Abstract
蒙特卡洛模拟程序（MCNP）常被用于计算机断层扫描（CT）所致受检者辐射剂量的计算。然而该模型的物理计算过程较为繁杂且程序的输入文件结构复杂，不支持几何模型的三维显示，从而导致研究者无法建立准确的CT辐射系统模型，影响剂量计算结果的准确性。针对这两大问题，本研究设计了一个可视化CT建模并自动生成输入文件的软件。在模型计算方面，融合各大研究者的CT建模改进方案来作为理论基础；在三维模型可视化方面，以LabVIEW为新的开发平台、实体几何构造法（CSG）为算法原理，引入MCNP输入文件的编辑方式来实现CT几何建模的可视化。相比一个近期研究所建立的CT模型，本可视化CT建模软件所模拟的结果与实际测量的均方根误差更小。该CT可视化建模软件不仅可以帮助研究者获得准确的CT辐射系统模型，而且为MCNP的几何建模可视化方法提供了新的研究思路。
Keywords: 辐射剂量, 计算机断层扫描辐射系统模型, 蒙特卡洛模拟程序, 可视化建模, 实体几何构造法
Abstract
The Monte Carlo N-Particle (MCNP) is often used to calculate the radiation dose during computed tomography (CT) scans. However, the physical calculation process of the model is complicated, the input file structure of the program is complex, and the three-dimensional (3D) display of the geometric model is not supported, so that the researchers cannot establish an accurate CT radiation system model, which affects the accuracy of the dose calculation results. Aiming at these two problems, this study designed a software that visualized CT modeling and automatically generated input files. In terms of model calculation, the theoretical basis was based on the integration of CT modeling improvement schemes of major researchers. For 3D model visualization, LabVIEW was used as the new development platform, constructive solid geometry (CSG) was used as the algorithm principle, and the introduction of editing of MCNP input files was used to visualize CT geometry modeling. Compared with a CT model established by a recent study, the root mean square error between the results simulated by this visual CT modeling software and the actual measurement was smaller. In conclusion, the proposed CT visualization modeling software can not only help researchers to obtain an accurate CT radiation system model, but also provide a new research idea for the geometric modeling visualization method of MCNP.
Keywords: Radiation dose, Computed tomography radiation system geometric model, Monte Carlo N-Particle, Visual modeling, Constructive solid geometry
0. 引言
计算机断层扫描（computed tomography，CT）自问世以来，迅速成为重要的医学影像诊断工具。随着CT使用频率越来越高，医学电离辐射对人体的危害性被广泛关注，如何准确评估一次CT检查中受检者的辐射剂量成为了研究热点[1]。目前，已有许多研究证明蒙特卡洛模拟是最可靠的计算方法。蒙特卡洛模拟程序（Monte Carlo N-Particle，MCNP）是由美国Los Alamos国家实验室研制的大型蒙特卡洛中子、光子和电子输运仿真程序输运计算的软件，在分析物理实验和反应堆设计、核保护无损检测系统和辐射屏蔽核仪器设计、材料活化和磁聚变中子学计算、核临界安全分析、物理保健问题研究等领域得到普遍使用[2]。由于MCNP的模拟准确且通用性高，研究者普遍利用该程序来计算CT扫描所致受检者的辐射剂量。
要保证MCNP模拟的准确性，首先要确保所构建的CT辐射系统模型尽量贴合实际。CT辐射系统模型中包含机架几何参数和物理参数。机架几何参数有源到等中心点的距离（the distance from the focal spot to the isocenter，SID）、源到探测器的距离（the distance from the focal spot to the detector，SDD）和源到过滤器的距离（the distance from the focal spot to the bowtie，SFD）；物理参数包括X射线发散角、过滤器的厚度和准直器的宽度[3]。然而当研究者们在MCNP程序中描述相应参数来构建CT辐射系统模型时，却因为该程序的输入文件结构复杂且不支持三维几何模型这两个因素而导致模型不够准确[3]。尤其是物理参数中的蝶形过滤器，因其几何结构复杂，且不同厂家CT机之间差异巨大，在很大程度上增加了建模工作的难度[4-5]。为了解决这一问题，需要对CT辐射系统的建模过程进行可视化并设计相关软件，通过选取合理的CT建模方法作为理论基础，并结合直接便利的三维模型构建法来帮助研究者观察、修改模型并获得相应输入文件。
对于CT模型的构建方法，1999年至2009年间，相继有研究者提出了不同的理论，所建的CT模型分别经历了从单排轴扫CT、多排轴扫CT到多排螺旋CT的过程。2003年以前，研究者们主要基于厂家给出的几何参数对CT进行建模[6-7]。2003年，美国的Jarry等[8]基于实测物理数据构建了一台GE LightSpeed 16排CT模型，并公开了标准体模表面的剂量分布曲线。2008年，Gu等[4]通过计算他们的实测数据来获得CT模型的几何参数，模拟结果与实测结果的百分比相对误差在8%以内。同时，Turner等[9]第一次提出了完全基于实测数据来计算获得CT几何参数的建模方案，发现基于这种方法建立的CT模型比基于厂家提供几何参数所建立的CT模型更加准确。后续更有研究者在其方法的基础上进行了改进，包括采用更精确的剂量仪器以及更准确、适用范围更广的能谱软件[10]。综合考虑下，本研究采用Turner等[9]提出的建模方法作为理论基础，并通过融合各研究者的改进方案来建立一个综合性的建模系统。
关于MCNP程序的三维模型可视化方法，目前大致分为两种：第一种，修改MCNP源程序直接采用计算机辅助设计（computer aided design，CAD）软件作为几何引擎。例如，MCNP5发行自带的可视化软件Visual Editor和美国白岩科学公司开发的Sabrina，使用MCNP粒子跟踪程序的源码来生成MCNP模型的二维、三维图像，应用的是光线跟踪技术[11]。但由于MCNP的源码不易获得，因此不利于二次开发与改进。
第二种，因为MCNP内部仅支持实体几何构造法（constructive solid geometry，CSG）模型，所以可以利用接口格式转换程序实现从CAD模型到CSG模型再到MCNP模型的转换。例如，清华大学李春艳等[12]基于C语言（Visual C++，VC）和开放图形库（open graphics library，OpenGL）实现了多个体素的MCNP三维建模；Theis等[13-14]开发了开源蒙特卡洛几何建模工具；朱晓林等[15]采用通用绘图（unigraphics NX，UG）二次开发实现了外部模型到MCNP计算模型的转换。但上述研究依赖于简单体素的CAD建模转换，因此对于复杂几何体的通用性不高。
为了加强通用性，中国科学院等离子体物理研究所FDS团队自主开发了自动建模可视化软件系统MCAM[16]；罗月童等[17]提出了基于面壳封闭的边界表示（boundary representation，BREP）模型转换算法；吴斌等[18]研究了一种基于辅助面的分解算法；赵瑛峰等[19]提出一种基于特征分解的模型BREP表达到半空间CSG表达转换算法。虽然改进模型转换算法可以在一定程度上提高转换效率，但是没有在根本上解决几何模型转换时的繁琐问题，且在模型转换时依旧容易出错。
分析国内外的相关工作后可知，目前没有针对CT辐射系统建模的MCNP可视化软件，而以往的三维几何模型可视化方法也都不够直观。因此，本研究设计了一个专门应用于CT辐射系统建模的MCNP可视化软件，以LabVIEW为新的开发平台、CSG构造法为几何建模原理，引入MCNP输入文件的编辑方式来实现几何建模可视化，以期帮助研究者直观、准确地获得完整的输入文件，从而提高CT建模的效率和准确性。
1. CT模型构建的理论方法
CT辐射系统建模的顺序为获取X射线能谱、计算蝶形过滤器厚度角分布、模拟准直器以及X球管的旋转运动[9]。其中X射线能谱和过滤器厚度角分布是通过对CT进行实际测量和计算获得的，具体的测量内容和模型构建方法如图1所示。
图 1.
Technical route of CT radiation system modeling
CT辐射系统建模的技术路线
半值层（half value laye，HVL）的定义为使辐射束的空气比释动能减少到其初始值一半的指定材料的厚度，通常用mmAL来表示[9]。半值层是X射线能量表达的重要参数，为了模拟简便，通常将焦点到固有滤过一同视作X射线放射源，因此可以通过匹配实验室测量与能谱软件输出的半值层来获得X射线等效能谱。
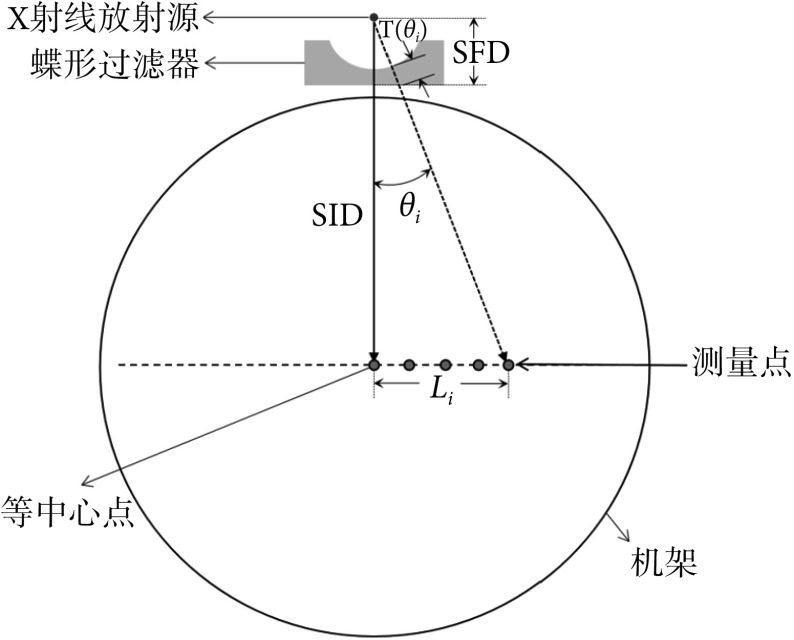
CT的蝶形过滤器结构是整个模型中最难构建的部分，可以用厚度角分布曲线来描述，即横坐标为X射线角，纵坐标为蝶形过滤器厚度的曲线，需要根据实测的等效能谱和X射线静态剂量曲线进行计算后拟合得到。根据Turner等[9]的研究，需要将X射线球管固定在一个位置来测量多个偏离等中心点处的空气比释动能，如图2所示，各个测量点等间距，计算每一个测量点相对于等中心点的比值r可以获得X射线静态剂量衰减曲线。衰减公式如式（1）所示，可以计算获得蝶形过滤器厚度角分布。
图 2.
Schematic diagram of the measurement of the static dose distribution curve of the tube
球管静态剂量分布曲线测量示意图
图中，T（θi）为θi角对应过滤器厚度，θi为X射线角度，L为测量点在X方向上的长度
in the figure, T(θi) is the thickness of the filter corresponding to the angle; θi is the X-ray angle; L is the length of the measurement point in the X direction
 |
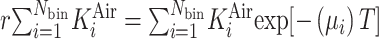1 |
式中，r为衰减比，K为空气比释动能，μi为过滤器材料的线性衰减系数，T为过滤器的厚度。
构建好放射源与蝶形过滤器模型后，需要限制光子的飞行范围来模拟CT的准直器模型，并根据一周放射源均匀抽样的方式来模拟X射线球管的旋转运动，因此需要将放射源和蝶形过滤器进行旋转阵列。
2. 软件的总体设计
LabVIEW是美国国家仪器有限公司（National Instruments，NI）的虚拟仪器开发软件，具有图形化编程环境、强大的仪器控制和仿真控制能力[20]。LabVIEW的程序设计通常分为前面板设计与功能面板设计两部分，前面板设计需要根据软件需求分析进行界面设计；后面板需要根据需求设计功能模块，并编写算法。根据上述CT辐射系统的建模方法，该软件的前面板在输入X射线在某一特定管电压下的等效能谱、静态剂量衰减曲线、SFD和SID后，可以获得蝶形过滤器的三维几何模型，后面板则需要根据输入的物理参数进行计算拟合，编写逻辑算法来生成几何体。
2.1. 前面板设计
在MCNP中构建复杂的几何模型需要通过数个曲面半空间进行布尔运算得到。模型构建的第一步是编写曲面卡来定义几个基本曲面；第二步，对曲面半空间进行布尔运算，这一步需要运用符号（“空格”代表交集，“：”代表并集，“#”代表余）连接带有方向的曲面编号（正号代表曲面正方向或曲面体的内部，负号代表曲面的负方向或曲面体的外部）；第三步，选择几何模型的材料，形成栅元[21]。
基于CT建模的方法和MCNP几何建模的流程，前面板需要设计一个友好界面来帮助用户输入CT的实测物理参数、材料选择以及输入文件导出等使用需求。另外，相应的曲面或几何体还可以进行修改调整。
2.2. 功能面板设计
针对于上述的使用需求，本软件分别设计了物理参数处理模块、标准曲面生成以及空间变换模块、几何布尔运算模块、材料库模块以及MCNP输入文件生成模块。
3. 实现功能模块的详细理论方法
对于物理参数处理模块，需要引入Matlab作为数据处理的接口，根据X射线等效能谱和蝶形过滤器厚度角分布来拟合出相应的形状曲线，而对于其余功能模块，则需要利用LabVIEW内部的几何运算功能来完成。
3.1. 标准曲面生成与空间变换
3.1.1. 标准曲面生成
空间中的任何一个标准曲面都可以由满足该曲面公式的坐标点集形成。LabVIEW（版本19.0）的三维曲面图形控件可以通过输入X、Y向量以及Z矩阵来生成对应的三维曲面图形，因此要生成标准曲面，只需根据不同的曲面类型内置好相应的曲面公式，然后通过坐标点的均匀抽样（对于平面采用均匀抽样，球面采用三角函数抽样）代入曲面公式后获得三维标准曲面图形[22]。多个曲面的生成可以通过将三维曲面控件进行连接的方式得到。
3.1.2. 曲面空间变换
曲面的空间变换包括平移、缩放、旋转。曲面在空间中的平移或者缩放可视作曲面上的坐标点集分别在X、Y、Z方向的平移或缩放，因此可以直接对曲面坐标点集中的每一个单位进行平移或乘以缩放系数等计算。对于曲面的空间旋转，利用罗德里格旋转公式来实现曲面上所有点向量的空间旋转，具体公式如下[23]：
 |
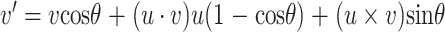2 |
其中，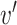
为旋转后的空间向量，v为旋转前的空间向量，θ为旋转角度，u为旋转轴的单位向量。
3.2. 曲面半空间的布尔运算
根据曲面的半空间表示法，每一个空间曲面都由满足该方程式的点集堆砌而成，设该曲面的方程为F (x, y, z) = 0，则其外侧（正向）半空间的点集表示为：
 |
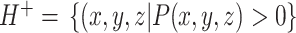3 |
其内侧（负向）半空间的点集表示为：
 |
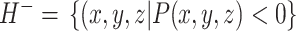4 |
式中H表示半空间[24]。
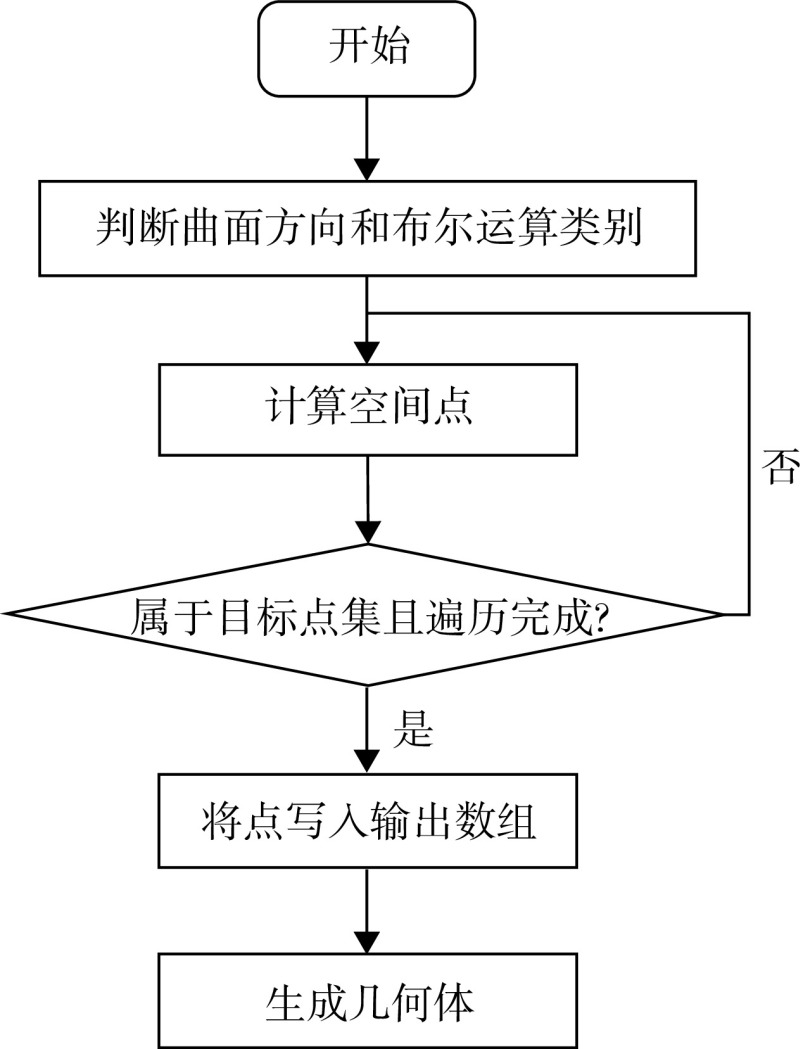
CSG构造法把复杂的实体看成若干个简单实体经过有序的布尔运算后得到，这些简单的实体称为体素[17]。一个曲面半空间可以视作一个CSG构造法的基本体素，而曲面半空间的布尔运算过程实质是对空间点的筛选过程，筛选的方法是对空间中的点进行边界条件限制，基于该原理的算法流程如图3所示。
图 3.
Algorithm flow chart of Boolean operation
布尔运算的算法流程图
假设需要布尔运算的两个标准曲面为P和Q，曲面半空间分别为P−和Q−，两个半空间里的坐标点表示为（x1, y1, z1）和（x2, y2, z2），则为了计算并筛选出目标坐标点，所设置的边界条件分别为：
（1）交：点集表示为：{(x2, y2, z2 | P (x, y, z)<0}或{(x1, y1, z1 | Q (x, y, z)<0}，即同时属于曲面半空间P−和Q−的点。
（2）并：点集表示为：{(x2, y2, z2 | P (x, y, z)>0}∪{(x1, y1, z1 | Q (x, y, z)>0}∪{(x2, y2, z2 | P (x, y, z)<0}，即曲面半空间P−和Q−在空间上覆盖的所有坐标点。
（3）余：点集表示为{(x2, y2, z2 | P (x, y, z)>0}或{(x1, y1, z1 | Q (x, y, z)>0}，即曲面半空间P−减Q−或Q−减P−的所有坐标点。
对于多个曲面半空间的布尔运算，由于新生成的点集通常不能再用标准曲面公式的半空间表示法来描述，因此需要在每一步布尔运算结束后，对点集进行保存记录，再进入下一轮布尔运算，生成最后的几何模型。
3.3. 材料库
本研究的可视化软件为用户构建了一个用以填充几何模型的材料库，其中包括金属、水、空气以及生物材料，所有材料的属性均摘自美国国家标准与技术研究院（National Institute of Standards and Technology，NIST）材料报告[25]。这些材料广泛应用于CT辐射剂量的蒙特卡洛估算中，是专门为CT几何建模研究而构建的材料库。材料库的具体构建方法为：首先使用Microsoft Access构建材料数据库，再利用LabVIEW的附加工具包LabVIEW SQL Toolkit进行数据库访问，用户只需选择材料名称即可获得相应的属性数据。
3.4. MCNP输入文件生成
把用户构建的曲面、布尔运算以及材料属性等信息转为MCNP语句的字符串形式，再通过LabVIEW中的写入文本文件模块将生成的字符串转为文本格式的文件，这个文件即为MCNP的输入文件。
4. 软件测试
4.1. 例题描述
为了验证本文可视化CT辐射系统建模软件的可行性，本研究在一台Windows10、32位的普通PC机上进行了测试，主要测试的内容是根据实测半值层和静态剂量衰减曲线来获得相应的蝶形过滤器模型。物理实测参数取自Hassan等在2018年发表的一篇论文，他们构建了一台西门子Definition 64 排螺旋CT，该CT的管电压为140 kV，半值层为9.4 mmAl，SID及SSD分别为59.5 mm和108.5 mm且具有两种形状的蝶形滤波。两种滤波器分别应用于小视野（small field of view，SFOV）扫描和大视野扫描（large field of view，LFOV），材料被是特氟龙，并通过匹配SpekCalc软件的半值层获得等效能谱。
4.2. 测试结果与讨论
与Hassan等一样，本研究使用均方根误差（root mean square error，RMSE）作为指标来验证本研究中构建的CT辐射系统模型的准确性。本研究中用于蒙特卡洛模拟的空气电离室参数、测量点和扫描条件的设置均与Hassan研究中的相同。两种形状的蝶形过滤器（SFOV和LFOV）的计算与几何模型构建结果如图4所示。图5展示了仿真结果与实际测量的归一化静态剂量衰减曲线（纵坐标为归一化的空气比释动能，横坐标为X射线角度）对比，SFOV和LFOV两种形状的过滤器对应的仿真与模拟的均方根误差分别0.97%和0.74%，而在Hassan等的研究中，在相同条件下，二者的均方根误差分别为1.16%和2.50%，这证明使用本研究开发的软件得到的CT辐射系统模型取得了更准确的模拟结果，且对于大视野的蝶形过滤器的模型精度提升效果更加明显。同时，利用该软件计算获取该模型的时间为5 s左右，相比传统逐步建模流程更加便利和高效。
图 4.
Two bowtie filter shape models constructed by the visual CT modeling software
可视化CT建模软件所构建的两种蝶形过滤器形状模型
图 5.
Comparison between the CT model constructed by this study and the reference model
本研究建立的CT模型与参照模型的比较结果
通过观察具有复杂曲面的蝶形过滤器模型，可知该模型是由三个基本曲面半空间进行布尔运算后获得，确定了本研究设计的可视化CT建模软件的可行性，可以帮助研究者观察、调整模型并快速获得相应的CT模型的输入文件。在几何模型的可视化方法方面，与修改MCNP源码法相比，由于LabVIEW层次化的结构，该软件可以把创建的VI程序当做子程序调用，因此后续对软件进行修改调试及二次开发时会更加便利，避免了修改MCNP源程序的不便利性，可以利用后续更多新型CT几何建模进行针对性的开发；与几何模型格式转换法相比，由于该软件不需要外部接口进行几何模型的格式转化，而是直接利用CSG构造法的原理进行几何模型构建，避免了格式转换的麻烦。
5. 结论
针对CT辐射系统在MCNP软件建模过程中遇到的两大问题，即模型准确计算和三维几何可视化，本研究首次以LabVIEW为开发平台，直接利用CSG构建法的原理设计了一个可视化CT辐射系统建模软件，并验证了其有效性和高效性，可以应用于各类CT模型的构建。该软件不仅可以弥补MCNP绘图功能的局限性，提升相关研究人员编写输入文件的效率和准确性，而且为MCNP可视化方法研究提供了新的思路。
本软件对于大型且复杂的几何建模可视化的交互速率还有待提高，未来会从算法以及可视化方法上进行改进，从而提高可视化效率。另外，需要继续对CT放射源模型和辐射剂量计数模型进行可视化，一方面提高软件的综合性，另一方面可以大大减少辐射剂量研究人员的工作量。
重要声明
利益冲突声明：本文全体作者均声明不存在利益冲突。
作者贡献声明：刘颖负责实验设计和数据采集；孟婷负责数据分析和软件编程；章浩伟和路鹤晴负责论文修改与完善。
Funding Statement
国家自然科学基金项目（82073474）
References
- 1.Zheng J Z, Gao L F, Zhuo W H, et al A trend study on radiodiagnosis and radiotherapy and radiological protection for medical exposure in Shanghai. Radiat Prot. 2014;34(5):265–273. [Google Scholar]
- 2.林茂松, 蔡勇, 王金诺 基于组件技术的MCNP三维可视化平台模型研究. 计算机应用研究. 2007;(2):225–226. doi: 10.3969/j.issn.1001-3695.2007.02.075. [DOI] [Google Scholar]
- 3.Hassan A I, Skalej M, Schlattl H, et al Determination and verification of the x-ray spectrum of a CT scanner. J Med Imaging. 2018;5(1):1–15. doi: 10.1117/1.JMI.5.1.013506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gu J, Bednarz B, Caracappa P F, et al The development, validation and application of a multi-detector CT (MDCT) scanner model for assessing organ doses to the pregnant patient and the fetus using Monte Carlo simulations. Phys Med Biol. 2009;54(9):2699–2717. doi: 10.1088/0031-9155/54/9/007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pan Y, Qiu R, Gao L, et al Development of 1-year-old computational phantom and calculation of organ doses during CT scans using Monte Carlo simulation. Phys Med Biol. 2014;59(18):5243–5260. doi: 10.1088/0031-9155/59/18/5243. [DOI] [PubMed] [Google Scholar]
- 6.Caon M, Bibbo G, Pattison J An EGS4-ready tomographic computational model of a 14-year-old female torso for calculating organ doses from CT examinations. Phys Med Biol. 1999;44(9):2213–2225. doi: 10.1088/0031-9155/44/9/309. [DOI] [PubMed] [Google Scholar]
- 7.Khursheed A, Hillier M C, Shrimpton P C, et al Influence of patient age on normalized effective doses calculated for CT examinations. Br J Radiol. 2002;75(898):819–830. doi: 10.1259/bjr.75.898.750819. [DOI] [PubMed] [Google Scholar]
- 8.Jarry G, DeMarco J J, Beifuss U, et al A Monte Carlo-based method to estimate radiation dose from spiral CT: from phantom testing to patient-specific models. Phys Med Biol. 2003;48(16):2645–2663. doi: 10.1088/0031-9155/48/16/306. [DOI] [PubMed] [Google Scholar]
- 9.Turner A C, Zankl M, DeMarco J J, et al The feasibility of a scanner-independent technique to estimate organ dose from MDCT scans: Using CTDIvol to account for differences between scanners. Med Phys. 2010;37(4):1816–1825. doi: 10.1118/1.3368596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Boone J M Method for evaluating bow tie filter angle-dependent attenuation in CT: theory and simulation results. Med Phys. 2010;37(1):40–48. doi: 10.1118/1.3264616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schwarz R A, Carter L L. Current state of Monte Carlo visualization tools// Kling A, Baräo F J C, Nakagawa M, et al. Advanced Monte Carlo for radiation physics, particle transport simulation and applications. Berlin, Heidelberg: Springer, 2000: 815-819.
- 12.李春艳, 李君利, 程建平, 等 MCNP可视化输入程序的开发. 清华大学学报(自然科学版) 2007;(S1):1089–1092. doi: 10.16511/j.cnki.qhdxxb.2007.s1.030. [DOI] [Google Scholar]
- 13.Theis C, Bucheger K, Brugger M, et al Interactive three dimensional visualization and creation of geometries for Monter Carlo calculation. Nucl Instrum Methods. 2006;562(2):827–829. doi: 10.1016/j.nima.2006.02.125. [DOI] [Google Scholar]
- 14.Theis C, Bucheger K, Feld G, et al Simple Geo-New developments in the interactive creation and geometries for Monte Carlo simulations. Nucl Sci Tech. 2011;2:587–590. [Google Scholar]
- 15.朱晓林, 蔡勇, 张建生 CSG模型到MCNP几何模型转换算法的研究与实现. 现代计算机. 2012;8:9–12. doi: 10.3969/j.issn.1007-1423-B.2012.04.003. [DOI] [Google Scholar]
- 16.Li Y, Lu L, Ding A, et al Benchmarking of MCAM 4. 0 with the ITER 3D model. Fusion Eng Des. 2007;82(15-24):2861–2866. [Google Scholar]
- 17.罗月童, 樊晓 基于面壳封闭的B-Rep到CSG转换算法. 计算机辅助设计与图形学学报. 2014;26(10):1673–1680. [Google Scholar]
- 18.吴斌, 俞盛朋, 程梦云, 等 反应堆中子学分析精准建模方法. 核科学与工程. 2016;36(1):72–76. doi: 10.3969/j.issn.0258-0918.2016.01.010. [DOI] [Google Scholar]
- 19.赵瑛峰, 刘检华, 武林林, 等 基于特征分解的半空间构造实体几何模型转换算法. 计算机集成制造系统. 2021;27(5):1382–1389. doi: 10.13196/j.cims.2021.05.014. [DOI] [Google Scholar]
- 20.孙文军, 阎慧, 高永明. 基于MapleSim和LabVIEW的航天器姿态控制仿真研究. 计算机应用研究, 2011, 28(11): 4202-4205, 4218.
- 21.X-5 Monte Carlo Team. MCNP―A general Monte Carlo N-Particle transport code, version 5, Volume II: User’s Guide. Los Alamos: Los Alamos National Lab, 2003.
- 22.Rob R, Panoiu C Using LabVIEW linx for creating 3d objects. IOP Conf Ser Mater Sci Eng. 2019;477(1):012027. [Google Scholar]
- 23.刘锋 罗德里格斯旋转公式的证明及应用. 江苏科技信息. 2020;37(28):37–40. doi: 10.3969/j.issn.1004-7530.2020.28.010. [DOI] [Google Scholar]
- 24.丁爱平, 李莹, 卢磊, 等 粒子输运计算模型MCNP模型的可视化实现. 原子核物理评论. 2006;(2):130–133. [Google Scholar]
- 25.Hubbell J H, Seltzer S M. Tables of X-ray mass attenuation coefficients and mass energy-absorption coefficients 1 keV to 20 MeV for elements Z= 1 to 92 and 48 additional substances of dosimetric interest. Gaithersburg: National Institute of Standards and Technology-PL, 1995.