Using Data Science for Mechanistic Insights and Selectivity Predictions in a Non-Natural Biocatalytic Reaction

Abstract

The study of non-natural biocatalytic transformations relies heavily on empirical methods, such as directed evolution, for identifying improved variants. Although exceptionally effective, this approach provides limited insight into the molecular mechanisms behind the transformations and necessitates multiple protein engineering campaigns for new reactants. To address this limitation, we disclose a strategy to explore the biocatalytic reaction space and garner insight into the molecular mechanisms driving enzymatic transformations. Specifically, we explored the selectivity of an “ene”-reductase, GluER-T36A, to create a data-driven toolset that explores reaction space and rationalizes the observed and predicted selectivities of substrate/mutant combinations. The resultant statistical models related structural features of the enzyme and substrate to selectivity and were used to effectively predict selectivity in reactions with out-of-sample substrates and mutants. Our approach provided a deeper understanding of enantioinduction by GluER-T36A and holds the potential to enhance the virtual screening of enzyme mutants.

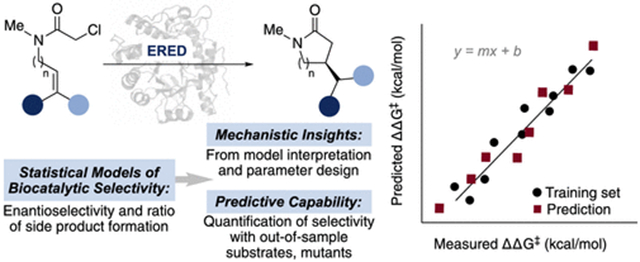
Graphical Abstract

INTRODUCTION

Enzymes play an expanding role as selective, efficient catalysts for biotechnology, biomedicine, biofuels, and industrial pharmacology.^1-4 The extension of enzymatic catalysis to non-native transformations generally relies on extensive screens of sequence space through protein engineering [e.g., directed evolution (DE)].^5,6 Advances in sequencing technologies and machine learning have enabled predictive modeling of biocatalyst reactivity. However, the widespread use of these methods is somewhat hindered due to the requirement for tremendous quantities of experimental data and the “black-box” nature of the algorithms used to guide optimization. Like DE, existing platforms for predictive biocatalysis do not necessarily capture or reveal the important mechanistic features of a given reaction and may not translate well to modified reactions (such as a similar reaction with a different substrate).

We were motivated to develop a strategy to simultaneously explore biocatalytic reaction space and gain insight into the molecular mechanisms behind non-native transformations. Specifically, we wanted to describe sequence space (enzyme mutants) and chemical space (substrate variants) in a quantitative manner using molecular descriptors and relate these descriptors to reaction outcomes, like enantioselectivity.⁷ Unlike black-box methods for predictive biocatalysis, we postulated that simple statistical models constructed from smaller datasets could deliver not only predictive power but also valuable molecular-level insights into the origins of selective biocatalysis. We anticipated that attention to conformational dynamics and the use of information-rich molecular descriptors (of both enzyme and substrate) would result in models with greater interpretability and generalizability compared to existing methods.^8-12

In this study, we demonstrate this approach in the context of non-native enantioselective photoenzymatic radical cyclization reactions catalyzed by “ene”-reductase (ERED) variants from Gluconobacter oxydans (GluER-T36A, Scheme 1).¹³ We created a statistical toolset that explored GluER-T36A reaction space and rationalized the observed and predicted selectivities of previously untested substrate/mutant combinations. The emphasis on both substrate and enzyme diversity in model training allowed us to predict the selectivity of out-of-sample substrates in combination with new GluER-T36A variants. We demonstrated the adaptability of statistical models through the incorporation of additional experimental data and hypothesis-driven parameter advancement. The inclusion of multiple substrates in model training and development complemented existing in silico protein engineering methods (which often require separate datasets/analyses for each substrate).^14-16 Our results showcase the advantages of these tools in predicting and rationalizing the molecular interactions that drive enantioselective biocatalysis.

Scheme 1.

Enantioselective Cyclization Catalyzed by GluER-T36A and Mutants

WORKFLOW DESIGN

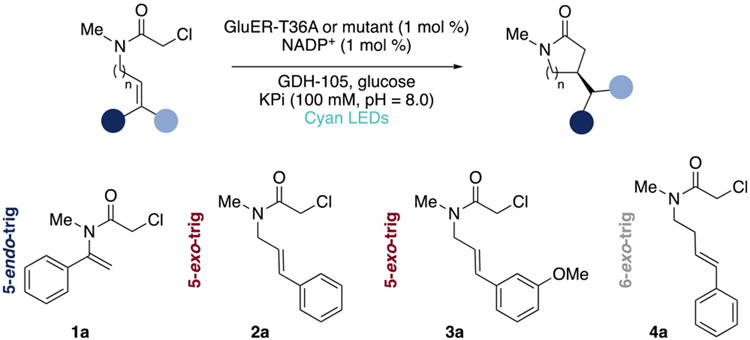
A major challenge associated with building statistical models of biocatalyst selectivity was the availability of balanced training data. We, therefore, sought a system with which we could construct a training set containing a range of reaction outcomes to develop the statistical modeling workflow. EREDs were selected as a model biocatalytic framework as they have been reliably utilized in a range of non-native enantioselective reactions.^17-21 GluER-T36A is a selective catalyst for the photoenzymatic cyclization of many α-chloroamides (Scheme 1); however, a number of substrates had to be paired with homologous EREDs to achieve high enantioselectivity in the initial report.¹³ Although effective in this instance, the general practice of shifting enzyme frameworks can lead to unexpected results (i.e., enantiodivergent transformations or byproducts) and introduce challenges including reoptimization of expression and reaction conditions.^20,21 To circumvent these challenges, we sought to develop explanatory statistical models. These models would relate structural features of a small but diverse sample of GluER-T36A variants and α-chloroamide substrates to selectivity and draw from all training data, including poorly performing substrate/mutant combinations. Notably, this strategy avoids the requirement for screening thousands of mutants and cyclic evaluation of mutant libraries to expand the reaction scope.

In this context, we designed a focused training set with diversity in both substrate characteristics and enzyme mutations. The transformation of substrates 1a–4a (Scheme 1) encompass three different cyclization modes (1a: 5-endo-trig, 2a, 3a: 5-exo-trig, and 4a: 6-exo-trig), varying electronic properties (as in 2a and 3a), and alkene substitution patterns (1a vs 2a–4a). Informed by previous studies on GluER-T36A, we identified five residues within the GluER-T36A active site for mutation: W66, Y177, Q232, F269, and Y343. Mutations at these sites were shown to retain activity while affecting selectivity in the cyclization, although the mechanism of selectivity modulation was not well-understood. We preformed site-directed mutagenesis to introduce residues W, F, D, L, or A at each of the five sites as these mutations would sample a range of residue properties. Substrates 1a–4a were subjected to reactions with each expressible mutant, resulting in a total of 50 datapoints to use in model training and selection. A full table of substrate/enzyme combinations and the resultant ee’s is included in Table S1.

We next considered strategies to computationally characterize both enzyme and ligand (substrate and product) structures for descriptor extraction. We have previously described methods to characterize small-molecule catalysts and compute chemical descriptors by pairing molecular mechanics (MM)-based structural analysis with density functional theory (DFT) calculations.^22,23 However, the shift to biocatalytic platforms presents several unique challenges. The size and elaborate dynamics of enzymes have necessitated bespoke computational strategies to study enzyme/ligand complexes [EL]; however, many of these are best suited for in-depth analysis of one or a few [EL] pairs due to their operational complexity and resource demands.^24,25 We therefore sought workflows that would account for the dynamic nature of biocatalysts while also introducing scalability and consideration of ligand interactions.

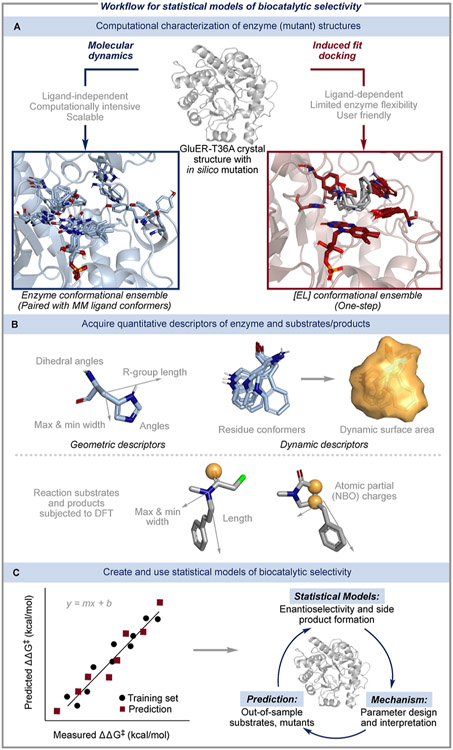
We identified two complementary conformational search platforms: molecular dynamics (MD) and induced fit docking (IFD) (Figure 1A). Typical MD simulations allow for flexibility in the entire enzyme; however, they also require substantial computational resources to sample enzyme conformations. To increase the scalability of the MD workflow, we utilized an enhanced sampling method, accelerated MD (aMD). This method artificially lowers the kinetic barriers in MD simulations through systematic perturbation of the potential energy surface.^26,27 We employed aMD to sample a larger number of GluER conformers without lengthening the MD simulation. Another step to reduce the computational cost of the aMD conformational search was to pair the enzyme structures with conformational ensembles of the free ligand (both substrate and product structures) from MM/DFT. The separate assembly of enzyme and ligand structures in the aMD sampling approach makes it easily applicable to large enzyme/ligand matrices and has potential for virtual screening (vide infra).

Figure 1.

Workflow to develop statistical models of biocatalytic reaction performance. (A) Two complementary approaches, aMD and IFD, were used to generate enzyme conformers from a GluER-T36A crystal structure (PDB ID: 6MYW) after introducing the desired mutation in silico. (B) Enzyme features were quantified using a residue-based approach. Geometric descriptors include the length, width, and backbone angles of each residue conformer and the fluctuations of these measurements. Dynamic descriptors were measured by overlaying a residue conformational ensemble, encapsulating it in a fictitious surface, and measuring the resulting surface area and volume. Ligands were subjected to both a geometric analysis and DFT calculations to acquire electronic descriptors, including the natural bond orbital (NBO) charges of atoms indicated by a yellow sphere. (C) Descriptors for each enzyme/ligand were regressed against the experimentally determined selectivities, resulting in statistical models that enabled mechanistic insights and predicted the outcomes of out-of-sample substrates and mutants.

As an alternative to the aMD conformer search, which requires supercomputing resources and expert knowledge, we directly probed the [EL] conformers with IFD. IFD is a MM-based docking protocol that approximates the docking pose of a ligand and the concomitant repositioning of nearby enzyme residues.^28-30 Previously, we applied IFD to engineer a more promiscuous variant of the prenyltransferase, NotF.³¹ Using the mechanistic insights gained from IFD simulations, we identified a NotF mutation that allowed the prenyltransferase to accept a more sterically demanding substrate. Here, we have expanded the use of IFD as a tool for collecting [EL] conformational ensembles. This conformational search method scales with the number of [EL] complexes, but unlike the aMD platform, it offers the advantage of directly probing the interactions between the small molecule and biocatalyst.

Upon acquisition of the enzyme and ligand conformational ensembles with either aMD or IFD, chemical descriptors were computed, automatically extracted, and curated for the ligands as well as for individual residues in the active site (Figure 1B). These descriptors included electronic (e.g., NBO charges),³² steric (e.g., sterimol values),³³ and dynamic descriptors, which measure the topographical properties of a collection of conformers [e.g., dynamic surface area (DSA)].³⁴ Although this initial parameterization strategy neglected the interactions between protein residues, we hypothesized that representing the active site by its individual residues in this manner could reveal the residues that have the most influence on reaction enantioselectivity (vide infra).

Finally, descriptors were regressed against the experimentally collected dataset (70:30 split of training and validation set data points, enantioselectivity expressed as ΔΔG^‡, which is proportional to the log of the measured enantiomeric ratio) using a forward-stepwise multivariate linear regression (MLR) algorithm, which resulted in numerous candidate models for each conformational search platform (Figure 1C).²²

RESULTS AND DISCUSSION

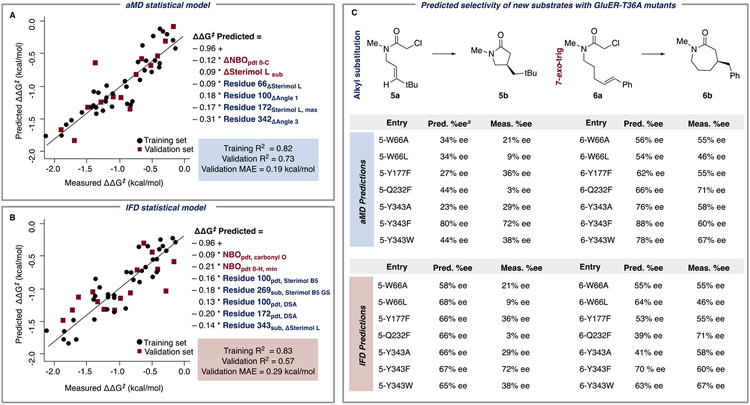
From the candidate models, we identified a representative high-performing aMD statistical model (Figure 2A) that had a training R² of 0.82 and a mean absolute error (MAE) in ΔΔG^‡ of 0.19 kcal/mol, indicating a good correlation between the measured and predicted values of the training set. The validation R² is the correlation between measured and predicted values for the validation set (the partition of data that was withheld from model training); the aMD model had a validation R² of 0.73 and a corresponding validation MAE = 0.19 kcal/mol. As for the parameters in the aMD model, ΔNBO_pdt,β-C is the difference in the maximum and minimum NBO charge on the product β-carbon; ΔSterimol L_sub is the difference in the maximum and minimum substituent length values (flexibility) of substrate structures. Residue 66_{ΔSterimol L} is the difference in the maximum and minimum residue length values (flexibility) of residue 66. Residue 100_{ΔAngle 1} and Residue 342_{ΔAngle 3} are the difference in the maximum and minimum of these angles (see Supporting Information). Residue 172_{Sterimol L,max} is the maximum length of residue 172.

Figure 2.

aMD and IFD statistical models with ligand descriptors (red) and enzyme descriptors (blue). (A) The aMD model had a training and validation R² of 0.82 and 0.73, respectively, a leave-one-out (LOO) R² of 0.70, and a 4-fold R² of 0.67. (B) The IFD model had a training and validation R² of 0.83 and 0.57, respectively, LOO R² of 0.73, and a 4-fold R² of 0.70. (C). Enantioselectivities of reactions with 5a and 6a to form 5b and 6b, respectively, predicted from the aMD and IFD models. ^aPredicted from aMD model 2, Figure S3.

The selected IFD statistical model (Figure 2B) demonstrated a training R² of 0.83 with a MAE of 0.18 kcal/mol, suggesting that the aMD and IFD models performed similarly in their capability to describe the data in the training set. The IFD model had a validation R² of 0.57 and a corresponding validation MAE of 0.29 kcal/mol. Identification of statistical models from both IFD and aMD workflows validated our hypothesis that molecular features of enzyme residues and ligands can describe the outcome of a biocatalytic reaction. NBO_{pdt,carbonyl O} is the NBO charge of the carbonyl oxygen on product structures. NBO_pdt,β-H,min is the minimum NBO charge of the hydrogen bound to the β-carbon in product structures. Residue 100_{pdt,Sterimol B5} is the maximum width of residue 100 from product-docked enzyme structures. Residue 269_{sub,Sterimol B5GS} is the GScore (docking-score) weighted maximum width of residue 269 from the substrate-docked enzyme structures. Residue 100_pdt,DSA and Residue 172_pdt,DSA are the DSAs of residues 100 and 172 from product-docked enzyme structures, respectively. Residue 343_{sub,ΔSterimol L} is the difference in the maximum and minimum length (flexibility) of residue 343 from substrate-docked enzyme structures.

Unlike established procedures to predict biocatalyst selectivity, the statistical models presented herein possess the ability to evaluate substrates that were not included in model training. We, therefore, used both aMD and IFD statistical models to predict the performance of various GluER-T36A mutants with two new substrates: 5a and 6a (Figure 2C). These were selected to incorporate substrate characteristics that were not represented in the training set, including an alkyl-substituted example (5a) and a different cyclization mode (6a, 7-exo-trig). For the aMD model, 5a and 6a conformers were collected and combined with existing enzyme trajectories, and for IFD, the relevant [EL] poses were generated. The enantioselectivities of 5a and 6a with each GluER-T36A variant were predicted using the statistical models from Figure 2a,b. Gratifyingly, in the experimental evaluation of these combinations, the models performed generally well in predicting the selectivity of GluER-T36A variants with the out-of-sample substrates. The aMD model was somewhat more successful, with a MAE of 0.38 kcal/mol for the out-of-sample substrate predictions, compared to a MAE of 0.48 kcal/mol for the IFD model.

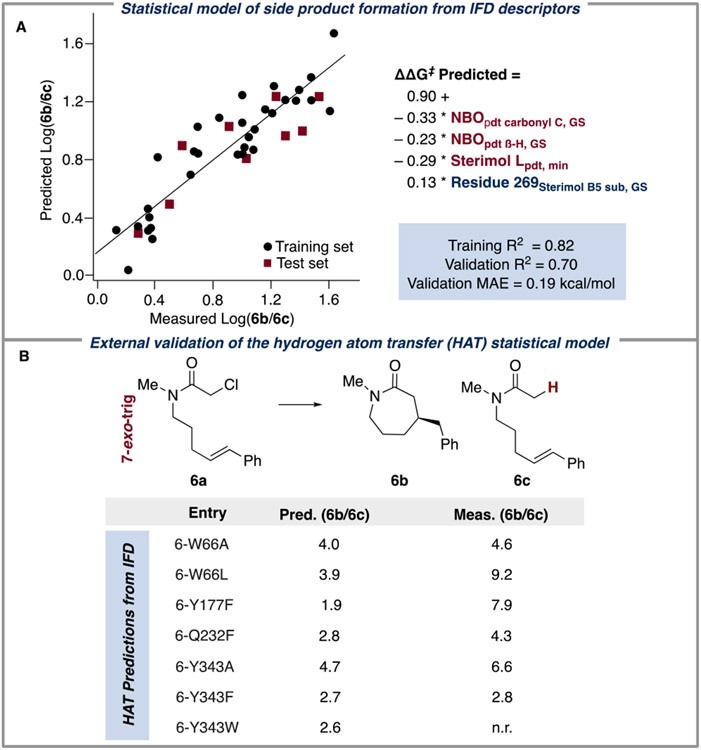
In addition to the competing diastereomeric transition states in the desired cyclization, a hydrodehalogenation pathway can also interfere with the cyclization process through H-atom transfer (HAT) to the putative α-acyl radical (as shown in Figure 3). The relative ratio of cyclization to HAT appeared to be primarily substrate-dependent, with the lowest levels of HAT detected in the 5-exo-trig cyclization of aryl substrates 2a and 3a. Despite the strong substrate dependence, some GluER-T36A variants modulate preference for the HAT pathway (Table S1), and we sought to capture GluER-T36A chemoselectivity through a separate statistical model.

Figure 3.

Statistical model of HAT side product formation. (A) Regressing experimental ratios of cyclization: HAT with the IFD descriptor set resulted in the best statistical model (training and validation R² of 0.82 and 0.70, respectively, LOO R² of 0.76, and a 4-fold R² of 0.70). The model had three ligand descriptors (red) and one enzyme descriptor (blue). (B) HAT model predictions on substrate 6a.

We found that regressing with the previously collected IFD descriptor set resulted in the best statistical model (training and validation R² of 0.82 and 0.70, respectively, Figure 3A). As expected from the observed substrate dependence, the HAT model primarily featured ligand descriptors: NBO_{pdt carbonyl C,GS} is the docking score-weighted NBO of the carbon atom of the product carbonyl. NBO_pdt,β-H,GS is the docking score-weighted NBO of the hydrogen atom bound to the β-carbon in product structures. Sterimol L_pdt,min describes the minimum length of the lactam substituent off the β-carbon in product structures. Simply put, the ligand features suggested that the electronic nature of the stereocenter formed in the cyclization and size of the lactam substituent when bound to the active site are largely responsible for the observed cyclization/HAT rate differences. Additionally, catalyst identity can modulate preference for the cyclization pathway, namely, through the repositioning of residue 269 (Residue 269_{Sterimol B5sub,GS} is the docking score-weighted maximum width of residue 269, generated from substrate-docked enzyme structures).

As an external validation of this model, we predicted the cyclization to HAT ratio of substrate 6a with a suite of GluER-T36A mutations. IFD appears to be particularly well suited for this analysis as it explicitly sampled ligand position for each GluER-T36A variant.

We next turned our attention to virtual screening GluER-T36A variants to predict how mutations impact selectivity in cyclization. We aimed to predict selectivity with multiple substrates and therefore utilized the aMD workflow, which scales with the number of enzyme variants screened rather than with the number of [EL] complexes. We took a rather ambitious tact by exploring a virtual library of GluER-T36A double and triple mutants even though only single mutants were initially used in the training data. The statistical models were used to predict the selectivity of each variant with the model substrate 2a and an alkyl substrate 5a. We selected only mutants that extrapolated beyond the enantioselectivities observed in the training data. The putative hits were expressed, but unfortunately, subjecting them to the reaction conditions resulted in little or no enantioenrichment of products 2b and 5b and other substrates (Table S2). This disappointing result suggested that poor extrapolation of the aMD model to new enzyme mutants was a result of the relatively small number of GluER-T36A single mutants used in model training and/or because the quantitative descriptors that were used to characterize the enzymes did not account for interactions between residues.

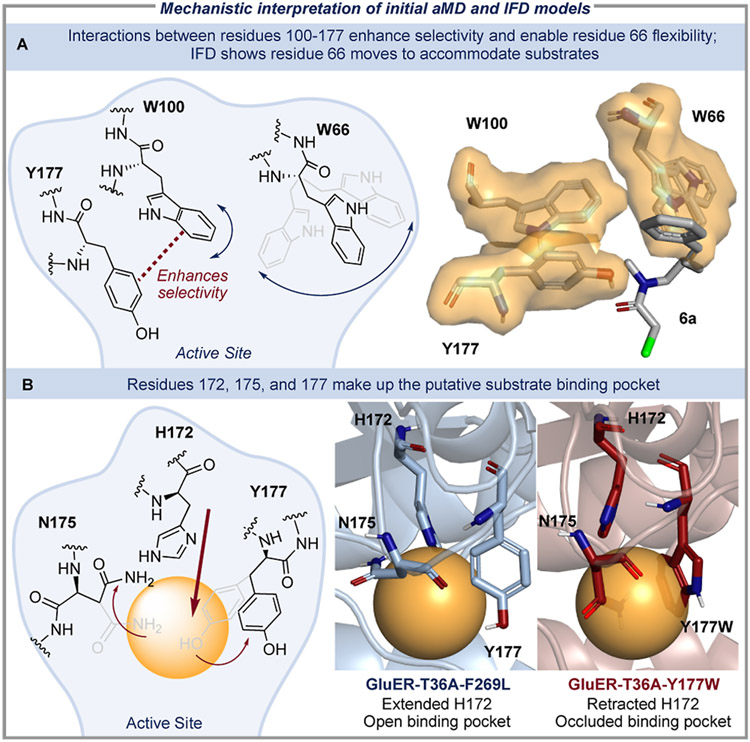
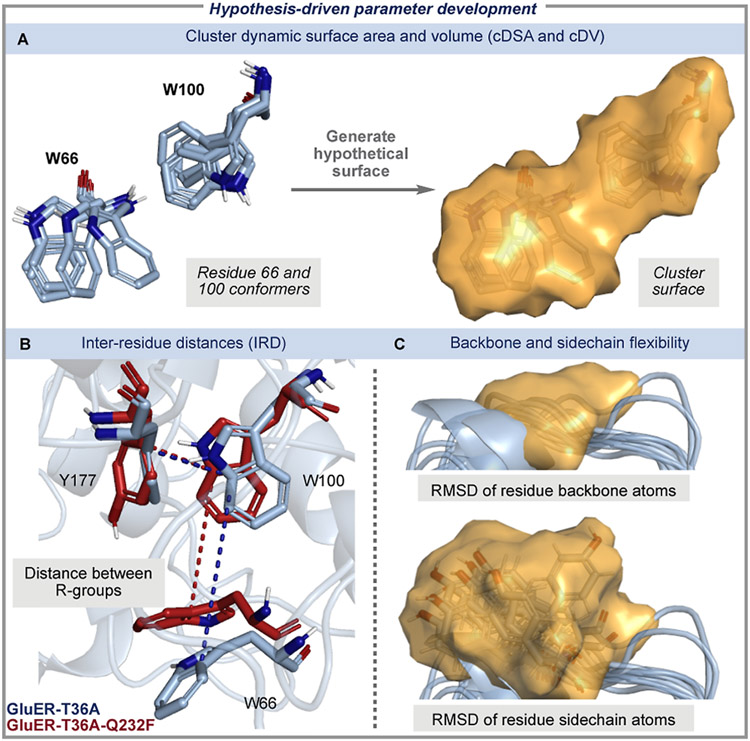
To address these challenges, we interrogated the initial statistical models and developed a mechanistic hypothesis that enabled us to create reaction-specific descriptors (Figure 4). The aMD and IFD models showed a correlation between GluER-T36A selectivity and the relative positioning of aromatic residues 66, 100, and 177, consistent with studies of homologous EREDs.^35-38 Features describing residue 100 conveyed that increased flexibility led to decreased enantioselectivity. Similarly, the negative coefficient associated with residue 66 (Residue 66_{Δ-Sterimol L}) in the aMD model indicated that the dynamic behavior of this residue contributes to enhanced selectivity in the cyclization. Inspection of the aMD conformers revealed that W100 is involved in a network of competitive non-covalent interactions with flanking residues 66 and 177, where a strong (rigid) integration between residues 100 and 177 enables residue 66 to have a wider range of motion. Interestingly, IFD revealed significant repositioning of residue 66 upon substrate 6a binding, suggesting that mobility of this residue is essential for proper substrate orientation (Figure 4A, right). We leveraged this insight to design new enzyme descriptors, which were focused on interactions between adjacent residues to better represent the contacts between residues 66, 100, and 177 (Figure 5). The DSA method was expanded to calculate the DSA of a group of proximal residues. For example, conformers of residues 66 and 100 were enclosed in a hypothetical surface, then the surface area and volume of the cluster were computed to determine the cDSA and cDV, respectively (Figure 5A). To further probe the interactions between residues 66, 100, and 177, R-group centroids were measured to describe inter-residue distances (IRD, Figure 5B).

Figure 4.

Mechanistic interpretation of descriptors from initial models. (A) The aMD conformers demonstrated that when aromatic residues 100 and 177 were closely associated, interactions between residues 66 and 100 were precluded, inducing residue 66 flexibility and higher selectivity. The IFD conformational ensembles (right) corroborated that the flexibility of residue 66 is necessary for substrate binding. (B) The term Residue 172_{Sterimol L,max} from the aMD model indicated that extended configurations of H172 facilitated selectivity. Examination of enzyme conformers where this term was large (GluER-T36A-F269L = 6.7 Å) showed H172 to be extended (blue) and revealed an open binding pocket (yellow sphere); this binding pocket was occluded in structures where values of this parameter were small (GluER-T36A-Y177W = 5.2 Å, red).

Figure 5.

Hypothesis-driven parameter development. (A) Cluster DSAs and (B) IRD were measured to explicitly describe the interactions between residues 66/100/177 and 172/175/177. (C) The overall residue flexibility was measured by computing the RMSD of residue backbone and side-chain atoms.

Having characterized the interactions between residues 66, 100, and 177, our focus then shifted to residues 172, 175, and 177. Both initial models found that the conformation of H172 is crucial for reaction selectivity. The aMD parameter for H172 measures its most extended conformation in each GluER-T36A variant; the aMD structures show that when H172 is extended, nearby residues N175 and Y177 are displaced, creating a distinct binding pocket (depicted as yellow spheres in Figure 4B, right). We suggest the open binding site observed in GluER-T36A-F269L allows for facile substrate binding and reduces the risk of substrate dissociation or rotation. Conversely, when H172 is retracted, as in the case of GluER-T36A-Y177W, the binding pocket is occluded by nearby residues, leading to reduced enantioselectivity.³⁹ To interrogate this hypothesis, the cDSA, cDV, and associated IRDs for residue 172 and neighboring residues 175 and 177 were added to our enzyme descriptor set.

In addition to investigating the residue–residue interactions that were informed by our statistical models, we aimed to better understand the role of overall dynamics and flexibility in reaction enantioselectivity through feature development. To achieve this, we measured a residue’s flexibility over the course of the entire aMD trajectory rather than just within the clustered conformational ensemble. The frames from each aMD trajectory were aligned, and the RMSD of the backbone atoms was measured for active site residues. Similarly, R-group flexibility was measured using the RMSD of side-chain nonhydrogen atoms (Figure 5C). A complete list of residues, cDSA, IRD, and RMSD measurements is available in Table S4.

PREDICTING SELECTIVITY OF NEW GLUER-T36A MUTANTS

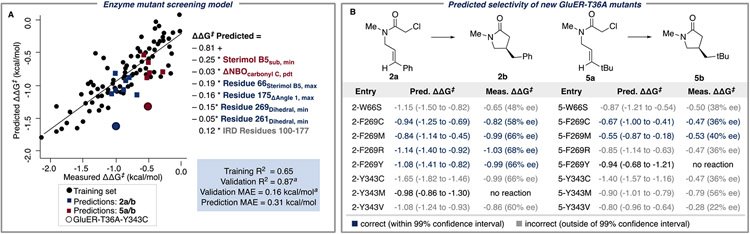
The newly designed enzyme descriptors (Figure 5) and additional experimental data from the previous virtual screen (Table S2) were merged with the initial dataset for a subsequent round of statistical modeling. In addition to training and validation set statistics (R² and MAE), a simulated virtual screening was used to identify three similar candidate models for prospective virtual screening (full details are available in the Supporting Information). To validate the models, a library of untested GluER-T36A variants was generated in silico for a virtual screen with substrates 2a and 5a. Using the aMD workflow, conformational ensembles for 39 single-point mutants at positions 66, 269, and 343 (sites at which mutations had previously preserved activity while affecting selectivity in the photoenzymatic cyclization) were collected, and the relevant parameters for the models were assembled. Unfortunately, the virtual screen did not suggest that any of these mutants would result in increased enantioenrichment in products 2b and 5b compared to previously tested GluER-T36A variants. Nonetheless, eight mutants, which were predicted to have a range of experimental outcomes, were selected from the in silico library for expression to validate the statistical model. Additional details of the virtual screening, mutant selection, and model comparison are available in the Supporting Information. The MLR models performed generally well in predicting how the new GluER-T36A mutants affected the enantioselectivity for products 2b and 5b. The best MLR model predicted the mutant performance with a MAE of 0.31 kcal/mol, and quantitative prediction of performance (within a 99% confidence interval computed from model bootstrapping with 1000 subsamples) was achieved for 6/14 of the reactions with out-of-sample enzymes (Figure 6). This performance was substantially better than the predictions from a regularized model trained on the complete feature set (Figure S6).

Figure 6.

Updated model enabled virtual screening and prediction of the selectivity of new GluER-T36A mutants. (A) Similar to the initial models, the updated statistical model has two ligand descriptors (red), several residue-based enzyme descriptors (blue), and one IRD parameter (gray) that measures the distance between residues 100 and 177. (B) Predicted enantioselectivities of 2a and 5a with untested GluER-T36A variants; the range for the predictions was computed at a 99% confidence interval using bootstrap subsampling. ^aTraining and validation set statistics were computed with a 70:30 split, as further described in the Supporting Information.

The updated statistical model is similar to the initial aMD model in several respects, including the use of a conserved electronic descriptor (the range in the charge on the carbonyl- or β-C in the lactam product, ΔNBO_{pdt,carbonyl-C} or ΔNBO_pdt,β-C, respectively) and a substrate steric descriptor (Sterimol B5_sub,min or ΔSterimol L_sub). Additionally, the models have similar enzyme parameters describing the flexibility of residue 66 (Residue 66_{Sterimol B5,max} and Residue 66_{ΔSterimol L}). The updated model also includes residue-specific descriptors for the maximum backbone angle of residue 175 (Residue 175_{Angle 1,max}), and the minimum backbone dihedral angles of residues 261 and 269 (Residue 261_dihedral,min and Residue 269_dihedral,min, respectively).

As described in the previous section, we postulated that when residue 100 preferentially interacts with residue 177, it disengages interactions with residue 66, enabling the necessary flexibility of that residue for proper repositioning upon substrate binding. Further supporting this hypothesis, the IRD parameter (IRD residues 100–177) in the updated model indicates that selectivity declines when residue 100 is far from residue 177. The new enzyme descriptors, informed from our mechanistic analysis of the initial statistical models, strengthened our understanding of GluER-T36A selectivity and enabled us to predict the effect of untested GluER-T36A mutations.

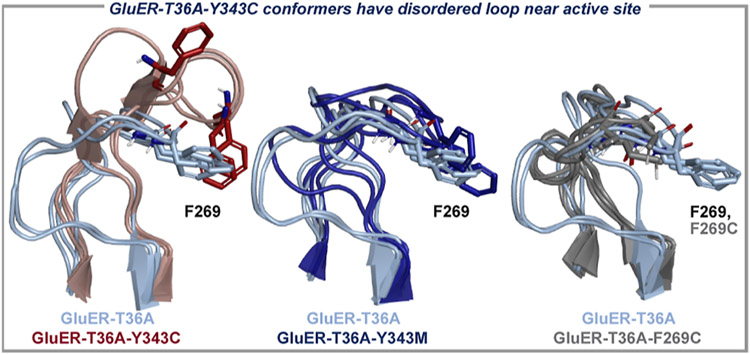
The GluER-T36A-Y343C variant was predicted to be most selective for both 2a and 5a, but the measured enantioselectivity was significantly over-predicted. To probe the origin of this apparent outlier, we compared the aMD conformers for GluER-T36A and the Y343C mutant, which revealed that adjacent residue W342 interacts with F269, a residue located on a loop adjacent to the active site. The loop is positioned to form a “lid” over the active site, and inspection of the GluER-T36A-Y343C conformational ensemble depicted a key difference from other GluER-T36A variants evaluated. The F269 loop is substantially displaced as a result of the Y343C mutation (Figure 7). Interestingly, similar mutations (Y343M) and even mutations to the loop (F269C, M, and R) do not result in comparable disorder. This structural anomaly supports that this prediction is likely an outlier as flexibility at this position is beneficial for enantioselectivity, but importantly, these models were not trained to recognize that major disruptions to the F269 loop are detrimental.

Figure 7.

GluER-T36A-Y343C is structurally unique. The aMD conformational ensemble of GluER-T36A-Y343C (red) displays disorder in the 269-loop region compared to GluER-T36A (light blue). Other variants such as GluER-T36A-Y343M (dark blue) and GluER-T36A-F269C (gray) maintain structures similar to GluER-T36A.

IFD experiments did not show alterations to the loop region as a result of the Y343 mutant, but an interesting change in the geometry of the bound lactam products was observed. These observations are seeding future studies to explore global [EL] features.

CONCLUSIONS

In summary, we have developed predictive tools to evaluate enzyme mutant performance on a non-native reaction while gaining a deeper mechanistic understanding. We identified two complementary conformational search platforms, aMD and IFD, to computationally characterize both enzyme and ligand structures for descriptor extraction and demonstrated how descriptors can be informed by evolving mechanistic hypothesis.

By utilizing a small, representative training set that encompasses a range of reaction outputs, we developed robust statistical models relating GluER-T36A structural features to function in an enantioselective cyclization. Although the focused training set used in this study was insufficient to predict reaction yields, we were able to construct a statistical model to capture the effects of the ligand and GluER-T36A variant on preference for a competing HAT pathway. These models allowed us to quantitatively predict the performance of out-of-sample substrates and substrate/mutant combinations, with a particular emphasis on substrate scope. Interpretation of the predictive model increased our understanding of the enantioinduction imparted by GluER-T36A, which complements contemporary approaches.^40,41 Future applications of this workflow will include the enhancement of enzymatic descriptors and virtual screening of enzyme mutants for reaction engineering.