Abstract
The incidence of stroke and stroke-related hemiparesis has been steadily increasing and is projected to become a serious social, financial, and physical burden on the aging population. Limited access to outpatient rehabilitation for these stroke survivors further deepens the healthcare issue and estranges the stroke patient demographic in rural areas. However, new advances in motion detection deep learning enable the use of handheld smartphone cameras for body tracking, offering unparalleled levels of accessibility. In this study we want to develop an automated method for evaluation of a shortened variant of the Fugl-Meyer assessment, the standard stroke rehabilitation scale describing upper extremity motor function.We pair this technology with a series of machine learning models, including different neural network structures and an XGBoost model, to score 16 of 33 (49%) Fugl-Meyer item activities. In this observational study, 45 acute stroke patients completed at least one recorded Fugl-Meyer assessment for training of the auto-scorers, which yielded average accuracies ranging from 78.1% to 82.7% item-wise. This novel method is demonstrated with potential to conduct telehealth rehabilitation evaluations and assessments with accuracy and availability.
Keywords: Stroke Rehabilitation, deep learning, telemedicine
Introduction
Studies report up to 85% of stroke survivors experience upper extremity (UE) hemiparesis in at least one arm 1 and 78% fail to achieve the average UE function for their age, even after 3 months of treatment and rehabilitation 2. Loss or partial loss of function in even one of the limbs can be extremely debilitating and depressive, as many basic daily tasks require bimanual function. In fact, dependence on bilaterality has been shown to increase with age 3. Common tasks like buttoning a shirt, writing, reaching for objects, and opening bottles mean the survivor must unlearn old habits and relearn new ones 4,5.
The growing issue of poor accessibility to healthcare exacerbates this functional decline, particularly for patients with disabilities in rural areas and largely attributable to a wide variety of factors6. In Texas, for example, the geographic disparities between rural and urban America are apparent; 71% of rural counties lack outpatient rehabilitation clinics for stroke patients, which greatly exceeds the 19% of urban counties 7. Parekh and Barton 8 describe other contributing factors and the complications of healthcare delivery to an aging and increasingly disabled population, citing 75 million people who have multiple chronic conditions. These comorbidities reduce patient compliance and stand in the way of treatment that is best realized by active participation. Current telerehab programs assess motor impairment utilizing technology that is expensive, out of reach for many, or utilize a hybrid in-person assessment, as there is limited availability of quantifiable remote motor assessment 9–11. Uninsured and underinsured patients tend to have increased disability after stroke, are less likely to be discharged to inpatient rehabilitation, and may have minimal or no access to outpatient therapies following a stroke 12–14. These reasons inspire us to advance technologies that can reach an increasingly isolated patient demographic.
An automated assessment of the UE post-stroke that can occur in an outpatient setting will provide clinicians with important data to guide decision-making and maximize session time for targeted intervention, whether it is in the home or via telerehab. Automation of the Fugl-Meyer assessment, which is used extensively as the primary metric to quantify post-stroke recovery, can provide objective data on range-of-motion, strength, and functional abilities that would otherwise require time and labor from healthcare professionals. In this paper, we present a novel approach to using machine learning for automatic scoring of the Fugl-Meyer assessment to measure upper extremity function in stroke patients. Our primary objective is to demonstrate the feasibility of using a single digital camera for motion detection and machine learning methods for automatic scoring. We developed and tested the predictive ability of four machine learning models on videos provided by consenting stroke patients and compared the results with scores provided by a trained healthcare professional. Our results show that machine learning models can achieve similar or better accuracy than human experts in predicting Fugl-Meyer assessment scores. This approach has the potential to reduce clinician burden and improve accessibility to marginalized groups.
Methods
A. Patient Recruitment
45 adult study participants with acute or subacute weakness or unilateral hemiplegia as a result of ischemic or hemorrhagic stroke were recruited after admission to inpatient rehabilitation facilities within the Memorial Hermann Health System. Patients were ineligible to participate in the study if they were younger than 18 years old and at the discretion of their attending physician; this refers to any limiting reason from the physician who is responsible for the patient’s well-being, including their current physical condition or interference with important treatment. No physicians recommended exclusion of any subject for this study. Subjects enrolled in the study if they could comprehend and follow basic instructions. All subjects provided in-person or electronic informed consent after an explanation of the study protocol and prior to any study activity, which was approved by the UT Health Institutional Review Board (IRB) and Committee for the Protection of Human Subjects (IRB number: HSC-MS-20–0767).
B. Study Activities
After enrollment, researchers performed Fugl-Meyer assessments with subjects every 2 days. Fugl-Meyer exercise items were recorded only after the activity was described by the investigator, demonstrated by the investigator, and the subject showed understanding by demonstration. For the recordings, study participants repeated each movement with both arms, first on their non-paretic side, between 3 and 5 times. Fugl-Meyer assessments were ended immediately upon request of the subject for any reason. The movements were captured by a video camera at a resolution of 1080p and a frame rate of 60 Hz placed 3–5 meters away on a tripod 1.5 meters in height. Consistent camera placement, ample lighting, and an unobscured subject improved the quality of motion detection. The Fugl-Meyer was scored in-person by the investigator leading the assessment and by a licensed occupational therapist after the video was spliced into individual activity items. The occupational therapist completed standardization training for an NIH trial and had BlueCloud certification for scoring visual recordings of Fugl-Meyer assessments. All identifiable patient health information, including raw audio- and visual-recording data, was stored locally on an encrypted hard drive and later on a secure UTHealth School of Biomedical Informatics (SBMI) server. Subject videos were separated into smaller clips consisting of individual Fugl-Meyer activity items for ease of scoring by both the model and by the licensed occupational therapist.
C. Deep-learning Motion Detection Algorithm and Feature Extraction
We modified a joint recognition pipeline15 to extract body joints locations from videos. The pipeline uses YOLO V316 object detection model to obtain bounding boxes of the patient’s presence in the image. The cropped bounding boxes are then fed to the HRDNet model17 to extract joints and other landmarks on the body. The output would be extracted -positional coordinates of body joints (nose, neck, hip center, and shoulder, elbow, wrist, hip, knee, ankle, eye, ear for both sides of body), which would be further used as input along the timeline of the patient’s video as an input to score classification model.
Besides major body joints, several Fugl-Meyer assessment items (exercises in hand or wrist groups) require high-precision location identification of hand joints from a patient’s video. A finger joint detection model18 is implemented which firstly fits a palm detector to provide a bounding box for the hand’s skeleton, and then lock joint landmark locations (wrist alone and 4 joints from all 5 fingers respectively for hand model).
For both models, the output is a () vector for each frame, where the first dimension is the number of features and the second dimension 3 contains the -positional coordinates and a confidence level. The number of features is 21 for each joint in the hand model and 19 for each joint in the body model. Normalization of joint position coordinates controlled for differences in subject size and allowed fair comparison between samples. A demonstration of two models on original videos are shown in Figure 1.
Fig 1.
Visual representation of normalized joint coordinates depicting final position of shoulder abduction performed poorly by subject (left, red) and correctly by investigator (middle, blue) with important joints identified (right, yellow). A hand detection model depicting joints (red) is superimposed on sample images of the subject (bottom left) and another investigator (bottom right).
The positional coordinates of features were extracted from video clips for analysis by the Fugl-Meyer Auto-Scoring Models described in section D. Due to symmetry across the sagittal plane, metrics could be calculated both on the left and right side of the subject without adaptations. A summary of the features extracted and final inputs for the auto-scoring models are described in Table A2. Additional information on individual features is provided in the appendix.
D. Fugl-Meyer Auto-Scoring Models
16 items of the Fugl-Meyer assessment (described in Table 2) are recorded using only a smartphone camera and scored using machine learning methods. Multiple deep learning models including a convolutional neural network (CNN), recurrent neural network (RNN) and dilated CNN were evaluated to find the highest performing model.
Table 2.
Modified Fugl-Meyer Assessment Items
| Group | Fugl-Meyer Item | Abbreviation |
|---|---|---|
| AI. Reflexes | Flexors Extensors |
R R |
| AII. Flexor Synergy | Shoulder retraction during hand to ear activity Shoulder elevation during hand to ear activity Shoulder abduction during hand to ear activity Shoulder external rotation during hand to ear activity Elbow flexion during hand to ear activity Forearm supination during hand to ear activity |
U U FM-0 U FM-1 FM-2 |
| AII. Extensor Synergy | Shoulder adduction during hand to ear activity Elbow extension during hand to knee activity Forearm pronation during hand to knee activity |
FM-3 FM-4 FM-5 |
| AIII. Mixed Synergies | Hand to lumbar spine Shoulder flexion to 90° Forearm pronation/supination with elbow at 90° |
U FM-6 FM-7 |
| AIV. Low Synergy | Shoulder abduction to 90° Shoulder flexion to 180° Forearm pronation/supination with shoulder flexed |
FM-8 FM-9 FM-10 |
| AV. Normal Reflexes | Biceps, triceps, and fingers | R |
| B. Wrist | Wrist stability with elbow at 90° Wrist flexion/extension with elbow at 90° Wrist stability with elbow at 180° Wrist flexion/extension with elbow at 180° Wrist circumduction |
S FM-11 S FM-12 FM-13 |
| C. Hand | Mass flexion Mass extension |
FM-14 FM-15 |
| C. Grasp | Hook grasp Thumb adduction Pincer grasp Cylinder grasp Spherical grasp |
S S S S S |
| D. Coordination/Speed | Tremor during finger from knee to nose activity Dysmetria during finger from knee to nose activity Time to complete finger from knee to nose activity |
FM-16* FM-17* FM-18* |
Note that 18 of 33 tests (55%) in the Fugl-Meyer can theoretically be scored using the presented model and are abbreviated with the prefix “FM-”.
Items listed with do not have prediction accuracies due to score class imbalances (FM-16 and FM-17) and the specific scoring criteria (FM-18). Abbreviations: R, requiring physical examination; U, undetectable motion; S, requiring strength assessment.
For each video, a 3D tensor of size for the body (for body actions such as shoulder flexion to 90°) or for the hand (for hand actions such as Wrist circumduction) is generated. and denote the number of joints for body and hand, respectively. Note that and coordinates of each joint are encoded as two channels in the 3D tensor, and we selected frames of equal interval along the video length
For the CNN model, our plain action recognition network was to extract spatial-temporal information from the frame-wise joint locations. It consisted of 3 convolution layers with a filter of 3 × 3, a stride of 1 and a padding of 1, and as the feature map size is halved, the channels (number of filters) is doubled. Two sets of filter numbers were tested: 64 and 128 for the number of filters in the first convolutional layer, respectively. Each convolutional layer is followed by batch normalization (BN).
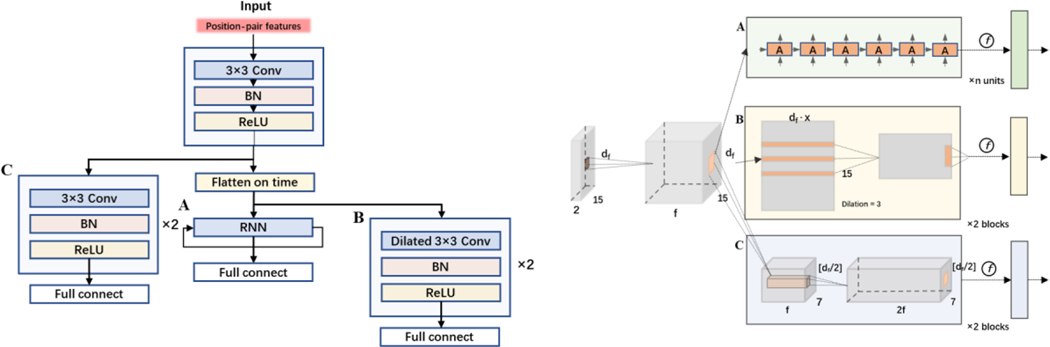
To further improve the action recognition performance, we used a CNN layer as a backbone for encoding, and then added a layer of RNN layer as a CNN-RNN model (hidden size = 64), and a layer of dilated CNN where the extracted encoded features are flattened and concatenated along the time dimension. A demonstration of the models’ structure can be found in Fig. A1. To compare prediction accuracies of deep learning models with advanced machine learning models, we chose eXtreme Gradient Boosting (XGBoost) to be the machine learning benchmark model.
E. Evaluation and Statistics
For each Fugl-Meyer assessment item score there are 3 possibilities: 0, 1 and 2, where 2 implies the patient performs no/little difference in this item with the weak side compared to the strong side, while 0 implies that the patient cannot finish/have great difficulty conducting such movement. The ground truth data used in calculating the accuracies was the experts’ scores of the same videos that were fed to the algorithm. The actual FMA scores were not used in the calculation. Our model was trained on the experts’ scores and then applied to reserved videos for testing.We treated item-wise Fugl-Meyer assessment scoring as a classification problem of 3 classes, did a 10-time cross-validation of randomly train-test split in item-wise level, and calculated the averaged accuracy, AUROC, and its standard deviation for comparison. In these cross-validations, training and testing sets were kept separate. Moreover, we then conducted group-wise Fugl-Meyer assessment scoring evaluation by fitting a linear regression model between predicted and actual group scores to calculate the coefficient of determination, and root-mean-square error (RMSE) of difference.
Results
A. Patient Characteristics
A total of 45 study participants completed at least one Fugl-Meyer assessment and are included in the analysis. A summary describing patient demographics and conditions is provided in Table 1. NIH Stroke Scores (NIHSS) were taken at admission and recorded by hospital staff on the patient’s electronic health record. Demographic information for one patient was missing due to a documentation glitch, but the subject provided informed consent and participated in all study activities.
Table 1.
Summary of Patient Population
| Characteristic | Missing, n (%) | Categories | Count, n (%) or |
|---|---|---|---|
| Demographics | |||
| Age | 1 (2.2 %) | 60.4 ∓ 16.5 | |
| Sex | 1 (2.2 %) | Male | 24 |
| Female | 20 | ||
| Race | 1 (2.2 %) | White | 12 |
| Black | 12 | ||
| Asian | 0 | ||
| Hispanic | 0 | ||
| Other / Unknown | 20 | ||
| Presenting Condition | |||
| Stroke Type | 1 (2.2%) | Ischemic | 30 |
| Hemorrhagic | 12 | ||
| Unspecified | 2 | ||
| Paretic Side | 0 (0%) | Left | 25 |
| Right | 10 | ||
| No difference | 10 | ||
| Lesion Location | 1 (2.2%) | Cortical | 7 |
| Subcortical | 24 | ||
| Other | 13 | ||
| NIHSS | 3 (6.7%) | 6.9 ∓ 5.8 |
Abbreviations: , mean; , standard deviation; NIHSS, National Institute of Health Stroke Scale.
B. Modified Fugl-Meyer Assessment Items
Table 2 categorizes and summarizes the Fugl-Meyer assessment and identifies scorable items with an abbreviation. Items that can not be scored fall under 1 of 3 categories:
Requiring physical examination (R)
Involving occluded joints or undetectable motion (U)
Requiring strength assessment (S)
C. Item-Wise and Group-Wise Prediction Accuracies
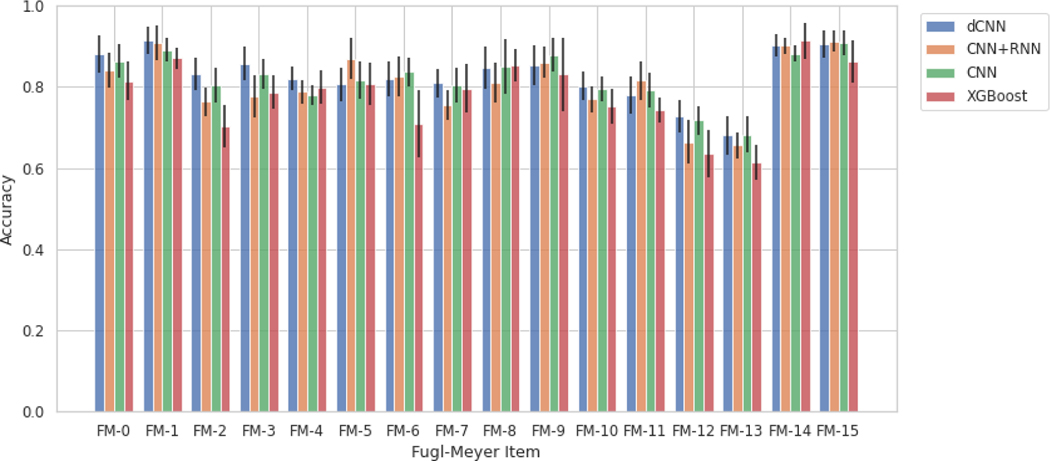
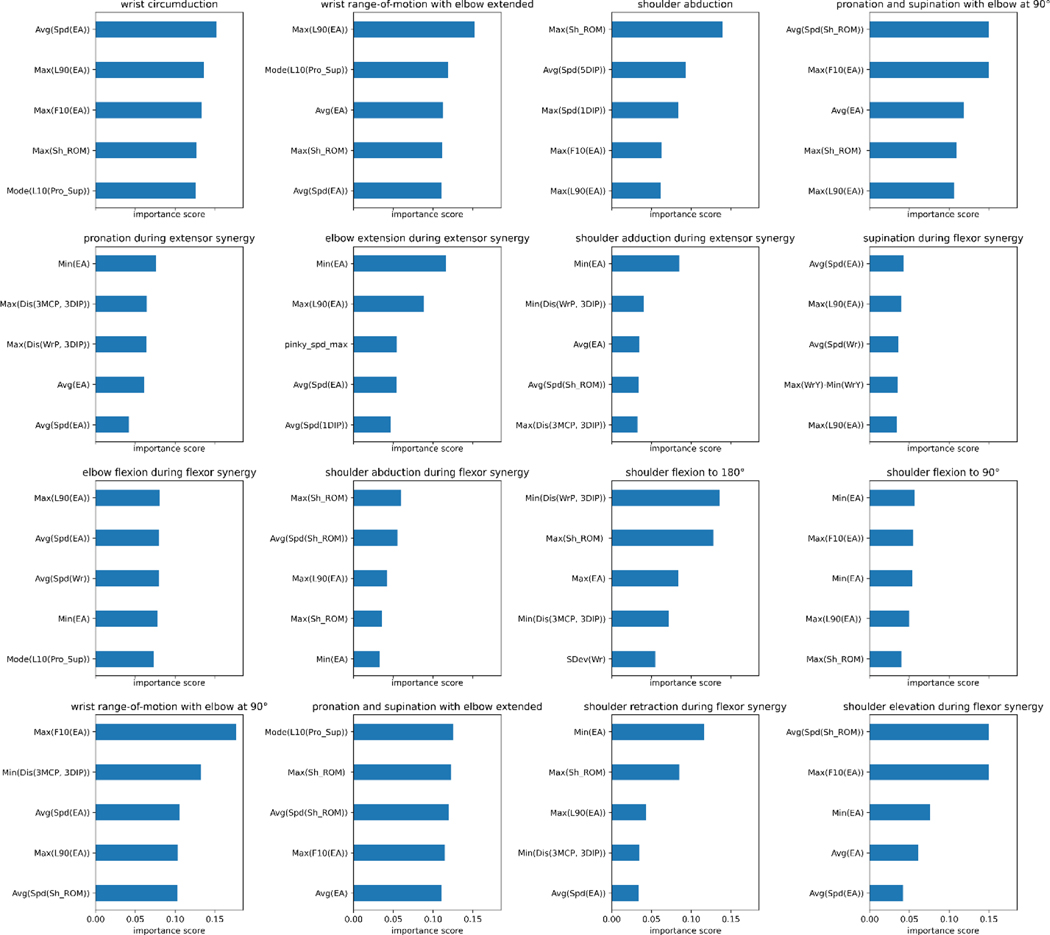
Table 3 illustrates various models’ ability to predict scores from the videos for each individual item, described as item-wise, and the predefined categories of the Fugl-Meyer, described as group-wise. It also lists the number of videos for each class (0, 1, 2) for each Fugl-Meyer item. To test accuracy and generalizability of the model at multiple structural levels, group-wise predictions were conducted for the dilated CNN model, described in Table 3b. Since in each group 2 or 3 items are included, we take the sum of scores for each patient with potential total score as 4 or 6, respectively, and treat it as a regression problem and evaluate the performance using root-mean-square deviation (RMSE). Figure 2 reiterates the tabular item-wise prediction accuracies in a graphical form. Average accuracies are 82.7∓1.6%, 80.7∓1.7%, 76.4∓1.6%, and 78.3∓2.2% for the dilated convolutional neural network, convolutional neural network and recurrent neural network, convolutional neural network, and XGBoost models respectively. Strong correlation between model prediction and actual scores are seen when analyzed group-wise; correlation coefficients range between 0.83 and 0.951 and average 0.89. For XGBoost models, we tried to identify features that contribute mostly to prediction on each items, and the results are shown in Figure A2. Moreover, we demonstrated the inter-rater agreement over scoring Fugl-Meyer items through video slices, and the details of comparison experiment can be found in Inter-rater Agreement Analysis part in Supplementary.
Table 3a.
Item-Wise Prediction Accuracies
| Items | N2 | N1 | N0 | Model performance | |||
|---|---|---|---|---|---|---|---|
| XGBoost (%) | CNN (%) | CNN+RNN (%) | Dilated CNN (%) | ||||
| FM-0 | 189 | 80 | 11 | 81.4∓4.8 | 86.3∓4.1 | 84.1∓4.4 | 88.1∓4.5 |
| FM-1 | 234 | 39 | 2 | 87.1∓2.6 | 89.1∓2.9 | 90.8∓4.3 | 91.4∓3.4 |
| FM-2 | 99 | 146 | 33 | 70.3∓5.1 | 80.4∓4.3 | 76.3∓3.6 | 83.2∓3.9 |
| FM-3 | 161 | 48 | 0 | 78.7∓4.1 | 83.2∓3.7 | 77.6∓5.2 | 85.7∓4.2 |
| FM-4 | 101 | 108 | 0 | 79.9∓4.1 | 77.9∓2.5 | 78.8∓3.0 | 82.1∓3.0 |
| FM-5 | 77 | 132 | 0 | 80.7∓5.2 | 81.6∓4.7 | 87.0∓5.1 | 80.6∓4.1 |
| FM-6 | 67 | 29 | 32 | 71.0∓8.3 | 83.7∓3.5 | 82.6∓4.9 | 81.9∓4.3 |
| FM-7 | 124 | 47 | 11 | 79.6∓6.0 | 80.5∓4.3 | 75.6∓3.7 | 81.0∓3.5 |
| FM-8 | 103 | 10 | 10 | 85.3∓4.1 | 85.1∓6.7 | 81.0∓5.0 | 84.7∓5.2 |
| FM-9 | 49 | 14 | 31 | 83.1∓9.1 | 87.9∓4.1 | 86.0∓3.8 | 85.2∓4.9 |
| FM-10 | 84 | 67 | 17 | 75.2∓4.2 | 79.5∓3.0 | 76.9∓3.3 | 80.2∓3.5 |
| FM-11 | 90 | 70 | 5 | 74.2∓3.1 | 79.2∓4.2 | 81.5∓4.7 | 78.0∓4.5 |
| FM-12 | 55 | 55 | 16 | 63.5∓5.8 | 71.7∓3.4 | 66.4∓5.3 | 72.7∓3.9 |
| FM-13 | 25 | 18 | 6 | 64.3∓6.3 | 67.6∓5.2 | 68.1∓5.3 | 71.4∓5.9 |
| FM-14 | 93 | 7 | 11 | 91.4∓4.5 | 88.1∓2.0 | 90.1∓1.9 | 90.2∓2.8 |
| FM-15 | 87 | 14 | 11 | 86.3∓5.2 | 90.9∓3.1 | 91.3∓2.6 | 90.5∓3.3 |
| FM-16 | 69 | 1 | 0 | / | / | / | / |
| FM-17 | 32 | 5 | 0 | / | / | / | / |
Abbreviations:
Table 3b.
Group-Wise Prediction Accuracies
| Groups | STotal | Savg (std) | RMSEpred | |
|---|---|---|---|---|
| AII. Flexor Synergy | 6 | 4.37∓1.337 | 0.865 | 0.643 |
| AIII. Extensor Synergy | 6 | 4.28∓1.284 | 0.883 | 0.619 |
| AIV. Mixed Synergy | 4 | 2.94∓0.739 | 0.897 | 0.587 |
| AV. Low Synergy | 6 | 4.82∓1.151 | 0.912 | 0.599 |
| B. Wrist | 6 | 4.15∓1.463 | 0.83 | 0.682 |
| C. Hand | 6 | 5.37∓0.061 | 0.951 | 0.476 |
| D. Coordination / Speed | 6 | / | / | / |
Abbreviations: Nₓ, count of videos scored x; CNN, convolutional neural network; RNN, recurrent neural network; /, unscorable due to class imbalances; STotal, total possible scores; Savg, total average of all available samples in group; std, standard deviation; , correlation coefficient; RMSEpred, root mean square error; /, unscorable due to class imbalances.
Fig 2.
Prediction accuracies with standard deviation bars generated from the various scoring models grouped by Fugl-Meyer item. Abbreviations: dCNN, dilated convolutional neural network; CNN, convolutional neural network; RNN, recurrent neural network; XGBoost, eXtreme Gradient Boosting.
Discussion
In this study, we demonstrate the feasibility of a low cost and very accessible method to automatically score components of the Fugl-Meyer Upper Extremity assessment. We used data provided from 45 study participants who share similar demographic and clinical diversity to the greater stroke patient population.
Traditional methods automating the Fugl-Meyer assessment rely on a combination of different motion capture devices and scoring techniques: Table A1 summarizes the recording apparatus, count of scorable Fugl-Meyer items, scoring methods, and results of several studies for reference. All related studies use at minimum one Kinect camera to capture motion for their automation. With this recording configuration, one model19 predicts Fugl-Meyer scores with accuracies ranging between 65% and 87% depending on the item, and another models’20 results, which are described as correlations between qualitative and quantitative scores, vary greatly depending on the activity, showing virtually no correlation for flexor synergy (0.03) and strong correlation for wrist flexion (0.97). Other methods21 use two Kinect cameras to capture 3D body representations and a random forest model to predict two Fugl-Meyer item scores at 91% and 59% accuracy. Studies23,24 also occasionally employ the use of force sensors and inertial measurement units to score up to 26 and 25 items, respectively; support vector machines and backpropagation neural networks for scoring achieved prediction accuracies of 86% and 93% for each model24 and scoring activities using a binary rule-based classification method23 yielded accuracies ranging between 66.7% and 100% depending on the Fugl-Meyer item.
Among the most important shortcomings of these studies is the employment of complex and costly technologies. All related studies rely heavily on depth sensing with the Microsoft Kinect camera. Issues with this camera include detection of subtle movements like supination and pronation, noise and inaccuracy when joints are occluded, reliance on infrared for motion capture, and poor hand tracking24. The use of external devices23,24 allow scoring of additional Fugl-Meyer items which improves clinical utility, but at the expense of reducing accessibility of the proposed technology, which is a focus of our study.
Video information analyzed by deep-learning motion detection models is the most accessible and least costly alternatives to Kinect depth sensors and marker-based motion capture technology. The smartphone is a ubiquitous tool among all generations and in all households, making it a prime candidate for reaching geographically and financially isolated populations; the methods presented in our study can be implemented practically with pre-existing technology in remote settings, although it will be important in future studies to assess our automated method on handheld devices. Most importantly, we show that these methods can compete with and even outperform traditional methods of automating the Fugl-Meyer assessment. Depending on the model, the average accuracy ranged between 78.1% and 82.7% for individual Fugl-Meyer items. Strong correlation () between model prediction and actual scores are observed when analyzed group-wise. These results further suggest the loss of information going from depth sensors to handheld video cameras is insignificant.
For item-wise accuracies, all models struggled the most with wrist circumduction, likely attributable to the low sample size of this activity. This item’s videos were not cut into individual repetitions because the activity is performed quickly and with poorly identifiable start and finish points. The group-wise accuracies presented in Table 3b suffer from low sample size due to the frequency of the therapist being unable to score items on the Fugl-Meyer assessment due to the subject’s unique disability in the acute hospital setting. This often led to samples with incomplete Fugl-Meyer assessment scores and exclusion from this table, even if only one item was unscored. We plan to conduct future studies in outpatient settings, in order to conduct more complete Fugl-Meyer recordings, which could inform us on the method’s errors and possible correlations with severity of stroke. However, this is not a focus of this study as our goal is to study the individual components of the Fugl-Meyer and we were able to obtain a sufficient number for each component to conduct the ML analyses (as indicated in Table 3a). Furthermore, we wanted to focus on the individual components of the score which are clinically more meaningful than the total score.
Alternative methods to auto-scoring machine learning models were attempted, most notably rule-based classification23. An assortment of features described in Table A2 were calculated from the joint positional coordinates and employed in a logical scoring system that was both clinically interpretable and unique to each item. However, noise generated by the motion detection algorithm and volatility of angles produced when joints were collinear with the camera line-of-sight led to poor performance overall: rule-based classification averaged an accuracy of 66.7% with 3 items failing to exceed 50% and 6 items failing to exceed 60%. Auto-scoring machine learning methods tolerate noise from the motion detection algorithm and the volatility natural to 2D joint extractions from 3D movements; a sufficiently large sample of training data could compensate for the associated loss in clinical interpretability.
Limitations of this study include some loss of clinical utility described previously, attributable to several factors. The motion detection model used in this study does not appreciate the real geometry of many joints and physical position of the upper extremities. The ball-and-socket glenohumeral joint allows for internal and external rotation of the arm, which is undetectable by the current model. This paired with obfuscation of the scapulothoracic joint reduces the number of scorable items and may limit the scope of the model’s clinical utility. These critical, unidentifiable movements reduce the total item count by 4. However, it is possible that this model could infer information about these joints and mitigate this occlusion with sufficient data. Other unscorable items involve UE functions that are invisible to cameras and require an in-person examiner, including reflexes, wrist strength, and grip strength.
The distribution of video scores among subject videos presents another challenge to model performance: imbalanced classes are most evident in items FM-3, FM-4, FM-5, FM-16, and FM-17. However, FM-3, FM-4, and FM-5 still have enough samples distributed between 2 of the 3 classes for differentiation by the auto-scorer. Fugl-Meyer items assessing tremors and dysmetria, abbreviated FM-16 and FM-17, were collected and scored by the occupational therapist, but severe imbalances prevented training of the models: there were 69, 1, and 0 videos scored 2, 1, and 0 for tremors and 32, 5, and 0 videos scored 2, 1, and 0 for dysmetria, respectively. For this reason, it is likely these items can be scored by these model architectures in theory with sufficient data, but it is not proven in this study.
FM-18, or the time taken during the coordination and speed activity item, can not be scored using the machine learning models because the criteria is strictly rule-based in design. Inputs for the neural networks and XGBoost do not include any reference to the total number of video frames, so differences in activity duration are undetectable. However, this item is scorable by other means very simply; if submitted videos begin at the start of the activity item and finish at the end of the activity item, the quantity of frames and frame rate of the camera provide a score for FM-18.
Conclusion
This paper presents a method for low-cost automatic assessment of upper extremity impairment in stroke patients. We show the designed models can score 16 of 33 (49%) items in the Fugl-Meyer assessment, with accuracies ranging from 78.1% and 82.7% for each item. When grouped by Fugl-Meyer category, strong correlations between model prediction and actual scores were achieved (). This system carries potential to reduce physician and therapist burden, increase monitoring of arm impairment, and improve the quality and access to care.
In future studies, we envision several changes that could help establish this method as an effective solution to the growing issue of healthcare inaccessibility among stroke patients in rural settings. We would also like to explore the feasibility of this method in a larger population; recording in an outpatient clinical setting or subject’s home would help acquire more data for training the models and test this technology’s ability to function in its intended environment. Utilizing automated Fugl-Meyer could be used in rehabilitation trials to provide intermittent assessments during interventions, easily performed in the patient’s own home. Linking the data obtained through automated Fugl-Meyer assessment could be further applied to define “rehabilitation success” and even “rehabilitation potential,” enabling clinicians to make informed decisions for patient care. However, before widespread applications of our method, we will first need to determine which additional components of the FM can be automated and then re-test its validity and reliability. We also need to determine in longitudinal studies whether this method will be able to discern minimal clinically important differences in FM. Lastly, we believe that consistent camera placement, ample lighting, and an unobscured subject are important for optimal quality of motion detection. Future studies will be helpful to determine which of these parameters are essential for optimal quality.
Acknowledgements
XJ is CPRIT Scholar in Cancer Research (RR180012), and he was supported in part by Christopher Sarofim Family Professorship, UT Stars award, UTHealth startup, the National Institute of Health (NIH) under award number R01AG066749 and U01TR002062, and the National Science Foundation (NSF) #2124789.
KT and SZ are partially supported by Giassell family research innovation fund through School of Biomedical Informatics.
Appendix
Table A1.
Related Research
| Study | Recording | Items | Scoring Method | Accuracy |
|---|---|---|---|---|
| (Eichler et al., 2018)21 | - 2x Kinect cameras - = 12, = 10 |
2 | SVM, Single Decision, RF | 59%, 91% |
| (Lee et al., 2018)22 | - 1x Kinect camera - Force sensors = 9, = 1 |
26 | Binary rule-based classification | 66.7% - 100% |
| (Otten et al., 2015)23 | - 1x Kinect camera - 1x IMU - 1x Glove sensor - = 10 |
25 | SVM and BNN | 86% and 93% |
| (Kim et al., 2016)19 | - 1x Kinect camera - = 41 |
13 | PCA and ANN | 65% - 87% |
| (Olesh et al., 2014)20 | - 1x LED-marker camera - 1x Kinect camera - = 9 |
10 | PCA | 0.03 < < 0.98 |
Abbreviations: , stroke subject sample size; , healthy subject sample size; IMU, inertial measurement unit; SVM, support vector machine; RF, random forest; BNN, backpropagation neural network; ANN, artificial neural network; , correlation coefficient. Accuracy is provided as a percentage compared to manual scores from trained healthcare professionals.
Table A2.
Features Extracted
| Feature Name | Description | Abbreviation |
|---|---|---|
| Initial Metrics | ||
| Shoulder ROM | List of angles between arm and torso | Sh_ROM |
| Elbow Angle | List of angles between axis of arm and forearm | EA |
| Wrist ROM | List of vertical distances between fingers and wrist joint | Wr |
| Pro.-Sup. | List containing classifications of “supination,” “pronation,” or “neutral” | Pro_Sup |
| First 10% | Isolates first 10% of video frames/the beginning of activity | F10 |
| Last 90% | Isolates last 90% of video frames/after the beginning of activity | L90 |
| Last 10% | Isolates last 10% of video frames/the end of activity | L10 |
| Speed | List of changes in values from another list, like speed | Spd |
| Maximum | Highest value of list | Max |
| Minimum | Lowest value of list | Min |
| Average | Average value of a list | Avg |
| Mode | Most common value in a list | Mod |
| Std. Dev. | Standard deviation of the values in a list | SDev |
| 1st Digit DIP | List of positions of the 1st digit’s distal interphalangeal joint | 1DIP |
| 3rd Digit MCP | List of positions of the 3rd digit’s metacarpophalangeal joint | 3MCP |
| 3rd Digit DIP | List of positions of the 3rd digit’s distal interphalangeal joint | 3DIP |
| 5th Digit DIP | List of positions of the 5th digit’s distal interphalangeal joint | 5DIP |
| Wrist Position | List of positions of the wrist | WrP |
| Distance between 2 joints | List of Euclidean distances between 2 joints labeled and | Dis (, ) |
| Ratio between 2 distances | A ratio of minimum distance to maximum distance between joints labeled and | R (, ) |
| Model Inputs | ||
| Max(Sh_ROM) | Highest angle between arm and torso achieved during exercise | |
| Avg(Spd(Sh_ROM)) | Average angular speed of the arm during abduction | |
| Max(Spd(Sh_ROM)) | The maximum angular speed of the arm during abduction | |
| Max(EA) | Greatest amount of elbow flexion | |
| Min(EA) | Greatest amount of elbow extension | |
| Max(F10(EA)) | Greatest angle of flexion in the first 10% of video frames | |
| Max(L90(EA)) | Greatest angle of flexion in the last 90% of video frames | |
| Avg(EA) | Average angle between arm and forearm during exercise | |
| Avg(Spd(EA)) | Average speed arm is flexed or extended during exercise | |
| Max(WrY)-Min(WrY) | The total vertical ROM of the wrist | |
| Max(WrX)-Min(WrX) | The total horizontal ROM of the wrist | |
| SDev(Wr) | Standard deviation from the mean position of the wrist | |
| Avg(Spd(Wr)) | Average speed the subject moves their wrist | |
| Mode(L10(Pro_Sup)) | At the end of an exercise, the highest frequency of hand positions classified as “supinated,” “pronated,” or “neutral” | |
| Max(Spd(5DIP)) | The maximum speed of the 5th digit | |
| Avg(Spd(5DIP)) | The average speed of the 5th digit | |
| Max(Spd(1DIP)) | The maximum speed of the thumb | |
| Avg(Spd(1DIP)) | The average speed of the thumb | |
| Min(Dis(WrP, 3DIP)) | The smallest distance between the wrist and 3rd digit | |
| Max(Dis(WrP, 3DIP)) | The greatest distance between the wrist and 3rd digit | |
| R(WrP, 3DIP) | The ratio of the smallest distance to greatest distance between the wrist and the 3rd digit | |
| Min(Dis(3MCP, 3DIP)) | The minimum distance between the 3rd digit’s metacarpophalangeal joint and the distal interphalangeal joint | |
| Max(Dis(3MCP, 3DIP)) | The maximum distance between the 3rd digit’s metacarpophalangeal joint and the distal interphalangeal joint |
Elements of the list correspond to frames in video clips. F10, L90, and L10 assess metrics based on their values at the beginning of the exercise, after the beginning of the exercise, or at the end of the exercise. Other abbreviations: ROM, range-of-motion; Pro.-Sup., pronation-supination status; Std. Dev., standard deviation.
Fig A1.
Model structure overview (left) and detailed neural network presentation (right). After feeding with the same input of extracted temporal features matrix, the data goes through a block of feature-wise convolution and then goes to one of three branches: A is the Recurrent Neural Network, B is temporal-wise dilated Convolutional Neural Network of two blocks, and C is feature-wise Convolutional Neural Network of two blocks. For all 3 branches, a fully connected layer is attached as the last layer for score classification.
Fig A2.
Extracted Feature importance of XGBoost models for different Fugl-Meyer upper extremity activity items.
Feature Extraction
Shoulder range-of-motion and elbow angle are calculated using the dot product of 2 vectors. For shoulder range-of-motion, these vectors were lines from the shoulder to the elbow and from the neck to the hip center. The elbow angle was the supplementary angle to the angle generated by vectors from the shoulder to the elbow and from the elbow to the wrist, such that greater angles on the range 0° to 145° correspond to greater flexion and less extension at the elbow joint: 0° would be defined as full extension and angles near 145° would be defined as full flexion.
Shoulder range-of-motion and elbow angle are vitally important features to create the model inputs. They are, however, the most susceptible to error. When the subject arms point forward or align with the camera line-of-sight, these features are prone to great variation and will often not represent the true angle of interest. A second version of shoulder range-of-motion and elbow angle were created to address this; distances from shoulder to elbow and from elbow to wrist were recorded from all video clips from one Fugl-Meyer. The greatest value represented the true length of the respective arm segment for that set of videos, at that respective camera angle. Assuming the torso of the body stays reasonably still and the chair minimizes leaning forward and backward, we could infer the 3-dimensional position of the elbow and wrist and approximate the true elbow angle and true angle between arm and torso, referred to as the shoulder range-of-motion. Both versions of both features were included as model inputs.
The wrist range-of-motion feature averaged the vertical coordinates of all metacarpophalangeal joints, excluding the thumb. Like the other features, this feature was recorded for each frame of a video clip. The maximum and minimum of this list yields information about the subject’s ability to flex and extend the wrist.
Using the hand joint detection model, pronation and supination were estimated using the positional coordinates of the thumb and pinky. For most exercises, if the vector pointing from the pinky to the thumb was outside the body and up to the 45° angle, that position in the video would be classified as supinated. Beyond the 45° angle, it would be classified as a neutral grip. If the vector pointed toward the body and up to the 45° angle, it would be classified as pronated. This rule did not apply to scoring supination during flexor synergy. To be classified as supinated, the hand pinky-to-thumb vector must be pointed upwards and with a large distance from start to finish, relative to the distance in other frames of the video.
Error Analysis
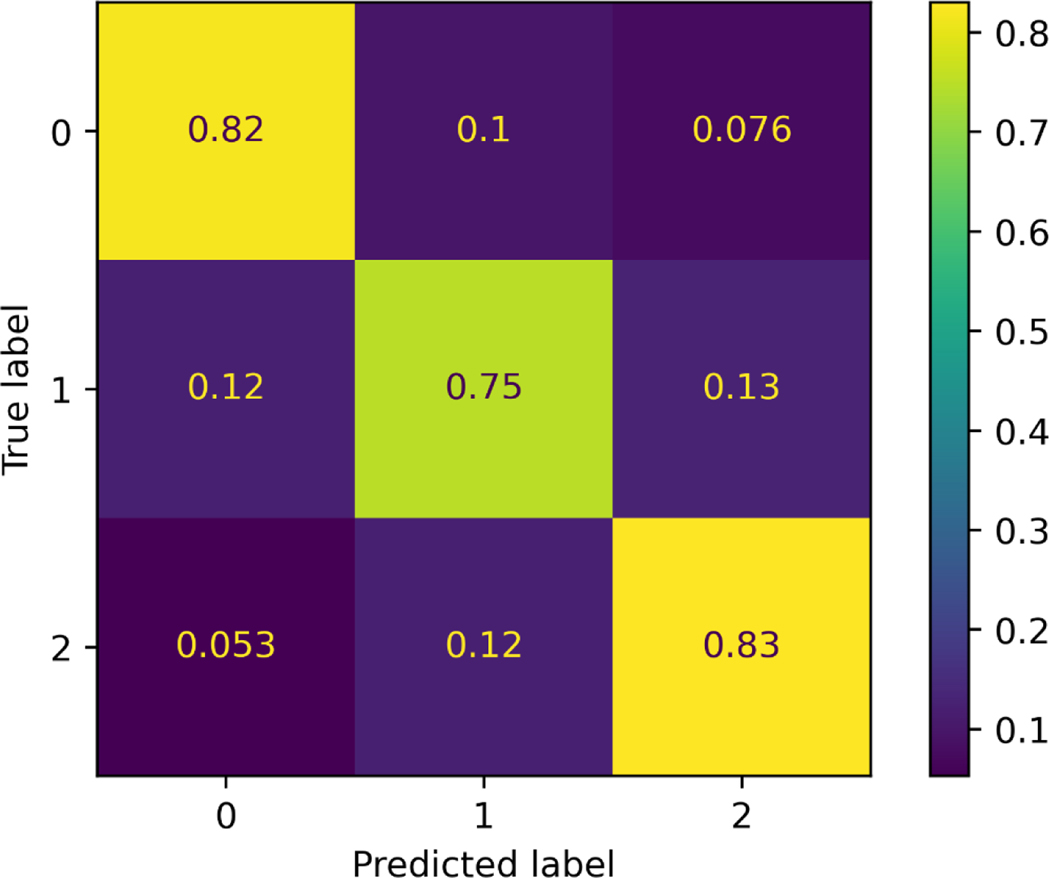
To gain a better understanding of the error distribution (0 vs. 1 or 1 vs. 2) over the dataset, confusion matrix of the model’s performance on the test set is plotted (Fig A3). Values are normalized along the true labels (row direction). As demonstrated in each sub-block, the error of distinguishing between satisfied completion and partial completion is higher than that between partial and inability of completion.”
Fig A3.
Confusion matrix plot of the test set. Accuracy in distinguishing scores of 2 vs. 1 exceeds that of distinguishing scores of 1 vs. 0.
Inter-rater agreement analysis
To explore the consistency between human experts over the method of utilizing videos slices to score Fugl-Meyer items, a subset of videos (consists of 9 patients randomly selected) were given to 2 physical therapists. The reviewers scored the videos individually while blinded to other examiner’s score. The scores were used to calculate Cohen’s Kappa Score, and the result table is shown below as Table A3. To help verify the proposed model in ideal clinical settings, we evaluate the model’s performance on the non-paretic side of patients, and the results are shown as in Table A4. It can be concluded that the high accuracy demonstrates that the model can classify unaffected activity patterns with high confidence.”
Table A3.
Cohen’s Kappa scores between two human experts.
| FM item | Slice count | Cohen’s Kappa score |
|---|---|---|
| FM-0 | 63 | 0.90 |
| FM-1 | 62 | 0.93 |
| FM-2 | 58 | 0.84 |
| FM-3 | 67 | 0.81 |
| FM-4 | 54 | 0.76 |
| FM-5 | 71 | 0.79 |
| FM-6 | 55 | 0.83 |
| FM-7 | 61 | 0.81 |
| FM-8 | 58 | 0.86 |
| FM-9 | 41 | 0.88 |
| FM-10 | 36 | 0.84 |
| FM-11 | 74 | 0.76 |
| FM-12 | 35 | 0.73 |
| FM-13 | 22 | 0.72 |
| FM-14 | 34 | 0.94 |
| FM-15 | 36 | 0.91 |
Table A4.
Model evaluation of non-paretic side. FM scores are evaluated with comparison to the unaffected side, so ideally the scores of the unaffected side would be all 2s, thus result in high prediction accuracy.
| Item | Accuracy (%) | Item | Accuracy (%) |
|---|---|---|---|
| FM-0 | 94.5 | FM-8 | 88.2 |
| FM-1 | 95.7 | FM-9 | 92.5 |
| FM-2 | 91.2 | FM-10 | 87.5 |
| FM-3 | 93.3 | FM-11 | 85.4 |
| FM-4 | 89.4 | FM-12 | 87.3 |
| FM-5 | 87.5 | FM-13 | 88.8 |
| FM-6 | 88.0 | FM-14 | 100.0 |
| FM-7 | 85.3 | FM-15 | 96.0 |
REFERENCES:
- 1.Levin MF, Kleim JA, Wolf SL. What do motor “recovery” and “compensation” mean in patients following stroke? Neurorehabil Neural Repair. 2009;23(4):313–319. [DOI] [PubMed] [Google Scholar]
- 2.Mayo NE, Wood-Dauphinee S, Ahmed S, et al. Disablement following stroke. Disabil Rehabil. 1999;21(5–6):258–268. [DOI] [PubMed] [Google Scholar]
- 3.Kalisch T, Wilimzig C, Kleibel N, Tegenthoff M, Dinse HR. Age-related attenuation of dominant hand superiority. PLoS One. 2006;1:e90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bailey RR, Klaesner JW, Lang CE. Quantifying Real-World Upper-Limb Activity in Nondisabled Adults and Adults With Chronic Stroke. Neurorehabil Neural Repair. 2015;29(10):969–978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wee SK, Hughes AM, Warner M, Burridge JH. Trunk restraint to promote upper extremity recovery in stroke patients: a systematic review and meta-analysis. Neurorehabil Neural Repair. 2014;28(7):660–677. [DOI] [PubMed] [Google Scholar]
- 6.Artnak KE, McGraw RM, Stanley VF. Health care accessibility for chronic illness management and end-of-life care: a view from rural America. J Law Med Ethics. 2011;39(2):140–155. [DOI] [PubMed] [Google Scholar]
- 7.Wozny J, Parker D, Sonawane K, et al. Surveying Stroke Rehabilitation in Texas: Capturing Geographic Disparities in Outpatient Clinic Availability. Archives of Physical Medicine and Rehabilitation. 2021;102(10):e29–e30. doi: 10.1016/j.apmr.2021.07.544 [DOI] [Google Scholar]
- 8.Parekh AK, Barton MB. The challenge of multiple comorbidity for the US health care system. JAMA. 2010;303(13):1303–1304. [DOI] [PubMed] [Google Scholar]
- 9.Cramer SC, Dodakian L, Le V, et al. Efficacy of Home-Based Telerehabilitation vs In-Clinic Therapy for Adults After Stroke: A Randomized Clinical Trial. JAMA Neurol. 2019;76(9):1079–1087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Baur K, Rohrbach N, Hermsdörfer J, Riener R, Klamroth-Marganska V. The “Beam-Me-In Strategy” - remote haptic therapist-patient interaction with two exoskeletons for stroke therapy. J Neuroeng Rehabil. 2019;16(1):85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yu L, Xiong D, Guo L, Wang J. A remote quantitative Fugl-Meyer assessment framework for stroke patients based on wearable sensor networks. Comput Methods Programs Biomed. 2016;128:100–110. [DOI] [PubMed] [Google Scholar]
- 12.MacDonald MR, Zarriello S, Swanson J, Ayoubi N, Mhaskar R, Mirza AS. Secondary prevention among uninsured stroke patients: A free clinic study. SAGE Open Med. 2020;8:2050312120965325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shen JJ, Washington EL. Disparities in Outcomes Among Patients With Stroke Associated With Insurance Status. Stroke. 2007;38(3):1010–1016. doi: 10.1161/01.str.0000257312.12989.af [DOI] [PubMed] [Google Scholar]
- 14.Medford-Davis LN, Fonarow GC, Bhatt DL, et al. Impact of Insurance Status on Outcomes and Use of Rehabilitation Services in Acute Ischemic Stroke: Findings From Get With The Guidelines-Stroke. J Am Heart Assoc. 2016;5(11). doi: 10.1161/JAHA.116.004282 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ludl D, Gulde T, Curio C. Simple yet efficient real-time pose-based action recognition. 2019 IEEE Intelligent Transportation Systems Conference (ITSC). Published online 2019. doi: 10.1109/itsc.2019.8917128 [DOI]
- 16.Redmon J, Farhadi A. YOLOv3: An Incremental Improvement. arXiv [csCV]. Published online April 8, 2018. http://arxiv.org/abs/1804.02767 [Google Scholar]
- 17.Liu Z, Gao G, Sun L, Fang Z. HRDNet: High-Resolution Detection Network for Small Objects. In: 2021 IEEE International Conference on Multimedia and Expo (ICME). ieeexplore.ieee.org; 2021:1–6.
- 18.Zhang F, Bazarevsky V, Vakunov A, et al. MediaPipe Hands: On-device Real-time Hand Tracking. arXiv [csCV]. Published online June 18, 2020. http://arxiv.org/abs/2006.10214
- 19.Kim WS, Cho S, Baek D, Bang H, Paik NJ. Upper Extremity Functional Evaluation by Fugl-Meyer Assessment Scoring Using Depth-Sensing Camera in Hemiplegic Stroke Patients. PLoS One. 2016;11(7):e0158640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Olesh EV, Yakovenko S, Gritsenko V. Automated assessment of upper extremity movement impairment due to stroke. PLoS One. 2014;9(8):e104487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Eichler N, Hel-Or H, Shmishoni I, Itah D, Gross B, Raz S. Non-Invasive Motion Analysis for Stroke Rehabilitation using off the Shelf 3D Sensors. 2018 International Joint Conference on Neural Networks (IJCNN). Published online 2018. doi: 10.1109/ijcnn.2018.8489593 [DOI]
- 22.Lee S, Lee YS, Kim J. Automated Evaluation of Upper-Limb Motor Function Impairment Using Fugl-Meyer Assessment. IEEE Trans Neural Syst Rehabil Eng. 2018;26(1):125–134. [DOI] [PubMed] [Google Scholar]
- 23.Otten P, Kim J, Son SH. A Framework to Automate Assessment of Upper-Limb Motor Function Impairment: A Feasibility Study. Sensors. 2015;15(8):20097–20114. [DOI] [PMC free article] [PubMed] [Google Scholar]