Measurement of the pK_a Values of Organic Molecules in Aqueous–Organic Solvent Mixtures by ¹H NMR without External Calibrants

Abstract

Aqueous–organic solvent mixtures are commonly used for reactions or analyses, where the components of a system are insoluble in pure water. The acid dissociation constant is an important property to measure in these media as it determines the charge state, solubility, and reactivity of a molecule. While NMR spectroscopy is an established tool for the measurement of pK_a in water, its use in aqueous–organic solvents is greatly hindered by the requirement for external calibrants on which a working pH scale is set. Such calibrants include buffer solutions, “anchor” molecules with known pK_a values, and pH electrodes that have undergone lengthy calibration procedures in the solvent mixture of interest. However, such calibrations are often inconvenient to perform, while literature pK_a data covering the required range may not be available at the solvent composition or the temperature of interest. Here, we present a method to determine pK_a in aqueous–organic solvents directly by NMR. We first determine pK_a of an organic acid such as 2,6-dihydroxybenzoic acid (2,6-DHB) by measuring its ¹H chemical shift as a function of concentration along a concentration gradient using chemical shift imaging (CSI). Using 2,6-DHB as a reference, we then determine pK_a of less acidic molecules in single CSI experiments via the variation of their ¹H chemical shifts along pH gradients. As proof of concept, we determine the pK_a values of organic acids and bases up to pK_a 10 in 50% (v/v) 1-propanol/water, 50% (v/v) dimethyl sulfoxide/water, and 30% (v/v) acetonitrile/water and obtain good agreement with the literature values.

Introduction

Mixtures of water and organic solvents are commonly used as media for analytical procedures,¹ synthetic reactions,² and work with biological tissues.³ The properties of these mixtures differ from those of the pure solvents, allowing modulation of the polarity, viscosity, and freezing point via the solvent composition.³ These properties in turn modulate the solubility,⁴ acidity/basicity,⁵ and reactivity² of the dissolved molecules. The acid dissociation constant of an organic molecule (K_a, normally expressed as the negative logarithm, pK_a) is very sensitive to the solvent composition and can be changed by more than one log unit relative to its aqueous value by inclusion of 50 wt % of an organic solvent.^6–8 Literature data are only available in a small number of solvent mixtures, while extrapolations of pK_a between different solvent mixtures are only possible within narrow classes of compounds and require reliable reference data.^9,10 For these reasons, it is often necessary to measure the pK_a values of organic molecules experimentally when working in aqueous–organic solvents.

The electrochemical measurement of pH requires careful calibration of electrodes⁵ either using solutions of known pH in the solvent mixture of interest^11–14 or by applying a specific correction to the pH reported by an electrode that has been calibrated using conventional aqueous buffers.^5,15 Alternatively, pH may be determined from the NMR chemical shifts or UV/vis spectra of compounds with known pK_a values.^8,16 However, electrode corrections and pK_a data are only available in a small number of aqueous–organic mixtures.^5,15 Finally, pK_a values can be measured without knowledge of pH using conductometric methods.¹⁷ However, such approaches require high-purity materials, and only one compound may be analyzed per titration.

Here, we demonstrate how pK_a values can be determined directly by ¹H chemical shift imaging (CSI) NMR in mixtures of compounds, without the use of electrochemical measurements or literature pK_a data. In our method, a concentration gradient of 2,6-dihydroxybenzoic acid (2,6-DHB) is established in an NMR tube by placing solid acid at the base of the tube and layering the solvent mixture of interest on top. Spatially resolved ¹H spectra are recorded at different positions along the gradient using CSI and a pK_a value extracted in a single experiment by analysis of how the ¹H chemical shift of 2,6-DHB varies with concentration. The experiment is then repeated in the presence of 1,2,4-triazole and a pK_a of this compound is determined, and the pK_a of 2,6-DHB is verified by considering the degree of proton transfer from 2,6-DHB to triazole. The pK_a values of organic molecules spanning pK_a 3–10 are then determined relative to 1,2,4-triazole and 2,6-DHB, allowing the determination of pH between 1 and 12 from their ¹H chemical shifts. We can, thus, establish a working set of indicator molecules to determine pH in an aqueous–organic mixture by running four ¹H CSI experiments (Scheme 1). These indicators allow the pK_a of organic molecules to be determined in single 20 min CSI experiments from the variation of their ¹H chemical shift along the pH gradients.^16,18

Scheme 1. Method to Determine pK_a of Organic Molecules in Aqueous–Organic Mixtures Using CSI and Concentration Gradients of 2,6-DHB.

The ¹H chemical shift of 2,6-DHB is measured as a function of concentration in the absence of base (a) and the presence of 40 mM 1,2,4-triazole (b) to determine the pK_a of both compounds. The pK_a values of other indicator molecules are determined relative to triazole and 2,6-DHB (c) allowing the determination of pH from their ¹H chemical shifts and pK_a of other organic molecules using pH gradients and CSI (d).

All experiments can be run under full automation on standard high-field NMR equipment, allowing for a convenient calibration of the indicators at the solvent composition and the temperature of interest. As proof of concept, we determine the pK_a of a range of acids and bases in 50% (v/v) 1-propanol/water, 50% (v/v) dimethyl sulfoxide-d₆ (DMSO)/water, and 30% (v/v) acetonitrile-d₃ (CD₃CN)/water at 298 K. The uncertainties in the fitted pK_a values are less than 0.5 units in most cases, while agreement with literature data is obtained within these uncertainties. While NMR is an established tool to determine the relative pK_a values of organic molecules,¹⁹ to the best of our knowledge, the direct measurement of absolute pK_a by NMR has not previously been described. All processing can be performed using the automation routines provided in Section S10 of the Supporting Information and the spreadsheet accompanying this work.

Experimental Section

Materials

All reagents were purchased from commercial suppliers and used as received. Phthalic acid was used as the monopotassium salt; otherwise, Na⁺ was the counterion in all experiments. Milli-Q water (18.2 MΩ cm) was used throughout the study. The DMSO-d₆ and CD₃CN had deuteration levels of 99.8 and 99%, respectively. The 50% (v/v) 1-propanol/H₂O mixture was prepared by combining D₂O (10 mL), H₂O (40 mL), and 1-propanol (50 mL).

Preparation of Samples

Solid 2,6-DHB was transferred to the base of 5 mm NMR tubes (Wilmad 528-PP) by pushing the tip of a 9 in. Pasteur pipet into the solid acid and emptying the tip at the base of the NMR tube. Four, 2 mm diameter glass beads were placed on top of the 2,6-DHB. Prior to use, the beads were rinsed with ethanol and dried. A solution containing indicators, organic analyte molecules, and DSS was layered slowly (10 s) on top of the beads up to a height of 40–45 mm from the base of the NMR tube. The sample was stood in the autosampler rack of the spectrometer (22 °C) prior to analysis. Samples for the determination of the pK_a of 2,6-DHB and 1,2,4-triazole contained 10 mM DSS to act as a reference for the chemical shift and integration. Other experiments in 50% DMSO/H₂O and 30% CD₃CN/H₂O were performed with 0.4 mM DSS, where only referencing of the chemical shift was required. All experiments in 50% 1-propanol/H₂O were performed with 10 mM DSS due to the strong background solvent signal. No 2,6-DHB was included as an indicator, with the ¹H signal arising from the acid diffusing up the NMR tube. Analytes were included as neutral bases or as sodium salts.

The time, t (hours), at which the gradient will have developed was estimated based on the viscosity, η (mPa s), of the solvent mixture as t = αη(Z₀² – Z_b²)/ln(C_b/C₀). Z_b is the height of the bottom of the NMR-active region, and Z₀ is the height of the midpoint of our sample above the top of the 2,6-DHB (9 and 19 mm in our instrument, respectively, with the top of the acid lying approximately 1–2 mm above the absolute base of the NMR tube—see the photograph of freshly prepared sample on Scheme 1a). C_b and C₀ are the concentrations at these positions. α is calculated as 0.1 h mPa^–1 s^–1 mm^–2 at 22 °C based on a self-diffusion coefficient of 2,6-DHB in 50% 1-propanol/H₂O of 2.8 × 10^–10 m² s^–1 at 298 K (Section S2, Supporting Information). Acceptable gradients are obtained at times calculated with the ratio C_b/C₀ between 400 and 6, giving theoretical concentrations (C_top) less than 2 mM at the top of the NMR active region (Z_top, 29 mm above 2,6-DHB in our instrument). The time windows are, thus, 12–41, 14–47, and 4–13 h for 50% 1-propanol/H₂O, 50% DMSO/H₂O, and 30% CD₃CN/H₂O, respectively. The pK_a,0 values determined over these time windows agree within uncertainties (Section S2). For determination of the pK_a,0 of imidazole (IM) in 50% 1-propanol/water, where an excess of a much stronger base was present [20 mM of dimethylglycine (DMG) Na salt] and only 32 points were collected in the CSI data set, a more gentle pH gradient was employed where appreciable acid was present at Z_top (C_b/C_top = 20, t = 66 h). The mass, m, of 2,6-DHB is calculated based on the desired C_b as 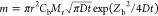, where r is the tube radius (2.1 mm), M_r is the molecular mass of 2,6-DHB (154.12 g/mol), and D is the diffusion coefficient of 2,6-DHB. For determination of the pK_a,0 of 2,6-DHB and triazole (Figure 1), 8–9 mg of 2,6-DHB was used, giving C_b between approximately 120 and 200 mM over the time window. A total of 4–5 mg was used for calibration of the other indicators (Table 1) and to determine the pK_a of the organic analytes (Table 2), unless otherwise stated, giving C_b between 60 and 100 mM. C_b is chosen to provide an excess of 2,6-DHB over the base at Z_b.

Figure 1.

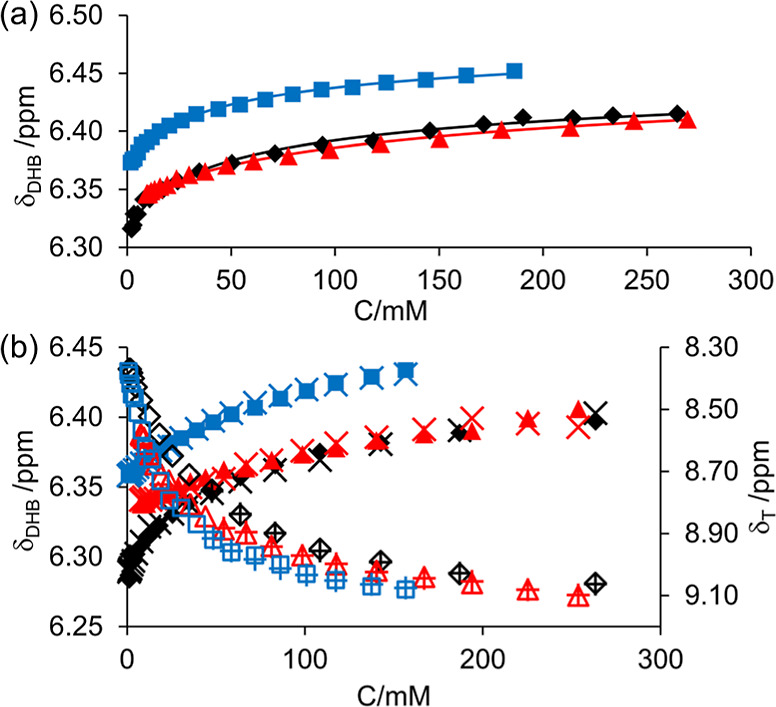
Plot of ¹H chemical shift of 2,6-DHB (solid symbols) vs C in the absence (a) and presence (b) of 40 mM 1,2,4-triazole in 50% 1-propanol/H₂O (black diamond), 50% DMSO/H₂O (red triangle), and 30% CD₃CN/H₂O (blue square). Solid lines are fits to eqs 1–4. ¹H chemical shift of 1,2,4-triazole (open symbols). Fits to eq 7 (vertical cross) and eqs 2 and 8 (diagonal cross).

Table 1. pK_a,0, δ_H, and δ_L for NMR Indicators.

50% 1-propanol/H2O				50% DMSO/H2O			30% CD3CN/H2O
indicator	pKa,0	δH/ppm	δL/ppm	pKa,0	δH/ppm	δL/ppm	pKa,0	δH/ppm	δL/ppm
2,6-DHBa	1.61 ± 0.29	6.4781	6.3113	1.02 ± 0.19	6.4911	6.3362	1.54 ± 0.40	6.4999	6.3680
1,2,4-triazole	1.80 ± 0.36	9.2221	8.3164b	1.77 ± 0.19	9.1934	8.3621b	2.33 ± 0.41	9.1539	8.3278b
DMGc				2.64 ± 0.21	4.0328	3.5755	2.45 ± 0.42	3.9985	3.6370
salicylic acid				3.33 ± 0.22	7.5679	7.3772
glycolic acid	4.47 ± 0.36	4.1722	3.9171d	4.82 ± 0.30	4.0994	3.7583d	4.43 ± 0.46	4.1716	3.8643d
acetic acid	5.47 ± 0.38	2.0516	1.9160d	5.72 ± 0.31	2.0293	1.8048d	5.46 ± 0.54	2.0583	1.8485d
IM	5.93 ± 0.44	8.7791	7.7155				6.61 ± 0.56	8.6442	7.7254
2MI	6.87 ± 0.47	2.6227	2.3574	6.66 ± 0.35	2.5790	2.3181	7.56 ± 0.59	2.5717	2.3233
4CN	8.54 ± 0.48	7.5160	7.2840	8.29 ± 0.37	7.6617	7.3510	8.44 ± 0.61	7.6370	7.4052
DMG	9.50 ± 0.50	2.9373e	2.2328e	9.45 ± 0.47	3.5870c	2.8685c	9.83 ± 0.69	3.6512c	2.9289c

^apK_a,0, δ_L, and δ_H obtained in the absence of 1,2,4-triazole using eqs 1–4, uncertainty obtained from experiment with 40 mM 1,2,4-triazole.

^bAverage of δ_L determined in solution of triazole (40 mM) and DSS and in acidic range sample.

^cCH₂ resonance of DMG.

^dAverage of acidic and basic range samples in the absence of 2,6-DHB.

^eMethyl resonance of DMG.

Table 2. Comparison of pK_a,0 of Analyte Molecules Determined by ¹H CSI with Literature Values.

50%1-propanol/H2O				50% DMSO/H2O				30% CD3CN/H2O
analyte	indicator	pKa,0 NMR	pKa,0Lit	analyte	indicator	pKa,0 NMR	pKa,0 Lit	analyte	indicator	pKa,0 NMR	pKa,0Lit
salicylic acida	2,6-DHB, triazole, glycolate, acetate	4.12 ± 0.37	4.1717	salicylic acida	2,6-DHB, triazole, DMG, glycolate, acetate	3.46 ± 0.21	3.488	salicylic acida	2,6-DHB, triazole, DMG, glycolate, acetate	3.69 ± 0.42	3.43,27 3.74,28 3.9329
benzoic acidb	2,6-DHB, triazole, glycolate, acetate, 2MI	5.52 ± 0.38	5.507	benzoic acid	triazole, glycolate, acetate, 2MI	5.25 ± 0.31	5.23,8 5.7330	benzoic acid	triazole, glycolate, acetate, 2MI	5.10 ± 0.49	4.78,31 5.10,29 5.2330
picolinic acidb	2,6-DHB, triazole, glycolate, acetate, 2MI	1.85c, 5.29 ± 0.38	2.16,32 5.5232	Besd	triazole, glycolate, acetate, 2MI	6.72 ± 0.34	7.03,12 7.1833	phthalic acid	triazole, glycolate, acetate, 2MI	3.48 ± 0.43, 6.07 ± 0.51	3.41,6 3.46,1 6.531
acetylacetone	IM, 2MI, DMG	9.23 ± 0.50e	9.7134	4CNf	2MI, DMG	8.25 ± 0.45	8.5635	quinineg	DMG, glycolate, acetate, IM, 2MI, DMG	3.55c, 8.35 ± 0.65	8.5436
pipecolic acid	triazole, 2MI, DMG	2.33c, 10.34 ± 0.50	2.87,32 10.4732	d-valinef	2MI, DMG	3.29c, 9.29 ± 0.47	9.6737	benzylamineh	DMG, 2MI, DMG	8.89 ± 0.69	9.2636

^aAcidic-range data set.

^b8–9 mg of 2,6-DHB.

^cApproximate pK_a1 from fitting to eq 14.

^dSample also contained DMG sodium salt (2 mM), tricine (2 mM), formate (4 mM), and tert-butylamine (10 mM), which were found unsuitable for use as indicators. A total of 5–6 mg of 2,6-DHB.

^eValue corrected for enol-ketone tautomerization.

^fSample also contained NaOH (10 mM), d-valine Na salt (2 mM), and 4CN sodium salt (20 mM).

^gBasic-range data set.

^hSample contained NaOH (10 mM) in addition to indicators. A total of 3–4 mg of 2,6-DHB.

NMR

All experiments were performed at 298 K on a Bruker 500 MHz Avance III spectrometer, locking and shimming to D₂O, DMSO-d₆, or CD₃CN. ¹H chemical shift images were acquired using a gradient phase encoding sequence based on that of Trigo-Mouriño et al.²⁰ For 50% 1-propanol/H₂O, a spin-echo sequence (π/2–τ–π–gp acquire) was used, where gp is a magnetic field gradient pulse of 166 μs duration that was ramped from −8 to 8 G/cm in 32 steps. τ is a delay to balance the gradient pulse and gradient recovery delay (200 μs). π/2 was 10 μs. Eight scans were acquired at each gradient increment with a signal acquisition time and relaxation delay of 2.15 and 3.0 s, respectively, and a sweep width of 20 ppm. A spoil gradient pulse (600 μs, 25 G/cm) and recovery delay (200 μs) were executed before the π/2 pulse. The spoil and phase encoding gradient pulses were in the form of smoothed squares. Sixteen dummy scans were performed prior to signal acquisition, giving a total experimental time of 23 min 30 s. The vertical range of the CSI experiment (cnst0, Section S11) was set to 3.2 cm, giving a theoretical resolution of 1.0 mm.

Experiments in 50% DMSO/H₂O and 30% CD₃CN/H₂O were performed with suppression of the H₂O resonance using a CSI sequence incorporating excitation sculpting with perfect-echo²¹ (Bruker library, zgesgppe) and 4 ms Gaussian inversion pulses. To determine the pK_a,0 of 2,6-DHB and 1,2,4-triazole, CSI data sets were collected with the same gradient, acquisition time, and relaxation delay described above for experiments in 50% 1-propanol/H₂O. To determine the pK_a values of other compounds in these solvents and acetylacetone in 50% 1-propanol/H₂O, the encoding gradient pulse was ramped from −16.5 to 16.5 G/cm in 64 steps with a signal acquisition time and relaxation delay of 1.17 and 1.0 s giving a total experimental time of 19 min 38 s. The vertical range of the CSI experiment was set to 3.0 cm.

Data Processing

¹H spectra and CSI data sets were processed with an exponential line broadening factor of 3 Hz and 64 K or 32 K points, respectively. CSI data sets were processed in phase-sensitive mode, with phase, baseline correction, and referencing to DSS (0 ppm) performed automatically using the scripts and routines described in Section S10, Supporting Information. Only rows 7–27 (32-point CSI data set) or 14–57 (64-point data set), covering the region approximately 11–31 mm from the base of the NMR tube, were used for analysis to avoid artifacts relating to off coil effects. Calculations are performed by the spreadsheet accompanying this work. The concentration of 2,6-DHB was determined from the integrals, h, of 2,6-DHB (3,5-position of aromatic ring) and DSS (methyl) as C = kh_2,6-DHB/h_DSS, where k = 44.0, 45.3, and 47.5 mM for 50% 1-propanol/H₂O, 50% DMSO/H₂O, and 30% CD₃CN/H₂O, respectively (Section S1, Supporting Information).

Results and Discussion

Determination of pK_a of 2,6-DHB

We first determine the pK_a of 2,6-DHB in the solvent mixture by layering a solution of sodium 3-(trimethylsilyl)-1-propanesulfonate (DSS, 10 mM) on top of 8–9 mg of 2,6-DHB. Dissolution and diffusion of the 2,6-DHB establishes a concentration gradient that can be predicted based on the viscosity of the solvent mixture (Section S2, Supporting Information). In the absence of other acids or bases, the fraction of 2,6-DHB in its deprotonated state, f, is given by eq 1

1

where K_a is concentration based and C is the total concentration of 2,6-DHB at each position along the sample. Assuming a fast exchange on the ¹H NMR time scale, the chemical shift of 2,6-DHB, δ_DHB, is given by

2

where δ_H and δ_L are the limiting chemical shifts of the protonated and deprotonated states, respectively. C is obtained by integrating the ¹H resonance of the 3,5-position of the aromatic ring of 2,6-DHB against the methyl resonance of DSS at each position along the sample using CSI. The molar ionic strength, I, of the solution at each position is calculated as the sum of the concentrations of DSS and dissociated 2,6-DHB. The activity coefficient of a univalent ion, γ, is obtained from eq 3

3

where A is taken as 1.32, 0.546, and 0.755 and B as 3.09, 2.22, and 4.45 for 50% 1-propanol/H₂O, 50% DMSO/H₂O, and 30% CD₃CN/H₂O, respectively (Section S3, Supporting Information).^22–24 In the absence of activity data, ionic strength can be ignored (A = 0) and our method will yield pK_a values uncorrected for ionic strength (Section S4, Supporting Information). The concentration-based K_a is calculated from the thermodynamic pK_a (pK_a,0) using eq 4

4

The pK_a,0 of 2,6-DHB is obtained by fitting the chemical shift of the 3,5-position to eqs 1–4, with pK_a,0, δ_H, and δ_L as free variables (Figure 1a). pK_a,0 is obtained as 1.61, 1.02, and 1.54 in 50% 1-propanol/H₂O, 50% DMSO/H₂O, and 30% CD₃CN/H₂O, respectively, in agreement with 1.80 interpolated from the data of Papadopoulos and Avranas in 50% 1-propanol/H₂O (Section S5, Supporting Information).¹⁷ Fitting the 4-position of 2,6-DHB yields the same pK_a,0 (Section S6, Supporting Information).

Determination of pK_a of 1,2,4-Triazole

To verify that the change in the ¹H chemical shift of 2,6-DHB with concentration is due to dissociation, the experiment is repeated in the presence of 40 mM 1,2,4-triazole. The pH is calculated from eq 5 using the values of pK_a,0, δ_H, and δ_L determined for 2,6-DHB in the absence of triazole.

5

The ionic strength is calculated from the ¹H chemical shift of 2,6-DHB and the concentration of DSS (eq 6).

6

The pK_a,0 of 1,2,4-triazole is obtained by fitting the chemical shift of the CH resonance of triazole (δ_T) to eq 7.

7

δ_L is taken as the ¹H chemical shift of 1,2,4-triazole in the solution prior to layering on top of the 2,6-DHB. Fitting to eq 7 is only performed for points where the uncertainty in the pH determined from the chemical shift of 2,6-DHB is less than 0.1 units based on the parameters of 2,6-DHB determined in the absence of triazole. To verify the pK_a,0 of 2,6-DHB, f is calculated from the pH and total concentration (T, 40 mM) of 1,2,4-triazole using eq 8 (Section S7, Supporting Information).

8

where and [H⁺] = γ^–110^–pH. The chemical shift of 1,2,4-triazole is fitted to eq 7 with pK_{a,0 triazole} and δ_H as free parameters and the chemical shift of 2,6-DHB to eqs 2 and 8 with pK_a,0 DHB*, δ_H, and δ_L as free parameters. The uncertainty in the pK_a,0 of 2,6-DHB is taken as the difference between pK*_a,0 DHB and pK_a,0 DHB as in the ideal case, the two values are equal. This uncertainty is used to calculate the average uncertainty in the pH in the fitting of eq 7, which is taken as the uncertainty in pK_{a,0 triazole} (Section S7, Supporting Information). Fitting data for the three solvent mixtures yield pK_a,0 values of triazole of 1.80 ± 0.36, 1.77 ± 0.19, and 2.33 ± 0.41 in 50% 1-propanol/H₂O, 50% DMSO/H₂O, and 30% CD₃CN/H₂O, respectively (Figure 1b). The pK_a values determined by homogeneous mixing of DSS, 2,6-DHB, and triazole agree with the CSI-derived values within fitted uncertainties (Section S1, Supporting Information).

Determination of pK_a of Indicators

Having determined the pK_a,0 of 2,6-DHB and 1,2,4-triazole in a solvent mixture, we can now obtain δ_H, δ_L, and pK_a,0 for a series of organic molecules with pK_a values up to 10. This set of indicators allows us to determine pH up to 12 via their ¹H chemical shifts.¹⁸ We chose a set of molecules possessing only one or two singlet ¹H resonances: DMG, glycolate, acetate, IM, and 2-methylimidazole (2MI). Sodium was the counterion in all samples. To determine δ_H and pK_a,0 for these indicators, two CSI experiments were run to span acidic (pH < 6) and basic (pH > 6) ranges. Salicylate and 4-cyanophenol (4CN) were used as additional indicators in these experiments. For the acidic range, 1,2,4-triazole (20 mM), DMG sodium salt (2 mM), glycolate (20 mM), acetate (20 mM), and salicylate (2 mM) were layered on top of 4–5 mg of 2,6-DHB. For 50% 1-propanol/H₂O, DMG was excluded due to spectral overlap with 1-propanol. Salicylate was included as an analyte only in 30% CD₃CN/H₂O and in 50% 1-propanol/H₂O, where it was included at a concentration of 20 mM.

The pH value reported by each indicator, pH_i, for which δ_H, δ_L, and pK_a,0 are known (initially only 2,6-DHB and 1,2,4-triazole) is calculated using eq 9

9

where δ_obs is the observed chemical shift of the indicator and Δz² is the difference in the square of the charge of the indicator between the protonated and deprotonated states (−1 and 1 for 2,6-DHB and 1,2,4-triazole, respectively). For these experiments, δ_L of 1,2,4-triazole was redetermined in the solution of indicators from a row of the CSI data set where the pH was sufficiently low for the anionic form to be absent and the triazole to be in its neutral form, as judged relative to the ¹H chemical shift of acetate (Figure S22, Supporting Information). γ was calculated using eq 3, with I at each point along the sample taken as the sum of the ionic strength of the solution of ligands in the absence of 2,6-DHB (I₀), the concentration of H⁺, and the concentration of protonated nitrogen bases (eq 10)

10

where the summation is carried out for all nitrogen bases of concentration C_i for which δ_H, δ_L, and pK_a,0 are known. The sensitivity, S_i, of the chemical shift of each indicator with respect to pH is calculated using eq 11(18,25)

11

The pH value at each position along the sample is calculated as the sensitivity-weighted average of pH_i calculated from each indicator for which δ_H, δ_L, and pK_a,0 are known.

12

where the summation is carried out for all indicators where the uncertainty in pH_i arising from the uncertainty in δ_obs, δ_H, and δ_L of the indicator is less than 0.05 units (Section S7, Supporting Information). This cutoff was increased to 0.1 units for the calibration of IM in 50% 1-propanol/H₂O due to the large uncertainty in pH determined from the known indicators (acetate, glycolate, triazole, and 2,6-DHB) when the pH approached the pK_a of IM. To determine δ_H, δ_L, and pK_a,0 for a new indicator, initial values are used to calculate pH_i for the indicator which is included in the calculation of the overall pH using eqs 9–12, provided the uncertainty in pH_i arising from the uncertainty in δ_obs, δ_H, and δ_L is less than 0.4 units. δ_H and pK_a,0 of the indicator are obtained by fitting δ_obs to eq 13 for each point along the sample for which pH can be determined using the known indicators.

13

δ_L was taken as the ¹H chemical shift measured in the solution of indicators prior to layering on 2,6-DHB, with the exception of DMG where δ_L for the acidic step was judged from the CSI data set relative to the ¹H chemical shift of acetate (Figure S22, Supporting Information). The 0.4 units cutoff in the calculation of pH_i for the new indicator was increased to 0.8 if no points with acceptable uncertainty in pH_i were detected following fitting to eq 13, so that an uncertainty in pK_a,0 could be calculated. This was only the case for 4CN in 50% 1-propanol/H₂O. Inclusion of the new indicator in the calculation of pH from eq 12 helps avoid the fitting to eq 13 being thrown by the high uncertainty when pH determined from the known indicators approaches their upper limit of quantitation. The uncertainty in pK_a,0 for an indicator is calculated as the highest uncertainty in pK_a,0 of the known indicators, plus the average difference between pH_i of the new indicator and the pH calculated from eq 12 using only the known indicators. Once δ_H, δ_L, and pK_a,0 and the uncertainty in pK_a,0 have been determined, the parameters of the next indicator with the higher pK_a can be determined until the full set is established. For 50% DMSO/H₂O, salicylate was used to improve the fitting of glycolate to eq 13 by bridging the gap in the pK_a between DMG and glycolate.

For the basic pH range, a solution of glycolate (20 mM), acetate (20 mM), IM (20 mM), 2MI (20 mM), 4CN sodium salt (20 mM), and DMG sodium salt (20 mM) was layered on the top of 4–5 mg of 2,6-DHB. Quinine hydrochloride (2 mM) was included as an analyte in the 30% CD₃CN/H₂O sample. The 50% DMSO/H₂O sample contained 2 mM N,N-bis(2-hydroxyethyl)-2-aminoethanesulfonate (Bes) as an analyte; however, the pH did not reach a sufficiently low value to determine the pK_a,0 of this compound. With the exception of DMG, δ_L of the indicator was measured in the solution prior to layering on the top of 2,6-DHB. δ_L for the fully deprotonated state of DMG (pK_a,0 > 9) was determined by fitting δ_obs to eq 13 with δ_H, δ_L, and pK_a,0 as free variables, and δ_L constrained to be less than or equal to the chemical shift measured prior to layering on 2,6-DHB. IM and 4CN bridged the gap in pK_a between acetate and 2MI and between 2MI and DMG, respectively. However, IM was not required as an indicator in 50% DMSO/H₂O due to the high pK_a of acetic acid in this solvent mixture.

The values of δ_H, δ_L, and pK_a,0 for the indicators are provided in Table 1. The pK_a,0 values of acetic acid determined in 50% 1-propanol/H₂O and 30% CD₃CN/H₂O (5.47 ± 0.38 and 5.46 ± 0.54, respectively) agree with the literature values of 5.71²⁶ and 5.40⁶ reported in these solvent mixtures. The plots of the ¹H chemical shifts of the indicators and fits to eq 13 in 50% DMSO/H₂O are provided in Figure 2. The plots for 50% 1-propanol/H₂O and 30% CD₃CN/H₂O are provided in Section S9 of the Supporting Information.

Figure 2.

Plot of ¹H chemical shifts of indicators vs pH in 50% DMSO/H₂O. Solid lines are fits to eq 13.

Determination of pK_a of Organic Molecules

Having established a set of indicator molecules to determine pH, we can measure the ¹H chemical shifts of organic analyte molecules and fit them to eq 13 with δ_H, δ_L, and pK_a,0 as free variables. With the exception of DMG in the determination of the pK_a,0 of salicylate (50% DMSO/H₂O and 30% CD₃CN/H₂O), all indicators were included at a 20 mM concentration, as sodium salts or neutral bases, to produce smooth pH gradients via buffering effects. As pK_a,0 and δ_H are known for each indicator, δ_L does not need to be redetermined. The pH of a row is calculated by grouping the indicators into pairs in order of pK_a,0 and calculating the sensitivity-weighted average pH_i of the pair with the highest combined sensitivity.¹⁸

Analytes were 2 mM in 50% DMSO/H₂O and 30% CD₃CN/H₂O and 20 mM in 50% 1-propanol/H₂O. A total of 4–5 mg of 2,6-DHB was used unless otherwise stated. Good fits to eq 13 are obtained for a range of monoprotic analytes (Figure 3), while the pK_a,0 values obtained agree with values reported in the literature (Table 2). These literature pK_a,0 values have been interpolated from published data to the solvent compositions used in the present work (Section S5, Supporting Information). The uncertainty in the fitted pK_a,0 was taken as the uncertainty in pH at the data point where the pH was closest to the value of pK_a,0 – Δz² log₁₀(γ).

Figure 3.

Plot of ¹H chemical shifts of monoprotic analytes vs pH in 50% 1-propanol/H₂O (a), 50% DMSO/H₂O (b), and 30% CD₃CN/H₂O (c) and fits to eq 13 (solid lines).

The pK_a,0 of the enol form of acetylacetone was determined from the ¹H chemical shift of the proton on the unsaturated carbon and converted to the overall pK_a,0 of acetylacetone as pK_a,0(enol) – log₁₀(j), where j is the fraction of compound in the enol form at low pH (Figure S21, Supporting Information).³⁸¹H spectra of analytes are provided in Section S8 of the Supporting Information.

For analytes possessing two protonation steps (picolinic acid, pipecolic acid, valine, phthalic acid, and quinine), eq 13 is modified to include two protonation steps

14

where the subscript denotes the deprotonation step and δ_L, δ_HL, and δ_H are the chemical shifts of the fully deprotonated, monoprotonated, and fully protonated states, respectively, and the pK_a values are thermodynamic. Fits to eq 14 are shown in Figure 4. All pK_a values and limiting chemical shifts were free fitting parameters. For all compounds, pK_a2 is determined with good accuracy. However, with the exception of phthalic acid, the pH does not attain a sufficiently low value to allow a reliable fitting of pK_a1. Nevertheless, an estimate of pK_a1 is obtained (Table 2). The pK_a1 of valine compares with the value of 3.00 reported by Dogăn et al.¹³ in 40% (v/v) DMSO/H₂O. For phthalic acid, complete titration curves are recorded, allowing both pK_a values to be fitted (Figure 4). The large number of pH values assessed in the CSI experiment also reveals the contrasting behavior of the two aromatic resonances.

Figure 4.

Plot of the ¹H chemical shifts of diprotic analytes. Solid lines are fits to eq 14. (a) Picolinic acid, 50% 1-propanol/H₂O. (b) Pipecolic acid, 50% 1-propanol/H₂O. (c) d-valine, 50% DMSO/H₂O. (d) Phthalic acid, 30% CD₃CN/H₂O. (e) Quinine, 30% CD₃CN/H₂O.

For quinine, the proton at position 2 of the quinoline ring exhibits a much larger change in chemical shift below pH 6 than the proton adjacent to the hydroxyl, implying that pK_a1 is associated with the protonation of quinoline nitrogen. Such information may not be apparent from a conventional NMR titration where fewer data points are collected or if pK_a was determined solely by potentiometric methods.

Conclusions

We have shown how a set of indicators for the measurement of pH in aqueous–organic solvents can be calibrated using four ¹H CSI experiments, avoiding completely the use of literature data or electrochemical measurements and liberating researchers to study pH-dependent processes at the solvent composition required by their work. The indicators allow the ¹H spectra of organic molecules, including active pharmaceutical ingredients, to be recorded as a function of pH using CSI techniques. The uncertainty in pK_a determined by our method is comparable to the spread in the pK_a values reported in the literature. As well as organic solvents, our method could potentially reveal the effect of additives, such as molecular crowding agents, on pK_a, thus providing a valuable tool to inform experimental design.

Data Availability Statement

The data underlying this study are openly available at https://research-portal.uea.ac.uk/en/datasets/data-for-measurement-of-the-pka-values-of-organic-molecules-in-aq.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.analchem.3c02771.

• Integration of 2,6-DHB; analysis of samples at different times since preparation; extraction of A and B (eq 3); interpolation of pK_a values from published data; extraction of pK_a of 2,6-DHB using 4-position; uncertainty analysis; example ¹H spectra; calibration plots of indicators; automated processing of data sets; and CSI pulse sequences (PDF)

• Spreadsheet for analysis of data sets (XLSX)

Author Contributions

All authors have given approval to the final version of the manuscript.

M.W. thanks UKRI for a Future Leaders Fellowship (MR/T044020/1). N.A. was funded by the Royal Society of Chemistry Analytical Chemistry Trust Fund (ACSS 21/015).

The authors declare no competing financial interest.