Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Oct 11;23(20):9538–9546. doi: 10.1021/acs.nanolett.3c03123

Bose Condensation of Upper-Branch Exciton-Polaritons in a Transferable Microcavity

Xingzhou Chen †, Hassan Alnatah ‡, Danqun Mao †, Mengyao Xu †, Yuening Fan †, Qiaochu Wan ‡, Jonathan Beaumariage ‡, Wei Xie †, Hongxing Xu †, Zhe-Yu Shi †, David Snoke ‡,*, Zheng Sun †,§,*, Jian Wu †,§,⊥,∥,*
PMCID: PMC10603810  PMID: 37818838

Abstract

graphic file with name nl3c03123_0005.jpg

Exciton-polaritons are composite quasiparticles that result from the coupling of excitonic transitions and optical modes. They have been extensively studied because of their quantum phenomena and potential applications in unconventional coherent light sources and all-optical control elements. In this work, we report the observation of Bose–Einstein condensation of the upper polariton branch in a transferable WS2 monolayer microcavity. Near the condensation threshold, we observe a nonlinear increase in upper polariton intensity accompanied by a decrease in line width and an increase in temporal coherence, all of which are hallmarks of Bose–Einstein condensation. Simulations show that this condensation occurs within a specific particle density range, depending on the excitonic properties and pumping conditions. The manifestation of upper polariton condensation unlocks new possibilities for studying the condensate competition while linking it to practical realizations in polaritonic lasers. Our findings contribute to the understanding of bosonic systems and offer potential for the development of polaritonic devices.

Keywords: Bose condensation, upper polariton branch, transferable microcavity, thermal equilibrium

The realization of exciton-polariton strong coupling in semiconductor microcavities from cryogenic temperatures1−3 to room temperature4,5 not only improves our understanding of the fundamental studies of many-body physics but also opens up opportunities for the exploration of potential all-optical control devices.6−10 Exciton-polaritons (called here simply “polaritons”) are hybridized half-light–half-matter quasiparticles that arise from the strong coupling of cavity photons and excitonic transitions. In the strong coupling regime, the rate of energy exchange between the cavity photons and the excitons becomes much greater than their dissipation rates, giving rise to new mixed states known as the upper polariton (UP) and the lower polariton (LP) branches. As interacting bosons, polaritons can exhibit Bose–Einstein condensation, which can be characterized by a strong coupling mechanism, e.g., a nonlinear increase in output strength, narrowing of spectra, continuous blue-shift, and an increase in temporal and spatial coherence across the threshold. The dual light–matter nature allows flexible control of the condensation of polaritons and facilitates its potential applications in quantum simulation,11,12 unconventional coherent light sources,13,14 all-optical polarization logic devices,15,16 neural morphology computing,17,18 and transistors.19,20

Polariton condensates allow the study of a range of behaviors as the cavity lifetime is changed. In the limit of long cavity lifetime, the scattering from UP to LP is fast, so that the dynamics approach the behavior of a single population model, making the UP hard to detect. As the cavity lifetime is decreased, it becomes comparable to the time for conversion from UP to LP, so the dynamics resemble those of two populations competing for condensation. The experiments we have performed here are in the latter case; the polaritons are in the strong-coupling limit with a lifetime comparable to their conversion time. This opens up new avenues for exploring out-of-equilibrium quantum phenomena. A few experiments have explored the upper polariton branch in a variety of microcavities based on different materials, including the transition from the upper polariton state to the dark exciton state,21 terahertz radiation originating from the scattering of upper polaritons to lower polaritons,22 and upper polaritons participating in parametric amplification.23 However, in these studies, the focus has largely been in a regime well below the threshold of condensation.

In this work, we have successfully demonstrated the upper polariton condensation formed in a symmetric transferable WS2 monolayer microcavity. Through a comprehensive investigation that combines experimental and theoretical approaches, we explored upper polariton condensation resulting from non-resonantly pumped polaritons. Our focus was on understanding the specific conditions necessary for the upper polariton to undergo condensation at a lower threshold than the lower polariton. Our findings have revealed that upper polariton condensation occurs within a particular range of particle density (<1013 cm–2). This behavior is consistent with an earlier prediction.24 The Bose condensation of the upper polariton can be attributed to several crucial factors. This discovery is greatly significant, as it contributes to the fundamental understanding of out-of-equilibrium quantum phenomena and unlocks new possibilities for further investigations. Additionally, our results hold practical relevance for the design and development of polaritonic lasers, where the competition between condensates of the lower and upper polariton states plays a crucial role.

The most intriguing feature of semiconductor-type two-dimensional transition metal dichalcogenides (2D TMDCs) is the emergence of fundamentally distinct electronic and optoelectronic properties as the material undergoes a transition from the bulk to the two-dimensional limit (monolayer).25,26 In addition, the 2D TMDCs possess a unique combination of properties, including a high oscillator strength,27 a large binding energy (a few hundred millielectronvolts),28−30 significant nonlinear properties,31−33 and compelling structural tunability.34−36 The strong excitonic effects in TMDCs present opportunities for studying light and matter interactions.37−42 This interaction can be further controlled by embedding the 2D TMDCs into an optical microcavity.43−46Figure 1a illustrates a schematic of the full structure design. The WS2 monolayer is sandwiched between two distributed Bragg reflectors (DBRs). The bottom DBR is made of alternating SiO2/SiNx layers with 12 periods and was grown by plasma-enhanced chemical vapor deposition (PECVD) with the center of the stopband at 628 nm. A spacer layer of quarter wavelength thickness SiO2 was then grown on top of the bottom DBR to form a λ/2 cavity. The WS2 monolayer, which was mechanically exfoliated from the bulk crystal (purchased from HQ), was then dry transferred onto the half-cavity. Finally, the top DBR, similar to van der Waals materials, was peeled off the substrate and transferred on top of the monolayer (see also Methods).47,48 The isolated WS2 monolayer with a size of 5 μm × 10 μm is circled with a red dashed line, as shown in the optical microscope image in Figure 1b. To show that the polaritons are in the strong-coupling regime, we made use of angle-resolved imaging at a temperature of 10 K (Figure 1c). The angle has a 1:1 correspondence with in-plane momentum (k∥) through the relation k∥ = (ω/c) sin θ, where c is the speed of light. A pump laser at 515 nm with a repetition frequency of 76 MHz was used to efficiently excite the sample (see also Methods). Figure 1c unambiguously shows the anticrossing feature of the dispersion illustrated together with the simulated absorption intensity (middle) showing the LP and UP branches via the transfer matrix method. The red lines are fits to the LP and UP dispersions, and the blue dotted lines are fits to the cavity and the exA mode using a coupled harmonic oscillator model, giving a Rabi splitting (Ω) of 30 meV and a cavity–exciton energy detuning (Δ) of −11 meV, respectively. The PL spectrum further shows strong coupling by summing for a narrow range of emission angles around k∥ = 0. The two dominant peaks in Figure 1c are assigned as the upper and lower polariton peaks, denoted with red dotted lines. Crucially, the emission of the upper polariton branch is brighter than that of the lower polariton branch in this sample. The strain applied to the monolayer during the transfer of the top DBR flakes results in a corresponding red-shift in the exciton bandgap.49,50

Figure 1.

Figure 1

Open in a new tab

Sample structure and optical properties of WS2 monolayer microcavity polaritons. (a) Schematic of the microcavity structure. The bottom DBR is composed of 12 SiO2/SiNx pairs grown by PECVD. The top DBR was mechanically separated from the substrate and transferred on top of the WS2 monolayer. (b) Optical microscopy image of the full microcavity. The dotted red line indicates the WS2 monolayer position. (c) Angle-resolved PL measurements (left) compared with the simulated absorption image (middle) of the WS2 monolayer microcavity, showing the same lower (LPB) and upper (UPB) polariton branches. The red lines are fitted to the LPB and UPB dispersion, and the blue dotted lines are fitted to the cavity and the exA mode with the coupled harmonic oscillator model, giving a Rabi splitting (Ω) of 30 meV and cavity–exciton energy detuning (Δ) of −11 meV, respectively. The strong coupling is illustrated by the PL spectrum (right), showing two dominant peaks assigned as the upper and lower polaritons, denoted with the red dotted lines.

The upper polariton condensation is observed as we increase the pump power across the phase transition, as shown in panels a and b of Figure 2. At low pump powers, the upper polariton occupation increases linearly with power. Near the condensation threshold, a nonlinear increase in intensity is observed, which becomes linear again at a much higher pump power. This sharp increase in intensity is accompanied by a decrease in the line width by a factor of 4, an energy blue-shift of ∼1 meV, that is 3.3% of the Rabi splitting, and an increase of the polariton temporal coherence, all of which are hallmarks of Bose–Einstein condensation. The saturation and the slight broadening of the line width above the threshold can be attributed to the increased polariton–polariton interaction. Recently, a red-shift of the upper polariton was observed in a stack consisting of multiple monolayers.51 Our interpretation is that the polariton density in our monolayer sample is relatively lower compared to multilayer configurations, which could account for the absence of a red-shift here. To gain more insight into the quantum statistics of the upper polariton, we make use of angle-resolved imaging, giving the intensity I(k, E), which is then converted into an occupation number N(E) using a single efficiency factor (for more details, see ref (52)). The measured UP occupation for different pump power values is shown in Figure 2c, where we defined the ground state energy in each case as E = 0.

Figure 2.

Figure 2

Open in a new tab

Power-dependent measurements at 10 K. (a) Angle-resolved PL measured at 0.25Pth (left) and 1.1Pth (right), where Pth = 110 μW is the threshold power of the condensation. Below the threshold, the emission is broadly distributed in momentum and energy in the UPB and LPB. Above the threshold, the emission comes almost exclusively from the k∥ = 0 lowest-energy state from the UPB. (b) Occupancy of the k∥ = 0 ground state (blue circles), line width (red circles), and energy blue-shift (green circles) vs the pump power for the upper polariton branch. At a low pump power, the ground state occupancy increases linearly with excitation and then increases exponentially after the threshold before becoming linear again. (c) Upper polariton occupation expressed in a semilogarithmic scale for various pump powers. The power values from low to high are 0.01, 0.1, 0.5, 1.1, 5.4, 9.1, and 13.6 times the threshold values. The solid curves are best fits obtained from the solution of the Boltzmann equation. The fitted temperature (T) is 89 K, and the reduced chemical potential (|μ/kBT|) is 0.168 for an excitation power of 1.1Pth, indicating the polariton gas is in the degenerate regime. For exciton powers larger than 1.1Pth, the experimental occupation becomes nonthermal, while our model predicts thermal equilibrium. Possible reasons for this are discussed in the text.

We find that when the pump power is below the condensation threshold, the occupation of the upper polaritons is described well by a Maxwell–Boltzmann distribution, indicating that the polariton gas is in thermodynamic equilibrium with a well-defined temperature. When the pump power is above the threshold, we observe a significant increase in the upper polariton ground state occupation. However, the high-energy tail becomes nonthermal. With an increase in pump power, this feature maintains the same behavior in the distribution, consistent with the other reported experiments carried out in short-lifetime polariton systems demonstrating nonequilibrium polariton condensates.2,53 Slightly above the threshold (∼1.1Pth), the upper polariton occupation is quasi-thermal, allowing us to obtain reasonable fits to a Bose–Einstein distribution as shown in Figure 2c. The fitted value of T is 89 K, and the corresponding chemical potential is −1.3 meV for the fourth occupation curve in Figure 2, leading to a reduced chemical potential |μ/kBT| = 0.168, which indicates the quantum degeneracy of the upper polariton gas under such pump powers.

To confirm the extended coherence expected of the condensation for the upper-branch exciton-polariton, we studied the temporal coherence using a Michelson interferometer. By tuning the relative distance between the two arms of the Michelson interferometer, we can introduce a time delay to study the temporal coherence of the upper polariton gas. We applied a conjugated lens to convert the real space to momentum space. Typical interference patterns below (0.6Pth) and above the threshold (2Pth) are shown in Figure 3a–d, with two different time delays, Δt = 0 ps (left column) and Δt = 0.1 ps (right column) respectively. The interference patterns without a time delay exhibit well-contrasted interference fringes, indicating the emergence of extended coherence in the system. As we introduced a time delay, we see a reduction in the visibility, allowing us to extract the coherence time. Here the visibility is defined as the ratio of the intensity difference of the maximum and minimum and the sum of them (Imax – Imin)/(Imax + Imin). In panels e and f of Figure 3, we plot the visibility as a function of the time delay. To determine the coherence time, the experimental visibility data were fitted with a Gaussian function. We find that the coherence time (δt) increased from 55 to 138 fs when the excitation power increased from 0.6Pth to 2Pth.

Figure 3.

Figure 3

Open in a new tab

Temporal coherence for upper polaritons. Typical interference patterns pumped (a and b) below and (c and d) above the threshold with two different time delays, Δt = 0 ps (left column) and Δt = 0.1 ps (right column), respectively. (e and f) Visibility as a function of the time delay for the corresponding pump powers. The experimental data were fitted with a Gaussian function. The coherence time (δt) is increased from 55 to 138 fs when the excitation power increases from 0.6Pth to 2Pth.

In addition, to further understand the underlying mechanism of the condensation in the upper polaritons, we carried out power-dependent dynamic measurements using a streak camera with a typical temporal resolution of 1 ps, as shown in panels a and c of Figure 4. The time-resolved photoluminescence spectra for UP/LP were extracted by using a two-peak fitting procedure. These time-resolved spectra allow us to extract several crucial parameters by fitting them to a population dynamics model as shown in panels b and d of Figure 4 (see the next section for details).

Figure 4.

Figure 4

Open in a new tab

Time-resolved photoluminescence spectra and underlying mechanism for the upper polariton condensate. (a and c) Time-resolved photoluminescence images for the pumping power at 0.8Pth and 1.2Pth, respectively, measured by a streak camera. The time-integrated spectra (yellow) were fitted by two Lorentzian peaks and assigned to the upper (red) and lower (blue) polaritons. (b and d) Experimental measurements (black) and simulated results (red), based on dynamic equations mentioned in the text and Methods, of the time-resolved upper and lower polariton photoluminescence spectra for different pumping powers [(b) 0.8Pth and (d) 1.2Pth]. 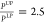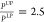(e) Occupation of the lower and upper polaritons obtained from the quantum Boltzmann simulations for the case in which Inline graphic. For this pumping ratio, the upper polariton undergoes condensation at a threshold power lower than that of the lower one. (f) Transition from UP to LP condensation at a higher power with the same ratio of pumping Inline graphic.

To model the dynamics of the polaritons, we used two different models, a coarse-grained model for describing the evolution of the total polariton density as a function of time, n(t), and a fine-grained model, namely, a full quantum Boltzmann equation solution, to describe the evolution of the polariton density as a function of both time and energy, n(t, E). The coarse-grained model allows us to extract parameters such as the conversion time between the UP and LP and characteristic lifetime parameters of the system, while the fine-grained model allows us to extract the occupation of the polaritons as a function of their energy.

First, we discuss the coarse-grained model. We use the following dynamic equations to simulate the conversion between the reservoir and the upper and lower polaritons:

graphic file with name nl3c03123_m001.jpg 1

where nres, nup, and nlp are the densities of reservoir excitons (i.e., excitons with momentum or spin states that do not couple to light) and polaritons in both upper and lower branches, respectively, and τres, τup, and τlp are the corresponding lifetimes. We also introduce two-particle collisional scattering from the reservoir to both polariton branches, represented by Ku and Kl.

Conversion time τconv describes the inverse of the rate of conversion between the upper and lower polaritons. Here we assume that it is dominated by the single-particle decay (e.g., phonon emission) and two-particle scattering processes (including the polariton–polariton and polariton–reservoir scattering). τconv thus depends on the densities of particles in both polariton branches as well as the reservoir and is written as τconv–1 = τ0–1 + A(nup + nlp) + Bnres, where τ0–1 represents the rate of single-polariton conversion, A(nup + nlp) and Bnres describe the polariton conversion due to scattering losses. Note that we have also introduced an inverse conversion term that is proportional to Boltzmann factor 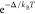Inline graphic in the dynamic equation. The term describes the conversion from lower polaritons to upper polaritons due to thermal fluctuations and guarantees that the fixed point of the dynamic equation would be a Boltzmann distribution were other loss processes to be ignored.

A comparison between the simulations and time-resolved photoluminescence spectra is shown in panels b and d of Figure 4. Although there are multiple fit parameters, the fits are highly constrained because we use the same equations to fit multiple initial pumping conditions for both polariton branches over the full range of temporal evolution. To compare the predictions of dynamic equations of eq 1 with the time-resolved spectra, we assume that at t = 0, there is no occupation in either polariton branch, while nres(0) = cP, with c being the pumping power–reservoir transfer rate. Time-resolved populations nup and nlp are then found by iterating the differential equations of eq 1. By fitting the simulated spectra with the experimental data as shown in panels b and d of Figure 4, we extract the following dynamic parameters: τup = 1.9 ps, τlp = 0.9 ps, τ0 = 30 ps, τres = 100 ns, c = 3.4 μW–1, Ku = 4.4 × 10–3 μm2 ps–1, Kl = 8.8 × 10–3 μm2 ps–1, A = 2.9 × 10–3 μm2 ps–1, and B = 1.5 × 10–3 μm2 ps–1. We find that the lifetimes of upper/lower polaritons extracted from the fits are very close to the expected lifetimes for upper and lower polaritons at k⃗ = 0 based on the Q of the cavity and the Hopfield coefficients for the photon fraction of each. Importantly, we find that conversion time τconv that describes the conversion process between the upper and lower polaritons is around 20–30 ps at low density, which is much longer than those of both τup and τlp. This indicates that the conversion between the upper and lower polariton branches due to spontaneous and two-particle collisions may be ignored within the time interval of interest and, more importantly, that it is possible for the upper polaritons to reach thermal (quasi) equilibrium without decaying to the lower branch. Our estimation of the conversion time is based on simulating the dynamic equations (eq 1), which simplify the WS2 monolayer microcavity. The real system may have additional effects like polariton–polariton interaction and polariton decay such as higher-order radiative processes54 and a nonradiative Auger process,55 which can alter the dynamic equations and impact the conversion time estimation. However, considering that our current estimation is much longer than the polariton lifetimes and these effects are higher-order, we can reasonably conclude that τconv ≫ τup, τlp in our experimental setup. However, this conversion time becomes faster as the polariton density increases due to stimulated scattering, eventually becoming fast enough that it is comparable to the lifetime of the polaritons.

Next, we discuss the fine-grained model, which uses the semiclassical Boltzmann equation to describe the dynamics of both lower and upper polariton branches. In general, the Boltzmann equation has the form

graphic file with name nl3c03123_m003.jpg 2

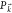where Inline graphic is the occupation number, Inline graphic is the characteristic lifetime, Inline graphic is the pumping term, and LP and UP refer to the lower and upper polariton branches, respectively. W(i) is the interaction term to be considered within each population. Our model includes four types of interactions: polariton–polariton interactions within the same branch, polariton–polariton interactions between different branches (i.e., upper polariton–lower polariton interaction), polariton–phonon interactions, and polariton–electron interactions (there are always typically some free carriers in these structures due to charged impurities). The details of the interactions considered in the model are discussed in the Supporting Information. This model is very similar to that used in ref (56), but crucially, our model treats the upper and lower polariton populations separately and accounts for conversions between these two populations via optical phonons.

Figure 2c shows the fits to the upper polariton occupation at low density measured by using the quantum Boltzmann equation. In agreement with the experimentally measured occupation, our model shows that at densities well below the condensation threshold, the upper polariton occupation becomes well described by a Maxwell–Boltzmann distribution. Because the interaction processes scale as the square of the density, the thermal equilibrium seen experimentally at a low density means that the polariton interactions are dominated by scattering with free charged carriers, which was also found in ref (56). We find that thermalization at a low density can be reproduced only by including a background free electron gas with a density of ∼1010 cm–2.

When quantum statistics become important [i.e., N(E0) ∼ 1], the shape of the distribution changes and an upturn at E = 0 appears, indicating the buildup of the ground state occupation. At a very high density, the experimental UP occupation becomes highly nonthermal, while our model predicts that the UP should remain in thermal equilibrium, hence the absence of the fit to the high-density data in Figure 2c. We speculate that the deviation from the thermal equilibrium at a high density in the experiment is due to two reasons. First, the optical system used in these experiments was polarizing, but the polarization of the condensate was not tracked, which can give rise to misleading N(E) values for the coherent part of the gas. Second, at a high density, rapid exciton–exciton annihilation can take place due to Auger recombination, which can lead to nonequilibrium. Our quantum Boltzmann model does not account for such processes.

The UP undergoing Bose–Einstein condensation before the LP can also be shown by our model. When the upper polariton is more excitonic than the lower polariton, it becomes more strongly interacting than the lower polariton, therefore enhancing the relaxation dynamics toward condensation. This is because the polariton–polariton interaction strength is proportional to the square root of the exciton fraction. Because the upper polariton is 0.7 excitonic and the lower polariton is 0.3 excitonic in our sample, the upper polariton is approximately an order of magnitude more interacting. In addition, because the upper polariton is more excitonic, it has a lifetime that is longer than that of the lower polariton, as the lifetime is inversely proportional to the photon fraction. Another important parameter is the ratio of pumping term PUP/PLP. In the model, we assumed that the pumping term is independent of k in each branch. We find that upper polariton condensation can happen only at a threshold pumping power lower than the lower polariton when PUP/PLP > 2.5 as shown in Figure 4e. The ratio of these pumping terms cannot be extracted experimentally, but our model can give us a lower bound of this ratio. Because the nonresonant pump in the experiment is at a higher energy than both the lower and upper polaritons, we expect that more upper polariton states are initially occupied than lower polariton states, which is in agreement with our simulations. Lastly, we mention that upper polariton condensation can happen only if the conversion time between the upper polariton and lower polariton is longer than or comparable to the lifetime of the polaritons. In the case of long-lifetime polaritons, the upper polariton population can decay much faster to lower polariton states than the decay outside of the cavity. Because of this, almost all of the upper polaritons first convert to lower polaritons before escaping the cavity, making the upper polariton branch hard to detect, as seen in long-lifetime GaAs microcavity experiments.52

At a very high pumping power, our model predicts a second transition from UP condensation to LP condensation. As the density of the polaritons increases, stimulated scattering from the UPB to the LPB becomes significantly enhanced. This in turn leads to a sudden “collapse” of the upper polariton particles to the lower polariton branch leading to LP condensation with a very large occupation at k = 0 (see Figure 3f). The threshold for such a transition is predicted to occur at a much higher power than we can observe experimentally. Another challenge is that at such a high power runaway heating might kick in first, making the observation of this transition difficult.

In this work, we demonstrated the nonequilibrium Bose condensation of polaritons in a transferable WS2 monolayer microcavity. The upper polariton gas exhibits quasi-thermal behavior at a high density and a well-defined temperature at a low density. Using Michelson interferometry, we observed extended coherence in k-space, with a coherence of 138 fs at 2 times the threshold. Our models, based on the semiclassical Boltzmann equation and population dynamics equations, provide insights into the conditions required for upper polariton condensation. The short lifetime and excitonic fraction of the upper polariton are crucial factors in observing this effect. Our work contributes to the understanding of condensation competition in open-dissipative quantum systems and its implications for practical laser technologies.

Acknowledgments

The work was supported by the National Key Research and Development Program of China (2021YFA1200803), the National Natural Science Foundation of China (12174111, 12227807 and 12174112), the Shanghai Pujiang Program (21PJ1403000), the Shanghai Sailing Program (20YF1411600) and the Natural Science Foundation of Shanghai (No. (23ZR1419800). D.S. and H.A. and J.B. and Q.W. acknowledge support from the U.S. National Science Foundation (DMR-2004570) and MURI (W911NF-17-1-0312), respectively.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.3c03123.

  • Standard procedure for making a transferable microcavity (section 1), angle-resolved reflectivity spectra for the samples (section 2), power-dependent PL spectra in real space (section 3), polarization properties of the upper polariton (section 4), temporal coherence setup (section 5), and numerical method (section 6 )(PDF)

Author Contributions

X.C. and H.A. contributed equally to this work. Z.S., D.S., and J.W. supervised the project. X.C., D.M., Y.F., and Z.S. fabricated the full samples and performed the optical measurements. H.A., M.X., Z.-Y.S., and D.S. performed the theoretical modeling. All of the authors contributed to the discussion of the results and writing of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

nl3c03123_si_001.pdf (1.2MB, pdf)

References

  1. Balili R.; Hartwell V.; Snoke D.; Pfeiffer L.; West K. Bose–Einstein condensation of microcavity polaritons in a trap. Science 2007, 316, 1007–1010. 10.1126/science.1140990. [DOI] [PubMed] [Google Scholar]
  2. Kasprzak J.; Richard M.; Kundermann S.; Baas A.; Jeambrun P.; Keeling J. M. J.; Marchetti F.; Szymańska M.; André R.; Staehli J.; et al. Bose–Einstein condensation of exciton polaritons. Nature 2006, 443, 409–414. 10.1038/nature05131. [DOI] [PubMed] [Google Scholar]
  3. Kim N. Y.; Kusudo K.; Wu C.; Masumoto N.; Löffler A.; Höfling S.; Kumada N.; Worschech L.; Forchel A.; Yamamoto Y. Dynamical d-wave condensation of exciton–polaritons in a two-dimensional square-lattice potential. Nat. Phys. 2011, 7, 681–686. 10.1038/nphys2012. [DOI] [Google Scholar]
  4. Su R.; Diederichs C.; Wang J.; Liew T. C.; Zhao J.; Liu S.; Xu W.; Chen Z.; Xiong Q. Room-temperature polariton lasing in all-inorganic perovskite nanoplatelets. Nano Lett. 2017, 17, 3982–3988. 10.1021/acs.nanolett.7b01956. [DOI] [PubMed] [Google Scholar]
  5. Plumhof J. D.; Stöferle T.; Mai L.; Scherf U.; Mahrt R. F. Room-temperature Bose–Einstein condensation of cavity exciton–polaritons in a polymer. Nat. Mater. 2014, 13, 247–252. 10.1038/nmat3825. [DOI] [PubMed] [Google Scholar]
  6. Peter E.; Senellart P.; Martrou D.; Lemaître A.; Hours J.; Gérard J.; Bloch J. Exciton-photon strong-coupling regime for a single quantum dot embedded in a microcavity. Phys. Rev. Lett. 2005, 95, 067401. 10.1103/PhysRevLett.95.067401. [DOI] [PubMed] [Google Scholar]
  7. Chikkaraddy R.; De Nijs B.; Benz F.; Barrow S. J.; Scherman O. A.; Rosta E.; Demetriadou A.; Fox P.; Hess O.; Baumberg J. J. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 2016, 535, 127–130. 10.1038/nature17974. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Feng J.; Wang J.; Fieramosca A.; Bao R.; Zhao J.; Su R.; Peng Y.; Liew T. C.; Sanvitto D.; Xiong Q. All-optical switching based on interacting exciton polaritons in self-assembled perovskite microwires. Sci. Adv. 2021, 7, eabj6627 10.1126/sciadv.abj6627. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Amo A.; Liew T.; Adrados C.; Houdré R.; Giacobino E.; Kavokin A.; Bramati A. Exciton–polariton spin switches. Nat. Photonics 2010, 4, 361–366. 10.1038/nphoton.2010.79. [DOI] [Google Scholar]
  10. Sun Z.; Snoke D. Optical switching with organics. Nat. Photonics 2019, 13, 370–371. 10.1038/s41566-019-0445-z. [DOI] [Google Scholar]
  11. Luo S.; Liao L.; Zhang Z.; Wang J.; Shen X.; Chen Z. Classical spin chains mimicked by room-temperature polariton condensates. Physical Review Applied 2020, 13, 044052. 10.1103/PhysRevApplied.13.044052. [DOI] [Google Scholar]
  12. Boulier T.; Jacquet M. J.; Maître A.; Lerario G.; Claude F.; Pigeon S.; Glorieux Q.; Amo A.; Bloch J.; Bramati A.; et al. Microcavity polaritons for quantum simulation. Adv. Quantum Technol. 2020, 3, 2000052. 10.1002/qute.202000052. [DOI] [Google Scholar]
  13. Zhang L.; Xie W.; Wang J.; Poddubny A.; Lu J.; Wang Y.; Gu J.; Liu W.; Xu D.; Shen X.; et al. Weak lasing in one-dimensional polariton superlattices. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 1516–1519. 10.1073/pnas.1502666112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Schneider C.; Rahimi-Iman A.; Kim N. Y.; Fischer J.; Savenko I. G.; Amthor M.; Lermer M.; Wolf A.; Worschech L.; Kulakovskii V. D.; et al. An electrically pumped polariton laser. Nature 2013, 497, 348–352. 10.1038/nature12036. [DOI] [PubMed] [Google Scholar]
  15. Liew T.; Kavokin A.; Shelykh I. Optical circuits based on polariton neurons in semiconductor microcavities. Phys. Rev. Lett. 2008, 101, 016402. 10.1103/PhysRevLett.101.016402. [DOI] [PubMed] [Google Scholar]
  16. Liew T.; Kavokin A.; Ostatnickỳ T.; Kaliteevski M.; Shelykh I.; Abram R. Exciton-polariton integrated circuits. Phys. Rev. B 2010, 82, 033302. 10.1103/PhysRevB.82.033302. [DOI] [Google Scholar]
  17. Berloff N. G.; Silva M.; Kalinin K.; Askitopoulos A.; Töpfer J. D.; Cilibrizzi P.; Langbein W.; Lagoudakis P. G. Realizing the classical XY Hamiltonian in polariton simulators. Nat. Mater. 2017, 16, 1120–1126. 10.1038/nmat4971. [DOI] [PubMed] [Google Scholar]
  18. Ballarini D.; Gianfrate A.; Panico R.; Opala A.; Ghosh S.; Dominici L.; Ardizzone V.; De Giorgi M.; Lerario G.; Gigli G.; et al. Polaritonic neuromorphic computing outperforms linear classifiers. Nano Lett. 2020, 20, 3506–3512. 10.1021/acs.nanolett.0c00435. [DOI] [PubMed] [Google Scholar]
  19. Ballarini D.; De Giorgi M.; Cancellieri E.; Houdré R.; Giacobino E.; Cingolani R.; Bramati A.; Gigli G.; Sanvitto D. All-optical polariton transistor. Nat. Commun. 2013, 4, 1778. 10.1038/ncomms2734. [DOI] [PubMed] [Google Scholar]
  20. Zasedatelev A. V.; Baranikov A. V.; Urbonas D.; Scafirimuto F.; Scherf U.; Stöferle T.; Mahrt R. F.; Lagoudakis P. G. A room-temperature organic polariton transistor. Nat. Photonics 2019, 13, 378–383. 10.1038/s41566-019-0392-8. [DOI] [Google Scholar]
  21. Groenhof G.; Climent C.; Feist J.; Morozov D.; Toppari J. J. Tracking polariton relaxation with multiscale molecular dynamics simulations. J. Phys. Chem. Lett. 2019, 10, 5476–5483. 10.1021/acs.jpclett.9b02192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kavokin K.; Kaliteevski M.; Abram R.; Kavokin A.; Sharkova S.; Shelykh I. Stimulated emission of terahertz radiation by exciton-polariton lasers. Appl. Phys. Lett. 2010, 97, 201111. 10.1063/1.3519978. [DOI] [Google Scholar]
  23. Dasbach G.; Schwab M.; Bayer M.; Krizhanovskii D.; Forchel A. Tailoring the polariton dispersion by optical confinement: Access to a manifold of elastic polariton pair scattering channels. Phys. Rev. B 2002, 66, 201201. 10.1103/PhysRevB.66.201201. [DOI] [Google Scholar]
  24. Hanai R.; Edelman A.; Ohashi Y.; Littlewood P. B. Non-Hermitian phase transition from a polariton Bose–Einstein condensate to a photon laser. Phys. Rev. Lett. 2019, 122, 185301. 10.1103/PhysRevLett.122.185301. [DOI] [PubMed] [Google Scholar]
  25. Mak K. F.; Lee C.; Hone J.; Shan J.; Heinz T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 2010, 105, 136805. 10.1103/PhysRevLett.105.136805. [DOI] [PubMed] [Google Scholar]
  26. Splendiani A.; Sun L.; Zhang Y.; Li T.; Kim J.; Chim C.-Y.; Galli G.; Wang F. Emerging photoluminescence in monolayer MoS2. Nano Lett. 2010, 10, 1271–1275. 10.1021/nl903868w. [DOI] [PubMed] [Google Scholar]
  27. Wang G.; Chernikov A.; Glazov M. M.; Heinz T. F.; Marie X.; Amand T.; Urbaszek B. Colloquium: Excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 2018, 90, 021001. 10.1103/RevModPhys.90.021001. [DOI] [Google Scholar]
  28. Chernikov A.; Berkelbach T. C.; Hill H. M.; Rigosi A.; Li Y.; Aslan B.; Reichman D. R.; Hybertsen M. S.; Heinz T. F. Exciton binding energy and nonhydrogenic Rydberg series in monolayer WS2. Phys. Rev. Lett. 2014, 113, 076802. 10.1103/PhysRevLett.113.076802. [DOI] [PubMed] [Google Scholar]
  29. He K.; Kumar N.; Zhao L.; Wang Z.; Mak K. F.; Zhao H.; Shan J. Tightly bound excitons in monolayer WSe2. Phys. Rev. Lett. 2014, 113, 026803. 10.1103/PhysRevLett.113.026803. [DOI] [PubMed] [Google Scholar]
  30. Ye Z.; Cao T.; O’brien K.; Zhu H.; Yin X.; Wang Y.; Louie S. G.; Zhang X. Probing excitonic dark states in single-layer tungsten disulphide. Nature 2014, 513, 214–218. 10.1038/nature13734. [DOI] [PubMed] [Google Scholar]
  31. Zhang L.; Wu F.; Hou S.; Zhang Z.; Chou Y.-H.; Watanabe K.; Taniguchi T.; Forrest S. R.; Deng H. Van der Waals heterostructure polaritons with moiré-induced nonlinearity. Nature 2021, 591, 61–65. 10.1038/s41586-021-03228-5. [DOI] [PubMed] [Google Scholar]
  32. Shahnazaryan V.; Iorsh I.; Shelykh I. A.; Kyriienko O. Exciton-exciton interaction in transition-metal dichalcogenide monolayers. Phys. Rev. B 2017, 96, 115409. 10.1103/PhysRevB.96.115409. [DOI] [Google Scholar]
  33. Zhao J.; Fieramosca A.; Bao R.; Du W.; Dini K.; Su R.; Feng J.; Luo Y.; Sanvitto D.; Liew T. C.; et al. Nonlinear polariton parametric emission in an atomically thin semiconductor based microcavity. Nat. Nanotechnol. 2022, 17, 396–402. 10.1038/s41565-022-01073-9. [DOI] [PubMed] [Google Scholar]
  34. Susarla S.; Kutana A.; Hachtel J. A.; Kochat V.; Apte A.; Vajtai R.; Idrobo J. C.; Yakobson B. I.; Tiwary C. S.; Ajayan P. M. Quaternary 2D transition metal dichalcogenides (TMDs) with tunable bandgap. Adv. Mater. 2017, 29, 1702457. 10.1002/adma.201702457. [DOI] [PubMed] [Google Scholar]
  35. Sun Z.; Xu K.; Liu C.; Beaumariage J.; Liang J.; Fullerton-Shirey S. K.; Shi Z.-Y.; Wu J.; Snoke D. Photoluminescence Switching Effect in a Two-Dimensional Atomic Crystal. ACS Nano 2021, 15, 19439–19445. 10.1021/acsnano.1c06016. [DOI] [PubMed] [Google Scholar]
  36. Jones A. M.; Yu H.; Ghimire N. J.; Wu S.; Aivazian G.; Ross J. S.; Zhao B.; Yan J.; Mandrus D. G.; Xiao D.; et al. Optical generation of excitonic valley coherence in monolayer WSe2. Nat. Nanotechnol. 2013, 8, 634–638. 10.1038/nnano.2013.151. [DOI] [PubMed] [Google Scholar]
  37. Sun Z.; Beaumariage J.; Wan Q.; Alnatah H.; Hougland N.; Chisholm J.; Cao Q.; Watanabe K.; Taniguchi T.; Hunt B. M.; et al. Charged bosons made of fermions in bilayer structures with strong metallic screening. Nano Lett. 2021, 21, 7669–7675. 10.1021/acs.nanolett.1c02422. [DOI] [PubMed] [Google Scholar]
  38. Galfsky T.; Sun Z.; Considine C. R.; Chou C.-T.; Ko W.-C.; Lee Y.-H.; Narimanov E. E.; Menon V. M. Broadband enhancement of spontaneous emission in two-dimensional semiconductors using photonic hypercrystals. Nano Lett. 2016, 16, 4940–4945. 10.1021/acs.nanolett.6b01558. [DOI] [PubMed] [Google Scholar]
  39. Wu S.; Buckley S.; Jones A. M.; Ross J. S.; Ghimire N. J.; Yan J.; Mandrus D. G.; Yao W.; Hatami F.; Vučković J.; et al. Control of two-dimensional excitonic light emission via photonic crystal. 2D Materials 2014, 1, 011001. 10.1088/2053-1583/1/1/011001. [DOI] [Google Scholar]
  40. Gan X.; Gao Y.; Fai Mak K.; Yao X.; Shiue R.-J.; Van Der Zande A.; Trusheim M. E.; Hatami F.; Heinz T. F.; Hone J.; et al. Controlling the spontaneous emission rate of monolayer MoS2 in a photonic crystal nanocavity. Appl. Phys. Lett. 2013, 103, 181119. 10.1063/1.4826679. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Liu X.; Galfsky T.; Sun Z.; Xia F.; Lin E.-c.; Lee Y.-H.; Kéna-Cohen S.; Menon V. M. Strong light–matter coupling in two-dimensional atomic crystals. Nat. Photonics 2015, 9, 30–34. 10.1038/nphoton.2014.304. [DOI] [Google Scholar]
  42. Lundt N.; Klembt S.; Cherotchenko E.; Betzold S.; Iff O.; Nalitov A. V.; Klaas M.; Dietrich C. P.; Kavokin A. V.; Höfling S.; et al. Room-temperature Tamm-plasmon exciton-polaritons with a WSe2 monolayer. Nat. Commun. 2016, 7, 13328. 10.1038/ncomms13328. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Sun Z.; Gu J.; Ghazaryan A.; Shotan Z.; Considine C. R.; Dollar M.; Chakraborty B.; Liu X.; Ghaemi P.; Kéna-Cohen S.; et al. Optical control of room-temperature valley polaritons. Nat. Photonics 2017, 11, 491–496. 10.1038/nphoton.2017.121. [DOI] [Google Scholar]
  44. Chakraborty B.; Gu J.; Sun Z.; Khatoniar M.; Bushati R.; Boehmke A. L.; Koots R.; Menon V. M. Control of strong light–matter interaction in monolayer WS2 through electric field gating. Nano Lett. 2018, 18, 6455–6460. 10.1021/acs.nanolett.8b02932. [DOI] [PubMed] [Google Scholar]
  45. Zhao J.; Su R.; Fieramosca A.; Zhao W.; Du W.; Liu X.; Diederichs C.; Sanvitto D.; Liew T. C.; Xiong Q. Ultralow threshold polariton condensate in a monolayer semiconductor microcavity at room temperature. Nano Lett. 2021, 21, 3331–3339. 10.1021/acs.nanolett.1c01162. [DOI] [PubMed] [Google Scholar]
  46. Anton-Solanas C.; Waldherr M.; Klaas M.; Suchomel H.; Harder T. H.; Cai H.; Sedov E.; Klembt S.; Kavokin A. V.; Tongay S.; et al. Bosonic condensation of exciton–polaritons in an atomically thin crystal. Nat. Mater. 2021, 20, 1233–1239. 10.1038/s41563-021-01000-8. [DOI] [PubMed] [Google Scholar]
  47. Rupprecht C.; Lundt N.; Wurdack M.; Stepanov P.; Estrecho E.; Richard M.; Ostrovskaya E. A.; Höfling S.; Schneider C. Micro-mechanical assembly and characterization of high-quality Fabry–Pérot microcavities for the integration of two-dimensional materials. Appl. Phys. Lett. 2021, 118, 103103. 10.1063/5.0034851. [DOI] [Google Scholar]
  48. Paik E. Y.; Zhang L.; Hou S.; Zhao H.; Chou Y.-H.; Forrest S. R.; Deng H. High Quality Factor Microcavity for Van der Waals Semiconductor Polaritons Using a Transferrable Mirror. Adv. Opt. Mater. 2023, 11, 2201440. 10.1002/adom.202201440. [DOI] [Google Scholar]
  49. Wang Y.; Cong C.; Yang W.; Shang J.; Peimyoo N.; Chen Y.; Kang J.; Wang J.; Huang W.; Yu T. Strain-induced direct–indirect bandgap transition and phonon modulation in monolayer WS 2. Nano Research 2015, 8, 2562–2572. 10.1007/s12274-015-0762-6. [DOI] [Google Scholar]
  50. Sun Z.; Beaumariage J.; Movva H. C.; Chowdhury S.; Roy A.; Banerjee S. K.; Snoke D. W. Stress-induced bandgap renormalization in atomic crystals. Solid State Commun. 2019, 288, 18–21. 10.1016/j.ssc.2018.11.006. [DOI] [Google Scholar]
  51. Zhao J.; Fieramosca A.; Dini K.; Bao R.; Du W.; Su R.; Luo Y.; Zhao W.; Sanvitto D.; Liew T. C.; et al. Exciton polariton interactions in Van der Waals superlattices at room temperature. Nat. Commun. 2023, 14, 1512. 10.1038/s41467-023-36912-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Sun Y.; Wen P.; Yoon Y.; Liu G.; Steger M.; Pfeiffer L. N.; West K.; Snoke D. W.; Nelson K. A. Bose–Einstein condensation of long-lifetime polaritons in thermal equilibrium. Phys. Rev. Lett. 2017, 118, 016602. 10.1103/PhysRevLett.118.016602. [DOI] [PubMed] [Google Scholar]
  53. Kasprzak J.; Solnyshkov D.; André R.; Dang L. S.; Malpuech G. Formation of an exciton polariton condensate: thermodynamic versus kinetic regimes. Phys. Rev. Lett. 2008, 101, 146404. 10.1103/PhysRevLett.101.146404. [DOI] [PubMed] [Google Scholar]
  54. Rajendran S. K.; Wei M.; Ohadi H.; Ruseckas A.; Turnbull G. A.; Samuel I. D. Low threshold polariton lasing from a solution-processed organic semiconductor in a planar microcavity. Adv. Opt. Mater. 2019, 7, 1801791. 10.1002/adom.201801791. [DOI] [Google Scholar]
  55. Hoshi Y.; Kuroda T.; Okada M.; Moriya R.; Masubuchi S.; Watanabe K.; Taniguchi T.; Kitaura R.; Machida T. Suppression of exciton-exciton annihilation in tungsten disulfide monolayers encapsulated by hexagonal boron nitrides. Phys. Rev. B 2017, 95, 241403. 10.1103/PhysRevB.95.241403. [DOI] [Google Scholar]
  56. Hartwell V.; Snoke D. Numerical simulations of the polariton kinetic energy distribution in GaAs quantum-well microcavity structures. Phys. Rev. B 2010, 82, 075307. 10.1103/PhysRevB.82.075307. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl3c03123_si_001.pdf (1.2MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES