Delineating the Specific Influence of Virus Isoelectric Point and Size on Virus Adsorption and Transport through Sandy Soils

Abstract

Many of the factors controlling viral transport and survival within the subsurface are still poorly understood. In order to identify the precise influence of viral isoelectric point on viral adsorption onto aquifer sediment material, we employed five different spherical bacteriophages (MS2, PRD1, Qβ, φX174, and PM2) having differing isoelectric points (pI 3.9, 4.2, 5.3, 6.6, and 7.3 respectively) in laboratory viral transport studies. We employed conventional batch flowthrough columns, as well as a novel continuously recirculating column, in these studies. In a 0.78-m batch flowthrough column, the smaller phages (MS2, φX174, and Qβ), which had similar diameters, exhibited maximum effluent concentration/initial concentration values that correlated exactly with their isoelectric points. In the continuously recirculating column, viral adsorption was negatively correlated with the isoelectric points of the viruses. A model of virus migration in the soil columns was created by using a one-dimensional transport model in which kinetic sorption was used. The data suggest that the isoelectric point of a virus is the predetermining factor controlling viral adsorption within aquifers. The data also suggest that when virus particles are more than 60 nm in diameter, viral dimensions become the overriding factor.

Numerous urban centers in the United States and around the world rely on groundwater as their only source of drinking water. Every year, almost one-half of the disease outbreaks in the United States can be attributed to contaminated groundwater (7). Wastewater effluents, sewage sludges, and leaking septic tanks have commonly been identified as the sources of bacterial and viral pathogens in contaminated groundwater. The primary factors relied on to prevent contamination of drinking water wells with viral pathogens from contaminating septic sources include natural viral inactivation within aquifers and viral adsorption to soil particles (10, 11, 19, 20, 27).

Virus survival within aquifers has been shown to be highly site specific and virus specific (8, 12, 14, 17, 29). The physical nature and chemical nature of aquifers have also been shown to influence viral adsorption (9, 13). Sobsey et al. (25) studied various soil materials to determine their ability to remove and retain viruses that were introduced via sewage effluent. These authors concluded that clayey materials having different pHs and organic contents efficiently adsorbed the viruses, especially at low pHs. They also reported that sandy soils were poor adsorbers except under intermittent unsaturated conditions. However, Sobsey et al. reported that even under unsaturated conditions the viruses could still be washed from sandy soils under rainfall conditions. Other investigators (14, 15) have placed viruses into two broad groups, groups I and II. Group I includes the phages and viruses which have been found to be influenced by soil factors, such as pH, organic matter, and exchangeable iron, while group II includes the viruses which are not influenced by any specific soil factor. Although there have been a number of studies which have correlated an aquifer’s physicochemical characteristics with viral survival, adsorption, and transport within aquifers, unfortunately many of the factors controlling viral transport are still poorly understood (16, 24).

The primary objective of this study was to identify the role(s) of specific virus characteristics, such as isoelectric point and dimensions, on the adsorption and transport of viruses in sandy soils. To do this, we employed five different bacteriophages (differing in size and isoelectric point) in conventional laboratory batch (flowthrough) columns and in a novel recirculating column. Our underlying hypothesis was that the viral isoelectric point is a critical parameter which influences viral transport in the subsurface. The null hypothesis was that no virus-associated factor or characteristic would correlate with viral transport.

MATERIALS AND METHODS

Bacteriophages.

Five bacteriophages having various sizes and various isoelectric points were employed in this study (Table 1). Two of these phages (MS2 and φX174) have been reported to belong to group I as described by Gerba and Goyal (14). These different phages (phages having different isoelectric points and dimensions) were chosen in order to observe their adsorption and transport under uniform saturated soil conditions. The appropriate host bacteria were used to enumerate the phages. The double agar overlay procedure was used to prepare high-titer lysates (2).

TABLE 1.

Physicochemical characteristics of the spherical bacteriophages used in this study

Bacterio- phage	Isoelectric pointa	Diam (nm)	Lipid content (%)	Host bacterium
MS2	3.9	24	0	Escherichia coli ATCC 15597
PRD1	4.2	63	16	Salmonella typhimurium LT-2
Qβ	5.3	24	0	Escherichia coli ATCC 17853
φX174	6.6	27	0	Escherichia coli ATCC 13706
PM2	7.3	60	13	Alteromonas espejia ATCC 2725

^apH at which the virus particle shows a net neutral charge (1). 

Aquifer material.

Sediment and groundwater were obtained from a previously well-studied sandy aquifer (95% sand, 7% silt, 2% clay) underlying the Brazos Alluvium (Burleson County, Tex.) (21, 28). The aquifer sediment had a pH of 7.1.

Column studies.

The following two types of columns were employed in this study: conventional batch (flowthrough) columns and a novel continuously recirculating column.

(i) Batch columns.

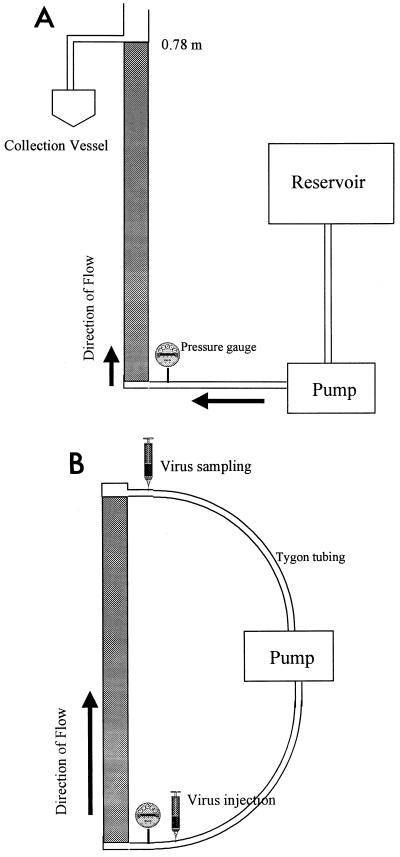
The batch columns were constructed by using clear rigid polyvinyl chloride tubing that was 0.05 m in diameter and 0.76 m long (Fig. 1A). Each column was sanded around the inner surface 90° to the flow path to prevent preferential flow along the walls of the column and was packed with aquifer sediment in 0.05-m increments. The sediment material was stirred and tapped with a rubber mallet to remove possible channels and to create a homogeneous soil matrix throughout the column. A peristaltic pump (Spenser Veristaltic pump; Manostat Corp., Barrington, Ill.) was used to create saturated conditions within the column. Saturated conditions were achieved by pumping 3 pore volumes of groundwater up through the bottom of the vertically oriented column, which forced gases trapped in pore spaces out and replaced them with groundwater. We did not attempt to pump carbon dioxide through the column to displace the oxygen (23) since we felt that this procedure might acidify the column. The transparency of the polyvinyl chloride permitted us to visually confirm that major preferential flow paths were not occurring and that the soil column appeared to be completely saturated.

FIG. 1.

Schematic diagram of the batch flowthrough column used in the viral batch transport studies. (B) Schematic diagram of the continuous column used in the viral transport studies.

Once the column was completely saturated, Tygon tubing was used to pump 2.1 pore volumes of virus-seeded groundwater (from a separate reservoir) into the column. Up to 10 pore volumes of virus-free groundwater was added after the viruses were introduced. Due to logistical considerations, MS2 and PRD1 were introduced together, while the other phages were introduced separately. The effluent was sampled as soon as the viruses were introduced into the columns. Multiple samples were also taken from the virus injectate to determine the injected or initial virus concentration (C₀).

Effluent samples (calibrated as pore volumes or fractions of pore volumes) were collected from the columns for phage enumeration. Samples were collected in sterilized flasks, and one 1-ml aliquot for every 50 ml of effluent sample was plated for phage analysis (e.g., if 200 ml of effluent sample was collected, then four 1-ml aliquots were used for the phage analysis). The detection limits of the assay were 0.1 PFU/ml for the first 2 pore volumes and 1.0 PFU/ml for subsequent samples.

(ii) Continuously recirculating column.

The continuously recirculating column was used to simulate an aquifer in a laboratory setting so that we could monitor the movement of virus particles over time and space. To our knowledge, this type of column approach for studying virus transport is novel. The recirculating column was designed to replace the conventional shaking microcosms that are normally used to study virus adsorption in the laboratory. Unlike batch columns, which can be used to study movement over a discrete distance only, a continuous column can be used to study movement over very long distances and over longer periods of time. The recirculating column adsorption studies were performed by using the basic column design described above, but the column was modified to make it recirculating (Fig. 1B). Clinical intravenous tube connections (Continu-flo; Travenol Laboratories, Inc., Deerfield, Ill.) were used to create ports at the top and bottom of the column; the needle ports were inserted into the peristaltic pump line, which created an injection port at the bottom of the column and a sampling port at the top. The column was saturated by passing 3 pore volumes through the system, after which the circuit was closed and the column was allowed to stabilize until it maintained a constant pressure (7.5 lb/in²) at the injection port. Virus particles (diluted in groundwater) were then injected by using a syringe and a 20-gauge needle. As in the batch column experiments, most of the phages were introduced separately; the exceptions were MS2 and PRD1, which were introduced together. Samples were obtained by injecting 1 ml of inoculum into the sampling port (to maintain constant groundwater volume within the column), waiting for several seconds, and then withdrawing a 1-ml aliquot. Samples for analysis were obtained 2.5, 5, 10, 20, 40, 60, 120, and 240 min after injection.

Statistical analysis.

A statistical analysis was performed by using Sigmastat software (Jandel Corporation, San Rafael, Calif.). (The applicability of this analysis was verified by using the software’s Wizard function.) The maximum viral adsorption percentage was calculated by dividing the C₀ in the supernatant in the system at time zero (prior to adsorption) by the resultant (effluent) virus concentration (C) in the supernatant after 2 h. A Spearman rank order correlation analysis was used to determine the viral characteristics which correlated to the maximum adsorption characteristics. The Spearman rank order correlation analysis was used to measure the strength of association between pairs of variables without specifying which variable was dependent or independent. A Pearson product moment correlation analysis was used to determine the association between the isoelectric points of the phages and experimental data. The Pearson product moment correlation analysis was used to measure the strength of association between pairs of variables without regard to which was dependent or independent.

Mathematical modeling.

The virus migration in the soil columns was described by using two separate one-dimensional mathematical models which took into account factors such as advection, diffusion, dispersion, adsorption, and decay. Modeling of microbial transport in saturated porous medium has been described by Corapcioglu and Haridas (5, 6). In this study, two models which represent bacteriophage sorption as equilibrium and as a kinetic sorption process were used.

Model A was developed with one-dimensional mass balance equations for bacteriophages exhibiting advective-dispersive transport, kinetic sorption, and first-order decay in a saturated medium. The governing equations used for model A are:

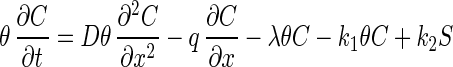1

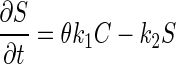2

where C is the mass concentration of bacteriophage in the aqueous phase (in PFU per liter), D is the hydrodynamic dispersion coefficient (in [units of length]² per unit of time), θ is the porosity, q is the specific discharge of water (in units of length per unit of time), λ is the decay rate (expressed as 1/unit of time), k₁ is the rate coefficient for bacteriophage capture to the solid matrix (expressed as 1/unit of time), k₂ is the rate coefficient for bacteriophage release from the solid matrix (expressed as 1/unit of time), S is the mass concentration of captured bacteriophage in the solid phase (in units of mass per unit of length³), t is time, and x is the distance from the source (in units of length). In the case of the 0.78-m column, the decay rate was neglected because of the relatively short travel time (11.3 min). Therefore, in model A, parameters k₁ and k₂ were determined by fitting the model results to the experimental data, and these optimized values were used in the analysis.

Numerical solutions to the bacteriophage mass balance equations were obtained by using a fully implicit finite difference method. This one-dimensional numerical solution was limited in application to simple geometry and to homogeneous media. Basic hydrogeologic parameters like dispersivity were obtained by applying the curve-fitting method to the experimental data for φX174, which had the highest C/C₀ value. The optimized value for dispersivity obtained by this method was 9.94 cm. The parameters used for model A are as follows: pore velocity, 0.176 cm/s; porosity, 0.3; column length, 0.78 m; injection duration, 824 s; decay rate, 0; hydrodynamic dispersion coefficient, 1.75 cm²/s.

Model B was used for one-dimensional advective-dispersive transport with a linear adsorption isotherm and first-order decay in saturated flow. The governing equation is

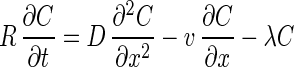3

and its analytical solution as described by van Genuchten and Alves (26) is

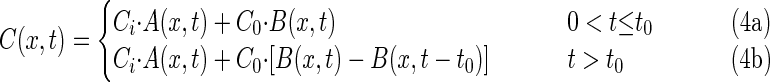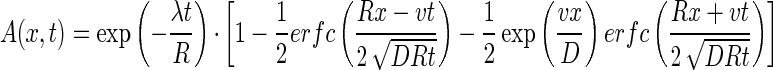5

where

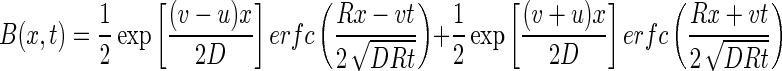6

and

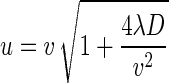7

where C₀ is the bacteriophage source concentration (in PFU per liter), C_i is the background bacteriophage concentration (in PFU per liter), erfc is the complementary error function, R is the retardation factor, t is the time (in seconds), and v is the pore velocity (in units of length per unit of time).

Model B was also fitted to the experimental data in order to provide simulation data. The parameters used for model A were also used for model B with the exception of rate coefficients k₁ and k₂. In model B, the retardation factor was used instead of the k₁ and k₂ parameters used in model A for each bacteriophage based on the best fit of the simulation to the column experimental data. The retardation factor is expressed as

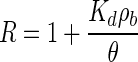8

where K_d is the partition coefficient of the virus and ρ_b is the bulk density of the soil.

RESULTS AND DISCUSSION

Batch columns. (i) MS2 transport.

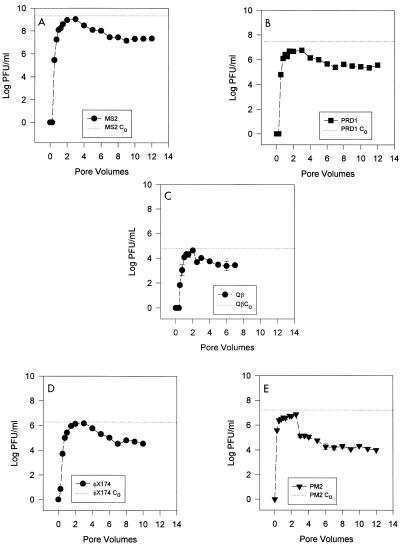
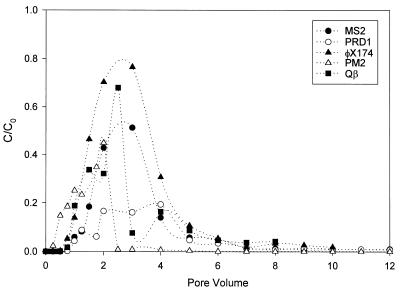
Two pore volumes (i.e., 1,052 ml) of groundwater containing 2.1 × 10⁹ PFU/ml was introduced into the batch column. The phage initially appeared after 0.5 pore volume had been introduced (Fig. 2A). A total of 1.23 × 10¹² PFU was recovered from 12 pore volumes; this value is 54% of the total amount of MS2 virus that was introduced (2.25 × 10¹² PFU). After the initial feed solution was switched to virus-free groundwater, there was a substantial increase in viral release for 1 pore volume, after which the concentration declined. The maximum C/C₀ was 0.50 at 3 pore volumes, after which the virus concentration slowly decreased through the 12th pore volume.

FIG. 2.

Breakthrough curves for bacteriophages in the flowthrough column. (A) MS2. (B) PRD1. (C) Qβ. (D) φX174. (E) PM2.

(ii) PRD1 transport.

A total of 3.09 × 10¹⁰ PFU of PRD1 was introduced into the column. More than 69% of the virus remained in the column after 12 pore volumes. The first breakthrough of PRD1 occurred after 0.5 pore volume, and the phage titer steadily increased until the virus-free groundwater flow was begun (Fig. 2B). As with MS2, the PRD1 virus level reached a peak after the beginning of the virus-free flow and then steadily declined through the 12th pore volume. The maximum C/C₀ at 3 pore volumes was 0.19.

(iii) Qβ transport.

A total of 6.69 × 10⁷ PFU of Qβ was introduced into the column, and the C₀ was 6.36 × 10⁴ PFU/ml (Fig. 2C). A total of 3.11 × 10⁷ PFU was recovered over 8 pore volumes, indicating that 3.6 × 10⁷ PFU of Qβ (53% of the viruses introduced) remained in the soil column. The first breakthrough of Qβ occurred within the first 0.5 pore volume, after which the concentration climbed quickly, reaching a peak value at 2.5 pore volumes, which corresponded to a C/C₀ of 0.68. After this peak, the concentration of the virus particles (in the effluent) declined rapidly over the next 6 pore volumes. The breakthrough characteristic of this virus was similar to that exhibited by MS2, φX174, and PRD1. The maximum C/C₀ was high compared to the C/C₀ values of MS2 and PRD1 in this column, although it was lower than the C/C₀ of ΦX174.

(iv) φX174 transport.

A total of 2.02 × 10⁹ PFU was introduced into the column, and the C₀ was 1.92 × 10⁶ PFU/ml. A total of 1.98 × 10⁹ PFU was recovered over 10 pore volumes (Fig. 2D), suggesting that 5.0 × 10⁷ PFU of φX174 (2.5% of the virus introduced) remained in the soil column. The first breakthrough of φX174 occurred within the first 0.25 pore volume, after which the concentration climbed quickly and reached a peak value at 3 pore volumes, which corresponded to a C/C₀ of 0.834. After this peak, the concentration of the virus particles in the effluent declined rapidly over the next 7 pore volumes. The overall curve and breakthrough characteristics are similar to those exhibited by MS2 and PRD1. The maximum C/C₀ was much higher than the C/C₀ values of MS2 and PRD1 in this column.

(v) PM2 transport.

A total of 1.72 × 10¹⁰ PFU of PM2 was introduced into the column, and the C₀ was 1.64 × 10⁷ PFU/ml. A total of 5.26 × 10⁹ PFU (Fig. 2E) was recovered over 12 pore volumes, which left 1.19 × 10¹⁰ PFU of PM2 (30.6% of the virus introduced) in the soil column. The first breakthrough of PM2 occurred within the first 0.25 pore volume, after which the concentration climbed quickly and reached a peak value at 2 pore volumes, which corresponded to a C/C₀ of 0.44. After this peak, the concentration of the virus particles (in the effluent) dropped drastically (2 logs) within the next 0.5 pore volume. After this drop, which corresponded to the addition of virus-free influent, the concentration in the effluent declined slowly over the next 10 pore volumes.

Continuously recirculating column studies.

The recirculating column was essentially a closed reactor which simulated transport and adsorption of phage through a soil matrix over time. We felt that this column provided a more realistic scenario of adsorption kinetics than the batch flowthrough columns used in conventional studies.

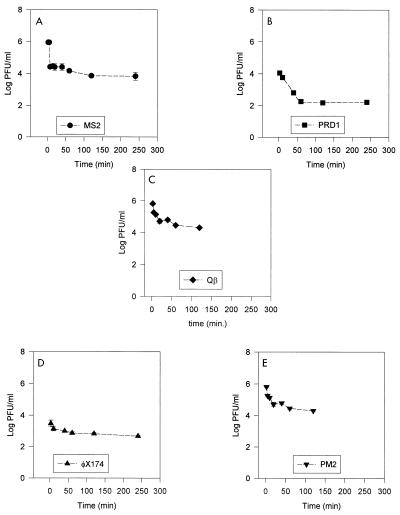
Based on preliminary studies, we found that 2 h of recirculation was sufficient for maximal adsorption to take place in the recirculating columns, while decay due to viral inactivation was limited (data not shown). At the end of 2 h, MS2 showed 99.4% adsorption, PRD1 showed 99% adsorption, Qβ showed 97% adsorption, φX174 showed 85% adsorption, and PM2 showed 80% adsorption. Plots of viral adsorption over time in the continuous columns are shown in Fig. 3. A Spearman rank order correlation analysis was used to determine if a specific viral characteristic, such as isoelectric point, molecular weight, buoyant density, or diameter, correlated with maximum level of adsorption. The only significant relationship that was found was the relationship between the level of adsorption and the isoelectric point of the phage. The correlation analysis showed that as the isoelectric point increased, adsorption decreased (r = −0.9, with 92% confidence) (data not shown). The results of flask adsorption studies also indicated that the degree of adsorption was negatively correlated with the isoelectric point of the viruses (r = −0.9, with 82% confidence) (data not shown).

FIG. 3.

Adsorption of bacteriophages in the continuous column. (A) MS2. (B) PRD1. (C) Qβ. (D) φX174. (E) PM2.

A Pearson product moment correlation analysis was performed to determine the correlation between the maximum flowthrough concentrations (C/C₀ values) of the smaller phages, MS2, Qβ, and φX174, and their isoelectric points. There was an exact correlation, with a coefficient of 1.0 at a 99.7% confidence level. This suggests that as the isoelectric point of the phage increases, the maximum C/C₀ also increases. The larger phages also exhibited the same type of effect in relation to their isoelectric points. Phage PM2, which had the highest pI, had a much higher C/C₀ than PRD1. When the larger phages were included in the analysis with the smaller phages, however, the correlation coefficient decreased (r < 0.7). This could be related to the lipid contents of the two larger phages (PRD1 and PM2) compared to the lipid contents of the other phages, which were devoid of any lipids (Table 1). This suggests that the larger phages have transport characteristics which are influenced by factors other than their isoelectric points.

Simulation results.

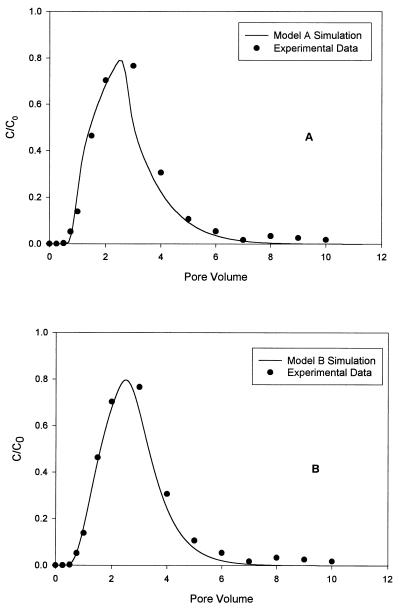
The experimental column data confirmed that the transport of bacteriophages was retarded by the sorption process. The sorption process characteristics for the phages used in this study were modeled by using one-dimensional transport model A, in which first-order kinetic sorption is used. The results of a statistical analysis in which we used a least-squares method to determine the capture rate coefficient (k₁) and the release rate coefficient (k₂) are given in Table 2, and the simulation results for φX174 are presented in Fig. 4. This figure shows the simulation results obtained when the kinetic (model A) and equilibrium (model B) results were used. The model parameters were obtained by curve fitting the model results to experimental data for φX174. MS2 and Qβ had similar rate coefficients for capture and release. The capture rates of the three smaller phages are consistent with the adsorption data, as well as the normalized transport data. The capture rate for PRD1 is much higher than the capture rates for the other phages, and the PRD1 release rate coefficient is much lower; these data are not consistent with the adsorption data but are related to the normalized transport curves. Phage PM2 (which has the highest isoelectric point) has the lowest capture rate coefficient, as well as the lowest release rate. This is consistent with the adsorption data (Fig. 3E) but, surprisingly, is not consistent with the normalized transport data (Fig. 5). The normalized experimental data in Fig. 5 show the retardation effects on transport due to sorption of phages to solids. When the experimental data were analyzed, the removal of phage due to decay and filtration was considered negligible because the duration of the experiment was short and because the phage size was relatively small (<100 nm). Therefore, the only property which could account for the differences in the breakthrough curves for the phages was the sorption process. The normalized data in Fig. 5 show the effects of phage sorption onto solids. The sorption properties of each phage can be characterized by the normalized peak time and the concentration. Model B is a one-dimensional transport model which uses equilibrium sorption along with retardation factors to fit the data set obtained by a least-squares treatment method. The retardation factor for each bacteriophage obtained with model B is shown in Table 2. PRD1 had the highest retardation factor, which conformed to the normalized transport curve (Fig. 5). The data for φX174 and Qβ, which had very similar retardation factors, were not consistent with the adsorption or transport data. The behavior of phage PM2, which had the lowest retardation factor, was consistent with the adsorption data but not the transport data. It is evident that low levels of viruses were present in the effluent for extended periods of time, suggesting that under natural conditions, low levels of virus particles may be present in pore waters (as a result of desorption) even after a particular point source of contamination ceases to exist.

TABLE 2.

Retardation factors and rate coefficients for virus capture and release

Phage	Model A		Model B retardation factor
	k1 (s−1)	k2 (s−1)
MS2	0.0053	0.0011	2.32
PRD1	0.0068	0.0004	2.70
Qβ	0.0054	0.0012	1.72
φX174	0.0029	0.0015	1.79
PM2	0.0024	0.0002	1.43

FIG. 4.

Comparison of 0.78-m column data for φX174 with simulation results obtained by using model A (A) and model B (B).

FIG. 5.

Normalized transport data for the five bacteriophages obtained by using the 0.78-m column.

The Brazos Alluvium aquifer material that was used in these studies had pH values that ranged between 6.9 and 7.1 (21, 28). This suggests that a virus particle’s net negative charge on its surface increases as its isoelectric point decreases from the ambient pH. This suggests that when a soil matrix which is essentially negatively charged is considered (22), some type of charge repulsion occurs between virus particles and soil particle surfaces. Thus, theoretically, bacteriophage MS2, which has an isoelectric point of 3.9, should be ionically repulsed from soil surfaces and exhibit less adsorption than viruses with higher pIs. The model described by Bohn et al. (3) could explain the apparent discrepancy between the theoretical predictions and the observed experimental data. This model describes how a negatively charged soil particle interacts with the chemical makeup of its surrounding liquid phase under saturated conditions. According to this model, there are two layers of cations associated with negatively charged soil particles; these layers are called the Stern double layer. The layer closest to the soil particles is a rigid layer of associated cations, and the layer next to this is a diffuse region of cations. These cation layers neutralize the negative charge of the soil mineral and in turn create a cation excess in a diffuse layer which attracts anions (such as virus particles) closer to the soil particles, where ion exchange with subsequent reversible and irreversible adsorption can theoretically occur (18).

When phage size is considered, it is tempting to hypothesize that some sort of straining occurs with the larger phages, such as PRD1 and PM2. PM2, which has the highest isoelectric point of the phages examined (pI 7.2), should be relatively unreactive with the soil (pH 7.1), yet it has a lower C/C₀ than the smaller phage φX174, which has a lower pI (pI 6.2). Considering that the pore spaces in the soil matrix are many times larger than the virus particles, straining should be negligible theoretically. The primary type of adsorption which occurs in the soil matrix has been described as adsorption due to London (van der Waals) forces (4). These forces or dipole interactions operate only over very short distances. The energy of this interaction varies by a factor of 1/r⁶, so that doubling the distance between particles decreases the energy by a factor of 2⁶ (3). Thus, the interacting particles (virus and soil) must be in close proximity in order for the forces to have any effect. It thus follows that the probability of a virus particle coming under the influence of these forces should increase with an increase in the surface area of the particle. This increase in reactivity is not related to an increase in charge strength but instead is related to an increase in the overall number of charges available for interaction. Thus, the chance of adsorption may increase with an increase in the diameter of the phage due to an increase in the number of surface charges available, especially when a larger virus particle is compared to a smaller virus particle. Thus, the viral isoelectric point should still have influence by increasing the strength of the charges. This is illustrated by the behavior of phages PM2 and PRD1, which have approximately the same dimensions but have different isoelectric points. PM2 has a higher C/C₀ and lower level of adsorption than PRD1. The effect of the isoelectric point can also be seen in the release rates (k₂) of the three smaller phages (MS2, Qβ, and φX174). As the pI increases, the k₂ increases, indicating that the adsorption which takes place is easily reversed. We acknowledge that the differences observed in the adsorption of the bacteriophages could be directly related to the underlying taxonomic differences among the phages (Table 1). Gerba and Goyal (14) reported previously that there are adsorption differences between strains of the same virus. However, a direct influence of pI on virus adsorption is seen when the release rate coefficients of MS2 and Qβ (belonging to the same family, the Leviviridae) are compared. MS2, which has a lower isoelectric point, has a lower release rate coefficient than Qβ, which has an isoelectric point closer to neutrality (Table 2).

Size is a significant factor and does have an obvious effect, as shown by the extremely low release rate coefficients of the two larger phages (PRD1 and PM2) compared to the smaller phages. The low release rate coefficients indicate that once adsorption of the larger virus particles occurs, there is a strong binding effect. The capture rates tended to agree with the adsorption data, both in the continuously recirculating column adsorption studies and in the flask adsorption studies. The model A results add strength to the hypothesis that isoelectric point and virus size are the major factors which influence both the capture rates and the release rates of the phages. Model B provides retardation factors for the viruses which are related to adsorption. One of the larger phages, PRD1, shows the greatest retardation, followed by MS2, which has the lowest pI, and by φX174, Qβ, and finally PM2, which shows the least retardation and which has the highest pI. It is thus obvious that different viruses display a wide variety of adsorptive characteristics. In continuously recirculating columns the adsorption of phage decreases with an increase in the pI. This effect is evident in batch transport columns when the maximum C/C₀ values of phages having the same relative size are considered. However, a size exclusion phenomenon was evident when the two larger phages were considered. PRD1 and PM2 showed increased retardation in their breakthrough curves when we compared their pIs, sizes, and maximum C/C₀ values with those of the smaller phages. The differences in the isoelectric points of viruses can be attributed to differences in the physicochemical properties of the viruses, which are important criteria in virus classification. However, our data also suggest that viral dimensions can become an overriding factor, especially when the virus particles are more than 60 nm in diameter.

Thus, this study sheds some new light on the role of a specific virus property (isoelectric point) on the control of virus adsorption to soil. Our results may help in the development of better numerical models to predict enteric virus transport in the subsurface or could be used in the development of methods (based on desorption) to selectively concentrate specific viruses from sediments.