Abstract
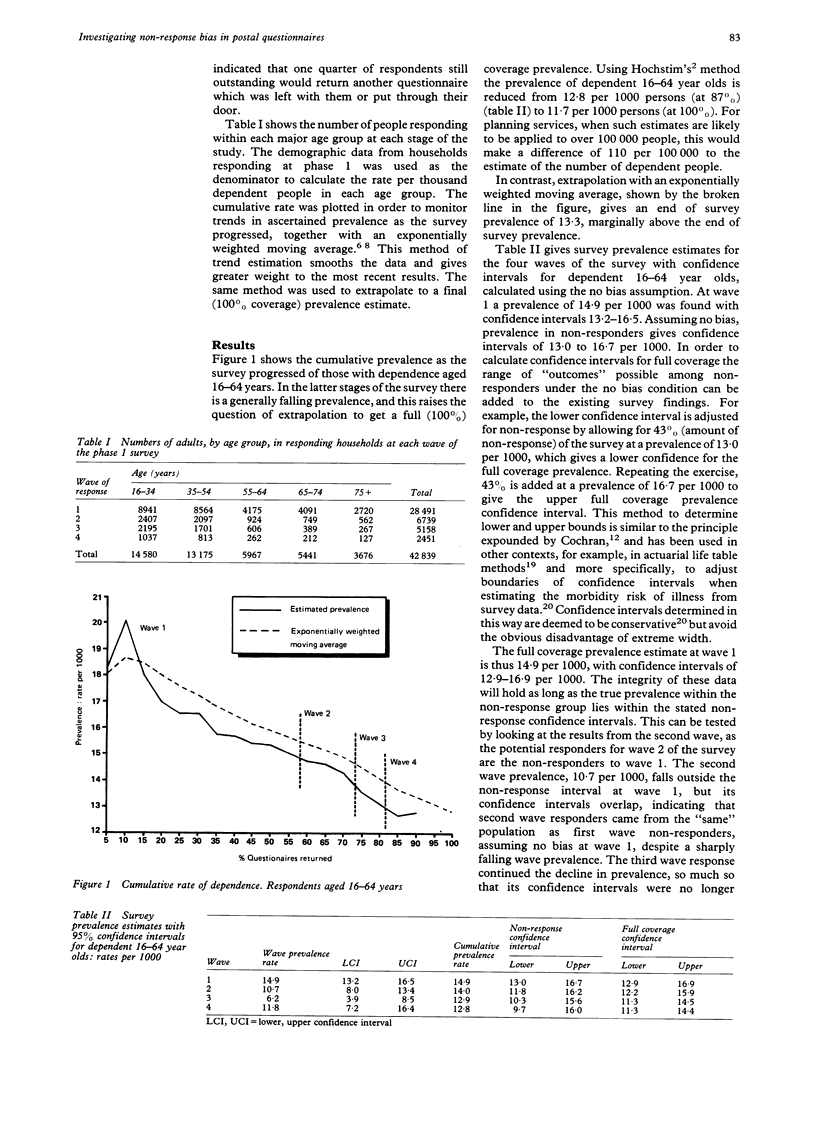
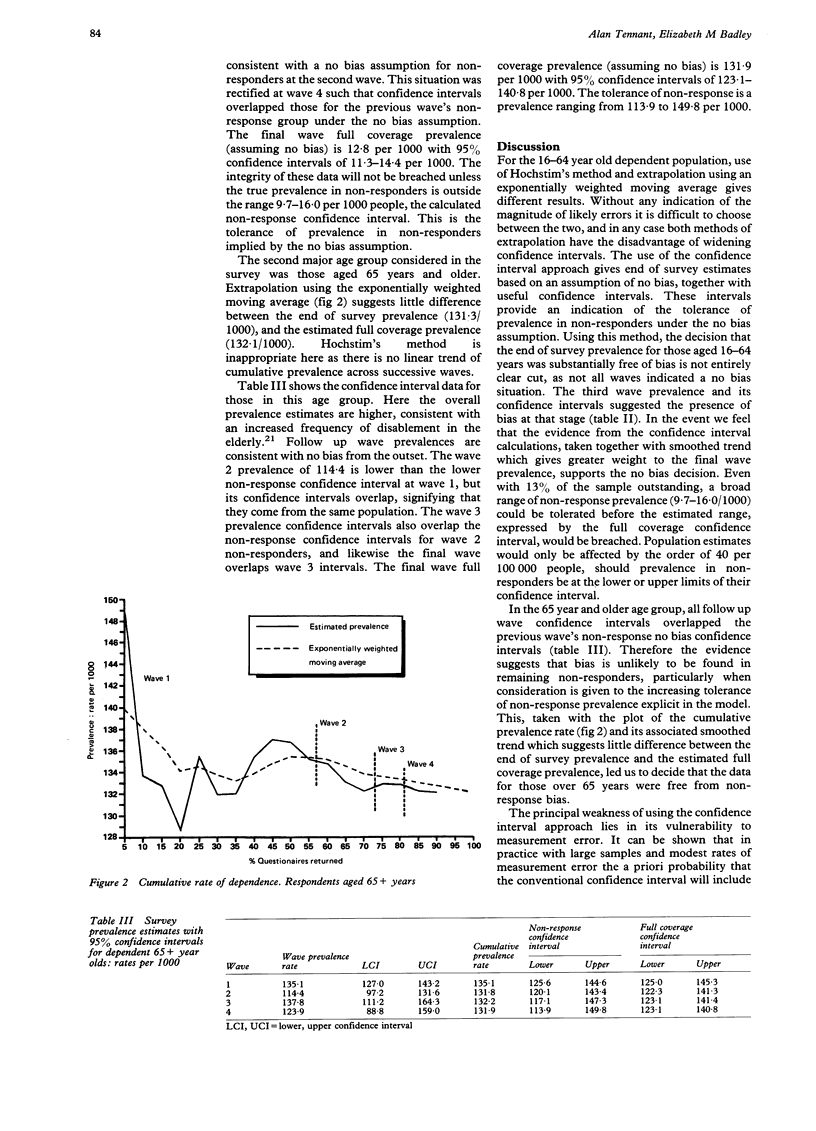
STUDY OBJECTIVE--The aim was to develop an alternative method of investigating non-response bias in postal surveys, including a method of calculating a final full (100%) coverage confidence interval which avoids the wide intervals of existing approaches. DESIGN AND SETTING--As part of a two stage survey of disablement in the community, a first phase postal questionnaire was sent to 25,168 households in Calderdale, West Yorkshire, England. Confidence intervals were calculated to investigate the precision of estimates using a "no bias" model, where the prevalence in non-responders is assumed to be the same as in responders. RESPONDENTS--A total of 21,889 postal questionnaires were returned (87%), representing households containing 42,826 people aged 16 years and over. This was achieved by the original post (1st wave, 57% response); two further postal follow ups (2nd and 3rd waves, taking the response to 73% and 81% respectively), the latter including a small personal call back; and a final postal follow up (the 4th wave). RESULTS--The cumulative estimated prevalence of those with dependence was plotted as the survey progressed. The final wave full coverage estimated prevalence for those aged 16-64 years was 12.8 per 1000 with 95% confidence intervals of 11.3-14.4 per 1000. The integrity of this estimate holds as long as the true prevalence in non-responders is within the calculated non-response confidence interval under the no bias assumption, 9.7-16.0 per 1000 people. This latter interval represents the tolerance of prevalence in non-responders implied by the no bias assumption. CONCLUSIONS--The findings have general implications for monitoring non-response bias in postal screening questionnaires. The confidence interval approach developed in this paper offers an alternative to existing regression based estimates, giving an indication of the range of prevalence amongst non-responders that could be tolerated before the no bias assumption used by the model is breached. It is suggested that this approach can be used to determine both the extent of bias, and to aid decision making about the appropriate juncture to terminate follow up. It highlights the potential, particularly in the context of a computerised survey operation, of methodological investigation occurring simultaneously with survey operation.
Full text
PDF


Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Bulpitt C. J. Confidence intervals. Lancet. 1987 Feb 28;1(8531):494–497. doi: 10.1016/s0140-6736(87)92100-3. [DOI] [PubMed] [Google Scholar]
- Gardner M. J., Altman D. G. Confidence intervals rather than P values: estimation rather than hypothesis testing. Br Med J (Clin Res Ed) 1986 Mar 15;292(6522):746–750. doi: 10.1136/bmj.292.6522.746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon I. Sample size estimation in occupational mortality studies with use of confidence interval theory. Am J Epidemiol. 1987 Jan;125(1):158–162. doi: 10.1093/oxfordjournals.aje.a114499. [DOI] [PubMed] [Google Scholar]
- Locker D., Wiggins R., Sittampalam Y., Patrick D. L. Estimating the prevalence of disability in the community: the influence of sample design and response bias. J Epidemiol Community Health. 1981 Sep;35(3):208–212. doi: 10.1136/jech.35.3.208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman S. C., Bland R. C. Estimating the morbidity risk of illness from survey data. Am J Epidemiol. 1989 Feb;129(2):430–438. doi: 10.1093/oxfordjournals.aje.a115147. [DOI] [PubMed] [Google Scholar]


