Abstract
SiOx thin films were prepared using magnetron sputtering with different O2 flow rates on a silicon substrate. The samples were characterized using Fourier transform infrared spectroscopy in transmission and reflection, covering a spectral range of 5 to 25 μm. By employing a multilayer model, the values of the complex refractive index that best fit the experimental transmission and reflection results were optimized using the Brendel–Bormann oscillator model. The results demonstrate the significance of selecting an appropriate range of O2 flow rates to modify the SiOx stoichiometry, as well as how the refractive index values can be altered between those of Si and SiO2 in the mid-infrared range.
Keywords: thin film, optical properties, mid-infrared, silicon oxide, refractive index
1. Introduction
The mid-infrared spectral region is an area of great scientific and technological interest, but in many cases, it has not been explored as extensively as the visible or near-infrared regions. Presently, it is necessary to develop a basic understanding of the optical properties of materials in the mid-infrared range.
The deposition of thin films using magnetron sputtering enables the deposition of a material under many different conditions [1,2,3,4,5], allowing for control of the stoichiometry of composite materials [6,7,8,9,10]. This allows for the production of materials with a wide range of optical properties [11,12,13,14,15].
Thin-film SiO2 is a material that has been extensively studied and is widely used in numerous applications, such as materials with a low refractive index, a barrier for thermal diffusion, and for improving adhesion or enhancing mechanical strength, among many others [16,17,18,19,20,21,22,23,24]. The properties of SiO2 and SiOx thin films have also been studied in the mid-infrared range [25,26,27], a spectral region that is of great interest in topics related to blackbody radiation at room temperature [28] or in astronomy, as well as in current research topics such as “epsilon near zero” metamaterials or the fabrication of perfect anti-reflective coatings at specific wavelengths [29,30,31,32,33,34]. In this regard, it is very interesting to have data on the refractive indices of different materials, which are often difficult to find. Therefore, it has been considered necessary to expand this knowledge by conducting a systematic study of the optical properties of thin films of SiOx with different stoichiometries in order to provide these basic data to the scientific community.
The optical properties of SiOx could be interesting since the properties of SiO2 do not always perfectly fit the requirements [35,36], for example, in the design of anti-reflective coatings with low angular dependence at a specific wavelength [31]. At this wavelength, the real part of the refractive index of a certain material equals one and the imaginary part is slightly higher than zero. This implies that, for a given material, these values of complex refractive indices occur at discrete and limited wavelengths. However, it is possible to modulate the wavelength at which this phenomenon occurs by controlling the stoichiometry of SiOx.
Other works, such as [37], have specifically studied the refractive indices of SiOx deposited by reactive sputtering while varying the reactive gas flow. However, although the results were useful and of high quality, the study did not determine the stoichiometry of the deposited SiOx under each deposition condition. Furthermore, from the results obtained in [37], it could be observed that there was little variation in the refractive indices obtained, which suggested that in all cases, the stoichiometry was close to that of SiO2.
In this study, we aimed to determine the refractive indices of SiOx in the mid-infrared range using FTIR spectroscopy by controlling the stoichiometry while varying the O2 flow during deposition and determining the stoichiometry through EDS. Special attention was given to the study of slightly sub-oxidized SiOx, which allowed for the modulation of the optical properties of SiO2.
2. Materials and Methods
In this study, we deposited SiOx thin films on a silicon substrate because it is transparent in the mid-infrared range. These silicon wafers had a thickness of 260~300 μm, 1~5 Ω/cm of resistance, and were orientated to <100> ± 1 deg.
These SiOx thin films were obtained using a prototype industrial magnetron sputtering installation, comprising three vacuum chambers. The loading chamber and the transfer chamber, which were smaller in size, facilitated rapid sample introduction and extraction without breaking the vacuum in the process chamber where the sputtering process took place. The achievable pressures in these chambers were in the order of 10−2, 10−7, and 10−7 mbar for the loading, transfer, and process chambers, respectively.
The installation included 8 distinct magnetrons, 4 on each side, enabling the deposition of up to 4 different materials on each sample. The targets used had dimensions of 600 × 100 mm. The silicon target used had a purity of 99.999%.
Additionally, two pulsed DC power supplies were available, capable of delivering up to 10 kW of power. For this study, a power of 2 kW was utilized. Gas flows were regulated using mass flow controllers (MFCs). The substrate holder linearly moved at a constant velocity, ensuring that each point at the same height received the same exposure during the deposition process. Furthermore, points within the same vertical line had equal exposure due to the larger dimensions of the magnetrons compared with the sample.
Once the SiOx thin film was deposited, its thickness was measured using a profilometer (DektakXT® model), which had a precision in the order of nanometers.
Transmission and reflection spectra were measured with an FTIR spectrophotometer, specifically the Perkin-Elmer Spectrum 100 model, which operates in the infrared range from 4000 to 200 cm−1 (2.5 to 50 µm) with a step size of 2 cm−1 and a resolution of 16 cm−1, which is the maximum resolution allowed by the spectrophotometer and was chosen in order to avoid interference from the substrate. Measurements were conducted in the air, ensuring that they were repeatable and unaffected by atmospheric effects.
Samples were also analyzed using a Field Emission Scanning Electron Microscope (FESEM) Carl Zeiss MERLIN™ in order to obtain images and determine the proportion of the Si and O in the SiOx thin films. This SEM equipment allowed for observations with a spatial resolution of up to 0.8 nm and acceleration voltages ranging from 0.02 to 30 kV. It was equipped with an EDS detector for energy analysis of the scattered X-rays, specifically an X-Max (20 mm2) detector with a Silicon Drift Detector (SSD) from Oxford Instruments. The EDS detector provided an energy resolution below 123 eV at the 5.9 keV Mn Ka.
3. Theoretical Background and Calculation
In this study, we experimentally determined the energetic factors of several SiOx thin films, including transmission factors, coating reflectance, and substrate reflectance. Our objective was to extract the complex refractive index, , which characterizes these materials.
First, the transmission, coating reflection, and substrate reflection spectra were measured using an FTIR spectrophotometer in the infrared range. To establish a relationship between these experimental energetic factors and the refractive index, a matrix formalism was employed, which was based on the foundations laid out in [38,39]. This formalism was derived from Maxwell’s equations while ensuring the continuity of the transverse components of the fields. To achieve this, the materials were assumed to be non-magnetic, linear, homogeneous, isotropic, without free charge density, and infinite in the plane of the layers.
In our model, we considered a thin film (indexed as one, as shown in Figure 1), a substrate material of silicon (indexed as zero), and the incident medium of air (indexed as two). Each material, denoted as , is characterized by its complex refractive index, , and its corresponding thickness, . The wave impinged on the thin film from the medium indexed as two. The analysis was divided into two parts: first, the reflection and transmission through the thin film without crossing the substrate, and then the subsequent consideration of the substrate’s effect.
Figure 1.
Schematic representation of the indices used for the mathematical model.
For the analysis of the thin film, it was assumed that media zero and two were infinite. Under normal incidence measurements, the transverse electric and magnetic components were equal. When transitioning from medium to medium , the relationship between the wave amplitudes is given by:
| (1) |
where is the transmission matrix at the interface between medium and medium :
| (2) |
Furthermore, as the wave propagated through a medium, its amplitude underwent a change, which is given by:
| (3) |
where represents the amplitudes after propagating a distance in medium , and is the propagation matrix in medium , which has the following expression:
| (4) |
where is the imaginary unit and is the wave number in a vacuum.
Using Equations (2) and (4), the amplitude in medium zero could be calculated from the amplitude in medium two as:
| (5) |
From this matrix, the transmission () and reflection () intensities in the thin film can be obtained as:
| (6) |
| (7) |
When studying the effect of substrate thickness, it is important to consider that the interferences occurring with the substrate have a much higher frequency than the spectral resolution of the spectrophotometer that we used. As a result, what was measured with the spectrophotometer was the incoherent sum of the intensities from multiple reflections at the interfaces. However, the resolution was enough to observe the monolayer interference.
Let represent the transmission of the coating, the reflection of the thin film if incident from air, the reflection of the thin film when incident from the substrate, the reflection at the substrate–air interface, the thickness of the substrate, and the absorption of the substrate, which can be related to the imaginary part of its refractive index, , as:
| (8) |
Then, the total transmission through the thin film and the substrate is given by:
| (9) |
and the reflection on the side of the thin film is:
| (10) |
and on the substrate side:
| (11) |
, , and are the experimental data that we obtained from the spectrophotometer. The substrate width, specified by the silicon manufacturer, was 00 μm, while the width of the SiOx thin film was measured using a profilometer.
First, the refractive index of silicon was calculated. For this purpose, the same mathematical approach was used, but with the consideration that , indicating the absence of a thin film. The spectra of the substrate were measured, and various values of and were considered. The values that best fit the experimental spectra were selected. Subsequently, the same method was applied to the thin films.
The results obtained for and using this method were quite noisy, so we adjusted them to a model. There were various mathematical models available to approximate and . In this study, we used the Brendel–Bormann oscillator model [40], which constructs a dielectric function that satisfies the Kramers–Kronig relations and yields with a Gaussian shape for the imaginary part. The dielectric constant is given by the addition of different vibrational modes:
| (12) |
where is the wavenumber, i.e., the inverse of the wavelength (); is the high-frequency permittivity; and refers to the different vibrational modes and the contribution of each one, , is defined by:
| (13) |
where is the standard deviation of the Gaussian distribution, is the center frequency, is the plasma frequency (which gives the oscillator strength), and is the damping constant.
As shown in Appendix A of [41], Equation (13) could be analytically solved and the result was:
| (14) |
where must be chosen in such a way that , i.e.,
| (15) |
| (16) |
where and refer to the real and imaginary parts, respectively, and is the Faddeeva function, defined by:
| (17) |
The complex refractive index, , is related to the dielectric function by , so that it is possible to obtain and from Equation (14), resulting in the following expressions:
| (18) |
| (19) |
Given these equations, we searched for the oscillator parameters that best fit the previously adjusted values of and . The number of oscillators considered was determined depending on the number of peaks in the spectrum.
4. Results and Discussion
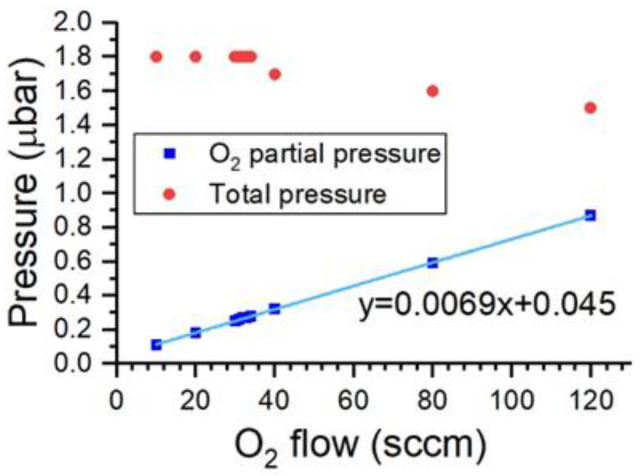
To obtain SiOx with different stoichiometries, the main parameter that needed to be controlled was the oxygen flow that was introduced into the vacuum chamber during the deposition process. All the coatings were deposited with a total flow of 200 sccm (sum of the Ar and O2 flows). As shown in Figure 2, the partial pressure of oxygen linearly increased with the O2 flow that was introduced by a mass flow controller (MFC). A linear fit of this trend is shown in Figure 2 along with the equation of the least-squares fit line. Moreover, in Figure 2, the total pressure of the chamber is shown as a function of the O2 flow. In this case, it can be observed that the pressure remained relatively constant, with a slight decrease observed for high values of the O2 flow.
Figure 2.
Relationship between pressure and the flow of gas introduced.
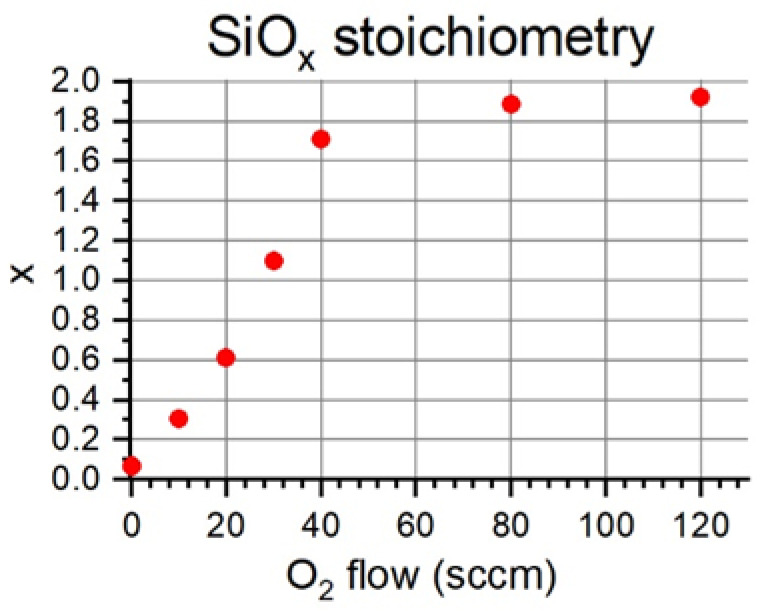
Figure 3 shows the evolution of the stoichiometry of the SiOx samples as a function of the O2 flow with which they were deposited. It can be seen that for a flow of 0 sccm of O2, x = 0.06 was obtained, a value very close to zero. The value of 0.06 took into account possible contamination when handling the samples, being very likely that they had been slightly oxidized in their exposure to the atmosphere. Between the flows of 0 and 20 sccm of O2, x approximately linearly grew, reaching a value of x = 0.61 for 20 sccm of O2. For values between 20 and 40 sccm of O2, the trend had a higher slope, reaching a value of x = 1.71 for a flow of 40 sccm of O2. This increase in slope was due to the entry into the reactive mode of the deposition process and its consequent decrease in deposition rate. The decrease in deposition rate entailed a higher degree of oxidation of the evaporated material. For flow values greater than 40 sccm, the value of x tended “asymptotically” toward the expected value for the stoichiometry of SiO2 of x = 2, reaching a value of x = 1.92 for a flow of 120 sccm of O2. Additionally, X-ray diffraction confirmed the amorphous nature of the SiOx samples, while Figure S1 in the Supplementary Material shows cross-sectional images of the thin films obtained using field emission scanning electron microscopy.
Figure 3.
SiOx stoichiometry as a function of the O2 flow introduced during the deposition process.
The fitting parameters for the dielectric permittivity value of each sample were determined using the Brendel–Bormann oscillator model. The obtained results are presented in Table 1 for the samples deposited with different O2 flows ranging from 10 to 120 sccm. The number of absorption peaks included in the model varied from four to six depending on the sample. This number was chosen in such a way that the model corresponded with the data, identifying the principal absorbance bands, which corresponded with those found in the literature [42,43,44]. This showed that resonances at approximately 440 and 810 cm−1 corresponded to Si-O-Si rocking and bonding bands, respectively, while the bands at 1060 and 1150 cm−1 corresponded to Si-O-Si stretching bands.
Table 1.
Brendel–Bormann oscillator parameters for SiOx deposited at different O2 flows between 10 and 120 sccm.
| O2 Flow | (F/m) | (cm−1) | (cm−1) | (cm−1) | (cm−1) |
|---|---|---|---|---|---|
| 10 | 9.50 | 400 | 71 | 0.89 | 34 |
| 547 | 609 | 3.82 | 414 | ||
| 978 | 430 | 0.58 | 69 | ||
| 1059 | 247 | 5.62 | 60 | ||
| 20 | 6.95 | 416 | 119 | 2.50 | 13 |
| 584 | 597 | 2.38 | 407 | ||
| 1005 | 508 | 0.99 | 62 | ||
| 1073 | 269 | 4.46 | 59 | ||
| 30 | 3.20 | 434 | 200 | 1.24 | 30 |
| 523 | 528 | 4.78 | 412 | ||
| 827 | 286 | 3.15 | 85 | ||
| 1030 | 650 | 0.76 | 57 | ||
| 1166 | 203 | 4.14 | 37 | ||
| 40 | 2.20 | 439 | 283 | 5.5 | 27 |
| 551 | 402 | 37.0 | 259 | ||
| 809 | 208 | 11.5 | 40 | ||
| 928 | 200 | 16.5 | 44 | ||
| 1046 | 664 | 4.0 | 39 | ||
| 1164 | 293 | 5.5 | 44 | ||
| 80 | 2.05 | 231 | 436 | 87.9 | 420 |
| 446 | 265 | 8.5 | 20 | ||
| 813 | 191 | 17.2 | 26 | ||
| 1052 | 690 | 5.0 | 34 | ||
| 1171 | 281 | 10.6 | 42 | ||
| 120 | 1.90 | 313 | 456 | 2.5 | 580 |
| 442 | 277 | 0.74 | 21 | ||
| 813 | 171 | 0.04 | 28 | ||
| 1049 | 662 | 0.01 | 35 | ||
| 1172 | 216 | 3.5 | 42 |
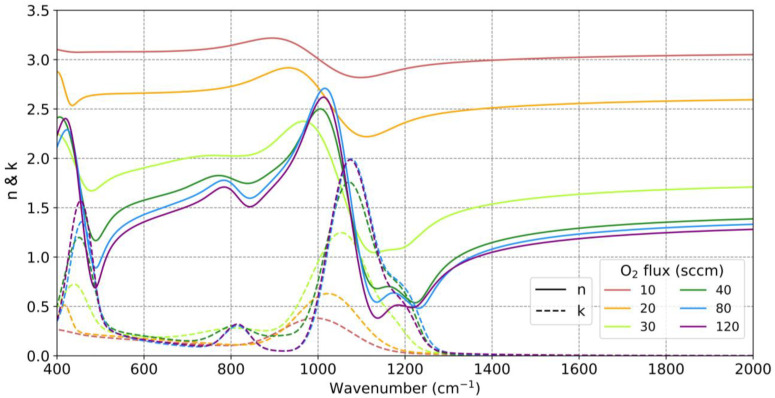
Using the values from these fittings, we can calculate the complex refractive indices of the different SiOx samples, as shown in Figure 4. It can be observed that the real part of the refractive index, , decreased as the O2 flow increased. While pure Si had a refractive index of approximately 3.42, the sample deposited with 10 sccm of O2 exhibited an value of around three for all wavelengths, accompanied by a weak absorption band around 1000 cm−1. The real part of the refractive index continued to decrease until reaching an approximate value of = 2.5 for the sample deposited at 20 sccm. On the other hand, the absorption in the approximately 1000 cm−1 band increased, and this absorption band shifted to higher wave numbers (shorter wavelengths) as the O2 flow increased. In [45], this effect was explained by O back-bonding or a variation of the Si–O–Si bond angles. In [46], researchers showed that the absorption strength in each band linearly scaled with the oxygen concentration and that this vibration was specifically determined by the detailed character of the bonding geometry. A further explanation about geometry and atomic displacements can be found in [44,46].
Figure 4.
Complex refractive indices for SiOx samples deposited with different reactive gas flows: real part n (solid line) and imaginary part k (dotted line).
For an O2 flow of 30 sccm (in which a value of x = 1.1 was obtained, indicating a stoichiometry very close to silicon monoxide), the trend in the complex refractive index followed the same pattern as in lower flows. However, at an O2 flow of 40 sccm (in which a value of x = 1.7 was reached), the complex refractive index values obtained bore a strong resemblance to those obtained at higher O2 flows, although they followed a similar trend as that of the previous cases. The similarity among the refractive indices deposited with flows of 40, 80, and 120 sccm suggested that starting from 40 sccm, the deposited material already exhibited characteristics very similar to those of SiO2. Despite the significant change in deposition conditions due to the substantial difference in the reactive gas flow, the samples barely altered their compositions, as observed in Figure 3, and the refractive indices showed minimal changes. The slight change in refractive indices when altering the O2 flow for high flow rates highlighted the significance of carefully selecting an appropriate range of reactive gas flows to effectively control the stoichiometry. In [37], samples were examined, each deposited with varying O2 flows, yet all displayed refractive indices similar to those of SiO2. This implied that these samples were likely deposited using high O2 flows that had a minimal impact on the stoichiometry.
However, it is interesting to note that the wavenumber at which = 1 could slightly vary was between 1322 and 1364 cm−1 (7.56 and 7.33 μm), corresponding to the values of the samples deposited with 40 and 120 sccm of O2. The sample deposited with 30 sccm of O2 never had a real part of the refractive index lower than one. However, it approached values close to one, indicating that the wavelength at which the real part of the refractive index equals one could potentially be controlled with flow rates between 30 and 40 sccm of O2. Therefore, the samples were subsequently deposited using an O2 flow slightly higher than 30 sccm. Additionally, the values of the dielectric permittivities are provided in Figures S2 and S3 of the Supplementary Material.
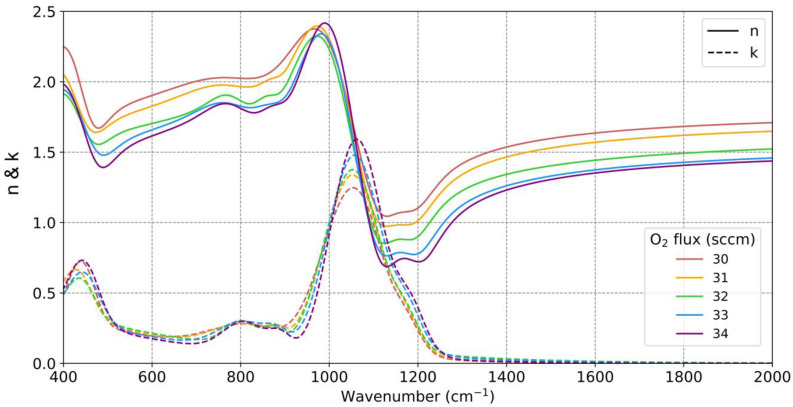
Following the same procedure as before, the samples were deposited with flows ranging from 31 to 34 sccm of O2. The fitting parameters for the dielectric permittivity using the Brendel–Bormann oscillator model are shown in Table 2. Likewise, Figure 5 displays the refractive indices obtained for these samples. A clear trend can be observed as the O2 flow increased, and this series of samples demonstrated the excellent reproducibility of the deposition process and the precise control of O2 flow achieved through the MFC. Starting from a flow of 31 sccm, regions with a real part of the refractive index lower than one appeared. For the case of 31 sccm, the cutoff point with = 1 occurred at 1194 cm−1 (8.375 μm), with a value of = 1.000 + 0.289i. In this case, the imaginary part had a significant value, but it would allow the production of an anti-reflective coating with a residual reflectance of 2% under a normal incidence. In the case of 32 sccm, the cutoff occurred at 1228 cm−1 (8.143 μm) with a value of = 1.007 + 0.126i. These results demonstrated how by modulating the O2 flow during SiOx deposition, we could customize the stoichiometry and adjust the refractive indices as desired. The values of the dielectric permittivity for these samples can be found in Figures S4 and S5 of the Supplementary Material.
Table 2.
Brendel–Bormann oscillator parameters for SiOx deposited at different O2 flows between 31 and 34 sccm.
| O2 Flow | (F/m) | (cm−1) | (cm−1) | (cm−1) | (cm−1) |
|---|---|---|---|---|---|
| 31 | 3.0 | 423 | 184 | 6.5 | 33 |
| 462 | 548 | 0.1 | 448 | ||
| 812 | 258 | 14.8 | 68 | ||
| 881 | 89 | 11.9 | 17 | ||
| 1028 | 651 | 5.8 | 51 | ||
| 1156 | 231 | 7.7 | 40 | ||
| 32 | 2.6 | 432 | 153 | 0.1 | 32 |
| 537 | 590 | 0.1 | 564 | ||
| 800 | 182 | 9.8 | 35 | ||
| 874 | 126 | 1.5 | 23 | ||
| 1027 | 627 | 0.1 | 51 | ||
| 1158 | 202 | 0.1 | 38 | ||
| 33 | 2.4 | 437 | 189 | 3.2 | 36 |
| 521 | 525 | 6.8 | 501 | ||
| 805 | 224 | 14.0 | 51 | ||
| 882 | 130 | 10.1 | 26 | ||
| 1031 | 636 | 5.3 | 46 | ||
| 1158 | 227 | 5.0 | 41 | ||
| 34 | 2.33 | 435 | 207 | 0.1 | 36 |
| 478 | 484 | 0.1 | 443 | ||
| 807 | 214 | 8.8 | 44 | ||
| 890 | 136 | 4.0 | 26 | ||
| 1036 | 644 | 0.6 | 44 | ||
| 1163 | 244 | 3.1 | 43 |
Figure 5.
Complex refractive indices for SiOx samples deposited with intermediate reactive gas flows: real part n (solid line) and imaginary part k (dotted line).
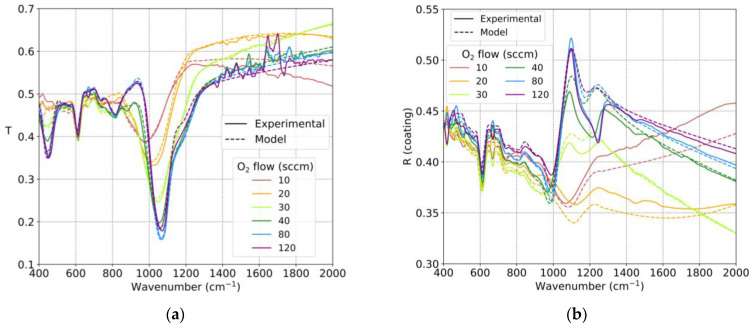
Figure 6a shows the transmittance spectra of the fabricated samples, while Figure 6b presents the reflectance spectra from the coating side (the reflectance spectrum from the substrate side is included in Figure S6 of the Supplementary Material). In Figure 6, the excellent agreement between the experimental measurements and the calculated values based on the obtained refractive indices can be observed. The drop in transmission in the characteristic absorption bands of SiOx is noticeable, with greater reductions for samples deposited with higher flows of O2. Additionally, there was an absorption peak around 600 cm−1 corresponding to crystalline Si originating from the substrate. It is also worth noting that the experimental measurements exhibited considerable noise between 1400 and 1800 cm−1 due to the absorption bands of gases present in the atmosphere. Regarding the reflectance values, a good agreement was also observed between the experimental measurements and the results calculated from the refractive indices using the employed model. However, it should be emphasized that the vertical scale was greatly amplified (the transmittance and reflectance spectra for the samples deposited with an O2 flow between 31 and 34 sccm are shown in Figures S7–S9 of the Supplementary Material). These results showed great agreement between the experimental values and the values calculated with the obtained refractive indices. The complex refractive index values for all the samples can be found in Table S1 of the Supplementary Material.
Figure 6.
(a) Experimental transmission spectra (solid line) and spectra calculated with the obtained refractive indices (dotted line) for SiOx samples deposited with different reactive gas flows. (b) Experimental reflectance spectra on the coated side (solid line) and spectra calculated with the obtained refractive indices (dotted line) for SiOx samples deposited with different reactive gas flows.
5. Conclusions
The results of this study demonstrated the controllability of SiOx thin film stoichiometry by adjusting the introduced O2 flow during the deposition process. It was crucial to carefully select an appropriate range of flow rates to effectively vary the stoichiometry. The refractive indices of SiOx thin films with different stoichiometries were determined using the Brendel–Bormann oscillator model. The findings highlighted the ability to modulate both the real part of the refractive index across the entire spectrum and the imaginary part in the absorption regions. Additionally, this study revealed the potential to modify the cutoff wavelength, where the real part of the refractive index equals unity. Furthermore, the agreement between the theoretically calculated transmittance and reflectance spectra based on the refractive indices and the experimentally obtained spectra was confirmed.
Acknowledgments
We gratefully acknowledge financial support from Cátedra Ariño Duglass and the “Departamento de Ciencia, Universidad y Sociedad del Conocimiento del Gobierno de Aragón” (group T20_20R). The authors would like to acknowledge the use of Servicio General de Apoyo a la Investigación-SAI, Universidad de Zaragoza. The authors gratefully acknowledge the continued support from the company Ariño Duglass.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/nano13202749/s1, Figure S1: Cross-section images of SiOx thin films deposited at different reactive gas flows; Figure S2: Real part of the relative dielectric permittivity in SiOx samples deposited with different reactive gas flows; Figure S3: Imaginary part of the relative dielectric permittivity in SiOx samples deposited with different reactive gas flows; Figure S4: Real part of relative dielectric permittivity in samples deposited with intermediate reactive gas flows; Figure S5: Imaginary part of relative dielectric permittivity in samples deposited with intermediate reactive gas flows; Figure S6: Experimental reflectance spectra on the substrate side (solid line) and calculated with the refractive indices obtained (dotted line) for SiOx samples deposited with different reactive gas flows; Figure S7: Experimental transmission spectra (solid line) and calculated with the refractive indices obtained (dotted line) for SiOx samples deposited with intermediate reactive gas flows; Figure S8: Experimental reflectance spectra on the coating side (solid line) and calculated with the refractive indices obtained (dotted line) for SiOx samples deposited with intermediate reactive gas flows; Figure S9: Experimental reflectance spectra on the substrate side (solid line) and calculated with the refractive indices obtained (dotted line) for SiOx samples deposited with intermediate reactive gas flows; Table S1: Complex refractive indices obtained. n is the real part, k is the imaginary part, the number after n and k refers to the O2 flow (in sccm) with which the sample was deposited.
Author Contributions
Conceptualization, N.H. and E.C.; methodology, N.H. and E.C.; software, N.H.; formal analysis, N.H.; investigation, N.H.; data curation, N.H.; writing—original draft preparation, N.H. and E.C.; writing—review and editing, N.H. and E.C.; visualization, N.H.; supervision, E.C.; project administration, E.C.; funding acquisition, E.C. All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
Data are available in the Supplementary Material.
Conflicts of Interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Enrique Carretero reports financial support provided by the Government of Aragon and Cátedra Ariño Duglass.
Funding Statement
This research was funded by Gobierno de Aragón, grant number T20_20R, and Cátedra Ariño Duglass.
Footnotes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
References
- 1.Wasa K. Handbook of Sputter Deposition Technology: Fundamentals and Applications for Functional Thin Films, Nano-Materials and MEMS. William Andrew; Norwich, NY, USA: 2012. [Google Scholar]
- 2.Kelly P.J., Arnell R.D. Magnetron Sputtering: A Review of Recent Developments and Applications. Vacuum. 2000;56:159–172. doi: 10.1016/S0042-207X(99)00189-X. [DOI] [Google Scholar]
- 3.Powell R.A. PVD for Microelectronics: Sputter Desposition to Semiconductor Manufacturing. Elsevier; Amsterdam, The Netherlands: 1998. [Google Scholar]
- 4.Helmersson U., Lattemann M., Bohlmark J., Ehiasarian A.P., Gudmundsson J.T. Ionized Physical Vapor Deposition (IPVD): A Review of Technology and Applications. Thin Solid Film. 2006;513:1–24. doi: 10.1016/j.tsf.2006.03.033. [DOI] [Google Scholar]
- 5.Ellmer K. Magnetron Sputtering of Transparent Conductive Zinc Oxide: Relation between the Sputtering Parameters and the Electronic Properties. J. Phys. D Appl. Phys. 2000;33:R17–R32. doi: 10.1088/0022-3727/33/4/201. [DOI] [Google Scholar]
- 6.Hoskins B.D., Strukov D.B. Maximizing Stoichiometry Control in Reactive Sputter Deposition of TiO2. J. Vac. Sci. Technol. A. 2017;35:020606. doi: 10.1116/1.4974140. [DOI] [Google Scholar]
- 7.Nair J.P., Zon I., Oron M., Popovitz-Biro R., Feldman Y., Lubomirsky I. Stoichiometry Control during Deposition by Ion Beam Sputtering. J. Appl. Phys. 2002;92:4784–4790. doi: 10.1063/1.1502916. [DOI] [Google Scholar]
- 8.Zhao W., Wang K., Li H., Yang Z., Liu Z., Sun J., Wang D., Liu S. (Frank) Stoichiometry Control of Sputtered Zinc Oxide Films by Adjusting Ar/O2 Gas Ratios as Electron Transport Layers for Efficient Planar Perovskite Solar Cells. Sol. Energy Mater. Sol. Cells. 2018;178:200–207. doi: 10.1016/j.solmat.2018.01.027. [DOI] [Google Scholar]
- 9.Kwok C.K.G., Wang Y., Egbo K., Hossain M.K., Shil S.K., Yu K.M. Enhancing the P-Type Conductivity of Pure Phase SnO via Stoichiometry Control and Annealing. Surf. Interfaces. 2022;35:102473. doi: 10.1016/j.surfin.2022.102473. [DOI] [Google Scholar]
- 10.Li H., Li J., Yan C., Huang J., Kong J., Wu Q., Shi Y., Xiong D. Deposition and Mechanical Properties of δ-TaNx Films with Different Stoichiometry by DC Magnetron Sputtering. Surf. Coat. Technol. 2020;404:126452. doi: 10.1016/j.surfcoat.2020.126452. [DOI] [Google Scholar]
- 11.Hirpara J., Malik G., Chandra R. Optical Properties Investigation of Reactively Sputtered Tantalum Oxynitride Films. Mater. Today Proc. 2022;57:202–210. doi: 10.1016/j.matpr.2022.02.352. [DOI] [Google Scholar]
- 12.Sarakha L., Bégou T., Goullet A., Cellier J., Bousquet A., Tomasella E., Sauvage T., Boutinaud P., Mahiou R. Influence of Synthesis Conditions on Optical and Electrical Properties of CaTiO3:Pr3+ Thin Films Deposited by Radiofrequency Sputtering for Electroluminescent Device. Surf. Coat. Technol. 2011;205:S250–S253. doi: 10.1016/j.surfcoat.2011.01.015. [DOI] [Google Scholar]
- 13.Pérez-Pacheco A., Prieto C., Castañeda-Guzmán R., García-López J. Influence of the Growth Conditions on the Stoichiometry and on the Optical Properties of Titanium Oxide Thin Films Prepared by Reactive Sputtering. Thin Solid Film. 2009;517:5415–5418. doi: 10.1016/j.tsf.2009.01.050. [DOI] [Google Scholar]
- 14.Mahata C., Park J., Ismail M., Kim S. Demonstration of Electronic and Optical Synaptic Properties Modulation of Reactively Sputtered Zinc-Oxide-Based Artificial Synapses. J. Alloys Compd. 2023;938:168539. doi: 10.1016/j.jallcom.2022.168539. [DOI] [Google Scholar]
- 15.Beliaev L.Y., Shkondin E., Lavrinenko A.V., Takayama O. Optical, Structural and Composition Properties of Silicon Nitride Films Deposited by Reactive Radio-Frequency Sputtering, Low Pressure and Plasma-Enhanced Chemical Vapor Deposition. Thin Solid Film. 2022;763:139568. doi: 10.1016/j.tsf.2022.139568. [DOI] [Google Scholar]
- 16.Cunha N.F., AL-Rjoub A., Rebouta L., Vieira L.G., Lanceros-Mendez S. Multilayer Passive Radiative Selective Cooling Coating Based on Al/SiO2/SiNx/SiO2/TiO2/SiO2 Prepared by Dc Magnetron Sputtering. Thin Solid Film. 2020;694:137736. doi: 10.1016/j.tsf.2019.137736. [DOI] [Google Scholar]
- 17.Tiron V., Velicu I.-L., Matei T., Cristea D., Cunha L., Stoian G. Ultra-Short Pulse HiPIMS: A Strategy to Suppress Arcing during Reactive Deposition of SiO(2)Thin Films with Enhanced Mechanical and Optical Properties. Coatings. 2020;10:633. doi: 10.3390/coatings10070633. [DOI] [Google Scholar]
- 18.Zambrano D.F., Villarroel R., Espinoza-González R., Carvajal N., Rosenkranz A., Montaño-Figueroa A.G., Arellano-Jiménez M.J., Quevedo-Lopez M., Valenzuela P., Gacitúa W. Mechanical and Microstructural Properties of Broadband Anti-Reflective TiO2/SiO2 Coatings for Photovoltaic Applications Fabricated by Magnetron Sputtering. Sol. Energy Mater. Sol. Cells. 2021;220:110841. doi: 10.1016/j.solmat.2020.110841. [DOI] [Google Scholar]
- 19.Zhao C., Zhao L., Liu J., Liu Z., Chen Y. Effect of Sputtering Power on the Properties of SiO2 Films Grown by Radio Frequency Magnetron Sputtering at Room Temperature. Opt. Quant. Electron. 2021;53:15. doi: 10.1007/s11082-020-02639-4. [DOI] [Google Scholar]
- 20.Zhang L., Li J., Zhang X.W., Jiang X.Y., Zhang Z.L. High-Performance ZnO Thin Film Transistors with Sputtering SiO2/Ta2O5/SiO2 Multilayer Gate Dielectric. Thin Solid Film. 2010;518:6130–6133. doi: 10.1016/j.tsf.2010.06.017. [DOI] [Google Scholar]
- 21.Tajima N., Murotani H., Matsudaira T. Optical Multicoating Using Low-Refractive-Index SiO2 Optical Thin Films Deposited by Sputtering and Electron Beam Evaporation. Thin Solid Film. 2023;776:139824. doi: 10.1016/j.tsf.2023.139824. [DOI] [Google Scholar]
- 22.Wang L., Zhao C., Zhao L., Fan X., Wang Q., Liu J. Effect of O2/Ar Flow Ratio and Heat Treatment on the Structure and Properties of SiO2 Film Prepared by Magnetron Sputtering. Phys. B Condens. Matter. 2022;630:413537. doi: 10.1016/j.physb.2021.413537. [DOI] [Google Scholar]
- 23.Joo S.Y., Loka C., Jo Y.W., Reddyprakash M., Moon S.W., Choi Y., Lee S.E., Cho G.S., Lee K.-S. ITO/SiO2/ITO Structure on a Sapphire Substrate Using the Oxidation of Ultra-Thin Si Films as an Insulating Layer for One-Glass-Solution Capacitive Touch-Screen Panels. Coatings. 2020;10:134. doi: 10.3390/coatings10020134. [DOI] [Google Scholar]
- 24.Tramarin L., Casquel R., Gil-Rostra J., Angel Gonzalez-Martinez M., Herrero-Labrador R., Murillo A.M.M., Laguna M.F., Banuls M.-J., Gonzalez-Elipe A.R., Holgado M. Design and Characterization of ITO-Covered Resonant Nanopillars for Dual Optical and Electrochemical Sensing. Chemosensors. 2022;10:393. doi: 10.3390/chemosensors10100393. [DOI] [Google Scholar]
- 25.Palik E.D. Handbook of Optical Constants of Solids. Academic Press; Cambridge, MA, USA: 1998. [Google Scholar]
- 26.Hass G., Salzberg C.D. Optical Properties of Silicon Monoxide in the Wavelength Region from 0.24 to 14.0 Microns*. J. Opt. Soc. Am. JOSA. 1954;44:181–187. doi: 10.1364/JOSA.44.000181. [DOI] [Google Scholar]
- 27.Paolone A., Placidi E., Stellino E., Betti M.G., Majorana E., Mariani C., Nucara A., Palumbo O., Postorino P., Sbroscia M., et al. Argon and Other Defects in Amorphous SiO2 Coatings for Gravitational-Wave Detectors. Coatings. 2022;12:1001. doi: 10.3390/coatings12071001. [DOI] [Google Scholar]
- 28.Eriksson T.S., Jiang S., Granqvist C.G. Dielectric Function of Sputter-Deposited Silicon Dioxide and Silicon Nitride Films in the Thermal Infrared. Appl. Opt. AO. 1985;24:745–746. doi: 10.1364/AO.24.000745. [DOI] [PubMed] [Google Scholar]
- 29.Dobrowolski J.A., Poitras D., Ma P., Vakil H., Acree M. Toward Perfect Antireflection Coatings: Numerical Investigation. Appl. Opt. AO. 2002;41:3075–3083. doi: 10.1364/AO.41.003075. [DOI] [PubMed] [Google Scholar]
- 30.Poitras D., Dobrowolski J.A. Toward Perfect Antireflection Coatings. 2. Theory. Appl. Opt. AO. 2004;43:1286–1295. doi: 10.1364/AO.43.001286. [DOI] [PubMed] [Google Scholar]
- 31.Dobrowolski J.A., Guo Y., Tiwald T., Ma P., Poitras D. Toward Perfect Antireflection Coatings. 3. Experimental Results Obtained with the Use of Reststrahlen Materials. Appl. Opt. AO. 2006;45:1555–1562. doi: 10.1364/AO.45.001555. [DOI] [PubMed] [Google Scholar]
- 32.Godinho V., Denisov V.N., Mavrin B.N., Novikova N.N., Vinogradov E.A., Yakovlev V.A., Fernández-Ramos C., de Haro M.C.J., Fernández A. Vibrational Spectroscopy Characterization of Magnetron Sputtered Silicon Oxide and Silicon Oxynitride Films. Appl. Surf. Sci. 2009;256:156–164. doi: 10.1016/j.apsusc.2009.07.101. [DOI] [Google Scholar]
- 33.Ando E., Suzuki S., Shimizu J., Hayashi Y. Sputtered Tin Silicon Oxide Films for Durable Solar Control Coatings. Thin Solid Film. 1999;351:301–307. doi: 10.1016/S0040-6090(99)00088-7. [DOI] [Google Scholar]
- 34.García-Valenzuela A., Alvarez R., Espinós J.P., Rico V., Gil-Rostra J., Palmero A., Gonzalez-Elipe A.R. SiOx by Magnetron Sputtered Revisited: Tailoring the Photonic Properties of Multilayers. Appl. Surf. Sci. 2019;488:791–800. doi: 10.1016/j.apsusc.2019.05.273. [DOI] [Google Scholar]
- 35.Song Q., Huang F., Li M., Xie B., Wang H., Jiang Y., Song Y. Graded Refractive-Index SiOx Infrared Filters Prepared by Reactive Magnetron Sputtering. J. Vac. Sci. Technol. A. 2008;26:265–269. doi: 10.1116/1.2837836. [DOI] [Google Scholar]
- 36.Wetzel S., Klevenz M., Gail H.-P., Pucci A., Trieloff M. Laboratory Measurement of Optical Constants of Solid SiO and Application to Circumstellar Dust. Astron. Astrophys. 2013;553:A92. doi: 10.1051/0004-6361/201220803. [DOI] [Google Scholar]
- 37.Kischkat J., Peters S., Gruska B., Semtsiv M., Chashnikova M., Klinkmüller M., Fedosenko O., Machulik S., Aleksandrova A., Monastyrskyi G., et al. Mid-Infrared Optical Properties of Thin Films of Aluminum Oxide, Titanium Dioxide, Silicon Dioxide, Aluminum Nitride, and Silicon Nitride. Appl. Opt. AO. 2012;51:6789–6798. doi: 10.1364/AO.51.006789. [DOI] [PubMed] [Google Scholar]
- 38.Berning P.H. Physics of Thin Films. Volume 1 Academic Press; Cambridge, MA, USA: 1963. Theory and Calculations of Optical Thin Films. [Google Scholar]
- 39.Thelen A. Design of Optical Interference Coatings. McGraw-Hill; New York, NY, USA: 1989. [Google Scholar]
- 40.Brendel R., Bormann D. An Infrared Dielectric Function Model for Amorphous Solids. J. Appl. Phys. 1992;71:1–6. doi: 10.1063/1.350737. [DOI] [Google Scholar]
- 41.Rakić A.D., Djurišić A.B., Elazar J.M., Majewski M.L. Optical Properties of Metallic Films for Vertical-Cavity Optoelectronic Devices. Appl. Opt. AO. 1998;37:5271–5283. doi: 10.1364/AO.37.005271. [DOI] [PubMed] [Google Scholar]
- 42.Kim Y.H., Hwang M.S., Kim H.J., Kim J.Y., Lee Y. Infrared Spectroscopy Study of Low-Dielectric-Constant Fluorine-Incorporated and Carbon-Incorporated Silicon Oxide Films. J. Appl. Phys. 2001;90:3367–3370. doi: 10.1063/1.1402152. [DOI] [Google Scholar]
- 43.Lucovsky G., Rayner G.B. Microscopic Model for Enhanced Dielectric Constants in Low Concentration SiO2-Rich Noncrystalline Zr and Hf Silicate Alloys. Appl. Phys. Lett. 2000;77:2912–2914. doi: 10.1063/1.1320860. [DOI] [Google Scholar]
- 44.Tsu D., Lucovsky G., Davidson B. Effects of the Nearest Neighbors and the Alloy Matrix on Sih Stretching Vibrations in the Amorphous Sior-H (0-Less-Than-R-Less-Than-2) Alloy System. Phys. Rev. B. 1989;40:1795–1805. doi: 10.1103/PhysRevB.40.1795. [DOI] [PubMed] [Google Scholar]
- 45.Einsele F., Beyer W., Rau U. Analysis of Sub-Stoichiometric Hydrogenated Silicon Oxide Films for Surface Passivation of Crystalline Silicon Solar Cells. J. Appl. Phys. 2012;112:054905. doi: 10.1063/1.4749415. [DOI] [Google Scholar]
- 46.Lucovsky G., Yang J., Chao S., Tyler J., Czubatyj W. Oxygen-Bonding Environments in Glow-Discharge Deposited Amorphous Silicon-Hydrogen Alloy-Films. Phys. Rev. B. 1983;28:3225–3233. doi: 10.1103/PhysRevB.28.3225. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data are available in the Supplementary Material.