ADME characterization and PBK model development of 3 highly protein-bound UV filters through topical application

Abstract

Estimating human exposure in the safety assessment of chemicals is crucial. Physiologically based kinetic (PBK) models which combine information on exposure, physiology, and chemical properties, describing the absorption, distribution, metabolism, and excretion (ADME) processes of a chemical, can be used to calculate internal exposure metrics such as maximum concentration and area under the concentration-time curve in plasma or tissues of a test chemical in next-generation risk assessment. This article demonstrates the development of PBK models for 3 UV filters, specifically octyl methoxycinnamate, octocrylene, and 4-methylbenzylidene camphor. The models were parameterized entirely based on data obtained from in vitro and/or in silico methods in a bottom-up modeling approach and then validated based on human dermal pharmacokinetic (PK) data. The 3 UV filters are “difficult to test” in in vitro test systems due to high lipophilicity, high binding affinity for proteins, and nonspecific binding, for example, toward plastic. This research work presents critical considerations in ADME data generation, interpretation, and parameterization to assure valid PBK model development to increase confidence in using PBK modeling to help make safety decisions in the absence of human PK data. The developed PBK models of the 3 chemicals successfully simulated the plasma concentration profiles of clinical PK data following dermal application, indicating the reliability of the ADME data generated and the parameters determined. The study also provides insights and lessons learned for characterizing ADME and developing PBK models for highly lipophilic and protein-bound chemicals in the future.

UV filters are used in sunscreen products to prevent sunburn or product photodegradation by inhibiting the infiltration of UV light (Matta et al., 2020). Safety evaluation of their use is critical to protect human health. A combination of consumer preference, a desire for greater human relevance, and an increasing number of bans on the animal testing of cosmetic ingredients and products in different geographies has resulted in rapid developments in non-animal approaches for safety assessment. Next-generation risk assessment (NGRA) is human-relevant, exposure-led, hypothesis-driven, and designed to prevent harm (Dent et al., 2018). Estimating human exposure as early as possible in the process of safety assessment of chemicals is crucial. Physiologically based kinetic (PBK) models combine information on exposure, physiology, and chemical properties, describing the absorption, distribution, metabolism, and excretion (ADME) processes of a chemical, to estimate time-dependent concentration in plasma and tissues (Paini et al., 2019; Rietjens et al., 2011). PBK modeling can be used to calculate internal exposure metrics such as maximum concentration (C_max) and area under the concentration-time curve (AUC) in plasma or tissues of a test chemical, which can help to identify tissues/organs with the highest exposure or accumulation (Li et al., 2021, 2022). These data can further guide the design and rationale of in vitro tests performed for risk assessment and derive a bioactivity:exposure ratio (BER) for decision-making (Health Canada, 2021). Without good quality PBK models describing internal exposure, safety decision-making using new, nonanimal approaches is severely limited.

Few clinical pharmacokinetic (PK) studies are available on sunscreen ingredients to help validate the PBK models, and performing such studies is expensive. When such human PK data are available, the study design is often an evaluation of the worst-case scenario, that is, an unrealistically high exposure is used, rather than mimicking the in-use situation (Schauer et al., 2006; Seirafianpour et al., 2022). For instance, a regulatory requirement on 16 sunscreen ingredients was proposed by the U.S. Food and Drug Administration, recommending assessment of human systemic absorption with a maximal usage clinical trial to ensure the safety of these ingredients, which are classified as drugs in the United States (Matta et al., 2020). The systemic exposure information obtained from these clinical trials could be of use to substantiate the human safety evaluation in certain extreme situations. However, this type of data could not easily be used to inform the safety decisions for any other realistic exposure scenarios which have different doses, formulations, exposure patterns or change of exposure settings in a quantitative way. Generating human PK data to validate the output of every PBK model for each cosmetic ingredient and for every exposure scenario and formulation is simply not feasible. Therefore, it is important to develop PBK models of sunscreen ingredients to estimate internal concentrations in the absence of any human data or for extrapolating existing PK data to other dose regimens in risk assessment.

In NGRA, the challenge for the PBK modelling community is to parameterize models partially or entirely based on data obtained from in vitro and/or in silico methods, with limited or no availability of in vivo kinetic data (especially for dermal absorption routes) to calibrate the models and validate the model outputs. This article discusses in vitro ADME data generation and PBK model development for 3 UV filters, that is, octyl methoxycinnamate (OMC), octocrylene, and 4-methylbenzylidene camphor (4-MBC), with a focus on their highly lipophilic and highly protein-bound characteristics. These types of chemicals exhibits different kinetic behaviors compared with other types of chemicals where human PK data are more common, such as drugs or pesticides (Seirafianpour et al., 2022). We focus on critical considerations in ADME data generation, interpretation, and parameterization to ensure valid PBK model development, to increase the confidence in using PBK modeling to help make safety decisions in the absence of human PK data. This is crucial to enable their acceptance in a regulatory context. Furthermore, our research findings may be important for understanding the kinetic behavior of other similarly lipophilic and highly protein-bound chemicals.

Materials and methods

 

ADME characterization

To characterize the ADME profile of the 3 chemicals and for PBK model parameterization, the following in vitro assays were conducted: ex vivo human skin penetration assay, blood partitioning assay for blood/plasma concentration ratio (Rbp), ultrafiltration assay for fraction unbound (Fup), and hepatocyte stability assay for hepatic intrinsic clearance (CL_int).

Ex vivo skin penetration study

Literature data were available for the ex vivo skin penetration of 4-MBC (Sasson et al., 2009) and octocrylene (SCCS, 2021), this was used to parameterize the dermal absorption of the compound. For OMC, no useful ex vivo skin penetration data were found in the literature. Therefore, new data were generated with the following methods, compliant with the requirements of Good Laboratory Practice, OECD guidance (OECD, 2004) and the SCCS Notes of Guidance (Bernauer et al., 2021). A summary of the methods is provided next. The output obtained from the skin absorption studies were kinetic data measured in receptor fluid as well as distribution in vehicle (skin wash) and skin layers.

The rate and extent of the in vitro dermal absorption of radiolabeled OMC in an emulsion formulation (the active ingredient [OMC] concentration was 10%) was investigated as follows. Thirty-seven samples of human abdominal skin were obtained from 5 donors (4 female and 1 male) aged 34–60 years old who gave informed consent (prior to undergoing routine surgery) for their surgical waste skin to be taken for scientific purposes. The skin was dermatomed to a thickness of 350–450 µm. Skin samples were mounted in flow-through dynamic diffusion cells (1 cm² dose application area) and the skin surface temperature was maintained at 32°C ± 1°C, with a fixed water bath integrated in the dynamic system. The receptor fluid (5% w/w bovine serum albumin, 0.9% NaCl in water) circulated at 1.5 ml/h giving a total volume of 36 ml for the volume obtained after dismantling 24 h after application on skin (and 12 ml for dismantling 8 h after application on skin). The solubility of the test item in the receptor fluid indicated that infinite sink conditions would be maintained throughout the experiment. Barrier integrity was assessed so only the skin meeting the criteria was included for subsequent absorption measurements. The test preparation was applied homogeneously at 2 mg/cm² (2 mg/cell) on each skin sample using a positive displacement pipette. The donor chambers of the cells were left unoccluded. The total experiment was stopped 24 h after application. Absorption of the test item was assessed by collection of receptor fluid in hourly fractions from t = 0 until the termination time point. Cells were washed at 30 min, 1 h, 2 h, 4 h, and 8 h (n = 5) and at 24 h (n = 12), respectively. The donor and receptor chambers were dismantled, the skin removed, then the chambers were each extracted with solvent. The stratum corneum was removed with maximum 20 successive tape strips (adhesive scotch Magic 3M); The epidermis of the exposed area was separated from the dermis by heat treatment. Radioactivity was determined by scintillation counting of each receptor solution fraction plus the receptor solution contained within the cell at termination, skin rinse, skin swab, donor and receptor chamber rinses, tape strip, epidermis, dermis, and flange skin.

The details of the ex vivo skin penetration study for octocrylene are reported in the literature (SCCS, 2021). Briefly, the absorption of radiolabeled octocrylene into and through human skin was assessed by single topical application of a target dose of 300 µg/cm² of test substance, formulated in a market representative cosmetic formulation, to split thickness skin preparations from 6 donors mounted in flow-through diffusion cells. The test preparation was applied homogeneously at 3 mg/cm² (3 mg/cell) on each skin sample, The active ingredient (octocrylene) concentration was 10%. Receptor fluid was collected from each cell in fractions by continuous collection over defined intervals over 24 h. After the exposure time of 24 h, skin membranes were washed with a mild soap solution followed by tap water and the test substance was recovered from all compartments of each diffusion cell.

The penetration of 4-MBC applied in an oil-in-water (O/W) emulsion (containing 4% 4-MBC) was taken from a preexisting in vitro (Franz cells) study found in the literature which used pig ear skin as described in Sasson et al. (2009). It is important to highlight that when conducting ex vivo skin penetration studies, human skin was the preferred option. However, in the case of 4-MBC, there is a lack of available data using human skin. Consequently, published quality data utilizing pig skin was utilized for dermal absorption model development as pig skin has historically been shown to be a good model for human skin. The 20 ± 0.2 mg/cm² emulsion was applied to the skin for a period of 24 h. The 4-MBC was readily soluble in the receptor fluid. At 8 h of experiment, the skin surface was washed with 3 ml of receptor fluid and quantified by HPLC. At 24 h, the skin was removed from the cells, stratum corneum (SC) was stripped with ±40 adhesive tapes (3M) that became in contact with methanol for 30 min in ultrasound to break the cells. At 0, 5, 8, and 24 h, 1.5 ml of receptor fluid was removed from the cell and analyzed by HPLC (assessment of possible permeation of 4-MBC).

Blood partitioning assay for determining Rbp

Whole blood (fresh, anticoagulant lithium heparin) was sourced from humans (mixed gender, pooled). Plasma (=blood supernatant) was separated by centrifugation from an aliquot of the whole blood used (reference plasma). Test item (OMC, octocrylene, or 4-MBC at 5 µM) was incubated in parallel with whole blood and reference plasma (n = 3). After 0 and 60 min of incubation at 37°C, reactions were stopped, and the Rbp was determined by comparing the test item concentration in control plasma with the test item concentration in the whole blood supernatant (LC-MS/MS analysis). Chlorthalidone (5 µM) was used as a positive control for the assay (expected high affinity to red blood cells).

Cross filtration for determining plasma protein binding/Fup

In this modified ultrafiltration procedure described by Taylor and Harker (2006), test chemical (10 µM of OMC, octocrylene, or 4-MBC) was incubated with plasma from humans (pooled, mixed gender) at 37°C for 60 min (n = 3), followed by ultrafiltration. In parallel with each experimental plasma sample (incubated with test chemical), a control plasma sample (blank) was also processed by ultrafiltration. The retentate from experimental and control plasma samples were mixed back into the filtrate of the partner sample. The resulting regenerated plasma samples, one representing the experimental filtrate and one representing the experimental retentate, were then analyzed by LC/MS/MS. Warfarin (10 µM) was included as specific high plasma protein binding (PPB) reference (positive control). The test item concentration in the 60 min stability control sample was compared with the nonincubated negative control sample concentration (=100%) to check test item plasma stability. The percentage of compound bound to plasma proteins (% PPB) was calculated using the following equations:

$$\text{PPB} \left[\%\right]=100-\frac{({\text{test} \text{item} \text{concentration}}_{\text{plasma} \text{filtrate}}/\text{RV})}{{\text{mean} \text{test} \text{item} \text{concentration}}_{\text{incubated} \text{plasma} }} *100$$

Results are expressed as mean PPB value calculated from plasma filtrate. In addition, the concentration of test item was corrected for the specific test item recovery (RV):

$$\text{RV}=\frac{({\text{concentration}}_{\text{plasma} \text{filtrate}}+{\text{concentration}}_{ \text{plasma} \text{retentate}})}{{\text{mean} \text{concentration}}_{\text{incubated} \text{plasma} }}$$

Fup was then calculated as Fup (%) = 100 − PPB (%).

Metabolic stability in primary human hepatocytes (PHH) in suspension

Test chemical (0.1, 1, and 10 µM of OMC, octocrylene, or 4-MBC) was incubated with cryopreserved suspensions of human hepatocytes (0.8 × 10⁶ cells/ml, 48-well format, 5 donor pool) in Williams E medium (25 mM HEPES, 2 mM l-glutamine) at 37°C, at 6 time points (0, 15, 60, 90, 180, and 240 min) (n = 3). The final solvent content was ≤0.5% DMSO or 1% ACN. Several controls were included: (1) negative control 1: test item incubated without cells (0 and 240 min); (2) negative control 2: test item incubated with heat-inactivated (boiling in a water bath, 10 min) suspension cells (0, 90, and 240 min); (3) in order to demonstrate adequate enzyme activity of the suspension hepatocytes during the metabolic stability assay, Naloxone (known intermediate CL_int) was incubated in parallel to test chemicals (0, 90, and 240 min) as positive control. Test chemicals were analyzed by LC-MS to determine the loss of parent compound and intrinsic clearance. The in vitro CL_int was calculated using −k * V, where k is the slope from the linear regression of log [test compound] versus time plot [1/min] and V is the ratio of incubation volume and cell number.

PBK software and model structure

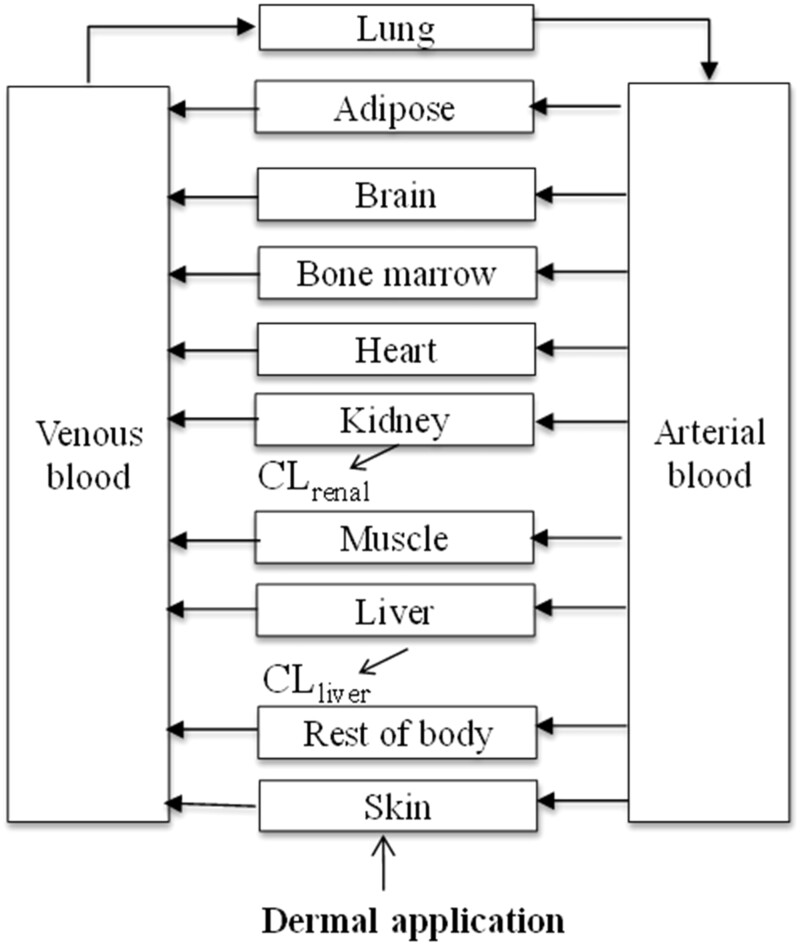
PBK modeling and simulations for the 3 chemicals were conducted using GastroPlus 9.8 (Simulation Plus, Lancaster, California). GastroPlus includes embedded databases for physiological and anatomical parameter values and includes modules to simulate several administration routes including dermal absorption. In GastroPlus, the most extensive PBK model configuration was chosen which is comprised of tissue compartments representing most major tissues in the body including liver, kidney, heart, and lungs, etc. Figure 1 shows the structure of the PBK model for the 3 chemicals.

Figure 1.

Schematic diagram of the human PBK model structure for the 3 chemicals.

PBK model parameterization

Chemical-specific parameters

Briefly, physicochemical and ADME properties were either predicted in silico or determined using in vitro methods. Log P (logarithm of octanol-water partition coefficient), pKa (logarithm of acid dissociation constant), and Madin-Darby canine kidney (MDCK) permeability were predicted with ADMET predictor (v.10.2). With the predicted properties (log P, molecular weight, pKa, and permeability), classification was conducted using the Extended Clearance Classification System (ECCS), which provides information about the dominant route of clearance from the body (Varma et al., 2015). The sensitivity indices (see Sensitivity analysis section), along with knowledge of the statistical performance and the applicability domain (eg, chemical space, parameter range, etc.) of the QSARs and ECCS classification, were used to guide the decisions on the need for generation of in vitro data. The other ADME parameters, that is, skin absorption, Fup, Rbp, hepatic CL_int, were obtained from the in vitro assays as described in ADME characterization section. Tissue-to-plasma partitioning coefficients (Kt:p) were calculated in Gastro-Plus using the Berezhkovskiy method (Berezhkovskiy, 2004), assuming chemical distribution into the tissues is perfusion limited. Kidney clearance rate was then predicted by the formula GFR * Fup, where GFR is the glomerular filtration rate (with 2.0 ml/s the default value in GastroPlus 9.8).

Dermal absorption model

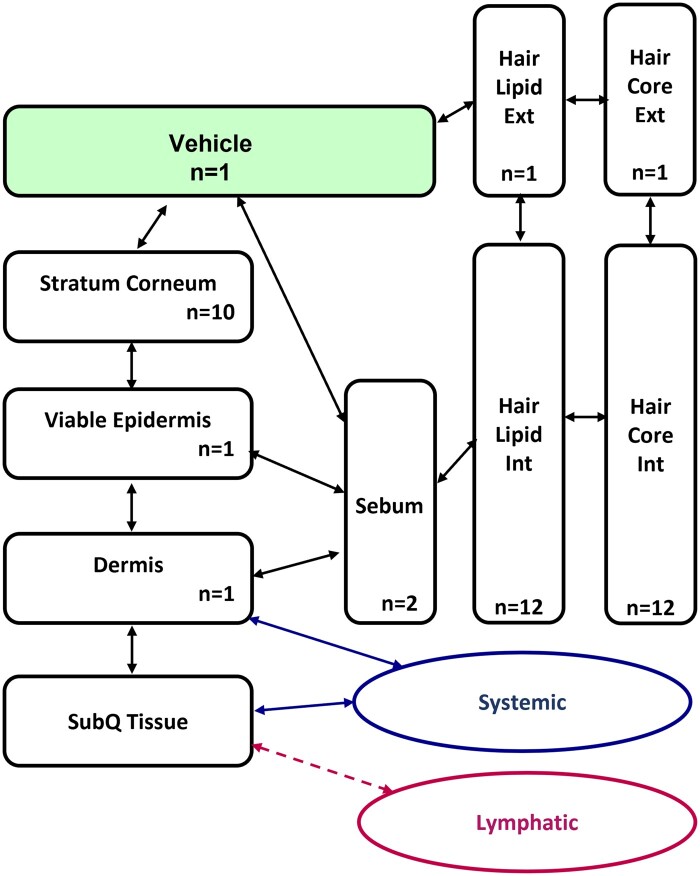
The dermal module (TCAT) in GastroPlus is a complex mechanistic model of dermal absorption, which can simulate a variety of transdermal dosage forms, including liquid formulations (solutions, lotions, suspensions) and semisolid formations (gels, creams, lotions, pastes). The transdermal chemical delivery model represents the skin as a collection of the following compartments (Figure 2): stratum corneum, viable epidermis, dermis, subcutaneous tissue, sebum, hair lipid, and hair core, to account for the chemical concentration gradient within each compartment due to chemical diffusion under nonsteady-state conditions. For the chemicals, key input parameters in the TCAT module, that is, diffusion and partitioning coefficients of the chemical in various skin layers (stratum corneum, epidermis, dermis, and sebum) are required. The dermal module also has the capability to include formulation-related parameters, such as partitioning between vehicle and water, evaporation, etc.

Figure 2.

Schematic diagram of the TCAT module in GastroPlus showing how the different compartments are connected to one another and the rest of the body. N represents the number of sublayers divided in vehicle or each skin layer for better reflection of concentration gradient.

For all the chemicals, dermal transport was modeled through the TCAT module in GastroPlus and parameterized using the ex vivo skin penetration data. Diffusivity and partition coefficient parameters were optimized from initially predicted values by fitting an in vitro skin penetration model set up in GastroPlus to the skin penetration data, that is, absorption into the receptor fluid and/or distribution in different skin layers (adjusting parameters until there is minimal difference between model output and the experimental data). The partition coefficients and diffusivity coefficient relevant to vehicle, stratum corneum, epidermis, and dermis determined in this fashion were then used as inputs into the human model of skin penetration.

Prediction of hepatic clearance

For the 3 chemicals, the liver compartment of the PBK model was provided with input data on hepatic clearance (CLliver), which was calculated in 2 steps.

First, the in vitro hepatic CL_int (l/h/million cells) determined from hepatocyte stability assay (Metabolic stability in primary human hepatocytes (PHH) in suspension section) was scaled to in vivo CL_int (l/h), accounting for the hepatocellularity and liver weight as described by Houston (1994):

$$invivo{\text{ CL}}_{\text{int}}=invitro{\text{ CL}}_{\text{int}}*\text{SF}$$

where SF (scaling factor) represents the million cells per gram of liver multiplied by the grams of liver weight. A hepatocellularity of 120 million cells/g of liver (Bayliss et al., 1990) and corresponding human liver weight of each clinical subject were used.

Second, the CLliver was calculated using the commonly used equation of the well-stirred liver model.

Two variations of the well-stirred liver model for CLliver calculation were considered (Buck et al., 2007),

$$\mathrm{CLliver}=\frac{\mathrm{Qliver}\times \frac{in \mathit{vivo}\mathrm{ }\mathrm{CLint}}{\mathrm{Fuinc}}\times \mathrm{Fup}}{\mathrm{Qliver}+\frac{in \mathit{vivo}\mathrm{ }\mathrm{CLint}\mathrm{ }}{\mathrm{Fuinc}}\times \frac{\mathrm{Fup}}{\mathrm{Rbp}}}\mathrm{ }$$ (1)

$$\mathrm{CLliver}=\frac{\mathrm{Qliver}\times in \mathit{vivo}\mathrm{ }\mathrm{CLint}\times \mathrm{Rbp}}{\mathrm{Qliver}+in \mathit{vivo}\mathrm{ }\mathrm{CLint}}$$ (2) (selected)

where CLliver is hepatic plasma clearance, Qliver is the hepatic blood flow (human, 90 l/h), and Fuinc is unbound fraction in hepatocyte incubation (Winiwarter et al., 2019). The first equation provides an estimate of in vivo CL of the unbound chemical, whereas the second equation describes the in vivo CL of the total, that is, bound and unbound chemical. As for the 3 studied chemicals, they are highly lipophilic and highly bound to plasma protein, the inclusion or exclusion of the fraction unbound parameters will have a huge impact on the determined CLliver. As there is no guidance on which liver model provides more appropriate estimation on CLliver for this type of chemical, literature review on hepatic clearance for highly plasma protein bound chemicals was conducted. The summarized findings could be found in Results section, based on which the second equation was selected for calculating the CLliver of all 3 chemicals.

Sensitivity analysis

To identify the parameters which have the biggest influence on the output, a sensitivity analysis was performed. As described previously (Moxon et al., 2020), this was carried out by adding a perturbation ($\epsilon$) to one parameter (${\theta }_i$) at a time, whilst keeping all the other parameters at the in silico predicted (nominal) values. A sensitivity index ($S_i$) was then calculated using the partial derivatives based on the nominal values (Hamby, 1994):

$$S_i=\left|\frac{y_n-y_i}{{\theta }_i-\mathrm{ }{\epsilon \theta }_i}\frac{{\theta }_i}{y_n}\mathrm{ }\right|$$ (3)

The sensitivity index is based on a certain endpoint $y$, here representing C_max and AUC with the subscript $n$ representing the endpoint when all parameters are at the nominal value and subscript $i$the endpoint when one parameter is perturbated. If the sensitivity index of a parameter is close to zero then it has little influence on the output (in the local parameter space), whereas a parameter with a higher sensitivity index will have a greater influence on the output even if small changes are made. The sensitivity analysis was carried out using the GastroPlus parameter sensitivity analysis function by calculating the effect of a parameter change (increase of 5% in parameter value) on the output (eg, C_max or AUC). Then the sensitivity indices were calculated based on equation 3. Indices were normalized by the nominal parameter value and the nominal output value, allowing the effect of the variation of a parameter upon the output to be compared directly.

Model simulation and performance

The GastroPlus built-in mathematical equations were used unaltered, and no additions were made to the modules available in GastroPlus (eg, TCAT module for simulation of dermal route of exposure). Besides, the model parameters and approach were recreated by an internal independent expert for quality control purpose.

Clinical PK data

Details of clinical PK studies following topical administration of each chemical are given next. The observed PK data were used for PBK model validation, and these studies were not used in model building, OMC, and octocrylene: Clinical data from a study assessing the systemic absorption and PK of UV filters was used to validate the PBK models for octocrylene and OMC (Matta et al., 2020). In the study, 12 healthy participants were randomized to 1 of 4 sunscreen products formulations. The PK data used for octocrylene and OMC involved a lotion and/or a nonaerosol spray applied at 2 mg/cm² to 75% of body surface area at 0 h on day 1 and 4 times on day 2 through day 4 at 2-h intervals. These conditions were replicated in the model and concentration-time profiles were simulated for comparison against observed data.

Four-MBC: The toxicokinetics of 4-MBC after dermal administration were investigated in human subjects (Schauer et al., 2006). Humans (3 male and 3 female subjects) were exposed to 4-MBC by topical application of a commercial sunscreen formulation containing 4% 4-MBC (w/w), covering 90% of the body surface and resulting in a mean dermal 4-MBC dose of 22 mg/kg bw. Concentrations of 4-MBC were monitored over 96 h in plasma and urine.

Population simulation and validation of PBK models

Once the in silico or in vitro parameters were obtained, population simulations of plasma concentrations corresponding to the clinical PK studies were then performed using GastroPlus. For OMC and octocrylene, the mixed multiple doses profile in GastroPlus was used to reflect multiple doses of specific amounts at varying intervals to closely simulate the clinical study design. The predicted plasma concentration data were compared with the observed PK data following dermal exposure. The Population Estimates for Age-Related Physiology module was used to match the exposure design-specific input parameter in GastroPlus to the corresponding observations of reported clinical studies. The built-in GastroPlus algorithm was used to account for sex, age, and body weight-dependent changes in the physiological and anatomical parameters, such as blood flow, cardiac output, and organ/tissue volumes. To this end, a virtual population of 1000 subjects was generated via Monte Carlo simulations. The population simulations incorporated 10%–30% variability on various systems and certain chemical-specific parameters and 40% for hepatic clearance, based on GastroPlus built-in values as well as literature-reported variability values. For the most influential parameters, that is, skin absorption-related diffusivity and partitioning parameters, 100% variability was set to cover the wide variability that was observed in the ex vivo skin penetration assay. Tenth and 90th percentile values were generated for the model-based population predictions on plasma concentration (C_max and AUC_0−t) to compare with measured human data.

Results

ADME characterization and PBK model parameterization

Physicochemical properties, ECCS classification, and ADME properties

Physicochemical properties were derived using ADMET predictor, including log P, ionization and MDCK permeability (Table 1). All 3 chemicals are highly lipophilic (log P: 4.63–6.17). Using the ECCS classification based on the log P, MW, and permeability values, all 3 compounds were predicted to be predominately cleared via liver metabolism (Class 2). For renal clearance rate, Fup × GFR were used to account for glomerular filtration.

Table 1.

Physico-chemical properties, ADME properties, and ECCS predictions of dominant clearance mechanism

Compound	MW g/mol	Log Pa	Ionizationa	MDCK Permeability cm/s × 10−7 a	ECCS Class b	Rbp c	PPB% c	Fup% c	Renal Clearance (l/h) d
OMC	290.4	5.7	Neutral	1369.9	Class 2 metabolism	0.73	99.96	0.04	0.003
Octocrylene	361.5	6.17	Neutral	1439.6	Class 2 metabolism	0.73	99.86	0.14	0.01
4-MBC	254.4	4.63	Neutral	801.6	Class 2 metabolism	0.88	99.96	0.04	0.003

^aPredicted using ADMET predictor 10.2 using the SMILES code for each structure as input.

^bThe ECCS (extended clearance classification system) class as determined by the criteria in Varma et al. (2015).

^cMeasured data.

^dCalculated by GFR * Fup.

Blood partitioning and plasma protein binding

The determined Rbp values were 0.73, 0.73, and 0.88 for OMC, octocrylene, and 4-MBC, respectively (Table 1).

Overall, no significant degradation of the 3 chemicals was observed during incubation with human plasma and they all showed high binding to human plasma proteins, as indicated by PPB values of 99.86 (octocrylene) and 99.96% (OMC and 4-MBC) (Table 1). Based on the PPB values, the calculated fraction unbound in plasma of all 3 chemicals are significantly low (0.04%, 0.14%, and 0.04% for OMC, octocrylene and 4-MBC, respectively).

Skin absorption

To aid parameterization of the skin absorption model (TCAT) in GastroPlus, ex vivo skin penetration studies were either carried out in the present study (OMC) or found in the literature (4-MBC and octocrylene). The mean total recovery for each condition was within the acceptance criteria (85%–115%) (OECD, 2004) for both the literature and the newly generated data. Because the penetration of OMC and octocrylene through the skin is extremely low, some large variances in the data at different time points in different skin layers could be seen. The rate and extent of the in vitro dermal absorption of radiolabeled OMC in an emulsion test formulation at target dose of 200 µg/cm² was investigated which showed that the dermal delivered fraction of the applied OMC was low, less than 0.5% of the applied dose for all the conditions (Table 2). The absorption of octocrylene into and through human skin was assessed by single topical application of a target dose of 300 µg/cm² of test substance formulated in a representative cosmetic formulation (SCCS, 2021). Under the test conditions used, the absorbed dose of octocrylene into receptor fluid was negligible (Table 3). The dermal delivered fraction of the applied octocrylene was low, less than 0.4% of the applied dose for all the conditions. The in vitro penetration of 4-MBC applied in a sunscreen formulation of oil-in-water (O/W) emulsion as reported from the literature showed that 24 h after application of the product, 4-MBC was detected in receptor fluid, epidermis in dermis. However, most was found in the stratum corneum (Table 4) (Sasson et al., 2009).

Table 2.

Distribution of ¹⁴C-OMC after application to human skin (% Mean and standard deviation [SD])

Test Item	OMC
Six conditions: application terminated at:	30 min		1 h		2 h		4 h		8 h		24 h
	n = 5		n = 5		n = 5		n = 5		n = 5		n = 12
	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
Total strips (1–20)	0.51	0.14	0.30	0.13	0.73	0.20	0.37	0.21	0.50	0.18	0.41	0.17
Skin excessa	91.04	3.62	112.02	5.78	89.22	6.47	100.26	10.39	113.76	7.10	100.26	10.53
Epidermis	0.07	0.02	0.04	0.02	0.06	0.03	0.05	0.02	0.10	0.09	0.21	0.16
Dermis	0.004	0.01	0.01	0.01	0.005	0.01	0.01	0.01	0.01	0.01	0.02	0.01
Receptor fluid	0.02	0.05	0.003	0.01	0.04	0.02	0.06	0.04	0.09	0.05	0.06	0.08
Dermal deliveryb	0.10	0.05	0.06	0.03	0.11	0.06	0.12	0.05	0.20	0.14	0.28	0.17
Total recovery	91.65	3.64	112.38	5.74	90.06	6.29	100.75	10.47	114.46	6.85	100.96	10.56

^aSkin excess corresponds to: Washing + Donor compartment rinsing + Remaining skin.

^bDermal delivery is Epidermis + Dermis + Receptor fluid according to SCCS Notes of Guidance.

Table 3.

Distribution of ¹⁴C-octocrylene after application to human skin (%mean and SD) as reported in SCCS (2021)

Test item	Octocrylene
Application terminated at:	24 h (n = 12)
	Mean	SD
Total strips (1–20)	0.69	0.31
Skin excessa	97.96	4.93
Epidermis	0.14	0.16
Dermis	0.012	0.016
Receptor fluid	0.0001	0.0003
Dermal deliveryb	0.15	0.17
Total recovery	98.8	4.92

^aSkin excess corresponds to: Washing + Donor compartment rinsing + Remaining skin.

^bDermal delivery is Epidermis + dermis + receptor fluid according to SCCS Notes of Guidance.

Table 4.

Distribution of 4-MBC after application to pig skin (% Mean and SD) as reported in Sasson et al. (2009)

Test item	4-MBC
Application terminated at:	24 h (n = 5)a
	Mean	SD
Skin excessb	4.5	0.72
Total strips (1–40)	80.1	6.19
Epidermis + Dermis	2.9	0.5
Receptor fluid	0.25	0.03
Dermal deliveryc	3.17	0.53
Total recovery	87.8	6.9

^aAt 8 h of postdosing, the skin surface was washed.

^bSkin excess corresponds to: Washing + Donor compartment rinsing + Remaining skin.

^cDermal delivery is Epidermis + dermis + receptor fluid according to SCCS guideline.

The initial in silico derived skin penetration parameters were refined by fitting the dermal kinetic model to the skin penetration data, that is, time course absorption into the receptor fluid, if available, and distribution in skin wash and different skin layers, by adjusting parameters until there was minimal difference between the model output and the experimental data. The refined parameters (Table 5) were then used as dermal exposure input in the PBK model for predicting clinical PK profile of the 3 chemicals following topically applied application in humans.

Table 5.

Skin absorption parameters as input in the PBK models

	OMC	Octocrylene	4-MBC	Source
Vehicle/water partition coefficienta	1.5E+05	4.0E+05	4.0E+04	Fitted
Vehicle diffusivity (cm2/s)	7.0E−12	6.2E−09	7.8E−06	Fitted
Stratum corneum/water partition coefficient	4.5E+02	2.0E+03	1.0E+03	Fitted
Stratum corneum diffusivity (cm2/s)	2.0E−10	2.0E−11	6.1E−11	Fitted
Epidermis/water partition coefficient	2.0E+01	6.0E+02	1.0E+02	Fitted
Epidermis diffusivity (cm2/s)	3.0E−08	2.0E−08	1.9E−09	Fitted
Dermis/water partition coefficient	7.0E−01	7.0E−01	2.0E+00	Fitted
Dermis diffusivity (cm2/s)	1.0E−07	6.0E−08	3.0E−08	Fitted
Sebum/water partition coefficient	5.5E+04	1.5E+05	5.4E+03	Lian-Yangb
Sebum diffusivity (cm2/s)	5.3E−08	1.6E−08	1.1E−07	Lian-Yangb

^aVehicle/water partition coefficient is vehicle/formulation specific that when a different vehicle/formulation is used, this parameter may differ accordingly.

^bLian-Yang method from GastroPlus.

Hepatic clearance

Assessment of the reliability of the hepatocyte stability data

Metabolic experiments using suspension PHH were performed to determine the hepatic clearance rate of the chemical. Due to the chemical characteristics of these chemicals with high lipophilicity and high protein binding, they could be considered as “difficult to test” chemicals, in that they were expected to be prone to nonspecific binding in in vitro cell assays. This could impact both, the acceptance of the assay data and interpretation of the results. For these types of chemicals, the quality of the control data played a significant role when assessing the reliability of the data and interpretation of the results. As a reference, Naloxone was investigated to monitor intermediate clearance in comparison with the test chemicals. As expected, Naloxone was metabolized with moderate in vitro CL_int of 16.4 ± 1.6 µl/min/million cells (4.8 ± 1.9% remaining after 240 min). To further assess the reliability of the hepatocyte stability data, several criteria (Table 6) were established for negative controls so that only data passing the criteria were used to estimate a clearance rate. Considering the type of controls used in the study is important, that is, we found that data generated in media only (no cells) were not the most appropriate control data for these chemicals as significant losses were observed in the controls due to nonspecific binding (data not shown), which did not occur in the presence of cells. Heat-inactivated control was shown to be more suitable as negative control for these types of chemicals.

Table 6.

Assessment criteria of the reliability of the hepatocyte stability negative control data

Passing criteria		Rationale
1	(a) t = 0 negative control within 20% of nominal concentration	(a) Reliability of quantification
	and/or	and/or
	(b) t = 0 negative control within 20% of t = 0 assay concentration	(b) Representative negative controls
2	Relative standard deviation (or CV%) <20% for t = 0 negative control	Reliability of quantification
3	<20% change in negative control over experiment	Negative control consistency, nonmetabolic losses ruled out

Hepatocyte stability results

Hepatic loss of OMC, octocrylene, and 4-MBC in human suspension hepatocytes assays are shown in Figure 3. It could be seen that they all displayed medium to fast depletion in suspension hepatocytes (they all have shown to have faster depletion rate than the reference chemical Naloxone with known intermediate CL_int). Based on the assessment criteria, most of the treatment data are acceptable, except for the 2 lowest concentrations of OMC failing criterial 1 or 2 (Table 6). For both octocrylene and 4-MBC, the in vitro clearance values decreased with increasing concentration, indicating saturated enzyme reactions at higher concentrations. However, as the calculated mean in vitro CLint was close to the clearance rate obtained at the 0.1 µM concentration which is a biologically relevant concentration for the 3 chemicals, the mean in vitro CL_int data were used to scale to in vivo CL_int values.

Figure 3.

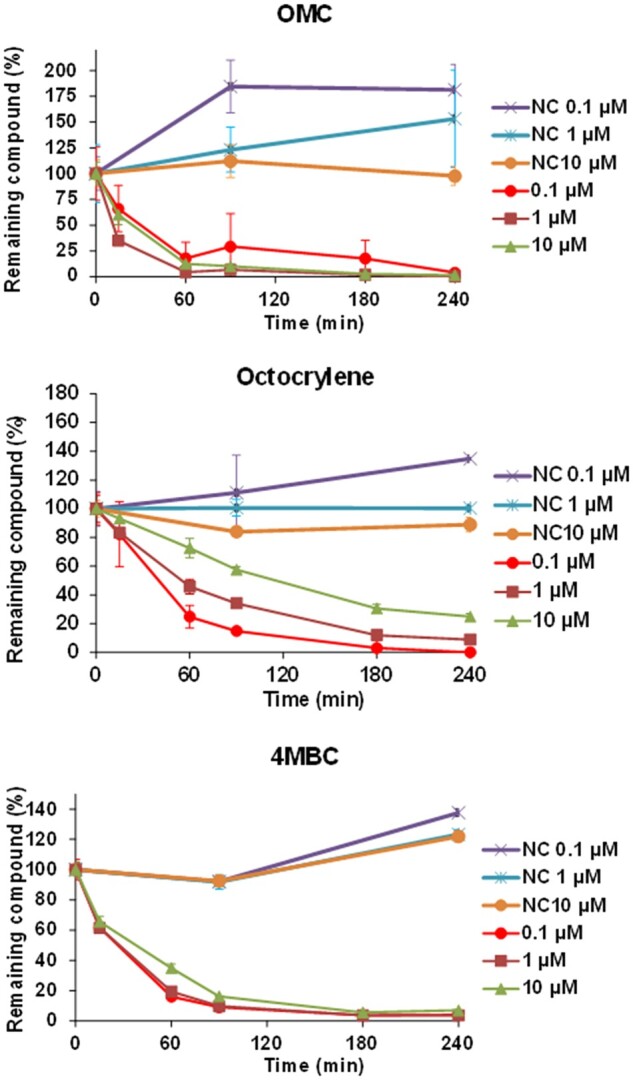
Hepatic loss of OMC, octocrylene, and 4-MBC in human suspension hepatocytes assays. NC, heat-inactivated negative control.

Hepatic clearance for highly plasma protein-bound chemicals and the determination of CLliver

After the in vitro CL_int values were scaled to in vivo CL_int values, 2 variations of the well-stirred liver model were considered to convert the in vivo CL_int to hepatic clearance (CLliver); the first equation provides an estimate of hepatic clearance of the unbound chemical, whereas the second equation describes the hepatic clearance of the total, ie, unbound and bound. As for the 3 studied chemicals, the inclusion or exclusion of the fraction unbound parameters will have a huge impact on the determined hepatic clearance. A literature review on hepatic clearance for highly plasma protein-bound chemicals was conducted.

Buck et al. found that in vitro CL_int may provide a better estimate of in vivo liver clearance of total rather than unbound chemical (Buck et al., 2007). Obach et al. found that for highly bound compounds (free fraction in plasma below 0.1), clearance can be severely underpredicted using a standard well-stirred model (Equation 1) for the liver (Obach, 1999) and Poulin and Hadded also suggested that more is available for metabolism than the free concentration (Poulin and Haddad, 2021). Baker and Parton also suggested that hepatic clearance was usually underestimated using scaled data obtained from hepatocytes and microsomes and that this underprediction of clearance was most common when the compound was highly bound (Baker and Parton, 2007). The relationship between Fup and clearance was investigated by Pang et al., too. They found that the clearance of a low extraction ratio chemical will be affected to a great extent by the chemical’s plasma protein binding. On the other hand, the clearance of highly extracted chemicals is unlikely to be affected by plasma protein binding (Pang and Rowland, 1977). For example, some chemicals may be eliminated or metabolized by mechanisms that have an even higher affinity for them than do the binding sites on their plasma protein. This is what happens in the case of propranolol, which is a highly bound chemical which is metabolized by such a high affinity hepatic enzyme system that its rate of clearance completely depends on the rate of its delivery to the liver. Although the chemical is 90%–95% bound to plasma, hepatic removal is so avid that both bound and free forms are extracted. Consequently, hepatic elimination is unaffected by chemical binding in blood (Shand, 1976). For the 3 tested UV filters, at biological relevant concentrations approximately 0.1 µM, in vitro CL_int values as determined in the hepatocyte stability assay are high, indicating high affinity for hepatic enzymes. Therefore, using the standard well-stirred equation including the corrections for the unbound fraction in vitro and in plasma, the in vivo hepatic clearance is very likely to be underestimated significantly. Based on these findings, the nonrestrictive equation (equation 2) was selected for calculating the liver clearance (CLliver) of all 3 chemicals (Table 7) and used as input in the PBK models in GastroPlus.

Table 7.

In vitro and in vivo clearance data

	In vitro CLint (µl/min/million cells)				In vivo CLint scaled (l/h/kg liver)a	CL liver l/h/kg bwb
	0.1 µM	1 µM	10 µM	Mean
OMC	—	—	43.34	43.34	312.0	1.1
Octocrylene	27.8	15.23	7.6	16.9	121.7	0.9
4-MBC	34.0	32.2	23.8	30.0	216	1.0

^a in vivo CL_int scaled from the mean in vitro CL_int.

^bCLliver calculated based on equation 2. Assuming average body weight 70 kg with 1.5 kg of liver weight and 90 l/h of Qliver.

—Data didn’t pass acceptance criteria.

Prediction of tissue-plasma partitioning

The distribution of the 3 chemicals in each compartment was modeled as perfusion limited. For calculating the tissue plasma partition coefficients (Table 8), the method published by Berezhkovskiy (2004) (an option available in GastroPlus) was used, which has shown to be a high performing method for calculating partitioning of neutrals (Mathew et al., 2021).

Table 8.

Kt:p: Tissue-to-plasma partition coefficient

Tissue	OMC	Octocrylene	4-MBC
Lung	0.84	1.21	0.49
Adipose	28.77	128.16	2.18
Muscle	3.13	5.64	0.81
Liver	4.98	9.19	1.08
Heart	2.07	3.60	0.66
Brain	7.86	14.71	1.52
Kidney	3.10	5.56	0.81
Skin	3.77	6.89	0.89
RedMarrow	8.49	16.07	1.46
YellowMarrow	28.77	128.16	2.18
RestOfBody	3.15	5.66	0.83

Sensitivity analysis

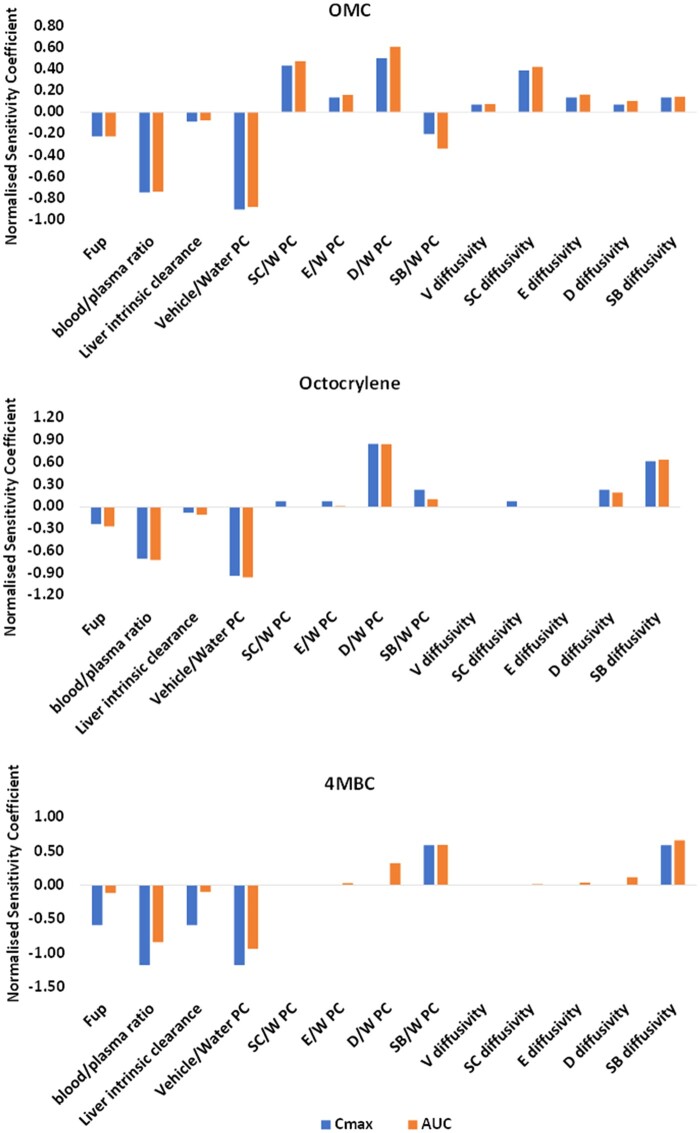
Sensitivity analysis was performed to provide a quantitative evaluation of how input parameters influence the model output. The normalized sensitivity coefficients for all chemical specific parameters were generated to determine the influence of parameter variation on the model output. This showed that C_max and AUC values are sensitive to chemical-specific parameters, for example, Rbp, Fup, skin absorption parameters, and liver clearance (Figure 4).

Figure 4.

Illustration of the output of sensitivity analysis of PBK model. A sensitivity coefficient of 1 implies that a 1% change in parameter value (ie, input) leads to a 1% change in output (ie, Plasma C_max and AUC predictions) of the model, indicating that the output is sensitive to that input parameter under the evaluated conditions. V, vehicle; SC, stratum corneum; E-epidermis, D-dermis, SB-sebum, PC-partition coefficient and W-water.

Model evaluation

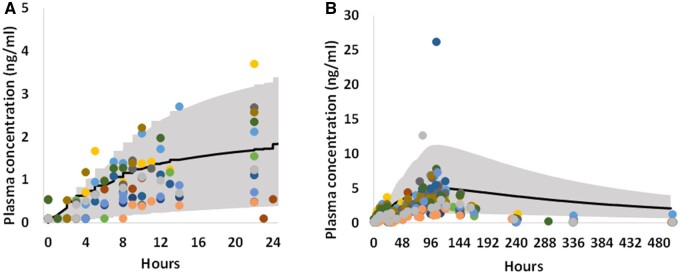
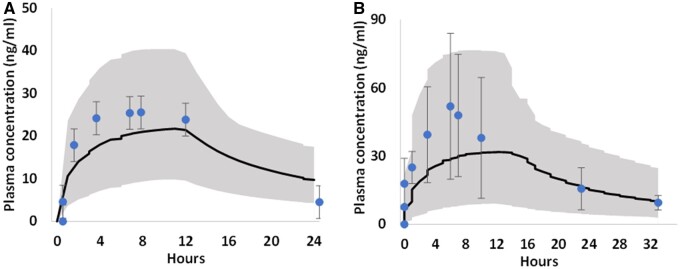
To evaluate the performance of the 3 human PBK models, which were developed using parameter values derived from in silico and in vitro data, the models were validated against independent plasma PK data from clinical studies, which were not used for model development. Figures 5–7 show the comparison of observed and simulated plasma concentration-time profiles of OMC, octocrylene, and 4-MBC following topical administration from 3 individual clinical studies. The model’s predictive performance was evaluated by calculating C_max and AUC_0−t ratios for simulations over observations.

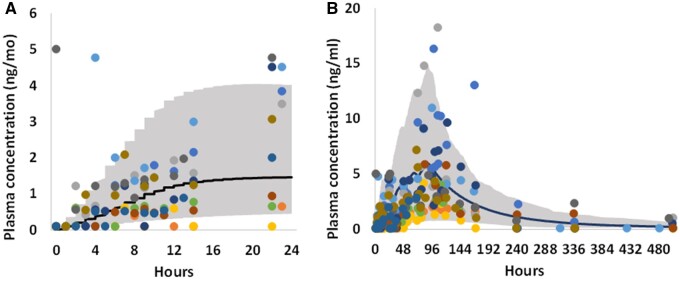
Figure 5.

For OMC, comparison between observed (dots, different color represents different subject data) (Matta et al., 2020) and PBK simulated (solid curve, mean) plasma concentration time profiles, for day 1 (A) and the entire study duration (B, 21 days) after dermal application of a nonaerosol Spray sunscreen product containing 7.5% OMC. The study product was applied 1 time on day 1 (0 h) and 4 times per day for the remaining 3 days. The shaded area represents the 90th percentiles interval of human population simulation.

Figure 6.

For octocrylene, comparison between observed (dots, different color represents different subject data) (Matta et al., 2020) and PBK simulated (solid curve, mean) plasma concentration time profiles, for day 1 (A) and the entire study duration (B, 21 days) after dermal application of a lotion sunscreen product containing 6% octocrylene. The study product was applied 1 time on day 1 (0 h) and 4 times per day for the remaining 3 days. The shaded area represents the 90th percentiles interval of human population simulation.

Figure 7.

For 4-MBC, comparison between observed (dot, mean ± SD; Schauer et al., 2006) and PBK simulated (solid curve, mean) plasma concentration time profiles in female (A) and male (B) human subjects after dermal application of a sunscreen formulation containing 4% 4-MBC (approximately 22 mg/kg bw). The shaded area represents the 90th percentiles of human population simulation.

The simulated/observed ratios for C_max and AUC_0−t of all 3 clinical trials were well within 2-fold limit (Table 9) (only exception is for OMC 4-day AUC_0−t, ratio was 2.7), indicating the model predicted values are in good agreement with the respective observed values, therefore the models were considered reasonable and validated (Jones et al., 2015).

Table 9.

Simulated against observed comparison on C_max (ng/ml) and AUC_0−t (ng × h/ml)

Chemical		Observed Cmax (ng/ml)		Predicted Cmax (ng/ml)		Fold Difference (Simulated Mean/Observed Mean)
		Geometric Mean	Range	Geometric Mean	Range
OMC	Day 1	2	0.6–5	2.9	0.22–7.6	1.5
	Day 4	7.9	2.6–30.6	9.9	1.1–24.7	1.3
Octocrylene	Day 1	1.5	0.5–3.6	1.7	0.4–3.3	1.2
	Day 4	7.8	2.6–38.7	5	1.3–11.3	0.6
4-MBC	Female	25.5	19.8–31.2	21.7	9.8–40.0	0.9
	Male	51.9	19.8–83.9	31.8	9.1–76.6	0.6

Chemical		Observed AUC0 − t (ng × h/ml)		Predicted AUC0 − t (ng × h/ml)		Fold Difference (Simulated Mean/Observed Mean)
		Geometric mean	Range	Geometric mean	Range
OMC	Day 1	21.6	2.7–57.7	32.9	1.9–81.0	1.5
	Day 4	103.4	45.1–213.5	276.0	87.3–705	2.7
Octocrylene	Day 1	20.0	6.4–38.1	28.7	5.0–49.7	1.4
	Day 4	94.7	41.4–210.0	128.6	26.6–245.2	1.4
4-MBC	Female	485.6	NA	373.8	160.1–692.2	0.8
	Male	987.9	NA	583.5	153.1–1374.9	0.6

NA, not available.

Discussion

Understanding the ADME and PK behavior of a chemical is critical for determining systemic exposure to enable safety decisions to be made using NGRA without animal testing. To date, no PBK models have been published on the 3 UV filters, OMC, octocrylene, and 4-MBC. This study for the first time provides a comprehensive collection of ADME data and a PBK modeling strategy for topical application for these highly plasma protein bound chemicals.

PBK modeling is a well-established tool for predicting the PK of chemicals in various species, exposure routes and dose regimens, the application of which can be traced back many decades (Andersen, 1995; Chen and Gross, 1979; Himmelstein and Lutz, 1979). Depending on the goal of the modeling exercise as well as the amount and quality of the available data, PBK models can be built based mainly on the observed clinical data (“top-down” approach) or based on the broader understanding of how a compound behaves in the body mechanistically (“bottom up” approach) (Jamei et al., 2009). Very few clinical PK studies are available on cosmetic ingredients to help verify PBK models, and performing such studies is expensive and time-consuming. Therefore, the modeling strategy for cosmetic ingredients, when human data are lacking, focuses on parameterizing models partially or entirely based on data from in vitro and in silico studies in a bottom-up manner. It is therefore of importance to use relevant and robust approaches for parameter determination to support the reliability of input parameters and provide a sound biological basis for the model structure.

The 3 UV filters in this work are highly lipophilic and have a high binding affinity for proteins and plastic, which makes them “difficult to test” chemicals. For these types of chemicals, the ADME parameter generation becomes very challenging as experimental data can be heavily impacted by the nonspecific binding. In this study, we demonstrated that the developed PBK models of the 3 chemicals can successfully simulate the plasma concentration profiles obtained from dermal clinical studies. Except for the human studies that are used for model verification, no other human PK data were used for model development/calibration, indicating the reliability of the ADME data generated and the parameters determined. This was achieved through careful fit for purpose study design, using assays/parameterization methods that have the suitable applicability domain and mechanistic relevance for the chemicals of interest, and establishment of acceptance criteria to ensure the quality/relevance of the generated data.

Capturing appropriate absorption in a PBK model is crucial, especially when human data for validating skin absorption model are unavailable. Depending on the context, the modeling strategy can range from describing percentage absorption to complex mechanistic models capturing flux rate over time in different skin compartments. Merely knowing the percentage absorbed is insufficient to parameter a PBK model, as different flux rates can result in the same percentage absorbed but different systemic exposure profiles. In this study, we employed a complex mechanistic model to capture the dynamic skin absorption process of 3 chemicals. However, determining input parameters for partitioning, diffusion in skin layers, and formulation effects are challenging due to variations among available in silico models and their poorly understood performance (Grégoire et al., 2021). To improve confidence in predictions, in vitro skin penetration data from literature or generated in this study were used to parameterize the dermal absorption model. Notably, the 3 UV filters exhibited low overall skin absorption, leading to high variability and fluctuation in observed data in skin layers and receptor fluid. Accounting for this variability through parameter distribution fitting and reflecting it in probabilistic modeling, such as population simulation, is important in the modeling process.

The ex vivo skin penetration studies included in this work for model development used radiolabeled chemicals without distinguishing between the parent compound and metabolites. Therefore, the skin absorption models developed didn’t include skin metabolism assuming everything going through is the parent. However, this can bring uncertainty to the model as the frozen skin has shown effective esterase activity, and skin metabolism of OMC through skin S9 incubation has been observed (through personal communication). Incorporating skin metabolism into the model would improve the accuracy of determining the penetration of the parent compound. However, the challenge is, apart from metabolizing rate, metabolism in the skin also depends on the abundance of skin S9, the duration of chemical residence, and the rate of chemical penetration. Currently, there is no well-established method for in vitro to in vivo extrapolation to incorporate in vitro skin S9 clearance rate into an in vivo situation. The significant variability in skin penetration data for the 3 chemicals could partially reflect varying esterase activity and different levels of skin metabolism among samples. This variability was accounted for by a high CV% of 100% integrated for all skin penetration-related parameters in human population simulation. This may explain why the predicted C_max still matches well with clinical PK data, despite not including skin metabolism in the absorption models.

Fup is a crucial parameter in PBK modeling, impacting the interpretation of ADME behavior of chemicals. However, accurately determining Fup for certain compounds is challenging with current methods. In vitro methods like equilibrium dialysis (Chen et al., 2019), ultracentrifugation (Weiss and Gatlik, 2014), and ultrafiltration (Banker and Clark, 2008) have been historically used for plasma protein-binding characterization, but their accuracy suffers for highly protein bound chemicals (ie, with Fup less than 1%) (Riccardi et al., 2015). Modified versions of these methods have been proposed to improve accuracy for highly bound chemicals (Chen et al., 2019; Riccardi et al., 2015; Toma et al., 2021). In this study, we used the cross-filtration method, a modified ultrafiltration technique suitable for chemicals with nonspecific binding and poor solubility. Validation using established chemicals, including highly protein bound ones, demonstrated good agreement with published figures (Taylor and Harker, 2006). The results for the 3 UV filters showed good recovery and captured their highly protein bound nature.

Improved methods for determining Fup in challenging chemicals primarily focus on the static measure of chemical binding in plasma at equilibrium. However, they do not describe binding affinity or kinetics, such as association and dissociation rates of the chemical-protein complex. This limitation may lead to significant underestimation of liver clearance for highly protein binding chemicals when using traditional well-stirred liver models with static Fup values. Due to the dynamic and reversible nature of chemical-protein binding, influenced by different association and dissociation rates, chemical-protein equilibrium is not instantaneous. For a highly protein bound chemical slow dissociation may restrict chemical retention in plasma, whereas fast dissociation may have a nonrestrictive or permissive effect (Li et al., 2015). The nonrestricted well-stirred liver model has been suitable for 3 UV filters, demonstrating a nonrestrictive effect of protein binding on liver clearance when compared with human-observed PK data. Various methodologies, such as surface plasmon resonance (Day et al., 2002), microdialysis (Wang et al., 2008), and enzyme reporter assay coupling with high-resolution mass spectrometry (Yan et al., 2023) have been investigated for determining chemical-protein binding kinetics. These methods measure association and dissociation rates (Day et al., 2002) or capture the dynamic and kinetic nature of chemical-protein binding through parameters like “dynamic free fraction” (Yan et al., 2023). They offer valuable insights into the impact of binding kinetics on chemical properties and can enhance our understanding of the effect of Fup on ADME for highly protein bound chemicals.

To determine the hepatic CL_int of the 3 UV filters, hepatocytes in suspension were used due to their higher metabolic activity compared with cultured cell lines and intact cellular membranes, which consider the impact of chemical movement across the cell membrane for low permeability chemicals. The experiments were preformed up to 240 min to ensure derivation of CL_int values in case of slow clearance and the results showed that for the 3 UV filters the curves are good enough to derive CL_int values. However, there are still gaps in achieving robust and reliable data generation using this widely used in vitro method. Harmonization frameworks are needed to address untargeted influences (eg, results that are not explainable/usable/variable), particularly for chemicals with unique physicochemical properties like instability, volatility, and nonspecific binding (Louisse et al., 2020). In hepatocyte stability assays, the commonly used medium control (when cells are absent) as a negative control is not appropriate for the 3 UV filters due to nonspecific binding to plastic, leading to data misinterpretation. A more suitable negative control would be heat-inactivated hepatocytes, which disable enzymatic activity while still including the chemical’s binding profile to cells.

The same PBK model structure was applied to the 3 UV filters. In the model, liver clearance was considered as the main clearance route, and that tissue distribution was perfusion limited. The validation against human PK data showed that the structure is valid for these chemicals. However, one should notice that this model structure may not be suitable for a chemical that is dominantly cleared via renal clearance or when active transport is relevant.

Conclusion

This study on the 3 UV filters showed that even when human PK data is limited for model validation/calibration, it is possible to develop valid PBK models in a bottom-up approach. To ensure successful PBK model development under such a strategy, the key is to use relevant and robust approaches for parameter determination to support the reliability of input parameters and provide a sound biological basis for the model structure. Some essential considerations and lessons have been learnt (Table 10) for the 3 UV filters which are highly lipophilic and highly protein bound, which need to be considered when developing PBK models for similar chemicals in the future.

Table 10.

Essential considerations and lessons learnt on the ADME characterization and PBK model development for the 3 UV filters which are highly plasma protein bound

1. Consider real-life use practices and habits in PBK model simulations of UV filters exposure

2. Variability in skin absorption parameters must be accounted for in PBK models

3. Highly lipophilic, protein-bound UV filters are difficult to test due to their nonspecific binding nature in in vitro assays, which could affect data acceptance and interpretation

4. Heat-inactivated controls are appropriate negative controls in hepatocyte stability assays for highly lipophilic, protein-bound chemicals

5. The correction for Fup in traditional well-stirred liver model may not be suitable for calculating liver clearance of highly protein-bound chemicals

6. Accumulation of UV filters occur with successive doses until steady state

7. ADME testing guidelines are needed for challenging chemicals

Declaration of conflicting interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article. H.L., F.B., R.P., R.C., B.N., S.S., M.B., S.C., and M.D. are or were employed by Unilever, which manufactures consumer products containing some of these UV filters.

Funding

Cosmetics Europe Long Range Science Strategy (lrsscosmeticseurope.eu).