Impact of Mobile Monitoring Network Design on Air Pollution Exposure Assessment Models

Abstract

Short-term mobile monitoring campaigns are increasingly used to assess long-term air pollution exposure in epidemiology. Little is known about how monitoring network design features, including the number of stops and sampling temporality, impacts exposure assessment models. We address this gap by leveraging an extensive mobile monitoring campaign conducted in the greater Seattle area over the course of a year during all days of the week and most hours. The campaign measured total particle number concentration (PNC; sheds light on ultrafine particulate (UFP) number concentration), black carbon (BC), nitrogen dioxide (NO₂), fine particulate matter (PM_2.5), and carbon dioxide (CO₂). In Monte Carlo sampling of 7327 total stops (278 sites × 26 visits each), we restricted the number of sites and visits used to estimate annual averages. Predictions from the all-data campaign performed well, with cross-validated R²s of 0.51–0.77. We found similar model performances (85% of the all-data campaign R²) with ~1000 to 3000 randomly selected stops for NO₂, PNC, and BC, and ~4000 to 5000 stops for PM_2.5 and CO₂. Campaigns with additional temporal restrictions (e.g., business hours, rush hours, weekdays, or fewer seasons) had reduced model performances and different spatial surfaces. Mobile monitoring campaigns wanting to assess long-term exposure should carefully consider their monitoring designs.

Graphical Abstract

1. INTRODUCTION

Evidence increasingly indicates that traffic-related air pollutants (TRAP) like ultrafine particles (UFP, particles with diameters less than 100 nm often measured as particle number concentration [PNC]), black carbon (BC), nitrogen dioxide (NO₂), and fine particulate matter (PM_2.5, particles with diameters less than 2.5 μm) may be associated with adverse health effects, including cardiovascular and pulmonary outcomes, mortality, and brain health.^1–4 Because unregulated TRAPs are not routinely measured at government monitoring sites; however, their use as exposures in epidemiologic cohort studies requires the adoption of special, and often costly, exposure assessment campaigns. Determining the most effective, feasible, and cost-effective approaches to improve exposure assessment for air pollution cohort studies will thus greatly enhance the quality of possible health effect inferences.

Short-term mobile monitoring campaigns, the collection of repeated short-term air samples at selected sites, are increasingly being used as an efficient and cost-effective approach for estimating multilocation long-term air pollution averages.^5–33 While many strategies have been employed, little is known about how monitoring network design features, including the number of stops and sampling temporality, impact exposure assessment models. Most campaigns, for example, collect limited data at each site consisting of ~1 to 5 repeat visits, sample during restricted time periods such as business hours, and/or have short monitoring durations lasting under a few months. The resulting exposure prediction models generally have moderate or poor coefficients of determination (R²), suggesting limited prediction accuracy and potentially less value for epidemiologic inference.

Hankey and Marshall, for example, collected repeated bicycle-based mobile measures of PNC, PM_2.5, and BC in Minneapolis, MN. Measurements were collected over a 2-month period on 42 occasions during morning and afternoon rush hours.^9,32 Their base land use regression (LUR) models of spatiotemporal data averaged every 1–300 s produced adjusted R² between 0.25 and 0.50. Weichenthal et al. collected mobile on-road PNC measures in Toronto, Canada, during weekday morning and afternoon hours over 2 weeks in the summer and 1 week in the winter.²⁹ The resulting LUR model of spatiotemporal road segment data had an out-of-sample R² value of 0.50. Kerckhoffs et al. measured PNC and BC at 2964 road segments and 161 stationary sites in Amsterdam and Rotterdam, Netherlands.¹² Samples were collected over two seasons (42 days) during non-rush-hour daytime hours (9 AM to 4 PM). R² values from spatiotemporal road segment data were 0.13 and 0.12 for PNC and BC, respectively.

A few studies have gained valuable insight regarding the impact of the number of sites and repeat site visits on the quality of the resulting exposure prediction models. Messier et al. used weekday daytime nitrogen monoxide (NO) and BC on-road measurements from a 2-year Google Street View monitoring campaign conducted in a 30 km² domain in Oakland, CA to investigate the impact of drive days (repeat visits) and road coverage (“sites”) on universal kriging models of long-term average measurements.³⁴ While their full data models had cross-validated R² values of 0.65 for NO and 0.43 for BC, they developed similarly performing models with only 30% of the roads in the modeling domain (~92 000 road segments) and 4–8 repeat visits per road segment. Saha et al. used continuous measurements of PNC at 32 fixed sites in Pittsburg (150 km² domain) during the winters of 2017 and 2018 to evaluate the influence of the number of sampling days (repeat “visits”) and sampling duration on LUR prediction models.²² While their base models had cross-validated R² values of 0.72–0.75, they found that at least 10–15 days with 1 h of sampling per day were required to produce PNC LUR models with good precision and low error. Hatzopoulou et al. used PNC and nitrogen dioxide (NO₂) measurements collected along ~1800 road segments in Montreal, Canada (470 km² domain), over 35 sampling days in the winter, summer, and fall of 2009 to evaluate the impact of repeat visits and number of road segments on LUR model stability.³³ They found that ~150 to 200 road segments and 10–12 visits per segment yielded stable long-term average LUR models. R² values were 0.60 for PNC and 0.51 for BC when road segments with at least three visits were included, and these increased to 0.74 for PNC and 0.55 for BC when road segments with at least 16 visits were included.

While these past investigations have added valuable knowledge to the field, their findings have been largely focused on nonstationary on-road measurement campaigns in relatively smaller geographic areas. Further work is needed to demonstrate whether exposure data from nonstationary, on-road campaigns are representative of residential human exposure levels.^12,35 Furthermore, cohort study applications often span large geographic areas and are interested in long-term exposures. Little is known about how long-term exposure prediction models are impacted by short-term, temporally restricted sampling campaigns.

To address these gaps, we leverage an extensive, multipollutant mobile monitoring campaign in the greater Seattle area (1200 km² domain) intended to assess annual average air pollution exposure levels in an epidemiologic cohort.³⁶ The campaign consisted of 309 stationary sites, each with ~29 temporally balanced visits per site, and measurements of PNC, BC, NO₂, PM_2.5, and CO₂. We use Monte Carlo sampling to collect subsamples and investigate how the mobile monitoring design features, including the number of stops (sites × visits) and sampling temporality (seasons, days, hours), impact the resulting exposure prediction models. Based on these findings, we recommend short-term mobile monitoring design approaches that are expected to improve the precision and accuracy of exposure prediction models and better support epidemiologic investigations of long-term air pollution exposure.

2. METHODS

2.1. Data.

We leverage data from an extensive air pollution mobile monitoring campaign conducted between March 2019 and March 2020 in a 1200 land km² (463 mi²) area within the greater Seattle, WA area.³⁶ A hybrid vehicle outfitted with equipment visited 309 stationary sites off the side of the road ~29 times throughout the campaign and collected 2-min measurements (visits) from various instruments, including PNC (TSI P-TRAK 8525), BC (AethLabs MA200), PM_2.5 (Radiance Research M903 nephelometer), NO₂ (Aerodyne Research Inc. CAPS), and CO₂ (Li-Cor LI-850). The vehicle operated by battery with its engine shut off during roadside measurements. All gas instruments were calibrated in our laboratory before the campaign and every few weeks thereafter. Particle instruments were purchased new and arrived with calibration certifications, or they were compared to like instruments that had been serviced prior to the study. Table S2 of the original monitoring campaign publication has additional instrumentation details, including measurement frequency.³⁶ Visits were temporally balanced over the course of 288 drive days such that all sites were visited during all seasons, days of the week, and most hours of the day (5 AM to 11 PM).

Since instruments used in this study collected measurements every 1–10 s, we calculated the median pollutant concentration of each 2-min visit. Concentrations were winsorized at the site level once (not after each subsample, see Section 2.2) by setting values below each site’s 5th or above 95th quantile concentration to that threshold, respectively, to reduce the influence of a few extreme observations on annual averages. We previously showed that winsorizing prior to averaging slightly improved PNC and PM_2.5 models due to the reduction of influential points, while using approaches completely robust to influential points (i.e., medians), produced worse-performing models of pollutants with already limited spatial variability like CO₂.³⁶

For comparability across pollutants, we excluded the ~10% of visits that had incomplete measurements (i.e., had fewer than five pollutants); the resulting dataset had an average of 26 (range: 21–31) visits per site during 251 drive days. We split sites into training-validation (90%, n = 278 sites, 7327 stops) and test (10%, n = 31 sites, 810 stops) sets (see Figure S1 for the spatial distribution of these sites). The training-validation set was used to select an initial set of modeling covariates based on variable variability in the region and was afterward used to perform validation (see below). The test set was a second out-of-sample set that was completely excluded from all modeling decisions and solely used to evaluate the performance of each full training model.

2.2. Samples with Reduced Data.

We used all of the training-validation data to calculate our best estimate (gold standard) of each site’s annual average and used Monte Carlo sampling to collect subsamples of these data following various sampling designs (Table 1). A spatial-temporal design sampled a fewer number of total stops (sites × visits per site) by randomly restricting both the number of sites (25–278) and visits (4–26). Table S1 lists the exact number of sites used and the respective monitoring densities (monitors per 100 km²). Since some sites only had 21–25 visits, the maximum number of stops in the Monte Carlo runs was 7080, lower than 7228 (278 sites × 26 visits), and lower than the 7327 stops in the all-data campaign, which included 143 sites with 27–31 visits each. Temporal designs, on the other hand, used all of the training-validation sites (n = 278) but were restricted to fewer random sampling seasons (1–4, with seasons randomly selected so samples were balanced across all included seasons), fewer days of the week (weekdays or weekends), or fewer hours (weekday business [9 AM to 5 PM] and/or rush hours [7–10 AM, 3–6 PM]). In additional analyses, we looked at the potential impact of specific season selection by sampling 1–2 prespecified seasons. Given the data availability in the most restrictive sampling approaches (e.g., one season or weekends only), only 12 site visits were collected following these temporal designs for a total of 3336 stops. The fewer hours design used sampling without replacement, while the fewer seasons and fewer days designs used sampling with replacement since, for example, sites had fewer than 12 samples on weekends or in one season. We calculated site annual averages for each reduced sampling campaign and repeated this process 30 times using the parallel package (v. 3.6.2) in R (v. 3.6.2; see Note S1 for code details).³⁷

Table 1.

Reduced Sampling Designs from an Extensive Mobile Monitoring Campaign (278 Sites × ~26 Visits Each)

design typea	design	versions	total stops	sites	visits per site
best estimate	all data	training-validation set	7327	278	26b
spatial and temporal	fewer total stopsc	fewer sites (25, 50, 100, 150, 200, 250, 278) and visits (4, 8, 12, 16, 20, 24, 26)	100−7080	25–278	4–26
temporal	fewer daysd	weekends or weekdays	3336	278	12
temporal	fewer hours	business, rush, or business and rush hours	3336	278	12
temporal	balanced seasonsd,e	1, 2, 3, or 4 seasons	3336	278	12

^aThe all-data sampling design has 1 campaign “sample”, while all others have 30 campaigns, where each campaign is defined as one sample from all of the data. The fewer total stops design has 30 campaigns for each site-visit combination.

^bSites each have an average of 26 (range: 21–31) visits.

^cSeventy-six sites only have between 21 and 25 visits to select from. The realized maximum total stops are thus 7080, lower than 7228 (278 sites × 26 visits), and 7327 stops in the all-data campaign. Sampling first selects the number of sites and then the number of visits. Table S1 lists the spatial density of monitors based on the number of monitoring sites included.

^dSampling with replacement because there are otherwise insufficient samples for the most restrictive sampling approaches (e.g., one season or weekends only).

^eSamples are distributed evenly across the randomly selected seasons (e.g., 12 site visits/4 seasons = 3 site visits/season).

2.3. Prediction Models.

We built universal kriging (UK) with partial least squares (PLS) covariate models for pollutant concentrations from each campaign using the gstat (v. 2.0–7),^38,39pls (2.7–2),⁴⁰ and sf (v. 0.9–5)⁴¹ R packages. The dependent variables in these models were the log-transformed annual average site concentrations (using the data described in Table 1). The independent variables were the first two PLS components, which summarized 188 geographic covariate predictors (e.g., land use, roadway proximity; eq 1). New PLS components were calculated for each model (five models per sampling campaign for fivefold cross-validation and one for test set validation). We selected this subset of covariates from 348 original covariates because these had sufficient variability and a limited number of outliers in the training-validation set.³⁶ The models were

$$\text{ln}\left({\text{conc}}_i\right)=\alpha +\sum _{m=1}^M{\theta }_m{Z}_{mi}+{\epsilon }_i$$ (1)

where conc_i is the pollutant concentration at the ith location, Z_m are the first two PLS principal component scores (M = 2), α and θ_m are estimated model coefficients, and ε is the residual term with mean zero and a modeled geostatistical structure. We selected a kriging variogram model for the geostatistical structure using the fit.variogram function in gstat, which chose the best-fitting model from exponential, spherical, and Matern options. In total, we had 1741 campaigns (1 all-data campaign; 1470 fewer total stops campaigns: 49 versions [7 site and 7 visit combinations] × 30 samples each; 60 fewer days campaigns: 2 versions × 30 samples; 90 fewer hours campaigns: 3 versions × 30 samples; and 120 balanced seasons campaigns: 4 versions × 30 samples), each with five models for cross-validation and one for test set validation for a total of 10 446 models.

2.4. Model Assessment.

We evaluated the performance of each campaign using non-normalized and normalized root-mean-square error (RMSE) and mean-square error (MSE)-based R². MSE-based R² was used instead of the more common regression-based R² because it evaluates whether predictions and observations are the same (i.e., are near to the one-to-one line), rather than merely correlated. As such, it assesses both bias and variation around the one-to-one line. In contrast, regression-based R² (which we did not employ), solely assesses whether pairs of observations are linearly associated, regardless of whether observations are the same or not. MSE-based R² performs similarly or worse than regression-based R². To calculate RMSE and MSE-based R², model predictions at cross-validation and test sites were compared to the respective all-data campaign annual average estimates (our best estimates). For the primary presentation, these were additionally normalized to (divided by) the RMSE and MSE-based R² of the all-data campaign, respectively. Normalized values of one indicate that the reduced sampling campaign performance was the same as the all-data campaign, while values of more than one for RMSE and less than one for MSE-based R² indicate worse model performance. Importantly, all normalized values were divided by the same, all-data campaign performance, thus facilitating comparisons of performances across study designs and pollutants. Non-normalized results are presented in the Supporting Information. In secondary analyses resembling traditional model assessment where a best or gold standard estimate is not known, we calculated RMSE and MSE-based R² by comparing model predictions to the reduced sampling campaign’s respective annual average site estimates.

For each campaign, we built five models for fivefold cross-validation and a final model using all of the training data (described in Table 1) to evaluate against a second out-of-sample se—the test set. Fivefold cross-validation performed similarly to 10-fold cross-validation but was less computationally intensive.

3. RESULTS

The median (and interquartile range [IQR]) 2-min median mobile monitoring stop concentrations used in this analysis were 5980 (3800–9324) pt/cm³ for PNC, 409 (250–709) ng/m³ for BC, 8 (4–13) ppb for NO₂, 4 (2.8–5.9) μg/m³ for PM_2.5, and 425 (415–442) ppm for CO₂ (Table S2). Looking at the ratio of the 95th–5th quantile (Q95/Q05), BC and NO₂ had the most overall variability (Q95/Q05: 13.9 and 11.3, respectively), followed by PNC (Q95/Q05: 7.5) and PM_2.5 (Q95/Q05: 5.2), while CO₂ had little variability (Q95/Q05: 1.2).

The distribution of annual average site estimates and model predictions from the all-data campaign are detailed in Table S3. PNC, NO₂, and BC show the most spatial variability for both estimates and predictions, with high- and low-concentration sites having a 1.9- to 2.7-fold difference (Q95/Q05 ratio). PM_2.5 and CO₂ show a much lower degree of spatial variability with high- and low-concentration sites having a 1.0- to 1.5-fold difference.

Figure S2 shows the annual average prediction error relative to the all-data campaign estimates for all of the sampling designs. Prediction errors for the all-data campaign are centered around zero, suggesting no systematic bias in the models. This is expected since the all-data campaign predictions were estimated from the all-data campaign estimates. Prediction errors from reduced sampling designs, on the other hand, are generally more variable when fewer total stops are used. While there is some variability across pollutants, designs that only sample on weekdays generally overpredict. The opposite is true for weekend-only sampling. When samples are only collected during business hours, models underpredict NO₂, PM_2.5, and CO₂ levels.

Pollutant models from the all-data campaign performed well in fivefold cross-validation and at test set locations (see Figure S3 for details). The cross-validated MSE-based R² estimates were 0.76 for PNC, 0.60 for BC, 0.77 for NO₂, 0.66 for PM_2.5, and 0.51 for CO₂. Test set locations performed slightly better, presumably due to the lack of high-concentration sites in the randomly chosen test set, which were generally underpredicted by the models. The lower cross-validation performance of BC, for example, seems to be driven by a few sites with large observations that do not have comparable sites in the test set.

Figure 1 shows the median normalized MSE-based R² for the fewer total stops design from 30 campaigns. Prediction performance parameters are calculated against reference estimates from the all-data campaign (Figures S6 and S7 show these results not normalized) and reduced sampling campaigns. Using the all-data campaign estimates to assess model performance (Figure 1, top), performance generally increases for all pollutants as the number of total stops increases. For a given number of total stops, R² is minimally impacted by whether those stops come from maximizing the number of sites (randomly distributed throughout the study area) or visits. The differences that are observed are small and can be explained by the variation in R² estimates across campaigns (Figure S4). There are diminishing returns on performance (normalized MSE-based R² > 0.85) at around 1000 stops for NO₂, 2000 stops for PNC, 3000 stops for BC, and 4000–5000 stops for PM_2.5 and CO₂. Table S4 details the site-visit combinations used to reach these total counts. While the increased performance of NO₂, PNC, and BC begins to flatten after this number, PM_2.5 and CO₂ continue to steadily increase, suggesting that only the latter two pollutants continue to substantially benefit from an increased number of total stops relative to the all-data campaign. Nonetheless, Figure S4 shows that R² and RMSE estimates become more precise (lower IQR values across the 30 campaigns) as the number of total stops increases. Thus, while campaigns with more total stops have diminishing returns on average, their resulting exposure models continue to become more stable and reproducible across campaigns.

Figure 1.

Median normalized MSE-based R² for the fewer total stops design. R² is calculated by comparing cross-validated predictions to annual average estimate references from either the all-data campaign (top) or the reduced sampling campaigns (bottom) and normalized (divided by) the R² from the all-data campaign. Normalized R² values below 1 indicate worse performances than the all-data campaign. Median performance parameters are each based on 30 campaigns.

Interestingly, when R² is evaluated using the reduced sampling campaign estimates rather than the all-data campaign estimates (Figure 1, bottom), the results are noisier and the number of stops to achieve the same performance benefit is larger. These performances are calculated based on noisier campaign annual average estimates, and they indicate that for all pollutants, increasing the number of visits is more important than the number of sites. For a given x-axis value, icons that are lighter in color (fewer sites, more visits per site) have better model performance than icons that are darker in color (more sites, fewer visits per site). Figure S5 shows similar findings for RMSE.

Figure 2 shows the median normalized MSE-based R² and RMSE for each temporal sampling design (Figures S6 and S7 show these results not normalized). The horizontal lines on each panel show the performances of the nontemporally restricted fewer total stops design with 278 sites and 12 random visits, which can serve as a reference. Overall, there is decreasing model performance for all pollutants as sampling is restricted to fewer days of the week, hours, or seasons. Weekday-only and weekend-only sampling exhibits poorer performance than sampling during all days of the week (horizontal lines). Restricting sampling to weekday rush hours (alone or with business hours) performs slightly worse, while restricting sampling to weekday business hours alone typically produces the worst model performances. Model performances clearly improve when 12 site visits are evenly distributed across more than one season, with limited improvements beyond two seasons for all pollutants other than PM_2.5. Additional analyses showed slightly improved performances for single-season sampling campaigns during the winter for PNC, BC, and NO₂ (Figure S8). There was no clear indication that sampling during two opposing seasons (winter and summer, or spring and fall) consistently improved model performances, although spring and summer sampling produced good PNC, NO₂, and BC performance. Plots showing the median performance seem to indicate that models perform slightly better when 12 site visits are collected randomly throughout the year than when they are forced to be evenly distributed across four seasons (balanced seasons design), although this is not meaningful based on overlapping campaign performance ranges (data not shown in Figure 2). Compared to PM_2.5 and CO₂, PNC, NO₂, and BC model performances are generally higher, and they appear to be less sensitive to restricted sampling times. When reduced sampling designs are evaluated against references from each respective campaign’s estimates, the fewer days and fewer hours designs show different trends. The weekend- and business-hours-only sampling, for example, seemingly perform better than less restrictive versions. The performances of all temporally restricted sampling designs are typically lower than the nontemporally restricted fewer total stops design with 278 sites and 12 random.

Figure 2.

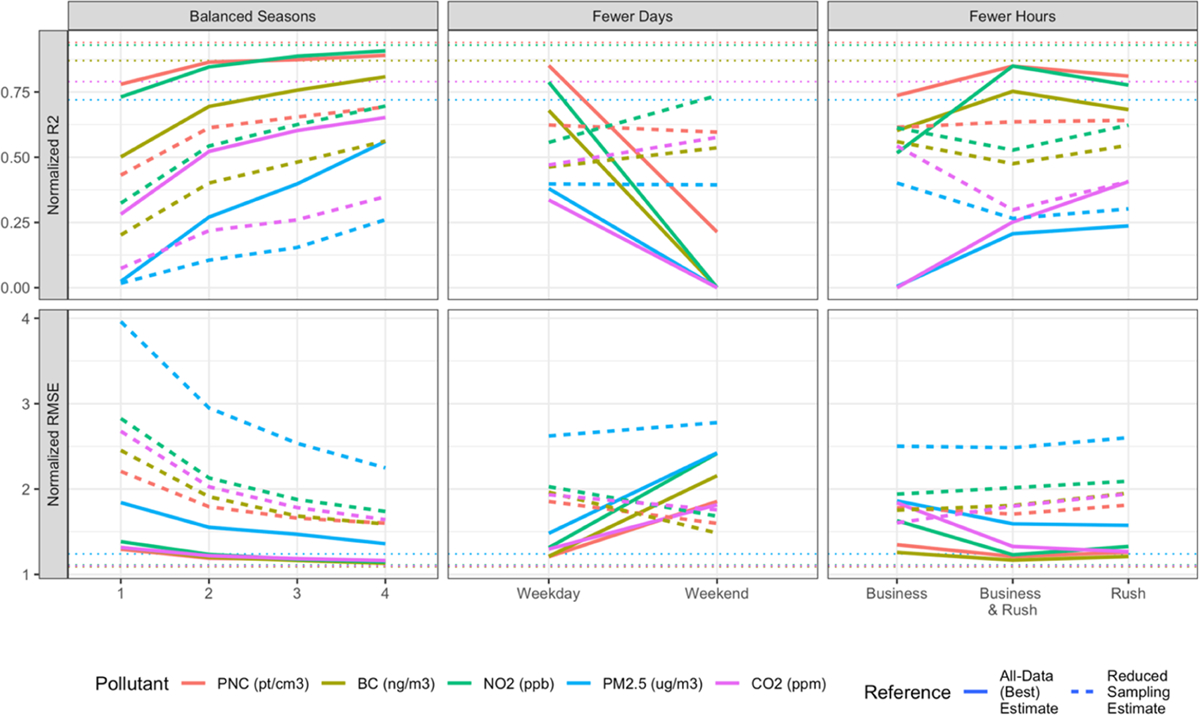
Median model performances (30 campaigns) calculated by comparing cross-validated predictions to annual average estimate references from the all-data campaign (best estimates; solid lines) and the reduced sampling campaigns (traditional model assessment; dashed lines). A value of 1 means that the design performs the same as the all-data campaign, while a value less than 1 for R² and more than 1 for RMSE means that the design performs worse. Horizontal lines show the median performance of the nontemporally restricted fewer total stops design with 278 sites and 12 random, which can serve as a reference.

Figure S9 shows the Pearson correlations (R) between cross-validated predictions from the all-data campaign and other sampling campaigns. Lower correlations are due to changes in the rank order of each campaign’s predictions and are indicative of different predicted exposure surfaces. Overall, the PNC, BC, and NO₂ exposure surfaces are less impacted by reduced sampling campaigns compared to PM_2.5 and CO₂. Correlations are generally lower and more variable as the number of total stops diminishes, due to prediction surfaces that are increasingly unstable and different from the all-data campaign. The correlations for weekend-only sampling are lower than weekday-only sampling, most strikingly for PM_2.5 and CO₂. Campaigns with only 12 visits divided among fewer seasons produce increasingly different exposure surfaces, primarily for PM_2.5 and CO₂. Figure 3 illustrates the resulting exposure surfaces for some example sampling designs. Sites with the highest PNC levels are found near the region’s largest airport, the Seattle-Tacoma International Airport. This area is consistently underpredicted using more restricted sampling designs. The Rush and Business hours designs show large-scale differences in spatial patterns for most pollutants. Figure S10 further shows that restricted sampling designs result in more variable predictions at higher concentration sites. This results in different predictions at these locations across campaigns.

Figure 3.

Comparison of the exposure surface from the all-data campaign with over 7000 stops (top) and the median prediction difference from some example reduced sampling campaigns with ~3000 stops (rounded). The ~3000 temporally balanced stops are from the fewer total stops design that randomly selects from the all-data campaign with no time restrictions and can serve as a reference for the other reduced sampling campaigns.

4. DISCUSSION

In this study, we show the impact of short-term mobile monitoring network design on the resulting air pollution exposure assessment results. Though there is some variability across pollutants, more robust exposure prediction results are generally produced with a greater number of total stops and increased temporal coverage. These findings are clearest when predictions are evaluated against a single set of best estimate observations (the all-data campaign), although this is not typically realistic in practice.

As expected, we obtained higher model performances as the number of monitoring sites and repeat site visits increased closer to that of the all-data campaign, with diminishing returns at higher stop counts. In fact, compared to the all-data campaign with ~7300 total stops (278 sites × 26 visits), reduced campaigns with about 1000–4000 stops (100–278 sites × 8–26 visits) for NO₂, PNC, and BC, and 4000–5000 stops (150–278 sites × 16–24 visits) for PM_2.5 and CO₂ produced similar model performances (82–88% of the all-data campaign R²; see Table S4 for details). Less expected was the finding that increasing sites versus visits did not have a meaningful impact on the model performances for any of the pollutants so long as the total stop count was met (e.g., 2400 total stops from 200 sites × 12 visits each or from 100 sites × 24 visits each). It’s notable that we randomly selected sites in these campaigns, and that these were distributed throughout the monitoring region. Particularly at the higher total stop count, campaigns thus did not necessarily capture less spatial variability.

We further showed that additional model improvements can be made by collecting temporally balanced samples, as seen in the sampling designs with more expansive sampling periods over more seasons, days of the week, and hours (Figure 2). And while collecting samples on all days of the week produces less biased predictions for all pollutant models, collecting samples beyond typical business hours is most critical for the more temporally variable pollutants like NO₂, PM_2.5, and CO₂ (e.g., Figures 3 and S10). While sampling during business hours is logistically practical and common in the literature, these and our previous results suggest that this can be problematic for predicting unbiased annual averages, for some pollutants more than others.⁴² Collecting samples over a period of more than about two seasons appears to have a relatively smaller impact on the PNC, NO₂, and BC model performances, suggesting that sampling campaigns lasting two to four seasons may still produce good prediction models for these pollutants as long as other design features such as the number of stops and temporally balanced samples are satisfied. In this study, seasons were randomly selected to allow for all season combinations that a campaign might choose to sample. Season-specific analyses indicated that single-season wintertime campaigns and two-season spring and fall campaigns could result in the best annual average PNC, NO₂, and BC model performances. Interpretation of these results should recognize that they are location-specific, as other work has suggested that combinations of opposing seasons might perform slightly better or worse than others,^5,10,43 which could be particularly true in locations with more extreme seasonal patterns. Further evaluation of season-specific local source emission and dispersion patterns will be valuable for studies that wish to restrict their sampling to specific time periods.

Interestingly, PM_2.5 and CO₂ had worse all-data campaign model performances than other pollutants, as quantified with non-normalized R². Performance also decayed quicker when sampling was reduced from the all-data campaign. These pollutants have relatively lower variability in their long-term average estimates and thus lower non-normalized R² (Figure S3), which scales the normalized R² of other designs. Performance is further reduced by designs with limited spatial or temporal sampling schemes, which at times produce R² estimates at or near 0 (Figures 1 and 2). Slight differences in patterns across pollutants when comparing R² with RMSE may be because ratio measures (i.e., R²) are less stable, particularly for pollutants with low variability such as PM_2.5 and CO₂ in this campaign. Still, it’s notable that PM_2.5 is not typically considered for mobile monitoring since widespread fixed site monitoring may already exist, and it is less spatially variable than other pollutants.

Campaigns with more total stops produced more consistent, less variable model performances, indicating that they create more stable prediction surfaces (see Table S4). Reduced sampling designs, on the other hand, produced very different predictions across campaigns. In line with these findings, correlations between predictions from the all-data campaign and those from reduced sampling campaigns were generally lower and more variable as the number of total stops diminished, further suggesting that exposure prediction surfaces become increasingly unstable and deviate from the all-data campaign. Importantly, differences in the exposure surfaces differed by location, with some high-concentration sites, for example, being less consistently predicted. These results may have implications for epidemiologic investigations, suggesting for instance that it is important to do sufficient sampling with an appropriate design so that the resulting predictions capture the richness of the underlying exposure surface. It may also be worth further research to determine what kinds of sites merit a larger number of visits to support better quality prediction surfaces.

Past studies have also reported more robust prediction models with an increased number of sites and visits, with some discrepancies. Hatzopoulou et al. reported that ~150 to 200 road segments (sites in a mobile sampling setting), each with 10–12 visits (1500–2400 total road samples), produced stable PNC and NO₂ models. We show, however, that these numbers can vary by pollutant (Figure S6 shows non-normalized results). Saha et al. found that 10–15 h-long visits at 32 sites produced robust PNC models with R² values near 0.7. Our PNC results were lower when using 320–480 total stops (32 sites × 10–15 visits) with median MSE-based R² closer to 0.5 for anything under 1000 stops. In addition to the longer visit duration, a notable difference between their study and ours was their focus on wintertime models. This restricted sampling period may not capture potentially important seasonal effects that impact annual averages such as nucleation events that form new particles during warmer seasons.⁴⁴ Still, Saha et al. argue that spatial patterns are expected to remain the same across seasons because such changes occur on the regional scale. Our temporal sampling designs suggest that limited seasonal, time of day, or day of week sampling affects both model performances and prediction surfaces (Figures 2 and S6–S10). Furthermore, while our measurements lasted only 2 min rather than 1 h, our past work has shown that both sampling durations produce similar long-term average estimates, where the shorter sampling duration has slightly more error.⁴² There were some discrepancies between the findings from this study and those from a 30 km² domain in Oakland reported by Messier et al. They reported that only 4–8 repeat visits per road segment (~92 000 segments) produced robust NO and BC models with R² values above ~0.50.³⁴ Using 1000–2000 total stop sites (278 sites × 4–8 visits), our median results were higher and closer to 0.6. Potential explanations for this discrepancy may be due to our collection of stationary measurements off the side of the road rather than nonstationary, on-road measurements; our expanded monitoring hours, which included rush hours, evenings, and weekends; and our larger modeling domain (1200 km², or about 40 times larger than for the Messier et al. study), which covered areas outside the Seattle city limits and is characterized by more geographic and seasonal variability. Another important distinction between our study and most others is our use of study design to capture temporal variability at the site level rather than using a reference site to afterward attempt to adjust temporally unbalanced samples. Furthermore, while the designs we described in this study were fairly balanced in terms of the number of visits we allowed each site to have, this is not true for many field campaigns, and this could possibly result in somewhat different conclusions.

One of this study’s strengths is that we used different out-of-sample sets of sites to characterize model performance, leveraging both cross-validation and pure out-of-sample validation with a test set that was not used at all in the model development stage. Model performances slightly varied when using these different out-of-sample sets. This is expected, since model performances are determined by how well site concentrations can be predicted, and better- or worse-performing sites may end up in different out-of-sample sets. Reassuringly, different out-of-sample test sets also produce similar trends and conclusions (results not shown).

In secondary analyses comparable to a situation where best or “gold standard” estimates are not known, we used estimates from the reduced sampling campaigns themselves as the reference concentrations to evaluate model performances (Figures 1 and 2). These produced slightly worse model performances. Others have similarly reported worse model performances when predictions are compared to short-term observations rather than longer-term averages.^12,34,42 Short-term observations are noisy representations of long-term averages. Furthermore, this approach to model assessment incorrectly implied that, for any given number of total stops, having fewer sites and more temporal coverage improved model performances for all pollutants. It also gave misleading performance results for the temporally unbalanced designs. Overall, these findings underscore the less documented point that traditional model assessment where a gold standard is not known (the default in the literature) can be misleading, particularly when assessing data collected from systematically biased designs such as the business hours design.

It is notable that our best estimate annual averages from the all-data campaign are themselves noisy and do not necessarily capture “true,” year-around annual averages. Stated differently, there is some level of error implicit in using only about 60 min of data from a fairly but not completely temporally balanced design to estimate annual averages. These data, for example, do not include overnight sampling between 12 AM and 4 AM, which is a limitation. The primary performance comparisons use these best estimates, and thus we are implicitly treating them as an appropriate representation of “true”, year-around annual averages in this paper. Based on our past work, however, we expect that this extensive all-data campaign with over 25 repeat samples collected in a temporally balanced way year-around achieved stable annual average estimates with low error despite not sampling during overnight hours.⁴² That work included the use of year-around measurements from fixed monitoring sites where a true long-term average can be assumed to be known.

We do not address monitor placement in this analysis, although past work has indicated that if the goal is out-of-sample prediction, monitors should be placed near the desired prediction locations to achieve spatial coverage (spatial compatibility) and in locations with similar covariate makeups to capture the covariate variability (covariate compatibility).^{22,33,45–47} Furthermore, if using model predictions from mobile-monitoring campaigns in epidemiological applications, ensuring both spatial and covariate compatibility in their sampling design is critical for minimizing exposure measurement error.⁴⁷ Spatial coverage may be especially important if the available modeling covariates do not capture the pollutant variability well and geostatistical approaches that take advantage of spatial correlation (e.g., kriging) are used. Some pollutant models may be more resilient to spatial extrapolation. The spatial variability of some pollutants, for example, NO₂, may be better captured by the model covariates (e.g., roadway proximity) compared to more regional pollutants like PM_2.5 or more spatially heterogeneous pollutants like PNC, as indicated by its higher model performances. That said, while the goal of this campaign was to develop exposure prediction models for epidemiological cohort applications, there are many other valuable spatial analyses that can be conducted using mobile monitoring data that do not involve modeling or epidemiologic application. This is beyond the scope of this paper.

Numerous short-term mobile monitoring designs have been used to assess long-term air pollution exposure in epidemiologic cohorts. Most, however, collect little data over limited time periods and produce moderately or poorly performing models. We leverage an extensive, multipollutant mobile monitoring campaign to better understand how a fine-tuned study design can improve model performances. In line with past work, we show that prediction model performances improve as the total number of stops increases. We add to the existing literature by further demonstrating how model performances can be improved when samples are temporally balanced, and how some pollutants may be more resilient to restrictive sampling designs, for example, NO₂ and BC. The measured pollutants are thus an important design consideration.

While this study used data from a stationary mobile monitoring campaign conducted in the greater Seattle area, findings from this study were in line with those from nonstationary monitoring campaigns in other regions regarding the importance of the number of sampling sites and visits for model performances.^33,35 We thus expect that the overall conclusions from this study will hold for other monitoring regions, for both stationary and nonstationary sampling. Of course, the exact results will vary based on regional sources, air pollution levels, sampling durations, proximity to major tailpipe emissions, modeling approaches, and other design features.