Real-Time Blood Pressure Estimation from Force-Measured Ultrasound

Abstract

Objective:

Our objective is to create a blood pressure measurement device which may provide a way to easily acquire frequent measurements. Common techniques to measure blood pressure include an arterial catheter, an oscillometric pressure cuff, or an auscultatory pressure cuff.

Methods:

The approach takes as input ultrasound images of an artery and contact force between the ultrasound array and subject. A subject may perform the self-measurements. Image and force data is analyzed for its quality and used to provide guidance or reject poor measurements. Tissue motions, due to probe contact forces and pulsing blood pressure, are estimated from the ultrasound image. Tissues elasticities and blood pressure are found by optimally fitting the observed tissue motion versus applied forces to a table of predicted motion - pre-generated with a finite element tissue deformation model. The output of the optimization is an estimate of systolic and diastolic blood pressure, arterial stiffness, and surrounding tissue stiffness.

Results:

The real-time implementation of the algorithm was validated on a cohort of 21 single-visit volunteers and on 4 volunteers self-monitored longitudinally. The systolic and diastolic pressures were compared to oscillometric cuff readings. Regression and Bland- Altman analyses were performed.

Conclusion:

Systolic pressure and diastolic pressure can be estimated in real-time and by the subject using this novel non-invasive ultrasound-based method (systolic accuracy/precision: −5.2 mmHg/10.7 mmHg; diastolic accuracy/precision: −3.9/8.0 mmHg).

Significance:

The method occupies a middle ground between the arterial catheter and cuff- based techniques. It has the potential to give calibration-free results.

I. INTRODUCTION

DOCTORS choose between three non-ideal techniques to measure blood pressure: an invasive arterial catheter, an oscillometric blood pressure cuff, or an auscultatory cuff. The catheter gives continuous and accurate data, but inserting the catheter is an invasive procedure. The oscillometric cuff cannot give pressure measurements continuously because it occludes the artery and it has been shown to significantly underestimate mean arterial pressure in patients with atherosclerosis [1]. The auscultatory cuff not only occludes the artery but also requires valuable time from medical professionals. Thus, there is a need for a blood pressure measurement device that serves as an intermediate option between the invasive catheter and cuff techniques.

We propose an approach using ultrasound to address the clinical arterial blood pressure measurement need. The inspiration to use ultrasound to non-invasively measure arterial blood pressure is quantitative ultrasound elastography [2], which is a well-known method that uses ultrasound to measure tissue stiffness, i.e. elastic modulus; a review of various elastography methods has been published [3].

In the proposed application of elastography methods to blood pressure estimation, strain elastography is made quantitative with the addition of the measured force between the probe and body applied as a boundary condition in the inverse problem formulation. The strain elastography formulation is further extended; the spatial distribution of tissue elasticities are calculated along with the addition of calculated pressure within a fluid filled vessel surrounded by the tissue. The estimation of variable pulse pressure is further decomposed into two estimation steps, first the mean arterial pressure, followed by the oscillatory pressure components. The inverse problem solution rate is increased by iteratively solving a multi-scale formulation; solutions are found iteratively on an increasingly resolved grid [4]–[6]. The results of the approach compared to a cuff were reported on a cohort of healthy volunteers [7].

In this paper we present the algorithm enhancements, and system innovations that are required to move the approach into a patient usable device with a specific focus on the use-model of serial examinations of an individual. Specifically, we report the real-time implementation of the approach. We report the results of the real-time implementation applied to a serial study of 4 volunteers self-examined over many days, and the results on a cohort of 21 single-visit healthy volunteers. The systolic and diastolic blood pressures were compared to oscillometric blood pressure cuff readings. Regression and Bland-Altman analyses were performed on the data and summarized.

A. Related Work

A brief review of a subset of the available arterial blood pressure (ABP) measurement techniques follows to put this work in context. The invasive arterial catheter, inserted most commonly at the radial artery near the wrist, gives a direct blood pressure measurement [8]. However, the invasive nature of the procedure increases the risk of infection and makes it impractical outside of a hospital.

The blood pressure cuff, also known as a sphygmomanometer, is a common blood pressure estimation method [9]. Automatic blood pressure cuffs are available for use in the home and use the oscillometric method. In the oscillometric method, the cuff inflates automatically and, as it is deflating, cuff pressure is sensed [10].

The manual auscultatory method is an alternative cuff-based method used by medical professionals. In the manual auscultatory method, after inflating the cuff and while decreasing cuff pressure, the doctor makes a judgment on systolic and diastolic pressures using the Korotkoff sounds, defined as the typical sounds blood makes as the cuff decreases in pressure [1]. While popular, the blood pressure cuff cuts off blood flow to the arm and thus is not suitable for continuous estimation.

Tonometry is a blood pressure measurement technique, originally developed for use at the wrist, in which a pressure transducer is placed next to an artery and the transducer readings are assumed to be related to the blood pressure within the artery [11]. While tonometry is very sensitive to placement of the device, some studies have shown good agreement with invasive arterial line data [1], [12]. A widely pursued approach for non-invasive and cuff-less ABP monitoring is pulse transit time [13]; several PWV-based approaches using ultrasound imaging are highlighted below.

B. Ultrasound-based ABP

A rich set of ultrasound-based approaches to ABP A rich set of ultrasound-based approaches to ABP measurement has been proposed. In one popular line of research, imaging or Doppler ultrasonography are used to determine local pulse-wave velocity (PWV), which is then calibrated to ABP through reference measurements. Benthin and co-workers [14] and Hoctor et al. [15] obtained long-axis images of the carotid artery and measured the diameter at multiple locations along the vessel to derive PWV. The Konofagou group extended this approach by placing 16 acoustic rays along the long-axis of the carotid artery and estimating the velocity of pulse propagation along the vessel wall by cross-correlation [16]. A different PWV-based approach, known as the flow-area or QA method, was introduced by Rabben [17] and updated by Beulen [18]. The method relies on Doppler ultrasonography to measure blood flow velocity and on imaging to measure cross-sectional area. PWV is computed as the ratio of the change in flow to the change in area. The Moens-Korteweg equation can be used to determine vessel compliance from PWV, which allows determination of pulse pressure, though most researchers have used calibration based on oscillometry to also get the mean value of ABP. In a different approach, Meinders and Hoeks [19] measured arterial cross-sectional area waveforms and converted these to pressure waveforms using an empirical relationship linking instantaneous vessel area to instantaneous luminal pressure. The method is made patient specific by supplying measurements of systolic and diastolic pressures.

These approaches all require calibration measurements to provide absolute ABP. Periodic recalibration is required due to changes in vessel properties. However, if the problem of calibration can be solved - for example by simultaneously measuring and correcting for vessel properties - these approaches also provide a tremendous opportunity for ABP measurement, as they can potentially all be implemented on the same ultrasound platform for redundant measurements and could be leveraged for frequent, intermittent or even continuous ABP measurements.

Other techniques are being developed by research groups to estimate arterial blood pressure non-invasively, and potentially continuously, using the behavior of ultrasound contrast agents in the blood stream [20]–[22]. By investigating cavitation frequency, radial oscillations, and general microbubble behavior, blood pressure can be estimated [20]. It has been reported that accuracy might be low with some variations of this technique [20]. Injection of microbubbles would not be ideal in every circumstance.

Our approach is based on controlled tissue deformation, and estimating the tissue properties and blood pressures which, via a model, predict tissue motions which agree with those observed. Tissue is deformed due to a combination of externally applied pressure, from the interaction of the probe with the body, and internally applied pressure, from blood in the artery. Tissue displacements are estimated from a sequence of ultrasound images. External, user applied, loads are measured. We model the tissue as an elastic medium, the artery as a pressurized non-linear elastic-walled tube, and the blood as a pressure source. Intuitively, for example, the higher the internal pressure in the artery the less the artery will be compressed due to externally applied loads. An algorithm estimates the elastic properties of the tissue surround the artery, the elastic properties of the artery, and the blood pressure (internally applied pressure) by comparing modeled and observed tissue motions from the observed tissue deformations and externally applied loads.

C. Contributions and Organization of Paper

The main contributions of the paper are the efficient real-time implementation of computationally-complex ultrasound-based blood pressure estimation algorithms, techniques to determine that quality-data has been acquired and which are used to give immediate feedback and guidance to the user, and the development of techniques to enable the subjects to perform their own self-measurements. In addition, we simplify the computational burden of iterative numerical simulations by pre- generating and storing results of the numerical models, and making the data processing algorithms real-time. The real-time approach is evaluated on a cohort of 21 healthy volunteers at Massachusetts General Hospital (MGH) in Boston, Massachusetts. Finally, the real-time and self-scan performance of the approach is evaluated on 4 volunteers performing self-measurements at time intervals of both minutes and days over a duration of 30 to 120 days.

The MGH Institutional Review Board and the Massachusetts Institute of Technology (MIT) Institutional Review Board approved this study. Volunteers for this study gave informed consent and only de-identified data were collected. Inclusion criteria included (a) being over 18 years of age and (b) non- pregnant mothers. Exclusion criteria included (a) volunteers with pacemakers and (b) overweight volunteers (BMI 30 kg/m² and greater).

The paper is organized into a hardware and algorithms section, a section on data acquisition methods and results for a cohort of healthy volunteers, a section on data acquisition methods and results for volunteers who performed self-scans over many days, a discussion section, and a conclusion sections.

II. SYSTEM OVERVIEW

A. Data Acquisition and Hardware

The procedure has three steps: (1) an image versus compression sequence is recorded - during which the user slowly increases the applied force of an ultrasound probe against the body while ultrasound images are acquired, see Fig. 2; (2) the tissue and artery displacement trajectories are found from the image sequence; (3) the tissue motions induced by applied pressures are optimally fit to a numerical tissue model. We model, and then estimate: the elasticity of the tissue surrounding the artery, elasticity of the arterial wall, and systolic and diastolic blood pressures which optimally agree with the observed tissue motions and externally applied loads. The solution method relies on iterative evaluation of the model and adjustment of the model parameters until the model output matches observations.

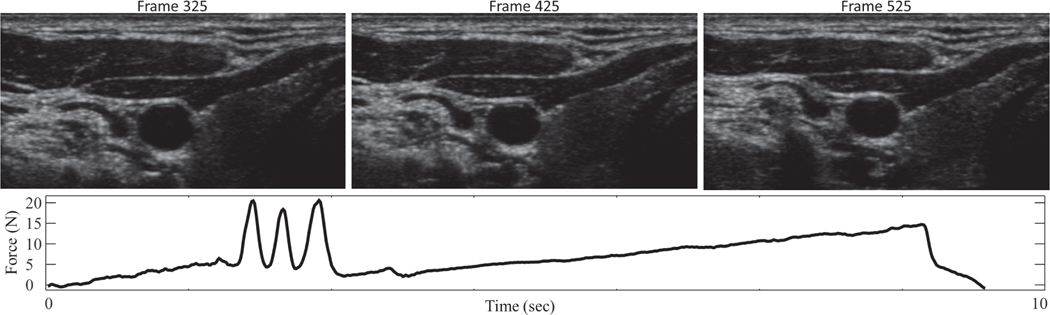
Fig. 2.

A representative compression sweep, with applied force between probe and subject (bottom) and associated ultrasound images (top). The three-taps at around 2.5 seconds are used for synchronization.

A force measurement system [23] is attached to a commercial ultrasound probe and consists of custom fit 3D printed parts, a rigidly supported load cell, and an accelerometer to compensate for gravity and tilt. In this application, the majority of the contact force during imaging is along the axis normal to the face of the ultrasound probe, thus the device described in [23] is modified to use a one-axis load cell to make the device both smaller and less expensive. The parts 3D-printed from ABS plastic and include a quick-release probe clamp and two halves of an outer shell that attach via magnets (Fig. 1). The electronics box contains a FUTEK load cell signal amplifier (Model IAA100, Futek, Irvine, California, USA) and a National Instruments Data Acquisition Device (DAQ) (USB-6001 DAQ, National Instruments, Austin, TX, USA) that acquires raw voltage signals. The DAQ connects to a laptop computer where a custom-designed LabVIEW LabVIEW (Version 2017, National Instruments, Austin, TX, USA) program is run to calculate, record, and display the contact force. The force sensor has an absolute accuracy from the factory of 0.5 N, with a repeatability of 0.05N. Therefore, after sensor characterization the force measurements are accurate to 0.05 N. The measurement resolution was characterized as better than 0.005 N. Applied contact pressure is estimated assuming the probe face is uniformly supported. A GE Logiq E9 ultrasound machine (General Electric, Boston, MA, USA) and a GE 9L-D linear probe is used. The dimensions of the face of this probe are l4 mm x 53 mm (an area of 7.4×l0⁻⁴ m²). Assuming the applied force is uniformly supported by the face of the probe, the applied pressure measurement is accurate to 67 N/m² or 0.5 mmHg. This device is used to gather force data as images are acquired during an ultrasound compression scan, where increasing probe pressure is applied throughout the scan.

Fig. 1.

Force measuring ultrasound probe, showing the assembly with quick- release probe clamp and ultrasound probe installed (top), as well as the underlying components (bottom, before assembly). Not pictured are one half of the outer shell and an attached box housing electronic components. A LabVIEW GUI displays contact force, pitch angle, and roll angle. The program is controlled via buttons and keyboard shortcuts. Additional features for clinical ease of use include ability to enter patient code and scan type.

Normal resting heart rate for adults ranges from l to 2 beats a second. In order to sample consecutive beats during a compression sequence, sampling theory dictates that the frame rate be at least 4 samples per second. To smoothly resolve the peaks and valley associated with maximum and minimum pressures, and to ensure smoothly varying segmentation results, we record ultrasound images at a rate of approximately 30 frames/second for l0 seconds.

The compression sweep is applied slowly compared to the heart rate. After the 3-taps, the target force profile for the compression sweep is a linear increase in applied load from l to ll Newtons over a l0 second interval. Again assuming the applied force is uniformly supported by the face of the probe, the applied pressure range is from l348 N/m² to l4825 N/m², or equivalently from l0 mmHg to lll mmHg. This pressure is felt by the tissue just under the probe, however it is supported and distributed over a large volume of tissue. Our simulations indicate that transmural pressure is always positive, and observations indicate the artery is never near collapse. During a l0 second compression sequence between 5 and l0 cardiac cycles are observed - sufficient for robust model fit.

B. Synchronization of Force Measurements with Ultrasound Jmage Stream

An automatic ‘three-tap’ synchronization method allows for automatic synchronization of force measurements and ultrasound images [24]. In this method, a three-tap signature is performed before the ultrasound compression sweep while both force measurements and ultrasound images are being acquired. As shown in Fig. 2, the three taps are easily identified in the force data, and these taps can be picked out in the ultrasound image streams as well as by analyzing the motion of image features.

Several approaches to extract motion signatures from the ultrasound image stream are used. One approach involves calculating grayscale intensity in a region of interest. As features in the ultrasound image move in and out of a region of the image, the grayscale values for the pixels in that region change. Summing the grayscale levels of each pixel in a fixed area of the frame for each image in the ultrasound recording is one metric correlated to the tapping motion. A second approach is template tracking of a user-chosen feature in the image [24], where the metric is the vertical position of the template. A third approach involves summing vertical optical flow over the entire image. Optical flow estimates the velocity of features throughout the image stream [25], and can be calculated to determine when and at what rate the features are moving upwards (corresponding to an increase in force) or downwards (corresponding to a decrease in force). Optical flow is preferred for its robustness and since it does not require user input [24].

The three-tap force signature is used as a matched filter. Normalized cross-correlation [26] is used to compute the temporal similarity and, therefore, alignment of the force signature and the motion signature extracted from the ultrasound images.

C. Algorithm and Model

The procedure has three steps: (l) a compression sweep is completed during which increasing probe pressure is applied and ultrasound images are acquired, see Fig. 2; (2) the tissue and artery motion is found from the image sequence; (3) the tissue motions induced by applied pressures are optimally fit to a tissue model with final output of systolic and diastolic blood pressure.

The approach for estimating ABP noninvasively from the inputs of applied probe pressure and corresponding ultrasound images is an inverse problem. We estimate the elasticity of the tissue surrounding the artery, elasticity of the arterial wall, and luminal pressure which optimally model the observed tissue motions due to applied pressures.

As described above, in the first step of the procedure, a user-applied compression sweep is completed. Fig. 2 shows a representative sweep and associated ultrasound images from a study subject. The three-tap method is used for synchronization. In the second step, the Star-Kalman filter is used to segment the carotid artery from the ultrasound images [27]–[29] (Fig. 3). In the third step, the optimization is performed. The optimization is a minimization of the difference between the segmented tissue-motion at systole and diastole and the prediction of a finite element model. The Levenberg-Marquardt [30] method is used to solve the inverse problem. The inverse problem proceeds in two stages. The first stage assumes that the artery is linear elastic and focuses on deformations within the physiological range to obtain an approximate estimate of pulse pressure. The second stage assumes a non-linear arterial stress-strain relationship and focuses on deformations of the artery starting with the undeformed (non-observable, nor physically realizable) geometry.

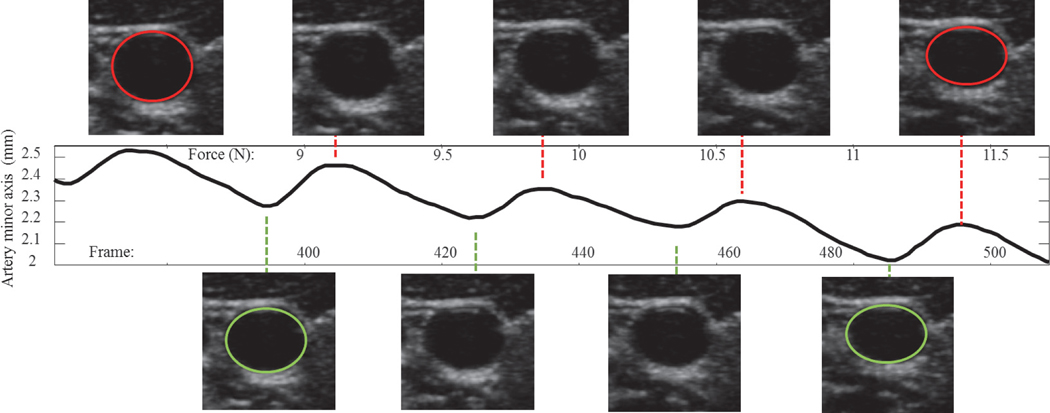
Fig. 3.

The Star-Kalman filter used to segment the carotid artery from the ultrasound images through the entire compression sequence. Versus applied external load, as expected, the artery is increasingly compressed (as noted by the reduction in minor axis) as external load is applied. The artery minor axis oscillates in size due to internal pulsing blood pressure. The size of the artery vs external applied load at peak size (systolic - top images of artery) and at valley size (diastolic - bottom images of artery) are used to look-up the stored results of the output of a finite element model and output systolic pressure and diastolic pressure.

The finite element model of the carotid artery should accurately represent the biomechanical properties of the tissue and arterial wall. The finite element model extends over a two-dimensional domain, semi-infinite in the horizontal directions and 35 mm in the vertical direction. Positive pressure, equal to the known applied pressure between the ultrasound probe and tissue, is applied to both the top and bottom of the domain. Displacement boundary conditions are applied in order to promote a symmetric deformation due to the symmetric loading and symmetric domain.

The tissue surrounding the artery is modeled as a linear elastic solid, assumed to be spatially homogeneous. There are two models for the artery that are used in the optimization process; the first model assumes that the artery is homogeneous and linear elastic with an elastic modulus while the second model assumes that the artery is homogeneous and non-linear. In particular, the second model assumes that the stress is exponentially related to the strain [31].

A large-deformation, plane strain formulation is used with four-node quadrilateral elements. A plane strain assumption, which has been used before to model the deformation of an artery’s cross-section [31], [32], is reasonable as deformations due to an expanding artery are in the plane and the artery can be thought of as long length-wise compared to other in-plane dimensions. The Poisson ratio of the tissue is assumed to be 0.495, which is typical for soft tissue [33]. A mesh was automatically generated and the finite element model was run using Abaqus (Version 6.8, Dassault Systems, Vélizy-Villacoublay, France). Abaqus’s hybrid displacement-pressure formulation is called automatically from Matlab (Version R2015a, MathWorks, Natick, Massachusetts, USA) in order to eliminate user interactions.

The three most significant assumptions in the approach are that (1) the surrounding tissue can be modeled as a homogeneous, semi-infinite slab, (2) the artery can be modeled as nonlinear elastic, and (3) the applied force can be modeled as an average force. The magnitude and direction of error introduced by these dominant modeling assumptions depends on the distribution of tissue heterogeneity and degree of tissue non-linearity. If modeled displacements are, on average, less then observed displacements, this means that either the modeled pressures required to achieve the same displacements must be increased, or that tissue stiffness should be decreased, or a combination of both. Increasing the complexity of the tissue model, by introducing spatial heterogeneity, such as bone and nominal tissue structures, is an option to improve performance – but in our tests this approach decreased the rate of convergence and numerical stability.

Pressure is variably amplified in the peripheral arteries compared with the central pressure [34]. This phenomenon is seen most significant in systolic pressure amplification [35]. It is due to differing arterial dimension and stiffness experienced by the pressure wave as it propagates along the arterial system [36]. Therefore, pressure measured in different arteries will be different. This difference is variable between individuals. In addition, gravity induced, hydrostatic pressure, differences will be present depending on artery’s location on the body with respect to gravity and the heart. In this work, measurements were taken while seated. The brachial cuff is taken on the arm with the cuff approximately level with the heart. The ultrasound measurements are taken at the neck, in the range of 20 to 30 cm about the heart depending on the individual.

We compensate for model assumptions, pulse pressure amplification differences between the brachial and carotid, and hydrostatic differences with a data driven correction.

A data-driven correction is applied in order to partially compensate for the biases introduced by the modelling assumptions, pulse pressure applications, and hydrostatic offset differences. The magnitude of the correction factor is different for systolic and diastolic pressures because the impact of the assumptions changes depending on the absolute value of blood pressure and the non-linear elasticity of the artery. This one- time correction could be applied based on an individual or on the average of a population; it is not a periodic recalibration.

The magnitude of the correction factor is obtained through the k-fold cross-validation method [37]. The k-fold cross- validation process amounts to a learning or training algorithm. After removing outliers, the data set is randomly split into a training set and a final test set, representing 2/3 and 1/3 of the entire set, respectively. During one iteration, the training set is randomly split into K folds; the first (K - 1) folds are used to find the fitting parameters and the Kth fold is used to calculate the error. The fitting parameters take the form of the parameters describing a line, with slope m and intercept b. To find the parameters, a line is fitted between two data sets: (1) a vector of training set algorithm measurements, and (2) a vector of corresponding cuff measurements minus corresponding algorithm measurements. This fitting is performed once for the diastolic results and once for the systolic results. A total of 1000 k-fold cross-validation iterations are completed on the training set and the parameter set corresponding to the iteration with the minimum error is chosen. Finally, the parameter set is applied to the final test set in order to report the relevant statistics.

Cuff measurements taken on the brachial artery are used to correct measurements taken at the carotid. This compensation may result in the absolute carotid systolic pressure values obtained using the algorithm to be equal or sometimes higher than the reference brachial systolic pressure recorded from the heart level.

We previously reported results of clinical evaluation on the same cohort of healthy volunteers comparing our proposed technique compared to a cuff. Here we present the techniques and results that move the approach into a real-time implementation and patient usable device.

D. Look-up Table Approach

A typical optimization as described above, with multiple iterations of the FEM model, requires about 24 hours to obtain a result. In order to improve the speed, a table look-up approach is used. In this approach, many sets of input parameters (tissue elasticity, artery elasticity, artery dimension and depth, blood pressures) are used to tabulate tissue deformation as a function of external applied load. Over a small force range, tissue deformation is further approximated by a linear fit of the artery minor dimension versus externally applied load, at both diastolic and systolic pressures.

In this way, the table models a hypersurface characterized by the input-indexes (slopes and intercepts of the artery minor axis dimension versus force at systolic and diastolic) and output-values (systolic and diastolic pressures, tissue and artery elasticities). Input data is linearly interpolated onto the table. The interpolation surface always passes through the table data points. See Table I for an abbreviated sample of the table calculated for this approach.

Table I -.

Sample portion of the look-up table used during the real-time optimization approach. The results displayed here are the raw algorithm results, before model correction.

Algorithm Input				Output
Change in Systole Diameter vs. Force	Zero-Force Diameter	Change in Diastole Diameter vs. Force	Zero-Force Diameter	Diastolic Pressure	Systolic Pressure
(mm/N)	(mm)	(mm/N)	(mm)	(mmHg)	(mmHg)
−0.15	2.50	−0.008	0.70	47.50	91.34
−0.02	2.50	−0.15	2.40	85.53	157.52
−0.15	4.50	−0.15	2.40	85.53	136.52
−0.02	4.50	−0.15	2.40	57.02	147.02
−0.03	3.00	−0.05	3.00	91.28	120.15

When the technique is used on a subject, their artery is segmented out of the ultrasound images. The artery minor axis versus external applied force are fit to a line. The linear fit parameters are interpolated onto the pre-calculated table of input parameters versus output results. The segmentation algorithm has been implemented in real-time [27]. Interpolation takes much less than one second to map input to output. The proposed technique is feasible for real-time estimation of blood pressure.

III. RESULTS - COHORT

In this work accuracy is defined as the mean of the errors (“measured cuff pressure” minus “pressure estimated via proposed technique”) and the precision is defined as the standard deviation of the errors (“measured cuff pressure” minus “pressure estimated via proposed technique”). The absolute relative error (ARE) is calculated as the absolute value of “measured cuff pressure” minus “pressure estimated via proposed technique” divided by the mean of “measured cuff pressure” and “pressure estimated via proposed technique”.

The real-time look-up table approach was tested on the healthy-volunteer data set first described in [7]. The average systolic and diastolic pressures reported by the oscillometric blood pressure cuff were 111 mmHg and 70 mmHg, with a standard deviation of 11 mmHg and 9 mmHg respectively. The same k-fold model correction was applied; the relevant real- time results are shown in Fig. 4. The accuracy and precision for systolic and diastolic blood pressure are −5.19 mmHg/10.68 mmHg and −3.85 mmHg/7.98 mmHg, respectively. The mean and median of the absolute relative error for systolic pressure are 8.3% and 5.3%, respectively, and for diastolic pressure are 8.3% and 4.7%, respectively.

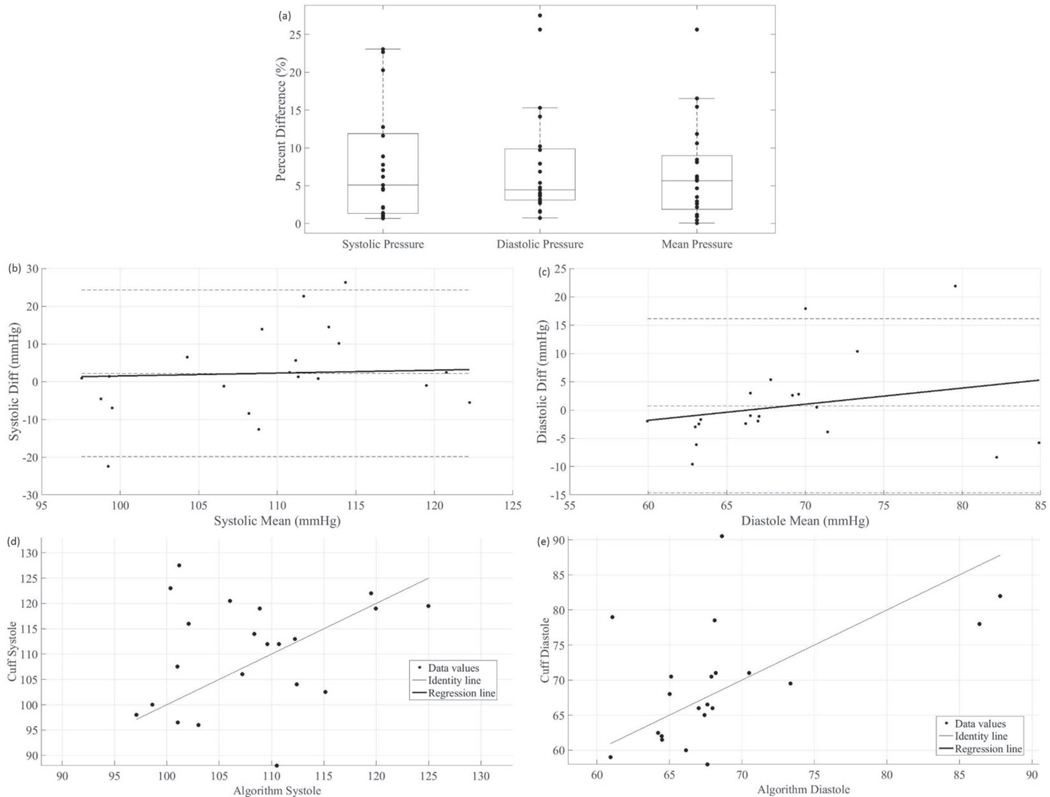
Fig. 4.

Statistical analyses from the 21 healthy volunteers. The k-fold determined model correction has been applied. In (a), a box plot of results is shown. Mean arterial pressure was calculated as 1/3 of the systolic pressure plus 2/3 of the diastolic pressure. In (b), the systolic Bland-Altman plot is displayed, i.e. the difference between the cuff and the algorithm’s systolic pressures is plotted against the mean of the cuff and the algorithm’s systolic pressures. In (c), the diastolic Bland-Altman plot is displayed. In (d), a correlation plot is displayed showing the systolic cuff result vs. the systolic algorithm result. The ordinary product regression is used to find the regression line displayed in the plot. In (d), a correlation plot is displayed for the diastolic pressure.

Every step of the process after the force sweep has the potential to be implemented in real-time. While the oscillometric cuff takes between 40 and 45 seconds to inflate, deflate, and report a blood pressure reading, the force sweeps above only took ten seconds each. Thus, the technique in this paper has the potential to be faster than the cuff measurements. Differences between the results presented above and the results presented in [7] are due to interpolation error and by reducing the force range to a small linearized regime. As more rows to the table are added, the interpolation error will decrease; the optimal force-range is an area of active investigation. Lower force sweep ranges can be used to gather data, as this would allow quicker data acquisition and a more comfortable experience for patients.

IV. RESULTS - LONGITUDINAL

A. High Quality Self-Scan

In order for the proposed technique to be deployed in a patient usable device, guidance must be provided to position and manipulate a device. To determine if the measurement that the subject completes is of high quality, certain metrics are used. The speed of the force sweep and the force range used during the force sweep is measured, with this information we reject force sweeps if they do not meet certain specifications. Measurements are automatically rejected if (1) the subject forgot to complete the three taps on the neck, (2) the force sweep was too fast, defined as a rate greater than 2 Newtons/second (2x the nominal), otherwise images may be motion blurred or too few cardiac cycles versus force are observed to enable robust model fitting (3) the artery moved laterally too much, defined as moving more than a radius in either the left or right direction over the duration of the force sweep, which generally indicates non-uniform application of pressure over the probe face, (4) the force sweep did not span a large enough force range to sufficiently characterize the variation in artery minor axis versus force required for the optimization algorithm, and (5) the carotid artery was accidentally imaged close to or at the bifurcation in the neck.

B. Method

Volunteers were first familiarized with the study, gave informed consent, and then received instruction on how to manually complete the three-taps and force sweep process. Each volunteer was shown the location of the carotid artery and practiced the three-taps and force sweep process. After taking a blood pressure measurement using an oscillometric cuff (Premium Automatic Blood Pressure Monitor, CVS Health, Woonsocket, RI, USA), the seated subject proceeded to complete 10 measurements, which include taps and force sweeps, on their own carotid artery while in view of the both the real-time ultrasound images and the real-time force data. In our experience, between 5 and 15 minutes of explanation and practice are required for an individual to then acquire quality scans 50% of the time.

Some types of undesired motions are easy to automatically detect and reject. The indicated errors encompass all measurement variation including that from motion artifacts from breathing, unspecified neck motions, and variation in how the user performed the compression sequence.

A GE Logiq E9 ultrasound machine (General Electric, Boston, MA, USA) and a GE 9L-D linear probe (General Electric, Boston, MA, USA) were used for data acquisition. During the scan, a study investigator announced the forces measured from the LabVIEW (Version 2017, National Instruments, Austin, TX, USA) program so that the volunteer could focus on the ultrasound images. In a next version of the application, force data will be conveyed to the user using visual clues or audio clues. After the scans were completed, a final cuff measurement was taken. We completed longitudinal studies of different duration and frequency on two healthy volunteer, one hypertensive volunteer, and one hypotensive volunteer.

C. Longitudinal Studies - Minutes

During the visit of volunteer 1, a self-scan was completed once every three minutes for a total of 90 minutes. Every nine minutes, an oscillometric cuff measurement was obtained; in order to do so, the cuff had to be placed on the arm and taken off after the measurement completed. Removing the cuff was important in order to facilitate the movement needed to complete a force sweep. However, removing the cuff resulted in subject movement that might have increased variability in the measurements.

The k-fold cross-validation algorithm was applied to determine a subject specific model correction. In order to make the following comparisons, the cuff pressures were interpolated onto the times at which the algorithm was used to measure blood pressure; this interpolation allowed direct comparison between cuff measurements and algorithm measurements. The algorithm was evaluated on the test set (about 10) and on the full set (about 30). The results are summarized in Table II.

Table II -.

Comparison between cuff and ultrasound approach for volunteer 1 minutes-study. Absolute relative error is abbreviated ARE.

		Mean (mmHg)	Standard Dev. (mmHg)	ARE Mean	ARE Median	Precision (mmHg)	Accuracy (mmHg)
Systolic	Test	135.6	2.5	2.0%	1.8%	0.2	3.3
	Full	135.7	2.1	2.2%	2.1%	0.06	3.7
Diastolic	Test	85.8	0.4	2.3%	1.6%	−1.3	2.2
	Full	85.8	0.8	2.5%	2.3%	−0.6	2.6

During the first visit of volunteer 2, the volunteer took data over the course of 15 minutes. Cuff measurements were taken at the beginning and end of the 15 minutes study. Algorithm measurements were taken throughout the 15 minutes. The k- fold cross-validation algorithm was applied to determine a subject specific model correction. The mean and standard deviation of the algorithm measurements, on full set (20), for systolic pressure were 119.2 mmHg and 2.0 mmHg, respectively, and for diastolic pressure were 72.4 mmHg and 0.1 mmHg, respectively. The mean and median of the absolute relative error for systolic pressure was 2.7% and 2.0%, respectively, and for diastolic pressure were 0.3% and 0.4%, respectively.

D. Longitudinal Studies - Days

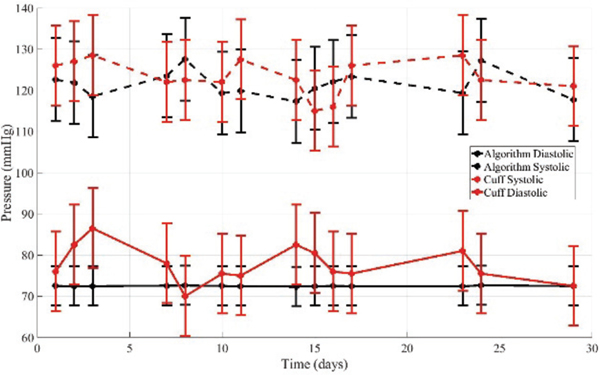
The same two volunteers completed longitudinal studies over 14 non-consecutive days. They repeatedly completed self- scans on the carotid artery. During each visit, an oscillometric cuff measurement was first taken, the ultrasound force sweeps were taken, and then a final oscillometric cuff measurement was completed. The purpose of this study was to evaluate if the algorithm measurements tracked the cuff measurements consistently over time on an individual. The corresponding subject-specific model correction from the minutes studies were applied. The results for volunteer 1 are summarized in Table III and Fig. 5. The results for volunteer 2 are summarized in Tables IV and Fig. 6.

Table III-.

Results for volunteer 1 in longitudinal study over 14 non-consecutive days.

Volunteer 1		Absolute relative error
		Mean	Median	Precision (mmHg)	Accuracy (mmHg)
Systolic	Full	7.6%	7.1%	9.1	7.3
Diastolic	Full	6.5%	7.1%	4.9	5.1

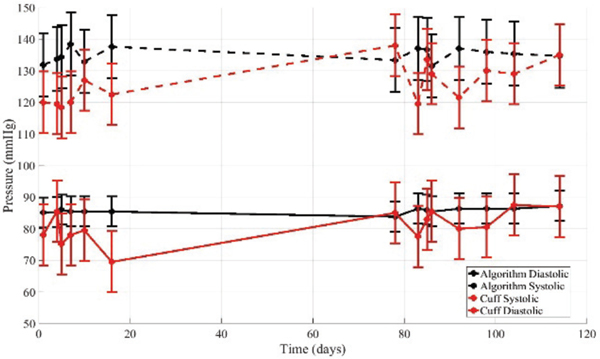
Fig. 5.

The algorithm applied to measurements on volunteer 1 over 14 non-consecutive days. A subject specific model correction determined from the minutes study was applied.

Table IV-.

Results for volunteer 2 in longitudinal study over 14 non-consecutive days.

Volunteer 2		Absolute relative error
		Mean	Median	Precision (mmHg)	Accuracy (mmHg)
Systolic	Full	4.2%	4.1%	−1.9	5.5
Diastolic	Full	7.3%	4.7%	−5.2	4.5

Fig. 6.

The algorithm applied to measurements on volunteer 2 over 14 non-consecutive days. A subject specific model correction determined from the minutes study was applied.

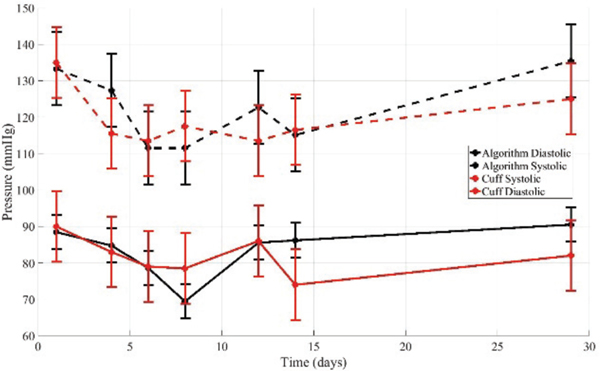
E. Hypertensive Longitudinal

A medicated hypertensive volunteer completed seven data acquisition sessions over the course of a month. Each session began with a resting period in order to stabilize blood pressure after walking to the testing site. After heart rate had decreased, measurements were administered by study personnel.

During the first visit, a 15 minute study was completed. Cuff measurements were taken at the beginning and end of the 15 minutes study. Algorithm measurements were taken throughout the 15 minutes. The cuff measurements were interpolated onto the time that the algorithm measurement was taken. The k-fold cross-validation algorithm was applied to determine a subject specific model correction. The mean and standard deviation of the algorithm measurements for systolic pressure were 123.2 mmHg and 82.8 mmHg for systolic and diastolic pressures, respectively. The standard deviations were 2.6 mmHg and 1.0 mmHg for systolic and diastolic pressures, respectively. The mean and median of the absolute relative error for systolic pressure were 2.7% and 1.6%, and for diastolic pressure were 2.7% and 2.3%, respectively.

During each subsequent visit, an oscillometric cuff measurement was first taken, ten ultrasound compression sequence measurements were taken, and then a final oscillometric cuff measurement was completed. One quality sweep was randomly selected for analysis. The subject specific model correction from the minutes studies were applied. The results are summarized in Table V and Fig. 7.

Table V-.

Results for hypertensive volunteer in longitudinal study over 7 non-consecutive days.

Hypertensive		Absolute relative error
		Mean	Median	Precision (mmHg)	Accuracy (mmHg)
Systolic	Full	5.0%	5.9%	2.9	6.7
Diastolic	Full	5.4%	6.0%	1.6	5.6

Figure 7.

The algorithm applied to measurements on medicated hypertensive volunteer over 7 non-consecutive days. A subject specific model correction determined from first visit was applied.

We see that both the cuff and algorithm pressures first decrease then increase over the 30 days. This is as expected considering the timing of the study relative to the volunteer’s medication regimen. Medication was taken the day before the first visit, and then not again until several days after the last visit.

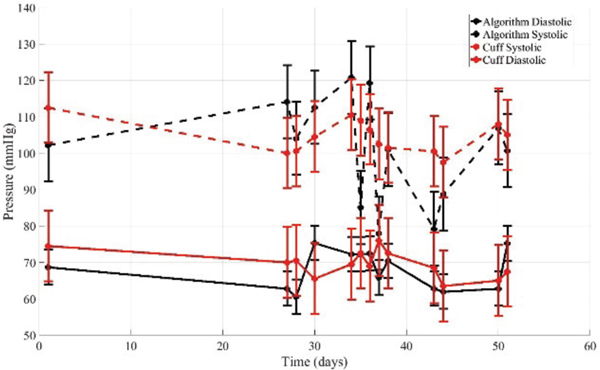
F. Hypotensive Longitudinal

The procedure for the hypotensive volunteer was analogous to that of the hypertensive volunteer, except that measurements were self-administered. This volunteer was diagnosed as hypotensive and, while not taking medication, is implementing life-style changes to address the condition, including a high sodium diet.

During the first visit, a 15 minute study was completed. Cuff measurements were taken at the beginning and end of the 15 minutes study. Algorithm measurements were taken throughout the 15 minutes. The cuff measurements were interpolated onto the time that the algorithm measurement was taken. The k-fold cross-validation algorithm was applied to determine a subject specific model correction. The means of the algorithm measurements were 104.2 mmHg and 67.4 mmHg for systolic and diastolic pressures, respectively. The standard deviations were 2.9 mmHg and 0.1 mmHg for systolic session, between three and six compression sweeps were completed, and then a final oscillometric cuff measurement was completed. One quality sweep was randomly selected for analysis. The subject-specific model correction from the minutes studies were applied. The algorithm results are summarized in Table VI and Fig. 8.

Table VI-.

Results for hypertensive volunteer in longitudinal study over 13 non-consecutive days.

Hypertensive		Absolute relative error
		Mean	Median	Precision (mmHg)	Accuracy (mmHg)
Systolic	Full	8.7%	9.0%	−2.0	11.1
Diastolic	Full	4.9%	3.8%	−2.1	3.7

Figure 8.

The algorithm applied to measurements on hypotensive volunteer over 13 non-consecutive days. A subject specific model correction determined from first visit was applied.

It is important to note that there was significant difficulty using the cuff on this volunteer. Results from the cuff were frequently of poor quality (either very high or very low, and inconsistent after repeated measurements).

V. LIMITATIONS

Oscillometry is subject to inaccuracy [38], [39]. It has been reported that different cuffs give different readings for blood pressure and that mean arterial pressure is typically underestimated by oscillometric blood pressure cuffs [1]. It has been reported that the agreement between oscillometric blood pressure cuffs and invasive pressure measurements is −6.7 +/−9.7 mmHg (p<.0001) [40]. In that study, 26.4% of measurements had a discrepancy, compared to the catheter, between 10 mmHg and 20 mmHg while 34.2% had a discrepancy of at least 20 mmHg [40]. Nevertheless, it is a convenient method to use for our studies. As is recommended [1] and noted above, the reported cuff measurement was the average of multiple measurements, separated by at least one minute. Individual cuff measurements are taken before and after a force-sweep sequence.

Cuff measurements on the brachial artery are used to correct measurements taken at the carotid. The correction technique used in this way will hide physically expected difference resulting from pulse pressure amplifications and hydrostatic pressure offset. This phenomena is observed by noting that the carotid systolic pressure values obtained, after correction, may be equal or sometimes higher than the reference brachial systolic pressure recorded at the heart level. The correction technique applied in this paper is well suited to longitudinal observations, monitoring change or trends over time, but can be improved.

In the future, direct comparisons between the proposed technique and cuff measurements will be made by using both approaches to measure brachial pressure. In addition, measurements performed with the proposed technique at both the carotid and brachial arteries will be made as close to the same time as possible; these measurements will be compared to expected differences arising from pulse pressure amplification and hydrostatic pressure offset. Expected hydrostatic pressure offset variation will be directly compared by taking measurements at the carotid and brachial when the subject is seated and lying prone.

Our technique is sensitive to the ability to track and extract tissue motion, for this reason we use a slow compression sweep. Artery segmentation and measurement in cross-sectional view introduces errors in diameter and distension measures, owing to poor definition of arterial wall boundaries (when analyzed in a single image). Owing to poor definition of arterial wall boundaries, it has been recommended to measure the dimension of an artery along the long axis [41] – in this way, the average artery wall boundary is made more visible as a line in the ultrasound image, in effect providing multiple measurements of boundary location. However, artery measurement made in this way are sensitive to precise location of the probe. It must be placed directly along the center line of the artery. We have observed that it is difficult to for a non-skilled operator to consistently find the center line. Similarly, we have observed that it is very difficult for skilled and non-skilled operators to keep the probe along the center line without slipping during a compression sequence, introducing significant variability in the measurement procedure. Finally, such an approach would require a different model which has not been the focus of this work. The cross-sectional view is robust to variable probe placement and is not sensitive to slipping from the longitudinal center line. Artery dimensions are robustly extracted by using the information from adjacent frames of the compression sequence.

The preferred motion sequence satisfies certain conditions - probe at a fixed location (i.e. no translation along the body) and oriented perpendicular to the artery, artery centered laterally in the images, and compression application smoothly applied over 5 to 10 cardiac cycles. Fast motions would introduce motion blur and reduce the quality of tissue motion tracking including artery segmentation and tracking. In the future, it would be straightforward to provide guidance to the patient or caregiver to after compression speed, or to provide audible visible or tactile cues in help keep the probe centered above the artery.

Methods directed to estimating measures related to local arterial stiffness include distensibility [42], stiffness index [43], local PWV imaging [44], arterial wall strain [45] and arterial wall strain-stress elastography [46] and others [47]. These methods are combined with tonometry based pressure measurements in the peripheral arteries. A transfer function is then applied to obtain the pressure waveform in the large central arteries [48]. Shear wave elastography (SWE) is a more direct method to quantitatively assess local tissue stiffness [49], [50]. Our model estimate of artery elasticity fell within the expected physiological range 60 – 300 kPa [49]–[51]. However, in our studies we did not separately estimate arterial elasticity via any of these techniques.

VI. DISCUSSION

In [7], results for a cohort of 24 healthy individuals, under a one-time visit protocol, were reported. A population-based correction was used. The mean precision / accuracy was 10.2 mmHg / −2.4 mmHg for systolic and 8.2 mmHg / −0.3 mmHg for diastolic pressure; the mean of the absolute relative error was 7.2% for systolic and 9.9% diastolic pressure. In the longitudinal studies presented here, a subject-specific correction, acquired at an initial visit, is used. Over these four longitudinal studies the mean precision / accuracy is 2.0 mmHg I 7.7 mmHg for systolic and −0.2 mmHg / 4.7 mmHg for diastolic pressure; the mean absolute relative error is 6.4% for systolic and 6.0% for diastolic pressure.

We presented results on a young normotensive population which included a one-time population-based correction. Such a correction would be appropriate for a clinical environment. For an in-the-home device, the cart, screen, knobs and standard interface of diagnostic imaging system are not available. What would be needed is a device with a compact hand-held form- factor, possessing the ability to generate and detect sound. Low-cost ultrasound-on-chip technology is now available commercially. These technologies could already enable the proposed approach to be used in-home. In an in-home environment, a user-specific calibration is feasible and would be appropriate.

Studies are underway to evaluate longitude performance for a larger population with an age range from 18 to 80 of normotensive and hypertensive subjects. As part of these studies a subject’s ABP is temporarily increased via exercise and physical stressors. These studies will be used to evaluate system performance over a wide range of ABP in a single subject, improve the tissue model, and to characterize subject-specific correction factors over a wide physiological ABP range.

Our vision is to create a hand-held blood pressure measurement device such as shown in Fig. 9. We target a use model in which a miniaturized ultrasound sensor package with integrated force measurement is housed in an ergonomic hand- held device that can be used by untrained users. This device easily fits into a purse or briefcase or sits next to your razor or toothbrush at home. A prototype probe integrating the force sensors with the ultrasound transducer array and integrated electronics within the body of the probe is a further step toward that vision [24]. Acoustic coupling is done with disposable gel pads.

Figure 9.

Rendering of a proposed device form factor that uses the techniques described in this paper.

An integrated design addresses the critical deficiencies of a retro-fit force measurement device. The main workflow issues in using the retro-fit force measurement device include the bulky size of the outer shell and additional steps necessary to prevent measurement inaccuracy (strain relieving the ultrasound transducer cable, zeroing out a bias force). Other improvements include obtaining more information about the pressure distribution across the transducer face. The recent introduction of the $2,000 ultrasound device from Butterfly networks [52] suggests that technology is not far off from making the proposed approach a cost feasible commercial option.

An additional application of this approach is for patients with a ventricular assist device (VAD) and no pulse. In the approach discussed here, a pulse is not required, pressure is estimated from tissue deformation assuming the arterial pressure is a constant at the fixed time along the pulse curve where measurement are made, such as at the peak and valley of systolic and diastolic pressures.

VII. CONCLUSION

In this paper we presented techniques and results that will help deploy an ultrasound based approach for estimation of arterial blood pressure into a patient usable device – this includes an automatic three-tap synchronization method and techniques for determine that quality-data has been acquired, which are used to give immediate feedback and guidance to the user. A real-time look-up-table is used to approximate an otherwise computationally expensive iterative optimization technique.

When the technique is used on a subject, their artery is segmented out of the ultrasound images and the segmentation results are interpolated onto the pre-calculated table of input parameters versus output results. This interpolation takes much less than one second. The segmentation algorithm can operate in real-time. The proposed technique is feasible for real-time estimation of blood pressure.

We report the real-time implementation of the algorithm validated on a cohort of 21 single-visit healthy volunteers and on four (4) volunteers monitored over many days. A one-time model correction factor was applied to the population analysis. A one-time model correction factor, determined on the first use, was applied for the longitudinal analyses. The systolic and diastolic blood pressure were compared to oscillometric blood pressure cuff readings. Maximum errors between cuff and algorithm were 10%.

This approach has potential to be used not only for arterial blood pressure but also pressure in veins and even to measure cyst pressure and embryonic fluid pressure. It also has potential to be used for patients with hypertension and atherosclerosis. It uses ultrasound, it is non-invasive, and it does not occlude the vessel. Further, assuming accurate force measurement, no manual calibration is needed with the method as calibration is completed on a fundamental level for this algorithm – in estimating ABP we also estimate tissue and arterial stiffness as a form of continuous self-calibration.

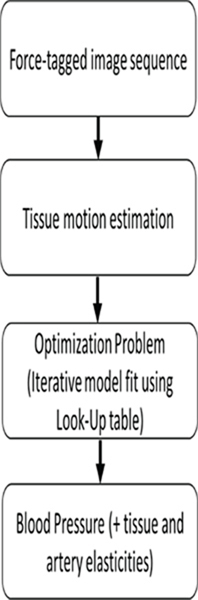
Fig. 0.

Algorithm work flow.