Abstract
Purpose
In this study an evaluation of the imaging performance of an electronic portal imaging device (EPID) is presented. The evaluation performed employing the QC-3V image quality phantom.
Methods
An EPID system of a 6 MV LINAC, was used to obtain images of a QC-3V EPID phantom. The X-ray source to phantom distance was 100 cm and the field size was 15x15 cm2. The irradiation conditions comprised Dose Rates (DR) of 200, 400 and 600 for a 2 MU–100 MU range. The Contrast Transfer Function (CTF), the Noise Power Spectrum (NPS), the Normalized Noise Power Spectrum (NNPS) and the Contrast-to-Noise Ratio (CNR) were studied. In addition, an alternative factor showing a frequency related output signal-to-noise ratio (SNR), the Signal-to-Noise-Frequency Response (SNFR), has been introduced. SNFR is a comprehensive quality index, easily determined in clinical environment.
Results
The CTF curves were found comparable to each other. The lowest values were measured at 2 MU and 200 MU/min. Concerning the NPS and NNPS graphs it was found that the values decrease up to approximately 0.3 lp/mm and demonstrate a white noise shape afterwards. SNFR values were found reducing with spatial frequency. Highest CNR were found between the region 7 and 11 of the phantom.
Conclusions
The influence of MU and DR on EPID performance were investigated. Image quality was assessed using the QC-3V phantom. The presented results can lead to image quality amelioration and act supportively to current image quality control routine protocols.
Keywords: Image quality, EPID, Detector, QC-3V, Phantom
1. Introduction
Electronic Portal Imaging Devices (EPIDs) were initially created to validate the geometric accuracy of patient positioning during radiotherapy [1,2]. The high-resolution images acquired by EPIDs, combined with the widespread adoption of modern radiotherapy techniques such as Intensity Modulated Radiation Therapy (IMRT) and Volumetric Modulated Arc Therapy (VMAT) extended their use to also assist the quality assurance (QA) of linear accelerators [3]. In specific, EPIDs can be utilized to verify jaws and multileaf collimator (MLS) positioning accuracy, collimator and gantry rotation isocenter accuracy, as well as X-ray output, flatness and symmetry constancy [4]. Moreover, their application has progressively expanded to include the acquisition of dosimetric data related to radiation treatment, either through in vivo dosimetry or via patient specific pretreatment QA [2]. The considerable challenges stemming from the extensive clinical integration of EPIDs [4] however, underscore the necessity for enhanced QA procedures to guarantee that the system operates as intended [5,6]. Image quality-based tests remain essential, since failure of these tests would result in a notably compromised functionality for dosimetry purposes. To this end, a methodology to assess EPID imaging performance with the QC-3V phantom, acting complementary to the other quality control tests, was developed and implemented in this work, based on fundamental parameters associated with image quality.
In previously published investigations methods for EPID quality assurance and image evaluation have been described, which are based on measuring the Signal to Noise Ratio (SNR), the Modulation Transfer Function (MTF), the Noise Power Spectrum (NPS), using specific methods, phantoms and dedicated software [1,5,[7], [8], [9]]. Studies, e.g. investigating various issues such as the effects of external aluminum target beam of the LINAC on EPID [10], the use of wavelet analysis to detect and isolate defective pixels and artifacts for quantitative quality assurance (QA) of EPIDs, characterizing the image noise, have been published [6]. In addition, a review is referred to the properties of dosimetry and imaging of radiation detectors, such as the physical principles of operation of calorimeters ionization, charge detectors, semiconductor, luminescent, chemical detectors, and radiochromic films [11]. Furthermore, the noise and contrast to noise ratio (CNR) were calculated using the PipsPro QC-3V phantom for evaluating a Tomotherapy MV Computed Tomography (MVCT) unit as well as the performance of Varian imaging devices [12,13]. The feasibility of patient positioning verification in electron beam radiotherapy, using the photon contamination detected by an EPID and RW3 slabs and a Gammex 467 phantom has been reported in literature. In this study image quality was evaluated calculating image contrast (CR) and Signal-to-Noise Ratio (SNR) [14]. Moreover, the QC-3V phantom has been utilized and metrics such as MTF, SNR and CNR have been investigated [15]. A drawback of EPID evaluation methods is the lack of a universally accepted comprehensive quality control protocol. This may bring diversity in the presented methodology as demonstrated in various studies [7,9,[16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28]].
Concerning the iViewGT portal imaging device, mounted on Elekta radiotherapy equipment is considered, the MTF with the edge method, the NNPS, Detective Quantum Efficiency (DQE) and the system response has been calculated for a range of Monitor Units (MUs) and by exploiting a Monte Carlo code for finding the number of X-ray photons needed for DQE calculation [1]. In addition, SNR, MTF and contrast for radiation incidence corresponding to 1–15 MUs for an Elekta iView EPID, measured with a PTW EPID QC phantom has been reported [5].
Similar methods employing image quality metrics, like those implemented in the previously referenced studies, have been also employed extensively in diagnostic radiology [12,15,16,28].
In the present study a systematic evaluation of the imaging performance of iViewGT™ R3.4.1 MV Portal Imaging EPID in interconnection with the Radiotherapy Information System Mosaiq® version 2–6.4.214 is presented. Within this framework we have introduced the Signal to Noise Frequency Response (SNFR), defined as a combination of the Contrast Transfer Function (CTF) and the Noise Power Spectrum (NPS), providing details about the signal and noise transfer in the spatial frequency domain and expressing a comprehensive image quality index that can be easily determined under clinical experimental conditions. The aforementioned spatial frequency related parameters may provide the limit of the EPID performance in detecting small dimensions. This can improve the visualization of the irradiation field, especially when healthy tissues with small radiation tolerance are next to the PTV. CTF was also employed to assess the MTF. In addition, complementary to CTF and NPS spatial domain quality metrics, such as CNR, SNR, Detector Response Curve, which may provide information regarding EPID performance changes, have been experimentally assessed for various monitor units (MU) and Dose Rates (DR). It is widely accepted that an in-depth and objective investigation of the fundamental imaging properties of a system, involves determination of image quality metrics in the spatial frequency domain. In the present study we have tried to achieve an accurate and objective assessment of detector performance, by employing an EPID phantom, commonly found under clinical settings, and thus facilitating the corresponding experimental procedures. The above parameters were assessed by imaging the QC-3V phantom on the EPID of an Elekta 6 MV LINAC with different MUs and DRs. The MU and DR values used are the ones that might be implemented during a clinical portal imaging procedure. Additionally, the default software setup parameters were kept unchanged. Our results present a thorough evaluation of iViewGT™ coupled with Mosaiq® under different MUs and DRs in conditions of clinical interest. Furthermore, the methodology provided can be used for assessing EPID performance of LINACs by utilizing the QC-3V phantom.
2. Methods
In the present study the EPID is comprised by a radiation sensitive scintillator layer on top of an amorphous silicon photodiode array. The system is incorporated in the Infinity™ Linac (Elekta AB, Stockholm, Sweden) equipped with the Agility™ Multileaf Collimator (MLC) of 160 leaves producing a 6 MV photon beam with a maximum DR of 600 MU/min.
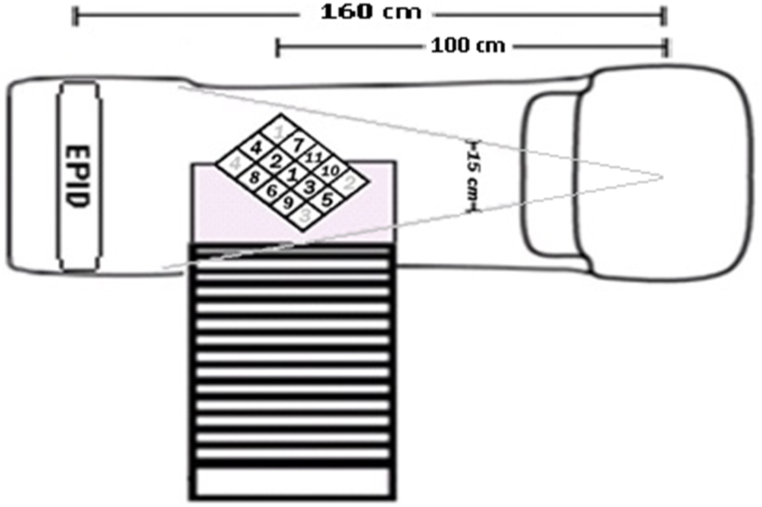
The irradiation conditions comprised 200 DR, 400 DR and 600 DR for a 2 MU–100 MU range. The X-ray source (in the LINAC head) to phantom distance was 100 cm, corresponding to the standard distance of the LINAC isocenter and the field size on the phantom surface was 15x15 cm2. The distance between the source and the EPID was 160 cm. The experimental setup is shown in Fig. 1.
Fig. 1.
LINAC set up, showing the QC-3V phantom (with numbered ROIs) standing on the plexiglass base.
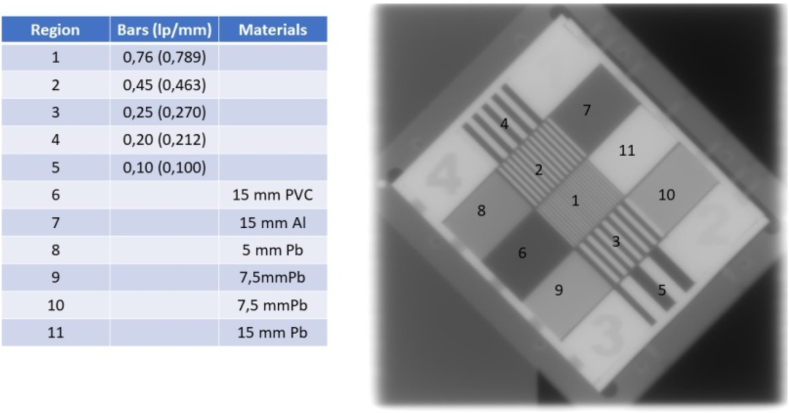
The QC-3V Phantom, shown in Fig. 2, is composed of five sets of high contrast rectangular bars with calibrated spatial frequencies of 0.100, 0.212, 0.270, 0.463 and 0.789 lp/mm and bar thickness of 15 mm. The frame of the phantom is made of aluminum, and the five test sections are made of lead and Delrin (Acetal) plastic (mass density 1.42 g/cm3). The phantom is 15 mm thin and has 3 mm acrylic and 2 mm aluminum cover plates on the top and bottom, respectively [29].
Fig. 2.
QC-3V phantom with regions of interest. The lp/mm in parenthesis are the vendor calibrated spatial frequency values of the specific phantom used in this work.
The images were transferred in Digital Imaging and Communications in Medicine (DICOM) RT format with a pixel size of 0.40 × 0.40 mm2 using the Radiotherapy Information System Mosaiq® version 2–6.4.214. The image analysis was performed via ImageJ and in-house code case specific Matlab software. The ROIs used for regions 1–5, shown in Fig. 2, were of 110 pixels, while the ROIs used for regions 7, 10, 11 as well as the background were 65x105 pixels.
The image quality and system performance metrics were determined as follows.
2.1. Contrast Transfer Function (CTF) and Modulation Transfer Function (MTF)
In the present study CTF was used as an index for determining spatial frequency response. In addition, the corresponding MTF, that describes the image signal variation in the spatial frequency domain, was approximated. MTF is regularly employed to assess a system's spatial resolution properties as well as the signal transfer accuracy through the imaging chain of a system. In the present study, MTF was expressed by the Coltman's formula [5,10,18,21,27,28,[30], [31], [32]]:
| (1) |
where CTF is the Contrast Transfer Function defined by Refs. [18,21,28]:
| (2) |
μmax(f) is the local maximum pixel value and μmin(f) is the local minimum pixel value for a given frequency f [24] corresponding to regions 1 to 5 that are shown in Fig. 2. The CTF was calculated for each of the corresponding line pairs 1 to 5 shown in Fig. 2 i.e., for each frequency.
2.2. Signal to noise ratio (SNR)
SNR was calculated with the following formula [15]:
| (3) |
where is the mean pixel value of the ROI and is the standard deviation corresponding to that ROI. SNR can be used as an estimate of the presence of signal within a noisy background and is a useful parameter for characterizing image quality.
2.3. Contrast to noise ratio (CNR)
Contrast to noise ratio expresses the ability of visual detection of an object of a given size and is used to determine the distinguishability of two ROIs in an image. It is a useful estimate of the effect of noise and was calculated with the following formula [23]:
| (4) |
where is the mean pixel value of the ROI, is the mean pixel value of the background or of another area of interest, is the variance of the ROI and are the corresponding variances.
2.4. Noise power spectrum (NPS)
NPS, expressing noise in the spatial frequency domain, is defined as the Fourier Transform (FT) of the signal fluctuations [28,33]:
| (5) |
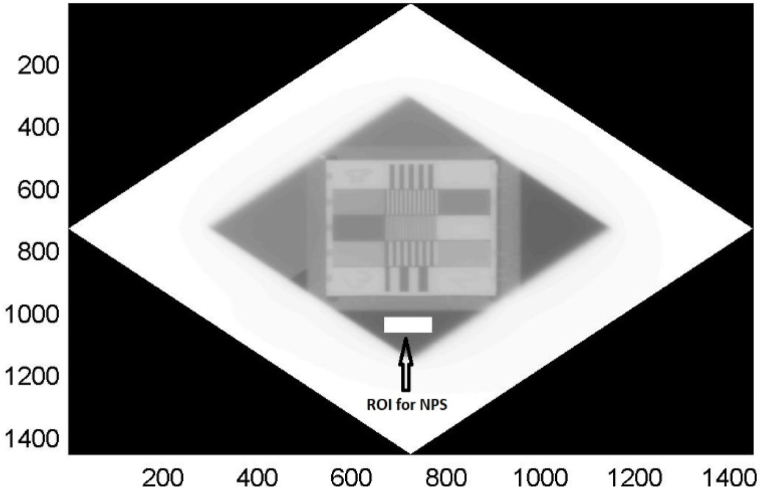
where p(x,y) is the difference between the average image signal, i.e. pixel value and the signal at point x,y. The p(x,y) is evaluated at a set of distinguished locations, x = nxΔx, nx = 0,1,2, …,N, y = nyΔy, ny = 0,1,2, …,N nx,ny stand for the number of samples, Nx and Ny are the x and y dimensions of each ROI or the numbers of pixels, lengthwise the two dimensions in the ROIs. The NPS then is calculated by ensemble averaging of the discrete Fourier transform of the average signal variation in the x and y directions, where ⟨ ⟩ represents the ensemble average. For this calculation a ROI of dimensions 100x50 pixels has been taken at the region indicated in Fig. 3 corresponding to air for each monitor unit and each dose rate combination. In addition to NPS, the normalized noise power spectrum (NNPS) is usually utilized to compare the noise features of different imaging systems. The NNPS is defined by Ref. [9]:
| (6) |
where is the square of the mean pixel value.
Fig. 3.
Area of NPS calculation in QC-3V phantom image corresponding to air.
2.5. Signal to Noise Frequency Response (SNFR)
The knowledge of CTFnorm and NPS enables the introduction of the SNFR, which is a variable that can be associated with the signal to noise ratio at the detector output, expressed in the spatial frequency domain. SNFR is calculated by using the following formula:
| (7) |
Where, CTFnorm is the normalized CTF to the lowest spatial frequency f. SNFR may act as a substitution of Detective Quantum Efficiency, DQE [1,8], since it does not require neither the knowledge of the X-ray spectrum properties, nor the air-kerma. In addition, the use of CTF instead of MTF in the nominator makes the calculation of SNFR more straight forward without the absolute need of specialized software.
2.6. EPID detector response
The EPID detector response, i.e., the variation of mean pixel value (MPV) where MPV = , as a function of MU, has been calculated by averaging the pixel values of uniform regions. The regions measured were: the background, region 7 (15 mm Aluminum thickness), region 10 (7.5 mm lead thickness) and region 11 (15 mm lead thickness) of the QC-3V phantom. The measurements were obtained for each MU and for three different DRs 200, 400, and 600.
3. Results
Table 1a, Table 1b, Table 1ca–1c shows the CTFnorm values and their corresponding error at 200 DR, 400 DR, 600 DR for 2 MU, 10 MU, 50 MU, 70 MU and 100 MU respectively. In general, the CTF responses are similar, something that might be expected if we consider that for the given EPID system, the LINAC energy is constant. It should be mentioned though that the 2 MU 200 DR combination showed the lowest CTFnorm whereas the 10 MU and 100 MU showed the highest CTFnorm at 600 DR. Αt a second glance a slight differentiation between all the values in the frequency range from 0.212 lp/mm to 0.789 lp/mm can be observed. If the spatial frequency of 0.463 lp/mm is considered the lowest CTFnorm values, was found at 2 MU with 200 DR, equal to 0.32 and the corresponding highest value, being equal to 0.39 was observed at 10 MU with 600 DR suggesting a 17.9 % difference between the highest and the lowest curve at the particular spatial frequency. The error of CTF per MU was obtained by calculating three different CTF's from three corresponding line profiles perpendicular to the bar orientation for each spatial frequency bar image, per MU, per DR. The error values are demonstrated in Table 1a, Table 1b, Table 1ca–1c accompanying the corresponding tabulated CTF values. The statistical similarity of the profile data was indicatively examined by considering two profiles of the 2MU 200DR image at 0.45(0.463) lp/mm bar pattern. A two tailed t-test between the max values and between the min values of two profiles was performed. The max values provided a t = 0.716 and the min values provided a t = 0.548. For 10 degrees of freedom and for a = 0.05 the critical value is 2.228. Since both calculated t values were found less than the aforementioned critical value, there is no statistical difference between the distributions. The statistical similarity is generally expected considering the specific LINAC output constancy of 1 % as well as the uniformity of the irradiation field.
Table 1a.
Tabulated CTF data with their corresponding errors for 200DR.
| lp/mm | 2MU 200DR | 10MU 200DR | 50MU 200DR | 70MU 200DR | 100MU 200DR |
|---|---|---|---|---|---|
| 0.100 | 1 ± 0.6 % | 1 ± 1.2 % | 1 ± 1.7 % | 1 ± 0.18 % | 1 ± 0.9 % |
| 0.212 | 0.80 ± 0.9 % | 0.80 ± 0.2 % | 0.79 ± 0.5 % | 0.80 ± 0.32 % | 0.80 ± 0.3 % |
| 0.270 | 0.57 ± 4.3 % | 0.57 ± 1.9 % | 0.57 ± 1.2 % | 0.58 ± 1.4 % | 0.57 ± 0.9 % |
| 0.463 | 0.32 ± 3.2 % | 0.35 ± 1.5 % | 0.35 ± 1.6 % | 0.36 ± 0.6 % | 0.36 ± 0.8 % |
| 0.789 | 0.20 ± 5.6 % | 0.24 ± 2.2 % | 0.23 ± 4.2 % | 0.23 ± 1.5 % | 0.23 ± 2.1 % |
Table 1b.
Tabulated CTF data with their corresponding errors for 400DR.
| lp/mm | 2MU 400DR | 10MU 400DR | 50MU 400DR | 70MU 400DR | 100MU 400DR |
|---|---|---|---|---|---|
| 0.100 | 1 ± 0.8 % | 1 ± 4.0 % | 1 ± 0.6 % | 1 ± 0.9 % | 1 ± 0.5 % |
| 0.212 | 0.82 ± 0.5 % | 0.80 ± 2.2 % | 0.79 ± 0.4 % | 0.79 ± 0.1 % | 0.79 ± 0.3 % |
| 0.270 | 0.56 ± 1.5 % | 0.58 ± 4.0 % | 0.57 ± 5.2 % | 0.58 ± 0.3 % | 0.56 ± 0.2 % |
| 0.463 | 0.36 ± 1.0 % | 0.35 ± 0.4 % | 0.35 ± 0.5 % | 0.36 ± 1.1 % | 0.36 ± 2.6 % |
| 0.789 | 0.22 ± 2.2 % | 0.22 ± 2.8 % | 0.23 ± 2.5 % | 0.24 ± 6.5 % | 0.24 ± 2.6 % |
Table 1c.
Tabulated CTF data with their corresponding errors for 600DR.
| lp/mm | 2MU 600DR | 10MU 600DR | 50MU 600DR | 70MU 600DR | 100MU 600DR |
|---|---|---|---|---|---|
| 0.100 | 1 ± 2.4 % | 1 ± 1.1 % | 1 ± 0.4 % | 1 ± 0.5 % | 1 ± 0.7 % |
| 0.212 | 0.80 ± 0.2 % | 0.82 ± 0.6 % | 0.79 ± 0.2 % | 0.80 ± 0.3 % | 0.80 ± 0.7 % |
| 0.270 | 0.56 ± 1.6 % | 0.58 ± 1.1 % | 0.57 ± 0.7 % | 0.58 ± 1.1 % | 0.58 ± 0.9 % |
| 0.463 | 0.35 ± 0.7 % | 0.39 ± 2.1 % | 0.35 ± 1.0 % | 0.36 ± 0.6 % | 0.37 ± 2.2 % |
| 0.789 | 0.22 ± 6.8 % | 0.23 ± 3.2 % | 0.22 ± 0.4 % | 0.24 ± 11.0 % | 0.24 ± 6.9 % |
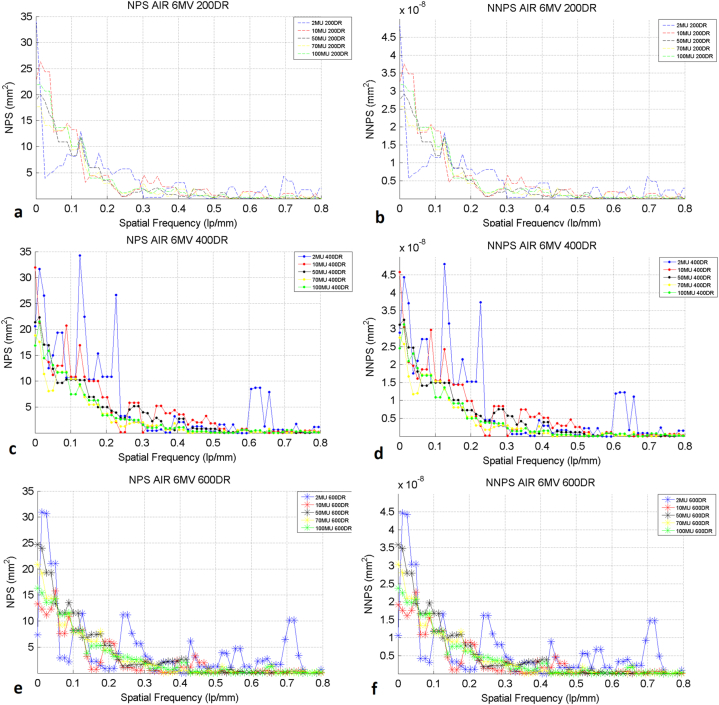
Fig. 4a–f shows the NPS and NNPS graphs, calculated in the air region indicated in Fig. 3. It is generally expected that if a detector is irradiated under quantum limited conditions, in the order of some μGy then quantum noise is dominant and the shape of NPS and NNPS falls with spatial frequency. In portal imaging clinical conditions, where the LINAC is usually calibrated to deliver 1cGy/MU at the depth of maximum dose in the tissue, quantum noise may not be the dominant noise in all spatial frequencies. Electronic noise or other noise sources also play an important role. The NPS curves shown in Fig. 4 fall with spatial frequency up to the frequency of 0.3 lp/mm and demonstrated a white noise like shape for higher spatial frequencies. Such a NPS trend in radiotherapy has also been reported in the literature [1,8,34,35]. There are distinct peaks in the NPS and NNPS curves for the 2MU at 400 DR and 600DR. This behavior is peculiar and is not generally expected in a NPS graph. It may be due to a failure of the image manipulation algorithms to assign reliable bit values in the image. The other NPS values for each DR were found comparable. There is not a significant difference in NPS and in NPPS values with different DRs. This is expected since noise and signal are mainly affected by the energy absorbed in the EPID, that is the cGy delivered by the beam. The clinical LINAC calibration to deliver 1cGy/MU is not expected to be affected by the choice of DR.
Fig. 4.
(a) NPS graphs in air of 200 DR, (b) NNPS graphs in air of 200 DR, (c) NPS graphs in air of 400 DR, (d) NNPS graphs in air of 400, (e) NPS graphs in air of 600 DR, (f) NNPS graphs in air of 600 DR.
Table 2α, Table 2b, Table 2ca–2c shows the SNFR values with their corresponding error at 200DR, 400DR, 600 DR for 2 MU, 10MU, 50MU, 70MU and 100 MU respectively. The highest SNFR values per MU and DR combination are observed in the low frequency region, ranging from 8.0x10+7 for 200 DR and 2MU, to5.7x10+8 for 600DR 2MU. SNFR generally decreases with spatial frequency and tends to zero when the EPID resolution limit is reached. This behavior can be explained if one considers the effect of CTFnorm and NPS variation with spatial frequency. Since, CTFnorm is found in the nominator of the ration defining SNFR (Equation (7)), it means that the drop of CTFnorm with respect to spatial frequency is reflected on SNFR values. Moreover, the NPS curves fell up to approximately 0.3lp/mm and present a constant trend with respect to spatial frequency afterwards. The SNFR statistical error in air was calculated by considering the CTF errors as mentioned before as well as the mean value and standard deviation of the air ROI. The error is demonstrated in Table 2α, Table 2b, Table 2ca–2c were the tabulated SNFR values are also shown.
Table 2α.
Tabulated SNFR data with their corresponding errors for 200DR.
| lp/mm | 2MU 200DR | 10MU 200DR | 50MU 200DR | 70MU 200DR | 100MU 200DR |
|---|---|---|---|---|---|
| 0.100 | 8.7E+07 ± 1.0 % | 1.3E+08 ± 1.4 % | 2.0E+08 ± 2.1 % | 1.8E+08 ± 1.2 % | 2.6E+08 ± 1.4 % |
| 0.212 | 9.4E+07 ± 1.2 % | 1.6E+08 ± 0.8 % | 1.9E+08 ± 1.2 % | 2.4E+08 ± 1.2 % | 2.2E+08 ± 1.2 % |
| 0.270 | 2.2E+07 ± 4.5 % | 2.5E+07 ± 2.0 % | 3.3E+07 ± 1.7 % | 3.5E+07 ± 1.8 % | 2.8E+07 ± 1.4 % |
| 0.463 | 1.1E+06 ± 3.3 % | 1.34E+06 ± 1.7 % | 1.5E+06 ± 2.0 % | 1.6E+06 ± 1.3 % | 1.5E+06 ± 1.4 % |
| 0.789 | 4.9E+06 ± 5.6 % | 5.2E+06 ± 2.3 % | 4.9E+06 ± 4.4 % | 5.Ee+06 ± 1.9 % | 4.7E+06 ± 2.4 % |
Table 2b.
Tabulated SNFR data with their corresponding errors for 400DR.
| lp/mm | 2MU 400DR | 10MU 400DR | 50MU 400DR | 70MU 400DR | 100MU 400DR |
|---|---|---|---|---|---|
| 0.100 | 3.1E+08 ± 1.0 % | 1.6E+08 ± 4.2 % | 1.6E+08 ± 1.1 % | 2.4E+08 ± 1.6 % | 1.9e+08 ± 1.4 % |
| 0.212 | 1.4E+08 ± 0.9 % | 1.9E+08 ± 2.4 % | 1.2E+08 ± 1.0 % | 1.5E+08 ± 1.3 % | 1.2E+08 ± 1.3 % |
| 0.270 | 5.1E+07 ± 1.7 % | 3.7E+07 ± 4.1 % | 3.6E+07 ± 5.3 % | 3.9E+07 ± 1.3 % | 3.8E+07 ± 1.3 % |
| 0.463 | 2.6E+06 ± 1.2 % | 1.3E+06 ± 1.1 % | 1.3E+06 ± 1.1 % | 1.4E+06 ± 1.7 % | 1.4E+06 ± 2.9 % |
| 0.789 | 3.6E+06 ± 2.3 % | 4.3E+06 ± 3.0 % | 4.2E+06 ± 2.7 % | 4.3E+06 ± 6.7 % | 6.E+06 ± 2.9 % |
Table 2c.
Tabulated SNFR data with their corresponding errors for 600DR.
| lp/mm | 2MU 600DR | 10MU 600DR | 50MU 600DR | 70MU 600DR | 100MU 600DR |
|---|---|---|---|---|---|
| 0.100 | 3.6E+08 ± 2.5 % | 2.0E+08 ± 1.5 % | 2.1E+08 ± 0.7 % | 2.2E+08 ± 1.1 % | 2.1E+08 ± 1.1 % |
| 0.212 | 5.7E+08 ± 0.8 % | 2.2E+08 ± 1.2 % | 1.1E+08 ± 0.6 % | 1.1E+08 ± 1.1 % | 1.3E+08 ± 1.2 % |
| 0.270 | 4.0E+07 ± 1.8 % | 3.0E+07 ± 1.5 % | 3.5E+07 ± 0.9 % | 4.1E+07 ± 1.5 % | 4.5E+07 ± 1.3 % |
| 0.463 | 1.7E+06 ± 1.0 % | 1.6E+06 ± 2.3 % | 1.3E+06 ± 1.1 % | 1.5E+06 ± 1.2 % | 1.4E+06 ± 2.4 % |
| 0.789 | 4.9E+06 ± 6.8 % | 3.7E+06 ± 3.3 % | 3.6E+06 ± 0.7 % | 4.8E+06 ± 11.0 % | 5.7E+06 ± 6.9 % |
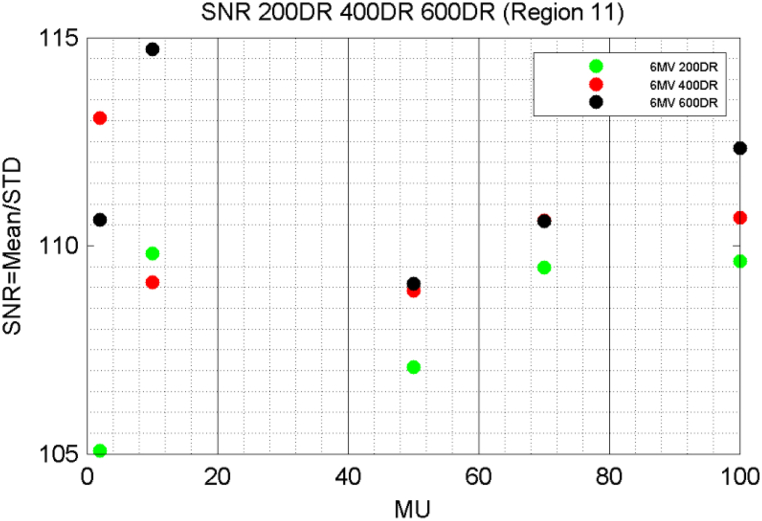
Fig. 5 demonstrates an example of the SNR graphs with respect to MUs that correspond to 200 DR, 400 DR and 600DR for region 11. It can be seen that SNR The SNR associated with 400 DR were lower than the corresponding calculated for 600 DR, except for the case of 2 MU whereas the 400 and 600 DR resulted in almost identical values at 50 and 70 MUs. Finally, if the 200 DR are considered, the corresponding SNR is the lowest, except for the case of 10 MU where its value is higher than the one of 400 DR. Taking into consideration a standard dose per MU, this could be attributed to the signal acquisition properties of the EPID electronics during image formation, as well as the image manipulation software.
Fig. 5.
SNR graphs of 200 DR, 400 DR and 600 DR at region 11.
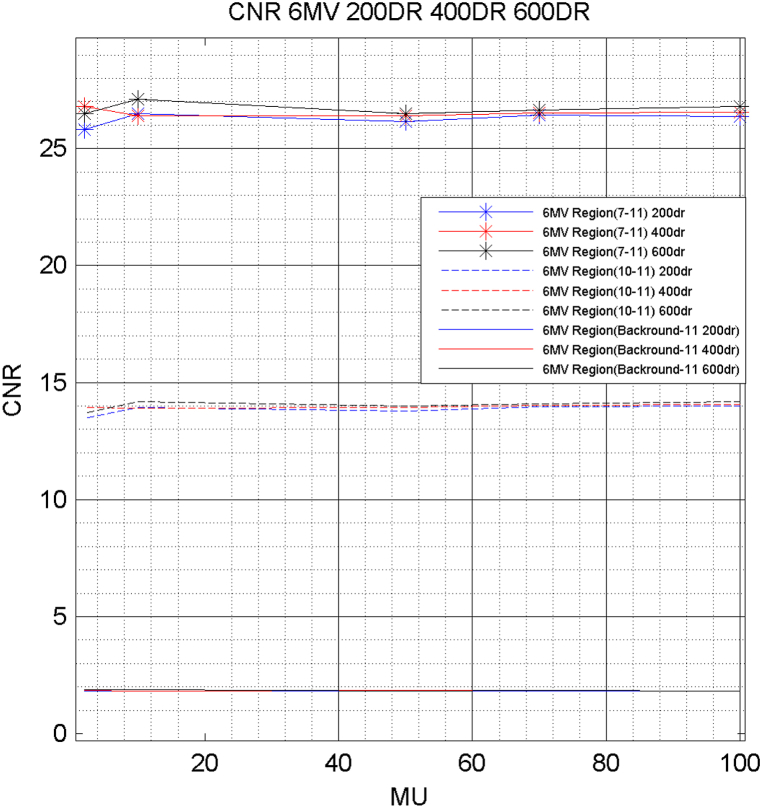
Fig. 6 shows the CNR between regions (a) 7 and 11, (b) 10 and 11 and (c) the background and 11 for 200 DR, 400 DR and 600 DR. The highest CNR values are observed between the regions 7 and 11. In addition, there is not a significant differentiation between the three Dose Rates. The variation of Monitor Units does not seem to affect the data. The graphs are almost straight and constant with respect to the MU values. The lowest values were observed between the background and region 11.
Fig. 6.
CNR graphs of 200 DR, 400 DR and 600 DR.
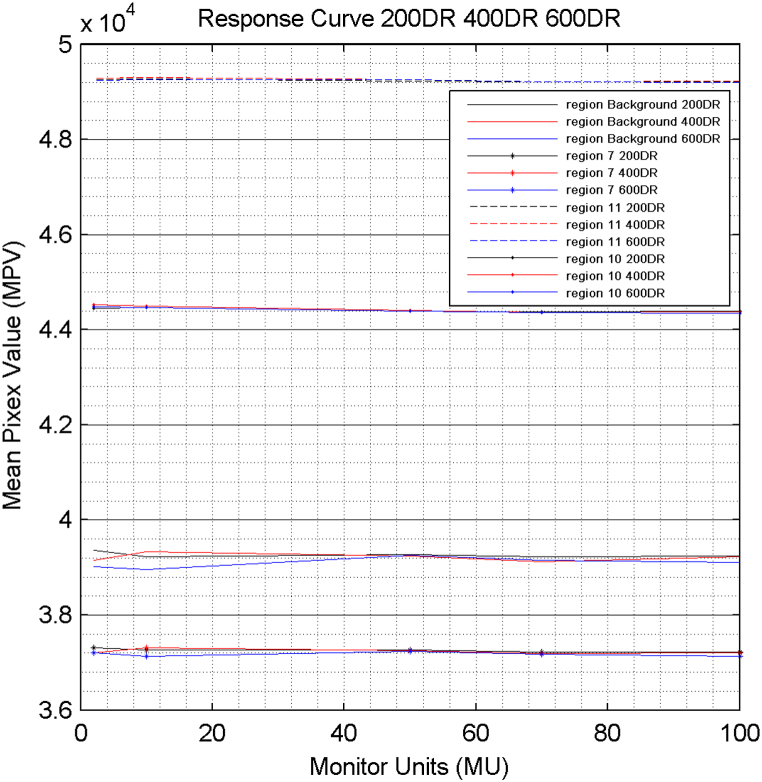
Fig. 7 shows the EPID response curve at 6 MV for 200 DR, 400 DR and, 600 DR and for four different uniformly irradiated regions of the QC-3V phantom. The detector presents remarkable stability over the whole range of MU under investigation, for each region. The highest values are shown in the region 11, which is a lead layer with total thickness of 15 mm. On the other hand, the lowest values were found for the region 7, which is an aluminum layer with 15 mm thickness and the background, which is the air.
Fig. 7.
Response curve of the EPID for 200 DR, 400 DR and 600 DR.
4. Discussion
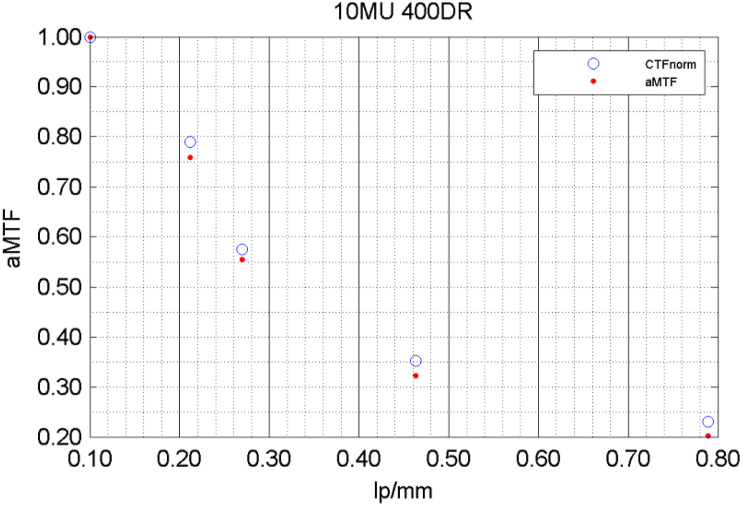
The calculation of MTF as shown in Equation (1), suggests that the CTF for all the frequencies 3f, 5f, 7f must be experimentally determined. However, the available frequencies of QC-3V EPID phantom are up to 0.789 lp/mm. A method to approximate a corresponding MTF, denoted hereafter as aMTF is demonstrated in Appendix A. Our aMTF(f) results for 10 MU and 400 DR, calculated in the Appendix, were found higher [8], or slightly inferior [5], in comparison with corresponding values reported in literature for portal imaging systems evaluation, for spatial frequencies up to 0.4 mm−1. On the other hand, the presented results were found inferior to those reported for a Varian TrueBeam™ flattening filter free system [1]. However, in the aforementioned works, MTF evaluation was performed by methods based on different instrumentation, e.g. the PTW EPID QC phantom [5], or on different techniques e.g., using either the edge technique [1], or the LSF method [8].
The NPS and NNPS curves, showed in Fig. 4a–f are affected: (a) by the statistical nature of the X-ray absorption, (b) the light creation processes in the scintillator, (c) the noise induced by the EPID electronics during image formation and (d) the software algorithms superimposed in the image. Our NPS results were higher than the corresponding NPS results reported in literature for an older amorphous silicon flat panel array irradiated with a 6 MV beam [8]. When newer systems are considered [1], our NPS results were found higher to those obtained for an EPID BEAMVIEWPLUS (Siemens) system an iX and TrueBeam (Varian) systems and another EPID iViewGT (Elekta) system [1]. The differences in the NPS results may be attributed to differences in EPID technology and the different phantoms that may be used in each measurement setup.
The differences among the regions are clearly due to the different materials in the phantom, e.g., lead, aluminum, air and their thicknesses, which affect the radiation propagation through each region of the phantom.
SNFR values were found decreasing with spatial frequency due to the effect of CTFnorm and NPS. CTF falls continuously with spatial frequency, reaching the limits of image resolution. On the other hand, NPS is usually falls slower in high frequencies than CTF. In our case it falls rapidly up to 0.3 lp/mm and keeps a constant like shape afterwards, resulting in a net fall of SNFR with respect to spatial frequency. However, in all cases the differences in SNFR values tend to minimize, with increasing spatial frequency. In addition, SNR was not found to follow some more or less smooth increase with MU.
The CNR values were found highest in the regions between 7 and 11. Also, no significant difference was observed between the three DRs. In addition, no dependency on MUs was observed. The Response of the EPID system can be optimized via the Response curves. The curves are affected principally by the X-ray absorption properties, i.e., differences among the regions, but are practically independent from the MU.
The presented MPV, SNR and CNR results are not expected if quantum limited exposure conditions and raw image data are used. In this case the MPV is expected to increase with MU. Furthermore, more photons always result in less noise and, therefore, higher SNR.
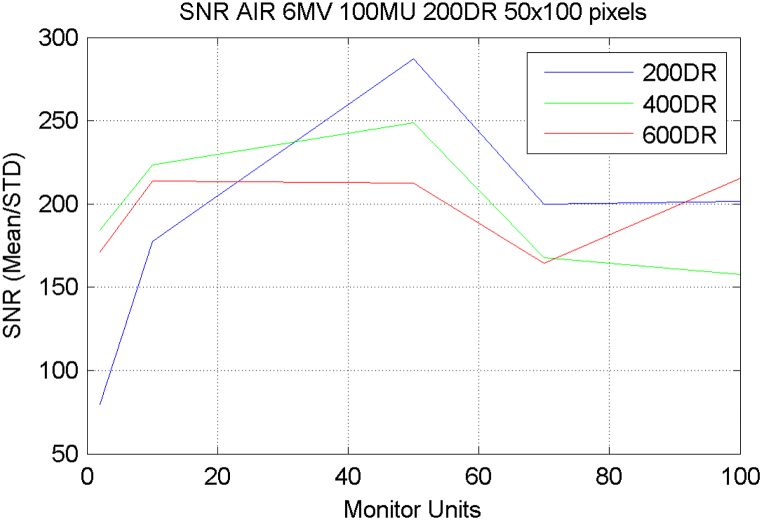
However, the irradiation conditions used in this work ranged from a few MU, which are of clinical interest, to higher MU. Furthermore, the small alteration of the mean pixel value with respect to MU, as well as the visibility of all the areas in every MU setting, are a result of the software processing algorithms applied by the IViewGT which include bad pixel mapping, electronic noise correction, image normalization, resulting in a processed image [36]. The effect of the above is clearly demonstrated in the mean pixel and CNR constancy over the MU. Additionally, the SNR curve of region 11 shown in Fig. 5 demonstrates a constancy with respect to MUs. Published literature [14] reports an increase in SNR of exposures up to 20 MU and a saturated behavior for higher MU. These values are however for a different phantom and material. In our case the X-ray absorption of 15 mm Pb which exist in region 11 may result in poor energy absorption statistics for low MU values. A trend closer to what is expected from the literature [14] may be observed if the SNR in air is calculated, as shown in Fig. 8.
Fig. 8.
SNR graphs of 200 DR, 400 DR and 600 DR at the air region.
From the previous discussion we could claim that, provided an appropriate phantom is available, the methodology of this study could be implemented routinely in radiotherapy departments. In addition, the accurate knowledge of the EPID performance can be an advantage in cases where electronic portal imaging dosimetry is applied, since the resolution of the detector and its noise properties can affect the calculated spatial distribution of the measured dose. The results of this study can lead to image quality amelioration and act supportively to current image quality checks routine protocols.
A simple methodology was developed in this work based on typical indices used for radiographic image quality assessment, in order to evaluate their suitability for QA of a clinical EPID system. Unlike the traditional qualitative portal imaging QA test which relies on user sensitivity, the quantitative metrics proposed in this study relative to spatial resolution, contrast and noise could serve as a robust QA tool that could be adopted in clinical testing procedures to establish relevant baseline values, as well as to monitor any loss in EPID performance due to unexpected mechanical or electronic damage. The verification of long-term stability of EPID is of utmost importance, particularly when it is employed for pre-treatment QA or in vivo dosimetry in IMRT and VMAT techniques, in order to be able to detect potential clinically relevant dose discrepancies that would compromise quality of treatment.
5. Conclusion
In the present study, the influence of the MU and DR choice, as LINAC irradiation parameters, on Electronic Portal Imaging Systems image quality was investigated via quantitative quality metrics. Image quality was assessed using the QC-3V EPID phantom. It was demonstrated that QC-3V phantom can be successfully used in quality control procedures where, in addition to metrics studied in the spatial domain, e.g., SNR and CNR, spatial frequency dependent image quality metrics related to signal and noise transfer properties of detectors, can be estimated. In this context, parameters, including MTF, NPS and SNFR (i.e., frequency dependent signal to noise response) were determined. SNFR can be useful for studying the overall system output performance and can be easily estimated in clinical environment. The previously mentioned metrics can be periodically used for the performance assessment of LINAC and EPID systems, acting supportively to current image quality procedures. Additionally, they can be helpful for the optimization of MU and DR settings during portal imaging procedures.
Data availability statement
The data associated with our study have not been deposited in a publicly available repository. The data generated during the current study can be made available on reasonable request.
Ethics declaration
Review and/or approval by an ethics committee was not needed for this study because there were no experiments to human, animals, or their related tissues involved in this study.
Informed consent was not required for this study because no human data, or opinions were involved in this study.
Funding
The APC was funded by the Special Account for Research Grants of the University of West Attica.
Additional information
No additional information is available for this paper.
CRediT authorship contribution statement
Marios K. Tzomakas: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. Vasiliki Peppa: Conceptualization, Methodology, Resources, Visualization, Writing – review & editing. Antigoni Alexiou: Conceptualization, Methodology, Resources, Visualization, Writing – review & editing. Georgios Karakatsanis: Conceptualization, Methodology, Resources, Visualization, Writing – review & editing. Anastasios Episkopakis: Investigation, Methodology, Resources, Validation. Christos Michail: Funding acquisition, Methodology, Validation, Writing – original draft, Writing – review & editing. Ioannis Valais: Funding acquisition, Methodology, Validation, Writing – original draft, Writing – review & editing. George Fountos: Funding acquisition, Project administration, Resources, Supervision, Writing – review & editing. Nektarios Kalyvas: Conceptualization, Methodology, Project administration, Supervision, Validation, Visualization, Writing – review & editing, Funding acquisition. Ioannis S. Kandarakis: Conceptualization, Formal analysis, Methodology, Project administration, Supervision, Writing – original draft, Writing – review & editing.
Declaration of competing interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:
Anastasios Episkopakis is an employee of Elekta Limited.
APPENDIX A. MTF approximation
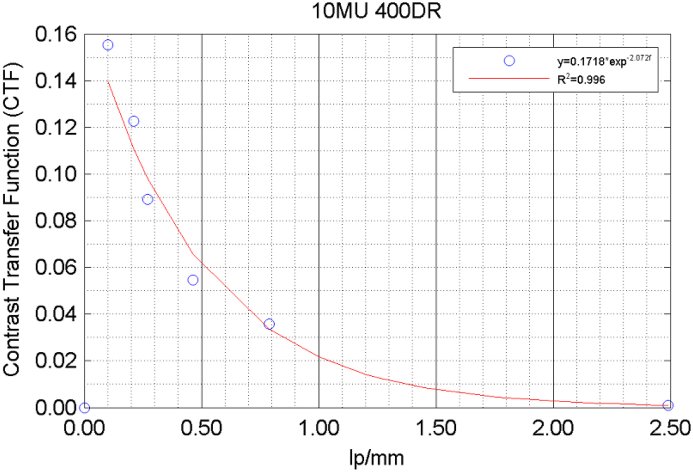
The calculation of MTF via the CTF function suggests that all the frequencies 3f, 5f, 7f must be experimentally determined. However, the available frequencies of QC-3V EPID phantom are up to 0.789 lp/mm. In order to overcome this deficit, the calculated CTF values for every frequency were fitted by an exponential function. Since the limiting resolution frequency corresponding to 400 μm pixel size is 2.5 mm−1, it was assumed that in 2.49 lp/mm the CTF value was assumed as 0.001. This value was considered as an end limit.
As an example, in Fig. A1, the fitted data for what we consider a typical CTF, at 10 MU, 400DR irradiation conditions, which lies with the majority of the calculated CTF, are shown.
Fig. A1.
CTF fitted values.
It may be observed that for the 10MU irradiation condition the CTF can be expressed as:
| (A1) |
The corresponding approximated MTF (aMTF), by using the formula presented in Equation (1) as well as the normalized CTFnorm are shown in Figure A2.
Fig. A2.
Comparison between CTFnorm and aMTF.
It may be seen from Fig. A2 that aMTF curve has a similar shape with CTFnorm, but its corresponding values per frequency are lower.
References
- 1.Son Soon-Yong, Choi Kwan-Woo, Kim Jung-Min, Jeong Hoi-Woun, Kwon Kyung-Tae, Cho Jeong-Hee, Lee Jea-Hee, Jung Jae-Yong, Kim Ki-Won, Young-Ah Lee, Son Jin-Hyun, Min Jung-Whan. Evaluation of image quality for various electronic portal imaging devices in radiation Therapy. Journal of Radiological Science and Technology. 2015;38:451–461. doi: 10.17946/JRST.2015.38.4.16. [DOI] [Google Scholar]
- 2.AAPM report No 57, clinical use of electronic portal imaging: report of AAPM radiation Therapy committee task group 58. Med. Phys. 2001;28:712–737. doi: 10.1118/1.1368128. [DOI] [PubMed] [Google Scholar]
- 3.Klein, et al. Task Group 142 report: quality assurance of medical accelerators. Med. Phys. 2009;36:4197–4212. doi: 10.1118/1.3190392. [DOI] [PubMed] [Google Scholar]
- 4.Dogan Nesrin, et al. AAPM task group report 307: use of EPIDs for patient-specific IMRT and VMAT QA. Med. Phys. 2023;50:e865–e903. doi: 10.1002/mp.16536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Das I.J., Cao M., Cheng C.-W., Misic V., Scheuring K., Schüle E., Johnstone P.A.S. A quality assurance phantom for electronic portal imaging devices. J. Appl. Clin. Med. Phys. 2011;12:391–403. doi: 10.1120/jacmp.v12i2.3350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lee S., Yan G., Bassett P., Gopal A., Samant S. Use of local noise power spectrum and wavelet analysis in quantitative image quality assurance for EPIDs. Med. Phys. 2016;43:4996–5008. doi: 10.1118/1.4959541. [DOI] [PubMed] [Google Scholar]
- 7.Borasi G., Nitrosi A., Ferrari P., Tassoni D. On site evaluation of three flat panel detectors for digital radiography. Med. Phys. 2003;30:1719–1731. doi: 10.1118/1.1569273. [DOI] [PubMed] [Google Scholar]
- 8.Cremers F., Frenzel Th, Kausch C., Albers D., Schönborn T., Schmidt R. Performance of electronic portal imaging devices (EPIDs) used in radiotherapy: image quality and dose measurements. Med. Phys. 2004;31:985–996. doi: 10.1118/1.1688212. [DOI] [PubMed] [Google Scholar]
- 9.Dobbins J.T., III, Samei E., Ranger N.T., Chen Y. Intercomparison of methods for image quality characterization. II. Noise power spectruma) Med. Phys. 2006;33:1454. doi: 10.1118/1.2188819. [DOI] [PubMed] [Google Scholar]
- 10.Baek J., Kim H., Kim B., Oh Y., Jang H. Assessment of portal image resolution improvement using an external aluminum target and polystyrene electron filter. Radiat. Oncol. 2019;14:70. doi: 10.1186/s13014-019-1274-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Seco J., Clasie B., Partridge M. Review on the characteristics of radiation detectors for dosimetry and imaging. Phys. Med. Biol. 2014;59:R303. doi: 10.1088/0031-9155/59/20/R303. [DOI] [PubMed] [Google Scholar]
- 12.Yadav P., Tolakanahalli R., Rong Y., Paliwal B.R. The effect and stability of MVCT images on adaptive TomoTherapy. J. Appl. Clin. Med. Phys. 2010;11:4–14. doi: 10.1120/jacmp.v11i4.3229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.McGarry C.K., Grattan M.W.D., Cosgrove V.P. Optimization of image quality and dose for Varian aS500 electronic portal imaging devices (EPIDs) Phys. Med. Biol. 2007;52:6865. doi: 10.1088/0031-9155/52/23/006. [DOI] [PubMed] [Google Scholar]
- 14.Ramm U., Köhn J., Dominguez R.R., Licher J., Koch N., Kara E., Scherf C., Rödel C., Weiß C. Feasibility study of patient positioning verification in electron beam radiotherapy with an electronic portal imaging device (EPID) Phys. Med.: Eur. J. Med. Plants. 2014;30:215–220. doi: 10.1016/j.ejmp.2013.06.001. [DOI] [PubMed] [Google Scholar]
- 15.de Moura F.M.G. master Thesis; 2008. Amorphous Silicon Detector Panel Damage: Correlating Physical Parameters to Clinical Usability.https://repositorio.ul.pt/handle/10451/1277?locale=en [Google Scholar]
- 16.El-Mohri Y., Antonuk L.E., Choroszucha R.B., Zhao Q., Jiang H., Liu L. Optimization of the performance of segmented scintillators for radiotherapy imaging through novel binning techniques. Phys. Med. Biol. 2014;59:797. doi: 10.1088/0031-9155/59/4/797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kanamori H., Matsumoto M. The information spectrum as a measure of radiographic image quality and system performance. Phys. Med. Biol. 1984;29:303. doi: 10.1088/0031-9155/29/4/001. [DOI] [PubMed] [Google Scholar]
- 18.Michail C., Spyropoulou V., Kalyvas N., Valais I., Dimitropoulos N., Fountos G., Kandarakis I., Panayiotakis G. The influence of software filtering in digital mammography image quality. J. Inst. Met. 2009;4 doi: 10.1088/1748-0221/4/05/P05018. [DOI] [Google Scholar]
- 19.Jarry G., Verhaegen F. Electron beam treatment verification using measured and Monte Carlo predicted portal images. Phys. Med. Biol. 2005;50:4977. doi: 10.1088/0031-9155/50/21/002. [DOI] [PubMed] [Google Scholar]
- 20.Daniels A. third ed. 2018. Field Guide to Infrared Systems, Detectors, and FPAs.https://spie.org/Publications/Book/2315934?print=2 Daniels | Publications | Spie, (2018) [Google Scholar]
- 21.Barnes G.T. Wiley; New York, NY, USA: 1979. The Physics of Medical Imaging: Recording System, Measurements and Techniques. [Google Scholar]
- 22.ICRU . nternational Commission on Radiation Units and Measurements; Bethesda, MD: 1986. Modulation Transfer Functions of Screen-Film Systems. [Google Scholar]
- 23.Kilic K., Erbas G., Guryildirim M., Konus O.L., Arac M., Ilgit E., Isik S. Quantitative and qualitative comparison of standard-dose and low-dose pediatric head computed Tomography: a retrospective study assessing the effect of adaptive statistical iterative reconstruction. J. Comput. Assist. Tomogr. 2013:37. doi: 10.1097/RCT.0b013e31828426de. [DOI] [PubMed] [Google Scholar]
- 24.Shaw R. American Association of Physicists in Medicine; New York, NY, USA: 1979. The Physics of Medical Imaging: Recording System, Measurements and Techniques. [Google Scholar]
- 25.Evans A.L. Adam Hilger Ltd; Bristol, UK: 1981. The Evaluation of Medical Images. [Google Scholar]
- 26.Liu J., Xu Y., Teymurazyan A., Papandreou Z., Pang G. Development of a novel high quantum efficiency MV x-ray detector for image-guided radiotherapy: a feasibility study. Med. Phys. 2020;47:152–163. doi: 10.1002/mp.13900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nill N.B. MITRE; 2001. Conversion between Sine Wave and Square Wave Spatial Frequency Response of an Imaging System.https://apps.dtic.mil/sti/citations/ADA460454 [Google Scholar]
- 28.Michail C.M., Kalyvas N.E., Valais I.G., Fudos I.P., Fountos G.P., Dimitropoulos N., Koulouras G., Kandris D., Samarakou M., Kandarakis I.S. Figure of image quality and information capacity in digital mammography. BioMed Res. Int. 2014;2014:1–11. doi: 10.1155/2014/634856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.SeeDOS Ltd . 2008. The Quality Control Phantom QC-3.http://www.seedos.co.uk/qc3_phantom.htm [Google Scholar]
- 30.Boreman G.D. SPIE, 1000 20th Street; Bellingham, WA 98227-0010 USA: 2001. Modulation Transfer Function in Optical and Electro-Optical Systems. [DOI] [Google Scholar]
- 31.Boone J.M., Yu T., Seibert J.A. Sinusoidal modulation analysis for optical system MTF measurements. Med. Phys. 1996;23:1955–1963. doi: 10.1118/1.597840. [DOI] [PubMed] [Google Scholar]
- 32.Podgorsak E.B. IAEA; Austria: 2005. Radiation Oncology Physics: A Handbook for Teachers and Students.http://inis.iaea.org/search/search.aspx?orig_q=RN:36071456 [Google Scholar]
- 33.Williams M.B., Mangiafico P.A., Simoni P.U. Noise power spectra of images from digital mammography detectors. Med. Phys. 1999;26:1279–1293. doi: 10.1118/1.598623. [DOI] [PubMed] [Google Scholar]
- 34.Rout B.K., Shekar M.C., Kumar A., Ramesh K.K.D. Quality control test for electronic portal imaging device using QC-3 phantom with PIPSpro. Int. J. Cancer Ther. Oncol. 2014;2 doi: 10.14319/ijcto.0204.9. [DOI] [Google Scholar]
- 35.Gopal Arun, Samant Sanjiv S. Use of a line-pair resolution phantom for comprehensive quality assurance of electronic portal imaging devices based on fundamental imaging metrics. Med. Phys. 2009;36:2006–2015. doi: 10.1118/1.3099559. 10.1118/1.3099559 2006-2015. [DOI] [PubMed] [Google Scholar]
- 36.McDermott L.N., Louwe R.J.W., Sonke J.-J., van Herk M.B. B. J. Mijnheera Dose–response and ghosting effects of an amorphous silicon electronic portal imaging device. Med. Phys. 2004;31:285–295. doi: 10.1118/1.1637969. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data associated with our study have not been deposited in a publicly available repository. The data generated during the current study can be made available on reasonable request.