Evaluation of contributors to amide proton transfer-weighted imaging and nuclear Overhauser enhancement-weighted imaging contrast in tumors at a high magnetic field

Abstract

Purpose:

The purpose is to evaluate the relative contribution from confounding factors (T_1w and MT) to the chemical exchange saturation transfer ratio (CESTR) quantified APT and NOE(−3.5) in tumors as well as whether the CESTR can reflect the distribution of the solute concentration (f_s).

Methods:

We first provided a signal model that shows the separate dependence of CESTR on these confounding factors and the clean CEST/NOE effects quantified by an apparent exchange-dependent relaxation (AREX) method. We then measured the change in these effects in the 9L tumor model in rats, through which we calculated the relative contribution of each confounding factor. f_s was also fitted, and its correlations with the CESTR and AREX was assessed to evaluate their capabilities to reflect f_s.

Results:

The CESTR-quantified APT shows ‘positive’ contrast in tumors, which mainly arises from R_1w at low powers and both R_1w and MT at high powers. CESTR-quantified NOE(−3.5) shows no or weak contrast in tumors, which is due to the cancellation of R_1w and NOE(−3.5) which have opposite contributions. CESTR-quantified APT has a stronger correlation with APT f_s than AREX-quantified APT. CESTR-quantified NOE(−3.5) has a weaker correlation with NOE(−3.5) f_s than AREX-quantified NOE(−3.5).

Conclusion:

CESTR reflects a combined effect of T_1w and CEST/NOE. Both of these factors depend on f_s, which contributes positively to the dependence of CESTR on f_s in APT imaging and enhances its correlation with f_s. In contrast, these factors have opposite contributions to its dependence on f_s in NOE(−3.5) imaging, thereby weakening the correlation.

INTRODUCTION

Chemical exchange saturation transfer (CEST) and nuclear Overhauser enhancement (NOE)-mediated saturation transfer are relatively new molecular MR imaging mechanisms which allow indirect detections of solute molecules with exchangeable protons or dipolar-coupled protons with enhanced sensitivity (1–6). In CEST/NOE imaging, a Z-spectrum, which is the plot of the water signal as a function of the frequency offset of the saturation pulses, is usually obtained so that different molecules with different resonance frequency offsets can be identified. Amide proton transfer (APT) is a variation of CEST imaging that detects the saturation transfer effect from mobile proteins/peptides and can be measured at approximately 3.5ppm from water (7). Nuclear Overhauser enhancement (NOE)-mediated saturation transfer imaging detects the saturation transfer effect from mobile macromolecular components with finite linewidth (e.g., large proteins, phospholipids) which can be measured at approximately −3.5ppm (8–12). These biomolecules are important tissue components that vary in multiple disorders. For example, protein overexpression (i.e., increased protein concentration) has been used as an imaging molecular biomarker for diagnosing tumors (13,14). Additionally, the concentration of most phospholipid species decreases in tumors, which has also been suggested as another cancer biomarker (15). Accurate and specific detection of variations in the concentration of these biomolecules in tissues is significant for both clinical diagnoses and research on the underlying pathologies.

However, as an indirect method for molecular imaging, CEST/NOE signals depend on not only the saturation transfer effect from the solute pool of interest but also on the water longitudinal relaxation time ($T_{\text{1w}}=1/R_{1\text{w}}$) as well as the background signal, including contributions from the direct water saturation (DS) and semisolid magnetization transfer (MT) effects (16). In addition, the saturation transfer effect has contributions from not only the solute concentration (f_s) but also other sample parameters, including the solute-water chemical exchange rate or cross-relaxation rate (k_sw) and the solute transverse relaxation rate (${\text{T}}_{2\text{s}}=1/{\text{R}}_{2s}$). These nonspecific factors may vary in different pathologies, thus reducing the accuracy and specificity of CEST/NOE imaging in detecting the solute molecular concentration leading to misinterpretations. Conventionally, a label signal that has contributions from both the CEST/NOE effect and the background signal and a reference signal that has contributions from only the background signal are first measured. The difference in the label and reference signals normalized to a control signal with no saturating pulses (1) or normalized to the reference signal (17–20), termed the chemical exchange saturation transfer ratio (CESTR), is then used to reduce the contributions from the background signal (1). However, CESTR cannot fully remove the nonspecific background signal. Previously, we have performed the first order Taylor series approximation of the CEST signal (21), in which the 0^th order term can be looked as the reference signal and the 1^st order term is the product of the square of the reference signal, T_1obs, and the CEST effect (T_1obs = 1/ R_1obs is the observed water longitudinal relaxation time). Although the reference signal in the 0^th order term can by removed by CESTR, the reference signal in the 1^st order term cannot be removed. It scales the CEST effect and introduces non-specificities to CESTR. This scaling effect has been also reported and termed ‘shine through’ effect in previous publications (16,22,23). Additionally, CESTR has a complex dependence on T_1w (21). Therefore, CESTR only provides a CEST/NOE-weighted signal. Evaluation of the relative contribution from each nonspecific factor to the CESTR contrast can help to interpret its contrast origin.

At low static magnetic fields in most clinical human imaging, the reference signal is usually obtained by an asymmetric analysis method, and is termed magnetization transfer ratio using asymmetric analysis (${\text{MTR}}_{\text{asym}}$). The asymmetric analysis method is simple, but may cause additional contaminations from other pools symmetrically on the other side of the water peak. At high fields, a more accurate reference signal can be obtained by using other quantification methods, such as the multiple-pool Lorentzian fit (12,24–26), chemical exchange rotation transfer (CERT) (27–32), and variable delay multiple pulse (VDMP) (33,34). Previously, we evaluated the dependence of the MTR_asym-quantified APT signal on T_1w with experiments and simulations focused on low fields where there is a significant DS effect (21). We found that there are two types of T_1w effects, termed T_1w recovery and T_1w-related saturation effects, which have opposite influences on the MTR_asym. The T_1w recovery effect reflects the dependence of MTR_asym on T_1w due to the recovery of water longitudinal magnetization. The T_1w-related saturation effect reflects the dependence of MTR_asym on T_1w due to the ‘shine through’ effect from DS. Specifically, with increasing T_1w, the T_1w recovery effect increases the MTR_asym, but the T_1w-related saturation effect decreases the MTR_asym. By choosing appropriate saturation powers so that the two T_1w effects can be counterbalanced, the MTR_asym could be roughly insensitive to T_1w. However, at high fields where the DS effect is usually weak, the insensitivity of the CESTR to T_1w may not be achieved. The dependence of CESTR on T_1w as well as other effects at high fields has not been evaluated.

In some diseases such as cancer, changes in both T_1w and MT effects have been observed. Although CESTR-quantified APT-weighted imaging and NOE-weighted imaging have been widely applied in tumors previously (14,35–46), the contributions from the change in these nonspecific factors to the CESTR contrast between tumors and normal tissues as well as its ability to reflect the distribution of corresponding molecular concentrations in tumors are unknown. To fully remove the contamination from T_1w, MT, and DS effects, an apparent exchange-dependent relaxation (AREX) method was also developed to quantify CEST/NOE effects. AREX values depend only on the solute exchanging parameters, including f_s, k_sw, and R_2s, but not other sample parameters which thus can provide more specific quantification of CEST/NOE effects than CESTR (16,22,47). However, whether AREX imaging can reflect the distribution of the corresponding molecular concentration in tumors is also unknown. In this paper, we first provided an approximate signal model to show the separate dependence of CESTR on the T_1w recovery effect, the background signal, and the CEST/NOE effects; we then measured the change of these effects in animal tumor models through which we can calculate the separate contribution from change in each of these effects to the CESTR contrast between tumors and normal tissues. Last, we fitted the proton concentration of the solute molecules and examined its correlations with the CESTR and AREX to determine whether they can reflect the distribution of the corresponding molecular concentration in tumors.

THEORY

In a three-pool model including CEST/NOE, DS, and MT, these effects acquired in steady state can be described simultaneously by superimposing their rotating frame relaxations (when the concentrations of CEST and MT pools are much less than 1) (16,22),

$$R_{1\rho }(\Delta \omega )\approx R_{eff}(\Delta \omega )+\frac{R_{ex}^{CEST}(\Delta \omega )}{1+f_m}+R_{ex}^{MT}(\Delta \omega )$$ (1)

Where $\mathrm{\Delta }\mathrm{\omega }$ is the RF saturation pulse frequency offset from water. ${\text{R}}_{\text{1ρ}}(\mathrm{\Delta }\mathrm{\omega })$, ${\text{R}}_{\text{eff}}(\mathrm{\Delta }\mathrm{\omega })$, ${\text{R}}^{\text{CEST}}{}_{\text{ex}}(\mathrm{\Delta }\mathrm{\omega })$, and ${\text{R}}^{\text{MT}}{}_{\text{ex}}(\mathrm{\Delta }\mathrm{\omega })$ are the water longitudinal relaxation, water relaxation, target CEST/NOE effect, and MT effect in the rotating frame, respectively. f_m is the semi-solid MT pool concentration. ${\text{R}}_{\text{1ρ}}(\mathrm{\Delta }\mathrm{\omega })$ can be described by (22,47),

$$R_{1\rho }(\Delta \omega )\approx \frac{S_0{R}_{1obs}}{S(\Delta \omega )}$$ (2)

where $\mathrm{S}(\mathrm{\Delta }\mathrm{\omega })$ is the measured CEST signal and S₀ is the control signal.

By substituting ${\text{R}}_{\text{1ρ}}(\mathrm{\Delta }\mathrm{\omega })$ in Eq. (1) with Eq. (2) and expanding it in powers of ${\text{R}}^{\text{CEST}}{}_{\text{ex}}(\mathrm{\Delta }\mathrm{\omega })$, we can obtain

$$\begin{gathered} S(\Delta \omega )\approx \frac{S_0{R}_{1obs}}{R_{eff}+\frac{R_{ex}^{CEST}(\Delta \omega )}{1+f_m}+R_{ex}^{MT}(\Delta \omega )} \\ \approx \frac{S_0{R}_{1obs}}{R_{eff}+R_{ex}^{MT}(\Delta \omega )}-\frac{S_0{R}_{1obs}{R}_{ex}^{CEST}(\Delta \omega )}{{\left(R_{eff}+R_{ex}^{MT}(\Delta \omega )\right)}^2(1+f_m)}+\cdots \end{gathered}$$ (3)

In APT and NOE imaging in biological tissues, ${\text{R}}^{\text{CEST}}{}_{\text{ex}}(\mathrm{\Delta }\mathrm{\omega })$ is much less than ${\text{R}}_{\text{eff}}+{\text{R}}^{\text{MT}}{}_{\text{ex}}(\text{Δω})$ (48). Therefore, the first two items in Eq. (3) dominate the CEST signal. Eq. (3) can represent ${\text{S}}_{\text{lab}}(\mathrm{\Delta }\text{ω})$. By setting ${\text{R}}^{\text{CEST}}{}_{\text{ex}}(\mathrm{\Delta }\mathrm{\omega })$ to zero, we can obtain ${\text{S}}_{\text{ref}}(\mathrm{\Delta }\text{ω})$,

$$S_{ref}(\Delta \omega )\approx \frac{S_0{R}_{1obs}}{R_{eff}+R_{ex}^{MT}(\Delta \omega )}$$ (4)

In this paper, we termed the CESTR with normalization to the control signal CESTR_I, and the CESTR with normalization to the reference signal was termed CESTR_Π. Using Eq. (3) and Eq. (4), an approximate model of CESTR_I and CESTR_Π can be then derived,

$$CEST{R}_{\text{I}}(\Delta \omega )\approx \frac{1}{R_{1obs}}·{(\frac{S_{ref(\Delta \omega )}}{S_0})}^2\frac{1}{1+f_m}·R_{ex}^{CEST}(\Delta \omega )$$ (5)

$$CEST{R}_{\text{Π}}(\Delta \omega )\approx \frac{1}{R_{1obs}}·\frac{S_{ref}(\Delta \omega )}{S_0}\frac{1}{1+f_m}·R_{ex}^{CEST}(\Delta \omega )$$ (6)

Here, we termed ‘1/R_1obs’ the T_1w recovery effect similar to that in our previous publication (21). The term ${\text{S}}_{\text{ref}}/{\text{S}}_0$ or ${({\text{S}}_{\text{ref}}/{\text{S}}_0)}^2$ represents the background signal (or reference signal), which should mostly arise from the MT effect at ±3.5 ppm at high fields and when relatively low saturation powers are used. ${\text{R}}^{\text{CEST}}{}_{\text{ex}}$ can be described by Eq. (7) (22) and quantified by the AREX defined in Eq. (8) (16),

$$R_{ex}^{CEST}(\Delta \omega )=\frac{f_s{k}_{sw}{\omega }_1^2}{{\omega }_1^2+(R_{2s}+k_{sw})k_{sw}+\frac{{(\Delta \omega -\Delta )}^2{k}_{sw}}{R_{2s}+k_{sw}}}$$ (7)

$$AREX(\Delta \omega )=\left(\frac{S_0}{S_{lab}(\Delta \omega )}-\frac{S_0}{S_{ref}(\Delta \omega )}\right)R_{1obs}(1+f_m)=R_{ex}^{CEST}(\Delta \omega )$$ (8)

where ${\text{R}}_{\text{2s}}(1/{\text{T}}_{\text{2s}})$ is the solute transverse relaxation rate and $\mathrm{\Delta }$ is the solute frequency offset. Simulations in Supporting Information Figs. S1–S4 show that the approximate model in Eq. (5) and Eq. (6) can provide a rough estimation of CESTR. Simulations in Supporting information Figs. S5–S8 further suggest that CESTR is roughly proportional to each contributor.

Inspired by the approximate model in Eq. (5) and Eq. (6), we defined ${\mathrm{C}}_{\mathrm{CESTR}}=\mathrm{CESTR}{\_}_{\mathrm{t}}/\mathrm{CESTR}{\_}_{\mathrm{n}}$, in which ‘t’ represents tumors and ‘n’ represents normal tissues, to analyze the separate contribution from change in the T_1w recovery effect, MT effect, and CEST/NOE effect to the CESTR contrast in tumors. C_CESTR can be then modeled by,

$$C_{CESTR}\approx C_{R_{1obs}}{C}_{MT}{C}_{R_{ex}^{CEST}}$$ (9)

where $C_{R_{1obs}}=\frac{R_{1obs\_n}}{R_{1obs\_t}}$ represents the contribution from the variation of the T_1w recovery effect to C_CESTR; $C_{MT}={(\frac{S_{ref\_t}}{S_{ref\_n}}\frac{S_{0\_n}}{S_{0\_t}})}^2\frac{1+f_{m\_n}}{1+f_{m\_t}}$ or $C_{MT}=\frac{S_{ref\_t}}{S_{ref\_n}}\frac{S_{0\_n}}{S_{0\_t}}\frac{1+f_{m\_n}}{1+f_{m\_t}}$ represents the contribution from the variation of the MT effect to C_CESTR for CESTR_I and CESTR_Π, respectively; and $C_{R_{ex}^{CEST}}=\frac{{AREX}_t}{{AREX}_n}$ represents the contribution from the variation of the CEST/NOE effect. Simulations in Supporting Information Figs. S9–S12 show that the approximate model in Eq. (9) can provide an accurate estimation of C_CESTR. Simulations in Supporting information Figs. S13–S16 further suggest that C_CESTR is also proportional to each contributor.

METHODS

Animal Preparation

Eight rats bearing 9L tumors were included in this study. For brain tumor induction, each rat was injected with 1 × 10⁵ 9L glioblastoma cells in the right brain hemisphere, and was then imaged after 2 to 3 weeks. All rats were immobilized and anesthetized with a 2%/98% isoflurane/oxygen mixture during data acquisition. Respiration was monitored to be stable, and a constant rectal temperature of 37°C was maintained throughout the experiments using a warm-air feedback system (SA Instruments, Stony Brook, NY, USA). All animal procedures were approved by the Animal Care and Usage Committee of Vanderbilt University Medical Center.

MRI

All measurements were performed on a Varian DirectDrive^™ horizontal 9.4 T magnet with a 38mm Litz RF coil (Doty Scientific Inc. Columbia, SC). CEST measurements were performed by applying a CW-CEST sequence with a 5s CW irradiation pulse with ${\mathrm{\omega }}_1$ of $0.25\mathrm{\mu }\mathrm{T}$, $0.5\mathrm{\mu }\mathrm{T}$, and $1\mathrm{\mu }\mathrm{T}$ followed by single-shot spin-echo echo planar imaging (SE-EPI) acquisition. Z-spectra were acquired with RF offsets at ±4000, ±3500, ±3000, and from −2000 to 2000 Hz with a step of 50 Hz (−10 to 10 ppm on 9.4 T) (49). S₀ were obtained by setting the RF offset to 100 kHz (250 ppm on 9.4T). Apparent water longitudinal relaxation rate (R_1obs) and semisolid MT pool concentration (f_m) were obtained using a selective inversion recovery (SIR) method with inversion times of 4, 5, 6, 8, 10, 12, 15, 20, 50, 200, 500, 800, 1000, 2000, 4000, and 6000 ms (50). All images were acquired with matrix size 64 × 64, field of view 30 × 30 mm², and one acquisition.

Multiple-pool Lorentzian fit and the fitting of exchange parameters

We used multiple-pool Lorentzian fitting to process the CEST Z-spectrum. Eq. (10) gives the model function of the Lorentzian fit method.

$$\frac{S(\Delta \omega )}{S_0}=1-{\sum }_{i=1}^N{L}_i(\Delta \omega )$$ (10)

Here, ${\text{L}}_{\text{i}}(\mathrm{\Delta }\text{ω})={\text{A}}_{\text{i}}/(1+{(\mathrm{\Delta }\text{ω}-{\mathrm{\Delta }}_{\text{i}})}^2/{(0.5{\text{W}}_{\text{i}})}^2)$, which represents a Lorentzian line with central frequency offset from water (${\mathrm{\Delta }}_{\mathrm{i}}$), peak full width at half maximum (W_i), and peak amplitude (A_i). N is the number of fitted pools. Specifically, a six-pool model Lorentzian fit was performed to process the Z-spectra. The model contains amide, amine, water, NOE at −1.6ppm (NOE(−1.6)) (12,51–55), NOE at −3.5ppm (NOE(−3.5)), and semisolid MT components. The number of fitted pools was estimated by observing exchange/coupling effects on Z-spectra. The fitting was performed to achieve the lowest root mean square (RMS) of residuals between the measured data and model. The Lorentzian fit was performed voxel by voxel. Supporting Information Table S1 lists the starting points and boundaries of the fit. The goodness of fit was observed by the sum of squared errors.

Since a CEST/NOE pool could be influenced by many other pools, we defined S_ref to have contributions from all other pools but not the corresponding CEST/NOE pool. So S_ref for APT, amine at 2ppm, NOE(−1.6), and NOE(−3.5) were obtained by the sum of all Lorentzians except the corresponding pool in Eq. (10); S_lab was obtained by the sum of all Lorentzians in Eq. (10) (56). Simulations in Supporting Information Figs. S17 and S18 show that the multiple-pool Lorentzian fit can provide accurate estimation of S_ref. CESTR_I- and CESTR_Π-quantified CEST/NOE effects were then obtained by subtracting S_lab from S_ref. AREX-quantified CEST/NOE effects were then obtained by inversely subtracting S_lab from S_ref and with T_1w normalization according to Eq. (8).

Previously, we have shown that the AREX metric using S_ref from the multiple-pool Lorentzian fit can provide relatively accurate estimation of $R_{ex}^{CEST}$ when ${\mathrm{\omega }}_1=<1\mathrm{\mu }\mathrm{T}$ at 9.4T (48). Here, $R_{ex}^{CEST}$ spectra were obtained using the AREX metric and the multiple-pool Lorentzian fit. f_s, k_sw, and R_2s were obtained by fitting $R_{ex}^{CEST}$ (with $\mathrm{\Delta }\mathrm{\omega }$ from 5ppm to 2ppm for APT and from −2ppm to −5ppm for NOE(−3.5)) acquired with the three ${\mathrm{\omega }}_1$ values to Eq. (7). Since the fitting of f_s, k_sw, and R_2s requires a high SNR, we do not provide their maps. Instead, we first averaged the $R_{ex}^{CEST}$ values from all voxels in a region of interest (ROI) of tumor or contralateral normal tissue, and then fit their values.

Numerical simulations

Numerical simulation of coupled Bloch equations were performed to evaluate the accuracy and reliability of the fitting method for quantifying f_s. Simulated CEST Z-spectra with RF saturation time of 5s and with ${\mathrm{\omega }}_1$ of $0.25\mathrm{\mu }\mathrm{T}$, $0.5\mathrm{\mu }\mathrm{T}$, and $1\mathrm{\mu }\mathrm{T}$ were first created using a seven-pool (amide at 3.5 ppm, fast exchanging amine at 3 ppm, intermediate exchanging guanidinium at 2ppm, water at 0mm, NOE(−1.6), NOE(−3.5), and semi-solid MT at −2.3ppm) model mimicking complex biological tissues. Sample parameters for the simulations are shown in Supporting information Table S2. Noises (S_n) were generated by randn function in MATLAB, and were added to the simulated CEST signals by ${({(\text{S}+{\text{S}}_{\text{n}})}^2+{\text{S}}_{\text{n}}{}^{\text{2}})}^{1/2}$. Other data processing to quantify AREX spectra from the simulated Z-spectra and to further fit f_s, k_sw, and T_2s was the same as that for processing the in vivo data. SNR was calculated using the ratio of the noise to the equilibrium water signal. At each noise level, 100 data sets were generated to determine the resulting variance in the fitted parameters.

The coupled Bloch equations can be written as $\frac{d\mathbf{M}}{\mathit{dt}}=\mathbf{AM}+{\mathbf{M}}_0$, where A is a 19 matrix for the seven-pool model. The water and solute pools each have three coupled equations representing their x, y, and z components. All numerical calculations of the CEST signals integrated the differential equations through the sequence using the ordinary differential equation solver (ODE45) in MATLAB 2018a (Math Works, Natick, MA, USA).

Data analysis and statistics

Student’s t-test was employed to evaluate the difference of all MRI/CEST parameters between tumors and contralateral normal tissues. Correlations between all MRI/CEST parameters and f_s were performed. Spearman’s r and p values were provided. The corresponding linear regression was also provided to indicate how these parameters are correlated in a linear manner. It was considered to be statistically significant when p < 0.05. ROIs of tumor were outlined from the f_m map with values less than a threshold of 7%. ROIs of contralateral normal tissue were chosen to mirror the tumor ROIs.

RESULTS

Fig. 1 and Fig. 2 show the Monte Carlo simulation of the fitting method for quantifying the APT f_s and the NOE(−3.5) f_s, respectively, with a variety of noise levels. The mean coefficient of variation is 11.97% for the fitting of APT f_s in Fig. 1d and is 3.54% for the fitting of NOE(−3.5) f_s in Fig. 2d when the SNR is 250. The normalized root mean square error (NRMSE) between the mean of the fitted f_s and the ground truth is 2.03% for the fitting of APT f_s in Fig. 1d and is 4.01% for the fitting of NOE(−3.5) f_s in Fig. 2d when the SNR is 250. The relatively low coefficient of variation and NRMSE suggest that the fitting method for quantifying f_s is accurate. Supporting Information Figs. S19 shows the Monte Carlo simulation of this fitting method for quantifying f_s for a variety of varied sample parameters, which suggests that the fitted f_s is roughly independent of other sample parameters and thus is reliable.

Fig. 1.

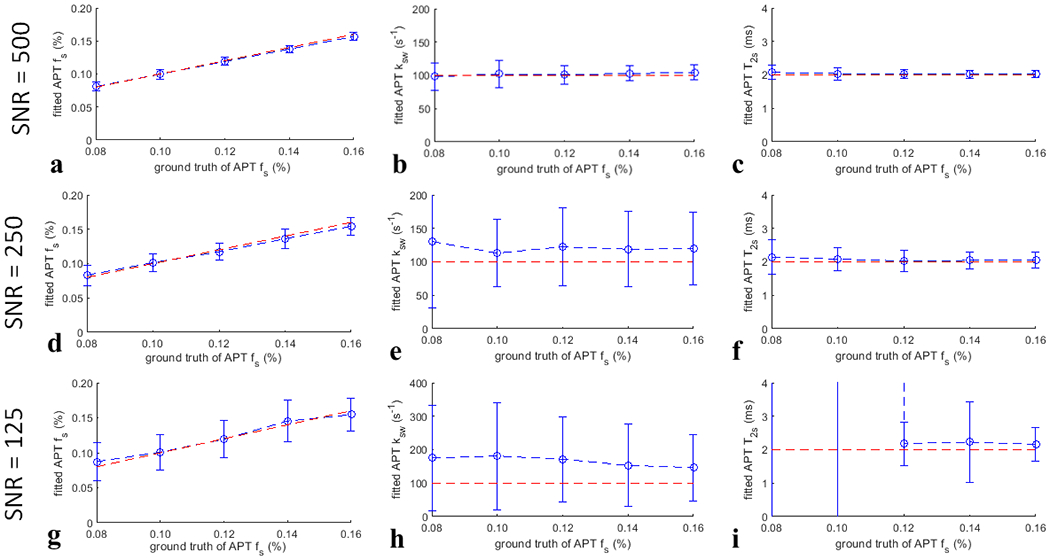
Monte Carlo simulation of the fitted APT f_s, APT k_sw, and APT T_2s (blue lines) from simulations with varied APT f_s, but constant APT k_sw and APT T_2s for different SNR. The ground truth of the fitted parameters (red lines) were also plotted for comparison.

Fig. 2.

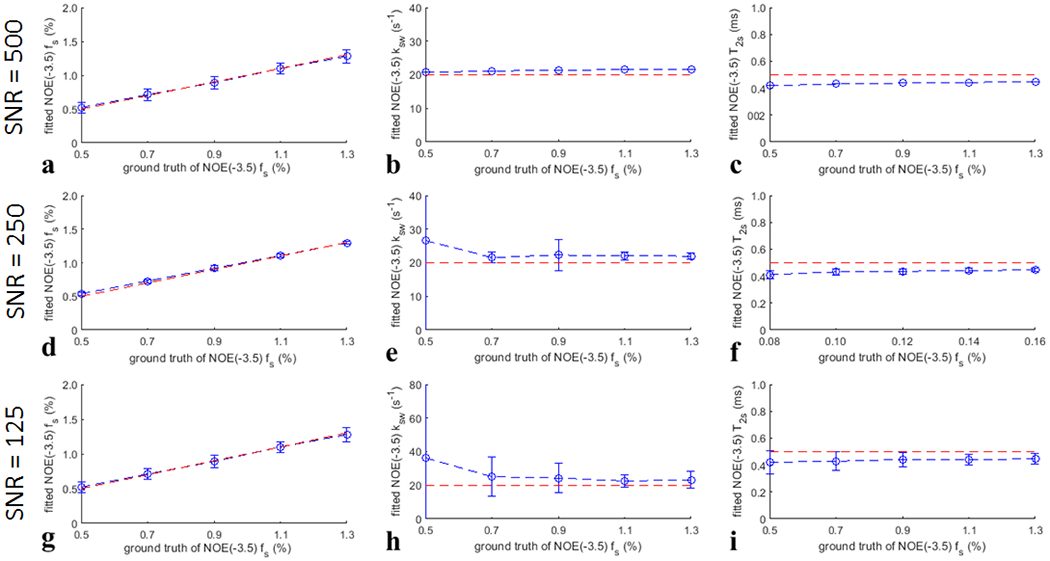
Monte Carlo simulation of the fitted NOE(−3.5) f_s, NOE(−3.5) k_sw, and NOE(−3.5) T_2s (blue lines) from simulations with varied NOE(−3.5) f_s, but constant NOE(−3.5) k_sw and NOE(−3.5) T_2s for different SNR. The ground truth of the fitted parameters (red lines) were also plotted for comparison.

Fig. 3a and 3b show the average CEST Z-spectra (or S_lab) and the corresponding S_ref for the multiple-pool Lorentzian fitting of APT and NOE(−3.5), as well as the fitting residuals from tumors and contralateral normal tissues of the eight rats with ${\mathrm{\omega }}_1$ of $1\mathrm{\mu }\mathrm{T}$. APT at 3.5ppm, amine at 2ppm, NOE at −1.6ppm and −3.5ppm, and the broad semisolid MT can be clearly observed on the CEST Z-spectra. The small residuals (< ±0.2%) in the frequency range of APT and NOE peaks indicate the success in the multiple-pool Lorentzian fit of these CEST/NOE effects. Fig. 3c–3h shows the spectra of CESTR_I, CESTR_Π, and AREX for APT and NOE(−3.5) with ${\mathrm{\omega }}_1$ of $1\mathrm{\mu }\mathrm{T}$. Supporting Information Fig. S20 and S21 show these spectra with ${\mathrm{\omega }}_1$ of $0.25\mathrm{\mu }\mathrm{T}$ and $0.5\mathrm{\mu }\mathrm{T}$, respectively.

Fig. 3.

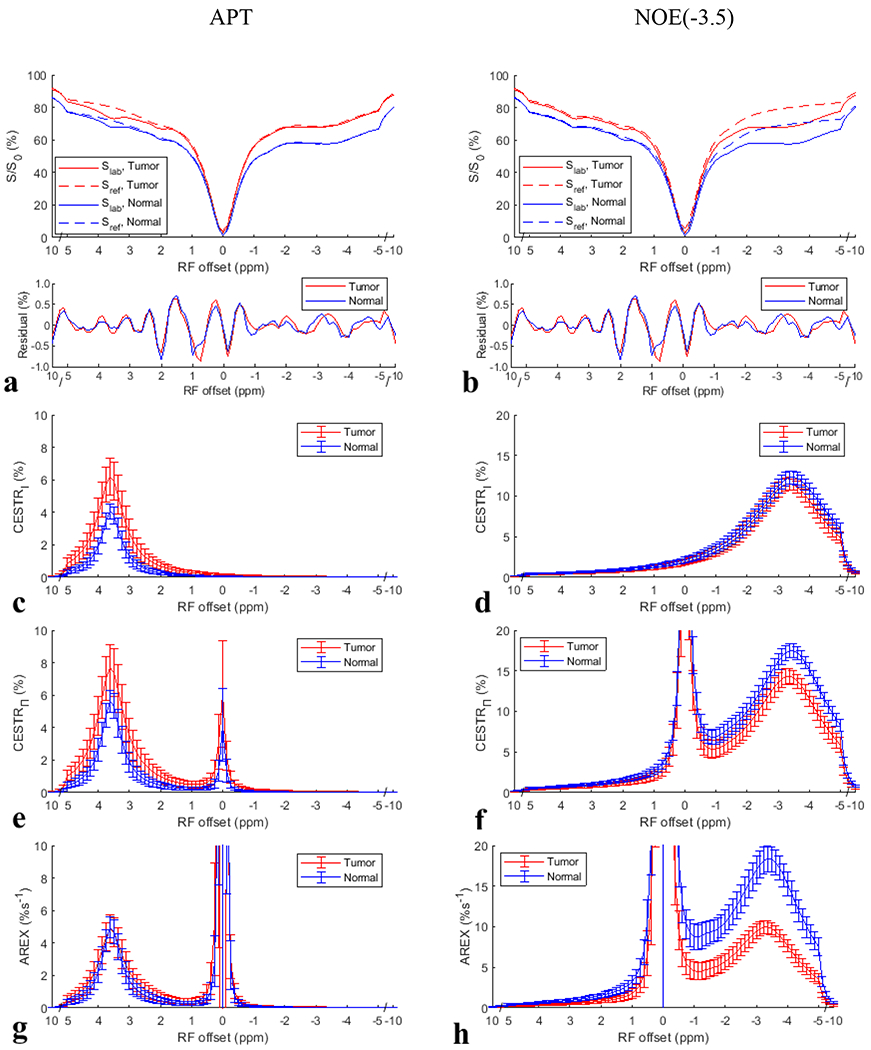
Average CEST Z-spectra (or S_lab) and the corresponding S_ref for the multiple-pool Lorentzian fitting of APT (a) and NOE(−3.5) (b) from tumors and contralateral normal tissues of the eight rats with a ${\mathrm{\omega }}_1$ value of $1\mathrm{\mu }\mathrm{T}$, as well as the fitting residuals. The CESTR_I, CESTR_Π, and AREX spectra obtained from these Z-spectra for APT (c, e, g) and NOE(−3.5) (b, f, h), respectively.

Table 1 lists the values of CESTR_I, CESTR_Π, S_ref/S₀, and AREX for APT at 3.5ppm and for NOE at −3.5ppm, R_1w, f_m, as well as the fitted f_s, k_sw, and R_2s from tumors and contralateral normal tissue. There were significant differences between tumors and contralateral normal tissues for CESTR_I- and CESTR_Π-quantified APT, R_1obs, f_m and APT f_s but not for AREX-quantified APT for all ${\mathrm{\omega }}_1$ values. In contrast, there were significant differences between tumors and contralateral normal tissues for both the CESTR- and AREX-quantified NOE(−3.5) as well as the NOE(−3.5) f_s for all ${\mathrm{\omega }}_1$ values, except the CESTR_I-quantified NOE(−3.5) with an ${\mathrm{\omega }}_1$ of $1\mathrm{\mu }\mathrm{T}$. Fig. 4 shows the maps of CESTR_I, CESTR_Π, and AREX for APT at 3.5ppm and for NOE at −3.5ppm with ${\mathrm{\omega }}_1$ of $1\mathrm{\mu }\mathrm{T}$ from a representative rat brain. Fig. S22 shows these maps with ${\mathrm{\omega }}_1$ of $0.25\mathrm{\mu }\mathrm{T}$ and $0.5\mathrm{\mu }\mathrm{T}$. Positive CESTR contrast, but no or weak AREX contrast, for APT imaging can be clearly observed, especially at higher ${\mathrm{\omega }}_1$ values. Negative AREX contrast, but no or weak CESTR contrast, for NOE(−3.5) imaging can be clearly observed, especially at higher ${\mathrm{\omega }}_1$ values.

Table 1.

lists of the values of CESTR_I, CESTR_Π, S_ref/S₀, and AREX for APT at 3.5ppm and for NOE at −3.5ppm, R_1w, f_m, as well as the fitted f_s, k_sw, and R_2s for APT and NOE(−3.5) from tumors and contralateral normal tissue.

	APT		NOE(−3.5)
	Tumor	Normal	Tumor	Normal
CESTRI $0.25\mathrm{\mu }\mathrm{T}$ (%)	1.62±0.23*	1.31±0.17	3.99±0.54*	4.56±0.43
CESTRI $0.5\mathrm{\mu }\mathrm{T}$ (%)	3.70±0.80*	2.81±0.30	8.54±0.42*	9.56±0.87
CESTRI $1\mathrm{\mu }\mathrm{T}$ (%)	6.27±1.10*	4.16±0.49	11.66±0.72	12.36±0.81
CESTRΠ $0.25\mathrm{\mu }\mathrm{T}$ (%)	1.66±0.25*	1.34±0.17	4.09±0.56*	4.73±0.45
CESTRΠ $0.5\mathrm{\mu }\mathrm{T}$ (%)	3.98±0.88*	3.14±0.35	9.22±0.43*	10.87±0.97
CESTRΠ $1\mathrm{\mu }\mathrm{T}$ (%)	7.79±1.37*	5.78±0.71	14.54±0.93*	17.55±0.87
R1w (s−1)	0.44±0.03*	0.56±0.02	0.44±0.03*	0.56±0.02
fm (%)	4.94±0.38*	9.99±1.26	4.94±0.38*	9.99±1.26
Sref/S0 $0.25\mathrm{\mu }\mathrm{T}$ (%)	97.80±0.58*	97.15±0.50	97.75±0.67	96.29±0.86
Sref/S0 $0.5\mathrm{\mu }\mathrm{T}$ (%)	92.74±0.68*	89.49±0.70	92.62±1.24*	87.55±1.11
Sref/S0 $1\mathrm{\mu }\mathrm{T}$ (%)	79.68±2.10*	71.50±1.85	80.35±1.61*	70.07±2.69
AREX $0.25\mathrm{\mu }\mathrm{T}$ (%s−1)	0.81±0.12	0.84±0.09	2.06±030*	3.11±0.34
AREX $0.5\mathrm{\mu }\mathrm{T}$ (%s−1)	2.07±0.38	2.17±0.21	5.18±0.29*	8.42±0.83
AREX $1\mathrm{\mu }\mathrm{T}$ (%s−1)	4.92±0.84	5.11±0.65	10.15±0.76*	18.46±1.57
fs (%)	0.13±0.03*	0.10±0.02	0.95±0.10*	1.53±0.26
ksw (s−1)	81.62±50.17	109.81±81.12	14.30±2.55*	19.93±4.27
T2s (ms)	1.20±0.34	1.70±0.54	0.52±0.09	0.45±0.06

^*p < 0.05

Fig. 4.

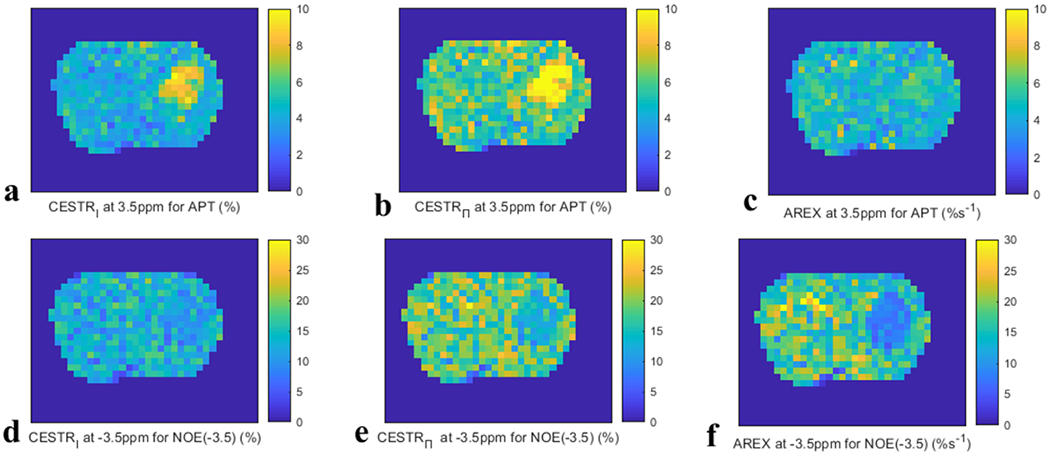
Maps of CESTR_I (left column), CESTR_Π (medium column), and AREX (right column) for APT at 3.5 ppm (a-c) and NOE at −3.5 ppm (d-f) with ${\mathrm{\omega }}_1$ of $1\mathrm{\mu }\mathrm{T}$ from a representative rat brain.

Fig. 5 and Fig. 6 show the C_CESTR and each of its contributors (i.e., $C_{R_{1obs}}$, C_MT, and $C_{R_{ex}^{CEST}}$) for APT and NOE(−3.5) from the eight rats. The average $|C_{R_{ex}^{CEST}}-1|$ for APT is very small compared with the average |C_CESTR-1| for all ${\mathrm{\omega }}_1$ values; the average |C_MT-1| for APT is also very small at ${\mathrm{\omega }}_1$ of $0.25\mathrm{\mu }\mathrm{T}$ and $0.5\mathrm{\mu }\mathrm{T}$ but increases at ${\mathrm{\omega }}_1$ of $1\mathrm{\mu }\mathrm{T}$; the average $|C_{R_{1obs}}-1|$ is comparable to the average |C_CESTR-1| for APT at ${\mathrm{\omega }}_1$ of $0.25\mathrm{\mu }\mathrm{T}$ and $0.5\mathrm{\mu }\mathrm{T}$ but is relatively smaller than it is at ${\mathrm{\omega }}_1$ of $1\mathrm{\mu }\mathrm{T}$; both the average $|C_{R_{1obs}}-1|$ and average |C_MT-1| are major contributors to |C_CESTR-1| at ${\mathrm{\omega }}_1$ of $1\mathrm{\mu }\mathrm{T}$. This result suggests that the change in R_1obs in tumors dominates the CESTR contrast at lower ${\mathrm{\omega }}_1$ values, and both R_1obs and the MT effect dominate the CESTR contrast at higher ${\mathrm{\omega }}_1$ values. Both the average $C_{R_{ex}^{CEST}}$ and the average C_CESTR for NOE(−3.5) are less than 1, and the average $|C_{R_{ex}^{CEST}}-1|$ is larger than the average |C_CESTR-1| for all ${\mathrm{\omega }}_1$ values. In contrast, both the average $C_{R_{1obs}}$ and average C_MT for NOE(−3.5) are greater than 1; similar to APT, the average |C_MT-1| for NOE(−3.5) is also very small at ${\mathrm{\omega }}_1$ values of $0.25\mathrm{\mu }\mathrm{T}$ and $0.5\mathrm{\mu }\mathrm{T}$, but increases at ${\mathrm{\omega }}_1$ values of $1\mathrm{\mu }\mathrm{T}$. This result suggests that changes in both R_1obs and NOE(−3.5) effect in tumors contribute to the CESTR contrast at lower ${\mathrm{\omega }}_1$ values and changes in R_1obs, MT effect, and NOE(−3.5) effect in tumors contribute to the CESTR contrast at higher ${\mathrm{\omega }}_1$ values. Additionally, the contributions from R_1obs and NOE(−3.5) effect are in opposite directions, causing the reduced CESTR contrast. In addition, compared with CESTR_I, CESTR_Π has a reduced contribution from the MT effect for both the APT and NOE(−3.5). However, CESTR_Π still cannot remove the contribution from R_1obs.

Fig. 5.

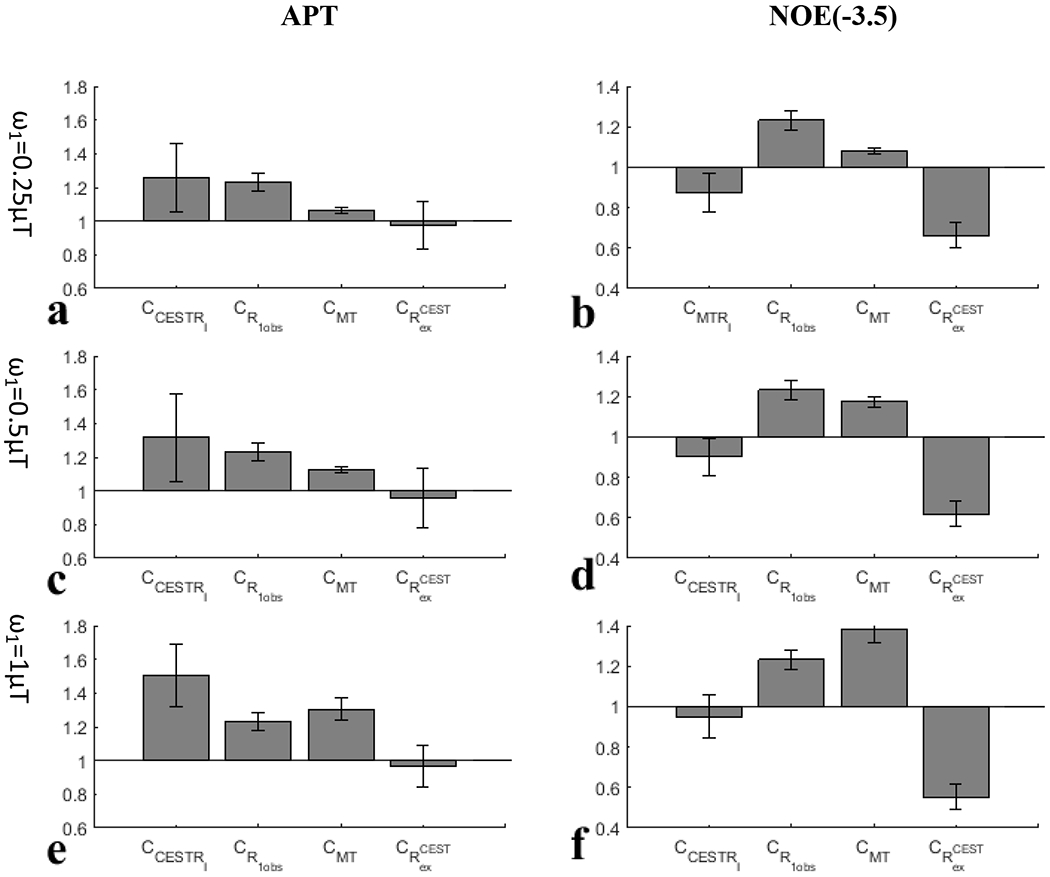
$C_{{CESTR}_I}$ and each of its contributors for APT (left column) and NOE(−3.5) (right column) with ${\mathrm{\omega }}_1$ values of $0.25\mathrm{\mu }\mathrm{T}$ (a, b), $0.5\mathrm{\mu }\mathrm{T}$ (e, f), and $1\mathrm{\mu }\mathrm{T}$ (i, j), respectively, from the eight rats.

Fig. 6.

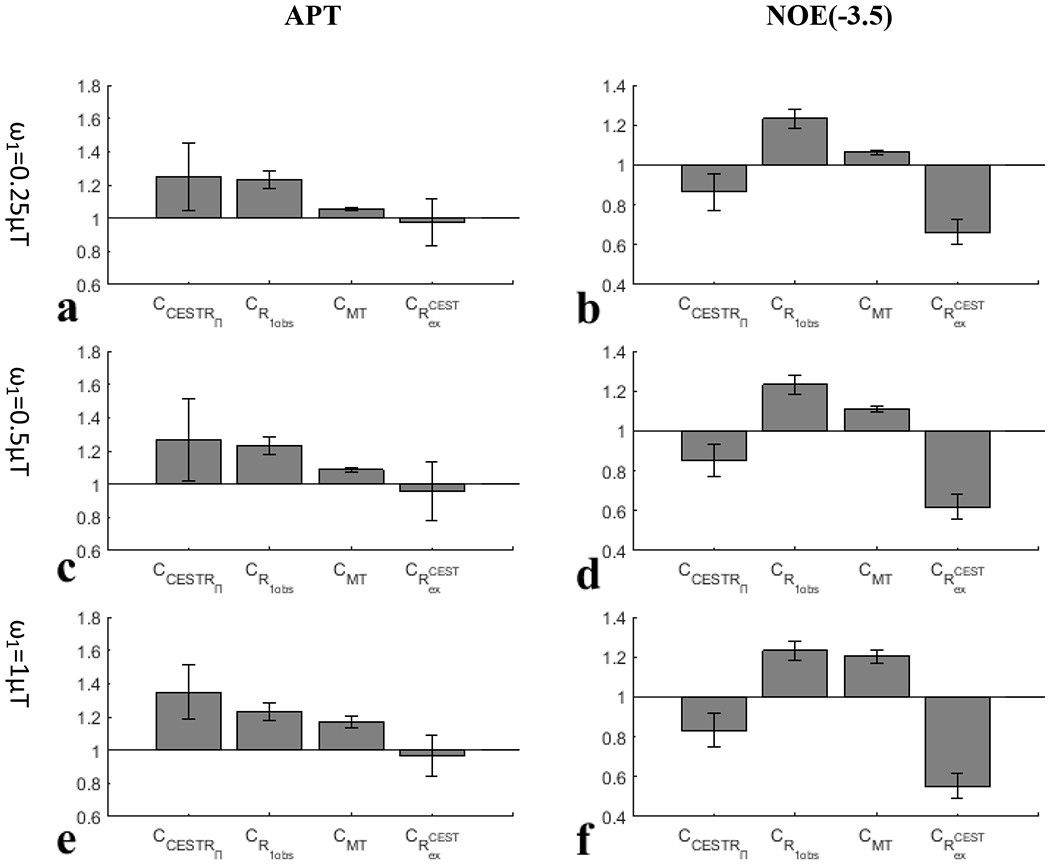
$C_{{\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{T}\mathrm{R}}_{\mathrm{\Pi }}}$ and each of its contributors for APT (left column) and NOE(−3.5) (right column) with ${\mathrm{\omega }}_1$ values of $0.25\mathrm{\mu }\mathrm{T}$ (c, d), $0.5\mathrm{\mu }\mathrm{T}$ (g, h), and $1\mathrm{\mu }\mathrm{T}$ (k, l), respectively, from the eight rats.

Fig. 7 summarizes the correlations between the APT effect quantified by the three CEST metrics (CESTR_I, CESTR_Π, AREX) and the corresponding APT f_s from both the tumors and the contralateral normal tissues. Significant correlations between the CESTR-quantified APT effect and the APT f_s, but not between the AREX-quantified APT effect and the APT f_s, for all ${\mathrm{\omega }}_1$ values were found. Fig. 8 summarizes the correlations between the NOE(−3.5) effect quantified by the three CEST metrics (CESTR_I, CESTR_Π, AREX) and the corresponding NOE(−3.5) f_s from both the tumors and the contralateral normal tissues. Significant correlations between the NOE(−3.5) effect quantified the three CEST metrics and the NOE(−3.5) f_s for all ${\mathrm{\omega }}_1$ values (except the CESTR_Π-quantified NOE(−3.5) for ${\mathrm{\omega }}_1$ value of $1\mathrm{\mu }\mathrm{T}$) were found. However, the correlation between the AREX-quantified NOE(−3.5) effect and the NOE(−3.5) f_s is stronger than the correlation between the CESTR-quantified NOE(−3.5) effect and the NOE(−3.5) f_s.

Fig. 7.

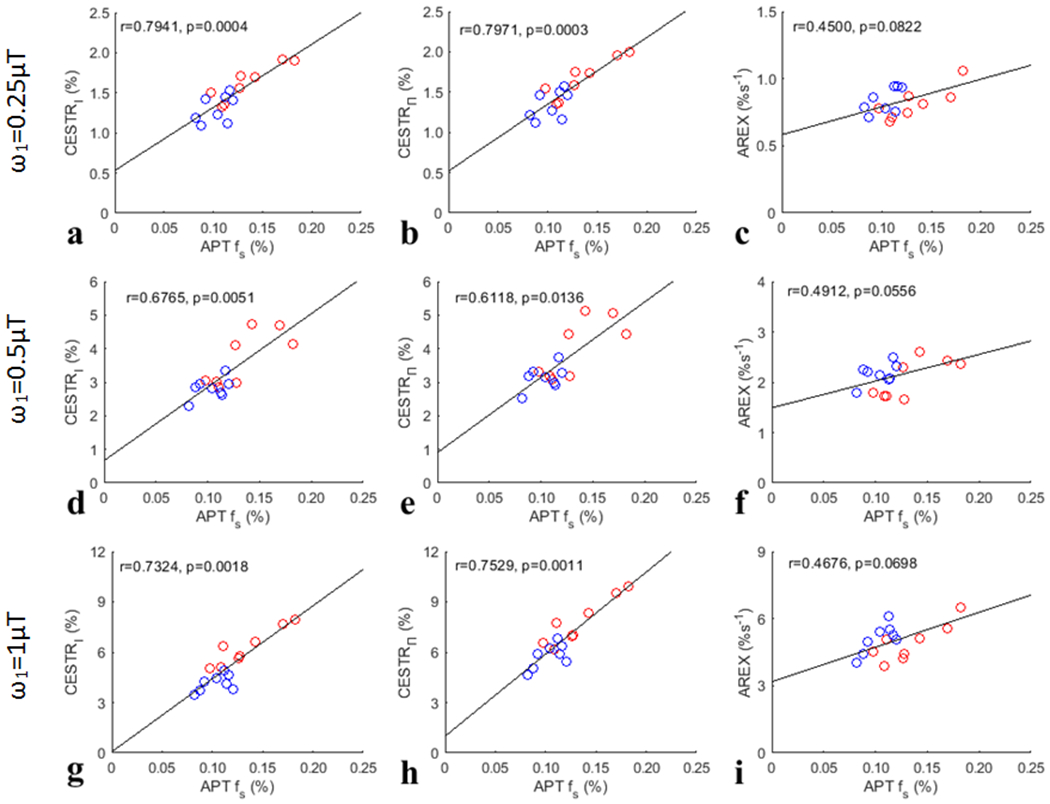
Summarized correlation of three CEST metrics (CESTR_I, CESTR_Π, AREX) at 3.5ppm for APT with the corresponding APT f_s from both the tumors and the contralateral normal tissues of the eight rats. The red circles represent the mean values of each tumor, and the blue circles are the mean values of each ROI of contralateral normal tissue. The Spearman’s rank correlation coefficient (r) and p value of each correlation are provided. The black lines represent the linear regression of all data points in each correlation subfigure.

Fig. 8.

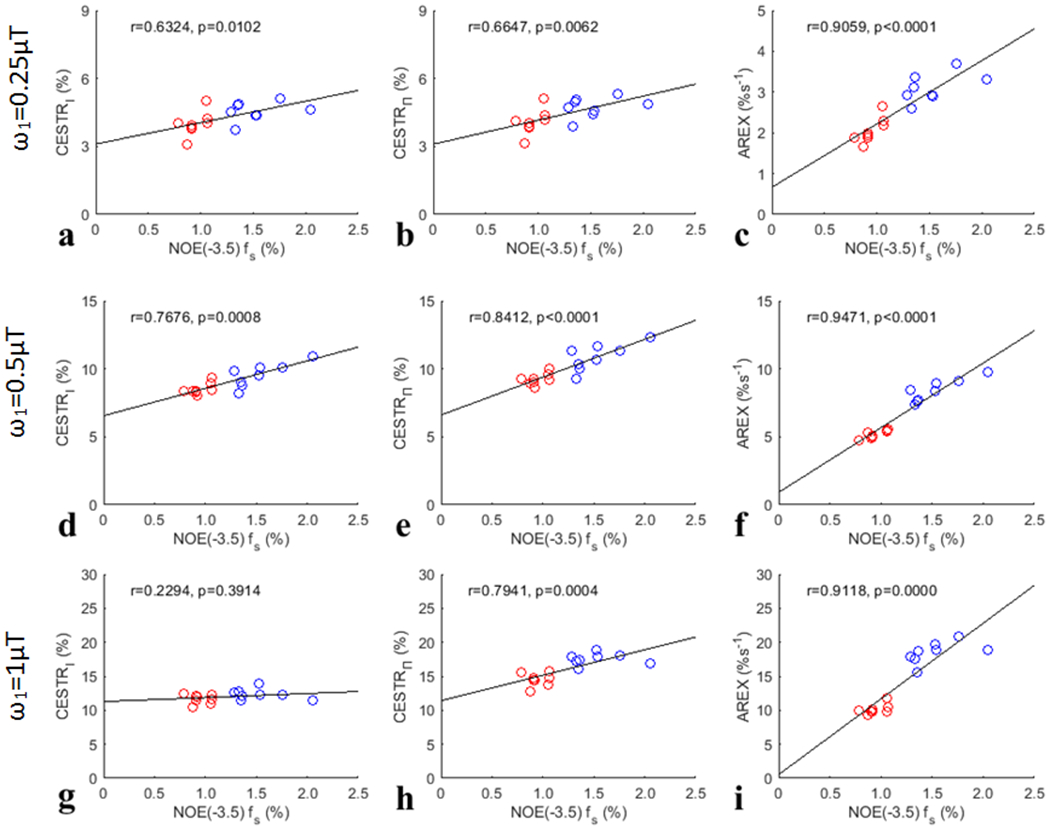
Summarized correlation of three CEST metrics (CESTR_I, CESTR_Π, AREX) at −3.5ppm for NOE(−3.5) with the corresponding NOE(−3.5) f_s from both the tumors and the contralateral normal tissues of the eight rats. The red circles represent the mean values of each tumor, and the blue circles are the mean values of each ROI of contralateral normal tissue. The Spearman’s rank correlation coefficient (r) and p value of each correlation are provided. The black lines represent the linear regression of all data points in each correlation subfigure.

Fig. 9 summarizes the correlations between the confounding factors (1/R_1obs, S_ref/S₀ with the three ${\mathrm{\omega }}_1$) and the APT f_s and NOE(−3.5) f_s, respectively, from both the tumors and the contralateral normal tissues. Although 1/R_1obs has positive correlation with APT f_s, it has negative correlation with NOE f_s. Supporting Information Fig. S23 and S24 summarizes the correlations between other MRI/CEST parameters (f_m, all CESTR- and AREX-quantified CEST/NOE effects with the three ${\mathrm{\omega }}_1$, NOE(−3.5) or APT f_s) and the APT f_s and NOE(−3.5) f_s, respectively, from both the tumors and the contralateral normal tissues. Significant correlations of 1/R_1obs, f_m, NOE(−1.6) and NOE(−3.5) quantified by the three metrics (except the AREX-quantified NOE(−3.5)) with the APT f_s were found. However, the correlation between these MRI/CEST parameters and the APT f_s is not as strong as that between the CESTR and the APT f_s. Significant correlations of 1/R_1obs, S_ref/S₀ with all ${\mathrm{\omega }}_1$ values, f_m, CESTR_I-quantified APT, CESTR_Π-quantified NOE(−1.6) and APT, as well as AREX quantified amine and NOE(−1.6) with the APT f_s were found. However, the correlation between these MRI/CEST parameters (except 1/R_1obs and S_ref/S₀ with a ${\mathrm{\omega }}_1$ value of $1\mathrm{\mu }\mathrm{T}$) and the NOE(−3.5) f_s is not as strong as that between the AREX and the NOE(−3.5) f_s.

Fig. 9.

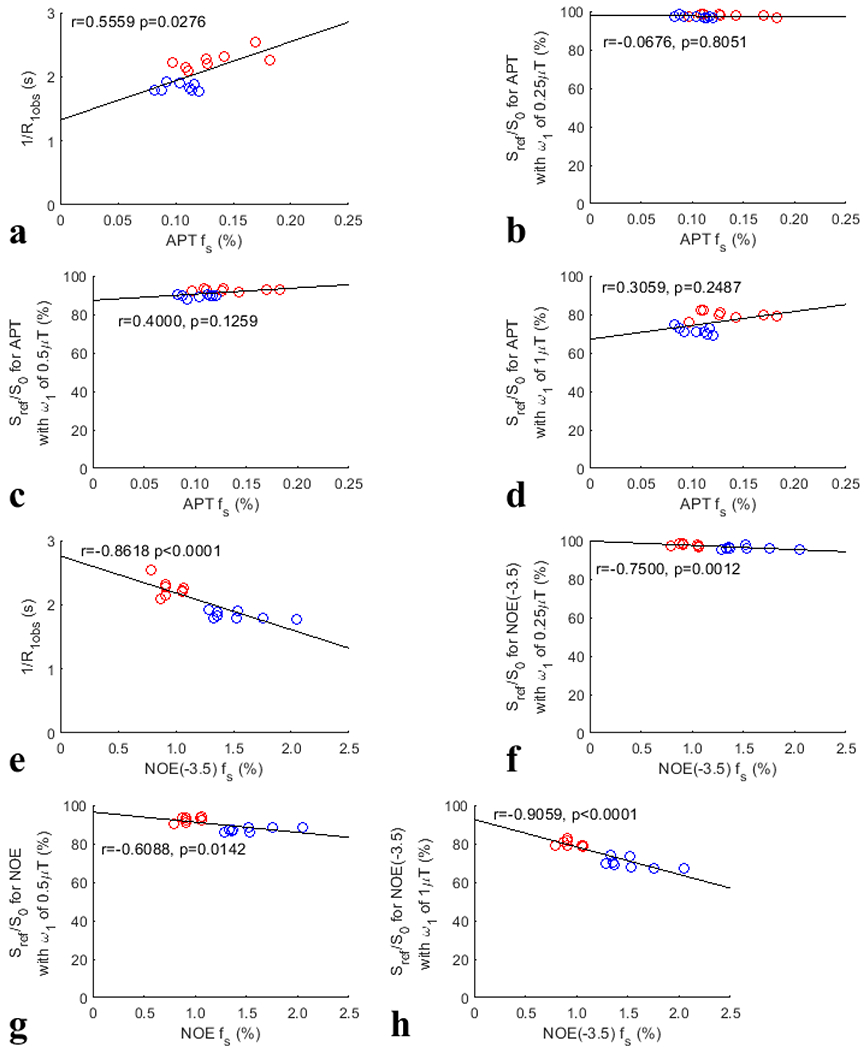
Summarized correlation of the confounding factors (1/R_1obs, S_ref/S₀ with ${\mathrm{\omega }}_1$ values of $0.25\mathrm{\mu }\mathrm{T}$, $0.5\mathrm{\mu }\mathrm{T}$, and $1\mathrm{\mu }\mathrm{T}$) with the APT f_s (a-d) and NOE(−3.5) f_s (e-h), respectively, from both the tumors and the contralateral normal tissues of the eight rats. The red circles represent the mean values of each tumor, and the blue circles are the mean values of each ROI of contralateral normal tissue. The Spearman’s rank correlation coefficient (r) and p value of each correlation are provided. The black lines represent the linear regression of all data points in each correlation subfigure.

DISCUSSION

Although it has been noticed that the APT/NOE-weighted imaging in tumors has contaminations from both T_1obs and MT effects (57), it is still not clear about how these confounding factors influence the APT/NOE-weighted imaging and how much their relative contributions are. This may be due the short of appropriate signal models for analyzing the contributions from the confounding factors. Although a few signal models have been previously derived from the coupled Bloch equations, they are very complex, especially when multiple pools for modeling biological tissues are considered, which do not show intuitive dependencies on the confounding factors and the CEST effects (3). In this paper, we provided a new approximate signal model which can be approximated as the multiplication of three independent terms, which are determined by the T_1w recovery effect, MT effect, and CEST/NOE effect, respectively. This approximate signal model allows us to analyze each of the contributors separately.

Although the CESTR-quantified APT is not specific to the APT effect, it has a stronger correlation with the APT f_s than the AREX-quantified APT. This is consistent with a previous report showing a strong correlation between the MTR_asym-quantified APT and protein content using proteomic analysis (13). Fig. 7 shows that there are positive correlations between the AREX-quantified APT and the APT f_s with relatively low p values (close to 0.05) although there are no statistical significance. Fig. 9 shows that there is a significant positive correlation between 1/R_1obs and the APT f_s. Since CESTR is roughly equal to the production of 1/R_1obs, S_ref/S₀/(1+f_m) or (S_ref/S₀)²/(1+f_m), and $R_{ex}^{CEST}$ as shown in Eq. (5) and Eq. (6), the strong correlation between the CESTR-quantified APT and the APT f_s may be due to the enhancement effect from both 1/R_1obs and the APT effect. Therefore, the CESTR-quantified APT contrast between tumors and normal tissues should reflect a combined effect from these two APT f_s-sensitive factors, which is thus more strongly related to the APT f_s than all other MRI/CEST parameters analyzed in this paper. CESTR is a widely used method to quantify APT effect which has shown interesting contrast in tumors, suggesting that it may reflect the underlying biomarker. Our results provide insight into the interpretation of the contrast origin of the APT/NOE-weighted imaging in tumors at high fields.

The CESTR-quantified NOE(−3.5) is not specific to the NOE(−3.5) effect. Different from the APT, the correlation between the CESTR-quantified NOE(−3.5) and the NOE(−3.5) f_s is not as strong as that between the AREX-quantified NOE(−3.5) and the NOE(−3.5) f_s. Fig. 8 shows that there are significant positive correlations between the AREX-quantified NOE(−3.5) and the NOE(−3.5) f_s. Fig. 9 shows that there are significant negative correlations between 1/R_1obs and the NOE(−3.5) f_s. The relatively weaker correlation between the CESTR-quantified NOE(−3.5) and the NOE(−3.5) f_s than that between the AREX-quantified NOE(−3.5) and the NOE(−3.5) f_s should be due to the cancellation effect from 1/R_1obs and the NOE(−3.5) effect which have opposite influences on the CESTR-quantified NOE(−3.5) contrast. The positive correlations of both the CESTR-quantified NOE(−3.5) and the AREX-quantified NOE(−3.5) with the NOE(−3.5) f_s suggest that the contribution from the NOE(−3.5) effect to the CESTR-quantified NOE(−3.5) dominates that from R_1obs. Therefore, the CESTR-quantified NOE(−3.5) contrast between tumors and normal tissues should mainly reflect the NOE(−3.5) effect, but has negative but small contributions from 1/R_1obs.

Previously, it was indicated that the APT f_s has little impact on R_1obs (16). But significant correlation between 1/R_1obs and APT f_s was found in Fig. 9a. This can be explained by that the amide concentration reflects the concentration of proteins which influence R_1obs through other fast exchanging protons (e.g., amines, hydroxyls) and/or dipolar-coupled protons. In addition, significant correlation between f_m and APT f_s was found in Supporting information Fig. S23a. The mechanism is unclear. Supporting information Fig17. Sj-Sl show that the multiple-pool Lorentzian fitted S_ref matches the ground truth simulated S_ref very well with varied f_m, suggesting that this correlation is not due to the failure of the multiple-pool Lorentzian fit in separating APT from MT.

Our conclusion about the relative contributions from confounding factors to the APT/NOE contrast in tumors relies on the accuracy of the approximate model in Eq. (9). In Supporting Information Fig. S1–S16, although the deviations of the approximate model in Eq. (5) and Eq. (6) are from a few percent to more than ten percent, the deviations of the approximate model in Eq. (9) are very small (<3%). The deviations in Eq. (5) and Eq. (6) are due to the ignorance of the higher order terms of the Taylor series. However, these higher order terms may have a roughly similar form of dependence on the contributing factors to that in Eq. (5) and Eq. (6). Thus, the ratio of two CESTR values from tumor and normal tissues in Eq. (9) has less influence from the ignorance of the higher order terms.

Our conclusion about the capability of the CESTR and AREX to reflect the solute molecular concentration relies on the accurate and robust fitting of f_s. Fig. 1 and Fig. 2 show that although the fitting of k_sw and R_2s are unreliable, the fitting of f_s is relatively accurate and robust. Our fitted APT f_s values are much smaller than those reported in previous publications (58–61). This may be due to the use of different models. Previously, we showed that the fast exchanging amine CEST effect is present at both high and low ${\mathrm{\omega }}_1$ values (e.g. $1\mathrm{\mu }\mathrm{T}$) and has significant contributions to the CEST signal at 3.5ppm (48,62). We also showed that the influence of the fast exchanging amine CEST effect on the quantification of APT can be significantly reduced by multiple-pool Lorentzian fit with ${\mathrm{\omega }}_1=<1\mathrm{\mu }\mathrm{T}$ at 9.4T. In this paper, we used low ${\mathrm{\omega }}_1$ values and the multiple-pool Lorentzian fit to reduce the contamination from the fast exchanging amine CEST effect. However, in previous papers, the contribution from the fast exchanging amine CEST effect was not considered.

In this paper, we used the ratio of two CESTR signals from tumors and normal tissues (i.e., C_CESTR = CESTR_t / CESTR_n) to reflect the CESTR contrast. Conventionally, CESTR contrast in tumors has been calculated by the subtraction of two CESTR signals from tumors and normal tissues (i.e., CESTR_t - CESTR_n) (63). By inputting C_CESTR, this conventional CESTR contrast becomes (C_CESTR-1)·CESTR_n or ($C_{R_{1obs}}{C}_{MT}{C}_{R_{ex}^{CEST}}-1$)·CESTR_n. From this equation, we can see that the relative size of $C_{R_{1obs}}$, $C_{MT}$, and $C_{R_{ex}^{CEST}}$ can still reflect their relative contributions to the conventional CESTR contrast.

Based on Eq. (7) and Eq. (8), the AREX metric reflects the production of f_s, k_sw, and a labeling efficiency related factor. In the full-saturation limit (64), AREX equals f_sk_sw. In this paper, we used % and s^-1 as units for f_s and k_sw, respectively. Therefore, we used %s⁻¹ as the unit for the AREX metric. It is worth noting that some previous publications have used Hz as the unit for the AREX metric which may look f_s as a dimensionless number (65–67).

Our experiments were performed on 9L tumor models in rat brains. In other animal tumor models and human patients, the change in the sample parameters may be different. Further studies related to the specificity of CESTR and its capability to reflect solute concentration in other tumor models are needed. Our conclusion does not fit for the MTR_asym-quantified APT at 3T, since it depends on not only the R_1obs and MT but also amine, DS and NOE effects, which are more complex.

CONCLUSION

CESTR measures a combined effect from the change in R_1w, MT, and CEST/NOE effects in tumors and thus is not a specific metric. However, in APT imaging, all these factors contribute positively to the dependence of CESTR on the amide concentration, which makes it a better method for detecting the increased protein concentration in tumors than other MRI/CEST parameters. In contrast, the AREX-quantified APT has no significant correlation with the amide concentration. In NOE(−3.5) imaging, these factors contribute to the dependence of CESTR on the macromolecular NOE pool concentration in opposite directions, which reduces its ability to detect the reduced macromolecular NOE pool concentration in tumors. In contrast, the AREX-quantified NOE(−3.5) has a significant and stronger correlation with the macromolecular NOE pool concentration.