Skip to main content
PMC home page
Applications in Plant Sciences logoLink to Applications in Plant Sciences
. 2023 Oct 31;11(5):e11551. doi: 10.1002/aps3.11551

How dense can you be? New automatic measures of vein density in angiosperm leaves

Walton A Green 1,✉, Juan M Losada 2
PMCID: PMC10617316  PMID: 37915435

Abstract

Premise

Because of the trade‐off between water loss and carbon dioxide assimilation, the conductivity of the transpiration path in a leaf is an important limit on photosynthesis. Closely packed veins correspond to short paths and high assimilation rates while widely spaced veins are associated with higher resistance to flow and lower maximum photosynthetic rates. Vein length per area (VLA) has become the standard metric for comparing leaves with different vein densities; its measurement typically utilizes digital image processing with varying amounts of human input.

Methods and Results

Here, we propose three new ways of measuring vein density using image analysis that improve on currently available procedures: (1) areole area distributions, (2) a sizing transform, and (3) a distance map. Each alternative has distinct practical, statistical, and biological limitations and advantages. In particular, we advocate the log‐transformed modal distance map of a vein mask as an estimator to replace VLA as a standard metric for vein density.

Conclusions

These methods, for which open‐source code appropriate for high‐throughput automation is provided, improve on VLA by producing determinate measures of vein density as distributions rather than point estimates. Combined with advances in image quality and computational efficiency, these methods should help clarify the physiological and evolutionary significance of vein density.

Keywords: automated leaf measurement, vein density, vein length per area (VLA)

Vein density has been measured for over a century (Zalenski, 1902) and described for even longer (von Ettingshausen, 1861; Ellis et al., 2009), but its physiological and evolutionary significance was not brought to prominence until a series of papers published in the early 21st century (Uhl and Mosbrugger, 1999; Roth‐Nebelsick et al., 2001; Sack and Holbrook, 2006; Noblin et al., 2008; Boyce et al., 2009; Rolland‐Lagan et al., 2009; Brodribb and Feild, 2010; Price et al., 2010). Note that here we distinguish between “vein density,” the general idea of how closely veins are packed in leaves, and vein length per area (VLA), a particular metric that has most frequently been used to approximate or estimate vein density. Because of the trade‐off between carbon acquisition and water loss along the transpiration stream, assuming that other factors are the same, veins that are packed more closely provide a shorter (and hence lower resistance) route for transpiration, which permits a higher maximum photosynthetic rate, with its associated evolutionary advantages.

The original method used by Zalenski (1902) for measuring VLA involved a mechanical curvimeter and camera lucida attached to a microscope at a magnification of 61×. The modern equivalent of this, which seems to have arisen organically as an updated version of Zalenski's procedure without significant methodological discussion, involves hand‐tracing a vein centerline or skeleton on a digital image. Image analysis software is then used to measure the length of the vein skeleton and divide by the total area represented by the image. Boyce et al. (2009) and Sack et al. (2014), among others, used the image analysis software ImageJ (Rasband, 1997–2018), but any appropriate software can be employed. A variation on this procedure involves hand‐tracing both sides of the vein and then relies on an algorithm to automate the process of reducing the vein tracing to a single pixel width and measuring the length of the resulting shape. Several attempts have been made to automate the whole procedure (Price et al., 2010; Bühler et al., 2015; Zhu et al., 2020; Xu et al., 2021), using varying degrees of computational complexity to facilitate the process. Fundamental disagreements about the repeatability and scale‐dependence of these measurements, however, have never been resolved. For example, Price et al. (2014) have pointed out the problems with a user‐dependent, manual procedure, while Sack et al. (2014) have maintained the general reliability of hand‐tracing and pointed out some of the biases that can be introduced by automation.

METHODS AND RESULTS

Disagreement about the details of how VLA should be measured has distracted from the point that VLA was merely chosen as a convenient proxy for the variable of physiological interest. The actual variable of interest is something more like the length of the mean free gaseous path from a xylem cell to the evaporation site on the cell wall of a spongy mesophyll cell in a substomatal cavity. If transport along cell boundaries is taken into account, we might also theoretically be interested in the shortest distance from xylem to mesophyll along cell boundaries in three dimensions. There has been no suggestion that VLA is anything more than a loose approximation of these distances. Although the complexity of these variables is well known (Wylie, 1939; Brodribb et al., 2007), the simplicity of VLA has increasingly eclipsed a more nuanced understanding of the physiologically relevant geometry.

Fundamentally limiting the accuracy of any measurement of vein density are the resolution and quality of the source images. At the finest level, many leaves have vascular networks that ramify to individual tracheids. These are only resolvable by a compound microscope at relatively high power (e.g., 400×). Any images at lower resolution (i.e., virtually all images on which VLA has been measured) display the problem illustrated by the simple theoretical model shown in Figure 1: a large proportion of aggregate length in a self‐similar network like angiosperm veins resides in the finest order of branching. Therefore, any methodology that fails to capture finer orders can underestimate VLA by a factor of 2 or more. Interestingly, most angiosperms show veins in three orders, distinguishable by development as well as morphology (Poethig, 1984; Nelson and Dengler, 1997; Tsiantis and Langdale, 1998; Piazza et al., 2005). The fourth and fifth (and even up to seventh) orders have been identified in the descriptive literature (Ellis et al., 2009), although Green et al. (2014) expressed skepticism as to whether orders 3–7 are ever quantitatively distinguishable. The greatest VLA that has been measured in angiosperms is under 30 mm/mm2 (Boyce et al., 2009), which closely matches the VLA that would be produced by fourth‐order venation in the theoretical model illustrated in Figure 1. Note that the units in which vein density is measured are typically mm/mm2, which would be scale‐independent (like a dimensionless unit) if and only if the vein network were self‐similar. In fact, vein networks are only approximately self‐similar over a small range of scales; hence the de facto standardization on mm/mm2.

Figure 1.

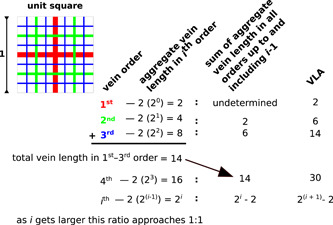
Figure 1

Open in a new tab

A simple theoretical model for vein density. Note that as the number of vein orders increases, the fraction of the total length occupied by the finest order approaches 50%. Therefore, missing the finest order of veins will underestimate the vein length per area (VLA) by a factor of 2.

In this paper, we attempt to sidestep some of these problems by separating the inherently subjective production of a binary mask (see Figure 2B) representing a vein network, from the entirely determinate measurement of vein density from that mask. A binary mask is a black‐and‐white image in which the vein network is black background and the areoles are white foreground. The white/black and background/foreground distinction is arbitrary. Production of such a binary mask from a color or grayscale photograph is a fundamentally difficult task in image analysis, often called image segmentation (Glasbey and Horgan, 1995). Image analysis algorithms can at times approach or exceed the accuracy of hand‐tracing, and of course can be replicated and scaled up in ways that no subjective, manual procedure can match in practice. For the purposes of this article, however, it is unimportant whether the mask comes from meticulous hand‐tracing or automatic image segmentation. Even given an acceptable binary mask, it is not a trivial problem to determine VLA using currently available procedures, as either an algorithm or a manual trace is needed to determine the centerline and measure the length of the vein network.

Figure 2.

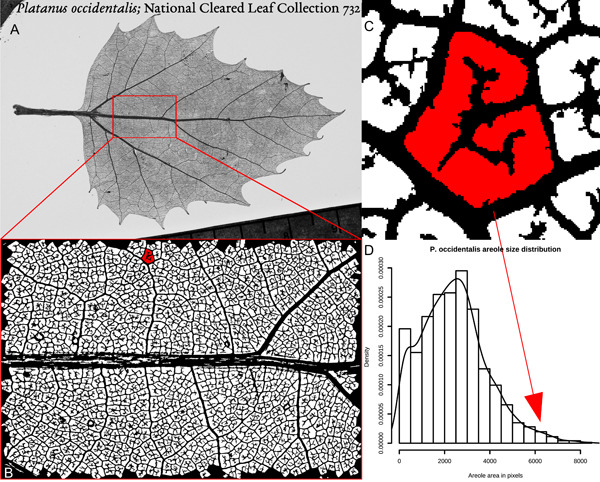
Figure 2

Open in a new tab

Vein density measurement using areole sizes. (A) Digital grayscale photograph of a cleared leaf of Platanus occidentalis (National Cleared Leaf Collection 732, National Museum of Natural History, Smithsonian Institution). (B) A region of interest (ROI) of approximately 9 × 13 mm, photographed at a larger scale and converted to a binary mask by the function clean(), with one areole colored red. (C) An expanded view of the shaded areole, which is 6228 pixels in size. (D) Histogram and density plot of the size distribution of all the areoles in the ROI. The arrow shows the location in the distribution of the shaded areole in (C).

The alternatives that we provide here avoid the problem of network length measurement entirely by restricting all subjective or tunable decisions to the process of image segmentation. Once the binary mask is created, the following three methods are algorithmically determined and require no tuning or user input. In all three cases, the measurement units are given in pixels (which, in the case of the image analyzed here, have width/height of 4.4 μm). Conversion to a physical distance is complicated by the fact that pixels fall on a square grid, so horizontal and vertical distances should be multiplied by 4.4 μm and diagonal distances by 4.42 = 6.2 μm. The image analyzed here is of a cleared leaf permanently mounted in polyester resin between glass slides. Such cleared leaves tend to provide the highest quality images, but depending on the leaf, it is possible to obtain satisfactory images by transillumination of a fresh leaf or sometimes even by simple reflected light photography. Images or manual tracings of fossils or damaged leaves can in principle be utilized. In practice, the theoretical pixel resolution is less important than the optical quality of the imaging system, which sets the minimum size of veins that can be seen in an image, as well as other confounding features like leaf hairs and fiber bundles, which are not part of the vein network but produce dark pixels on the image.

The first alternative to VLA presented here has already been described by Green et al. (2014) and consists of measuring the size of each areole in an image. The whole leaf can be used, but it is still computationally difficult to image an entire leaf at a resolution that permits fine venation to be distinguished. Experiments by Green et al. (2014) and Sack et al. (2014) have agreed that in most cases a region of interest (ROI) of 1‐cm2 scale does a satisfactory job of estimating whole‐leaf summary statistics.

Figure 2A shows a photograph of the cleared leaf analyzed throughout this paper. The particular ROI quantified is shown in Figure 2B and is about 9 × 13 mm, imaged at 2000 × 3008 pixels on a sensor of 16 × 24 mm (Nikon D70 [Nikon, Tokyo, Japan] with macro lens on bellows), giving about 4× optical magnification and a theoretical pixel size of approximately 4.4 μm. The mask (Figure 2B) was obtained from the original image using the function clean() (see source code in Appendix S1). clean() is an adaptive thresholding algorithm, in which a grayscale image is converted to black‐and‐white one region at a time. In this case, the region is a 30‐pixel‐square window, and the threshold at which each pixel in a window is converted to black or white varies based on the overall distribution of light and dark pixels within the window, modified by a dimensionless, user‐tunable sensitivity parameter. After thresholding, clean() removes all black/vein pixels that are not connected to the largest black region (the vein network), and then removes all white/areole regions smaller than 81 pixels in size (the equivalent of a 9 × 9‐pixel square). All three of these user‐settable parameters—window size, sensitivity, and the minimum allowable areole size—were tuned to create a mask that subjectively best seemed to represent the vein network visible in the grayscale image; however, it should be noted that obvious artifacts remain, such as the presence of white gaps in the midrib that are not areoles. Finally, clean() removes any areoles that intersect the edge of the ROI.

The areole size distribution shown in Figure 2D is an improvement over VLA, especially if robust estimators like the median or mode are used to summarize the distribution, because it provides a range of values, inherently quantifying variability as well as vein density. It still, however, has the flaw that large areoles with elaborate, dichotomously branching terminal veinlets are not distinguished from large, empty areoles. Recall that the physiological variable of interest is how easy it is for water vapor to get from the nearest vein to the site of evaporation; freely ending veinlets ramifying into large areoles will affect the hydraulics but are not reflected in the areole size distribution.

A second alternative is known in image analysis as a sizing transform (function st() in the source code; Appendix S1). For each pixel in the (white, areole) foreground, a sizing transform calculates the maximal ball (i.e., the largest circular area including that pixel) that can be fit entirely in the foreground. Because each ball is centered on a single pixel, calculations are only made for balls with an odd‐numbered diameter. Figure 3A shows the same ROI as Figure 2, with the foreground pixels shaded by sizing transform radius; Figure 3B–D show the same magnified areole and the location of a representative ball in the distribution of sizing transform radii.

Figure 3.

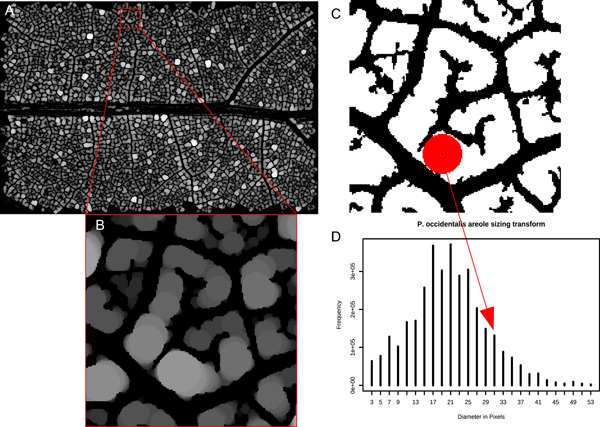
Figure 3

Open in a new tab

Vein density measurement using sizing transforms. (A) The ROI from Figure 2B shown after applying a sizing transform; the lighter shades correspond to larger balls that fit into foreground areas. (B) An expanded view of the same areole as is shown in Figure 2C. (C) Another view of the expanded area showing a pixel surrounded by a ball with a diameter of 31 pixels. (D) The distribution of ball sizes for the entire ROI. The arrow indicates the location in this distribution of the pixel identified in (C).

The distribution of balls fitted in the foreground at each pixel shares with areole size measurement the benefit of providing a distribution of values for each pixel in the image (by analogy, for each location in the leaf mesophyll). The average (mean or modal) ball size in this distribution gives a measure of the average size of the spaces between veins. This corresponds fairly well to VLA (Uhl and Mosbrugger, 1999), but again is not quite what we are looking for physiologically.

Another alternative is provided by a distance map (function distmap(), in Pau et al., 2010), in which each foreground (white, areole) pixel is given a value equal to its Euclidean distance from the nearest (black, background) vein. The distribution of these distances is exponential (because there are more pixels close to veins than far away from them), but the log‐transformed distribution typically has a well‐defined mode. Figure 4 shows the complete ROI, shaded by distance transform, as well as the same single areole detail (Figure 4B, C) and its location in a distribution of distances (Figure 4D). This distance corresponds relatively well to the quantity we are looking for, i.e., the distance from each piece of mesophyll to the nearest vein.

Figure 4.

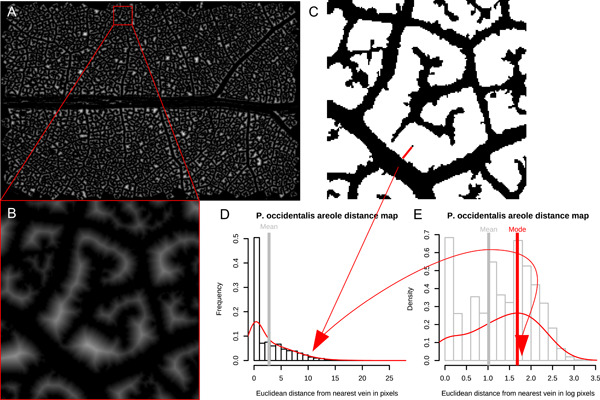
Figure 4

Open in a new tab

Vein density measurements using distance maps. (A) The ROI shown in Figure 2B after applying a distance map; the lighter shades indicate pixels farthest from the nearest vein. (B) An expanded view of the same areole shown in Figures 2 and 3. (C) Another view of the expanded area, showing the value given by the distance transform for the same pixel identified in Figure 3C. (D) The distribution of distances for all foreground pixels in the ROI. (E) Log‐transform of the histogram and density shown in (C), again with the location of the same pixel in the distribution identified.

Whichever of these methods is used for measuring vein density, it is dependent on an accurate binary mask. Creation of a binary mask that reflects venation remains inherently subjective, but is becoming technically more feasible, as can be seen from the image in Figure 5 of a vein from Illicium parviflorum Michx. ex Vent., stained with Schiff's solution and imaged with a confocal microscope. Figure 5A is multispectral; Figure 5B is the same region thresholded from the 415–735‐nm spectral band. Note that the pixel resolution is only about one factor of 10 greater than that of the other images shown, but the improved image clarity gives much greater confidence that the binary mask accurately reflects small details of xylem geometry. In order to obtain images at this resolution that cover a representative portion of the leaf, it would be necessary to stitch together many images from a confocal microscope with a high‐power objective. Dealing with file sizes at this resolution and size becomes computationally intensive, but it is within the realm of possibility that in the foreseeable future, it will be possible to make measurements in three dimensions on images like this one, in which individual tracheary elements are identifiable.

Figure 5.

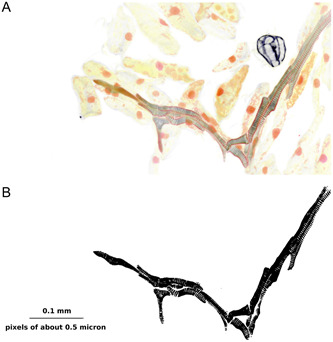
Figure 5

Open in a new tab

Higher‐resolution imaging of leaf primordium venation. (A) Multispectral image of a portion of a leaf of Illicium parviflorum. (B) Binary mask of (A), showing the full complexity of the leaf vasculature at a resolution at which individual traceids can be identified.

To demonstrate the ease with which the tools provided in this article can be automated, we also provide the source code for an example batch script (Appendix S2). We applied this script to 230 images across the angiosperm tree (available in the supplementary archive for Green et al. [2014] on Dryad, see Data Availability Statement); the resulting table of summary statistics is available in Appendix S3 with an explanatory text file as Appendix S4.

These 230 images represent 80 families, 118 genera, and 120 species (in most cases with two separate ROIs per specimen). Of these, 207 images are from woody plants and 19 are from herbs. An example of one obvious problem in this data set can be seen in images 0089.jpg, 0093.jpg, and 0094.jpg (the ericaceous herbs Moneses uniflora (L.) A. Gray and Pyrola asarifolia Michx. [listed as “acerifolia” in the metadata] [Ericaceae]), which crash the function clean() because they have poorly organized, weakly staining venation. It is possible that tuning the user‐defined parameters for binary mask production could fix this issue. Images 0081.jpg and 0082.jpg (the floating aquatic Nuphar microphylla (Pers.) Fernald [listed as “microphyllum” in the metadata] [Nymphaeaceae]) are successfully processed by clean(), but in the resulting binary masks, dark‐staining trichomes completely obscure the venation pattern, meaning that the measurements do not reflect any relevant hydraulic variable. In general, the best images are obtained from chartaceous leaves from arborescent woody plants with well‐lignified vein networks; the poorest images come from coriaceous herbs with poorly organized venation or abundant trichomes.

A more detailed analysis of these measurements is beyond the scope of this article, but the output of the batch script is included in Appendix S3 to demonstrate the generalizability of the tools provided here. The complete image set and metadata associated with the image numbers detailed in Appendix S3 are available in Green et al. (2015), and the raw images included in Figures 1A and 5A are provided as Appendix S5 and S6.

CONCLUSIONS

These three proposed metrics are not the only alternatives (e.g., Blonder et al. [2011] and Rolland‐Lagan et al. [2009] offer additional approaches), but all have the following advantages over VLA: (1) they are algorithmically determined given a binary mask (i.e., there are no parameters to tune and no user‐variability is possible); (2) they are entirely automated, and can therefore be applied to large image databases; (3) they provide a distribution of values rather than a single summary statistic; and (4) they correspond more closely to the measurement assumed to be hydraulically important—the distance from a photosynthesizing mesophyll cell to the nearest xylem conduit. Remaining areas needing improvement include a continued dependence on accurate binary masks, and computational limits on processing very large image sizes.

Despite the observation of large‐scale patterns in vein density across vascular plants (e.g., Boyce et al., 2009) and the hypothesized role of closer vein packing in the success of the angiosperms (e.g., Brodribb and Feild, 2010), there is not yet a consensus as to the precise physiological significance of vein density, especially within closely related angiosperm groups. A complete understanding of leaf venation must account for not only the hydraulic factors on which the majority of vein density literature focuses, but also the role played by venation in the structural support of the leaf (Givnish, 1978; Niinemets et al., 2007) and its function in translocating photosynthate.

Targets for future work could include systematic surveys of vein density across the angiosperm tree, ecological studies looking for patterns across environment and life history, and direct comparisons examining vein functions other than transpiration. Such surveys are beyond the scope of this article, and before this sort of comparative work can be pursued, raw image files need to be published routinely and kept digitally available, so that alternative analytic methods can be applied to the same original images. The supplemental archive referenced above (Green et al., 2015) is still available (see Data Availability Statement), but it is notable that two other online sources of images cited in Green et al. (2014) are no longer maintained.

One of the appeals of VLA seems to have been that it produces a single scalar quantity that can be published without images, but our experiences with measuring vein density suggest that continuing merely to collect more measurements of VLA will not lead to any better understanding of the physiological and biophysical role of leaf venation. Instead, the improved procedures for quantifying vein density that are proposed here, along with a commitment to publishing raw imagery and open‐source analytic code and continued advances in microscopy and computational speed that make larger, high‐resolution files tractable, will make possible a more comprehensive understanding of the biology of leaf venation.

AUTHOR CONTRIBUTIONS

W.A.G. conceived the study and wrote the software; J.M.L. provided specimens and images. Both authors approved the final version of the manuscript.

Supporting information

Appendix S1. Functions.

Click here for additional data file. (10.3KB, R)

Appendix S2. Code snippets.

Click here for additional data file. (8.6KB, txt)

Appendix S3. Output data from batch script.

Click here for additional data file. (13.9KB, csv)

Appendix S4. Text file describing output data from batch script.

Click here for additional data file. (1.4KB, txt)

Appendix S5. Raw image of Platanus occidentalis leaf pictured in Figure 2.

Click here for additional data file. (857.4KB, jpg)

Appendix S6. Raw images of Illicium parviflorum leaf primordia pictured in Figure 5.

Click here for additional data file. (1.3MB, tif)

ACKNOWLEDGMENTS

The authors thank N. M. Holbrook, K. E. Black, and two anonymous reviewers for comments on the manuscript, and Beth Parada for copyediting. J.M.L. is funded by the Spanish Ministry of Science and Innovation, through the Agencia Estatal de Investigación (reference PID2021‐129074O‐BI00).

Green, W. A. , and Losada J. M.. 2023. How dense can you be? New automatic measures of vein density in angiosperm leaves. Applications in Plant Sciences 11(5): e11551. 10.1002/aps3.11551

This article is part of the special issue “Advances in Plant Imaging across Scales.”

DATA AVAILABILITY STATEMENT

All data analyzed are provided in the Supporting Information (Appendices S1–S6), or are available in the supplementary archive to Green et al. (2014), found at https://datadryad.org/stash/dataset/doi:10.5061/dryad.8h022 (Green et al., 2015), which contains images and their related metadata from a prior study. All analysis was done with the open source software R (R Core Team, 2018) and the library EBImage (Pau et al., 2010).

REFERENCES

  1. Blonder, B. , Violle C., Bentley L. P., and Enquist B. J.. 2011. Venation networks and the origin of the leaf economics spectrum. Ecology Letters 14: 91–100. [DOI] [PubMed] [Google Scholar]
  2. Boyce, C. K. , Brodribb T. J., Feild T. S., and Zwieniecki M. A.. 2009. Angiosperm leaf vein evolution was physiologically and environmentally transformative. Proceedings of the Royal Society B 276: 1771–1776. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Brodribb, T. J. , and Feild T. S.. 2010. Leaf hydraulic evolution led a surge in leaf photosynthetic capacity during early angiosperm diversification. Ecology Letters 13: 175–183. [DOI] [PubMed] [Google Scholar]
  4. Brodribb, T. J. , Feild T. S., and Jordan G. J.. 2007. Leaf maximum photosynthetic rate and venation are linked by hydraulics. Plant Physiology 144: 1890–1898. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bühler, J. , Rishmawi L., Pflugfelder D., Huber G., Scharr H., Hülskamp M., Koornneef M., et al. 2015. phenoVein: A tool for leaf vein segmentation and analysis. Plant Physiology 169: 2359–2370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ellis, B. , Daly D. C., Hickey L. J., Mitchell J. D., Johnson K. R., Wilf P., and Wing S. L.. 2009. Manual of leaf architecture. Cornell University Press, Ithaca, New York, USA. [Google Scholar]
  7. Givnish, T. J. 1978. Ecological aspects of plant morphology: Leaf form in relation to environment. Acta Biotheoretica 27: 83–142. [Google Scholar]
  8. Glasbey, C. A. , and Horgan G. W.. 1995. Image analysis for the biological sciences. Wiley, Chichester, United Kingdom. [Google Scholar]
  9. Green, W. A. , Little S. A., Price C. A., Wing S. L., Smith S. Y., Kotrc B., and Doria G.. 2014. Reading the leaves: A comparison of leaf rank and automated areole measurement for quantifying aspects of leaf venation. Applications in Plant Sciences 2(8): 1400006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Green, W. A. , Little S. A., Price C. A., Wing S. L., Smith S. Y., Kotrc B., and Doria G.. 2015. Data from: Reading the leaves: A comparison of leaf rank and automated areole measurement for quantifying aspects of leaf venation [Dryad]. 10.5061/dryad.8h022 [accessed 27 September 2023]. [DOI] [PMC free article] [PubMed]
  11. Nelson, T. , and Dengler N.. 1997. Leaf vascular pattern formation. Plant Cell 9: 1121–1135. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Niinemets, Ü. , Portsmuth A., Tena D., Tobias M., and Valladares F.. 2007. Leaf shape and venation pattern alter the support investments within leaf lamina in temperate species: A neglected source of leaf physiological differentiation? Functional Ecology 21: 28–40. [Google Scholar]
  13. Noblin, X. , Mahadevan L., Coomaraswamy I. A., Weitz D. A., Holbrook N. M., and Zwieniecki M. A.. 2008. Optimal vein density in artificial and real leaves. Proceedings of the National Academy of Sciences, USA 105(27): 9140–9144. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Pau, G. , Fuchs F., Sklyar O., Boutros M., and Huber W.. 2010. EBImage–an R package for image processing with applications to cellular phenotypes. Bioinformatics 26(7): 979–981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Piazza, P. , Jasinski S., and Tsiantis M.. 2005. Evolution of leaf developmental programmes. New Phytologist 167: 693–710. [DOI] [PubMed] [Google Scholar]
  16. Poethig, S. 1984. Cellular parameters of leaf morphogenesis in maize and tobacco. In White R. A. and Dickison W. C. [eds.], Contemporary problems in plant anatomy, 235–259. Academic Press, Orlando, Florida, USA. [Google Scholar]
  17. Price, C. A. , Symonova O., Mileyko Y., Hilley T., and Weitz J. S.. 2010. Leaf extraction and analysis framework graphical user interface: Segmenting and analyzing the structure of leaf veins and areoles. Plant Physiology 155(1): 236–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Price, C. A. , Munro P. R. T., and Weitz J. S.. 2014. Estimates of leaf vein density are scale dependent. Plant Physiology 164: 173–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. R Core Team . 2018. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. Website: https://www.R-project.org/ [accessed 25 September 2023]. [Google Scholar]
  20. Rasband, W. S. 1997–2018. ImageJ. U. S. National Institutes of Health, Bethesda, Maryland, USA. Website: https://imagej.nih.gov/ij [accessed 25 September 2023].
  21. Rolland‐Lagan, A.‐G. , Amin M., and Pakulska M.. 2009. Quantifying leaf venation patterns: Two‐dimensional maps. The Plant Journal 57: 195–205. [DOI] [PubMed] [Google Scholar]
  22. Roth‐Nebelsick, A. , Uhl D., Mosbrugger V., and Kerp H.. 2001. Evolution and function of leaf venation architecture: A review. Annals of Botany 87: 553–566. [Google Scholar]
  23. Sack, L. , and Holbrook N. M.. 2006. Leaf hydraulics. Annual Review of Plant Biology 57: 361–381. [DOI] [PubMed] [Google Scholar]
  24. Sack, L. , Caringella M., Scoffoni C., Mason C., Rawls M., Markesteijn L., and Poorter L.. 2014. Leaf vein length per area is not intrinsically scale dependent: Avoiding measurement artifacts for accuracy and precision. Plant Physiology 166: 829–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Tsiantis, M. , and Langdale J. A.. 1998. The formation of leaves. Current Opinion in Plant Biology 1998(1): 43–48. [DOI] [PubMed] [Google Scholar]
  26. Uhl, D. , and Mosbrugger V.. 1999. Leaf venation density as a climate and environmental proxy: A critical review and new data. Palaeogeography, Palaeoclimatology, Palaeoecology 149(1): 15–26. [Google Scholar]
  27. von Ettingshausen, C. R. 1861. Die Blatt‐Skelete der Dikotyledonen. Druck und Verlag der Kais. Kön. Hof‐ und Staatdruckerei, Vienna, Austria.
  28. Wylie, R. B. 1939. Relations between tissue organization and vein distribution in dicotyledon leaves. American Journal of Botany 26(4): 219–225. [Google Scholar]
  29. Xu, H. , Blonder B., Jodra M., Malhi Y., and Fricker M.. 2021. Automated and accurate segmentation of leaf venation networks via deep learning. New Phytologist 229: 631–648. [DOI] [PubMed] [Google Scholar]
  30. Zalenski, W. v. 1902. Über die Ausbildung der Nervation bei verschiedenen Pflanzen. Bericht der Deutschen botanischen Gesellschaft 1902(7): 433–440. [Google Scholar]
  31. Zhu, J. , Yao J., Yu Q., He W., Xu C., Qin G., Zhu Q., et al. 2020. A fast and automatic method for leaf vein network extraction and vein density measurement based on object‐oriented classification. Frontiers in Plant Science 11: 499. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Citations

  1. Green, W. A. , Little S. A., Price C. A., Wing S. L., Smith S. Y., Kotrc B., and Doria G.. 2015. Data from: Reading the leaves: A comparison of leaf rank and automated areole measurement for quantifying aspects of leaf venation [Dryad]. 10.5061/dryad.8h022 [accessed 27 September 2023]. [DOI] [PMC free article] [PubMed]

Supplementary Materials

Appendix S1. Functions.

Click here for additional data file. (10.3KB, R)

Appendix S2. Code snippets.

Click here for additional data file. (8.6KB, txt)

Appendix S3. Output data from batch script.

Click here for additional data file. (13.9KB, csv)

Appendix S4. Text file describing output data from batch script.

Click here for additional data file. (1.4KB, txt)

Appendix S5. Raw image of Platanus occidentalis leaf pictured in Figure 2.

Click here for additional data file. (857.4KB, jpg)

Appendix S6. Raw images of Illicium parviflorum leaf primordia pictured in Figure 5.

Click here for additional data file. (1.3MB, tif)

Data Availability Statement

All data analyzed are provided in the Supporting Information (Appendices S1–S6), or are available in the supplementary archive to Green et al. (2014), found at https://datadryad.org/stash/dataset/doi:10.5061/dryad.8h022 (Green et al., 2015), which contains images and their related metadata from a prior study. All analysis was done with the open source software R (R Core Team, 2018) and the library EBImage (Pau et al., 2010).

Articles from Applications in Plant Sciences are provided here courtesy of Wiley

RESOURCES