Abstract
Chemical reactions that couple to systems that phase separate have been implicated in diverse contexts from biology to materials science. However, how a particular set of chemical reactions (chemical reaction network, CRN) would affect the behaviours of a phase separating system is difficult to fully predict theoretically. In this paper, we analyse a mean field theory coupling CRNs to a combined system of phase separating and non-phase separating materials and analyse how the properties of the CRNs affect different classes of non-equilibrium behaviour: microphase separation or temporally oscillating patterns. We examine the problem of achieving microphase separated condensates by statistical analysis of the Jacobians, of which the most important motifs are negative feedback of the phase separating component and combined inhibition/activation by the non-phase separating components. We then identify CRN motifs that are likely to yield microphase by examining randomly generated networks and parameters. Molecular sequestration of the phase separating motif is shown to be the most robust towards yielding microphase separation. Subsequently, we find that dynamics of the phase separating species is promoted most easily by inducing oscillations in the diffusive components coupled to the phase separating species. Our results provide guidance towards the design of CRNs that manage the formation, dissolution and organization of compartments.
Keywords: phase separation, chemical reaction networks, reaction–diffusion
1. Introduction
The ability of mixtures of molecules to separate into distinct compartments has major implications in chemistry, materials science and biology, and offers intriguing hypotheses on the origin of life [1–3]. Within cells, phase separated biomolecular condensates form in response to internal and external stimuli [4], operating as microscopic organelles without a membrane that enable precise regulation of cell physiology and chemistry [5,6]. Among the biological questions pertaining to phase separation observed in living cells, the interplay between biochemical reactions and phase separation is of particular interest, because it can explain the dynamic nature of biomolecular condensates in the homeostatic cellular environment [7,8]. In parallel, the combination of artificial phase separating systems and designed chemical reactions is making it possible to design artificial organelles [9–11] and functional materials with precise spatio-temporal responses [12–14]. Chemically active droplets can also be made to self-propel, acting as potential carriers of material [15,16].
With mean field theories, it has been possible to observe that chemical reactions fuel ‘life-like’ behaviours such as droplet splitting [17,18], providing that there are sufficient free energy sources available to keep the system out of equilibrium. Prior work has shown that chemical reactions can control condensate properties, with focus on examples that allow for the derivation of exact conditions [19–21], or that include enzymatic reactions particularly relevant in specific biological processes [18,22–27].
The space of possible chemical reaction networks (CRNs) that can be coupled to phase separating systems is large. It is difficult to say a priori how the features of a particular CRN would manifest themselves on the spatial patterning and dynamical behaviour of a phase separating system. Here, we seek general design rules for chemical reactions that can provide a means to control macroscopic non-equilibrium behaviours of phase separated condensates. Motivated by the rapid expansion of programmable molecular substrates that enable the synthesis of nearly arbitrary CRNs [28,29], we consider the following general questions: over many different CRNs coupled with a phase separating material, are there any broad features that arise in the CRNs themselves that lead to particular features of the material? Furthermore, if the chemical species have some non-chemical coupling (such as non-specific interactions leading to spatial agglomeration of different species), how do these couplings impact the CRNs that lead to those defined features? Answers to these questions will provide guidance for the design of chemical reactions that can regulate the properties of phase separating materials [30]. Previous works have considered coupling phase transitions to non-equilibrium chemical thermodynamics [31–33], (see [34] for review). In particular, [33] demonstrated that spinodal decomposition can be controlled through autocatalyis using a linear irreversible thermodynamics approach. We use a similar extension of Cahn–Hilliard theory with focus on the structure of the CRN coupled to multiple components that can diffuse in space, of which only one is phase separating.
Rather than asking whether phase separation is stable or not, we examine two particular features of phase separating systems. One feature relates to average size of the observed condensates. This question can be examined through a mean field model that combines spatial and chemical interactions among species, and corresponds to the problem of studying linear stability of equilibria [35–37]. Standard phase separation kinetics, such as in the Cahn–Hilliard model, feature coarsening, i.e. the distinct phases continue to grow until the system has been separated into macroscopic compartments (macrophase separation). We seek to identify general chemical reactions that can arrest coarsening [36], and lead to a case in which the stationary state of the system contains many droplets with a defined length scale, and the system exhibits microphase separation. The other feature we are interested in is dynamical instability. Are there any CRNs which lead to continual (or at least long-lived) dynamical oscillations of the system with phase separation?
To answer these general questions, we analyse a non-equilibrium dynamical theory of phase separation kinetics coupled to an arbitrary CRN. Through computations, we explore which features of a CRN are sufficient to produce non-equilibrium phenomena, such as condensate size limitation (microphase separation) [27] and oscillatory dynamics. Introducing such a question poses a theoretical challenge, as the number of parameters involved in the problem proliferates very rapidly with the number of components. We therefore seek simplified ‘design rules’ that can allow us to gain an intuitive understanding of how different parameters affect different features. We achieve this by analysing the system over the entire parameter space and seeing whether any strong signals exist in lower dimensional representations of the system. To that end, the paper is organized as follows: In the first section, we describe our mathematical model. We then show an analytical example for a system with a small number of components as a description of our method. Subsequently, we consider numerically the same problem with a larger number of components, using random matrix representation of the CRNs. Next, we introduce real CRNs and extend our analysis over structural features of the CRNs. Finally, we use our method towards prediction of oscillatory dynamics.
2. Modelling phase separation in the presence of chemical reactions
We introduce a set of N density fields in space corresponding to the concentrations of different chemical species, , where , . We assume these species are coupled through conserved dynamics (which we also call spatial coupling), that affect how the density fields arrange in space while keeping their total concentration constant, and through non-conserved chemical reactions that determine how the density fields locally inter-convert.
To model spatial coupling, we introduce the following equilibrium free energy for the different chemical fields:
| 2.1 |
where γ is a parameter related to the surface tension, and ν is some effective energy scale. In principle, this ν can depend on other parameters [38], such as , but we suppress this dependence here. A fuller theory could start from Flory–Huggins free energy and obtain more explicit parametrizations of the effective parameters above. This free energy corresponds to a system where component 1 undergoes phase separation, under Cahn–Hilliard form, to two phases with density ρ1 and ρ2, ρ2 > ρ1 (figure 1). The symmetric matrix introduces some additional spatial coupling between all the fields. As the interaction of c1 with itself is already included in the Cahn–Hilliard term, the corresponding matrix component is taken to be . In principle, we could include higher-order couplings of different fields, however, for simplicity, we truncate the series after approximately c2. We additionally ignore problems related to the total packing fraction of different components and of surface effects of the non-phase separating chemicals (γi where i ≥ 2).
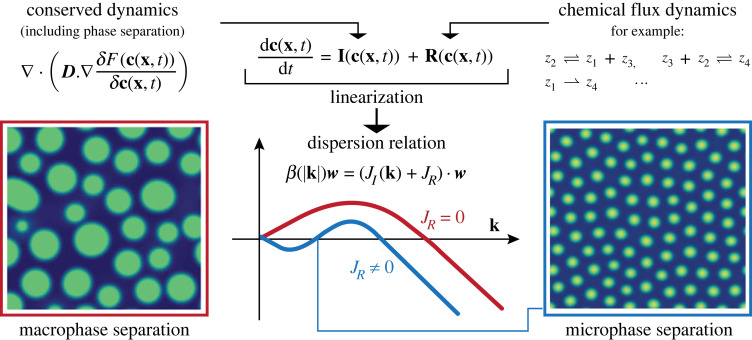
Figure 1.
We are considering the interplay of chemical reactions and phase separation following Cahn–Hilliard dynamics. Through linearization, we obtain dispersion relations from the Jacobians associated with the model. There are two different categories of dispersion relation for phase separating systems: in red, we illustrate the case of macrophase separation, corresponding to standard phase separation where the phases continue to grow inside until they are macroscopically separated, which is typical in the absence of chemical reactions. In blue, we illustrate the case of microphase separation, where large droplets (small |k|) and small ones (large |k|) have a negative growth rate, stabilizing droplets to a particular size near the mid-intersection point. In this paper, we seek methods to shape the dispersion relation to yield microphase separation through the presence of chemical dynamics. Snapshots show actual solutions of equation (2.4) with and without chemical reactions, illustrating macrophase and microphase separation for a chemical model (A) given in the electronic supplementary material.
The time evolution of this system can be inferred using model B dynamics [39]
| 2.2 |
For simplicity, we assume the mobility matrix is given by where is a constant and Id is the identity matrix. The presence of the conserved interactions in leads to effective cross-diffusion terms, which are important for pattern formation in their own right [40].
We are left with how to specify the chemical dynamics. Previous literature uses different choices for deriving non-conserved dynamics based on variations of model A dynamics, involving specification of a free energy functional [41]. We do not make this choice, and for now, we merely specify that chemical dynamics must obey the following equation:
| 2.3 |
where R are the reaction fluxes generated from the law of mass action by a set of different chemical reactions. We restrict our analysis to chemical reactions which conserve the total mass (no spontaneous creation or destruction of mass). We keep deliberately general the precise form of R in equation (2.3) for the moment, in order to analyse the generic effects of chemistry on phase separation.
We finally combine the conserved dynamics (the dynamics that moves the concentration fields around in space while keeping their total amount constant) and the chemical dynamics (the dynamics that inter-converts concentration fields between one another, thus changing total amounts of individual components) via the following combined equation:
| 2.4 |
This equation is inherently non-equilibrium, as the origins of the two different terms differ. An equilibrium theory would have both terms arising from the functional derivative of the same free energy functional [41]. This can also be constrasted to other equilibrium methods in the liquid–liquid phase separation (LLPS) literature [42]. We do not focus on this case as we are only interested in non-equilibrium properties resulting from the action of chemistry, as opposed to equilibrium phenomena that can lead to microphase separation (e.g. copolymers or micellar solutions [43,44]). In contrast to previous studies, such as Li & Cates [41], we do not assert a functional to derive the term R(c(x, t)), in fact, for anything other than the simplest form of reactions, there would not be a single unique functional that describes mass-action kinetics in a CRN. Our approach is instead a specification of the rates at which different reactions proceed rather than from specification of the energies. This would correspond to a free energy source being constantly consumed to maintain these reactions at the specified rates [21,24], an approach that was used to study problems such as protein aggregation [45]. We use (2.4) for reasons of analytical tractability, as a full theory containing phase separating dynamics and CRNs is beyond the present scope of the manuscript. Our approach assumes that each of the chemical species contains sufficient complexity to have reactions that can change their conserved dynamics with other molecules, either through mechanisms such as allostery or additional steric effects, as previously considered in [46].
Equation (2.4) is at the base of the rest of the paper; however, in most instances, we do not study it directly. Instead, we study matrices that result from linear stability analysis of this equation. This general strategy results in the fact that terms that combine in the same entry of the matrix can be combined without loss of generality. When we do study it directly, we solve it numerically with a Fourier spectral method in two dimensions, the full details of which are available in the electronic supplementary material.
We analyse our model (2.4) through a linear stability analysis near equilibrium, , where is small, . Inserting this form into (2.4) allows us to define a dispersion relation β(|k|) (growth rate as a function of wavenumber), where β(|k|) is the dominant eigenvalue (the eigenvalue with the largest real part). The initial state is the stationary state of the chemical dynamics, cs, as this is the stable homogeneous equilibria. In the absence of any chemical reactions, our system is in the spinodal region of the phase diagram. We do not consider nucleation effects. While it could plausibly be the case that the homogeneous state is stable to small perturbations but not stable globally, we do not study this in this paper.
The dynamics are linearized around cs, by defining the Jacobians
| 2.5 |
where JI(k) is the Jacobian matrix of the conserved interactions and JR is the Jacobian matrix of the chemical interactions term. We obtain a generic relationship in
| 2.6 |
where it can be seen that is an eigenvalue of the combined matrix (JI(k) + JR). We are interested in the occurrence of unstable wavelengths with finite size (microphase separation). This case arises when the real part of β(k) satisfies for small |k|, for intermediate |k|, and for large |k|. We illustrate this with a scalar example in figure 1, where we compare two dispersion relation curves in red (macrophase separation) and in blue (microphase separation). The red curve is typical of phase separating systems that do not include chemical reactions: condensates either coalesce or dissolve completely. The blue curve indicates that large wavelengths and small wavelengths have a negative growth rate, while wavelengths of intermediate size can have a positive growth rate. This results in the emergence of a crossing point that is a stable fixed point for the wavenumber in the linearized regime, i.e. condensate size is stabilized. (In practice, the nonlinear system will exhibit a number of different wavenumbers, depending on the precise nonlinearity.) We will also refer to this type of dispersion curve as size-controlled condensation.
The matrix JI(k) has an exact form that depends on the parameters, which is given by
| 2.7 |
Entry (1,1) of JI can be described as a function a|k|2 − γ2|k|4, with a is a constant that depends on many parameters. We shall study what happens to our system in the region where it already undergoes phase separation. We therefore set a = 1, which amounts to effective selection of quantities such as ν, ρ1, ρ2 and cs such that the system is undergoing phase separation. This means that the propensity of our system to phase separate in the absence of chemical reactions or additional couplings to be precisely the same. A random choice of the matrix JI(k) can be generated by generating random values of all the parameters appearing in (2.7).
In the next sections, we follow two different approaches for generating Jacobians of the chemical reactions JR that can ‘reshape’ the dispersion relation. In the first approach, we will generate a random matrix for JR, analyse the resulting features of matrix itself, and infer design principles for candidate reaction networks. In some sense, this approach is ‘model-free’ so long as the reaction terms contain no derivatives (as they should not). It tells us generically how linearized source/sink terms in a phase separating system modify the dispersion relation. In the second approach, we will generate random CRNs using mass action kinetics [47], derive their Jacobian algebraically, and evaluate whether the network can induce microphase separation under a parameter sweep. These approaches lead to qualitatively different types of ‘design rules’ towards the design of chemical networks. While the first approach can tell us about what the mean relationships between species are necessary (i.e. ‘component zi should repress component zj’), the second approach can tell us more about the actual networks themselves, which is more useful for experimental design. Another major difference between these two approaches is that the second approach yields Jacobians whose entries are correlated, due to the law of mass action.
3. Computational analysis of randomly generated Jacobian matrices
Here, we describe the computational method we adopted to ascertain whether the model we considered produces a microphase behaviour for a particular choice of parameters. For this purpose, we build and evaluate a function PJ that takes as inputs the Jacobian arising from the chemistry and the Jacobian arising from the conserved interactions, and generates two possible outputs, either microphase separation (1) or macrophase separation (0)
| 3.1 |
The output of PJ(JI(k), JR) is determined through analysis of the dispersion curve: in other words, given that the entire form of dispersion curves (figure 1) is determined by the Jacobians JI(k) and JR, we can associate any pair of a particular instance of the matrices with a single number corresponding to whether those Jacobians display microphase or macrophase separated dispersion curves. This is a deterministic function, in that every unique pair of matrices JI(k) and JR will map onto the Boolean value. (We ignore cases where there is no phase separation at all, as it is trivial to infer the rule that leads to no phase separation: not enough phase separating material is present.)
A major issue is that the dimension of arguments to this function is rather large. For example, a two-component system would include four independent arguments corresponding to all the entries in the matrix JR as well as the independent parameters in the matrix JI(k) (such as the interaction between components 1 and 2, , the surface parameter γ, the mobilities etc.). If our goal is to understand how particular features of the resulting condensates result from a consideration of these parameters, the explosion of parameters as one goes to larger amounts of components impedes understanding.
To address this problem, and to focus our attention on the interplay of phase separation and chemical reactions, we made judicious assumptions about the parameter values:
-
—
All mobilities are set to be the same. . Different diffusion rates can lead to Turing patterns even in the absence of phase separation [48], thus we exclude studying the effects of varying diffusion coefficients in order to focus our attention on the effects of chemical reactions. This is achieved by setting the mobilities of all species to be identical and setting for i > 1. ( as the squared contribution to the free energy for the first component arises from the Cahn–Hilliard functional.) In principle, differing models of mobility in the Cahn–Hilliard equation (see [49]) could be used, and our choice corresponds to the Mullins–Sekerka model. Due to the additional terms in the free energy contribution of component 1, the diffusivity has a different form for the first component than other components.
-
—
The propensity of different systems to phase separate is kept constant in the absence of chemical reactions or additional conserved couplings. As mentioned previously, this corresponds to fixed choices of parameters a, ρ1, ρ2, ν, γ such that the growth rates are identical for any two separate systems. We set a = 1 and γ = 0.44.
-
—
We perturb around chemical dynamics with a stationary state. We select chemical reactions that have a stationary state, and perturb the system from this homogeneous stationary state. This is equivalent to restricting our analysis to CRNs which have Jacobians that have eigenvalues with negative real parts. As we assume mass conservation, at least one of the eigenvalues of JR must be zero, and its determinant is also zero. Taken together, this ensures that the k = 0 perturbation has a growth rate of zero. In other words, this choice satisfies the requirement that the homogeneous state we perturb from is stable.
In the electronic supplementary material, we demonstrate both that in the absence of surface tension there is no microphase separation (the purely diffusive model), and that in the absence of chemical reactions there is also no microphase separation. This indicates that the observed effects we see are due to the interplay of chemistry and phase separation, as we wished.
However, despite setting some parameters to be fixed, we still face an explosion of parameters, and require a method to obtain discernable rules. Fortunately, such methods have already been established in diverse contexts. However, for completeness, we below sketch what this would entail; for a full discussion, see [50].
We first aggregate all the relevant parameters of the problem in a set . This set contains all the terms that enter into the matrices JI(k) and JR, for example where Jij are entries of the Jacobian matrix JR. Given the set of parameters , we can reconstruct the Jacobians (i.e. the Jacobians are trivially functions of all their parameters ), and therefore whether the system is microphase or macrophase separated. We seek to understand how each of the members of the set affect the value of PJ through the following decomposition:
| 3.2 |
where ψ and θ are a single element of the set . This means that we express the full function P as sums of subfunctions that depend on zero parameters, one parameter, two parameters etc. For example, consider a generic function such as : the subfunction of zero parameters would be f0 = 1, the subfunction of one parameter would be and and the subfuncion of two parameters would be , each of these terms therefore gives information about the action of a parameter independently or in concert on the value of the total function.
Each term in equation (3.2) represents how the propensity to observe our feature of interest is modified through changing only a single parameter, two parameters concurrently etc. Due to the difficulty in analysing higher-order correlations, we focus on two-point correlation functions and lower, and we determine the subfunctions Pψ through functional ANOVA [51,52]. While it is plausible that the design principles of the problem at hand are too complex to be represented in lower-dimensional form, we focus on this simplified case in order to identify easily discernible, pragmatic rules.
Given the focus only on lower dimensional rules, we can represent the subfunctions more explicitly as the following. Imagine a two-component system where ; then we can write out the following functions:
| 3.3 |
This corresponds to the average observation of microphase or macrophase separation over the entire range of parameters. The first-order decomposition, for a particular component (e.g. as a function of J11) is given by
| 3.4 |
and then using the first-order decomposition one can obtain the second-order decomposition in a pair of components (e.g. J11, J12) by
| 3.5 |
One can see that these functions are generically computing the net effect of changing a single parameter or two parameters in concert on the observation as to whether we are likely to be observing microphase or macrophase separation. To try to make this subfunction intuitive, imagine performing an experiment where one can only change one parameter (e.g. J11), but each experiment is instantiated with random values of the other parameters. One sets e.g. J11 = −0.2 and performs M experiments, noting whether the system is microphase or macrophase separated. One repeats this for every value of J11. By looking at the mean of the set of observations for each J11 one is effectively computing the subfunction , once the mean propensity of observing microphase separation is subtracted. Higher-order subfunctions of more than one variable are more involved, but the same intuitive picture should be kept in mind. Additionally, as the measured values are either 0 or 1, the standard deviation and mean should be simply related to one another (no additional information comes from the standard deviation). In brief, while a standard approach to multi-parameter problems is to hold certain parameters fixed and change the others, in this approach we ‘average’ over the parameters that are not being explored in order to see the net effect of one parameter across the entire space.
It can be seen that were we to study a system with only two parameters, the addition of equations (3.3), (3.4) and (3.5) would recapitalute the original function P. Full details about performing these integrations numerically as well as comparisons with data generated for a specified Jacobian are presented in the electronic supplementary material.
4. Results
4.1. Exact analysis of a two-component system
We illustrate our approach using a two-component example, in which it is possible to determine analytically the conditions necessary for chemical dynamics to introduce microphase separation. We can then compare exact conditions on the parameters with the outcomes of a statistical evaluation of (3.2).
For a two-component system, the Jacobians of the spatial interactions and the chemistry are
The set of parameters we are interested in is: . (In the previous section, we described how we set the parameters not involved in this set.)
To study the impact of JR on the dispersion relation, we analyse the determinant of the sum of JI(k) and JR
| 4.1 |
This is a helpful expression, as we know that the determinant itself is given by the product of the eigenvalues . Due to the presence of a conservation law , and this leads to the following expression:
| 4.2 |
In the case of microphase separation, a necessary (but not sufficient) condition is that the determinant of JI(k) + JR must have at least three zeroes as a function of |k| (crossing points of the blue curve in figure 1). Thus, microphase separation corresponds to situations where (4.2) has three real zeros in k ≥ 0. We can translate this requirement into conditions on the entries of JR and , and are an example of the function P defined earlier in (3.1). Restricting our analysis to the range where (due to the truncation of the expansion), these conditions are
| 4.3 |
This function should be interpreted as a complicated logical sentence. Either all the clauses within the first brace are true, or all the clauses within the second brace are true. If the sentence is true, the set of parameters corresponds to microphase separation, and if not it corresponds to macrophase separation. It is immediately apparent how complex these expressions can become, even for a two-component systems. In fact, even the above expressions required computer algebra software (Mathematica) to extract closed-form expressions.
While these expression are complex, the inequality is simple enough that we can offer an interpretation of its meaning. For occurrence of microphase separation, it is beneficial for term J11 − J22 to be negative. In a matrix where the real parts of the eigenvalues are negative, both J11 and J22 are generally both negative, so it is desirable that |J11| > |J22|. This means that upon a perturbation, it is preferable for the concentration of species 1 to relax faster back to its equilibrium state, when compared with the concentration of species 2. In a two-component system, we can understand this simply enough through the idea that components 1 and 2 both suppress their own concentration through reactions: given that there are only two species, the only way that this can occur is through the inter-conversion of the two species into one another. This condition implies more of species 1 is being converted to species 2 than vice versa, which is a necessary condition for the formation of a microphase separation as species 1 has the inbuilt tendency to phase separate, which has to be balanced by chemical flux (as has been observed before [27]).
As for term , if the spatial interaction between species 1 and 2 is repulsive (), then it is preferable for species 1 and 2 to produce each other (positive off-diagonals); if it is attractive (, then it is preferable for species 1 and 2 to inhibit each other (such as by reacting together to form a different substrate). In other words, it is preferable for the chemical interactions to have an effect on the concentration that is opposite from the effect of the spatial interaction. This opposite effect is beneficial to maintaining microphase separation. While the remaining conditions are not easy to interpret, they can be computationally decomposed to reveal the interplay between terms.
4.2. Designing two-component networks
The conditions on the Jacobian elements in equations (4.3) can guide the design of chemical reactions that promote the emergence of microphase separation in the presence of uncertainty or fluctuations of the spatial interaction parameters, making the structure of the chemical Jacobian more robust with respect to such uncertainties. For example, consider a system in which the following chemical reactions occur:
| 4.4 |
where z1 is the phase separating species. We do not have much latitude to design networks where there are only two components; however, additional autocatalytic reactions can be added to the above. For example, the following reaction:
| 4.5 |
or the following reaction:
| 4.6 |
The addition of either one of these reactions changes the elements of the Jacobian in predictable ways, and therefore using the conditions we have derived above, we can know whether they are helpful or harmful to microphase separation. Reaction (4.5) adds an additional negative term to J11, a positive and negative term to J22, and the important term J12 + J21 becomes more positive. A similar analysis but with the labels swapped applies for reaction (4.6). Therefore, the addition of autocatalytic cycles will help or hinder depending precisely on the sign of ; if these reactions tend to hinder microphase separation, but they are helpful when . Thus, there does not exist a general relationship between the presence of autocatalytic reactions and the emergence of microphase separation.
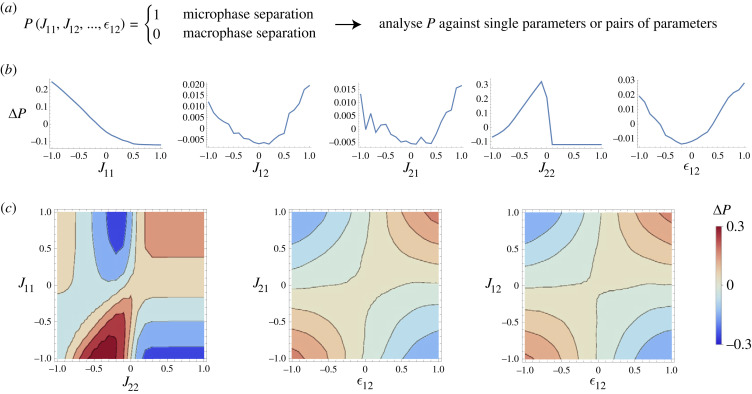
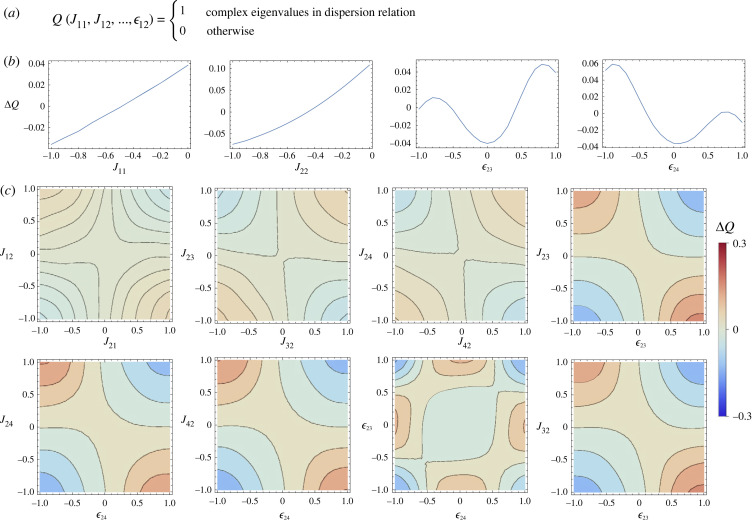
The preceding discussion allows us to reason about relatively simple rules in the design of two-component systems. These rules are rather intuitive in this case, yet it is tricky to generate them and evaluate them. Therefore, next, we use decomposition method in the previous section to graphically illustrate how the likelihood of microphase separation is affected by changes in the parameters of the Jacobians in (4.1). Figure 2 shows the decompositions in which a selection of individual or of pairs of parameters are changed (the remaining sets are in electronic supplementary material, figure S1). Some of these relationships are consistent with those inferred from (4.3), for example figure 2b confirms that the likelihood of microphase separation increases if J11 is more negative than J22. This means the deactivation of species 1 (the phase separating component) has to proceed most strongly, which is natural if we consider that phase separation causes a local increase of concentration, a process that needs to be counteracted by chemical deactivation to avoid predominance of macroscopic separated phases. We also confirm our expectation that spatial interactions () and chemical reactions (Jij) between the two species should have opposite effects on the concentration. This illustrative example generates simple rules; however, we can extend it to larger systems and see how much the logic described here holds.
Figure 2.
How the various parameters of the Jacobian matrices impact the propensity to observe microphase separation, when a = 1 and γ = 0.44. (a) The function P maps a set of parameters onto a binary yes–no function that tells us whether the system is microphase separated or macrophase separated. Decompositions of this function are displayed as a function of both changing a single variable (b) and as a function of changing two variables simultaneously (c). Many such relationships could be generated, but we here show only those that have the largest impact on the function P. In particular, the interaction between J12 and the spatial coupling is important, while components J11 and J22 are important in themselves.
4.3. Random Jacobian analysis of systems with four components
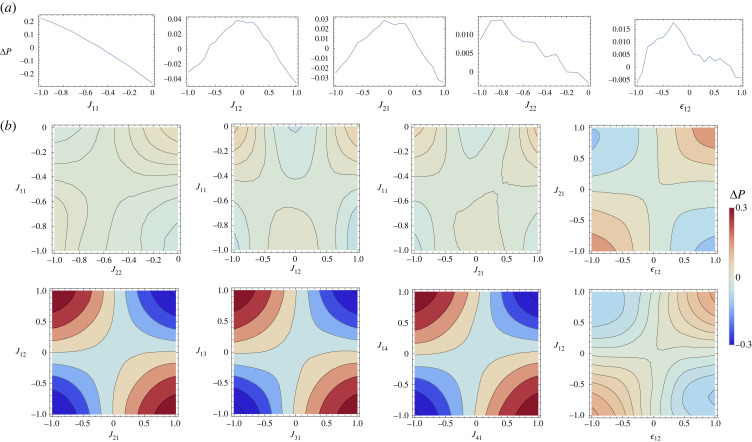
We use computational analysis to consider another example that includes four distinct species. For ease of comparison with the two-component system, we restrict the spatial interactions between components to be between species 1 and 2, with all other components set to zero (only the component in the interaction matrix of (2.1) are non-zero). Figure 3 shows how the likelihood of microphase separation changes as parameters are varied. For ease of comparison with the two-components system, we varied the same single parameters (top row panels in figure 3), identifying some similarities. For example, there is a strong dependence on the parameter J11 where systems with more negative J11 (strong self-deactivation) are more likely to undergo microphase separation. The other components, however, display differences to the two component example, the generic behaviour of the other components seem to be inverted in comparison with the two component example, and the effect of each other component is much weaker (see electronic supplementary material, figure S2).
Figure 3.
Modification of the function P, propensity to observe a microphase separation as a function of various components of the Jacobians when a = 1 and γ = 0.44. For comparison, we show the complementary parameters as appeared in figure 2. (a) The modification of the propensity due to changing a single component and (b) the modification of the propensity when two components are being modified simultaneously. While some features of the analysis remain for the case of four species, several qualitative differences emerge as to what confluence of parameters leads to high propensity of observing microphase separation.
The relation between J12 and is similar to the two-component example: spatial and chemical interactions should have opposite effects on concentration to promote the emergence of condensates of finite size. However, and in contrast to the observations made for the two-component example, we can now observe that there are very strong interactions between the complementary components of the first row and first column, i.e. J12 and J21. We can interpret this heat map by observing that the preference appears to be strongly in favour in terms of J12 and J21 being of different signs. Microphase separation is generally disrupted if the odd-diagonal terms are the same. This suggests that in order to design chemical networks leading to microphase separation it is necessary to produce a network where component 2 activates component 1 and component 1 inhibits component 2 or vice versa. This corresponds to instability in the level of components 1 and 2 when they are mixed together, i.e. the creation of fluxes, which would always be a precondition of fixed size condensates. Analysis of figure 3, furthermore, reveals an element of frustration [53] in the problem. As J12 and J21 should have opposite signs, and yet each of them as they appear in the plots of and would prefer to have an which matches their own sign. It is not possible to satisfy this constraint, which may explain why is relatively less important for systems above more than two components. In general, we believe that increasing the number of components in this system increases the chances that constraints such as these occur, suggesting an intriguing problem of optimization in parameter space for design of robust networks.
4.4. Identifying chemical reaction networks that achieve condensate size control
The prior sections expounded on the mathematical features necessary towards the realization of chemical reactions that produce condensates of finite size, which was conducted through analysis of the properties of the Jacobians arising from the interplay of spatial and chemical interactions among species. This leads to generic rules on the level of activation/inhibition in the Jacobian; however, it is usually not possible to design Jacobians directly, rather, we are more used to introducing specific chemical reactions into a system. In this section, we seek design rules for chemical reactions that produce microphase separation, following the workflow illustrated in figure 4a.
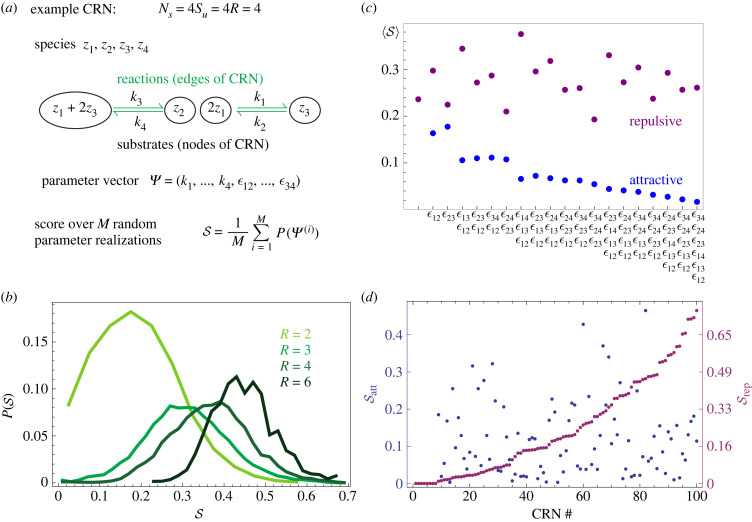
Figure 4.
Comparing relative efficacy of different chemical reaction networks and spatial interactions to produce a system with microphase separation when a = 1 and γ = 0.44. (a) Schematic of the CRN scoring approach. We begin with a system with a set number of species, and then randomly generate Su substrates and R reactions between them. We then interrogate how often the feature we are interested in arises across random choices of all the parameters . (b) The average score changes depending on the number of reactions across different CRNs; here we assume Ns = 4, Su = 4. More reactions have a positive impact on . (c) Impact of spatial interactions on the average score across different chemistries for purely repulsive or attractive interactions; each of the x-axis labels is the subset of spatial couplings that is non-zero. (d) Scores against 100 distinct labelled chemistries when the interactions are changed to be positive or negative. The same chemistries which do well for repulsive interactions do not correlate with the score for attractive interactions.
We consider general CRNs that can be described by a tuple (Ns, Su, R), where Ns is the number of species, Su is the number of substrates (where a substrate is a set of reactants appearing in the reactions) and R is the total number of reactions [47]. Given a particular set of reactions, a CRN can be associated with an incidence graph whose nodes correspond to the substrates, and arcs corresponds to the reactions inter-converting the substrates. (Note that many different graphs can be associated with a particular tuple (Ns, Su, R), depending on the reactions chosen.) Each graph admits a multitude of parameter realizations (reaction rate parameters). Once reactions and parameters are specified, we can generate the time evolution equations of each CRN via the law of mass action. Now the entries Jij of the chemical reaction Jacobian matrix JR are specified by physical reaction rates and concentrations that populate the parameter vector . To test whether a CRN introduces microphase separation, we determine the algebraic form of its Jacobian JR, and analyse the resulting dispersion relation that includes algebraic expression with random parameters. Our automated process for defining and examining random CRNs takes advantage of definitions in [47] and is described in electronic supplementary material, §1.
An actual chemistry being a symbolic representation of interconversions between species, e.g. etc., what can we say about the structural features of CRNs that make size control more or less likely? There is a degree of arbitrariness to this problem, in that the structure of the CRN (defined by the number of species Ns, the number of substrates Su, the number of reactions R in the system and the substrate/reaction graph) is not sufficient to define whether the Jacobians will yield microphase or macrophase separation, which is influenced by a myriad of parameters involved, such as the reaction rates, diffusion coefficients, surface tensions, interaction parameters etc. However, broadly stated, we can define this problem as one of optimization, introducing the following score metric:
| 4.7 |
where we use the function PJ defined in (3.1) that maps the Jacobian matrices to a dispersion relation (with microphase separation = 1 and macrophase separation = 0). The function defines some probability distribution of parameters in the system. Maximization of leads to a system which displays microphase separation over many different choices of parameters. Such a system would therefore be ‘robust’ to uncertainty in parameters towards achieving microphase separation. This optimization problem will also make it possible to identify patterns in the Jacobian JR (non-zero entries and their sign) that maximize the number over all parameter values, and those patterns are consistent with those identified via the reaction-agnostic approach described in electronic supplementary material, §B. We choose because the probability distribution of parameters, which would depend on experimental conditions, uncertainty and temporal fluctuations etc. is not known in principle. In this case, the set includes all the parameters necessary for full definition of the CRN (e.g. rates and free concentrations) and all the spatial interactions . We restrict the range of the reaction rates in these calculations to be between 0 and 1, and the interactions to be between −1 and 1.
We use in (4.7) as a metric to compute a ‘size control score’ and rank the capacity of various CRNs to yield microphase separation (figure 4a). By taking advantage of the structured nature of chemical reactions [47], we generated CRNs by considering all possible combinations of Ns = 4, Su ∈ [2, 4], and R ∈ [2, 6]. For each combination of (Ns, Su, R), we generated a series of graphs; for each interaction graph, we generated 1000 random parametric realizations. More details on our CRN generation algorithm are in the electronic supplementary material, §1. For physically meaningful results, as done earlier, we restricted our attention to closed networks conserving the total mass, and networks admitting a stable fixed point. We evaluated using Monte Carlo integration by obtaining a score (1 or 0) for each set of parameters, and we computed an average score for each CRN (for this purpose, we used the fully connected interaction matrix JI). Figure 4b shows the distribution of scores over networks with the same number of reactions. Interestingly, the more fully connected the network structure is, the more likely it is to generate microphase separation. By contrast, we found that CRNs with only two chemical reactions (R = 2) have the lowest values of score , as shown in figure 4b. Consideration of the analysis of the Jacobian JR in the previous section leads to a plausible mathematical hypothesis regarding why, as with larger numbers of reactions the entries in the Jacobian JR become less correlated and can also take values with opposite signs. Highly correlated entries in the Jacobian could constrain the off-diagonal elements in such a way as to be destructive to the existence of microphase separation, as illustrated in figure 3.
We show the networks with the highest score in table 1. By observing this table, we note that the best-performing CRNs in terms of achieving microphase separation include the following class of reactions:
| 4.8 |
and
| 4.9 |
where we can use i, j (i ≠ j) interchangeably for any of the non-phase separating chemicals in our system. The CRN should include a reaction that converts z1 to some other chemical zi, and in addition this chemical zi can itself sequester z1, thereby generating another chemical zj. As a consequence, a local increase in z1 is counterbalanced by sequestration of z1 itself, which is qualitatively equivalent to self-repression and generates a negative feedback loop. In other words, size control is promoted by the presence of chemical reactions introducing a self-regulation mechanism in the local level of z1. This is the best-performing motif in a system where the spatial interactions can take random values.
Table 1.
Example highly scoring chemistries for Ns = 4, Su = 4, R = 2
| chemical reactions | score |
|---|---|
| 0.596 | |
| 0.595 | |
| 0.591 | |
| 0.583 | |
We can use the Jacobian analysis of the previous section to understand why the form of CRN shown in equations (4.8) and (4.9) is so good for microphase separation, (using i = 2, j = 3), the Jacobian corresponding to this CRN is given by
| 4.10 |
where we consider the equilibrium concentration [z2] to be a free parameter. We see that the structure of the CRN leads to a Jacobian where the off-diagonal entries at {1, 2}, {2, 1}, {1, 3}, {3, 1}, which are most important towards the realization of microphase separation, depend on largely different parameters. Therefore, even when these parameters cannot be controlled, they will be more likely take different values, which is useful for size control, as can be seen from our map in figure 3. This is related to the results for the more highly connected networks being better for microphase separation, as small CRNs tend to produce off-diagonals that are positively correlated, or off-diagonals that can only take positive values, which as was seen in the previous section, is an impediment to realizing size control. Sequestration reactions of z1 are helpful motifs, more so than others such as autocatalysis.
We are left with the question of what is the impact of the spatial coupling terms on the size control score . Figure 4c shows the average value of when only a subset of couplings have a finite value (as specified in the x-axis), while all others are set to zero. Several trends can be observed. The best-performing system is the one in which component 1 has a repulsive interaction to all the other species 2, 3, 4. It can also be seen that the more attractive interactions the system has, the more difficult it is to realize a microphase separation (low average scores). A simple intuitive picture that would explain this is that components tend to get concentrated together when there are attractive interactions, and this makes it difficult to achieve a flux out of the dense phase that is necessary to arrest coarsening.
To examine to what extent a CRN is likely to achieve size control under different types of spatial interactions, we compare the scores of the same CRN against repulsive and attractive spatial interactions in figure 4d. In other words, the chemistry is the same, and all that is changed is that the entries of are either all repulsive or attractive. One way to test this is by generating the average score for 100 distinct CRNs for repulsive interations, and plotting them in a rank-ordered manner. These same CRNs can be used to compute the scores for attractive interactions. If the curves were to display similar trends, this would suggest that a CRN that is good in a system with repulsive interactions also tends to be good in a system with attractive interactions. The lack of correlation between the two curves in figure 4d suggests a well-performing chemistry in the presence of repulsive spatial interactions will not necessarily be good when the interactions are attractive. The problem of designing CRNs for size-controlled condensates is quite sensitive to the sign of the spatial interactions in the system.
4.5. Controlling dynamics of condensates through chemical reactions
The approach we have described can be adapted for different conditions. One interesting extension is the emergence of dynamical phenomena. This cannot be exactly predicted from linear stability analysis, but a condition we can obtain from the dispersion relation β(|k|) is
| 4.11 |
which would correspond to oscillations. Obviously, in the real system, we have many different wavelengths, each of which has its own real and imaginary value of the eigenvalues of the Jacobian matrix, and therefore (4.11) is not a sufficient condition for the realization of sustained oscillations in our system. However, it is still interesting to analyse what kinds of patterns in the Jacobian elements could possibly lead to oscillations. To that end, we define a new function,
| 4.12 |
In words, we look for dispersion relations where both and exists for some value k.
We can do the same decomposition we did searching for microphase separation for a four species system, shown in figure 5. Patterns similar to those in figures 2 and 3 emerge in the relationships between field couplings and Jacobian elements Jij. However, the variables most of interest in the Jacobian towards oscillatory behaviours are the components that were relatively unimportant towards microphase separation, such as the coupling between components 2 and 3 (which are not the components that phase separate). The Jacobian elements themselves display a coupling feature where it is advantageous for both components to have the same magnitude. Altogether, this would mean that the best way towards achieving dynamical oscillations of condensates would be to couple the condensates to another reaction–diffusion system which already displays oscillatory behaviour, rather than attempting to induce dynamical oscillations of the condensates themselves.
Figure 5.
Function describing the presence of a dispersion relation with both imaginary and real components, see (4.12), with arguments as the Jacobians when a = 1 and γ = 0.44. The presence of imaginary eigenvalues would be indicative of long-lived dynamical states. Only the features which have the strongest impact on the propensity to observe imaginary eigenvalues are shown, both for varying a single parameter (b) and for varying two different parameters simulataneously (c). In contrast to the observations for microphase separation, different sets of components are most important to the observation of imaginary eigenvalues, suggesting the possibility that these two different features need not interfere with one another. Unlike size control, the presence of continued dynamics depends more strongly on the details of the spatial interactions, which means that chemical motifs are of relatively less importance.
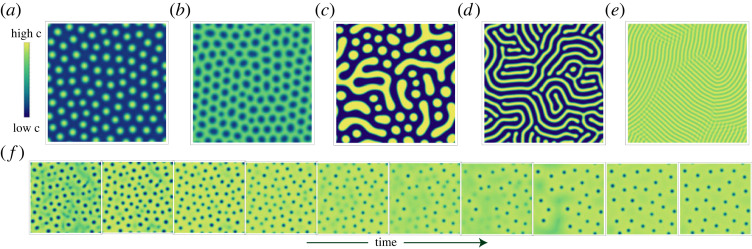
As is well understood, linear stability analysis is not fully predictive of the properties of the long-time behaviour of reaction–diffusion systems, nor can it precisely enumerate exactly how the long-time behaviour will ‘look’ [54]. In order to fully understand what these systems do, there are as yet few alternatives towards complete solution of the equations involved. Given the thousands of different possible CRNs, full enumeration of the possibilities here are prohibitive, but we can take a taxonomic approach towards the problem by simulating a few examples with interesting dispersion relations and observing the time evolution. The subset we are interested in here shall be those dispersion relations which display both microphase separation and dynamic oscillations. These can be generated by generating many CRNs and finding the parameter sets that display both of these features. The taxonomy is displayed in figure 6 (the corresponding reactions are in the electronic supplementary material §3). Microphase separation arises rather commonly in our system, though the precise structure of this phase itself displays plentiful variance, including droplets and stripes (as is well established). Whether the exact features of the final states displayed here depend on ‘thermodynamic’ or ‘chemical’ factors would require further analysis of individual reaction schemes. However, we show in electronic supplementary material, §2 that in the absence of chemical reactions none of the observed states could occur, as such systems will only display macrophase separation. Chemical reactions are therefore necessary towards the achievement of size limited patterns, but the precise form these patterns take will depend on the interplay of the conserved and non-conserved dynamics. All such patterns exhibit the finite size instability, in contrast to expected equilibrium behaviour for monomers but discernable via field theoretic techniques for polymeric systems [42]. Despite the fact our equations do not minimize a functional, they exhibit similar kinds of order to equilibrium microphase separated systems.
Figure 6.
Examples illustrating the taxonomy of possible (real) solutions (concentration of the phase separating material) found through the condition (4.11) after relaxation over the same amount of time. These solutions display significant visual differences, although they all exhibit microphase separation. Under these schemes, we observe (a) droplets of finite size (b) anti-droplets (droplets of low density) (c) irregular droplets (d) stripes (e) stripes of smaller width. (f) Condensation dynamics introduced by a particular CRN. The dynamics shows droplets coming into and out of existence; however, the concentration field eventually settles into a static state. The CRNs corresponding to each example are in the electronic supplementary material, §3.
When looking for dynamics, the linear stability analysis is not strongly predictive of long-lasting dynamic oscillations. In fact, most chemistries we attempted led to slow exponential relaxation to a steady state as opposed to long-lasting oscillations, despite the presence of complex eigenvalues. From this, we would surmise that the conditions required to obtain long-lasting oscillatory dynamics would require some additional analysis accounting for the nonlinearities. Another possibility is that the presence of a noise term in our system may lead to excitation of dynamical modes, but we have forgone the study of noise in this paper.
5. Discussion and conclusion
While biomolecular phase separation can be controlled over time by modulating temperature and ionic conditions [55], changes in these properties are often limited by the necessity to maintain conditions compatible with life. This obstacle can be circumvented by controlling phase separation through a change of subunit concentration, which is easily achieved via CRNs that allow for interconversion between species [19]. We have discussed how the coupling of phase separating molecules with chemical reactions can lead to the emergence of non-equilibrium behaviours, such as the existence of condensates with size showing a well-defined length scale or with size that undergoes continuous temporal dynamics. Through computational simulations, we have identified patterns on the interaction parameters and we scored CRN structures that support the realization of these features. We have not considered the effects of either momentum transport, or random noise, and we acknowledge that both of these elements could conceivably alter some of the relationships we have observed, though we expect our broad findings to hold.
Stabilization of condensate size in a binary mixture has been computationally demonstrated before through the introduction of externally provided fuel and waste species, or through an enzyme that self-segregates into the droplets generating diffusive fluxes [19]. Coarse-grained simulations of individual molecules in a system that contains phase separating species showed that a particular class of chemical reactions proceeding at a given rate can lead to novel non-equilibrium behaviours, including molecular sorting, spatial and temporal oscillations and tunability of chemical production [46]. However, exploring chemical rules that lead to non-equilibrium behaviour cannot be done efficiently via coarse-grained molecular simulation. Capitalizing on these studies, our work considers a broad set of CRNs with the goal of identifying useful design rules.
By framing the problem in terms of the properties of the Jacobians, we were able to identify parameter trends that should be satisfied to achieve particular behaviours. For microphase separation to occur (size control), we found that (i) chemical reactions should deactivate the phase separating species, by converting it into a species that does not participate in condensation and rather diffuses in the system; and (ii) the impact of other chemicals on the phase separating species should have opposite effects relative to the impact on them of the phase separating species. For example, if the phase separating molecule is species 1, and species 2 is another molecule, we found that either 1 should produce 2 and 2 should inhibit 1, or that 2 should produce 1 and 1 should inhibit 2, and the system is at rest only when the level of 1 or 2 is zero. This shows that size control benefits from the presence of chemistry that makes it unlikely for species 1 and 2 to coexist in the same region of space, and may indicate the presence of a negative feedback loop. We illustrate this idea in figure 7 using a network diagram often used in biology to represent activator/inhibitor interactions [56]. When exploring the capacity of randomly generated CRNs to generate microphase separation by analysing their Jacobian, we found a recurring CRN motif in which the deactivated phase separating molecules further deactivate other active molecules via molecular sequestration, which has been associated with perfect adaptation in biology [57,58]. This reaction introduces negative feedback, because the higher the level of phase separating species, the more self-repression occurs. This leads to large fluxes of material out of condensates, counteracting the influx of phase separating species. Yet, the existence of negative feedback does not represent a necessary or sufficient condition towards achieving microphase separation, because all the patterns we have described here are only statistical in nature. This finding is still interesting because negative feedback has a well-known role in the context of stabilization and emergence of oscillations in biomolecular networks [57,59]. Such relationships only arise when considering more than two components, demonstrating the delicate nature of trying to understand the behaviour of many coupled fluids.
Figure 7.
Two different kinds of motifs in terms of generalized chemical reactions that are most helpful towards the realization of microphase separation. Component 1 (the phase separator) should self-inhibit, and either inhibit another component 2 that activates 1, or activate a component 2 that inhibits 1.
Curiously, we observed that the more coupled the CRN is, the better it performs in terms of size control. It appears as a general effect, therefore, that the more chemical fluxes are included in the system, the more likely is the realization of microphase separation, even if individual fluxes might not be optimized towards that actual goal. This would suggest that the presence of any random chemical flux corresponding to some energy-consuming reaction in a phase separating system rarely has the effect of stabilizing the macroscopically separated state, rather, it would appear to be the opposite. A mathematical explanation for this phenomenon can be gained from the full analysis of the function P.
We also found that spatial interaction parameters have a major influence on the design of CRNs achieving microphase separation. We found that repulsive couplings, i.e. the different species like to spatially segregate, are generally beneficial. By contrast, attractive couplings make it more difficult to design CRNs for size control. This is consistent with the common-sense notion that it would be harder to regulate the size of condensates were all the spatial interactions in the system attractive, for this would tend to promote the aggregation of all objects, to the detriment of control over their size. This finding is important in the context of experimentally designing molecular subunits, for example using peptides or nucleic acids, that can present non-specific, undesired attractive interactions often classified as ‘cross-talk’ [60]. These interactions can perturb the system’s parameters enough to suppress its intended behaviour, an effect that is particularly critical in non-equilibrium molecular systems [61]. In the case of microphase separation, the presence of any kind of spatial attractive interaction would make it much harder to realize that goal. Indeed, the design of a CRN that does not take this into account could mean the theoretical result would be hard to reproduce. A way around this problem would be to include the unknown parameters as a constraint, and identify the CRN forms that lead to the best performance given that attractive spatial interactions exist. While here we explored CRNs assuming that all the chemicals are coupled randomly, our analysis can be repeated including experimental limitations and constraints like the presence of unwanted attractive couplings.
When considering the emergence of periodic behaviours over time in our phase separating system, we noted that couplings between all the non-phase separating components appear to be most important (for example mediated by the interaction between species 2 and 3, and 2 and 4). We speculate that having stable oscillations in the phase separating material itself is difficult due to the fact that aggregation compromises the conditions required for the presence of sustained oscillations. In this case, the other species in the system may oscillate when decoupled from the phase separating species, and oscillations observed in the condensates may be a secondary effect of oscillations of chemicals in the dispersed phase. In practice, it is rare to observe stable oscillations in this system when the full partial differential equations were solved, though we have observed systems with limited oscillations of droplets popping into and out of existence.
A major advantage of using CRNs to control separation, when compared with introducing global environmental changes in temperature and solvent, is that CRNs could direct independently numerous coexisting condensates. Although theory points out that multi-component phase separating materials can display a multitude of morphologies [62] even in the absence of chemical reactions, which can be tuned through control over the self-attraction of the phase separating materials [63] (which can also be framed as a sequence design problem [64]), morpologies can also be controlled through hydrostatic pressure and osmolytes [65]. The analysis of biological CRNs will help formulate hypotheses on how cells manage a multitude of types of condensates with distinct composition, function, structure and temporal dynamics [19,27,66]. Our results will also provide guidance towards the design of novel materials in the context of a rapidly expanding set of designable molecular substrates that could be used to implement a variety of CRNs [28,29], as well as a variety of condensates [13,67,68]. We have used the general model presented here to gain insight on the behaviour of artificial DNA condensates in which subunits are activated and deactivated through chemical reactions, and we found experiments to be consistent with theoretical predictions [12]. We thus expect that our approach will be useful to explore whether chemical reactions could provide instructions to manage condensate formation, dissolution, organization and other macroscopic properties.
Ethics
This work did not require ethical approval from a human subject or animal welfare committee.
Data accessibility
The data are an analysis of the equations presented in the main text. The work is entirely theoretical. The mathematica notebooks for generating the equations are available from the GitHub repository: https://github.com/osmanovicdino/CRNData [69].
The data are provided in the electronic supplementary material [70].
Declaration of AI use
We have not used AI-assisted technologies in creating this article.
Authors' contributions
D.O.: conceptualization, formal analysis, investigation, methodology, writing—original draft, writing—review and editing; E.F.: conceptualization, formal analysis, funding acquisition, supervision, writing—original draft, writing—review and editing.
Both authors gave final approval for publication and agreed to be held accountable for the work performed therein.
Conflict of interest declaration
We declare we have no competing interests.
Funding
E.F. and D.O. acknowledge support from NSF FMRG:Bio award 2134772 to E.F. and from the Sloan Foundation through award G-2021-16831.
References
- 1.Alberti S, Hyman AA. 2021. Biomolecular condensates at the nexus of cellular stress, protein aggregation disease and ageing. Nat. Rev. Mol. Cell Biol. 22, 196-213. ( 10.1038/s41580-020-00326-6) [DOI] [PubMed] [Google Scholar]
- 2.Brangwynne CP, Eckmann CR, Courson DS, Rybarska A, Hoege C, Gharakhani J, Jülicher F, Hyman AA. 2009. Germline P granules are liquid droplets that localize by controlled dissolution/condensation. Science 324, 1729-1732. ( 10.1126/science.1172046) [DOI] [PubMed] [Google Scholar]
- 3.Hyman AA, Weber CA, Jülicher F. 2014. Liquid-liquid phase separation in biology. Annu. Rev. Cell Dev. Biol. 30, 39-58. ( 10.1146/annurev-cellbio-100913-013325) [DOI] [PubMed] [Google Scholar]
- 4.Riback JA, Katanski CD, Kear-Scott JL, Pilipenko EV, Rojek AE, Sosnick TR, Drummond DA. 2017. Stress-triggered phase separation is an adaptive, evolutionarily tuned response. Cell 168, 1028-1040. ( 10.1016/j.cell.2017.02.027) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Frottin F, et al. 2019. The nucleolus functions as a phase-separated protein quality control compartment. Science 365, 342-347. ( 10.1126/science.aaw9157) [DOI] [PubMed] [Google Scholar]
- 6.O’Flynn BG, Mittag T. 2021. The role of liquid–liquid phase separation in regulating enzyme activity. Curr. Opin. Cell Biol. 69, 70-79. ( 10.1016/j.ceb.2020.12.012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Alberti S. 2017. Phase separation in biology. Curr. Biol. 27, R1097-R1102. ( 10.1016/j.cub.2017.08.069) [DOI] [PubMed] [Google Scholar]
- 8.Banani SF, Lee HO, Hyman AA, Rosen MK. 2017. Biomolecular condensates: organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 18, 285-298. ( 10.1038/nrm.2017.7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Klosin A, Oltsch F, Harmon T, Honigmann A, Jülicher F, Hyman AA, Zechner C. 2020. Phase separation provides a mechanism to reduce noise in cells. Science 367, 464-468. ( 10.1126/science.aav6691) [DOI] [PubMed] [Google Scholar]
- 10.Reinkemeier CD, Girona GE, Lemke EA. 2019. Designer membraneless organelles enable codon reassignment of selected mRNAs in eukaryotes. Science 363, eaaw2644. ( 10.1126/science.aaw2644) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schuster BS, Reed EH, Parthasarathy R, Jahnke CN, Caldwell RM, Bermudez JG, Ramage H, Good MC, Hammer DA. 2018. Controllable protein phase separation and modular recruitment to form responsive membraneless organelles. Nat. Commun. 9, 1-12. ( 10.1038/s41467-018-05403-1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Agarwal S, Osmanovic D, Klocke M, Franco E. 2022. Biochemical control of DNA condensation. Research Square (preprint). ( 10.21203/rs.3.rs-1654835/v1) [DOI]
- 13.Gong J, Tsumura N, Sato Y, Takinoue M. 2022. Computational DNA droplets recognizing miRNA sequence inputs based on liquid–liquid phase separation. Adv. Funct. Mater. 32, 2202322. ( 10.1002/adfm.202202322) [DOI] [Google Scholar]
- 14.Heckel J, Batti F, Mathers RT, Walther A. 2021. Spinodal decomposition of chemically fueled polymer solutions. Soft Matter 17, 5401-5409. ( 10.1039/D1SM00515D) [DOI] [PubMed] [Google Scholar]
- 15.Michelin S. 2022. Self-propulsion of chemically-active droplets. Annu. Rev. Fluid Mech. 55, 77-101. ( 10.1146/annurev-fluid-120720-012204) [DOI] [Google Scholar]
- 16.Toyota T, Maru N, Hanczyc MM, Ikegami T, Sugawara T. 2009. Self-propelled oil droplets consuming ‘fuel’ surfactant. J. Am. Chem. Soc. 131, 5012-5013. ( 10.1021/ja806689p) [DOI] [PubMed] [Google Scholar]
- 17.Browne KP, Walker DA, Bishop KJM, Grzybowski BA, Browne KP, Walker DA, Bishop KJM, Grzybowski BA. 2010. Self-division of macroscopic droplets: partitioning of nanosized cargo into nanoscale micelles. Angew. Chem. Int. Ed. 49, 6756-6759. ( 10.1002/anie.201002551) [DOI] [PubMed] [Google Scholar]
- 18.Zwicker D, Seyboldt R, Weber CA, Hyman AA, Jülicher F. 2016. Growth and division of active droplets provides a model for protocells. Nat. Phys. 13, 408-413. ( 10.1038/nphys3984) [DOI] [Google Scholar]
- 19.Kirschbaum J, Zwicker D. 2021. Controlling biomolecular condensates via chemical reactions. J. R. Soc. Interface 18, 20210255. ( 10.1098/rsif.2021.0255) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Longo TJ, Anisimov MA. 2022. Phase transitions affected by natural and forceful molecular interconversion. J. Chem. Phys. 156, 084502. ( 10.1063/5.0081180) [DOI] [PubMed] [Google Scholar]
- 21.Zwicker D. 2022. The intertwined physics of active chemical reactions and phase separation. arXiv. (http://arxiv.org/abs/2202.13646)
- 22.Brackley CA, Liebchen B, Michieletto D, Mouvet F, Cook PR, Marenduzzo D. 2017. Ephemeral protein binding to DNA shapes stable nuclear bodies and chromatin domains. Biophys. J. 112, 1085-1093. ( 10.1016/j.bpj.2017.01.025) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Carati D, Lefever R. 1997. Chemical freezing of phase separation in immiscible binary mixtures. Phys. Rev. E 56, 3127-3136. ( 10.1103/PhysRevE.56.3127) [DOI] [Google Scholar]
- 24.Cates ME, Tjhung E. 2018. Theories of binary fluid mixtures: from phase-separation kinetics to active emulsions. J. Fluid Mech. 836, P1. ( 10.1017/jfm.2017.832) [DOI] [Google Scholar]
- 25.Weber CA, Zwicker D, Jülicher F, Lee CF. 2019. Physics of active emulsions. Rep. Prog. Phys. Phys. Soc. (Great Britain) 82, 064601. ( 10.1088/1361-6633/ab052b) [DOI] [PubMed] [Google Scholar]
- 26.Zwicker D, Decker M, Jaensch S, Hyman AA, Jülicher F. 2014. Centrosomes are autocatalytic droplets of pericentriolar material organized by centrioles. Proc. Natl Acad. Sci. USA 111, E2636-E2645. ( 10.1073/pnas.1404855111) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zwicker D, Hyman AA, Jülicher F. 2015. Suppression of Ostwald ripening in active emulsions. Phys. Rev. E 92, 012317. ( 10.1103/PhysRevE.92.012317) [DOI] [PubMed] [Google Scholar]
- 28.Chen Y-J, Dalchau N, Srinivas N, Phillips A, Cardelli L, Soloveichik D, Seelig G. 2013. Programmable chemical controllers made from DNA. Nat. Nanotechnol. 8, 755-762. ( 10.1038/nnano.2013.189) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chen Z, Elowitz MB. 2021. Programmable protein circuit design. Cell 184, 2284-2301. ( 10.1016/j.cell.2021.03.007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Shrinivas K, Brenner MP. 2021. Phase separation in fluids with many interacting components. Proc. Natl Acad. Sci. USA 118, e2108551118. ( 10.1073/pnas.2108551118) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Avanzini F, Penocchio E, Falasco G, Esposito M. 2021. Nonequilibrium thermodynamics of non-ideal chemical reaction networks. J. Chem. Phys. 154, 094114. ( 10.1063/5.0041225) [DOI] [PubMed] [Google Scholar]
- 32.Bazant MZ. 2013. Theory of chemical kinetics and charge transfer based on nonequilibrium thermodynamics. Accounts Chem. Res. 46, 1144-1160. ( 10.1021/ar300145c) [DOI] [PubMed] [Google Scholar]
- 33.Bazant MZ. 2017. Thermodynamic stability of driven open systems and control of phase separation by electroautocatalysis. Faraday Discuss. 199, 423-463. ( 10.1039/C7FD00037E) [DOI] [PubMed] [Google Scholar]
- 34.Berry J, Brangwynne CP, Haataja M. 2018. Physical principles of intracellular organization via active and passive phase transitions. Rep. Prog. Phys. 81, 046601. ( 10.1088/1361-6633/aaa61e) [DOI] [PubMed] [Google Scholar]
- 35.Cross MC, Hohenberg PC. 1993. Pattern formation outside of equilibrium. Rev. Mod. Phys. 65, 851-1112. ( 10.1103/RevModPhys.65.851) [DOI] [Google Scholar]
- 36.Glotzer SC, Di Marzio EA, Muthukumar M. 1995. Reaction-controlled morphology of phase-separating mixtures. Phys. Rev. Lett. 74, 2034. ( 10.1103/PhysRevLett.74.2034) [DOI] [PubMed] [Google Scholar]
- 37.Menou L, Luo C, Zwicker D. 2023. Physical interactions in non-ideal fluids promote Turing patterns. R. Soc. Interface 20, 20230244. ( 10.1098/rsif.2023.0244) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lin Y-H, Brady JP, Forman-Kay JD, Chan CH. 2017. Charge pattern matching as a ‘fuzzy’ mode of molecular recognition for the functional phase separations of intrinsically disordered proteins. N. J. Phys. 19, 115003. ( 10.1088/1367-2630/aa9369) [DOI] [Google Scholar]
- 39.Hohenberg PC, Halperin BI. 1977. Theory of dynamic critical phenomena. Rev. Mod. Phys. 49, 435-479. ( 10.1103/RevModPhys.49.435) [DOI] [Google Scholar]
- 40.Vanag VK, Epstein IR. 2009. Cross-diffusion and pattern formation in reaction–diffusion systems. Phys. Chem. Chem. Phys. 11, 897-912. ( 10.1039/B813825G) [DOI] [PubMed] [Google Scholar]
- 41.Li YI, Cates ME. 2020. Non-equilibrium phase separation with reactions: a canonical model and its behaviour. J. Stat. Mech: Theory Exp. 2020, 053206. ( 10.1088/1742-5468/ab7e2d) [DOI] [Google Scholar]
- 42.Lin Y-H, Wessén J, Pal T, Das S, Chan HS. 2022. Numerical techniques for applications of analytical theories to sequence-dependent phase separations of intrinsically disordered proteins. In Phase-separated biomolecular condensates: methods and protocols (eds H-X Zhou, J-H Spille, PR Banerjee), pp. 51–94. New York, NY: Springer.
- 43.Gompper G, Schick M, Milner S. 1995. Self-assembling amphiphilic systems. San Diego, CA: Academic Press. [Google Scholar]
- 44.Laradji M, Guo H, Grant M, Zuckermann MJ. 1991. Phase diagram of a lattice model for ternary mixtures of water, oil, and surfactants. Phys. Rev. A 44, 8184. ( 10.1103/PhysRevA.44.8184) [DOI] [PubMed] [Google Scholar]
- 45.Chan HY, Lubchenko V. 2019. A mechanism for reversible mesoscopic aggregation in liquid solutions. Nat. Commun. 10, 1-11. ( 10.1038/s41467-019-10270-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Osmanović D, Rabin Y. 2019. Chemically active nanodroplets in a multi-component fluid. Soft Matter 15, 5965-5972. ( 10.1039/C9SM00826H) [DOI] [PubMed] [Google Scholar]
- 47.Van Der Schaft A, Rao S, Jayawardhana B. 2011. On the mathematical structure of balanced chemical reaction networks governed by mass action kinetics. SIAM J. Appl. Math. 73, 953-973. ( 10.1137/11085431X) [DOI] [Google Scholar]
- 48.Turing A. 1952. The chemical basis of morphogenesis. Phil. Trans. R. Soc. Lond. B 237, 37-72. ( 10.1098/rstb.1952.0012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Dai S, Du Q. 2016. Computational studies of coarsening rates for the Cahn–Hilliard equation with phase-dependent diffusion mobility. J. Comput. Phys. 310, 85-108. ( 10.1016/j.jcp.2016.01.018) [DOI] [Google Scholar]
- 50.Molnar C. 2020. Interpretable machine learning. Lulu.com.
- 51.Hooker G. 2004. Discovering additive structure in black box functions. KDD-2004 – Proc. of the 10th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, Seattle, WA, 22–25 August, pp. 575–580.
- 52.Hooker G. 2012. Generalized functional ANOVA diagnostics for high-dimensional functions of dependent variables. J. Comput. Graph. Stat. 16, 709-732. ( 10.1198/106186007X237892) [DOI] [Google Scholar]
- 53.Chowdhury D. 1986. Spin glasses and other frustrated systems. Princeton, NJ: Princeton University Press. [Google Scholar]
- 54.Riaz SS, Sharma R, Bhattacharyya SP, Ray DS. 2007. Instability and pattern formation in reaction-diffusion systems: a higher order analysis. J. Chem. Phys. 127, 064503. ( 10.1063/1.2759212) [DOI] [PubMed] [Google Scholar]
- 55.Dignon GL, Zheng W, Kim YC, Mittal J. 2019. Temperature-controlled liquid–liquid phase separation of disordered proteins. ACS Central Sci. 5, 821-830. ( 10.1021/acscentsci.9b00102) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Alon U. 2006. An introduction to systems biology: design principles of biological circuits. Boca Raton, FL: Chapman and Hall/CRC. [Google Scholar]
- 57.Briat C, Gupta A, Khammash M. 2016. Antithetic integral feedback ensures robust perfect adaptation in noisy biomolecular networks. Cell Syst. 2, 15-26. ( 10.1016/j.cels.2016.01.004) [DOI] [PubMed] [Google Scholar]
- 58.Samaniego CC, Franco E. 2021. Ultrasensitive molecular controllers for quasi-integral feedback. Cell Syst. 12, 272-288. ( 10.1016/j.cels.2021.01.001) [DOI] [PubMed] [Google Scholar]
- 59.Blanchini F, Franco E, Giordano G. 2014. A structural classification of candidate oscillatory and multistationary biochemical systems. Bull. Math. Biol. 76, 2542-2569. ( 10.1007/s11538-014-0023-y) [DOI] [PubMed] [Google Scholar]
- 60.Zhang DY, Seelig G. 2011. Dynamic DNA nanotechnology using strand-displacement reactions. Nat. Chem. 3, 103-113. ( 10.1038/nchem.957) [DOI] [PubMed] [Google Scholar]
- 61.Green LN, Subramanian HK, Mardanlou V, Kim J, Hariadi RF, Franco E. 2019. Autonomous dynamic control of DNA nanostructure self-assembly. Nat. Chem. 11, 510-520. ( 10.1038/s41557-019-0251-8) [DOI] [PubMed] [Google Scholar]
- 62.Mao S, Kuldinow D, Haataja MP, Košmrlj A. 2019. Phase behavior and morphology of multicomponent liquid mixtures. Soft Matter 15, 1297-1311. ( 10.1039/C8SM02045K) [DOI] [PubMed] [Google Scholar]
- 63.Mao S, Chakraverti-Wuerthwein MS, Gaudio H, Košmrlj A. 2020. Designing the morphology of separated phases in multicomponent liquid mixtures. Phys. Rev. Lett. 125, 218003. ( 10.1103/PhysRevLett.125.218003) [DOI] [PubMed] [Google Scholar]
- 64.Statt A, Casademunt H, Brangwynne CP, Panagiotopoulos AZ. 2020. Model for disordered proteins with strongly sequence-dependent liquid phase behavior. J. Chem. Phys. 152, 075101. ( 10.1063/1.5141095) [DOI] [PubMed] [Google Scholar]
- 65.Cinar H, Fetahaj Z, Cinar S, Vernon RM, Chan HS, Winter RH. 2019. Temperature, hydrostatic pressure, and osmolyte effects on liquid–liquid phase separation in protein condensates: physical chemistry and biological implications. ChemA Eur. J. 25, 13 049-13 069. ( 10.1002/chem.201902210) [DOI] [PubMed] [Google Scholar]
- 66.Shin Y, Brangwynne CP. 2017. Liquid phase condensation in cell physiology and disease. Science 357, eaaf4382. ( 10.1126/science.aaf4382) [DOI] [PubMed] [Google Scholar]
- 67.Kaur T, Raju M, Alshareedah I, Davis RB, Potoyan DA, Banerjee PR. 2021. Sequence-encoded and composition-dependent protein-RNA interactions control multiphasic condensate morphologies. Nat. Commun. 12, 1-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Mountain GA, Keating CD. 2019. Formation of multiphase complex coacervates and partitioning of biomolecules within them. Biomacromolecules 21, 630-640. ( 10.1021/acs.biomac.9b01354) [DOI] [PubMed] [Google Scholar]
- 69.Osmanović D, Franco E. 2023. Chemical reaction motifs driving non-equilibrium behaviours in phase separating materials. GitHub repository. (https://github.com/osmanovicdino/CRNData) [DOI] [PubMed]
- 70.Osmanović D, Franco E. 2023. Chemical reaction motifs driving non-equilibrium behaviours in phase separating materials. Figshare. ( 10.6084/m9.figshare.c.6888329) [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- Osmanović D, Franco E. 2023. Chemical reaction motifs driving non-equilibrium behaviours in phase separating materials. GitHub repository. (https://github.com/osmanovicdino/CRNData) [DOI] [PubMed]
- Osmanović D, Franco E. 2023. Chemical reaction motifs driving non-equilibrium behaviours in phase separating materials. Figshare. ( 10.6084/m9.figshare.c.6888329) [DOI] [PubMed]
Data Availability Statement
The data are an analysis of the equations presented in the main text. The work is entirely theoretical. The mathematica notebooks for generating the equations are available from the GitHub repository: https://github.com/osmanovicdino/CRNData [69].
The data are provided in the electronic supplementary material [70].