A two-scale numerical study on the mechanobiology of abdominal aortic aneurysms

Abstract

Abdominal aortic aneurysms (AAAs) are a serious condition whose pathophysiology is related to phenomena occurring at different length scales. To gain a better understanding of the disease, this work presents a multi-scale computational study that correlates AAA progression with microstructural and mechanical alterations in the tissue. Macro-scale geometries of a healthy aorta and idealized aneurysms with increasing diameter are developed on the basis of existing experimental data and subjected to physiological boundary conditions. Subsequently, microscopic representative volume elements of the abluminal side of each macro-model are employed to analyse the local kinematics at the cellular scale. The results suggest that the formation of the aneurysm disrupts the micromechanics of healthy tissue, which could trigger collagen growth and remodelling by mechanosensing cells. The resulting changes to the macro-mechanics and microstructure of the tissue seem to establish a new homeostatic state at the cellular scale, at least for the diameter range investigated.

1. Introduction

An abdominal aortic aneurysm (AAA) is a condition in which the shape of the abdominal aorta is permanently altered. It is typically characterized by a local and irreversible bulging of the vessel wall, which is recognized in clinical practice when the infrarenal aortic diameter exceeds 30 mm [1,2]. It is a life-threatening cardiovascular pathology that can go unnoticed for years and has a high mortality rate if it progresses to rupture [3,4]. Current treatment is based on surgical intervention, either with a traditional open abdominal procedure or with endovascular repair by deploying a stent-graft into the aneurysmal vessel [5,6]. In any case, the risks associated with the procedure, which are often amplified by factors such as advanced age and concomitant cardiovascular pathologies, require specific medical criteria to evaluate the need for an intervention [7]. The most commonly used criterion is based on a correlation between the probability of rupture and the size of the aneurysm. In general, current guidelines recommend surgery when the maximum diameter of the aneurysm reaches 55 mm in men or 50 mm in women, or when it increases by more than 5–10 mm within a year [8–10]. However, autopsy studies and clinical reports have shown that small AAAs can still rupture [11,12], while some large ones do not [13,14], suggesting that alternative approaches should be pursued [7,15,16].

Various prospective studies have explored biomechanics-based indicators such as maximum wall stress and rupture potential index and, based on the analysis of large patient cohorts, have argued their superiority in relation to the diameter criterion [17–21]. Despite promising achievements, the reliability of these indicators depends on the accuracy of the computational biomechanical simulations used to calculate them, which are closely linked to the modelling framework. Significant advances have been made over early models based on Laplace’s law, including the use of advanced constitutive laws, three-dimensional patient-specific geometry and fluid–structure interaction simulations [22–27]. Nevertheless, the complex pathogenesis of the disease requires a more thorough examination of the mechanical behaviour of the aortic wall. A detailed study of the aortic wall microstructure and its components and how these evolve during aneurysm growth can lead to the development of structure-based, multi-scale constitutive models with improved predictive abilities [28–31].

The healthy human aorta can be described as a thick-walled tube composed of three layers (intima, media and adventitia), each of which has a specific hierarchical arrangement of components at different scales ranging from molecules to cells, fibrils and fibres to tissue [32–34]. As with other soft tissues, it is the extracellular matrix (ECM) that maintains tissue integrity and provides the structural and biochemical environment in which cells are embedded. The ECM of vascular tissues appears as a network of collagen fibres, elastic fibres, elastin layers and proteoglycans [34,35]. Their specific organization is maintained by the mechanotransduction activity of smooth muscle cells and fibroblasts, which can sense and respond to mechanical stimuli to maintain mechanical homeostasis [36,37]. More relevant to the present study is the disruption of this equilibrium and the resulting changes in ECM structure and composition, as they may provide insights into disease progression [38]. In the context of AAA pathogenesis, recent work by Niestrawska et al. [39–41] identified significant differences in the microstructure and mechanical behaviour of aneurysmal tissue compared with healthy aortas. The authors then proposed a three-stage model for describing disease development [40], based on a widely accepted pathophysiological theory of aneurysm formation and growth [2,42]. In summary, loss of elastic fibres and smooth muscle cells initiates dilatation, followed by extensive growth and remodelling (G&R) of the collagen fibres and inflammation. The later stage of AAAs is characterized by the presence of a thick neo-adventitial layer at the abluminal side of the wall, which stiffens the tissue and shows a highly isotropic orientation of collagen fibres [40].

Given these recent findings, it seems obvious that an answer to the evolution of aneurysms, and in particular to the mechanobiological aspects involved, suggests a multi-scale modelling approach, where simulation and experiment go hand in hand. In this direction, Dalbosco et al. [43] recently evaluated the mechano-pathological theory of Niestrawska et al. [40] by simulating the equibiaxial loading of representative volume elements (RVEs) of the arterial microstructure in the healthy tissue and in different stages of AAA, with a special focus on the changes in collagen arrangement. However, a major limitation of [43] is that only the micro-scale of the tissue, subjected to an equibiaxial macroscopic deformation of 10%, was modelled. In reality, given the bulging of the wall as the disease progresses and a thrombus is built up—as observed in approximately 75% of AAAs [44,45]—it is to be expected that the macroscopic mechanics of the wall will also change, affecting the microscopic mechanical state of the tissue.

To fill this gap, we propose here a two-scale computational finite-element (FE) model that describes the passive behaviour of the abdominal aorta. The macro-scale is located at the tissue level, and the micro-scale consists of RVEs in which a network of collagen fibres is embedded in a ground substance identified as the non-collagenous part of the tissue [43,46]. First, the healthy abdominal aorta is simulated as a three-layered cylindrical segment under in vivo loading conditions. The deformation of points at the abluminal side of the vessel is then applied to (microscopic) RVEs whose geometry is based on the collagen configuration of the healthy adventitia [39,43]. The resulting deformation fields in the RVEs are then interpreted as the homeostatic mechanical state experienced by vascular cells, particularly fibroblasts, in the healthy non-aneurysmal tissue.

Subsequently, models of the aneurysms are created with an idealized fusiform geometry [47], including the presence of an intraluminal thrombus (ILT), for different disease stages [40,43] and varying diameters. As in the previous case, the deformation from the abluminal side of each AAA is then applied to RVEs representing the microstructural configuration of the corresponding disease stage. The resulting deformation fields at the micro-scale are then compared with the healthy case and evaluated along AAA (stage) progression and diameter increase. The goal is to correlate changes in the micro-mechanical state of the tissue with possible mechanobiological cues that might drive G&R through vascular cells, with a focus on the formation of the neo-adventitia.

2. Methods

2.1. Macroscopic simulations

This section describes geometries, boundary conditions and constitutive models employed in the macroscopic simulations at the tissue scale. In such models, a distinction is made between an unknown stress-free reference configuration ${\mathit{\Omega }}_{\mathrm{ref}}$, a load-free but residually stressed configuration ${\mathit{\Omega }}_0$ which represents the ex vivo state of the vessel, and finally the loaded current configuration $\mathit{\Omega }$, which e.g. can be observed through medical imaging [48]. While inverse design analyses have been proposed to identify the reference configuration of the FE model [49,50], we instead chose a simplified approach combining experimental observations and simulations. All macroscopic analyses were performed with the commercial FE software Abaqus/Standard 2018 (Dassault Systèmes Simulia Corp, Providence, RI, USA) using the implicit static solver, custom Python scripts and a user material definition.

2.1.1. Healthy abdominal aorta

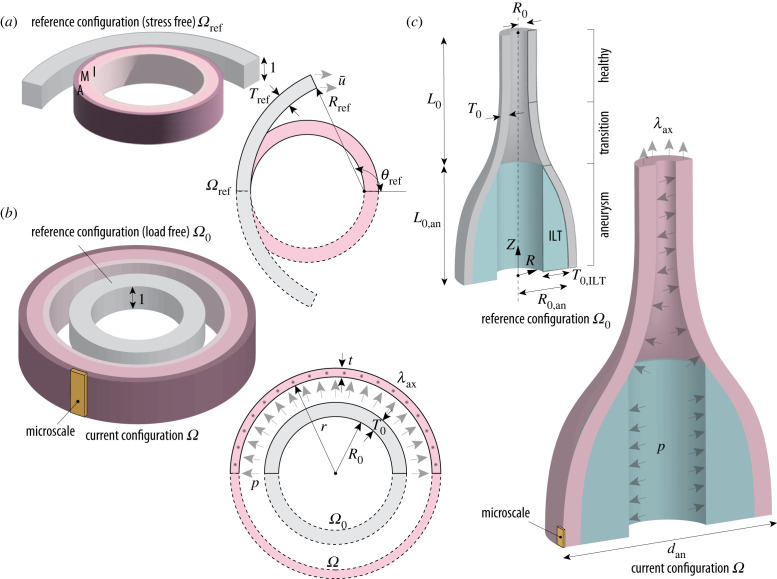
The healthy aorta in the load-free configuration ${\mathit{\Omega }}_0$ is modelled as a thick-walled cylindrical segment with inner radius R₀, thickness T₀ and unit length in the axial direction [51]. A three-layered structure including the intimal layer is adopted, which is thought to be representative of elderly individuals—who are more prone to developing AAA [3,4,42]—with non-atherosclerotic intimal thickening [52,53]. The intima, media and adventitia correspond, respectively, to 20%, 50% and 30% of the wall thickness [52]. Only a quarter of the aortic segment is simulated with appropriate boundary conditions to enforce symmetry. The geometry is meshed using linear hexahedral elements with a mixed stress-displacement formulation for material incompressibility and an appropriate mesh refinement in the wall thickness to resolve the layer-specific stress fields.

The configuration ${\mathit{\Omega }}_0$ is characterized by the presence of unknown residual stresses. Therefore, the finite-element simulations consist of two different stages. First, residual stresses are computed based on the concept of the opening angle, which can be measured ex vivo on excised rings of the aorta [52]. From a biomechanical perspective, the role of residual stresses is to reduce the stress gradient within each layer of the arterial wall in the physiologically loaded configuration. In the absence of consistent information on the opening angle for the layer properties of the aortic wall adopted in this work [39], we have identified an optimal value 2θ_ref that minimizes the intramural layer-specific stress gradients in the final deformed configuration [54]. In the unknown reference configuration, the healthy aortic wall is described as an open circular segment with an inner radius R_ref, thickness T_ref and unit length in the axial direction (figure 1a). Closing is simulated by specifying displacements on a free edge of the ring, so that the load-free radius R₀ corresponds to the measured ex vivo value [52]. The stress field obtained defines the initial residual state, i.e. a self-equilibrated stress state in the undeformed, load-free configuration ${\Omega }_0$ [55].

Figure 1.

(a) Sketch of closure simulation on a healthy aortic segment with referential inner radius R_ref, thickness T_ref and opening angle θ_ref using a displacement $\overline{u}$, to calculate residual stresses with the three-layered arrangement of intima, media and adventitia; (b) sketch of the main simulation on the residually stressed, healthy aortic segment with initial inner radius R₀ and thickness T₀, which deforms to a final radius r and thickness t due to the effect of axial stretch λ_ax and intraluminal pressure p; (c) sketch of the simulation on the model with the abdominal aneurysm consisting of three regions: the aneurysm sac, with initial length L_0,an and inner radius R_0,an, a transition zone (neck) and a healthy cylindrical part with inner radius R₀; the initial combined length of both is given by L₀ and the wall thickness T₀ is assumed to be constant. The model also contains an axisymmetric intraluminal thrombus (ILT) with initial thickness T_0,ILT at the luminal side of the aneurysm sac. The aneurysm is subject to the same axial stretch λ_ax and intraluminal pressure p as the healthy aorta, resulting in a deformed outer diameter d_an. In (b) and (c), the solid elements shown in yellow are representative regions whose final deformation state is passed to the RVE as input for the micro-scale simulations. Symmetry along the longitudinal axis of the aorta is always assumed.

In the second stage, in vivo loading is simulated by applying an axial stretch and an internal pressure with the load-free configuration ${\mathit{\Omega }}_0$ serving as a reference (figure 1b). The in vivo axial prestretch λ_ax contributes significantly to mechanical homeostasis as it allows the axial force in the artery to remain unchanged during the cardiac cycle [56]. Importantly, this value is generally larger than the in situ stretch λ_ax,0, which was determined experimentally from the length of excised aortic segments [57]. Therefore, an iterative procedure was adopted to identify the axial in vivo prestretch as the optimal stretch at which the reduced axial force [48] remains approximately constant, in the range of physiological pressures [54]. A summary of the quantities of interest employed in the FE simulations is provided in table 1.

Table 1.

Parameters employed in the FE element simulations of the healthy abdominal aorta.

geometry and loading
parameter	description	numerical value		refs.
Rref (mm)	radius of the open segment	8.05
Tref (mm)	thickness of the open segment	1.46
2θref (deg)	opening angle	100.0
R0 (mm)	radius of aortic wall ex vivo	5.61		[52]
T0 (mm)	thickness of aortic wall	1.46		[52]
λax,0 (−)	axial prestretch in situ	1.07		[58]
λax (−)	axial prestretch in vivo	1.184
p (mmHg)	internal pressure	120.0
material parameters
parameter	description	intima [39]	media [39]	adventitia [39]
μA (kPa)	shear modulus of matrix	6.88	30.52	3.77
k1 (kPa)	shear modulus of fibres	4.90	22.81	0.36
k2 (−)	exponential parameter of fibres	41.95	22.78	45.88
κip (−)	in-plane fibre dispersion	0.261	0.208	0.232
κop (−)	out-of-plane fibre dispersion	0.484	0.487	0.466
α (deg)	in-plane fibre mean anglea	3.25	6.91	77.53

^aWith respect to the circumferential direction.

2.1.2. Abdominal aortic aneurysm

The abdominal aneurysm is defined as an axisymmetric solid with a fusiform section in the axial-radial plane, described by

$$R(Z)=R_0+(R_{0,\mathrm{an}}-R_0-c_3\frac{Z^2}{R_0})\exp (-c_2\left|{\frac{Z}{R_0}}^{c_1}\right|),$$ 2.1

where R_0,an is the maximum radius of the aneurysm in the reference configuration, and c₁, c₂, c₃ are geometric coefficients [24].

The initial length of the aneurysm L_0,an=f₁ R_0,an depends on the maximum radius by a geometric parameter f₁ [24] while the thickness T₀ is here assumed to correspond to the healthy aorta. Although aneurysms can lead to a thickening of the aortic wall, other studies have found that a thrombus-covered wall can be significantly thinner [59]. Moreover, Niestrawska et al. [40] reported that the intima and media of some of their AAA samples appeared to have split open and therefore, despite collagen accumulation and formation of the neo-adventitia on the abluminal side of some specimens, there was no significant difference in thickness between different tissue stages.

The geometry extends in the axial direction for an additional length L₀ = L_0,an, which includes a portion of the healthy aortic wall and an intermediate transition zone (figure 1c). To the best of the authors’ knowledge, there is no clear characterization of such a region in the literature. However, it appears reasonable to define a zone corresponding to the geometrical change from the healthy to the aneurysmal wall and include also here a transition in terms of mechanical response, see §2.1.3 and appendix A.

The ILT is simplified as a hollow, axisymmetric solid adjacent to the luminal side of the aneurysm sac. The reference thickness T_0,ILT is computed from Tong et al. [60] where experimental observations revealed an empirical correlation between the maximum thickness of the thrombus and the maximum in vivo diameter of the aneurysm d_an. Both the wall and the ILT are each described by a single material layer. Only a quarter of the model is simulated with appropriate boundary conditions to enforce symmetry. The geometry is meshed using linear hexahedral elements with a mixed stress-displacement formulation for material incompressibility. Preliminary studies of mesh convergence have been performed.

In contrast to the simulations of the healthy aorta, the current configuration $\Omega$ of the aneurysm under physiological loading is considered to be known, in particular the in vivo maximum outer diameter d_an, which is used in clinical practice to assess the risk of rupture of AAAs [9]. The unknown reference configuration is determined by an inverse procedure that finds the optimal value of the initial radius R_0,an of the aneurysm such that the deformed external diameter corresponds to d_an. To illustrate the changes along the AAA growth, three values of d_an (45, 55 and 65 mm) were simulated. In order to estimate the influence of mechanical and microstructural alterations along AAA pathogenesis, two different disease stages—the early and the late [40,43]—were considered for each diameter (six simulations in total). Since no relationship between tissue stage and aneurysm size could be found [40], using the same diameters for different tissue stages was aimed at investigating the interplay between microstructural remodelling and AAA growth.

In vivo loading is simulated by applying axial stretch to the healthy portion of the aorta and internal pressure throughout the vessel (figure 1c). The in vivo axial prestretch λ_ax is taken from the previous simulation on the healthy wall, since no more detailed experimental characterization on AAAs is available. For the same reason, residual stresses in the circumferential direction of the aneurysm are neglected. A summary of the quantities of interest employed in the FE simulations can be found in table 2.

Table 2.

Parameters employed in the FE element simulations of abdominal aortic aneurysms.

geometry and loading
parameter	description	early AAA	late AAA	refs.
R0 (mm)	radius of healthy aortic wall	____________ 5.61 _____________		[52]
T0 (mm)	thickness of aortic wall	____________ 1.46 _____________		[52]
dan (mm)	maximum diameter of AAA in vivo	___________ 45-55-65 ___________
2R0,an (mm)	initial diameter of the AAA (for each dan)	36.4-45.0-53.6	39.7-49.0-56.6
f1 (−)	geometric parameter	_____________ 4.0 _____________
c1 (−)	geometric parameter	_____________ 0.5 _____________
λax (−)	axial prestretch in vivo	____________ 1.184 ____________
p (mmHg)	internal pressure	____________ 120.0 ____________
material parameters
parameter	description	early AAA [40]	late AAA [40]	ILT [45]
μA (kPa)	shear modulus of matrix	0.59	3.78	—
μI (kPa)	stress-like parameter for ILT	—	—	9.26
b (−)	non-dimensional parameter for ILT	—	—	1.62
k1 (kPa)	shear modulus of fibres	1.30	8.96
k2 (−)	exponential parameter of fibres	47.51	636.29
κip (−)	in-plane fibre dispersion	0.242	0.224
κop (−)	out-of-plane fibre dispersion	0.433	0.402
α (deg)	in-plane fibre anglea	6.55	22.90

^aWith respect to the local circumferential direction.

2.1.3. Constitutive models

The mechanical behaviour of both the healthy and aneurysmal aortic wall is described by the anisotropic strain-energy function ${\Psi }_A$ proposed by Holzapfel et al. [61] (the subscript A stands for anisotropic), which contains two families of fibres with non-symmetric fibre dispersion. Assuming incompressible behaviour, the strain-energy function reads

$$\begin{array}{r}{\Psi }_A=\frac{{\mu }_A}{2}(I_1-3)+\sum _{i=4,6}\{\frac{k_1}{2k_2}\exp [k_2{(I_i^{\star }-1)}^2]-1\}-p(J-1),\end{array}$$ 2.2

where μ_A > 0 and k₁ > 0 are stress-like material parameters, and k₂ > 0 is a dimensionless parameter. In equation (2.2), $I_1=\mathbf{C}\hspace{0.17em}:\hspace{0.17em}\mathbf{I}$ is the first invariant of the right Cauchy–Green tensor $\mathbf{C}$, where $\mathbf{I}$ is the second-order identity tensor, $J=\sqrt{det\mathbf{C}}>0$ is the volume ratio and p is a Lagrange multiplier that enforces material incompressibility. The invariant $I_i^{\star }$ with respect to the stretch of a single family of fibres is expressed by

$$\begin{array}{rl}& I_i^{\star }=\mathbf{C}\hspace{0.17em}:\hspace{0.17em}{\mathbf{H}}_{\mathit{i}},\mathrm{with}\hspace{0.17em}{\mathbf{H}}_{\mathit{i}}=A\mathbf{I}+B{\mathit{M}}_{\mathit{i}}\otimes {\mathit{M}}_{\mathit{i}}\\ & +(1-3A-B){\mathit{M}}_{\mathit{n}}\otimes {\mathit{M}}_{\mathit{n}},i=4,6,\end{array}$$ 2.3

where H_i is a second-order symmetric structure tensor, M_i with ‖M_i‖=1 represents the reference mean orientation of the ith fibre family, M_n is an out-of-plane unit vector, and A, B are coefficients related to the in-plane and out-of-plane dispersion of fibres κ_ip and κ_op [61].

The model described in (2.2) has been implemented as user material for the FE solver Abaqus/Standard, with an analytical derivation of the Cauchy stress tensor and of the spatial elasticity tensor. The material parameters adopted in the simulations of the three-layered healthy aorta can be found in table 1. Two sets of parameters were employed for the aneurysmatic tissue to account for the different stages of the disease [40,43], as shown in table 2.

The healthy portion of the wall in the geometry with the aneurysm was modelled as a single layer with homogenized mechanical behaviour, while in the intermediate region, we assumed a continuous transition from the behaviour of the homogenized healthy wall to the behaviour of the aneurysm. We performed this homogenization process directly on the stress–strain response of the tissue under equibiaxial tension (appendix A), not on the material properties, because of the nonlinear nature of (2.2).

Although a layered structure with an anisotropic luminal layer is observed in aged thrombi [45], for simplicity the ILT is modelled as a single layer of homogeneous material with isotropic properties. The layer-specific experimental data from biaxial tests reported in Tong et al. [45] were homogenized using the same procedure mentioned above and fitted with the exponential isotropic strain-energy function ${\Psi }_I$ proposed by Demiray [62] (the subscript I stands for isotropic)

$${\Psi }_I=\frac{{\mu }_I}{2}[\exp [b(I_1-3)]-1]-p(J-1),$$ 2.4

where μ_I > 0 is a stress-like material parameter and b > 0 is a non-dimensional parameter. The model described in (2.4) has been implemented as a hyperelastic user material for the FE solver Abaqus/Standard. The material parameters adopted in the simulations can be found in table 2.

2.2. Microscopic simulations

In this section, geometries, boundary conditions and constitutive models for the multi-scale simulations of arterial tissue at the cellular level are described. The methods presented here were previously employed by Dalbosco et al. [43]; therefore, only the main features of the multi-scale model are presented. The goal of these simulations is to shed light on possible micro-mechanical cues sensed by vascular cells, especially fibroblasts, since smooth muscle cells are largely absent in AAAs [40,63]. Such cells are responsible for collagen G&R during AAA pathogenesis and their activity is at least partially driven by mechanotransduction [64,65].

2.2.1. Geometry, mesh and boundary conditions

RVEs, which represent a tissue-level point (figure 2) and consist of two families of collagen fibres embedded in a ground substance of non-collagenous micro-constituents, were constructed for three different stages of AAA pathogenesis, namely:

• — the fibroblast-rich adventitia of a healthy aorta, whose collagen fibres are preferentially aligned in an axial direction [39,43] (figure 2a);
• — the abluminal side of an early AAA [40,43], in which there is a realignment of collagen fibres towards the circumferential direction (figure 2b);
• — the abluminal side of a late AAA [40,43], with a stiff neo-adventitia characterized by a highly isotropic distribution of collagen fibres in the circumferential-axial plane (figure 2c).

Figure 2.

The micro-scale model consists of representative volume elements (RVEs) of (a) the tunica adventitia of a healthy aorta and AAAs at (b) an early and (c) late microstructural stage. For each stage, five realizations of the microstructure were created and simulated according to the deformation gradients F of the macro-scale models with different diameters d_an. The heatmaps in (a–c), reproduced from [39,40], illustrate the characteristic arrangement of collagen fibres for each stage; the colours red and blue indicate high and low concentrations, respectively, of fibres aligned according to a specific in-plane angle between the circumferential (circ) and axial (axi) directions of the tissue for each radial (rad) layer between the luminal (LU) and the abluminal (AL) side of the vessel. (d) Since the two fibre families in the RVEs are represented as (red and blue) straight lines, the waviness of collagen in the real tissue is simulated by assigning a recruitment stretch ${\lambda }_r^i$ to each ith fibre by sampling a value P_s (ratio between the end-to-end distance L₀ and the arc length L_f of a wavy fibre) from a stage-specific beta distribution [43]; the probability density functions (PDFs) ρ_r for each stage can be seen in the graph.

Five RVEs for each stage were generated using a stochastic algorithm described in [43], which gradually adds collagen fibres (red and blue lines in figure 2a–c) to the ground substance (shown in pink in figure 2a–c) by sampling the direction of the fibre from a specific von Mises distribution, characterized by a mean fibre angle α, an in-plane dispersion parameter κ_ip and an out-of-plane dispersion parameter κ_op. For each of the three stages, values for these parameters were taken from the literature [39,40]; these are the same ones from our previous work [43] and in the macroscopic models (§2.1).

Each RVE measures 500 × 500 × 100 μm along the circumferential, axial and radial directions of the arterial tissue. This size was chosen to ensure a representative network of collagen fibres, accounting for volume fractions of 40% for the healthy adventitia and 60% for the aneurysmatic tissue, see [43] for more details. After each RVE was generated, the set of fibre directions was fitted to the von Mises distribution to obtain the effective values of α, κ_ip and κ_op for that particular RVE. In general, there is good agreement between the microstructural parameters reported in the literature for each of the three stages and the corresponding (effective) parameters for the three sets of five RVEs (table 3), suggesting that the fibre networks are sufficiently representative of each microstructure.

Table 3.

Experimental (target) and numerical (effective) parameters of the bivariate von Mises distributions for the three microstructural stages of the arterial tissue considered in the present study. Values are given as medians and interquartile ranges.

	healthy adventitia		early AAA		late AAA
	exp. [39]	num.	exp. [40]	num.	exp. [40]	num.
	(n=16)	(n=5)	(n=6)	(n=5)	(n=6)	(n=5)
α (deg)	77.53	77.35	6.55	7.59	0.00a	0.00
	[67.04–84.02]	[73.46–79.92]	[5.19–11.62]	[5.88–8.41]		[0.00–0.00]
κip (−)	0.232	0.217	0.242	0.236	0.500a	0.500
	[0.192–0.282]	[0.205–0.239]	[0.234–0.260]	[0.231–0.259]		[0.500–0.500]
κop (−)	0.466	0.468	0.433	0.432	0.402	0.401
	[0.459–0.479]	[0.465–0.471]	[0.425–0.441]	[0.432–0.435]	[0.379–0.421]	[0.400–0.403]

^aAssuming an isotropic in-plane fibre dispersion, κ_ip = 0.5 and the mean in-plane angle α becomes superfluous.

The ground substance of each RVE is meshed with second-order hexahedrons. The element size was defined as 12.5 μm after mesh convergence analyses [43]. The collagen fibres are meshed with second-order truss elements in such a way that each fibre element is fully contained in a particular hexahedron to which it is attached by a no-slip kinematic bond—the so-called embedded elements technique, see [43,46] for more details.

Since they represent a tissue-level point, RVEs are assumed to undergo incompressible biaxial deformation in the circumferential-axial plane, characterized by the deformation gradient $[[\mathbf{F}]]=\mathrm{diag}$(λ_circ, λ_axial, λ_rad), in which the principal stretches λ_circ, λ_axial and λ_rad are obtained from the tissue-level simulations (figure 2).

A volume-averaging multi-scale framework is used to simulate the biaxial deformation of the RVEs while ensuring energy consistency between the macro and micro-scales; details on this theory can be found elsewhere [66,67]. As suggested in [46], periodic displacement fluctuations are enforced at the boundary of the RVEs.

2.2.2. Constitutive models

The ground substance of the RVEs is modelled as a nearly incompressible neo-Hookean material whose strain-energy function ${\Psi }_g$ is given in the decoupled form

$${\Psi }_g(\overline{\mathbf{C}})=\frac{G_g}{2}({\overline{I}}_1-3)+\frac{K_g}{2}{(J-1)}^2,$$ 2.5

where $\overline{\mathbf{C}}=J^{-2/3}\mathbf{C}$ is the isochoric right Cauchy–Green tensor, with ${\overline{I}}_1=\overline{\mathbf{C}}\hspace{0.17em}:\hspace{0.17em}\mathbf{I}$ its first principal invariant, G_g is the shear modulus of the ground substance and K_g is a penalty (volumetric) parameter, which was chosen to be K_g = 100G_g to ensure nearly incompressible behaviour. The values of the shear modulus for each of the three tissue stages are summarized in table 4.

Table 4.

Constitutive parameters employed in the RVE simulations.

material parameters
parameter	description	healthy adventitia	early AAA	late AAA	refs.
Gg (kPa)	shear modulus of ground substance	3.77	0.59	3.78	[39,40]
$E_{\hspace{0.17em}f}^i$ (MPa)	collagen fibre stiffness (normal distribution)	54.3 ± 25.1 (mean ± s.d.)			[68]
a (−)	waviness parameters	4.84	4.00	3.29	[41,43]
b (−)	(beta distribution)	1.54	1.10	0.64

Since collagen fibres in the unloaded arterial tissue are wavy [41,69], a fact not taken into account in the geometry of the RVEs (figure 2a–c), each ith fibre is assigned a strain-energy function ${\Psi }_{\hspace{0.17em}{f}_i}$ of the form [43,46]

$${\Psi }_{{\mathrm{f}}_i}(\lambda )=\{\begin{array}{cc}0& \mathrm{if}\hspace{0.17em}0<\lambda <{\lambda }_r^i,\\ \frac{E_{\hspace{0.17em}f}^i}{2}{(\lambda -{\lambda }_r^i)}^2& \mathrm{if}\hspace{0.17em}\lambda \ge {\lambda }_r^i,\end{array}$$ 2.6

where $E_{\hspace{0.17em}f}^i$ is the fibre stiffness, λ is the stretch applied to the fibre and ${\lambda }_r^i$ is the recruitment stretch of the fibre. Therefore, it is assumed that fibres only bear load when they are recruited, i.e. when the stretch λ applied to the fibre is higher than ${\lambda }_r^i$. This simulates the well-known phenomenon of gradual fibre recruitment responsible for the characteristic nonlinear mechanical response of arterial tissue [33,70,71].

To account for variability of waviness and stiffness between the fibres, each ith fibre is assigned to different values of $E_{\hspace{0.17em}f}^i$ and ${\lambda }_r^i$. The former is taken from a normal distribution with a mean of 54.3 MPa and a standard deviation of 25.1 MPa (table 4), while the latter is taken from a beta distribution with the form

$${\rho }_r(P_s)=\frac{{P_s}^{a-1}{(1-P_s)}^{b-1}}{B(a,b)},$$ 2.7

where B(a, b) is the beta function and $P_s^i$ is a measure of the waviness of the ith fibre with respect to its recruitment stretch ${\lambda }_r^i=1/P_s^i$ (figure 2d). The parameters {a, b}, which are different for each tissue stage, are given in table 4. The beta distributions for each parameter set are shown in figure 2d, where it can be seen that fibres tend to be straighter ($P_s^i\to 1$) in diseased tissue as experimentally identified by Niestrawska et al. [41].

2.3. Statistical analyses

Simulation results were analysed at the macro- and micro-scales; regarding the latter, results were organized in groups of five RVEs according to the three tissue stages (healthy, early AAA and late AAA) and the maximum diameter of the aneurysms (45, 55 and 65 mm). Since normality of the data could not be assumed, the non-parametric Mann–Whitney U test was used to check for differences between groups.

3. Results and discussion

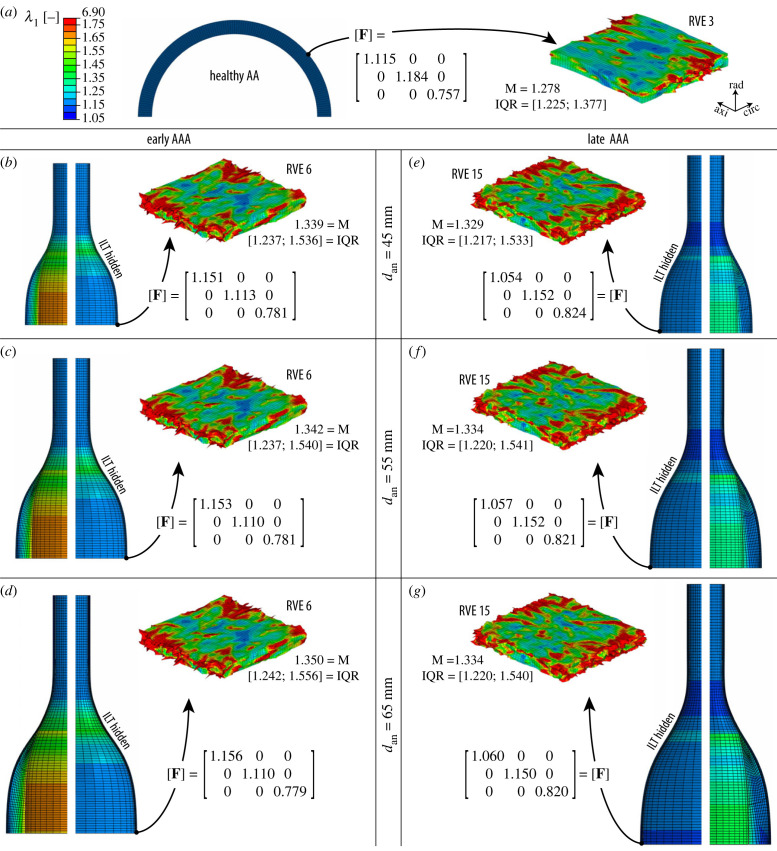
The results of the finite-element simulations are summarized in figure 3, where the field of maximum principal stretches λ₁ is plotted (a) for the healthy aorta and (b–g) for AAAs with a maximum (deformed) diameter ranging from 45 to 65 mm. For the latter, results are shown for each size for (b–d) AAAs at an early stage and (e–g) at a late stage, after formation of the neo-adventitia ([40,43], see also figure 2 and table 2).

Figure 3.

Maximum principal stretch λ₁ of the macro- and micro-scale models of (a) the healthy abdominal aorta (AA) and of AAAs with diameters ranging from 45 to 65 mm with (b–d) an early and (e–g) late microstructure. Half of the intraluminal thrombus (ILT) was hidden for each macro-scale model to better represent the stretches in the wall, and only one (of five) exemplary representative volume element (RVE), simulated according to the macro-deformation gradient F, is shown. M and IQR refer to the median and interquartile range, respectively, of the λ₁ values for each RVE. The colour scale applies to all models.

Macroscopic results show a fairly homogeneous deformation field in the healthy aorta (a), resulting in a hoop stress of about 100 kPa in the medial layer, which is widely accepted as the physiological stress value in a healthy abdominal aorta [72]. However, the AAA models (b–g) show important inhomogeneities in the deformation field due to the altered mechanical properties of the wall and its fusiform shape. In both early (b–d) and late (e–g) AAAs, the intraluminal thrombus, which is more compliant, deforms considerably more than the aortic wall. This could indicate a protective (mechanical) function of the thrombus, as previous works suggested [23,73], although other concurrent effects (e.g. inflammatory processes [74] or hypoxia of the aortic wall due to isolation from blood flow [75,76]) associated with the presence of an ILT are not captured by the present model.

Also in terms of the macro-models, the stretches in the aortic wall of early AAAs (b–d) are higher than their late counterparts (e–g), consistent with the observations in Niestrawska et al. [40], which reported a significant increase in the stiffness of the aortic tissue at a later stage. For early AAAs, stretches tend to be higher at the neck region of the wall, which has also been reported for real aneurysms [77]; on the other hand, the stretches in the late AAAs are lower in this region. In this context, it has to be taken into account that the mechanical properties in the transition zone (i.e. the neck) are actually not derived from experiments but are interpolated from the parameters of the healthy and diseased tissue, see §2.1.3 and appendix A. Moreover, the reference geometries for early and late AAAs are different in order to have the same deformed diameter, as discussed in §2.1.2. Both assumptions of the model might also influence these contrasting results in the neck region, which, however, is not the region of interest in the present study.

The field of maximum principal stretches λ₁ in the ground substance of exemplary RVEs is shown at the micro-scale for each of the seven cases of figure 3. Since the ground substance encompasses all non-collagenous micro-constituents of the tissue, including mechanosensitive vascular cells such as fibroblasts, the microscopic deformations are interpreted here as possible mechanotransduction cues [64,65] sensed by cells, see Dalbosco et al. [43] for a more detailed discussion on this particular choice. For the three exemplary RVEs shown in figure 3, important differences between the healthy (a) and diseased (b–g) states can be seen; on the other hand, these differences are much less pronounced in RVEs of early AAAs (b–d) and late AAAs (e–g) with the same diameter. Likewise, there are only negligible changes to the distribution of λ₁ with increasing diameter for each disease stage, at least qualitatively.

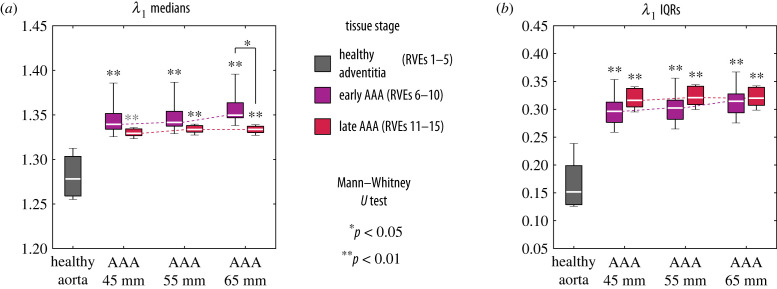
In order to quantitatively compare the seven cases from figure 3, the median (M) and interquartile range (IQR) of the maximum principal stretches λ₁ were calculated from all integration points of each individual RVE mesh. These quantities were then organized in groups of five RVEs according to the three tissue stages (healthy, early AAA and late AAA) and the maximum diameter of the aneurysms (45, 55 and 65 mm). Boxplots of M and IQR values grouped according to the three tissue stages (healthy, early AAA and late AAA) and the maximum diameter of the aneurysms (45, 55 and 65 mm) are presented in figure 4.

Figure 4.

Boxplots of (a) the median and (b) the interquartile range (IQR) values of the maximum principal stretch λ₁ grouped by the three microstructural stages of the tissue and, in case of AAAs, also by maximum diameter. Each of the seven groups contains the results of five representative volume elements (RVEs). For both quantities, the grey asterisks indicate the results of the Mann–Whitney U test for differences between each diseased group and the healthy group. When comparing the AAA stages, the same test showed a significant difference only for λ₁ medians of an AAA with a diameter of 65 mm (asterisk).

From figure 4, one can see that in general both the median (figure 4a) and the IQR (figure 4b) values of λ₁ are significantly higher in the diseased tissue compared with the healthy aorta, as indicated by the asterisks. This means that fibroblasts in AAAs would, on average, experience higher and more dispersed levels of deformation than the levels of deformation of the healthy adventitia, which could have mechanobiological implications. On the one hand, it is known from in vitro studies [65,78,79] that fibroblasts can sense their mechanical environment and respond accordingly—among other things, by promoting collagen G&R—when it deviates too far from healthy, homeostatic levels. In this respect, the differences predicted by the model between the micro-mechanics of healthy and diseased tissue could drive the changes in the collagen network in AAAs, as observed by Niestrawska et al. [40]. Importantly, this G&R process could be enhanced by the activation of fibroblasts to myofibroblasts (a cell phenotype often associated with pathological tissues), which is known to occur in response to altered mechanics at the cellular level [36,80,81].

On the other hand, it can be seen that for all aneurysm diameters that the median and IQR values of λ₁ for RVEs of early and late AAAs are remarkably similar, although the geometric and material properties of each disease stage, as well as the macroscopic deformation gradients applied to each of them (figure 3), are different. This motivates the hypothesis that both the macroscopic mechanics and the microstructure of the tissue—according to the mechano-pathogenic model of Niestrawska et al. [40]—change symbiotically in the course of the disease in order to keep the level of deformation in the micro-scale approximately constant. In this case, the fact that this level is above the healthy one could mean that cells in the tissue have reached a new homeostatic state [37]. Importantly, a previous study using the same micro-scale model [43] showed significantly different levels of λ₁ when the same macroscopic deformation gradient is applied to RVEs of early and late AAAs. Therefore, changes at both scales are required for the model to provide similar deformation fields at the micro-scale.

Finally, one can see that for RVEs of early AAAs the levels of λ₁ tend to be slightly higher with larger diameters, although this increase is not significant (Kruskal–Wallis test: p = 0.26 for the medians, figure 4a, and p = 0.44 for the IQRs, figure 4b). Nevertheless, this trend, which is mostly absent in RVEs of late AAAs, leads to a significantly higher level of deformation in RVEs of early AAAs compared with their late counterparts for aneurysms with 65 mm of diameter (figure 4a). Since this is not the case for smaller diameters (for which p > 0.05), it could mean that the microstructure of early AAAs is less effective in maintaining homeostasis at larger diameters than the late AAA microstructure with a thick abluminal neo-adventitia (figure 2c). This in turn could be a reason why the microstructure of the tissue continues to change from early to late as the aneurysm expands. It also underscores a hypothetical protective function of the neo-adventitia in late AAAs, as proposed in [43]—in this case, especially for larger aneurysmal diameters. In fact, clinical evidence linking faster AAA growth to an increased rupture risk [10] may indicate a failure of the tissue to adapt its microstructure to a rapidly changing geometry.

As a final remark to this section, it is emphasized that all seven models shown in figure 3 exhibit an important amplification effect from the macro to the micro-scale. For the healthy wall, e.g. the median value of the maximum principal stretch λ₁ of the exemplary RVE 3 shown in figure 3a is 80% higher than the value of λ₁ in the macroscopic model. In diseased tissue, this difference is even more pronounced. This contrast between kinematics at macro- and micro-scales (i.e. tissue and cell levels), which has been observed experimentally [82,83] for arterial tissue, could have important consequences for microscopic phenomena, e.g. cell mechanotransduction. Therefore, this should be taken into account if meaningful results on the micro-scale are to be obtained [84].

4. Limitations and outlook

Despite the important insights into the mechanobiology of AAA pathogenesis provided by the model, some limitations to the present work can be mentioned. In the macroscopic simulations, an idealized geometry was used to model different AAA diameters, which did not take into account possible changes in the overall shape of a real aneurysm during its growth. Likewise, the thrombus was simplified into a homogeneous axisymmetric solid with isotropic mechanical behaviour, while in real AAAs it usually has an asymmetric shape [8] and a three-layered structure with a certain degree of anisotropy [45]. In this context, applying the same modelling strategy to more complex, potentially patient-specific geometries of both the aneurysm and the thrombus could be the subject of future works. In particular, regional variations in curvature and wall thickness, which are common in real AAAs [21,23], could have a significant influence on the local deformation gradient. This in turn would also change the results at the micro-scale, which could be related to mechanobiological phenomena, e.g. the transition from fibroblasts to myofibroblasts [80,81]. Likewise, considering the external support of the perivascular tissues and spine [85,86] could help to improve the fidelity of macro-scale models.

Another limitation is that the mechanical behaviour in the transition zone between healthy and diseased tissue in AAAs had to be inferred from their respective material properties (appendix A) due to the lack of specific experimental data. It is hoped that future studies on the spatial variability of mechanical properties of AAA tissues will provide better inputs to FE models like the present one.

Despite the intricate microstructure of arterial tissue [32–34], both in health and disease, the RVEs employed in the present work were simplified to a network of collagen fibres embedded in a ground substance with all non-collagenous components of the tissue. While this is reasonable from a purely mechanical point of view (since collagen is much stiffer than the other micro-constituents), further refinements of the model could include e.g. proteoglycans and elastin [34,35] as separate phases. In particular, the inclusion of elastin as a separate phase in the RVEs would make it possible e.g. to investigate the consequences of elastin degradation (which is known to occur already in early stages of AAA formation [2,38,40]) on cell mechanobiology, which is also an interesting question for future studies.

Finally, it should be noted that in the present model, only the passive behaviour of the wall was modelled at both scales. In this context, the active behaviour of aortic tissue and chemo-mechanical phenomena, among others, could also have important implications for AAA pathogenesis and cell mechanotransduction. These concurring effects also represent an interesting field of study for future work.

5. Conclusion

In this study, a two-scale FE model of the aortic tissue in health and disease was presented. At the macro-scale (tissue level), the healthy aorta and AAAs of increasing size were modelled to simulate their passive mechanical behaviour in vivo. At the micro-scale (cell level), the deformation gradient obtained from the macro-models was used as input to simulate RVEs of the healthy and diseased tissues.

In the context of mechanobiology, the microscopic deformations observed in the RVEs were interpreted as possible mechanotransduction cues sensed by vascular cells. The results suggest that the formation of an aneurysm disrupts the healthy micro-mechanical state of the tissue and thus represents a possible reason for the collagen G&R by mechanosensing cells (e.g. fibroblasts) along the AAA development [40]. After the formation of the aneurysm, an attempt seems to be made to keep the level of the microscopic deformations approximately constant with increasing diameter by altering both the microstructure and the macroscopic mechanics of the tissue, which could mean that a new homeostatic state was reached [37], at least for the diameter range investigated here.

Finally, it is emphasized that these conclusions are inextricably linked to the many hypotheses put forward to construct the model. However, since, to the best of the authors’ knowledge, the micro-mechanical state of the aortic tissue simply cannot be visualized in vivo with current experimental techniques, the present numerical approach represents a valuable tool to improve our understanding of the multi-scale pathogenesis of AAAs.

Appendix A. Mechanical properties of the transition zone

The geometries used in the macroscopic AAA simulations (§2.1.2) consist of a healthy aortic cylinder and a diseased aneurysm sac. Since these two regions are microstructurally and mechanically different, it is reasonable to assume that there is a transition zone between them, which here was taken to coincide with the aneurysm neck (figure 1c).

To the best of the authors’ knowledge, the material properties of this hypothetical transition zone are not known from experiments. Therefore, they were derived from the equibiaxial response of the healthy and diseased parts, calculated from the parameters of table 1 and table 2, respectively, with the aim to model the transition zone as a mechanically graded material. Assuming a single material layer in such a zone, the mechanical parameters of the healthy wall were also averaged from the three different layers to obtain a consistent transition.

Considering an incompressible equibiaxial stretch λ in the circumferential-axial plane of the tissue, described by the deformation gradient $[[\mathbf{F}]]=\mathrm{diag}({\lambda }_{\mathrm{circ}},{\lambda }_{\mathrm{axial}},{\lambda }_{\mathrm{rad}})=\mathrm{diag}(\lambda ,\lambda ,1/{\lambda }^2)$, the second Piola–Kirchhoff stress tensor S was calculated from (2.2) as [61]

$$\mathbf{S}=2\frac{\mathrm{\partial }{\Psi }_A}{\mathrm{\partial }\mathbf{C}}-p{\mathbf{C}}^{-1}={\mu }_A\mathbf{I}+\sum _{i=4,6}2k_1(I_i^{\star }-1)\exp [k_2{(I_i^{\star }-1)}^2]{\mathbf{H}}_{\mathit{i}}-p{\mathbf{C}}^{\mathbf{-}\mathbf{1}},$$ A 1

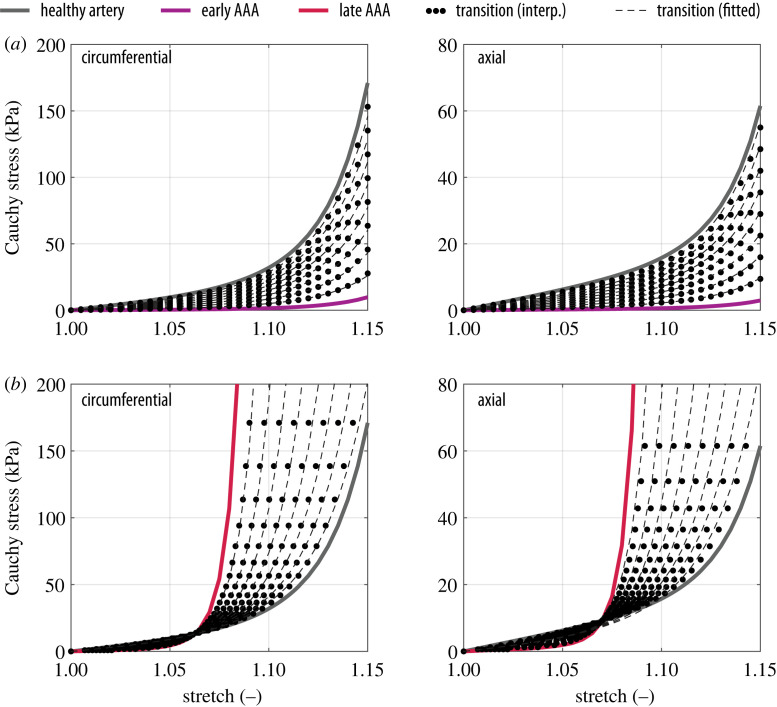
where p is the Lagrange multiplier that enforces the incompressibility condition calculated here from the plane stress condition (S₃₃=0). Finally, the Cauchy stress tensor was computed by a push-forward operation, i.e. σ=FSF^T. The resulting stress–stretch curves are shown in figure 5 for the healthy aorta (grey), early AAA (purple) and late AAA (red). A series of fictitious stress–stretch responses (dotted curves in figure 5) was then interpolated from the curves of healthy and diseased tissue. To get the constitutive parameters for each generated response, the structural parameters α, κ_ip and κ_op of the model (A1) were fixed to values between the healthy and diseased stages (table 5) and the mechanical parameters μ_A, k₁ and k₂ were then fitted to each generated response. The results are shown in figure 5 as dashed curves, where it can be seen that a good fit (R² ≥ 0.99) could be achieved for all interpolated responses. The parameters obtained in this way for each curve of figure 5 are presented in table 5.

Figure 5.

Fitted equibiaxial mechanical response of the transition zone; (a) early AAAs and (b) late AAAs.

Table 5.

Parameters of the interpolated curves shown in figure 5.

interpolated material parameters: healthy aorta → early AAA
parameter	numerical value
μA (kPa)	11.61	10.17	8.74	7.31	5.87	4.44	3.01	1.57
k1 (kPa)	18.80	16.62	14.44	12.27	10.09	7.92	5.74	3.58
k2 (−)	30.71	30.66	30.60	30.51	30.38	30.18	29.81	28.92
κip (−)	______________________________________ 0.240 _________________________________________
κop (−)	______________________________________ 0.460 _________________________________________
α (deg)	______________________________________ 15.0 _________________________________________
interpolated material parameters: healthy aorta → late AAA
parameter	numerical value
μA (kPa)	5.61	5.87	6.10	6.30	6.49	6.66	6.79	6.88
k1 (kPa)	40.24	38.06	35.24	31.65	27.17	21.77	15.56	9.02
k2 (−)	36.70	44.76	55.33	69.51	89.11	117.2	159.6	228.5
κip (−)	_______________________________________ 0.230 ________________________________________
κop (−)	______________________________________ 0.440 _______________________________________
α (deg)	_____________________________________ 23.5 _______________________________________

The method described above was implemented in Matlab (The MathWorks Inc., Natwick, USA) to generate any desired number of interpolated curves. Based on the finite-element mesh, each line of elements in the transition zone of macro-scale models is assigned a different set of parameters, considering equally spaced intervals along the longitudinal direction from healthy to diseased properties to ensure a smooth transition of deformation fields (figure 3) along the length of the AAA, as one would expect from a biological material.

Ethics

This work did not require ethical approval from a human subject or animal welfare committee.

Data accessibility

This article has no additional data.

Declaration of AI use

We have not used AI-assisted technologies in creating this article.

Authors' contributions

M.D.: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing—original draft, writing—review and editing; M.T.: conceptualization, investigation, software, validation, writing—review and editing; T.A.C.: investigation, software, writing—review and editing; E.A.F.: investigation, writing—review and editing; G.A.H.: conceptualization, funding acquisition, investigation, methodology, project administration, resources, supervision, validation, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

No funding has been received for this article.