Facilitating cooperation in human-agent hybrid populations through autonomous agents

Summary

Cooperative AI has shown its effectiveness in solving the conundrum of cooperation. Understanding how cooperation emerges in human-agent hybrid populations is a topic of significant interest, particularly in the realm of evolutionary game theory. In this article, we scrutinize how cooperative and defective Autonomous Agents (AAs) influence human cooperation in social dilemma games with a one-shot setting. Focusing on well-mixed populations, we find that cooperative AAs have a limited impact in the prisoner’s dilemma games but facilitate cooperation in the stag hunt games. Surprisingly, defective AAs can promote complete dominance of cooperation in the snowdrift games. As the proportion of AAs increases, both cooperative and defective AAs have the potential to cause human cooperation to disappear. We then extend our investigation to consider the pairwise comparison rule and complex networks, elucidating that imitation strength and population structure are critical for the emergence of human cooperation in human-agent hybrid populations.

Graphical abstract

Highlights

• •Modeling cooperative and defective autonomous agents in social dilemmas
• •In snowdrift/stag hunt games, a minority of autonomous agents drives full cooperation
• •More autonomous agents can disrupt cooperation
• •Autonomous agents at hub nodes wield influence

Statistical physics; Computer science; Artificial intelligence

Introduction

Cooperation, which serves as a fundamental social behavior,^1,2 plays a crucial role in ensuring human prosperity. It not only facilitates the resolution of individual conflicts, such as hunting and driving, but also mitigates burdensome catastrophes such as global climate change and disease transmission.^3,4 However, cooperation often struggles to survive in the face of competition with defection due to lower payoffs.⁵ Although mutual cooperation is beneficial to collective interests, individuals are frequently tempted to choose defection. The concept of social dilemma captures the inherent challenge in the evolution of cooperation, referring to a situation where an individual’s interests conflict with collective interests. Two-player social dilemma games such as prisoner’s dilemma (PD) game, stag hunt (SH) game, and snowdrift (SD) game, are employed ubiquitously, portraying the rational decision-making of two participants using a strategy set and payoff matrix.^6,7 This type of matrix game allows for equilibrium analysis and has been extensively utilized in research within the fields of social science, biology, and artificial intelligence (AI).^8,9

With the integration of AI into various aspects of human life, advancements in science and technology have allowed humans to delegate decision-making tasks to machines.^10,11,12 Although previous studies have suggested fascinating solutions to encourage cooperation in human-human interactions,^13,14 they do not address this problem within human-agent hybrid populations. Consequently, research on human-agent coordination has gained significant attention and encompasses diverse areas. One typical example is autonomous driving,¹⁵ where humans relinquish decision-making power to cars, thereby freeing themselves from the physical demands of driving and making travel easier and more enjoyable. However, most of these researches focus on situations where humans and agents share a common goal.^16,17 When conflicts of interest arise, it becomes crucial to investigate the evolution of human behavior in a human-agent hybrid environment.¹⁸ For instance, studying human-AI interaction within the general-sum environment and the trust-revenge game provides a comprehensive understanding of these domains.^19,20 As social interactions have become more hybrid,^16,21 involving humans and AAs, there lies an opportunity to gain new insights into how human cooperation is affected.^18,22 This work aims to examine the influence of AAs on human cooperative behavior when social dilemmas exist.

Understanding how human behavior changes in the presence of robots or AAs is a challenging but essential topic.^23,24 To accurately capture human cooperation toward agents, previous studies have predominantly concentrated on the development and design of algorithms for AAs.^18,25,26 These studies mainly focused on repeated games where human players (HPs) can make decisions based on historical information about AAs. A repeated game involves the repetition, either finite or infinite, of a base game, which is represented in the strategic form.²⁷ However, the impact of one-shot settings, where players lack prior experience and information about their counterparts, has been generally ignored with few exceptions.^28,29 In this article, we focus on how cooperative and defective AAs affect human cooperation in two-player social dilemma games, and we ask: Are cooperative AAs always beneficial to human cooperation? Do defective AAs consistently impede the evolution of human cooperation? How do population dynamics change in structured and unstructured populations when the ratio of human-human interaction to human-agent interaction varies?

To address the research questions mentioned above, we utilize an evolutionary game theoretic framework to study the conundrum of cooperation in social dilemma games with a one-shot setting. As shown in Figure 1, the typical games involve PD, SD, and SH games. Previous evidence has proved (or hypothesized) that human players update strategies according to payoff differences, with social learning being the most well-known modality.^30,31,32 Therefore, we examine the evolutionary dynamics of human cooperation by employing replicator dynamics (RD) and pairwise comparison.^32,33,34 The main difference between these two dynamics lies in the consideration of AAs. In the pairwise comparison rule, human players can adopt the strategies of AAs, whereas replicator dynamics do not incorporate such imitation.

Figure 1.

Schematic representation of the human-agent hybrid population

(A) The well-mixed population consists of human players and AAs interacting with each other. The frequencies of human-human and human-agent interactions depend on the composition of the population, specifically the ratio of AAs to human players. The red and blue solid circles respectively represent cooperators and defectors in the human players.

(B) The two-player two-strategy games in human-human and human-agent interactions. Mutual cooperation yields a reward $R$ to both players, while mutual defection results in a punishment $P$. Unilateral cooperation leads to a sucker’s payoff $S$, while the corresponding defector receives a temptation to defect $T$. By setting $R=1$ and $P=0$, there are four kinds of games, including prisoner’s dilemma game, snowdrift game, stag hunt game, and harmony game.

In the human-agent hybrid population, the fraction of cooperation among human players is denoted as ${\rho }_C$ (${0\le \rho }_C\le 1$). Assuming human players are one unit, add y units of AAs to the hybrid population. Specifically, AAs are programmed to choose cooperation with a fixed probability $\phi$ that remains constant over time. The summary of the notations is given in Table 1. Our findings indicate that in well-mixed populations with replicator dynamics, AAs have little impact on cooperation in games with a dominant strategy. Cooperative agents facilitate cooperation in the SH game but undermine cooperation in the SD game. Counterintuitively, seemingly harmful defective agents can support the dominance of cooperation in the SD game. Additionally, we conduct stability analysis and establish the conditions for the prevalence of cooperation. Our results demonstrate that even a minority of defective (or cooperative) AAs can significantly enhance human cooperation in SD (or SH) games. However, when cooperative (or defective) AAs constitute a majority, they may trigger the collapse of cooperation in SD (or SH) games. These findings are further corroborated by pairwise comparison rule when strong imitation strength is considered. In scenarios with weak imitation strength, cooperative AAs are more likely to stimulate human cooperation. In contrast to well-mixed populations, where players can interact with others with an equal probability, structured populations restrict interactions to locally connected neighbors. Such a difference in interactive environments is deemed a determinate factor influencing the emergence of cooperation.³⁵ To investigate this, we conduct experimental simulations on complex networks and observe that structured populations yield comparable results to well-mixed scenarios, except in the case of heterogeneous networks. This divergence can be attributed to the influential role of nodes with higher degrees. Our results, taken together, provide valuable insights into the impact of AAs on human cooperation.

Table 1.

Summary of notations

Notation	Meaning
$y$	The ratio of autonomous agents to human players
$\varnothing$	The cooperation probability of autonomous agents
${\rho }_C$	The frequency of human cooperation among human players
${\dot{\rho }}_C$	${\rho }_C$’s derivative with respect to time
$K$	The imitation strength of human player

Results

In this section, we mainly present the theoretical results of well-mixed populations in the PD, SD, and SH games by analyzing the replicator equations and pairwise comparison rule. The replicator equation is a differential equation, depicting the growth of a specific strategy based on the payoff difference ${\pi }_C-{\pi }_D$, where ${\pi }_C$ and ${\pi }_D$ mean the expected payoff of cooperation and defection, respectively. Pairwise comparison, guided by the Fermi rule, elucidates the process of strategy updating. Lastly, we introduce an extension to incorporate complex networks into the analysis.

Replicator dynamics

Prisoner’s dilemma game and harmony game

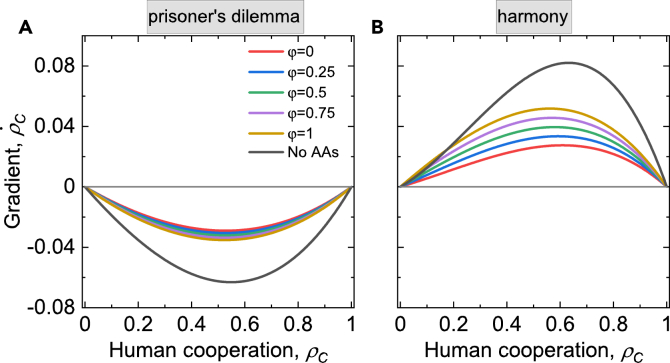
In the PD game, despite the presence of AAs, defection remains the dominant strategy, and the expected payoff for defection is either equal to or greater than that of cooperation, leading to ${\dot{\rho }}_C\le 0$. Therefore, evolutionary dynamics reach a full defection equilibrium state, and human cooperation diminishes irrespective of its initial frequency. This finding remains robust against any cooperation probability of AAs, as shown in Figure 2A. Although the equilibrium remains constant, the gradient is influenced by the values of y and $\phi$. In contrast, the expected payoff of cooperation is equal to or larger than defection (see Figure 2B) in the harmony game, leading to ${\dot{\rho }}_C\ge 0$. Thereby, the population evolves to a full cooperation equilibrium state. The results show that both cooperative and defective AAs have no effect on the convergent state in the games with a dominant strategy.

Figure 2.

Phase portrait of PD and harmony games

(A) In the PD game, additional AAs have no influence on the equilibrium. Regardless of whether cooperative or defective AAs are involved, the population inevitably evolves toward a state of complete defection due to the constant condition ${\dot{\rho }}_C\le 0$.

(B) In the harmony game, the introduction of additional AAs also has no effect on the equilibrium. Since ${\dot{\rho }}_C\ge 0$ consistently holds, the population evolves to a full cooperation state despite cooperative or defective AAs. The black line means the situation in the absence of AAs. The parameters are fixed as $y=0.95$, $S=-0.2$, $T=1.3$ for the PD game and $S=0.1$, $T=0.5$ for the harmony game.

Snowdrift game

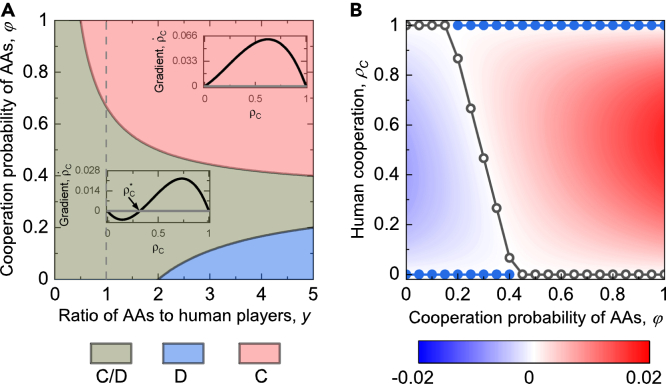
In the SD game, when AAs are absent, replicator dynamics have demonstrated that the interior equilibrium ${\hat{\rho }}_C=\frac{P-S}{R+P-T-S}$ is the unique asymptotically stable state, while the equilibria ${\rho }_C=0$ and ${\rho }_C=1$ are always unstable. However, the results will be different if we take AAs into consideration. We find that the population converges to a full cooperation equilibrium state regardless of the initial frequency of human cooperation, provided the condition $\frac{1+y\phi }{1+y}\le \frac{P-S}{R+P-T-S}$ is satisfied. Interestingly, to achieve a full cooperation equilibrium state with as few AAs as possible, the optimal approach is to introduce AAs with a cooperation probability of $\phi =0$. Correspondingly, the minimum value for y is $\frac{T-R}{S-P}$. On the other hand, when $\frac{\phi }{1+y}\ge \frac{P-S}{R+P-T-S}$ , the population converges to a full defection equilibrium state regardless of the initial frequency of human cooperation. Therefore, we reveal that defective AAs can actually stimulate human cooperation in the SD games.

We then present analytical results regarding how AAs affect the equilibrium by setting T = 1.2 and S = 0.5 in Figure 3. Panel A depicts the $\phi -y$ phase diagram, which consists of three parts: full C state, full D state, and coexistence state of C and D. We find that a minority of defective AAs (see the area with y < 1) can shift the equilibrium state from a coexistence state to a full cooperation equilibrium state, whereas a sufficiently large fraction of cooperative AAs drives the system to a full defection equilibrium state (blue color). To better understand how such an unexpected full defection state happens, we examine the frequency of human cooperation as a function of AAs’ cooperation probability $\phi$ at y = 4 in Figure 3B. We observe that with a fixed ratio of AAs to human players y, the lower the cooperation probability of AAs, the higher the level of human cooperation. In detail, the unique asymptotically stable state moves from full cooperation to the coexistence of C and D, and ultimately to complete defection with the increase of $\phi$.

Figure 3.

Equilibrium and phase diagram in the SD game

(A) A phase diagram of stable equilibrium state as a function of $(\phi ,y)$ pair. The blue, purple, and red areas mean the full C state, the coexistence state of C and D, and the full D state, respectively. The insets are phase portraits of human cooperation ${\rho }_C$. In the full C state, the gradient of ${\rho }_C$ is always not less than 0. In the region where cooperation and defection coexist, the gradient of ${\rho }_C$ is non-negative when ${\rho }_C<{\rho }_C^{\ast }$, and non-positive otherwise. The dashed line $y=1$ indicates an equal contribution of human players and AAs, each accounting for 0.5.

(B) The stable (solid circles) and unstable (open circles) equilibrium states as a function of $\phi$ with $y=4$. The background means the gradient of ${\rho }_C$, which reveals the evolutionary direction of this population. The change of stable equilibrium shows that compared with cooperative AAs, defective AAs are more beneficial to the evolution of cooperation. Other parameters are fixed as $S=0.5$ and $T=1.2$.

Stag hunt game

In the absence of AAs, replicator dynamics have revealed that the coexistence of C and D is an unstable equilibrium state, whereas the full cooperation and defection equilibrium states are both asymptotically stable. The equilibrium state that the population evolves in depends on the initial frequency of human cooperation. However, the full cooperation equilibrium state provides each player with a higher payoff compared to the full defection equilibrium state. Consequently, the question arises of how to steer the population toward a full cooperation equilibrium state that is independent of the initial frequency of human cooperation. This can be addressed by incorporating AAs, particularly cooperative AAs. In detail, when $\frac{y\phi }{1+y}\ge \frac{P-S}{R+P-T-S}$, the full cooperation equilibrium state becomes a unique asymptotically stable solution, implying that the population converges to full cooperation irrespective of initial frequency of human cooperation. In particular, to achieve full cooperation with as few AAs as possible, the best option is to introduce AAs with cooperation probability $\phi =1$. On the other hand, the population converges to full defection regardless of the initial frequency of human cooperation when $\frac{1+y\phi }{1+y}\le \frac{P-S}{R+P-T-S}$.

In Figure 4A, we present the phase diagram of analytical solutions. There exist three phases, including a full C state, a full D state, and a bistable state of C or D. The results demonstrate that the higher the cooperation probability of AAs, the lower the threshold for the proportion of AA required to achieve a full cooperation equilibrium state. Notably, when $y<1$, we showcase that even a minority of cooperative AAs can stimulate a full cooperation equilibrium state. On the other hand, AAs with a lower cooperation probability can result in the collapse of cooperation in a population containing a large fraction of AAs (see blue area). We then show how the equilibrium of the population varies as a function of $\phi$ by fixing $y=4$. In the monostable state, the equilibrium is insensitive to the initial frequency of human cooperation. However, in the bistable state, increasing $\phi$ decreases the unstable interior equilibrium and expands the area capable of reaching a full cooperation equilibrium state.

Figure 4.

Equilibrium and phase diagram in the SH game

(A) Phase diagram showing the stable equilibrium state as a function of the $(\phi ,y)$ pair. Introducing cooperative AAs in the population increases the likelihood of achieving a full cooperation equilibrium state, while introducing a large fraction of defective AAs may lead to cooperation collapse. The blue and red areas show the unique asymptotically stable states of full cooperation and full defection, respectively. The brown area indicates a bistable state that includes both full cooperation and full defection. The insets display phase portraits of ${\rho }_C$. The dashed line $y=1$ means that human players and AAs each account for 0.5.

(B) Stable (solid circles) and unstable (open circles) equilibrium states as a function of $\phi$ with a fixed $y=4$. The background illustrates the gradient of ${\rho }_C$. Cooperative AAs have a more positive impact on the evolution of cooperation compared to defective AAs. The parameters are fixed as $S=-0.2$ and $T=0.6$.

Overall, we find that a minority of defective (or cooperative) AAs can trigger a pronounced phase transition toward a full cooperation equilibrium state in the SD (or SH) games. In contrast, if AAs take a larger proportion, although a full cooperation equilibrium state is easy to reach, there is a risk of transitioning to a full defection equilibrium state. Given the recognition of social learning as a means of describing human strategy updating,³⁴ we further investigate the results by considering pairwise comparison rule, focusing on the situation where human players can not only imitate the strategy of human player but also AAs.

Pairwise comparison rule

In the pairwise comparison rule, we investigate the influence of AAs as well as the imitation strength K. Note that, $K\to +\infty$ and $K\to 0$ mean strong and weak imitation strength, respectively. The probability given by Fermi function is totally affected by the sign of payoff difference ${\pi }_C-{\pi }_D$ if $K\to +\infty$, or tends to 0.5 if $K\to 0$. To illustrate how human cooperation evolves under pairwise comparison rule, we present theoretical and agent-based simulation results in this section. A fascinating finding is that results are qualitatively consistent with replicator dynamics if we consider strong imitation strength in pairwise comparison. However, the results vary as the imitation strength weakens.

We utilize the same values of $T$ and $S$ as in the replicator dynamics section and present the results in Figure 5. Note that we here represent cooperative and defective AAs as $\phi =0.1$ and $\phi =0.9$, respectively. The details of the agent-based simulation process are given in the STAR Methods. In the PD game, human cooperation, either in $\phi =0.1$ or $\phi =0.9$ condition, is difficult to emerge under strong imitation strength (see Figure 5A). In detail, when $K=100$, human cooperation is insensitive to the strategy and fraction of AAs, which is consistent with replicator dynamics. However, when we reduce the imitation strength, the results change. Both AAs’ proportion and cooperation probability positively influence the evolution of human cooperation. In particular, cooperative AAs promote human cooperation more effectively than defective AAs. This effect becomes more significant with lower imitation strength (see $K=1$). In the SD game (see Figure 5B), human cooperation increases (or decreases) with AA’s proportion when $\phi =0.1$ (or $\phi =0.9$) under strong imitation strength. Defective AAs boost the evolution of human cooperation, consistent with the results obtained through RD. In particular, this effect is insensitive to the initial fraction of human cooperation, as shown in Figure S1 (electronic supplementary material). However, the results become totally contrary when imitation strength weakens (see $K=1$): cooperative AAs are more beneficial to human cooperation. In the SH game (see Figure 5C), there exists two kinds of state: a unique asymptotically stable state ${\rho }_{C1}^{\ast }$ (or ${\rho }_{C2}^{\ast }$) and a bistable state ${\rho }_{C1}^{\ast }$ and ${\rho }_{C2}^{\ast }$, where ${\rho }_{C1}^{\ast }$ means the coexistence of C and D with a higher frequency of cooperation and ${\rho }_{C2}^{\ast }$ means the coexistence of C and D with a lower frequency of cooperation. As shown in Figure S2 (electronic supplementary material), in a bistable state, which equilibrium the system evolves to is affected by the initial frequency of human cooperation. Furthermore, similar to the findings in the RD section, AAs with lower (or higher) cooperation probability $\phi =0.1$ (or $\phi =0.9$) are more feasible to cause the state ${\rho }_{C2}^{\ast }$ (or ${\rho }_{C1}^{\ast }$) as y increases under strong imitation strength. This finding is still robust when imitation strength becomes weak.

Figure 5.

Equilibrium in three types of social dilemma games under the pairwise comparison rule

Consistently to the findings in replicator dynamics, under strong imitation strength, (A) cooperative AAs have no significant influence on cooperation in the PD game.

(B) Cooperative AAs inhibit cooperation in the SD game.

(C) However, cooperative AAs stimulate cooperation in the SH game. In contrast, when imitation strength is weak, cooperative AAs promote cooperation in all three games. From left to right, each column shows the results for the PD ($S=-0.2$, $T=1.3$), SD ($S=0.5$, $T=1.2$), and SH ($S=-0.2$, $T=0.6$) games. The lines show theoretical results and the squares show the agent-based simulation results. The solid and dashed lines show stable and unstable equilibria, respectively. The top and bottom panels are obtained with $\phi =0.1$ and $\phi =0.9$, respectively.

Our findings demonstrate consistent results in both the replicator dynamics and pairwise comparison rule under strong imitation strength. However, if weak imitation strength is taken into account, cooperative AAs are more beneficial to the evolution of human cooperation in all three types of games. While our previous discussions primarily focused on well-mixed populations, exploring the outcomes within networks that incorporate local interactions is also pertinent.

Extension to complex networks

We present the average human cooperation frequency ${\rho }_C$ as a function of $\phi$ for square lattice, Barabasi Albert (BA) scale-free, and Erdos Renyi (ER) random network in Figure 6. In the PD game, cooperation is consistently promoted with increasing $\phi$, regardless of the network type. The results are qualitatively consistent with previous theoretical analyses. This finding is further verified in Figures S3 and S4 (electronic supplementary material). Turning our attention to SD games, we find that AAs inhibit cooperation compared to scenarios without AAs, regardless of the network type. In the square lattice, cooperation weakens further as $\phi$ increases. However, a contrasting phenomenon emerges when considering heterogeneous networks, such as ER random and BA scale-free networks. We infer that this discrepancy may be attributed to AAs occupying the hub nodes of the networks. To verify this inference, we conduct simulation experiments on a BA scale-free network under two scenarios (see Figure S5 in electronic supplementary material): (i) By assigning 4871 nodes (to maintain a similar number of AAs as in Figure 6) with the highest degrees as AAs, Figure S5 presents results similar to those in Figure 6B. (ii) By assigning 4871 nodes with the lowest degrees as AAs, we arrive at the conclusion that defective AAs effectively promote cooperation once again. This finding highlights the significant influence of AAs’ location on human cooperation. Next, in the SH game (see Figure 6C), AAs with higher cooperation probability are more beneficial for human cooperation compared to defective AAs. In particular, the increase in $\phi$ triggers tipping points in three types of networks. Given the significance of hub nodes, we conduct additional analysis by focusing on ten nodes in three different types of games, as shown in Figure 7. When AAs are assigned to nodes with the highest degrees, the strategy of AAs has a profound impact on human cooperation. Even a slight change in the behavior of AAs, especially in the PD games (see Figure 7A), can lead to a significant increase in overall human cooperation. Conversely, when these ten AAs are randomly allocated across the network, they have little influence on human behavior and exhibit limited utility in altering cooperation levels.

Figure 6.

The frequency of human cooperation as a function of $\mathit{\phi }$ in complex networks with $\mathit{y}=\mathbf{0.95}$

(A) Human cooperation is promoted by AAs in the PD game across all three networks. In particular, the higher the value of $\phi$, the higher the frequency of cooperation.

(B) Compared to the results without AAs, human cooperation is prohibited by AAs in the SD games regardless of network type. With the increase of $\phi$, human cooperation decreases (or increases) in the square lattice (or heterogeneous networks).

(C) Cooperative AAs are more conducive to the evolution of human cooperation. The circles show simulation results averaged over 60 iterations, and the shaded regions show the standard deviation. The dashed lines indicate the frequency of human cooperation in the absence of AA. The parameters are fixed as $S=-0.2$, $T=1.3$ in the PD game, $S=0.5$, $T=1.4$ in the SD game, and $S=-0.5$, $T=0.6$ in the SH game.

Figure 7.

The frequency of human cooperation as a function of $\mathit{\phi }$ in BA scale-free network with ten AAs

We examine two scenarios, one involves assigning AAs to the nodes with the largest degree (blue), while the other assigns AAs to randomly selected nodes (red). Panels (A–C) show the results of the PD, SD, and SH games, respectively. Human cooperation closely approximates the results without AAs when AAs are randomly assigned to nodes. However, if AAs are assigned to nodes with the largest degree, even with only 10 nodes, they can boost human cooperation effectively, particularly in the PD and SH games. The circles show agent-based simulation results averaged over 60 times, and the shaded regions show standard deviation. The parameter settings are the same as Figure 6.

Discussion

In this study, we investigate human cooperation in hybrid populations, involving interactions between human players and AAs. AAs, who are programmed to choose cooperation with a specific probability, are employed to answer our motivation questions. The human player is assumed to update strategy according to the payoff difference given by replicator dynamics and pairwise comparison rule. Theoretic analysis and experimental simulations mainly proceed following well-mixed population and network structures, respectively. Using replicator dynamics, we investigate the impact of AAs on the equilibrium of various social dilemma games, such as the PD, SH, and SD games. We showcase that cooperative AAs effectively promote human cooperation in the SH game, but their influence is limited in games with dominant strategies. Surprisingly, in the SD game, cooperative AAs can even disrupt cooperation. To achieve a full cooperation state with as few AAs as possible in the SH game, introducing AAs with fully cooperating probability is proved to be the most effective approach. Furthermore, our results also show that defective AAs are not useless, as they can stimulate cooperation in the SD games. Correspondingly, to achieve a cooperation-dominant state with as few AAs as possible, the best choice is to introduce AAs with always defection. These findings are further verified using pairwise comparison rule with strong imitation strength. On the other hand, if taking weak imitation strength (which includes irrational options of human players) into account, we demonstrate that cooperative AAs are beneficial for promoting human cooperation regardless of social dilemmas.

In an extended study, we implement experimental simulations involving three types of complex networks. By incorporating spatial structures into the interaction environment, we obtain qualitatively consistent results in the homogeneous network. The differences in heterogeneous networks are mainly due to the location of AAs. By controlling AAs’ location, we find that assigning AAs to hub nodes, even in a small proportion, can significantly affect evolutionary outcomes. Thus far, we have contributed a model for studying human cooperation in hybrid populations, showing that it is essential to consider environments related to social dilemmas, networks, and imitation strength when designing AAs. The insights gained from our results have practical implications for developing AI algorithms to foster human cooperation.

Our research distinguishes itself from previous studies mainly in several key aspects. Firstly, in addition to considering the committed minorities,^36,37 we incorporate a substantial number of autonomous agents into our model. These AAs cooperate with their counterparts with a certain probability. The inclusion of a substantial number of AAs is motivated by recent advancements in social network research,³⁸ which suggests that machine accounts make up approximately 32\% of all tweets based on empirical evidence from Twitter data. Moreover, there is an increasing trend in the number of machine accounts, posing significant challenges in terms of reducing their potential risks.³⁹ In the context of human-agent games, we validate that minority cooperative AAs stimulate cooperation, which aligns with existing literature.^40,41,42 However, our research reveals an unexpected result: the inclusion of a large number of AAs leads to a breakdown of the cooperative system, surpassing the effects observed with a mere minority of AAs, as demonstrated in the defective region depicted in the left panel of Figures 3 and 4. This discovery emphasizes the potential risks posed by the growing prevalence of AAs in relation to human cooperation.

Secondly, we introduce defective AAs, whose role in fostering cooperation in two-player social dilemma games has been largely overlooked in the context of human-agent interaction. Either replicator dynamics or pairwise comparison rule, we find that the inclusion of defective AAs can indeed trigger the dominance of cooperation in SD games, an effect that remains hidden when solely focusing on cooperative AAs. Furthermore, although several existing studies primarily use AAs to address fairness or collective risk problems,^28,29 they have not introduced AAs in structured populations.⁴³ These interactive environments have been recognized as important factors in the context of human-human interactions. By introducing structured populations, we reveal tipping points that are triggered by AAs in the SH games. Meanwhile, we investigate the effect of nodes with higher degrees on triggering human cooperation. These additional critical extensions provide a comprehensive understanding of the role of cooperative and defective AAs in the evolution of human cooperation. They offer a more realistic representation of interactive environments in human-agent interactions, shedding light on the complex dynamics at play in social systems.

There are still intriguing avenues for future exploration in this field. In human-human interactions, punishment has been proven to be a powerful behavior in eliciting cooperation.⁴⁴ It’s also essential to understand its utility in human-agent populations, particularly in solving second-order free-rider problems.⁴⁵ Even though theoretical analysis helps identify critical values, it neglects human players' emotional and social factors. Conducting experiments involving structured and unstructured populations to test these findings will open up exciting avenues for research in human-agent interaction.

Limitations of the study

The current study has some limitations that should be acknowledged. Firstly, it focuses solely on the simplest social dilemmas involving two decisions: cooperation and defection. While we have shown that artificial agents (AAs) with even simple intelligence can facilitate cooperation in social dilemmas where players have no prior information about counterparts, it remains uncertain how they would perform in more complex scenarios, such as stochastic games and sequential social dilemma games.^46,47 The interaction among players in these scenarios may be influenced by historical information or the state of the environment, which necessitates addressing these complex problems. Moreover, although simple algorithms may be effective in stimulating cooperation,⁴⁸ developing algorithms with more intelligence would further benefit the development of artificial intelligence, particularly for human-machine or human-robot interaction.²⁴

Furthermore, it is important to acknowledge that a purely theoretical study may overlook the complex motivations behind human behavior. Conducting human experiments is crucial for testing predictions from theoretical models and gaining insights into various aspects, including psychological effects, emotions, and cultural differences.^20,26 Mechanisms such as communication sentiment, reward, and punishment in human-human interactions have provided clear evidence of prosocial behavior.^49,50,51 Empirical experiments not only test theoretical possibilities but also reveal what actually occurs. As artificial agents increasingly integrate into human life, the study of human-agent cooperation from both theoretical and experimental perspectives becomes necessary. Building upon experimental findings of human-human interactions, we can construct a theoretical model of human-agent interaction and explore the influence of cooperative and defective artificial agents on human cooperation. Although our current work does not include human behavior experimental results, we believe that our theoretical work can serve as a valuable starting point for future human behavior experiments.

Several subsequent studies have examined the impact of the information level on human cooperation, specifically the extent to which human players know their opponents are artificial agents.²⁴ These studies have revealed that human cooperation is often higher when human players have no information about the true nature of their opponents.⁵² Conversely, even when participants recognize that artificial agents perform better than human players at inducing cooperation, human players tend to reduce their willingness to cooperate. However, Shirado and Christakis conducted human-agent interactions on network structures and presented contrasting results, showing that human cooperation can still be promoted even if the identity of the agents is transparent.⁴⁸ In social dilemma games with one-shot settings, the answer is still not deterministic. Our study did not account for the intrinsic properties of artificial agents and focused on a scenario without learning bias between humans and artificial agents. Therefore, it is crucial to consider the true nature of agents, particularly in one-shot settings, to expand our understanding of their behavior and implications.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
T together with R, S, and P for social dilemma games	Macy et al.53	https://doi.org/10.1073/pnas.09208009
y together with $\varnothing$ for autonomous agents	Cardillo and Masuda36	https://doi.org/10.1103/PhysRevResearch.2.023305
Software and algorithms
Dev C++	Bloodshed	https://www.bloodshed.net/
OriginLab	OriginLab Corporation	https://www.originlab.com/

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Zhen Wang (zhenwang0@gmail.com).

Materials availability

No materials were newly generated for this paper.

Experimental model and subject details

Our study does not use typical experimental models in the life sciences.

Method details

Social dilemma games

Two-player social dilemma game, a typical subclass of social dilemma, depicts the rational decision-making of two participants by introducing a strategy set and payoff matrix. In the simplest version, each player selects a strategy from a strategy set $\mathcal{S}=\{C,D\}$, where C and D represent cooperation and defection, respectively. Mutual cooperation yields a reward $R$ to both players, while mutual defection results in a punishment $P$. Unilateral cooperation leads to a sucker’s payoff $S$, while the corresponding defection receives a temptation to defect $T$. The above process can be represented by a payoff matrix:

$$\mathcal{A}=\left(\begin{array}{cc}R& S\\ T& P\end{array}\right)\text{.}$$ (Equation 1)

Using this payoff matrix, the so-called social dilemma is meeting if it follows these four conditions simultaneously:⁵³

• (i)$R>P$. Players prefer to cooperate with each other than to defect from each other.
• (ii)$R>S$. Mutual cooperation is preferred over unilateral cooperation.
• (iii)$2R>T+S$. Mutual cooperation is more beneficial for the collective than defecting against a cooperator.
• (iv)Either $T>R$ (greed) or $P>S$ (fear). The former condition means players prefer exploiting a cooperator to cooperating with him. The latter condition means players prefer mutual defection over being exploited by a defector.

According to the ranking order of these parameters, these two-player social dilemma games can be classified into four different kinds of games,⁷ which are PD games ($T>R>P>S$), SD games ($T>R>S>P$), SH games ($R>T>P>S$), and harmony (HG) game ($R>T,S>P$). It is noteworthy that the first three games exhibit social dilemmas,^47,53 while the harmony game does not. Without a specific declaration, we set $R=1$ and $P=0$ throughout this paper.

Population setup and autonomous agents

We consider a well-mixed and infinitely large population $\mathcal{P}=\{\mathrm{1,2},\cdots ,N\}$, where $N\to +\infty$, and each player can interact with each other with equal probability. In the population, player $i\in \mathcal{P}$ can choose one of two strategies from set $\mathcal{S}=\{C,D\}$. We denote the strategy of player $i$ as a vector ${\mathcal{X}}_i={(x_1,x_2)}^{\prime }$, where $x_j=1$ if the $j$ th strategy is chosen and the other element is equal to 0. To investigate how AAs affect the cooperative behavior among human players, we consider a hybrid population consisting of human players and AAs (see Figure 1A). Human players participate in the game and update their strategies through a social learning process. AAs, on the other hand, follow a pre-designed algorithm to make their choices: they cooperate with a fixed probability $\phi (0\le \phi \le 1)$ and defect with probability $1-\phi$. We refer to them as cooperative AAs if $0.5\le \phi \le 1$, and defective AAs if $0\le \phi <0.5$. In the human-agent hybrid population, each player has an equal chance to engage in a two-player game with other players (see Figure 1B). Consequently, the interaction probability between humans and AAs significantly depends on the composition of this population.

Hybrid population game

In the hybrid population, the fraction of cooperation among human players is denoted as ${\rho }_C$ (${0\le \rho }_C\le 1)$. Assuming human players are one unit, add $y$ units of AAs to the hybrid population. Consequently, the fraction of human cooperation is denoted by $f_C=\frac{{\rho }_C}{1+y}$. The parameter $y$ can also be used to quantify the composition of the population: if $0<y<1$, it implies that the fraction of AAs is lower than that of human players; whereas $y>1$ indicates a higher proportion of AAs. Accordingly, the expected payoff of cooperation and defection among human players in a hybrid population can be calculated as follows:

$${\pi }_C=\frac{1}{1+y}\left({\rho }_{C}R+\left(1-{\rho }_C\right)S\right)+\frac{y}{1+y}\left(\phi R+\left(1-\phi \right)S\right)\text{,}$$

$${\pi }_D=\frac{1}{1+y}\left({\rho }_{C}T+\left(1-{\rho }_C\right)P\right)+\frac{y}{1+y}\left(\phi T+\left(1-\phi \right)P\right)\text{,}$$ (Equation 2)

where the first term on the right-hand represents the payoff from interacting with human players, and the second term signifies the payoff obtained from interacting with AAs.

Replicator dynamics

The replicator equation³³ is a widely used differential equation that depicts evolutionary dynamics in infinitely large populations. Following this rule, the growth of a specific strategy is proportional to the payoff difference. Therefore, the dynamics of human cooperation can be represented by the following differential equation:

$${\dot{\rho }}_C=\left(1+y\right){\dot{f}}_C$$

$$=\left(1+y\right)\frac{{\rho }_C}{1+y}\frac{{1-\rho }_C}{1+y}\left({\pi }_C-{\pi }_D\right)$$

$$=\frac{{{\rho }_C(1-\rho }_C)}{1+y}\left({\pi }_C-{\pi }_D\right)\text{,}$$ (Equation 3)

where

$${\pi }_C-{\pi }_D=\frac{{\rho }_C+y\phi }{1+y}\left(R-T-S+P\right)+S-P\text{.}$$ (Equation 4)

By solving ${\dot{\rho }}_C=0$, we find that there exists two trivial equilibrium ${\rho }_C=0$ and ${\rho }_C=1$, and a third equilibrium ${\rho }_C^{\ast }$ that is closely associated with game models and AAs. By solving ${\pi }_C-{\pi }_D=0$, one can derive:

$${\rho }_C^{\ast }=\frac{P-S}{R+P-T-S}+y\left(\frac{P-S}{R+P-T-S}-\phi \right)$$

$$={\hat{\rho }}_C+y\left({\hat{\rho }}_C-\phi \right)\text{,}$$ (Equation 5)

where ${\hat{\rho }}_C=\frac{P-S}{R+P-T-S}$. It is easy to deduce that the restriction $T>R>S>P$ or $R>T>P>S$ guarantees $0<{\hat{\rho }}_C<1$. Moreover, ${\rho }_C^{\ast }$ increases with $y$ if ${\hat{\rho }}_C-\phi >0$, whereas decreases with $y$ if ${\hat{\rho }}_C-\phi <0$. Since ${\rho }_C^{\ast }$ measures cooperation rate in human players, this equilibrium will vanish if ${\rho }_C^{\ast }<0$ or ${\rho }_C^{\ast }>1\text{.}$ Note that ${\hat{\rho }}_C$ is also the interior equilibrium when the population consists only of human players,⁵⁴ i.e., the scenario $y=0$. Subsequently, the stability of the equilibrium will be discussed from three types of social dilemmas. As evidence has revealed that human players may update their behaviors through social learning,³⁴ one may ask: what results can be obtained when considering pairwise comparison rule? Under this rule, we can also examine the effect of imitation strength on the outcomes.

Pairwise comparison rule

Pairwise comparison is a well-known cultural process that effectively portrays game dynamics. Note that we employ the Fermi rule during the strategy updating stage.⁵ In this process, strategy updating takes place within a randomly chosen pair of players, denoted as $i$ and $j$, with strategy $\mathcal{X}$ and $\mathcal{Y}$ ($\mathcal{X}$, $\mathcal{Y}\in \mathcal{S}$). If $\mathcal{X}\ne \mathcal{Y}$, player $i$ takes $j$ as a reference and imitates its strategy with a probability determined by the Fermi function,

$$W_{\mathcal{X}\leftarrow \mathcal{Y}}=\frac{1}{1+e^{-K({\pi }_{\mathcal{Y}}-{\pi }_{\mathcal{X}})}}\text{,}$$ (Equation 6)

where $K$ represents selection intensity (which is also known as imitation strength) and measures the irrational degree of human players (or the extent players make decisions by payoff comparisons).^5,30 In the hybrid population defined, the probability of a cooperator taking a defector as an indicator is given by:

$$P_1=\frac{{\rho }_C(1-{\rho }_C+y(1-\phi ))}{1+y}\text{.}$$

Subsequently, the probability that cooperators decrease by one is

$$Q^{-}=P_1{W}_{C\leftarrow D}=\frac{{\rho }_C(1-{\rho }_C+y(1-\phi ))}{1+y}\frac{1}{1+e^{-K({\pi }_D-{\pi }_C)}}\text{.}$$ (Equation 7)

Similarly, the probability that a defector taking a cooperator as an indicator is

$$P_2=\frac{({\rho }_C+y\phi )(1-{\rho }_C)}{1+y}\text{.}$$

Consequently, the probability that cooperators increase by one is

$$Q^{+}=P_2{W}_{D\leftarrow C}=\frac{({\rho }_C+y\phi )(1-{\rho }_C)}{1+y}\frac{1}{1+e^{-K({\pi }_C-{\pi }_D)}}\text{.}$$ (Equation 8)

In total, the dynamics of cooperation can be represented as follows:

$${\dot{\rho }}_C=Q^{+}-Q^{-}=\frac{\left({\rho }_C-{\rho }_C^2+y\phi -{\rho }_{C}y\phi \right)e^{K\left({\pi }_C-{\pi }_D\right)}}{\left(1+y\right)\left(1+e^{K\left({\pi }_C-{\pi }_D\right)}\right)}-\frac{{\rho }_C-{\rho }_C^2+{\rho }_{C}y-{\rho }_{C}y\phi }{\left(1+y\right)\left(1+e^{K\left({\pi }_C-{\pi }_D\right)}\right)}\text{.}$$ (Equation 9)

We can derive the equilibrium by solving ${\dot{\rho }}_C=0$. Since the denominator is larger than 0 evidently, the equilibrium is mainly determined by the numerator. We then denote the numerator as ${f(\rho }_C)$ and examine the condition:

$$f\left(0\right)=y\phi e^{K\left(\frac{y\phi }{1+y}\left(R-T-S+P\right)+S-P\right)}\text{,}$$

$$f\left(1\right)=y\phi -y\text{.}$$ (Equation 10)

In the presence of AAs, $f\left(0\right)\ge 0$ and $f\left(1\right)\le 0$ are established. The equality holds when $\phi =0$ and $\phi =1$, respectively. Therefore, there exists at least one interior equilibrium when $0<\phi <1$. Note that $\phi =1$ is the so-called zealous cooperator.³⁶ In addition to analytical results, we verify our findings through agent-based simulations. The simulation procedure includes the following steps: (i) Initially, each human player is assigned either cooperation with probability $p$ or defection with a probability $1-p$ initially, where $p$ controls the initial frequency of cooperation. Each AA adopts cooperation and defection with probability $\phi$ and $1-\phi$ in each round. (ii) With a specific strategy, a randomly chosen player (presumed to be human), denoted as $i$, obtains an expected payoff by interacting with other $N-1$ individuals. (iii) Individual $i$ decides whether to imitate the strategy of a randomly chosen individual $j$, who obtains a payoff in the same way, according to the Fermi function. Repeat (ii) and (iii) until the population reaches an asymptotically stable state. We get the simulation results by setting $N=1000$.

Simulation for complex networks

Building upon the aforementioned results, we further study the network structure effect on human-agent cooperation in this section. Since interaction, in reality, is not limited to well-mixed populations, we also implement experiments in complex networks that contain local interactions. This means that players can only interact with a limited set of neighboring individuals. To assess the effect of network structure on cooperation, we employ pairwise imitation as a strategy updating rule and measure the expected cooperation rate among human players. Following this, players are matched in pairs and imitate their opponent's strategy based on a probability determined by their payoff difference.³⁵ We begin by introducing three types of complex networks.

Network settings

Denote $\mathcal{G}=\{\mathcal{V},\mathcal{E}\}$ as a complex network, where $\mathcal{V}=\left\{\mathrm{1,2},\cdots N\right\}$ represents node set, and $\mathcal{E}\subset \mathcal{V}\times \mathcal{V}$ is link set. Each node $i\in \mathcal{V}$ represents either a human player or an AA. For the edge $(i,j)\in \mathcal{E}$, each player $i$ is paired up with another player $j$ to play a two-player social dilemma game. We consider a network with $N=10000$ players and an average degree of 4$<k>=$.

• •Square lattice is a homogeneous network. Each player interacts with their four neighbors and receives a payoff by playing with its north, south, east, and west neighbors. It is noteworthy that here we consider lattice with periodic boundary.
• •Barabasi Albert scale-free network is generated following the growth and preferential attach rules.⁵⁵ The degree distribution of the ultimate network satisfies a power-law function.
• •Erdos Renyi random network is generated by linking two different nodes with a random probability.⁵⁶ The degree distribution of the ultimate network satisfies the Poisson distribution.

Agent-based model

Agent-based simulation

We utilized the Monte Carlo simulation to examine the variation of cooperation across different networks. Initially, each human player is assigned either cooperation or defection with a probability of 0.5, whereas each AA adopts cooperation and defection with probability $\phi$ and $1-\phi$, respectively. With the specific strategy, a randomly chosen player (assumed to be human), denoted as $i$, obtains the payoff by interacting with connected neighbors

$$F_i=\sum _{y\in {\mathrm{\Omega }}_i}{\mathcal{X}}_i^{\prime }\mathcal{A}{\mathcal{X}}_j\text{,}$$ (Equation 11)

where ${\mathrm{\Omega }}_i$ represents neighbor set of player $i$, $\mathcal{A}$ is the payoff matrix given by Figure 1B. After calculating the cumulative payoff, player $i$ decides whether to adopt one of his/her neighbors' strategies with the probability given by the Fermi function

$$W_{{\mathcal{X}}_i\leftarrow {\mathcal{X}}_j}=\frac{1}{1+e^{-K(F_j-F_i)}}\text{,}$$ (Equation 12)

where $j$ is a randomly chosen neighbor. We set $K=10$ in the simulations. Results are calculated by conducting 60 realizations. For each realization, we fix the total step as 50000, and each value is averaged over 5000 steps when the network reaches an asymptotic state.

Quantification and statistical analysis

Our study does not use typical statistical analysis.

Published: October 12, 2023

Data and code availability

• •The data that support the results of this study are available from the corresponding authors upon request.
• •The code used to generate the figures is available from the corresponding authors upon request.
• •All other items: any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.