Deciphering the ‘gut–brain axis’ through microbiome diversity

Abstract

Incentivised by breakthroughs and data generated by the high-throughput sequencing technology, this paper proposes a distance-based framework to fulfil the emerging needs in elucidating insights from the high-dimensional microbiome data in psychiatric studies. By shifting focus from traditional methods that focus on the observations from each subject to the between-subject attributes that aggregate two or more subjects’ entire feature vectors, the described approach revolutionises the conventional prescription for high-dimensional observations via microbiome diversity. To this end, we enrich the classical generalised linear models to articulate the multivariable regression relationship between distance-based variables. We also discuss a robust and computationally feasible semiparametric inference technique. Benefitting from the latest advances in the semiparametric efficiency theory for such attributes, the proposed estimators enjoy robustness and good asymptotic properties that guarantee sensitivity in detecting signals between clinical outcomes and microbiome diversity. It offers a readily implementable and easily interpretable solution for deciphering the gut–brain axis in mental health research.

Introduction

The human microbiome is the totality of the microbes (microbiota), their genetic elements (metagenome) and the interactions they have with surrounding environments throughout the human body.¹ In contrast to the human genome, the human microbiome is highly variable, displays substantial intra-individual variation at different body sites (gut, skin, lung, vagina, oral cavity, etc), inter-individual variation at the same body sites and intra-individual variation at different times in longitudinal studies.²

The human microbiome plays a key role in human disease and health. A preponderance of human microbiome studies have implicated the human microbiome in the pathogenesis of many human diseases, such as obesity, diabetes, alcoholic liver disease, vaginosis and even cancers.^{1 3} The genotypic effect on the microbiome may explain the missing link between genetics and disease since a disease-susceptibility genotype may affect the disease outcome through the alteration of the microbiome composition.^{4 5} Therefore, identifying potential factors that influence the microbiome composition and discovering their relationship with biological or clinical outcomes help demystify the inherent disease mechanism and enable the possibility of modulating the microbiome composition for therapeutic purposes.

Fuelled by the technological advancement of next-generation sequencing, the human microbiome can be interrogated using high-throughput sequencing. One strategy amplifies and sequences the bacterial 16S ribosomal RNA from the samples. We then cluster the similar sequences into operational taxonomic units (OTUs). By comparing OTUs with reference databases, we identify existing species in the samples and also obtain the OTU abundance profiles. The OTU abundance profiles refer to a matrix with the (i, j)-th element referring to the number of sequence reads that represent the j-th OTU (or species, roughly speaking) in the i-th subject. This count matrix forms the foundation for statistical analyses.⁶ The notable features of OTU abundances are high-dimensional (p>>n) and skewed counts with a preponderance of zeros. One line of research aims to advance statistical tools to directly tackle such data features to find individual OTU culprits for certain diseases of interest.^{7 8} Another emerging paradigm, however, shifts gears to study the impact of the overall microbiome composition represented as diversity metrics, such as alpha-diversity and beta-diversity,⁶ which we introduce and focus on in this paper.

Microbiome diversity metrics

Alpha-diversity

Alpha-diversity is a subject-level metric summarising OTU abundance into a scalar value for each person. Consider a sample of $n$ subjects and a vector ${\mathbf{y}}_i={\left(y_{i1,}{y}_{i2,}...,y_{ip}\right)}^{\mathrm{T}}$ denoting the counts of the $p$ OTUs for subject $i$ . Alpha-diversity for subject $i$ is:

$${\displaystyle {\displaystyle S_i^{\left(m\right)}={\left(\sum _{j=1}^p‍p_{ij}^m\right)}^{\frac{1}{1-m}},p_{ij}=\frac{y_{ij}}{\sum _{j^{\prime }=1}^p‍y_{i{j}^{\prime }}}}}$$ (1)

where $m$ is the order controlling the weight allocation among taxa. Varying $m$ permits different alpha diversities. For example, $m=0$ yields the observed species index ${\displaystyle S_i^{\left(0\right)}=\sum _{j=1}^p‍I\left(p_{ij}>0\right)}$ that counts the total number of species present, hence weighing more on the rare taxa and indexes the richness of microbe in total.⁹ On the other hand, $m=2$ leads to the Simpson index ${\displaystyle S_i^{\left(2\right)}=1/\sum _{j=1}^p‍p_{ij}^2}$ that assigns more weight towards abundant taxa, hence indicating species evenness.⁹ When $m=1,$ (1) is undefined but the resulting limit is the Shannon index, ${\displaystyle S_i^{\left(1\right)}=-\sum _{j=1}^p‍p_{ij}\mathrm{l}\mathrm{o}\mathrm{g}\left(p_{ij}\right)}$ .

Beta-diversity

Unlike the OTU abundance or alpha-diversity that describes features within each subject, beta-diversity is a between-subject attribute⁶ indexing the dissimilarity between any two individuals or a pair. Essentially, beta-diversity compares the feature differences between any pair $\mathbf{i}=\left(i_1,i_2\right)\in C_2^n$ using a dissimilarity or distance metric, denoted as $d_{\mathbf{i}}=d\left({\mathbf{y}}_{i_1},{\mathbf{y}}_{i_2}\right)$ , where $d\left(\cdot \right)$ : ${\displaystyle {\mathbb{R}}^p\times {\mathbb{R}}^p\to \mathbb{R}}$ is a mapping from the high-dimensional OTUs to a scalar value for that pair. Different choices of $d\left(\cdot \right)$ lead to distinct versions of beta-diversity, with the commonly used ones including Aitchison, Bray-Curtis, Jaccard, Unifrac, and so on. For example, the Aitchison beta-diversity¹⁰ is defined as:

$${\displaystyle \begin{array}{ll}{\displaystyle d_A\left({\mathbf{y}}_{i_1},{\mathbf{y}}_{i_2}\right)=}& {\left[\sum _{k=1}^p‍{\left\{\mathrm{l}\mathrm{o}\mathrm{g}\frac{y_{i_{1}k}}{g\left({\mathbf{y}}_{i_1}\right)}-\mathrm{l}\mathrm{o}\mathrm{g}\frac{y_{i_{2}k}}{g\left({\mathbf{y}}_{i_2}\right)}\right\}}^2\right]}^{1/2},\\ & g\left({\mathbf{y}}_i\right)={\left(\prod _{k=1}^p‍y_{ik}\right)}^{1/p}\end{array}}$$ (2)

By integrating information from high-dimensional features, beta-diversity represents a totality measure of dissimilarity between two subjects across all the OTUs, which constitutes a biologically relevant indicator of human health¹¹ and merits interest. It is non-negative, with $0$ (bigger values) indicating the same (very different) taxonomic abundances. Also, its dimension does not change with the number of taxonomic units $p,$ hence can be viewed as a dimension reduction.

Statistical methods

The research community is primarily interested in using statistical methods to link various diversity metrics introduced above to clinical variables, such as disease status.

Alpha-diversity

The alpha-diversity is composed of data from one subject; therefore, most standard statistical methods are readily applicable for the analysis of alpha-diversity. For example, popular tools for associating a phenotype with alpha-diversity include the Kruskal-Wallis H (or Mann-Whitney U) test¹² for categorical variables and the Spearman’s correlation for continuous phenotype variables. When controlling for covariates (eg, demographics) is needed in more complex settings, the robust regression framework is often suggested to ensure valid inferences given the non-normality nature of alpha-diversity. For a study with size $n$ , let $Y_i$ denote a response, and $X_i$ an explanatory variable for the $i$ -th subject. The semiparametric GLM characterising the within-subject relationship between $Y_i$ and $X_i$ is:

$${\displaystyle E\left(Y_i|X_i\right)=h\left(X_i;\mathit{\beta }\right),1\le i\le n}$$ (3)

where $h\left(\cdot \right)$ is the inverse of some link functions. Compared with the classical parametric GLM, (3) is more flexible. It removes the distributional assumption on $Y_i$ , thus yielding valid inference even when the data deviate from such an assumption. Hence, it is especially suited for modelling the alpha-diversity by specifying $Y_i=S_i^{\left(m\right)}$ in (1). It is worth noting that the same method can be used if alpha-diversity is the predictor.

Beta-diversity

Given a main factor ${\mathbf{X}}_i$ with $K$ levels for the group membership, let ${\mu }_k=E\left[d_{\mathbf{i}}I({\mathbf{X}}_{\mathbf{i}}=\left\{k,k\right\}\right]$ and ${\sigma }_k^2=Var\left[d_{\mathbf{i}}I({\mathbf{X}}_{\mathbf{i}}=\left\{k,k\right\}\right]$ denote the mean and variance of $d_{\mathbf{i}}$ for the $k$ -th group. We can formalise the scientific question into a hypothesis to test the mean beta-diversity distance across the $K$ groups:

$$\begin{gathered} {\displaystyle H_0:{\mu }_k=\mu \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}1\le k\le K\mathrm{v}.\mathrm{s}. \\ {H}_{\mathrm{A}}:{\mu }_j\ne {\mu }_k\mathrm{f}\mathrm{o}\mathrm{r}1\le j\ne k\le K} \end{gathered}$$ (4)

However, unlike the case with alpha-diversity, the $d_{\mathbf{i}}$ involves the OTU abundances from a pair, so it introduces rather complex correlation structures that are difficult, if not impossible, to model using parametric form.

Permutational Multivariate Analysis of Variance Using Distance Matrices

One solution is the distance-based Permutational Multivariate Analysis of Variance Using Distance Matrices (PERMANOVA).¹³ It defines a pseudo-F statistic as:

$${\displaystyle pseudo-F=\frac{tr\left(\mathbf{H}\mathbf{G}\mathbf{H}\right)/\left(p-1\right)}{tr\left[\left(\mathbf{I}-\mathbf{H}\right)\mathbf{G}\left(\mathbf{I}-\mathbf{H}\right)\right]/{\left(n-p\right)}^{\prime }}}$$

where $tr(.)$ is the trace of a matrix, $\mathbf{H}=\mathbf{X}({\mathbf{X}}^{\mathrm{\top }}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathrm{\top }}$ is the hat matrix of the design matrix $\mathbf{X},$ and $\mathbf{G}$ is the Gower’s centred matrix obtained from $\mathbf{D}.$ Due to the complexity of beta-diversity (usually non-Euclidean) distance, the limit of this pseudo- $F$ is unlikely to follow the $F$ -distribution, and the non-parametric permutation is thus adopted for p values.

Although routinely being used, some concerns have been raised regarding PERMANOVA. First, it does not provide any coefficient estimators for explanatory variables, which hinders generating interpretable results on the direction or size of the effects or discerning the sources of differences. Second, it only describes relationships between beta-diversity (a between-subject attribute) and a within-subject main categorical factor, not with their between-subject counterpart or any other types of variables, such as a continuous variable. Third, it requires a large number of permutations for stable results, and thus carries more overhead in terms of the computational burden. Last but not least, it is difficult to extend PERMANOVA to longitudinal studies (especially with missing data) to discover valuable scientific insights from dynamic and highly personalised microbiome data.

To resolve those limitations, recently, a more flexible alternative has been proposed.⁶ Granted by its distance-based regression setup, this approach permits elucidating the association between the beta-diversity $d_{\mathbf{i}}$ and a categorical variable (eg, group difference) or even more general variable types, such as perceived stress, a continuous instrument in mental health research.¹⁴

Distance-based regression

Modelling the between-subject attributes

To enlarge the semiparametric GLM framework for beta-diversity, consider a column vector of multivariate response and an explanatory variable $({\mathbf{Y}}_i^{\mathrm{\top }},{\mathbf{X}}_i^{\mathrm{\top }})$ for the $i$ -th subject, where ${\displaystyle {\mathbf{Y}}_i\left({\mathbf{X}}_i\right)\in {\mathbb{R}}^h\left({\mathbb{R}}^m\right)}$ , and where $h,m\ge 1$ . By concatenating ${\mathbf{Y}}_i$ into a (scalar) functional response from two subjects with some scalar-valued function, such as the beta-diversity $d_{\mathbf{i}}=f\left({\mathbf{Y}}_{i_1},{\mathbf{Y}}_{i_2}\right)$ in (2), we can model $d_{\mathbf{i}}$ as a function of ${\displaystyle {\mathbf{X}}_{\mathbf{i}}={\left({\mathbf{X}}_{i_1}^{\mathrm{\top }},{\mathbf{X}}_{i_2}^{\mathrm{\top }}\right)}^{\mathrm{\top }}}$ :

$${\displaystyle E\left(d_{\mathbf{i}}|{\mathbf{X}}_{\mathbf{i}}\right)=h\left({\mathbf{X}}_{\mathbf{i}};\mathit{\beta }\right),\mathbf{i}=\left(i_1,i_2\right)\in C_2^n}$$ (5)

where $h\left(\cdot \right)$ is some smooth function (eg, with continuous derivatives up to the second order), and $\mathit{\beta }$ is a vector of parameters. Akin to (3), (5) remains semiparametric by imposing minimum distributional assumption on $d_{\mathbf{i}}$ . This introduces greater flexibility in practice.

The distance-based regression introduced above is a special case of a class of semiparametric functional response models (FRM).⁶ Equation (5) achieves effective dimension-reduction (with the mapping $d_{\mathbf{i}}$ ) and is well-suited for data entailing the intrinsic between-subject nature, that is, outcomes that are composed of pairs of subjects. With this setup, we can formalise the scientific question by regressing $d_{\mathbf{i}}$ on the explanatory variables to test their associations, adjusting for covariates.

To illustrate, consider a categorical variable $X_i$ (such as the group membership) with $K$ levels. We transform $X_i$ into a between-subject attribute by defining a set of pairwise indicators (or dummy variables) for ${\displaystyle X_{\mathbf{i}}=\left\{X_{i_1},X_{i_2}\right\}}$ through the one-hot encoding function $\delta \left(\cdot \right):\{1,...,K\}\times \{1,...,K\}\mapsto \{\mathrm{0,1}{\}}^{K+C_2^K}:$

$${\displaystyle {\delta }_{k_1{k}_2}\left(X_{\mathbf{i}}\right)=\{\begin{array}{ll}1,& \mathrm{i}\mathrm{f}{X}_{\mathbf{i}}=\left\{X_{i_1},X_{i_2}\right\}=\left\{k_1,k_2\right\}\\ 0,& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}}$$ (6)

$${\displaystyle \begin{array}{ll}\mathit{\delta }\left(X_{\mathbf{i}}\right)=& {\left({\delta }_{11}\left(X_{\mathbf{i}}\right),\dots ,{\delta }_{\left(K-1\right)K}\left(X_{\mathbf{i}}\right),{\delta }_{KK}\left(X_{\mathbf{i}}\right)\right)}^{\mathrm{\top }},\\ & 1\le k_1\le k_2\le K\end{array}}$$

where ${\delta }_{k_1{k}_2}\left(X_{\mathbf{i}}\right)$ indicates the pair with the same $k$ -th concordant ( $k_1=k_2=k$ ) or discordant ( $k_1\S amp;lt;k_2$ ) levels for $X_{\mathbf{i}}$ . For example, if $X_i$ is a binary indicator of disease, we use $\mathit{\delta }\left(X_{\mathbf{i}}\right)={\left({\delta }_{DD}\left(X_{\mathbf{i}}\right),{\delta }_{HH}\left(X_{\mathbf{i}}\right),{\delta }_{HD}\left(X_{\mathbf{i}}\right)\right)}^{\mathrm{\top }}$ to index the respective diseased-diseased, healthy-healthy and healthy-diseased pairs. With $d_{\mathbf{i}}=f\left({\mathbf{Y}}_{i_1},{\mathbf{Y}}_{i_2}\right)$ the beta-diversity for the $\mathbf{i}$ -th pair, we can model its conditional mean among subgroups with (5):

$${\displaystyle E\left(d_{\mathbf{i}}|{\mathbf{X}}_{\mathbf{i}}\right)=\mathrm{e}\mathrm{x}\mathrm{p}\left[{\mathit{\beta }}^{\mathrm{\top }}\mathit{\delta }\left(X_{\mathbf{i}}\right)\right],\mathit{\beta }={\left({\tau }_{11},\dots ,{\tau }_{KK}\right)}^{\mathrm{\top }}}$$ (7)

here $\mathrm{e}\mathrm{x}\mathrm{p}\left(\cdot \right)$ is adopted since the response beta-diversity is non-negative.

The coefficients $\mathit{\beta }$ reveal the heterogeneity in $d_{\mathbf{i}}$ among different subgroups. Constructing tests among subgroups also helps disentangle different types of heterogeneity. These insights, in terms of effect sizes and directions, are of considerable interest to researchers but are difficult to achieve for PERMANOVA. Additional strengths of FRM include the computational scalability over permutation-based mainstream for such data, as well as the ease of including covariates in (7), either between-subject or within-subject.⁶

A more generalised variation can be specified in this distance-based regression. For example, by switching the response and explanatory variable, we can define the ‘difference indices’ $f_{\mathbf{i}}^y$ $=y_{i_1}-y_{i_2}$ for some clinical outcomes (such as body mass index difference) and model their relationship with beta-diversity (as a predictor):

$${\displaystyle E\left(f_{\mathbf{i}}^y|d_{\mathbf{i}}\right)=\beta d_{\mathbf{i}},\mathbf{i}=\left(i_1,i_2\right)\in C_2^n}$$ (8)

One glitch is that while $d_{\mathbf{i}}$ is non-negative, $f_{\mathbf{i}}^y$ here can be positive or negative. This can be readily fixed by setting $d_{\mathbf{i}}$ to ${\displaystyle d_{\mathbf{i}}sign\left(\mathbf{i}\right)}$ , where $sign\left(\mathbf{i}\right)$ denotes the sign function with $sign\left(\mathbf{i}\right)=1$ if $i_1-i_2\S amp;gt;0,$ $sign\left(\mathbf{i}\right)=-1$ if ${\displaystyle i_1-i_2<0}$ and $sign\left(\mathbf{i}\right)=0$ otherwise. For brevity, we continue to denote $d_{\mathbf{i}}$ $sign\left(\mathbf{i}\right)$ by $d_{\mathbf{i}}$ in what follows.

Now for (8), $\left|\beta \right|$ represents the differential response $f_{\mathbf{i}}^y$ per unit difference in the beta-diversity $d_{\mathbf{i}}$ for the $\mathbf{i}$ -th pair. This generalisation is especially useful when interest lies in evaluating the role of alpha-diversity and beta-diversity metrics together on a clinical outcome (see section ‘Real data analysis’). Furthermore, (8) even permits multivariate clinical outcomes ${\displaystyle Y_iϵ{\mathbb{R}}^m}$ , where some domain-specific distance can be prespecified as $f_{\mathbf{i}}^y=d({\mathbf{Y}}_{i_1},{\mathbf{Y}}_{i_2})$ .

Statistical inference and hypothesis testing

As the response function in (5) or (8) involves pairs of subjects, inferences about $\mathit{\beta }$ must tackle their interlocking dependencies. A class of U-statistics-based GEE (UGEE) has been proposed accordingly¹⁵ for this. Let

$$\begin{gathered} {\displaystyle S_{\mathbf{i}}\left(\mathit{\beta }\right)=f_{\mathbf{i}}^y-h_{\mathbf{i}}\left(\mathit{\beta }\right),{\mathbf{D}}_{\mathbf{i}}=\frac{\mathrm{\partial }}{\mathrm{\partial }\mathit{\beta }}{h}_{\mathbf{i}}\left(\mathit{\beta }\right), \\ {V}_{\mathbf{i}}=Var\left(f_{\mathbf{i}}^y|{\mathbf{x}}_{\mathbf{i}}\right),\mathbf{i}=\left(i_1,i_2\right)\in C_2^n,} \end{gathered}$$ (9)

In practice, $V_{\mathbf{i}}$ is unknown and substituted by a working variance such as $V_{\mathbf{i}}\left(h_{\mathbf{i}}\right)={\tau }^2{h}_{\mathbf{i}}$ , with ${\tau }^2$ as an unknown constant. Thus, the UGEE takes a familiar form

$${\displaystyle {\displaystyle {\mathbf{U}}_n\left(\mathit{\beta }\right)=\sum _{\mathbf{i}\in C_2^n}‍{\mathbf{U}}_{n,\mathbf{i}}\left(\mathit{\beta }\right)=\sum _{\mathbf{i}\in C_2^n}‍{\mathbf{D}}_{\mathbf{i}}{V}_{\mathbf{i}}^{-1}{S}_{\mathbf{i}}\left(\mathit{\beta }\right)=0,}}$$ (10)

where the estimates ${\displaystyle \hat{\mathit{\beta }}}$ are obtained through the Newton-Raphson method.

The theory of U-statistics guarantees that ${\displaystyle \hat{\mathit{\beta }}}$ by solving for (10) is consistent and asymptotically normal (CAN) under mild regularity conditions:

$${\displaystyle \sqrt{n}\left(\hat{\beta }-\beta \right){\to }_{d}N\left(0,{\mathbf{\Sigma }}_{\mathit{\beta }}\right)}$$ (11)

where ${\to }_d$ denotes convergence in distribution and a consistent ‘sandwich’ variance estimator of ${\displaystyle {\mathbf{\Sigma }}_{\mathit{\beta }}={\mathit{B}}^{-1}{\mathbf{\Sigma }}_U{\mathit{B}}^{-1},\mathit{B}=\mathit{E}\left({\mathbf{D}}_{\mathbf{i}}{V}_{\mathbf{i}}{\mathbf{D}}_{\mathbf{i}}^{\mathit{T}}\right)}$ and ${\displaystyle {\mathbf{\Sigma }}_U=4Var\left(E\left({\mathbf{U}}_{n,\mathbf{i}}|{\mathbf{y}}_{{\mathbf{i}}_1},{\mathbf{x}}_{{\mathbf{i}}_1}\right)\right)}$ , which can be obtained by substituting consistent estimates of $\mathit{\beta }$ and moments of the respective quantities.

This can be readily applied to testing any linear hypotheses concerning $\mathit{\beta }$ through the linear contrast $H_0:\mathbf{C}\mathit{\beta }=0$ vs $H_a:\mathbf{C}\mathit{\beta }\ne 0$ , where $\mathbf{C}$ is a matrix of known constants with rank $s$ . Under the null, the Wald statistic has an asymptotic ${\chi }^2$ distribution:

$${\displaystyle W_n=n{\left(\mathbf{C}\hat{\mathit{\beta }}\right)}^{\mathrm{\top }}{\left(\mathbf{C}{\hat{\mathrm{\Sigma }}}_{\mathit{\beta }}{\mathbf{C}}^{\mathrm{\top }}\right)}^{-1}\left(\mathbf{C}\hat{\mathit{\beta }}\right){\to }_d{\chi }_s^2}$$ (12)

where ${\chi }_s^2$ denotes a (central) ${\chi }^2$ distribution with $s$ df. A score test can also be constructed if needed.⁶

More importantly, ${\displaystyle \hat{\beta }}$ is also semiparametrically efficient whose asymptotic variance ${\mathbf{\Sigma }}_{\mathit{\beta }}$ is the smallest among all models satisfying the same moment restriction in (7) or (8), which can lead to reduced sample size requirements for clinical studies in detecting a given effect size.¹⁶ Altogether, this semiparametric inference technique ensures both robustness and sensitivity to help facilitate data-driven scientific findings.

Real data analysis

Recent studies suggest that the gut microbiome plays a major role in the development and functioning of the central nervous system via the microbiome–gut–brain axis.¹⁷ Although numerous pieces of evidence have implicated strong relationships among psychosocial factors, few have investigated their relationship with the gut microbiome. A recent study¹⁸ fills this gap by collecting both self-reported psychosocial measurements and faecal samples from 184 community-dwelling adults (aged 28–97 years). Participants completed the validated measures, including physical and mental health 36-Item Short Form Survey (SF-36), resilience, optimism, loneliness, wisdom, compassion and social support. DNA extraction and 16S rRNA amplicon sequencing were completed using the Earth Microbiome Project standard protocols. The feature dimension of the microbiome taxonomic units was quite high (m = 12 131).

The original paper¹⁸ focuses primarily on the predicting role of Faith’s phylogenetic alpha-diversity on the psychosocial variables, using a robust regression model. The study revealed that lower levels of loneliness and higher levels of wisdom, compassion, social support and social engagement were all associated with greater alpha-diversity of the gut microbiome, and age plays an important moderating role. Partial least squares (PLS) analysis was first applied to all the collected psychosocial variables to summarise them into PLS components of the negative impact of loneliness on gut health. The results supported the previous findings and related literature on the negative impact of loneliness on gut health.¹⁹ These encouraging findings motivated us to further investigate the role of microbiome beta-diversity on psychosocial outcomes, intending to uncover different aspects from the between-subject attributes. Below, we present the results of applying the distance-based model to elucidate the impact of beta-diversity on perceived stress and positive states (traits). For illustration, we did not correct for multiple comparisons.

Perceived stress as a continuous response

Perceived stress was assessed by the standardised instruments of the Perceived Stress Scale (PSS)¹⁴; it can be viewed as continuous with larger values indicating higher levels of perceived stress. The distance-based model in (8) with predictors of beta-diversity $d_{\mathbf{i}}^x$ , alpha-diversity difference $d_{\mathbf{i}}^{z1}$ , age difference $d_{\mathbf{i}}^{z2}$ and the one-hot encoded gender $\mathit{\delta }\left({\mathbf{w}}_{\mathbf{i}}\right)$ can be specified as ${\displaystyle E\left(f_{\mathbf{i}}^y|d_{\mathbf{i}}^x,d_{\mathbf{i}}^{z1},d_{\mathbf{i}}^{z2},{\mathbf{w}}_{\mathbf{i}};\mathit{\beta }\right)={\beta }_x{d}_{\mathbf{i}}^x+{\beta }_{z1}{d}_{\mathbf{i}}^{z1}+{\beta }_{z2}{d}_{\mathbf{i}}^{z2}+{\beta }_w{\delta }_{12}\left({\mathbf{w}}_{\mathbf{i}}\right)}$ , where $f_{\mathbf{i}}^y=y_{i_1}-y_{i_2}$ denotes the difference score for the perceived stress of the $\mathbf{i}$ -th pair.

Here, $\left|{\beta }_x\right|$ represents the mean difference between the perceived stress per unit difference in the beta-diversity $d_{\mathbf{i}}^x$ , ${\beta }_{z1}$ $\left({\beta }_{z2}\right)$ indicates the directional mean difference between the perceived stress per unit difference in the alpha-diversity (age), and $\left|{\beta }_w\right|$ is the mean difference between the perceived stress comparing male–female pairs with homogeneous gender pairs.

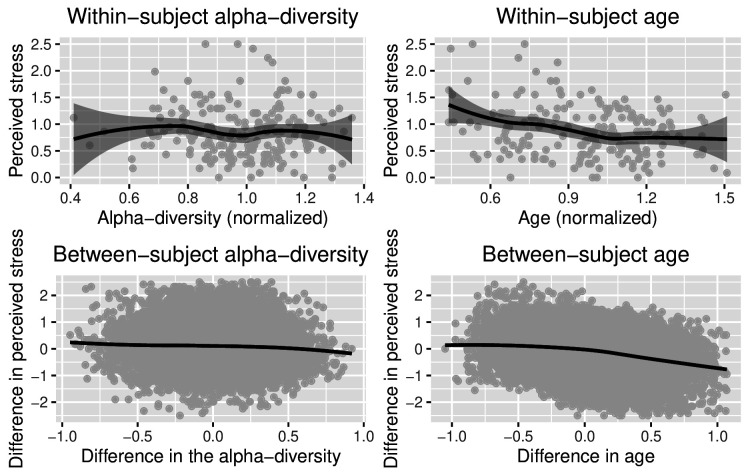
When the response and explanatory variable are both continuous, the between-subject regression will preserve their corresponding relationships among within-subject attributes. We demonstrate this in the continuous alpha-diversity (age) in figure 1. Shown at the top of figure 1 are the scatter plots with locally estimated scatterplot smoothing (LOESS) curves for the perceived stress (within-subject) with alpha-diversity and age, respectively. On average, the perceived stress did not correlate strongly with alpha-diversity, but it showed a negative relationship with age, which was confirmed by the univariate linear regression where the alpha-diversity effect was insignificant (t-statistic=−0.3145, p=0.448) but had a significant negative age effect (t-statistic=−1.1021, p<0.001). The bottom of figure 1 shows the scatter plots for their between-subject counterparts. As expected, the within-subject relationships were well-preserved in the between-subject regression.

Figure 1.

Real data analysis. The first row shows the scatter plots and LOESS curves for the perceived stress (within-subject) against alpha-diversity (left) and age (right). The second row shows scatter plots and LOESS curves for the difference in perceived stress against the difference in alpha-diversity (left) and the difference in age (right). LOESS, locally estimated scatterplot smoothing.

Shown at the top of table 1 are the results of perceived stress from the robust distance-based regression model. Per unit difference in a pair’s beta-diversity is associated with a 0.1457 (Wald=2.9752, p=0.085) unit difference in their perceived stress, suggesting that a larger difference between two subjects’ microbiome profiles implies more discrepancies in their stress levels. The mean (directional) stress score difference for any pair was −0.0270 per unit difference in their alpha-diversity but was not significant (Wald=0.1869, p=0.666). Per unit age difference was significantly associated with a 0.2520 unit decrease in the mean perceived stress difference (Wald=10.7857, p=0.001). This is expected since the scatter plots in figure 1 suggest that age is negatively related to perceived stress. The mean perceived stress difference comparing male–female pairs versus homogeneous gender pairs (male–male and female–female pairs) was 0.0218 (Wald=0.343, p=0.558); that is, we did not find strong evidence implicating perceived stress in distinct gender pairs being different from homogeneous gender pairs. Although signals between perceived stress and the microbiome composition were not strong, the negative association between age and stress shown here has been demonstrated in the literature.²⁰

Table 1.

Estimates, asymptotic SEs, Wald statistics, p values for the real study data using distance-based model, controlling for body mass index (continuous) and gender (binary)

Continuous outcome (perceived stress)
Parameter	Est.	SE	Statistic (Wald)	P value (Wald)
${\beta }_x$	0.1457	0.0845	2.9752	0.085
${\beta }_{z1}$	0.0270	0.0625	0.1869	0.666
${\beta }_{z2}$	0.2520	0.0767	10.7857	0.001
${\beta }_w$	0.0218	0.0371	0.3431	0.558
Composite outcome (positive traits/states)
Parameter	Est.	SE	Statistic (Wald)	P value (Wald)
${\beta }_x$	2.1210	0.1575	181.3488	<0.001
${\beta }_{z1}$	0.0292	0.0384	0.5804	0.446
${\beta }_{z2}$	0.1185	0.0618	3.6775	0.055
${\beta }_{w1}$	0.1912	0.1762	1.1775	0.278
${\beta }_{w2}$	0.1095	0.0815	1.8043	0.179

Est., estimates; SE, standard error.

Positive states (traits) as a multivariate response

In mental health studies, some traits are evaluated as a composite outcome.⁹ Particularly, resilience, optimism, mental well-being and wisdom all belong to positive states (traits). We devised the distance-based regression notion to link this four-dimensional multivariate outcome ${\displaystyle {\mathbf{y}}_i}$ to the microbiome composition by constructing the composite pairwise outcomes with the Euclidean distance and adopting (8) with a log link to decipher their relationships.

At the bottom of table 1 are the results of the positive states. Significant associations were found between the mean distance (variability) in the positive states and beta-diversity ( ${\displaystyle {\hat{\beta }}_x=2.1210}$ , Wald=181.3488, p<0.001) but not with the variability in alpha-diversity ( ${\displaystyle {\hat{\beta }}_{z1}=0.0292,}$ Wald=0.5804, p=0.446). This non-significant alpha-diversity is similar to the case of perceived stress as the univariate outcome. Hence, the microbiome beta-diversity may be a more sensitive indicator in capturing the between-subject attributes of mental health than the alpha-diversity in this dataset. Age variability was only marginally significant ( ${\displaystyle {\hat{\beta }}_{z2}=0.1185}$ , Wald=3.6775, p=0.055). The mean distance (variability) in the positive states for male–male pairs was $exp(-0.1912)=82.6\mathrm{\%}$ the distance for female–female pairs (Wald=1.1775, p=0.278); the mean distance (variability) for male–female pairs was $exp(-0.1095)=89.6\mathrm{\%}$ of that for female–female pairs (Wald=1.8043, p=0.179) but neither effect was significant. Hence, no significant gender effect was observed, similar to the case with perceived stress.

Taken together, those findings help support the existence of the microbiome–gut–brain axis^{17 19} and, more importantly, provide clinical implications for developing microbiota-related interventions to improve mental health and mitigate its related consequences. For example, given the positive association between beta-diversity and positive states, strategies that modulate patients’ microbiome composition may be beneficial to improve their mental health in general.

Conclusion and discussion

In this paper, we discussed both prevailing and emerging statistical approaches to demystifying the microbiome–gut–brain axis by studying the relationship between the univariate or multivariate clinical outcomes and various microbiome diversity metrics. Depending on its attribute (within-subject or between-subject), each type of microbiome diversity metric merits its own clinical and scientific exploration and, hence, well-designed statistical tools.

We introduced the definition and characteristics of popular alpha-diversity (within-subject) and beta-diversity (between-subject) measures. Specifically, for the between-subject beta-diversity, a semiparametric distance-based regression was discussed in detail. This distance-based framework has unique advantages in dealing with the complex dependency structures in between-subject attributes such as beta-diversity, which is difficult for traditional approaches. The regression setup also provides coefficient estimates to characterise the associations, facilitating in-depth scientific findings in mental health research. We briefly discussed their theoretical properties as well.

By further augmenting the choice set for both the response and explanatory variables, this framework permits elucidating the relationship among multiple high-dimensional variables. We illustrated predicting univariate or multivariate clinical variables using microbiome diversity by first transforming those clinical outcomes into between-subject attributes. This strategy is especially relevant to mental health research as many psychometric measures are evaluated as a composite rather than a univariate outcome. We also presented the analyses of an actual study to implicate the essential role of the microbiome on mental health. The compelling evidence was consistent with previous findings to support the bridge between the gut and mental health. Simultaneously, this timely demonstration offers a new angle to analyse complex omics data or other types of data of similar format to prepare for the new line of interdisciplinary research in psychiatry.

Biography

Jinyuan Liu obtained her PhD in Biostatistics in 2022 from UC San Diego in the USA. She is currently working as an Assistant Professor of Biostatistics at Vanderbilt University Medical Center in the USA, with a secondary appointment at the Department of Psychiatry. Her main research interests include semiparametric efficiency, causal inference, psychometrics, and building effective dimension-reduction and efficient integrative modeling of high-dimensional data from various disciplines, including genomics, imaging, and wearables.

Ethics statements

Patient consent for publication

Not applicable.

Ethics approval

Not applicable.