Statistical Approaches to Study Exposome-Health Associations in the Context of Repeated Exposure Data: A Simulation Study

Abstract

The exposome concept aims to consider all environmental stressors simultaneously. The dimension of the data and the correlation that may exist between exposures lead to various statistical challenges. Some methodological studies have provided insight regarding the efficiency of specific modeling approaches in the context of exposome data assessed once for each subject. However, few studies have considered the situation in which environmental exposures are assessed repeatedly. Here, we conduct a simulation study to compare the performance of statistical approaches to assess exposome-health associations in the context of multiple exposure variables. Different scenarios were tested, assuming different types and numbers of exposure-outcome causal relationships. An application study using real data collected within the INMA mother-child cohort (Spain) is also presented. In the simulation experiment, assessed methods showed varying performance across scenarios, making it challenging to recommend a one-size-fits-all strategy. Generally, methods such as sparse partial least-squares and the deletion-substitution-addition algorithm tended to outperform the other tested methods (ExWAS, Elastic-Net, DLNM, or sNPLS). Notably, as the number of true predictors increased, the performance of all methods declined. The absence of a clearly superior approach underscores the additional challenges posed by repeated exposome data, such as the presence of more complex correlation structures and interdependencies between variables, and highlights that careful consideration is essential when selecting the appropriate statistical method. In this regard, we provide recommendations based on the expected scenario. Given the heightened risk of reporting false positive or negative associations when applying these techniques to repeated exposome data, we advise interpreting the results with caution, particularly in compromised contexts such as those with a limited sample size.

Short abstract

This simulation study tests and compares statistical approaches to study the association between multiple and repeated exposures and a health outcome.

1. Introduction

The exposome encompasses all the environmental (i.e., nongenetic) factors that an individual experiences from conception onward.¹ The exposome concept aims at considering many environmental stressors simultaneously, as opposed to the one-by-one approach classically used in epidemiological research. The exposome approach leads to some statistical challenges due to the high number of exposures that need to be considered, which are sometimes highly correlated. Even though the exposome is not a statistic, most exposome-health studies to date have assessed these associations with an exposome measured at a single time point. The exposome is a life-course concept, covering all exposures from conception onward, and variations of the exposome over time can have an influence on health outcomes. Currently, several cohort studies are collecting repeated exposome data in order to better capture exposomes at different points of life. Still, even though some results have been published on the properties of some statistical methods aiming to link health outcomes with exposome data assessed at a single time point,^2,3 there is no guidance on how to conduct the statistical analysis when repeated exposome are available.

Having repeated measurements of the exposome has the advantage of increasing the odds of assessing exposure at the toxicologically relevant time window. However, it further increases the dimensionality problem and may also aggravate the problems associated with correlated variables, as the different time points of the same variable are expected to have some degree of correlation, although this can vary according to the type of exposure.

Here, we conduct a simulation study to compare the performance of different statistical approaches to assess exposome-health associations in the context of multiple and repeated exposure variables and a distal health outcome assessed once. Then, the most promising methods were applied to a real showcase of exposome data with repeated exposure measurements from pregnancy to 11 years old.

2. Methods

2.1. Data Simulation

2.1.1. Exposome Simulation

We simulated 100 independent data sets, each of them being composed of 500 variables representing 100 exposures assessed at 5 time points, in 1200 participants. The exposure matrix was obtained by summing two components: (1) a subject random effect that induces correlation between repeated measures from the same subject; and (2) a residual term that induces correlation between exposures measured at the same time point. To generate the random effects, we sampled from a mean-zero normal distribution with a variance according to three values for the intraclass correlation coefficient (ICC): low (0.1), medium (0.5), and high (0.9). Each ICC was used with the same probability, so that simulated data sets approximately had the same number of variables with each ICC. Variables with an ICC of 0.9 represent exposures that are expected to remain similar over time (e.g., exposures with a long half-life), while those with an ICC of 0.1 are expected to vary a lot over time (e.g., compounds with a short half-life). To generate exposure variables with a realistic correlation structure, we relied on the existing HELIX project, in which more than 200 environmental factors were assessed in 1301 mothers–child pairs during pregnancy and childhood through questionnaires, geospatial modeling, and biological monitoring.⁴ Assessed variables in the HELIX cohort included macrolevel factors such as climate, urban environment, and societal factors and an individual external domain including agents such as environmental pollutants, tobacco smoke, diet, and physical activity, among others. Specifically, the residual component for each time point was generated from a multivariate normal distribution with a mean zero and a covariance matrix equal to the observed correlation matrix from HELIX. The correlation matrix of the simulated data is shown in Figure S1.

2.1.2. Outcome Simulation

The health outcome Y was simulated by choosing a reduced subset of exposures that were assumed to be the only ones that directly influenced the outcome (hereafter “causal exposures”), according to two scenarios:

• Scenario 1, where all the five exposure time windows of the causal exposures are directly influencing Y

• Scenario 2, where only a single exposure time window of the causal exposures is directly influencing Y

For each scenario, Y was simulated with k = 3, 5, and 10 true exposures. For scenario 1, it means that the total number of terms in the data-generating model (apart from the intercept) was 15, 25, and 50 variables (i.e., k multiplied by 5 time points). For scenario 2, this means that the data-generating model includes k terms (apart from the intercept). Let X₁,... X₁₀₀, and let l = (l₁,... l_k) be a set of indices that indicate which are the k true exposures. The mean of Y was calculated as m = ∑_j=1^kβ_jX_lj. Then, the response variable was generated from a normal distribution with a mean m and a variance that resulted in an R² of the model of 5%.

2.2. Statistical Methods to Estimate the Exposome-Health Association

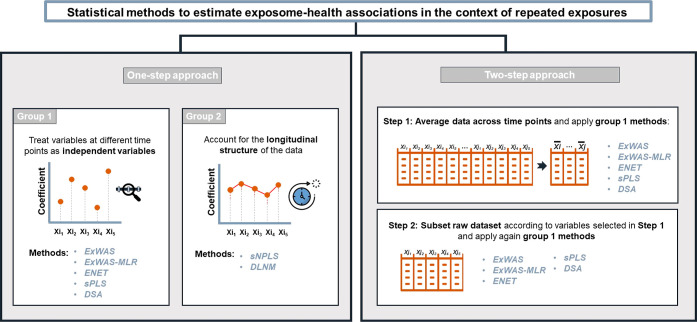
Different statistical methods that aimed to select the exposures and time points associated with the outcome were applied (Figure 1). Two approaches were tested. In the first one, the statistical methods were applied directly on the raw data (1-step approach), i.e., including all time-specific exposures. In the second one, the statistical methods were applied after averaging the exposure levels across the five time-windows, and once the averaged exposures were selected, the same methods were applied in a second step to a data set that included all time-specific exposures but was restricted to the averaged exposures selected in the first step (2-step approach).

Figure 1.

Overview of the statistical methods tested to estimate exposome-health associations in the context of repeated exposure data. Schematic view of the statistical approaches tested in the simulation study. The statistical methods tested following the one-step approach were performed using all time-specific exposures; among those, some statistical methods ignore the repeated design, while others consider it. In the 2-step approach, only the statistical methods that ignore the repeated design of the exposome data were tested. These methods were first performed on an averaged exposure level across the time points and then performed on the time-specific exposures. For more details, we kindly refer the reader to the Methods section. Abbreviations: DSA, deletion-substitution-addition algorithm; ExWAS, exposome-wide association study; ENET, elastic net; FDR, false discovery rate; sPLS, sparse partial least-squares.

For the 1-step approach, we first tested a number of methods that ignore the repeated design of the exposure data (i.e., variables corresponding to an exposure measured at different time points were considered as independent variables):

2.2.1. Exposome-Wide Association Study

Exposome-wide association study (ExWAS) consists of fitting as many regression models as there are exposure variables in order to evaluate the association between each exposure variable and Y independently for each exposure.⁵ For the present study, 500 linear regression models were fitted to assess the association between each exposure variable and Y, independently of the other exposure variables and ignoring the dependency between time points. The results are reported with no correction for multiple testing and with correction for multiple testing using the Bonferroni, the Benjamini–Hochberg, and the Benjamini–Yekutieli correction.

2.2.2. ExWAS-Multiple Linear Regression

ExWAS-multiple linear regression (ExWAS-MLR) is an extension of the ExWAS where the statistically significant variables from the ExWAS are introduced simultaneously in a single multiexposure regression model. Each exposure variable is considered statistically significant if the two-sided p-value obtained in the multiexposure regression model is below 5%. The candidate variables to be introduced into the multiexposure model were selected according to the ExWAS results, with and without correction for multiple testing.

2.2.3. Elastic Net

Elastic net (ENET) is a penalized regression method that performs both regularization and variable selection.⁶ It combines the L1 penalty from LASSO, which shrinks the coefficient of the uninformative variable to 0, and the L2 penalty from RIDGE, which accommodates correlated variables and ensures numerical stability. The tuning parameters were determined by defining the optimal calibration parameters (in order to prevent overfitting) as those providing the sparsest model among those yielding an RMSE within 1 standard error of the minimum RMSE.

2.2.4. Sparse Partial Least-Squares Regression

Sparse partial least-squares regression (sPLS) performs both variable selection and dimension reduction simultaneously.⁷ sPLS is an extension of the partial least-squares regression—a supervised dimension reduction technique that builds latent variables as linear combinations of the original set of variables—which additionally imposes sparsity using a L1 penalty in the estimation of the linear combination coefficients. The tuning parameter and the number of components to be included in the regression model were calibrated by minimizing the RMSE using 5-fold cross-validation.

2.2.5. Deletion-Substitution-Addition Algorithm

The deletion-substitution-addition algorithm (DSA) is an iterative regression model search algorithm performing variable selection.⁸ It searches for the best model, starting with the intercept model and identifying an optimal model for each model size. At each iteration, the following three steps are allowed: (a) removing a term, (b) replacing one term with another, and (c) adding a term to the current model. The final model is selected by minimizing the value of the RMSE using 5-fold cross-validated data. For this simulation study, we did not allow polynomial nor interaction terms and considered models of size up to 25 variables.

In addition, the following statistical methods that account for repeated measures of exposure variables were tested:

2.2.6. Penalized Distributed Lag (Non-)Linear Models (DLNMpen) with Variable Selection

Distributed lag models are regression models that assess how exposure measured at different time points affects the outcome. Constrained distributed lag models allow putting constraints on the regression coefficients at each time point in order to improve efficiency and to avoid collinearity problems. For example, it is common to constrain regression coefficients to vary smoothly over time, thus assuming that the effects of exposure at two periods that are close in time will be more similar than the effects for two exposure periods that are further apart.⁹ DLNMs describe the bidimensional dose-lag-response associations, potentially varying nonlinearly in the dimensions of predictor intensity and lag. Particularly, here we employed an extension of the standard DLNM framework to penalized splines within generalized additive models (gam).¹⁰ For the specification of the model, we built a cross-basis matrix (one basis for the predictors and one basis for the lags) for each exposure and introduced them all into a linear regression model. To build the basis for each predictor, we assumed a linear effect on the outcome (Y). Regarding the shape of the lag space, we assumed it follows a cubic B-spline with five equally spaced knots (one per time point). The employed model further incorporated an extra penalty controlling the degree of smoothing of each term so that it can be penalized to zero, removing the term from the model and therefore performing variable selection. To evaluate the statistical significance of the exposure-outcome association, we first evaluated the significance of the entire cross-base, applying a correction for multiple testing. Then, among the significant cross-bases (with p-value multiple-testing correction), we considered that a particular lag was statistically significant if the estimated effect for that lag had a confidence interval that excluded 0.

2.2.7. Sparse N-Way Partial Least-Squares

Sparse N-way partial least-squares (NPLS) is an extension of the ordinary sPLS regression algorithm to temporal data where the bilinear model of predictors is replaced by a multilinear model.¹¹ sNPLS studies relationships between some three-way (or N-way) X data structure (individuals-variables-times) and any Y data. As sPLS, sNPLS tries to find latent spaces that maximize the covariance between X and Y. Additionally, sNPLS imposes sparsity using an L1 penalty in the estimation of the linear combination coefficients, so feature-selection is performed at both the level of variables and time points influencing the latent variables. Thanks to that, sNPLS improves the interpretability of the results and also greatly reduces the variables involved in performing new predictions from the model. This model is especially suitable for data structures showing strong correlations over time. The optimal hyperparameters (number of latent components and variables/time points contributing to them) were estimated through 50-times repeated fold-cross validation.

For the 2-step approach, the first step aims to summarize the exposure levels measured at different time points into a single measure by calculating the averaged level of exposure across time points, which could be seen as being proportional to cumulative exposure. This step reduces the number of variables from 500 to 100. Methods 1 to 5 are then applied to the reduced data set. At the second step, we applied methods 1 to 5 to the subset of exposures selected in the first step but now including all time points. The 2-step approach was not performed for DLNM nor sNPLS, which both considered the temporal structure of the data and required time-specific variables as input variables. All selected methods were methods that provided an estimate for the linear relationship of an individual exposure and the health outcome. This choice was motivated by the practical applicability of our findings, since many exposome researchers prefer to obtain this type of results.

2.3. Statistical Performance Assessment

For all methods and under each scenario, we calculated the sensitivity as a measure of the capacity to identify the true exposure and the false discovery rate (FDR) as a measure of the proportion of false discoveries. The performance of each method was assessed at two different levels:

• (1)at the variable level, to calculate the performance of identifying the true exposure at the true time point (denominator = 500 variables = 100 exposures measured at 5 time points)
• (2)at the exposure level, to calculate the performance of identifying the true exposure independently of which time point was selected (denominator = 100 exposures).

For example, if exposure X₁ at time 2 was selected while the true exposure was X₁ at time 4, this is considered as a false positive at the variable level (wrong time point) but as a true positive at the exposure level (right exposure).

We also compared the performance of the methods to identify the true exposure at the true time point according to the ICC of the exposures across time points.

The threshold for the statistical significance was set to 0.05. All of the analyses were performed using R software. The main packages used included MASS, glmnet, spls, DSA, dlnm, sNPLS, splines, and mgcv. The code used to generate the simulated data, to apply the methods, and to compare the performances is available on GitHub repository (see Supporting Information).

2.4. Application with Real Data

The top methods, according to their performance in the simulated data, were applied to a real exposome data set with repeated exposure measurements from pregnancy to 11 years old. The real data set belongs to the INMA mother-child cohort, a prospective population-based cohort for the study of the associations between pre- and postnatal environmental exposures and growth, health, and development from early fetal life until adolescence in Spain.¹² For the present study, the study population was composed of 495 Spanish children from Sabadell.

The outcome of interest here was the waist circumference z-score of children at the age of 11 years old, properly standardized by sex and age using the reference values of children aged 5–19 y in NHANES III.¹³ The population was composed of 82 children with overweight and obesity and 413 normal-weight individuals (Table S1).

As exposures, repeated data on the lifestyle patterns and environmental factors to which children are exposed during pregnancy and early childhood were investigated (Table S2). Specifically, environmental exposure data concerning air pollution, built environment, natural spaces and noise and traffic were assessed at 5 time points (ages of 4, 6, 7, 9, and 11). Additionally, diet was assessed through food frequency questionnaires at 3 time points (pregnancy, and at the age of 4 and 7 years old). Diet data constituted average intakes of macronutrients (total sugars, fats, and proteins) and micronutrients (vitamins, essential minerals, etc.).

Categorical variables, or those with more than 70% of the missing values, were excluded. Additionally, variables with more than 80% of zeros were transformed to binary exposures and treated as numeric (values >0 were converted to 1). For the built environment domain, measurements were taken at a buffer of 300 m from home. Normalization of all exposures was conducted using the bestNormalize R package, which renders data Gaussian through the use of different functions according to the Pearson P statistic, as calculated by the nortest package. The transformations contained in the package and implemented in bestNormalize are reversible (i.e., 1–1), which allows for straightforward interpretation and consistency. In other words, any analysis performed on the normalized data can be interpreted using the original unit. Imputation was performed with multivariate imputation by chained equations. Only the first imputed data set was used for the showcase.

In total, the number of exposure features in the data set was 83, of which 32 had repeated measures at 3 time points and 51 had repeated measures at 5 time points. The cross-sectional and longitudinal cumulative effect of multiple and repeated exposures on the waist circumference of children at 11 years old was evaluated following the approaches described in the Methods section.

3. Results

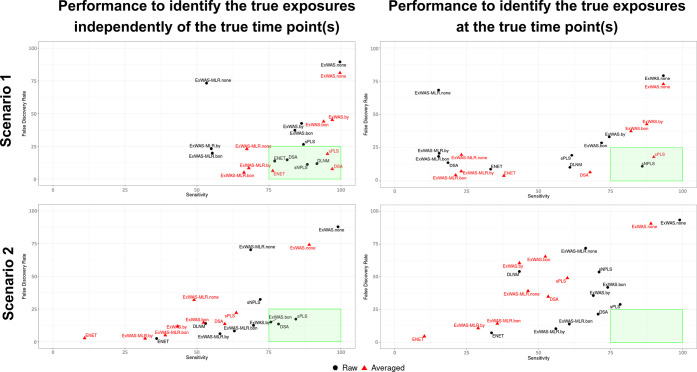
The performances of each method are detailed in Tables 1 and 2 for Scenario 1 and Scenario 2, respectively. Figure 2 visually summarizes the performances of each method when the number of true predictors is fixed to k = 3.

Table 1. Performances of Each Method When All Time Points Are Truly Associated with Y (Scenario 1)^a.

	performance to identify the true exposures independently of the true time point (s)						performance to identify the true exposures at the true time point (s)
	sensitivity			FDR			sensitivity			FDR
N true predictors (×5)b	3	5	10	3	5	10	3	5	10	3	5	10
Raw Data (1-Step Approach)
ExWAS.none	99.7 (3.3)	97.4 (6.8)	91.1 (8.7)	89.5 (2.9)	84.8 (3.6)	76.5 (3.9)	93.3 (8.6)	86.2 (9.2)	72.6 (9.4)	79.1 (6.8)	72.2 (7.7)	63.9 (6.7)
ExWAS.bon	84 (18.6)	68 (19.3)	43.5 (14.5)	37.2 (27.5)	29.1 (24.3)	25.7 (19.3)	71.9 (19.7)	51.8 (15.7)	26 (12.4)	28.6 (24.8)	22.4 (22.1)	19.8 (17.6)
ExWAS.by	86.3 (17.8)	74.6 (19.9)	49.1 (19.4)	42.5 (28.4)	34.7 (24.2)	30.8 (19.9)	74.5 (19.9)	57.4 (17.5)	32.2 (15.9)	33.1 (26.3)	27 (23.1)	23 (18)
ExWAS-MLR.none	53.3 (30)	37.2 (23.1)	27.7 (16.4)	73.3 (16.1)	71.8 (19.4)	64.7 (18.3)	15.3 (11.3)	8.8 (6.2)	6.1 (3.7)	68.3 (19.3)	70.2 (20.6)	63.5 (18.9)
ExWAS-MLR.bon	55.3 (30.4)	34.6 (20.3)	21.9 (11.8)	19.8 (27.2)	17.9 (26)	19.1 (24.7)	15.3 (10)	7.7 (4.5)	4.8 (2.7)	18.5 (26.6)	17.4 (25.5)	18.3 (24.3)
ExWAS-MLR.by	55 (27.8)	37 (20.2)	22.7 (11.6)	23.1 (27.9)	23.6 (29.4)	20 (23.9)	15.5 (9.9)	8.5 (4.9)	5 (2.7)	20.8 (26.5)	22.8 (29.1)	19.3 (23.3)
ENET	77 (25.8)	60.8 (29.8)	40 (27.1)	13.7 (19.8)	17 (21.9)	15.8 (18.3)	33.3 (16)	21.8 (14.1)	11.8 (9.2)	8.9 (13.6)	13.4 (18.7)	13.6 (16)
sPLS	87 (17.6)	82.6 (18.8)	72.6 (22.5)	26.5 (30.2)	34.8 (27.3)	49.8 (27.4)	61.5 (27.5)	55.3 (24.9)	49.4 (26.3)	19.3 (24.2)	25.3 (22.5)	39.8 (24.9)
DSA	81.3 (22.4)	67.6 (20.1)	41.4 (20.1)	14.7 (22.2)	11.1 (16.7)	14.4 (18.6)	18.5 (7.9)	13.7 (4.3)	8.3 (4)	13.7 (21.1)	11 (16.8)	14.5 (18.6)
sNPLS	88.3 (16)	78.6 (19.1)	68.1 (18.1)	11.1 (20.8)	24.5 (22.3)	39.1 (19.2)	86 (18.8)	75.6 (21.5)	62.2 (21.5)	11 (20.5)	24.4 (22.2)	38.7 (19)
DLNM	91.7 (15.2)	71.4 (18)	35.4 (17.4)	11.7 (16.9)	12.2 (16.1)	9.6 (15.4)	60.9 (16.2)	39 (15.3)	16.4 (9.3)	10.2 (15.9)	12.4 (16.7)	10.4 (17.8)
Averaged Data (2-Step)
ExWAS.none	99.7 (3.3)	96.8 (7.4)	86.5 (9.5)	81 (7.8)	73.7 (9)	65.2 (7.4)	93.3 (8.6)	86 (9.4)	71.5 (9.8)	72.8 (11.8)	64.6 (12.3)	57.6 (8.9)
ExWAS.bon	94 (12.9)	79.2 (16.1)	52.3 (13.8)	43.9 (25.2)	35.2 (21.7)	28.5 (17.5)	82.1 (15.4)	65.3 (14.8)	38.7 (11.5)	37.4 (24.7)	30.2 (21.2)	24.7 (16.7)
ExWAS.by	97 (9.6)	83.4 (16.6)	58.5 (16.8)	45.2 (27)	36.8 (23.2)	34.6 (18.1)	87.5 (13.8)	73.3 (15.2)	50 (15.2)	42.6 (26.7)	34.9 (22.6)	31.2 (17.6)
ExWAS-MLR.none	67.3 (29.2)	44.8 (24.6)	29.9 (16.6)	23 (27.9)	21.6 (27)	16.5 (23)	23.2 (15.3)	12.4 (8.6)	7.3 (4.5)	19.6 (26.7)	20.6 (27.2)	16.2 (23.1)
ExWAS-MLR.bon	66.3 (29)	38.6 (23)	23.4 (13.8)	5 (16.3)	9.6 (21.3)	7.5 (18.8)	21.2 (13.8)	9.6 (6.6)	5.3 (3.3)	4.4 (15.2)	9 (20.5)	7.2 (18.5)
ExWAS-MLR.by	68 (27.6)	40.8 (24.6)	23.1 (13.1)	8.3 (19.6)	8.7 (20.6)	7.3 (17.1)	23.1 (14.6)	10.6 (7.8)	5.5 (3.4)	7.3 (18.4)	8.4 (20.3)	6.9 (16.6)
ENET	76.3 (25.2)	65 (25.3)	44.1 (26.1)	6.2 (14.6)	10.9 (14.4)	14.3 (18.5)	37.9 (19.6)	30.1 (17.6)	16.9 (11.6)	3.9 (9.6)	7.9 (11.8)	11.8 (16.5)
sPLS	95.3 (11.6)	84.4 (16.5)	70.1 (19.4)	19.2 (23.7)	19.8 (24.2)	31.8 (23.7)	90 (18.2)	80.5 (18.7)	65.5 (23.3)	18 (22.8)	19.1 (23.6)	30.9 (23.5)
DSA	97 (9.6)	85.6 (15.6)	63.4 (19.8)	7.7 (15)	10 (15.1)	19.2 (16.5)	67.9 (23.3)	48.1 (24.4)	23.1 (11.7)	6.5 (13.2)	8.5 (13.4)	18.1 (16.4)

^aAbbreviations: DSA, deletion-substitution-addition algorithm; ExWAS, exposome-wide association study; ENET, elastic net; FDR, false discovery rate; MLR, multiple linear regression; sPLS, sparse partial least-squares.

^bThe number of true predictors refers to the number of features presenting a causal relationship with the outcome in the simulated data. Since we here present results from scenario 1 (where all time points are truly associated with Y), the number of true predictors needs to be multiplied by 5 time points.

Table 2. Performances of Each Method When Only a Single Time Point Is Truly Associated with Y (Scenario 2)^a.

	performance to identify the true exposures independently of the true time point (s)						performance to identify the true exposures at the true time point (s)
	sensitivity			FDR			sensitivity			FDR
N true predictors	3	5	10	3	5	10	3	5	10	3	5	10
Raw Data (1-Step)
ExWAS.none	99 (5.7)	93.8 (10.5)	78.5 (11.8)	87.9 (3.1)	82.4 (4.1)	73.4 (6.1)	99 (5.7)	92 (11.7)	72.5 (14)	93.5 (1.9)	90.3 (3.4)	87 (4)
ExWAS.bon	75.7 (24.1)	39.4 (20.2)	16 (13.1)	15 (22.3)	14.6 (22.5)	20.9 (28.3)	74 (24.9)	38.4 (20)	15.1 (12.6)	42 (30.4)	34.1 (31.8)	34.1 (33.8)
ExWAS.by	69.7 (29.2)	35.2 (23.6)	11.8 (14.7)	12.5 (20.7)	12.6 (22.7)	16.6 (26.2)	69 (29.3)	34.8 (23.5)	11.5 (14.4)	35.7 (33.3)	28.7 (33.3)	24.1 (32.4)
ExWAS-MLR.none	68.7 (28)	51 (19.8)	25.4 (13.8)	70.3 (14.7)	66.3 (14)	64.4 (15.5)	66.3 (27.4)	47.6 (20.1)	20.7 (13.9)	71.9 (14.5)	69.4 (13.9)	72.6 (15.9)
ExWAS-MLR.bon	63 (28)	29.6 (19)	11.1 (11.9)	8.2 (22.7)	5.7 (14.8)	14.7 (30.1)	60.7 (28.2)	28 (18.9)	10.2 (11.1)	14 (26.4)	10.5 (21.8)	18.9 (32.2)
ExWAS-MLR.by	58 (30.2)	27.4 (19.6)	7.7 (10.8)	6.2 (20)	7.5 (20)	11.2 (24.8)	56 (29.9)	26 (19.4)	7.2 (10.3)	10.4 (24.1)	11.2 (25.2)	12.9 (27.3)
ENET	36 (34.7)	15.2 (23.8)	5.5 (11.8)	2.5 (10.3)	4.1 (15.2)	8.2 (25)	33.7 (33.3)	13 (20.4)	4.9 (10.7)	7.2 (18.9)	9.3 (22.9)	12.2 (30.5)
sPLS	84.3 (22.4)	58.2 (26.2)	28.8 (23.6)	17.3 (22.9)	23 (25.3)	28.8 (30.7)	78.3 (24.8)	54.2 (26.1)	25.6 (22.5)	29 (29.8)	35.5 (30)	43.4 (34.9)
DSA	78.3 (27)	45.6 (27.3)	15.1 (15.1)	13.5 (20.6)	14.8 (21.8)	14.3 (26.6)	70.7 (27.7)	39.6 (24.9)	12.2 (12.4)	21.5 (24.4)	22.3 (27.6)	23 (32.5)
sNPLS	72 (23.6)	54.4 (27.6)	42.5 (29.3)	32.4 (32)	43.8 (33.5)	46.6 (29.8)	71 (23.5)	52.4 (28.3)	40.4 (29.8)	53.7 (33.1)	65.7 (27)	60.6 (31.7)
DLNM	53 (29.3)	25 (20.2)	6.7 (9.2)	14 (23.7)	14.3 (26.3)	24.7 (38.7)	43.3 (26.6)	19.2 (16.3)	4.7 (7.2)	54.1 (31.7)	49.4 (35.8)	48.4 (43.2)
Averaged Data (2-Step)
ExWAS.none	89 (15.7)	73.6 (21.6)	51.2 (15.5)	74.1 (10.2)	66.7 (15.2)	60.2 (14.6)	89 (15.7)	72.6 (22)	49.4 (15.9)	90.7 (4)	87.8 (6)	86.3 (5.8)
ExWAS.bon	52.3 (27.3)	23.8 (20.4)	11.4 (12.1)	14.7 (24.2)	12.9 (24.5)	24.3 (32.9)	52.3 (27.3)	23.6 (20.2)	11.3 (12)	65.5 (27.4)	53.2 (37.2)	55 (38.5)
ExWAS.by	43.3 (32.3)	21.2 (23.4)	8.2 (12.8)	11.8 (23.3)	11.6 (24.4)	13 (24.9)	43.3 (32.3)	21.2 (23.4)	8.2 (12.8)	60.5 (35.5)	47.3 (40.8)	33.5 (41.6)
ExWAS-MLR.none	49 (29)	31.6 (20.9)	12.1 (9.5)	32 (30.7)	31.5 (32.4)	30.7 (37.3)	46.3 (27.6)	28.6 (21.1)	9.7 (8.2)	39.2 (31.2)	42.5 (33.9)	43.6 (38.6)
ExWAS-MLR.bon	39 (26.8)	14.2 (14.6)	5.6 (6.7)	5 (19.5)	4.3 (17.3)	7.5 (24)	35.7 (26.5)	12.4 (13.9)	4.7 (6.1)	14.3 (29.7)	13.8 (30.2)	14.3 (31.9)
ExWAS-MLR.by	32 (29.2)	12.6 (15.2)	3.3 (5.7)	2.5 (14.9)	3.7 (16.8)	3 (13.9)	29 (27.9)	10.4 (13.8)	2.7 (5.1)	10.8 (26.7)	13.8 (30.7)	7.5 (24)
ENET	11 (22.7)	2.6 (10.1)	1.4 (5.9)	2.8 (15)	1.3 (10.5)	0.7 (5.3)	10.3 (22.1)	1.2 (5.6)	1.2 (5)	4.6 (19.3)	6.3 (23.5)	1.8 (11.6)
sPLS	63.7 (29.6)	42.8 (28.7)	29 (23.3)	22.1 (28.4)	28.8 (31.2)	28.9 (32.3)	60 (31.1)	39.8 (28.4)	26.8 (23.9)	49.1 (36)	56.9 (33.8)	59.1 (36.5)
DSA	59.7 (29.3)	27.6 (26.8)	13 (14)	13.6 (23.1)	19.6 (30.6)	18 (28.5)	53.3 (29.6)	21.6 (23)	10.1 (11.3)	34.9 (33.2)	43.9 (37.8)	35.6 (35.7)

^aAbbreviations: DSA, deletion-substitution-addition algorithm; ExWAS, exposome-wide association study; ENET, elastic net; FDR, false discovery rate; MLR, multiple linear regression; sPLS, sparse partial least-squares.

Figure 2.

Comparison of the performances of each method under scenarios 1 and 2 (when k = 3). Scatter plot representing the sensitivity (x-axis) and the FDR (y-axis) obtained from each method under scenario 1 (all time points are associated with Y) and scenario 2 (a single time point is associated with Y). Labels are in black if the performances correspond to a method performed using raw data and in red if the performances correspond to a method performed using averaged data (2-step). The green square represents the area under which the sensitivity is above 75% and the FDR is below 25%. Abbreviations: Bon; Bonferroni multiple-testing correction; BY; Benjamini–Yekutieli multiple-testing correction (FDR); DSA, deletion-substitution-addition algorithm; ExWAS, exposome-wide association study; ENET, elastic net; FDR, false discovery rate; none, no multiple-testing correction applied; sPLS, sparse partial least-squares.

3.1. Scenario 1. All Time Points Are Truly Associated with Y

3.1.1. Performance to Detect the True Exposure (Independently of the True Time Points) (Table 1)

The best performance to identify the “causal” exposures was achieved when the number of true predictors k was low (k = 3) for all methods. We start describing the performance for this scenario (k = 3). All methods but ExWAS-MLR had a good sensitivity (>75%) but showed varying levels of FDR. When using all time-specific exposures (raw data), DSA, sNPLS, DLNM, and ENET showed a good performance, with sensitivities close to or higher than 80 and FDRs below 20%.

The strategy of averaging the exposure at all time points and performing variable selection using the average variable provided, in general, some improvements in both sensitivity and FDR when we evaluated the capacity to select the true exposures. Still focusing on k = 3, DSA, which already provided good results with raw data, improved performance. sPLS reached high sensitivity and had an FDR close to 20%. For DLNM, we did not see a difference in performance if we tested the entire crossbasis (i.e., an association across all time points, similar to testing the average) or if we tested the specific time points. ENET also improved, although its performance was worse than that of the previously mentioned methods. ExWAS did not provide a good performance. Further testing of the separate time points among the ones selected using the average (i.e., implementing a 2-step process) did not change much the performance, except for ExWAS-MLR.by, which decreased its performance and performed worse than ENET (results in the supplement).

As the number of true predictors k increased, the sensitivity of all methods decreased. DSA, DLNM, and ExWAS-MLR managed to keep FDR low, but sPLS and sNPLS showed increases in FDR when k increased.

3.1.2. Performance to Detect the True Exposure at the True Time Points (Table 1)

In scenario 1, selecting the true time points means selecting all time points, as all of them were associated with the outcome by design. When performance was evaluated in terms of selecting the true time points, only sNPLS provided acceptable performance for k = 3, with sPLS and DLNM providing results that were not optimal but were substantially better than the other methods. DSA, which performed well in selecting the variable regardless of the time point (as described in the previous paragraph), had a very low sensitivity for selecting all time points. Taking a two-step strategy in which (1) we take the average across time points and perform selection based on the average and (2) we test individual time points among the selected in the first step provided improvements for sPLS and DSA, which obtained acceptable results. Still, DSA had low sensitivity, while sPLS had worse FDR, which worsened when increasing k.

3.2. Scenario 2. A Single Time Point Is Truly Associated with Y

3.2.1. Performance to Detect the True Exposure (Independently of the True Time Point) (Table 2)

As in previous cases, performance was better for k = 3. Focusing on k = 3, when using the raw data, the methods that had a sensitivity greater than 70% and a FDR lower than 20% were DSA, ExWAS.bon, and sPLS. ExWAS-MLR and DLNM performed slightly worse, while ENET had low sensitivity and sNPLS had high FDR. Increasing the true number of predictors reduced the sensitivity for all methods and increased the FDR for all methods except DSA.

3.2.2. Performance to Detect the True Exposure at the True Time Point (Table 2)

When we evaluated the capacity to detect the true time point, the performance of the different methods was reduced, as expected. DSA was still among the best methods, now with an FDR slightly higher than 20%, followed by sPLS but showing a higher FDR. ExWAS-MLR had a much lower FDR but with a sensitivity close to 60%. The strategy of doing a 2-step approach using the average across time points provided much worse results than using the raw data directly (1-step approach).

3.3. Influence of the ICCs between Time-Specific Exposures on Models’ Performance

The performances of each method according to the ICC between time points are presented in Figure S2.

Scenario 1. In comparison with the main results, we observed that in case of low ICC between time points (<0.1), then several methods did not show good performances (ENET, sPLS, DSA, including in the 2-step approach). Conversely, the performances of sPLS, sNPLS, DSA, ExWAS, ExWAS_AVG, and sPLS_AVG were improved in the case of moderate to high ICC between time points (>0.5), including when the number of true predictors increased to k = 5 and, in a lesser extent, when k = 10.

Scenario 2. Results observed with different ICCs were similar to the results that did not consider the ICC; none of the methods performed well for k = 5 and 10. Overall, for k = 3, ExWAS-MLR, sPLS, and DSA seem to perform slightly better in identifying the true exposure at the true time point when the ICC between time points is low (<0.1) to moderate (>0.1 to <0.5). The 2-step approaches did not perform well, whatever the ICC between time points.

3.4. Application to Real Data

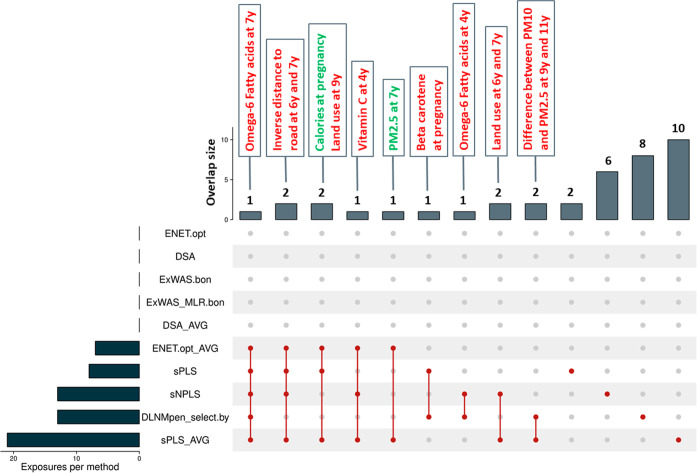
According to their performance in the different scenarios with simulated data, a total of 10 methods were selected and applied to the real showcase with INMA data: ExWAS.bon, ExWAS-MLR.bon, ENET, sPLS, DSA, sNPLS, DLNM, ENET_AVG, sPLS_AVG, and DSA_AVG. In Table 3, the number of selected variables and the top 10 most relevant associations (according to the reported effect sizes among those selected features) for each method are presented. The overlaps between the different methods can be observed in Figure 3. None of the ExWAS approaches, the ENET, and DSA (including DSA_AVG) found any significant association in this real data set (to be selected, an exposure needs to present a P-value <0.05 for the EWAS or DLNM or a beta distinct from 0 for the rest of algorithms). Conversely, sPLS on averaged data (2-step approach) and sNPLS and DLNM on raw data (1-step approach) were the methods identifying the highest number of associations (21, 13, and 13, respectively). The most singular method (giving results more different from the rest) was the DLNM.

Table 3. Results from the Real Showcase on INMA Data; Number of Selected Variables and the Top 10 Most Relevant Associations with Waist Circumference Z-Score at the Age of 11 Years Old^a.

method	N significant features	N significant features (−coef)	N significant features (+coef)	top 10 most relevant features (estimate)
ExWAS.bon	0	0	0
ExWAS-MLR.bon	0	0	0
ENET	0	0	0
sPLS	8	1	7	land use other at 9 y (0.15)
				calories at pregnancy (−0.12)
				beta carotene at pregnancy (0.11)
				total sugars at 4 y (0.10)
				omega 6 fatty acid at 7 y (0.08)
				polyunsaturated fat at 7 y (0.08)
				inverse distance to nearest road at 7 y (0.07)
				inverse distance to nearest road at 6 y (0.07)
DSA	0	0	0
sNPLS	13	4	9	vitamin C at 4 y (0.17)
				folato at 4 y (−0.14)
				inverse distance to nearest road at 6 y (0.09)
				omega 6 fatty acid at 7 y (0.09)
				land use other at 6 y (0.09)
				omega 6 fatty acid at pregnancy (0.09)
				vitamin C at 7 y (0.07)
				folato at 7 y (−0.06)
				inverse distance to nearest road at 7 y (0.06)
				land use other at 7 y (0.05)
DLNM	13	5	8	PM10fe at 4 y (−0.33)
				PM10fe at 7 y (0.33)
				PM10fe at 11 y (−0.33)
				omega 6 fatty acid at 7 y (0.13)
				difference between PM10 and PM2.5 at 11 y (0.12)
				traffic load all roads at 4 y (−0.12)
				traffic load all roads at 11 y (0.12)
				beta carotene at pregnancy (0.12)
				beta carotene at 4 y (−0.10)
				omega 6 fatty acid at 4 y (0.07)
ENET AVG	7	2	5	omega 6 fatty acid at 7 y (0.032)
				inverse distance to nearest road at 7 y (0.03)
				calories at pregnancy (−0.02)
				PM2.5v at 7 y (−0.01)
				land use other at 9 y (0.01)
				inverse distance to nearest road at 6 y (0.006)
				vitamin C at 4 y (0.002)
sPLS AVG	21	5	16	vitamin C at 4 y (0.17)
				folato at 4 y (−0.14)
				inverse distance to nearest road at 6 y (0.09)
				omega 6 fatty acid at 7 y (0.09)
				land use other at 6 y (0.09)
				omega 6 fatty acid at pregnancy (0.09)
				vitamin C at 7 y (0.07)
				folato at 7 y (−0.06)
				inverse distance to nearest road at 7 y (0.06)
				land use other at 7 y (0.05)
DSA_AVG	0	0	0

^aEnvironmental exposure data concerning air pollution, built environment, natural spaces and noise and traffic were assessed at 5 time points (ages of 4, 6, 7, 9, and 11 y). Additionally, diet was assessed through food frequency questionnaires at 3 time points (pregnancy, and at the age of 4 and 7 y). Top 10 most relevant features were selected according to the reported effect sizes among those selected features (a feature was considered as selected if P-value <0.05 for the EWAS or DLNM or if beta distinct from 0 for the rest of algorithms). Abbreviations: DSA, deletion-substitution-addition algorithm; ExWAS, exposome-wide association study; ENET, elastic net; FDR, false discovery rate; MLR, multiple linear regression; sPLS, sparse partial least-squares.

Figure 3.

Overlaps in selected exposures by each of the tested methods on the real INMA data set. The lower left part of the upset plot shows the number of selected exposures by each of the methods (a feature is considered as selected if its P-value <0.05 for the EWAS or DLNM, or if its beta is distinct from 0 for the rest of algorithms). The vertical red lines and upper histogram part of the figure refer to the overlapping findings between methods (e.g., the first vertical line connecting ENET.opt_AVG, sPLS, sNPLS, DLNMpen_select.by, and sPLS_AVG refers that all these methods identified the same feature, omega-6 fatty acids at the age of 7 y, associated with the waist circumference Z-score at the age of 11 y). The red/green color in exposure names indicates that the exposure has been evidenced as a risk/protective factor by the methods. Abbreviations: DSA, deletion-substitution-addition algorithm; ExWAS, exposome-wide association study; ENET, elastic net; FDR, false discovery rate; MLR, multiple linear regression; sPLS, sparse partial least-squares.

Regarding the findings, the daily intake of polyunsaturated fatty acids omega-6 at the age of 7 years and the inverse distance to the nearest road from home at the age of 6 and 7 years were identified as risk factors for increased waist circumference at the age of 11 years by most of the methods.

According to simulated data, sNPLS was among the top methods for scenario 1 (in which all time points or windows of exposures were associated with the outcome), especially in referring to the identification of the true time point associated with the outcome (Table 1). Since we reckon that this might be the scenario that best fits the INMA exposome data (at least for the air pollution and built environment domain), we focused on its interpretation. The estimated coefficients for each of the significant variables identified by the method can be found in Figure S3. Interestingly, the intake of omega 6 fatty acids at pregnancy and at the age of 7 years was identified by sNPLS as risk factors for higher waist circumference values at 11 years. Another factor identified by the method, not previously highlighted by the rest methods, was the intake of folate at pregnancy, 4 and 7 years, which was inversely associated with waist circumference. Similarly, urban environmental factors such as the distance to the nearest road and the proximity to areas dedicated to other human uses (e.g., dump sites, mineral extraction sites) at the age of 6 and 7 years old were reported to negatively affect waist circumference at 11 years. Interestingly, these associations reinforce previous evidence for the negative effect of omega 6 intake on obesity,^14,15 the protective role of folate (B9 vitamin) on metabolic health and adiposity,^16,17 as well as the obesogenic role of some built environmental factors.¹⁸ Although these findings would need to be validated in replication cohorts, they could be argued on the fact that the developmental processes ongoing during those stages (pregnancy, 4, 7, and 9 years old) are crucial for the future health status of the children and raise awareness of the importance of initiating preventive measurements already from the very early stages of life.

Some unexpected associations were also found by the method, highlighting the risk association between vitamin C intake at pregnancy, 4 and 7 years, and the outcome, which would need further investigation, or the protective role of omega 6 intake at age of 4 years, which could be actually a falsely detected signal since its estimate was very close to zero.

4. Discussion

In this article, we used simulations to test the performance of different methods and strategies to perform variable selection in an exposome context with repeated exposome data that affects a health outcome at a single time point. If the analysts expect that an exposure causally linked to the outcome will have an effect at all time points, good strategies include. sPLS and sNPLS also provided good performance, but their FDR tended to increase more rapidly as the number of exposures associated with the outcome increased. Taking a 2-step strategy, in which the average across time points is screened first, is a good strategy to improve performance, and this is especially true in the case of high correlation between time points. If, alternatively, the analyst expects that only a single time point will be associated with the outcome, DSA (used in a single step) is still a good option; the 2-step approach using the average drastically reduces performance. ExWAS with Bonferroni multiple testing correction also produced good results to detect the right exposure (regardless of the true time point).

Overall, ExWAS with no correction for multiple testing shows a good sensitivity, whatever the scenario. However, it should be kept in mind that this is also the method that showed the highest FDR (∼70–90%; i.e., the methods tend to select many variables, which allows to capture the true ones but also many noncausal exposures, which is overall not very informative); applying a correction for multiple testing, such as a Bonferroni or Benjamini–Hochberg, drastically reduced the FDR (∼20–40%) but also the sensitivity. Similar trends were observed for ExWAS-MLR, but with a clearly lower sensitivity compared to ExWAS. Applying the 2-step approach did not improve the performance of ExWAS but slightly lowered the FDR of ExWAS-MLR, especially under scenario 1. In addition, we observed that, under scenario 1, the ExWAS performances were reasonable in the case of high ICC between the time points. In summary, ExWAS would be the method of choice in the context of a discovery study in which one does not want to leave out predictors truly associated with the outcome, but in view of the high FDR, other methods should be considered in a validation study.

The other variable selection methods tested (ENET, sPLS, and DSA) had an opposite performance to EXWAS: overall, these methods showed low FDR (∼10–30%) but relatively low sensitivity (mostly <60%) in both scenarios. However, acceptable sensitivity (∼70–90%) was reached by sPLS and DSA under scenario 2 and after applying the 2-step approach under scenario 1. The ICC between time points had little impact on these performances. Finally, for the two methods that considered the structure of the data, i.e., that the same variable was measured at different time points, sNPLS and DLNM, we observed good sensitivity for sNPLS but not for DLNM in both scenarios, along with low FDR under scenario 1 and high FDR under scenario 2. The ICC between time points had little impact on these performances.

Data sets were simulated to be as realistic as possible by taking the correlation structure from the existing exposome study HELIX project, which presents many variables from multiple exposome domains (including factors such as climate, urban environment and societal factors, environmental pollutants, tobacco smoke, diet, and physical activity, among others). However, we acknowledge that even though we have explored several scenarios, there are countless possibilities for exposome studies, and indeed, we cannot generalize our findings to all settings. For example, for a given health outcome in a real exposome study, it is difficult to know a priori the number of truly associated exposures. Normally, the variables that are included in an exposome analysis are preselected because there is some plausibility that they may have an effect (usually small) on studied outcomes, so a situation with many causal hits is in principle plausible. Nevertheless, this will always depend on the context, facing sometimes scenarios with just a few causal exposures or others with many of them. Keeping this in mind and considering that some of the most important conducted exposome studies have found between ∼5 and ∼25 factors associated with the examined health outcomes,^18,21–23 we here opted for simulating three different scenarios ranging from only a few to 15 truly associated exposures. This approach, though an oversimplification of the complex realities faced in exposome research, is still the first one providing some guidance in a reasonably realistic setting.

At the same time, we acknowledge that we explored a nonexhaustive list of statistical methods in this simulation study, and there may be many other methods or strategies that could be tested. For example, we a priori ruled out mixture models (i.e., statistical models estimating the combined effect of multiple exposures). In the context of a few numbers of exposure to be tested, some mixture models might be a good alternative, such as the lagged weighted quantile sum regression (which estimates the mixture effect using a weighted index and attempts to model the complex exposure trajectory as a continuous function of time) or the Bayesian kernel machine regression distributed lag model (which estimates nonlinear and nonadditive effects of exposure mixtures while assuming these effects vary over time).^19,20 Strategies involving dimension reduction techniques or classifiers could also be of interest but were not considered in the present study. For all intents and purposes, the code used to simulate data and evaluate the results is available on GitHub repository (see Supporting Information), which gives the possibility to the research community to try other approaches and methods and compare the results. In addition, the situation with repeated measures of both the exposome and the outcome, as frequently encountered in longitudinal cohort studies, was not explored. Some methods, such as penalized generalized estimating equations²⁴ or penalized generalized mixed effect models,²⁵ may be suitable to deal with such design but would need to be tested in the context of a very high number of exposure data. In such a longitudinal study, more scenarios and techniques (e.g., those focusing on trajectories) could be envisioned. Advice on which statistical methods to use in longitudinal exposome studies is still needed.

Besides the simulation experiment, we further applied all tested methods to a “real-world” problem using the prospective population-based Spanish INMA cohort,¹² which shared some common characteristics with the HELIX cohort employed for simulations. For example; INMA is one of the 6 cohorts composing the HELIX population. Likewise, it presents variables belonging to exposome domains that are also present in the full exposome HELIX data (mainly, urban environment, air pollution, and diet). The inclusion of the INMA data as a “real-world” problem, complementary to the “full exposome” simulation experiment, allowed us to highlight some problems not covered during the simulation (“ideal situation”), which are indeed closer to what is of practical applicability for individuals performing exposomic studies. For example, some methods cannot handle categorical exposure variables that were part of the original real data set (e.g., smoking status). We decided to exclude these variables for the demo, but an alternative could be to create dummy variables. Another constraint related to differences in the number of repeated time measurements available by exposure and exposome domains; some exposures were assessed at 3 time points (i.e., diet), while others were available at 5 time points (i.e., air pollution). In that case, we were not able to introduce all exposure variables in a single sNPLS model, and two separated models had to be run, i.e., one with all variables measured three times and another with the variables measured five times. Other specificities of the analysis plan that should be considered before choosing the statistical method are related to the need to be able to adjust for the effects of potential confounding variables and/or to deal with the presence of missing data or multiple imputed data sets. A summary of the main strengths and weaknesses of each method is presented in Table 4.

Table 4. Strengths and Weaknesses of the Different Methods^a.

method	strengths	weaknesses
ExWAS	high sensitivity	high FDR
	easy to implement	repeated design not explicitly considered
	can handle categorical variable
	can handle multiple imputed data sets
ENET	low FDR	repeated design not considered
	can handle multicollinearity	cannot handle categorical variable
		a posteriori inference needed
sPLS	can handle multicollinearity	repeated design not considered
	can model multiple outcomes	not possible to adjust for confounders
		cannot handle categorical variables
		a posteriori inference needed
DSA	low FDR	repeated design not considered
	can handle categorical variable	computing time
	can handle multiple imputed data sets	a posteriori inference needed
DLNM	consider repeated design	cannot handle categorical variables
	flexibility in dose–response shape modeling
sNPLS	consider repeated design	need equal number of time points for all exposures
	can handle multicollinearity	cannot handle categorical variables
	can model multiple outcomes

^aAbbreviations: DSA, deletion-substitution-addition algorithm; ExWAS, exposome-wide association study; ENET, elastic net; FDR, false discovery rate; sPLS, sparse partial least-squares.

The results of the simulation study suggest that DSA is one of the best-performing methods in the context of the tested data structure. When these were applied to the real data, no exposures were selected by this method. DSA is known to be restrictive in including terms, which protects against false positives.² Even though the true result could be that there are no associations or that they cannot be detected with the available sample size, it is likely that analysts seek other methods if no exposures are selected. This could be seen as p-hacking and could increase the number of false positives. However, relevant information could be obtained using other methods with more sensitivity, and more trust in the results can be placed on exposures that are selected by several methods. In our application study, 2 exposures (omega-6 fatty acid intake and proximity to near road) have been selected by almost all the other methods. Ideally, analysts should specify a priori the set of methods that they are going to apply to their data and interpret the results cautiously, owing to the imperfect sensitivity and FDR of these methods, as shown in our simulation study.

In summary, our simulation study based on a realistic exposome study shows that available statistical methods show variable performance across scenarios, making it hard to recommend a strategy that fits all scenarios. Still, some recommendations could be done based on the expected scenario. Our results also show that data-driven results from repeated exposome studies should be interpreted with caution, especially in contexts with a limited sample size, given the elevated chance of reporting false positive or negative associations.

Our approach does not fully cover the complex reality of the exposome, and other exposome studies can reflect issues not covered here. This therefore suggests that more methodological studies are needed for the definition of the best analytical strategy to approach the life-course concept of the exposome, encouraging future research in the field.

Data Availability Statement

All scripts and data set used for this study are available on GitHub repository available here: https://github.com/AugustoAnguita/simulation_repeated_exposures.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.est.3c04805.

• Tables and plots with additional details for the simulation experiment and the real showcase with INMA data including plots on the correlation structure of simulated data, additional results from the simulation experiment not presented in the main text, and the general description of the INMA population and the list of assessed exposome variables (PDF)

Author Contributions

^∇ C.W. and A.A.-R. equally contributed to this work.

The authors declare no competing financial interest.

Special Issue

Published as part of the Environmental Science & Technologyvirtual special issue “ The Exposome and Human Health ”.