Improvement of Norm Score Quality via Regression-Based Continuous Norming

Abstract

The interpretation of psychometric test results is usually based on norm scores. We compared semiparametric continuous norming (SPCN) with conventional norming methods by simulating results for test scales with different item numbers and difficulties via an item response theory approach. Subsequently, we modeled the norm scores based on random samples with varying sizes either with a conventional ranking procedure or SPCN. The norms were then cross-validated by using an entirely representative sample of N = 840,000 for which different measures of norming error were computed. This process was repeated 90,000 times. Both approaches benefitted from an increase in sample size, with SPCN reaching optimal results with much smaller samples. Conventional norming performed worse on data fit, age-related errors, and number of missings in the norm tables. The data fit in conventional norming of fixed subsample sizes varied with the granularity of the age brackets, calling into question general recommendations for sample sizes in test norming. We recommend that test norms should be based on statistical models of the raw score distributions instead of simply compiling norm tables via conventional ranking procedures.

The Significance of Norm Scores in Applied Psychometrics

Critical life decisions in education, medicine, and even the judicial system, are often based on the results of psychometric tests. Individual test results are usually interpreted in comparison to a reference population, that is, a subset of the target population that serves as a standard (cf. American Psychological Association, n.d.). This standard is predominantly reported in the form of norm scores. One of the most drastic applications of norm scores is, for example, the preclusion of people with mental retardation (i.e., with an IQ score <70) from the death penalty in the United States (Duvall & Morris, 2006). Less dramatic but yet very important decisions based on test norms are, for example, school placement or advanced placement (American Educational Research Association, American Psychological Association, National Council on Measurement in Education, 2014), granting of rehabilitative measures (e.g., diagnosis of learning disorders based on a performance of less than the 7th percentile; American Psychiatric Association, 2013), job recruitment (Arthur, 2012), access to elite universities (Duncan & Stevens, 2011) and many more. In all these examples, the comparison between an individuals’ test result and the distribution of test results in the reference population is the basis of the decision. Given that this distribution is usually unknown, it must be inferred from the test results of a normative sample, that is, a subsample of the reference population which is much smaller than the reference population but as representative for it as possible. The statistical procedures used for this inference significantly affect the test outcome and therefore play a vital role in applied psychometrics and applied psychology (cf. Lenhard et al., 2016).

The Origins of Norm Scores in Psychometry

The establishment of norm scores in psychometry is tightly linked to intelligence assessment (e.g., Wasserman, 2018). The first attempts of William Stern (1912) and Lewis Terman (1916) to measure intelligence in such a way that the test results could be compared across different psychometric tests and different age groups drew on the definition of an intelligence quotient (IQ) as mental age divided by chronological age multiplied with 100, thus trying to take into account the growth of cognitive abilities during childhood. This definition had multiple drawbacks, most notably the missing linearity of mental growth across age.

It was the distribution-based approach of David Wechsler (1939) in the Bellevue Intelligence Scale that paved the way for a more statistically sound approach. Wechsler suggested to z-standardize the subtest raw scores drawing on the age-specific distribution parameters M and SD in the reference sample. The resulting z-scores were subsequently transformed into the well-known Wechsler subtest scores (with M = 10 and SD = 3), summed up and transformed into IQ scores (with M = 100 and SD = 15).

Wechsler’s approach was not only driven by the motivation to make test results comparable across different tests and age groups but also to determine the relative location of a test person among the reference group with which this person was compared. In his seminal work “The measurement of adult intelligence” (Wechsler, 1939, p. 34) he even stated that “the important fact about it is this relative standing and not the numerical rating which we may happen to assign to it.” In fact, determining the relative location of a persons’ latent trait (e.g., in the form of percentiles) is still the core aspect of psychometric assessment today, as already described in the introductory section, since the diagnosis of mental disorders and the granting of subsequent treatment is often based on defined cut-points based on percentiles.

Requirements and Limitations of Conventional Norming Procedures

Measurement is generally defined as the assignment of numbers to features in such a way that the numbers reflect the relationships between the features to be measured (e.g., Brosius et al., 2008). Since psychometric tests usually aim at measuring personality traits or abilities, the numeric test scores must therefore reflect these traits. For example, the raw scores obtained in an intelligence test must convey the ranking information with regard to the different intellectual levels of the test persons as precisely as possible. To put it in more technical terms, tests have to be constructed in such a way that the raw scores are a homomorphous function of the latent traits or abilities. To achieve this goal, test constructors put major efforts in item construction, analysis, and selection to establish high test quality in terms of reliability, validity, unidimensionality, homogeneity, and so on (e.g., Eid & Schmidt, 2014; Kline, 2015; McDonald, 1999). Unfortunately, the calculation of norm scores is often viewed more as a routine task. There are, however, a number of challenges which must be mastered in the norming process.

First of all, the normative sample has to be as representative as possible of the reference population. To establish this representativeness, some test authors rely on random sampling (cf. Bracken, 1988; Gregory, 1996). In case of unbalanced data sets, the sample should additionally be stratified according to covariates that influence the test results most significantly, such as sex, region, or ethnical background. Stratification is especially necessary in the case of small sample sizes, since they are more prone to imbalances.

If, however, the confounding variable in question does not only affect the raw score but also defines the reference population, stratification will not even suffice to get to the desired result. For example, in the case of IQ assessment, the location of a test person is determined with respect to a reference population of the same age only. (In the following, we will generally refer to such variables as explanatory variables.) Therefore, the normative samples must usually be partitioned into smaller subsamples (e.g., age brackets). For conventional norming procedures, subsample sizes of n = 250 to n = 500 are recommended to generate norms with sufficiently high precision (depending on the intended diagnostic purpose and the scale properties; Eid & Schmidt, 2014; Oosterhuis et al., 2016).

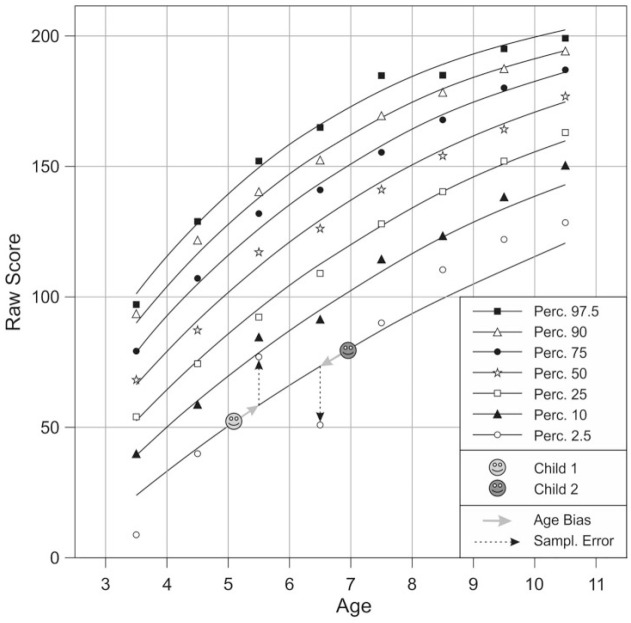
An important question in this context is how the width of the age brackets affects the accuracy of the norm scores. In the case of intelligence assessment or developmental tests, the raw scores change rather quickly with age. If, in such cases, the age brackets are chosen too large, significant jumps between the norm tables of the subsamples will occur (Lenhard et al., 2016; Bracken, 1988; Voncken et al., 2019a; Zachary & Gorsuch, 1985). These jumps lead to errors because the age of a test person might deviate considerably from the average age of the respective age bracket. For example, children at the lower boundary of an age bracket are mainly compared with older children, and vice versa. Consequently, the performance of children at the lower boundary of the age bracket is underestimated, while the performance of children at the upper boundary is overestimated. This age-related norm score bias, which increases with the width of the age brackets and the gradient of the measured ability across age, is depicted in Figure 1. The data are taken from an unstratified data pool of a vocabulary test for children (Lenhard et al., 2015). The sample was split up into age brackets of 1 year each to illustrate the effect. The solid lines represent the assumed continuous development of the raw scores across age. The smileys represent two children, the first one (light gray) being 5 years and 1 month old with a raw score of 52, the second one (dark gray) being 6 years and 11 months old with a raw score of 79. According to the solid lines, both children should be assigned a percentile of 2.5. However, in the age bracket of the 5-year-olds, children at percentile 2.5 have expected raw scores spanning from 50 to 70 with an average raw score of approximately 60. Therefore, Child 1 will be assigned a percentile below 2.5. In contrast, the opposite effect occurs with the second child (cf. Bracken, 1988). It might seem that the age bracket of 1 year is chosen deliberately large in this example to depict the effect overly dramatic. Yet some intelligence tests in fact deliver such coarse-grained norms (e.g., Kubinger & Holocher-Ertl, 2014).

Figure 1.

Sources of error with conventional norming. A first source of error originates from age brackets of finite width. As a consequence, test persons are compared with a reference group that may be younger or older on average. The second source of error is due to random sampling.

The age brackets should therefore under no circumstances be chosen too wide. On the other hand, splitting up into narrow age brackets quickly leads to enormously large sizes of the total sample. Imagine, for example, an intelligence test spanning 10 years. If the age brackets were chosen with a width of 3 months and a subsample size of n = 500 each, the total size of the normative sample would have to be N = 20,000-a figure that in most cases probably lies far beyond feasibility. Therefore, the trade-off between total sample size and width of the age brackets must be balanced carefully.

Once the subsamples have been established, the next crucial step is to convert the raw scores into norm scores. As already described above, the numeric test scores assigned to the test persons must reflect the latent traits and abilities to be measured. This requirement applies not only to the raw scores but also to the norm scores. What is even more, the transformation of raw scores into norm scores must not only maintain the ranking order between any two individuals. In addition, the norm scores must exactly indicate, how many people in the reference population have a lower or the same level of the latent trait, that is, they are supposed to indicate the location of the test person with respect to the reference population. Technically speaking, norm scores must represent a specific bijective function of the latent trait. From the well-known law of large numbers, it can be derived that latent traits or abilities must be normally distributed, because they are usually shaped by a large number of variables (cf. Andersen & Madsen, 1977). This is especially true for abilities such as intelligence. If the raw scores were perfectly normally distributed, too, then the norming procedure suggested by Wechsler would actually return norm scores that could be transformed into percentiles by simply using the cumulative normal distribution. But perfect normal distribution of the raw scores is rarely given. Instead, raw score distributions are almost always more or less skewed, at least in some age groups. What remains constant, though, is the ranking information. Therefore, many test constructors apply inverse normal transformation (INT), that is, they start by determining the cumulative distribution function (CDF) of the raw scores and subsequently use the inverse normal CDF to assign norm scores to the observed percentiles, thereby mapping the raw score distribution onto a normal distribution. We will refer to this method as conventional norming in the following. It is important to note that the resulting norm scores do not indicate how many standard deviations the raw score of an individual is below or above the average raw score of the reference population. Instead, they are supposed to indicate how many standard deviations the hypothesized latent trait of an individual is below or above the average latent trait.

Many test constructors consider the norming process to be finished at this point. For example, we know of only one school achievement test in Germany using advanced modelling techniques instead of the conventional norming. (It happens to be our own test, Lenhard et al., 2017). Although it has occasionally been discussed, whether INT should be applied in the case of large deviations from the normal distribution (Soloman & Sawilowsky, 2009), other severe drawbacks of this data-driven norming procedure have received less attention.

A first drawback is that errors resulting from random sampling are either completely included in the norm tables or they are at best poorly corrected by hand. The sampling errors are usually of varying magnitude in the different subsamples, which may be even exacerbated by the fact that sometimes not all subsamples can be stratified accurately. As a consequence, the sequence of raw scores assigned to a certain percentile across age usually is not smooth but rather jagged. This effect is also depicted in Figure 1. The dots in this figure represent the CDFs calculated per age bracket. In some cases, they deviate considerably from the solid lines, which represent the expected smooth developmental curve. For example, the dot representing the 2.5th percentile in the age bracket of 5-year-olds corresponds to a raw score of 77 whereas the according dot in the age bracket of 6-year-olds corresponds to a raw score of only 51. A 5-year-old would therefore need a higher raw score than a 6-year-old to attain the same percentile. Obviously, the numbers in this case do not reliably reflect the relationships between the latent traits to be measured. Note that the term reliability, as defined in classical test theory, is supposed to specify the proportion of error variance contained in test scores. Interestingly, though, the standard methods used to determine reliability indices exclusively draw on raw scores. Yet the confidence intervals—which are based on these indices—are specified for the norm scores, not for the raw scores. As a consequence, the error variance contained in norm scores is not fully covered by conventional confidence intervals, that is, they do not reflect the error variance resulting from the norming procedure. Unfortunately, this shortcoming has seldom been the subject of scientific debate (Voncken et al., 2019b). Therefore, we designed our study in such a way that we could determine the error variance caused by the test items and the error variance caused by the norming method separately. We will later on analyze the proportion of error variance, the norming procedure adds to the test scores. Furthermore, we will define a reliability index to evaluate the different norming procedures. This index is an equivalent to the classical reliability index for test scales. It specifies the proportion of error variance introduced to test scores by a specific norming procedure and could theoretically be used to calculate more realistic confidence intervals. Furthermore, it can be used to compare the error variance the norming process alone contributes to the test scores with the error variance produced by the items. To the best of our knowledge, this has never been done numerically before. It is particularly important, though, because some test constructors are of the opinion that norming is far from being as important as is generally assumed, specifically if the impact of norming is compared with the impact of item selection (e.g., Lienert & Raatz, 1998).

A final problem of conventional norming we want to mention here is that the norm tables can be plagued with gaps because of missing raw scores in some subsamples (cf. Bracken, 1988). For example, in the data set depicted in Figure 1, the lowest raw score was 55 in the age bracket of 5-year-olds, but 24 in the age bracket of 6-year-olds. The higher the number of items and the lower the subsample size, the higher is, of course, the number of missings. Moreover, some achievement tests contain norm tables that apply to specific points in time only, for example, to the midterm and/or the end of a school year (e.g., Stock et al., 2017). This means that sometimes, there are not only missings within norm tables but also large gaps between norm tables. These gaps are particularly problematic because in diagnostic practice the existing norm tables are often applied whenever an achievement test is needed, that is, they are used beyond the specified time slots.

Semiparametric Continuous Norming

To overcome some of the problems of conventional norming, different continuous norming methods have been developed modelling norm scores as functions of the explanatory variable. Again, the development of these advanced methods was mainly inspired by intelligence assessment, starting with the WAIS-R (Gorsuch, 1983, quoted from Zachary & Gorsuch, 1985) in the United States and the SON-R 5 $\frac{1}{2}$ –17 (Snijders et al., 1989) in the Netherlands. As far as we know, the application of these methods is still rather restricted to the field of intelligence assessment (e.g., WISC-V, Wechsler, 2014; KABC-2, Kaufman & Kaufman, 2004; SON-R 6-40, Tellegen & Laros, 2012; IDS-2, Grob & Hagman-von Arx, 2018). Clearly, intellectual assessment strongly profits from continuous norming, since intellectual performance heavily depends on age (e.g., Horn & Cattell, 1967). Yet this does not mean that advanced norming methods can only be applied to intelligence tests. After all, there are many other abilities and personality traits that develop with age. In addition, quite different continuous covariates are conceivable, which could be important at least for some diagnostic purposes, such as duration of schooling, socioeconomic level, weight, and so on. For example, we ourselves have used continuous norming to successfully model not only vocabulary acquisition (Lenhard et al., 2015), reading fluency and reading comprehension (Lenhard et al., 2017) or competence levels in foreign language acquisition (Lenhard et al., in press) but also body mass index and reaction times (Lenhard al., 2018). Other examples for the application of advanced norming procedures have been demonstrated with regard to clinical questionnaires (van Breukelen & Vlaeyen, 2005) and attention deficits (Stemmler et al., 2017).

Although the different continuous norming methods vary in their assumptions about the raw score distributions and modeling procedures, they do share the common feature of a statistical model being established based on the normative data. These models are subsequently used to interpolate between the age brackets (horizontal interpolation), close the missings between the achieved raw scores (vertical interpolation), and smooth the norm score distributions horizontally and vertically. They can as well be used to extrapolate to ability or age levels beyond the ones contained in the normative data, though extrapolation should be applied cautiously, of course. The norming methods do not only reduce the required total sample size (e.g., Zhu & Chen, 2011), but they can also decrease the error variance introduced into the test scores through the norming procedure (Lenhard et al., 2016; Oosterhuis et al., 2016).

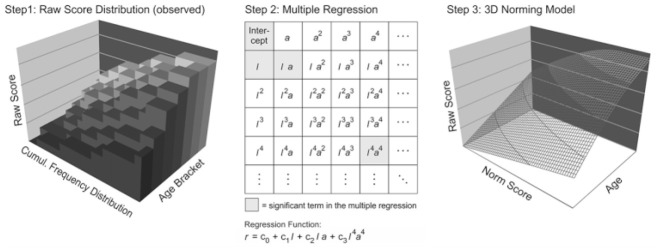
In this article, we focus on a semiparametric continuous norming approach (SPCN; Lenhard et al., 2016, 2018, 2019). The essential steps of the method are illustrated in Figure 2.

Figure 2.

Steps in modeling three-dimensional norming functions with semiparametric continuous norming (SPCN). The raw scores are modeled as a function of person location and age via multiple regression, thus, fitting a hyperplane to the data that reduce noise and interpolate missings.

The approach draws on the assumption that the expected raw score r of an individual is a function f of his or her person location with respect to a latent ability θ and one or several explanatory variables a. In the following, we will concentrate on the explanatory variable that probably plays the most important role in norming, namely age. In this specific simulation, we will use it together with a one-parameter logistic (1-PL) measurement model. SPCN starts the modeling process by using INT to compute conventional norm scores per age bracket, which are used as preliminary estimates l of the age-specific person locations (Figure 2, Step 1). The aforementioned function f can subsequently be modeled via the following polynomial (Lenhard et al., 2016, 2019):

$$r=\sum _{s,t=0}^k{c}_{\mathrm{st}}{l}^s{a}^{t.}$$ (1)

In this equation, k denotes a smoothing parameter which can be chosen as needed with higher values leading to higher explanation of variance and lower values leading to smoother curves (Figure 2, Step 2). Based on our experience, a value of 4 will in most cases lead to smooth curves while at the same time fitting the model with a multiple R² > .99 (Lenhard et al., 2016, 2019). The polynomial described in Equation (1) contains a total of 2k+k² variable terms plus the intercept, which are used to predict the raw scores. The mathematical background of this approach has been described in more detail elsewhere (Lenhard et al., 2016, 2019). Therefore, in the present article we would like to summarize these descriptions by pointing out that the principal polynomial approach can be used to model virtually any function with sufficiently high accuracy as long as the function is smooth and continuous. To meet these requirements, the discrete raw scores must be underlaid with a continuum. The assumption of an underlying continuum has, however, been proven to be generally valid for modeling purposes (cf. Hansen, 2004) and applies to all forms of continuous norming (e.g., Oosterhuis et al., 2016; Voncken et al., 2019a).

In order to avoid overfit, it is advisable not to include the full number of 2k+k² terms in the regression function, but to select a minimum number of terms with the highest relevance. This selection problem can be solved via different approaches as, for example, stepwise regression, ridge, lasso and elastic net regularization (e.g., “glmnet” package, Friedman et al., 2010) and other methods. In the current version of our approach, we use best subset regression (Miller, 2002; R package “leaps”; Lumley, 2017) to select the respective coefficients c_st (Figure 2, Step 2; Lenhard et al., 2019). The subset regression approach tests all possible combinations of predictors and returns the models with the highest $R_{\mathrm{adjusted}}^2$ for any specified number of terms. $R_{\mathrm{adjusted}}^2$ increases with the number of terms included in the regression equation. As a consequence, the number of terms is a second, more fine-tuned smoothing parameter, with low numbers again leading to smooth curves and high numbers leading to a more detailed mapping of the empirical raw data. In most practical cases, a very small number of terms in the regression function (e.g., four) is sufficient to model the norming data with a data fit of $R_{\mathrm{adjusted}}^2$ > .99 (Lenhard et al., 2019), that is, the regression leads to very efficient models while minimizing noise and error variance. Graphically speaking, the procedure approximates the observed data through fitting a hyperplane to the empirical data (Figure 2, Step 3). In order to reduce the danger of overfit, it is advisable to keep the number of terms as low as possible and to cross-validate the retrieved models.

Rationale and Goals of the Present Study

The conditions, under which a new method performs better or worse than other methods, have to be assessed carefully. For example, we have already compared SPCN with another continuous norming approach, namely, parametric continuous norming. SPCN in general performed very well and its application was particularly favorable when applied on skewed raw score distributions and when using subsample sizes less than n = 250 (Lenhard et al., 2019). In the study reported here, we will compare its performance with regard to conventional norming under different sample sizes. To this end, we drew normative samples of different sizes from a simulated population with known population parameters. These normative samples were subjected to fictitious item response theory (IRT)–based test scales with varying item difficulties and item numbers, thereby simulating test results with different skewness of the raw score distributions. We subsequently generated norm scores with SPCN and conventional norming. In a previous study, we showed that SPCN is largely invariant to the width of the age brackets (Lenhard et al., 2016). The same does not hold true for conventional norming. We expected that the age bias of the conventional norms would increase with the width of the age brackets, since the age variance within each bracket increases. If, on the other hand, the total sample size is fixed, the subsample size increases with the width of the age brackets, which simultaneously reduces the sampling error. Therefore, we additionally varied the width of the age brackets in four levels (1 month, 3 months, 6 months, 12 months) when using conventional norming, in order not to disadvantage this method by selecting a particular unfavorable condition. The real-world analogy would be a normative data set with a continuous age distribution where the test constructor has to decide, how fine-grained the age brackets should be, taking into account the trade-off between age bias and subsample size.

The quality of the norming methods was determined by use of a very large and representative cross-validation sample. On the basis of the “ideal norms” determined in the cross-validation sample, we calculated different measures of norm score quality. Furthermore, we compared the proportion of error variance the different norming procedures add to the test scores. In line with the existing continuous norming literature (e.g., Lenhard et al., 2016; Oosterhuis et al., 2016; Zhu & Chen, 2011), we assumed that conventional norming would lead to a higher proportion of error variance than SPCN, particularly when used together with small sample sizes, because the regression draws on the complete normative sample instead of the subsamples only. In addition, we also expected to find the obvious advantages of continuous norming procedures, namely, a reduction of missings in the norm tables.

Specifically, we assessed the following hypotheses:

• Hypothesis 1: The overall norming error will be lower when SPCN is used as compared with conventional norming.

• Hypothesis 2: The size of the normative sample will have a lower impact on the overall norming error when SPCN is used as compared with conventional norming.

• Hypothesis 3: Conventional norming will lead to a considerably larger number of missings in the norm tables compared with SPCN. The number of missings will increase as the subsample size decreases and as the number of items increases.

Method

Procedure

To simulate normative data, we repeatedly drew random samples from a predefined population and subsequently generated test results for test scales with three different difficulties (syntax, data, a complete simulation cycle, descriptives of the raw data distributions, and aggregated results are available via https://osf.io/ntydc/). We delineate only the most important features below, because this simulation procedure was described in detail in Lenhard et al. (2019).

The simulation process included the following central steps: (a) simulation of normative samples on the basis of the population model, (b) simulation of test scales with n items of varying average item difficulty, (c) using the test scales to generate raw score distributions for the normative samples and a representative cross-validation sample by means of a 1-PL measurement model, (d) retrieving norm scores based on the normative samples by using INT per age group (conventional norming) or SPCN, (e) cross-validation of the different approaches by computing conventional norm scores for the large cross-validation sample and comparing them with the norm scores that would have been assigned to each person based on the much smaller normative samples.

Simulation of Normative Samples Based on the Population Model

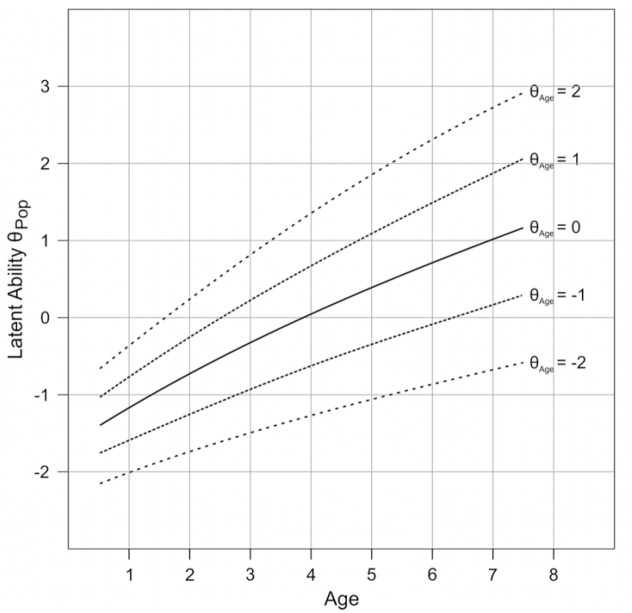
Each person in the simulated population was assigned an age variable a and a fictitious latent ability θ_Pop. The uniformly distributed age variable comprised 7 years, starting with 0.5 and ending with 7.5. It is important to note that θ_Pop was normally distributed at each single age level, but not across the whole age range. Instead, it increased curvilinearly across age with a slight scissor effect (see Figure 3). This means, the development across age was not linear, but slowed down with increasing age, while the standard deviation slightly increased. This type of development is common for many ability domains in childhood and adolescence and can be found in our own psychometric tests on vocabulary (Lenhard et al., 2015) and reading comprehension (Lenhard et al., 2017), too. The precise numeric description of the population model is available in Lenhard et al. (2019). θ_Pop was z-standardized across the whole age range, in order to be able to apply it together with the 1-PL model to produce test scores. In addition, we z-standardized θ_Pop per age level, which led to a second latent trait score θ_Age. This second latent trait score was used to determine the “true” location of the person with respect to other persons of the same age. Consequently, each person was characterized by three variables: (a) age (uniformly distributed across the whole age range), (b) the latent ability θ_Pop, which indicated the person location with respect to the whole population, and (c) θ_Age, which referred to the same latent ability, however, this time with regard to persons of the same age only.

Figure 3.

Population model: The normally distributed θ_Age specifies the person location determined with respect to persons of the same age only. By contrast, θ_Pop corresponds to the person location with respect to the total population (cf. Lenhard et al., 2019).

The normative samples consisted of N = 700, 1,400, 2,800, 5,600, 11,200, or 22,400 in total, and thus covered the complete range of rather small normative samples (100 cases per year with N = 700) up to very large samples, which would probably only be available through large-scale assessments. The samples were randomly drawn from the population, that is, the normative samples were afflicted with the regular but unsystematic sampling error.

For the cross-validation sample, we generated a completely representative sample of n = 10,000 cases per month, amounting to a total of N = 840,000 cases per simulation cycle. To avoid age bias (as described in the introduction) in the cross-validation, we set the age of each person in this cross-validation sample exactly to the center of the respective months. The person locations in the cross-validation sample followed the same population model as in the normative samples but were not randomly drawn either. Instead, θ_Age was perfectly normally distributed within each age bracket, with equidistant percentiles ranging from $\frac{0.5}{n}$ to $\frac{n-0.5}{n}$ . These properties of age and latent ability θ_Age in the cross-validation sample remained constant in all simulation cycles. The raw scores of the cross-validation sample were, however, generated anew in each cycle based on the simulated test scales (see the “Simulation of Test Scales” and “Generating Raw Scores for the Normative and Cross-Validation Sample” subsections).

Simulation of Test Scales

We simulated test scales with 10, 20, 30, 40, or 50 items. We used these item numbers to cover a broad range of possible test scenarios, with 10 items representing a rather small and unreliable test scale, and 50 items representing a medium to large test scale. For instance, most test scales of the WISC-V (Wechsler, 2014) and the KABC-2 (Kaufman & Kaufman, 2004) range between a maximum raw score of 20 and 50. We refrained from including larger item numbers, since the computational effort for the entire simulation was already enormously high and we did not expect qualitatively different results with higher item numbers. In each simulation cycle, the item difficulties δ _i were drawn randomly from normal distributions with mean item difficulties of M_easy = −1, M_medium = 0 or M_difficult = 1 and a standard deviation of SD = 1 for all scales. Thus, the range of item difficulties was not restricted, but the scales exhibited differences in the mean scale difficulty. The medium test scale mimicked a test scenario, where most of the ability levels are covered well across all age levels. The accumulation of item difficulties in the medium difficulty range for this scale corresponds to real test construction, as items with extreme difficulties are sorted out more often than items with medium difficulty due to their lower discriminative power. In contrast to the medium test scale, the easy and difficult scales were designed such that they differentiated best in the lower or upper age ranges, respectively. The easy scale resulted in mild to medium ceiling effects at older age levels, and the difficult test scale resulted in medium to large bottom effects at the younger age levels. Again, our aim was to cover all kinds of test scenarios as realistically as possible. For example, even a widespread intelligence test like the KABC-2 (Kaufman & Kaufman, 2004) displays considerable skewness of the raw score distributions at extreme age levels in more than half of all subtest scales.

Generating Raw Scores for the Normative and Cross-Validation Sample

For each person of the normative and the cross-validation sample, we simulated the item responses in accordance with a 1-PL IRT model. We chose this model for three major reasons. First, the item response theory is one of the most important theoretical models to explain how a latent ability interacts with items and scale parameters and finally results in a raw score distribution. It therefore offers a rather simple but plausible way to generate raw score distributions corresponding to real-world data. More precisely, we do not need to make specific assumptions about the raw score distributions themselves, apart from the assumption that they result from an interaction between the latent trait of a certain individual and the test items. Second, both the normative data and the representative cross-validation data could be generated in the exact same way. Third, since we started by assigning a “true” latent ability to each person, it was not only possible to compare the raw score distributions in the normative sample with the raw score distributions in the cross-validation sample. Additionally, and even more importantly, we could determine how well the raw scores and the resulting norm scores cover the latent ability.

To generate the response of person i to item j of a test scale, we computed the probability of success of that person on each item via the 1-PL logistic function (De Ayala, 2009; Embretson & Reise, 2000; Rasch, 1980; Wright & Stone, 1979; source code available as the “simRasch” function in cNORM, Lenhard et al., 2018):

$$p(x_{\mathrm{j}}=1|{\mathrm{\theta }}_{\mathrm{Pop}i},{\mathrm{\delta }}_{\mathrm{j}})=\frac{e^{{\mathrm{\theta }}_{\mathrm{Pop}\mathrm{i}}-{\mathrm{\delta }}_j}}{1+e^{{\mathrm{\theta }}_{\mathrm{Pop}\mathrm{i}}-{\mathrm{\delta }}_j}}.$$ (2)

p(x_j = 1| θ_{Pop i}, δ_j) specifies the probability that a person i with the latent ability θ_{Pop i} succeeds on an item j with the given difficulty δ _j . For each item j and person i, we drew a uniformly distributed random number ranging from 0 to 1 and compared this number with the person’s probability to succeed. In case p(x_j) was equal or higher than the random number, the person scored one point, otherwise zero points. Eventually, the item responses were summed up to a total score, which served as the raw score this person received in the test scale.

On average, the simulated raw score distributions showed a negative skew of g_m = −0.506 for the easy, a small positive skew of g_m = 0.145 for the medium, and a highly positive skew of g_m = 0.859 for the difficult scales. Detailed descriptive data on the raw score distributions per half year age bracket are available for the normative and cross-validation sample in the OSF repository. The repository also includes the data of one complete simulation cycle with item difficulties, raw data, and cross-validation data per condition.

Statistical Modeling of the Raw Score Distributions and Compilation of Norm Score Tables

To establish norming models according to the SPCN approach, we used the cNORM package (Lenhard et al., 2018) available for the R platform. The ranking function needed for the estimation of the location l was set to “rankByGroup” with a width of 6 months, which means that the percentiles for each person were estimated for each half-year bracket of the norm sample before applying the statistical modeling. The results of the procedure are, however, relatively invariant against the bracket width with 6 and 12 months returning almost identical models (Lenhard et al., 2016). The multiple regression was performed with the default setting of k = 4 as the maximum degree of the polynomial, resulting in a polynomial with 24 terms at most. We started with four as the default number of terms and only searched for different solutions when the resulting model showed violations against monotonicity, that is, when the relation between raw scores and norm scores at a given age was not monotonically increasing throughout the whole data set. The monotonicity check was based both on determining the polynomial roots of the first-order derivative of the regression function and on numeric search (method “checkConsistency” of the cNORM package). In case of violations, we repeated the modeling beginning with three terms and subsequently increased the number of terms in the regression function until a model without such inconsistencies was found. In 70% of all simulation cycles, this procedure resulted in a norming model with only six terms or less.

In order to disentangle the effects of sample size and width of the age brackets, we split up the normative samples in subsamples of the width of 1 month, 3 months, 6 months, and 12 months, respectively, when using conventional norming. Table 1 gives an overview over the average subsample sizes as a function of the total sample size and the width of the age brackets.

Table 1.

Subsample Sizes as a Function of Total Sample Size and Width of the Age Brackets.

	Total sample size N
Age bracket	N = 700	N = 1,400	N = 2,800	N = 5,600	N = 11,200	N = 22,400
1 Month	8.3	16.7	33.3	66.7	133.3	266.7
3 Months	25	50	100	200	400	800
6 Months	50	100	200	400	800	1,200
12 Months	100	200	400	800	1,600	3,200

We subsequently performed INT for each age bracket and automatically compiled norm score tables for the transformation of raw scores into norm scores, which included all raw scores that had occurred in the respective subsamples.

Since all norm scores will be expressed as T-scores (M_T = 50 and SD_T = 10) in the following analyses, we will subsequently refer to norm scores produced with a certain method as T_Method. The different conventional norming conditions will be abbreviated to CN1, CN3, CN6, and CN12 for the respective age brackets of 1 month, 3 months, 6 months, and 12 months.

Cross-Validation

In the cross-validation sample, we also applied INT to the empirical CDF of the raw scores in each subsample. Given that the total sample was perfectly representative and included 840,000 cases with n = 10,000 per subsample, we assumed that the resulting norm scores contained almost no norming error and therefore represented an upper boundary for the quality of any norming procedure. The fact that these norm scores are nevertheless no perfect predictors of the latent abilities (R² < 1) can therefore be completely traced back to limitations of the scales (distribution of item difficulties; bottom and ceiling effects, limited number of items . . .), but not to the norming procedure. We will refer to these norm scores as T_Ideal in the analyses.

To be able to compare the different norming methods, we also assigned to each person in the cross-validation sample the five different norm scores that had been assigned to the raw score of this person on the basis of the much smaller normative sample, namely, T_SPCN, T_CN1, T_CN3, T_CN6, and T_CN12.

Assessment of Model Fit and Definition of the Dependent Measures

We used various measures to determine different aspects of the model fit.

Root Mean Square Error (RMSE) and Mean Signed Difference (MSD)

RMSE is the standard measure of model fit. In our simulation, it was defined as follows:

$$\mathrm{RMSE}=\sqrt{\frac{1}{840,000}\times \sum _{i=1}^{840,000}{(T_{\mathrm{Method}}-T_{\mathrm{Ideal}})}^2}.$$ (3)

The RMSE reflects an overall measure of the error introduced by the norming procedure, that is, it captures constant as well as variable errors of the norming procedure.

The MSD, by contrast, only reflects constant dislocations of the norm scores within each simulation cycle. It is defined as

$$\mathrm{MSD}=\frac{1}{840,000}\times \sum _{i=1}^{840,000}(T_{\mathrm{Method}}-T_{\mathrm{Ideal}}).$$ (4)

Since the average sampling error is expected to be zero in this simulation, the MSD should also be zero when averaged over multiple simulation cycles, regardless of the total sample size. If it is not, this may be due to the fact that a certain method produces constant dislocations of the norm scores in one specific direction under certain conditions (e.g., for certain scale difficulties). Therefore, the MSD is a measure of how accurately the method can cover raw score distributions with specific properties as, for example, skewness.

Proportion of Error Variance

For the following comparisons, the latent variable θ_Age was also transformed from a z-score to a T-score for each person in the cross-validation sample so that the variances of the different scales could directly be compared.

In classical test theory, the reliability of a test scale is usually expressed as the proportion of variance in the true score that can be predicted from the raw scores. Under the assumption that raw scores can be converted into norm scores without additional error or loss of information (as is approximately the case for T_Ideal), the coefficient of determination R² between θ_Age and T_Ideal therefore equals the reliability REL_Raw of the respective scale:

$$\mathrm{RE}{L}_{\mathrm{Ideal}}=\mathrm{RE}{L}_{\mathrm{Raw}}=\frac{\mathrm{Var}\left({\mathrm{\theta }}_{\mathrm{Age}}\right)}{\mathrm{Var}\left(T_{\mathrm{Ideal}}\right)}=R^2({\mathrm{\theta }}_{\mathrm{Age}};T_{\mathrm{Ideal}}).$$ (5)

The proportion of error variance (PEV) contained in the ideal norm scores respectively in the raw scores can subsequently be calculated as follows:

$$\mathrm{PE}{V}_{\mathrm{Ideal}}=\mathrm{PE}{V}_{\mathrm{Raw}}=1-\frac{\mathrm{Var}\left({\mathrm{\theta }}_{\mathrm{Age}}\right)}{\mathrm{Var}\left(T_{\mathrm{Ideal}}\right)}=1-R^2({\mathrm{\theta }}_{\mathrm{Age}};T_{\mathrm{Ideal}}).$$ (6)

Note that this proportion of error variance is not due to the norming procedure but only due to the deficiencies of the test scale.

Since the norm scores are, however, flawed with errors, the proportion of error variance contained in T_SPCN, T_CN1, T_CN3, T_CN6, and T_CN12 is higher than the proportion of error variance contained in the ideal norm scores. We will refer to the proportion of error variance contained in the norm scores as PEV_Total in the following, because it contains measurement error on the level of the raw scores as well as additional error due to the norming procedure:

$$\mathrm{PE}{V}_{\mathrm{Total}}=1-\frac{\mathrm{Var}\left({\mathrm{\theta }}_{\mathrm{Age}}\right)}{\mathrm{Var}\left(T_{\mathrm{Method}}\right)}=1-R^2({\mathrm{\theta }}_{\mathrm{Age}};T_{\mathrm{Method}}).$$ (7)

The proportion of error variance caused exclusively by the norming procedure can therefore be calculated by the following equation:

$$\mathrm{PE}{V}_{\mathrm{Norm}}=\mathrm{PE}{V}_{\mathrm{Total}}-\mathrm{PE}{V}_{\mathrm{Ideal}}=R^2({\mathrm{\theta }}_{\mathrm{Age}};T_{\mathrm{Ideal}})-R^2({\mathrm{\theta }}_{\mathrm{Age}};T_{\mathrm{Method}}).$$ (8)

Definition of Reliability Index for Norming Procedures

We furthermore define the reliability REL_Norm of a specific norming procedure as the proportion of variance in the latent ability the actual norm scores can predict, divided by the proportion of variance ideal norm scores can predict:

$$\mathrm{RE}{L}_{\mathrm{Norm}}=\frac{\mathrm{Var}\left({\mathrm{\theta }}_{\mathrm{Age}}\right)}{\mathrm{Var}\left(T_{\mathrm{Method}}\right)}:\frac{\mathrm{Var}\left({\mathrm{\theta }}_{\mathrm{Age}}\right)}{\mathrm{Var}\left(T_{\mathrm{Ideal}}\right)}=\frac{\mathrm{Var}\left(T_{\mathrm{Ideal}}\right)}{\mathrm{Var}\left(T_{\mathrm{Method}}\right)}=\frac{R^2({\mathrm{\theta }}_{\mathrm{Age}};T_{\mathrm{Method}})}{R^2({\mathrm{\theta }}_{\mathrm{Age}};T_{\mathrm{Ideal}})}.$$ (9)

Finally, REL_Total, which is the proportion of variance the norm scores share with the true latent score, can be expressed as the product of REL_Raw and REL_Norm:

$$\mathrm{RE}{L}_{\mathrm{Total}}=\mathrm{RE}{L}_{\mathrm{Raw}}.\mathrm{RE}{L}_{\mathrm{Norm}}=R^2({\mathrm{\theta }}_{\mathrm{Age}};T_{\mathrm{Ideal}}).\frac{R^2({\mathrm{\theta }}_{\mathrm{Age}};T_{\mathrm{Method}})}{R^2({\mathrm{\theta }}_{\mathrm{Age}};T_{\mathrm{Ideal}})}=R^2({\mathrm{\theta }}_{\mathrm{Age}};T_{\mathrm{Method}}).$$ (10)

REL_Norm can be interpreted as a global measure of the precision of a certain norming procedure that is independent of the specific scale on which the procedure is applied. Moreover, it can be multiplied with classical reliability indices to retrieve the total reliability of a norm score, that is, the degree to which this norm score is able to predict the latent ability. If, for example, the conventionally computed reliability index of a test was REL_Raw = .90 and the norming procedure had a reliability of REL_Norm = .95, the de facto reliability of the norm scores would only be REL_Total = .90 * .95 = .86. REL_Norm is easy to interpret, but it only accounts for the general shape and course of the modeled distributions. It does not capture dislocations or constant biases that affect all norm scores equally. Therefore, it is only applicable to those norming methods with an MSD close to zero.

Number of Missings

Finally, we also counted the missings. They were defined as percentage of persons in the cross-validation sample for whom no norm score could be determined because the corresponding raw score had not occurred in the normative sample.

Data

The simulation was repeated 1,000 times for each combination of parameters, resulting in a total number of 6 (size of the normative sample) × 3 (scale difficulty) × 5 (number of items) × 1,000 repetitions = 90,000 cycles.

Statistical Analyses

We analyzed RMSE, MSD, and the number of missings in the norm tables with repeated-measures analyses of variance (ANOVAs), with method (SPCN, CN1, CN3, CN6, and CN12) serving as within factor and total sample size (N = 700, 1,400, 2,800, 5,600, 11,200, and 22,400), item number (10, 20, 30, 40, and 50) and scale difficulty (easy, medium, and difficult) serving as the between factors. For specific hypotheses and post hoc analyses, we drew on one-way ANOVAs. Due to the high number of repetitions for all combinations of the independent variables, the ANOVA was very robust against violations of homoscedasticity and normality requirements (cf. Eid et al., 2017). Furthermore, the significance level for all tests was set to α = .001 to reduce Type I errors. A power analysis with GPower (Faul et al., 2009) showed a β > .9999 for all analyses on main effects, interactions and post hoc tests. This means that the ANOVA was robust yet extremely powerful enough to detect even the smallest main effects and interactions.

Given that the statistical power was extremely high, we will additionally report effect sizes in the form of partial η² and interpret only effects with η² > 3%, which approximately corresponds to at least small effect sizes (Cohen, 1988).

Since PEV_Norm and REL_Norm are different measures of the proportion of error contained in test scores, the inferential statistical analysis of these scores does not provide any other results than the evaluation of the RMSE with regard to the different methods. What is different, however, is the fact that the two parameters are not absolute but relative measures of error, that is, they are independent of the used scaling, and therefore provide easy interpretation. Moreover, the impact of the norming procedure can be compared with the impact of the item selection. For this reason, we will provide only descriptive data for the two parameters, but we will add a few fictitious calculation examples using realistic test parameters in order to demonstrate the importance of a balanced norming procedure.

Results

Precision and Accuracy of the Norm Scores in Terms of RMSE and MSD

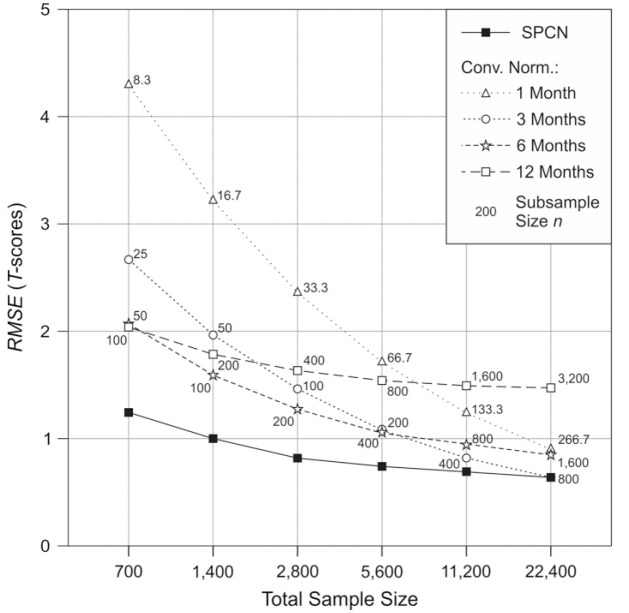
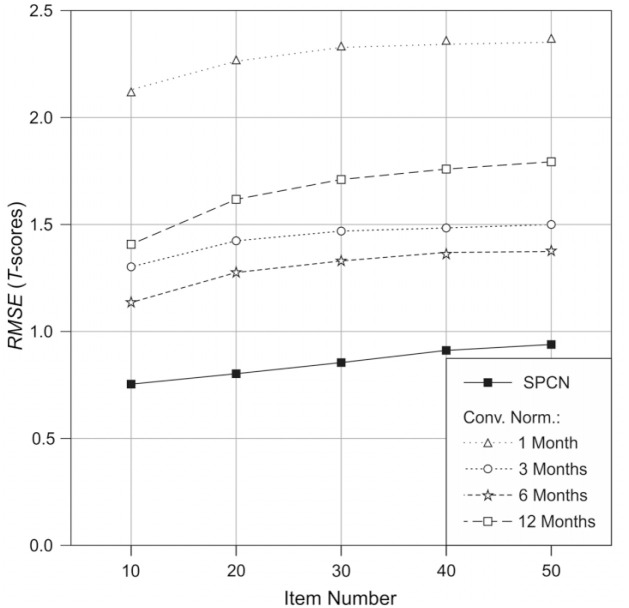
The RMSE was analyzed as a function of method, total sample size and item number to investigate the overall quality of the different norming procedures. With regard to Hypotheses 1 and 2, the analysis of the RMSE revealed a main effect of method, F(4, 359980) = 544560.527, p < .001, ${\eta }_{\mathrm{part}}^2$ = .858, with SPCN delivering on average a much lower RMSE (RMSE_SPCN = .862) than the four conventional norming procedures (RMSE_CN1 = 2.293, RMSE_CN3 = 1.445, RMSE_CN6 = 1.305, and RMSE_CN12 = 1.665). We also found a main effect of total sample size (Hypothesis 2), F(5, 89970) = 397945.050, p < .001, ${\eta }_{\mathrm{part}}^2$ = .957, which was qualified by a significant Method × Total Sample Size interaction, F(20, 359880) = 65863.247, p < .001, ${\eta }_{\mathrm{part}}^2$ = .785. This interaction is illustrated in Figure 4. The effect of total sample size was only η² = .184 for SPCN, but much higher for the conventional norming procedures (η² = .978 for CN1; η² = .957 for CN3; η² = .896 for CN6, and η² = .600 for CN12). Even with the lowest total sample size of N = 700 (i.e., 100 persons per year), the RMSE was only 1.25 T-scores for SPCN. In contrast, the best conventional method required four times the total sample size to approach such a low value. Moreover, for the SPCN approach, the change in RMSE between the lowest and the highest total sample size was only ΔRMSE_SPCN = 0.613. Although the impact of total sample size was similarly low in the CN12 condition (ΔRMSE_CN12 = 0.572), it must be noted that CN12 showed a significantly higher RMSE at any total sample size. For all other conventional procedures, the impact of the total sample size was much larger (ΔRMSE_CN1 = 3.392; ΔRMSE_CN3 = 2.021, and ΔRMSE_CN6 = 1.198). Thus, conventional norming is much more dependent on the total sample size. In general, an equally low RMSE requires four times the total sample size when conventional norming is applied as compared with SPCN. Moreover, this result only holds true if an optimal age bracket is selected. As can be seen from Figure 4, the same subsample size yields a significant differences in RMSE between the conventional norming conditions. In case no optimum age bracket is selected, the total sample sizes would have to be even higher when conventional norming is applied.

Figure 4.

RMSE in the cross-validation as a function of method and sample size. The numbers indicate the subsample sizes for the conventional norming conditions.

Note. All SEs < 0.01. Dashed lines represent conventional norming, the solid line represents semiparametric continuous norming (SPCN).

The ANOVA also revealed a main effect of the item number, F(4, 89970) = 13777.134, p < .001, ${\eta }_{\mathrm{part}}^2$ = .380, with higher item numbers leading to higher RMSE. This effect is illustrated in Figure 5.

Figure 5.

RMSE in the cross-validation as a function of method and item number.

Note. All SEs < 0.01. Dashed lines represent conventional norming, the solid line represents semiparametric continuous norming (SPCN).

Due to the huge test power, there were also significant interactions of the item number with all other independent variables, but the respective effect sizes were too small to be of any practical relevance (η² < .02 for all interactions).

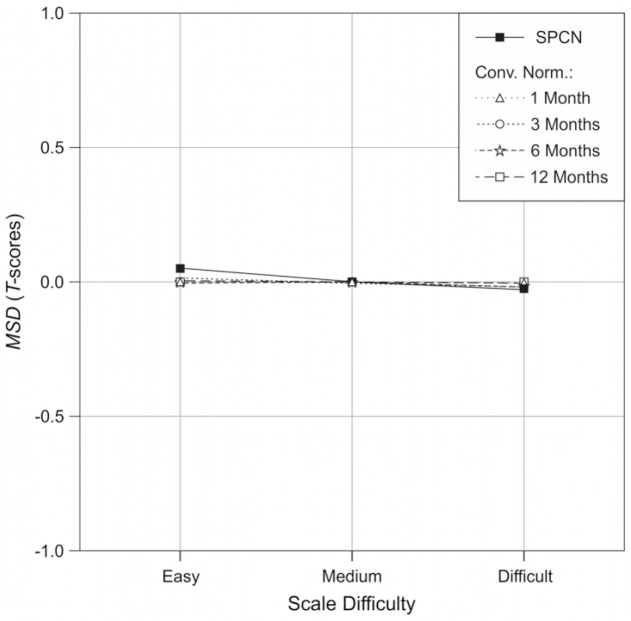
As a next step, the MSD in the cross-validation was analyzed as a function of method and scale difficulty to search for constant dislocations. The scale difficulty was chosen as independent variable in this case, since high skewness of the raw score distributions is most likely to cause a general dislocation in continuous norming in general. The MSD for the different scales is depicted in Figure 6. There was in fact a significant interaction between method and scale difficulty, F(8, 359864) = 2300.986, p < .001, ${\eta }_{\mathrm{part}}^2$ = .049. The interaction was caused by the fact that SPCN showed a slightly higher MSD than conventional norming at easy scales only. However, with MSD = 0.054 T-scores, the absolute size of the dislocation was so tiny that it was irrelevant compared with the other error sources. Moreover, the size of the dislocation is far below the accuracy with which real test results are actually ever reported.

Figure 6.

MSD in the cross-validation as a function of method and scale difficulty (i.e., skewness of the raw score distribution).

Note. All SEs < 0.01. Dashed lines represent conventional norming, the solid line represents semiparametric continuous norming (SPCN).

Analysis of Missing Norm Scores

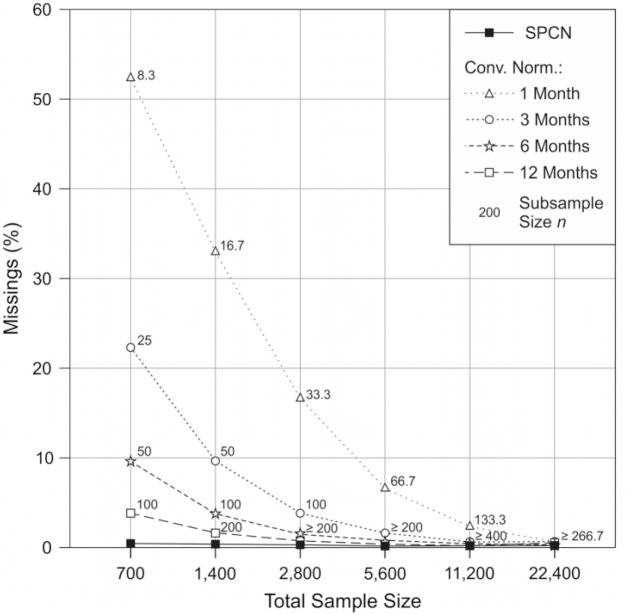
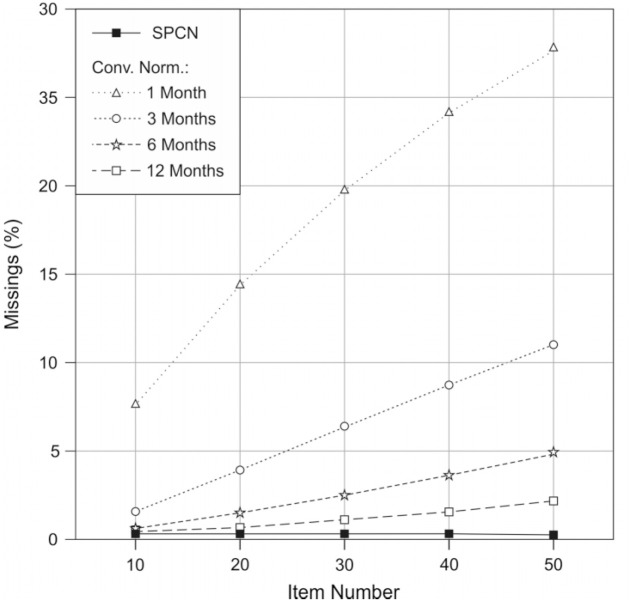
With regard to the analysis of the missings (Hypothesis 3), the reader should note that SPCN in most cases allows to compute norm scores to all achievable raw scores, which is the central advantage of this method, let alone closing gaps between norm tables. However, on some rare occasions, SPCN cannot return a norm score because of an incoherent model. The analysis of the missings as a function of method, total sample size and item number confirmed these expectations. There was a very strong main effect of method, F(4, 359880) = 3952101.067, p < .001, ${\eta }_{\mathrm{part}}^2$ = .978, with SPCN delivering only 0.258% missings on average. Moreover, in 50% of all simulation cycles, the number of missings was even below 0.031%. There was, in fact, a small main effect of the total sample size in the SPCN condition, F(5, 89994) = 716.923, p < .001, ${\eta }_{\mathrm{part}}^2$ = .038, with the smallest total sample size delivering more missings (0.478%) than the largest one (0.137%). However, conventional norming achieved similarly low numbers only when the total sample size was four to eight times larger. Moreover, the different conventional norming procedures showed very large main effects of total sample size and item number, which were qualified by twofold and threefold interactions (all ps < .001; all ${\eta }_{\mathrm{part}}^2$ > .82). Under balanced conditions (i.e., age bracket = 6 months, N = 5,600 and item number = 40) the number of missings was 0.713 %. The effects are depicted in Figures 7 and 8.

Figure 7.

Missings in the cross-validation as a function of method and sample size. The numbers indicate the subsample sizes for the conventional norming conditions.

Note. All SEs < 0.01. Dashed lines represent conventional norming, the solid line represents semiparametric continuous norming (SPCN).

Figure 8.

Missings in the cross-validation as a function of method and item number.

Note. All SEs < 0.01. Dashed lines represent conventional norming, the solid line represents semiparametric continuous norming (SPCN).

Descriptive Analysis of PEV_Norm and REL_Norm

Since the conditions in our study were numerous and covered a wide range of item numbers and total sample sizes, some of the combinations of conditions would certainly not occur in reality, for example, conventional norming with N = 700 and an age bracket of 1 month. Therefore, we will not report PEV_Norm and REL_Norm for all combinations of conditions in the following. Instead, we will focus on the conventional norming procedure that performed best under a specific combination of conditions (= Best CN). That is, we assume that a test constructor is able to divide the total sample into age brackets with optimal width. Table 2 gives an overview over PEV_Norm and REL_Norm under the different combinations of total sample size and item number analyzed in this study.

Table 2.

PEV_Norm and REL_Norm as Functions of Approach (Continuous vs. Conventional), Total Sample Size, and Item Number.

			Total Sample Size N
			700	1,400	2,800	5,600	11,600	22,400	Total
10 Items	PEVNorm	SPCN	0.97%	0.53%	0.35%	0.37%	0.27%	0.19%	0.45%
		Best CN	3.29%	2.07%	1.37%	0.78%	0.49%	0.33%	1.39%
	RELNorm	SPCN	.982	.990	.994	.993	.995	.997	.992
		Best CN	.941	.963	.975	.986	.991	.994	.975
20 Items	PEVNorm	SPCN	1.27%	0.87%	0.49%	0.41%	0.37%	0.26%	0.61%
		Best CN	5.24%	3.32%	2.17%	1.26%	0.82%	0.51%	2.22%
	RELNorm	SPCN	.982	.988	.993	.994	.995	.996	.991
		Best CN	.925	.953	.969	.982	.988	.993	.968
30 Items	PEVNorm	SPCN	1.39%	1.00%	0.71%	0.47%	0.43%	0.33%	0.72%
		Best CN	6.32%	4.09%	2.63%	1.55%	1.01%	0.64%	2.71%
	RELNorm	SPCN	.982	.987	.991	.994	.994	.996	.991
		Best CN	.918	.947	.966	.980	.987	.992	.965
40 Items	PEVNorm	SPCN	1.59%	1.08%	0.75%	0.61%	0.52%	0.49%	0.84%
		Best CN	7.12%	4.60%	2.96%	1.74%	1.15%	0.71%	3.05%
	RELNorm	SPCN	.980	.987	.991	.992	.994	.994	.990
		Best CN	.913	.944	.964	.979	.986	.991	.963
50 Items	PEVNorm	SPCN	1.57%	1.16%	0.82%	0.74%	0.52%	0.49%	0.88%
		Best CN	7.67%	5.02%	3.17%	1.90%	1.25%	0.77%	3.30%
	RELNorm	SPCN	.981	.986	.990	.991	.994	.994	.989
		Best CN	.909	.941	.962	.978	.985	.991	.961
Total	PEVNorm	SPCN	1.36%	0.93%	0.62%	0.52%	0.42%	0.35%	0.70%
		Best CN	5.93%	3.82%	2.46%	1.45%	0.94%	0.59%	2.53%
	RELNorm	SPCN	.981	.987	.992	.993	.994	.995	.990
		Best CN	.921	.949	.967	.981	.988	.992	.966

Note. For the conventional norming procedure, we selected the best fitting model. SPCN = semiparametric continuous norming.

First of all, the numbers indicate that the proportion of error variance added to the test scores through the norming procedure decreases with growing total sample size, but increases with the number of items, as was already reported with regard to RMSE. What we find interesting, though, is the possibility to interpret the error variance independently of the scaling. For example, when SPCN was applied, the error variance added to the test scores through the norming procedure, varied between 0.194% and 1.594% (M = 0.70%). As a consequence, the proportion of true variance of the latent trait contained in the norm scores, was slightly reduced by a factor ranging between .980 and .997, with REL_Norm = .990 on average. Imagine, for example, a highly reliable test scale with an indicated reliability of r_tt = .90, that is, a proportion of error variance of about 10% in the raw scores. In the worst case, SPCN would increase this variance to a total of 11.6%, that is, the “effective” reliability of the norm scores would be REL_Total = .90 × .98 = .88, which is still high. With conventional norming, on the other hand, the introduced error variance varied between 0.328% and 7.673% (M = 2.53%), corresponding to a factor REL_Norm between .994 and .901 (M = .966). As a consequence, the reliability of a fictitious test scale of r_tt = .90 would decrease to an effective reliability of REL_Total = .90 × .90 = .81 in the worst case. The error variance contributed by the norming procedure would be about three quarters as high as the error variance contributed by the test items in this case. Admittedly, the total sample size was only N = 700 with age brackets of 12 months in this worst-case scenario, that is, the subsample size was below the generally recommended one for conventional norming. Under more optimal conditions, that is, with subsample sizes between n = 200 and n = 400, but an attainable total sample size of up to N = 5,600, the error variance added to the test scores with conventional norming ranged between 1% and 5%. Again, conventional norming required about four times the total sample size to achieve the same quality as continuous norming.

Discussion

This simulation study compared continuous with conventional norming, taking into account that the quality of conventional norms often depends on whether continuous explanatory variables (e.g., age) are considered in building sufficiently narrow normative subsamples. To investigate the effects of the different norming procedures under multiple conditions, we additionally varied the number of items, the difficulty of the used test scales (i.e., the skewness of the raw score distributions) and the total sample size.

Regardless of the total sample size, the scale difficulty and the number of test items, the specific continuous norming method we used in this study (SPCN) produced less error variance and therefore provided a more reliable estimation of the person location than conventional norming. Even with an optimal balance between the total sample size and the width of the age brackets, conventional norming required about four times the total sample size to achieve the same data fit as continuous norming. In reality, however, it is anything but certain that a test constructor would always find this optimal balance between the width of the age brackets and the size of the subsamples. Only with unrealistically high total sample sizes, the quality of both approaches was similar. At the same time, as indicated in Figure 4, the general recommendations for sample sizes per age bracket are not sufficient to guarantee optimal results, since the bias resulting from finite width of the age brackets is neglected.

Since the statistical test power was extremely high in our study, there is the additional question of whether the size of the effect plays a role for practical applications. On the one hand, the mean absolute error was mostly within the range of 95%-confidence intervals for both conventional and continuous norming—even for scales with very high reliability. On the other hand, many diagnostic decisions are made on the basis of clear cut-points where the confidence intervals do not play any role at all. Therefore, one T-score more or less can definitely make the difference here. More important, however, the norming errors are never evenly distributed across all levels of the latent trait. Generally, they are U-shaped, with the slopes on both sides varying with the average RMSE (cf. Lenhard et al., 2019). Therefore, the difference between the methods might be irrelevantly small for average test results but significantly high for test results strongly above or below average. Unfortunately, extreme test results are precisely those results that are most relevant in diagnostic practice.

Furthermore, conventional norming also leads to a considerably higher number of missings in the norm tables. Again, conventional norming required about four to eight times the total sample size to approach the low number of missings of continuous norming. Furthermore, the missings almost exclusively concern the extreme test results, that is, the range of diagnostically relevant cases. Hence, the percentage of test results affected by missings in diagnostic practice is probably much higher than in our study. Continuous norming can improve the quality of the test norms because it not only closes these gaps but also smooths the data along the ability dimension.

Finally, we directly compared the error variance contributed to test scores by the different norming procedures with the error variance produced by the test items. For continuous norming, the error variance added by the norming procedure was much smaller than the one that is usually contributed by the test items. Hence, the norming procedure only slightly impaired the explanatory power of the test results. By contrast, the proportion of error variance added with conventional norming considerably increased the total error variance at least under some conditions. This finding suggests that the selection and accurate implementation of an adequate norming procedure can be almost as important for the explanatory power of test scores as all item selection efforts (e.g., increasing the number of items, analyzing the item fit and removing those that deteriorate homogeneity). In case, relevant covariates like age exist, continuous norming can help to represent a latent ability more precisely than conventional norming. Our study thus adds support to the finding of Zhu and Chen (2011) and Oosterhuis et al. (2016) that with continuous norming, substantially smaller samples are sufficient to reach the same quality of norm scores or even surpass conventional norming.

Limitations

The advantage of SPCN and other continuous norming procedures is to model the effects of a covariate on the relation between raw scores and norm scores. This advantage should increase with the proportion of variance in the raw scores that can be explained by that covariate. If, on the other hand, a covariate like, for example, age does not exert a relevant influence on the raw scores, there is no reason to construct norm tables for distinct age brackets and consequently continuous norming models are unnecessary as well (at least as far as this particular covariate is concerned). The effects demonstrated in this norming study should therefore increase with an increasing slope of the age trajectories of the measured trait and decrease with a decreasing slope.

In this simulation study, SPCN returned very robust solutions for the predefined population model we used, which mimicked the vocabulary development in childhood and adolescence. Yet it might fail with other application scenarios. In other conceivable scenarios, for example, the mean raw scores could remain constant across age, while only the variance might change. We have not modeled such scenarios yet and it is therefore impossible to generalize the results of the present study to all conceivable conditions. On the other hand, our own experiences with SPCN showed very good results in many domains other than the originally intended psychometric use cases. More precisely, we successfully modeled fetal length in dependence of gestation week, body mass index and body height growth in childhood and adolescence in dependence of age, world-wide life expectancy at birth and mortality rates on country level in the course of the last 50 years (Lenhard et al., 2018). The approach might therefore be useful for other application scenarios from biometrics to macroeconomics as well.

A second limitation concerns the number of covariates. So far, we have mainly focused on taking only one covariate into account, namely age. For the application scenarios we mainly target, such as intelligence tests or developmental tests, other covariates (e.g., sex or ethnical background) are usually controlled via stratification of the sample. Although from a theoretical point of view, SPCN is not necessarily restricted to the inclusion of one covariate only, other approaches (e.g., Rigby & Stasinopoulos, 2005; Van Breukelen & Vlaeyen, 2005) might be better suited for this demand. Whether it is advisable to compute separate norm scores for covariates other than age (e.g., sex-specific IQ scores), cannot be solved by statistical procedures, though. It rather depends on the exact use case.

Conversely, of course, it could also happen that no covariates have to be included at all, but that the norm score is to be predicted as a function of the raw score only. Equation (1) would thus be reduced to a simple polynomial regression. At the moment we cannot precisely determine how significant the advantages of such a regression would be compared with the conventional calculation of norm scores. While the procedure certainly loses many of its advantages in that case, it nonetheless closes missings in the tables more precisely than a simple interpolation between the available data points. Moreover, it smooths the transformation function between raw scores and norm scores and thus might help to mitigate sampling errors in the normative sample, though it is not possible to repair completely unrepresentative normative data this way.

Another drawback of the present study might be the use of measures that cannot be determined in real norming procedures. Since in applied diagnostics, the latent ability is unknown, the factor REL_Norm, specifying the relative amount of error variance added by the norming procedure, can only be estimated in simulation studies like the present one. Strictly speaking, the determined values therefore only apply to the conditions established in this simulation. For SPCN, however, REL_Norm remains constant at around .99 even under simulation conditions other than those implemented in this study, whereas for other methods it obviously depends more on the actual conditions. We therefore think it is important to keep in mind that in real life the “effective” reliability of norm scores (as defined by the explained variance of the latent trait) is usually lower than the reliability of the raw scores, which is typically specified in the handbooks.

Of course, a simulation study like the present one is always based on specific assumptions. For example, we drew the samples from a perfectly representative population. In real-life scenarios, however, it is not always possible to perfectly stratify each age bracket. As the regression-based approach in SPCN always draws on information from the total sample to determine the mathematical models, such imbalances can at least partially be compensated. The same does not hold true for conventional norming, though. As a consequence, the differences between continuous and conventional norming would even increase in real-life scenarios.

Furthermore, we assumed that the latent trait is normally distributed at each level of the explanatory variable. We believe that this assumption is justified because of the universality of the law of large numbers. Additionally, the 1-PL IRT measurement model we used to produce test results makes specific assumptions about the interaction between latent traits and test items (e.g., constant discriminative power for all test items). We chose to draw on a 1-PL IRT model due to three main reasons. First, the method is suitable to generate sample raw data that align with real-world normative samples. Second, we constructed both the normative and the representative cross-validation sample from the same population model and subjected them to the same, randomly generated test scales in order to cross-validate different modelling techniques. Third, the item response theory is one of the most important theoretical models to explain how a latent ability interacts with items and scale parameters and finally results in a raw score distribution. That way, we could determine how well the raw scores and consequently the normed raw scores represent the latent ability. It is important to note, though, that a specific measurement model is neither required for the application of conventional norming nor for SPCN. The latter is based on the mathematical principle that any function can be modelled with polynomials as long as it is smooth and finite. Therefore, it can be applied to all kind of distributions like biometric and sociometric data. As psychometry most often aims at measuring latent variables, the application of an IRT model was the most plausible candidate for data simulation purposes in our specific use case. Furthermore, SPCN is not restricted to 1-PL IRT models. For example, we successfully applied this method to normative data of a test constructed on the basis of a complex measurement model including power and speed components as well as discrimination parameters for both (2 × 2 PL model sensu; Fox et al., 2007; Lenhard et al., 2017). Moreover, it was also used to model observed biometric data without any measurement model at all like, for instance, the BMI growth curves in childhood and youth (sample dataset CDC of the cNORM package). Therefore, we are convinced that the results can in fact be transferred to various other conditions. We even believe that the universality and simplicity of the SPCN approach is one of its great strengths.

Finally, we only compared one specific continuous norming method with conventional norming, namely SPCN. As described above, this particular method makes no specific assumptions about the raw score distributions and can therefore be used very flexibly. However, there are other continuous norming methods that may lead to somewhat different results (e.g., Cole & Green, 1992; Rigby & Stasinopoulos, 2005; Zachary & Gorsuch, 1985, as demonstrated by Voncken et al., 2019a). When we compared SPCN with parametric continuous norming methods, it mainly showed superior performance when applied on scales with medium to high skewness of the raw score distributions (Lenhard et al., 2019). When applied on test scales with very low skewness, both methods performed equally well, with a slight advantage of SPCN in smaller norming samples and a slightly better performance of parametric models in larger samples. However, the latter result was only achieved under the condition that an optimal modelling function was used in the parametric condition. Hence, the search for such an optimal modelling function is of high importance when applying parametric approaches. If the search is successful, then parametric and semiparametric continuous norming deliver comparable results. Consequently, and just like SPCN, parametric continuous norming will very likely outperform conventional norming in most cases as well.

Conclusion

Our results have clearly shown that test scales contain less error variance and will therefore be more reliable if continuous models are used to capture the effects of relevant explanatory variables as such as age. We therefore recommend not only to resort to simple ranking procedures but also to complete the analysis by modeling the continuous relation between raw scores, norm scores, and explanatory variables when necessary. One way to perform this modeling is the regression-based continuous norming method we have described in this study. The method not only provides higher norming quality than conventional norming procedures but also outperforms other continuous norming methods under various conditions (Lenhard et al., 2019). Moreover, the software is available as an R package with a graphical user interface (online demonstration, see https://cnorm.shinyapps.io/cNORM/) and online tutorials (https://www.psychometrica.de/cNorm_en.html). It can be freely used even with limited prior knowledge in R. More experienced psychometricians can choose between different norming methods, for example, semiparametric or parametric continuous norming. The sample size, the impact of covariates and the properties of the raw score distribution are important factors when it comes to the selection of the most appropriate method.

In recent years, research and published work in the field of norming has increased. We consider this development to be of paramount importance, because it has the potential not only to improve the explanatory power of psychometric tests but also to make them more cost-effective and therefore more widespread. We hope that we can significantly contribute to this field with this simulation study.