Modelling the Growth Limits (Growth/No Growth Interface) of Escherichia coli as a Function of Temperature, pH, Lactic Acid Concentration, and Water Activity

Abstract

The form of a previously developed Bělehrádek type of growth rate model was used to develop a probability model for defining the growth/no growth interface as a function of temperature (10 to 37°C), pH (pH 2.8 to 6.9), lactic acid concentration (0 to 500 mM), and water activity (0.955 to 0.999; NaCl was used as the humectant). Escherichia coli was unable to grow in broth in which the undissociated lactic acid concentration exceeded 11 mM or, with two exceptions, at a pH of 3.9 or less with no lactic acid present. Under experimental conditions at which the pH and the undissociated acid concentrations were the major growth-limiting factors, the growth/no growth interface was essentially independent of temperature at temperatures ranging from 15 to 37°C. The interface between conditions that allowed growth and conditions at which growth did not occur was abrupt. The inhibitory effect of combinations of water activity and pH varied with temperature. Predictions of the model for the growth/no growth interface were consistent with 95% of the experimental data set.

The increasing number and severity of food-borne disease outbreaks in developed countries have resulted in an increased focus on the control of food-poisoning organisms, such as pathogenic Escherichia coli. Various approaches, such as better detection techniques for E. coli, improved disease surveillance, and research on the virulence factors of the organism, are being used to study this problem. Another approach which has been proposed is formal risk analysis (8). This approach requires, in part, knowledge of the growth limits and rates of growth and death of pathogenic bacteria in response to the relevant environmental factors in foods.

The growth, survival, and death of E. coli in foods have been examined with particular reference to organic acids and low pH values. However, most studies have involved inoculating E. coli into food and monitoring survival or growth (1, 10, 30). The information provided by such studies may be limited to the specific food formulation and conditions used. The effects of different sets of conditions cannot be predicted by this type of study. Furthermore, the specific mechanisms by which pH and organic acids cause inhibition in prokaryotes at a subcellular level are not completely understood (9, 21, 22).

Therefore, studies such as those described above are not adequate to determine the safe minimum preservative levels and storage conditions for foods in general. For example, some observations of microbial survival and death in foods in response to pH are counterintuitive (30).

Predictive microbiology is concerned with the systematic development of mathematical models which summarize and describe the responses of microorganisms to environmental conditions experienced in foods (12, 26). Ratkowsky and Ross (20) proposed a logistic regression model for modelling the growth/no growth interface for several conditions, including temperature, pH, and additives, such as salt and sodium nitrite. A Bělehrádek type of growth rate or kinetic model was used as a basis for that model. By using the data of Zaika et al. (27–29) for Shigella flexneri, it was shown that the model described the data well. A limitation, however, was that the data used to illustrate the approach were not genuine growth/no growth data, but rather data for “growth observable within 24 h.” Thus, Ratkowsky and Ross (20) concluded that the suggested connection between the probability approach and kinetic models may have been an artifact resulting from using time-limited kinetic data to test a probability model.

This report describes the application of the same modelling approach to another organism, a nonpathogenic strain of E. coli, for pH, water activity, temperature, and lactic acid concentration conditions that are suboptimal for growth. In this work we allowed sufficient time and used specific strategies to ensure that growth, if possible, would be observed. Thus, the present study generated growth/no growth data that were not time limited and that enabled a more rigorous assessment of the use of a kinetic model to create a probability model. The model used predicts the probability of growth at any combination of the factors examined and can be used to define the growth/no growth interface for combinations of factors.

MODEL DEVELOPMENT

A Bělehrádek type of model developed to study the combined effects of water activity, temperature, pH, and lactic acid concentration on the growth rate of E. coli M23 has been described previously (18). The form of this model is:

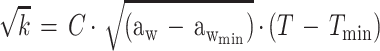1

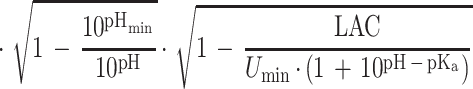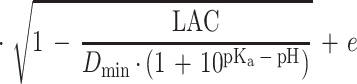where k is the growth rate (defined as 1/generation time [in minutes]), C is a constant of proportionality, a_w is the water activity, a_wmin is a theoretical minimum water activity for growth, T is the temperature, T_min is a notional value of temperature when the growth rate is zero, pH_min is a theoretical maximum pH which prevents growth, LAC is the total concentration of lactic acid (concentration of undissociated lactic acid plus concentration of dissociated lactic acid), D_min is the theoretical minimum concentration of dissociated lactic acid required to prevent growth, U_min is the theoretical minimum concentration of undissociated lactic acid required to prevent growth, pK_a is the acid dissociation constant (which for lactic acid is 3.86 [6]), and e is the error term. The square root of the growth rate is used to homogenize the variance of the growth rate data.

Equation 1 differs from the model used previously (20) because a different term for pH is included and new terms for the effect of lactic acid are added. In the present study the mathematical transformation of Ratkowsky and Ross (20) was used on equation 1 to construct a new model for the probability of growth of E. coli M23 in response to water activity, temperature, pH, and lactic acid concentration. The form of this model is:

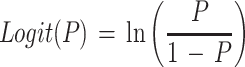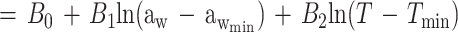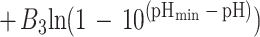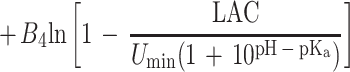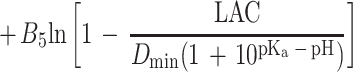2

where P is probability (0 to 1), ln is the logarithm to base e, B₀ to B₅ are fitted coefficients, and all other terms are as defined above. The model is an example of a generalized linear regression model with binomial error and logit link function if the parameters a_wmin, T_min, pH_min, D_min, and U_min are taken to be fixed constants.

MATERIALS AND METHODS

The data set used to fit and evaluate the growth/no growth interface model (equation 2) was derived from three separate experiments.

Lactic acid growth/no growth experiment.

The lactic acid growth/no growth experiment was designed to determine the growth/no growth interface of E. coli M23 as dictated by temperature, pH, and lactic acid concentration. Data were collected at 10, 15, 20, 25, 30, and 37°C for total lactic acid concentrations of 0, 25, 50, 100, 200, and 500 mM with a pH range of 3 to 7. The broad range of conditions under which the organism could grow and the conditions which prevented growth were known (18). Narrow pH intervals (down to 0.1 pH unit) were tested near the expected interface to improve the precision with which the interface was defined.

Organism.

E. coli M23 (a nonpathogenic laboratory strain) was obtained from the Department of Agricultural Science Culture Collection, University of Tasmania.

Growth medium preparation.

A 26-g portion of nutrient broth (catalog no. CM1; Oxoid) was dissolved in 800 ml of distilled water. Lactic acid (88%, wt/wt; Univar, AR, Ajax Chemicals, Auburn, New South Wales, Australia) was added to 800-ml volumes to obtain the following total lactic acid concentrations: 500, 200, 100, 50, and 25 mM (102.24, 40.92, 20.44, 10.23, and 5.11 g, respectively). In addition, broth with no lactic acid was included. Each broth preparation was divided equally by weight into 10 flasks. Each flask was kept refrigerated until the pH was adjusted with several HCl and NaOH solutions containing various concentrations (to give the final pH values shown in Tables 1 and 2), and then distilled water was added to obtain the final volume. pH values were selected to fall on both sides of the anticipated growth/no growth interface. pH was measured with a portable meter (model 250A; Orion Research Inc.) equipped with calomel-sealed flat-tip probe (model AEP433; Activon). Each broth preparation was filter sterilized with type CA sterile filter units (pore size, 0.45 μm; diameter, 25 mm; Activon). The water activity of each broth preparation was measured with an Aqualab CX2 dew point instrument (Decagon Devices, Pullman, Wash.). Broth preparations were kept for 1 week at room temperature to reveal possible contamination. Contaminated preparations were discarded.

TABLE 1.

pH (measured after inoculation) and total lactic acid concentration combinations evaluated at 10, 15, 20, 25, 30, and 37°C in growth/no growth experiment 1 performed with E. coli M23

Broth prepn	pH used with a total lactic acid concn of:
	0	25 mM	50 mM	100 mM	200 mM	500 mM
1	2.8	3.0	3.2	4.0	4.5	4.5
2	3.4	3.9	4.1	4.4	4.7	5.0
3	3.6	4.1	4.4	4.6	4.9	5.3
4	3.8	4.2	4.5	4.7	5.0	5.5
5	3.9	4.3	4.6	4.9	5.1	5.4
6	4.0	4.4	4.7	5.0	5.1	5.5
7	4.4	4.5	4.8	5.2	5.3	5.6
8	4.6	4.6	5.1	5.4	5.4	5.6
9	5.3	—a	6.0	5.7	—	5.8
10	6.9	6.6	6.8	6.2	6.1	5.9

^a—, combination was not tested because the broth was contaminated before the experiment was started. 

TABLE 2.

Combinations of pH (measured after inoculation) and water activity (with NaCl as the humectant) evaluated at 10, 20, 25, 30, and 37°C in growth/no growth experiment 2 performed with E. coli M23

Broth prepn	pH used with a water activity of:
	0.955	0.965	0.975	0.985
1	4.2	4.2	4.1	4.0
2	4.7	4.6	4.6	4.2
3	5.2	5.1	5.1	4.8
4	5.8	5.7	5.7	5.4
5	6.2	6.1	6.2	6.0
6	6.8	6.9	6.9	6.8

Culture preparation.

The inoculum was prepared by pipetting 5 ml of an overnight static culture (37°C) of E. coli M23 into 45 ml of nutrient broth. This preparation was incubated at 37°C with shaking until the absorbance at 540 nm was 0.8 (i.e., the culture was in the late exponential phase of growth). Inocula were prepared separately for each lactic acid concentration and for the water activity experiment due to logistical constraints. Inocula grown under the same conditions and at the same optical density were presumed to be in the same physiological condition. Inocula occasionally had to be kept at 15°C for up to 20 min until all media could be inoculated, but this had little effect on the inoculum density (the generation time of E. coli at 15°C is approximately 120 min; within 20 min a maximum of 0.17 generation would be expected).

Data collection.

To simplify detection of growth, turbidimetric methods were used primarily; these methods were supported by cultural methods when necessary. To ensure that even slight growth was detected, 2 ml of the inoculum was pipetted into 200 ml of each of the individually pH-adjusted broth preparations so that the broth preparations were just visibly turbid compared to a sterile, growth medium blank. The pH was measured again after inoculation, and the resulting value could be significantly different from the preinoculation pH value. The cultures were then kept at 4 to 10°C to ensure that growth was minimized until the inoculated broth preparations were dispensed aseptically into sterile well plates (Linbro tissue culture multiwell plates with covers; 24 flat-bottom wells that were approximately 1.7 by 1.6 cm; Flow Laboratories, Inc., McLean, Va.). Each well plate contained quadruplicate 2-ml cultures of 5 of the 10 different pH broth preparations used for each lactic acid concentration. The sixth set of four wells contained sterile nutrient broth (pH 7.2) as a contamination control. Thus, two well plates were used for each lactic acid concentration at each of six temperatures (10, 15, 20, 25, 30, and 37°C).

Evaluation of growth/no growth.

Growth was recorded to have occurred if there was a visible increase in the turbidity of the broth in a well. In almost all cases when growth occurred there was a significant change in turbidity. When the results were doubtful, possible growth was recorded and the well was reexamined subsequently to confirm growth based on further increases in turbidity.

The presence of E. coli was verified by growing a pure culture on nutrient agar (catalog no. CM1; Oxoid) and then producing typical E. coli colonies on Eosin methylene blue agar (Levine) (catalog no. CM69; Oxoid). Turbidity was assessed by eye and was recorded daily for approximately the first 21 days, and thereafter turbidity was assessed less frequently for up to 51 days, when the experiment was terminated. When there was no overt increase in turbidity or only a deposit of cells in the base of a well, a semiquantitative evaluation of cell numbers was performed for each well separately by using the ecometric technique (14), with the following changes: four streaks were used instead of five, lines were streaked by following a template placed under the plate, and, for standardization, all plates contained 15.0 ml of agar. Previous work (17) showed that this technique is sensitive to changes from the initial inoculum level. Generally, a spread plate containing 0.1 ml of the well culture was also prepared, and this spread plate could be used to confirm the ecometric technique results when few or no colonies were recovered on the ecometric plates. The final pH of each broth preparation was measured.

Water activity growth/no growth experiment.

The water activity growth/no growth experiment was designed to determine the growth/no growth interface of E. coli M23 as dictated by temperature, pH, and water activity with no added lactic acid. Data were collected at 10, 20, 25, 30, and 37°C for water activities of 0.985, 0.975, 0.965, and 0.955 and at pH values ranging from 4 to 7; pH intervals of approximately 0.5 pH unit were used. Broth preparations with lower water activities were prepared by using the methods described above except that NaCl, a common humectant in the food industry, was added at the following concentrations: 7, 5.25, 3.5, and 2% (wt/vol) for water activities of 0.955, 0.965, 0.975, and 0.985, respectively, in nutrient broth. At each water activity six pHs were tested; the pHs used ranged from 4 to 7 at approximately 0.5-pH unit intervals. A 0.5-ml portion of inoculum was added to 30 ml of each broth preparation. As only six pHs were used at each water activity level, only one well plate per water activity at each of five temperatures (10, 20, 25, 30, and 37°C) was used. In all other respects, the procedures used were the same as those described above for the lactic acid experiment.

Lactic acid growth rate experiments.

In previous studies (18) E. coli M23 cultures were monitored for long periods of time (up to 3 weeks) to verify that growth did not occur. The data obtained also revealed growth limits and were included in the present data set. Only single observations were made under each set of conditions.

Modelling.

The data set contained 627 conditions consisting of pH, lactic acid concentration, water activity, and temperature. Most conditions consisted of four observations; the exceptions were the growth rate experiments (18), in which only single observations were made for each condition. In a few cases there were eight observations for one set of conditions when a set of conditions was duplicated due to a change in pH after inoculation.

Equation 2 was fitted to the data by using SAS PROC LOGISTIC (SAS Institute Incorporated, Cary, N.C.), a procedure for logistic regression modelling. The model was used as a generalized linear regression model with the following fixed parameter values: T_min = 4.0; a_wmin = 0.934; pH_min = 3.90; D_min = 823.4; and U_min = 10.7. These values were derived from previous work (18).

Experimental pH values less than the pH predicted to prevent growth (pH_min) were tested, as were undissociated lactic acid concentrations higher than the concentration predicted to prevent growth (U_min). The form of the model does not allow evaluation of conditions that are beyond the limits for growth due to generation of negative values for which the logarithm cannot be calculated. The experimental temperatures did not approach T_min, and the water activity was always more than a_wmin.

The probabilities of growth predicted by the fitted model were compared with the original data. Using the Solver routine of Microsoft Excel, we calculated the growth/no growth interface predicted by the model at probabilities of 0.1, 0.5, and 0.9.

RESULTS

Evaluation of growth/no growth.

The ecometric method (14), modified as described previously (17), reliably showed that in wells in which no turbidity was visible after 50 days, the cell numbers had decreased from the initial levels. With this technique, precise estimates of cell numbers were not possible or required. In the case of very low bacterial counts not detectable by the ecometric technique, the reduction in cell numbers was confirmed by examining a spread plate containing 0.1 ml of culture. For cultures in which growth was observed there was always an increase of 2 or more pH units.

Growth limits: pH.

The range of pH values used for each total lactic acid concentration spanned the growth/no growth interface, except in the case of 500 mM lactic acid. For the latter concentration of lactic acid, growth occurred only at the highest pH values tested, and growth did not occur at 10 and 25°C (Table 3). In some cases the measured pH was lower than the value intended due to changes in the pH of the broth after the inoculum was added. This phenomenon was observed particularly at the highest concentrations of lactic acid.

TABLE 3.

Highest pH at which E. coli M23 growth was not observed and lowest pH at which growth was observed at each combination of temperature and total lactic acid concentration

Temp (°C)	Total lactic acid concn
	0		25 mM		50 mM		100 mM		200 mM		500 mM
	No growth pHa	Growth pHb	No growth pH	Growth pH	No growth pH	Growth pH	No growth pH	Growth pH	No growth pH	Growth pH	No growth pH	Growth pH
10	3.9	4	4.4 (6)c	4.5 (5)	4.7 (6)	4.8 (5)	5.0 (7)	5.2 (4)	5.3 (7)	5.4 (6)	5.9 (5)	—d
15	3.8	3.9	4.4 (7)	4.3 (6)	4.6 (8)	4.7 (6)	4.9 (8)	5.0 (7)	5.0 (14)	5.1 (11)	5.8 (6)	5.9 (5)
20	3.6	3.8	4.4 (7)	4.3 (6)	4.6 (8)	4.7 (6)	5.0 (7)	5.2 (4)	5.1 (11)	5.3 (7)	5.8 (6)	5.9 (5)
25	3.9	4	4.4 (7)	4.3 (6)	4.6 (8)	4.7 (6)	4.9 (8)	5.0 (7)	5.3 (7)	5.4 (6)	5.9 (5)	—
30	3.4	3.6	4.4 (7)	4.3 (6)	4.6 (8)	4.7 (6)	4.9 (8)	5.0 (7)	5.1 (11)	5.1 (11)	5.6 (9)	5.8 (6)
37	3.8	3.9	4.4 (7)	4.3 (6)	4.6 (8)	4.7 (6)	4.9 (8)	5.0 (7)	5.1 (11)	5.3 (7)	5.8 (6)	5.9 (5)

^aHighest pH at which E. coli M23 growth was not observed. 

^bLowest pH at which E. coli M23 growth was observed. 

^cThe numbers in parentheses are the millimolar concentrations of undissociated lactic acid present. 

^d—, growth was not observed under the conditions used. 

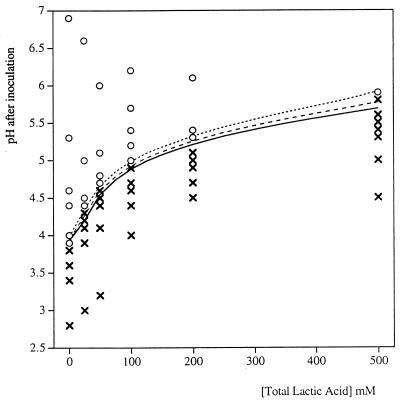
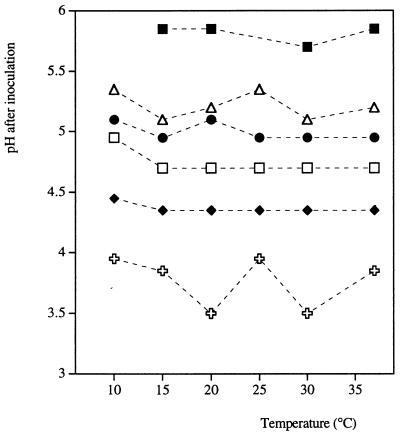
At all temperatures, as the total lactic acid concentration increased, there was an increase in the pH at which the growth/no growth interface occurred (Fig. 1). When 25, 50, or 100 mM lactic acid was used, the interface occurred at slightly higher pH values at 10°C than at other temperatures (Table 3 and Fig. 2). There was variation in the observed growth/no growth interface for pH and temperature when no lactic acid was present, although no trend correlated with temperature was discernible (Fig. 2).

FIG. 1.

Growth/no growth of E. coli M23 in the presence of lactic acid at 37°C: comparison of the observed data for growth (○) and no growth (×) and predictions of the growth/no growth interface model (see equation 2 and Table 5) at probabilities of growth of 0.1 (solid line), 0.5 (dashed line), and 0.9 (dotted line). The total lactic acid concentration was the concentration of undissociated lactic acid plus the concentration of dissociated lactic acid.

FIG. 2.

Growth/no growth interface of E. coli M23 as a function of lactic acid concentration, pH, and temperature. The interface plotted was obtained from Table 3 by averaging the highest pH at which growth was not observed and the lowest pH at which growth was observed in the presence of no lactic acid ( ) and total lactic acid concentrations of 25 mM (⧫), 50 mM (□), 100 mM (•), 200 mM (▵), and 500 mM (▪). The total lactic acid concentration was the concentration of undissociated lactic acid plus the concentration of dissociated lactic acid.

Data from the growth/no growth experiments suggested that the pH limit for E. coli growth is between pH 3.4 and 3.6 at both 20 and 30°C; this was in contrast to the results of the experiments performed at 20 to 22°C, which consistently showed that the observed growth/no growth interface was between pH 3.8 and 4.0. A subsequent experiment revealed a decline in E. coli numbers (i.e., death of E. coli) at pH 3.7 and 3.8, which suggested that the two observations of growth at pH values of <3.9 were anomalous.

Growth limits: undissociated lactic acid.

At 10°C the observed growth/no growth interface occurred at an undissociated lactic acid concentration of 5.75 mM (average of growth and no growth concentrations for all total lactic acid concentrations from 25 to 200 mM as calculated from the data in Table 3). This interface occurred at average undissociated lactic acid concentrations of 8.4, 7.0, 6.9, 8.0, and 7.5 mM at 15, 20, 25, 30, and 37°C, respectively (calculated from the data in Table 3 as described above). There was no other discernible trend in temperature or lactic acid concentration. A growth/no growth interface was not observed for a total lactic acid concentration of 500 mM at 10 or 25°C because growth did not occur at any experimental pH, although an interface must have occurred at a concentration less than the lowest undissociated lactic acid concentration tested (5 mM). The observed growth/no growth interface occurred at undissociated lactic acid concentrations ranging from 5.5 to 12.5 mM for all other combinations of temperature, pH, and total lactic acid concentration.

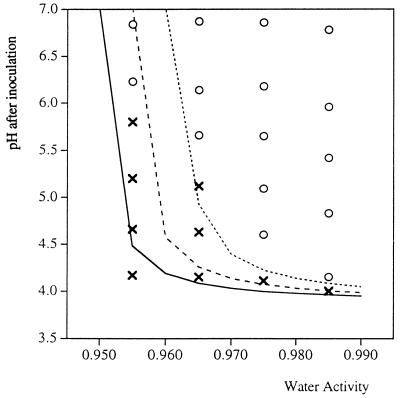
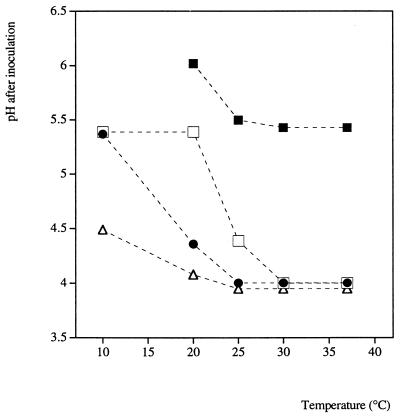
Growth limits: water activity.

At reduced water activity values the minimum pH at which growth occurred increased (Table 4 and Fig. 3). This effect was most evident at low temperatures (10 and 20°C) and water activities (0.955 and 0.965) and was almost undetectable at higher temperatures and water activities. At 25, 30, and 37°C and water activities of 0.985 and 0.975 the minimum pH at which growth occurred was approximately 4 (Fig. 4).

TABLE 4.

Highest pH at which E. coli M23 growth was not observed and lowest pH at which growth was observed at each combination of temperature and water activity (with NaCl as the humectant)

Temp (°C)	Water activity
	0.955		0.965		0.975		0.985
	No growth pHa	Growth pHb	No growth pH	Growth pH	No growth pH	Growth pH	No growth pH	Growth pH
10	6.8	—c	5.2	5.7	5.1	5.7	4.2	4.8
20	5.8	6.2	5.2	5.7	4.1	4.6	4.0	4.2
25	5.8	6.2	4.2	4.6	—	4.1	—	4.0
30	5.8	6.2	—	4.2	—	4.1	—	4.0
37	5.8	6.2	—	4.2	—	4.1	—	4.0

^aHighest pH at which E. coli M23 growth was not observed. 

^bLowest pH at which E. coli M23 growth was observed. 

^c—, growth or no growth was not observed under the conditions used. 

FIG. 3.

Growth/no growth of E. coli M23 in the absence of lactic acid at 20°C with lowered water activity (when NaCl was used as the humectant): comparison of the observed data for growth (○) and no growth (×) and predictions of the growth/no growth interface model (see equation 2 and Table 5) at probabilities of growth of 0.1 (solid line), 0.5 (dashed line), and 0.9 (dotted line).

FIG. 4.

Growth/no growth interface of E. coli M23 as a function of water activity (when NaCl was used as the humectant), pH, and temperature. The interface plotted was obtained from Table 4 by averaging the highest pH at which growth was not observed and the lowest pH at which growth was observed for water activities of 0.955 (▪), 0.965 (□), 0.975 (•), and 0.985 (▵). (If the interface between growth and no growth was not described by the water activity data, the pH limit [3.9] was substituted for no growth to calculate the average.)

Modelling.

Overall, only 413 of the 627 conditions examined could be used to fit the model; for the other 214 conditions either the pH was less than pH_min or the concentration of undissociated lactic acid was more than U_min. For the 413 conditions used, 804 observations of growth and 311 observations of no growth were obtained. The fitted model is:

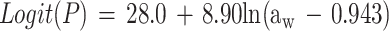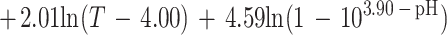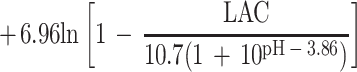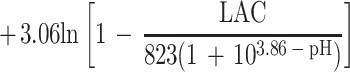3

Parameter estimates and their standard errors are shown in Table 5.

TABLE 5.

Fitted values for the coefficients of the growth/no growth interface model for E. coli M23 (equation 3)

Coefficient	Estimated value	SE
Intercept (B0)	27.9783	2.4500
Water activity (B1)	8.8969	0.7424
Temp (B2)	2.0132	0.2500
pH (B3)	4.5865	0.4690
Undissociated lactic acid concn (B4)	6.9637	0.5726
Dissociated lactic acid concn (B5)	3.0646	0.4876

To evaluate the goodness of fit of the model, predictions of the model were compared to all observations. To do this, observed growth was recorded if ≥50% of the replicate cultures incubated under a set of experimental conditions grew, and a predicted probability of growth of >0.5 was considered predicted growth. When this criterion was used, the results obtained for 41 of the 627 conditions (6.5%) disagreed with the model predictions; in 19 cases there was no growth when growth was predicted, and in the remaining 22 cases growth occurred when growth was not predicted. Only 6 of these 41 disagreements fell outside a predicted probability range of 0.1 to 0.9 (Fig. 1 and 3). As determined with a concordance index described by SAS (24), the degree of agreement between the probabilities predicted by the fitted model and all observations was 97.3% concordant and 2.7% discordant. The total data set (627 conditions) was used to test the model as the conditions outside the individual theoretical limits for growth (i.e., T_min, a_wmin, etc.) were considered to be predictions that growth was not possible.

DISCUSSION

Reducing the pH by adding acids is an important food preservation technique, as are fermentations in which acids and other inhibitory metabolites are produced in the food by lactic acid bacteria (4, 25). Weak acids are popular food preservatives because they are effective at low concentrations and can lower the pH sufficiently to prevent the growth of spoilage organisms. Reducing water activity is another widely used food preservation technique, and the combination of reduced water activity, reduced pH, and weak organic acids is a key element in the stability of many shelf-stable foods.

Outbreaks of E. coli O157:H7 infections obtained from foods that were previously considered too acidic to support the survival of enteric pathogens have challenged the safety of current practices in the food industry (3). Such outbreaks also challenge the perception that prevention of spoilage reflects conditions sufficiently stringent to ensure that pathogens are not able to survive (3). Some bacteria, including pathogenic E. coli, have been found to have a high tolerance to low pH (2). It has been proposed that this tolerance is a reason that outbreaks of E. coli infections caused by certain acidic foods occur (13, 31), and tolerance to low pH is believed to be a virulence factor for such food-borne pathogens (i.e., pathogens that are able to survive the gastric acidity barrier) (16).

Equation 3 describes combinations of pH, temperature, lactic acid concentration, and water activity that interact to prevent growth of E. coli M23. Although E. coli M23 is not a pathogenic strain, its growth responses and limits have been well characterized (5, 18, 23) and do not appear to be unusual compared to other strains, including pathogenic E. coli strains (5, 23).

It may be argued that for low-infectious-dose pathogens, such as some pathogenic E. coli strains (11), the growth rates and limits of the organisms are irrelevant because any number of organisms results in a high risk of illness (15). However, while it is currently possible to minimize the incidence of pathogens, it is not possible to guarantee the absence of pathogens in all units of all foods. The scale and nature of modern food-processing operations are such that even at levels undetectable by routine methods, a significant risk to human health from these pathogens can exist.

It is important to take steps to quantify and minimize this risk and the factors that affect it, such as the potential for, and extent of, proliferation of the pathogens. In this context, models such as equation 3 are useful tools for food safety management.

The experimental design used here included conditions beyond the pH and undissociated lactic acid concentration limits to growth in the absence of any other limiting factors. In contrast, the experimental design did not include conditions beyond the temperature and water activity limits for E. coli in the absence of any other limiting factors. For each concentration of lactic acid tested the data revealed a consistent pH for the observed growth/no growth interface for temperatures ranging from 15 to 37°C. Each of the pH values corresponded to an undissociated lactic acid concentration within a narrow range, which implies that it was this factor which consistently prevented growth at all total lactic acid concentrations. While it has been reported that pH, temperature, lactic acid concentration, and water activity act additively to affect the growth rate (18), it is clear from this study that the effects on limiting the growth of E. coli are synergistic. For example, at water activities of 0.985 and 0.975 and at temperatures of 25°C and above, the minimum pH at which growth occurs is approximately 4, but when the temperature is lower, the minimum pH rises slightly. For a water activity of 0.955, the minimum pH is more than 4 at all temperatures. If, in addition, temperature was limiting (<25°C), the minimum pH permitting growth was even higher, and growth was not observed at any pH at 10°C (Table 4 and Fig. 4).

Previous reports on the variability of the microbial growth rate under almost growth-limiting conditions suggested that growth responses become increasingly variable under these conditions (13, 19). For this reason, Ratkowsky and Ross (20) advocated a probability approach for modelling the growth/no growth interface. In the current study quadruplicate cultures were tested with the expectation that there would be a gradual change in the number of cultures able to grow as conditions traversed the growth/no growth boundary. The transition between pH conditions which permitted growth and pH conditions which did not was abrupt, however, and it was at the limit of resolution of the experimental methods (0.1 pH unit). There were very few examples of conditions under which only some of the quadruplicate cultures did or did not grow. For water activity, the same behavior was observed, but the experimental values used were more widely spaced.

Narrower intervals of water activity have been used in tests performed with E. coli (23). In that work the transition from conditions at which growth is highly probable (90% likelihood) to conditions at which growth is highly improbable (10% likelihood) also occurred over a narrow water activity range at the limit of resolution of the experimental method (0.001 relative humidity unit).

Similarly, the fitted model predicts a transition from conditions at which growth is highly probable (90% likelihood of growth) to conditions at which growth is highly improbable (10% likelihood of growth) over a narrow pH range and a wider water activity range (Fig. 1 and 3). Possible inferences from these results are that it may not be necessary to calculate probabilities and that for practical applications from a food safety perspective it may be sufficient to use the model simply to define the interface at a selected level of probability.

The bacterial growth/no growth interface has been likened to a high cliff which bacteria cannot climb (7). The narrow transition zone described here is consistent with this analogy. If the concept of a cliff is used, it should be very beneficial to the food industry to be able to define the position of the cliff in terms of food preservation factors, so that it can formulate foods that are just beyond the edge of the cliff (i.e., foods that have the minimum combination of preservative factors which satisfy consumer preferences for freshness but which also minimize the risk of pathogen proliferation).

This study supports the hypothesis of Ratkowsky and Ross (20) that a kinetic model may be used to generate a probability model to describe growth/no growth. While the previous work relied on essentially kinetic data, in the current study special measures were taken to ensure that the observed response differentiated the ability of E. coli M23 to grow or not grow under specified environmental conditions. This joining of the kinetic and probability approaches to modelling is important as there are limitations to each method. In kinetic models only the growth rates are used, so that the observations of no growth cannot be used. In probability modelling the amount of information given by a result is more limited because the information is reduced to a binary response. Growth/no growth models of the type used in this study (equation 2) can utilize both probability data and kinetic data developed for other purposes to describe the bacterial growth/no growth interface. The reasons for this apparent link between the forms of the kinetic and probability models are unclear.

As more knowledge of the physiological basis of microbial growth, survival, and death in response to environmental conditions is obtained, it may be possible to relate this knowledge to the forms of models used in order to enhance their performance. Nevertheless, the current model provides a useful way to describe the growth/no growth interface and should help workers explore further the effects of environmental conditions on microbial growth, survival, and death.