The Cellular and Mechanical Basis for Response Characteristics of Identified Primary Afferents in the Rat Vibrissal System

SUMMARY

Compared to our understanding of the response properties of receptors in the auditory and visual systems, we have only a limited understanding of the mechanoreceptor responses that underlie tactile sensation. Here, we exploit the stereotyped morphology of the rat vibrissal (whisker) array to investigate coding and transduction properties of identified primary tactile afferents. We performed in vivo intra-axonal recording and labeling experiments to quantify response characteristics of four different types of identified mechanoreceptors in the vibrissal follicle: ring-sinus Merkel; lanceolate; clublike; and rete-ridge collar Merkel. Of these types, only ring-sinus Merkel endings exhibited slowly adapting properties. A weak inverse relationship between response magnitude and onset response latency was found across all types. All afferents exhibited strong ‘‘angular tuning,’’ i.e., their response magnitude and latency depended on the whisker’s deflection angle. Although previous studies suggested that this tuning should be aligned with the angular location of the mechanoreceptor in the follicle, such alignment was observed only for Merkel afferents; angular tuning of the other afferent types showed no clear alignment with mechanoreceptor location. Biomechanical modeling suggested that this tuning difference might be explained by mechanoreceptors’ differential sensitivity to the force directed along the whisker length. Electron microscopic investigations of Merkel endings and lanceolate endings at the level of the ring sinus revealed unique anatomical features that may promote these differential sensitivities. The present study systematically integrates biomechanical principles with the anatomical and morphological characterization of primary afferent endings to describe the physical and cellular processing that shapes the neural representation of touch.

Graphical Abstract

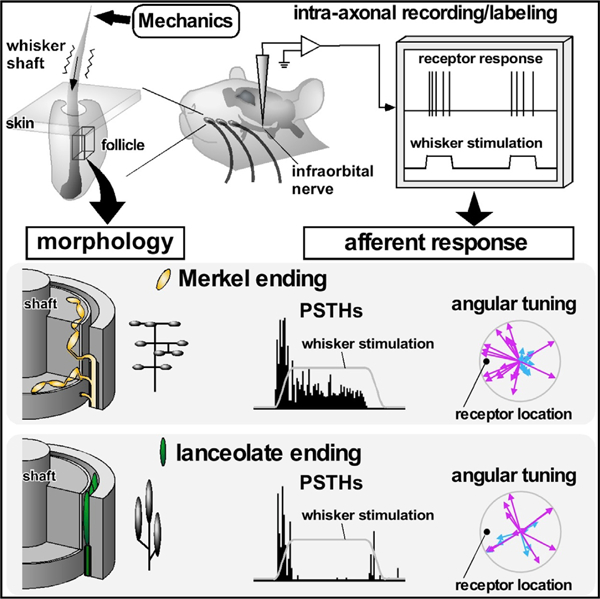
In Brief

Using intra-axonal recordings, Furuta et al. quantified response properties of four different types of identified mechanoreceptors in the whisker system. Each type had different response magnitudes, latencies, and angular tunings. Mechanical modeling and electron microscopy helped explain the responses in terms of sensor and tissue morphology.

INTRODUCTION

Compared to sensory transduction in the visual and auditory systems, transduction mechanisms for mechanical stimuli in the somatosensory periphery are as yet poorly understood. Mechanoreceptors have been classified based on morphology (e.g., Merkel, Meissner, Pacinian, and lanceolate), but only recently have studies begun to characterize responses of identified endings [1–3]. We lack a general understanding of relationships between tactile stimulus features (e.g., amplitude, velocity, and direction); mechanoreceptor characteristics, including type, size, number, and location of endings; and response properties, such as magnitude, latency, and angular (‘‘direction’’) sensitivity.

Recent studies of mechanosensory neurons innervating the skin have begun to improve our understanding of tactile receptor responses. For example, recent work showed that the strong caudal-rostral tuning of Ad innervated lanceolate nerve endings in mouse body hair is largely attributable to the angular location of mechanoreceptors within the follicle [4]. Other recent computational work predicted population responses of distinct receptor types in the human hand to simulated touch [5]. To date, however, studies of afferents innervating body hairs have not linked morphological and anatomical identity of the transduction machinery (i.e., mechanoreceptor location and identity) with detailed quantification of stimulus-response properties.

The rodent vibrissal (whisker) system offers a unique opportunity to probe responses of primary afferents to well-controlled tactile stimulation [3, 6, 7]. Two features of this system make it a particularly appropriate model for the study of receptor coding properties, complementary to study of mouse hairy skin and the primate hand. First, there are no mechanoreceptors along the vibrissa length; instead, all tactile information is transmitted to the follicle at the whisker base [8, 9]. Well-established models of vibrissal mechanics [10–12] allow tactile input to the follicle to be precisely quantified [6, 7, 13, 14]. Second, the follicle incorporates diverse mechanoreceptor types [8], many of which are analogous to those in the hand. These types include Merkel endings at the ring-sinus level (RS-Merkel), lanceolate endings, club-like endings, and Merkel endings at the rete-ridge collar (RRC-Merkel). Each of the ~150 myelinated axons innervating the follicle receives input from only a few mechanoreceptors, all of a single type [15].

Here, we performed intra-axonal recordings of rat vibrissal primary afferents while deflecting individual vibrissae with a piezoelectric transducer in four orthogonal directions. We then labeled and visualized the 3D morphology of each recorded nerve ending to identify the associated mechanoreceptor type. We aimed to reveal the correspondence between four mechanoreceptor types and their associated afferents’ suprathreshold spiking response characteristics, including number of stimulusevoked action potentials, temporal latency from stimulus onset to first evoked spike, variability of spike timing precision, adaptation properties, and angular tuning.

Results showed that piezoelectric stimulation evoked distinct response profiles across all mechanoreceptor types and that all types exhibit strong angular tuning. Only RS-Merkel neurons exhibited slowly adapting (SA) characteristics. Both RS- and RRC-Merkel endings showed angular tuning that coincided with the mechanoreceptor’s angular location within the follicle. In contrast, angular tuning of lanceolate and club-like receptors was not well predicted solely by mechanoreceptor location. A simple biomechanical model suggested that different receptor types may also be differentially sensitive to the ‘‘axial force,’’ i.e., the force directed along the whisker length. Electron microscopic studies suggested these differential mechanical sensitivities may be partially explained by the anatomical location of mechanoreceptors in the whisker-follicle complex.

RESULTS

The Morphology of Primary Afferents Associated with Four Identified Mechanoreceptor Types

The vibrissal nerve innervates several morphologically distinct types of mechanoreceptors, including RS-Merkel, lanceolate endings, club-like endings, and RRC-Merkel. Bulk tracer injections (Figure S1) showed that each mechanoreceptor cluster associated with a single primary afferent axon spanned only a small angular region of a follicle, although the totality of mechanoreceptors encircled the entire root of vibrissal shaft.

To investigate the correlation between mechanoreceptor type and its response properties, we performed intra-axonal recordings and then injected the axon with biotynilated dextran amine (BDA) to visualize the morphology of the nerve endings derived from single afferent fibers. Representative labeling of these endings for all four mechanoreceptor types is shown in Figure 1A. Each afferent responded to stimulation of one and only one vibrissa, and we analyzed recordings from 21 afferent fibers: 8 RS-Merkel; 3 RRC-Merkel; 6 lanceolate; and 4 club-like. Labeled axons were reconstructed in 3D (Figure 1B) to visualize axon terminal location within the follicle. A schematic of the recording setup and an example voltage trace are provided in Figure S2, along with a size comparison of the recording electrode and infraorbital nerve axons. All 21 3D reconstructions are shown in Figure S3.

Figure 1. Representative Primary Afferents and Endings: RS-Merkel, RRC-Merkel, Lanceolate, and Club-like.

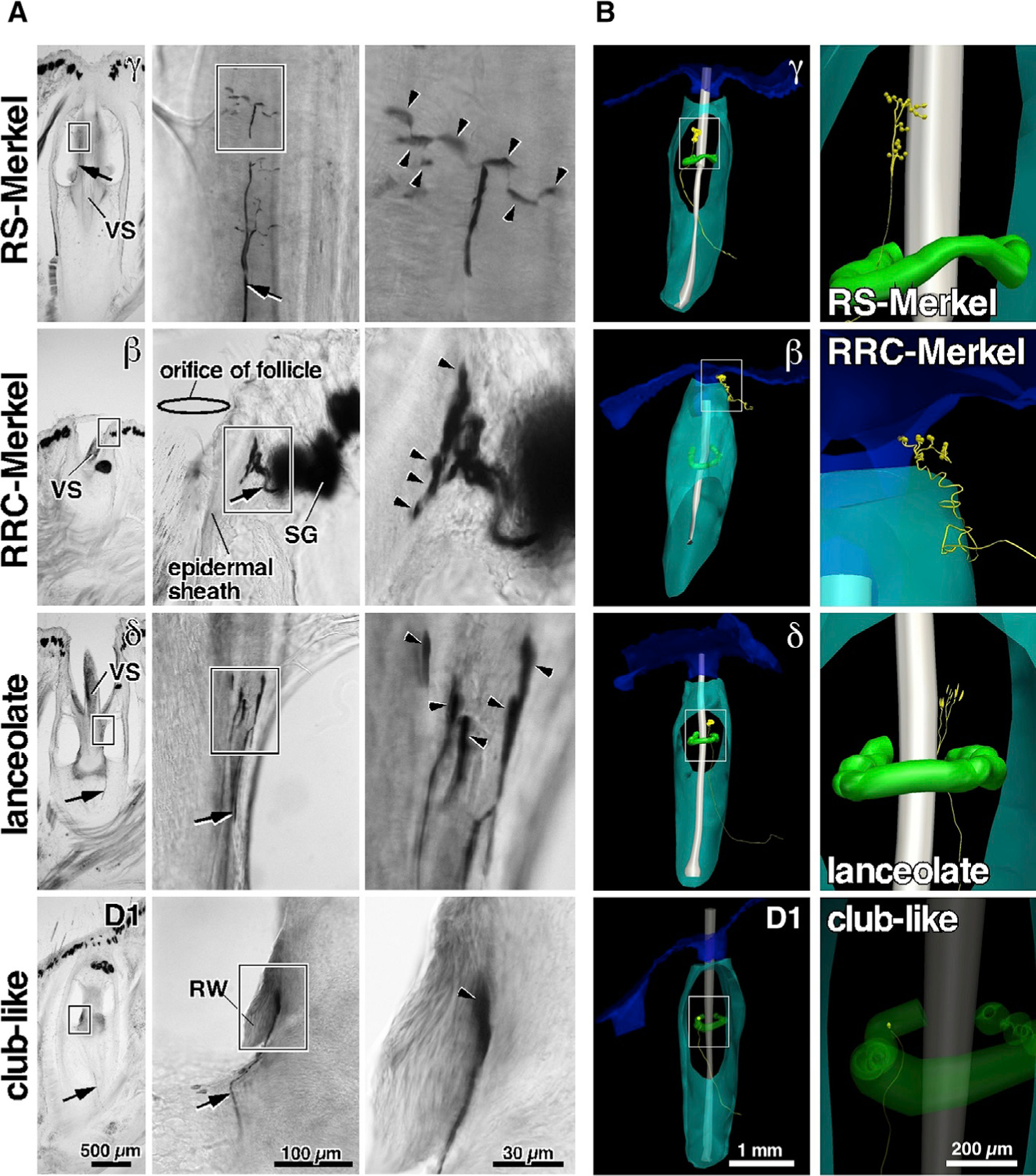
(A) Morphologies labeled via intra-axonal injection. Arrows indicate trunks of labeled afferents. Arrowheads indicate peripheral endings.

(B) Example 3D reconstructions of follicles that contained recorded axons. Axons and terminals are yellow. Skin, follicle capsule, vibrissal shaft, and Ringwulst are blue, cyan, gray, and green, respectively. Axon thickness and terminal size are exaggerated for clarity. Expanded views for each reconstruction (right column) show semiquantitative renderings of mechanoreceptor terminal shapes. The scale for the longest dimension of the mechanoreceptor is quantitatively accurate, although the scale for the other two dimensions is approximate, due to limitations of the microscope and 3D Neurolucida tracing system.

RW, Ringwulst; SG, sebaceous gland; VS, vibrissal shaft. See also Figures S1, S2, and S3 and Table S1.

Response Characteristics of Identified Primary Afferents when the Vibrissa Is Deflected in an Afferent’s ‘‘Best Direction’’

Vibrissae were trimmed to 5 mm and deflected in four orthogonal directions with a 10–50-10 ms ramp-and-hold stimulus during intra-axonal recording for 20 trials per stimulus direction. The ON response was defined to occur during the 10-ms onset ramp and the OFF response during the 10-ms offset ramp.

Unsurprisingly, all afferents exhibited distinct ‘‘angular tuning,’’ i.e., responses varied strongly with whisker deflection angle [16–23]. Many axons exhibited strong ON and OFF responses in multiple directions. The direction of strongest response (i.e., the most spikes elicited in ON or OFF windows) was considered the afferent’s best direction.

Representative responses to whisker deflection in the best direction are shown for single afferents of each type in Figure 2A. Consistent with previous results [18, 24], these raster plots and single-axon histograms show that each afferent exhibited highly repeatable, temporally precise firing patterns. As shown in Figure 2B, all 21 afferents exhibited very small onset timing jitter: the standard deviation of time to first spike was <1 ms. Within the 10-ms onset ramp, nine of 21 afferents fired the same number of spikes on all trials and nine showed maximum variation of a single spike. All three RRC-Merkel endings, as well as two of six lanceolate endings, always produced exactly one spike in the first 10 ms of firing.

Figure 2. Response Properties of Primary Afferents to Whisker Deflection in the Afferent’s Best Direction.

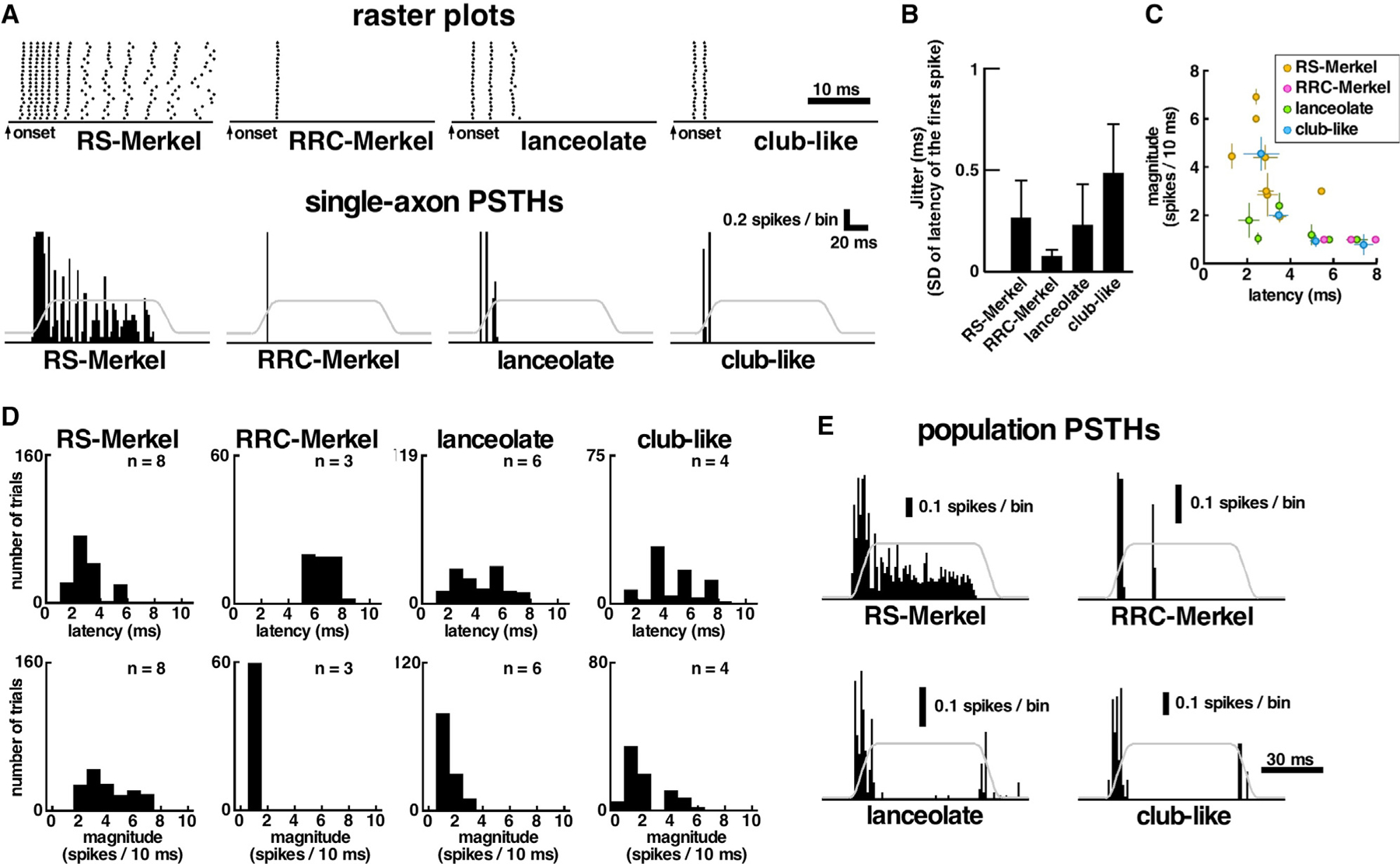
All histograms use bin width = 1 ms; error bars in (B) and (C) indicate standard deviations.

(A) Representative raster plots (20 trials) and post-stimulus time histograms (PSTHs) for each mechanoreceptor type. Gray lines represent piezoelectric stimulator motion (5° amplitude). ON/(OFF) responses were defined to occur during the 10-ms onset/(offset) ramp.

(B) For each receptor type, spike timing variability is quantified as the standard deviation of the latency to first spike across 20 trials. Error bars indicate SD across all afferents in each type.

(C) Inverse relationship between onset latency (ON responses) and spiking magnitude for each recorded afferent. Error bars indicate SD across 20 trials in each afferent.

(D) Histograms of ON latencies and ON magnitudes for all trials from all afferents, categorized by afferent type. n, number of afferents.

(E) Population PSTHs constructed by averaging all best-direction responses for all endings of the same type.

See also Figure S2.

At the level of individual axons, magnitude and latency of ON responses tended to exhibit a weak inverse relationship (Figure 2C). Shorter latency ON responses were also associated with more variable response magnitudes.

When averaged by receptor type, RS-Merkel exhibited the shortest latency (mean ± SD: 2.35 ± 0.58 ms) and largest magnitude responses, although RRC-Merkel exhibited the longest latency (6.75 ± 1.2 ms) and the lowest magnitude (Figure 2D). Lanceolate and club-like endings tended to have intermediate latencies (4.05 ± 1.69 ms and 3.36 ± 1.64 ms, respectively) and intermediate magnitudes. RS-Merkel response magnitudes were significantly larger than those of the other three afferent types (Tukey-Kramer test; p < 0.01 for each comparison), and club-like endings exhibited larger response magnitude than lanceolate and RRC-Merkel endings (Tukey-Kramer test; p < 0.01for each comparison). RRC-Merkel endings responded at longer latencies than other types (Tukey-Kramer test; p < 0.01 for each comparison), although RS-Merkel endings showed the shortest response latencies (Tukey-Kramer test; p < 0.01 for each comparison).

Considering each subpopulation, only RS-Merkel endings reliably showed slow-adaption characteristics; lanceolate endings, club-like endings, and RRC-Merkel endings showed rapidly adapting (RA) responses (Figure 2E). It is notable that the two types of Merkel endings, distinguished primarily by their location in the follicle, showed strikingly different adaptation properties. Full quantification of each afferent’s responses, including number of spikes (magnitude), latency from stimulus onset to first spike, and direction tuning, are provided in Table S1.

The responses shown in Figure 2E also indicate that some, but not all, afferent types generated OFF responses when the whisker was deflected in the afferent’s best direction. No OFF responses were observed for either RS-Merkel or RRC-Merkel endings but were present for two of six lanceolate endings and two of four club-like endings.

Angular Tuning of Merkel Endings, but Not Lanceolate or Club-like Afferents, Coincides with Mechanoreceptor Location

Studies of Aδ lanceolate endings in mouse hairy skin describe preferential responses to hair deflection in the direction of the mechanoreceptor [4]. We therefore expected to find that each afferent’s best stimulus direction was aligned with its associated mechanoreceptor’s angular location within the follicle. To test this expectation, we reconstructed the 3D angular location of each mechanoreceptor relative to the vibrissa and thus to the stimulation directions. An example reconstruction for an RS-Merkel ending is shown in Figure 3. We then compared the responses of each identified afferent with the reconstructed mechanoreceptor location.

Figure 3. Identifying the 3D Location of the Mechanoreceptor in the Follicle.

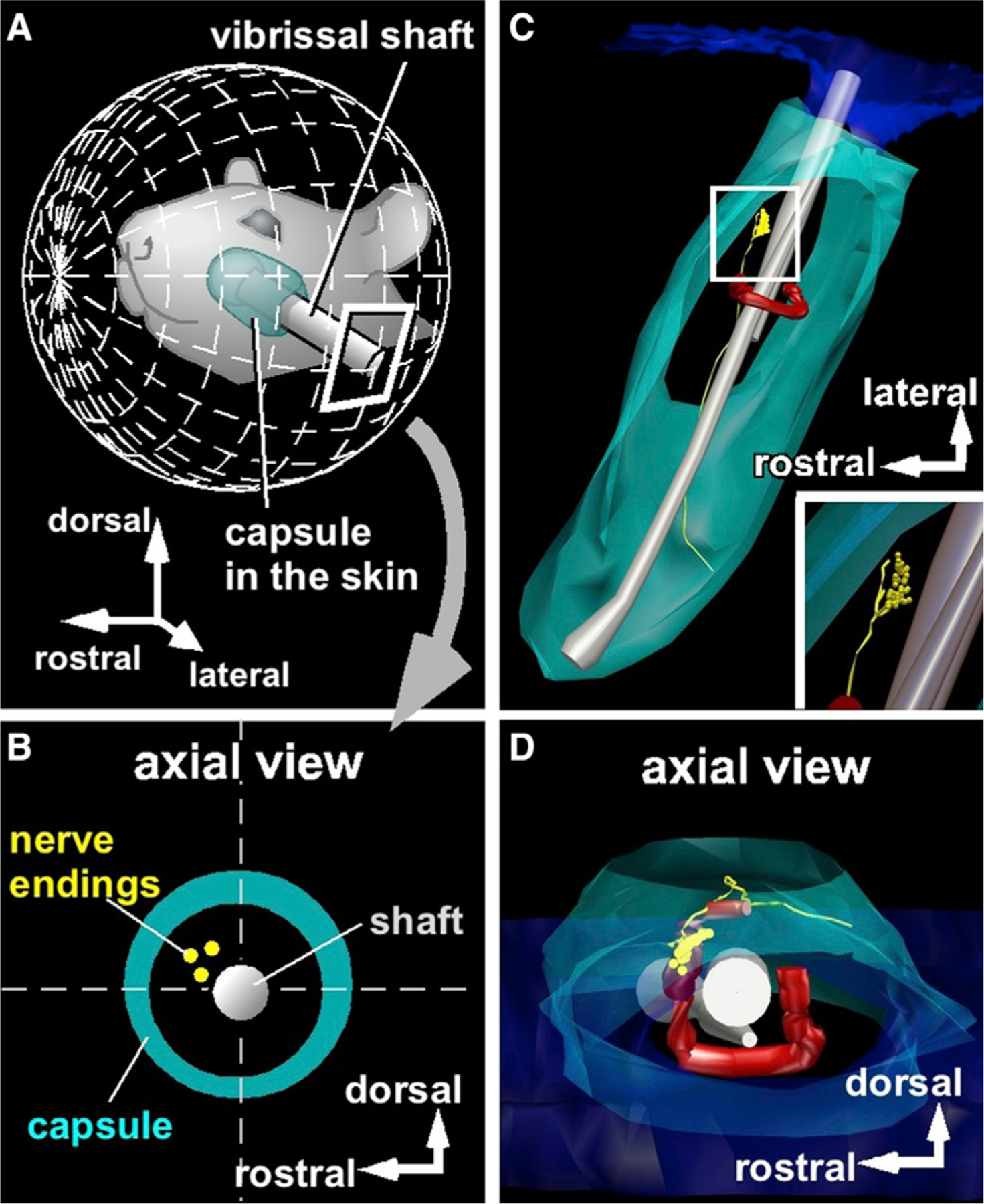
(A) Vibrissa orientation relative to mystacial pad.

(B) Locations of peripheral endings were projected into a plane normal to the vibrissal length.

(C) Representative 3D reconstruction of a vibrissal follicle. Peripheral endings are yellow.

(D) Reconstructed data are observed from a direction along the vibrissal length.

See also Figures S2 and S3.

Both RS-Merkel and RRC-Merkel afferents tended to exhibit the strongest ON responses when deflected in the general direction of the mechanoreceptor ending (Figure 4A). The angular difference between each neuron’s best direction and the mechanoreceptor ending location is shown in Figure S4A.

Figure 4. Axons Exhibit a Diversity of Angular Tuning Profiles Relative to Location of Endings and Preferred Angle.

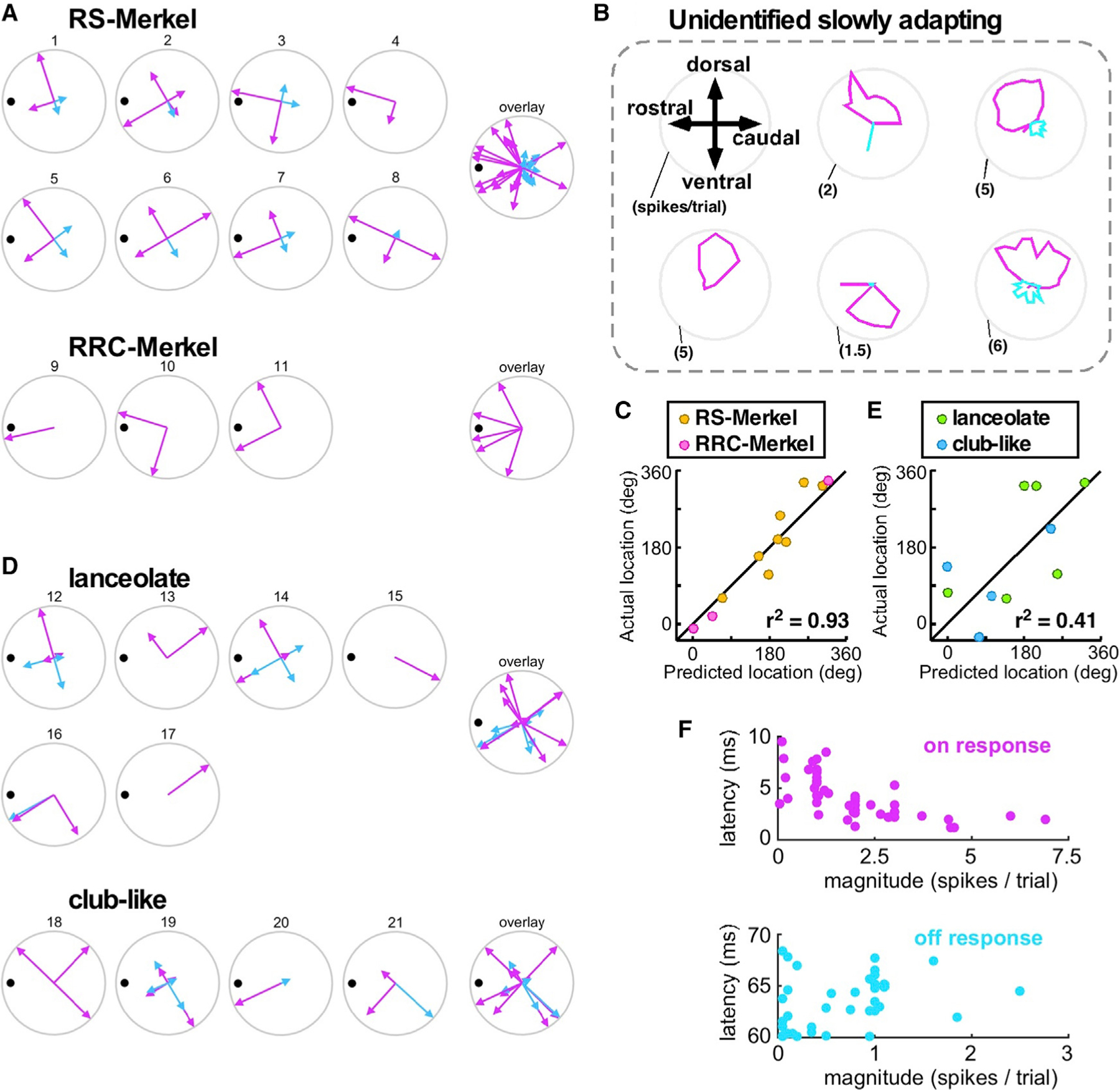
(A) Responses of 11 identified Merkel afferents to deflections in four directions with respect to the laboratory frame (up, forward, back, and down). All subplots are rotated to place the mechanoreceptor (black dot) at the same angular location, permitting results from all afferents to be overlaid. Pink and cyan vectors indicate ON and OFF response magnitudes for the four deflection directions. For afferent 2, one pair of overlapping pink and cyan vectors is rotated approximately ±5° from nominal for visual clarity.

(B) Angular tuning curves for six unidentified, slowly adapting primary afferents during whisker deflections in either 32 or 16 different directions. Pink/cyan polar plots indicate ON/OFF response magnitudes, respectively.

(C) For Merkel neurons, mechanoreceptor angular locations were well predicted by a cosine function.

(D)Responses of ten identified lanceolate and club-like neurons to deflections in four directions. Conventions are as in (A). For afferents 12 and 16, one pair of overlapping pink and cyan vectors is rotated approximately ±5° from nominal for visual clarity. Two pairs are similarly rotated for afferent 19.

(E)For lanceolate and club-like neurons, mechanoreceptor angular locations were not well predicted by cosine fits.

(F)Relationships between response latency and magnitude (number of spikes/10-ms ON or OFF window) are variable.

See also Figure S4.

To quantify angular tuning at higher resolution, we recorded from six additional, unidentified but slowly adapting (putative Merkel) afferents while stimulating in either 32 or 16 different directions. Five of six afferents were strongly directionally tuned, just like the eight identified RS-Merkel afferents in Figure 4A. Responses of these five unidentified afferents are shown in Figure 4B. The sixth unidentified afferent exhibited very little if any angular tuning; it responded at an unusually high firing rate and with nearly equal strength in all stimulus directions (Figure S4B).

Visual inspection of Figure 4B suggested that these responses could be modeled with a cosine function. Cosine fits (Equation 3 in STAR Methods) to all six unidentified afferents are shown in Figure S4B. Responses predicted using cosine fits were generally a good match for experimental responses (Pearson correlation value > 0.81) for all but the sixth afferent.

Given the cosine-like tuning observed in these high-resolution (but unidentified) recordings, we performed cosine fits to the responses of the identified Merkel neurons. These cosine fits yielded a preferred angle (between 0° and 360°), taken to be a prediction of mechanoreceptor location. The preferred angle is distinct from ‘‘best direction,’’ which is constrained to be one of the four tested stimulation directions. For all Merkel neurons, cosine fits yielded preferred angles (predicted mechanoreceptor locations) that matched well with actual mechanoreceptor locations (Figure 4C).

In contrast, identified lanceolate and club-like endings did not generally exhibit the strongest ON responses when deflected toward the mechanoreceptor ending (Figure 4D). Accordingly, their ON responses were not adequately recapitulated by a cosine fit, and preferred angle estimates from identified lanceolate and club-like endings were poorly correlated with mechanoreceptor location (Figure 4E). Only three of ten axons show preferred angles within ±45° of the mechanoreceptor location.

OFF responses also differed between mechanoreceptor types. Although Merkel neurons never exhibited OFF responses when stimulated in their best direction (cf., Figure 2E), seven of eight RS-Merkel endings exhibited OFF responses when stimulated in directions approximately opposite their best direction. No OFF responses were observed in RRC-Merkel endings for any stimulation direction (Figure 4A). Six of ten lanceolate and club-like endings had OFF responses, often strong and in multiple directions, although the remaining four had no OFF response at all (Figure 4D).

Finally, ON and OFF response latencies both exhibited considerable variability (Figure 4F); latency and magnitude are not strongly related. Furthermore, stimulation in the best direction does not necessarily ensure the shortest latency response: four of 21 axons had a shorter latency response in a direction other than that which generated the largest magnitude response.

Summarizing, these results indicate thata cosine fit based on the angular location of the mechanoreceptor offers a good (but not complete) explanation for ON responses of Merkel endings. However, responses of lanceolate and club-like afferents cannot be captured with this approach. Thus, we next constructed a simple but more general biomechanical model that accounted for mechanoreceptor location to explain the latencies and magnitudes of both ON and OFF responses, for all 21 axons, in all four directions.

A Simple Biomechanical Model Predicts Spiking Responses across Afferents

Details for creating a simple biomechanical model are provided in STAR Methods. When the whisker is deflected in a particular direction, the mechanical signals generated at the whisker base depend on whisker geometry and orientation (Figure S5). Both experimental and modeling work [6, 7, 10] indicate that primary afferent responses depend strongly on these mechanical signals. In the present experiments, the signals that determine mechanoreceptor deformation are chosen to be (1) how the whisker bends in the direction of the mechanoreceptor; (2) the axial force, directed along the whisker’s length; and (3) the time derivatives of these two signals.

We performed simulations to calculate bending moment (M_B) and axial force (F_X) during the stimulus onset ramp. The M_B signal was then weighted by a cosine function maximum in the direction of mechanoreceptor location. At stimulation offset, the whisker quickly detaches from the piezo (Figure S6A) and relaxes to rest based on surrounding tissue mechanics. We generated a total of four mechanical signals (M_B; F_X , and their derivatives) to represent the complete ramp and hold trajectory (Figure S6B).

Linear, weighted pairwise combinations of these four mechanical signals were then optimized to predict afferent responses. Because only pairwise combinations were tested, each model had two parameters (Equation 5 of STAR Methods). To determine firing latencies, each simulated response was considered to occur the first time it crossed a simulated threshold, which was the third and final parameter optimized in each model. For each afferent, the number of incorrect ON and OFF responses was minimized, followed by minimizing the absolute value of the difference between observed and simulated response magnitude and between observed and simulated response latency. Notably, the model does not contain an adaptation term, so it cannot predict responses during the hold period.

Model fitness was assessed with F1 scores (Equations 6, 7, and 8 of STAR Methods) and by computing the ratio of correct (binary) responses to the total number of responses. There were 88 total responses for Merkel neurons (11 neurons × 4 directions × 2 ON/OFF) and 80 total responses for lanceolate and club-like neurons (10 neurons × 4 directions × 2 ON/OFF). Model fitness was also assessed by comparing total magnitude error and latency error.

We first tested how well the direction-weighted M_B signal and its derivative could explain afferent responses. Because M_B and its derivative are directionally weighted, we expected these signals to yield high-quality predictions for Merkel responses (which exhibit strong angular tuning) and lower quality predictions for lanceolate and club-like responses (which exhibit weaker angular tuning). Meeting this expectation (Figure 5), this model explained most (81/88; F1 = 0.90) of the Merkel responses but fewer of the lanceolate and club-like responses (62/80; F1 = 0.69). Note that the model failed to capture any ON responses in directions opposite the mechanoreceptor location. Magnitude error in all directions is visualized by comparing the overlay plots in the second columns of Figures 5A and 5B with experimental data in the first columns and quantified in the magnitude error histograms of Figures 5C and 5D. Note that, because the maximal response for each afferent was normalized to 1 (see STAR Methods), the magnitude error histograms can be compared across models: if the histograms look similar to each other, the models performed similarly.

Figure 5. Mechanical Modeling Suggests Differential Mechanical Sensitivities across Afferent Types.

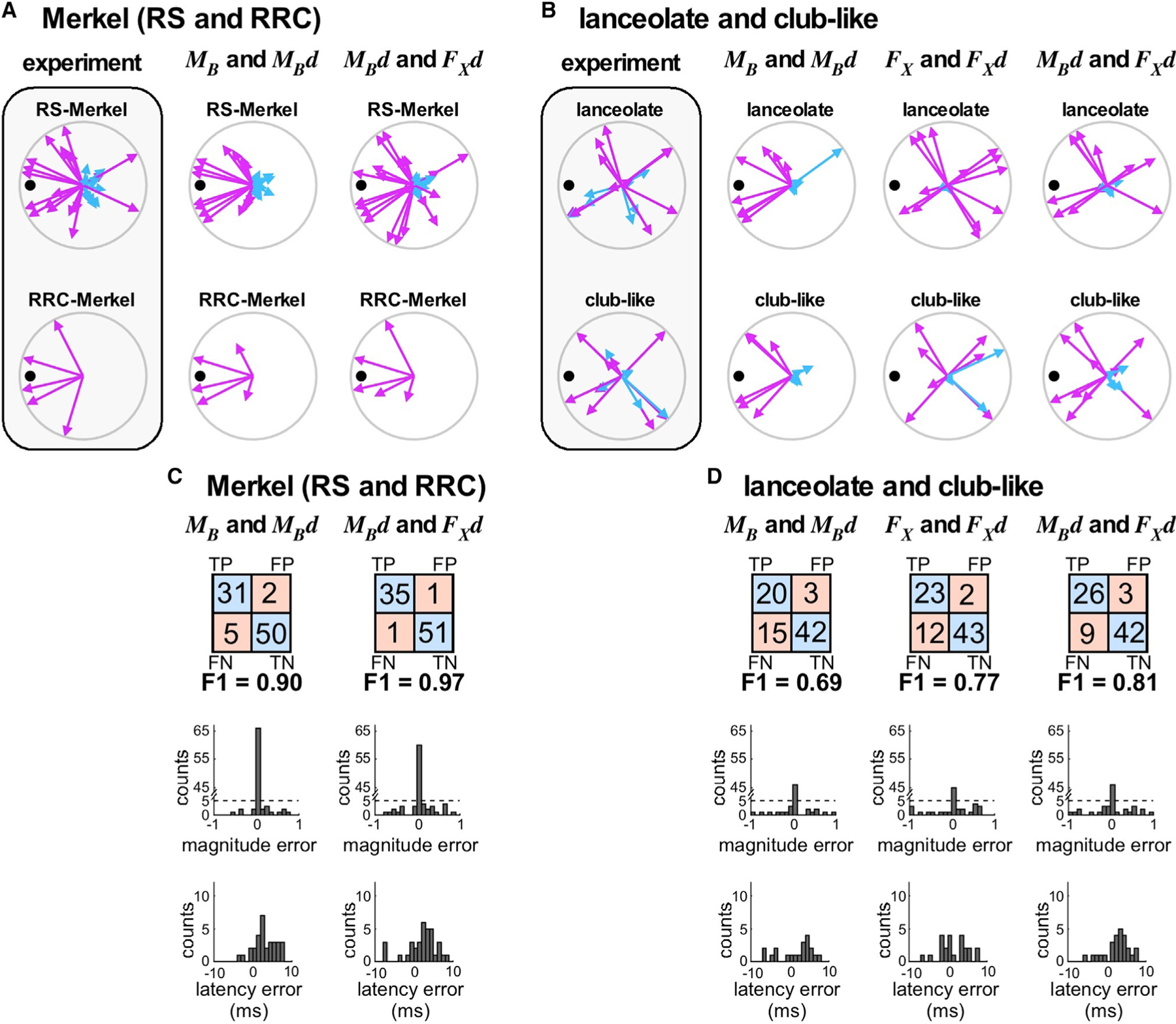
(A) Experimental ON and OFF responses for Merkel neurons.

(B) Experimental ON and OFF responses for lanceolate neurons.

(A and B) Column 1 (shaded) shows experimental data. The remaining columns show results of models based on specific mechanical signals, as labeled. F_X , axial force; F_X d, derivative of axial force; M_B, bending moment; M_Bd, derivative of bending moment. ON (pink) and OFF (cyan) response magnitudes for each direction are plotted as vectors and sorted by mechanoreceptor type.

(C and D) Confusion matrices and magnitude error and latency error histograms for Merkel (C) and lanceolate and club-like endings (D). Each column shows results for a single modeling choice; abbreviations are as in (A) and (B). Each 2 × 2 array shows the number of true positives (TPs), false positives (FPs), false negatives (FNs), and true negatives (TNs) of predicted spiking responses compared to observed spiking responses. F1 scores (see STAR Methods) are indicated below each array. Histograms quantify error between experimental and modeled stimulus responses. Latency error histograms have 1-ms bins. Magnitude error histograms are binned at 0.1 units, where maximum response magnitude for each afferent has been normalized to 1.

See also Figures S5 and S6.

We next asked whether axial force (F_X) and its derivative would improve the F1 scores for either ending type. These mechanical signals do not incorporate mechanoreceptor location but are strongly modulated by whisker shape and angle of emergence (Figure S5). As shown in Figures 5B and 5D, model performance improved slightly for lanceolate and club-like responses (66/80 correct; F1 = 0.77). In contrast, shuffling simulations (see STAR Methods) indicated that this combination of variables did not predict Merkel responses with greater success than if the neural responses were randomized with respect to those variables, and so this combination is omitted from Figures 5A and 5C.

Finally, we noted that the model aims to predict responses during the ‘‘ramp’’ period, when mechanical signals change as functions of time. We therefore tested model performance using a linear combination of the two derivatives (M_Bd and F_X d). This combination successfully predicted 98% (86/88; F1 = 0.97) of Merkel responses and 85% (68/80; F1 = 0.81) of lanceolate and club-like responses.

Summarizing, this simple model indicates that all receptor types are broadly responsive to many different mechanical variables but that lanceolate and club-like endings may incorporate more information about F_X and its derivative than do Merkel neurons. For Merkel cells, ON responses in the hemifield of the mechanoreceptor location, and OFF responses in the opposite hemifield, are well explained by cosine-tuned bending moment and its derivative. Lanceolate and club-like neurons can be moderately well predicted by this mechanical signal, but observed responses outside this hemifield can be captured with addition of F_X . The axial force and its derivative help explain responses outside the hemifield. Differences between types are likely driven by differences in mechanoreceptor biophysics, geometry, orientation, branching pattern, and location in the follicle.

Anatomical Location of Afferent Types Suggests a Physical Substrate for Differential Mechanical Tuning

RS-Merkel endings and lanceolate endings exhibit quite different response characteristics, even though they are found at similar locations relative to the ring sinus and might therefore be expected to receive similar mechanical input (Figures 1 and S1). To try to explain these differences, we compared the detailed architecture of the two ending types at the electron microscopic level.

Myelinated axons running in the mesenchymal sheath and traversing the intermediary zone were found to give off thin branches that pierced the glassy membrane (Figures 6A–6C). At increased spatial resolution, RS-Merkel endings—presumed to connect with these thin branches—were localized in the deepest layer of the epithelial sheath (Figure 6D). In contrast, lanceolate endings were located in a loose space between the glassy membrane and mesenchymal sheath (Figure 6E) [25]. 3D reconstruction of ultrastructure at the ring sinus level (Figures 6F and 6G) clearly revealed the different spatial arrangements of these two mechanoreceptor types.

Figure 6. Ultrastructure of RS-Merkel and Lanceolate Endings.

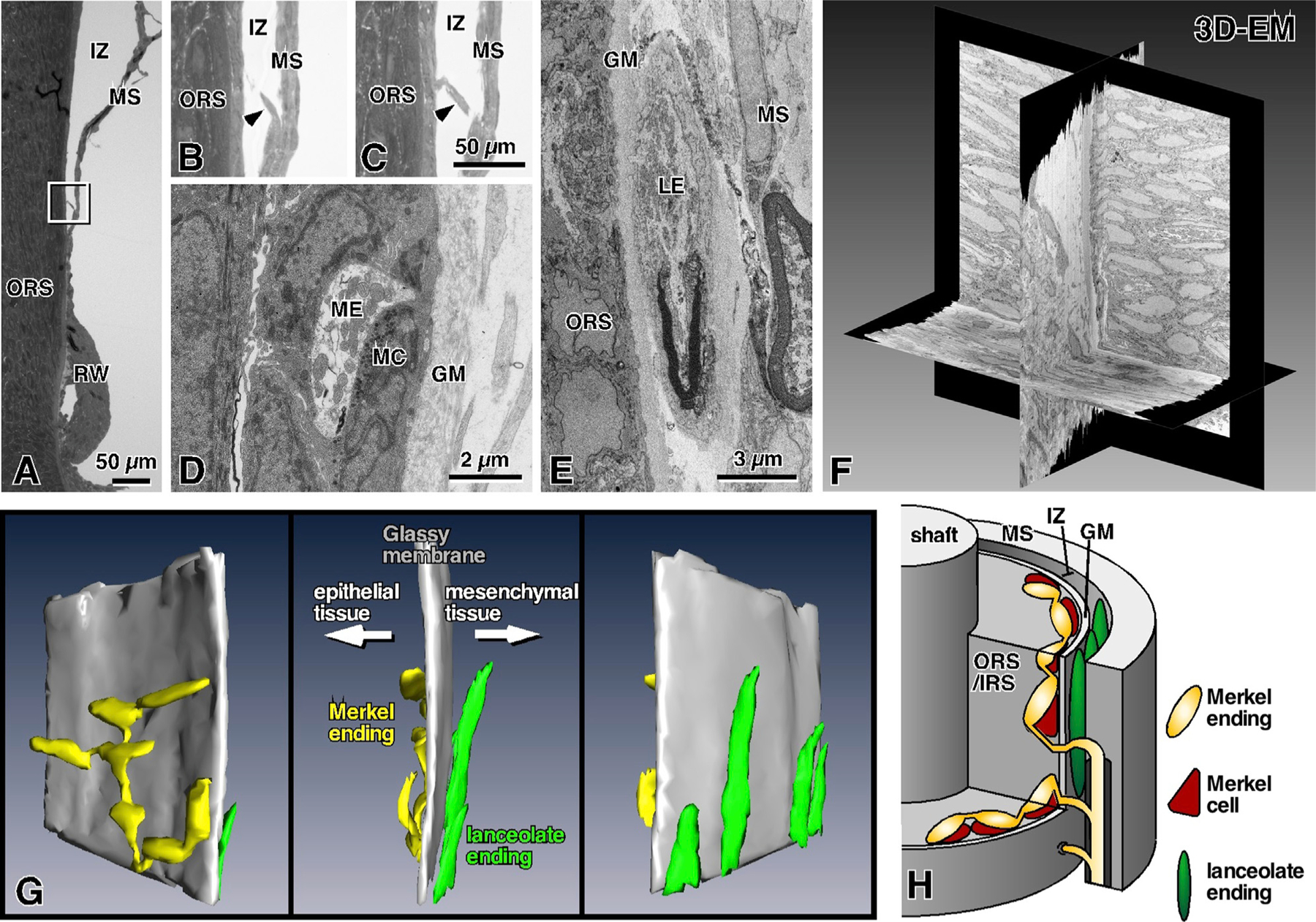
GM, glassy membrane (basement membrane); IRS, inner root sheath; IZ, intermediary zone; LE, lanceolate ending; MC, Merkel cell; ME, Merkel ending; MS, mesenchymal sheath; ORS, outer root sheath; 3D-EM, three-dimensional electron microscopy.

(A) Semi-thin section parallel to the axis of the vibrissa.

(B and C) Magnified views of the rectangle in (A) obtained from two sequential semi-thin sections. Arrowheads indicate an axon branch piercing the glassy membrane to enter the ORS.

(D)RS-Merkel endings are distributed in the most lateral layer of the ORS.

(E) Ultrastructure of a lanceolate ending.

(F) Three orthogonal planes of stack data obtained with a scanning electron microscopic system.

(G) Sequential EM images of nerve endings at the ring sinus level were reconstructed in 3D (gray, glassy membrane; yellow, Merkel ending; green, lanceolate ending). RS-Merkel endings are located in the epithelial sheath although lanceolate endings are localized in the loose space between the glassy membrane and the mesenchymal tissue.

(H) Schematic representation of Merkel and lanceolate ending innervation at the level of the ring sinus.

Based on analogy with hairy skin of cats and primates [26], we expected to find the discoid varicosities of Merkel endings localized between Merkel cells and the glassy membrane (basement membrane). Surprisingly, however, the reconstructions of Figures 6F and 6G clearly show that each Merkel cell was always localized between the discoid varicosity of its associated Merkel ending and the glassy membrane—a geometry exactly reversed from the spatial relationship found in the skin.

In the case of lanceolate endings (Figure 6E), we confirmed that one side of the longitudinal axon terminal contacted the deeper side of the glassy membrane, although the other side of the axon terminal made contact with the mesenchymal sheath [25].

The anatomical differences between RS-Merkel and lanceolate endings are summarized in Figure 6H. Intuitively, the schematic suggests that these two mechanoreceptors types will experience different mechanical signals during vibrissa stimulation.

Specifically, the intra-axonal recordings, the theoretical model for angular tuning, and the three-dimensional electron microscopy (3D-EM) analysis suggest the perspective depicted in Figure 7. Mechanical input near the vibrissal tip is transmitted by the vibrissal shaft, whose intrinsic curvature and emergence angle alter mechanical signals at its base. Each mechanoreceptor is differentially sensitive to the mechanical components, depending on its type, location, and orientation. Primary afferent responses are determined by a combination of the mechanical processing of the vibrissa itself and differential mechanoreceptor sensitivity.

Figure 7. An Explanation for Response Variations across Mechanoreceptor Type Based on Differential Sensitivity to Mechanical Signals at the Whisker Base.

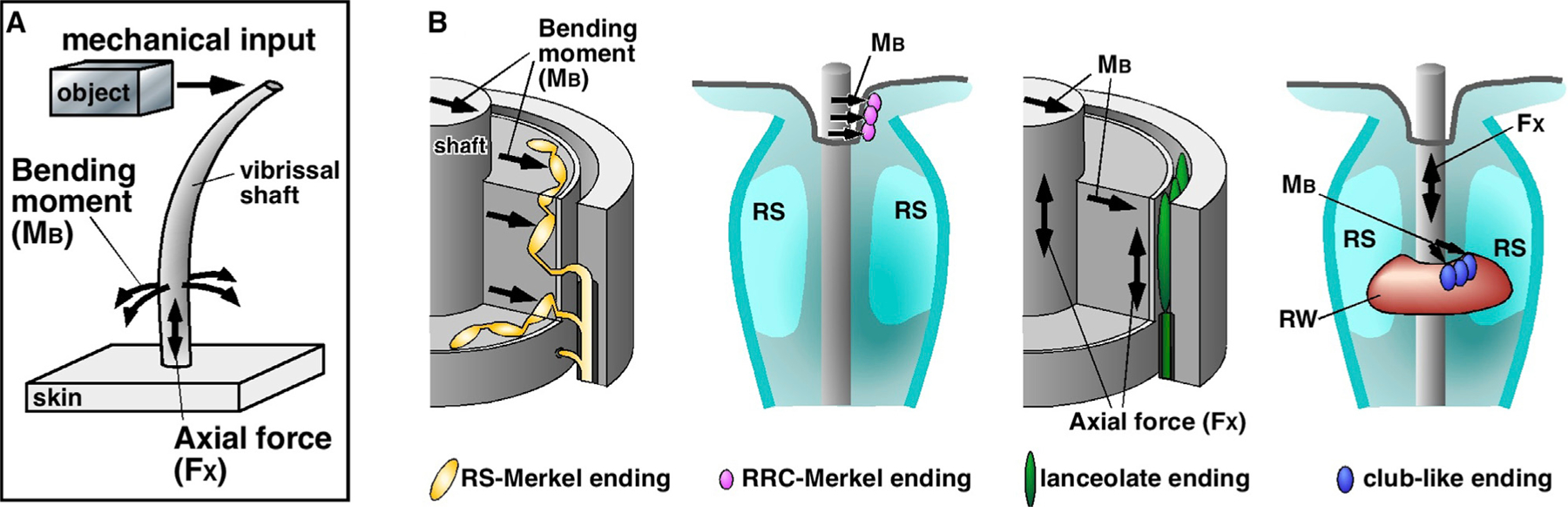
(A) Mechanical input near the vibrissa tip is transduced by the vibrissa, which has an intrinsic curvature. The mechanical signal is decomposed into mechanical components that include bending moment (M_B) and axial force (F_X).

(B) Each mechanoreceptor’s sensitivity will be influenced by its location and the surrounding structure of the follicle complex.

Merkel endings, which are embedded between the glassy membrane and the epithelial tissue, are ideally positioned to respond strongly, and at short latency, to bending moment in directions that generally correspond to mechanoreceptor location. In contrast, the effect of the axial force F_X is isotropic, regardless of mechanoreceptor location. A lanceolate ending is ideally positioned to respond to F_X because its two sides are connected between the glassy membrane and the mesenchymal sheath: it will respond to shearing between these two structures. The isotropic nature of the axial force helps explain why lanceolate axonal responses do not appear well correlated with ending location.

DISCUSSION

The present work delineates for the first time direct correspondences between morphological characteristics of four different mechanoreceptor types and response properties. Each type shows characteristic latencies, magnitudes, and angular tunings to punctate stimuli. Biomechanical modeling suggests that all afferents are broadly tuned but may differ in sensitivity to particular mechanical signals. Our results complement recent genetic approaches that have focused on the molecular mechanisms underlying tactile sensing [27–29] and offer a detailed quantification of the sensing machinery underlying vibrissal somatosensation: the stimulus is precisely controlled; mechanics and geometry are quantified; and morphology and anatomy of recorded afferents are verified.

A Potential Explanation for Variable Adaptation Characteristics of Lanceolate Endings in Mouse Hairy Skin

In mouse hairy skin, lanceolate endings are associated with guard hairs, zigzag hairs, and awl/auchene hairs [1]. Recent work tested the prediction that these endings should exhibit RA characteristics [1, 30] and found that lanceolate endings associated with A-beta or A-delta fibers were always RA, but those associated with C-fibers exhibited intermediate adaptation characteristics. The present work finds that lanceolate endings in the vibrissal follicle always exhibit RA responses, consistent with the strong resemblance of vibrissae to guard hairs, which are innervated only by A-beta fibers.

In addition, the anatomy shown in Figures 6 and 7 suggests a potential explanation for the variable adaptation characteristics observed for lanceolate endings in hairy skin. Namely, the intrinsic curvature of Awl/Auchene hairs and the eponymous shape of zigzag hairs seem likely to generate high variability in the axial force. If lanceolate endings are particularly sensitive to this signal (as suggested by Figures 5, 6, and 7), subtle differences in mechanoreceptor location, surrounding structure, or receptor morphology between the three lanceolate subtypes of hairy skin could significantly change response properties.

A Unique Location for RS-Merkel Cells: between the Glassy Membrane and the Neuronal Terminal

Recent papers have explored the function of the channel protein Piezo2 in Merkel cells, the primary site of mechanical transduction associated with Merkel endings [2, 31–36]. Deprivation of Piezo2 or Merkel cells reduced SA responses, indicating that Merkel endings are SA type. The present intra-axonal labeling studies confirm that, in the vibrissal follicle, RS-Merkel endings exhibit SA responses but also show that RRC-Merkel endings respond with RA characteristics. We suggest that these distinct adaptation characteristics may be driven by tissue properties rather than by intrinsic cellular differences in the endings themselves (Figure 6). Although Merkel cells associated with RRC-Merkel endings lie between the neuronal terminal and the epithelial cell, we show that Merkel cells associated with RS-Merkel endings lie between the glassy membrane and the neuronal terminal, exactly opposite the situation in hairy skin. This anatomical difference may drive afferent response variability among populations of genetically and physiologically similar mechanoreceptors.

Factors that Contribute to the Neural Response

Afferent encoding mechanisms thus involve the architecture of the tactile sensing apparatus and surrounding tissue as well as the intrinsic physiological properties of each mechanoreceptor type.

The results of Figure 4 highlight that mechanoreceptor location is the primary (though not the complete) factor that determines Merkel responses. However, mechanoreceptor location alone is not sufficient to predict lanceolate and club-like responses: the mechanoreceptor’s angular location generally does not correspond to the afferent’s preferred angle. This result contrasts with the finding in mouse hairy skin that Aδ lanceolate endings exhibit strong rostrocaudal tuning in the angular direction of the mechanoreceptor [4]. We suggest that the follicular ring sinus, a complicated anatomical structure with complex biomechanical properties, might help explain these different relationships between ending location and preferred angle for lanceolate endings.

The morphology of the sensor (the vibrissa) also plays a key role in determining the signals to which the primary afferents respond. In particular, the axial force (F_x) often varies with deflection angle in unintuitive ways (Figure S5) and may be a strong driver of neural responses. The ramp-and-hold stimulus employed here is relatively simple: on each trial, the stimulation is applied at the same position along the whisker (arc length), with the same linear displacement, and at the same velocity. In addition, the whisker was trimmed so short that it was essentially straight. Therefore, the twisting moment (M_X ) could not contribute to the neural response, and F_x is strongly correlated with M_B.The stimulus space explored here therefore does not allow for widely varying response profiles between afferents, either within or across mechanoreceptor types.

When vibrissae are untrimmed, the effects of vibrissal 3D geometry on primary afferent responses will be even larger [11–14, 37]. Future work should include the study of deflections with the whiskers intact, so as to observe any contribution of M_X to the generation of afferent signals. Nevertheless, the distinctive response patterns seen, even for this simple stimulus, suggest that different afferent types may show some degree of selectivity for particular regions of the stimulus space.

Advantages, Limitations, and Implications of the Biomechanical Model

The association between mechanical signals and neural response was further investigated using a simple biomechanical model to explain response magnitude and latency as a function of deflection direction. This approach complements previous detailed models of mechano-electrical transduction that have included integrate and fire models of primary afferents and use a total of either 17 [38] or 9 [39] parameters. A significant limitation of the present model is that it cannot predict responses during the ‘‘hold’’ portion of the stimulus.

As expected, modeling showed that responses of Merkel endings are predominantly driven by the bending moment (M_B) scaled by the angular location of the mechanoreceptor [3], but models improve when the derivative of axial force (F_xd) was included; this signal depends strongly on vibrissal geometry relative to stimulation direction but is independent of the mechanoreceptor’s angular location within the follicle.

A striking aspect of the modeling results (Figure 5) is that quite accurate performance can be obtained using multiple different combinations of mechanical signals. For example, Merkel neurons respond nearly equally well to a combination of M_B and its derivative or to the combination of the derivatives of M_B and F_x. Many lanceolate and club-like responses are also explained by these two combinations, as well as by the combination of F_x and its derivative. These results suggest that afferents are broadly tuned to a wide range of mechanical signals and their derivatives, regardless of cell type. However, confirmation of this idea will require testing under conditions in which M_B and F_x are decoupled (e.g., during axial stimulation of the whisker).

At first glance, the results presented here may appear inconsistent with those of Severson et al. [3], which indicated that Merkel neurons respond to bending moment. However, that work did not test models without components of moment and therefore cannot evaluate the sensitivity of Merkel endings to F_x alone. The results of Severson et al. [3] as well as results of the present study are both consistent with the idea that Merkel neurons are strongly driven by the amplitude and direction of bending. Whether Merkel endings are sensitive to F_x because this signal is correlated with M_B or because they are additionally tuned to F_x is as yet unclear and will require further experiments.

The Vibrissal System Offers Unique Advantages for the Study of Mechanoreceptor Responses

The present results underscore that primary afferent responses depend on both sensor morphology and intrinsic mechanoreceptor properties. To disentangle the contributions of these factors, the vibrissal system offers some unique advantages compared to the skin.

Direct stimulation of the skin is complicated by viscoelasticity, nonlinear deformation, sweat, friction, and hysteresis. Models of skin primary afferent responses often require hundreds of parameters [40–42]. Recent work [5] in the primate hand has reduced the number of parameters using a combined quasistatic/dynamic approach and simulated quasistatic skin deflections to predict responses of RA and SA afferents. However, the model simulated the immobile hand, neglected friction, shear forces, and 3D hand geometry, and the quasistatic input was estimated heuristically, based on quantities empirically found to be associated with afferent responses over different frequency ranges.

The vibrissal system offers complementary costs and benefits to study of the primate hand. Unlike the hand, the 3D geometry and mechanics of the vibrissa can be quantified, even during motion [10–14]. Although our understanding of internal follicle mechanics is limited [9, 38], the vibrissa is itself a tool for applying a highly repeatable stimulus to a mechanoreceptor. By stimulating at different positions along the vibrissa arc length, the effects of applying a particular force can be decoupled from the effects of applying a particular displacement. Furthermore, a wide range of complex, realistic active sensing conditions can be explored using different frequencies and amplitudes of vibrissal stimulation.

The vibrissa’s simplicity, combined with robust physiological and morphological data, offers the ability to examine how each mechanoreceptor type differentially deconstructs tactile input. The present results underscore that the architecture of the tactile sensory apparatus helps determine neural response properties, an idea equally applicable to the study of other tactile organs. Given the homology of receptor types between vibrissa and hand, we anticipate that complementary experiments in these two systems will progressively help us ‘‘break the code’’ of the tactile periphery.

STAR★METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Takahiro Furuta (furuta@dent.osaka-u.ac.jp). This study did not generate new unique reagents.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Experiments were performed with 38 male rats (250–350 g; Sprague-Dawley). The animals were kept on a 12/12 h light/dark cycle at 28°C. Experiments were conducted in accordance with the animal care and use guidelines of the Institute of Laboratory Animals, Graduate School of Medicine (Kyoto University, approval number: MedKyo16573). All efforts were made to minimize the number of animals required as well as pain and discomfort of the animals.

METHOD DETAILS

Recording and labeling of primary afferents

Experiments were performed under ketamine (75 mg/kg, xylazine 5 mg/kg) anesthesia. The animal was placed in a stereotaxic apparatus, breathed freely, and body temperature was maintained at 37.5°C with a heating pad controlled thermostatically. The height of the animal’s body was adjusted to maximize the stability of electrophysiological recordings and the animal’s head tipped so that bregma and lambda were in the horizontal plane. Throughout the experiment, a deep level of anesthesia was maintained (stage III-3) by delivering additional doses of anesthetic (20 mg/kg ketamine plus 0.3 mg/kg xylazine, i.m.) as needed to abolish the reflex response to sharp pinch of the hindlimbs. The eyeball and adipose tissue in the orbit were removed to expose the surface of the infraorbital nerve small slits were made in the sheath of the nerve.

Glass micropipettes (beveled tip) filled with a solution of potassium acetate (0.5M) and biotynilated dextran amine (10% BDA-3000; Invitrogen, Eugene, OR) were slowly lowered into the infraorbital nerve. When a micropipette mechanically impaled an axon it caused a sudden increase in action potential amplitude (> 10 mV), and drop in resting potential (> 20 mV). We assessed the receptive field of the recorded axon by deflecting individual vibrissae with a hand-held probe under a dissecting microscope. Signals were amplified and bandpass filtered (100 Hz - 3 kHz) and an audio monitor and a computer display were used to monitor the responses. Each axon responded to deflection of one and only one vibrissa.

The vibrissa was cut 5 mm from the skin, and its tip inserted into the groove of a beveled straw attached to a ceramic bimorph bender (Physik Instrumente, Karlsruhe, Germany). The vibrissa was pushed in a given direction at stimulus onset, but returned passively at a neutral position at stimulus offset. Care was taken to align the axis of the stimulator with that of the hair shaft (Figure S6A). Ramp-and-hold waveforms (rise/fall times, 10 ms; hold duration, 50 ms; amplitude, 0.4 mm, or ~5°; angular velocity, ~1,000°/sec; interstimulus interval, 1.0 s) were used to deflect vibrissae from their resting position in four directions spanning 360° (i.e., in 90° increments relative to the horizontal alignment of the vibrissa rows). As measured with a photodiode, the first-mode resonance frequency of the bimorph was 200 Hz (amplitude ~5% of peak displacement; i.e., ~20 µm for the first period). Stimuli were repeated 20 times, the probe was rotated by 90°, and the sequence was repeated. As during hand-held stimulation, all signals were amplified and bandpass filtered between 100 Hz – 3 kHz, and were then and sampled at 10 kHz.

After recordings of the axonal responses to the vibrissa stimulation were complete (5–10 min), BDA was injected intra-axonally by passing 10–50 nA positive pulses of 200 ms duration at 2.5 Hz for 10–30 min. During the intra-axonal injection, injected axons continued to show sensory-evoked spikes until the injection was complete. The size of spikes was monitored continuously in order to ensure that the axon was not lost, and pipette location was adjusted to maximize the spike size. For the bulk tracer injection, a glass electrode was used to inject 10% BDA-3000 in 0.5M potassium acetate solution into the infra orbital nerve by passing 2A positive current pulses 7 s in duration once every 14 s (50% duty cycle) for 4 minutes. After completing this protocol, the skin was sutured, rats were given analgesics (5 mg/kg Anafen), and returned to the animal facility.

Histology

After 5 days, rats were perfused under deep anesthesia with phosphate buffered saline (PBS) followed by a fixative containing 4% paraformaldehyde and 0.5% glutaraldehyde in phosphate buffer (PB, 0.1 M). After cryoprotection in 30% sucrose, the vibrissal pad was cut horizontally at 100 µm on a freezing microtome. Sections were incubated overnight in ABC-Elite (Vector Laboratories, Burlingame, CA) at room temperature. After three rinses in PBS, sections were reacted for 30 min with 2.5 µM biotinylated tyramine, 3 µg/ml glucose oxidase and 2 mg/ml glucose [43]. This procedure was followed by incubation for 2 h in ABC-Elite, and peroxidase was revealed using nickel-diaminobenzidine as a substrate. Photomicroimages were obtained under a light microscope equipped with objectives (10X, 20X, 40X).

Classification of morphological types of peripheral nerve endings

Previous work [8] has shown that the infraorbital nerve gives rise to both deep and superficial vibrissal nerves, which innervate several morphologically-distinct types of mechanoreceptors (Figure S1). Disk-like nerve endings associated with Merkel cells are known as Merkel endings [26]. The deep vibrissal nerve innervates Merkel endings at the level of the ring sinus (RS); these endings are called RS-Merkel and are illustrated in Figures S1E and S1F. The deep vibrissal nerve also innervates lanceolate receptors and club-like receptors. Lanceolate endings (Figures S1G–S1J) consist of longitudinal nerve endings and Schwann sheaths, and are located mainly at the level of the ring sinus. Club-like receptors (Figures S1K and S1L), consist of club-like endings enveloped by Schwann sheaths, and in the present work were invariably found to be associated with the ringwulst. The superficial vibrissal nerve innervates a second category of Merkel cells, distinguished by their position near the rete ridge collar (RRC). These endings are termed RRC-Merkel endings and are illustrated in Figures 1M and 1N. In addition to the four types of endings identified in Figures S1E–S1N, vibrissal follicles and the surrounding skin also contain other types of nerve endings, for example, circumferential fine- and small-caliber innervations, reticular endings, palisade endings, and free nerve endings. These ending types are illustrated in Figure S1, but were not investigated further in the present study.

Follicle reconstruction and analysis of anatomical data

The axonal arbor and mechanoreceptors of labeled primary axons were examined with a light microscope equipped with a computerized tracing system (Neurolucida, MicroBrightField Japan, Chiba, Japan). Axons, mechanoreceptors, and contours of sections were mapped with a CCD camera using a 30-inch flat panel monitor connected to the Neurolucida system. This system had an intermediate magnification lens (5x) in front of the CCD camera. Thus, with an objective lens of 40x, the final magnification was ~2,000. The traced structures were then reconstructed to build 3D data with software (Neurolucida Explorer, MicroBrightField Japan).

We obtained 30 labeled afferent fibers. Nine fibers were excluded from analysis: two fibers were excluded because they terminated in the skin between the vibrissae and appeared to have palisade endings; an additional seven fibers were excluded because BDA labeling was insufficient to determine receptor type. This left a total of 21 afferent fibers available for further analysis. Of these 21, eight afferents had RS-Merkel endings, six afferents had lanceolate endings, four fibers had club-like endings and three had RRC-Merkel endings. Examples of each type are shown in the four rows of Figure 1A. All 21 labeled axons were then reconstructed in three dimensions so that the location of axon terminals within the follicle could be clearly visualized. Four representative examples are shown in Figure 1B, and all 21 3D reconstructions are shown in Figure S3.

The position of a nerve ending was digitized as an angle between a vector indicating the nerve ending from the center of the vibrissal shaft and a vector indicating caudal direction in the 2D data, which was generated by projecting the 3D data of the follicle to a perpendicular plane to the vibrissal shaft. Because each primary afferent (except club-like endings) had multiple nerve endings, the position of mechanoreceptors of each axon was defined as the average of angles of nerve endings derived from the axon. The position of mechanoreceptors of each axon was compared with the preferred angle which was computed from the response magnitudes in the four stimulus directions.

Electron microscopy

Procedures for the electron microscopic approach used in the present study have been described previously [44]. Briefly, fixed vibrissal pads from three rats were cut into 100 µm-thick horizontal sections. After wash, sections were treated with a mixture of 2% OsO4 and 3% potassium ferrocyanide for 1 hour on ice. Sections were then incubated in 1% thiocarbohydrazide for 20 min followed by a treatment with 2% OsO4 for 30 min. After staining with uranyl acetate and lead aspartate, sections were dehydrated in ethanol and propylene oxide and embedded in resin. Small blocks of the tissue embedded in the resin were mounted on specimen pins and coated with platinum-palladium. The 3D ultrastructure data within the follicle was obtained with 3View system (Zeiss, Oberkochen, Germany) and reconstructed with image processing software (Amira, Visage Imaging, Inc., San Diego, CA).

Mechanical model: Simulating the piezoelectric displacement of the vibrissa

To simulate vibrissa mechanics during physiological experiments we oriented an anatomical model of the rat head and vibrissa array [45] so that bregma and lambda were in the horizontal plane. In experiments the vibrissae were trimmed to 5 mm, so in simulation the vibrissa had a length between 4.9692 and 5.1020 mm to account for the vibrissa’s slip on the piezoelectric stimulator as well as the discretization of the vibrissa into nodes.

Piezo deflection of each vibrissa was simulated by rotating each vibrissa about its basepoint by 5°. Vibrissae were displaced in the same four directions as in the experiments, i.e., rostral, caudal, dorsal, and ventral. Simulated displacements for the trimmed gamma and D5 whisker are illustrated in Figure S5.

We next computed the mechanical signals generated by these piezo displacements. Although piezo stimulation displaces the vibrissa in head-centered coordinates, the mechanical effect of these displacements must be computed in vibrissa-centered coordinates [6, 10, 13, 14, 46]. Vibrissa-centered coordinates depend on the geometry of each individual vibrissa, with the origin placed at the vibrissa base. The x-y plane is defined as the plane in which the proximal ~60% of the vibrissa lies [45, 47, 48]. The x axis is parallel to the vibrissa’s length near its base, with positive pointing away from the vibrissa base. The y axis is perpendicular to the x axis, with positive pointing toward the vibrissa tip.

Using a 3D quasi-static model for vibrissa bending, we computed all six components of moment and force at the vibrissa base due to the piezo deflection. Details of the model have been described previously [10, 13, 14], but briefly, vibrissae are divided into nodes (100 in the present study), and the two bending moments M_Y and M_Z for each segment are calculated based on curvature and Young’s modulus.

The twisting moment of each segment (M_X) is derived from the torsional constant and Poisson’s ratio. With all three moments calculated, the three components of the force normal to the vibrissa can be calculated at the contact point location.

Figure S5B shows that the magnitude of the bending moment $\left({\mathrm{M}}_{\mathrm{B}}=\sqrt{{\mathrm{M}}_{\mathrm{Y}}^2+{\mathrm{M}}_{\mathrm{Z}}^2}\right)$ is nearly constant for all deflection directions of all 31 vibrissae. In contrast, the magnitude of F_X varies greatly between vibrissae, as seen in Figure S5C. More importantly, even for a single vibrissa, the magnitude of F_X varies with deflection direction, as does its slope during onset. Note that these variations are completely unrelated to mechanoreceptor location within the follicle; they are entirely due to differences in each vibrissa’s angle of emergence and intrinsic curvature.

Mechanical model: Simulating detachment from the piezoelectric stimulator and tissue relaxation

After the hold period, the piezoelectric stimulator returns to its rest position faster than the whisker can return to rest, and thus the ‘‘OFF’’ phase of the stimulus is dictated by the dynamics of the tissue surrounding the follicle. In order to determine the time course of this relaxation (to be used in the ‘‘OFF’’ phase of the biomechanical model), we performed a separate set of experiments in anesthetized rats. We recorded high-speed video at 500 frames per second during manual deflections (n = 44) of a D2 whisker from an adult (~3 mo) Long Evans female rat. The whisker was released from a deflected position and the angular motion of the base segment of the whisker was tracked as the whisker relaxed back to rest. Figure S6D shows the mean, normalized relaxation trajectory over time, from fully deflected to rest position. The negative temporal derivative of that average trajectory is shown in Figure S6E. Based on the empirical shape of these curves, we fit a trajectory to be used in all biomechanical models with the following construction:

$$\theta \left(t\right)=\left(\tau t+1\right)e^{-\tau t}$$ Equation 1

so that

$$\theta \prime \left(t\right)=-{\tau }^{2}t{e}^{-\tau t}$$ Equation 2

Several values of τ are shown in Figures S6D and S6E; the optimal match between the observed whisker motion was found at τ = 0:075 seconds

Mechanical model: Fitting experimental data to cosine tuning functions

To generate the cosine tuning curves shown in Figure S4B, we used the MATLAB ‘‘fit’’ function to find optimal values for w₁ and ϕ in the equation:

$$Response\hspace{0.17em}Magnitude\left(\theta \right)=w_1\cos \left(\theta +\varphi \right),$$ Equation 3

where θ ranged from 0 to 2π radians. The value of ϕ determined the direction (angle) of maximal response, while the value of w₁ scaled the magnitude of the fit response to the experimental magnitudes.

This identical fit was also used to predict the preferred angles of each of the 21 identified neurons shown in Figures 4A and 4D. The fit value for ϕ is taken to be a prediction of mechanoreceptor location. These predicted values are compared with the measured mechanoreceptor locations in Figures 4C and 4E.

Mechanical model: Optimization

As described in the main text, we hypothesized that primary afferent responses could be explained by differential sensitivity to mechanical signals at the whisker base. Because the whiskers were trimmed short (to 5 mm), they had essentially zero intrinsic curvature, so the twisting moment M_X was negligible. The bending moment $\left({\mathrm{M}}_{\mathrm{B}}=\sqrt{{\mathrm{M}}_{\mathrm{Y}}^2+{\mathrm{M}}_{\mathrm{Z}}^2}\right)$ and the axial force (F_X)and their temporal derivatives were therefore the only mechanical signals used in the model.

High resolution recordings of putative RS-Merkel afferents indicated that their responses were well fit with a cosine function (Figure S4B). We therefore weighted the bending moment term by a cosine function:

$$M_{B\_directional}=\frac{1}{2}{M}_B\cos \left(\Delta \theta \right)$$ Equation 4

where Δθ represents the angular difference between the direction of whisker deflection and measured mechanoreceptor location.

The mechanics associated with the ‘‘ON’’ ramp were modeled as a combination of M_B__direcitonal, F_X , and their derivatives.

At stimulation offset the whisker quickly detaches from the piezo (Figures S6A–S6C) and is free to relax to its resting state. The mechanical signals generated during this rebound will depend on the mechanics of the tissue surrounding the follicle, and not on individual whisker mechanics. The tissue will relax with a time constant (τ). We measured τ in separate experiments in which we deflected the D2 whisker of an anesthetized rat and tracked its base angle as it returned to rest. The value of τ that best fit the tissue relaxation was 75 ms (Figures S6B and S6C). The mechanics associated with the ‘‘OFF’’ ramp was therefore modeled as a decaying function with τ = 75 ms for all neurons and all directions.

The mechanics associated with the complete ramp-and-hold trajectory was created by combining the mechanics of the ON ramp, the static hold, and tissue relaxation mechanics during the OFF ramp. Schematics of the four mechanical signals associated with the ramp-and-hold stimulation are shown in Figures S6B and S6C. The signals were M_B__directional and its derivative, and F_X and its derivative. Pairwise, linear, weighted combinations of these four mechanical signals were then optimized to predict the afferent response, according to Equation 5

$$f=w_1\left(mechanicalsignal1\right)+w_2\left(mechanicalsignal2\right)$$ Equation 5

Thus w₁ and w₂ were two parameters optimized in the model; the third parameter was a simulated threshold that determined firing latencies. For each afferent, the threshold was required to be identical for all four deflection directions, and for both ON and OFF responses.

A response was considered ‘‘incorrect’’ either if the weighted sum did not cross threshold during the 10-ms ON or OFF window and spiking responses were observed experimentally (false negative), or if the weighted sum crossed threshold when no experimental response was observed (false positives). For each afferent, the number of incorrect ON and OFF responses was minimized, followed by minimizing the absolute value of the difference between observed and simulated response magnitude and between observed and simulated response latency. Notably, the model contains no term that would permit simulated neural responses to adapt; it cannot predict responses during the hold period.

Mechanical model: shuffling analysis

To confirm the explanatory power of each combination of mechanical signals in the model, we performed a shuffling analysis. Specifically, we fit the model to data in which the relationship between stimulation direction and afferent response was randomized by shuffling the data.

We performed 72 data shuffles, ensuring that each direction was shuffled independently for ON and OFF responses. The number 72 was chosen because there are nine shuffles that ensure that all four ON directions are associated with shuffled neural responses. If the original direction/response match is represented as (1,2,3,4), then the nine shuffles are: (2,1,4,3); (2,3,4,1); (2,4,1,3); (3,1,4,2); (3,4,2,1); (3,4,1,2); (4,1,2,3); (4,3,1,2); (4,3,2,1). Each of those nine ON response shuffles can then be associated with eight non-matching OFF response shuffles, for a total of 72 non-matching shuffles.

For each shuffle, we re-optimized the model weights to find the best match to the experimental data. We quantified the F1 scores for each shuffle and for each combination of mechanical variables. However, we noted that – even after shuffling in this manner – approximately 40% of the shuffled response/direction pairs will be identical to the unshuffled response/direction pairs. The primary reason is that many responses are zero in more than one direction. Shuffling the location of the zero responses results in no change. It is therefore expected that some shuffles will do as well or nearly as well as the unshuffled data, purely by chance.

The threshold for inclusion as a potential explanatory model was therefore set at 90%. In other words, the F1 score of the unshuffled data had to exceed the F1 score of at least 90% of the 72 shuffled trials. In Figure 5, the unshuffled Merkel neuron responses had higher F1 scores than 100% of the shuffled trials for the combinations (M_B, M_Bd) and (M_Bd, F_xd). In contrast, the F1 score of the unshuffled Merkel response for the combination (F_x; F_xd) was higher than only 62% of the F1 scores from the shuffled trials. The F1 score for unshuffled lanceolate and club-like responses was higher than 100% of the shuffled trials for the combination (M_B, M_Bd), and higher than 90% of the shuffled trials for the combinations (M_Bd, F_xd) and (F_x; F_xd).

QUANTIFICATION AND STATISTICAL ANALYSIS

Data analysis

Spike events elicited by vibrissa deflection were collected in peristimulus time histograms (PSTHs) of 20 responses with 1 ms bin width. Response magnitude was estimated as the mean number of spikes per stimulus within a time window of 10 ms after stimulus onset. We defined response onset as the first bin (poststimulus) displaying counts that significantly exceeded (99.99% confidence interval) spontaneous activity levels estimated over a prestimulus time window of 100 ms, or as the first two consecutive bins displaying significantly larger counts (99% confidence interval) than the spontaneous activity levels. Data were analyzed with IgorPro (WaveMetrics, Inc, Lake Oswego, OR) and Excel (Microsoft, Redmond, WA) software. Results are reported as mean ± SD.

Because RS-Merkel cells are slowly adapting it was sometimes challenging to distinguish between a true OFF response and a persistent response to the ‘‘hold’’ portion of the stimulus which continued into the OFF ramp. Some of these spikes happen to overlap with the OFF window. To distinguish persistent ON responses from OFF responses, the following procedure was used.

For each stimulus direction we performed a running average of the spike train (window size = 15 ms) over the entire duration of the ramp-and-hold stimulus to obtain the spike rate. We then averaged the spike rate in the 10 ms window immediately before the OFF ramp, and in the 10 ms window during the OFF ramp. The difference between the averages in the two windows was compared with a threshold, set to 5% of the maximum of the running average. If the difference was positive and smaller than the threshold, the response was counted as a persistent ON response and removed as an OFF response. This procedure eliminated a total of 14 OFF responses that were actually persistent ON responses. Results were identical regardless of whether the running average was computed over a 5, 10, or 15 ms window size.

Model accuracy in Figure 5 was assessed using the F1-score, computed as:

$$F1=2\frac{precision\ast recall}{precision+recall}$$ Equation 6

where

$$precision\equiv \frac{TruePositives}{TruePositives+FalsePositives}$$ Equation 7

$$recall\equiv \frac{TruePositives}{TruePositives+FalsePositives}$$ Equation 8

DATA AND CODE AVAILABILITY

Data and code available upon request to the Lead Contact, Takahiro Furuta (furuta@dent.osaka-u.ac.jp).

KEY RESOURCES TABLE

REGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Biotinylated dextran, 3000 MW, Lysine Fixable	Thermo Fisher Scientific	D7135
Experimental Models: Organisms/Strains
Rat (Sprague-Dawley)	Shimizu Laboratory Supplies	http://www.shimizu-ls.co.jp/index.html
Software and Algorithms
MATLAB	MathWorks	https://www.mathworks.com/
Neurolucida	MBF Bioscience	https://www.mbfbioscience.com/

Highlights.

• Intra-axon recordings from four different mechanoreceptor types in whisker follicle

• Types have different response magnitudes, latencies, and adaptation properties

• Angular tuning explained by both mechanoreceptor location and mechanics

• Electron microscopy shows unique geometry for Merkel endings near ring sinus