Correlation of extended Martin/Hopkins equation with a direct homogeneous assay in assessing low‐density lipoprotein cholesterol in patients with hypertriglyceridemia

Abstract

Background

The Friedewald or Martin/Hopkins equation is widely used to estimate low‐density lipoprotein cholesterol (LDL‐C) at triglyceride (TG) levels <400 mg/dL. In this study, we aimed to validate the recently developed Sampson and extended Martin/Hopkins equations intended for use in patients with TG levels up to 800 mg/dL by comparing them to a direct homogenous assay.

Methods

In total, 8676 participants with serum TG levels <800 mg/dL were enrolled in this study. LDL‐C was directly measured using Abbott homogeneous assay (DLDL) and estimated using the Friedewald (FLDL), Martin/Hopkins (MLDL), extended Martin/Hopkins (EMLDL), and Sampson equations (SLDL). The overall concordance between the DLDL and LDL‐C estimates was calculated. The performance of the four equations was also compared using Bland–Altman plots and mean absolute difference (MAD).

Results

The EMLDL was more accurate than other LDL‐C equations particularly for patients with TG≥400 mg/dL (MAD = 10.43; vs. FLDL: MAD = 21.1; vs. SLDL: MAD 11.62). The overall concordance of FLDL, MLDL, EMLDL, and SLDL with DLDL in TG values ranging from 200 to 799 mg/dL were 52.2, 70.5, 71.6, and 65.7%, respectively (p < 0.001), demonstrating the EMLDL as the most optimal estimation method, particularly for high TG levels (≥200 mg/dL).

Conclusion

Both the original and extended Martin/Hopkins method are optimal in estimating LDL‐C levels in clinical laboratories using the Abbott analyzer in patients with TG levels of 200–399 and 400–799 mg/dL, respectively. Meanwhile, caution is need that considerable underestimation of Friedewald and Sampson equation could lead to undertreatment in hypertriglyceridemia.

We found that the extended Martin/Hopkins equation (EMLDL) shows superior concordance with directly measured LDL‐C by Abbott chemistry analyzer (DLDL), compared to Friedewald equation (FLDL), Martin/Hopkins equation (MLDL), and Sampson equation (SLDL) with TG 400‐799  mg/dL.

1. INTRODUCTION

Cardiovascular diseases (CVDs) are the leading cause of death worldwide. An estimated 17.9 million people died from CVDs in 2019, representing 32% of all global deaths. Of these deaths, 85% were due to heart attack and stroke. ¹ Over three‐quarters of CVD deaths occur in low‐ and middle‐income countries.

Risk assessment and clinical management of CVD are critically dependent on the level of low‐density lipoprotein cholesterol (LDL‐C), with the 2018 American Heart Association/American College of Cardiology (AHA/ACC) cholesterol guidelines focusing on LDL‐C as a primary target. ² Traditionally, the following Friedewald equation has been the standard method for LDL‐C calculation: LDL‐C = (Total Cholesterol)—(Triglycerides/5)—(High‐Density Lipoprotein Cholesterol) in mg/dL. Although this equation is sufficiently accurate in most cases, it is associated with very low‐density lipoprotein cholesterol (VLDL‐C) overestimation and LDL‐C underestimation under conditions of low LDL‐C and high triglyceride (TG) levels, given a fixed TG: VLDL‐C ratio of 5:1, which could lead to cardiovascular risk misclassification. Therefore, Martin et al. developed a novel method of applying an adjustable factor for the TG/VLDL‐C ratio based on the triglyceride and non‐high‐density lipoprotein cholesterol (non‐HDL‐C) concentrations. ³ The Martin/Hopkins equation was calculated using the median ratio of triglycerides to VLDL‐C by non‐HDL‐C and triglyceride strata acquired from 900,605 individuals, which are now available as calculators on the website (https://ldlcalculator.com/). The Martin/Hopkins equation is more accurate than the Friedewald equation, particularly at low LDL‐C levels (<70 mg/dL) and TG levels between 150 and 400 mg/dL. Thus, this equation provides superior CVD risk classification compared to the Friedewald equation. ⁴ , ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰

Sampson et al. recently published a novel equation that uses a multiple least‐squares regression approach to estimate VLDL‐C. This equation has been reported to be more accurate than the Friedewald equation at low LDL‐C and TG levels between 400 and 799 mg/dL. ¹¹ Initially, Sampson's method was validated in an external dataset using beta quantification or a direct homogeneous assay from Roche or Beckman Coulter, and this novel equation correlated well with directly measured LDL‐C levels. Several studies that have applied this novel equation have been reported. Song et al. reported that the Martin/Hopkins equation has superior performance compared to the Sampson's equation in populations with relatively high prevalence of mild‐to‐moderate hypertriglyceridemia. ¹² Sajja et al. developed an extended Martin/Hopkins equation for TG levels of 400–799 mg/dL and concluded that this method offers greater LDL‐C accuracy than the Friedewald and Sampson equations. ¹³

Patients should be monitored using the same method (calculation or direct assay) to avoid between‐method variations. ¹⁴ Hence, in this study, the Sampson equation was compared to the Friedewald equation and the Martin or extended Martin/Hopkins equation with the Abbott direct homogeneous assay for estimating LDL‐C, to explore which method could be the best alternative in clinical laboratories utilizing the Abbott chemistry analyzer.

2. MATERIALS AND METHODS

2.1. Study population

A total of 8717 individuals who underwent a general health checkup and completed an examination of total cholesterol, HDL‐C, TG, DLDL, and coronary CT angiography at the Seoul National University Hospital Healthcare System Gangnam Center between January 2020 and October 2022 were retrospectively reviewed. This study was approved by the Institutional Review Board of the Seoul National University Hospital (IRB No. H‐2209‐109‐1359), and the requirement of informed consent was waived due to its retrospective nature. After excluding individuals who had TG levels ≥800 mg/dL, 8676 participants were finally enrolled.

2.2. Demographic characteristics, anthropometric data, and laboratory findings

Demographic characteristics and anthropometric data were acquired via medical questionnaires, nurse interviews, and health examinations.

Blood samples were collected after a 12‐hour fast. Serum samples were collected in tubes containing a clot activator and serum gel separator. Centrifugation was performed at 3000 rpm for 10 min within 30 min of blood withdrawal to prevent glycolysis. All analyses were performed immediately after centrifugation. Total cholesterol, TG, LDL‐C (DLDL), and HDL‐C levels were measured using the Architect Ci 16000 and Alinity C (Abbott Laboratories, Abbott Park, IL, USA). The total coefficient of variation (CV) of Architect C 16000 and Alinity C were <1.2% and <2.0% for total cholesterol, <1.6% and <1.9% for HDL‐C, <1.2% and <1.6% for TG, and <1.9% and <2.2% for LDL‐C, respectively. The mean bias based on Bland–Altman plots for the comparison of Architect C 16000 and Alinity C in measuring total cholesterol, HDL‐C, TG, and LDL‐C was between −2.6 and 1.7 (Figure S1). The total cholesterol, HDL‐C, TG, and LDL‐C levels measured by Architect C 16000 and Alinity C showed a very strong correlation (R ² ≥ 0.9799) based on Deming regression (Figure S2).

The LDL‐C estimation by Friedewald equation (FLDL), Martin/Hopkins equation (MLDL), extended Martin/Hopkins equation (EMLDL), and Sampson equation (SLDL) were calculated as previously described. ³ , ¹¹ , ¹³ , ¹⁵ FLDL levels were calculated using a fixed VLDL‐C: TG ratio of 5 in mg/dL. Thus, FLDL was expressed as (total cholesterol minus HDL‐C) minus TG/5 in mg/dL. MLDL was calculated using the median ratio of TG to VLDL‐C in the non‐HDL‐C and TG strata acquired from 900,605 people. Thus, MLDL was expressed as total cholesterol minus HDL‐C minus TG/ (strata‐specific median VLDL‐C: TG ratio). In the original Martin/Hopkins equation, the strata‐specific median VLDL‐C: TG ratio of TG levels between 400 and 13,975 mg/dL was defined only by non‐HDL‐C levels (Non‐HDL‐C < 100 mg/dL, 11.9; Non‐HDL‐C 100–129 mg/dL, 10.0; Non‐HDL‐C 130–159 mg/dL, 8.8; Non‐HDL‐C 160–189 mg/dL, 8.1; Non‐HDL‐C 190–219 mg/dL, 7.5; Non‐HDL‐C ≥ 220 mg/dL, 6.7). In contrast, the extended Martin/Hopkins equation was calculated using the Strata‐specific median VLDL‐C TG ratio derived from a very large database of lipids with TG levels of 400–799 mg/dL using 240‐cell methods ¹³ (Table S1). SLDL was calculated as TC/0.948 – HDL‐C/0.971 – (TG/8.56 + [TG × Non‐HDL‐C]/2140 – TG²/16100) − 9.44 in mg/dL. ¹¹

Coronary CT was performed using a 256‐slice multidetector CT scanner (Brilliance iCT 256; Philips Medical Systems, Cleveland, OH, USA). Coronary artery calcium score (CACS) was calculated onsite on a dedicated workstation with the analysis software Wizard VB10B (Somaris/5 VB10B‐W, Syngo; Siemens, Erlangen, Germany), and quantitative CACS was calculated according to the method described by Agatston et al. ¹⁶

2.3. Statistical analysis

All statistical analyses were performed using the SPSS Statistics 27.0 for Windows (IBM SPSS Statistics, Armonk, NY, USA) and MedCalc version 20.211(MedCalc Software, Mariakerke, Belgium). All statistical outcomes were based on two‐sided tests, and p values <0.05 were considered significant.

For continuous variables, data were expressed as the median and interquartile ranges when their distribution was not normal according to the Kolmogorov–Smirnov test (p < 0.05) and were otherwise expressed as a mean ± SD. Categorical variables were expressed as percentages. Bland–Altman plots were created to compare DLDL and FLDL or MLDL or EMLDL or SLDL. The difference between the DLDL and LDL‐C estimates was evaluated using residual error plots with the mean absolute difference (MAD) according to TG levels. Cochran's Q test was performed to compare the overall concordance between the LDL‐C and LDL‐C estimates and evaluate whether their concordance differed from the DLDL category or the TG group.

3. RESULTS

The demographic characteristics and lipid profiles or overall concordance of FLDL, MLDL, EMLDL, and SLDL with the DLDL of the participants in our study are shown in Table 1. A total of 8676 participants were included. The proportion of participants taking antihypertensive drugs, oral hypoglycemic agents, or lipid‐lowering agents was 28.2, 9.9, and 34.7%, respectively. The median and interquartile ranges of DLDL, FLDL, MLDL, EMLDL, and SLDL levels were as follows: DLDL, 118 (92–144) mg/dL; FLDL, 114 (87–140) mg/dL; MLDL, 115 (89–141) mg/dL; EMLDL, 115 (89–141); and SLDL, 116 (90–143) mg/dL. The median CACS and interquartile ranges were 2.7 and 0.0–75.6, respectively. Most of estimates using FLDL, MLDL, EMLDL and SLDL were within 2 SD compared with DLDL, as depicted by the Bland–Altman plot (Figure 1 and Figure S3). Interestingly, the mean difference between DLDL and MLDL or DLDL and EMLDL was lower than that between the DLDL and FLDL or DLDL and SLDL with TG level of 200–799 mg/dL (Figure 1). According to the residual error plots for the difference between DLDL and various equations, the MAD values indicated the overall superiority of EMLDL over the other equations (MAD = 4.18; FLDL: MAD = 4.96; MLDL: MAD = 4.20; SLDL: MAD = 4.38; Figure 2). EMLDL was shown to provide the smallest MAD values even in patients with TG levels ≥400 mg/dL (EMLDL, 10.43 vs. FLDL, 21.10 vs. MLDL, 12.44 vs. SLDL, 11.62).

TABLE 1.

Baseline patient characteristics (n = 8676).

Age, years	59.8 ± 8.9
Male, n (%)	5977 (68.9)
On anti‐hypertensive drug, n (%)	2443 (28.2)
On oral hypoglycemic agent, n (%)	863 (9.9)
On insulin, n (%)	103 (1.2)
On lipid‐lowering agent, n (%)	3013 (34.7)
Current smoker, n (%)	4249 (49.0)
Ex‐smoker, n (%)	342 (3.9)
BMI (kg/m2)	24.1 ± 3.1
HbA1c, %	5.7 (5.4–6.0)
Fasting serum glucose, mg/dL	101 (94–110)
Total cholesterol, mg/dL	190 (161–219)
Triglyceride, mg/dL	97 (69–137)
HDL cholesterol, mg/dL	51 (44–60)
Non‐HDL cholesterol, mg/dL	136 (108–165)
DLDL, mg/dL	118 (92–144)
FLDL, mg/dL	114 (87–141)
MLDL, mg/dL	115 (89–141)
EMLDL, mg/dL	115 (89–141)
SLDL, mg/dL	116 (90–143)
CACS	2.7 (0.0–75.6)

Note: SI conversion factor: To convert low‐density lipoprotein cholesterol levels to millimoles per liter, multiply by 0.0259; and to convert TGs to millimoles per liter, multiply by 0.0113. Values are presented as the mean ± SD, median (interquartile range), or a number (percentage), unless otherwise indicated.

Abbreviations: BMI, body mass index; CACS, coronary artery calcium score; DLDL, directly measured LDL‐cholesterol; EMLDL, LDL‐cholesterol estimated using extended Martin/Hopkins equation; FLDL, LDL‐cholesterol estimated using Friedewald equation; HbA1c, glycated hemoglobin; HDL, high‐density lipoprotein; MLDL, LDL‐cholesterol estimated using Martin/Hopkins equation; SLDL, LD,‐cholesterol estimated using Sampson equation; VLDL‐C, very‐low‐density lipoprotein cholesterol.

FIGURE 1.

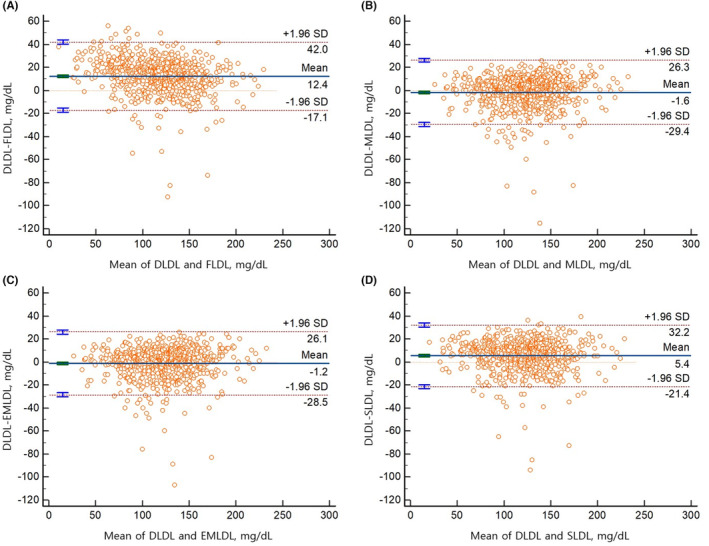
Bland–Altman plot for the comparison of directly measured LDL‐C (DLDL) and Friedewald equation (A) or Martin/Hopkins equation (B) or extended Martin/Hopkins equation (C) or Sampson equation (D) with TG levels 200–799 mg/dL.

FIGURE 2.

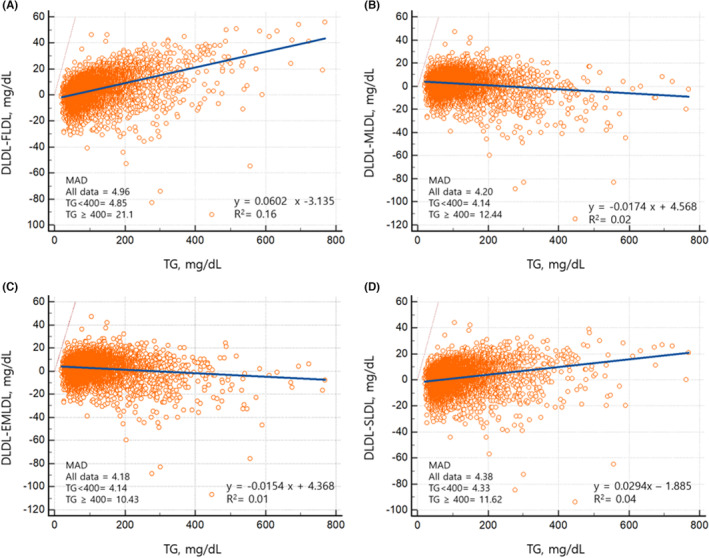
Residual error plots for low‐density lipoprotein cholesterol estimated by Friedewald equation (A), Martin/Hopkins equation (B), extended Martin/Hopkins equation (C), and Sampson equation (D) against TG level.

Overall, concordance between DLDL and LDL‐C estimates, in agreement with LDL‐C treatment classes, showed that MLDL, EMLDL, and SLDL showed better agreement with DLDL classification compared to FLDL (MLDL, 76.7%; EMLDL, 76.8%; SLDL, 76.2%; FLDL, 74.2%; p < 0.001).

The concordance of FLDL, MLDL, EMLDL, and SLDL with individual DLDL treatment classes and TG level groups is shown in Table S2. For DLDL levels of 40–159 mg/dL, MLDL and EMLDL predicted the DLDL classes better than FLDL. In DLDL levels of ≥190 mg/dL, SLDL predicted DLDL classes better than FLDL and MLDL/EMLDL. However, at this DLDL level, 91.2% of TG levels were <200 mg/dL. Therefore, we performed a subgroup analysis using TG levels of 200 mg/dL as the cutoff value. With TG level <200 mg/dL, MLDL or EMLDL or SLDL showed better concordance with DLDL compared to FLDL (FLDL, 76.2%; MLDL or EMLDL 77.2%; SLDL 77.1%; p < 0.001). In contrast, with TG levels of 200–799 mg/dL, the concordance of DLDL with MLDL or EMLDL was significantly higher than that of FLDL and SLDL (FLDL, 52.2%; MLDL, 70.5%; EMLDL, 71.6%; SLDL, 65.7%; p < 0.001). The SLDL had 2.9–4.0% additional concordance gain with LDL‐C treatment classes compared to FLDL with TG levels of <200 mg/dL and DLDL levels ≥160 mg/dL (Table 2). In contrast, EMLDL demonstrated at least 8.6%–29.1% additional concordance gain compared to FLDL with TG levels of 200–799 mg/dL and DLDL levels ≥70 mg/dL. In addition, with TG levels of 200–799 mg/dL and DLDL levels of 130–189 mg/dL, EMLDL showed significantly better concordance with DLDL than with SLDL. A similar tendency was observed when the TG level was subdivided into TG levels of 200–399 mg/dL and TG levels of 400–799 mg/dL; however, the lack of specimens failed to show statistical significance with TG levels of 400–799 mg/dL in certain DLDL level groups (Table S3).

TABLE 2.

Concordance of directly measured LDL‐cholesterol with estimated cholesterol using Friedewald equation, Martin/Hopkins equation, Extended Martin/Hopkins equation, Sampson equation according to TG levels.

DLDL, mg/dL	TG < 200 mg/dL					TG 200–799 mg/dL
	n	FLDL	EMLDL	SLDL	p value a	n	FLDL	EMLDL	SLDL	p value a
<40	26	100.0	100.0	100.0	1.000	6	100.0	100.0	100.0	1.000
40–69	646	84.8	87.3	85.5	<0.001 b	38	84.2	84.2	84.2	1.000
70–99	1947	76.7	78.0	76.6	0.028 c	148	43.9	73.0	66.9	<0.001 f
100–129	2319	75.7	77.7	76.4	0.001 d	204	55.4	73.5	69.6	<0.001 f
130–159	1979	74.7	75.3	76.2	0.093	225	48.0	70.7	60.9	<0.001 g
160–189	784	71.8	72.5	74.7	0.009 e	81	51.9	60.5	58.0	0.005 c
≥190	249	75.9	69.1	79.9	<0.001 b	24	54.2	66.7	58.3	0.097

Note: Values shown are n/N in group (%).

Abbreviations: DLDL, directly measured LDL‐cholesterol; EMLDL, LDL‐cholesterol estimated using extended Martin/Hopkins equation; FLDL, LDL‐cholesterol estimated using Friedewald equation; SLDL, LDL‐cholesterol estimated using Sampson equation; TG, triglyceride.

^a p values were calculated with Cochran's Q test.

^b FLDL versus EMLDL; EMLDL versus SLDL <0.05.

^c EMLDL versus SLDL <0.05.

^d FLDL versus EMLDL <0.05.

^e FLDL versus SLDL <0.05.

^f FLDL versus EMLDL; FLDL versus SLDL <0.05.

^g FLDL versus EMLDL; FLDL versus SLDL; EMLDL versus SLDL <0.05.

The reclassification rates of FLDL, MLDL, EMLDL, and SLDL in the TG group are shown in Table 3. The maximal underestimation and overestimation rates of FLDL, MLDL, EMLDL, and SLDL across the TG groups were as follows: FLDL: 68.9 and 10.2%; MLDL: 18.5 and 42.6%; EMLDL: 18.5 and 27.9%; SLDL: 36.1 and 14.3%. Also, with TG levels of 400–799 mg/dL, EMLDL had a significantly decreased overestimation rate compared to MLDL (27.9 vs. 42.6%). Even with TG levels of 200–399 mg/dL, FLDL and SLDL underestimated 42.6% and 26.6% of LDL‐C values, respectively. In contrast, the underestimation and overestimation rates of MLDL and EMLDL for TG levels of 200–399 mg/dL were only 15.6% and 13.1%, respectively. Conversely, the underestimation rates of FLDL and SLDL for TG levels of 400–799 mg/dL were 68.9 and 36.1%, respectively, while the overestimation rate of EMLDL was 27.9% for TG levels of 400–799 mg/dL.

TABLE 3.

Overall discordance of estimated LDL‐cholesterol using Friedewald equation, Martin/Hopkins equation, extended Martin/Hopkins equation, and Sampson equation according to TG level by NCEP‐ATP III guideline classification.

Triglyceride, mg/dL	FLDL		MLDL		EMLDL		SLDL
	Underestimation	Overestimation	Underestimation	Overestimation	Underestimation	Overestimation	Underestimation	Overestimation
<100	12.2	10.2	15.8	7.2	15.8	7.2	11.1	11.8
100–149	20.1	4.7	16.5	5.6	16.5	5.6	15.0	7.5
150–199	28.8	4.2	18.5	8.0	18.5	8.0	19.9	14.3
200–399	42.6	5.4	15.6	13.1	15.6	13.1	26.6	7.8
400–799	68.9	6.6	4.9	42.6	6.6	27.9	36.1	13.1

Abbreviations: EMLDL, LDL‐C cholesterol estimated using extended Martin/Hopkins equation; FLDL, LDL‐cholesterol estimated using Friedewald equation; MLDL, LDL‐cholesterol estimated using Martin/Hopkins equation; SLDL, LDL‐cholesterol estimated using Sampson equation.

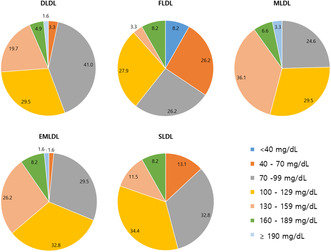
The distribution of LDL‐C values for TG levels of 400–799 mg/dL according to DLDL, FLDL, MLDL, EMLDL, and SLDL levels is shown in Figure 3. EMLDL showed the most similar results to DLDL, whereas FLDL and SLDL tended to underestimate LDL‐C levels and MLDL tended to overestimate LDL‐C levels when compared to DLDL. MLDL showed the most similar results to DLDL with TG levels of 200–399 mg/dL (Figure S4).

FIGURE 3.

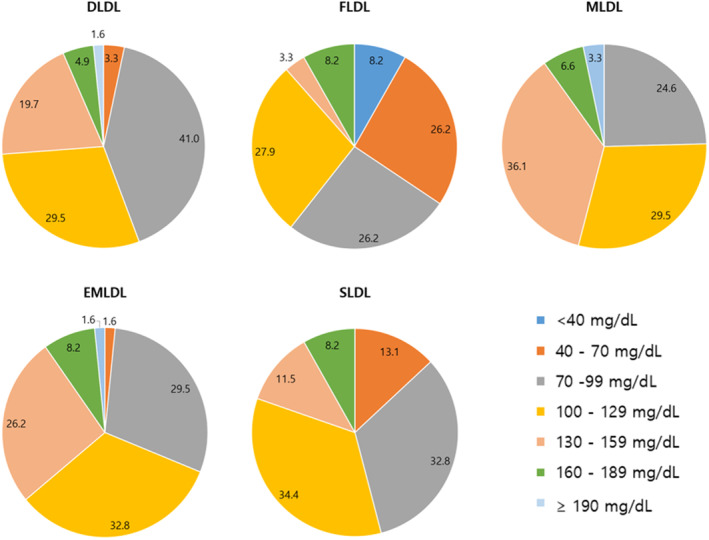
Distribution of low‐density lipoprotein cholesterol (LDL‐C) values with TG 400–799 mg/dL by direct measurement (DLDL), Friedewald equation (FLDL), Martin/Hopkins equation (MLDL), extended Martin/Hopkins equation (EMLDL), and Sampson equation (SLDL). The data are presented as percent.

4. DISCUSSION

This study aimed to verify the performance of a novel equation (the Sampson equation) and compare it to other widely used equations for LDL‐C estimation (the Friedewald and Martin/Hopkins equations or the extended Martin's equation) using a sample direct homogeneous assay with an Abbott analyzer. Sampson et al. suggested that the novel equation would calculate LDL‐C more accurately than the Friedewald or Martin/Hopkins equations ¹¹ for TG levels of <800 mg/dL. However, in our study, the extended Martin/Hopkins equation showed optimal performance in classifying directly measured LDL cholesterol levels with TG levels of 200–799 mg/dL.

The use of the extended Martin/Hopkins equation was associated with 34.5% or fewer misclassifications compared with the Sampson equation (49.2%) across all TG levels. There was a considerable underestimation of LDL‐C across all methods, particularly with the Friedewald and Sampson equations, which could lead to undertreatment. The underestimation increased with hypertriglyceridemia, reaching 68.9% for Friedewald equation and 36.1% for Sampson equation in patients with TG levels of 400–799 mg/dL. Therefore, more than one‐third of individuals with TG levels of 400–799 mg/dL could be undertreated if the LDL‐C level has been estimated using Sampson equation.

In the original Sampson's study, the novel equation was derived from beta‐quantification with samples including highly skewed lipid levels (LDL‐C levels) of 200–800 mg/dL, and TG levels of ≥2880 mg/dL, which are rare in routine clinical practice. ¹⁰ , ¹² The median and interquartile ranges of LDL‐C and TG in Sampson's derivation dataset were 143 mg/dL (103–199 mg/dL) and 149 mg/dL (98–253), respectively. The median and interquartile ranges of LDL‐C and TG in our dataset were similar to those from the Martin/Hopkins equation derivation dataset and were as follows: LDL‐C, 118 (92–144) versus 108 (84–135) mg/dL; TG, 97 (69–137) versus 115 (82–166) mg/dL. Furthermore, Sampson et al. validated their novel equation with external datasets using the Roche and Beckman DLDL analyzer. ¹¹ Although they have demonstrated the MAD value and residual error plots and insisted that the Martin/Hopkins method showed increased negative bias compared to the Sampson equation for TG levels of 1000 mg/dL or more (Roche 0.08 vs. 0.01%; Beckman, 0.08% vs. 0.02%), in routine clinical laboratories, direct measurement is usually performed rather than the calculation of the TG level. Additionally, in this study, the Martin/Hopkins equation was the optimal choice for estimating LDL‐C levels.

Piani et al. compared several LDL‐C estimation methods using a direct homogeneous assay with a Coulter instrument. ¹⁷ Although the correlation coefficients of LDL‐C estimated using the Martin/Hopkins and Sampson methods with the direct measure assay were similar for the entire population (0.973 vs. 0.976) with TG levels ≥400 mg/dL, the correlation coefficient of the Sampson method was markedly decreased compared to that of the Martin/Hopkins method (0.852 vs. 0.941).

Rossouw et al. demonstrated that the Friedewald and Martin/Hopkins equations were comparable at LDL‐C levels of 40–190 mg/dL in both Abbott and Roche analyzers; however, the Friedewald and Sampson equations were comparable only on the Abbott analyzer and not the Roche analyzer. Furthermore, the Martin‐Hopkins and Sampson equations were comparable only on the Abbott analyzer and not on the Roche analyzer. The TG distribution in this study showed that both the Abbott and Roche analyzer datasets contained only 2% of TG values ≥400 mg/dL. The original Sampson study validated the equation in the dataset using a Roche and Beckman analyzer, including considerable samples with extensively high TG levels (>1000 mg/dL). These findings suggest that for TG values frequently observed in routine clinical practice, the Sampson equation cannot be extrapolated to other widely used equations in certain chemistry analyzers, and further evaluations using various chemistry analyzers with moderate to high TG values are required.

Additionally, several studies have validated the Martin/Hopkins equation, especially for use in patients with LDL‐C levels <70 mg/dL and TG levels of 150–399 mg/dL. ³ , ⁹ , ¹² , ¹⁸ The 2018 AHA/ACC/Multi‐Society Cholesterol Guidelines provided a Class IIa recommendation for the use of the Martin‐Hopkins equation in patients with LDL‐C levels <70 mg/dL. ¹² , ¹⁹ The 2022 ACC Expert Consensus Decision Pathway on the Role of Nonstatin Therapies clarified that although Friedewald equation is widely used, the Martin/Hopkins equation provides a more accurate assessment of LDL‐C in individuals with very low levels of LDL‐C or with hypertriglyceridemia. ²⁰ Meanwhile, the expert consensus noticed that Sampson equation may also be more precise, but additional validation is needed. Based on proficiency test surveys, most laboratories still calculate LDL‐C since the direct assay does not provide major significant clinical benefit that would outweigh the additional cost. ²¹ However, those laboratory would use direct measurement assay for LDL‐C with TG >400 mg/dL. Therefore, to prevent errors caused by between‐method variations which might affect therapeutic decision, Martin/Hopkins equation would be suitable equation method for laboratory utilizing Abbott chemistry analyzer.

This study has some limitations in that the various LDL‐C estimating equations were compared to only a single chemistry analyzer by Abbott and the comparison analysis between Abbott direct homogeneous assay and β‐quantification was unable. The direct homogeneous assays have been reported to perform well in a heathy population; however, they have shown an unacceptable total error for patients being treated for CVDs or those with conditions likely to affect lipoprotein methods. ²² Nonetheless, the method used in our institution is suitable for routine clinical application. It provides assay precision within the acceptable limits, as per the National Cholesterol Education Program performance criteria according to the accuracy‐based lipid proficiency testing program performed by the Korean Association of External Quality Assessment Service. ²³ Furthermore, the Committee of Clinical Practice Guidelines of the Korean Society of Lipid and Atherosclerosis recommends the use of direct LDL‐C measurement when TG levels are ≥400 mg/dL. ²⁴ Similarly, 2019 European Society of Cardiology and European Atherosclerosis Society guidelines stated that both homogeneous assay and β‐quantification are useful at TG levels ≥400 mg/dL. ¹² , ²⁵ The 2018 AHA/ACC cholesterol guidelines also recommend the use of direct LDL‐C measurement along with the Martin/Hopkins equation for adults with an LDL‐C level <70 mg/dL. ²

This study demonstrated that the original Martin/Hopkins equation is the most optimal estimation method in clinical laboratories using the Abbott chemistry analyzer for the direct measurement of LDL‐C, particularly in patients with moderate hypertriglyceridemia (TG, 200–399 mg/dL). With TG levels of 400–799 mg/dL, although caution is advised with all kinds of LDL‐C equation within this TG range, the extended Martin/Hopkins equation showed better correlation with the Abbott direct measurement assay compared to the Friedewald or Sampson equations.

FUNDING INFORMATION

No funding was received for this work.

CONFLICT OF INTEREST STATEMENT

No conflict of interest to declare.

Supporting information

Data S1

Chung S. Correlation of extended Martin/Hopkins equation with a direct homogeneous assay in assessing low‐density lipoprotein cholesterol in patients with hypertriglyceridemia. J Clin Lab Anal. 2023;37:e24963. doi: 10.1002/jcla.24963

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions