Sex Differences and Similarities in Relations Between Mathematics Achievement, Attitudes, and Anxiety: A Seventh-to-Ninth Grade Longitudinal Study

Abstract

There are consistent correlations between mathematics achievement, attitudes, and anxiety, but the longitudinal relations among these constructs are not well understood nor are sex differences in these relations. To address this gap, mathematics achievement, attitudes, and anxiety were longitudinally assessed for 342 (169 boys) adolescents from 7th to 9th grade, inclusive, and Latent Growth Curve Models were used to assess the relations among these traits and developmental change in them. Spatial abilities (7th, 8th grade) and trait anxiety (8th, 9th grade) were also assessed and used for control for sex differences in these traits. Overall, boys had stronger spatial abilities and more positive mathematics attitudes and were less anxious than girls, but there were no sex differences in mathematics achievement. Across grades, mathematics achievement improved, attitudes became less positive, and anxiety increased for both boys and girls. Higher than average cross-grade growth in mathematics achievement mitigated boys’ developmental declines in mathematics attitudes and increases in anxiety. Girls with strong spatial abilities had lower mathematics anxiety, but girls overall maintained higher mathematics anxiety and less positive mathematics attitudes relative to boys, even when they showed strong cross-grade gains in mathematics achievement. The study demonstrated that longitudinal gains in mathematics are associated with cross-grade changes in attitudes and anxiety but with several different developmental patterns for boys and girls.

Success in the modern world depends to some extent on the mathematical competencies that people develop during schooling. These competencies create opportunities to pursue math-intensive careers in college and beyond and contribute to success in other occupations and areas of life (National Mathematics Advisory Panel, 2008; Ritchie & Bates, 2013). Sex differences in mathematical development are extensively studied, in part because they contribute to differences in the pursuit of math-intensive careers (Halpern et al., 2007). At the mean, sex differences in mathematics achievement are small or nonexistent (Else-Quest et al., 2010; Hutchinson et al., 2019; Hyde et al., 2008), although larger differences emerge in some specific areas (Geary et al., 2000) and at the high end of performance (Wai et al., 2018). At the same time, the question of whether different factors support the mathematical development of boys and girls has received some empirical attention (Crombie et al., 2005; Jiang et al., 2020), but has not been as systematically explored as the factors that mediate sex differences in mathematics outcomes.

Spatial abilities, for instance, contribute to sex differences in some mathematics domains (e.g., word problems, number line; Bull et al., 2013; Casey et al., 1997; Geary et al., 2000; Halpern et al., 2007), but contribute to mathematics learning for both sexes. Differences emerge in some areas only because there are more boys than girls with strong spatial abilities (Geary et al., 2021). Similarly, the importance of attitudes and anxiety to mathematical development and the pursuit of math-intensive occupations have been well-documented (Eccles & Wang, 2016; Eccles & Wigfield, 2002; Casey & Ganley, 2021; Levine & Pantoja, 2021), but sex differences in the developmental relations among achievement, attitudes, and anxiety are not as well understood. Accordingly, the current 7th-to-9th grade longitudinal study examined sex differences in the pattern of cross-grade relations between mathematics achievement and mathematics attitudes and anxiety.

Mathematics Attitudes and Mathematical Development

Mathematics self-efficacy (i.e., positive self-appraisals about one’s math competencies) and beliefs about the long-term utility or perceived usefulness of mathematics are two core attitudes that are correlated with mathematics achievement and predict enrollment in mathematics courses in high school and college (Crombie et al., 2005; Eccles & Wang, 2016). Lauermann et al. (2017) found that self-efficacy and utility beliefs are moderately correlated (rs = .50 to .61), and their combination contributed to adolescents’ math-related career aspirations and their later career choices. Early studies revealed boys had stronger utility beliefs than girls (Eccles et al., 1984), but more recent ones indicate nuance (Crombie et al., 2005; Lauermann et al., 2017; Steinmayr & Spinath, 2008). Mean differences are now small, but boys’ utility beliefs may be more strongly influenced by future job aspirations and those of girls by their intentions to take future mathematics courses (Gaspard et al., 2015). In other words, adolescent boys’ evaluation of the usefulness of mathematics is related to their occupational plans, whereas girls’ evaluation is related to preparation for future schooling.

Even with small or no sex differences in utility beliefs, boys typically have modestly higher mathematics self-efficacy than do girls (Hedge’s g = .18; Huang, 2013). Jiang et al. (2020) confirmed adolescent boys’ higher mathematics self-efficacy (d = .23), but higher efficacy was associated with more mathematics and science course taking for both sexes (see also Lauermann et al., 2017). Sheu et al.’s (2018) meta-analysis showed that self-efficacy in mathematics and science is related in part to prior experiences in the area, such as class grades, for both boys and girls, but did not provide an assessment of longitudinal change in these relations.

A meta-analysis of longitudinal studies indicated a modest relation between students’ academic self-efficacy and their later grades or achievement in the same domain; for mathematics self-efficacy and later mathematics achievement, $\beta =.11$; Valentine et al., 2004). However, prior self-efficacy and achievement levels were not controlled in most of the studies included in this meta-analysis and thus the direction of the relation is unclear (Wen & Dubé, 2022). Cross-lagged panel studies that included these controls found evidence for reciprocal effects in adults (Talsma et al., 2018). However, for elementary and older students, prior achievement was related to later self-efficacy ($\beta =.13$), but not the reverse. The relations appeared to be similar for boys and girls, but the method used in this meta-analysis to assess sex differences (proportion of boys in the study) was not optimal. Thus, the question of whether there are sex differences in the longitudinal relations between mathematics self-efficacy and mathematics achievement has not been fully answered.

One large-scale longitudinal study revealed that both self-efficacy (defined as perceived competence) and utility (defined as valuation of math) beliefs declined as students moved into the middle and high school years for both sexes, but with more shallow declines in self-efficacy for girls than boys and similar declines in utility beliefs (Fredricks & Eccles, 2002). A related study confirmed that utility beliefs declined from middle to high school and that the relation with achievement was reciprocal (Ma & Xu, 2004a). However, prior achievement was a stronger predictor of later utility than utility was of later achievement for boys and girls.

The overall results suggest that mathematics achievement has a stronger influence on mathematics attitudes than the reverse and that these relations are similar for girls and boys, although the latter are not well studied. Attitudes generally become less positive as students’ move through middle school into high school, but the relation between developmental changes in mathematics achievement and changes in attitudes are not well understood.

Mathematics Anxiety and Mathematical Development

Higher mathematics anxiety is associated with lower mathematics achievement and avoidance of mathematics coursework for both sexes (Caviola et al., 2022; Dowker et al., 2016; Hembree, 1990; Ma, 1999; Meece et al., 1990). However, the long-term effects might be more severe for girls and women because they experience higher levels of mathematics anxiety than do boys and men (Hyde et al., 1990; Stoet et al., 2016). Stoet et al.’s large-scale study (n = 761,655) revealed higher mathematics anxiety in adolescent girls than boys, controlling mathematics achievement (ds = .21 to .25). One possibility is that the excess (beyond achievement levels) mathematics anxiety is related to the sex difference in test anxiety (Caviola et al., 2022). However, Devine et al. (2012) found that higher mathematics anxiety was associated with lower mathematics performance for girls and boys, but this relation disappeared with control of test anxiety but only for boys. In other words, girls appear to have higher levels of mathematics anxiety, even with control of mathematics achievement and test anxiety.

Related studies have shown the sex difference in spatial abilities might also contribute to girls’ higher mathematics anxiety, mediated in part by spatial anxiety (Ferguson et al., 2015; Maloney et al., 2012). A largely unexplored question is whether the sex difference in general anxiety that emerges during adolescence (Bandelow & Michaelis, 2015) contributes to the sex differences other forms of anxiety. This emerging sex difference could in theory result in a sex difference in the susceptibility to develop anxiety in specific areas, including mathematics. In short, controlling for other forms of anxiety, including trait anxiety, provides a more robust assessment of the sex difference in mathematics anxiety and its relation to mathematics achievement.

Whatever is contributing to the sex differences in mathematics anxiety, Devine et al. (2012) and Geary et al. (2019) suggested that the magnitude of the relation between mathematics anxiety and mathematics outcomes might be larger for girls than boys when assessed in the same grade. Caviola et al.’s (2022) meta-analysis also revealed a stronger correlation between mathematics anxiety and achievement for girls (r = −.29) than boys (r = −.20), but the difference was only a trend (p = .075). They note that most studies in their meta-analysis did not explore the relation between mathematics achievement and mathematics anxiety independently for girls and boys, and so the issue of whether the relation is stronger in girls than boys remains unsettled.

Developmental relations are also uncertain but research to date suggests that prior mathematics achievement is more strongly related to later anxiety than prior mathematics anxiety is to later achievement. Gunderson et al. (2018), for instance, found that higher achieving first and second graders had lower mathematics anxiety six months later ($\beta =-.20$, d = −.41), and students with lower mathematics anxiety had higher mathematics achievement six months later ($\beta =-.06$, d = −.12). These relations held for girls and boys. Geary et al. (2019) in contrast found that girls but not boys with lower mathematics achievement in sixth grade had higher mathematics anxiety in seventh grade, but there was no relation between sixth grade mathematics anxiety and seventh grade mathematics achievement. Wang et al. (2020) found the same for high school students, that is, mathematics grades predicted later mathematics anxiety, but anxiety did not predict later grades. In a study of the transition from middle school to high school, Ma and Xu (2004b) also found that achievement predicted later anxiety, but this relation was more consistent for boys than girls.

In sum, mathematics achievement is generally a stronger predictor of later anxiety than anxiety is of later achievement but sex differences in this relation are mixed. Concurrent assessments sometimes reveal stronger relations between anxiety and achievement for girls than boys, whereas Ma and Xu’s (2004b) large-scale study revealed more consistent cross-grade relations for boys than girls during the transition from middle to high school. At this point, no definitive conclusions can be drawn about sex differences in the patterns of relations between mathematics achievement and anxiety. To further complicate the issue, it is not certain how other forms of anxiety might influence the relation between mathematics achievement and anxiety in girls and boys.

Current Study

The study used Latent Growth Curve Models (LGCM) to examine developmental change in girls’ and boys’ mathematics achievement, attitudes (combined self-efficacy and utility beliefs) and anxiety as they transitioned from middle school into high school, that is, from 7th to 9th grade, inclusive. LGCM is a powerful technique that models change over time in a latent, unobservable variable (e.g., an anxiety factor), and it is more flexible than alternative approaches (e.g., multilevel modeling) because it can be used to model different functional forms of a trajectory and to analyze the relations between different predictors and the initial (intercept) value of an outcome and its trajectory (slope) across time (Duncan et al., 2013). Modeling these relations across middle school to high school is important because this transition is associated with declines in attitudes about mathematics and the stabilization of high levels of mathematics anxiety for some students (Fredricks & Eccles, 2002; Ma & Xu, 2004a; Ma & Xu, 2004b). A better understanding of the factors that influence attitudes and anxiety during this transition has implications for interventions to arrest the decline in mathematics attitudes and to reduce anxiety.

The first goal was to assess whether the direction of the relations was stronger from achievement to attitudes and anxiety or from attitudes and anxiety to achievement. We hypothesized that the relation from mathematics achievement to mathematics attitudes and anxiety would be stronger than the relation from attitudes and anxiety to achievement (e.g., Ma & Xu, 2004a). In a LGCM this would manifest as significant paths from the mathematics start point (intercept for seventh grade achievement) to the mathematics attitudes and anxiety slopes, such that higher starting mathematics achievement would be associated with improving attitudes and declining anxiety across grades. The growth models also enable an assessment the relations between developmental change (i.e., slope) in achievement (or attitudes and anxiety) and developmental change in attitudes and anxiety (or achievement). We were agnostic as to whether significant slope to slope effects would emerge but if they did, we expected cross-grade gains in achievement to predict improvement in attitudes and declines in anxiety rather than change in attitudes and anxiety predicting change in achievement.

The second goal was to assess whether these relations differed for boys and girls. Based on prior results, we expected higher beginning mathematics achievement (intercept) to be associated with more positive beginning mathematics attitudes and lower anxiety for girls and boys, but we also expected the relation between the mathematics intercept and anxiety intercept to be stronger for girls. The latter is based on the finding that the correlation between achievement and anxiety is often higher for girls than for boys (Caviola et al., 2022; Devine et al., 2012; Geary et al., 2019). Based on Ma and Xu’s (2004b) finding, the mathematics achievement (intercept) to anxiety slope was expected to be stronger for boys than girls during the transition from middle to high school, but the mathematics achievement (intercept) to attitudes slope was expected to be similar (Jiang et al., 2020; Lauermann et al., 2017).

As noted, boys’ advantage in spatial abilities has been implicated as a potential source of sex differences in certain mathematics domains (Casey & Ganley, 2021; Geary, 1996, 2022) and thus we controlled for the relation between spatial abilities and mathematics achievement. We did not have measures of spatial anxiety and so could not directly test the hypothesis that spatial abilities influence mathematic anxiety in part through spatial anxiety (Ferguson et al., 2015; Maloney et al., 2012). We did however conduct a post-hoc analysis, after testing the just described predictions, controlling for the relation between spatial abilities and mathematics anxiety. We also assessed trait anxiety in 8th and 9th grade to confirm that the sex differences in mathematics anxiety (below) were not due to a sex difference in trait anxiety.

Methods

Participants

The participants were 342 (169 boys) adolescents in a 6th to 9th grade longitudinal study conducted in collaboration with the public schools in Columbia MO (USA). The sex of the students was provided by the schools that in turn obtained the information when students enrolled. Only data from 7th to 9th grade were included here because a nationally standardized mathematics achievement test was not administered in sixth grade. They were recruited from a group of 1,926 students who participated in a district-wide assessment of arithmetic competencies (see Scofield et al., 2021). The latter occurred across two cohorts in consecutive years, the first of which (n = 1,091) included all middle schools in the district and about 86% of sixth graders; the remaining students were absent the day of the assessment or unable to participate. The second cohort (n = 835) included all but one of the same schools; the one school was omitted because of over-representation of first cohort students in the longitudinal sample.

All 1,926 students were invited to participate in a 7th to 9th grade longitudinal component and 342 of them and their parents agreed (n = 226, 116 for cohorts 1 and 2, respectively). A locally standardized (M = 100, SD = 15) mathematics score was created from the sixth-grade assessments and indicated that these 342 participants had modestly higher (M = 104.27, SD = 14.80) scores than the students who did not participate in the 7th to 9th grade assessments (M = 99.08, SD = 14.89), t(1924) = 5.85, p < .001, d = .35. Demographic information was obtained through a parent survey for students in the longitudinal component (n = 281). Six percent of the students were 6% Hispanic or Latino (across racial categories), and 70% were White, 14% Black or African American, 3% Asian, 1% American Indian or Alaska Native, 10% More than One Race, and the remaining Not Reported. Self-reported annual household income was as follows: $0-$24,999 (12%); $25,000-$49,999 (18%); $50,000-$74,999 (12%); $75,000-$99,999 (22%); $100,000-$149,999 (19%); and $150,000+ (17%). Seventy-one percent of the students had at least one parent with a college degree. Sixteen percent of families received food assistance, and six percent housing assistance.

A prior study reported on 6th grade data from the first cohort (n = 1,091) and a 6th to 7th grade assessment of the relations between mathematics achievement, attitudes, and anxiety for 190 students from the longitudinal component (Geary et al., 2019). The 6th grade mathematics achievement measure was a composite based on several arithmetic tests administered in 6th grade and the 7th grade mathematics achievement measure was the Numerical Operations test (below). The 6th grade mathematics achievement measure could not be used for the LGCM because it is on a different scale then the Numerical Operations measure. In all, the only overlap between the prior and current studies is the 7th grade measures administered to the first cohort.

Informed written consent was obtained from students’ parents, alongside assent obtained from adolescents for each assessment. This study was approved by the University of Missouri Institutional Review Board (IRB; Algebraic Learning and Cognition, Approval # 2002634).

Mathematics Attitudes and Anxiety Measures

Mathematics attitudes.

The 7-item measure assesses students’ mathematics self-efficacy and their beliefs about the long-term utility of mathematics (Eccles & Wigfield, 2002). Students responded to each item using a 1-to-7 Likert scale rated from 1 (“a little”) to 7 (“a lot”). The utility score was the mean of the four associated items (e.g., “How useful do you think math will be for what you want to do after you graduate and go to work?”; $\alpha =.71$to .82 across grades). The self-efficacy score was the mean of the three associated items (e.g., “How good are you at math?”; $\alpha =.78$ to .81 across grades). Initial Latent Growth Curve Models (below), however, revealed that latent intercept scores for efficacy and utility were highly correlated (r = .86) and represented a single mathematics attitudes construct. Thus, we used the mean of these measures as an overall indicator of general mathematics attitudes for each grade.

Mathematics anxiety.

The measure included 9 items adapted from the Abbreviated Math Anxiety Scale (Hopko et al., 2003), and one additional item, “In general, how anxious are you about math?” The latter was included because Ashcraft (2002) noted that single general items provide a good broad assessment of math anxiety. Each item was rated on a 1 (low anxiety) to 5 (high anxiety) scale. Following prior studies (Baloglu & Koçak, 2006; Geary et al., 2019) and patterns of factors loadings, the mean of 5 items assessed mathematics anxiety for evaluations (e.g., “Taking an examination in a math course”; $\alpha =.86$ to .88 across grades) and the mean of 5 items assessed mathematics anxiety for learning (e.g., “Listening to a lecture in math class”; $\alpha =.77$ to .84 across grades). Separate measures for evaluations and learning often emerge for single grades. However, a principle components factor analysis (SAS, 2014) that included these two measures across 7th to 9th grade, inclusive, revealed a single mathematics anxiety construct that explained 62% of the covariance among the measures. Thus, we used the mean of the 10 items to create a single mathematics anxiety measure for each grade.

Trait anxiety.

The measure was based on a six-item anxiety survey described in Marteau and Becker (1992; see also Tluczek et al., 2009). For each item participants are asked to reflect on how they generally feel, using the terms “calm,” “tense,” “upset,” “relaxed,” “content,” and “worried.” Participants rated items on a 1- (almost never) to 4-point (almost always) scale; positive valence items were reverse-coded such that higher scores reflected higher anxiety. The score was the mean of the six items ($\alpha s=.81$ and .85 for 8th and 9th grade, respectively).

Spatial Measures

The tasks were administered on iPads using customized programs developed through Inquisit by Millisecond (https://www.millisecond.com). We used the mean score across 7th and 8th grades and estimated the reliabilities $(\rho )$ of these summary scores using the Spearman-Brown Prophecy formula applied to the test-retest correlations.

Spatial ability.

The first measure was the Judgment of Line Angle and Position test (JLAP; Collaer & Nelson, 2002; Collaer et al., 2007), which assesses visuospatial attention. The task requires students to match the angle of a single line to one of 15-line options in an array below the target line. There are 20 sequentially presented test items, with students using the touch screen of the iPad to select the correct angle. Each trial began following the student response, or after 10 sec. The score was the number correct ($\rho =.70$).

The 24-trial Mental Rotations Test (MRT) was the second measure (MRT; Peters et al., 1995). On each trial, students viewed 3D images of 10 connected cubes, including one target image and four choice options. The task was to select the two options that matched the target image, only rotated to various degrees. Four self-paced practice problems were administered, followed by two blocks of 12 problems each (3 min per block). The score was the number of problems on which both correct options were chosen ($\rho =.83$).

Spatial span.

Corsi Block Tapping Task was used to assess visuospatial working memory (Kessels et al., 2000). Students were presented with a display of nine squares that appeared to be randomly arranged. The squares “lit up” for 1000 ms in a pre-determined sequence, and students then tapped the squares in the same order. The sequence length started at two squares (level = 2) and could increase to up to nine squares. Students had two attempts at each sequence length. If one of the sequences was recalled correctly, the next sequence level began; if both sequences at a level were incorrect, the task was terminated. The score was the total number of correct sequences across the task ($\rho =.68$).

Standardized Measures

Intelligence.

Students were administered the Vocabulary and Matrix Reasoning subtests of the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999). Based on standard procedures, subscale scores were used to generate an estimated full-scale IQ, which was average (M = 104.57, SD = 13.09).

Achievement.

Mathematics achievement was assessed with the Numerical Operations subtest from the Wechsler Individual Achievement Test–Third Edition (Wechsler, 2009). The test items were solved with pencil and paper and included basic arithmetic and continued through fractions, algebra, geometry, and calculus. Standardized scores were average (Ms = 98 to 100, SDs = 17 to 19). Raw scores were used in the analyses.

Procedure

The students participated in the assessments shown in Table 1. Each assessment was conducted one-on-one in a quiet location at the school site and lasted about 45 min. As noted, data were collected across 2 cohorts in consecutive school years. Due to Covid-19 related closure of schools, the Numerical Operations test was administered remotely for 38 of the 158 students in cohort 1 in ninth grade, six of the 112 students in cohort 2 in eighth grade, and all of cohort 2 students in ninth grade. For the remote sessions, a sealed envelope containing supplies and paper forms was delivered to the participant’s home. After entering the session and enabling the computer camera, the session began with verbal assent and instructions. Throughout the session, the administrator observed testing progress. Upon completion, the participant was asked to place the test in a postage-paid return envelope and seal it in view of the camera, and then a plan was made to facilitate mailing. Numerical Operations scores did not differ across in-person and remote assessments (ps > .25).

Table 1.

Age of Administration and Timing of Assessments

Task Name	Seventh Grade		Eighth Grade		Ninth Grade
	Fall	Spring	Fall	Spring	Mid-year	Spring
Mean Age (months) at test	153	157	164	168	178	181
Numerical Operations		√		√		√
Mathematics attitudes		√		√	√
Mathematics anxiety		√		√	√
Trait anxiety				√	√
Corsi	√		√
Judgment of Line Angle and Position	√		√
Mental Rotations Test	√		√
Intelligence		√

Note: Age is in months, SDs range between 4.26 and 4.51 months.

Analyses

Mean sex differences are reported as Cohen’s (1988) $d\left[d=\left(M_{\text{boys}}-M_{\text{girls}}\right)/\text{ overall }SD\right]$, with positive values indicating higher scores for boys and negative values higher scores for girls. The 5.9% of missing values were estimated using the multiple imputations procedure in SAS (2014). The imputations were based on all key variables and were the average across 5 imputations. The key constructs were mathematics achievement, mathematics attitudes (mean of utility and efficacy), and mathematics anxiety (mean of anxiety for evaluations and learning) and any associated changes from 7th to 9th grade, inclusive. The focus was on assessing the developmental relations between mathematics achievement and mathematic attitudes and anxiety, as well as overall sex differences for these constructs and sex differences in developmental change.

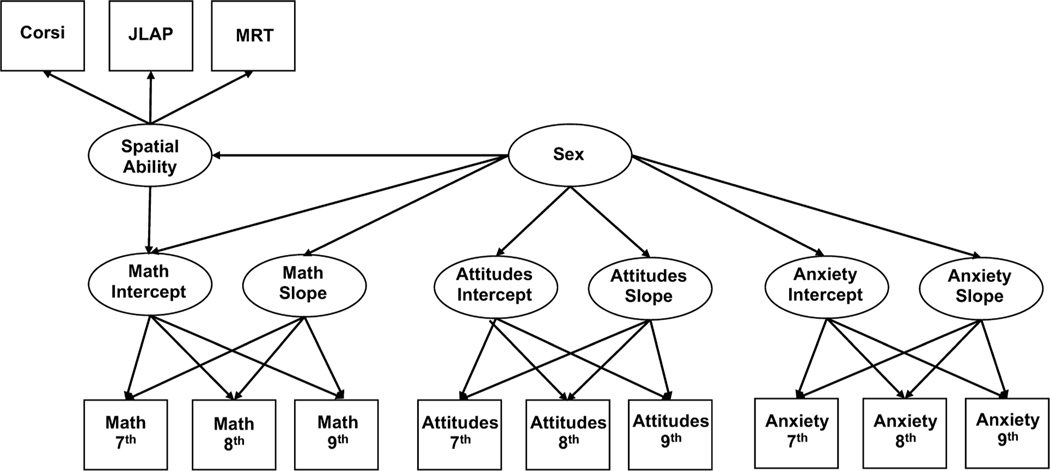
Latent Growth Curve Models, using the lavaan package in R (R Core Team, 2022; Rosseel, 2012), were used to achieve these ends. The basic structure of the target LGCM is shown in Figure 1 (the variances and covariances of all manifest and latent variables were estimated). The intercept factors represent the average scores across all participants in seventh grade, whereas the slope factors represent the average trajectory in an outcome across grades. To ensure the intercept represents the mean of each outcome in seventh grade, the factor loadings on the manifest indicators for the slope factors were fixed at 0 in 7th grade and coded 1 and 2 for 8th and 9th grade, respectively. Factor loadings on the manifest indicators for the intercept factors were all fixed to 1. The latent Spatial Ability variable was defined by the Corsi, JLAP, and MRT measures, and used to control for the relation between spatial abilities and mathematics achievement, as previously described. We also estimated sex differences in all intercepts and slopes (0 = girls, 1 = boys) and for the Spatial Ability factor.

Figure 1.

Basic Latent Growth Model, where all intercept paths are set to 1 and slope paths at 0, 1, 2 for 7th to 9th grade, respectively. JLAP = Judgment of Line Angle and Position, MRT = Mental Rotations Test.

The relations between achievement, attitudes, and anxiety were assessed in two separate sets of analyses. First, we tested whether the intercept and slope for mathematics achievement predicted slopes for attitudes and anxiety. The model tested whether 7th grade scores on the Numerical Operations test and changes in these scores across grades predicted changes in attitudes or anxiety across grades. In the second set, we tested whether the intercepts and slopes for attitudes and anxiety predicted the slope for Numerical Operations scores.

Model fit was assessed using the comparative fit index (CFI), the Tucker-Lewis Index (TLI), and the root mean square error of approximation (RMSEA). Hu and Bentler (1999) suggested that good fit is obtained when CFI and TLI > .95 and RMSEA < .06. However, others have recommended a more graded set of guidelines for RMSEA, such that an RMSEA < .05 is considered good, values between .05 and .08 are considered acceptable, and values between .08 and .10 are considered marginal (Fabrigar et al., 1999).

In all, we initially estimated and compared two sets of five models. One set focused on mathematics to attitudes and anxiety relations, whereas the other focused on attitudes and anxiety to mathematics relations. We had to run these separately because reciprocal paths could not be simultaneously estimated. This is because the estimates (e.g., math slope to anxiety slope) were based on a single covariance which would not support the two-estimates needed for running bidirectional models. For both sets, in Model 1 (M1) all paths from sex were fixed at 0 (i.e., we estimated no sex differences) as were all paths from intercepts and slopes. The latter means that we did not estimate paths from the Mathematics Achievement Intercept and Slope to the Attitudes and Anxiety Slopes, nor the Attitudes and Anxiety Intercepts and Slopes to the Mathematics Achievement Slope. In model 2 (M2), we freely estimated all regressions of the latent variables on sex, but we retained the intercepts and slopes constraints. In model 3a (M3a), we freed the regressions predicting Attitudes and Anxiety Slopes (or Mathematics Achievement Slope) from the Mathematics Achievement Intercept (or Attitudes and Anxiety Intercepts) but kept the constraint on the slope-to-slope effects. In contrast, in model 3b (M3b), we freed the parameters for the slope-to-slope effects but constrained the intercept-to-slope paths to 0. Model 4 (M4) was the target model in which all regression parameters were freely estimated.

These models addressed our basic goals, but it is possible that they underestimate the influence of spatial abilities on the pattern of sex differences, especially for the Mathematics Anxiety Intercept and Slope, as noted (Ferguson et al., 2015; Maloney et al., 2012). Accordingly, once the preferred model was determined from our planned analyses, we added Spatial Ability to Anxiety Intercept and Slope paths to this model, as well as a path from Spatial Ability to Mathematics Achievement Slope; our original intent was to control for the overall relation between spatial abilities and mathematic achievement (i.e., the Spatial Ability to Mathematics Achievement Intercept) but an anonymous reviewer suggested this path should be estimated as well.

Models were compared with chi-square difference tests and based on Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC; lower values are preferred for both indicators). After determining the best model, we assessed modification indices to identify potential sources of misfit, although any such modifications should be considered as post-hoc relative to the proposed structure of the model.

Openness and Transparency

All the raw data and R code for the LGCM models have been deposited in Open Science Framework, https://osf.io/zdkm4/. The study was not preregistered.

Results

Sex Differences

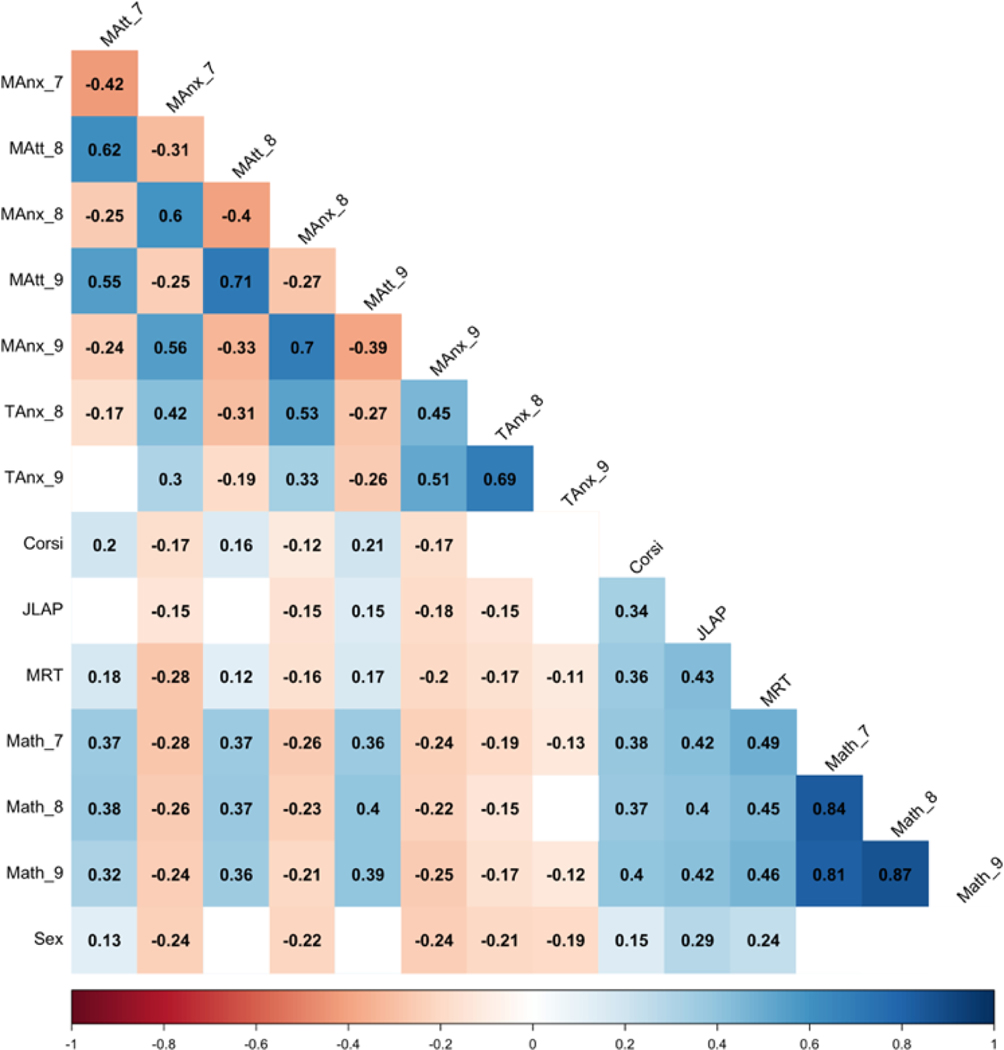
Table 2 shows overall means and means for boys and girls, and Figure 2 shows correlations among the variables (separate correlation figures for boys and girls are in the Supplementary Online Material, SOM). There were no sex differences for mathematics achievement, but boys reported better mathematics attitudes (ds = .20 to .26) and had higher scores on the spatial measures (ds = .29 to .58). Girls reported higher levels of mathematics anxiety (ds = −.44 to −.48), as well as higher trait anxiety in 8th (d = −.41) and 9th (d = −.39) grade. With control of same-grade trait anxiety, the sex difference in mathematics anxiety remained significant in 8th (p = .019) and 9th (p = .001) grade, indicating higher mathematics anxiety in girls above and beyond the sex difference in trait anxiety.

Table 2.

Mean Sex Differences

	Overall		Boys		Girls					Range
	M	SD	M	SD	M	SD	t	p	d	Min	Max
Mathematics Attitudes 7th	5.13	0.89	5.25	0.81	5.02	0.95	2.39	.018	.26	1	7
Mathematics Anxiety 7th	2.17	0.75	1.99	0.66	2.35	0.79	−4.51	.000	−.48	1	5
Mathematics Attitudes 8th	4.92	1.01	5.02	0.97	4.82	1.04	1.81	.071	.20	1	7
Mathematics Anxiety 8th	2.18	0.77	2.01	0.65	2.35	0.84	−4.08	.001	−.44	1	5
Mathematics Attitudes 9th	4.69	0.98	4.79	0.93	4.58	1.01	1.96	.051	.21	1	7
Mathematics Anxiety 9th	2.25	0.70	2.08	0.59	2.42	0.76	−4.63	.000	−.46	1	5
Trait Anxiety 8th	1.94	0.54	1.83	0.47	2.05	0.58	−3.95	.000	−.41	1	4
Trait Anxiety 9th	1.99	0.56	1.88	0.53	2.10	0.57	−3.59	.000	−.39	1	4
Numerical Operations 7th	35.70	7.30	35.96	7.39	35.43	7.21	0.66	.502	.07	16	61
Numerical Operations 8th	37.13	7.75	37.26	7.94	37.01	7.59	0.30	.767	.03	16	61
Numerical Operations 9th	38.25	8.25	38.25	8.52	38.25	8.01	0.00	.999	.00	16	61
Corsi	8.83	1.68	9.07	1.66	8.59	1.66	2.71	.007	.29	0	16
JLAP	13.83	2.82	14.66	2.70	13.02	2.71	5.58	.000	.58	0	20
MRT	10.05	4.26	11.09	4.58	9.03	3.65	4.62	.000	.48	0	24

Note. $d=\left(M_{\text{m}}-M_{\text{f}}\right)/S{D}_{\text{overall}}$; JLAP = Judgment of Line Angle and Position; MRT = Mental Rotations Test. The 16 minimum for Numerical Operations is the start point, that is, students are credited with 16 easier items if they get items 17 to 19 correct. Theoretically, the minimum could be lower, but the lowest scores for this sample were 17, 19, and 20 for grades 7 to 9, respectively.

Figure 2.

MAtt = Mathematics Attitudes, MAnx = Mathematics Anxiety, TAnx = Trait Anxiety, JLAP = Judgment of Line Angle and Position, MRT = Mental Rotations Test. Math = raw Numerical Operations Scores. Blanks cells are insignificant (p > .05).

Repeated measures Analyses of Variance, with sex as a between-subjects factor and grade a within-subjects factor, confirmed the sex differences for overall mathematics attitudes, F(1,340) = 5.55, p = .019, and revealed significant declines in attitudes across grades, F(2,680) = 49.57, p < .001, d = .49 (comparing 7th to 9th grade, using 7th grade SD); the grade by sex interaction was not significant (p = .934). These analyses also confirmed the overall sex difference for mathematics anxiety, F(1,340) = 26.51, p < .001, and revealed an increase in anxiety across grades, F(2, 680) = 3.08, p = .047, d = .11(comparing 7th to 9th grade, using 7th grade SD); the grade by sex interaction was not significant (p = .939). Raw scores on the Numerical Operations test improved across grades, F(2, 680) = 57.01, p < .001, d = .35 (comparing 7th to 9th grade, using 7th grade SD), but there was no sex (p = .746) or grade by sex (p = .544) effects.

Longitudinal Relations

Initial models.

The top section of Table 3 shows fit statistics (CFI, TLI, and RMSEA) and comparison indices (AIC, BIC) for the five initial models assessing mathematics achievement as a predictor of Attitudes and Anxiety Slopes, and the bottom section for the five models assessing attitudes and anxiety as predictors of Mathematics Achievement Slopes. In both sets of analyses, Model M3b was preferred, that is, the model in which all sex effects and slope-to-slope effects were freely estimated but intercept-to-slope effects were constrained to 0. Indeed, compared to the target model (M4), in which the intercept-to-slope effects were freely estimated, AIC and BIC were lower for M3b, and the chi-square difference tests were not statistically significant, with ${\chi }^2(2)=1.62$, p = .445 for the first set of models, and ${\chi }^2(2)=.04$, p = .980 for the second set of models. These results indicate the more restricted model (M3b) was preferred in both sets of analyses. Additionally, none of the intercept-to-slope effects (i.e., Mathematics Achievement Intercept predicting Attitudes and Anxiety Slopes in the first set, and Attitudes and Anxiety Intercepts predicting Mathematics Achievement Slopes in the second set) were significant (M4, ps > .05).

Table 3.

Model Fit Statistics

Model	${\chi }^2$	df	$\Delta {\chi }^2$	P	CFI	TLI	RMSEA	AIC	BIC
Achievement Predicting Attitudes and Anxiety Intercepts and Slopes
M1 (Base)	248.19	65	---		.921	.905	.091	15117	15258
M2 (Sex effects)	171.66	58	76.53	.000	.951	.934	.076	15054	15223
M3a (Regressions on Intercepts)	168.14	56	3.52	.172	.952	.932	.077	15054	15231
M3b (Regressions on Slopes)	161.72	56	9.94	.007	.954	.936	.074	15048	15224
M4 (Full model)	160.10	54	1.62	.445	.954	.934	.076	15050	15234
M5 (M3b + modifications)	101.60	54	60.12	.000	.979	.970	.051	14992	15176
M6 (M5 + 3 spatial paths)	86.42	51	15.18	.002	.985	.977	.045	14983	15174
M6b (M6b drop spatial to AnxS)	87.94	52	1.52	.217	.984	.977	.045	14982	15174
Attitudes and Anxiety Predicting Achievement Intercept and Slope
M1 (Base)	303.27	69	---		.899	.886	.100	15164	15290
M2 (Sex effects)	226.90	62	76.37	.000	.929	.910	.088	15101	15225
M3a (Regressions on Intercepts)	225.95	60	0.95	.622	.928	.907	.090	15104	15265
M3b (Regressions on Slopes)	216.67	60	10.23	.006	.932	.912	.087	15095	15256
M4 (Full model)	216.63	58	0.04	.980	.931	.908	.089	15099	15268
M5 (M3b + modifications)	156.66	58	60.01	.000	.957	.943	.071	15039	15208

Note. AIC = Aikake Information Criterion. BIC = Bayesian Information Criterion. CFI = Comparative Fit Index. df = Degrees of freedom. RMSEA = Root Mean Square Error of Approximation. TLI = Tucker-Lewis Index. AnxS = Mathematics Anxiety Slope.

The fit statistics for M3b were satisfactory for CFI and acceptable for RMSEA in the first set of analyses (mathematics achievement to attitudes and anxiety) but short of an acceptable TLI in the second set of analyses (attitudes and anxiety to mathematics achievement). An assessment of the models’ modification indices suggested that M3b would better account for the data if it included random intercepts on two of the manifest indicators (Corsi and MRT) of the Spatial Ability latent variable. Incorporating these into the model improved all fit statistics in the first set (see M5 in top section of Table 3), and for the second set the CFI and RMSEA values were acceptable while TLI was marginally below the criterion (see M5 in bottom section of Table 3). Chi-square tests indicated that M5 was preferred over M3b in both comparisons (ps < .001) and by AIC and BIC metrics. Comparisons of the ${\chi }^2$ values and AIC and BIC metrics indicate that the models in which mathematics achievement predicts changes in attitudes and anxiety are preferred to parallel models in which attitudes and anxiety predicts changes in mathematics achievement. Results from M5 (boys and girls combined, Table 1a) and for boys and girls separately (Table 2a) are in the SOM, as are corresponding tables in which attitudes and anxiety predict mathematics achievement (Table 3a, Table 4a).

The key findings for Model 5 were that cross-grade gains in mathematics achievement were associated with cross-grade improvement in mathematics attitudes ($\beta =.27$, p = .004) and showed a trend for cross-grade declines in mathematics anxiety ($\beta =.-14$, p = .086). As shown in Table 2a, cross-grade gains in mathematics achievement were associated with gains in mathematics attitudes for boys ($\beta =.70$, p = .004), which mitigated a general cross-grade deterioration of attitudes ($\beta =-1.33$, p < .001). Similarly, cross-grade gains in mathematics achievement were associated with cross-grade reductions in anxiety for boys ($\beta =-.50$, p =.018), which slowed a general trend for anxiety to increase across grades ($\beta =.73$, p = .003). Neither the mathematics achievement slope to attitudes slope ($\beta =.14$, p = 322) nor the mathematics achievement slope to anxiety slope ($\beta =-.16$, p = .300) were significant for girls. The 90% CI did not overlap for estimates for either the mathematics achievement slope to the attitudes slope, or for the mathematics achievement slope to the anxiety slope, confirming stronger relations for boys than girls.

Spatial ability and mathematics anxiety.

Model 5 addressed our basic goals but as mentioned we then added the Spatial Ability to Anxiety Intercept and Slope paths and a path from Spatial Ability to the Mathematics Achievement Slope. The result was M6, which fitted the data significantly better than did M5, ${\chi }^2(3)=15.18$, p = .002 (Table 3). However, the path from Spatial Ability to the Mathematics Anxiety Slope was not significant, z = 1.22, p = .226. Dropping this path resulted in Model 6b, which did not differ significantly in fit from M6, ${\chi }^2(1)=1.52$, p = .217. Thus, we report estimates for M6b (below). These results confirm a relation between spatial abilities and mathematics anxiety start point (intercept) but not changes in anxiety.

Mathematics achievement predicting attitudes and anxiety.

The core unstandardized and standardized coefficients for model M6b, with mathematics achievement predicting attitudes and anxiety, are shown in Table 4. The non-significant Mathematics Achievement Intercept and Slope effects were due to the estimation of the Spatial Ability to Mathematics Achievement Intercept and Slope paths. When these two paths are dropped, the Mathematics Achievement Intercept (z = 12.03, p < .001) and Slope (z = 4.19, p < .001) are significant, but the overall model did not fit the data as well as M6b, ${\chi }^2(2)=153.22$, p < .001.

Table 4.

Latent Growth Curve Model with Achievement Predicting Attitudes and Anxiety for Full Sample

Model Component	Unstandardized Estimate (SE)	Standardized Estimate (SE)	z	p
Math Achievement Intercept	−0.79 (4.19)	−0.12 (0.64)	−0.19	.850
Math Achievement Slope	−1.65 (1.21)	−1.03 (.78)	−1.36	.174
Attitudes Intercept	5.03 (.07)	6.61 (.43)	75.86	.000
Attitudes Slope	−0.31 (.05)	−0.92 (.18)	−6.71	.000
Anxiety Intercept	3.15 (.31)	5.05 (.54)	10.34	.000
Anxiety Slope	0.07 (.03)	0.25 (.12)	2.10	.036
Spatial Ability → Math Intercept	5.95 (.79)	0.78 (.05)	7.52	.000
Spatial Ability → Math Slope	0.50 (.20)	0.27 (.11)	2.51	.012
Spatial Ability → Anxiety Intercept	−0.13 (.05)	−0.18 (.07)	−2.68	.007
Sex → Spatial Ability	0.64 (.13)	0.38 (.06)	5.18	.000
Sex → Math Intercept	−3.31 (.77)	−0.26 (.06)	−4.29	.000
Sex → Math Slope	−0.58 (.29)	−0.18 (.09)	−2.03	.042
Sex → Attitudes Intercept	0.22 (.09)	0.15 (.06)	2.37	.018
Sex → Attitudes Slope	0.01 (.05)	0.01 (.07)	0.15	.884
Sex → Anxiety Intercept	−0.27 (.08)	−0.21 (.06)	−3.25	.001
Sex → Anxiety Slope	0.00 (.04)	0.00 (.07)	0.00	.997
Math Slope → Attitudes Slope	0.07 (.02)	0.31 (.10)	2.87	.004
Math Slope → Anxiety Slope	−0.019 (.01)	−0.12 (.08)	−1.34	.180

Note. Bolded p values are significant at an alpha of .05. z and p values are for unstandardized estimates.

In keeping with the univariate results, boys had better spatial competencies, more positive mathematics attitudes (Intercept), and lower anxiety (Intercept) than did girls. Inconsistent with the univariate results, girls had better initial mathematics achievement scores (Intercept) and more cross-grade gains (Slope) than did boys, but these sex differences were no longer significant (ps > .321) when the Spatial Ability to Mathematics Achievement Intercept and Slope paths were dropped. There were no sex differences in developmental change (slopes) in mathematics attitudes or anxiety (ps > .884), in keeping with the results from the ANOVAs.

For the full sample, cross-grade gains in mathematics achievement were associated with slower cross-grade declines in mathematics attitudes, that is, the Mathematics Achievement Slope to Attitudes Slope was significant and positive ($\beta =.31$, p = .004) which partially countered the more general decline in attitudes (i.e., Attitudes Slope, $\beta =-.92$, p < .001). Similarly, the cross-grade increase in mathematics anxiety (Anxiety Slope, $\beta =.25$, p = .036) was partially mitigated by gains in mathematics achievement, that is, the Mathematics Achievement Slope to Anxiety Slope, although the latter was not significant ($\beta =-.12$, p = .180).

There were differences across the models for girls and boys, as shown in Table 5. For girls, gains in mathematics achievement were unrelated to development change in attitudes (Mathematics Achievement Slope to Attitudes Slope, $\beta =.03$, p = .303) or anxiety (Mathematics Achievement Slope to Anxiety Slope, $\beta =.-06$, p = .564), as found in the initial models. For boys, gains in mathematics were positively associated with developmental improvement in mathematics attitudes (Mathematics Achievement Slope to Attitudes Slope, $\beta =.48$, p = .009), partially mitigating the general decline in attitudes ($\beta =-1.07$, p < .001). Gains in mathematics achievement were also associated with a trend for developmental declines in mathematics anxiety (Mathematics Achievement Slope to Anxiety Slope, $\beta =-.29$, p = .09), partially mitigating the overall increase in anxiety (Anxiety Slope, $\beta =.46$, p = .009). Higher spatial abilities were associated with lower mathematics anxiety for girls ($\beta =.-36$, p < .001) but the relation was not significant for boys ($\beta =.-66$, p = .194). However, in each of these cases and contra the initial models, the 90% confidence intervals overlapped for girls and boys and thus the evidence for differences should be considered suggestive and in need of follow-up studies.

Table 5.

Latent Growth Curve Model with Achievement Predicting Attitudes and Anxiety by Sex

Model Component	Unstandardized Estimate (SE)	Standardized Estimate (SE)	z	p
Girls
Math Achievement Intercept	−3.88 (6.52)	−0.57 (.95)	−0.60	.551
Math Achievement Slope	0.31 (1.68)	0.19 (.99)	0.19	.853
Attitudes Intercept	5.03 (.07)	6.11 (.51)	71.16	.000
Attitudes Slope	−0.26 (.05)	−0.72 (.18)	−5.37	.000
Anxiety Intercept	4.26 (0.54)	6.18 (.83)	7.91	.000
Anxiety Slope	0.06 (.04)	0.17 (.12)	1.45	.147
Spatial Ability → Math Intercept	4.91 (.81)	0.73 (.06)	6.09	.000
Spatial Ability → Math Slope	0.14 (.21)	0.08 (.13)	0.65	.514
Spatial Ability → Anxiety Intercept	−0.24 (.07)	−0.35 (.09)	−3.60	.000
Math Slope → Attitudes Slope	0.03 (.03)	0.12 (.12)	1.03	.303
Math Slope → Anxiety Slope Boys	−0.01 (.02)	−0.06 (.10)	−0.58	.564
Math Achievement Intercept	−17.05 (9.02)	−2.55 (.1.32)	−1.89	.059
Math Achievement Slope	−3.86 (2.10)	−2.44 (1.40)	−1.84	.066
Attitudes Intercept	5.25 (.06)	7.48 (.73)	83.72	.000
Attitudes Slope	−0.34 (.05)	−1.07 (.26)	−6.28	.000
Anxiety Intercept	2.65 (.51)	5.79 (1.28)	5.18	.000
Anxiety Slope	0.09 (.03)	0.46 (.22)	2.61	.009
Spatial Ability → Math Intercept	7.80 (1.65)	0.84 (.07)	4.74	.000
Spatial Ability → Math Slope	0.73 (.32)	0.34 (.15)	2.29	.022
Spatial Ability → Anxiety Intercept	−0.10 (.08)	−0.16 (.12)	−1.30	.194
Math Slope → Attitudes Slope	0.10 (.04)	0.48 (.16)	2.60	.009
Math Slope → Anxiety Slope	−0.04 (.02)	−0.29 (.18)	−1.70	.090

Note. Bolded p values are significant at an alpha of .05. z and p values are for unstandardized estimates. The variance for 9th grade anxiety was slightly negative (unstandardized estimate = −.004) in the model for girls but did not differ significantly from zero (z = −0.08, p = .936).

Covariances among mathematics achievement, attitudes, and anxiety.

The covariances between the latent intercept and slope factors are shown in Table 6. Except for the covariance between the intercept and slope for mathematics attitudes, all effects were significant for the full sample. Students who started with higher initial levels of mathematics anxiety showed shallower increases in anxiety across grades (p = .011). Students with higher initial mathematics achievement had lower initial levels of mathematics anxiety and more positive mathematics attitudes, whereas students with higher initial mathematics anxiety had less positive mathematics attitudes (ps < .006). Perhaps counterintuitively, students with higher initial mathematics anxiety had gains in mathematics attitudes across grades (p = .003). Nevertheless, cross-grade increases in anxiety were associated with cross-grade decreases in mathematics attitudes (p < .001).

Table 6.

Full Sample Covariances for Achievement Predicting Attitudes and Anxiety

Covariance	Unstandardized Estimate (SE)	Standardized Estimate (SE)	z	p
Full sample
Anxiety Intercept and Anxiety Slope	−0.05 (.02)	−0.34 (.09)	−2.53	.011
Attitudes Intercept and Attitudes Slope	−0.04 (.03)	−0.18 (.11)	−1.35	.178
Math Achievement Intercept and Anxiety Intercept	−0.56 (.21)	−0.21 (.07)	−2.72	.006
Math Achievement Intercept and Attitudes Intercept	1.87 (.27)	0.56 (.07)	6.86	.000
Anxiety Intercept and Attitudes Intercept	−0.24 (.03)	−0.53 (.07)	−6.88	.000
Anxiety Intercept and Attitudes Slope	0.05 (.02)	0.26 (.09)	3.01	.003
Anxiety Slope and Attitudes Slope Girls	−0.05 (.01)	−0.57 (.12)	−5.87	.000
Anxiety Intercept and Anxiety Slope	−0.07 (.03)	−0.34 (.10)	−2.28	.023
Attitudes Intercept and Attitudes Slope	−0.03 (.05)	−0.09 (.14)	−0.61	.540
Math Achievement Intercept and Anxiety Intercept	−0.61 (.32)	−0.21 (.10)	−1.89	.059
Math Achievement Intercept and Attitudes Intercept	1.63 (.44)	0.43 (.10)	3.72	.000
Anxiety Intercept and Attitudes Intercept	−0.23 (.05)	−0.43 (.08)	−4.65	.000
Anxiety Intercept and Attitudes Slope	0.03 (.02)	0.13 (.10)	1.37	.171
Anxiety Slope and Attitudes Slope Boys	−0.05 (.01)	−0.38 (.11)	−3.88	.000
Anxiety Intercept and Anxiety Slope	−0.01 (.03)	−0.11 (.27)	−0.35	.725
Attitudes Intercept and Attitudes Slope	−0.04 (.05)	−0.19 (.18)	−0.83	.405
Math Achievement Intercept and Anxiety Intercept	−0.25 (.26)	−0.15 (.16)	−0.95	.345
Math Achievement Intercept and Attitudes Intercept	1.28 (.40)	0.51 (.13)	3.16	.002
Anxiety Intercept and Attitudes Intercept	−0.10 (.03)	−0.32 (.10)	−2.97	.003
Anxiety Intercept and Attitudes Slope	0.03 (.02)	0.27 (.16)	1.83	.068
Anxiety Slope and Attitudes Slope	−0.03 (.01)	−0.63 (.29)	−3.38	.001

Note. Bolded p values are significant at an alpha of .05. Covariances could not be modeled with Math Slope, because it was a predictor in the model. Covariances could not be modeled for Math Intercept and Attitudes and Anxiety slopes as these were constrained-to-zero paths in the final model.

For girls, higher initial mathematics anxiety was associated with more rapid cross-grade declines in anxiety (Anxiety Intercept with Anxiety Slope, $\beta =.-34$, p = .023), but this relation was not significant for boys ($\beta =.-11$, p = .725). There was also a stronger relation between initial mathematic achievement and mathematics anxiety for girls ($\beta =.-21$, p = .059) than boys ($\beta =.-15$, p = .345). Again, the 90% confidence intervals overlapped and thus the evidence for the differences here are only suggestive.

The key findings were that cross-grade mathematics attitudes decreased and mathematics anxiety increased, but these relations were less pronounced for students showing relatively large cross-grade achievement gains. The latter effects were significant for mathematics attitudes for the full sample and for boys and a trend for mathematics anxiety for boys; the latter was significant for our initial models. Neither of these potential mitigating effects were significant for girls, although the relation between spatial abilities and mathematics anxiety was significant for girls but not boys.

Discussion

The current study provided a unique longitudinal assessment of the relations among mathematics achievement, attitudes, and anxiety through the middle school years and the transition to high school. The use of LGCM models enabled the assessment of mean sex differences in each construct and sex differences in the relations among these core constructions in seventh grade, as well as the relation between mathematics achievement (attitudes and anxiety) and change in attitudes and anxiety (mathematics achievement) across grades. The first goal was to assess the direction of these relations and confirmed our expectation that the mathematics achievement to attitudes and anxiety relations were stronger than the reverse (Ma & Xu, 2004a, 2004b; Wang et al., 2020). This is not to say that there were no reciprocal attitudes and anxiety to mathematics achievement relations, but rather models with achievement affecting attitudes and anxiety better fitted the data. Our expectation that mathematics start point (intercept) would predict cross-grade changes in attitudes and anxiety was not confirmed, but there was a relation between gains in mathematics achievement and developmental change in attitudes and anxiety (elaborated below).

The finding of no overall sex differences in mathematics achievement is in keeping with prior studies (Else-Quest et al., 2010; Hutchinson et al., 2019; Hyde et al., 2008), but was not the focus here. Our second goal was to examine if the developmental relations between mathematics achievement, attitudes, and anxiety differed for girls and boys. For both sexes, mathematics attitudes declined with the transition from middle to high school, but the decline was mitigated for boys but not girls with larger cross-grade mathematics achievement gains. A similar pattern emerged for anxiety, but the effects were not as robust as those found for attitudes. The control of spatial abilities confirmed a relation to mathematics achievement but more critically replicated prior findings of a relation to mathematics anxiety that might be stronger for girls than for boys (Ferguson et al., 2015; Maloney et al., 2012). We also expected a stronger concurrent relation between mathematics achievement and mathematics anxiety (7th grade intercepts) for girls than boys (Geary et al., 2019). This pattern emerged (significant for girls but not boys), but the magnitude of the sex differences was small.

Mathematics Attitudes and Mathematical Development

Mathematics self-efficacy (or perceived ability) and utility beliefs are core components of students’ mathematics attitudes and are often independently assessed (e.g., Lauermann et al., 2017), although they are moderately correlated. Our initial LGCM results also reflected this correlation but at a level (r = .86) that suggested they were capturing similar attitudes toward mathematics. Our correlation might have been higher than those found by Lauermann et al., (2017, rs = .50 to .61) because the latter were based on manifest variables and ours was based on latent variables which often produce more reliable estimates and higher correlations among related constructs.

In any case, the finding of better mathematics attitudes among boys than girls, despite no sex difference in mathematics achievement, replicates many previous findings (Huang, 2013; Jiang et al., 2020). There were also developmental declines in mathematics attitudes as students moved from middle school to high school as found in prior studies (Fredricks & Eccles, 2002; Ma & Xu, 2004a). Unlike Fredricks and Eccles who found more shallow declines in girls’ than boys’ mathematics attitudes and thus a narrowing of the sex difference, we found similar declines for girls and boys. The reason is likely because Fredricks and Eccles’ models covered 1st to 12th grade, inclusive, with the largest differences in earlier grades.

Previous studies that have used cross-lagged panel models have shown that prior mathematics achievement typically predicts next-grade mathematics attitudes (self-efficacy and utility), controlling prior grade attitudes (Ma & Xu, 2004a; Talsma et al., 2018). The achievement to attitudes relation is typically stronger in these studies than the attitudes to achievement relation (although they are sometimes reciprocal), as we found. However, our results suggest that it is not baseline mathematics achievement (seventh grade here) but cross-grade gains in achievement that influence change in mathematics attitudes. Moreover, the cross-lagged analyses suggest more similarities than differences in these relations for boys and girls, that is, prior mathematics achievement is equally predictive of next grade attitudes for girls and boys. Our approach went beyond this by examining the relation between cross-grade change in mathematics achievement and cross-grade change in attitudes (i.e., Mathematics Achievement Slope to Attitudes Slope), which suggested a stronger effect for boys ($\beta =.48$) than girls ($\beta =.12$; Table 5). In other words, gains in achievement were more strongly associated with mitigation of the developmental decline in mathematics attitudes for boys than girls.

The reason for this sex difference was not apparent from the main results and so in a post-hoc analysis we examined the pattern of relations between mathematics achievement and self-efficacy and utility beliefs across grades (see Figure 3a, Figure 4a in SOM). For girls, the same-grade and cross-grade correlations between mathematics achievement and self-efficacy (rs = .35 to .45) and between mathematics achievement and utility beliefs (rs = .20 to .31) were stable, showing no discernable developmental pattern. The same was true for boys’ self-efficacy and mathematics achievement (rs = .34 to .48) but not their utility beliefs (rs = .12 to .34). For the latter, correlations among mathematics achievement and same-grade utility beliefs rose from 7th to 9th grade (r = .19 to .26 to .34, respectively), and these were lower than the correlations between mathematics achievement and next grade utility beliefs. More specifically, 7th grade achievement was more strongly correlated with 8th grade (r = .26) than 7th grade (r = .19) utility beliefs and 8th grade achievement was more strongly correlated with 9th grade (r = .34) than 8th grade (r = .26) utility beliefs.

These patterns suggest that boys’ middle-school achievement is directly influencing their evaluations about the long-term usefulness of mathematics. In the context of Gaspard et al.’s (2015) finding that adolescent boys’ but not girls’ utility beliefs were related to their future job aspirations, it could be that boys who are relatively good at mathematics might now be considering it as a potential competitive niche. Adolescence is a time where social competitiveness increases and for boys is often associated with activities that provide a competitive edge in culturally valued domains (Geary, 2021). Similar processes might be occurring for girls, but more boys than girls have a comparative advantage (i.e., their best academic subject; Stoet & Geary, 2020) in mathematics that in turn might bias them to consider mathematic-intensive areas as a long-term niche.

In contrast, Lauermann et al. (2017) did not find that ninth grade utility beliefs differentially predicted boys’ and girls’ math-intensive career aspirations or later career choices. One potential reason is that Gaspard et al. (2015) used more differentiated utility belief items, including several specifically related to future careers, whereas Lauermann et al. used more generic items. With respect to the current study, Lauermann et al. started with 9th graders, whereas our endpoint was 9th grade. It could be that most of the gains in boys’ utility beliefs, as related to gains in mathematics achievement, occur by the end of 9th grade, but this remains to be determined. In any case, future studies of adolescents’ mathematics utility beliefs and mathematics attitudes more generally might include Gaspard et al.’s items on future careers.

Mathematics Anxiety and Mathematical Development

The commonly found sex difference in mathematics anxiety was replicated (Dowker et al., 2016; Kazelskis, 1998; Stoet et al., 2016; Wigfield & Meece, 1988), and remained significant with control of trait anxiety. Even so, higher levels of trait anxiety were consistently associated with higher levels of mathematics anxiety (Figure 2), but importantly the correlations between same-grade trait and mathematics anxiety were similar for boys (rs = .51, .53 Figure 1A SOM) and girls (rs = .50, .46 Figure 2A SOM), suggesting that adolescents who are generally anxiety prone might be at higher risk of developing mathematics anxiety, independent of sex, as suggested by Wang et al.’s (2014) behavior genetic study. In other words, girls may have higher levels of mathematics anxiety because they have higher mean levels of anxiety generally, and boys with similarly high anxiety levels may also be prone to developing mathematics anxiety. By analogy, strong spatial abilities are associated with gains in mathematics achievement for both boys and girls, and boys have advantages in mathematical areas that have a spatial component to them because there are more boys than girls with strong spatial abilities not because they are boys per se (Geary et al., 2021; Geary et al., 2022).

From a broader perspective, mathematics is an evolutionarily novel academic domain (Geary, 1995), and thus inherent math-specific anxiety is unlikely. Rather, mathematics anxiety must emerge through some type of conditioning, whereby anxiety prone individuals (more adolescent girls than boys) are more likely to acquire math anxiety than their calmer peers, if they experience anxiety during mathematics learning (e.g., through exposure to math anxious teachers or parents) or evaluations (Levine & Pantoja, 2021). Indeed, individuals with high levels of math anxiety have physiological and other responses like those found with phobias (Hembree, 1990; Lyons & Beilock, 2012; Ramirez et al., 2018), and the genetic risks associated with general anxiety contribute to mathematics anxiety, independent of math competencies (Wang et al., 2014). This interpretation is consistent with Young et al.’s (2012) finding that mathematics anxiety is correlated with engagement of an amygdala nucleus that contributes to fear conditioning.

In this scenario, mathematics learning and evaluations may be stressful and anxiety provoking for most girls and boys, but adolescent girls and young women may be more prone to form anxiety-related memories during these experiences (Cover et al., 2014), and will eventually form math-specific anxiety that is independent of trait anxiety. Any such relation might be related, in part, to spatial abilities (Ferguson et al., 2015; Maloney et al., 2012). This is because some aspects of mathematics learning (e.g., word problems; Casey & Ganley, 2021; Geary et al., 2022) are facilitated by spatial abilities and students (more girls than boys) with less developed spatial competencies (including low-spatial boys) might experience more anxiety when encountering these types of mathematics problems than other students, potentially resulting in both mathematics and spatial anxiety. Indeed, controlling the relation between spatial abilities and mathematics anxiety reduced the magnitude of the relation between cross-grade gains in mathematics and cross-grade change in anxiety, suggesting they are all interrelated.

In any case, if we assume that mathematics anxiety is a conditioned fear response, then repeated success with mathematics should contribute to fear extinction or a reduction in mathematics anxiety over time (Graham & Milad, 2011). This was found for boys without control of the spatial ability to mathematics anxiety relation (our initial models) and was a trend with control of this relation. Boys who had relatively large gains in mathematics achievement across 7th to 9th grade experienced a mitigation of the general cross-grade increase in anxiety ($\beta =-.29$, Table 5). The same pattern emerged for girls ($\beta =-.06$) but with a weaker and not statistically significant effect. One possibility is that higher achieving adolescent girls are showing slower fear extinction, at least in this context. However, much remains to be learned about sex differences in fear extinction (Velasco et al., 2019) and so this interpretation remains to be fully evaluated. It is also possible that girls and boys interpret their difficulties or successes with mathematics differently, which would result in influences (e.g., stereotypes) on the sex difference in mathematics anxiety above and beyond success in mathematics (Levine & Pantoja, 2021; Ramirez et al., 2018).

Whatever the underlying reason, the consequences of high mathematics anxiety might be more severe for girls than boys. As noted in the introduction, the mean sex difference in mathematics anxiety could result in more girls than boys avoiding future mathematics courses (Dowker et al., 2016; Ma, 1999; Meece et al., 1990). The combination of higher mathematics anxiety and more negative attitudes will likely contribute to the sex difference in interest in and pursuit of math-intensive careers (Lauermann et al., 2017), although there are other factors that contribute to these differences, such as intra-individual strengths in reading and mathematics and interests in math-related professions (Stoet & Geary, 2015, 2018, 2020, 2022).

Limitations

The correlational nature of the data is the primary limitation. One way to further test the relations found in this study is to integrate anxiety and attitudes measures into mathematics interventions to determine if intervention students show greater reductions in anxiety and gains in attitudes relative to students in control groups. We chose mathematics attitudes and anxiety measures that had shown sex differences in previous studies and controlled for the potential confounds from spatial abilities and trait anxiety, both of which also show sex differences. Still, there could be other traits or more nuanced measures of attitudes, especially utility beliefs (Gaspard et al., 2015), or anxiety that could yield different results. Spatial anxiety is one construct that was not measured here but should be considered as a potential contributor to the sex difference in mathematics anxiety (Delage et al., 2022; Sokolowski et al., 2019).

The analytic approach did not support the estimation of reciprocal relations between mathematics achievement, attitudes, and anxiety slopes, and thus our findings should not be taken to mean that attitudes and anxiety do not affect later achievement, only that any such effects are weaker than the mathematics achievement to attitudes and anxiety relations. Moreover, it is possible that change in spatial abilities and trait anxiety from 7th to 9th grade, which we were unable to assess, could influence the sex differences we found here. Finally, the majority (70%) of the students were White and from middle- to upper-middle class backgrounds and thus the extent to which these findings will generalize to other samples remains to be determined.

Conclusions

Despite these limitations, the use of LGCM revealed more nuanced sex differences in the relations between mathematics achievement, attitudes, and anxiety than have previous studies. Broadly, the findings indicate that studying developmental change in mathematics achievement as related to developmental change in attitudes and anxiety (slope to slope effects in LGCM) might be more informative than the more typical focus on the relation between earlier achievement (intercepts in LGCM) and later attitudes and anxiety. Specifically, our results suggest that strong cross-grade gains in mathematics might mitigate the general decline in mathematics attitudes and increase in mathematics anxiety for boys but not girls, although both effects need replication. Our results also confirm the relation between spatial abilities and mathematics anxiety and suggest this relation might be more important for girls’ than boys’ mathematical development, potentially mediated through spatial anxiety. Overall, the finding that cross-grade mathematics gains were more consistently related to developmental change in mathematics attitudes and anxiety in boys than girls suggests that different approaches to addressing mathematics anxiety and development declines in attitudes might be needed for boys and girls (Ramirez et al., 2018).

Educational Impact and Implications Statement.

Students with strong mathematical competencies are less mathematically anxious and have more positive mathematics attitudes. For boys, mathematics achievement gains across the middle school years and into high school slowed developmental declines in mathematics attitudes and increases in anxiety. Girls maintained higher levels of mathematics anxiety and less positive attitudes than did boys, even when they showed strong mathematics achievement gains across grades.