Automatic Segmentation of Abdominal Aortic Aneurysms from CT Angiography Using a Context-Aware Cascaded U-Net

Abstract

We delineate abdominal aortic aneurysms, including lumen and intraluminal thrombosis (ILT), from contrast-enhanced computed tomography angiography (CTA) data in 70 patients with complete automation. A novel context-aware cascaded U-Net configuration enables automated image segmentation. Notably, auto-context structure, in conjunction with dilated convolutions, anisotropic context module, hierarchical supervision, and a multi-class loss function, are proposed to improve the delineation of ILT in an unbalanced, low-contrast multi-class labeling problem.

A quantitative analysis shows that the automated image segmentation produces comparable results with trained human users (e.g., DICE scores of 0.945 and 0.804 for lumen and ILT, respectively). Resultant morphological metrics (e.g., volume, surface area, etc.) are highly correlated to those parameters generated by trained human users. In conclusion, the proposed automated multi-class image segmentation tool has the potential to be further developed as a translational software tool that can be used to improve the clinical management of AAAs.

1. Introduction

Abdominal aortic aneurysm (AAA) is the pathologic local dilation of the abdominal aorta. According to epidemiological studies [1, 2], the incidence of AAAs is increasing. Despite the advance in our understanding and treatment of AAAs, high rates of morbidity and mortality persist [3, 4]. Once the aortic diameter reaches 5.5 cm in men or 5.0 – 5.4 cm in women, the current clinical guidelines recommend elective repairs [5], which is the most reliable strategy to prevent death due to a ruptured AAA. Smaller AAAs are managed with guideline-directed atherosclerotic risk reduction through serial surveillance imaging performed at time intervals dictated by aneurysm size.

Recent advances in medical imaging technology have led to the development of analytic tools to improve the management of AAAs. Approximately 10% of aneurysms have minimal to no growth, while 30% display rapid growth [6]. Repeated imaging can put an economic strain on patients with slow-growing AAAs [7, 8]. Consequently, tools capable of identifying aneurysms with a propensity for rapid growth would be immensely useful clinically and anticipated to inform resource allocation for serial monitoring. Motivated by the clinical need, much research has been devoted to analyzing medical imaging data associated with AAAs. Infrared thermography (IRT) [9, 10] can be a promising imaging technique to detect AAAs. Still, its accuracy may be affected by the thermal effect of other abdominal organs, tissues, fats, etc. In five recently published studies [11–15], derivatives of medical imaging data (geometrical and biomechanical metrics) were used to predict aneurysm growth (i.e., fast-growing versus slow-growing) or aneurysm diameter. Their results (i.e., the area under the curve = 0.78 ~ 0.85) are promising, suggesting that this methodology has excellent translational potential.

An important component of those software tools is identifying the extent of AAAs from medical images. In all five studies mentioned above, manual or semi-automatic image segmentation was performed. This manual or semi-automatic image segmentation process is labor-intensive (up to 2 hours per case) and has considerable operator dependency.

Leveraging our experience in medical image classification [16] and segmentation [17] tasks, our primary objective is to develop a supervised deep-learning-based multi-label method for AAA segmentation. The availability of such an image segmentation tool could facilitate the standardization of morphological analyses of AAAs. In addition to predicting AAAs’ growth status, such information is also valuable for surgical planning of AAAs’ repair, e.g., optimal sizing of the endografts [18]. However, automatic segmentation of an AAA is challenging because of the heterogeneity of AAA morphology and the low discrimination between an AAA and its surroundings. Particularly, low image contrast between intraluminal thrombosis (ILT) and its ambient anatomies on computed tomography angiography (CTA) poses significant difficulties in the required delineation. Other technical challenges of the ILT segmentation include: (1) a label/class imbalance issue due to the small ILT volume; and (2) the ILT morphology is irregular, making it impossible to geometrically parameterize ILT for better outcomes.

It is important to note that the extent of ILT in AAAs is of clinical significance for several reasons. First, ILT has a high prevalence in AAA patients (70–80%). Second, clinical work found that the growth of thrombosis was a better indicator of AAAs’ rupture risk [19] as compared with using the maximal diameter of AAAs [5]. Third, unstable ILT may trigger peripheral embolization with subsequent ischemia.

We are motivated to develop a novel deep-learning framework to address the unmet clinical need. By learning from the annotated data, a supervised model transforms the input variables into the output variable, and a robust transformation (i.e., a trained, supervised model) allows reliable predictions post-training. In the framework of deep learning, a key to supervised learning is constructing efficient rules for parameter adjustments. We made efforts to optimize our proposed supervised model for AAA segmentation mainly from three aspects: (1) exploring a two-stage cascade CNN structure at different resolutions to ensure deep supervision and better convergence; (2) configuring the network model with an anisotropic context module to capture both short-range and long-range dependencies to improve positional encoding; (3) developing a rebalanced multi-class error loss function to measure the deviation between actual and expected outputs to increase the tolerance of imbalanced classes during supervised learning.

Prior work related to the automated segmentation of AAAs is briefly summarized in Section 2 to highlight the necessity of devising a novel context-aware deep-learning convolutional neural network configuration. Section 3 presents essential details of the proposed context-aware cascaded U-Net, of which the architecture is illustrated in Figure 1, followed by our experimental design (Section 4) and preliminary testing results (Section 5). Then, our observations are discussed in Section 6 before some closing remarks.

Figure 1:

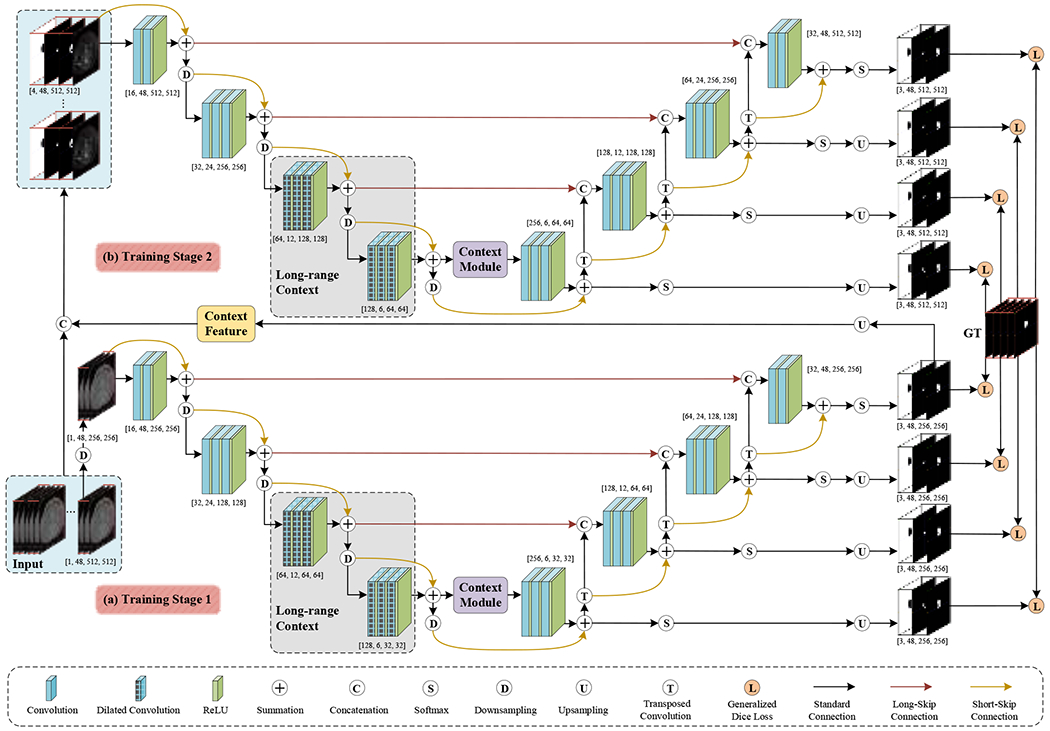
A schematic illustration of the proposed CACU-Net: (a) a residual 3D U-Net architecture, (b) an auto-context 3D U-Net structure.

2. Prior Work

Our brief literature review below is concentrated on image segmentation methods of ILT, which can be roughly divided into two categories: (1) semi-automatic and (2) fully automatic models.

Five published semi-automatic approaches for ILT segmentation were found. One weakness is that all five methods need AAAs’ lumens to be identified and/or some user interactions, as described below. Olabarriaga et al. [20] developed a nonparametric grey-level modeling method to segment thrombosis based on the generated lumen surface. User interactions (i.e., specifying two positions) were required to identify the lumen. Freiman et al. [21] segmented the thrombosis by iteratively growing it from an initially depicted aortic lumen using a graph minimum-cut algorithm. In another attempt, Lee et al. [22] first secured a manual initialization of the aortic lumen. They then employed a triangular mesh-based graph search method to segment the lumen and thrombus surfaces. Maiora et al. [23] performed thrombus segmentation in AAAs using active learning and a supervised random forest method. Some user interactions are needed in active learning. Lalys et al. [24] proposed to first estimate an aorta centerline to acquire an initial lumen with minimal user interaction. Then, they separated ILT from the lumen and its surroundings by exploring gradient information of the imaging data. Another weakness of these semi-automated methods is that they involved a large number of parameters. Optimization of their parameters led to dataset-dependent outcomes, significantly reducing their repeatability and robustness.

Referring to fully automatic approaches, we found seven published studies, six of which adopted deep learning models. Hong and Sheikh [25] presented a deep belief network (DBN) for detecting and segmenting the preoperative AAA region of 2D CTA. López-Linares et al. [26] exploited a 2D segmentation method for AAA thrombosis only, using a fully convolutional network (FCN) and a modified holistic nested edge detection (HED) network. In another study from the same group, López-Linares et al. [27] extended their prior work by introducing a 3D CNN for segmenting the aneurysms from both preoperative and postoperative CTA scans. However, their 3D CNN model failed when ILT regions were thin. Lu et al. [28] proposed a modified 3D U-Net [29] architecture by combining the elliptic fitting for aorta segmentation and AAA detection, which used both contrast and non-contrast CT scans for training. Hwang et al. [30] employed an improved Mask R-CNN [31] for thrombus segmentation, but they merely transformed 2D results into 3D images for qualitative evaluation. In one more traditional segmentation method by Lareyre et al. [32], they first located the aortic lumen using the boundary propagation method and then segmented ILT regions based on the active contours of the identified lumen.

Limitations of these existing fully automated methods are briefly discussed below. First, most of them are based on 2D images. Although these methods can detect thrombosis with the same precision as neuroradiologists, the resultant volume and spatial consistencies are low compared with the known ground truth. Second, these methods can only perform binary classifications. We stipulate that multi-class segmentation was avoided in part due to the class imbalance issue mentioned.

In this study, we propose a novel automatic method, context-aware cascaded U-Net (CACU-Net, Figure 1), to perform AAA segmentation in a multi-class (lumen and thrombosis) fashion. One significant advantage of the proposed CACU-Net is to utilize multi-scale contextual information [33] through two-stage training. In the first training stage, one residual 3D U-Net captures contextual information from the low-resolution levels and generates preliminary segmentation maps. The contextual information fusion is implemented by the cascaded networks [34, 35]; that is, the output layer of the residual 3D U-Net is directly connected to the input layer of the auto-context 3D U-Net. In the second training stage, an auto-context 3D U-Net can extract contextual information at a higher resolution (i.e., the original high-resolution CTAs), which is fused together with the above-said preliminary prediction maps. Notably, in the auto-context 3D U-Net, auto-context architectures [36, 37] are added to the classic U-Net. Thus, by balancing context information and image features, our algorithm can give consideration to low-level appearance features and high-level shape information. Furthermore, we explore dilated convolutions and anisotropy context modules to enrich the long-range dependencies of in-depth supervision. Last, to mitigate the known label imbalance issue, a rebalancing multi-class hierarchical surveillance strategy is exploited to balance the number of samples per class in training and to facilitate a detailed perception of lumen and thrombosis.

In short, the main contributions of the proposed CACU-Net include: (1) a two-stage context-aware cascaded U-Net that fully considers the surrounding context to guide more coherent multi-class segmentation, (2) an auto-context algorithm involving deep supervision at different resolutions, (3) an anisotropic context module with low computational cost to capture the short-range and long-range dependency information, and (4) a rebalancing multi-class loss function to improve the deep network’s tolerance for severely imbalanced classes. Our proposed auto-context algorithm mentioned above was applied to a 3D residual U-Net, in which posterior inferences were carried into later network components as priors to generate more discriminative results in a coarse-to-fine manner.

3. Methods and Materials

This section provides essential details of our CACU-Net (see Figure 1) and multi-stage training. Upon publication, source codes of the proposed CACU-Net will be made available through Github or an equivalent to improve reproducibility.

3.1. Overview of CACU-Net

The CACU-Net comprises a residual 3D U-Net and an auto-context 3D U-Net. In the first (training) stage, the residual 3D U-Net with long-range dependencies is trained on the subsampled CTA images of lower resolution to capture abundant context. The output of the first training stage is an initial segmentation map covering the entire aneurysm, with most of the background voxels excluded. At the end of the first (training) stage, the initial segmented map is up-sampled to exactly the same resolution as the original CTA image.

In the second (training) stage, the original CTA image and the initial segmentation map are supplied to the auto-context 3D U-Net for training at a higher resolution. The second stage considers the surrounding information to modify the initial map iteratively. Training in Stages 1 and 2 interleaves, and the model parameters are continuously updated by measuring and back-propagating errors between the prediction and the ground truth. This two-stage training continues until a pre-set convergence is reached.

The details of each stage are illustrated in the following two subsections.

3.2. Stage 1: Residual 3D U-Net

The residual 3D U-Net architecture shown in Figure 1(a) is based on the fully convolutional U-Net [38] and consists of encoding and decoding paths. Each path has four layers of different resolutions obtained by ReLU-activated convolution and transposed convolution, respectively. Basically, short-skip connections and long-skip connections are used for feature fusion of adjacent layers and cross-layers, respectively, thereby maximizing the utilization of feature information in each layer. In particular, a series of 3×3×3 convolutions with small receptive fields are adopted to capture finer detail. As complements, the dilated convolutions are leveraged in the last two layers of the encoder path to enlarge the receptive field of a CNN to probe the long-range context. Typically, the anisotropy context module enables the network to aggregate both local (within-object) and global (between-objects) contexts. Furthermore, hierarchical supervision is achieved by executing Softmax activations on all four layers of the decoding path and then training to minimize the total losses between these four predictions and the ground truth.

3.2.1. Anisotropy Context Module

The anisotropy context module (as shown in Figure 2) mainly adopts mixed pyramid pooling to extract different types of neighborhood context information, namely short-range context (see Figure 2(a)) and long-range context (see Figure 2(b)), making the feature expression more discriminative. In other words, standard spatial pooling and strip pooling [39] are exploited to capture short-range and long-range dependencies within different locations, both of which are crucial for multi-class object segmentation.

Figure 2:

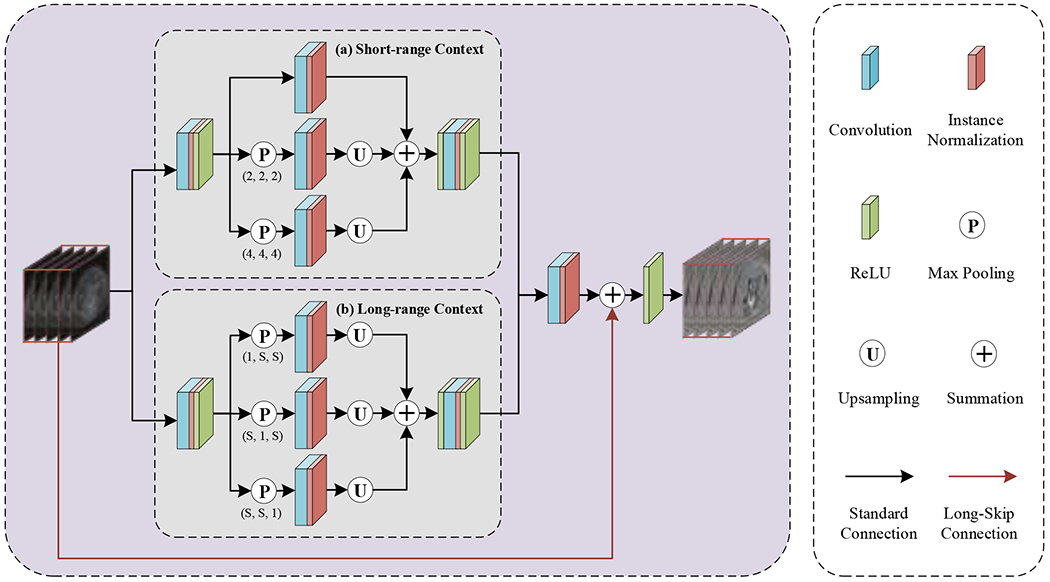
A workflow illustrating the proposed anisotropy context module: (a) short-range context and (b) long-range context.

To collect short-range dependencies, two maximum pooling operations with strides 2×2×2 and 4×4×4 followed by 3×3×3 convolutions plus a 3D convolutional layer that preserves the original spatial information are aggregated to handle tightly distributed semantic information with short-range context. Meanwhile, to achieve long-range dependencies, strip pooling operations with three different orientations of receptive fields (i.e., kernel size) 1×S×S, S×1×S, and S×S×1 are configured to connect the object regions discretely and encode the candidate object with band structure, where S denotes the size of the input feature map to allow the network to perceive long-range contextual information. Notably, the adaptive parameter S will differ in the two-stage cascaded network due to different resolutions. It is important to note that this design is particularly suitable for segmenting long cylindrical objects such as AAAs. Next, the above two sub-modules are concatenated and fed to a 1×1×1 convolutional layer for channel expansion and then merged with the initial feature map using a long-skip connection to obtain the final anisotropy context.

3.2.2. Hierarchical Supervision Strategy

Given n training CTA images containing $m$ voxels (denoted as $X^{(j)}(x_i)$, $i=1,\cdots ,m$, $j=1,\cdots ,n$) and their corresponding ground truth (GT; denoted as $Y^{(j)}(y_i)$, $y_i\in \{0,1,2\}$ representing the background, lumen, and ILT, respectively), the gist of the proposed network is to learn segmentation model parameters $\theta$ based on training samples. Briefly, the predicted segmentation map (denoted as $Y\prime (y_i^{\prime })$, $y_i^{\prime }\in \{0,1,2\}$) is obtained by maximizing the posterior probability (denoted as $P_d$, $d\in \{1,2,3,4\}$ representing the four decoding layers in Figure 1(a)–(b)) for a given observed CTA image:

$$Y\prime (y_i^{\prime })=\arg \max P_d(y_i=l|X(x_i);\theta ),$$ (1)

where the posterior probability $P_d$ of a voxel set $M_i$ with the label $l\in \{0,1,2\}$ can be calculated by performing the Softmax function on the last ReLU activation map (denoted as $A(x_i)$) of each decoding layer via:

$$P_d(y_i=l|X(M_i);\theta )=\frac{e^{A_l(M_i)}}{{\sum }_{k=0}^2{e}^{A_k(M_i)}}.$$ (2)

Subsequently, the network learnable hyper-parameter set $\theta$ is iteratively updated by backpropagation of the error between $P_d(M_i)$ and $Y(M_i)$, which can be computed by a loss function. Since the ILT region accounts for a very small fraction of the whole aneurysm (typically 10% or less), we run into a classic label imbalance problem. As a result, the prior information on class proportions learned by the network inevitably leads to suboptimal ILT segmentation. Therefore, the purpose of our proposed rebalancing multi-class loss (denoted as $L_d$, $d\in \{1,2,3,4\}$, which stands for four decoding layers in Figure 1(a)–(b)) must be more conducive to ILT prediction. The proposed loss function reads,

$$L_d=1-2\frac{{\sum }_{l=1}^2{w}_l{\sum }_i{Y}_l(M_i)P_d(y_i=l|M_i)}{{\sum }_{l=1}^2{w}_l{\sum }_i(Y_l(M_i)+P_d(y_i=l|M_i))},$$ (3)

where $w_l$ is used to balance the contribution of each class to reduce the dominant influence of a particular label set with a considerable volume. In practice, a larger weight $w_l$ is applied to the class with a small proportion, thereby helping improve the tolerance level of the deep network for imbalanced labels.

Also, we used a hierarchical supervision strategy that fully considers multi-level predictions with different resolutions. Hence, our model’s ability to express objects at various scales is enhanced to facilitate the perception of detailed aneurysm information.

3.3. Stage 2: Auto-Context 3D U-Net

The auto-context 3D U-Net (Figure 1(b)) is inspired by the auto-context algorithm [33]; the underlying idea is to utilize multiple stages for segmentation. Particularly, the later stage network can take advantage of the features processed by its previous network. Correspondingly, we take the generated segmentation map $Y\prime (y_i^{\prime })$ of the first stage, which has large quantities of contextual localizations, as a new channel plus the original image $X(x_i)$ to constitute the training set for the second stage. In other words, the posterior trained by residual 3D U-Net (Stage 1) is used as the prior of auto-context 3D U-Net (Stage 2) to realize the concatenation of deep features and context features (also called shape features). Consequently, our segmentation problem becomes seeking an optimal solution to the conditional probability distribution $P(Y″|X,Y\prime )$, which can be achieved by determining the maximum posterior as follows:

$$Y″(y_i^{″})=\arg \max P_d(y_i=l|X(x_i),Y\prime (y_i^{\prime });\theta )$$ (4)

Next, the same procedure as residual 3D U-Net is repeated until the algorithm converges. Mathematically, how to calculate the weight sequence in the network to construct the segmentation model parameters $\theta$ is provided below as Algorithm 1. Finally, the learned weights are employed to make predictions during testing.

Compared with the current U-Net structure, there are three main advantages of our auto-context U-Net. First, in the second stage, we input raw images of low-level appearance features along with predicted probability maps of high-level shape information. Thus, the classifier can gradually correct early prediction errors by exploiting new contextual features. Second, since the posterior distribution of labels contains the target’s learned local shape and connectivity, the proposed network can more effectively perform discriminative mining of contextual information around the target to improve segmentation performance. Third, capitalizing on deeper supervision and flexible configuration of the proposed network, the proposed model naturally handles the balance between image features and contextual knowledge.

3.4. Implementation details

In the training stage, the proposed CACU-Net is learned using patches of size 48×512×512 voxels randomly cropped along the vertical axis of the CTA image, with a batch size of 2. The first stage starts by running the residual 3D U-Net on downsampled input images 1×48×256×256. This process generates a three-channel binary segmentation map 3×48×256×256, including the lumen, ILT, and background. By upsampling this initial segmentation map to the original resolution and adding it to the raw CTA image patch, a 4×48×512×512 image patch is generated and used as the input to the second stage. In the second stage, a full-resolution auto-context 3D U-Net is configured. The initial learning rate of the network is set to 0.0001 and optimized by the Adam algorithm [41]. Guided by empirical convergence results, a multi-step learning rate (MultiStepLR) schedule approach is adopted to reduce the learning rate by 0.2 per 30 epochs. On configuration, our CACU-Net is implemented in PyTorch framework and trained on dual Tesla V100 PCIe GPUs (32 GB RAM each) for a total of 600 epochs, taking 10 hours.

In the testing stage (as shown in Figure 3), the overlapping 3D patches of size 48×512×512 are extracted from the test images with a stride of 6×512×512. This deployment ensures that each voxel belonging to a different test patch is predicted eight times, and the prediction class with the highest frequency is determined as the final label for that voxel. Indeed, using overlapping patches during testing enriches the context information, which is helpful for accurately segmenting the ILT. Furthermore, the maximum 3D connected components of the lumen and ILT regions are calculated as the final segmentation result.

Figure 3:

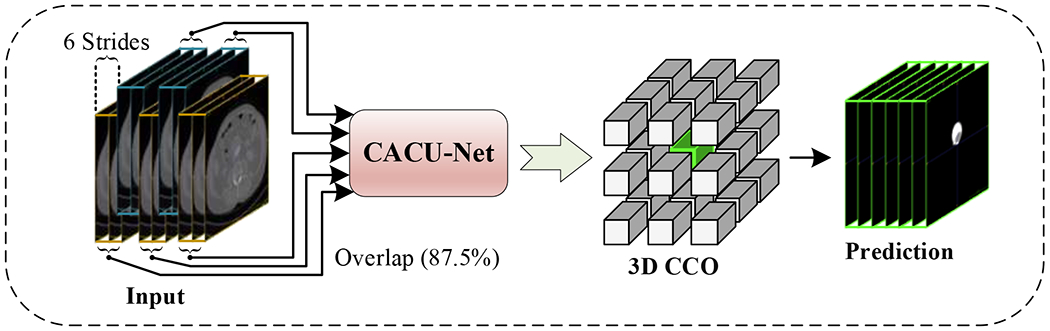
A graphical diagram showing the testing stage. Connected component optimization (CCO) is used in the post-processing step.

3.5. Dataset

All data were acquired at Mayo Clinic during routine imaging follow-up for patients with AAAs, who underwent multidetector CT scans with intravenous injection of contrast liquid. The protocol was approved by the institutional review boards at Michigan Technological University and Mayo Clinic. The CTA volume images we used for training and testing were converted from the provided Digital Imaging and Communications in Medicine (DICOM) format to NIFTI-type 3D images of 512×512 pixels with 214-2,433 slices. Since our multi-class segmentation model was designed to segment both lumen and ILT, we discarded the AAA patient data without ILT and selected CTA data contained ILT with varying sizes (approximately 9-79% in terms of volume percentage) and shapes . In more than 70% of the AAA patient data, the number of voxels corresponding to the ILT was much smaller than that corresponding to the lumen. The ground truth labels for each CTA image were manually annotated with software tools (Mimics v24.0 and 3-Matic v16.0, Materialise, Leuven, Belgium) by two experienced operators.

4. Experiments

We performed extensive numerical experiments to evaluate the performance of the proposed CACU-Net. Specifically, we qualitatively and quantitatively compared CACU-Net’s performance against that of five published state-of-the-art models: Graph-Cuts [42], 3DUNet [29], SegNet [43], 3DResUNet [44], and KiU-Net [45]. Seventy CTA datasets with ground truth (GT) were selected from our internal database for the above-said performance evaluation. Inclusion criteria were: (1) contrast-enhanced CTA to delineate both aorta lumen and ILT and (2) sufficient image quality and complete CTA image to identify abdominal aorta and iliac arteries. The flowchart of inclusion and exclusion criteria for selecting our experimental cases is shown in Figure 4.

Figure 4:

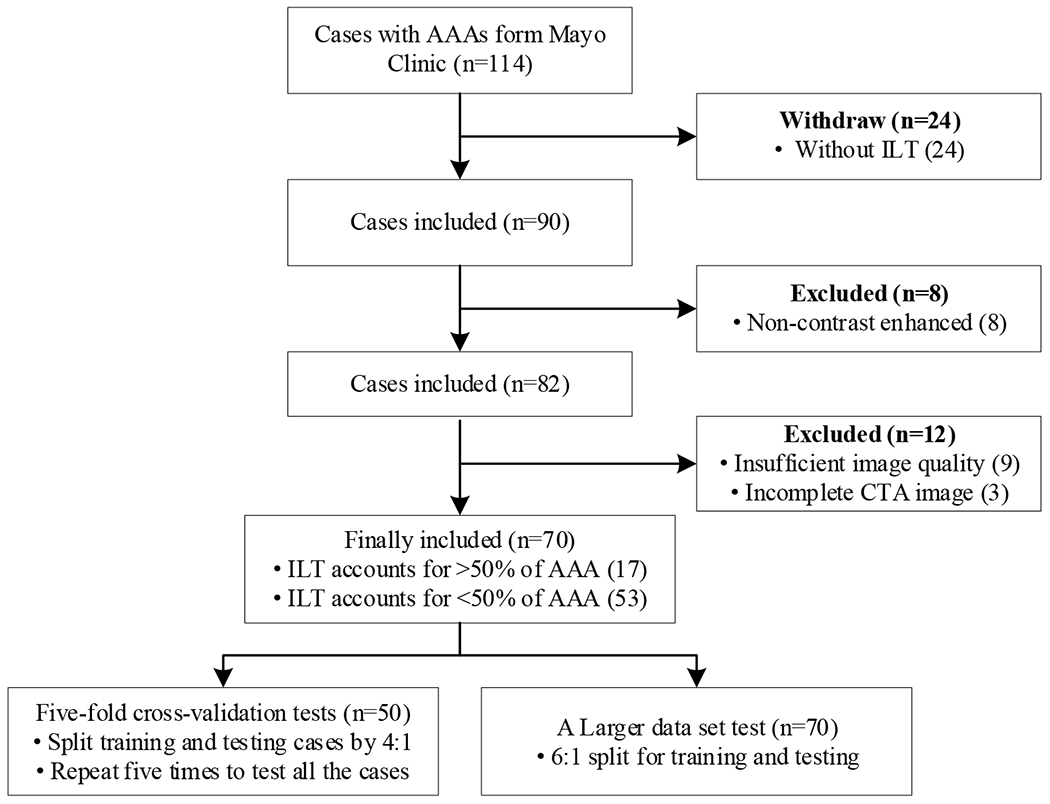
A flow chart showing the data selection process. “Incomplete CTA” means that imaging data failed to include a complete AAA.

We conducted two experiments to evaluate model effectiveness and reproducibility: (1) five-fold cross-validation tests on 50 cases. In each run, an 80:20 (non-overlapping) split was used for training and testing, respectively. As a result, after five runs, this 5-fold cross-validation strategy produced computer-segmented results for all 50 cases. (2) A larger data set test with 70 cases. The cases were randomly divided into a training set (60 cases) and a testing set (10 cases).

The segmentation results were evaluated by comparing with GT in terms of six metrics, viz., DICE coefficient, $2TP/(2TP+FP+FN)$, relative volume error (RVE), $|FN-FP|/(TP+FN)$, sensitivity, $TP/(TP+FN)$, specificity, $TN/(TN+FP)$, 95% Hausdorff distance (HD) [46], and surface distance (ASSD) [47], where TP, TN, FP, and FN denote the true positive, true negative, false positive, and false negative, respectively. Specifically, we singled out the lumen and ITL regions from the predicted segmentation map and GT, respectively, to form two binary maps for comparison and utilized the above six metrics to calculate the similarity/difference of volume/surface between the voxels contained in the two 3D maps. An ablation experiment was also conducted to investigate the contributions of various context-aware components (see Figure 1) to the segmentation outcomes.

Furthermore, a morphological analysis of the proposed CACU-Net was conducted and compared with the morphology of the GT. Statistical methods, i.e., Pearson correlation coefficient (PCC), linear regression (LR), and Bland-Altman (B-A), were used.

5. Results

5.1. Comparative Experiments

Extensive quantitative and qualitative evaluations were performed to verify the superiority and reproducibility of our CACU-Net model.

5.1.1. Quantitative Results

Five-fold cross-validation tests.

The quantitative comparison of multi-class segmentation results obtained by cross-validation of the various models is shown in Table 1. The results show that the proposed CACU-Net outperformed all other models on average scores of six metrics for lumen and ILT segmentation of 50 3D CTA images. In terms of DICE scores, our segmentations for lumen and ILT are 0.203 and 0.323 higher, respectively, than the second-ranked 3DResUNet model. In addition, our model achieved minimum values in RVE and two surface distance metrics: 95% HD and ASSD; the proposed CACU-Net was far superior to the respective second-ranked models (see Table 1).

Table 1:

Quantitative performance comparisons of multi-class segmentation results obtained by various models on six metrics. The up arrow ↑ indicates that the larger the average value, the better the model performance, and the down arrow ↓ has the opposite meaning. The dash (−) means that the model cannot produce the corresponding class to compute the metric. Both 95% HD and ASSD are given in mm. The best results are shown in bold fonts.

Classes	Models	DICE↑	RVE↓	Sensitivity↑	Specificity↑	95% HD(mm)↓	ASSD(mm)↓
Lumen	Graph-Cuts	0.426±0.046	0.778±0.360	0.843±0.027	0.996±0.002	142.986±23.077	23.358±5.579
	3DUNet	0.643±0.056	0.795±0.233	0.797±0.072	0.957±0.056	71.025±19.437	17.554±5.807
	SegNet	0.663±0.052	0.667±0.165	0.788±0.069	0.958±0.055	59.819±18.253	13.284±4.924
	3DResUNet	0.742±0.041	0.779±0.246	0.965±0.021	0.997±0.001	68.811±10.225	16.828±3.705
	KiU-Net	0.705±0.050	0.571±0.236	0.835±0.060	0.998±0.000	50.772±15.332	14.743±6.338
	CACU-Net	0.945±0.008	0.076±0.018	0.971±0.010	1.000±0.000	6.644±1.833	1.108±0.178
ILT	Graph-Cuts	-	-	-	-	-	-
	3DUNet	-	-	-	-	-	-
	SegNet	-	-	-	-	-	-
	3DResUNet	0.481±0.036	1.422±0.317	0.758±0.042	0.996±0.000	47.413±7.168	9.806±1.580
	KiU-Net	0.220±0.035	0.728±0.161	0.199±0.050	0.999±0.000	40.925±12.474	10.684±3.425
	CACU-Net	0.804±0.021	0.157±0.033	0.829±0.028	0.999±0.000	6.169±1.427	1.301±0.241

Notably, our CACU-Net demonstrated superior performance for ILT segmentation, achieving a DICE value of 0.804, with minimum RVE and maximum sensitivity values also indicating the successful suppression of false positives. Of note, Graph-Cuts, 3DUNet, and SegNet failed to provide meaningful outcomes for thrombosis segmentation. Although 3DResUNet and KiU-Net models yielded some useful results, their DICE values were low (0.481 and 0.220, respectively). Overall, Table 1 indicated that the performance of all five comparative models was indeed problematic for ILT segmentation. It is also interesting to note that our 95% HD and ASSD are 6.169 mm and 1.301 mm, respectively. Given the aneurysm size (typically > 60 mm for AAAs under surgery), our predictions could be helpful for the surgeon’s clinical decision-making process.

Larger data set test.

To verify how imaging data size influenced the model performance, we expanded the training data cases from 40 to 60; the quantitative performance comparison of various deep learning models is shown in Table 2. The performance of all four benchmark deep learning models (3DUNet, SegNet, 3DResUNet, and KiU-Net) has been improved. Referring to the lumen segmentation, the improvement of 3DUNet was most apparent (see Table 1 vs. Table 2); e.g., the DICE score was improved by 0.098. In the case of ILT segmentation, the DICE scores of 3DResUNet and KiU-Net increased by 0.076 and 0.327, respectively. It is worth mentioning that the SegNet could detect ILT after expanding the training set. Initially, SegNet failed when it had been trained with 40 cases (see Table 1). However, the DICE score was still low (0.268). In contrast, our CACU-Net model was stable, as its performance showed no significant changes. It is worth noting that our CACU-Net model achieved state-of-the-art performance (Tables 1 and 2).

Table 2:

Quantitative performance comparisons of various deep learning models when 70 cases were used.

Classes	Models	DICE↑	RVE↓	Sensitivity↑	Specificity↑	95% HD(mm)↓	ASSD(mm)↓
Lumen	3DUNet	0.741±0.054	0.406±0.172	0.832±0.100	0.999±0.001	19.476±4.513	4.835±0.869
	SegNet	0.700±0.073	0.436±0.309	0.777±0.126	0.999±0.001	18.927±4.817	5.458±1.073
	3DResUNet	0.770±0.090	0.607±0.379	0.977±0.020	0.998±0.001	44.933±16.055	9.459±3.832
	KiU-Net	0.750±0.075	0.158±0.132	0.691±0.083	1.000±0.000	22.770±17.591	4.906±1.745
	CACU-Net	0.935±0.039	0.114±0.111	0.985±0.012	0.968±0.028	12.929±6.970	1.553±0.667
ILT	3DUNet	-	-	-	-	-	-
	SegNet	0.268±0.073	0.667±0.339	0.288±0.057	0.998±0.001	23.027±3.294	6.417±0.894
	3DResUNet	0.557±0.114	1.084±0.703	0.785±0.052	0.997±0.001	39.960±12.500	8.233±2.348
	KiU-Net	0.547±0.075	0.775±0.437	0.703±0.107	0.998±0.000	24.637±8.725	5.205±0.949
	CACU-Net	0.810±0.070	0.169±0.102	0.798±0.096	0.967±0.013	7.267±4.254	1.308±0.348

5.1.2. Qualitative Results

Figure 5 visually compares the lumen and ILT segmentation results obtained by the proposed CACU-Net and five other benchmark models on the five-fold cross-validation tests (training: 40 cases + testing: 10 cases). Note that our results from CACU-Net were highly consistent with GT, successfully separating the ILT from surrounding tissues, e.g., veins and colons. Consistent with results in Table 1, for Graph-Cuts, 3DUNet, and SegNet models (see Figure 5(b–d)), ILT could not be segmented, and the lumen extent was also difficult to determine. In terms of the 3DResUNet model (see Figure 5(e)), there were a large number of regions that were mis-segmented as lumen (indicated by the blue arrows) and ILT (indicated by the yellow arrows). In contrast, the ILT volumes predicted by the KiU-Net model (see Figure 5(f)) were smaller than those of manual segmentation, with some peripheral structures falsely detected. Overall, all other models were unable to segment the ILT regions correctly. We drew this conclusion based on both subjective and objective performance assessments.

Figure 5:

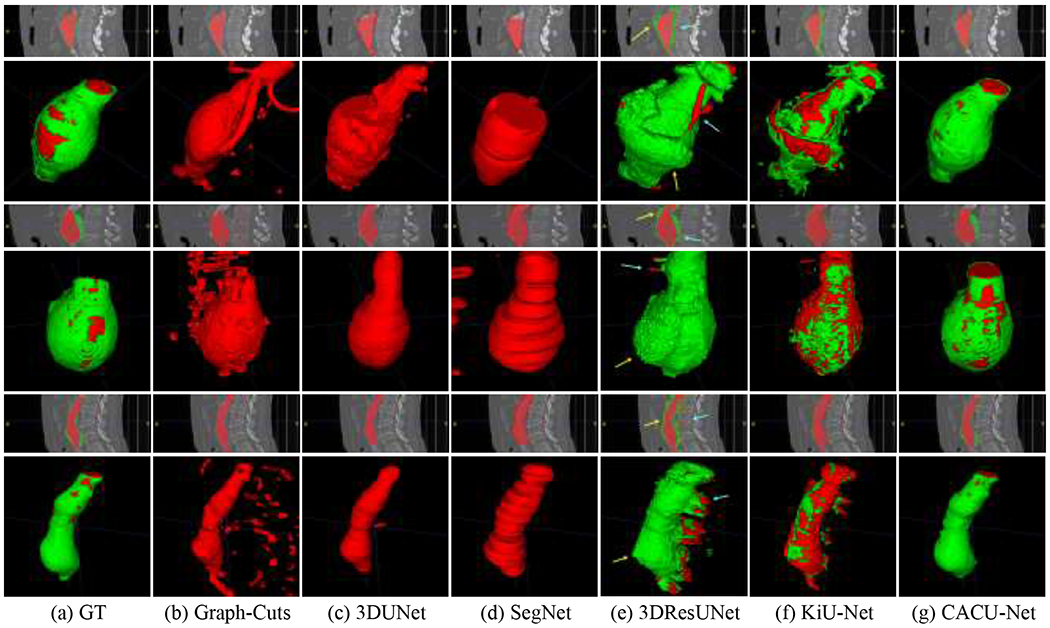
Representative visualization of multi-class segmentation results for CACU-Net and 5 other benchmark models: (a) Ground truth (manual annotation). (b-g) Different segmentation models. Coronal and 3D views are provided. Arrows in (e) point to some regions of interest where errors occur.

5.2. Ablation Experiments

To verify the effectiveness of different components of the proposed CACU-Net, we extended our experiments to evaluate the performance of six ablations, including: (1) the first-stage residual 3D U-Net framework without anisotropy context module and hierarchical supervision strategy (i.e., ResU); (2) the base auto-context 3D U-Net framework (i.e., AutoU); (3) adding anisotropy context module to ablation 2 (i.e., AutoU+C); (4) adding hierarchical supervision strategy to ablation 2 (i.e., AutoU+H); (5) adding anisotropy context module and hierarchical supervision strategy to ablation 2 (i.e., AutoU+C+H); (6) complete structure with post-processing, i.e., overlapping patches and maximum 3D connected components (i.e., AutoU+C+H+P).

We chose one fold of five-fold cross-validation tests for testing (10 cases) and the remaining four folds for training (40 cases). The objective performance comparisons of the six ablations are provided in Table 3. The results show that all other ablations outperform ResU ablation; e.g., its lumen and ILT DICE scores are only 0.814 and 0.609, respectively. The performance of AutoU was superior to ResU in all six metrics, indicating that configuring the network as an auto-context structure would significantly improve the network’s performance. For AutoU+C, AutoU+H, and AutoU+C+H ablations, the performance of each metric increased when the anisotropy context module or/and hierarchical supervision strategy was/were integrated into AutoU. The results indicate that both the proposed anisotropy context module and hierarchical supervision strategy played critical roles in the final lumen and thrombosis segmentation. The ablation results with and without post-processing show that overlapping patches and 3D connected components optimization boost the performance of the test.

Table 3:

Objective performance comparisons of the proposed CACU-Net and its ablations.

Classes	Ablations	DICE↑	RVE↓	Sensitivity↑	Specificity↑	HD95(mm)↓	ASSD(mm)↓
Lumen	ResU	0.814±0.054	0.420±0.176	0.973±0.008	0.998±0.000	38.562±7.652	7.128±1.883
	AutoU	0.864±0.032	0.273±0.079	0.980±0.011	0.999±0.000	33.562±7.800	4.379±1.350
	AutoU+C	0.885±0.032	0.205±0.091	0.971±0.026	0.999±0.000	26.079±7.730	3.542±1.252
	AutoU+H	0.872±0.031	0.234±0.100	0.971±0.026	0.999±0.000	29.706±7.595	3.936±1.198
	AutoU+C+H	0.907±0.019	0.167±0.051	0.979±0.021	0.999±0.000	18.646±6.842	2.339±0.684
	AutoU+C+H+P	0.941±0.015	0.078±0.024	0.974±0.018	1.000±0.000	11.011±5.388	1.372±0.493
ILT	ResU	0.609±0.076	0.681±0.263	0.784±0.040	0.998±0.001	29.908±8.961	6.207±1.820
	AutoU	0.756±0.063	0.242±0.113	0.841±0.052	0.999±0.001	28.358±7.654	3.892±1.426
	AutoU+C	0.778±0.063	0.221±0.114	0.850±0.052	0.999±0.000	20.582±7.381	2.893±1.095
	AutoU+H	0.761±0.070	0.213±0.136	0.821±0.061	0.999±0.000	23.202±6.957	3.121±1.133
	AutoU+C+H	0.792±0.044	0.086±0.031	0.775±0.048	0.999±0.000	11.094±5.333	1.776±0.632
	AutoU+C+H+P	0.815±0.039	0.169±0.075	0.877±0.049	0.999±0.000	9.078±4.024	1.450±0.461

Representative visualizations of our ablative experiments are shown in Figure 6. Comparing Figure 6(c) with Figure 6(b), we found that results from the second-stage auto-context network were dramatically improved from that of the first-stage prediction. The first stage prediction over-segmented the lumen and ILT (see Figure 6(b)). This is a showcase example of the advantages of using residual 3D U-Net in an auto-context fashion. By employing the anisotropy context module (see Figure 6(e)) and hierarchical supervision strategy (see Figure 6(f)), details of the segmented lumen and ILT were further enhanced. Overall, the anisotropy context module can guide the segmentation network to learn both short-range and long-range contexts to distinguish ILT from neighboring tissues; a hierarchical supervision strategy that simultaneously considers predictions at different resolutions has the ability to focus on the details of the segmentation structure. In addition, it can be seen from the final results (see Figure 6(g)) that, to some extent, the overlapping of sliding windows during testing also improves the segmentation results.

Figure 6:

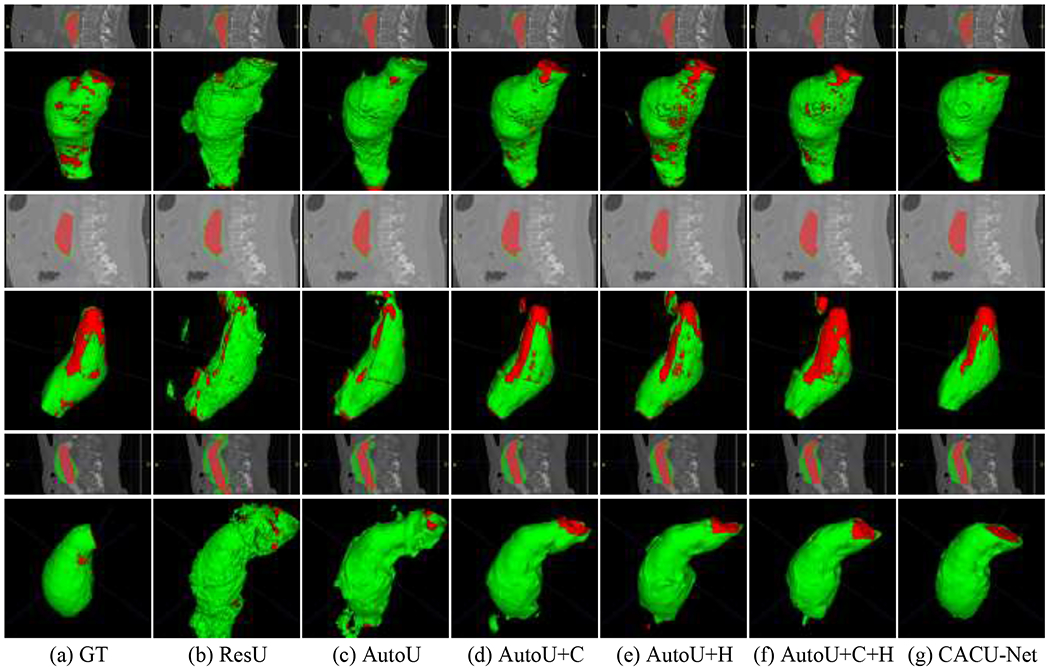
Visualization of segmentation results for different variants of the proposed model. (a) Ground truth. (b-g) CACU-Net and different combinations used during the ablative experiment.

5.3. Morphological Analysis

We selected seven widely used morphological metrics, i.e., length, surface, volume, max-radius, mean-radius, undulation index, and tortuosity, to further assess whether CACU-Net results can be used for machine learning-based predictions, as reported by others [11–15]. As shown in Table 4, morphological parameters derived from CACU-Net results were compared with those from manual segmentation in terms of Pearson correlation coefficient (PCC), linear regression (LR), and Bland-Altman (B-A) plot.

Table 4:

Statistical analysis of the proposed CACU-Net model in terms of morphological metrices.

Classes	Statistical Criteria		Length (mm)	Surface Area (mm2)	Volume (mm3)	Max-Radius (mm)	Mean-Radius (mm)	UI	Tortuosity
Lumen	PCC*		0.975	0.992	0.994	0.991	0.961	0.967	0.863
	LR	Slope*	1.003	1.035	1.043	1.000	0.961	0.951	0.684
		Y-intercept	1.617	60.395	−25.943	0.152	0.672	0.022	0.390
	B-A	Bias	1.942	416.402	3306.644	0.159	0.923	0.013	0.011
		Lower-Limit	−9.07	−505.015	−6329.38	−0.81	−1.369	−0.039	−0.073
		Upper-Limit	12.953	1337.818	12942.668	1.128	1.643	0.065	0.095
Lumen+ ILT (AAA)	PCC*		0.976	0.966	0.981	0.904	0.851	0.618	0.610
	LR	Slope*	1.006	1.033	0.946	0.910	0.744	0.514	0.398
		Y-intercept	−1.414	359.306	12277.584	1.911	4.701	0.074	0.759
	B-A	Bias	−0.776	836.597	4503.800	−0.271	−0.071	0.013	−0.001
		Lower-Limit	−12.136	−1596.315	−20634.295	−3.419	−3.315	−0.125	−0.196
		Upper-Limit	10.585	3269.510	29641.895	2.877	3.174	0.151	0.195

^*The star indicates that the closer the value in the row is to 1, the more similar it is to GT.

Pearson Correlation Coefficients -- PCC, Linear Regression -- LR; Bland-Altman (B-A) plots are calculated as prediction minus GT; Undulation Index -- UI.

In all cases, significant correlations between our segmentations and GTs were found. Regarding lumen prediction, all the PCC values are higher than 0.85 (six of them above 0.96; Table 4), and six of the slopes in LR analysis were around 1 with a discrepancy less than 0.05, demonstrating the strong linear correlation. The positive biases of B-A plots indicated that the predicted results slightly overestimated the AAA geometries; however, the overestimation was only around 3-6% on a relative scale. After combining lumen geometries with thrombosis, the PCC results of most metrics (except length) decreased, among which the UI and Tortuosity decreased by 0.349 and 0.253, respectively, and the remaining four metrics decreased by no more than 0.1. In general, the PCC values of the five metrics were still greater than 0.85. The LR slopes of UI and Tortuosity had distinctly dropped, but there were still four indicators whose slopes were around 1 with a gap less than 0.1. Again, slightly positive and negative biases were found through the B-A plots, and their relative scales were small (<6%).

6. Discussions

We used contrast-enhanced CTA; thus, sufficient imaging contrast allowed us to delineate lumens, and the proposed CACU-Net’s performance was excellent (see Table 1). However, locating the ILT around the outer boundary of the lumen without leaking into the adjacent tissues is very challenging. Technically, segmenting ILT is equivalent to the interference of the lumen’s neighboring tissues with highly similar image intensity.

In response, we investigated a two-stage context-aware-based approach to simultaneously segment lumen and thrombosis in CTA images. Three key strategies enabled us to achieve good outcomes for ILT segmentation. First, compared with the traditional 3D residual U-Net (see Figure 5(e)), our improved residual U-Net model is equipped with dilated convolutions and a rebalancing multi-class loss. As a result, our design effectively reduces the interference of the background to thrombosis segmentation, thus mitigating the negative impacts of class imbalance (shown in Figure 5(e) vs. Figure 6(b)). Second, our crucial contribution and innovation are to incorporate rich contextual features in an auto-context manner. Iteratively, our context-aware network structure considers the surrounding information of each voxel to enhance the reliability and rationality of multi-class segmentation. Compared with the prediction results of the first-stage network, the two-stage cascaded network based on the auto-context algorithm was more conducive to distinguishing lumen and ILT classes (Figure 6(b) vs. Figure 6(c)). This observation suggested that contextual features were more discriminative for multi-class segmentation. Also, notably, comparing ResU to AutoU, the DICE scores of lumen and thrombosis predictions increased from 0.814 and 0.609 to 0.864 and 0.756, respectively, as shown in Table 3. Third, we introduced an anisotropic context module, which used a mixture of spatial pooling and strip pooling operations to gain insight into short-range and long-range dependency information. Such exploration was critical for determining whether the voxels belonged to the same or different classes. It can be seen from Table 3 that, compared with AutoU without the anisotropic context module, AutoU+C improved the DICE scores of lumen and thrombosis by 0.021 and 0.022, respectively. Furthermore, after configuring hierarchical supervision (AutoU+C+H) to extend the effect of short-long-range context to multi-layer predictions, the DICE scores of lumen and ILT were improved to 0.907 and 0.792, respectively. Collectively, our experiments verified that (1) the contextual information (including auto-context and anisotropic context) was an important complement to optimizing the AAA results, and (2) the hierarchical supervision of rebalancing multi-class loss further amplified the extraction of contextual information.

To our knowledge, this is the first deep-learning network for automatic multi-class segmentation of AAAs in the medical image domain, predicting lumen and ILT simultaneously. Our proposed CACU-Net outperforms traditional and recent deep learning models on this task, and, as expected, the results of these models deteriorate significantly when performing multi-class segmentation. As seen in Table 1, the DICE values of our model for lumen and thrombosis segmentation are 0.945 and 0.804, respectively, which are significantly higher (p-value < 0.01) than the second-ranked 3DResUNet model (only 0.742 and 0.481, respectively). In addition, most of the benchmark models (Graph-Cuts, 3DUNet, and SegNet) failed to predict ILT completely. We stipulate that those three methods cannot deal with (1) unbalanced classes (i.e., normally, an ILT accounts for only 10% or less of the entire AAA) and (2) subtle image contrast between the ILT and its neighboring tissues.

Now, referring to the lumen segmentation result, the traditional method Graph-Cuts performed the worst compared with other 3D networks. The graph-based approach failed because strong responses from adjacent anatomical objects (e.g., spines and calcifications) distracted the model from finding the proper lumen boundaries. Simple 3DUNet and SegNet achieved the worst and second worst performance, respectively, among all 3D networks, and thus, their encoder-decoder structure was insufficient to represent the AAA information. In contrast, the 3DResUNet model with added residual structure and the KiU-Net model with parallel multi-network structure were able to segment both lumen and ILT. However, their results were poor. As shown in Figure 5(e–f), 3DResUNet and KiU-Net have a large number of over-segmented or under-segmented regions for thrombosis. In fact, due to the small size of ILT, high individual variability in shape and location, and blurred boundaries with surrounding tissue, these state-of-the-art networks largely failed to depict ILT regions from CTA data. In contrast, our two-stage context-aware cascade scheme obtained considerably better results and outperformed these state-of-the-art benchmark models.

Regarding the effect of sample size on training performance, we compared the performance of the different deep learning models in Table 1 and Table 2, where the training samples are 40 and 60 cases, respectively. Interestingly, the performance of the four comparison models was slightly improved after increasing the training data. This observation is not surprising and indicates that the parameter optimization of these supervised models is highly dataset-dependent. In contrast, the results of our model are relatively stable. Conceptually, the auto-context manner of our CACU-Net facilitates the gradual correction of errors in model predictions during training, which is crucial given the very small number of training samples. Additionally, our anisotropic context module provides more contextual information for high-level features; thus, our model can learn the discriminative features needed to segment large or small regions from small 3D patches. These all ensure that our model can converge better in training with limited data.

The morphological analysis also confirmed the superior performance offered by the proposed CACU-Net. Table 4 shows that the PCCs of Surface Area, Volume, and Max-Radius between our predicted lumen and GT were higher than 0.99. Although the performance of ILT segmentation results was degraded, the PCCs of Length, Surface Area, and volume were still greater than 0.96. This observation demonstrated that our CACU-Net could accurately delineate the gross regions of the lumen and ILT.

When UI and Tortuosity were used for comparisons, consistency between the GT and CACU-Net results decreased, particularly for geometries including both lumen and ILT. Recall that UI utilizes the volume of the convex hull. Thus, the inclusion of less accurate and highly irregular ILT surfaces resulted in (relatively) large changes in the convex hull size. Table 4 shows that tortuosity was a sensitive metric and was low when the lumen segmentation was evaluated. Thus, its reductions in PCC and slope values were not unexpected.

Lastly, the importance of the proposed segmentation model and its potential impacts are summarized as follows. First, we developed a fully automated methodology to segment the lumen and ILT of AAA simultaneously. The availability of such a tool allows us to reconstruct accurate AAA geometries (both the lumen and ILT) using standard CTA imaging data in the clinical workflow. This new capability may promote interest in more advanced morphological analyses of AAAs beyond their diameter. Morphological parameters are relevant for the diagnosis and endovascular treatment planning of AAAs. Certainly, a computerized morphological analysis tool is expected to reduce inter- and intra-operator variabilities. Second, our pipeline brought novel insights to multi-class image segmentation tasks with severely imbalanced classes and low discrimination between objects and their surrounding tissues.

Auto-context algorithms’ shape/context information is often implicitly used and has certain limitations for discriminative learning. Thus, the proposed CACU-Net inherited those limitations from general auto-context algorithms. We found additional limitations of the proposed CAVU-Net: (1) the context information of the features in the encoding layer is still limited; (2) our predicted ILTs had relatively large errors in diameter and volume when an AAA had thin ILT regions; and (3) the model was fully supervised, relying on a set of well-annotated ground-truth data. To further improve, in our future work we will (1) consider a Transformer-based self-supervised mechanism to build encoders for modeling long-range dependencies and (2) explore weakly-supervised or semi-supervised learning to reduce the burden of annotating ground truth.

7. Conclusion

In this study we developed a two-stage context-aware cascaded U-Net, i.e., CACU-Net, to perform accurate lumen and thrombosis segmentation from CTA images. The core contribution of this work is to incorporate contextual information into deep networks for multi-class predictions. Experimental results show that both the auto-context architecture and anisotropic context module significantly improved the segmentation accuracy. Our 5-fold cross-validations using standard CTA data acquired from clinical workflow demonstrated the feasibility of using the proposed CACU-Net for human investigations.

Given the promising results, work is ongoing to improve CACU-Net in terms of its ability for morphological analysis. Our ultimate goal is to translate such a deep-learning neural network model into the clinical workflow, aiding cardiologists, surgeons, and radiologists in making clinical decisions.