High-Throughput Linear Optical Stretcher for Mechanical Characterization of Blood Cells

Abstract

This study describes a linear optical stretcher as a high-throughput mechanical property cytometer. Custom, inexpensive, and scalable optics image a linear diode bar source into a microfluidic channel, where cells are hydrodynamically focused into the optical stretcher. Upon entering the stretching region, antipodal optical forces generated by the refraction of tightly focused laser light at the cell membrane deform each cell in flow. Each cell relaxes as it flows out of the trap and is compared to the stretched state to determine deformation. The deformation response of untreated red blood cells and neutrophils were compared to chemically treated cells. Statistically significant differences were observed between normal, diamide-treated, and glutaraldehyde-treated red blood cells, as well as between normal and cytochalasin D-treated neutrophils. Based on the behavior of the pure, untreated populations of red cells and neutrophils, a mixed population of these cells was tested and the discrete populations were identified by deformability.

Introduction

CELL mechanical properties are a label-free biomarker indicative of cell health (1–3); for example, in cases such as malaria (1–4), sickle cell anemia (5), and sepsis (6), cells stiffen with onset of disease. Also, in breast (7,8) and oral (9) cancers, changes in deformability are sufficient to differentiate between cells of varying metastatic potential. Cell mechanics may also be used to assess drug efficacy (1) because various anti-cancer drugs including cytochalasins, vinca alkaloids, and taxanes disrupt the cytoskeleton, inhibiting proliferation by disrupting the cell cycle (10–12) and altering cell mechanics (13,14). In the context of personalized medicine, the effectiveness of chemotherapeutic agents could be evaluated based on their ability to alter cancer cell mechanics on a per-patient basis (12). However, significant differences exist not only with separate patients but, due to the heterogeneity of tumor tissue and cell response, with individual cells as well. Motivated by this, single cell mechanical properties have been measured by micropipette aspiration (15,16), atomic force microscopy (8,17), and optical tweezing (18,19). These methods, however, employ static testing conditions with low measurement throughput and restricted sample sizes of ~100 cells (20). Because of the inherent heterogeneity of biological samples (21), populations on the order of 10³–10⁴, similar to those generated by techniques such as fluorescence-activated cell sorting (FACS) (22,23), are required to make confident diagnoses based on deformability as a clinical biomarker.

Deforming cells in flow similar to traditional cytometry techniques could increase throughput. One approach is the microfluidic cell deformability cytometer which are inexpensive to prototype, use small sample volumes (nanoliters), and employ laminar flow characteristics (24) allowing for predictable and controllable flow. For example, physical constrictions (25–28) or inertial focusing flow (29–31) have been used to create contact or shear forces (> 1 nN (30)) capable of significantly deforming flowing cells. Large strains (>10% deformation) however, can damage cells and should be avoided when cell isolation and viability post-analysis are of interest. Lower strain (<10% deformation) methods including optical stretchers (7,32) can apply non-destructive, non-contact forces sufficient to differentiate cell states (9,33,34). Optical stretching relies on the changing momentum of laser light by refraction at the surface of a soft dielectric object, generating non-contact optical forces (35). In specific laser configurations (36,37) and when operated at powers that minimize heating from optical absorption (38,39), these forces can deform trapped cells. In the case of a linear optical trap, antipodal stretching forces generated parallel to the trap long axis act to elongate the cell (37), while the relative deforming influence of the hydrodynamic forces remains low (40). By applying optical forces independent of flow forces cell viscoelastic behavior has been accurately quantified via a mechanical model (41). Such techniques can maintain flow velocities capable of deforming 10³–10⁴ cells in 10–20 min while employing geometries very similar to current light-scattering and fluorescence-based imaging cytometers. Because of this and the small perturbations associated with linear optical stretching, direct incorporation of mechanical properties as an additional biomarker within imaging flow cytometers utilizing light and fluorescence-based detection is quite feasible.

Here, we use linear optical stretchers described previously (41,42) to stretch cells continuously in flow. To avoid changes in laser intensity and beam profile due to the linear emitter geometry (43–45), custom optics (37) were used to focus the stretcher at the optimal numerical aperture (NA) with efficient 1:1 imaging of the source (46). In this system, imaging optics are decoupled from the stretching optics.

To test the potential of this system as a high-throughput deformation cytometer, we measured the deformation of normal and chemically treated cells. First, normal human red blood cells (RBCs) were compared to those treated with diamide and glutaraldehyde and the results showed statistically significant increases in stiffness in subsequent populations. As a model for leukemic cells, we isolated and measured the response of normal neutrophils and those treated with cytochalasin D, an actin-disrupting drug. In this, we observed a statistically significant increase in aspect ratio in the treated cell population. Finally, two distinct populations of cells were observed in a mixture of untreated RBCs and neutrophils and differentiated based on aspect ratio.

Materials and Methods

Optical Assembly

Figure 1 shows the optical assembly that was previously described in Ref. 46. A 0.54 NA aspheric lens (A230-C, Thor-Labs, Newton, NJ) first collimates the output from a 1064 nm, 8 W, 1 × 100 μm² linear diode bar laser (Lumics GmbH, Germany). The linear geometry of the source results in the collimated output extending along the long axis of the bar. A pair of cylindrical lenses (LJ1567RM, ThorLabs, Newton, NJ) forms a telescope to correct for this extension. A second aspheric lens then refocuses the laser after reflection by a dielectric mirror (BB1-E03, ThorLabs, Newton, NJ), forming a 1:1 image of the source through the polydimethylsiloxane (PDMS) layer of a microfluidic device. The near-infrared wavelength of the laser minimizes absorption by biological samples, preventing optical damage (38,39). The laser imaging optics described in Figure 1 are used to create the linear stretcher, shown as a green line in the schematic and images in Figure 2. Sample imaging is achieved through an independent optical train. Light from a 200 W source (Prior Scientific Inc., Rockland, MA) passes through an aperture, condensing lens, dichroic mirror, and aspheric lens to illuminate the sample plane. A ×40 microscope objective (Zeiss LD Achroplan 40×/0,60, Jena, Germany) forms an image (0.1395 μm/pixel) on a Phantom v341 high-speed camera (Vision Research, Wayne, NJ) after a shortpass filter (FES0900 ThorLabs, Newton, NJ) and focusing lens.

Figure 1.

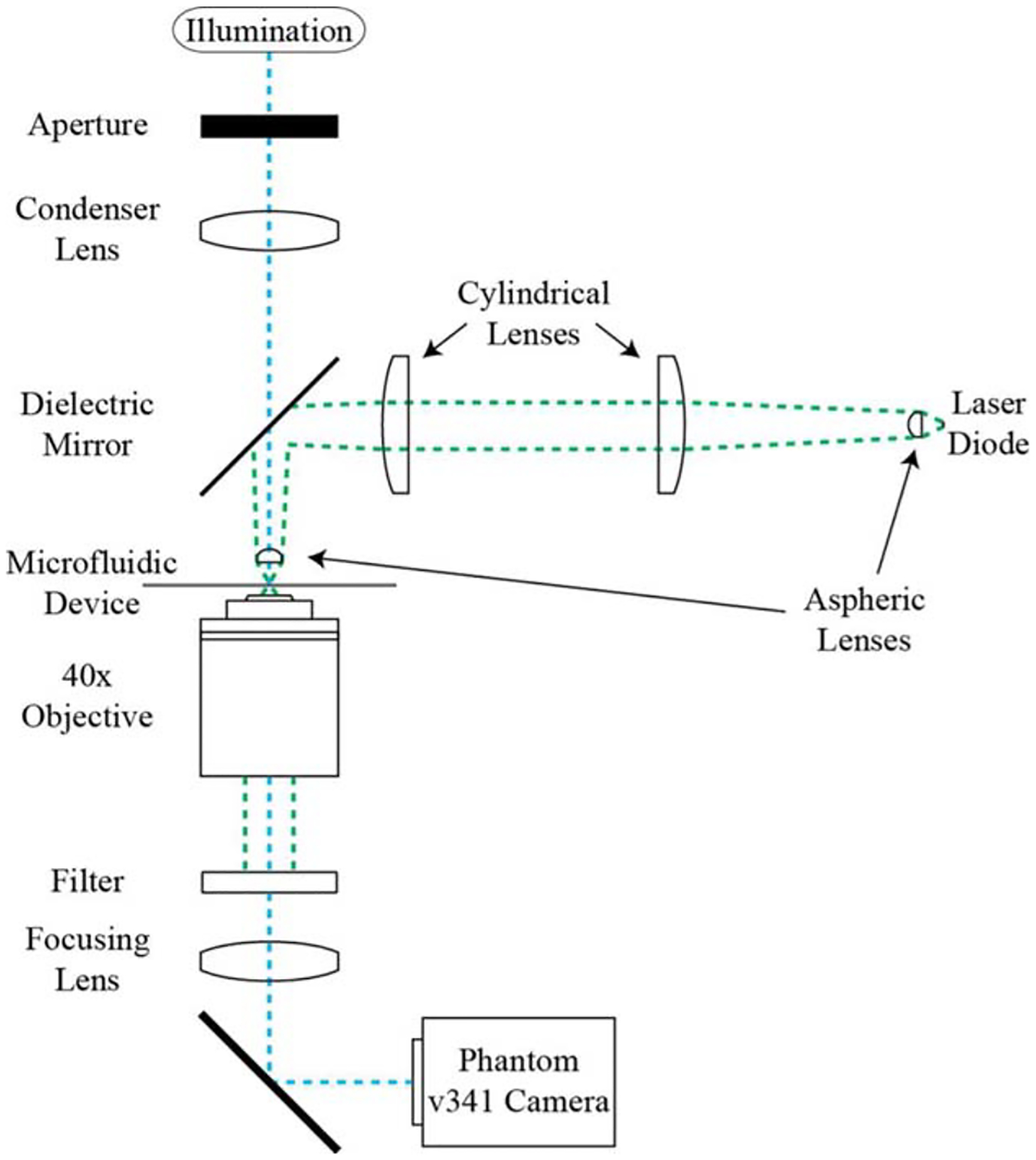
Linear stretcher optical assembly. A 1:1 image of the laser diode source is formed at the focal plane of a 40× objective. An aspheric lens collimates the laser output, a cylindrical lens telescope corrects for the source geometry, and an identical aspheric lens refocuses the laser. The sample is illuminated from above and an image is formed below on the camera.

Figure 2.

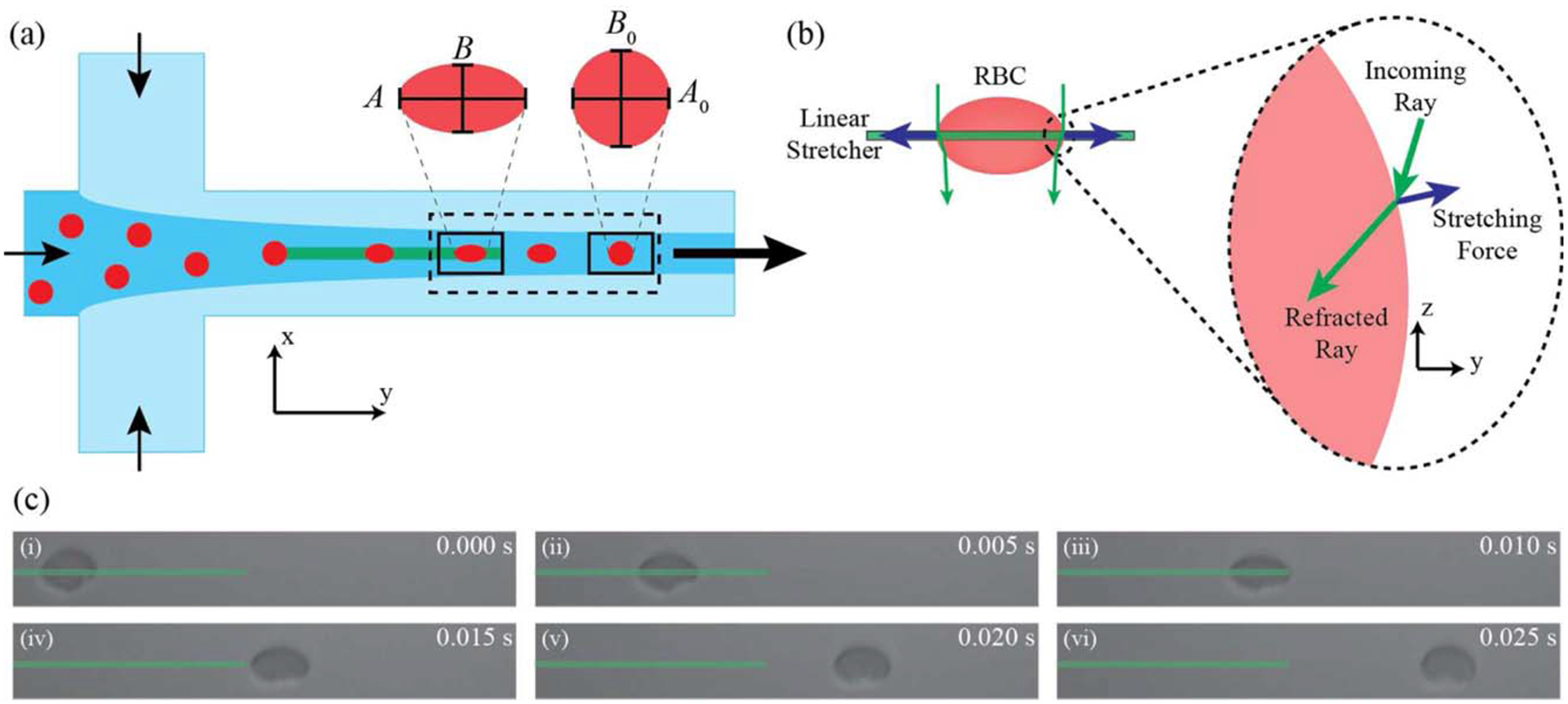
(a) Hydrodynamic focusing device design: Cells enter the focusing region and are guided toward the optical stretcher. Cells are then observed in the rectangular region of interest (125 μm × 15 μm) from stretched to a relaxed state in flow. The solid boxes illustrate the regions of cell stretch and relaxation used to calculate deformation parameters corresponding to the panels of a RBC stretching in flow. (b) Optical stretching forces: As an incoming ray of light is refracted at the cell surface, the resulting change in momentum imparts a force on the cell membrane. The resulting net optical force acts to stretch the cell along the line of the trap (37). (c) A typical RBC stretch and relaxation cycle. The green bar shows the position of the linear optical stretcher.

Cell Preparation

Blood was obtained according to the Declaration of Helsinki and under either Colorado Multiple Institutional Review Board or the University of Colorado, Boulder Institutional Review Board approved protocols for RBC or neutrophil experiments, respectively. Blood used in the RBC experiments was acquired via finger-poke with a contact-activated safety lancet (BD, Franklin Lakes, NJ). Twenty microliters of blood was then collected via micropipette and suspended in 150 mOsm phosphate buffered saline (PBS) solution with 0.1% wt/vol bovine serum albumin (BSA, Sigma, St. Louis, MO) to prevent non-specific cell interactions and 1.0% wt/vol sodium citrate (Sigma) as anticoagulant. RBCs were swollen to make image processing more uniform. Untreated RBC experiments were performed without the addition of any additional chemicals to the blood suspension. Chemically treated RBCs were suspended in either 3.8 mM diamide (Sigma) or 0.05% vol/vol glutaraldehyde (Sigma) solutions. Regardless of treatment, cells were incubated at room temperature (~25°C) for 20 min before three washes in PBS buffer at 300g for 5 min. Cells were suspended in 500 μL of PBS buffer (~2 × 10⁵ cells/μL) for cytometry experiments.

Neutrophils were isolated using a previously described isolation protocol with minor changes (47). Whole blood was collected by standard phlebotomy techniques via venipuncture in 3.2% sodium citrate vacutainers (4.5 mL, BD, Franklin Lakes, NJ). First, the blood was carefully layered over 3 mL of lympholyte poly separation media (Cedarlane Labs, Burlington, Ontario, Canada) and centrifuged at 500g for 50 min at 25°C. Second, the neutrophil layer was then removed, diluted to 10 mL with Hank’s balanced salt solution without calcium chloride (HBSS, Invitrogen, Grand Island, NY), and spun down at 200g for 5 min. Finally, the supernatant was removed and the pellet resuspended in HBSS with 2.4% human serum albumin (HSA, Sigma). For neutrophils receiving drug treatment, cytochalasin D (Sigma) suspended in DMSO was added to a final concentration of 10 μM and incubated for 10 min at 37°C. For the mixed cell experiment, in addition to the neutrophil isolation, 4 μL of whole blood was washed in HBSS and centrifuged at 200g for 5 min. The unswollen RBCs were then re-suspended in HBSS/HSA buffer before being added to the isolated neutrophils.

Microfluidic Device Preparation

Microfluidic devices were fabricated in PDMS (Slygard 184, Dow Corning, Midland, MI) using standard soft lithography techniques (48,49). The resulting devices, with channel cross-sectional area of 20 μm × 200 μm and an overall length of 2.5 cm, were ~1.1 mm thick. This thickness of PDMS allows the aspheric lens to focus the optical stretcher through the PDMS layer into the flow channel (46). To prevent leaking in such thin devices, an additional block of PDMS (0.5 cm × 0.5 cm × 1.5 mm) was bonded over the inlet and exit wells to act as a connector between tubing and the device. Channels were incubated with PBS buffer for RBC experiments or HBSS buffer for neutrophil experiments for 1 h. Cells were then flowed through the device at a free-stream cell velocity of ~2000 μm/s, achieved by varying the hydrostatic head 5 ± 2 cm. Initially, free-stream velocity was measured in the absence of optical forces by manually tracking cell position in flow. We define an applied optical intensity in units of mW/μm as the power of the laser is distributed along the length of the 1 μm × 100 μm source. With this, optical intensity was 26.3 mW/μm for the RBC experiments and 40.9 mW/μm for neutrophil and mixed-cell experiments. Exposure for each cell type and condition can be determined by multiplying the optical intensity by the cell cross-section within the trap. With cells spending ~0.01 s in the trap while flowing, they experience a total energy exposure of ~2.0 mJ; low enough to prevent cell damage (50,51).

Image Processing

All videos were captured using the Phantom Camera Control software (Vision Research) at 1,000 fps. Dynamic cell relaxation was processed using a custom C program with functions from the OpenCV computer vision library (52). Briefly, in each frame imaging noise was first removed by cvSmooth before applying an adaptive threshold with cvAdaptiveThreshold. Cell contours were then detected with cvFind-Contours and fit to ellipses using cvFitEllipse2. The ellipse fit chooses the major and minor axes diameters and centroid position. Using size and position information, cell trajectories were tracked and used to store raw data for individual cells. The image analysis and data processing codes are available on GitHub (https://github.com/marrgroup/imageanalysiscode).

Cell data across the region of interest (125 μm × 15 μm), illustrated in Figure 2a as a dotted rectangle, were separated further into two regions (solid boxes in Fig. 2a): maximum cell deformation at the end of the optical stretcher and cell relaxation 30 μm downstream of the stretcher. The time available and the hydrodynamic forces in the system limit any cell rotation in this distance after the optical stretcher. The average cell size parameters in these boxed regions were used to calculate deformation parameters including percent deformation of the major axis, (A – A0)/A₀, percent deformation of the minor axis, (B – B₀)/B₀, stretched aspect ratio, D = (A/B), and relaxed aspect ratio, D₀ = (A₀/B₀), where A and B represent the stretched major and minor cell diameters, and A₀ and B₀ represent the relaxed cell diameters. Scatter plots for data visualization were generated with a custom Matlab function, dscatter, available on the Mathworks File Exchange (File ID: #8430).

Flow Cytometry

To measure the relative concentration of cells in our mixed population, we performed cytometry analysis with a Guava easyCyte Single Sample Flow Cytometer (EMD Millipore, Billerica, MA). Isolated neutrophils were stained in a 5 μM solution of DiOC6 (Sigma) for identification. RBCs were then mixed with the neutrophils as described above for the mixed cell samples and run in the cytometer. Gating was determined based on fluorescence and confirmed with pure neutrophils.

Statistical Analysis

Statistical significance between groups was determined by two-sample t-tests in Matlab. A P value of less than 0.01 was considered significant. Data was plotted on a log–log scale to more readily differentiate between small differences in population deformation.

Results and Discussion

Microfluidic devices were designed to create a hydrodynamic focusing flow profile (53) (Fig. 2a). Cells in suspension were guided to the linear optical stretcher by focusing the center inlet with two buffer streams. The stretcher has a steep intensity gradient along the short beam axis allowing cells to be tightly held in that direction. The long beam axis lacks the same steep gradient, allowing cells to freely travel along the stretcher long axis as they are driven down the channel by flow. Upon entering the stretcher, cells experience an optical force at the membrane surface from a change in momentum of refracted laser light (Fig. 2b). The magnitude of the resulting force is strongly dependent on the angle of the incoming light, described by the focusing NA. For a linear optical trap where the width is shorter but the length is longer than a cell diameter, we have previously demonstrated that an NA of ~0.5 will generate the maximum stretching force (37). The anisotropic intensity distribution creates antipodal stretching forces and cell elongation along the long beam axis (Fig. 2b) (37). Here, the beam is aligned with flow, allowing cells to stretch (Fig. 2c) as they translate along the long axis of the stretcher. After cells exit the stretcher they relax back to their pre-stretched state. To quantify this, the camera is positioned to observe both the point of maximum deformation at the end of the stretcher and the cell relaxation down the channel, shown as a dotted region in Figure 2a. RBCs were fully relaxed 30 μm downstream of the end of the trap. However, the technique does not require full relaxation to determine differences because only relative differences are used to discriminate cell state or type.

Untreated, diamide-treated, and glutaraldehyde-treated RBCs were measured at throughputs averaging 15.0 ± 10.0 cells/s, with a range of 5–50 cells/s (Fig. 3) at an optical intensity of 26.3 mW/μm. Considering an average cell spacing of 20 μm to ensure accurate image processing, the theoretical maximum measurement throughput for a flow rate of 2,000 μm/s is ~100 cells/s. Rigid colloids were employed as a control for image processing as they do not deform under applied optical force and used to generate the solid line in the aspect ratio plots corresponding to zero deformation (Supporting Information Fig. 1a). We present our data in Figure 3 as stretched (D) vs. unstretched (D₀) aspect ratios where data further from the origin denote increasing cell asymmetry and data above the line greater cell deformability. Normal RBCs (Fig. 3a) deform 6.5 ± 6.0% with respect to the major axis (Fig. 3d). RBCs treated with diamide (Fig. 3b) deform an average of 3.9 ± 8.5% (Fig. 3d). Diamide causes disulfide bonds to form between membrane spectrin proteins resulting in a stiffening of the cell membrane (54–56). RBCs treated with glutaraldehyde (Fig. 3c) remained undeformed, on average, by the same optical force (Fig. 3d) due to the non-specific crosslinking of membrane proteins by glutaraldehyde (57–59). Note that despite the spread in cell morphology distribution (e.g. Fig. 3a), measured deformations are consistent as indicated by the data falling parallel to the line, an observation verified by plotting the major axis percent deformation directly (Supporting Information Figs. 1b and 1d).

Figure 3.

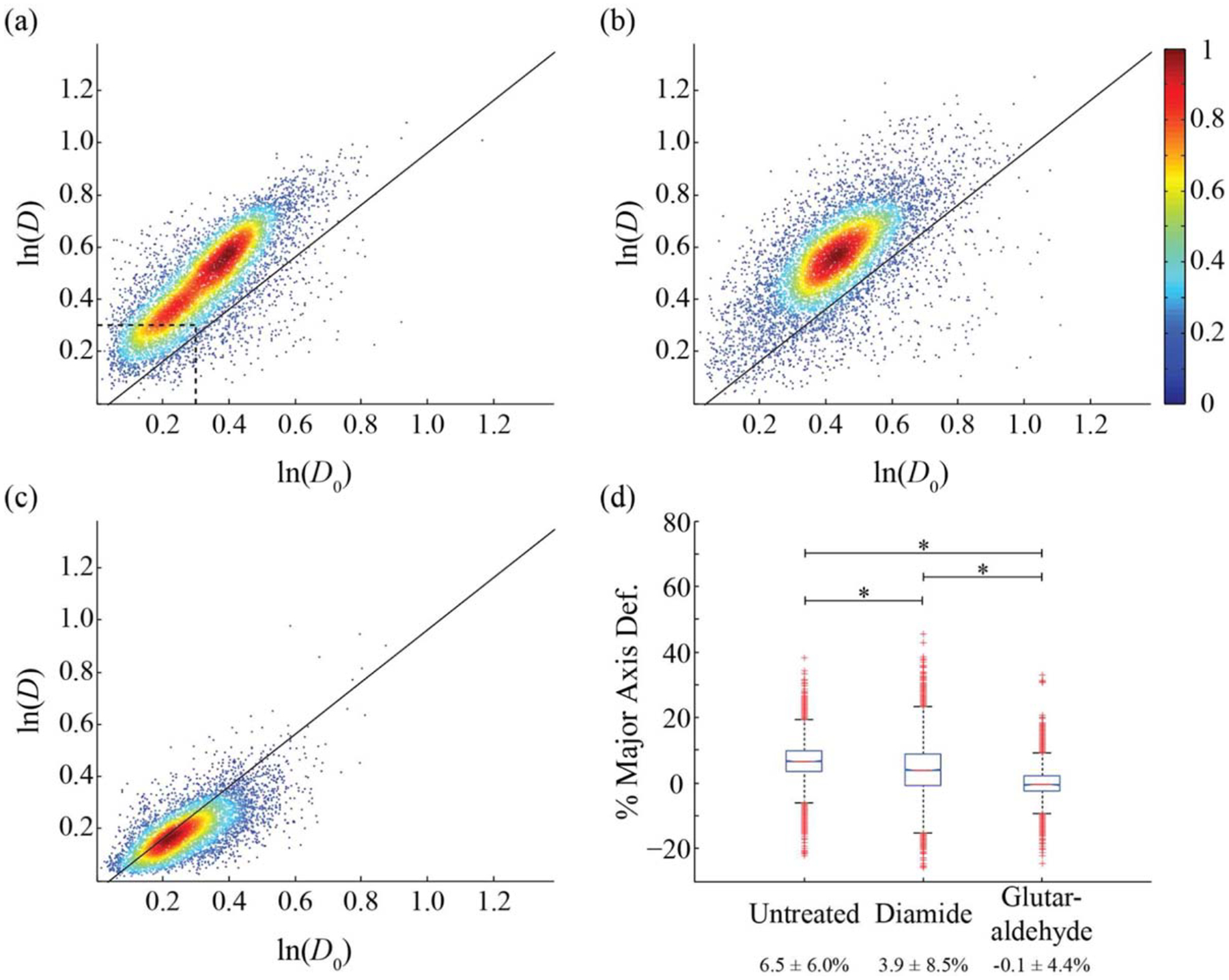
Cell aspect ratio for pure RBCs. D corresponds to the ratio of the cell’s major and minor axis diameters at the end of the optical stretcher, D₀ represents the same ratio 30 μm down the flow channel. (a) Untreated (n = 8,098), (b) treated with 3.8 mM diamide (n = 7,917), (c) treated with 0.05% vol/vol glutaraldehyde (n = 5,883). Solid lines correspond to measurements on rigid colloids. (d) Box plot of the average percent deformation of the major axis with average values and standard deviations from data in panels (a–c). (*) corresponds to a P values of 10⁻⁴ for a two-sample t test. The color bar shows a scale for the normalized population density. The dashed line in (a) identifies the location of the neutrophil population in Figure 4a.

Deformation of normal and cytochalasin D-treated neutrophils was measured at an average throughput of 3.0 cells/s, limited by the concentration of the isolated neutrophil suspension. Normal neutrophils (Fig. 4a) were measured to have an average of D = 1.15 ± 0.16 (Fig. 4c), with 86% of the population found in the region bounded by ln(D) and ln(D₀) < 0.3. Neutrophils treated with cytochalasin D experience cell softening (60,61) via disruption in cytoskeletal Factin (62,63). Such softening is observed in the upward shift of the cytochalasin D-treated neutrophils (Fig. 4b) to D = 1.21 ± 0.18 (Fig. 4c). Neutrophils have a reported cortical tension (26.8 μN/m (63)) three- to fourfold stiffer than the shear elastic modulus of RBCs (6–9 μN/m (64,65)) and thus require a larger optical power (40.9 mW/μm) to induce measurable deformation. Although the average percent deformation of the neutrophil major axis (~1%) is low at this increased optical intensity, it is sufficient to differentiate between behavior of normal and treated cells.

Figure 4.

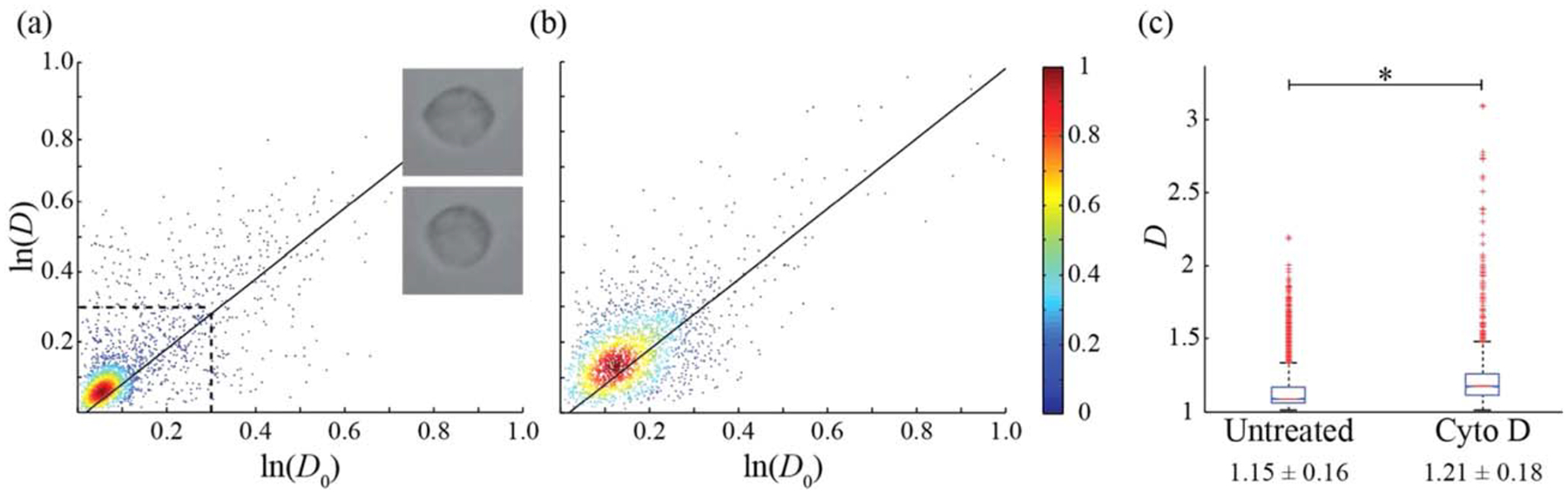
Cell aspect ratio for neutrophils. (a) Untreated (n = 2,389), (b) Cytochalasin D treated (n = 2,199). Solid lines correspond to measurements on rigid colloids. (c) Box plot of D with average values and standard deviations for data in panels (a) and (b). (*) corresponds to a P values of 10⁻⁴ for a two-sample t test. The dashed line in (a) corresponds to the region containing 86% of the total neutrophil population with images of a stretched (top) and relaxed neutrophil (bottom) provided for clarification.

RBC and neutrophils were mixed in a suspension at relative concentrations of 48.7% and 51.3%, respectively, as determined using a fluorescent marker for neutrophils in a flow cytometer (Fig. 5a), and stretched at an optical power of 40.9 mW/μm and measurement throughput of 3 cells/s. Two gating styles were applied to discriminate the two cell types by aspect ratio. Figure 5b shows a scatter plot of deformation data with gating criteria extracted from the untreated pure cell population plots. The neutrophils in the mixed population are found in the same location as the untreated neutrophils in Figure 4a bounded by ln(D) and ln(D₀) < 0.3. RBCs are found above this region in the area of ln(D) and ln(D₀) > 0.3 and above the rigid colloid line. In Figure 3a, 77% of the RBCs are found in this region. Although the RBCs in Figure 3 were deformed at a lower optical power (26.3 mW/μm) than in the mixed cell experiment (40.9 mW/μm), it is reasonable that the vast majority of the RBCs deformed at the higher power will fall in or above this same region. In the mixed cell experiment, 88.0% of the cells in the mixed population are positively identified in either of the two gating regions, of which 43% are identified as neutrophils (815) and 57% are identified as RBCs (1,080). We also gated samples based on cell size, using a cell diameter of 5.5 μm for discriminating RBC and neutrophils (Fig. 5b). The larger cells, corresponding to the neutrophils, comprised 46% of the cell population with the remaining 54% identified as the smaller RBCs; percentages consistent with identification based on deformability as well as measured by flow cytometry. The slight drop in measured neutrophils in the aspect ratio measurements is likely due to neutrophil adhesion at the device inlet leading to a decrease in concentration.

Figure 5.

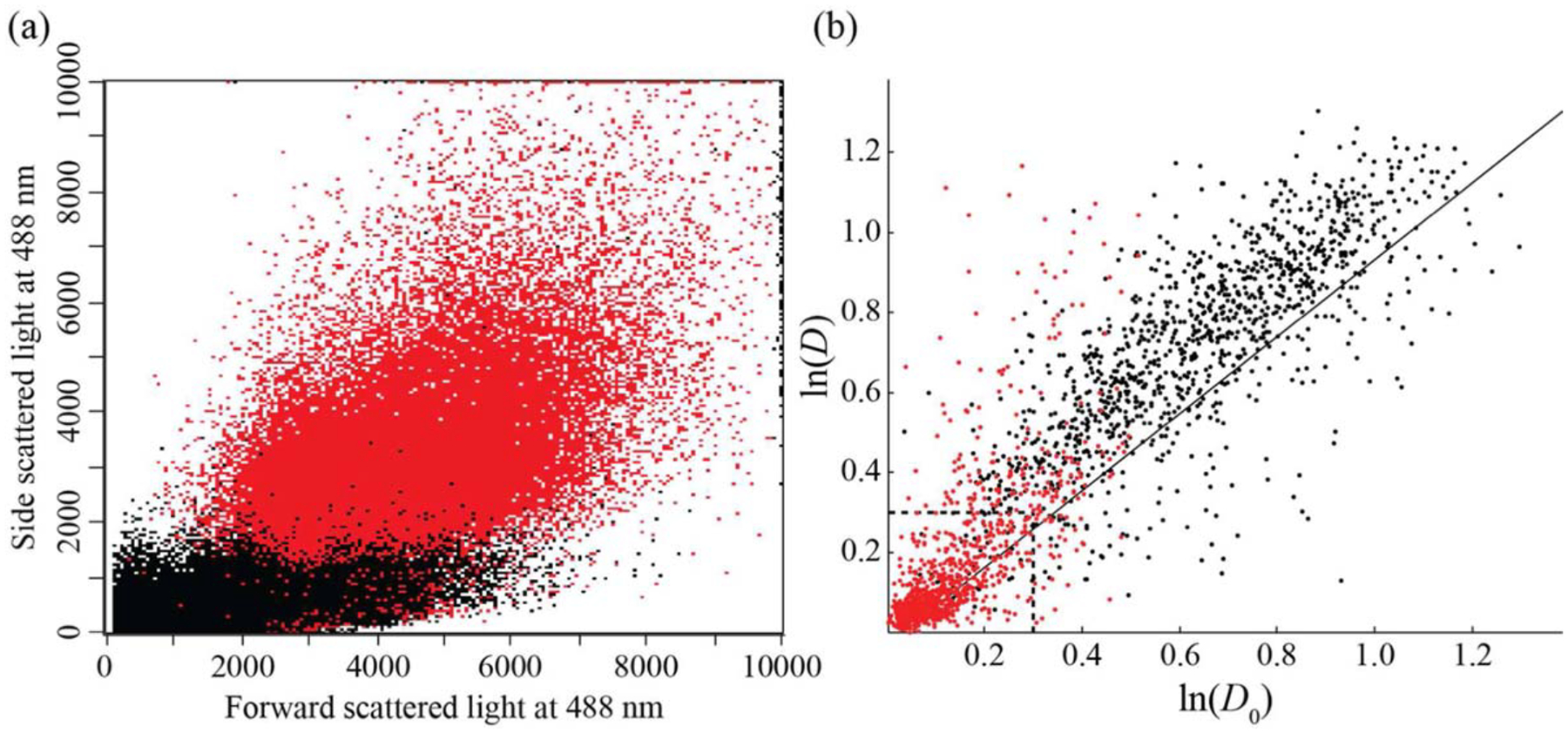
RBC and neutrophil mixed population. (a) Flow cytometry data of forward and side scatter for a mixed cell population (n = 113,981), with neutrophils shown in red and RBCs in black. Neutrophil gating was based on the fluorescence of a pure population of neutrophils. Neutrophils (red) comprise 51.3% of the population (mean fluorescence intensity of 1,146.09 with 88.10% CV), while RBCs (black) comprise the balance (mean fluorescence intensity of 3.41 with 302.14% CV). (b) Mixed cell population (n = 2,154) gated by size. The red population corresponds to minor axis diameters above 5.5 μm (n = 993), the black population corresponds to minor axis diameters below 5.5 μm (n = 1,161).

In this study, we used a linear optical stretcher to measure deformation response by applying a non-contact force on flowing blood cells. This approach is capable of distinguishing differences in cell populations, either by chemical treatments that affect the mechanical properties of the plasma membrane or cytoskeleton or in mixtures of RBC and neutrophils. The ability to apply optical forces decoupled from cell size is unique, as size is directly coupled to applied force via flow rate in other high-throughput methods (28,29). By separating deforming force from flow rate, one can fix hydrodynamic conditions while varying the applied force, allowing direct comparison between cell types of different stiffness and size at the same velocity. As the optical train is independent of the characterization optics (46), the optics could be potentially integrated with existing imaging cytometery platforms (66) utilizing existing image capture and processing software (66) to quantify cell deformation.