Single-cell mechanical analysis and tension quantification via electrodeformation relaxation

Abstract

The mechanical behavior and cortical tension of single cells are analyzed using electrodeformation relaxation. Four types of cells, namely, MCF-10A, MCF-7, MDA-MB-231, and GBM, are studied, with pulse durations ranging from 0.01 to 10 s. Mechanical response in the long-pulse regime is characterized by a power-law behavior, consistent with soft glassy rheology resulting from unbinding events within the cortex network. In the subsecond short-pulse regime, a single timescale well describes the process and indicates the naive tensioned (prestressed) state of the cortex with minimal force-induced alteration. A mathematical model is employed and the simple ellipsoidal geometry allows for use of an analytical solution to extract the cortical tension. At the shortest pulse of 0.01 s, tensions for all four cell types are on the order of 10⁻² N/m.

I. INTRODUCTION

Cortical tension of cells plays ubiquitous roles in the organization of cell aggregates, tissues, and cell clusters and in biological processes such as mechanotransduction, morphogenesis, cancer metastasis, and wound healing [1–8]. Coactive with adhesion and other mechanisms, they determine the tissue surface tension and cell sorting [9,10], the rigidity transition in a confluent tissue [11], and the translocation behavior of a cluster of circulating tumor cells [12]. They are the key cellular-level properties affecting the collective behavior, especially in regimes where strong bonds between the cells and extracellular matrix are absent or not yet formed.

Quantifying cortical tension, however, is a challenging task, as it is a state variable and subtly different although closely related to other properties such as the apparent moduli. In typical studies using atomic force microscopy or pipetting methods, the force (indentation or suction pressure, respectively) is usually applied for 1–100 s and the cortical tension is extracted via a cortical-shell–liquid-core or elastic-shell model [13–18]. While these approaches indeed provide cues on the cell mechanical behavior, from a quantitative perspective, the properties already deviate from those in the naive undisturbed state due to prolonged force application. For example, Trepat et al. demonstrated that a single transient biaxial stretch of 10% and 4 s can decrease cell stiffness by 50% [19]. This is not surprising; an extensive body of data exists and establishes the mechanically adaptive nature of cells, in part because the cell cortex is a nonpermanent network [20]. Prior studies commonly indicate different regimes of behavior as a function of force application time or frequency [18,20–23]. In the lower-frequency regime, cell deformation follows a well-established power-law behavior with a typical exponent around 0.2–0.4; in the high-frequency regime, the exponent may eventually approach 3/4. From a theoretical perspective, the former is interpreted with soft glassy rheology (SGR) [24,25], characterized by yielding events. In the case of cells, these yielding events are presumably due to unbinding of cross-linked actin filaments [20,22,26–28]. On the other hand, the exponent of 3/4 on the high-frequency side can be readily derived from a wormlike-chain theory in the low-tension limit and the measured properties better reflect the viscoelastic behavior of the actin filaments per se [29]. The demarcating frequency is typically around several hertz, corresponding to an unbinding timescale around 1 s [28,30]. These prior works therefore allude to the possibility that cortical tension in its naive state is best quantified in the moderate- to high-frequency (low force application time) regime where the structure-modifying unbinding events are not or minimally initiated.

This work tackles single-cell mechanical analysis and cortical tension quantification via electrodeformation. Electrodeformation is a contactless method where whole-cell deformation is induced via electrostatic forcing, through the application of an external direct- or alternating-current electric field [31–33]. Forces (known as the Maxwell stress) focus on the membrane or cortex, which is the primary conductance barrier separating the cytoplasm and the surroundings. Both stress and strain distributions are usually simple, an advantage that avoids difficulty in analysis due to complex geometry. Indeed, deformations are typically ellipsoidal, which is the leading-order mode in spherical harmonics [34–36]. This technique is largely implemented in a microfluidic setting and hence has the potential to achieve high throughput [37–42]. On the other hand, these studies all probe the cells in the low-frequency SGR regime, with very long-pulse durations ranging from 25 to 75 s. In contrast, the present work intends to achieve two objectives. First, we will systematically vary pulse duration by three orders of magnitudes to quantify the frequency-dependent behavior of whole-cell deformation in this scheme and to identify regimes of behavior. Second, with particular attention on the short-pulse (high-frequency) regime, we will extract cortical tension based on the deformation relaxation. We achieve this objective by using an analytical solution derived from a rigorous mathematical model describing the viscoelastic behavior of the cortex in a tensioned or prestressed state.

II. MATERIALS AND METHODS

A. Cell culture

MDA-MB-231, MCF-7, and MCF-10A cells were obtained from American Type Culture Collection (Manassas, VA). Glioblastoma multiforme (GBM) cells were provided by one of our laboratories (R.A.F.) and were previously isolated and characterized [43]. Cells were maintained in a cell culture incubator (5% CO₂, 37 °C) in Dulbecco’ s Modified Eagle’ s Medium (Sigma-Aldrich, St. Louis, MO) supplemented with 10% fetal bovine serum, 1% Penicillin-Streptomycin, and 1% L-glutamine (Sigma-Aldrich). Cells were trypsinized for 5 min in the incubator using 0.5% trypsin/ethylenediaminetetraacetic acid (Sigma-Aldrich) followed by centrifugation for 2 min at 2000 rpm (Allegra X-21, Beckman Coulter, Brea, CA) in culture media and then twice in electrodeformation isotonic buffer containing 250 mM sucrose. The osmolarity and electrical conductivity were measured with an osmometer (3D3 Osmometer, Advanced Instruments, Norwood, MA) and conductivity meter (CON 6, Oakton Instruments, Vernon Hills, IL) and adjusted to 310 mOsm/kg and 10 μS/cm, respectively. To ensure the cell viability and membrane integrity during the experiment 1% (vol %) 40 μg/ml propidium iodide (Molecular Probes, Inc., Eugene, OR) was added to the electrodeformation buffer.

B. Device fabrication and experimental setup

An indium tin oxide (ITO) (140 nm) coated glass slide was purchased from Structure Probe, Inc. (West Chester, PA). The ITO coated glass slide was soaked in acetone, isopropanol, and deionized water, respectively, for 10 min each, dehydrated in 200 °C for 30 min, and then an S1818 photoresist layer was deposited on top. The electrodes’ gap pattern was developed by a photomask with a 35-μm gap fabricated by CAD Art Services, Inc. (Bandon, OR). The photomask and general design followed prior work [44,45]. The coated glass slide was exposed to UV light through a mask aligner and the parallel microelectrodes were developed on the photoresist. Unprotected ITO regions were etched with 5% hydrochloric acid for 15–20 min and photoresist was removed with acetone. An exemplary image of the chip near the electrode gap is shown in Fig. 1(a).

FIG. 1.

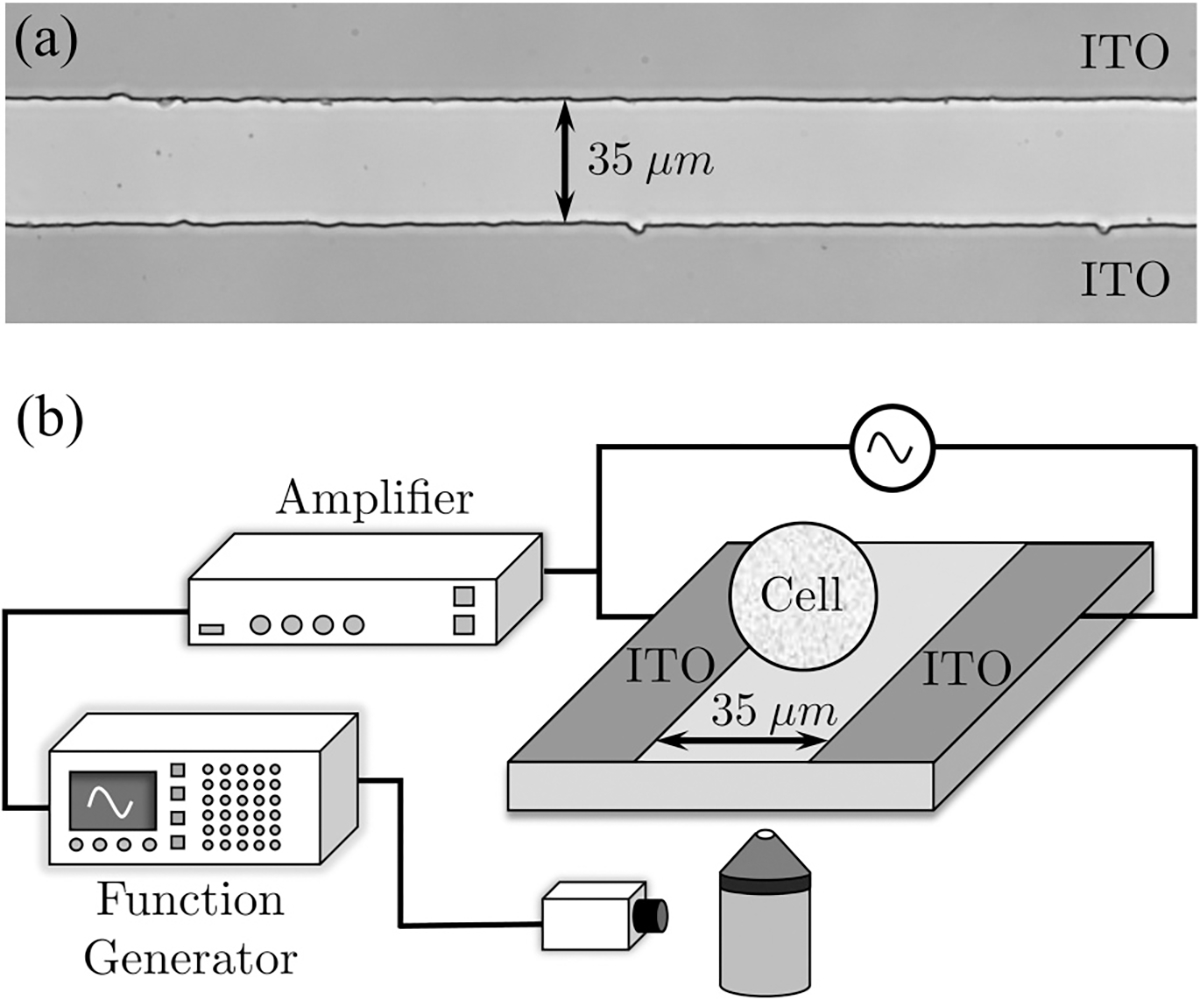
(a) Exemplary image of the etched ITO slide where the conductive coating is separated by a 35-μm gap. (b) Schematic of the experimental setup.

The chip was placed on an inverted microscope (Olympus IX71, Center Valley, PA) with a 40× objective and was connected via conductive tapes to a high-voltage, high-frequency amplifier (Trek Model PZD 350, Lockport, NY), which in turn connected to a function generator [Tektronix AFG3022C, Melrose, MA, Fig. 1(b)]. Pulses were delivered to the chip which resulted in electrodeformation. Images of the cells were recorded with a synchronized high-speed camera (pco.edge sCMOS, PCO AG, Kelheim, Germany) at 20–1000 frames/s.

C. Electrodeformation protocol

Approximately 40 μl of cell solution (200 cells/μl) was dropped on the chip. A coverslip was gently placed on top to contain the drop and to minimize motion due to flow. A small AC voltage ($V_{pp}=4\mathrm{V}$ and $f=5\mathrm{M}\mathrm{H}\mathrm{z}$) was first applied to capture the cells near one of the electrode edges via dielectrophoresis. This minimized the translation of cells during deformation relaxation. Subsequently, a high-amplitude, high-frequency AC pulse was applied to deform the cells (1–15 kV/cm, 5–8 MHz, and 0.01–10 s). This pulse range was carefully designed to effectively deform the cells without electroporation; the high-frequency range led to small transmembrane potentials [0.06–0.62 V per calculation using a COMSOL simulation (see Appendix E)]. Upon pulse cessation, the deformed cell shape relaxed to its original shape. Before and after the electrodeformation-relaxation process, cell membrane integrity was assayed by a standard propidium iodide test; cases (around 5% of total) showing membrane permeabilization are not included in the analysis due to the compromised structure. In addition, Joule heating is estimated to cause a temperature rise of 1 °C–3 °C for typical pulse conditions, which we regard as negligible.

Exemplary images of cell deformation relaxation are shown in Fig. 2. A custom-made image-processing code was developed in MATLAB (MathWorks, Natick, MA) to automatically detect the cell boundaries (dashed lines in Fig. 2) and also to automatically identify $a$ and $b$ with Fourier analysis, following one of our prior works [46].

FIG. 2.

Exemplary images of the cell deformation-relaxation process. (a) An MDA-MB-231 cell at rest prior to the deformation pulse ($t=0\mathrm{s}$ and $\delta =0$); the horizontal line is one of the electrode edges. (b) The same cell is deformed with a high-amplitude, high-frequency pulse ($t=0.5\mathrm{s},\delta =0.12,V_{pp}=40\mathrm{V}$, and $f=5\mathrm{M}\mathrm{H}\mathrm{z}$). Here $a$ and $b$ denote the long and short axes of the ellipse, respectively. (c) The cell begins to relax once the pulse ceases ($t=0.6\mathrm{s}$ and $\delta =0.05$). (d) The cell eventually recovers its shape at the end of relaxation ($t=2\mathrm{s}$ and $\delta =0$).

III. RESULTS

A. Data and analysis

Figure 3 demonstrates an exemplary deformation-relaxation process for pulse durations of $t_p=0.01$ and 0.5 s, respectively, for MDA-MB-231 cells. The applied voltage was 40 and 25 V (peak to peak, denoted by $V_{pp}$), respectively. Here we use a shape factor $\delta =a/a_0-1$ (see Fig. 2 for definitions of $a$ and $a_0$) to quantify the degree of deformation, and data from the measurements are shown in green. We apply two different approaches of analysis to all data. The first one accords with a standard power-law model [22,23,41,47–49]

$$\delta \left(t\right)=\frac{T_0}{\lambda \mathrm{\Gamma }\left(\alpha +1\right)}\left[t^{\alpha }H\left(t\right)-{\left(t-t_p\right)}^{\alpha }H\left(t-t_p\right)\right],$$ (1)

where $T_0$ denotes applied stress, $\lambda$ is a modulus, $\mathrm{\Gamma }$ is the Gamma function, $\alpha$ is the exponent, and $H$ is the Heaviside step function. (For details see Appendix B.) The second is in the form of a single-timescale deformation relaxation

$$\begin{gathered} \delta \left(t\right)=\frac{F_0}{4{\gamma }_s{a}_0}\sqrt{\frac{5}{4\pi }}[\left(1-e^{-t/t_r}\right)H\left(t\right) \\ -(1-e^{-\left(t-t_p\right)/t_r})H\left(t-t_p\right)], \end{gathered}$$ (2)

where the coefficients $F_0$ and ${\gamma }_s$ are force and surface viscosity, respectively, derived from a viscoelastic surface model introduced later, and $t_r$ is the single timescale. (For details see Appendix A.) In both panels, power-law fitting per (1) is shown as a black dashed line and single-exponential fitting per (2) is shown as a red dashed line. The coefficients of determination ${\mathrm{R}}^2$ are also provided. Implications of these two different approaches of analysis are deferred to later. Note that in Fig. 3 and in general, $\delta$ may not begin and/or end in 0 in the process, denoting a deviation from sphericity in the cell’ $\mathrm{s}$ relaxed shape. This arises due to the combined effects of the cell shape and numerical errors in our imaging and edge detection algorithm. To account for this deviation, we have used an offset value (less than 0.004) in both the power-law and the exponential fittings above.

FIG. 3.

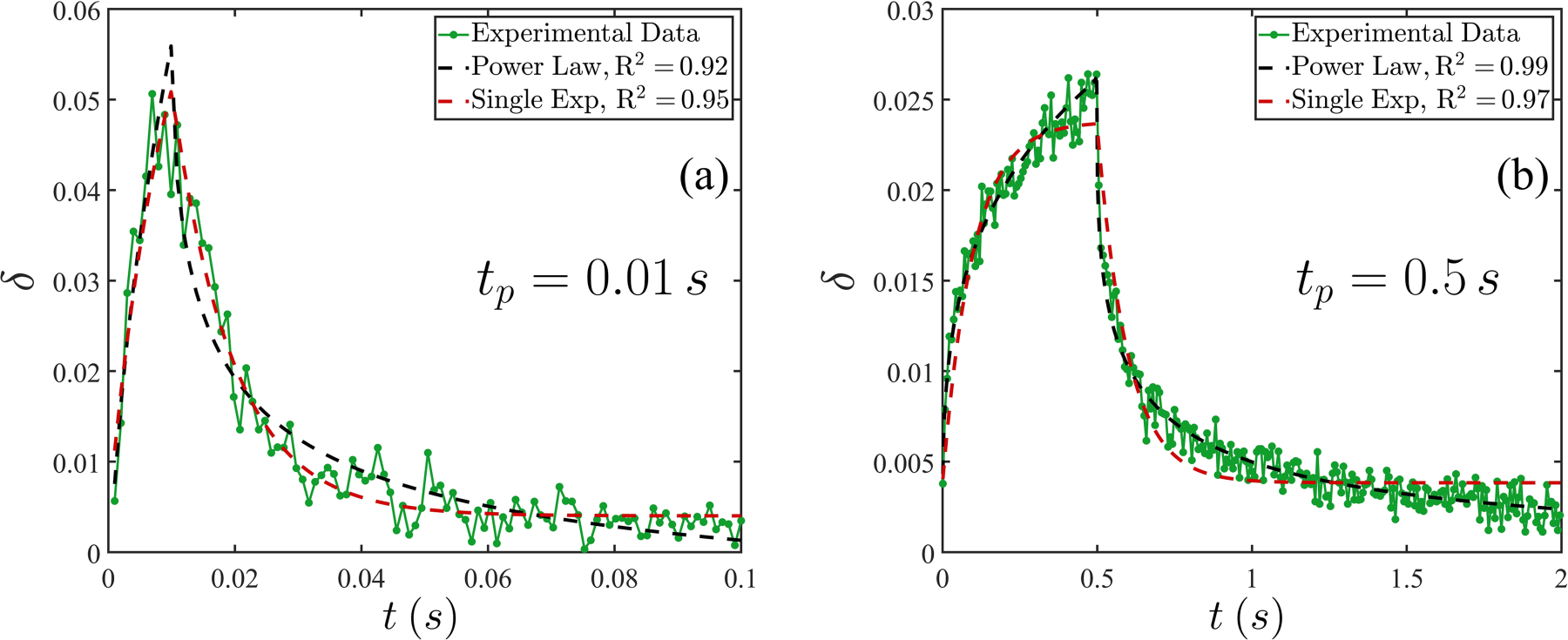
Evolution of the shape factor for two different pulse durations for a single MDA-MB-231 cell. Here $\delta =a/a_0-1$ (see Fig. 2) and (a) $t_p=0.01\mathrm{s},V_{pp}=40\mathrm{V}$, and $f=5\mathrm{M}\mathrm{H}\mathrm{z}$ and (b) $t_p=0.5\mathrm{s},V_{pp}=25\mathrm{V}$, and $f=7\mathrm{M}\mathrm{H}\mathrm{z}$. For both cases, two analytical strategies are attempted: a power-law model (black dashed line) and a single-exponential model (red dashed line). The coefficients of determination R² are provided for both cases.

We investigate a total of four cell types, namely, MCF-10A, MCF-7, MDA-MB-231, and GBM, following the protocol established above. For each case, we vary the pulse duration $t_p$ from 0.01 to 10 s, spanning four orders of magnitude. For MCF-10A, MCF-7, MDA-MB-231, and GBM, the total number of measurements are 42, 47, 52, and 42, respectively. The details on the number of repeats for each pulse duration are tabulated in Table III. For all cases we also vary the amplitude of the applied voltage and find a consistent correlation between the maximum degree of deformations and the electric stress (Appendix D, Fig. 11). However, the key quantity, such as the exponent $\alpha$ from the power-law model, depends primarily on the pulse duration $t_p$, which we demonstrate in Fig. 4(a). Evidently, $\alpha$ assumes the highest value for the shortest pulse duration, ranging from 0.48 to 0.58 for all cell types. As $t_p$ increases, $\alpha$ decreases to the range of 0.27–0.4 at $t_p=0.1\mathrm{s}$, but no obvious trend is observed beyond this duration.

FIG. 4.

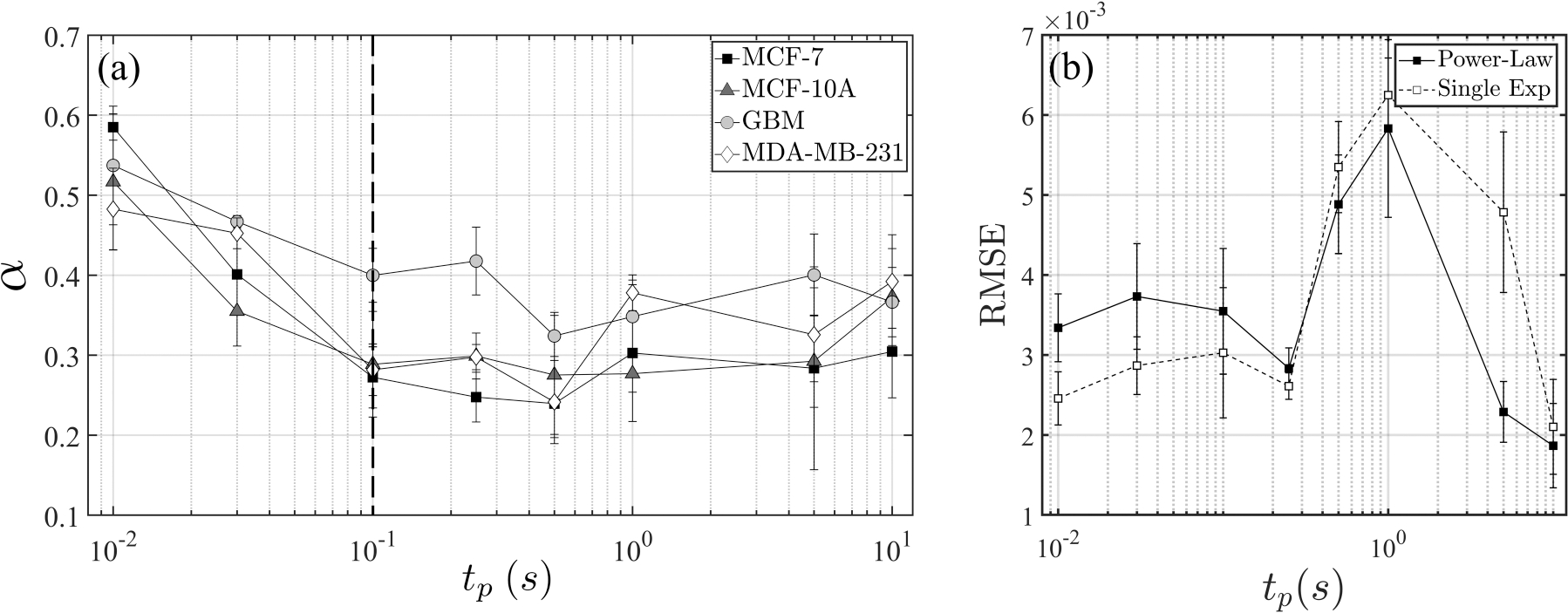
(a) Power-law exponent $\alpha$ versus pulse duration $t_p$. Error bars indicate standard deviation. The number of cells examined in each data point is tabulated in Table III. (b) Error quantification [rms error (RMSE)] for MCF-7. Results for other cell types are found in Fig. 14.

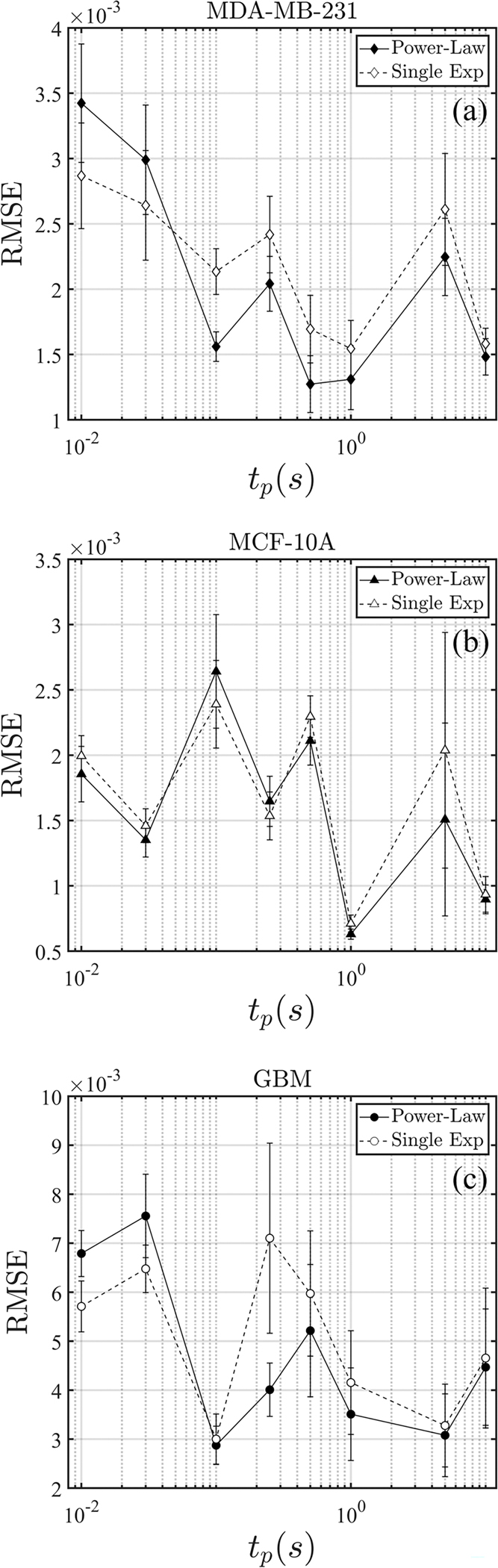
We also quantify the error of fitting for both models. Figure 4(b) shows the rms error differences between the data and the fitting (denoted by RMSE) for MCF-7. In general, the power-law model performs better for longer pulse durations, whereas the single-timescale model demonstrates more accuracy for $t_p$ shorter than 0.1 s. This trend is consistently corroborated in both MDA-MB-231 and GBM cells, shown in Fig. 14. For MCF-10A, the two approaches provide comparable results for $t_p⩽1\mathrm{s}$, whereas the superiority of the power-law fitting becomes evident only for the longer pulse durations of 5 and 10 s (see Appendix F).

These results corroborate prior work [20–23,28,50] which found that distinguishable regimes exist in the response of cells to external mechanical forcing. In the limit of long timescales, the SGR theory is commonly accepted, which predicts the power-law behavior [24,25]. For this regime ($t_p⩾0.1\mathrm{s}$), our power-law exponents are consistent with those reported previously [49,51–53]. On the other hand, for the shorter timescales, the material properties of the cell cytoskeleton are thought to be mediated by the elastic response of the actin filaments in conjunction with thermal fluctuation [21,29,54]. In particular, our data indicate that, in general, a single-timescale fitting outperforms power-law fitting. This timescale reflects the mechanical state of the actin filaments themselves without the structure-modifying unbinding events and is consistent with the behavior predicted by Broedersz et al. [20] for intermediate frequency ranges (further discussed in Sec. IV). The two regimes are demarcated by a value of $t_p$ around a fraction of a second, in agreement with those reported in literature, namely, around 0.1–1 s [27,28,30,50,55–58]. Note, however, that the transition between the regimes is gradual and selection of the threshold value is approximate.

B. Model interpretation

We further elaborate on the two model analyses based on the observation above. Evidence from both data and prior theory indicate that a single-timescale model is more appropriate for the shorter pulse times. We present a spatially resolved analysis assuming that the cell cortex is a viscoelastic “membrane” (in the sense of a mechanical entity) with surface tension (Fig. 9). This model allows us to extract cortical tension in a regime better capturing properties in the naive state without structural modification. For the longer timescales, we use a standard power-law model, in which the power-law behavior derives from the structure-modifying yielding events per standard SGR model. Details are presented below.

FIG. 9.

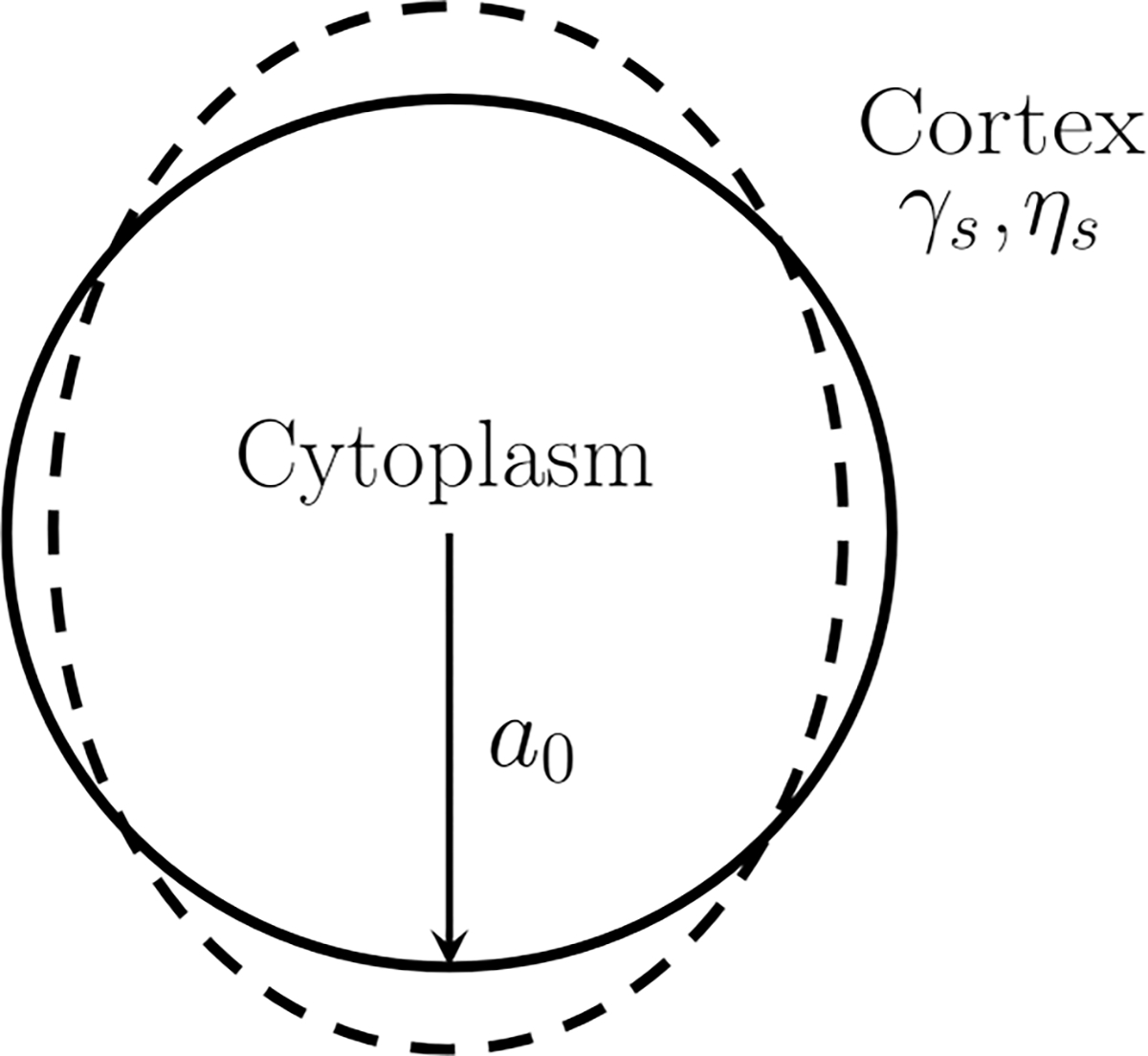
Model schematic. The cell is simplified as an infinitesimally thin, viscoelastic cortex with cortical tension ${\gamma }_s$ and surface viscosity ${\eta }_s$.

1. Surface tension model

In the first model we focus on the cell cortex, which is assumed to be an infinitesimally thin shell with a surface tension ${\gamma }_s$ and a surface viscosity ${\eta }_s$ (Fig. 9). In the regime of small to moderate deformation, the problem can be solved analytically for the dominant ellipsoidal mode as the leading-order term in a spherical harmonic expansion [34,59]. The full governing equations are reduced to a single ordinary differential equation

$$\frac{4}{3}{\eta }_s{\dot{X}}_2\left(t\right)+4{\gamma }_s{X}_2\left(t\right)=F_{0}H\left(t_p-t\right),$$ (3)

where $X_2$ is the coefficient of spherical harmonic model $Y_{\mathrm{2,0}}$ and is related to $\delta$ via

$$X_2=\sqrt{\frac{4\pi }{5}}{a}_0\delta .$$ (4)

On the right-hand side, $F_0$ corresponds to electrostatic forcing in the $Y_{\mathrm{2,0}}$ mode, which is calculated using a COMSOL simulation capturing the electrode geometry and pulsing conditions realistically (Appendix E). The Heaviside function takes into account that the pulse has a finite duration of $t_p$. Details on the model and derivation are given in Appendix A as well as our recent work [59]. Solving (3) and considering (4) reveals (2) as the final solution used for fitting, and the timescale is

$$t_r=\frac{{\eta }_s}{3{\gamma }_s}.$$ (5)

Figure 5 summarizes results analyzed with this model, in which we temporarily focus on the three shorter pulse durations, namely, $t_p=0.01,0.03$, and 0.1 s. More complete results are shown in Fig. 10 in Appendix A and Fig. 7 below. In Fig. 5(a), the timescale $t_r$ is extracted. The values for the first two pulse durations are comparable and do not depend on the applied voltages or electric fields. Appreciable increases are demonstrated at $t_p=0.1\mathrm{s}$, which we speculate correlates with the onset of actin cross-link unbinding and the transition to the power-law (SGR) regime.

FIG. 5.

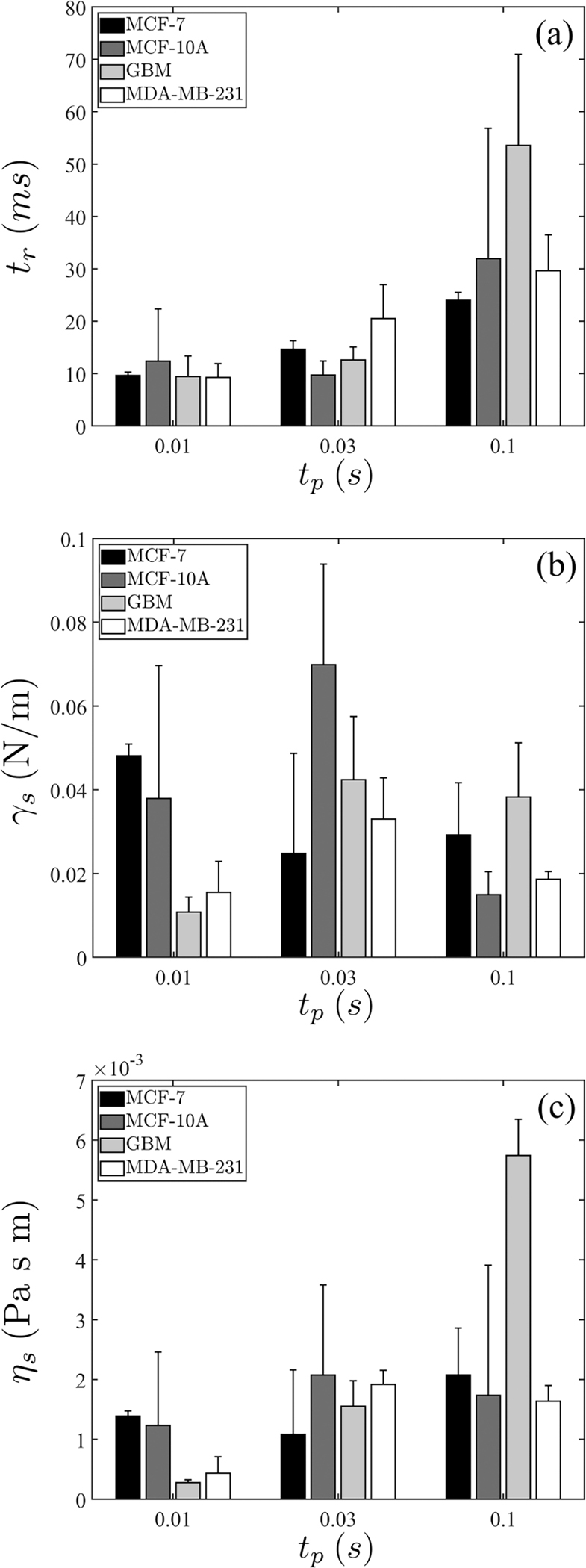
(a) Extracted timescale $t_r$, (b) surface tension ${\gamma }_s$, and (c) surface viscosity ${\eta }_s$. Error bars indicate standard deviation. The number of repeats is provided in Table III.

FIG. 10.

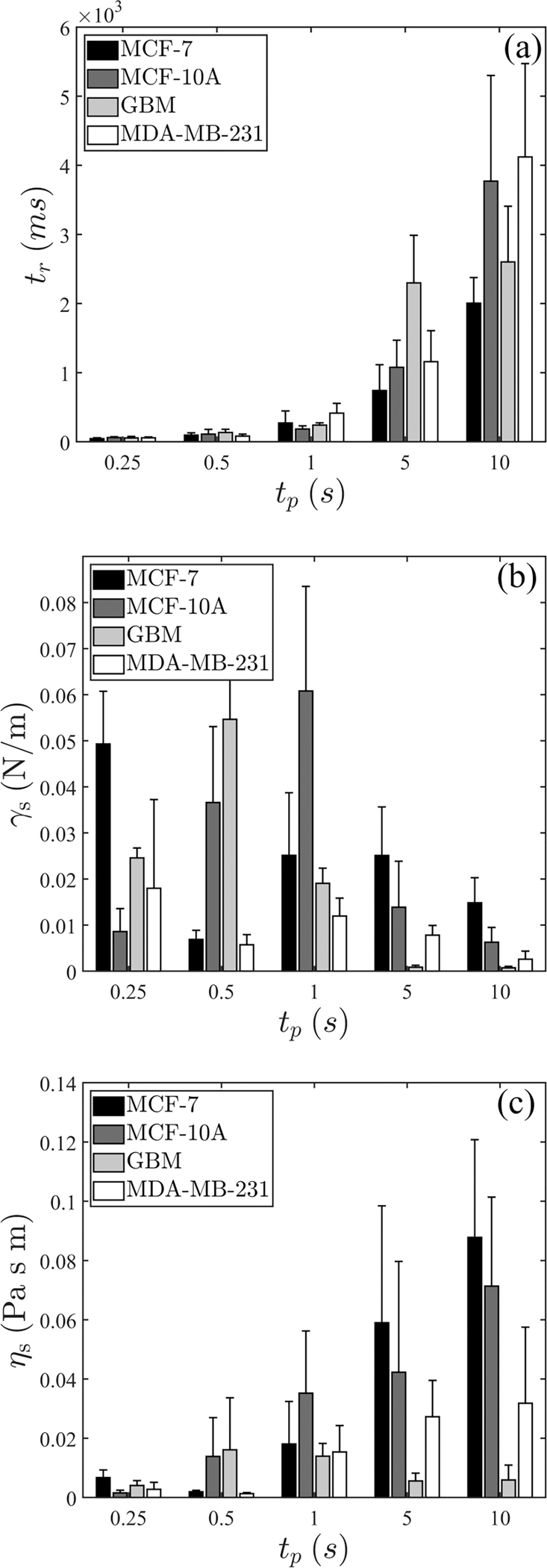
(a) Extracted timescale $t_r$, (b) surface tension ${\gamma }_s$, and (c) surface viscosity ${\eta }_s$ for $t_p>0.1$. Error bars indicate standard deviation. The number of repeats is provided in Table III.

FIG. 7.

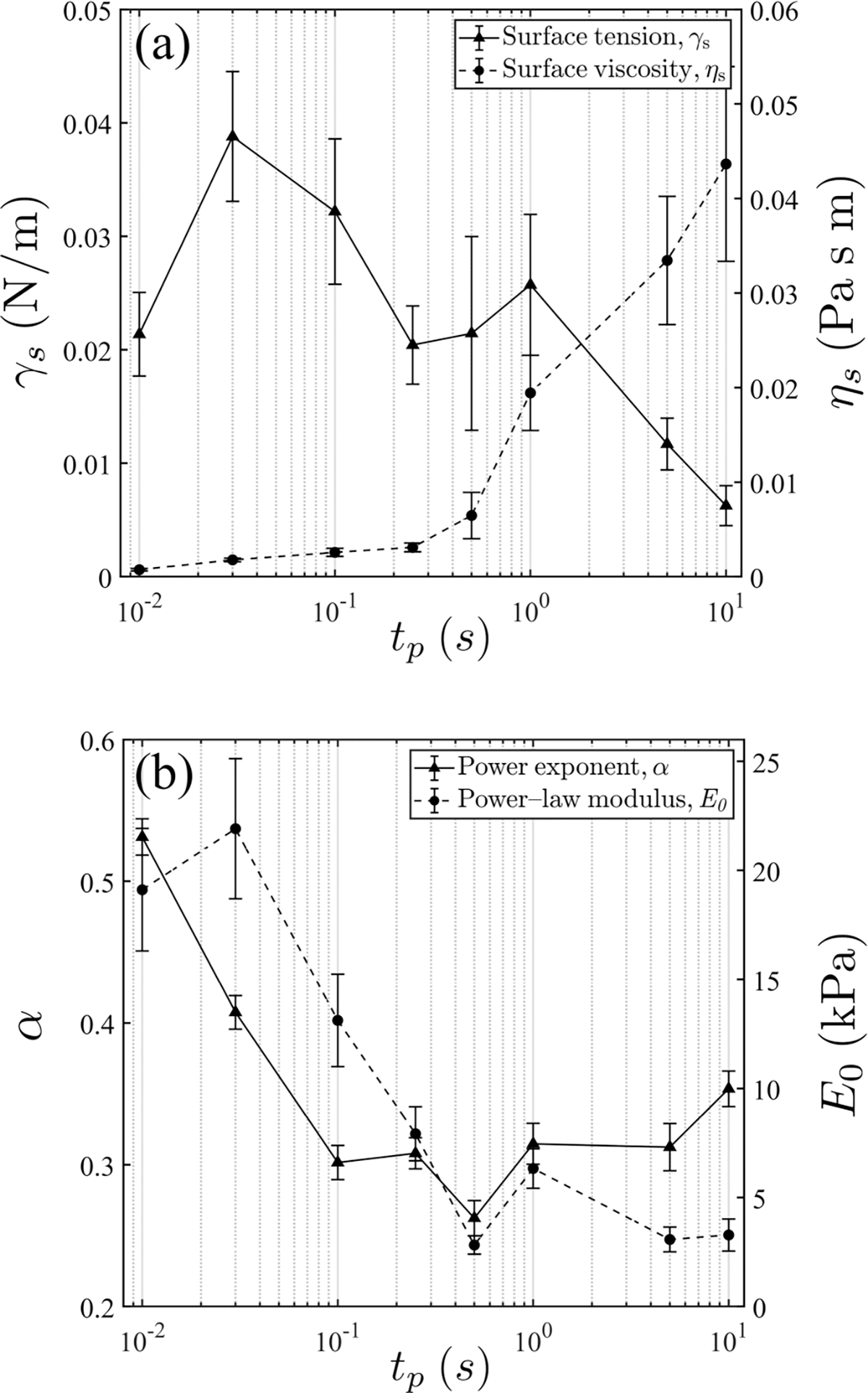
Pooled results for all cell types and pulse durations: (a) ${\gamma }_s$ and ${\eta }_s$ from the surface tension model and (b) $\alpha$ and $E_0$ from the power-law damping model. Error bars indicate standard error. The number of repeats is provided in Table III.

The availability of $t_r$ and $F_0$ allows us to extract the mechanical properties ${\gamma }_s$ and ${\eta }_s$, which are shown in Figs. 5(b) and 5(c), respectively. Using this analysis, cortical tension demonstrates values in the range of 10⁻²–10⁻¹N/m, whereas surface viscosity is on the order of 10⁻³Pa sm.

2. Power-law model

We now turn to the power-law model, in which we used a lumped stress-strain relation but with a fractional derivative

$$\lambda D_t^{\alpha }\left(\delta \left(t\right)\right)=T_{0}H\left(t_p-t\right),$$

where $D_t^{\alpha }(\cdot )$ is Riemann’s fractional derivative, $T_0$ is constant applied stress, $\delta$ is strain, $\alpha$ is the power exponent, and $\lambda$ is the corresponding module in the power-law regime which is constant. Solution using a Laplace transform leads to the creep response (1); details are elaborated in Appendix B. Data analysis leads to the extraction of $\alpha$, shown in Fig. 4(a). The combination $T_0/\lambda$ can also be determined, but not independently. We thus again can resort to simulation to compute $T_0$ and to subsequently extract the modulus $\lambda$ (Appendix E). However, following prior work, we more conveniently transform to the frequency domain so that the storage and loss moduli are

$$E^{\prime }=\lambda {\omega }^{\alpha }\cos \frac{\pi \alpha }{2},$$ (6)

$$E^{\prime \prime }=\lambda {\omega }^{\alpha }\sin \frac{\pi \alpha }{2},$$ (7)

respectively, where the frequency is calculated as $\omega =2\pi /t_p$, and the magnitude of the complex modulus is

$$E_0=\lambda {\omega }^{\alpha }.$$

The loss tangent is related to the power exponent via

$$\eta =\frac{E^{\prime \prime }}{E^{\prime }}=\tan \frac{\pi \alpha }{2}.$$ (8)

This is a simple monotonic relationship relating $\eta$ to $\alpha$, and hence we do not show results on the former for brevity. On the other hand, extracted values of $E_0$ for $t_p⩾0.1\mathrm{s}$ are shown in Fig. 6. Despite more significant variabilities being present in the data in this regime, we observe that $E_0$ values are appreciably greater for $t_p=0.1$ and 0.25 s, particularly for MCF-7, and decrease to the 1–10 kPa range when $t_p$ assumes longer durations.

FIG. 6.

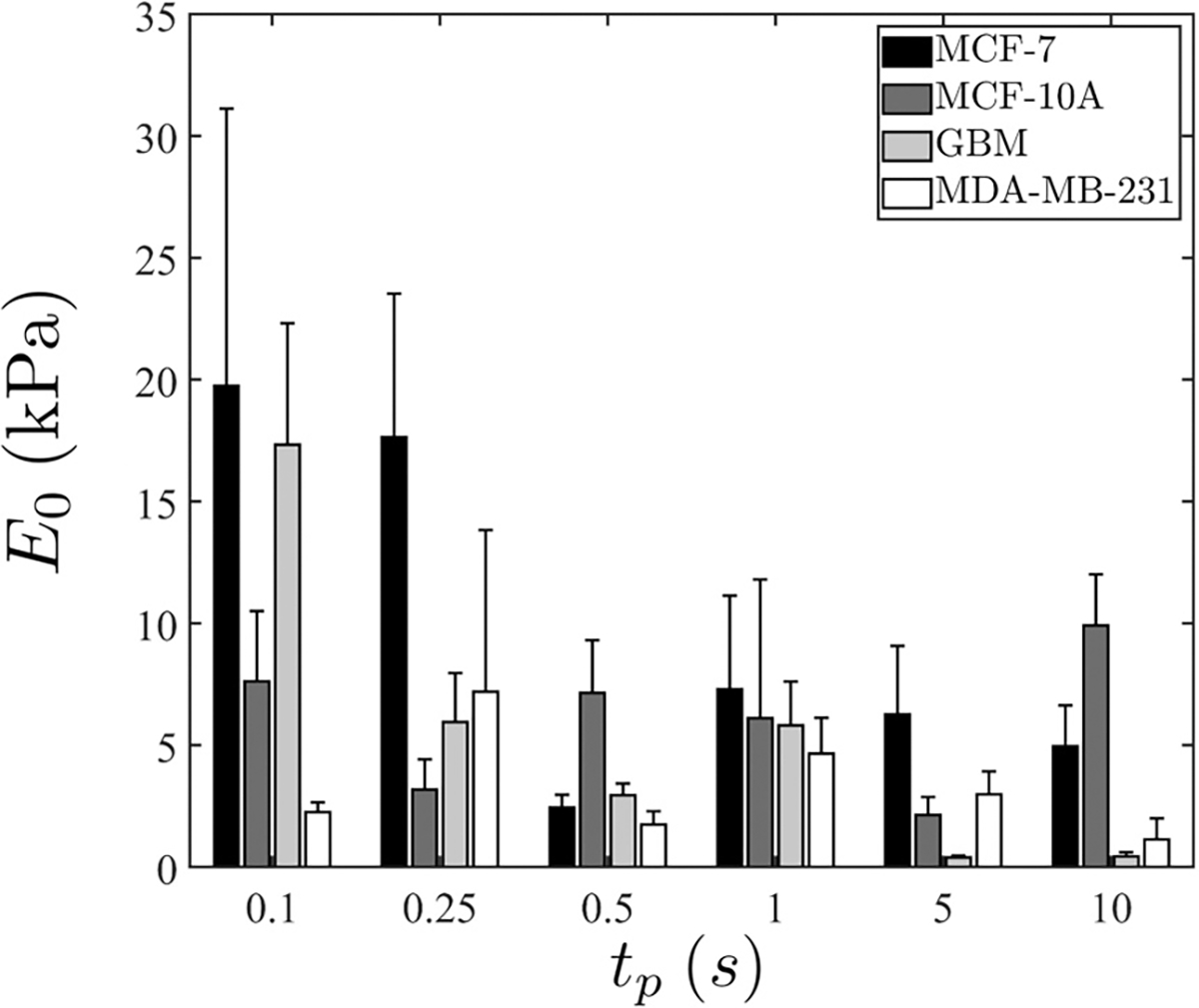
Extracted $E_0$ for $t_p⩾0.1\mathrm{s}$. Error bars indicate standard deviation. The number of repeats is provided in Table III.

The above trends become more apparent when we apply the model analysis to all cell types with all pulse durations (regardless of the relative model accuracy and validity in the pulsing regimes). These results are presented in Fig. 7. In general, both ${\gamma }_s$ and $E_0$ decrease with an increasing $t_p$ while ${\eta }_s$ increases. These trends again reflect transitional behavior from the elastic to the SGR regime, where cortical strength weakens and effective viscosity increases. Further discussion of these trends and comparisons with those in the literature are found in the next section.

Finally, it would be of interest to directly compare results from the two models. For this purpose, we first convert surface tension and viscosity to an effective, lumped elastic modulus and viscosity via (Appendix C)

$$E_{\mathrm{e}\mathrm{f}\mathrm{f}}^{\prime }=\frac{24}{23}\frac{{\gamma }_s}{a_0},$$ (9)

$${\mu }_{\mathrm{e}\mathrm{f}\mathrm{f}}=\frac{8}{23}\frac{{\eta }_s}{a_0},$$ (10)

respectively. Note that these quantities are effectively averages over the entire cell, which also facilitate comparison with similar bulk measurements from the literature below. On the other hand, they are different from the effective cortex modulus which is obtained by scaling with cortical thickness [18,60]. The magnitude of the complex modulus is

$$E_{0,\text{eff}}=\sqrt{{E_{\text{eff}}^{\prime }}^2+{E_{\text{eff}}^{\prime }}^2},$$ (11)

$$E_{\text{eff}}^{\prime \prime }=\omega {\mu }_{\text{eff}}.$$ (12)

Results suggest that both total and loss moduli are in good agreement. On the other hand, the power-law model tends to overestimate the elastic modulus by several times, in particular in the short-pulse regime. We thus conclude that the single-timescale, surface-based model (2) is not only appropriate but necessary for valid quantitative mechanical analysis in the intermediately- to high-frequency regime.

IV. DISCUSSION

A. Cortical tension in the short-pulse regime

Above we observed two regimes consistent with the understanding in the literature: an SGR regime that is characterized by a low power exponent $\alpha$ for the long-pulse durations (lower frequencies) and a regime for the short-pulse durations (higher frequencies) where the response is characterized by a single timescale. Indeed, an interpretation is provided by prior work that this is because in this regime unbinding is not initiated and modes longer than cross-link spacing are suppressed, so “only small-scale bending fluctuations between cross-links can relax” [20]. Consequently, the theory also predicts a plateau in $E^{\prime }$ [20], which is observed in, for example, [61]. In our data [Fig. 8(a)], even though such a plateau is not rigorously seen, we do observe a slight decrease in $E_{\text{eff}}^{\prime }$ toward the shortest pulse $t_p=0.01\mathrm{s}$. It is unclear from the data whether this is due to its intrinsic large variability or this decrease is actually mechanistically driven. We are not observing the high-frequency regime where $\alpha =\frac{3}{4}$, even if we force a power-law analysis [Fig. 4(a)]. Similar to [28], we speculate that our shortest-pulse duration $t_p=0.01$ is not sufficient to reach that regime, although we do see $\alpha$ values are higher around 0.48–0.58. On the other hand, relaxation of the bending fluctuations may be a cause of the weak dependence on the $t_p$ shown in Fig. 7(a) at the short-pulse times.

FIG. 8.

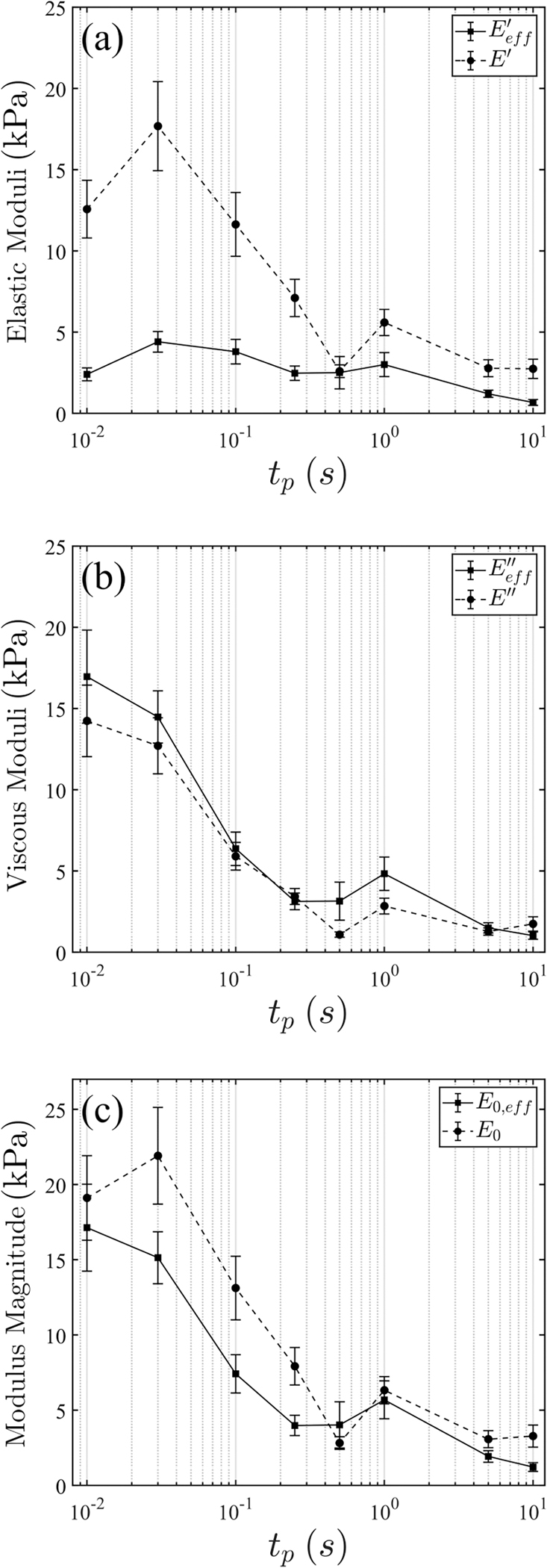
Direct property comparison between the two models. Error bars indicate standard error. The number of repeats is provided in Table III.

One particular thesis of the present work is that cortical tension is more faithfully quantified in the short-pulse regime. The rationale is straightforward, given the above data trend as well as previously established theories. We aim to establish that under short-pulse (~0.01 s), small-amplitude (several percent of strain) electrodeformation, the extracted tension or prestress reflects that in a state where the cortical structure is close to the undisturbed state.

B. Comparison with literature values

A vast body of literature exists on measuring mechanical properties of cells. Importantly, a recent study by Wu et al. systematically examined the properties of MCF-7 with various techniques and observed that moduli vary by as much as three orders of magnitude, depending on the particular method, the state of the cells (attached or suspended), the target (partial membrane, cortex, or whole cell), and interrogation strength and frequency [62]. Indeed, this reflects the very complex and adaptive nature of cells as a living mechanical entity.

In the literature, the cortical tension is commonly measured with the micropipette aspiration technique, which reports values in the range of 30–3000 pN/μm for various cell types [14,60,63,64], which is in general weaker than values extracted by this work. Trends from the present work suggest that this may be due to the much longer force application times, e.g., a few hundred seconds for typical aspiration measurements [16,60,65]. On the other hand, measurements from real-time deformability cytometry do reveal a tension of 0.02 N/m, matching the present results [66]. Note that, interestingly, an upper cutoff time for the power-law regime was also observed in [18].

Against those here we only selectively compare our results on an elastic modulus with the most similarity in configuration, namely, whole-cell measurements in a similar frequency range, and with the same cell types. The results are summarized in Table I and depend on cell type. For MDA-MB-231, our data are in good agreement with prior work measured with different techniques [37,51]. On the other hand, the properties for MCF-7 are greater in value when compared with those from other work, by several times or even an order of magnitude. The cause of this difference is unknown, yet one possible difference lies within the force distribution on the whole-cell level, e.g., when comparing optical stretching and plate rheometry with electrodeformation. In this regard, the latter has a comparative advantage: Both the stress and strain fields have a relatively simple cosinusoidal distribution to the leading order, and hence allow spatially resolved model construction (Appendix A).

TABLE I.

Comparison with prior data in similar frequency ranges. Here timescales refer to force application times in optical stretching or parallel-plate rheometry (first and second rows, respectively) [62], electrodeformation (third and fourth rows) [37], and residence time translocating a constriction (fifth and sixth rows) [51]. For properties, the notation follows that of this work (the last two columns).

Source	Cell type	Properties (kPa)	Timescale (s)	This work (kPa)	$t_p(\mathrm{s})$
[62]	MCF-7	$E_{\text{eff}}^{\prime }$ = 0.018 ± 0.024	8	1.87 ± 0.23	10
[62]	MCF-7	$E^{\prime }$ = 0.95 ± 0.15	1	6.38 ± 3.38	1
[37]	MCF-7	$E_{\text{eff}}^{\prime }$ = 0.358 ± 0.053	25	1.87 ± 0.23	10
[37]	MDA-MB-231	$E_{\text{eff}}^{\prime }$ = 0.327 ± 0.052	25	0.35 ± 0.21	10
[51]	MCF-7	$E_{\text{eff}}^{\prime }$ = 2.1 ± 0.1	0.1	7.10 ± 1.52	0.1
[51]	MDA-MB-231	$E_{\text{eff}}^{\prime }$ = 0.8 ± 0. 19	0.1	0.70 ± 0.11	0.1

Note that, although at each pulse duration we do observe differences in the cell types, a consistent trend is not seen at all pulse times. On the other hand, the variation with respect to $t_p$ provides major variability in the system and such is the rationale of pooling data from all cell types as a function of pulse time in Fig. 7. Further controlled study via various drug treatment such as those following [18,33,51] will help shed light on the biological regulators of cortical tension and genotype similarities and/or differences.

V. CONCLUSION

In this work we have presented an electrodeformation-relaxation assay to probe mechanical properties of whole suspended cells. We vary pulse duration by four orders of magnitudes, from 0.01 to 10 s, which is equivalent to a frequency range of approximately $\omega ~0.6-600\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$ (or $~0.1-100\mathrm{H}\mathrm{z}$). Expectedly, mechanical properties depend strongly on pulsing time. We observe an SGR regime characterized by a low-exponent power-law behavior in the long-pulse regime, whereas we are able to capture a single-timescale deformation-relaxation behavior with subsecond pulse durations. Within the simplifications and using a rigorous, spatially resolved (versus lumped) mathematical model, we extract cortical tension that closely approximates that in the naive cell state, the state that is the least mechanically disturbed. This work demonstrates that electrodeformation can be developed as a contactless technique to rapidly assay cell mechanical properties in a wide frequency range and to analyze tension statistics using its short-pulse capability.

APPENDIX A: SURFACE TENSION MODEL

Consider a spherical cell of radius $a_0$ in a fully relaxed state and the displacement is defined by $\mathbf{u}(\cdot ,t):\partial B\to {\mathbb{R}}^3\left(B=\{\mathbf{x}\in {\mathbb{R}}^3:\left|\mathbf{x}\right|=a_0\}\right)$. The elastic energy $ℰ$ and the dissipation potential $𝒟$ of the cortex are given by

$$ℰ\left[\mathbf{u}\right]={\int }_{\partial B}\frac{1}{2}{\nabla }_s\mathbf{u}\cdot {\mathbb{C}}_{\mathrm{s}}{\nabla }_s\mathbf{u},$$ (A1)

$$𝒟\left[\mathbf{u}\right]={\int }_{\partial B}2{\eta }_s{\left|\frac{1}{2}[{\nabla }_s\dot{\mathbf{u}}+{\left({\nabla }_s\dot{\mathbf{u}}\right)}^{\mathrm{T}}]\right|}^{2}dS,$$ (A2)

where ${\mathbb{C}}_{\mathrm{S}}$ is the surface elasticity tensor which is proportional to surface tension, ${\gamma }_s$ and ${\eta }_s$ represent surface viscosities associated with the cortex (Fig. 9), and ${\nabla }_s$ is the surface gradient [59]. Moreover, assuming conservation of the cell interior volume and local surface area at the leading order implies the constraints

$${\nabla }_s\cdot \mathbf{u}={\nabla }_s\cdot \dot{\mathbf{u}}=0\text{on}\partial B.$$ (A3)

In terms of spherical harmonic modes and assuming axisymmetry, $E$ and $D$ are given by

$$ℰ\left[\mathbf{u}\right]=\sum _{l=2,4,6,\dots }^{\infty }{\gamma }_s\left(\frac{l(l+1)-2}{2}\right)X_l^2,$$ (A4)

$$𝒟\left[\mathbf{u}\right]=\sum _{l=2,4,6,\dots }^{\infty }{\eta }_s\frac{2\left[l(l+1)-2\right]}{l(l+1)}{\dot{X}}_l^2,$$ (A5)

where $X_l$ is the $l$ th-mode coefficient of the radial displacement $u^r$,

$$X_l=\frac{1}{a_0^2}{\int }_{\partial B}{u}^r(R,\theta )Y_l(\theta )dS,$$ (A6)

$$u_r=\sum _{l=2,4,6,\dots }^{\infty }{X}_l(r)Y_l.$$

Let $\mathbf{t}:\partial B\to {\mathbb{R}}^3$ be the surface traction on the cell. The rate of work done by the force is given by

$$\dot{𝒲}={\int }_{\partial B}\mathbf{t}\cdot \dot{\mathbf{u}}dS=\sum _{l=2,4,6,\dots }^{\infty }\left[t_l^r+\frac{2}{l(l+1)}{t}_l^{\theta }\right]{\dot{X}}_l,$$ (A7)

where $t_l^r$ and $t_l^{\theta }$ are the $l$ th modes in radial and tangential traction, respectively,

$$t_l^r={\int }_{\partial B}{t}^r\left(R,\theta \right)Y_l\left(\theta \right)dS,$$ (A8)

$$t_l^{\theta }={\int }_{\partial B}{t}^{\theta }\left(R,\theta \right)Y_l\left(\theta \right)dS,$$ (A9)

By neglecting the higher modes of spherical harmonics, the balance of work for the system in the second mode (ellipsoidal) leads to

$$\dot{𝒲}-\frac{d}{dt}ℰ\left[X_2(t)\right]=𝒟\left[X_2(t)\right]$$ (A10)

or

$$\frac{4}{3}{\eta }_s{\dot{X}}_2\left(t\right)+4{\gamma }_s{X}_2\left(t\right)=t_2^r+\frac{1}{3}{t}_2^{\theta }=F_{0}H\left(t_p-t\right),$$ (A11)

where $F_0$ denotes the total electrostatic force exerted on the cell cortex and $H$ is the Heaviside step function to capture the effects of a finite pulse time. The following relationship converts between $\delta$, the shape factor, and $X_2$:

$$X_2=\sqrt{4\pi /5}{a}_0\delta .$$ (A12)

In (A11), the traction terms are to be evaluated from the Maxwell stress tensor induced by the applied electric field [67,68],

$$\mathbf{T}=ϵ(\mathbf{E}\mathbf{E}-\frac{1}{2}|\mathbf{E}{|}^2\mathbf{I}),\mathbf{t}={\mathbf{T}\mathbf{e}}_r,$$ (A13)

where $ϵ$ is electrical permittivity. Solving Eq. (A11) with constant traction (applicable to our studies) yields

$$\begin{gathered} \delta (t)=\frac{F_0}{4{\gamma }_s{a}_0}\sqrt{\frac{5}{4\pi }}[(1-e^{-t/t_r})H(t)-(1-e^{-(t-t_p)/t_r}) \\ \times H(t-t_p)], \end{gathered}$$ (A14)

where the deformation-relaxation timescale is given by

$$t_r=\frac{{\eta }_s}{3{\gamma }_s}.$$ (A15)

FIG. 11.

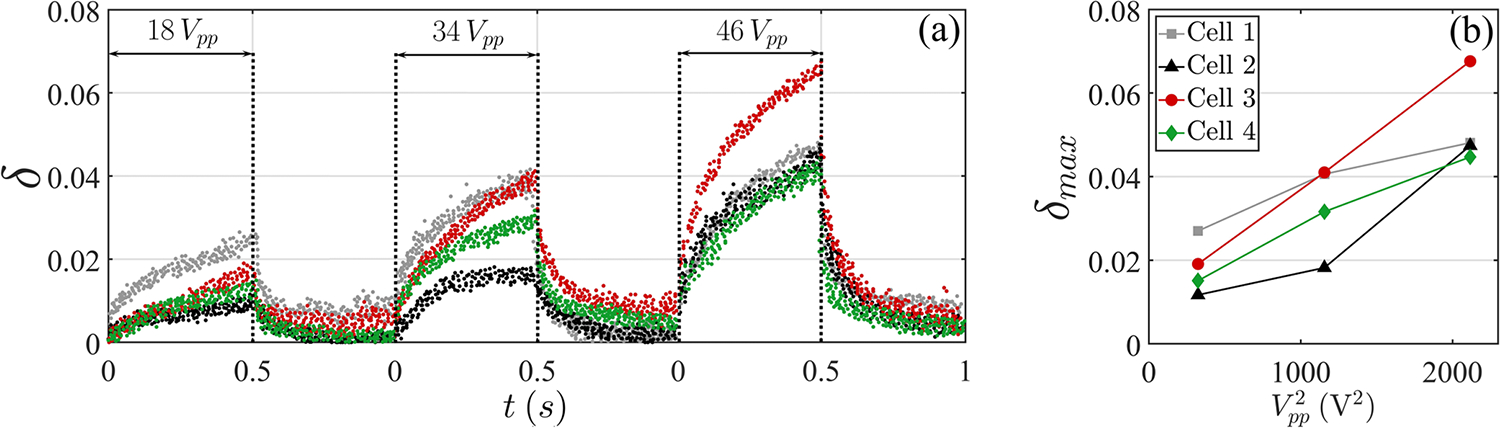
(a) Shape factor changes of four different MDA-MB-231 cells under consecutively increasing pulsing, each 0.5 s at 7 MHz. (b) The maximum deformation achieved at the end of pulsation ${\delta }_{max}$ shows approximately a linear correlation with $V_{pp}^2$.

The calculated values with this model for $t_p⩽0.1$ for each cell type is provided in Fig. 5 in the proper text. However, to provide complete data, we provide the trends of changes for these properties in relatively longer-pulse durations $\left(t_p>0.1\right)$ in Fig. 10.

APPENDIX B: POWER-LAW MODEL

In the power-law regime, the lumped stress-strain relation is given by

$$T\left(t\right)=T_{0}H\left(t_p-t\right)=\lambda D_t^{\alpha }\left(\delta \left(t\right)\right),$$ (B1)

where $D_t^{\alpha }(f)$ is the Riemann’s fractional derivative, $T_0$ is a constant applied stress, $\delta$ is strain (quantified by $a/a_0-1$ in our case), $\alpha$ is the power exponent, and $\lambda$ is the modulus. The creep response is obtained using a Laplace transform

$$ℒ\{T(t)\}=\lambda ℒ\left\{D_t^{\alpha }(\delta (t))\right\},$$ (B2)

$$\delta \left(t\right)=\frac{T_0}{\lambda \mathrm{\Gamma }\left(\alpha +1\right)}\left[t^{\alpha }H\left(t\right)-{\left(t-t_p\right)}^{\alpha }H\left(t-t_p\right)\right],$$ (B3)

where $T_0$ is determined via

$$T_0=\frac{F_0}{\pi a_0^2}.$$ (B4)

Rewriting Eq. (B1) in the frequency domain using a Fourier transform provides the storage $\left(E^{\prime }\right)$ and loss moduli $\left(E^{\prime \prime }\right)$

$$E^{\prime }=\lambda {\omega }^{\alpha }\mathrm{c}\mathrm{o}\mathrm{s}\frac{\pi \alpha }{2},$$ (B5)

$$E^{\prime \prime }=\lambda {\omega }^{\alpha }\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi \alpha }{2},$$ (B6)

where $\omega$ is frequency ($\omega =2\pi /t_p$ for our case). The loss tangent or structural damping coefficient $\eta$ is given by

$$\eta =\frac{E^{\prime \prime }}{E^{\prime }}=\tan \frac{\pi \alpha }{2}.$$ (B7)

The modulus $E_0$ is related to $\lambda$ via

$$E_0=\lambda {\omega }^{\alpha }.$$ (B8)

APPENDIX C: EFFECTIVE ELASTIC AND VISCOUS MODULI

Based on a general model in [59], if the cell is to be considered a bulk material with an effective elastic modulus $E_{\text{eff}}^{\prime }$ and bulk viscosity ${\mu }_{\text{eff}}$ the energy functionals are

$$\begin{gathered} {ℰ}_{\text{bulk}}[\mathbf{u}]={\int }_B{E}_{\text{eff}}^{\prime }{\left|\frac{1}{2}[\nabla \mathbf{u}+{(\nabla \mathbf{u})}^{\text{T}}]\right|}^{2}dV \\ ={\int }_{\partial B}\frac{1}{2}{E}_{\text{eff}}^{\prime }{\left|{\nabla }_s\mathbf{u}\right|}^{2}dS \\ =a_0\sum _{l=2,4,6,\dots }^{\infty }{E}_{\text{eff}}^{\prime }(\frac{2l^3+3l^2-5}{2l(l+1)})X_l^2, \end{gathered}$$ (C1)

$$\begin{array}{l}{𝒟}_{\text{bulk}}[\mathbf{u}]={\int }_{B}2{\mu }_{\text{eff}}{\left|\frac{1}{2}\left[\nabla \stackrel{.}{\mathbf{u}}+{(\nabla \stackrel{.}{\mathbf{u}})}^{\text{T}}\right]\right|}^{2}dV\\ ={\int }_{\partial B}{\mu }_{\text{eff}}{\left|{\nabla }_s\stackrel{.}{\mathbf{u}}\right|}^{2}dS\\ =a_0\sum _{l=2,4,6,\dots }^{\infty }{\mu }_{\text{eff}}(\frac{2l^3+3l^2-5}{l(l+1)}){\dot{X}}_l^2.\end{array}$$ (C2)

FIG. 12.

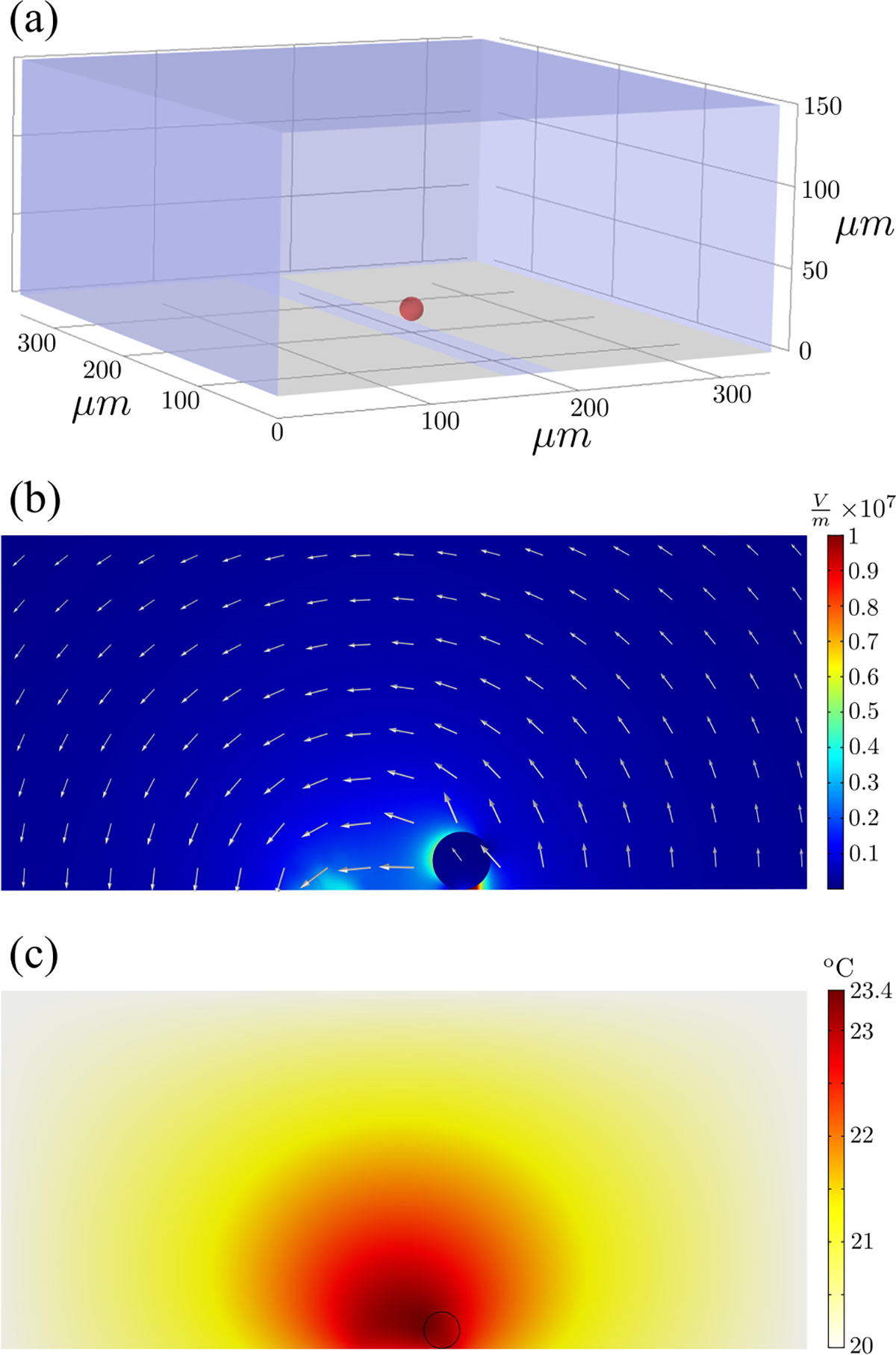
(a) Model geometry. (b) Exemplary electric field distribution. (c) Exemplary heat map due to Joule heating; the ambient temperature is assumed to be 20 °C. The cross section is taken perpendicular to the electrode edges and at the cell equator. The simulation parameters are $a_0=7.5\mu \mathrm{m},V_{pp}=50\mathrm{V}$, and $f=5\mathrm{M}\mathrm{H}\mathrm{z}$.

TABLE II.

Parameters for simulation.

Domain	Relative permittivity	Conductivity (S/m)	Thermal conductivity (W/mK)	Heat capacity (J/kgK)
Media	80	10−2	0.611	4180.9
Cytoplasm	80	0.4	0.611	4180.9
Membrane	2	5×10−9

Comparing the above with (A4) and (A5) for the second mode of spherical harmonics $l=2$, we have

$$E_{\mathrm{e}\mathrm{f}\mathrm{f}}^{\prime }=\frac{24}{23}\frac{{\gamma }_s}{a_0},{\mu }_{\mathrm{e}\mathrm{f}\mathrm{f}}=\frac{8}{23}\frac{{\eta }_s}{a_0}.$$

FIG. 13.

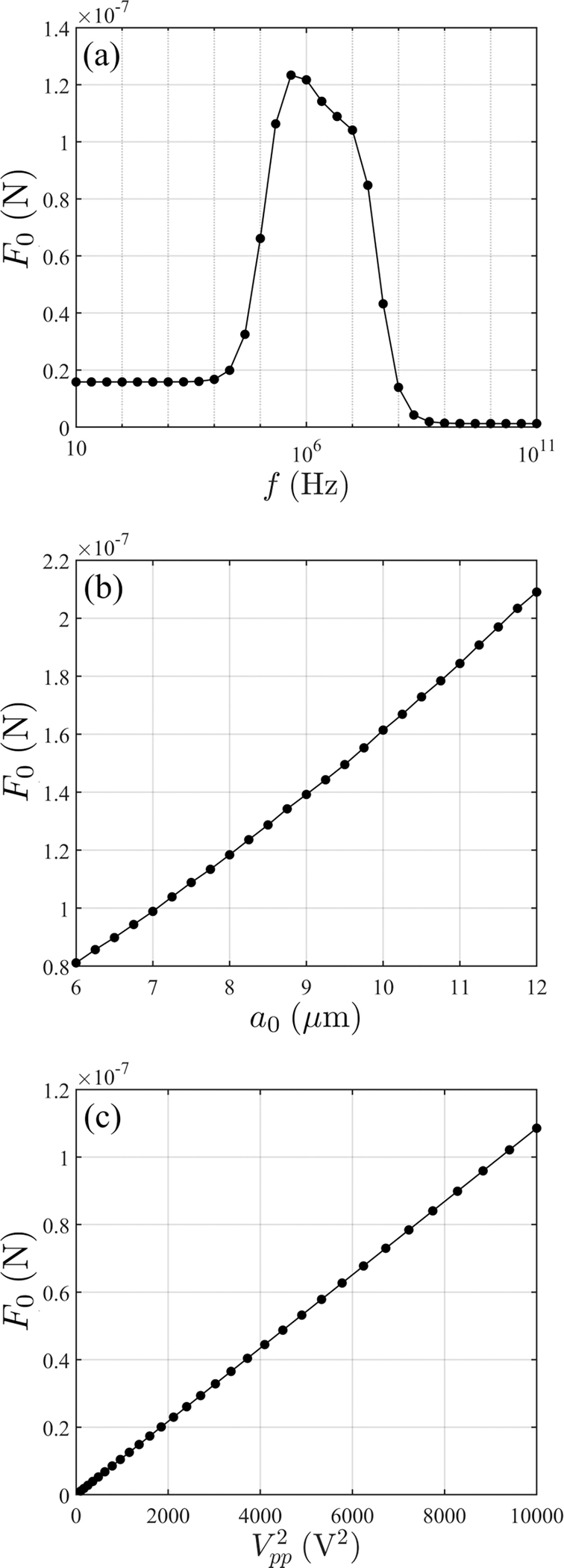
Dependence of $F_0$ on (a) frequency, (b) cell radius, and (c) applied voltage. The reference case is $a_0=7.5\mu \mathrm{m},V_{pp}=100\mathrm{V}$, and $f=5\mathrm{M}\mathrm{H}\mathrm{z}$.

Note that as the coefficient of $\frac{24}{23}$ is very close to 1, one can conveniently convert between storage modulus and surface tension via a simple estimate $E_{\text{eff}}^{\prime }~{\gamma }_s/a_0$.

FIG. 14.

The RMSE for the two analytical approaches. The number of repeats is provided in Table III.

APPENDIX D: DEFORMATION VS APPLIED VOLTAGE

We performed limited experiments to confirm the scaling law of deformation and electrostatic forcing. The Maxwell stress scales with $|\mathbf{E}{|}^2$ per (A13); therefore, we expect that deformation scales with $V_{pp}^2$, although the field distribution is nonuniform (see Appendix E below). Exemplary results are demonstrated with four MDA-MB-231 cells in Fig. 11, where indeed a general correlation between the maximum strain ${\delta }_{max}$ and $V_{\mathrm{p}\mathrm{p}}^2$ is observed.

APPENDIX E: NUMERICAL SIMULATION

Simulation is performed with COMSOL MULTIPHYSICS (COMSOL Inc., Burlington, MA) and includes studies of the electric field, Maxwell stress, and Joule heating. Electric currents and heat transfer in fluid modules with both transient and frequency domain studies are employed. A 350×350×150 μm³ size box with electrodes on the bottom surface, spaced 35 μm apart, is used as the geometry to realistically simulate the chip setup (Fig. 12). A spherical cell of given radius is seated on the bottom near one of the electrodes; the location is not arbitrary, but is found as a translational force equilibrium for dielectrophoresis, approximating realistic physics. In the simulation, deformation is not considered; the electric field distribution in ellipsoids with small deformations (a strain of only a few percent, $\delta ~{10}^{-2}$) presents a negligible deviation [36,69,70].

Properties and parameters are listed in Table II. The electrical conductivity of the suspending media is measured as described in the main text. The membrane and cytoplasmic properties are chosen from the literature [71–76]. Permittivity, density, and thermal properties of the media and cytoplasm are assumed to be that of water.

TABLE III.

Number of cases $n$ for each pulse duration.

$t_p(\mathrm{s})$	MCF-7	MCF-10A	MDA-MB-231	GBM	$n_{\text{total}}$
0.01	6	7	8	9	30
0.03	3	7	6	5	21
0.1	9	6	5	4	24
0.25	6	8	8	7	29
0.5	7	3	6	4	20
1	5	3	3	3	14
5	5	5	6	4	20
10	6	3	10	6	25

The total traction $F_0$ as defined in Eq. (A11) is computed as a function of cell radius, applied voltage, and frequency and the results are shown in Fig. 13. Variations in parameters are based on the reference case of $a_0=7.5\mu \mathrm{m},V_{pp}=100\mathrm{V}$, and $f=5\mathrm{M}\mathrm{H}\mathrm{z}$. Note that the relationship with respect to radius and $V_{pp}^2$ are almost linear (this is expected) and the results allow us to use the correlations as a quick lookup table without repeated, additional simulations.

The effect of Joule heating is also evaluated, and an exemplary temperature map for $a_0=7.5\mu \mathrm{m},V_{pp}=50\mathrm{V},f=5\mathrm{M}\mathrm{H}\mathrm{z}$, and $t_p=10\mathrm{s}$ is shown. The maximum temperature rise is 3.4 °C, which is considered insignificant in modifying the cortical mechanical response.

APPENDIX F: ERROR QUANTIFICATION

The rms error for MDA-MB-231, MCF-10A, and GBM cells is shown in Fig. 14 to compare the two analytical methods; the numbers of cells measurements were made in are shown in Table III.