Abstract
Inference of deep phylogenies has almost exclusively used protein rather than DNA sequences based on the perception that protein sequences are less prone to homoplasy and saturation or to issues of compositional heterogeneity than DNA sequences. Here, we analyze a model of codon evolution under an idealized genetic code and demonstrate that those perceptions may be misconceptions. We conduct a simulation study to assess the utility of protein versus DNA sequences for inferring deep phylogenies, with protein-coding data generated under models of heterogeneous substitution processes across sites in the sequence and among lineages on the tree, and then analyzed using nucleotide, amino acid, and codon models. Analysis of DNA sequences under nucleotide-substitution models (possibly with the third codon positions excluded) recovered the correct tree at least as often as analysis of the corresponding protein sequences under modern amino acid models. We also applied the different data-analysis strategies to an empirical dataset to infer the metazoan phylogeny. Our results from both simulated and real data suggest that DNA sequences may be as useful as proteins for inferring deep phylogenies and should not be excluded from such analyses. Analysis of DNA data under nucleotide models has a major computational advantage over protein-data analysis, potentially making it feasible to use advanced models that account for among-site and among-lineage heterogeneity in the nucleotide-substitution process in inference of deep phylogenies.
Keywords: Amino acid models, codon models, deep phylogeny, nonhomogeneous processes, nucleotide substitution, phylogenetic information
In the post-genome age of molecular systematics, we have the luxury of collecting thousands of genes from a large number of species to infer phylogenetic relationships across the tree of life. However, our ability to use genome scale datasets is often compromised by the computational burden of phylogenomic analyses. Despite the continuous development of algorithms for speeding up and parallelising phylogenetic likelihood calculation (Kobert et al. 2014, 2017), inference can take weeks or months on computer clusters for realistically sized datasets. One important factor that drastically affects running times is the data type: analysis of protein sequences under amino acid models requires far more computation than analysis of DNA sequences under nucleotide-substitution models. Codon models (Goldman and Yang 1994; Muse and Gaut 1994) are usually not used in phylogenetic analysis due to their computational cost even though simulations suggest that they have advantages at shallow or intermediate levels of species divergences (Ren et al. 2005; Seo and Kishino 2008).
There is no debate over the use of DNA sequences to resolve relationships of closely related species. For inference of deep phylogenies, such as the origin of the eukaryotes or the diversification of animal phyla, it is generally accepted that protein rather than DNA sequences should be used (Simion et al. 2017; Philippe et al. 2019; Williams et al. 2020). Exclusive use of proteins has become such a standard practice in reconstruction of deep phylogenies that often only protein sequence alignments are archived and provided in the publications while the corresponding DNA alignments are lost, even though the original sequencing projects produced DNA sequences. Claimed advantages of protein sequences include at least the following. First, orthology prediction and multiple sequence alignment are easier at the protein level than at the DNA level (Abascal et al. 2010). Second, protein sequences are less prone to saturation or homoplasy than DNA sequences because of the slower rate of evolution and the larger alphabet (20 amino acids instead of 4 nucleotides). In particular, the third codon positions of the coding genes are known to suffer from saturation. Proteins are also suggested to be more informative because of the larger alphabet. Third, heterogeneous substitution processes may lead to different nucleotide or amino acid compositions among species but protein sequences should be less affected than DNA sequences. Thus protein sequences may be advantageous over DNA sequences because misidentification of orthologous sequences, errors in sequence alignments, and violation of homogeneous substitution models are known to affect phylogenetic accuracy and have been associated with topological and branch length artefacts in reconstructing ancient radiations (Foster 2004; Lartillot et al. 2007; Kapli and Telford 2020; Kapli et al. 2021; Natsidis et al. 2021).
We suggest that those perceived advantages of protein over DNA sequences are largely misconceptions. Given the coding DNA sequences, the protein sequences are available and one can easily identify protein orthologs and align protein sequences to construct the DNA alignment, so it is not harder to get reliable DNA data than proteins. Many of the amino acids are determined by the first two codon positions so one may expect the use of nucleotide-substitution models to analyze the first two codon positions should give similar performance as analysis of the amino acid sequences.
Here, we use theory and computer simulation to demonstrate that DNA sequences (or the first and second codon positions of a coding gene) may be as good as protein sequences for inference of deep phylogenies. Previously, Seo and Kishino (2009) discussed the test of the goodness of fit of nucleotide, amino acid, and codon models applied to the alignments of the same protein-coding gene. Here, our objective is to examine the utility of the different types of models and data for inferring deep phylogenies. We note that nucleotide models have a computational advantage over amino acid models. If nucleotide models are as useful as amino acid models for inferring deep trees, it may be feasible to develop and apply sophisticated models of DNA sequence evolution to accommodate well-known features of the evolutionary process. In particular, while there has been much effort to accommodate heterogeneous substitution rates and nucleotide or amino acid compositions among sites in the sequence (Yang 1994b; Yang et al. 2000; Lartillot and Philippe 2004), compositional heterogeneity among lineages is often not accommodated properly in real data analysis even though it is known to have a strong detrimental impact on inference of deep phylogenies (Lockhart et al. 1994; Yang and Roberts 1995; Foster and Hickey 1999; Foster 2004; Ho and Jermiin 2004; Jermiin et al. 2004; Blanquart and Lartillot 2006, 2008; Jayaswal et al. 2014). This may be because likelihood implementations under amino acid models that account for both among-site and among-lineage compositional heterogeneities involve many parameters and costly computation. However, likelihood methods under similar heterogeneous nucleotide models may be computationally feasible (Yang and Roberts 1995; Foster 2004; Matsumoto et al. 2015).
We first present a theoretical analysis of a Markov chain model for the evolution of codons, amino acids, and nucleotides under a “regular” genetic code to demonstrate that the larger amino acid than nucleotide alphabet does not mean there is more phylogenetic information in protein sequences; indeed under the idealized code, analysis of the protein data is equivalent to analysis of the first two codon positions. We then conduct a simulation study, generating protein-coding gene sequences under models of heterogeneous substitution processes across codons or amino acids in the sequence and among evolutionary lineages on the tree, and analyzing either the DNA or protein sequence alignments using maximum likelihood (ML) to infer the tree (Felsenstein 1981; Stamatakis et al. 2012; Nguyen et al. 2015). We consider different tree shapes, substitution models, and data sizes, as well as strategies of data analysis (DNA versus proteins). We also apply the same strategies of data analysis to an empirical dataset of metazoan protein coding genes. Our analyses of both simulated and real datasets suggest that DNA alignments produce as good trees as the corresponding protein alignments. We discuss future research directions suggested by our results.
Theory: Gene-Sequence Evolution under a Regular Genetic Code
To see that DNA sequences are likely to contain as much information as protein sequences, unrelated to the size of the alphabet, consider a “regular” genetic code, in which all codons are 4-fold degenerate (Yang 2014, p. 64–65). In this code, every substitution at the third position is synonymous (amino acid-preserving) and every substitution at the first or second positions is nonsynonymous (amino acid-altering), with 64 sense codons encoding 16 amino acids. We use this idealized code as a proof of principle, while the real “universal” code is used in later simulation and empirical analyses. Suppose nucleotide substitutions at the three codon positions occur according to the GTR model (Yang 1994a), except that the rate at the first or second positions is reduced by a factor  (which is the nonsynonymous/synonymous rate ratio). We illustrate that under this code, the evolutionary process of the gene sequence can be modeled equivalently at the level of codon triplets or at the level of nucleotides, likelihood analyses under both models will produce identical results, and the size of the alphabet makes no difference. Similarly likelihood analyses of DNA data at the first two codon positions under the nucleotide model and of protein data under the amino acid model are equivalent.
(which is the nonsynonymous/synonymous rate ratio). We illustrate that under this code, the evolutionary process of the gene sequence can be modeled equivalently at the level of codon triplets or at the level of nucleotides, likelihood analyses under both models will produce identical results, and the size of the alphabet makes no difference. Similarly likelihood analyses of DNA data at the first two codon positions under the nucleotide model and of protein data under the amino acid model are equivalent.
Specifically, at the nucleotide level, let the substitution rate from nucleotides  to
to  at the third codon position be
at the third codon position be
| (1) |
with 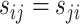 to be the symmetrical part of the rate matrix (the so-called exchangeability rates), where,
to be the symmetrical part of the rate matrix (the so-called exchangeability rates), where, 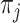 is a frequency or propensity parameter used to account for the bias toward nucleotide
is a frequency or propensity parameter used to account for the bias toward nucleotide 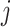 in the mutational process, with
in the mutational process, with  (Yang 1994a; Yang and Nielsen 2008). At the first or second codon position, we multiply the rate by
(Yang 1994a; Yang and Nielsen 2008). At the first or second codon position, we multiply the rate by 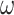 . The substitution process at all three codon positions is then described by a partition model with two partitions, with codon positions 1 and 2 in one partition and codon position 3 in another, and with rates for the two partitions in the ratio
. The substitution process at all three codon positions is then described by a partition model with two partitions, with codon positions 1 and 2 in one partition and codon position 3 in another, and with rates for the two partitions in the ratio  (Yang et al. 1995b; Yang 1996b). The expected number of nucleotide substitutions per site accumulated over time
(Yang et al. 1995b; Yang 1996b). The expected number of nucleotide substitutions per site accumulated over time 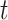 (which may represent the branch length in a species phylogeny or the distance between two sequences) is given as
(which may represent the branch length in a species phylogeny or the distance between two sequences) is given as
| (2) |
at the three codon positions.
At the codon level, let 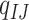 be the substitution rate from codon triplets
be the substitution rate from codon triplets 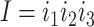 to
to 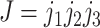 . Substitutions occur independently at the three codon positions, as the rate at one position does not depend on the nucleotide states at the other two positions. Ignoring simultaneous changes at two or three positions in a small time interval, which occur at negligible rates, we get the rate
. Substitutions occur independently at the three codon positions, as the rate at one position does not depend on the nucleotide states at the other two positions. Ignoring simultaneous changes at two or three positions in a small time interval, which occur at negligible rates, we get the rate 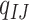 from codons
from codons 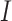 to
to 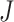 to be nonzero if
to be nonzero if 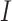 and
and 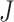 differ at only one position (let the different position be
differ at only one position (let the different position be 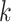 ):
):
| (3) |
where 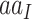 represents the amino acid coded by codon
represents the amino acid coded by codon  . The diagonal elements of the rate matrix,
. The diagonal elements of the rate matrix, 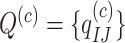 , are given by the requirement that each row of the matrix sums to 0. This model predicts the equilibrium codon frequency
, are given by the requirement that each row of the matrix sums to 0. This model predicts the equilibrium codon frequency
| (4) |
(Yang and Nielsen 2008, Equation (4)). The nucleotide frequencies at each codon position implied by the codon model are given by summing 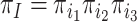 over the other codon positions and are clearly
over the other codon positions and are clearly 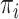 , as in Equation (1). Here, we use
, as in Equation (1). Here, we use 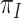 for the frequency of codon
for the frequency of codon 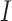 and
and 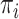 for the frequency of nucleotide
for the frequency of nucleotide  .
.
Let 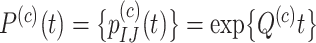 be the transition probability matrix over time
be the transition probability matrix over time 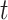 for codons, and
for codons, and 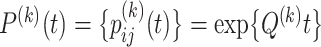 be the transition probability matrix under the nucleotide-substitution model for codon position
be the transition probability matrix under the nucleotide-substitution model for codon position 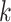 . Then we have, for example,
. Then we have, for example,
| (5) |
because substitutions at the three codon positions are independent (see also Seo and Kishino, 2009, Equation (6), for a more detailed argument). The branch length under the codon model is defined as the expected number of nucleotide substitutions per codon (Goldman and Yang 1994), given as
| (6) |
where 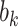 is the branch length at codon position
is the branch length at codon position 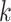 (Equation (2)), with
(Equation (2)), with 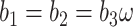 . Note that the sum over
. Note that the sum over  in Equation (6) is in effect over all codon pairs
in Equation (6) is in effect over all codon pairs 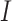 and
and 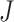 that differ at exactly one position (Equation (3)).
that differ at exactly one position (Equation (3)).
At the codon level, there are 64 letters in the alphabet (sense codons), while at the level of nucleotides there are 4, but the likelihood analyses under the two models at the nucleotide and codon levels are equivalent, with an exact correspondence in the parameters between the models such as the branch lengths. There is no gain in information when the size of the alphabet changes from 4 to 64.
Similarly, if we exclude the third codon positions, the evolutionary process at codon positions 1 and 2 can be described, equivalently, using either an amino acid model with 16 amino acid states or a nucleotide model with 4 nucleotide states. The amount of information in the sequence data remains the same whether the data are treated as protein sequences with 16 amino acids or as DNA sequences with 4 nucleotides. Note that with either type of data, parameter 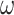 is unidentifiable.
is unidentifiable.
In the real genetic code, not all substitutions at the third codon position are synonymous and also some changes at the first position are synonymous. Seo and Kishino (2008) made an attempt to establish a correspondence between the nucleotide and codon models under the real (“universal”) genetic code. Note that with the real genetic code, if the process of gene sequence evolution is described by a Markov chain at the codon level, it is impossible to construct a Markov chain to describe the changes between amino acids: in other words, under a Markov chain model of codon substitution the synonymous codons for the same amino acid are not “lumpable” (Kemeny and Snell 1960) and the process of amino acid substitution is not Markovian (Curnow 1988; Kosiol and Goldman 2011; Weber et al. 2021; see also Foster et al., 2023; Vera-Ruiz et al. 2022). At any rate, our analysis of the regular code illustrates that the important model assumptions concern the independence or lack thereof of substitutions at the codon positions, rather than the size of the alphabet, and that the larger size of the alphabet for amino acids than for nucleotides does not necessarily mean more information in amino acid sequences. While real-world genetic codes have differences from the idealized code, we expect our conclusions to apply broadly: nucleotide data may be as informative as amino acid data about deep phylogenies. In inference of deep phylogenies, assumptions concerning compositional heterogeneities among sites and among lineages appear to be far more important than the non-Markovian nature of the substitution process: the common practice of using nucleotide models to analyze protein-coding DNA sequences (possibly with the third codon positions excluded) ignores the non-Markovian nature of the substitution process but has produced highly reliable phylogenies, at least at shallow timescales.
Our main objective in this paper is to evaluate the phylogenetic utility of the different types of data in such inference. In theory, codon sequences including all three positions should contain more information than either the first two codon positions or amino acid sequences. However, codon models involve heavy computation, especially if used in phylogenetic tree search. Furthermore current codon models do not accommodate rate and compositional heterogeneity among sites and among lineages, making them unsuitable for inference of deep trees. Thus, in this paper, our main focus is on analysis of DNA data under nucleotide models and of protein data under amino acid models.
Materials and Methods
Simulation of Codon Sequences
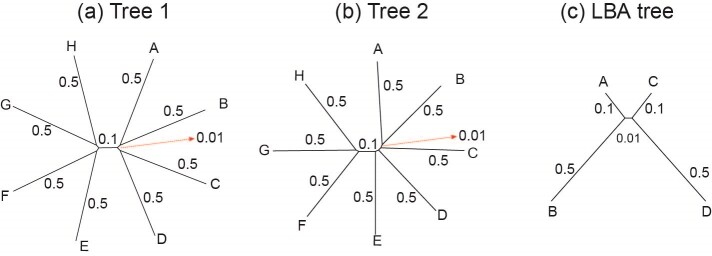
We conducted simulations to assess the performance of different strategies to analyze data of protein-coding genes and the corresponding protein sequences. We simulated codon sequences using INDELible (Fletcher and Yang 2009), using two trees of eight species and a long-branch-attraction (LBA) tree for four species (Fig. 1). In trees 1 and 2, the 8 terminal branches have the length of 0.5 nucleotide substitutions per codon, the 4 short internal branches have the length 0.01 and one longer internal branch has length 0.1. Trees 1 and 2 are unrooted versions of balanced and unbalanced rooted trees, respectively. The LBA tree has two long branches of 0.5 substitutions per codon and two short branches of lengths 0.1, with the internal branch length to be 0.01 (Fig. 1). For each of the three topologies, we created a longer version in which all branch lengths are multiplied by a factor of 4, except for the internal branches of length 0.1 in trees 1 and 2, which were not changed. These are called “deep trees.” In total, six true trees were used, three “shallow,” and three “deep.”
Figure 1.
(a and b) Two eight-taxa trees and (c) a 4-taxa long-branch-attraction (LBA) tree used in the simulation. Branch lengths are in the expected number of nucleotide substitutions per codon. The 4 short branches in trees 1 and 2 have length 0.01. These are the “shallow” trees. We also used three “deep” trees with branches 4 times as long.
Our study focuses on the inference of challenging deep phylogenies. Such phylogenies often include a mixture of very short and very long branches, and the protein-coding genes used tend to be highly conserved with heterogeneous rates and compositions both among sites in the protein sequence and among evolutionary lineages. The model of codon substitution we used to generate gene sequence alignments had two components (Fig. 2). The first concerns possible variation in selective pressure among amino acid residues along the protein sequence reflected in the nonsynonymous/synonymous rate ratio 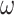 . We used two models: M0 (one-ratio, with one
. We used two models: M0 (one-ratio, with one 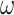 ) and M3 (discrete, with 3
) and M3 (discrete, with 3 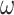 s) (Nielsen and Yang 1998; Yang et al. 2000). Under M0 we used the ratio
s) (Nielsen and Yang 1998; Yang et al. 2000). Under M0 we used the ratio 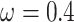 , while under M3 we used 3 site classes in proportions 0.5, 0.4, and 0.1, with
, while under M3 we used 3 site classes in proportions 0.5, 0.4, and 0.1, with 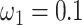 ,
, 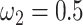 , and
, and 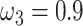 . Note that data simulated under M0 will show different substitution rates at the three codon positions because
. Note that data simulated under M0 will show different substitution rates at the three codon positions because 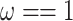 , while M3 will, in addition, cause different substitution rates among amino acid sites of the protein. The same transition/transversion rate ratio is assumed for both models.
, while M3 will, in addition, cause different substitution rates among amino acid sites of the protein. The same transition/transversion rate ratio is assumed for both models.
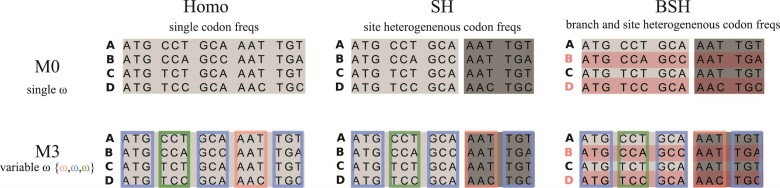
Figure 2.
Illustration of models of gene sequence evolution used in the simulation. The models have two components: (i) M0 (one-ratio or one 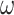 ) versus M3 (discrete or 3
) versus M3 (discrete or 3 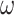 ) concerning the nonsynonymous/synonymous rate ratio (
) concerning the nonsynonymous/synonymous rate ratio (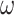 ) among codons in the gene, and (ii) homogeneous or heterogeneous codon frequencies among sites and branches (homo, site-heterogeneous (SH), and branch-site-heterogeneous (BSH)). The homogeneous (homo) model assumes one set of equilibrium codon frequencies, the SH (for SH1 and SH2) models assume multiple sets of codon frequencies among sites (indicated by the grey and dark-gray shading), while the BSH model assumes that the codon frequencies vary both among sites and among lineages (A and C differ in codon compositions from B and D).
) among codons in the gene, and (ii) homogeneous or heterogeneous codon frequencies among sites and branches (homo, site-heterogeneous (SH), and branch-site-heterogeneous (BSH)). The homogeneous (homo) model assumes one set of equilibrium codon frequencies, the SH (for SH1 and SH2) models assume multiple sets of codon frequencies among sites (indicated by the grey and dark-gray shading), while the BSH model assumes that the codon frequencies vary both among sites and among lineages (A and C differ in codon compositions from B and D).
The second component of the simulation model concerns equilibrium codon frequencies. We considered three scenarios, namely homogeneous model (homo), site-heterogeneous model (SH1 and SH2), and branch-site-heterogeneous model (BSH) (Fig. 2).
Homogeneous model (homo) assumes one set of codon frequencies for all sites and all lineages, which were based on the
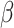 -globin genes from 17 vertebrates and provided in the MCcodon.dat file in the PAML package (Yang 2007).
-globin genes from 17 vertebrates and provided in the MCcodon.dat file in the PAML package (Yang 2007).Site-heterogeneous model 1 (SH1) assumes a mixture of 5 sets of codon frequencies in equal proportions. For one set we used the
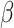 -globin frequencies, while for the other 4 sets, we used codon frequencies based on 4 coding genes from 2 mammals (human and mouse). The genes were selected from a collection available in the OrthoMaM database (https://orthomam.mbb.cnrs.fr/) and the codon frequencies were calculated with codeml.
-globin frequencies, while for the other 4 sets, we used codon frequencies based on 4 coding genes from 2 mammals (human and mouse). The genes were selected from a collection available in the OrthoMaM database (https://orthomam.mbb.cnrs.fr/) and the codon frequencies were calculated with codeml.Site-heterogeneous model 2 (SH2) assumes a mixture of 10 sets of codon frequencies in equal proportions based on the amino acid frequencies of C10 profile mixture model (Si Quang et al. 2008). The frequency for each codon is calculated by the frequency of the amino acid divided by the number of synonymous codons for the amino acid and multiplied by the frequency for the nucleotide at the third codon position, with
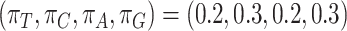 .
.Branch-site-heterogeneous (BSH) model assuming among-site codon frequency heterogeneity as in SH2, but with among-branch nucleotide frequency heterogeneity. As in SH2, the frequency for each codon is calculated by the frequency of the amino acid divided by the number of synonymous codons for the amino acid, and then multiplied by the nucleotide frequency for the nucleotide at the third codon position. The nucleotide frequencies are
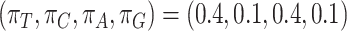 for branches B, D, F, and G in tree 1 and tree 2 and branches B and D in the LBA tree, and by
for branches B, D, F, and G in tree 1 and tree 2 and branches B and D in the LBA tree, and by 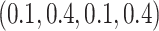 for other branches in the trees including the internal branches.
for other branches in the trees including the internal branches.
Note that models SH1 and SH2 introduce constraints on nonsynonymous substitutions when we consider the whole protein sequence; for each site class certain amino acids are rare and not tolerated at sites belonging to that site class. In addition, our simulation assumes purifying selection removing nonsynonymous mutations due to the use of the  ratio in the M0 and M3 models. Overall there may be strong selection against nonsynonymous mutations as well as extreme heterogeneity in the substitution process among sites. This seems to mimic analysis of very deep phylogenies, which often relies on highly conserved protein sequences.
ratio in the M0 and M3 models. Overall there may be strong selection against nonsynonymous mutations as well as extreme heterogeneity in the substitution process among sites. This seems to mimic analysis of very deep phylogenies, which often relies on highly conserved protein sequences.
In total, we used eight different evolutionary models, with a total of 96 parameter combinations: 6 trees  2
2  models
models  2 data-sizes
2 data-sizes  4 codon frequency-heterogeneity models. The number of codons in the sequence is either 2000 or 5000. The number of simulated replicates is 1000.
4 codon frequency-heterogeneity models. The number of codons in the sequence is either 2000 or 5000. The number of simulated replicates is 1000.
Analysis of Simulated Data
The simulated codon sequences were analyzed at the nucleotide, amino acid, and codon levels to infer the ML tree under different substitution models using the IQ-tree software (Minh et al. 2020). The nucleotide-based analysis used either all three codon positions or only the first two, and as either one partition or separate partitions according to the codon positions. These are referred to as DNA-123 (1 partition), DNA-123-P (three partitions), DNA-12 (1 partition), and DNA-12-P (two partitions). The GTR+G substitution model (Yang 1994a, b) was assumed. For partitioned analysis, branch lengths are assumed to be proportional between partitions, while the exchangeability parameters and base frequencies in the GTR model are estimated separately for the codon positions (Yang et al. 1995b; Yang 1996b).
The translated amino-acid sequences were analyzed under the WAG+G model incorporating rate variation across sites (Whelan and Goldman 2001; Yang 1994b). WAG is a widely used empirical model for amino acid substitution, constructed from large alignments of many proteins (Whelan and Goldman 2001). The relative substitution rates are fixed and not adapted to the protein sequences being analyzed, whereas in the nucleotide-based analysis, the parameters in the GTR model are estimated from the data. To assess the impact of the assumed substitution model, we re-analyzed a subset of the data, those of 5000 codons simulated under the homogeneous (homo) model, under the GTR+G model specified using the IQ-tree option of user-defined amino acid model. This was carried out in two steps. First, for each simulation condition (or tree-model combination), we analyzed one replicate dataset of 5000 sites to estimate the GTR exchangeability rates under the GTR+G model for amino acids using codeml (with the option model = 9) (Yang et al. 1998). The true phylogeny was used. Second, the estimated GTR matrix for each simulation condition was used by IQ-tree to analyze all 1000 replicates to conduct ML tree search.
model for amino acids using codeml (with the option model = 9) (Yang et al. 1998). The true phylogeny was used. Second, the estimated GTR matrix for each simulation condition was used by IQ-tree to analyze all 1000 replicates to conduct ML tree search.
Finally, the gene sequences were also analyzed under the codon model M0 (one ratio), assuming a single 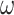 ratio for all sites in the gene sequence and all branches on the tree (Nielsen and Yang 1998). The M3 (discrete) model, which allows variable selective pressures among site classes (
ratio for all sites in the gene sequence and all branches on the tree (Nielsen and Yang 1998). The M3 (discrete) model, which allows variable selective pressures among site classes (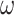 ) (Yang et al. 2000), is not implemented in IQ-tree (Minh et al. 2020) or RAxML-ng (Kozlov et al. 2019). We performed bootstrap analysis with 100 bootstrap replicates.
) (Yang et al. 2000), is not implemented in IQ-tree (Minh et al. 2020) or RAxML-ng (Kozlov et al. 2019). We performed bootstrap analysis with 100 bootstrap replicates.
Assembly of an Empirical Dataset of Metozoan Genes
To assess the performance of the different data types under realistic conditions we assembled an empirical dataset of 22 animal species representing the major metazoan clades. The metazoan phylogeny is vitally important to our understanding of major transitions in evolution such as the origin and evolution of different body plans in animal phyla. However, the relationships among several groups on the phylogeny remain controversial, defying decades of efforts in molecular systematics. Our intention here is not to attempt to resolve the long-standing phylogenetic problem but instead to examine the relative utility of DNA versus protein sequences for inferring deep phylogenies. Studies of metazoan phylogenies have almost exclusively relied on protein sequences (Philippe et al. 2011; Laumer et al. 2015; Telford et al. 2015; Kocot et al. 2017; Cannon et al. 2016; Laumer et al. 2019; Marlétaz et al. 2019; Philippe et al. 2019; Kapli and Telford 2020; Kapli et al. 2021), and no corresponding DNA alignments for the protein sequences analyzed in those studies are easily available. As a result, we have very limited knowledge of whether DNA sequences would yield similar phylogenetic results to protein sequences.
For each of the 22 species, we retrieved raw sequence reads of RNA-seq from NCBI or other resources (Supplementary Table S1) and assembled them de novo using the Trinity pipeline (Grabherr et al. 2011). Protein coding regions were extracted from each assembly using TransDecoder (Haas et al. 2013), as follows: (i) initially, open reading frames of a minimum of 100 amino acids were predicted; (ii) they were scanned against the Pfam (Finn et al. 2014); and the Uniprot (UniProt-Consortium et al. 2018) databases; (iii) the likely coding sequences were predicted, ensuring that the peptides with either a blast or Pfam hit were kept in the final set of coding sequences.
To identify orthologous genes among the 22 transcriptome samples we used the 42 pipeline (Simion et al. 2017), which attempts to enrich a given multiple sequence alignment with corresponding orthologous sequences from multiple transcriptomes of genome samples. We used the metazoa BUSCO (Benchmarking Universal Single-Copy Orthologs) genes available in OrthoDB9 (Zdobnov et al. 2017) as the reference genes and ran 42 for each of them. We used 9 reference proteomes available in OrthoDB9, such that they cover as many different animal phyla as possible and they are present in the majority of the BUSCO genes (i.e., Homo sapiens, Amphimedon queenslandica, Bombus impatiens, Capitella teleta, Lottia gigantea, Saccoglossus kowalevskii, Strongylocentrotus purpuratus, Trichoplax adhaerens, and Nematostella vectensis). However, only the best 4 of them were used in each run (i.e., ref_org_mul-=0.4). The e-value threshold for all blast comparisons was set to 1e-6, the alignment option was disabled, and all the 22 transcriptome samples and the 9 query organisms were converted to blast databases using the makeplastdb application (Camacho et al. 2009), which were used as input for the 42 pipeline. In the case of multiple transcripts per species for a given orthologous group, we selected the longest one and discarded the rest. To align the amino acid and corresponding nucleotide sequences, we used mafft-linsi (Katoh et al. 2005) with the TranslatorX wrapper (Abascal et al. 2010). From the alignment we removed codons represented by fewer than two species. The procedure led to a super-alignment of 941 orthologous coding loci (with 440,195 codons or 1,320,585 bps).
Phylogenetic Analysis of Metazoan Dataset
The DNA and protein alignments were analyzed under nucleotide and amino acid models implemented in IQ-tree. For the nucleotide data (either including or excluding the third codon positions), each codon position is assigned to a separate partition with a GTR+G model (Yang 1994a, b). Branch lengths were assumed to be proportional among partitions (-p option in IQ-tree). These are the DNA-123-P and DNA-12-P analyses described above.
For the amino acid alignment we performed two analyses with IQ-tree, under the WAG+G and GTR+G models. For GTR+G, the exchangeability parameters were estimated using codeml (Yang 2007; Yang and Nielsen 2008) under GTR+G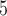 , assuming the tree inferred with IQ-tree under the WAG+G model, and then used in ML tree search by IQ-tree, specified as a user-defined model. For all IQ-tree inferences we also performed bootstrap analyses using the ultrafast bootstrap approximation (Hoang et al. 2018).
, assuming the tree inferred with IQ-tree under the WAG+G model, and then used in ML tree search by IQ-tree, specified as a user-defined model. For all IQ-tree inferences we also performed bootstrap analyses using the ultrafast bootstrap approximation (Hoang et al. 2018).
Models that allow heterogeneous nucleotide or amino acid compositions both among sites and among branches are currently lacking in ML programs such as IQ-tree (Minh et al. 2020) and RAxMLKozlov et al. (2019). We used the Bayesian program PhyloBayes (Lartillot et al. 2013) to analyze the protein data under the CAT+GTR+G model, which accommodates heterogeneous amino acid compositions across sites (Lartillot and Philippe 2004). As the program involves heavy computation, we constructed two data subsets with 40,000 randomly sampled amino acid residues each. The analysis for each subset was conducted twice, each with 10,000 MCMC steps, with the first 2500 samples discarded as burnin. Convergence of the MCMC was assessed by examining the differences in split frequencies between runs: for the first subset we achieved 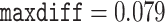 and
and 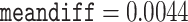 while for the second subset they were
while for the second subset they were 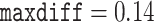 and meandiff 0.0056. As the recommendation was for to assume convergence, we extended the second run to a total of 15,000 MCMC iterations and 5000 samples discarded as burnin which resulted in
and meandiff 0.0056. As the recommendation was for to assume convergence, we extended the second run to a total of 15,000 MCMC iterations and 5000 samples discarded as burnin which resulted in 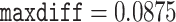 .
.
Simulation Based on the Metazoan Data
We performed a small simulation using parameters estimated from the metazoan dataset. We used two of the inferred tree topologies (trees a and c, Fig. 3) with branch lengths, the transition/transversion ratio (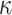 ), and the
), and the 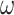 values and proportions for three site classes under the M3 (discrete) model, estimated using codeml (Yang et al. 2000; Yang 2007). We used two data sizes, with 2000 and 5000 sites, respectively. We did not use the homogeneous models; instead, we assumed the site-heterogeneous (SH2) and branch-site-heterogeneous (BSH) models of codon frequencies described above. For both trees we assigned different nucleotide frequencies to the protostomes (Lophotrochozoa and Ecdysozoa) and the Porifera, which were also different from frequencies for the rest of the tree. In total there were 8 parameter combinations (2 trees
values and proportions for three site classes under the M3 (discrete) model, estimated using codeml (Yang et al. 2000; Yang 2007). We used two data sizes, with 2000 and 5000 sites, respectively. We did not use the homogeneous models; instead, we assumed the site-heterogeneous (SH2) and branch-site-heterogeneous (BSH) models of codon frequencies described above. For both trees we assigned different nucleotide frequencies to the protostomes (Lophotrochozoa and Ecdysozoa) and the Porifera, which were also different from frequencies for the rest of the tree. In total there were 8 parameter combinations (2 trees 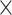 2 data sizes
2 data sizes 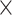 2 models) and for each we generated 100 replicate datasets.
2 models) and for each we generated 100 replicate datasets.
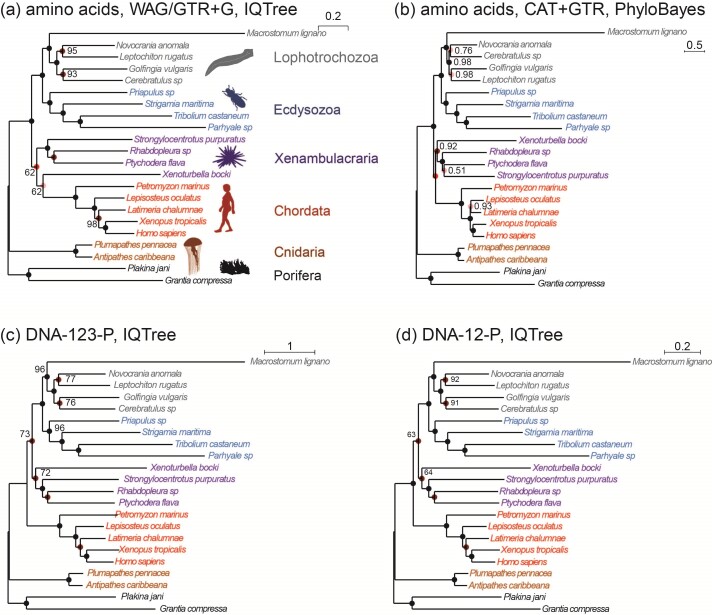
Figure 3.
Phylogenies of 22 animal species reconstructed from ML and Bayesian analyses of an dataset of 941 orthologous genes (440,195 codons or amino acids). (a) The protein sequences are analyzed using IQ-tree under the WAG+G and GTR+G models. (b) The protein alignment for one of the two data subsets (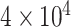 sites) is analyzed under the CAT+GTR model using PhyloBayes (the topology for the second subset is shown in Supplementary Fig. S1). (c) The DNA sequence data are analyzed under a nucleotide partition model with three partitions for the 3 codon positions. (d) The first and second codon positions are analyzed using IQ-tree under a nucleotide partition model. Note that trees C and D are identical. The color of the circles on the nodes indicates whether the node is recovered in all 4 (black), in 3 (dark red), or in two (red) analyses or in only one analysis (pink). The number next to each internal node represents the bootstrap support (or the posterior probability for phylobayes) for the node (not shown if 100%).
sites) is analyzed under the CAT+GTR model using PhyloBayes (the topology for the second subset is shown in Supplementary Fig. S1). (c) The DNA sequence data are analyzed under a nucleotide partition model with three partitions for the 3 codon positions. (d) The first and second codon positions are analyzed using IQ-tree under a nucleotide partition model. Note that trees C and D are identical. The color of the circles on the nodes indicates whether the node is recovered in all 4 (black), in 3 (dark red), or in two (red) analyses or in only one analysis (pink). The number next to each internal node represents the bootstrap support (or the posterior probability for phylobayes) for the node (not shown if 100%).
Results
Results of the Simulation Experiment
We simulated coding sequences using the three trees of Figure 1, with branch lengths representing “shallow” and “deep” trees. Our simulation incorporated variable selective pressure among sites (model M0: one-ratio versus model M3: discrete with 3 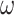 s), as well as compositional heterogeneity among sites (SH1, SH2) and among both branches and sites (BSH). The data were analyzed at the nucleotide, amino acid, and codon levels. The results are summarized in Figures 4 and 5. Note that in all analyses the model was misspecified except the codon-based analysis of codon sequences generated under the M0 and the homo models. Current likelihood programs do not have models that accommodate both branch- and site-heterogeneity of the substitution process, although IQ-tree has models that accommodate among-site heterogeneity in amino acid compositions.
s), as well as compositional heterogeneity among sites (SH1, SH2) and among both branches and sites (BSH). The data were analyzed at the nucleotide, amino acid, and codon levels. The results are summarized in Figures 4 and 5. Note that in all analyses the model was misspecified except the codon-based analysis of codon sequences generated under the M0 and the homo models. Current likelihood programs do not have models that accommodate both branch- and site-heterogeneity of the substitution process, although IQ-tree has models that accommodate among-site heterogeneity in amino acid compositions.
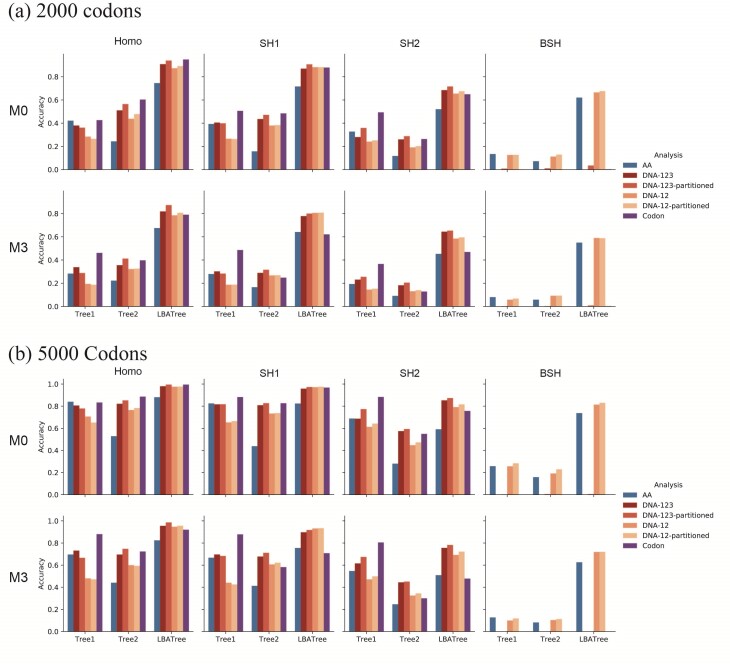
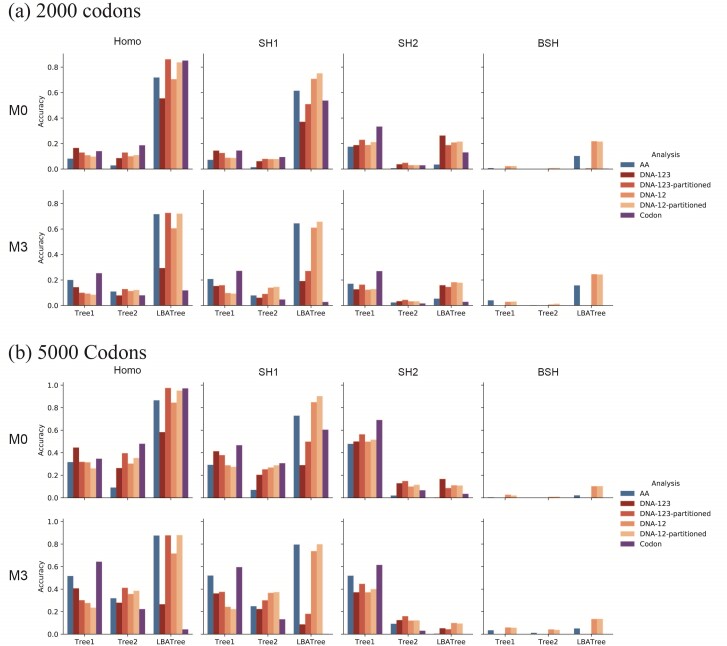
Figure 4.
Probability of recovering the correct tree in 1000 replicate datasets with (a) 2000 sites or (b) 5000 sites simulated assuming the shallow trees of Figure 1. The models assumed to generate data are as follows. The selective pressure on nonsynonymous mutations was either homogeneous among sites (M0: 1 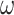 ) or variable (M3: 3
) or variable (M3: 3 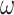 s) (Nielsen and Yang 1998)). The codon frequencies are modelled using four different models (homo, SH1, SH2, and BSH). Homo is the homogeneous model with one set of codon frequencies for all sites in the sequence and all branches on the tree. SH1 assumes site-heterogeneous codon-frequencies generated from observed codon frequencies in coding genes from two mammal species. SH2 assumes site-heterogeneous codon-frequencies generated using the amino acid frequencies in the C10 mixture model, multiplied by nucleotide frequencies at the third codon position. BSH assumes branch-site-heterogeneous codon frequencies as in SH2, but with additional among-branch nucleotide-frequency heterogeneity. The six data-analysis strategies are “AA”: analysis of amino acid sequences under the WAG+G model; “DNA-123”: analysis of nucleotide sequences of all three codon positions using the nucleotide model GTR+G; ‘DNA-123-P’: analysis of all three codon positions using a nucleotide partition model that assigns different rates and base frequencies to the three codon positions (Yang et al. 1995b; Yang 1996b)); “DNA-12”: analysis of codon positions 1 and 2 using the nucleotide model GTR+G; “DNA-12-P”: analysis of codon positions 1 and 2 using a nucleotide partition model; and “codon”: analysis of the codon sequences (all three codon positions) using the codon model M0 (one-ratio) (Nielsen and Yang 1998).
s) (Nielsen and Yang 1998)). The codon frequencies are modelled using four different models (homo, SH1, SH2, and BSH). Homo is the homogeneous model with one set of codon frequencies for all sites in the sequence and all branches on the tree. SH1 assumes site-heterogeneous codon-frequencies generated from observed codon frequencies in coding genes from two mammal species. SH2 assumes site-heterogeneous codon-frequencies generated using the amino acid frequencies in the C10 mixture model, multiplied by nucleotide frequencies at the third codon position. BSH assumes branch-site-heterogeneous codon frequencies as in SH2, but with additional among-branch nucleotide-frequency heterogeneity. The six data-analysis strategies are “AA”: analysis of amino acid sequences under the WAG+G model; “DNA-123”: analysis of nucleotide sequences of all three codon positions using the nucleotide model GTR+G; ‘DNA-123-P’: analysis of all three codon positions using a nucleotide partition model that assigns different rates and base frequencies to the three codon positions (Yang et al. 1995b; Yang 1996b)); “DNA-12”: analysis of codon positions 1 and 2 using the nucleotide model GTR+G; “DNA-12-P”: analysis of codon positions 1 and 2 using a nucleotide partition model; and “codon”: analysis of the codon sequences (all three codon positions) using the codon model M0 (one-ratio) (Nielsen and Yang 1998).
Figure 5.
Probability of recovering the correct tree when data are simulated assuming the deep trees of Figure 1. See legend to Figure 4.
Shallow trees.—The shallow trees were easy to reconstruct when the data were simulated under the site-homogeneous and even site-heterogeneous models (homo, SH1, and SH2) (Fig. 4), and all methods performed well. Furthermore, performance for all methods was better for large datasets of 5000 codons than for 2000 codons, suggesting that all methods are consistent in estimating the tree topology despite the model misspecification, and that they are expected to become increasingly accurate when the sequence length increases. Consistent with this interpretation, the average bootstrap support was higher when the estimated tree was the correct tree than when it was any wrong tree (Supplementary Table S2). All 4 nucleotide-based analyses (DNA-123, DNA-123-P, DNA-12, and DNA-12-P) performed similarly well regardless of whether or not the sequences were partitioned. Including third positions in the data often improved performance, despite the high level of sequence divergence at the third codon positions (Supplementary Table S3). This is particularly the case for trees 1 and 2 with 8 taxa, for which the codon-based analysis was often much better than the protein-based analysis (Fig. 4).
When the data were simulated under the BSH model with compositional differences among both branches and sites, the methods performed drastically differently. Analyses of nucleotide data including third codon positions (DNA-123, DNA-123-P, and codon) were the worst, with the probability of recovering the true tree at 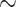 0% at both 2000 and 5000 sites (or codons). Not only was the ML tree incorrect, the incorrect estimate was supported with very high bootstrap probabilities (Supplementary Table S2). We conclude that those methods are statistically inconsistent in this setting. Note that in the simulation under the BSH model, the among-lineage compositional heterogeneity affected the third codon positions only. Nucleotide-based analyses excluding third codon positions (DNA-12 and DNA-12-P) and amino acid-based analysis performed much better than nucleotide-based analysis including all three positions (DNA-123 and DNA-123-P), with DNA-12 and DNA-12-P being very slightly better than amino acid-based analysis. All these three methods (DNA-12, DNA-12-P, and AA) appeared to be statistically consistent, as the performance was better at 5000 sites than at 2000 sites, and as the bootstrap support for incorrect ML trees were lower than for correct ML trees (Table S2).
0% at both 2000 and 5000 sites (or codons). Not only was the ML tree incorrect, the incorrect estimate was supported with very high bootstrap probabilities (Supplementary Table S2). We conclude that those methods are statistically inconsistent in this setting. Note that in the simulation under the BSH model, the among-lineage compositional heterogeneity affected the third codon positions only. Nucleotide-based analyses excluding third codon positions (DNA-12 and DNA-12-P) and amino acid-based analysis performed much better than nucleotide-based analysis including all three positions (DNA-123 and DNA-123-P), with DNA-12 and DNA-12-P being very slightly better than amino acid-based analysis. All these three methods (DNA-12, DNA-12-P, and AA) appeared to be statistically consistent, as the performance was better at 5000 sites than at 2000 sites, and as the bootstrap support for incorrect ML trees were lower than for correct ML trees (Table S2).
Note that the performance of the methods showed large differences depending on the substitution model used to generate the data, even though the same phylogeny and the same branch lengths were used. The models assumed in the IQ-tree analyses, such as GTR+G for nucleotides and WAG+G for amino acids, accommodated the among-site variation in substitution rates, but not among-site variation in nucleotide or amino acid compositions or among-lineage variation in nucleotide or amino acid compositions. Method performance was good if the true substitution process was homogeneous, in which case the simulation model and the analysis model nearly matched each other, while performance was far poorer when the data were simulated under the heterogeneous models (SH1, SH2, and BSH). The variable selective pressures among amino acid residues (model M3 with three 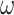 s instead of M0 with one
s instead of M0 with one 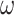 ) had relatively minor adverse effects, perhaps because the analysis model already accommodated among-site variation in rates (even if imperfectly). Among-site compositional heterogeneity (as in data simulated under SH1 and SH2) added challenges to the inference, while among-lineage compositional heterogeneity (as in the BSH model) made the trees very difficult to recover.
) had relatively minor adverse effects, perhaps because the analysis model already accommodated among-site variation in rates (even if imperfectly). Among-site compositional heterogeneity (as in data simulated under SH1 and SH2) added challenges to the inference, while among-lineage compositional heterogeneity (as in the BSH model) made the trees very difficult to recover.
Deep trees.—When the deep trees were used to simulate data, the sequences were much more divergent, and the different methods performed far more poorly and also showed greater differences among them than under the shallow trees (Fig. 5). Overall, the relative performance of the different methods showed similar patterns as in the simulation under the shallow trees. Under the homogeneous model (homo), nucleotide-based analyses including third codon positions (DNA-123, DNA-123-P, codon) were most often superior to amino acid-based analyses at recovering trees 1 and 2, with the codon-based analysis showing much better performance. Note that the third codon positions in those simulations were highly divergent, with, for example, 2.51 nucleotide substitutions per site in data simulated under the LBA tree and the BSH+M3 model (Supplementary Table S2). The result is consistent with the early observation that likelihood-based phylogenetic analyses are robust to multiple substitutions at the same site (i.e., saturation or homoplasy) (Yang 1998). However, high divergences are often associated with many other issues such as orthology identification errors, alignment errors, and serious model violations due to compositional heterogeneity among sites and among lineages.
On the LBA tree, codon-based analysis was much worse and appeared to be inconsistent, as the probability of recovering the true tree was lower at 5000 sites than at 2000 sites. We used the codeml program in the paml package (Yang 2007) to compare candidate trees under the M3 (discrete) model, assuming 3 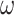 classes, which confirmed that ML under M3 was indeed consistent, with higher probability of recovering the correct tree at 5000 sites than at 2000 sites (88.2% vs. 75.2%). The inconsistency of the M0 model here is similar to the well-known inconsistency of ML under the one-rate model (and parsimony) when the data are generated on an LBA tree with variable rates among sites (e.g., Yang 1997; Swofford et al. 2001).
classes, which confirmed that ML under M3 was indeed consistent, with higher probability of recovering the correct tree at 5000 sites than at 2000 sites (88.2% vs. 75.2%). The inconsistency of the M0 model here is similar to the well-known inconsistency of ML under the one-rate model (and parsimony) when the data are generated on an LBA tree with variable rates among sites (e.g., Yang 1997; Swofford et al. 2001).
The results under the SH1 model were similar to those under the homo model. Under SH2, codon-based analysis was superior on tree 1 but much worse on the LBA tree. Similarly, including third codon positions (DNA-123 and DNA-123-P vs. DNA-12 and DNA-12-P)was slightly beneficial for reconstructing tree 1 but not for tree 2 and was worse for the LBA tree. For the LBA tree and when the substitution process involved extreme among-site and among-lineage compositional heterogeneity (BSH), amino acid-based analysis and nucleotide-based analysis of the first two codon positions (DNA-12 and DNA-12-P) were much more robust.
In summary, inclusion of third codon positions (DNA-123, DNA-123-P, and codon) improved performance for trees 1 and 2 if the substitution model was homogeneous or only mildly heterogeneous (as in SH1), but when the substitution process is highly heterogeneous (SH2 and BSH), model violations caused the analyses of all three codon positions to fail. In all our simulations, DNA-based analyses of the first two codon positions (DNA-12 and DNA-12-P) were sometimes considerably better, but never much worse, than protein-based analyses.
In contrast to simulations under shallow trees, performance sometimes worsened with the increase of data size in simulations under the deep trees, in particular under the deep LBA tree (Fig. 5 and Supplementary Table S4), indicating that the methods were inconsistent. In those cases, the bootstrap support was higher for the wrong trees than for the correct tree (Supplementary Table S4).
Note that in the DNA-based analysis, we used the GTR+G model, with the GTR exchangeability rates estimated by ML from the data. However, in amino acid-based analysis, the empirical WAG model was assumed and the amino acid exchangeability rates were not optimized to fit the data being analyzed. To assess the effects of the assumed substitution model, we re-analyzed the datasets of 5000 codons simulated under the homogeneous (homo) model. One replicate dataset was analyzed using codeml to estimate the GTR matrix, which was then used as the user-defined model by IQ-tree for phylogenetic tree search. The results are shown in Table 1. Compared with WAG+G, use of the GTR+G model performed slightly worse on data simulated under tree 1 and model M3 (discrete), but considerably better on data simulated under tree 2 and the LBA tree. We suspect that the use of the true tree to estimate the rate matrix does not matter much as previous studies have noted that the MLEs of the rate matrix are relatively insensitive to the tree topology as long as the tree is a reasonably good one (e.g., Yang et al. 1995a; Sullivan et al. 2005). However, there are substantial sampling errors in the estimates even with long sequences of 5000 amino acids, possibly because all three trees are small with only 4 or 8 sequences. Indeed estimates from two replicate datasets of the same simulation condition (tree-model combination) are just as different as those from different simulation conditions (Supplementary Fig. S2).
Table 1.
Probability of recovering the correct tree in 1000 replicate datasets with 5000 codons simulated under the homogeneous (homo) model
| Homo, short trees | Homo, deep trees | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tree 1 | Tree 2 | LBA Tree | Tree 1 | Tree 2 | LBA Tree | |||||||
| Sim model | M0 | M3 | M0 | M3 | M0 | M3 | M0 | M3 | M0 | M3 | M0 | M3 |
| AA-WAG+G | 0.84 | 0.70 | 0.53 | 0.44 | 0.88 | 0.82 | 0.32 | 0.52 | 0.09 | 0.32 | 0.87 | 0.88 |
| AA-GTR+G | 0.80 | 0.62 | 0.78 | 0.63 | 0.97 | 0.93 | 0.32 | 0.41 | 0.36 | 0.55 | 0.92 | 0.90 |
| DNA-123 | 0.81 | 0.73 | 0.82 | 0.70 | 0.98 | 0.96 | 0.45 | 0.41 | 0.26 | 0.28 | 0.58 | 0.27 |
| DNA-123-P | 0.78 | 0.67 | 0.85 | 0.75 | 1.00 | 0.99 | 0.32 | 0.30 | 0.40 | 0.41 | 0.97 | 0.88 |
| DNA-12 | 0.71 | 0.48 | 0.76 | 0.60 | 0.98 | 0.95 | 0.31 | 0.28 | 0.30 | 0.36 | 0.84 | 0.72 |
| DNA-12-P | 0.65 | 0.47 | 0.78 | 0.59 | 0.98 | 0.96 | 0.26 | 0.24 | 0.35 | 0.39 | 0.95 | 0.88 |
| Codon (M0) | 0.83 | 0.88 | 0.89 | 0.72 | 1.00 | 0.92 | 0.35 | 0.64 | 0.48 | 0.22 | 0.97 | 0.04 |
Note: The AA-GTR+G model used the GTR exchangeability rates for amino acids estimated from one of the simulated replicates using codeml (Supplementary Fig. S2). The other 6 data-analysis strategies are defined in the legend to Figure 4, and the results are plotted in Figures 4 and 5 (homo).
Phylogenetic Analysis of the Metazoan Dataset
We analyzed a super-alignment of 941 orthologous genes (1,320,585 bp) at the amino acid, nucleotide, and codon levels using IQ-tree. For the nucleotide data, we either included or excluded the third codon position, with the sites partitioned by codon position and with the GTR+G model applied to each partition. For the protein data, we used the WAG+G model with homogeneous amino acid frequencies. We also applied PhyloBayes (Lartillot et al. 2013) to analyze a subset of the protein data under the CAT+GTR+G model.
All 4 analyses produced similar tree topologies (Fig. 3). In particular, the two DNA-based analyses (DNA123-P and DNA12-P) produced the same tree. The WAG+G and GTR+G models for the amino acid data produced the same tree, which differed from the DNA tree. The CAT+GTR+G model applied to the two protein data subsets produced two different trees, which also differed from all others. The two PhyloBayes analyses differed in the recovered relationships of the Lophotrochozoa lineages with the exception of the flatworm (Macrostomum lignano). Overall, the differences among all inferred trees concern parts of the phylogeny that had low bootstrap support or posterior probability and are known controversial parts of the animal phylogeny (Philippe et al. 2011; Laumer et al. 2015; Telford et al. 2015; Kocot et al. 2017; Cannon et al. 2016; Laumer et al. 2019; Marlétaz et al. 2019; Philippe et al. 2019; Kapli and Telford 2020; Kapli et al. 2021).
One of the topological differences concerns the Deuterostome monophyly (clustering of Chordata and Xenambulacraria), which is recovered with the amino acid data under the WAG+G and the CAT+GTR+G model but not in the DNA-based analyses. Deuterostomes have been a long-trusted clade in the animal phylogeny. However, it was not supported in recent phylogenomic studies (Marlétaz et al. 2019; Philippe et al. 2019), and was hypothesized to be an artefact of model misspecification (Kapli et al. 2021). Similarly, the placement of Xenacoelomorpha is uncertain, either sister to Nephrozoa (Lophotrochozoa, Ecdysozoa, Ambulacraria, Chordata) (Cannon et al. 2016) or to Ambulacraria (Philippe et al. 2019; Kapli and Telford 2020). Both topologies were recovered using amino acid data under different taxon sampling or substitution models (Cannon et al. 2016; Philippe et al. 2019; Kapli and Telford 2020). Here, the Xenambulacraria hypothesis was supported by all analyses except the protein-based analysis underWAG+G, which places Xenoturbella as sister to Chordates.
Another topological difference concerns the relationships among the Lophotrochozoa lineages, which were recovered similarly by all analyses except the two PhyloBayes analyses of the protein data subset under CAT+GTR+G. Previous analyses of protein sequences sampled across the genome under similar models produced multiple and conflicting phylogenetic relationships among the Lophotrochozoa phyla (Laumer et al. 2015; Kocot et al. 2017; Marlétaz et al. 2019). Therefore, the fragile phylogenetic signal for this clade may be the main reason for the different topologies recovered. Our use of a reduced dataset to runPhyloBayes may also be a factor, and may explain other unique relationships in the analysis, such as the grouping of Ptychodera with Strongylocentrotus, and Lepisosteus with Latimeria. Both these relationships are weakly supported and appeared to be incorrect.
Overall, these results suggest that the differences among the 4 recovered topologies are not surprising and reflect the challenges in reconstructing the relationships of different animal phyla no matter what types of data are used. Similarly the DNA trees for the metazoa are just as plausible as the protein trees. We note that none of the models used in the ML analyses here accommodates the among-site and among-branch compositional heterogeneity considered in our simulations. The Bayesian analysis using PhyloBayes accounts for among-site compositional heterogeneity but not among-lineage compositional heterogeneity.
Simulations Based on the Metazoan Data
We used parameter estimates from the metazoan data to perform simulations that resemble more closely an empirical case for which phylogenomic analysis is traditionally conducted using protein data. We used trees A and C of Figure 3, with estimates of the transition/transversion rate ratio 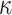 and
and 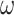 obtained using codeml under M0 (one-ratio) (Yang 2007). We used the same site-heterogeneous (SH2) and branch-site-heterogeneous (BSH) models to simulate replicate datasets, as described before (the homo model was not used), and each simulated dataset was analyzed as amino acid, nucleotide, and codon sequences as before.
obtained using codeml under M0 (one-ratio) (Yang 2007). We used the same site-heterogeneous (SH2) and branch-site-heterogeneous (BSH) models to simulate replicate datasets, as described before (the homo model was not used), and each simulated dataset was analyzed as amino acid, nucleotide, and codon sequences as before.
The estimated terminal branch lengths for trees A and C ranged from 0.5 to 8.7 (with the mean of 2.9) substitutions per codon, which resembled the terminal branch lengths of the “deep” trees used in our simulations before. The internal branch lengths in the empirical trees ranged from 0.16 to 2.5 (with a mean of 0.56), substantially greater than the internal branch lengths assumed before (0.01), suggesting that the empirical trees may be easier to recover, and that the deep simulations may be relevant to even more challenging instances of deep divergences than the animal phylogeny.
Indeed the two empirical trees were recovered by all methods/strategies with high probabilities when the data were simulated under the SH2 model (Table 2). Under the BSH model, the third codon positions are drifting toward different nucleotide frequencies, and the DNA-based analyses including third codon positions (DNA-123, DNA-123-P, codon) did not recover the true tree in any of the replicates, as the models did not accommodate the compositional heterogeneity among lineages. The other methods performed well. Nucleotide-based analyses of the first two positions, with and without site partitioning (DNA-12 and DNA-12-P) performed at least as well as analysis of the amino acid sequences (Table 2). The results are in good agreement with the simulations using the smaller trees of Figure 1.
Table 2.
Probability of recovering the metazoan phylogenies A and C of Figure 3 by different methods in 100 replicate datasets of 2000 and 5000 sites simulated under the site-heterogeneous (SH2) and branch-site-heterogeneous (BSH) models
| SH2 | BSH | |||||||
|---|---|---|---|---|---|---|---|---|
| tree A | Tree C | Tree A | Tree C | |||||
| Method | 2K | 5K | 2K | 5K | 2K | 5K | 2K | 5K |
| AA | 83 | 98 | 72 | 98 | 57 | 81 | 51 | 88 |
| DNA-123 | 84 | 100 | 76 | 100 | 0 | 0 | 0 | 0 |
| DNA-123-P | 92 | 100 | 78 | 100 | 0 | 0 | 0 | 0 |
| DNA-12 | 86 | 98 | 76 | 100 | 66 | 89 | 58 | 87 |
| DNA-12-P | 82 | 98 | 72 | 100 | 65 | 90 | 59 | 94 |
| Codon | 63 | 88 | 46 | 91 | 0 | 0 | 0 | 0 |
Note: Datasets were simulated assuming trees A and C of Figure 3, using parameter estimates from the empirical dataset.
Discussion
Challenges of Inferring Deep Phylogenies
In our simulation, the accuracy of phylogeny reconstruction varied considerably depending on a number of factors, such as the shape of the phylogeny (relative lengths of the internal and external branches and relative placement of long branches on the tree), the sequence divergence levels (shallow vs. deep trees), and the complexity of the substitution process, such as variable strength of natural selection removing deleterious nonsynonymous mutations (the 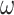 ratio), among-site heterogeneity in substitution rates and in nucleotide and amino acid compositions, and among-lineage compositional heterogeneity. The multiple factors also interact in complex ways, so that we found it challenging to explain many of the simulation results of Figures 4 and 5, even though we verified their correctness. The differences between trees 1 and 2 are particularly intriguing. For example, amino acid-based analysis under WAG+G was substantially worse for tree 2 than for tree 1 (Figs. 4 and 5). This seems to be related to the different placements of the short internal branches in the two trees. While both trees have four short internal branches, tree 1 may be easier to recover than tree 2, as its short branches are separate, creating fewer nearly equally supported trees around the very short branches, out of which one is the true tree. In tree 1, there are 15 nearly equally good resolutions for the taxa
ratio), among-site heterogeneity in substitution rates and in nucleotide and amino acid compositions, and among-lineage compositional heterogeneity. The multiple factors also interact in complex ways, so that we found it challenging to explain many of the simulation results of Figures 4 and 5, even though we verified their correctness. The differences between trees 1 and 2 are particularly intriguing. For example, amino acid-based analysis under WAG+G was substantially worse for tree 2 than for tree 1 (Figs. 4 and 5). This seems to be related to the different placements of the short internal branches in the two trees. While both trees have four short internal branches, tree 1 may be easier to recover than tree 2, as its short branches are separate, creating fewer nearly equally supported trees around the very short branches, out of which one is the true tree. In tree 1, there are 15 nearly equally good resolutions for the taxa  , and
, and 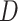 and 15 for
and 15 for 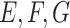 , and
, and 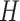 , making a total of 225 nearly equally good trees. In tree 2, there are 105 resolutions for
, making a total of 225 nearly equally good trees. In tree 2, there are 105 resolutions for  , and
, and  , and three resolutions for
, and three resolutions for  , and
, and 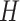 , making a total of 305 nearly equally good trees. This may be a contributing factor for the lower accuracy in recovering tree 2, but it does not explain the substantially lower accuracy of amino acid-based inference than DNA-based analysis. Use of the GTR+G model for amino acids improved the performance under tree 2 considerably (Table 1), suggesting that part of the difficulty may be the poor fit of the WAG matrix to protein data simulated under tree 2. However, it is unclear why similar poor model-fit did not cause poor performance for data simulated under tree 1. There seems to be a disconnect between the goodness of fit of the assumed model and the accuracy of the inferred phylogeny, as noted previously in analyses of both simulated and empirical data (e.g., Yang 1997; Abadi et al. 2019; Spielman 2020).
, making a total of 305 nearly equally good trees. This may be a contributing factor for the lower accuracy in recovering tree 2, but it does not explain the substantially lower accuracy of amino acid-based inference than DNA-based analysis. Use of the GTR+G model for amino acids improved the performance under tree 2 considerably (Table 1), suggesting that part of the difficulty may be the poor fit of the WAG matrix to protein data simulated under tree 2. However, it is unclear why similar poor model-fit did not cause poor performance for data simulated under tree 1. There seems to be a disconnect between the goodness of fit of the assumed model and the accuracy of the inferred phylogeny, as noted previously in analyses of both simulated and empirical data (e.g., Yang 1997; Abadi et al. 2019; Spielman 2020).
Multiple factors contribute to the challenge of inferring deep phylogenies. Here, we discuss some of them with reference to the choice of DNA versus protein data for phylogeny reconstruction. At deep divergences, data quality can become a major issue, including possible errors in orthology prediction, sequence alignment, and so on. These issues should not affect one’s choice of DNA versus protein data, since it is equally difficult to obtain high-quality protein versus DNA data. Choice of data types should thus depend on the information content in the DNA and protein alignments, the violation of assumptions in the assumed model and the resulting systematic biases in the inference methods applied to the different types of data. Availability of sophisticated nucleotide or amino acid models that accommodate heterogeneous substitution processes as well as the computational load may also be an important factor.
In our simulation, when the phylogeny is relatively easy and the substitution process is homogeneous or involves only mild among-site compositional heterogeneity, codon models or nucleotide-based analyses, including all three codon positions (DNA-123, DNA-123-P, and codon), tend to be most accurate. This may be explained by the fact that there is an important phylogenetic information in data of third codon positions. Previous studies also highlighted the advantages of codon models for reconstruction of shallow phylogenies for closely related species (Ren et al. 2005; Seo and Kishino 2008). However, if the phylogeny is challenging, involving long-branch attraction, and if the substitution process involves extreme among-site and among-lineage compositional heterogeneity, the homogeneous models performed poorly (Figs. 4 and 5). Removing third codon positions improved the performance of DNA-based analyses in our simulation as it improved the model fit to the remaining first and second position data. Our simulation highlighted the dramatic effects of among-lineage compositional heterogeneity on inference of deep phylogenies (Figs. 4 and 5 and Table 2). Different nucleotide or amino acid frequencies are commonly observed in real data for deep phylogenies (Feuda et al. 2017; Laumer et al. 2018). When such process heterogeneity is not accommodated, reconstruction methods may be misled to group species according to nucleotide or amino acid compositions rather than the evolutionary history of the species (Lockhart et al. 1994; Yang and Roberts 1995; Foster and Hickey 1999).
The impacts of heterogeneous processes on phylogenetic reconstruction have been noted in numerous empirical studies. Rota-Stabelli et al. (2013) reconstructed phylogenies for Pancrustacean (a clade of animals) using both DNA and protein sequences, and found that the protein phylogeny depended on whether the model assumed homogeneous or heterogeneous compositions among sites, while the DNA phylogeny was affected by serine codon usage (with TCN codons used in some clades and AGY in others), highlighting the importance of accommodating among-lineage compositional heterogeneities. Holder et al. (2008) evaluated the utility of nucleotide and amino acid models in phylogeny inference when the data were simulated assuming heterogeneous amino acid frequencies among sites, and found that DNA-based analysis was more accurate than amino acid and codon-based analyses.
One approach to mitigating the problem ofsubstitution-process heterogeneity is to identify and remove problematic taxa or aberrant genes or proteins (e.g., Brinkmann and Philippe, 1999; Canbäck et al. 2004; Nesnidal et al. 2010). While data quality control is important in inference of deep phylogeny, such data filtering, if used as a general strategy for meeting the challenges of inferring deep phylogenies, may be arbitrary and ineffective. The rogue taxa may be critical to the phylogenetic problem, and most genes and proteins may be evolving under heterogeneous mutation biases and selective pressures. Furthermore, data filtering may introduce biases in the analyses. Here, we emphasize the use of heterogeneous nucleotide and amino acid substitution models in phylogenetic tree search as the major approach to dealing with challenging deep phylogenies.
Limitations of Our Simulation and Utility of DNA and Protein Sequences for Inferring Deep Phylogenies
As our focus in this paper is on inference of deep phylogenies using phylogenomic datasets, we have simulated relatively large datasets, with 2000 or 5000 codons or amino acids. In modern phylogenomic analysis, systematic biases due to model violations are often more important than random sampling errors due to limited number of sites in the alignment (Thomson and Brown 2022). We simulated data under site- and branch-site-heterogeneous models to represent realistic situations in inference of deep phylogenies, and analyzed them using modern phylogeny-reconstruction software. However, the models assumed in the software may not fully account for the heterogeneous substitution process assumed in the simulation of the data. Here, we discuss a few limitations of our simulation, and their impact on our conclusions concerning the utility of DNA versus protein sequences for inference of deep phylogenies.
In simulating data with among-lineage compositional heterogeneity (under the BSH model), we multipliedthe codon-frequency parameters in the rate matrix by the nucleotide frequency (or propensity) parameter for the nucleotide at the third codon position. This may introduce slight among-lineage heterogeneity in amino acid compositions (as some third-position substitutions are nonsynonymous), but not in the first and second codon positions, thus placing amino acid-based analysis (AA) in a slight disadvantage relative to nucleotide-based analysis using the first two codon positions (DNA-12 and DNA-12-P).
A better way of simulating the heterogeneous substitution process of protein-coding genes, suggested by a reviewer (Dr. Nicolas Lartillot), may be to adopt the mutation-selection formulation of codon substitution and specify the rate of codon substitution as the product of the mutation rate multiplied by the fixation probability for the mutant (Halpern and Bruno 1998; Yang and Nielsen 2008), as in Holder et al. (2008) and Spielman (2020). To use the notation of Equation (3) (but assuming any genetic code), the substitution rate from codons 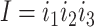 to
to 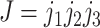 is
is
| (7) |
where, 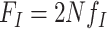 is the population-scaled fitness for codon
is the population-scaled fitness for codon 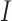 and
and 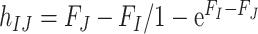 is the fixation probability of the mutant codon
is the fixation probability of the mutant codon 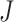 in a population of codon
in a population of codon  , with the population size to be
, with the population size to be  (Fisher 1930). Here, the codon fitness
(Fisher 1930). Here, the codon fitness 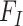 may depend on the encoded amino acid
may depend on the encoded amino acid 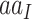 so that the synonymous codons for the same amino acid have the same fitness. The model of Equation 7 is time-reversible, with the equilibrium codon frequency to be
so that the synonymous codons for the same amino acid have the same fitness. The model of Equation 7 is time-reversible, with the equilibrium codon frequency to be 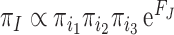 (Yang and Nielsen 2008: Equation (3)). The model attributes among-lineage heterogeneity in nucleotide and amino acid compositions to mutational bias and predicts more variable nucleotide compositions at the third codon position than at the first and second, and than amino acid compositions, because of the constraints due to amino acid fitness (Latrille and Lartillot 2022). Those model predictions agree with the empirical observation that amino acid compositions may vary among species, although not to the same extent as nucleotide compositions at the third codon position (Foster et al. 1997; Singer and Hickey 2000). Currently, neither indelible (Fletcher and Yang 2009) nor evolver (Yang 2007) includes the mutation-selection model of codon substitution. We leave it to future study to use such advanced codon models to evaluate the impacts of heterogeneous mutational biases among lineages on the use of nucleotide models to infer deep phylogenies.
(Yang and Nielsen 2008: Equation (3)). The model attributes among-lineage heterogeneity in nucleotide and amino acid compositions to mutational bias and predicts more variable nucleotide compositions at the third codon position than at the first and second, and than amino acid compositions, because of the constraints due to amino acid fitness (Latrille and Lartillot 2022). Those model predictions agree with the empirical observation that amino acid compositions may vary among species, although not to the same extent as nucleotide compositions at the third codon position (Foster et al. 1997; Singer and Hickey 2000). Currently, neither indelible (Fletcher and Yang 2009) nor evolver (Yang 2007) includes the mutation-selection model of codon substitution. We leave it to future study to use such advanced codon models to evaluate the impacts of heterogeneous mutational biases among lineages on the use of nucleotide models to infer deep phylogenies.
Another unrealistic feature of our simulation is the use of one nonsynonymous/synonymous rate ratio for all pairs of amino acids; in other words, 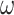 in Equation (3) is independent of the source and target amino acids (
in Equation (3) is independent of the source and target amino acids (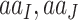 ), whether
), whether 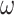 is allowed to vary among sites (as in M3 discrete) or not (as in M0 one-ratio). It is well-known that amino acids with similar physico-chemical properties tend to exchange with each other at high rates (Grantham 1974). This is reflected in all empirical amino acid models such as the Dayhoff (Dayhoff et al. 1978), JTT (Jones et al. 1992), WAG (Whelan and Goldman 2001), and LG (Le and Gascuel 2008) for nuclear proteins, and mtREV (Adachi and Hasegawa 1996) and mtMam (Yang et al. 1998) for mitochondrial proteins. Nucleotide substitution models usually do not account for such effects of amino acid chemical differences. Our simulation model did not incorporate such amino acid chemical differences and may not reflect the advantage of empirical amino acid models in analysis of real data and may thus have favored nucleotide-based analysis. Again the mutation-selection framework may be used to simulate codon substitutions incorporating amino acid chemical properties. It will be interesting to evaluate the performance of different data-analysis strategies under more realistic codon-substitution models.
is allowed to vary among sites (as in M3 discrete) or not (as in M0 one-ratio). It is well-known that amino acids with similar physico-chemical properties tend to exchange with each other at high rates (Grantham 1974). This is reflected in all empirical amino acid models such as the Dayhoff (Dayhoff et al. 1978), JTT (Jones et al. 1992), WAG (Whelan and Goldman 2001), and LG (Le and Gascuel 2008) for nuclear proteins, and mtREV (Adachi and Hasegawa 1996) and mtMam (Yang et al. 1998) for mitochondrial proteins. Nucleotide substitution models usually do not account for such effects of amino acid chemical differences. Our simulation model did not incorporate such amino acid chemical differences and may not reflect the advantage of empirical amino acid models in analysis of real data and may thus have favored nucleotide-based analysis. Again the mutation-selection framework may be used to simulate codon substitutions incorporating amino acid chemical properties. It will be interesting to evaluate the performance of different data-analysis strategies under more realistic codon-substitution models.
Despite these shortcomings in our simulation design, we suggest that our overall conclusion that nucleotide models applied to DNA data may be as useful as amino acid models for protein data for inferring deep phylogenies is well supported. In our simulation, nucleotide-based analysis (DNA-12-P, say) often performed a better and never much worse than amino acid based analysis. In the analysis of the metazoan data, nucleotide-based analyses produced at least as good trees as the protein data. We suggest that both DNA and protein data should be useful for inferring deep phylogenies, and DNA data should not be discarded without any serious evaluation, as is the current practice. Our simulations highlight the importance of accommodating the rate and compositional heterogeneity in the substitution model whether DNA or protein data are analyzed.
Finally, our study has focused on phylogeny reconstruction. It may also be interesting to examine the relative utility of DNA and protein data for estimating branch lengths and dating species divergences.
Developing Heterogeneous Models of Coding Sequence Evolution
Our simulation (Figs. 4 and 5) highlights theimportance of accounting for heterogeneous substitution process in inference of deep phylogenies, in particular compositional heterogeneity among sites and among lineages. The relative advantages of DNA versus protein sequences may to some extent depend on whether appropriate heterogeneous models are available and computationally feasible for the different data types.
For analysis of DNA sequences under nucleotide models, current ML programs such as IQ-tree and RAxML have implemented models to deal with among-site rate heterogeneity, but models of among-site compositional heterogeneity are less developed. In the Bayesian context, the CAT mixture model in PhyloBayes is available for nucleotide data (Lartillot and Philippe 2004; Lartillot et al. 2009). Models of among-lineage compositional heterogeneity often involve even heavier computation. The nhomo models in baseml, with pre-specified branch classes with different substitution models (Yang and Roberts 1995), may be used to compare candidate trees but are not available for tree search. The break-point (BP) model in PhyloBayes (Blanquart and Lartillot 2006, 2008) uses a nonstationary breakpoint process to accommodate changes to the substitution pattern on the tree. The BP and CAT-BP models involve heavy computation and MCMC mixing issues. The program p4 (Foster 2004; Foster et al. 2009) implements the so-called node-discrete composition-heterogeneous (NDCH) model for nucleotide data.
For analysis of protein sequences under amino acid models, the CAT models implemented in PhyloBayes account for among-site compositional heterogeneity. Similarly in the ML program IQ-tree, empirical mixture models are available with site classes having different amino acid compositions (Le et al. 2012). A recent approximate method implemented in IQ-tree, called the posterior mean site frequency (PMSF), performed well in simulations (Wang et al. 2018). This uses a guide tree to fit the mixture model and “estimate” the amino acid frequencies for each site (or site pattern) by using posterior means given data at the site, and then to use such estimated amino acid frequency profiles as fixed during phylogenetic tree search. The strategy in effect uses a partition model to approximate a mixture model, and was used to deal with among-site rate heterogeneity in the “fixed-rates” model of Yang (1994b) or the CAT model in RAxML (Stamatakis et al. 2012; note that this is different from the CAT model in PhyloBayes). A mixture model involves more computation because the probability for a site is an average over the mixing classes, whereas in a partition model each site is assigned a partition or site class a priori so that averaging is avoided (Yang 1996a). Currently, no efficient models appear to be available for among-lineage compositional heterogeneity for amino acid sequences.
With the advancements of computational power, it may also be worthwhile to explore the use of codon models to infer deep phylogenies, using either codon or amino acid sequences. For analysis of amino acid sequences under codon models, two approaches may be taken. The first is to treat amino acids as ambiguous codon states, using the approach to dealing with missing data in phylogenetic likelihood calculation (Felsenstein 2004, p. 255–256; Yang, 2014, p. 110–112; Weber et al., 2021). Likelihood calculation under the model then involves similar amounts of computation as under the codon model and one has to estimate the nonsynonymous/synonymous rate ratio parameter ( ) even though the protein sequences contain little information about the synonymous substitution rate (Weber et al. 2021). The second approach is to construct an approximate Markov chain for amino acids by lumping synonymous codons into the same state (Yang et al. 1998). This involves less computation than the former model and avoids semi-identifiable parameters such as the
) even though the protein sequences contain little information about the synonymous substitution rate (Weber et al. 2021). The second approach is to construct an approximate Markov chain for amino acids by lumping synonymous codons into the same state (Yang et al. 1998). This involves less computation than the former model and avoids semi-identifiable parameters such as the  ratio. Both models are implemented in codeml, but their utility in phylogenetic tree search is not tested.
ratio. Both models are implemented in codeml, but their utility in phylogenetic tree search is not tested.
One could use the same strategies to implement a Markov chain model for nucleotide data of the first and second codon positions, using 16 states in the Markov chain. Compared with amino acid models, this has the disadvantage of being unable to distinguish between amino acids that differ at the third codon position only (such as histidine and glutamine) but have the advantage of being able to distinguish the two serines (encoded by codons TCN and AGY).
Acknowledgments
The authors are grateful to two reviewers (Drs. Nicolas Lartillot and Jeff Thorne) and the associate editor (Dr. Lars Jermiin) for many constructive comments that have led to improvement of the paper.
Contributor Information
Paschalia Kapli, Department of Genetics, University College London, Gower Street, London WC1E 6BT, UK.
Ioanna Kotari, Department of Genetics, University College London, Gower Street, London WC1E 6BT, UK; Institut für Populationsgenetik, Vetmeduni Vienna, Vienna, 1210, Austria.
Maximilian J Telford, Department of Genetics, University College London, Gower Street, London WC1E 6BT, UK.
Nick Goldman, European Molecular Biology Laboratory - European Bioinformatics Institute, Wellcome Genome Campus, Hinxton, Cambridge CB10 1SD, UK.
Ziheng Yang, Department of Genetics, University College London, Gower Street, London WC1E 6BT, UK.
Funding
This study has been supported by Biotechnology and Biological Sciences Research Council grants (BB/T012951/1 and BB/R016240/1), a BBSRC equipment grant (BB/R01356X/1), a Templeton Foundation grant (to Z.Y.), and a Leverhulme Trust grant (RPG-2021-433) to M.T. N.G. is supported by the European Molecular Biology Laboratory.
Supplementary Material
Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.sbcc2fr85.
REFERENCES
- Abadi S., Azouri D., Pupko T., Mayrose I.. 2019. Model selection may not be a mandatory step for phylogeny reconstruction. Nat. Commun. 10(1):934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abascal F., Zardoya R., Telford M.J.. 2010. TranslatorX: multiple alignment of nucleotide sequences guided byamino acid translations. Nucl. Acids Res. 38(Suppl. 2): W7–W13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adachi J., Hasegawa M.. 1996. Model of amino acid substitution in proteins encoded by mitochondrial DNA. J. Mol. Evol. 42:459–468. [DOI] [PubMed] [Google Scholar]
- Blanquart S., Lartillot N.. 2006. A Bayesian compound stochastic process for modeling nonstationary and nonhomogeneous sequence evolution. Mol. Biol. Evol. 23:2058–2071. [DOI] [PubMed] [Google Scholar]
- Blanquart S., Lartillot N.. 2008. A site- and time-heterogeneous model of amino acid replacement. Mol. Biol. Evol. 25:842–858. [DOI] [PubMed] [Google Scholar]
- Brinkmann H., Philippe H.. 1999. Archaea sister group of bacteria? Indications from tree reconstruction artifacts in ancient phylogenies. Mol. Biol. Evol. 16(6):817–825. [DOI] [PubMed] [Google Scholar]
- Camacho C., Coulouris G., Avagyan V., Ma N., Papadopoulos J., Bealer K., Madden T.L.. 2009. BLAST: architecture and applications. BMC Bioinf. 10(1):1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canbäck B., Tamas I., Andersson S.G.. 2004. A phylogenomic study of endosymbiotic bacteria. Mol. Biol. Evol. 21(6):1110–1122. [DOI] [PubMed] [Google Scholar]
- Cannon J.T., Vellutini B.C., Smith J., Ronquist F., Jondelius U., Hejnol A.. 2016. Xenacoelomorpha is the sister group to Nephrozoa. Nature. 530(7588):89–93. [DOI] [PubMed] [Google Scholar]
- Curnow R. 1988. The use of Markov chain models in studying the evolution of the proteins. J. Theor. Biol. 134:51–57. [DOI] [PubMed] [Google Scholar]
- Dayhoff, M.O., Schwartz, R.M., Orcutt, B.C.. 1978. A model of evolutionary change in proteins. In: Atlas of protein sequence and structure, Vol. 5, Suppl. 3. Washington (DC): National Biomedical Research Foundation. p. 345–352. [Google Scholar]
- Felsenstein J. 1981. Evolutionary trees from DNA sequences: a maximum likelihood approach. J. Mol. Evol. 17:368–376. [DOI] [PubMed] [Google Scholar]
- Felsenstein, J. 2004. Inferring phylogenies. Sunderland, MA: Sinauer Associates. [Google Scholar]
- Feuda R., Dohrmann M., Pett W., Philippe H., Rota-Stabelli O., Lartillot N., Wörheide G., Pisani D.. 2017. Improved modeling of compositional heterogeneity supports sponges as sister to all other animals. Curr. Biol. 27(24):3864–3870. [DOI] [PubMed] [Google Scholar]
- Finn R.D., Bateman A., Clements J., Coggill P., Eberhardt R.Y., Eddy S.R., Heger A., Hetherington K., Holm L., Mistry J., Sonnhammer E.L.L., Tate J.. 2014. Pfam: the protein families database. Nucl. Acids Res. 42(D1):D222–D230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher, R. 1930. The genetic theory of natural selection. Oxford: Clarendon Press. [Google Scholar]
- Fletcher W., Yang Z.. 2009. INDELible: a flexible simulator of biological sequence evolution. Mol. Biol. Evol. 26:1879–1888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster P.G., Jermiin L., Hickey D.. 1997. Nucleotide composition bias affects amino acid content in proteins coded by animal mitochondria. J. Mol. Evol. 44:282–288. [DOI] [PubMed] [Google Scholar]
- Foster P.G., Hickey D.A.. 1999. Compositional bias may affect both DNA-based and protein-based phylogenetic reconstructions. J. Mol. Evol. 48(3):284–290. [DOI] [PubMed] [Google Scholar]
- Foster P.G. 2004. Modeling compositional heterogeneity. Syst. Biol. 53:485–495. [DOI] [PubMed] [Google Scholar]
- Foster P.G., Cox C., Embley T.. 2009. The primary divisions of life: a phylogenomic approach employing composition-heterogeneous methods. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 364:2197–2207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster P.G., Schrempf D., Szollosi G.J., Williams T.A., Cox C.J., Embley T.M.. 2023. Recoding amino acids to a reduced alphabet may increase or decrease phylogenetic accuracy. Syst. Biol. 72:723–737. [DOI] [PubMed] [Google Scholar]
- Goldman N., Yang Z.. 1994. A codon-based model of nucleotide substitution for protein-coding DNA sequences. Mol. Biol. Evol. 11:725–736. [DOI] [PubMed] [Google Scholar]
- Grabherr M.G., Haas B.J., Yassour M., Levin J.Z., Thompson D.A., Amit I., Adiconis X., Fan L., Raychowdhury R., Zeng Q.. 2011. Trinity: reconstructing a full-length transcriptome without a genome from rna-seq data. Nat. Biotechnol. 29(7):644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grantham R. 1974. Amino acid difference formula to help explain protein evolution. Science. 185:862–864. [DOI] [PubMed] [Google Scholar]
- Haas B.J., Papanicolaou A., Yassour M., Grabherr M., Blood P.D., Bowden J., Couger M.B., Eccles D., Li B., Lieber M.. 2013. De novo transcript sequence reconstruction from RNA-seq using the Trinity platform for reference generation and analysis. Nat. Protoc. 8(8):1494–1512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halpern A.L., Bruno W.J.. 1998. Evolutionary distances for protein-coding sequences: modeling site-specific residue frequencies. Mol. Biol. Evol. 15:910–917. [DOI] [PubMed] [Google Scholar]
- Ho S., Jermiin L.. 2004. Tracing the decay of the historical signal in biological sequence data. Syst. Biol. 53:623–637. [DOI] [PubMed] [Google Scholar]
- Hoang D.T., Chernomor O., Von Haeseler A., Minh B.Q., Vinh L.S.. 2018. UFBoot2: improving the ultrafast bootstrap approximation. Mol. Biol. Evol. 35(2):518–522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holder M.T., Zwickl D.J., Dessimoz C.. 2008. Evaluating the robustness of phylogenetic methods to among-site variability in substitution processes. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 363(1512):4013–4021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jayaswal V., Wong T.K., Robinson J., Poladian L., Jermiin L.S.. 2014. Mixture models of nucleotide sequence evolution that account for heterogeneity in the substitution process across sites and across lineages. Syst. Biol. 63(5):726–742. [DOI] [PubMed] [Google Scholar]
- Jermiin L., Ho S.Y., Ababneh F., Robinson J., Larkum A.W.. 2004. The biasing effect of compositional heterogeneity on phylogenetic estimates may be underestimated. Syst. Biol. 53(4):638–643. [DOI] [PubMed] [Google Scholar]
- Jones D.T., Taylor W.R., Thornton J.M.. 1992. The rapid generation of mutation data matrices from protein sequences. CABIOS. 8:275–282. [DOI] [PubMed] [Google Scholar]
- Kapli P., Telford M.J.. 2020. Topology-dependent asymmetry in systematic errors affects phylogenetic placement of Ctenophora and Xenacoelomorpha. Sci. Adv. 6(50):eabc5162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kapli P., Natsidis P., Leite D.J., Fursman M., Jeffrie N., Rahman I.A., Philippe H., Copley R.R., Telford M.J.. 2021. Lack of support for Deuterostomia prompts reinterpretation of the first Bilateria. Sci. Adv. 7(12):eabe2741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katoh K., Kuma K.-I., Toh H., Miyata T.. 2005. MAFFT version 5: improvement in accuracy of multiple sequence alignment. Nucl. Acids Res. 33(2):511–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kemeny JG, Snell JL.. 1960. Finite Markov Chains. Princeton, N.J., USA: Van Nostrand. [Google Scholar]
- Kobert, K., Flouri, T., Aberer, A., Stamatakis, A.. 2014. The divisible load balance problem and its application to phylogenetic inference. In: Algorithms in Bioinformatics: 14th International Workshop, WABI 2014, Wroclaw, Poland, September 8–10, 2014. Proceedings 14 (pp. 204–216). Berlin Heidelberg Springer. [Google Scholar]
- Kobert K., Stamatakis A., Flouri T.. 2017. Efficient detection of repeating sites to accelerate phylogenetic likelihood calculations. Syst. Biol. 66(2):205–217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kocot K.M., Struck T.H., Merkel J., Waits D.S., Todt C., Brannock P.M., Weese D.A., Cannon J.T., Moroz L.L., Lieb B., et al. 2017. Phylogenomics of Lophotrochozoa with consideration of systematic error. Syst. Biol. 66(2):256–282. [DOI] [PubMed] [Google Scholar]
- Kosiol C., Goldman N.. 2011. Markovian and non-Markovian protein sequence evolution: aggregated Markov process models. J. Mol. Biol. 411:910–923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozlov A.M., Darriba D., Flouri T., Morel B., Stamatakis A.. 2019. RAxML-NG: a fast, scalable and user-friendly tool for maximum likelihood phylogenetic inference. Bioinformatics. 35(21):4453–4455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lartillot N., Philippe H.. 2004. A Bayesian mixture model for across-site heterogeneities in the amino-acid replacement process. Mol. Biol. Evol. 21(6):1095–1109. [DOI] [PubMed] [Google Scholar]
- Lartillot N., Brinkmann H., Philippe H.. 2007. Suppression of long-branch attraction artefacts in the animal phylogeny using a site-heterogeneous model. BMC Evolut. Biol. 7(1):1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lartillot N., Lepage T., Blanquart S.. 2009. PhyloBayes 3: a Bayesian software package for phylogenetic reconstruction and molecular dating. Bioinformatics. 25(17):2286–2288. [DOI] [PubMed] [Google Scholar]
- Lartillot N., Rodrigue N., Stubbs D., Richer J.. 2013. PhyloBayes MPI: phylogenetic reconstruction with infinite mixtures of profiles in a parallel environment. Syst. Biol. 62(4):611–615. [DOI] [PubMed] [Google Scholar]
- Latrille T., Lartillot N.. 2022. An improved codon modeling approach for accurate estimation of the mutation bias. Mol. Biol. Evol. 39(2):1. doi:0.1093/molbev/msac005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laumer C.E., Bekkouche N., Kerbl A., Goetz F., Neves R.C., Sørensen M.V., Kristensen R.M., Hejnol A., Dunn C.W., Giribet G.. 2015. Spiralian phylogeny informs the evolution of microscopic lineages. Curr. Biol. 25(15):2000–2006 [DOI] [PubMed] [Google Scholar]
- Laumer C.E., Gruber-Vodicka H., Hadfield M.G., Pearse V.B., Riesgo A., Marioni J.C., Giribet G.. 2018. Support for a clade of Placozoa and Cnidaria in genes with minimal compositional bias. Elife. 7:e36278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laumer C.E., Fernández R., Lemer S., Combosch D., Kocot K.M., Riesgo A., Andrade S.C., Sterrer W., Sørensen M.V., Giribet G.. 2019. Revisiting metazoan phylogeny with genomic sampling of all phyla. Proc. Royal Soc. B. 286(1906):20190831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le S.Q., Gascuel O.. 2008. An improved general amino acid replacement matrix. Mol. Biol. Evol. 25:1307–1320. [DOI] [PubMed] [Google Scholar]
- Le S.Q., Dang C., Gascuel O.. 2012. Modeling protein evolution with several amino acid replacement matrices depending on site rates. Mol. Biol. Evol. 29(10):2921–2936. [DOI] [PubMed] [Google Scholar]
- Lockhart P.J., Steel M.A., Hendy M.D., Penny D.. 1994. Recovering evolutionary trees under a more realistic model of sequence evolution. Mol. Biol. Evol. 11(4):605–612. [DOI] [PubMed] [Google Scholar]
- Marlétaz F., Peijnenburg K.T., Goto T., Satoh N., Rokhsar D.S.. 2019. A new spiralian phylogeny places the enigmatic arrow worms among gnathiferans. Curr. Biol. 29(2):312–318. [DOI] [PubMed] [Google Scholar]
- Matsumoto T., Akashi H., Yang Z.. 2015. Evaluation of ancestral sequence reconstruction methods to infer nonstationary patterns of nucleotide substitution. Genetics. 200:873–890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minh B.Q., Schmidt H.A., Chernomor O., Schrempf D., Woodhams M.D., von Haeseler A., Lanfear R.. 2020. IQ-TREE 2: new models and efficient methods for phylogenetic inference in the genomic era. Mol. Biol. Evol. 37(5):1530–1534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muse S.V., Gaut B.S.. 1994. A likelihood approach for comparing synonymous and nonsynonymous nucleotide substitution rates, with application to the chloroplast genome. Mol. Biol. Evol. 11:715–724. [DOI] [PubMed] [Google Scholar]
- Natsidis P., Kapli P., Schiffer P.H., Telford M.J.. 2021. Systematic errors in orthology inference and their effects on evolutionary analyses. Iscience. 24(2):102110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nesnidal M.P., Helmkampf M., Bruchhaus I., Hausdorf B.. 2010. Compositional heterogeneity and phylogenomic inference of metazoan relationships. Mol. Biol. Evol. 27(9):2095–2104. [DOI] [PubMed] [Google Scholar]
- Nguyen L.T., Schmidt H.A., von Haeseler A., Minh B.Q.. 2015. IQ-TREE: a fast and effective stochastic algorithm for estimating maximum-likelihood phylogenies. Mol. Biol. Evol. 32(1):268–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R., Yang Z.. 1998. Likelihood models for detecting positively selected amino acid sites and applications to the HIV-1 envelope gene. Genetics. 148:929–936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philippe H., Brinkmann H., Copley R.R., Moroz L.L., Nakano H., Poustka A.J., Wallberg A., Peterson K.J., Telford M.J.. 2011. Acoelomorph flatworms are Deuterostomes related to Xenoturbella. Nature. 470(7333):255–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philippe H., Poustka A.J., Chiodin M., Hoff K.J., Dessimoz C., Tomiczek B., Schiffer P.H., Müller S., Domman D., Horn M.. 2019. Mitigating anticipated effects of systematic errors supports sister-group relationship between Xenacoelomorpha and Ambulacraria. Curr. Biol. 29(11):1818–1826 [DOI] [PubMed] [Google Scholar]
- Ren F., Tanaka H., Yang Z.. 2005. An empirical examination of the utility of codon-substitution models in phylogeny reconstruction. Syst. Biol. 54:808–818. [DOI] [PubMed] [Google Scholar]
- Rota-Stabelli O., Lartillot N., Philippe H., Pisani D.. 2013. Serine codon-usage bias in deep phylogenomics: pancrustacean relationships as a case study. Syst. Biol. 62(1):121–133. [DOI] [PubMed] [Google Scholar]
- Seo T.-K., Kishino H.. 2008. Synonymous substitutions substantially improve evolutionary inference from highly diverged proteins. Syst. Biol. 57(3):367–377. [DOI] [PubMed] [Google Scholar]
- Seo T.K., Kishino H.. 2009. Statistical comparison of nucleotide, amino acid, and codon substitution models for evolutionary analysis of protein-coding sequences. Syst. Biol. 58(2):199–210. [DOI] [PubMed] [Google Scholar]
- Si Quang L., Gascuel O., Lartillot N.. 2008. Empirical profile mixture models for phylogenetic reconstruction. Bioinformatics. 24(20):2317–2323. [DOI] [PubMed] [Google Scholar]
- Simion, P., Philippe, H., Baurain, D., Jager, M., Richter, D.J., Di Franco, A., Roure, B., Satoh, N., Quéinnec, E., Ereskovsky, A.. 2017. A large and consistent phylogenomic dataset supports sponges as the sister group to all other animals. Curr. Biol. 27(7):958–967 [DOI] [PubMed] [Google Scholar]
- Singer G.A., Hickey D.A.. 2000. Nucleotide bias causes a genomewide bias in the amino acid composition of proteins. Mol. Biol. Evol. 17(11):1581–1588. [DOI] [PubMed] [Google Scholar]
- Spielman S.J. 2020. Relative model fit does not predict topological accuracy in single-gene protein phylogenetics. Mol. Biol. Evol. 37(7):2110–2123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stamatakis A., Aberer A., Goll C., Smith S., Berger S., Izquierdo-Carrasco F.. 2012. RAxML-Light: a tool for computing terabyte phylogenies. Bioinformatics. 28:2064–2066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan J., Abdo Z., Joyce P., Swofford D.L.. 2005. Evaluating the performance of a successive-approximations approach to parameter optimization in maximum-likelihood phylogeny estimation. Mol. Biol. Evol. 22:1386–1392. [DOI] [PubMed] [Google Scholar]
- Swofford D.L., Waddell P.J., Huelsenbeck J.P., Foster P.G., Lewis P.O., Rogers J.S.. 2001. Bias in phylogenetic estimation and its relevance to the choice between parsimony and likelihood methods. Syst. Biol. 50:525–539. [PubMed] [Google Scholar]
- Telford M.J., Budd G.E., Philippe H.. 2015. Phylogenomic insights into animal evolution. Curr. Biol. 25(19):R876–R887. [DOI] [PubMed] [Google Scholar]
- Thomson R.C., Brown J.M.. 2022. On the need for new measures of phylogenomic support. Syst. Biol. 71:917–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- UniProt-Consortium. 2018. Uniprot: the universal protein knowledgebase. Nucl. Acids Res 46(5):2699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vera-Ruiz V.A., Robinson J., Jermiin L.S.. 2022. A likelihood-ratio test for lumpability of phylogenetic data: is the Markovian property of an evolutionary process retained in recoded DNA? Syst. Biol. 71(3):660–675. [DOI] [PubMed] [Google Scholar]
- Wang H.C., Minh B., Susko E., Roger A.J.. 2018. Modeling site heterogeneity with posterior mean site frequency profiles accelerates accurate phylogenomic estimation. Syst. Biol. 67:216–235. [DOI] [PubMed] [Google Scholar]
- Weber C., Yang Z., Goldman N.. 2021. Ambiguity coding allows accurate inference of evolutionary parameters from alignments in an aggregated state-space. Syst. Biol. 70(1):21–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whelan S., Goldman N.. 2001. A general empirical model of protein evolution derived from multiple protein families using a maximum likelihood approach. Mol. Biol. Evol. 18:691–699. [DOI] [PubMed] [Google Scholar]
- Williams T.A., Cox C.J., Foster P.G., Szöllősi G.J., Embley T.M.. 2020. Phylogenomics provides robust support for a two-domains tree of life. Nat. Ecol. Evol. 4(1):138–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z. 1994a. Estimating the pattern of nucleotide substitution. J. Mol. Evol. 39:105–111. [DOI] [PubMed] [Google Scholar]
- Yang Z. 1994b. Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J. Mol. Evol. 39:306–314. [DOI] [PubMed] [Google Scholar]
- Yang Z. 1996a. Among-site rate variation and its impact on phylogenetic analyses. Trends Ecol. Evol. 11(9):367–372. [DOI] [PubMed] [Google Scholar]
- Yang Z. 1996b. Maximum-likelihood models for combined analyses of multiple sequence data. J. Mol. Evol. 42:587–596. [DOI] [PubMed] [Google Scholar]
- Yang Z. 1997. How often do wrong models produce better phylogenies? Mol. Biol. Evol. 14:105–108. [DOI] [PubMed] [Google Scholar]
- Yang Z. 1998. On the best evolutionary rate for phylogenetic analysis. Syst. Biol. 47:125–133. [DOI] [PubMed] [Google Scholar]
- Yang Z. 2007. PAML 4:Phylogenetic analysis by maximum likelihood. Mol. Biol. Evol. 24:1586–1591. [DOI] [PubMed] [Google Scholar]
- Yang, Z. 2014. Molecular evolution: a statistical approach. Oxford: Oxford University Press. [Google Scholar]
- Yang Z., Nielsen R.. 2008. Mutation-selection models of codon substitution and their use to estimate selective strengths on codon usage. Mol. Biol. Evol. 25:568–579. [DOI] [PubMed] [Google Scholar]
- Yang Z., Roberts D.. 1995. On the use of nucleic acid sequences to infer early branchings in the tree of life. Mol. Biol. Evol. 12:451–458. [DOI] [PubMed] [Google Scholar]
- Yang Z., Goldman N., Friday A.E.. 1995a. Maximum likelihood trees from DNA sequences: a peculiar statistical estimation problem. Syst. Biol. 44:384–399. [Google Scholar]
- Yang Z., Lauder I.J., Lin H.J.. 1995b. Molecular evolution of the hepatitis b virus genome. J. Mol. Evol. 41:587–596. [DOI] [PubMed] [Google Scholar]
- Yang Z., Nielsen R., Hasegawa M.. 1998. Models of amino acid substitution and applications to mitochondrial protein evolution. Mol. Biol. Evol. 15:1600–1611. [DOI] [PubMed] [Google Scholar]
- Yang Z., Nielsen R., Goldman N., Pedersen A.-M.K.. 2000. Codon-substitution models for heterogeneous selection pressure at amino acid sites. Genetics. 155:431–449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zdobnov E.M., Tegenfeldt F., Kuznetsov D., Waterhouse R.M., Simao F.A., Ioannidis P., Seppey M., Loetscher A., Kriventseva E.V.. 2017. OrthoDB version 9.1: cataloging evolutionary and functional annotations for animal, fungal, plant, archaeal, bacterial and viral orthologs. Nucl. Acids Res. 45(D1):D744–D749. [DOI] [PMC free article] [PubMed] [Google Scholar]