A universal description of stochastic oscillators

Significance

Many natural systems exhibit oscillations that show sizeable fluctuations in frequency and amplitude. This variability can arise from a wide variety of physical mechanisms. Here, we develop a general theory for stochastic oscillators, based on a canonical nonlinear transformation of variables. We show that under our (complex-valued) description, the statistics of the oscillator’s spontaneous activity, of its response to external perturbations, and of the coordinated activity of (weakly) coupled oscillators are brought into a universal and greatly simplified form. We test the theory for three theoretical models of noisy oscillators arising from fundamentally different mechanisms: a damped harmonic oscillator with dynamical noise, a fluctuation-perturbed limit-cycle system, and an excitable system in which oscillations require noise to occur.

Abstract

Many systems in physics, chemistry, and biology exhibit oscillations with a pronounced random component. Such stochastic oscillations can emerge via different mechanisms, for example, linear dynamics of a stable focus with fluctuations, limit-cycle systems perturbed by noise, or excitable systems in which random inputs lead to a train of pulses. Despite their diverse origins, the phenomenology of random oscillations can be strikingly similar. Here, we introduce a nonlinear transformation of stochastic oscillators to a complex-valued function $Q_1^{*}$(x) that greatly simplifies and unifies the mathematical description of the oscillator’s spontaneous activity, its response to an external time-dependent perturbation, and the correlation statistics of different oscillators that are weakly coupled. The function $Q_1^{*}$ (x) is the eigenfunction of the Kolmogorov backward operator with the least negative (but nonvanishing) eigenvalue λ₁ = μ₁ + iω₁. The resulting power spectrum of the complex-valued function is exactly given by a Lorentz spectrum with peak frequency ω₁ and half-width μ₁; its susceptibility with respect to a weak external forcing is given by a simple one-pole filter, centered around ω₁; and the cross-spectrum between two coupled oscillators can be easily expressed by a combination of the spontaneous power spectra of the uncoupled systems and their susceptibilities. Our approach makes qualitatively different stochastic oscillators comparable, provides simple characteristics for the coherence of the random oscillation, and gives a framework for the description of weakly coupled oscillators.

In the age of big data, the human mind craves simple explanations of complex phenomena. The general category of “stochastic oscillations” embraces a bewildering array of natural and engineered systems in which one or more measurable quantities vary repeatedly but irregularly. Examples range from the molecular scale [oscillations in genetic regulatory circuits (1)] to the macroscopic scale [fluctuations in predator-prey systems (2, 3)], from physical and chemical systems [lasers (4, 5), chemical oscillations (6), swaying of bridges (7), oscillations in aircraft wings (8, 9)] to living systems [oscillations in hair cell bundles (10, 11), in glycolytic yeast activity (12, 13), in locomotor CPG activity (14), and in cortical networks (15, 16)], and from millisecond time scales [neuronal firing (17, 18)] to hours [circadian rhythms (19, 20)] and longer [menstrual cycle (21)].

A universal framework for understanding and comparing stochastic oscillations would seem to be an impossible goal, not only because nonlinear stochastic dynamical systems are intrinsically difficult to analyze but because stochastic oscillations arise from a wide variety of underlying dynamical mechanisms. In the simplest case, one may obtain irregular oscillations by incorporating noise into a deterministic limit-cycle system. Examples of noisy oscillations generated by such mechanisms include spontaneously active hair bundles in the auditory system (22), tonically active nerve cells in the sensory periphery, that produce trains of action potentials perturbed by “channel noise” (random gating of ion channels) (23, 24), and oscillations in genetic regulatory circuits perturbed by copy-number noise (1). In addition, there are multiple types of noise-induced oscillations: systems in which the oscillatory activity would die out in the absence of noise. A well-known class of noise-induced mechanisms arises when a deterministic excitable system is perturbed by noise. Below its activation threshold, such an excitable system will not produce sustained activity. But when perturbed by dynamical noise, an excitable system may produce an ongoing train of pulsatile activations (25). A nerve cell receiving a subthreshold current provides a familiar example (26–29). Another important class of noise-induced oscillators includes quasicycle systems. Quasicycles arise when a system has a stable equilibrium (with complex eigenvalues), perturbed by fluctuating inputs (30).

Many physical and biological systems show random oscillations attributed to quasicycle dynamics. Examples include underdamped linear mass-spring system immersed in a heat bath (31), subthreshold oscillations in nerve cells sustained by channel noise (32), models of EEG oscillations and intermittent cortical network activity (33–36), and oscillations in predator-prey systems sustained by demographic (finite-population) noise (2). Demographic fluctuations can also sustain oscillations in systems with rock–paper–scissors interactions by yet another mechanism: noisy heteroclinic cycle dynamics (37–40).

Despite this diversity in the origins of noisy oscillations, each of the mechanisms above can be instantiated as a Markov process, for example, as a system of stochastic differential equations. Previous investigations of such systems have relied on empirical quantities such as the power spectrum (for a single unit), the cross-correlation (for multiple units), or the linear response to small-amplitude perturbations. The possibility of a simpler, unifying description of Markovian oscillators remains an important open question. Ideally, one would aim to find the stochastic analogue of the well-known “phase reduction.” In deterministic limit-cycle systems, the phase reduction (41, 42) and also the phase-amplitude reduction (43–46) provide low-dimensional descriptions that have yielded far-reaching insights into regulation, entrainment, and synchronization of oscillating systems (47–50). Although the deterministic phase concept can also be applied to some noisy systems, e.g., single linear and nonlinear oscillators (51) and coupled stochastic systems (52), generally, the notion of phase has to be redefined in a stochastic framework in order to make it applicable to cases of pure noise-induced oscillations for which a deterministic phase does not exist (53–58). Here, we go beyond such a simple extension of the phase definition and suggest a transformation to a complex-valued function that brings about a tremendous simplification in the description of stochastic oscillators. We show that by transforming the system’s output to a complex eigenfunction of the backward Kolmogorov operator, we obtain a surprisingly simple, unified treatment of irregular oscillations, regardless of their underlying mechanisms. Importantly, using our complex-valued eigenfunction description, we show that both the power spectrum and the susceptibility for single oscillators, and the cross-spectrum for multiple oscillators, take dramatically simplified, universal forms.

Stochastic Oscillators Described by Eigenfunctions

The key step in finding a universal description comes from the observation that stochastic systems may be described not just by individual trajectories but by an ensemble of trajectories, described by a probability density. Nonlinear stochastic dynamical systems are difficult to analyze (25, 59–61), in particular, if they violate detailed balance (62). However, their densities evolve following linear dynamics, making the densities amenable to analysis as linear systems.

We suppose that a stochastic oscillator obeys the Langevin equation (which we interpret in the sense of Itô)

$$\begin{array}{c}\hfill \frac{d\mathbf{x}}{\mathit{dt}}=\mathbf{f}(\mathbf{x})+\mathbf{g}(\mathbf{x})\xi (t),\end{array}$$ [1]

where ξ represents k-dimensional white Gaussian noise with uncorrelated components ⟨ξ_i(t)ξ_j(t′)⟩ = δ(t − t′)δ_{i, j}. For Eq. 1, the conditional probability of the state vector x, given initial condition x₀, obeys the forward Kolmogorov equation (62):

$$\begin{array}{ll}\frac{\partial }{\partial t}P(x,t|x_0,s)\hfill & =\mathcal{L}[P]\hfill \\ \hfill & =-{\nabla }_x\text{}·\text{}\left(f(x)P\right)+{\displaystyle {\displaystyle \sum }_{i,j}}\frac{{\partial }^2}{\partial x_i{x}_j}\left(D_{ij}(x)P\right),\hfill \end{array}$$ [2]

where $D=\frac{1}{2}g{g}^{⊺}$. The formal adjoint of the operator ℒ is Kolmogorov’s backward operator ℒ^† (also known as the generator of the Markov process Eq. 1 and closely related to the Koopman operator), which satisfies the equation

$$\begin{array}{ll}-\frac{\partial }{\partial s}P(\mathbf{x},t|{\mathbf{x}}_0,s)\hfill & ={\mathcal{L}}^{†}[P]\hfill \\ \hfill & =\mathbf{f}({\mathbf{x}}_0)·{\mathrm{\nabla }}_{{\mathbf{x}}_{\mathbf{0}}}\left(P\right)+{\displaystyle \sum _{i,j}}{D}_{\mathit{ij}}({\mathbf{x}}_0)\frac{{\partial }^{2}P}{\partial x_{0,i}{x}_{0,j}}.\hfill \end{array}$$ [3]

Let us assume that the operators ℒ, ℒ^† possess a discrete set of eigenvalues with corresponding eigenfunctions

$$\begin{array}{c}\hfill \mathcal{L}[P_{\lambda }]=\lambda P_{\lambda },{\mathcal{L}}^{†}[Q_{\lambda }^{\ast }]=\lambda Q_{\lambda }^{\ast }.\end{array}$$ [4]

Under the natural inner product, we have the biorthogonality condition

$$\begin{array}{c}\hfill ⟨Q_{{\lambda }^{\prime }}|P_{\lambda }⟩=\int d\mathbf{x}{Q}_{{\lambda }^{\prime }}^{\ast }(\mathbf{x})P_{\lambda }(\mathbf{x})={\delta }_{{\lambda }^{\prime }\lambda },\end{array}$$ [5]

so that the transition probability can be expressed as (62)

$$\begin{array}{c}\hfill P(\mathbf{x},t|{\mathbf{x}}_0,s)=P_0(\mathbf{x})+{\displaystyle \sum _{\lambda \ne 0}}{e}^{\lambda (t-s)}{P}_{\lambda }(\mathbf{x})Q_{\lambda }^{\ast }({\mathbf{x}}_0),\end{array}$$ [6]

for t > s. That is, as established for many stochastic systems (60, 62, 63), the transition probability P can be regarded as a sum of modes, each of which decays at a rate given by the real part of its respective eigenvalue λ, leading in the long-time limit to the stationary distribution P₀(x), which we assume to be unique. The latter is the eigenfunction for the eigenvalue λ₀ = 0; the corresponding eigenfunction for this eigenvalue for the operator ℒ^† is Q₀ = 1. N.b. Even in the stationary state, the system will maintain a steady circulation of probability.

The decaying modes in Eq. 6 have been shown to contain important information about the stochastic oscillation (54, 58, 64); the most prominent mode being the one whose associated eigenvalue has least negative nonvanishing real part—as this is the mode that decays the slowest. Some of us suggested a definition of a stochastic oscillator and its stochastic phase along these lines: according to ref. 54, the stochastic system in Eq. 1 qualifies as robustly oscillating if the following conditions are met:

1. There exists a nontrivial eigenvalue with least negative real part λ₁ = μ₁ + iω₁ which is complex-valued and unique;

2. The oscillation is pronounced, i.e., the quality factor |ω₁/μ₁| is much larger than one;

3. All other nontrivial eigenvalues λ′ are significantly more negative in their real parts, i.e., |ℜ[λ′]| ≥ 2|ℜ[λ₁]|.

If these conditions are fulfilled, then one can extract the stochastic asymptotic phase ψ(x) as the complex argument of the slowest decaying eigenfunction $Q_1^{*}$ (x), i.e., ψ(x) = arg($Q_1^{*}$ (x)). We can then ascribe at any time t a phase variable to the state x(t) of the system by making the nonlinear transformation to a real-valued phase of the system ψ(t) = ψ(x(t)) (modulo 2π).

Here, we pursue this eigenfunction perspective further by demonstrating that the nonlinear transformation of the system, using the complex eigenfunction $Q_1^{*}$ (x), i.e.,

$$\begin{array}{c}\hfill \mathbf{x}(t)\to Q_1^{\ast }(\mathbf{x}(t)),\end{array}$$ [7]

leads to a universal description of stochastic oscillations, independent of the specific stochastic mechanism responsible for their generation. The transformation to the complex-valued variable $Q_1^{*}$ (x(t)) entails a tremendous simplification for all of the oscillator’s essential aspects. First, we derive unifying and strikingly simple formulas for its spontaneous spectral statistics; this enables a systematic comparison of different stochastic oscillators. Second, we also calculate its linear response to external time-dependent stimuli and find a fluctuation–dissipation theorem. Third, we put forward a simple but quantitatively successful theory of cross-correlations of weakly coupled stochastic oscillators. Hence, using the full function $Q_1^{*}$ (x) (instead of using only its complex argument ψ(x)) as the stochastic analog of the asymptotic phase, we achieve a true simplification and capture the universal characteristics of stochastic oscillations.

Before proceeding, we note that $Q_1^{*}$ (x(t)) has a zero stationary mean value, in the sense that

$$\begin{array}{c}\hfill 〈Q_1^{\ast }(\mathbf{x}(t))〉=\int d\mathbf{x}{Q}_1^{\ast }(\mathbf{x})P_0(\mathbf{x})=0,\end{array}$$ [8]

which follows from the biorthogonality relation Eq. 5. Furthermore, we normalize it to have unit variance

$$\begin{array}{c}\hfill 〈|Q_1^{\ast }{(\mathbf{x}(t))|}^2〉=\int d\mathbf{x}{|Q_1^{\ast }(\mathbf{x})|}^2{P}_0(\mathbf{x})=1.\end{array}$$ [9]

Finally, we note that the complex argument of $Q_1^{*}$ (x) (the abovementioned asymptotic phase of a stochastic oscillator) is only defined up to a constant phase shift.

Example Models

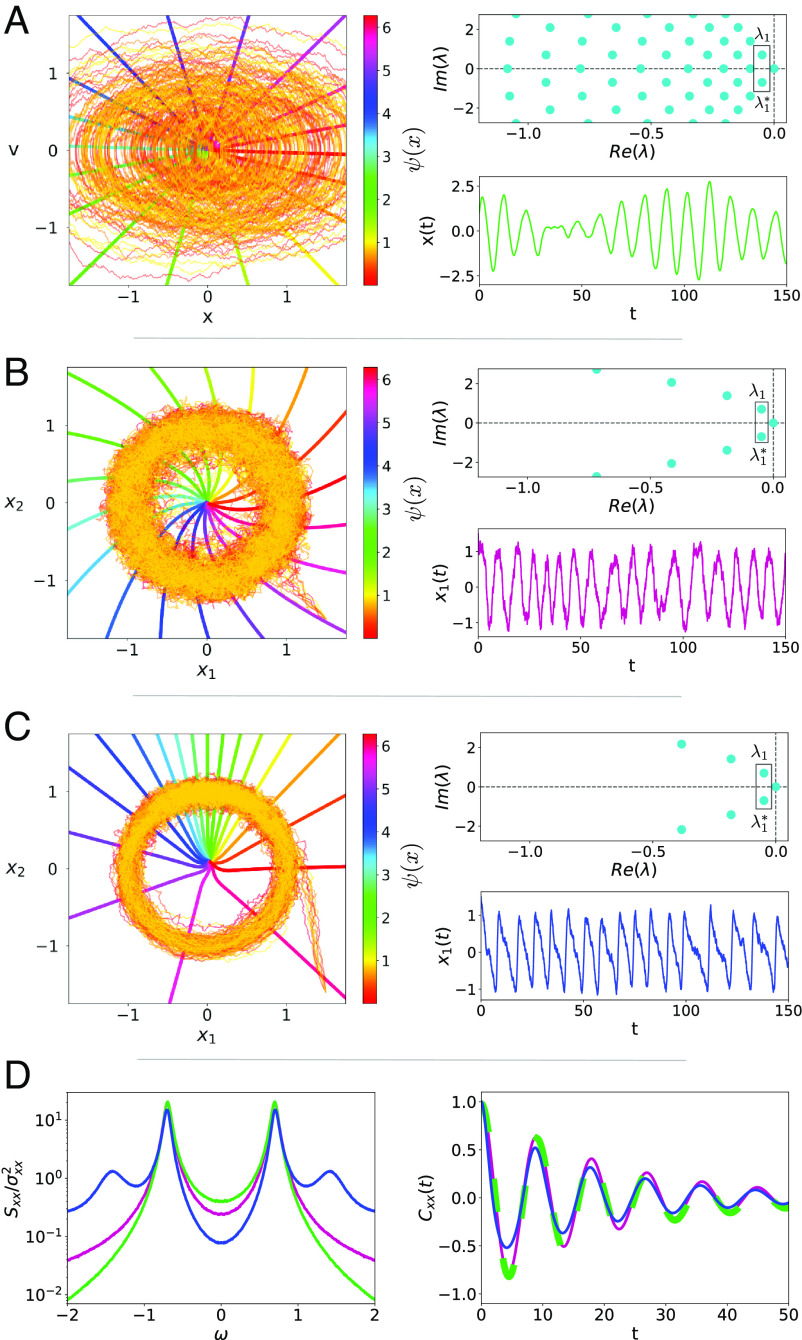
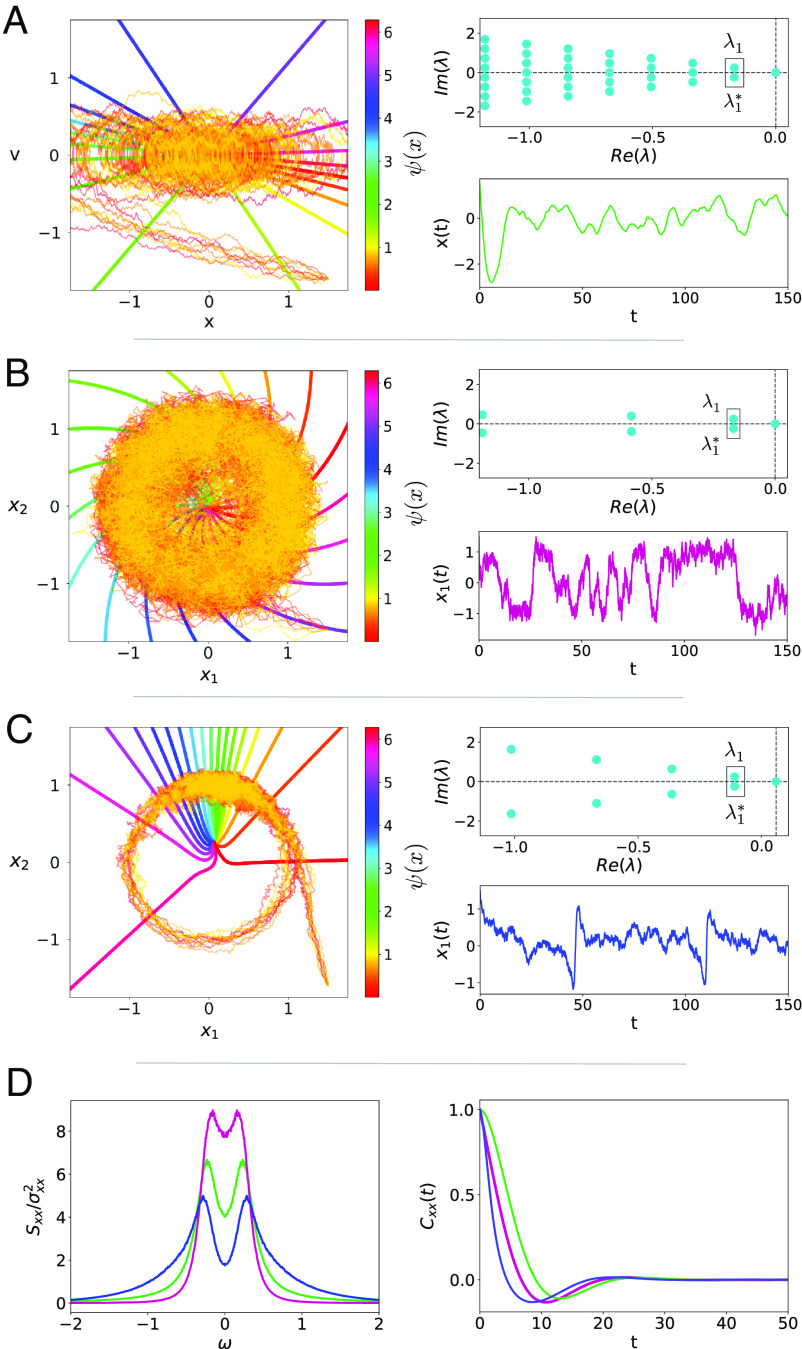
Throughout the paper, we will illustrate our unified theory by applying it to three models in which stochastic oscillations arise from qualitatively different mechanisms. We will use each model at two different parameter sets—one corresponding to a more coherent (cf. Fig. 1) and one to a less coherent (cf. Fig. 2) stochastic oscillation. We tune parameters such that all models in the more coherent case have the same leading nontrivial eigenvalue λ₁ = −0.048 + i0.698 and thus also the same quality factor of |ω₁/μ₁|=14.5, thereby satisfying condition (ii) for a robust stochastic oscillation well. Likewise, we find parameters such that all models in the less coherent case have the same λ₁ = −0.168 + i0.241 and thus also the same quality factor of |ω₁/μ₁|=1.43 which obeys condition (ii) for a robust stochastic oscillation only barely but represents the interesting limit case in which fluctuations definitely cannot be regarded as weak.

Fig. 1.

Three models of “robust” stochastic oscillations. In the three panels, we show for each model ten sample trajectories in phase space together with the stochastic asymptotic phase ψ(x) (Left), a time series of one of the components (Lower Right), and the spectrum of eigenvalues (Top Right). For the three models, parameters have been tuned so they have the same value for the eigenvalue λ₁ = −0.048 + 0.698i with the smallest nonvanishing real part. (A) Damped noisy harmonic oscillator for M = 1, γ = 0.096, ω₀ = 0.699, D = 0.01125. (B) Noisy Stuart–Landau for a = 1, b = −0.3, D₁ = D₂ = 0.04. (C) Noisy SNIC model (beyond the bifurcation, i.e., in the limit-cycle regime) for m = 1.216, n = 1.014, and D₁ = D₂ = 0.0119. (D) Power spectra (Left) and correlation function (Right) of x(t) (harmonic oscillator, green), x₁(t) (noisy Stuart–Landau model, purple), and x₁(t) (SNIC model, blue).

Fig. 2.

Three models of stochastic oscillations. In the three panels, we show for each model ten sample trajectories in phase space together with the stochastic asymptotic phase ψ(x) (Left), a time series of one of the components (Lower Right), and the spectrum of eigenvalues (Top Right). For the three models, parameters have been tuned, so they have the same value for slowest decaying eigenvalue λ₁ = −0.168 + 0.241i. (A) Damped noisy harmonic oscillator for M = 1, γ = 0.337, ω₀ = 0.294, D = 0.01125. (B) Noisy Stuart–Landau for a = 1, b = −0.713, and D₁ = D₂ = 0.0995. (C) Noisy SNIC model (prior to the bifurcation, i.e., in the excitable regime) for m = 0.99, n = 1, and D₁ = D₂ = 0.01125. (D) Power spectra (Left) and correlation function (Right) of x(t) (harmonic oscillator, green), x₁(t) (noisy Stuart–Landau model, purple), and x₁(t) (excitable SNIC model, blue).

Damped harmonic oscillator with white noise—As a first illustration, we consider an elementary physical model that is analytically treatable (31): a one-dimensional harmonic oscillator with mass M which is subject to Stokes friction and white Gaussian noise and obeys the stochastic differential equations

$$\begin{array}{c}\hfill \dot{x}=v,M\dot{v}=-\gamma v-M{\omega }_0^{2}x+\sqrt{2D}\xi (t).\end{array}$$ [10]

The model is already formulated in nondimensional variables (space and time) and parameters (friction coefficient γ, eigenfrequency ω₀, and noise intensity D) and will be considered exclusively in the underdamped limit (ω₀ > γ/(2M)). We show sample trajectories and the time courses of the stochastic oscillation for a high-quality factor of |ω₁/μ₁|=14.5 in Fig. 1A and for a less coherent oscillation with |ω₁/μ₁|=1.43 in Fig. 2A. The trajectories in phase space spend most time around the origin and in the time series of the position variable strong stochastic variations in amplitude and phase are seen. The eigenvalue spectra (Upper Right in Figs. 1A and 2A) on the left side of the complex plane are in part complex-valued, but some are also purely real; the next eigenvalue to λ₁ fulfills the condition (iii) with the equal sign (the spectrum is discussed in ref. 60).^*

Noisy Stuart–Landau oscillator—This is the canonical model for a supercritical Hopf bifurcation, which we consider in a version endowed with white Gaussian noise

$$\begin{array}{cc}\hfill {\dot{x}}_1& =a{x}_1-x_2-a(x_1^2+x_2^2)(x_1+b{x}_2)+\sqrt{2D_1}{\xi }_1(t),\hfill \\ \hfill {\dot{x}}_2& =a{x}_2+x_1-a(x_1^2+x_2^2)(x_2-b{x}_1)+\sqrt{2D_2}{\xi }_2(t),\hfill \end{array}$$ [11]

with a, b ∈ ℝ. In the absence of noise, this system has a limit cycle of period T = 2π/(1 + ba). Because of the existing limit cycle, the amplitude variations of the stochastic oscillations are much smaller than for the harmonic oscillator (see Left and Bottom Right of Figs. 1B and 2B). The eigenvalue spectra (Top Right of Figs. 1B and 2B) are, in the displayed region, far less populated than for those of the harmonic oscillator. We note that there are also purely real eigenvalues outside the shown range; these are related to the amplitude of the stochastic oscillation (58).

Noisy SNIC system—A two-dimensional system that, in its deterministic version, undergoes a saddle-node bifurcation on an invariant circle (SNIC) is given by

$$\begin{array}{cc}\hfill {\dot{x}}_1& =n{x}_1-m{x}_2-x_1(x_1^2+x_2^2)+\frac{x_2^2}{\sqrt{x_1^2+x_2^2}}+\sqrt{2D_1}{\xi }_1(t),\hfill \\ \hfill {\dot{x}}_2& =m{x}_1+n{x}_2-x_2(x_1^2+x_2^2)-\frac{x_1{x}_2}{\sqrt{x_1^2+x_2^2}}+\sqrt{2D_2}{\xi }_2(t).\hfill \end{array}$$ [12]

Without noise, the saddle-node bifurcation from the excitable to the oscillatory regime occurs at m = 1. Here, we consider this model endowed with white Gaussian noise once set in the oscillatory regime (leading to the more coherent stochastic oscillation, see Fig. 1C) and once set in the excitable regime (leading to the less coherent stochastic oscillation, see Fig. 2C). In marked contrast to the first two models, the x₁ variable of the SNIC model has a temporally asymmetric time series; however, we observe this asymmetry to be more pronounced in the excitable case. In this case, the trajectory stays most of the time close to the stable node and occasionally the noise causes a transition across the unstable saddle. Similarly to the Stuart–Landau case, we have fewer eigenvalues in the displayed range compared to the harmonic oscillator; again, there exist purely real eigenvalues outside the range shown.

As Figs. 1D and 2D show, despite having chosen the parameters of the three models such that they all have the same value of λ₁ = μ₁ + iω₁ and thus share the same long-term evolution time dependence^† in Eq. 6, the power spectra and autocorrelation functions of the models at one λ₁ differ. The differences are more pronounced for the less coherent oscillation (Fig. 2D), and they reflect the specific nature of the system. For instance, the SNIC system with its highly temporally asymmetric time series shows pronounced higher harmonics, while the harmonic oscillator does not. Except for the harmonic oscillator (31), it is difficult to calculate power spectra or correlation functions for these stochastic oscillators analytically (for the Stuart–Landau oscillator, some approximations for power spectrum and linear response have been put forward in refs. 66–68).

By contrast, and as we show next, the heterogeneous profiles for the statistics of spontaneous fluctuations, as given by the power spectra or correlation functions, will be reduced to a universal form when we observe the processes through the lens of the leading backward eigenfunction $Q_1^{*}$ (x(t)).

Correlation Functions and Power Spectra

Generally, for any eigenfunction $Q_{\lambda }^{*}$(x(t)), the correlation function is given by C_{λ, λ}(τ) = ⟨$Q_{\lambda }^{*}$(x(τ))Q_λ(x(0))⟩ and its Fourier transform, the power spectrum, by $S_{\lambda ,\lambda }(\omega )={\int }_{-\infty }^{\infty }{C}_{\lambda ,\lambda }(\tau )e^{-i\omega \tau }d\tau$. Following ref. 60, we can write the autocorrelation function as an integral over the formal solution of the Fokker–Planck equation using the stationary probability density P₀(x)

$$\begin{array}{c}\hfill C_{\lambda ,\lambda }(\tau )=\int d\mathbf{x}{Q}_{\lambda }^{\ast }(\mathbf{x})e^{\mathcal{L}(\mathbf{x})\tau }[Q_{\lambda }(\mathbf{x})P_0(\mathbf{x})].\end{array}$$

If we expand the function Q_λ(x)P₀(x) = ∑_λ′κ_λ′P_λ′(x) in terms of the forward eigenfunctions and use the biorthogonal properties Eq. 5 of these functions (see SI Appendix for an alternative derivation), we arrive for τ > 0 at

$$\begin{array}{c}\hfill C_{\lambda ,\lambda }(\tau )=⟨|Q_{\lambda }^{\ast }{|}^2⟩e^{\lambda \tau }.\end{array}$$ [13]

This is a strikingly simple result: The correlation function is given by the product of the stationary variance of $Q_{\lambda }^{*}$ and a complex exponential function. Specifically, for our variable $Q_1^{*}$ (x), taking into account Eq. 9 and generalizing the formula to both negative and positive time lags τ, the correlation function reads

$$\begin{array}{c}\hfill C_1(\tau )=exp\left[{\mu }_1|\tau |+i{\omega }_1\tau \right].\end{array}$$ [14]

Real and imaginary parts of this function display damped oscillations corresponding to the finite coherence of the stochastic oscillations. One characteristic of the oscillation is the quality factor |ω₁/μ₁| that tells us how many cycles (in multiples of 2π) are seen in the correlation function before the exponential envelope has decayed to 1/e.

The even simpler expression for the power spectral density corresponds to a (purely real-valued) Lorentzian, peaked at ω = ω₁ with a half-width of μ₁

$$\begin{array}{c}\hfill S_1(\omega )=\frac{2|{\mu }_1|}{{\mu }_1^2+{(\omega -{\omega }_1)}^2}.\end{array}$$ [15]

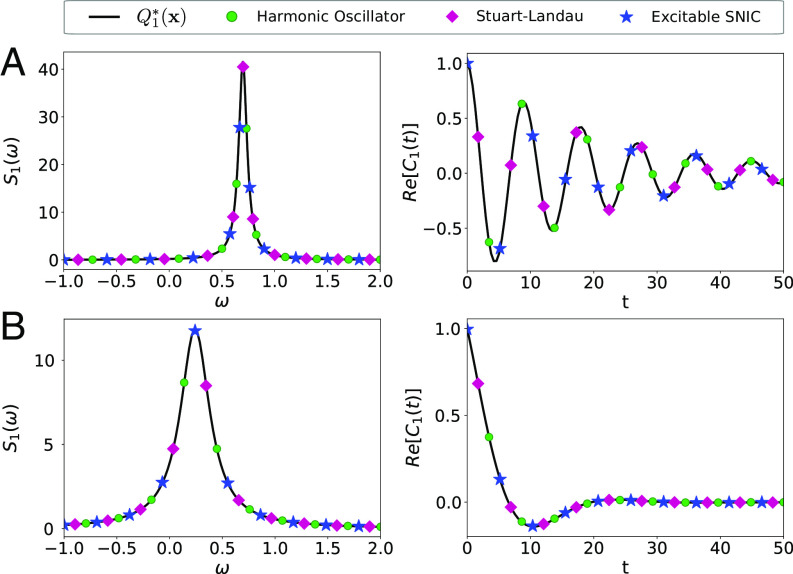
In Fig. 3 we show the power spectra of $Q_1^{*}$ (x) and the real part of the autocorrelation function C₁(τ) for the parameters chosen in Figs. 1 and 2 (Fig. 3 A and B, respectively). As we show in Figs. 1D and 2D, the power spectra and correlation functions of the models in the original variables exhibit different shapes. However, when transforming to $Q_1^{*}$ (x), since we tuned parameters such that all three models in Figs. 1 and 2 have the same complex eigenvalue with the smallest real part, λ₁, the three very different systems possess identical power spectra. This is confirmed by our simulations (symbols) which all fall on the line predicted by Eq. 15 (Fig. 3). Therefore, by means of the function $Q_1^{*}$ , we have made the three systems quantitatively comparable and, moreover, characterizable with a simple analytical expression and two informative parameters—the frequency and the half-width of the spectral peak (or, equivalently, the frequency and the quality factor).

Fig. 3.

Power spectra S₁(ω) and real part of the autocorrelation function C₁(t) of $Q_1^{*}$ (x(t)) for the different models with parameters in A and B as in Figs. 1 and 2, respectively. (A) For parameters from Fig. 1 (chosen such that λ₁ = μ₁ + iω₁ is approximately the same for all models with μ₁ = −0.048, ω₁ = 0.698, leading to a more coherent oscillation with a quality factor of |ω₁/μ₁|=14.3), we compare Eq. 15 (solid line) to stochastic simulations of the three models (symbols). (B) For parameters from Fig. 2 (chosen such that λ₁ = μ₁ + iω₁ is approximately the same for all models with μ₁ = −0.168, ω₁ = 0.241, leading to a less coherent oscillation with a quality factor of |ω₁/μ₁|=1.43), we compare Eq. 15 (solid line) to stochastic simulations of the three models (symbols).

By a procedure similar to that for the correlation functions and power spectra for $Q_{\lambda }^{*}$(x(t)), we can also calculate expressions for the cross-correlation functions C_{λ, λ′}(τ)=⟨$Q_{\lambda }^{*}$(x(τ))Q_λ′(x(0))⟩ (see SI Appendix for details):

$$\begin{array}{c}\hfill C_{\lambda ,{\lambda }^{\prime }}(\tau )=〈Q_{\lambda }^{\ast }{Q}_{{\lambda }^{\prime }}〉\left\{\begin{array}{cc}{e}^{-{\lambda }^{\prime \ast }\tau },\hfill & \tau <0\hfill \\ e^{\lambda \tau },\hfill & \tau >0\hfill \end{array}\right.,\end{array}$$ [16]

and for the cross-spectra $S_{\lambda ,\lambda \prime }(\omega )={\int }_{-\infty }^{\infty }d\tau C_{\lambda ,\lambda \prime }(\tau )e^{-i\omega \tau }$

$$\begin{array}{c}\hfill S_{\lambda ,{\lambda }^{\prime }}(\omega )=-〈Q_{\lambda }^{\ast }{Q}_{{\lambda }^{\prime }}〉\left(\frac{1}{\lambda -i\omega }+\frac{1}{{\lambda }^{\prime \ast }+i\omega }\right).\end{array}$$ [17]

We will need these expressions below for the theory of coupled stochastic oscillators.

Linear Response and Fluctuation–Dissipation Theorem

We now consider how the stochastic oscillators respond to a weak time-dependent forcing εp(t) that enters the system via a perturbation vector e. That is, we consider

$$\begin{array}{c}\hfill \frac{d\mathbf{x}}{\mathit{dt}}=\mathbf{f}(\mathbf{x})+\epsilon p(t)\mathbf{e}+\mathbf{g}(\mathbf{x})\xi (t),\mathbf{x},\mathbf{e}\in {\mathbb{R}}^n.\end{array}$$ [18]

How the time-dependent mean value of our variable $Q_1^{*}$ (x(t)) is affected by the perturbation p(t) can be described in terms of linear response theory (60, 61, 69, 70)

$$\begin{array}{c}\hfill 〈Q_1^{\ast }(\mathbf{x}(t))〉=\epsilon {\int }_{-\infty }^{t}d{t}^{\prime }{K}_{\mathbf{e}}(t-t^{\prime })p(t^{\prime }),\end{array}$$ [19]

where we have taken into account Eq. 8 and introduced the complex-valued linear-response function K_e(τ) (the index indicates the dependence on the direction of perturbation, e). Equivalently, we can use the susceptibility χ_e(ω) = ${\int }_{\mathrm{-\infty }}^{\infty }$dτe^−iωτK_e(τ), the Fourier transform of the response function.

In order to derive an expression for K_e(τ), we follow Risken (60), chapter 7] and express the Fokker–Planck operator by an unperturbed part ℒ and a perturbation part ℒ_e = −e ⋅ ∇, leading to the Fokker–Planck equation

$$\begin{array}{c}\hfill {\partial }_{t}P(\mathbf{x},t)=(\mathcal{L}(\mathbf{x})+\epsilon p(t){\mathcal{L}}_{\mathbf{e}}(\mathbf{x}))P(\mathbf{x},t).\end{array}$$ [20]

Expanding the density in powers of ε, P(x, t) = P₀(x) + εP_e(x, t) + 𝒪(ε²), taking only the leading linear order and expressing this by an integral over the formal time-dependent solution, we obtain

$$\begin{array}{c}\hfill P_{\mathbf{e}}(\mathbf{x},t)={\int }_{-\infty }^{t}d{t}^{\prime }p(t^{\prime })e^{\mathcal{L}(\mathbf{x})(t-t^{\prime })}[{\mathcal{L}}_{\mathbf{e}}(\mathbf{x})[P_0(\mathbf{x})]].\end{array}$$ [21]

By expressing the time-dependent mean value ⟨$Q_1^{*}$ (x(t))⟩ by the integral over P_e(x, t) and comparing to Eq. 19, we obtain for the linear-response function the intermediate result

$$\begin{array}{c}\hfill K_{\mathbf{e}}(\tau )=\int d\mathbf{x}{Q}_1^{\ast }(\mathbf{x})e^{\mathcal{L}(\mathbf{x})\tau }[{\mathcal{L}}_{\mathbf{e}}(\mathbf{x})[P_0(\mathbf{x})]],\tau >0.\end{array}$$ [22]

We expand ℒ_e(x)[P₀(x)] = ∑_λ′β_{e, λ′}P_λ′(x) into forward eigenfunctions, use the eigenvalue equations and the biorthogonality relation Eq. 5, and finally take into account causality (which implies K_e(τ) ≡ 0 for τ < 0) to arrive at a simple expression for the linear-response function (see SI Appendix for details)

$$\begin{array}{c}\hfill K_{\mathbf{e}}(\tau )={\beta }_{\mathbf{e}}\left\{\begin{array}{cc}{e}^{{\lambda }_1\tau },\hfill & \tau >0\hfill \\ 0,\hfill & \text{else}\hfill \end{array}\right.,\end{array}$$ [23]

where the complex-valued coefficient β_e = β_{e, λ1} (we omit the second index for ease of notation) is given by

$$\begin{array}{c}\hfill {\beta }_{\mathbf{e}}=-\int d\mathbf{x}{Q}_1^{\ast }(\mathbf{x})[\mathbf{e}·\mathrm{\nabla }{P}_0(\mathbf{x})],\end{array}$$ [24]

where ∇P₀(x) is the gradient of the stationary density in our n-dimensional phase space. We note that for a stationary density P₀(x) obeying natural boundary conditions, β_e = e ⋅ ⟨∇$Q_1^{*}$ (x)⟩, i.e., the coefficient is related to the mean change of $Q_1^{*}$ (x) in the direction of the perturbation.

The susceptibility of the stochastic oscillator is given by

$$\begin{array}{c}\hfill {\chi }_{\mathbf{e}}(\omega )={\int }_{-\infty }^{\infty }d\tau K_{\mathbf{e}}(\tau )e^{-i\omega \tau }=\frac{{\beta }_{\mathbf{e}}}{-{\mu }_1+i(\omega -{\omega }_1)},\end{array}$$ [25]

i.e., a simple bandpass filter centered at ω = ω₁. Its modulus and its phase are given by,

$$\begin{array}{cc}\hfill |{\chi }_{\mathbf{e}}(\omega )|& =\frac{|{\beta }_{\mathbf{e}}|}{\sqrt{{\mu }_1^2+{(\omega -{\omega }_1)}^2}},\hfill \\ \hfill arg({\chi }_{\mathbf{e}}(\omega ))& =arg({\beta }_{\mathbf{e}})+arctan({\omega }_1-\omega ,-{\mu }_1).\hfill \end{array}$$ [26]

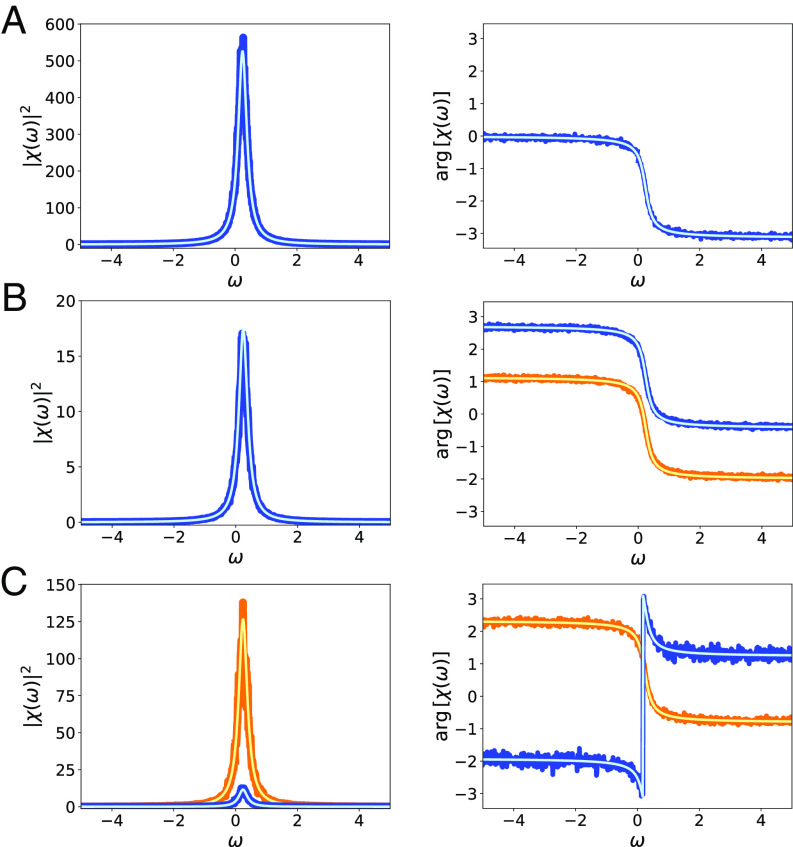
We confirm these results via numerical simulations of all three models in Fig. 4 (see SI Appendix for details on measuring susceptibilities). For the harmonic oscillator, we show only the susceptibility for the physically relevant case of a perturbation of the velocity equation. For the Stuart–Landau model, the susceptibilities for perturbations in the x₁ and x₂ directions are shown separately but coincide because of the symmetry of the model; the phase shifts are also the same up to a constant (we recall that the phase of our output variable $Q_1^{*}$ is only determined up to a constant phase). In contrast to the rotational symmetry of the Stuart–Landau oscillator, the excitable SNIC model differs in its response to perturbations in the x₁ and x₂ directions: perturbations in the x₁ direction are more efficient in kicking the system out of the stable fixed point and thus in evoking a response; consequently, χ_ex1 > χ_ex2 for all frequencies.

Fig. 4.

Susceptibility functions χ_e(ω) of the variable $Q_1^{*}$ (x(t)) for the different models with the same parameters as in Fig. 2 and different perturbation vectors e as indicated. For each model, we show the squared of the absolute value, |χ_e(ω)|², (Left) showing a Lorentzian profile and its angle arg(χ_e(ω)) (Right). The perturbation vectors are e₁ = (1, 0)^⊤ and e₂ = (0, 1)^⊤. (A) The harmonic oscillator β_ev = −3.87i (blue, computations; cyan, theory); (B) Stuart–Landau model β_e1 = 0.641 − 0.297i (orange, computations; yellow, theory), β_e2 = 0.297 + 0.641i, (blue, computations; cyan, theory); (C) SNIC excitable system β_e1 = 1.38 + 1.3i (orange, computations; yellow, theory), β_e2 = −0.54 + 0.19i (blue, computations; cyan, theory).

We note that we can calculate the response functions and susceptibilities of the higher eigenfunctions $Q_{\mathrm{\lambda \prime }}^{*}$(x(t)) in an analogous fashion, resulting in very similar formulas, Eqs. 23 and 25. The main differences are that i) we have to use λ′ instead of λ₁, and ii) in the computation of the coefficient β_e in Eq. 24, we use $Q_{\mathrm{\lambda \prime }}^{*}$(x) instead of $Q_1^{*}$ (x).

Turning back to the statistics of $Q_1^{*}$ (x(t)), we stress that the simple expressions for the autocorrelation function of the oscillator and its response function permit a simple connection between them, which can be regarded as a fluctuation–dissipation theorem (FDT). FDTs are relations between the spontaneous activity of a system and its response to external perturbations and have been derived for thermodynamic equilibrium (60, 69, 71) as well as for nonequilibrium settings (61, 72–76). For our broad model class, we obtain the simplest relation in the time domain as follows:

$$\begin{array}{c}\hfill K_{\mathbf{e}}(\tau )={\beta }_{\mathbf{e}}{C}_1(\tau ),\tau >0.\end{array}$$ [27]

This relation resembles, formally, the generalized FDT (61, 72, 73, 77), but differs from the latter, because the generalized FDT is based on the (purely real-valued) conjugated variable. Our result Eq. 27 constitutes a simple fluctuation–dissipation theorem holding true for the general class of stochastic oscillators, most of which operate far from thermodynamic equilibrium. For relations between the power spectrum and the susceptibility that are formally closer to the standard FDT of equilibrium systems in the Fourier domain (71), see SI Appendix.

Two Weakly Coupled Stochastic Oscillators

We now demonstrate that the transformation to the variable $Q_1^{*}$ (x) also allows for a simplified description of the statistics of weakly coupled stochastic oscillators. For simplicity, we consider only two coupled oscillators; however, the general method can be applied for larger systems of interacting units too.

We couple the two oscillators with the scalar functions H_x(x, y) = H_xx(x) + H_yx(y) and H_y(x, y) = H_xy(x) + H_yy(y) along the directions e_x and e_y, respectively, and scale the coupling terms by a small parameter ε

$$\begin{array}{cc}\hfill \dot{\mathbf{x}}& ={\mathbf{f}}_{\mathbf{x}}(\mathbf{x})+\epsilon {\mathbf{e}}_{\mathbf{x}}[H_{\mathbf{x}\mathbf{x}}(\mathbf{x})+H_{\mathbf{y}\mathbf{x}}(\mathbf{y})]+{\mathbf{g}}_{\mathbf{x}}(\mathbf{x}){\xi }_{\mathbf{x}}(t),\hfill \\ \hfill \dot{\mathbf{y}}& ={\mathbf{f}}_{\mathbf{y}}(\mathbf{y})+\epsilon {\mathbf{e}}_{\mathbf{y}}[H_{\mathbf{x}\mathbf{y}}(\mathbf{x})+H_{\mathbf{y}\mathbf{y}}(\mathbf{y})]+{\mathbf{g}}_{\mathbf{y}}(\mathbf{y}){\xi }_{\mathbf{y}}(t).\hfill \end{array}$$ [28]

Here, the terms with mixed indices H_yx(y) (H_xy(x)) describe the effect of the y (x) oscillator on the x (y) oscillator; the diagonal terms H_xx(x) and H_yy(y) can in principle be lumped into the drift terms f_x(x) and f_y(y), respectively (which will then also change our $Q_1^{*}$ functions). Here, we keep for clarity the diagonal terms as a perturbing input such that the eigenfunctions $Q_{1_{\text{x}}}^{*}(\text{x})$ and $Q_{1_{\text{y}}}^{*}(\text{y})$ are those of the uncoupled oscillators (see SI Appendix for a discussion of the alternative treatment of the problem).

We use the response functions Eq. 23 in a realization-wise version

$$\begin{array}{cc}\hfill Q_{1_{\mathbf{x}}}^{\ast }& =Q_{1_{\mathbf{x}},0}^{\ast }+\epsilon {\displaystyle \underset{-\infty }{\overset{t}{\int }}}d{t}^{\prime }{K}_{{\mathbf{e}}_{\mathbf{x}}}(t-t^{\prime })[H_{\mathbf{x}\mathbf{x}}(\mathbf{x}(t^{\prime }))+H_{\mathbf{y}\mathbf{x}}(\mathbf{y}(t^{\prime }))],\hfill \\ \hfill Q_{1_{\mathbf{y}}}^{\ast }& =Q_{1_{\mathbf{y}},0}^{\ast }+\epsilon {\displaystyle \underset{-\infty }{\overset{t}{\int }}}d{t}^{\prime }{K}_{{\mathbf{e}}_{\mathbf{y}}}(t-t^{\prime })[H_{\mathbf{x}\mathbf{y}}(\mathbf{x}(t^{\prime }))+H_{\mathbf{y}\mathbf{y}}(\mathbf{y}(t^{\prime }))],\hfill \end{array}$$ [29]

and similarly for the other backward eigenmodes $Q_{{\lambda }_x^{\prime }}^{\ast }$ and $Q_{{\lambda }_y^{\prime }}^{\ast }$ (SI Appendix). In Eq. 29, the functions $Q_{1_x,0}^{\ast }$ and $Q_{1_y,0}^{\ast }$ denote the spontaneous activity of the uncoupled oscillator, respectively. A similar approximation (using the response function for the time-dependent mean value to approximate the realization-wise response of the system) has been successfully applied in the past to stochastic network models of recurrently coupled spiking neurons (78, 79).

We assume that we can expand the coupling functions into the backward eigenfunctions as follows:

$$\begin{array}{cc}\hfill H_{\mathbf{x}\mathbf{x}}(\mathbf{x})+H_{\mathbf{y}\mathbf{x}}(\mathbf{y})& ={\displaystyle \sum _{{\lambda }_{\mathbf{x}}^{\prime }}}{\gamma }_{{\lambda }_{\mathbf{x}}^{\prime }}{Q}_{{\lambda }_{\mathbf{x}}^{\prime }}^{\ast }+{\displaystyle \sum _{{\lambda }_{\mathbf{y}}^{\prime }}}{\alpha }_{{\lambda }_{\mathbf{y}}^{\prime }}{Q}_{{\lambda }_{\mathbf{y}}^{\prime }}^{\ast },\hfill \\ \hfill H_{\mathbf{x}\mathbf{y}}(\mathbf{x})+H_{\mathbf{y}\mathbf{y}}(\mathbf{y})& ={\displaystyle \sum _{{\lambda }_{\mathbf{x}}^{\prime }}}{\alpha }_{{\lambda }_{\mathbf{x}}^{\prime }}{Q}_{{\lambda }_{\mathbf{x}}^{\prime }}^{\ast }+{\displaystyle \sum _{{\lambda }_{\mathbf{y}}^{\prime }}}{\gamma }_{{\lambda }_{\mathbf{y}}^{\prime }}{Q}_{{\lambda }_{\mathbf{y}}^{\prime }}^{\ast },\hfill \end{array}$$ [30]

where the coefficients γ_λ′x, α_λ′x are given by

$$\begin{array}{cc}\hfill {\gamma }_{{\lambda }_{\mathbf{x}}^{\prime }}=\int d\mathbf{x}{P}_{{\lambda }_{\mathbf{x}}^{\prime }}(\mathbf{x})H_{\mathbf{x}\mathbf{x}}(\mathbf{x}),& {\alpha }_{{\lambda }_{\mathbf{x}}^{\prime }}=\int d\mathbf{x}{P}_{{\lambda }_{\mathbf{x}}^{\prime }}(\mathbf{x})H_{\mathbf{x}\mathbf{y}}(\mathbf{x}),\hfill \\ \hfill {\gamma }_{{\lambda }_{\mathbf{y}}^{\prime }}=\int d\mathbf{y}{P}_{{\lambda }_{\mathbf{y}}^{\prime }}(\mathbf{y})H_{\mathbf{y}\mathbf{y}}(\mathbf{y}),& {\alpha }_{{\lambda }_{\mathbf{y}}^{\prime }}=\int d\mathbf{y}{P}_{{\lambda }_{\mathbf{y}}^{\prime }}(\mathbf{y})H_{\mathbf{y}\mathbf{x}}(\mathbf{y}).\hfill \end{array}$$ [31]

In addition to introducing these coefficients, we now also consider the finite-time-window Fourier transforms of the observables (see SI Appendix for details) and thus obtain from Eq. 29

$$\begin{array}{cc}\hfill {\tilde{Q}}_{1_{\mathbf{x}}}^{\ast }& ={\tilde{Q}}_{1_{\mathbf{x}},0}^{\ast }+\epsilon {\chi }_{{\mathbf{e}}_{\mathbf{x}}}({\displaystyle \sum _{{\lambda }_{\mathbf{x}}^{\prime }}}{\gamma }_{{\lambda }_{\mathbf{x}}^{\prime }}{\tilde{Q}}_{{\lambda }_{\mathbf{x}}^{\prime }}^{\ast }+{\displaystyle \sum _{{\lambda }_{\mathbf{y}}^{\prime }}}{\alpha }_{{\lambda }_{\mathbf{y}}^{\prime }}{\tilde{Q}}_{{\lambda }_{\mathbf{y}}^{\prime }}^{\ast }),\hfill \\ \hfill {\tilde{Q}}_{1_{\mathbf{y}}}^{\ast }& ={\tilde{Q}}_{1_{\mathbf{y}},0}^{\ast }+\epsilon {\chi }_{{\mathbf{e}}_{\mathbf{y}}}({\displaystyle \sum _{{\lambda }_{\mathbf{x}}^{\prime }}}{\alpha }_{{\lambda }_{\mathbf{x}}^{\prime }}{\tilde{Q}}_{{\lambda }_{\mathbf{x}}^{\prime }}^{\ast }+{\displaystyle \sum _{{\lambda }_{\mathbf{y}}^{\prime }}}{\gamma }_{{\lambda }_{\mathbf{y}}^{\prime }}{\tilde{Q}}_{{\lambda }_{\mathbf{y}}^{\prime }}^{\ast }),\hfill \end{array}$$ [32]

and similarly for the remaining modes. From this linear system of equations, by a systematic expansion in the weak coupling strength ε, we obtain the cross-spectrum between $Q_{1_{\text{x}}}^{*}$ and $Q_{1_{\text{y}}}^{*}$ in terms of the susceptibilities Eq. 25 and cross-spectra between the modes of one oscillator Eq. 17 (SI Appendix):

$$\begin{array}{c}\hfill S_{1,\mathbf{y}\mathbf{x}}^c=\epsilon ({\chi }_{{\mathbf{e}}_{\mathbf{x}}}^{\ast }{\displaystyle \sum _{{\lambda }_{\mathbf{y}}^{\prime }}}{\alpha }_{{\lambda }_{\mathbf{y}}^{\prime }}^{\ast }{S}_{1_{\mathbf{y}},{\lambda }_{\mathbf{y}}^{\prime }}+{\chi }_{{\mathbf{e}}_{\mathbf{y}}}{\displaystyle \sum _{{\lambda }_{\mathbf{x}}^{\prime }}}{\alpha }_{{\lambda }_{\mathbf{x}}^{\prime }}{S}_{{\lambda }_{\mathbf{x}}^{\prime },1_{\mathbf{x}}}).\end{array}$$ [33]

From this formula, we can extract the following information. First of all, for weak coupling, the cross-spectrum between oscillators is proportional to ε. Second, the first term in the parenthesis consists of the susceptibility of the x oscillator and a weighted sum of cross-spectra between the different eigenfunctions of the y oscillator with the most important term being the power spectrum S_1y. The complex-valued coefficients of this sum are determined by H_yx(y), the coupling function from y to x, via Eq. 31. The second term in the parenthesis is similar, only the roles of x and y are switched. For two statistically identical oscillators with symmetric coupling, the second term is the complex conjugate of the first one and hence the cross-spectrum will be real-valued; any nonvanishing imaginary part thus reflects a heterogeneity in the oscillators or the coupling. For the interesting case of a purely unidirectional coupling from y to x, for instance, the second term in the parenthesis in Eq. 33 will simply vanish.

Our result for the cross-spectrum of the oscillators Eq. 33 still contains an infinite sum of terms. However, as all of our numerical examples below show, just a few terms in the sums will effectively contribute. Specifically, for the case of coherent stochastic oscillators with similar frequencies, we may restrict the sums just to the first terms (involving the spectra associated with λ₁ and ${\lambda }_1^{*}$) and still obtain accurate results.

We start testing our formula for the cross-spectrum of two identical harmonic oscillators that are weakly coupled by a spring (Fig. 5A). In this case, of course, the cross-spectrum between the original position variables of the two oscillators can be easily calculated and is shown in the Left panel (and calculated in the SI Appendix): a purely real function with a positive lobe for ω < ω₀, a negative lobe for ω > ω₀ and everything mirrored at negative frequencies. When computing the cross-spectrum of the variables $Q_{1_x}^{\ast }$, $Q_{1_y}^{\ast }$, we can take advantage of the analytical expression for $Q_1^{*}$ (SI Appendix) to find that the coupling function is exactly given by a linear combination of $Q_1^{*}$ and Q₁ (hence, higher coefficients ${\alpha }_{{\lambda }_y^{\prime }}^{\ast }$ and ${\alpha }_{{\lambda }_{\text{x}}^{\prime }}$ in the expansion are identically zero; see SI Appendix for further details). Therefore, the infinite sum in Eq. 33 reduces to

$$\begin{array}{c}\hfill S_{1,\mathbf{y}\mathbf{x}}^c\approx 2\epsilon \mathfrak{R}({\chi }_{\mathbf{e}}^{\ast }{\alpha }_1^{\ast }{S}_1+{\chi }_{\mathbf{e}}^{\ast }{\alpha }_1{S}_{1,1}),\end{array}$$ [34]

Fig. 5.

Cross-spectra of two coupled units for weak coupling strength ε = 0.01. In all panels, the thin (thick) lines indicate simulations (theory); blue (green) corresponds to real (imaginary) part. (A) For two harmonic oscillators with parameters as in Fig. 1, we show cross-spectra between the position variables of each oscillator (Left) and between the $Q_1^{*}$ functions, $S_{1,\mathbf{\text{yx}}}^c$. (B) For two symmetrically coupled but nonidentical Stuart–Landau oscillators, we show the cross-spectrum between the $Q_1^{*}$ functions; Left: oscillators slightly detuned with one oscillator as in Fig. 1 and the other one with a changed value of b = −0.25; Right: the second oscillator is more strongly detuned with b = −0.1. (C) For two coupled identically SNIC systems, we show the cross-spectra $S_{1,\mathbf{\text{yx}}}^c$ with parameters as in Fig. 1 (Left) and Fig. 2 (Right). In the Right, two versions of the theory are shown: approximations by one mode (dashed line) and by the five leading terms (solid line, see text).

where we have omitted the x, y dependences of the functions on the r.h.s. since both oscillators are assumed to be identical.

As we observe in Fig. 5A, Right, Eq. 34 displays an excellent agreement with numerical simulations. If we compare the cross-spectrum of the $Q_{1_x}^{\ast }$, $Q_{1_y}^{\ast }$ functions with the cross-spectrum in the original position variables, we note that they look very similar with the only difference being that in $S_{1,\mathbf{\text{yx}}}^c$(ω) everything happens exclusively at positive frequencies (we consider rotating pointers in the complex plane instead of real-valued time series) and the zero crossing of the function is at ω₁ (here close to ω₀). Hence, the cross-spectrum of the two systems described in terms of the backward eigenfunctions reflects the interdependence of the two systems appropriately. We note that, while the largest contribution to $S_{1,\mathbf{\text{yx}}}^c$ in Eq. 34 is given by the power spectra term S₁, the additional term S_{1, 1}, even if it is small, has to be included to match the asymmetry between the two lobes (sizes of minimum and maximum are slightly different); including only power spectra terms would result in a strictly odd function with respect to ω = ω₁.

Next, we employ our formula Eq. 33, to study a case of symmetrically coupled but nonidentical oscillators. We consider two different noisy Stuart–Landau oscillators diffusively coupled by their first coordinates x₁ and y₁. We study two cases to inspect how inhomogeneities of the oscillators affect the cross-spectrum: we set parameters such that i) both oscillators are slightly detuned (λ_1x = −0.048 + 0.698i, λ_1y = −0.047 + 0.748i) and ii) oscillators are more strongly detuned (λ_1x = −0.048 + 0.698i, λ_1y = −0.045 + 0.9i). As all quality factors in this example are small and the system is rotationally symmetric (which according to our numerical observations implies S_{1, 1}(ω) ≡ 0), we expect that the cross-spectrum is approximately given by

$$\begin{array}{c}\hfill S_{1,\mathbf{y}\mathbf{x}}^c=\epsilon ({\chi }_{{\mathbf{e}}_{\mathbf{x}}}^{\ast }{\alpha }_{1_{\mathbf{y}}}^{\ast }{S}_{1_{\mathbf{y}}}+{\chi }_{{\mathbf{e}}_{\mathbf{y}}}{\alpha }_{1_{\mathbf{x}}}{S}_{1_{\mathbf{x}}}).\end{array}$$ [35]

This formula agrees well with numerical simulations for both cases (Fig. 5B). We note that, as the oscillators are nonidentical, the cross-spectrum has both nonvanishing real and imaginary parts. The effect of inhomogeneities is clearly seen by comparing Left and Right panels in Fig. 5B. For small detuning (Left panel), we observe a similar profile for the real and imaginary parts of $S_{1,\mathbf{\text{yx}}}^c$: a one lobe function, which is only different from zero around a narrow frequency band in the neighborhood of both eigenfrequencies. As the detuning is small in case (i), the real part of $S_{1,\mathbf{\text{yx}}}^c$ is larger than the imaginary part. By contrast, in case (ii) with stronger detuning, the situation is reversed, and the imaginary part has a larger absolute value than the real part; also now the two frequencies of the oscillator become visible by two distinct peaks in both real and imaginary parts. Indeed, the larger degree of inhomogeneity is not only captured by the increase of power in the imaginary part of $S_{1,\mathbf{\text{yx}}}^c$, but also in the appearance of two secondary peaks around the individual eigenfrequencies of each unit.

Finally, we illustrate how for less coherent oscillators, more terms in the sum are required to yield a quantitatively correct result in Eq. 33. To this end, we consider first two identical SNIC systems with parameters of the more coherent case (chosen as in Fig. 1) and coupled symmetrically through their first coordinates. Here, we expect that, again, few modes are needed, and, indeed, similarly to the Stuart–Landau case, we just need the power spectra term

$$\begin{array}{c}\hfill S_{1,\mathbf{y}\mathbf{x}}^c=2\epsilon \mathfrak{R}({\chi }_{\mathbf{e}}{\alpha }_1{S}_1),\end{array}$$ [36]

(due to symmetry, we can drop the index again and obtain a purely real-valued cross-spectrum). This formula shows an excellent agreement with numerical simulations (Fig. 5C, Left). However, changing the parameters to the less coherent case (parameters as in Fig. 2) (so now both coupled units are in the excitable regime), we find that Eq. 36 does not suffice (compare dashed and solid curves in Fig. 5C, Right). Besides the power spectra contribution, we find that obtaining an accurate prediction in this noncoherent case requires including cross-spectral contributions between $Q_1^{*}$ and the neighboring backward eigenmodes associated with the eigenvalues ${\lambda }_1^{*}$, λ₂, λ₃, and λ₄ (the contributions associated with ${\lambda }_2^{*}$, ${\lambda }_3^{*}$, and ${\lambda }_4^{*}$ have negligible covariance values).

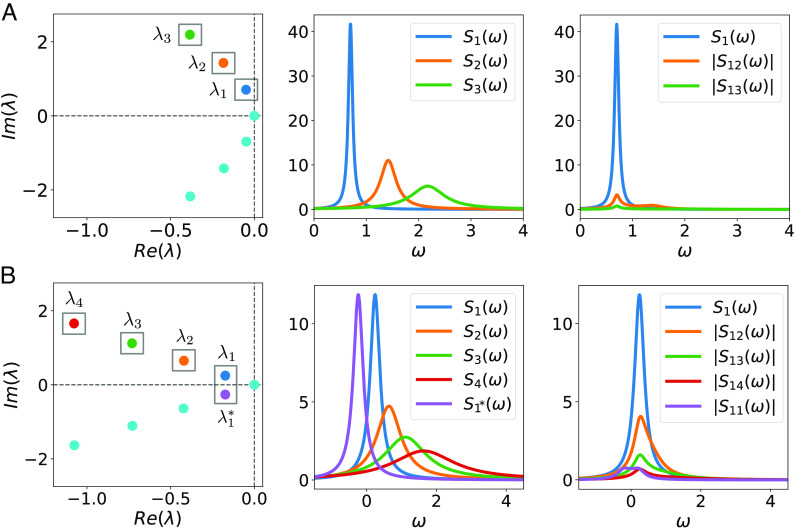
Why did this last example require more modes than any other of the cases considered? There is no general answer to this question as Eq. 33 depends on the coefficients α_λ′x, α_λ′y which depend in turn on the specific systems and the specific coupling functions. However, the dependence of Eq. 33 on the cross-spectra S_{1, λ} can shed some light on this question. As Eq. 17 shows, our formula for the cross-spectra S_{1, λ} between $Q_1^{*}$ and any other backward mode is weighted by their covariance ⟨$Q_1^{*}$Q_λ⟩. The more robustly oscillatory a system is, the smaller we would expect the covariance between $Q_1^{*}$ and the rest of the backward modes. The reason for such expectation is illustrated in Fig. 6. In Fig. 6A, we consider the SNIC model in the coherent regime and show its eigenvalue spectrum (Left panel). We observe that the closest eigenvalue to λ₁ = −0.048 + 0.698i is λ₂ = μ₂ + iω₂ = −0.18 + 1.42i. Consequently, the power spectrum of $Q_2^{*}$, which is also given by a Lorentzian centered at ω₂ and half-width of μ₂, shows very little overlap with the power spectrum of $Q_1^{*}$ (Mid panel). Hence, it is not surprising that the cross-spectrum S_{1, 2} is small (Right panel). By contrast, if we now consider the SNIC in the less coherent case (Fig. 6B), this scenario changes. As we see in Fig. 6B, Right, the eigenvalues are much closer in their imaginary parts (also real parts are larger) than in the coherent case (now λ₁ = −0.168 + i0.241, λ₂ = −0.42 + i0.64, and λ₃ = −0.73 + i1.11). Therefore, there is an effective overlap between their respective power spectra (Mid panel) leading to non-negligible cross-spectra between $Q_1^{*}$ and its neighboring modes (Right panel), and these contributions have to be taken into account in the theory.

Fig. 6.

Spectral overlap and cross-spectra between $Q_1^{*}$ and the rest of the backward modes for a more (A) and less (B) coherent oscillator. Spectrum of eigenvalues (Left), power spectrum S_λ of different eigenmodes (Mid), and the cross-spectra between $Q_1^{*}$ and different eigenmodes (Right). SNIC model with parameters in A and B as in Figs. 1 and 2, respectively.

Summary and Discussion

In this paper, we have developed a simplifying framework for stochastic oscillators that can be described by systems of stochastic differential equations. By mapping the system’s n-dimensional state vector to a complex-valued oscillator given by the eigenfunction $Q_1^{*}$ (x) of the backward Kolmogorov operator to the eigenvalue λ₁ = μ₁ + iω₁ with the least negative real part, we achieve a significant reduction in complexity. By using the transformed variable $Q_1^{*}$ (x), i.e., the pair (ℜ[$Q_1^{*}$ (x(t))], ℑ[$Q_1^{*}$ (x(t))]), we accomplish three major simplifications. First, we can describe the single oscillator’s spontaneous activity by a simple correlation function consisting of a single exponential, or, equivalently, by a Lorentzian power spectrum with frequency ω₁, half-width μ₁, and quality factor |ω₁/μ₁|. Second, we can quantify the response to an external stimulus with a simple linear response function of the form K(τ)∝Θ(τ)exp(λ₁τ), a function that is related to the correlation function by a simple proportionality. This result constitutes a fluctuation–dissipation theorem for a nonequilibrium system that is distinct from other theorems that have been derived in the past (e.g., refs. 72, 73, and 75). Third, by mapping the oscillator state to the $Q_1^{*}$ (x) function, we can predict the form of the cross-correlations of coupled noisy oscillators.

We illustrated the working of the general theory by three models that have distinct mechanisms for generating stochastic oscillations; mathematically speaking, these were a linear system with a stable focus driven by fluctuations, the canonical model for a supercritical Hopf bifurcation endowed with noise, and a system with a saddle-node on invariant circle bifurcation likewise with uncorrelated noise. It is important to note that the first and the third example would not perform any oscillations (at least in the long-time limit) in the absence of noise. These oscillations are noise generated in both cases, though by different mechanisms. The second system constitutes a limit-cycle system perturbed by noise, and thus, here, the effect of the fluctuations is easier to grasp: More noise will reduce the phase coherence of the oscillation. Although the three systems are very different in their dynamical mechanism, they become similar and, moreover, comparable when viewed through the lens of the $Q_1^{*}$ (x) function. Even in our framework, we still see characteristic aspects of the system, when we look at their response to external stimuli or the cross-correlation statistics for coupled systems.

While results on the theory of the single power spectrum and the linear response are exact, the case of coupled stochastic oscillators required an additional idea for the analytical calculation; we used an ansatz that employs linear response theory (proceeding as if the dynamics in the variables $Q_{1,\text{x}}^{*}$ and $Q_{1,\text{y}}^{*}$ were linear). We illustrated the resulting expressions for a number of numerical examples: for the three models, for identical and nonidentical oscillators, for rather coherent, and for more noisy oscillators. In all cases and for sufficiently weak coupling, we found excellent agreement between the predicted and the simulated cross-spectra of the $Q_1^{*}$ variables of the two systems. We take this as an indication that the true dynamics of the variables $Q_{1,\text{x}}^{*}$ and $Q_{1,\text{y}}^{*}$ are effectively linear. The reasons why this is so merit further exploration.

The universal description of stochastic oscillations put forward here may also be used to better highlight the characteristic differences between the different systems. Given that two oscillators have the same λ₁ (i.e., the same quality factor), what sets them apart? Should we combine the information for the leading complex-valued eigenvalue and its eigenfunction with that of the first purely real-valued eigenvalue and the associated eigenfunction, which can be used to define the stochastic limit cycle (80)? Or should we rather compare the higher oscillatory modes $Q_{\mathrm{\lambda \prime }}^{*}$ (with |ℜ(λ′)|> |μ₁| and ℑ(λ′) ≠ 0), that play such a prominent role in our theory of coupled oscillators? It seems to us that both comparisons offer a novel perspective for the finer categorization of stochastic oscillators.

The relation between our universal description of stochastic oscillators and the classical phase description of deterministic oscillators bears further discussion. Recall that, in deterministic limit-cycle systems, the phase can be obtained from the argument of the principal eigenfunction of the Koopman operator with purely imaginary eigenvalue (81, 82). Upon introducing noise into the system, this eigenvalue develops a negative real part. Indeed, it becomes λ₁, and its associated eigenfunction becomes $Q_1^{*}$ . This connection between the deterministic phase and the $Q_1^{*}$ function in the noise vanishing limit is not coincidental since the Kolmogorov backward operator ℒ^† corresponds to the stochastic version of the Koopman operator (83). Indeed, the relationship between the stochastic asymptotic phase (the complex argument of $Q_1^{*}$ ) and the deterministic phase in the limit D → 0 has already been noted (54, 64, 84, 85). Hence, our transformation also embraces the deterministic case and connects cleanly with the well-established deterministic Koopman-operator framework (86).

Returning to the specific results of our paper, we note that they can be generalized in different directions. First of all, even if our general setup includes multiplicative noise, for simplicity, we restricted all of our examples to Langevin systems with additive white Gaussian noise. Nothing keeps us from finding the eigenfunction to the eigenvalue with the least negative real part and to make the transformation to this complex-valued variable in a system with multiplicative noise. Likewise, we are not restricted to systems with Gaussian white noise but can also apply the method to Markov processes described by a master equation (for which there exist also a backward operator with eigenfunctions; one such example has been already treated in ref. 54 for the extraction of the asymptotic phase of a stochastic neuron model with discrete channel noise). More generally even, any jump-drift-diffusion process (62) described by a master equation (with additional drift and diffusion terms) that shows the hallmarks of robust stochastic oscillations, can be captured by our universal description in terms of the $Q_1^{*}$ (x) function. Our formulas for the main characteristics will not change, and, for instance, the power spectrum of such systems in the variable $Q_1^{*}$ will still be a pure Lorentzian, the response function a pure exponential, etc. Another straightforward generalization concerns the external perturbation: This could (and will in certain cases) also depend on the state of the system. This will mainly affect the definition of the complex-valued coefficient β that appears in the response function.

An exciting challenge is to extend our analysis of two coupled oscillators to the general case of N weakly coupled oscillators with their obvious applications to neural (87–89), mechano-sensory (90–92), genetic (1, 93), metabolic (94), and energy supply networks (95), to name but a few examples. Because our analytical approach can be generalized to this case, different scenarios of connectivity (sparse, random, or structured) and heterogeneity (in the single oscillator properties or in the connections) can be studied analytically. Moreover, the summed activity of subgroups of oscillators at the mesoscopic level can be calculated from the cross-spectral statistics of single stochastic oscillators.

Our theory was here applied to stochastic models, but applications to data are conceivable. In ref. 54, it was demonstrated how the stochastic asymptotic phase (the complex argument of the function $Q_1^{*}$ ) can be extracted from data. In the same way, the function $Q_1^{*}$ itself can be found, provided the data are consistent with a robustly oscillatory Markov process. We suggest that if one were to propose a method for extracting either $Q_1^{*}$ , or higher modes $Q_{\lambda }^{*}$, our results offer a test: whether the resulting power spectra fit simple Lorentzians at the respective eigenfrequencies. Thus, in light of the direct link between the Kolmogorov backward operator and the stochastic Koopman operator, our work may help advance methods for extracting Koopman eigenfunctions from data (96–99), as well as for providing physical interpretations of particular modes (54, 58).

Our framework also offers a test of a key assumption, namely that the stochastic oscillation arises from a Markov process. Markovianity is an important characteristic of stochastic processes, and different methods to test for it are currently under debate (see, e.g., refs. 76, 100, and 101). For the important class of stochastic oscillators, computing the statistics of $Q_1^{*}$ (x(t)), and specifically probing for a purely Lorentzian line shape, may provide another independent tool to test for Markovianity.

In summary, there are many open problems that can be studied within the framework put forward here.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

There are no data underlying this work.