Decoupling of catalysis and transition state analog binding from mutations throughout a phosphatase revealed by high-throughput enzymology

Significance

Transition state analogs (TSAs) resemble fleeting high-energy transition states and have been used to inhibit enzymes in nature and medicine, to learn about enzyme active-site features, and to design and select new enzymes. While TSAs mimic transition states, they differ from actual TSs, and we exploit these differences here. Systematic TSA affinity measurements for 1,004 mutants of PafA (a model phosphatase enzyme) revealed effects in and around the active site that mirror their effects on catalysis, but TSA-binding and deleterious catalytic effects diverge more distally. These observations suggest that residues throughout an enzyme shape its conformational landscape on the tenth-Ångström scale to optimize the active site for catalysis, rendering allostery more evolvable in nature but likely complicating enzyme design.

Abstract

Using high-throughput microfluidic enzyme kinetics (HT-MEK), we measured over 9,000 inhibition curves detailing impacts of 1,004 single-site mutations throughout the alkaline phosphatase PafA on binding affinity for two transition state analogs (TSAs), vanadate and tungstate. As predicted by catalytic models invoking transition state complementary, mutations to active site and active-site-contacting residues had highly similar impacts on catalysis and TSA binding. Unexpectedly, most mutations to more distal residues that reduced catalysis had little or no impact on TSA binding and many even increased tungstate affinity. These disparate effects can be accounted for by a model in which distal mutations alter the enzyme’s conformational landscape, increasing the occupancy of microstates that are catalytically less effective but better able to accommodate larger transition state analogs. In support of this ensemble model, glycine substitutions (rather than valine) were more likely to increase tungstate affinity (but not more likely to impact catalysis), presumably due to increased conformational flexibility that allows previously disfavored microstates to increase in occupancy. These results indicate that residues throughout an enzyme provide specificity for the transition state and discriminate against analogs that are larger only by tenths of an Ångström. Thus, engineering enzymes that rival the most powerful natural enzymes will likely require consideration of distal residues that shape the enzyme’s conformational landscape and fine-tune active-site residues. Biologically, the evolution of extensive communication between the active site and remote residues to aid catalysis may have provided the foundation for allostery to make it a highly evolvable trait.

Transition state analogs (TSAs) have been used by nature to control enzyme function (1, 2), in research to provide insights into the properties of enzyme active sites and enzymatic catalysis (3–6), and in medicine to provide highly effective drugs (6–10). Catalysis can be defined as preferential stabilization of a transition state over a reaction’s ground state (3, 11–16). Thus, it is expected—and has been observed—that compounds with electrostatic and geometric features resembling the transition state but not the ground state bind more strongly to enzymes than substrates or standard inhibitors. For example, lactone and sugar analogs serve as TSAs of glycosidases by mimicking the planar geometry and positive charge accumulation at the reactive carbon in the oxycarbenium-like transition state (17, 18); for serine proteases, TSAs mimic the charge and tetrahedral geometry of their transition states upon forming adducts with the nucleophilic serine (19). In addition, many strong inhibitors are bisubstrate analogs, mimicking the partial bond formed in the transition state and taking advantage of the lower entropic cost in binding a single transition state-like species relative to the two substrates independently (20). Despite these many successes, it has also been widely recognized that no transition state analog is perfect—none can exactly replicate the geometry and electronic distribution of a species with partial bonds that exists at the peak of the reaction pathway (21–23).

Efforts to use TSAs to develop artificial enzymes highlight their strengths and weaknesses. The selection of antibodies with catalytic activity via TSA binding—so-called “catalytic antibodies”—demonstrated the fundamental concept of transition state complementarity of enzyme active sites (24, 25). Nevertheless, the catalytic power of antibodies falls well short of naturally evolved enzymes (22, 26). These shortcomings led to speculation about what may be missing in these proteins and their design. These observations, and the general inability to design de novo enzymes that rival the rate enhancements of the most proficient natural enzymes, further highlights that there are gaps in or limits to our understanding of enzyme catalysis (27).

Enzyme research has understandably focused on the interactions made directly with substrates and transition states. Nevertheless, it is common to find residues remote from the active site that substantially influence enzyme activity (28–31). Despite much discussion about the roles of these remote residues and of the overall folded protein (32–49), our knowledge of the mechanism by which they impact catalysis is limited, at least in part due to a dearth of data. We recently developed high-throughput microfluidic enzyme kinetics (HT-MEK), an approach that allows parallel expression, purification and quantitative kinetic and thermodynamic assays for multiple substrates, concentrations, and inhibitors for ~1,500 enzyme variants in parallel. In prior work, we generated a mutant library comprised of systematic glycine and valine substitutions (with native glycine and valine residues mutated to alanine) within PafA, a phosphomonoesterase of the alkaline phosphatase superfamily, and applied HT-MEK to study these 1,036 mutants. Glycine and valine were chosen because they have widely different side-chain properties and provide distinct biochemical perturbations to increase the chance of observed functional effects from perturbations at individual positions. Indeed, functional effects at positions beyond the active site were typically observed for one or the other mutation but not both. In total, substitutions at 161 of PafA’s 526 residues significantly reduced catalysis, including many distal residues (50).

Here, we systematically interrogated the effects of these mutations on binding of the TSAs vanadate and tungstate (51, 52). We explored active-site specificity for the reaction’s transition state versus the TSAs using catalysis of the substrate methyl phosphate (MeP; k_cat/K_M) for which the chemical step of catalysis is rate limiting (51, 53). Our results revealed extensive specificity effects from mutations remote from the active site, including catalytically deleterious mutations that increase TSA binding. These results suggest that residues throughout the enzyme are involved in precise positioning at the active site. This complex connectivity presents a challenge in understanding and engineering enzymes, but, from a practical perspective, a potential pathway to more effectively optimize enzymes for promiscuous reactions and from an evolutionary perspective, a potential pathway for the widespread emergence of allostery.

Results

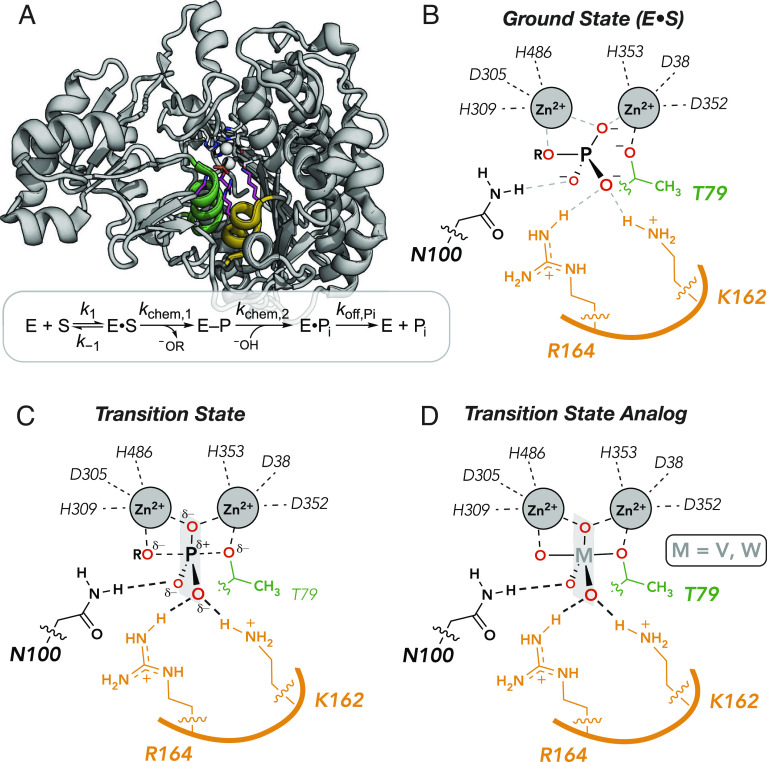
PafA and other members of the alkaline phosphatase superfamily are extraordinary catalysts, providing rate enhancements of up to 10²⁷-fold for the hydrolysis of phosphate monoester substrates, formally equivalent to a transition state stabilization of ~37 kcal/mol (51, 54). PafA is a 526-residue enzyme with a Rossmann fold and an active site comprised of a bimetallo Zn²⁺ core, a nucleophilic threonine residue (T79), and three additional residues (K162, R164, and N100); these three residues and the amide backbone of T79 contact the phosphoryl oxygen atoms of the substrate (Fig. 1 A and B). Following substrate binding, hydrolysis proceeds through nucleophilic attack by T79 to form a covalent phosphoryl enzyme intermediate (E-P) that is subsequently hydrolyzed by an attacking zinc-liganded hydroxide ion to generate inorganic phosphate (P_i), which is released from the enzyme (Fig. 1A). During both chemical steps, one Zn²⁺ ion within the bimetallo core activates the nucleophile and the other stabilizes the developing negative charge on the leaving group (Fig. 1B). Mutations of the substrate-contacting residues yield much larger deleterious effects on catalysis than on binding P_i (the reaction product and substrate for the reverse reaction), indicating that these side chains preferentially stabilize the transition state (51).

Fig. 1.

PafA catalysis and binding. (A) PafA active site and catalytic cycle showing helices containing the nucleophilic threonine (green) and active-site residues K162 and R164 (orange). (B–D) Schematics of ground state (B), transition state (C), and transition state analog-bound state (D). The semitransparent plane contains the equatorial oxygen atoms expected in the trigonal bipyramidal geometry of the transition state and of bound analogs.

Vanadate and tungstate bind strongly to many phosphoryl transfer enzymes and adopt trigonal bipyramidal geometries that mimic the reaction’s transition state (Fig. 1 C and D) (52, 55–60). Consistent with expected TSA behavior, vanadate and tungstate affinity correlate closely with catalysis for 27 combinations of active-site mutations in Escherichia coli alkaline phosphatase and for four ablative active site mutations in PafA (51, 52). Nevertheless, crystal structures of these molecules in isolation and bound to proteins reveal differences in bond lengths and bond angles (see below). Here, we exploit transition state mimicry and these subtle differences to learn more about molecular specificity in active sites and the protein features that are responsible.

HT-MEK Reliably Measures Transition State Analog–Binding Affinities.

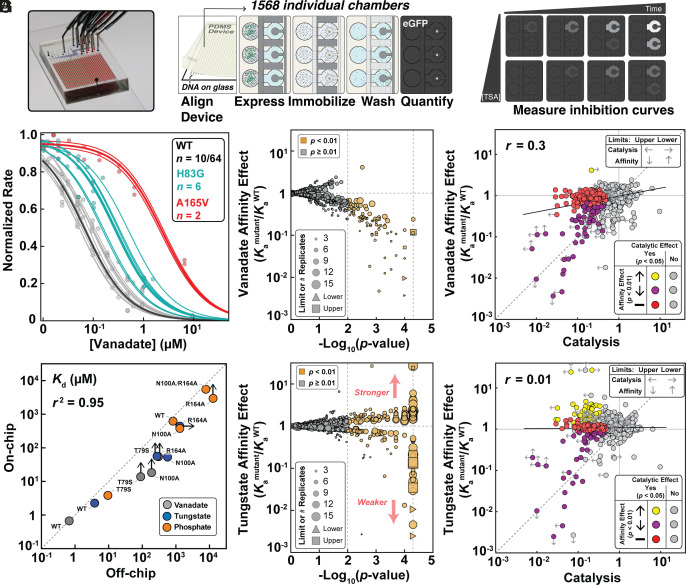
To determine the impact of mutations throughout the enzyme on transition state analog-binding affinity and specificity, we turned to HT-MEK (50). In HT-MEK, reaction chambers within valved microfluidic devices (Fig. 2 A, Left) are programmed with specific enzyme mutants by aligning devices to printed arrays of a library of plasmids encoding C-terminally eGFP-tagged PafA mutants. Following alignment, cell-free expression reagents are introduced into all chambers to express the mutants in parallel. After expression, eGFP-tagged mutants are recruited to anti-eGFP-patterned surfaces within each chamber to purify the enzymes in parallel (Fig. 2 A, Middle); measured eGFP fluorescence intensities along with an eGFP calibration curve report on the concentration of immobilized mutant enzyme. After immobilization, integrated valves that protect device surfaces make it possible to start and stop reactions as well as introduce fresh reagents without loss of surface-attached enzyme. To quantify TSA binding, we iteratively introduced the fluorogenic substrate 7-(dihydroxyphosphoryloxyl)coumarin-4-acetic acid [cMUP; (50)] in the presence of increasing TSA concentrations (7 to 13 concentrations ranging from 0.1 µM to 1 mM) and measured initial reaction rates via time-resolved fluorescence imaging (Fig. 2 A, Right). Increasing concentrations of vanadate and tungstate inhibited catalysis as expected, with behavior well fit by a competitive inhibition model (Fig. 2B and see below). Dissociation constants for vanadate, tungstate, and P_i obtained from these data for WT PafA and four active-site mutants on-chip agreed well with values from traditional measurements (r² = 0.95; Fig. 2C), as is also the case for kinetic constants (50, 51).

Fig. 2.

HT-MEK experimental pipeline and TSA-binding measurements for PafA mutant library. (A) Device photo (A, Left) and schematic showing experimental measurements of inhibition. (B) Representative vanadate inhibition curves. Thin lines indicate per-chamber curve fits; thick lines show fit behavior predicted by median K_i for WT (black), H83G (cyan), and A165V mutants (red); for WT, 10 of 64 total measurements are shown for clarity. (C) Comparison between dissociation constants (K_Ds) measured on- and off-chip for vanadate, tungstate, and P_i. Arrows denote K_d limits (see below and Materials and Methods). These limits were not used to calculate the correlation coefficient. (D and E) Volcano plots of vanadate (D) and tungstate (E) association constants (K_a^mutant/K_a^WT) for PafA glycine and valine scanning libraries; marker size indicates the number of replicates and limits are of affinity effects. (F) Comparison of vanadate affinity effects (K_a^mutant/K_a^WT) and catalytic effects (k_cat/K_{M, mutant}/k_cat/K_{M, WT}) for PafA mutants. (G) Comparison of tungstate affinity effects (K_a^mutant/K_a^WT) and catalytic effects. In F and G, the points are colored by the statistical significance of each mutant’s catalytic and affinity effect using statistical tests comparing the effects of each mutant against the WT PafA measurements: mutants that do not differ significantly in catalysis from WT are shown in gray; mutants with significant catalytic defects are colored based on vanadate (F) or tungstate affinity (G) effect (yellow, increase in affinity; purple, decrease in affinity; red, WT-like affinity). The dashed line is the identity line and the solid line the best-fit correlation line. Vertical arrows denote upper and lower K_a limits, affinities too weak to be measured using the range of inhibitor concentrations used or stronger than measured due to low K_M values, respectively. Left arrows denote upper limits for mutants with catalytic activities below the dynamic range of the assay, and right arrows denote lower limits for mutants with MeP K_M values below the lowest substrate concentration used (Materials and Methods).

Systematic HT-MEK Measurements Reveal Hundreds of Mutations That Impact Transition State Analog Binding.

Over 17 experiments, we determined inhibition constants or limits for 1,004 of the 1,036 PafA glycine and valine variants in the presence of vanadate or tungstate, corresponding to the measurement of 1,944 equilibrium constants, with the remaining variants too catalytically impaired to quantify inhibition. We report inhibition curves for each mutant in each experiment in per-experiment and per-mutant reports in our Open Science Foundation (OSF) data repository (https://osf.io/k8uer/), corresponding to a dataset of 9,278 inhibition curves. The high number of replicate measurements obtained via HT-MEK (n_average = 4.5; SI Appendix, Fig. S1) allowed us to resolve statistically significant affinity differences of < twofold via bootstrap hypothesis testing, in which we compare the distribution of measured inhibition constants for each mutant to the WT PafA distribution (a significance threshold of P < 0.01 is used; Fig. 2D and SI Appendix, Fig. S2) (50, 61). Even with this high sensitivity, ~90% of the mutants showed wild-type-like vanadate inhibition (897/979 mutants), with 82 mutants decreasing affinity and one increasing affinity (Fig. 2E and SI Appendix, Fig. S2). Tungstate measurements revealed similar numbers of mutants with decreased affinity (76/964 mutants) (P < 0.01; Fig. 2E and SI Appendix, Fig. S3). Unexpectedly though, a large number of mutants (155) significantly enhanced tungstate binding (Fig. 2E). Off-chip measurements for 8 distal mutants that either increased or decreased tungstate affinity on-chip measurements strongly supported the on-chip results (r² = 0.81 & RMSD of 1.6-fold); SI Appendix, Fig. S4).

Many Mutations Reduce Catalysis without Impacting Transition State Analog Binding.

Traditionally, a compound is considered a good TSA if changes to the enzyme (e.g., via mutation) or the analog (e.g., via chemical modification) yield equal magnitude changes in binding and catalysis (52, 58). Active-site mutants of PafA and another alkaline phosphatase family member, E. coli alkaline phosphatase, give strong correlations between vanadate or tungstate binding and catalysis [(51, 52) & see below]. Indeed, 50 mutations that reduced k_cat/K_M of MeP hydrolysis [a substrate for which chemistry is rate-limiting (51, 53)] also reduced vanadate and/or tungstate affinity (Fig. 2 F and G). Yet an additional 123 catalytically deleterious PafA mutations (51, 53) did not significantly weaken binding of either TSA (Fig. 2 F and G).

This result is not a consequence of differences in statistical resolution between experiments; indeed, HT-MEK-binding measurements have higher accuracy than HT-MEK kinetic measurements (due to errors in determining enzyme concentration that affect kinetic but not inhibition constants), so this differential is likely still larger (50). Furthermore, for mutations giving the largest deleterious catalytic effects (>10-fold), some yield similar reductions in vanadate and tungstate binding, but many yield little or no reduction in binding (Fig. 2 F and G). Below, we evaluate which residues and substitutions give rise to equal effects and which give rise to disparate effects, and we develop models to account for these results.

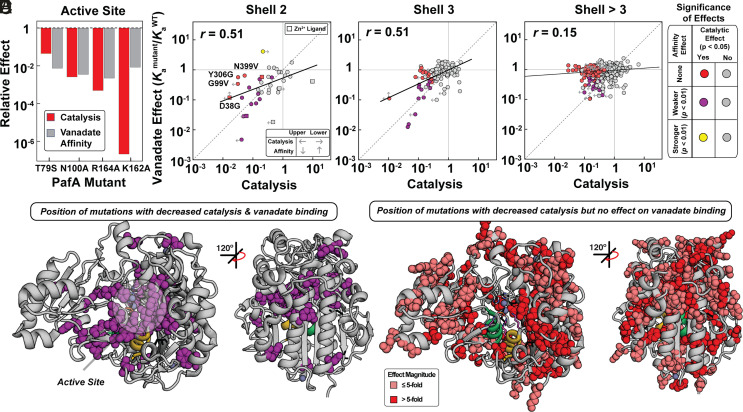
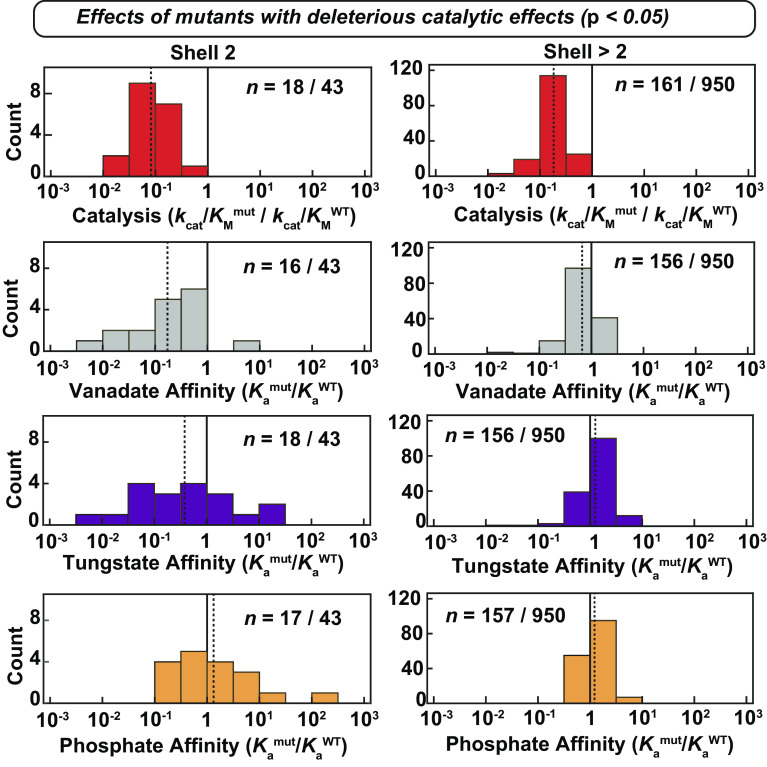
Larger Deleterious Effects on Catalysis Compared to Vanadate Binding from Mutations Distal to the Active Site.

Prior mutations of active-site residues measured off-chip gave nearly equal (within twofold to threefold) effects on catalysis and vanadate binding, consistent with expectations for removing interactions with a TSA that contribute to catalysis (Fig. 3A) (51). The sole exception is K162A, which gave a >10⁶-fold deleterious catalytic effect but a much smaller effect on vanadate binding (~10²). Moving out from the active site to residues that directly contact the catalytic residues or zinc ions (“second shell” residues), we were able to obtain data for 39 of the 50 total possible mutations. Of these 39 mutants, 17 were compromised in catalysis, with most having similar impacts on catalysis and affinity; indeed only four of the 39 measured gave larger deleterious impacts on catalysis by threefold or more (D38G, G99V, Y306G, and N399V) (Fig. 3B and SI Appendix, Fig. S5). For the second-shell mutants to the six catalytic Zn²⁺ ligands (12 mutations total), six had measurable catalytic activity and only one, D38G, gave different deleterious effects on catalysis and vanadate binding (Fig. 3B, squares and SI Appendix, Table S1).

Fig. 3.

Effects of mutations on vanadate binding and catalysis as a function of distance from the PafA active site. (A) Comparison of catalytic and vanadate affinity effects for PafA active-site mutants, measured previously (51). (B–D) Comparison of catalytic (P < 0.05) and vanadate affinity effects (P < 0.01) for mutants of residues in the (B) second shell, (C) third shell, and (D) more distal shells. Labeled points in B denote mutants with significant catalytic but not affinity effects. Colored and gray points denote statistically significant and insignificant effects, respectively, based on statistical tests (bootstrap hypothesis tests) comparing each mutant distribution to the WT PafA distribution. Left arrows denote upper limits for mutants with catalytic activities below the dynamic range of the assay, right arrows denote lower limits for mutants with MeP K_M values below the lowest substrate concentration used, and vertical arrows denote upper and lower vanadate K_a limits (Materials and Methods). (E) PafA structure with spheres shown for residues with significantly deleterious catalytic and vanadate affinity effects when mutated to either glycine or valine (35 of 520 measurable residues). (F) PafA structure with spheres shown for residues with significant catalytic but not significant affinity effects (125 of 520 measurable residues). Catalytic data are from reference (50).

Moving further from the active site, we observed decreasing congruence between catalytic and vanadate-binding effects. In the third shell, few mutations gave similar effects (Fig. 3C, purple), with the majority affecting catalysis more than vanadate binding; beyond the third shell (shells 4 to 8) there was essentially no correlation, even for distal mutants with large detrimental catalytic effects (Fig. 3D and SI Appendix, Fig. S6 and Tables S2 and S3). This loss of congruence between catalytic and vanadate binding effects with increasing distance from the active site is also apparent from the decreasing slopes of correlation lines and decreasing correlation coefficients in Fig. 3 A–D. Projecting these results onto the PafA structure provides a striking visualization of the diminishing correlation of catalytic and TSA-binding effects with distance from the active site (Fig. 3 E and F).

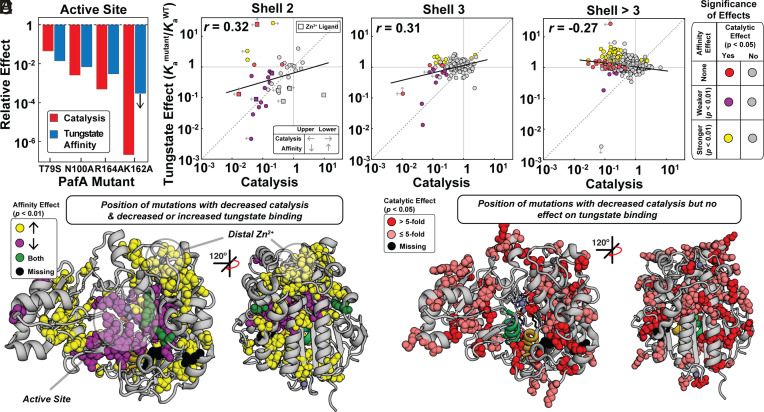
Increased Tungstate Binding from Many Distal Mutations.

We carried out the same analyses as above for vanadate with the second TSA, tungstate. Active-site mutants again gave similar effects on catalysis and tungstate binding, but with enhanced agreement for the K162A mutant relative to that observed for vanadate (Fig. 4A) (51). Also as for vanadate, tungstate binding and deleterious catalytic effects were strongly correlated for second-shell mutants, with only a small number of outliers (Fig. 4B), and the correlation decreased substantially for third-shell residues and beyond (Fig. 4 C and D and SI Appendix, Fig. S7 and Tables S4 and S5). Unlike vanadate, however, many mutants in distal shells increased tungstate affinity, with the largest enhancements (10-fold) for mutations clustering near PafA’s distal Zn²⁺ ion (Fig. 4 E and F).

Fig. 4.

Effects of mutations throughout the PafA structure on tungstate binding and catalysis as a function of distance from the PafA active site. (A) Comparison of catalytic and tungstate affinity effects of PafA active-site mutants, measured previously (51). (B–D) Comparison of catalytic and tungstate affinity effects for mutants of residues in the (B) second shell, (C) third shell, and (D) more distal shells. Colored and gray points denote statistically significant and insignificant effects, respectively, based on statistical tests (bootstrap hypothesis tests) comparing each mutant to WT PafA. Left arrows denote upper limits for mutants with catalytic activities below the dynamic range of the assay, right arrows denote lower limits for mutants with MeP K_M values below the lowest substrate concentration used, and vertical arrows denote upper and lower tungstate K_a limits (Materials and Methods). (E) PafA structure showing locations of residues with significant catalytic and either deleterious (28 of 522 measurable residues) or enhanced (57 of 522 residues) tungstate affinity effects when mutated to either glycine or valine. (F) PafA structure showing positions in PafA that have significant catalytic effects but do not have significant affinity effects (80 of 522 residues). Catalytic data are from reference (50).

At least 40% of the mutations (62 of 155) that increased tungstate affinities decreased catalysis, and more may have small or modest deleterious catalytic effects that are not detectable given the lower precision of our catalytic measurements (SI Appendix, Fig. S8 & see Many mutations reduce catalysis without impacting transition state analog-binding above). Also, the small number of mutations that give apparent increases in catalysis is consistent with the number of expected false positives for our statistical cutoff and give small effects (50 expected for a library of 1,004 mutants at a threshold of P < 0.05; mean 2.7 ± 1.7-fold effect) (50); thus, mutations appear to enhance TSA binding but not the enzyme’s cognate catalytic activity.

Correlations of TSA Affinity with Catalysis and Ground-State Analog (GSA) Affinity.

A formal requirement for catalysis is preferential stabilization of the transition state relative to the ground state. Consistent with this expectation, mutational effects throughout PafA have much larger effects on catalysis than they do on binding of P_i (a GSA and substrate for the reverse reaction) (SI Appendix, Fig. S9) (50). As also expected, and as noted above, the effects from first and second-shell mutants on vanadate and tungstate binding correlated with deleterious catalytic effects (Figs. 3 A and B, 4 A and B, and 5) Nevertheless, the correlations between TSA binding and catalysis are largely lost beyond the second shell, as noted above, as are the correlations between the TSAs themselves (Fig. 5 and SI Appendix, Fig. S10). These results are consistent with the more distal residues tuning conformational states with a precision that discriminates between the actual transition state and the TSAs (Discussion).

Fig. 5.

Comparison of catalytic effects and affinities of transition state and ground-state analogs. Distributions of catalytic and affinity effects (relative to WT PafA) for second-shell mutants with significantly deleterious catalytic effects (P < 0.05). For each plot, the two numbers denote the number of mutants with significant deleterious catalytic effects and which were measured for each parameter, and the number of mutants whose catalytic effects were measured, respectively. The solid black gridlines denote the WT value, and the dashed gridlines denote the mean fold-effect on each parameter for these mutants. The P_i affinity data are from reference (50).

Intriguingly, mutational effects that increase either tungstate or P_i binding (50, 62) correlate with one another for more distal residues compared to proximal residues (SI Appendix, Fig. S10) despite apparently different underlying causes for these effects—the relief of electrostatic destabilization that increases P_i binding (50, 51, 62) and the increased occupancy of alternative conformational states that are more complementary to the TSA, as described in the Discussion.

Discussion

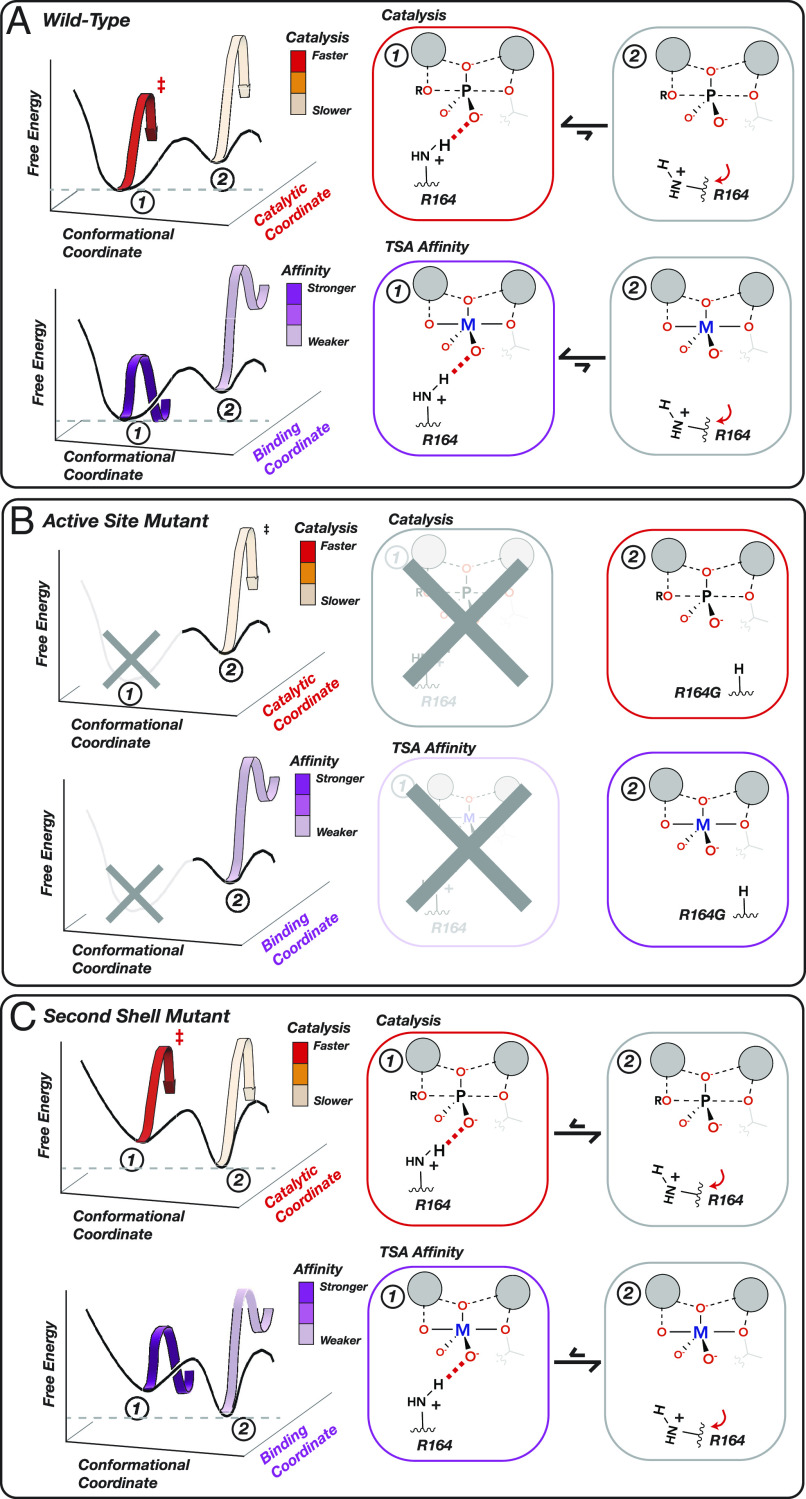
Our measurements of 1,944 affinity constants for vanadate and tungstate binding to 1,004 PafA variants combined with our prior data detailing impacts on catalysis and for P_i binding for these same mutants yielded some expected and unanticipated results (50). The correspondence of deleterious catalytic (transition state, TS) and TSA effects in and around the active site matches the expectation that direct interactions to TS or TSA atoms with similar charge and positioning contribute similar amounts of binding energy (Fig. 6 A and B) and that removing groups that help position these contacting residues (second shell) yield similar (but smaller) energetic consequences (Fig. 6C). In the simplest case, this reduction in the magnitude of observed effects would report on how a mutation alters the fraction of time spent by an active-site residue in a state that is competent for catalysis (Fig. 6C). For example, the active-site arginine of E. coli alkaline phosphatase (R166) is mispositioned when its flanking aspartate residues (D101 and D153) are removed, leading to losses in catalysis and TSA binding but with effects that are smaller than those from removal of the arginine (41, 42). Analogous positioning effects of non-active-site mutations on the positioning of active-site residues have been observed in many other enzymes (e.g., refs. 63–66).

Fig. 6.

Physical models accounting for observed effects of mutating active-site and second-shell residues. (A) A WT PafA active-site residue shown in a conformational equilibrium between two states. In State 1 (favored), R164 donates a hydrogen bond to an oxygen atom in the TS and TSA, promoting catalysis and TSA binding (M = V, W). In State 2 (disfavored), R164 is mispositioned so that the hydrogen bond no longer forms, reducing both catalysis and TSA binding. (B) Ablation of the R164 side chain eliminates State 1, reducing catalysis and TSA binding to the same extent [to the level of WT State 2 alone (A)]. (C) Mutating a second-shell residue that positions R164 destabilizes State 1 and increases occupancy of State 2. This change in the conformational equilibrium equally reduces catalysis and TSA binding, proportional to the increased occupancy of State 2.

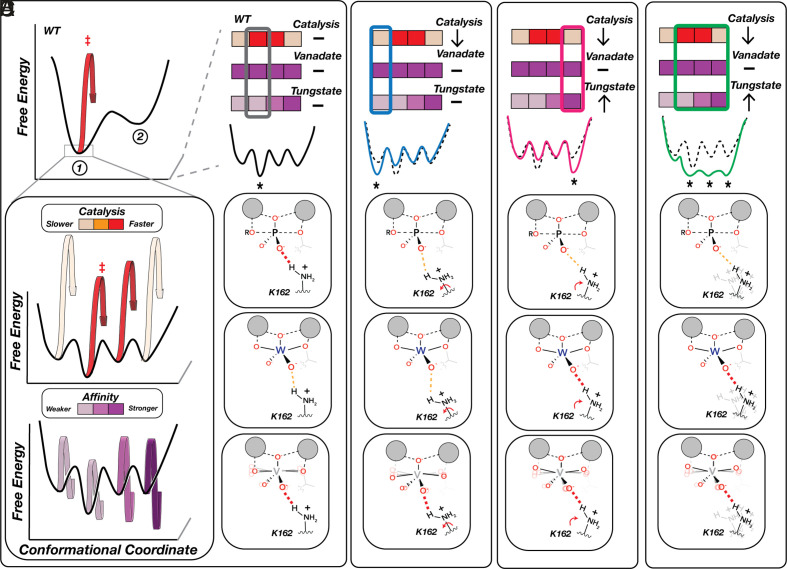
Data from the mutations in and contacting the active site can be described and interpreted using two-state models like those in Fig. 6, where a residue is either positioned or not positioned and the fraction of time it is correctly positioned determines the amount of catalysis that is observed. However, our full dataset paints a more complex picture, telling us that many positions throughout the enzyme communicate to the active site but do so in complex ways distinct from one another. Some mutations decrease catalysis while not affecting vanadate or tungstate binding, and others decrease catalysis while either decreasing or differentially impacting vanadate and tungstate binding, as summarized in Fig. 7. In principle, we could expand from our two-state model (Fig. 6) to a four-state model as shown in Fig. 7. In this model, the observed functional parameters are determined by the functional properties of each of the four states, weighted by the population of each. However, measuring more kinetic and thermodynamic constants for more mutants would likely reveal still more states, leading to far greater complexity. Further, we know from first principles that proteins exist as conformational ensembles defined by energy landscapes where the population of individual states can vary subtly or extensively with sequence (66–81). We therefore consider our functional results in terms of energy landscapes and the conformational ensembles they specify.

Fig. 7.

Physical models for the impacts of distal residue mutations that decouple catalytic and TSA affinity effects. (A) WT-favored State 1 is itself an ensemble of microstates (that is, states with smaller conformational changes than illustrated for the mutants in Fig. 6) with different levels of catalysis (Middle) and TSA binding (Bottom), denoted by color bars. The most populated WT microstate is optimal for catalysis but not for tungstate binding, whereas vanadate’s conformational flexibility allows the ligand to adopt more optimal geometries in each microstate. (B–D) Examples of distal mutational effects with differential impacts on catalysis and TSA binding due to alternation in microstate distributions. (B) Stabilization of a less catalytically competent microstate that maintains WT TSA affinities (blue). (C) Stabilization of a less catalytically competent microstate that preferentially binds the distorted tungstate geometry (pink). (D) Flattening of the conformational landscape due to increased flexibility results in similar occupancies of multiple microstates, including some with increased affinity for the distorted geometry of tungstate (green). Not shown are distal effects that phenocopy the effects described in Fig. 6B. For simplicity we show changes that do not alter vanadate affinity; additional states are required to account for mutants that alter vanadate affinity the same or differently than catalysis and tungstate affinity.

Overall, our results reveal two remarkable features about PafA’s energy landscape. First, they indicate that many positions throughout the enzyme communicate to the active site. Second, they tell us that this communication can yield exquisite specificity, discriminating between species that differ on the scale of tenths of Ångströms. Vanadate and tungstate are larger than phosphate, with mean bond lengths of 1.8 Å for vanadate and 1.7 Å for tungstate, compared to 1.5 Å for phosphate (SI Appendix, Fig. S11), and there are additional differences in charge distributions and geometries between the TSAs and the reaction’s transition state that may also lead to discrimination (SI Appendix, Figs. S12 and S13) (82). Structural data further support this model and the high degree of positioning. Tungstate bound to the related E. coli alkaline phosphatase has a 164° axial O-W-O bond angle, more acute than expected for a pentavalent trigonal bipyramidal species (SI Appendix, Fig. S12), suggesting a suboptimal fit for the larger tungstate in sites evolved for the phosphoryl transition state and that distal mutations may allow the active site to better accommodate tungstate (Fig. 7 C and D).

As is typical when new properties are revealed, our results raise additional questions. For example, what determines which sites communicate to the active site and which do not? Conceptually, we can think of these effects in terms of dissipation of a perturbation. If the alterations from the mutation can be accommodated by local rearrangements or if the alterations propagate away from rather than toward the active site, then effects on function and binding in the active site are not expected. If instead the conformational perturbations propagate to the active site, then function can be altered. What is surprising (to us) is the large number of positions that propagate effects to the active site (e.g., 161 positions with deleterious catalytic effects and 200 positions with significant changes to tungstate affinity when mutated). While we have observed this behavior only for one enzyme to date, we speculate that extensive connectivity to the active site may be a common feature of enzymes, perhaps more extensive for enzymes that must precisely fine-tune active-site conformational properties to achieve strong transition state stabilization and high discrimination between the transition state and ground state. Discrimination is required for catalysis and to prevent substrate or product inhibition (83–88).

If evolutionary forces led to the extensive use of long-range interactions to tune active-site conformations, then protein scaffolds would contain the innate potential for allostery. In other words, if communication to the active site is used to optimize function, then these evolved functional conduits could be further coopted by evolution to provide long-range communication in allostery and also in coupled conformational processes such as molecular motors and pumps that must coordinate conformational states at sites distal from the active site but depend on the reaction cycle that occurs at the active site (89, 90).

Evolution, to be efficient even on its long timescales, requires that complex changes occur in steps and follow pathways that provide selective advantages along the way. According to this model, early steps in the evolution of allostery would not be based on direct selection for allosteric regulation but rather based on the catalytic advantage from extensive connectivity to the active site. Analogously, enzymes evolved to catalyze new reactions appear to arise from enzymes having preexisting promiscuous activities that subsequently undergo selection to improve catalysis of the new reaction (91, 92).

This model of tuning precision is supported by the greater number of Gly than Val mutations that increase tungstate binding (95 Gly vs. 50 Val mutants, SI Appendix, Figs. S14–S16 and Tables S6–S9), as Gly substitutions allow greater freedom of motion and thus would be more likely to relax tuning. Val mutations can also of course disrupt this tuning but are less likely to broaden the enzyme’s conformations and thus less likely to increase occupancy of states that bind other molecules more strongly. Increased P_i binding also arises more frequently from Gly than Val mutations (222 Gly vs. 109 Val mutants) (SI Appendix, Fig. S16) (50). Presumably the broadened conformational possibilities help the E•P_i complex adopt conformations that lessen electrostatic repulsion between P_i and the active-site threonine alkoxide (51, 62) as well as accommodate the larger tungstate. More generally, these differential Gly and Val effects also emphasize the interpretative benefits of measuring the effects of more than one type of mutation.

There is overlap between the mutations that increase tungstate and P_i binding, with 109 mutations increasing both tungstate and P_i binding, 45 increasing tungstate binding only, and 204 increasing P_i binding only (SI Appendix, Table S10). The overlap may reflect a flattening of portions of the energy landscape and thus a broadening of the conformational ensemble that increases the representation of different states that bind tungstate or P_i more strongly. Alternatively or in addition, there may be common states that bind both more effectively, perhaps creating space to sterically accommodate the longer W–O bonds and for movement of P_i away from the nucleophilic threonine alkoxide to reduce their electrostatic destabilization. No mutants favor vanadate binding, possibly because such states are more difficult to access. These findings speak to the complexity of the conformational landscape and underscore the need to investigate protein ensembles to understand these effects (66–81).

Our findings also provide an alternative model for the frequent observation of greater catalytic promiscuity of ancestrally reconstructed enzymes (93, 94). While many or all reconstructed enzymes may accurately reproduce greater catalytic promiscuity present in the actual ancestors, lowered specificity could instead reflect imperfect reconstruction that lacks some active-site interconnections and thereby increase the population of states within the ensemble that are more efficient in catalyzing alternative reactions.

Practically, our results suggest a need to consider residues and interactions well beyond the active site to engineer new enzymes that rival those from nature. Our results also suggest a potential approach to reengineer existing enzymes for new functions: Adding glycine residues at remote positions with active-site connectivity may identify positions that allow access to conformations that are more proficient in the desired activity; then, directed evolution targeting positions at and near these favorable sites might identify variants that favor states that are more active and that thereby improve the desired new activity.

Finally, we consider the type of models that may be needed to understand enzyme catalysis. On the one hand, scientists strive to find patterns in their data and simpler models. However, applying standard dimensionality reduction approaches to our multiparameter PafA mutational data revealed a complex pattern without well-separated clusters (SI Appendix, Fig. S17). The absence of distinct clusters presumably reflects the underlying complexity of effects of individual mutations. The effects of each mutation on catalysis and vanadate, tungstate, and P_i affinities can be directly compared in SI Appendix, Fig. S18. More sophisticated clustering and dimensionality reduction techniques that consider multiple functional parameters and three-dimensional spatial relationships may help reveal common physical features that alter particular aspects of catalysis and may guide the development of models. Nevertheless, protein conformational landscapes are complex and, given this complexity, the basic rules of physics and chemistry (i.e., energetics of bond rotamers, hydrogen bonds, electrostatic interactions, van der Waals interactions and sterics) may provide a firmer foundation for models that are interpretable and testable (66–81).

It is also possible that more complex models are required to account for enzyme catalysis. For example, Klinman has recently suggested that protein “quakes” are involved in transmitting thermal energy from an enzyme’s surface to its active site (95–97). Nevertheless, our TSA-binding data indicate that long-range effects can arise through equilibrium effects on an enzyme’s conformational landscape. Thus, the presence of long-range effects does not necessarily indicate a need to invoke nonequilibrium functional models.

We now face a major and exciting challenge of relating the vast amounts of multidimensional quantitative data that can now be obtained to quantitative models and then testing those models via new, nontrivial predictions that they make. Overall, ensemble models seem to provide an appropriate level of complexity and rigor for framing models that are built from fundamental physical and chemical properties, do not compress and oversimply data, and can be tested and modified, extended or rejected as dictated by extensive and quantitative data that can be obtained via HT-MEK.

Materials and Methods

On-Chip Expression, HT-MEK Device Setup, and Expression and Purification of PafA Mutants.

HT-MEK devices were used to recombinantly express PafA mutants as described previously (50). Briefly, devices were fabricated using standard soft lithography techniques and then aligned to PafA-eGFP mutant plasmid arrays deposited on epoxy-coated slides using a custom microarray printer. Following alignment, device surfaces were specifically patterned with anti-GFP antibody beneath “button” valves and passivated with BSA elsewhere; after surface patterning, cell-free expression mix was introduced into each chamber, solubilizing printed plasmid DNA. PafA-eGFP mutants were expressed at 37 °C for 45 min, incubated at room temperature for 90 min, and then immobilized on the surface of anti-GFP-patterned button valves and purified via washing with button valves closed.

Measuring Vanadate and Tungstate Affinities Using HT-MEK.

Inhibition constants (K_i) for vanadate and tungstate were determined via competitive inhibition assays with the fluorogenic substrate cMUP (50 μM) as previously described for measurements of inorganic phosphate (P_i) inhibition (50). Vanadate measurements used concentrations of 0, 0.25, 0.5, 1, 2, 5, and 10 μM for vanadate, in some cases with 100 μM vanadate added to the series; tungstate measurements used concentrations of 0, 0.5, 1, 2, 5, 10, 25, 100, 250, 500, and 1,000 μM for all experiments except two, which went up to 100 μM and 500 μM, respectively. For each mutant replicate, we fit initial rates of cMUP hydrolysis at each inhibitor concentration and then fit these initial rates to a standard competitive inhibition model, as previously described (50).

To ensure accurate quantification of TSA affinities (K_d), all experiments used a substrate concentration (50 µM) that is below the previously measured cMUP K_M (50) for nearly all (>90%) of PafA variants and provides high signal to noise in fluorescence time-course measurements. As observed, K_i values are proportional to both the substrate K_M and the intrinsic affinity (K_d), we used the Cheng–Prussoff relationship (98) and previously measured K_M values for cMUP hydrolysis for each mutant (50) to correct for these modest systematic differences between the measured K_i and the K_d. Returned K_d values were within two-fold of the measured K_i values for 88% of mutants (SI Appendix, Fig. S19).

We used multiple quality control metrics to ensure that measurements from each chamber were due to the mutant printed in that chamber and not from cross-contamination between chambers, as described previously (50). To ensure each mutant expressed and immobilized successfully, we manually confirmed that each chamber contained a measurable eGFP spot (corresponding to [E] > 0.3 nM) and that each spot was free of fluorescence artifacts. To ensure high-quality activity measurements, we included a catalytically inactive “fiducial” mutant T79G or chamber lacking a mutant DNA template (“Skipped”) in every 7th chamber, considered measured rates within these chambers to represent a local “background” rate, and culled data from any chambers in which measured activity was less than fivefold greater than an interpolated local background rate. To further ensure accurate activity measurements for the most catalytically compromised mutants, we implemented a tiered measurement strategy in which all mutants within the glycine and valine scanning libraries were measured together initially, and then the slowest mutants were selected, reprinted, and assayed again separately.

As described previously for P_i (50), we first normalized fitted K_D values for each mutant to the median K_D of the wild-type replicates within a given experiment and then calculated the median values for each mutant across experiments. K_d values from experiments containing only the slowest mutants (which did not include wild-type PafA) were not normalized. We determined the statistical significance of K_D effects for each mutant relative to WT PafA using bootstrap hypothesis testing (P < 0.01) as previously described (50).

All progress curves, initial rate fits, inhibition curves, fitted K_i values, and K_d values after correction for each individual replicate measurement of each mutant, as well as median K_d values and measures of statistical significance for each mutant, are available in CSV and PDF files in the associated OSF repository (https://osf.io/k8uer/).

Identifying Upper and Lower Limits on Inhibition and Catalytic Measurements.

Lower K_d limits (or upper K_a limits) arise when the measured (apparent) K_i is greater than the highest concentration of inhibitor assayed; that is, the inhibitor affinity is too weak to be accurately measured (three mutants total in our Val and Gly scanning libraries). Upper K_d limits (lower K_a limits) arise when a particular mutant’s cMUP K_M was too low to be measured (50). In these cases, the K_d value obtained using the Cheng–Prussoff relationship is overestimated (five mutants total). To identify these limit cases, we flagged K_d values as lower K_d limits if the measured K_i was greater than two-fold above the highest vanadate or tungstate concentration for >50% of all measured replicates of that mutant, as previously implemented for P_i affinity measurements (50). For mutants whose measured cMUP K_M values are upper limits, K_d values were denoted as upper limits; that is, the affinities are likely to be stronger than measured. For catalytic effects, upper limits are denoted for mutants with catalytic activities below the dynamic range of the assay, and lower limits are denoted for mutants with MeP K_M values below the lowest substrate concentration used, as previously described (50). For both catalytic and inhibition measurements, upper and lower limits are denoted by arrows in the main text and SI Appendix, Supplementary Figures.

Recombinant E. coli Expression of WT PafA and Mutants and Tungstate Affinity Measurements.

To ensure that observed inhibition effects are not due to the presence of the C-terminal eGFP tag, surface immobilization, or any other potential artifact of the HT-MEK platform, we recombinantly expressed and purified WT PafA and eight mutants in E. coli as previously described (51). Tungstate affinities were determined in 0.1 M sodium MOPS, pH 8.0, 500 mM NaCl, 100 mM ZnCl₂ at 25 °C using the commercial chromogenic substrate p-nitrophenyl phosphate (pNPP), a tungstate concentration range of 0 to 1 mM, and a Tecan Infinite M200 plate reader.

Assignment of Residues to Active-Site Interaction Shells.

To determine the minimum number of interactions between each residue and the active site and assign residues to interaction shells, we used GetContacts (https://getcontacts.github.io) to identify all contacts between residues in the WT PafA crystal structure. We then defined the active site as composed of all residues or ions making direct contacts with the substrate (T79, N100, K162, and R164, and the two Zn²⁺s.) The set of residues making at least one contact to any of these active-site components was then defined as the second shell. Residues making at least one contact to any of the second-shell residues but not contacting the active site were defined as third-shell residues. Residues were then successively assigned to the more distal shells in the following general manner: For shell N, residues were defined as residues making contacts to shell N-1, but not to any of the residues in the lower shells.

Multiparameter Data Visualization Using UMAP.

UMAP (99) was performed using its implementation in skikit-learn (100) in a Jupyter notebook (available at the OSF repository). The catalytic (k_cat/K_{M, chem.}) effects and vanadate, tungstate, and P_i affinities (log₁₀ transformed) for all glycine and valine mutants for which these parameters were experimentally measurable (n = 928) were imported, and the UMAP reducer was trained and the two-dimensional dimensionality-reduced array was output using the “reducer.fit_transform” function.

Obtaining Geometric Parameters of Vanadium, Tungsten, and Phosphorus Compounds from the Cambridge Structural Database (CSD).

We used the CSD Python API to search for all molecules containing at least one M-O bond, where M denotes vanadium, tungsten, or phosphorus. We then used the GeometryAnalyzer function to determine the number of bonds to the M atom, identify each M-O bond, assess if the oxygen was esterified or nonesterified, and determine all M-O bond lengths and bond angles. We then classified the valency of each molecule based on the number of bonds to the M atoms, and classified its geometry (tetrahedral, square pyramidal/planer/octahedral, trigonal bipyramidal, or undefined) based on bond angle values, as defined previously (52).

For the comparisons of tetrahedral forms, we selected all molecules containing only M-O oxides. We also included M-O oxide distances measured previously in the literature but not deposited in the CSD (101, 102). For the comparisons of tetrahedral esters, we selected all molecules containing a mixture of oxides and M-O-C esters and compared the bond length distributions of each type. As the number of esterifying atoms on each oxygen strongly affects M-O bond lengths, we only considered singly esterified oxygens when comparing lengths of esterified M-O bonds.

For the comparisons of pentavalent molecules, the total number of molecules was limited, (especially for tungsten compounds). We therefore selected all pentavalent molecules containing a mixture of oxide bonds and at least one M-O-C ester, again only comparing oxides or singly esterified oxygens.

All codes used to download, parse, and analyze these data are available at the OSF repository (https://osf.io/k8uer/).

Geometric Parameters of Vanadium and Tungsten Compounds Bound to Proteins in the PDB.

PDB structures containing tungstate and vanadate compounds bound to proteins were analyzed using the Bio.PDB package in Python. To infer connectivity and geometry of the bound molecules in each structure, we first identified all neighboring atoms within 2.5 Å of the metal atom. For each neighboring oxygen atom, we then calculated the number of atoms bonded to that atom within 2.5 Å. We assigned oxygens forming only one bond as oxides and others as esters and then calculated all bond lengths and angles involving the metal atom. Structures with five atoms bonded to the metal atom and one (and only one) bond angle larger than 160° (the angle between axial atoms) were defined as having pentavalent trigonal bipyramidal geometry; structures with four atoms bonded to the metal atoms (based on the above criteria) were assigned as tetrahedral.

Supplementary Material

Appendix 01 (PDF)

Dataset S01 (CSV)

Movie S1.

Three-dimensional PafA structure (5TJ3, (1)), first showing positions with mutational effects on the chemical step of catalysis (red spheres), followed by a comparison of the effects of these mutations on vanadate affinity. All significant catalytic effects are initially presented (red), followed by the subset of these mutations that have weaker-than-WT vanadate affinities (purple), then the subset that have unchanged inhibitor affinities (red), and finally these sets shown together. Numbers of mutations in each category are given in SI Appendix, Table S8, and all data are given in Dataset S1.

Movie S2.

Three-dimensional PafA structure (5TJ3, (1)), first showing positions with mutational effects on the chemical step of catalysis (red spheres), followed by a comparison of the effects of these same mutations on tungstate affinity. All significant catalytic effects are initially presented (red), followed by the subset of these mutations that have weaker-than-WT tungstate affinities (purple), the subset that have unchanged inhibitor affinities (red), the subset that have strongerthan-WT affinities (yellow), and finally these sets shown together. Numbers of mutations in each category are given in SI Appendix, Table S8, and all data are given in Dataset S1.

Movie S3.

Three-dimensional PafA structure (5TJ3, (1)), first showing positions with mutational effects on the chemical step of catalysis (red spheres), followed by a comparison of the effects of these same mutations on Pi affinity. All significant catalytic effects are initially presented (red), followed by the subset of these mutations that have weaker-than-WT Pi affinities (purple), the subset that have unchanged inhibitor affinities (red), and the subset that have stronger-than-WT affinities (yellow), followed by these sets shown together. Numbers of mutations in each category are given in SI Appendix, Table S8, and all data are given in Dataset S1.

Data, Materials, and Software Availability

All experimental data are provided as a CSV file in Dataset S1. Additionally, all experimental data, including per-experiment and per-mutant summary reports of the on-chip measurements, as well as all code used to process the data are available in the Open Science Foundation repository (https://osf.io/k8uer/) (103).