Significance
Rivers have been found only on Earth, Mars, and Saturn’s moon Titan. We use a universal framework for river geometry to unlock clues about the climates of all three worlds. On Earth, our method can predict sediment and water fluxes in regions where field surveys are impractical. On Mars, our results imply that the river deposits explored in situ by NASA’s Perseverance and Curiosity rovers required prolonged time periods when conditions favorable for life were maintained. On Titan, we show that its active methane rivers may have substantially different geometry than rivers on Earth. NASA’s Dragonfly mission to Titan can test our predictions and may witness active sediment transport.
Keywords: Titan, Mars, rivers, hydrology, planetary landscapes
Abstract
Alluvial rivers are conveyor belts of fluid and sediment that provide a record of upstream climate and erosion on Earth, Titan, and Mars. However, many of Earth’s rivers remain unsurveyed, Titan’s rivers are not well resolved by current spacecraft data, and Mars’ rivers are no longer active, hindering reconstructions of planetary surface conditions. To overcome these problems, we use dimensionless hydraulic geometry relations—scaling laws that relate river channel dimensions to flow and sediment transport rates—to calculate in-channel conditions using only remote sensing measurements of channel width and slope. On Earth, this offers a way to predict flow and sediment flux in rivers that lack field measurements and shows that the distinct dynamics of bedload-dominated, suspended load-dominated, and bedrock rivers give rise to distinct channel characteristics. On Mars, this approach not only predicts grain sizes at Gale Crater and Jezero Crater that overlap with those measured by the Curiosity and Perseverance rovers, it enables reconstructions of past flow conditions that are consistent with proposed long-lived hydrologic activity at both craters. On Titan, our predicted sediment fluxes to the coast of Ontario Lacus could build the lake’s river delta in as little as ~1,000 y, and our scaling relationships suggest that Titan’s rivers may be wider, slope more gently, and transport sediment at lower flows than rivers on Earth or Mars. Our approach provides a template for predicting channel properties remotely for alluvial rivers across Earth, along with interpreting spacecraft observations of rivers on Titan and Mars.
Rivers are among the clearest manifestations of the hydrologic systems of Earth, Saturn’s moon Titan, and ancient Mars, but a scarcity of field measurements hampers our ability to study these systems on all three worlds. On Earth, although field measurements are frequently made, many rivers remain unsurveyed and difficult to access. On Titan, an active hydrologic cycle is currently shaping the landscape (1, 2), generating river networks (3–5) (Fig. 1 F and G), apparent river deltas (6), and vast seas of liquid methane and ethane (3, 7) that may be experiencing sea-level change (3, 7, 8). However, much remains unknown about Titan’s hydrologic cycle and climate, including rates of precipitation and runoff, the resulting rates of erosion and sediment deposition, and spatial and temporal climate variations (9). On Mars, ancient river channels crossing many of its landscapes (10) and depositional fans and deltas in some impact craters (11; Fig. 1 D and E) imply past runoff (12). Yet, the intensity and duration of these runoff events remain poorly constrained, and the nature of the ancient climate that produced precipitation events continues to be intensely studied (12).
Fig. 1.
Alluvial rivers on Earth, Mars, and Titan. (A) The Yellowstone River, with gravel bed and banks (photo: J. Peaco); Images of gravel on both Mars (B) and Titan (C) from the Curiosity rover and Huygens lander. The larger grains in the Huygens image are ~10 cm in diameter; (D) Peace Vallis fan, an alluvial fan within Gale Crater on Mars; (E) The western delta within Jezero Crater on Mars, the target of exploration for the Perseverance Rover; (F) Saraswati Flumen on Titan, terminating in two delta-like lobes along the western shoreline of Ontario Lacus; (G) Vid Flumina on Titan, a large tributary network that terminates at Ligeia Mare. Yellow regions indicate locations where channel widths and slopes were measured.
River channels offer clues about the environments in which they form and may therefore hold the keys to unlock some of these mysteries about Titan and Mars. In particular, alluvial rivers, which construct their own channels with the sediment they carry (Fig. 1A), adjust their width, depth, and slope according to the fluxes of fluid and sediment they convey. Fluid and sediment fluxes in turn reflect various aspects of a planet’s surface environment, from the rates of precipitation and runoff that produced the flow to the upstream erosion that generated the sediment.
Previous estimates of fluid and sediment discharge in rivers on Titan (13) and Mars (14–16) have typically relied on presumptions about flow depth, bed sediment grain size, or sediment concentration, each of which is difficult or impossible to measure without direct surface observations or active flow. Titan’s active river flows are not well resolved by current spacecraft data, and Mars’ rivers no longer flow. Although granular sediment exists on both Mars (Fig. 1B) and Titan (Fig. 1C), such surface observations are rare. Therefore, it would be preferable to reconstruct planetary rivers using quantities that can be measured from orbit even in the absence of active flow.
On Earth, empirical equations calibrated from field measurements are commonly applied to relate a river channel’s width, depth, and slope—its hydraulic geometry—to flow discharge, sediment flux, and other properties (17–20). This approach has the advantage of using characteristics that can be measured remotely, such as width and slope, but it has not been widely applied to planetary rivers. This is because the empiricisms underlying conventional hydraulic geometry equations do not account for conditions that differ from Earth—such as gravity (which differs on Titan and Mars) and fluid and sediment densities [which differ substantially on Titan (21) (SI Appendix, Table S1)—and because it is currently impossible to calibrate hydraulic geometry equations for Titan and Mars with field measurements.
Here, we adapt dimensionless hydraulic geometry equations (17–19) to reconstruct characteristics of planetary rivers using only channel width and slope, both of which can be measured from orbit. We calibrate these equations, which explicitly account for gravity as well as fluid and sediment density, with a compilation of alluvial river characteristics on Earth. This analysis shows that bedload-dominated, suspended load-dominated, and bedrock rivers (where bedrock is emergent on the bed or banks) have distinct channel characteristics that reflect distinct channel-forming processes, and our approach enables predictions of river characteristics on Earth where field measurements are impractical. Applying this theory to rivers on Titan and Mars, we estimate rates of flow and sediment discharge that offer insights into Titan’s active hydrologic cycle and Mars’ ancient climate as well as highlighting observational targets for landed and orbiting spacecraft.
1. Dimensionless Hydraulic Geometry
Downstream hydraulic geometry relationships describe the state of a river channel at a formative fluid discharge, typically the “bankfull” discharge at which the flow completely fills the channel (20). The observed consistency of these relationships reflects feedbacks that cause an alluvial river to alter its width, depth, and slope such that the bankfull flow at any point along the channel conveys the fluid discharge and sediment flux imposed by the upstream drainage basin (17–19, 22). Terrestrial hydraulic geometry relationships typically take the form of a power law. For example, channel width scales with fluid discharge raised to a power, with the coefficient and exponent for a particular river determined by empirical fits to field data.
Parker et al. (17) and Wilkerson and Parker (18) proposed universal hydraulic geometry relationships for bedload-dominated and suspended-load dominated rivers on Earth that express dimensionless bankfull channel width ( ), slope ( ), depth ( ), and sediment flux ( ) as power-law functions of the dimensionless flow discharge ( ):
| [1a] |
| [1b] |
| [1c] |
| [1d] |
| [1e] |
where B (m), H (m), Q (m3/s), and Qs (m3/s) are the dimensional quantities, and D50 (m) is the median bed grain diameter. Because of the elevated importance of suspended sediment transport in the latter category of rivers (18), their power-law relationships depend on the particle Reynolds number ( ), and therefore fluid kinematic viscosity ( ), in addition to the dimensionless discharge (Eqs. 1a–e; SI Appendix).
There are separate dimensionless hydraulic geometry relationships for bedload-dominated (17) and suspended load-dominated (18) rivers because river reaches in nature tend to be bimodally distributed (23, 24). Even individual alluvial rivers commonly have an abrupt spatial transition between upstream reaches where sediment moves dominantly along the bed and downstream reaches where sediment moves dominantly in suspension within the fluid (23). On Earth, this transition in dominant transport mode generally corresponds to a transition from gravel-sized (D50 > 15 mm) to sand-sized (D50 < 1.5 mm) bed sediment. As a result, relatively few rivers on Earth have bed grain sizes intermediate between sand and gravel (~1.5 to 15 mm; refs. 24 and 25). This gravel–sand transition, thought to result from size-selective sediment transport, rapid abrasion, or a bimodal sediment supply to the channel network (23), is a fundamental characteristic of alluvial rivers on Earth, so it is reasonable to expect a similar phenomenon on Titan and Mars. The grain size at which the transition occurs on Mars and Titan may be somewhat coarser than the boundary between sand and gravel (25), so we hereafter refer to rivers as either bedload-dominated (corresponding to gravel-bedded rivers on Earth) or suspended load-dominated (sand-bedded on Earth). This difference in the expected grain size of the transition does not affect our calculations for Titan or Mars (25).
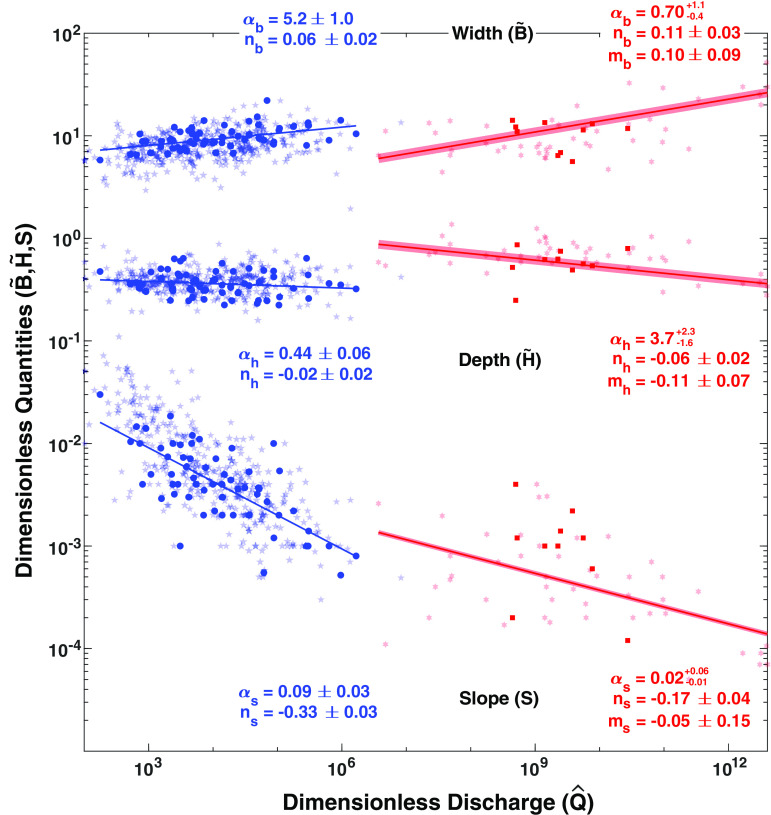
To constrain the constants in the dimensionless hydraulic geometry relationships, we compiled field measurements of B, H, S, Q, and D50 for 491 different suspended load- and bedload-dominated rivers and fit Eqs. 1a–d to these data (Fig. 2; Materials and Methods). We fit these two alluvial river types separately, as is standard (17, 18). For suspended load-dominated rivers, we fit the data with a multivariate technique (18) to determine the values of , n, and m independently, while for bedload-dominated rivers we fit a simple power law (17). For both river types, we used a Monte Carlo technique to estimate the empirical constants and uncertainties (SI Appendix, Fig. S1 and Table S2; Materials and Methods).
Fig. 2.
Dimensionless width ), depth ( ), and slope ( ), as functions of the dimensionless discharge ( ) for 491 suspended load-dominated (red) and bedload-dominated (blue) rivers on Earth. Rivers with floodplains are plotted with solid colors; semitransparent points indicate rivers with widths potentially constrained by topography or with some bedrock on their beds or banks. For suspended load-dominated rivers, we plot the fits according to Eq. 1 assuming a constant Rep, adopting the median grain size of our suspended load-dominated river dataset and 1-sigma of the D50 distribution as shaded lines. Suspended load-dominated rivers are in red (Right), with bedload-dominated rivers in blue (Left).
The hydraulic geometry measurements from many different rivers spanning more than 10 orders of magnitude in dimensionless discharge collapse to consistent trends that are well described by the predicted power laws (Fig. 2). These consistent trends appear despite other complicating factors that can influence channel dimensions but are not accounted for directly in our theory, such as bank cohesion and human impacts (SI Appendix, Fig. S2; Materials and Methods). The observation that bedrock rivers, which have channel dimensions controlled by a different mechanism, do not follow the same trends (black points in SI Appendix, Fig. S3) indicates that the hydraulic geometry relationships for alluvial rivers are a signature of their channel-forming processes and differing bank materials and properties.
Unlike conventional dimensional hydraulic geometry relations, the dimensionless quantities in Eqs. 1a–e account for gravity (g), and the power-law coefficients ( ’s in Eqs. 1a–e) are functions of the sediment ( ) and fluid densities ( ). Specifically, Parker et al. (17) derived gravity- and density-dependent expressions for the coefficients for bedload-dominated rivers using a set of equations that prescribe how energy is dissipated within the flow and how sediment is mobilized and transported, combined with a theory for channel width in open rectangular channels with alluvial bed and banks (SI Appendix). These equations, combined with the fits to the new data compilation (Fig. 2 and SI Appendix, Table S2), yield coefficients for bedload-dominated rivers of
| [2] |
and for suspended load-dominated rivers, based on analogous expressions from Wilkerson & Parker (18; SI Appendix), of
| [3] |
where . The exponents in the power-law fits ( ’s in Eqs. 1a–e) are independent of gravity and sediment or fluid properties. The use of these dimensionless hydraulic geometry relations implicitly assumes that the sediment grains in bedload-dominated and suspended load-dominated rivers on Titan and Mars are dynamically similar to gravel and sand on Earth. We checked this assumption by comparing particle Reynolds numbers (19), Rouse numbers, and Froude numbers, and indeed, find dynamic similarity (SI Appendix).
2. Calibrating Remote Predictions of River Properties on Earth
Although river channel width, slope, bed grain size, flow depth, flow discharge, and sediment flux can be measured in the field, most rivers on Earth remain unsurveyed, and many are difficult to access. This hinders our ability to estimate their fluid discharge and sediment flux, both of which are important in studies of Earth’s actively changing landscapes and climate. Similarly, river characteristics on Titan and Mars must be measured from remote sensing data. On Titan, the Cassini spacecraft’s images of the surface (typical resolution ~1 km, finest resolution 175 m) make it possible to place bounds on channel width (5), and Cassini RADAR altimetry data permit measurements of channel width and slope in a few locations (26, 27). On Mars, remote sensing images and topographic data provide meter-scale views of the surface in many locations. However, most features of interest have been degraded by billions of years of erosion. Thus, river characteristics that can be estimated most reliably are derived from the present-day widths and slopes of inverted channel beds (28–30).
Due to these limitations, we rearrange Eqs. 1a–e to make bankfull channel width and slope the independent variables (Materials and Methods). This yields equations for predicting dimensional characteristics (D50, Q, and H) of bedload-dominated rivers (Eqs. 4a–c, Materials and Methods) and suspended load-dominated rivers (Eqs. 5a–c, Materials and Methods). For a river on a given world, we can use measurements of channel slope and bankfull width, along with assumed sediment and fluid densities (R in Eqs. 2 and 3), to calculate bed grain size, D50 (Eqs. 4b or 5b). Bed grain size is then used to calculate flow discharge (Eqs. 4a or 5a) and then channel depth (Eqs. 4c or 5c). Finally, with the discharge and bed grain size both assessed, we calculate the sediment flux, Qs (Eq. 6, Materials and Methods), which is the bedload in bedload-dominated rivers and the total load in suspended load-dominated rivers (SI Appendix).
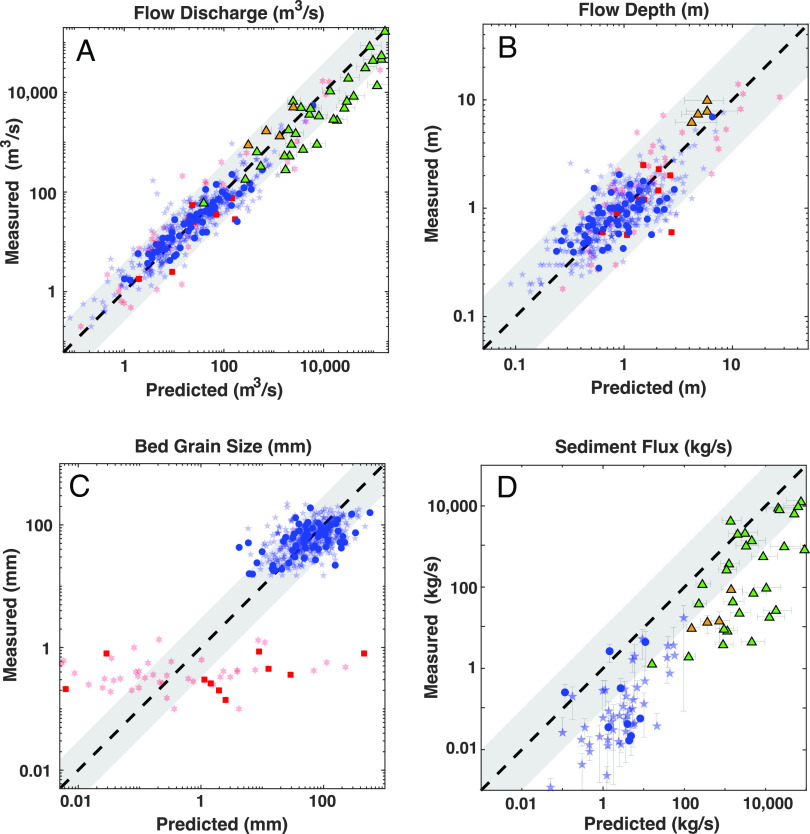
To gauge the uncertainties in this approach, we used the measured width and slope of each terrestrial river in our dataset to predict the dimensional quantities of interest. We then compared these predicted values to field measurements (Fig. 3). The predicted flow discharges (Fig. 3A), flow depths (Fig. 3B), and bed grain size (for bedload-dominated rivers; Fig. 3C) match the measured values to within ~3× for >90% of the data. There is a residual trend in the grain size predictions, likely reflecting an influence on D50 not included in the theory, but this does not substantially influence our predictions of H, Q, or Qs because they depend only weakly on grain size (Eq. 4). We also slightly underpredict discharge for rivers with restricted channel or floodplain widths, which is expected given that our theory assumes channels can widen to accommodate the imposed discharge. It is not feasible to estimate grain size accurately for suspended load-dominated rivers based on channel width and slope because the dimensionless hydraulic geometry relationships for slope in suspended load-dominated rivers (Eq. 1c) are relatively insensitive to grain size. The predicted sediment fluxes agree with the measured fluxes to within ~10× for >60% of the rivers with reported Qs (Fig. 3D). Although the sediment flux uncertainty is large in an absolute sense for any given river, it is surprisingly good for estimates based only on channel width and slope, especially given that sediment flux measurements in the field can have similar uncertainties (31) (Fig. 3D). These comparisons confirm that remote measurements of channel width and slope can yield useful order-of-magnitude estimates of bankfull flow and sediment transport, even for rivers without D50 or H measurements (triangles in Fig. 3 A and D). This makes it possible to predict river characteristics where field measurements are lacking and also to perform these predictions over far greater spatial scales than would be practical for field surveys.
Fig. 3.
Comparing the predictions of dimensionless hydraulic geometry with measurements. In all plots, the 1:1 line is in black, with the gray shaded regions representing 1:3 and 3:1 bounds (A–C) and 1:10 and 10:1 bounds (D). Colors are as in Fig. 2. In panels A/B/D, the orange and green triangles represent calculations for the Rhine River and rivers in the Amazon Basin, respectively. All Rhine and Amazon rivers are suspended load-dominated, but we do not have measurements of D50 for either, or H for those in the Amazon. For these select rivers, all Qs measurements are lower bounds, as only the suspended sediment loads are reported. Error bars represent 16th and 84th percentiles and derive from uncertainties in the measurements and hydraulic geometry fits. To compare our predicted volumetric sediment fluxes to the measured mass fluxes, we assume sediment with a density of 2.65 g/cm3.
3. Results
Having calibrated and tested the dimensionless hydraulic geometry relationships with rivers on Earth, we use these relationships to estimate the bankfull characteristics of rivers on Mars and Titan (SI Appendix, Tables S3–S6) and explore the implications for Mars’ ancient climate and Titan’s active hydrologic cycle. In doing so, we assume that the same physical mechanisms govern alluvial channel form on all three worlds. This assumption could eventually be tested when field observations of an active river are acquired on Titan.
We selected two rivers on Mars and two on Titan where width and slope can be measured remotely. Bed grain size is uncertain for three of these four, making it unclear whether the rivers are bedload-dominated or suspended load-dominated. Therefore, we performed both bedload-dominated (Eqs. 2 and 4) and suspended load-dominated (Eqs. 3 and 5) hydraulic geometry calculations for the Mars and Titan rivers, with the two calculations bracketing a range of possible estimates.
3.1. Estimates for Rivers on Mars.
On Mars, we selected two locations where alluvial rivers formed sedimentary deposits that were explored in situ by rovers: the Peace Vallis fan in Gale Crater, and the Western Jezero delta in Jezero Crater. The Peace Vallis fan is a broad, gently sloping alluvial fan draining off Gale Crater’s northern rim (30) (Fig. 1D). Along the western margin of Jezero Crater is a river delta (28, 32, 33) that appears to have been built by a series of avulsive channels (Fig. 1E). Images of the delta from Perseverance show possible alluvial sediment and possible river beds (32). Thus, both locations provide opportunities to constrain Mars’ paleoclimate and are currently the only locations beyond Earth where the grain size of a particular alluvial river’s sediment has been measured (32, 34, 35).
The fluvial conglomerates at the distal end of the Peace Vallis fan imaged by Curiosity in Gale Crater (Fig. 1B) confirm that gravel, with D50 (15th to 85th percentiles D15–D85) ranging from 0.5 (0.3–0.7) cm to 1.0 (0.6–1.6) cm, comprised the bed and banks of past channels (35). Using previous measurements of the width and slope of channels on the fan (30) (SI Appendix, Table S3; Materials and Methods), we calculate a median bed grain size of D50 = 2.0–7.7 cm (Eq. 4b), similar to, but slightly coarser than, the Curiosity measurements (35). Assuming a slope of S= 0.001, a typical lower limit for gravel-bedded rivers on Earth (17), we calculate D50 = 1.0 ± 0.6 cm, consistent with the observed grain sizes. Our grain size estimates for the steeper middle portion of the fan are in the gravel-to-boulder range (SI Appendix, Table S3), consistent with those of Palucis et al. (30).
At Jezero crater, we use previously estimated widths and slopes measured along stratigraphic boundaries exposed on the upper surface of the delta, focusing our analyses on the lower end of the slope estimates from Mangold et al. (32) (SI Appendix, Table S4; Materials and Methods). We calculate a bed grain size for a bedload-dominated river on the Jezero delta of D50 = 3.4–26 cm. These estimates overlap with Perseverance measurements (32) of D50 = 16.4 ± 2.2 cm (84th percentile D84 = 25.9 ± 2.2 cm). Although it is not certain that the observed grains at Gale and Jezero are representative of the beds of ancient bedload-dominated rivers that formed the bulk of the two deposits, the overlap of our estimates with the only available observations lends confidence to our methods. This agreement is especially promising given the level of predictability of D50 observed with our terrestrial data (Fig. 3C), the lognormal distribution of grain size that is commonplace in nature, and uncertainties on the slopes and widths of the source channels (Materials and Methods).
At both locations, we assume that only one channel was actively transporting sediment at any given time. For Gale, we only consider bedload transport and use our estimate of D50 (Eq. 4b) with Eq. 4a to estimate flow discharges in the range of Q = 6–190 m3/s. These estimates overlap almost exactly with those of Palucis et al. (30); however, our approach does not require assumptions of channel width-to-depth ratios or critical shear stress values, as in ref. 30. At Jezero, we consider that the channels that formed the bulk of the deposit may have been either bedload-dominated or suspended load-dominated (Eq. 5) and estimate larger flow discharges of Q = 15–3,200 m3/s, consistent with previous estimates (36, 37). Assuming that these discharges are sourced from runoff uniformly distributed over the upstream drainage areas (A), the required runoff rates (M = Q/A) of M = 0.03–0.9 mm/h (Gale) and M = 0.004–0.9 mm/h (Jezero) are consistent with past estimates (30, 34, 35) and predictions by climate models, which estimate runoff production from seasonal snowmelt or precipitation to be ~0.01–1 mm/h (38–40).
We then use the estimated bankfull sediment fluxes at Gale (Qs = 1 × 10−3–4 × 10−2 m3/s) and Jezero (Qs= 5 × 10−4–3 × 10−2 m3/s) to estimate the active bankfull flow time (t) required to construct the measured volumes of the Peace Vallis fan and Jezero delta (30, 33), accounting for the fraction of the total sediment load that is washload (Materials and Methods). For Gale, we estimate t > 5 × 106–1 × 108 h, ignoring any interstitial fine materials measured at the alluvial fan’s toe (41). For the Jezero delta, which is >10× larger than the Peace Vallis fan (33), we estimate longer bankfull flow times of t > 5 × 107–3 × 109 h if the channels are suspended load-dominated and t > 5 × 107–8 × 109 h if bedload-dominated.
Converting these active bankfull flow times to absolute formation times requires knowledge of the intermittency and duration of bankfull flow events as well as the contribution of sub-bankfull flows to the cumulative sediment discharge (Materials and Methods). Using an intermittency factor (42, 43)—defined as the fraction of time bankfull flow would have to occur to yield the actual time-averaged sediment flux—of 0.01, consistent with ephemeral, arid-region rivers on Earth (42) and Mars snowmelt runoff models (39), we estimate a formation time for the Peace Vallis fan of ≳50 kyr to 2 Myr and formation times for the Jezero delta of ≳0.6 Myr to 33 Myr if suspended load-dominated and ≳0.5 Myr to 87 Myr if bedload-dominated. For a larger intermittency factor of 0.1, consistent with both perennial arid region rivers and the Mississippi River on Earth (42), formation times would be 10× shorter. A smaller intermittency factor of 0.5–1 × 10−4, estimated from climate models that produce runoff via rainfall (44, 45), would yield formation timescales of hundreds of millions of years or longer, which are less consistent with the duration of fluvial activity inferred from the geologic record (46). Moreover, our longest formation time estimates correspond to the gentlest slopes and narrowest channel widths, a combination of extremes that we consider less likely. For comparison, we apply the same approach to the Holocene Rhine River delta on Earth based on the measured (47) volume of deltaic sediments (Materials and Methods) and the sediment fluxes predicted from hydraulic geometry (Fig. 3D). We estimate a formation time of ~1,200–21,000 y, bracketing the true formation time of ~8,000 y (47).
Although we consider the lower end of these estimated formation times for martian deltas (~50 kyr) to be conservatively short, a few factors could conceivably shorten them further. These possibilities include channel widths and slopes larger than our estimates, an outsized influence of sub-bankfull flows, an increased fraction of the total sediment load being composed of washload (Materials and Methods), or the Jezero delta being constructed largely by debris flows (32). While we consider each of these scenarios unlikely, especially in combination, substantial durations of fluvial activity are nevertheless implied even in such scenarios (Materials and Methods).
3.2. Estimates for Rivers on Titan.
For Titan, Cassini topographic and imaging data permit measurements of slope and channel width for only two major rivers: Vid Flumina and Saraswati Flumen (SI Appendix, Fig. S4). The hydraulic geometry relations could in principle be applied to other mapped fluvial networks on Titan (4, 5), but currently available topographic data are insufficient to measure slopes reliably in other locations (27). Saraswati Flumen is the largest and longest (>360 km) river flowing into Ontario Lacus (Fig. 1F) in Titan’s south polar region (3, 5, 6), and terminates near what appear to be two lobes of a river delta (6). The Vid Flumina tributary network drains into Ligeia Mare in Titan’s north polar region (Fig. 1G) and has been observed to be liquid-filled (26).
Using our measured widths and slopes for Saraswati Flumen (SI Appendix, Table S5; Materials and Methods) and Vid Flumina (SI Appendix, Table S6; Materials and Methods), our calculations show that both rivers are capable of transporting gravel as bedload with a D50 on the order of centimeters (SI Appendix, Tables S5 and S6). These results are broadly consistent with previous findings (48, 49) and comparable to the grain sizes observed at the Huygens Landing site (50). However, the Huygens Landing site is far away from either river, and it remains unclear if the gravel observed there was deposited by a river or by a different process.
For Saraswati Flumen, we calculate the bankfull fluid discharge within this single channel to be Q = 40–50,000 m3/s. The larger end of this range is far higher than the studied Martian channels, instead comparable to the Mississippi and Mekong rivers on Earth. Due to limited data coverage, it is only possible to estimate channel characteristics for one tributary into Vid Flumina’s main stem (Fig. 1G and SI Appendix, Fig. S4 A–C; Materials and Methods). For this tributary, our measurements of channel width and slope (SI Appendix, Table S6; Materials and Methods) suggest a flow discharge of Q = 10–2,000 m3/s. As with the Jezero delta, these estimated discharges span large ranges because they encompass both bedload-dominated and suspended load-dominated conditions. At Vid Flumina, where it is possible to estimate drainage basin area, the estimated discharge implies runoff rates of M > 0.04–5.2 mm/h. Permitting losses to infiltration and evaporation (51), the lower end of this range is consistent with climate models (52, 53), which predict precipitation rates of ~0.001–0.1 mm/h for yearly storms.
Our estimate of Saraswati Flumen’s bankfull sediment flux is also large (SI Appendix, Table S5), requiring t > 7 × 103–2 × 105 h of bankfull flow to form the small delta (V ≈ 0.36 km3) if suspended load-dominated and t > 1 × 105–1 × 108 h if bedload-dominated (SI Appendix, Table S5). Both estimates assume no washload (Materials and Methods). Given the similar widths and slopes of Vid Flumina and our narrower estimate of Saraswati Flumen (SI Appendix, Tables S5–S6; Materials and Methods), we predict a similar flux of sediment from the Vid Flumina tributary into the main river. This suggests that sedimentary deposits with volumes like those seen at Ontario Lacus could be constructed if Vid Flumina transports sand. The apparent absence of a river delta at the mouth of Vid Flumina (like most rivers entering Titan’s large lakes and seas) despite this large estimated sediment flux raises questions about how the sediment delivered to Titan’s coasts is deposited in the lakes and distributed along the shorelines.
Assuming precipitation intermittencies and durations from global climate models (52) (Materials and Methods), which equate to an intermittency factor of 0.01, we convert the active bankfull flow time for Saraswati Flumen to an absolute time required to construct the largest delta lobe at Ontario Lacus of >100–3,000 y for a suspended load-dominated river and >2 kyr to 2 Myr if bedload-dominated. If Saraswati Flumen is suspended load-dominated, which seems likely given its large drainage area and proximity to a river delta (Fig. 1F), then Ontario Lacus’ deltas may have formed much faster than a single sea-level cycle, which are hypothesized to occur over tens to hundreds of thousands of years in response to orbitally induced climate change and appear to be consistent with the asymmetric hemispheric distribution of surface liquids (1, 54).
4. Discussion
For the fluvial deposits in both Jezero and Gale Craters, we estimate formation times of hundreds of thousands of years or more. Even for the most optimistically frequent, washload-heavy flows, tens of thousands of years of active flow are required, suggesting prolonged periods when surface liquid water was stable. Although the time required for life to begin is debated, these formation time estimates, which are consistent with past work that uses independent methods (16, 30, 33, 34, 36, 37), suggest that the conditions favorable for life on Mars were not merely fleeting. If Perseverance were to measure slopes and thicknesses of fluvial stratigraphic layers, our methods could be applied to further refine sediment flux estimates and more tightly constrain the timing of fluvial activity in Jezero crater. The possibility of applying the dimensionless hydraulic geometry approach to other river networks and fluvial deposits presents an exciting prospect for the continued exploration of Mars’ paleoclimate.
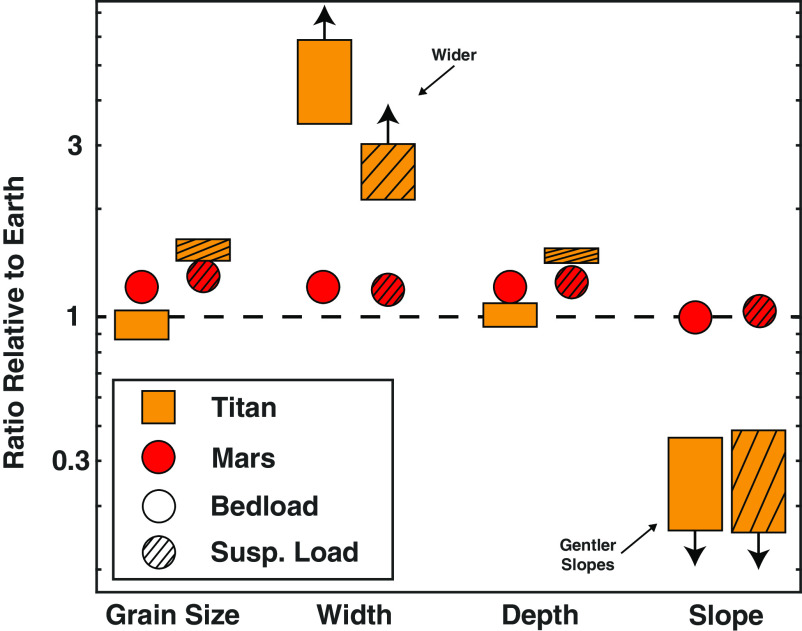
The dependence of the hydraulic geometry relationships on gravity, fluid properties, and sediment properties implies notable differences among rivers on Earth, Mars, and Titan. An alluvial river at equilibrium must convey the sediment supply from its watershed with the runoff supplied over that same watershed. To examine how the resulting river geometries depend on differences in gravity, fluid properties, and sediment properties, we solve Eqs. 1a–e for dimensional width, depth, slope, and bed grain size for a given discharge and sediment flux and express the ratios of these quantities between two planetary bodies (Materials and Methods). This exercise predicts that channel width, depth, and slope should differ little between Mars and Earth due to the nearly identical fluid and sediment properties and the weak dependence on gravity (Fig. 4; Materials and Methods), which helps explain why past estimates (14–16, 30, 33, 34, 36, 37) of flow discharge on Mars have yielded plausible values. In contrast, both river types on Titan should be at least ~3× to 6× wider and have ~2× to 5× gentler slopes than analogous terrestrial rivers (Fig. 4). These differences arise from Titan’s more buoyant sediment (Materials and Methods), which can be entrained or suspended by shallower flows over gentler slopes (55). The Dragonfly rotorcraft should be able to test these predictions on Titan if it encounters active, or recently active, rivers draining the rim of Selk Crater.
Fig. 4.
Relative bed grain size, width, depth, and slope of planetary and terrestrial rivers. Bedload-dominated river ratios are shown with solid colors, while suspended load-dominated rivers are shown with a striped pattern. Assuming equivalent flow discharge and sediment flux, bedload-dominated and suspended load-dominated rivers on Titan may be both wider and more gently sloping than comparable rivers on Earth, while depth and bed grain size are less affected. Values for Titan are more extreme if even more buoyant sediment is assumed (arrows). Both river types on Mars are only marginally different from those on Earth, as gravity only weakly affects relative geometries.
Alternatively, we can solve for the relative fluid discharges that would produce the same river channel geometry (equal width and slope) on different planets (Materials and Methods). On Mars, the relative discharge is ~90% that of an equal-sized river on Earth, as the somewhat denser sediment compensates for the lower gravity. On Titan, however, the relative discharge is just 2% to 6% of an equal-sized river on Earth because Titan’s more buoyant sediment permits transport at lower flows (55). The fact that relatively modest discharge can transport sediment on Titan increases the likelihood that Dragonfly will observe active sediment transport, despite Titan’s semi-arid climate (52).
Finally, we note that our work is limited by the relative paucity of data for rivers on Mars and Titan. Our general framework is, however, of sufficient generality that it can be amended to incorporate new data that adds new perspectives.
5. Materials and Methods
5.1. Global Alluvial River Dataset and Sources.
We gathered hydraulic geometry data for 634 terrestrial rivers from multiple compilations, ensuring that all reported data on channel width, depth, slope, discharge, and bed grain size were measured, not calculated. The entire data compilation is shown in SI Appendix, Fig. S3. For clarity, in Fig. 2 of the main text, we only show the bedload- and suspended load-dominated single-thread rivers, with all other river types removed. The full dataset is available as a supplementary file in the online version of our manuscript.
For our alluvial rivers (491 total), we compiled hydraulic geometry data from multiple past compilations and datasets (SI Appendix). Rivers with measured sediment fluxes are fewer in number, as we only found measurements for 58 of the bedload-dominated rivers in our dataset, and none of the suspended load-dominated rivers. Most of the data for rivers with measured sediment fluxes are derived from the BYU Sediment Transport database (31) (SI Appendix). We acquired 4 additional sediment flux data points from the Rhine River and 33 from Amazon basin rivers (Fig. 3 of the main text). Data for these 37 points did not include D50, hence their exclusion from Fig. 3C, but did include all the other measures (Fig. 3). The Rhine River data came from the BYU database (31), while the Amazon rivers were from Filizola and Guyot (56) and Goldberg et al. (57).
5.2. Calibrating Hydraulic Geometry Relationships on Earth.
In total, this dataset provided bankfull depth, width, slope, and discharge, along with the median bed grain size, for 491 different bedload-dominated (D50 > 15 mm) and suspended load-dominated (D50 < 1.5 mm) rivers in a multitude of different climates and geographic regions on Earth (Supplementary Data File). For the bedload-dominated rivers, we fit hydraulic geometry relationships only to those with clear floodplains (opaque blue points in Figs. 2 and 3), which are the rivers most likely to have entirely self-formed channel widths. Floodplains were identified through visual inspection of Google Earth images for approximately two-thirds of the data that recorded reliable latitude and longitude information. This resulted in 57 bedload-dominated rivers with clear floodplains. Bedload-dominated rivers flowing through constricted valleys, with heavy vegetation, deeply incised into the surrounding topography, or with no latitude or longitude information were fitted separately (351 transparent blue points in Figs. 2 and 3 and SI Appendix, Fig. S1). We performed a similar analysis for suspended load-dominated rivers, but the smaller number of sites (only 10 total, plotted with opaque red points in Figs. 2 and 3, had available latitude/longitude information and clear floodplains) required fitting the hydraulic geometry relations to all the locations. When performing predictions (Fig. 3), we also compared the results with data from four locations on the Rhine River and 33 within the Amazon Basin, which were not included in the fits due to a lack of bed grain size measurements. These additional suspended load-dominated rivers provided a way of gauging the uncertainty in the predicted flow discharge and sediment flux when lacking grain size measurements, a scenario we encounter on Titan and Mars.
Data for three other river types were included in the compilation for comparison but were not used to calibrate hydraulic geometry relationships. We gathered data for 57 bedrock rivers from a variety of climatic and tectonic settings (SI Appendix), a smaller dataset due in large part to the infrequent reporting of bed grain size and the difficulty in estimating a bankfull discharge. We gathered data for 12 braided rivers, which show trends that are similar to the bulk of the bedload-dominated river dataset. Finally, we gathered data from two gauged ephemeral rivers that have reported field observations for the bankfull width, depth, slope, and discharge. The entire compilation, plotted in SI Appendix, Fig. S3, includes data for 634 rivers for which the bankfull depth, width, slope, discharge, and bed grain size (except the Rhine and Amazon rivers) have been measured in the field (SI Appendix).
After dividing the rivers into separate classes, we fit the hydraulic geometry equations (Eq. 1) for bedload-dominated and suspended load-dominated rivers separately. For bedload-dominated rivers, we fit a simple power law. Specifically, for a given set of data (e.g., and for bedload-dominated rivers with floodplains), we randomly sampled data pairs, with replacement, N times, where N represents the total number of rivers in that class. We fit this randomly sampled dataset using an orthogonal least-squares method applied to log-transformed data. These two steps were then iteratively repeated 1,000 times to obtain an estimated probability distribution of the fitted parameters (SI Appendix, Fig. S1). For suspended load-dominated rivers, we performed a similar routine, but instead fit a multivariate power-law to both and Rep. For each class of river, we report the medians of these distributions along with the 16th and 84th percentiles (Fig. 2 and SI Appendix, Table S2).
To check for statistical differences between bedload-dominated rivers with and without floodplains and with our entire suspended load-dominated river dataset, we performed fits on all three classes separately. This analysis showed that the two classes of bedload-dominated rivers are broadly similar, differing primarily in their fitted values for slope (SI Appendix, Fig. S1). Further, as found by Parker et al. (17), we observe that the dimensionless depth is almost statistically constant (i.e., ) for bedload-dominated rivers, despite the addition in this study of hundreds more rivers from diverse locations around the world. This is consistent with the use of Q0.4 to nondimensionalize flow depth and channel width (Eq. 1), which follows the original observation by Leopold and Maddock (20) that flow depth typically varies as Q0.4. Similarly, the observation (20) that channel width typically varies as Q0.5 helps explain why dimensionless channel width increases only weakly with dimensionless discharge (Fig. 2 and SI Appendix, Table S2). The suspended load-dominated rivers showed substantial, statistically significant differences in most fitted parameters relative to the bedload-dominated rivers (Fig. 2 and SI Appendix, Fig. S1 and Table S2). We use the resulting constants (SI Appendix, Table S2) for the entire suspended load-dominated river dataset and the sub-selected bedload-dominated rivers with floodplains in the hydraulic geometry relationships throughout our work.
5.3. Dimensional Hydraulic Geometry Predictions.
From our dimensionless relations (Eq. 1), we seek to predict the flow discharge and sediment flux using only measurements made from remote sensing platforms. Channel width and slope can both be measured from images and topographic data collected by orbiting spacecraft. However, bed grain size and flow depth generally require in situ measurement by field scientists or spacecraft such as rovers or rotorcraft.
As such, we rearranged Eq. 1 to express the dimensional bed grain size (D50), flow discharge (Q), sediment flux (Qs), and depth (H) as functions of the dimensional width (B) and slope (S). For bed grain size, we solved both Eqs. 1a and 1c for Q and equated the two expressions. For bedload-dominated rivers, this yields
| [4aa] |
Solving Eq. 4a for D50 then yields
| [4bb] |
The dimensional depth is then obtained by substituting Eq. 1d into Eq. 1b and solving for H,
| [4c] |
The same approach for suspended load-dominated rivers yields
| [5a] |
| [5b] |
| [5c] |
For the flow discharge (Eqs. 4a and 5a), either the slope or width relation can be chosen. For our work, we chose the width relation because uncertainties on measured widths on Mars or Titan were less than for slope. Finally, the sediment flux is given by
| [6] |
where for bedload-dominated rivers Qs is the bedload, and for suspended-load dominated rivers Qs is the total load.
Alternatively, there may be scenarios where channel depth is better constrained than slope. Although this is not the case for the Titan examples presented here, the caprock thickness of inverted channels on Mars appears to be a useful indicator of channel depth (29, 58). If one were to expand this work to other channels or deposits on Mars, a width–depth formulation may be preferred. In that case, the approach would be to solve for D50 by combining the equations for channel width (Eq. 1a) and channel depth (Eq. 1b),
| [7] |
making the approximation (SI Appendix, Table S2), and solving for D50:
| [8] |
This form for bedload-dominated rivers (and the equivalent for suspended load-dominated rivers) could be used in place of (Eqs. 4b and 5b) where measurements of slope on Mars are more difficult due to stratigraphic uncertainties and erosional modification.
5.4. Influence of Bank Cohesion on Mars and Titan.
Two factors that can affect hydraulic geometry are bank cohesion and human impacts (SI Appendix, Fig. S2). While we can confidently neglect any human influences on Mars or Titan, it is less clear how bank cohesion might differ among worlds. Bank cohesion is thought to have a relatively minor effect on the hydraulic geometry of bedload-dominated channels on Earth, with the position of the channel banks set by the threshold of motion of sediment along the banks (17; SI Appendix). However, the distinct hydraulic geometry relations for suspended load-dominated rivers (Fig. 2) have been interpreted as a consequence of cohesion from vegetation or fine sediment (59).
On Mars, there is evidence of cohesive banks in ancient river channels (60, 61), which suggests that cohesion-related errors in our flow and sediment flux estimates for Mars should be minor. Specifically, inverted channels on Mars preserve evidence of single-thread rivers, implying that some bank cohesion was present when the rivers were active. Detrital mud or ice (60) on Mars may have played a similar role to vegetation and mud in Earth’s riverbanks (59, 61). Although the flow discharges required to produce the observed channel geometry on Mars would need to have been slightly higher than our estimates if the absolute magnitude of bank cohesion on Mars was equal to that found on Earth, such differences would likely be small compared to the inherent variability encountered on Earth (Fig. 2). Therefore, both our suspended load-dominated and bedload-dominated calculations on Mars are unlikely to be strongly affected by differences in bank cohesion.
The cohesion of sediment on Titan is unknown. However, if there were no bank cohesion, suspended load-dominated rivers would be wider and shallower than our estimates, likely forming multiple threads. Cassini’s RADAR would be unable to observe such rivers directly, as absorption of the radar signal through tens of meters of liquid is required for the liquid to be detected in images (8). RADAR altimeter measurements showing Vid Flumina to be liquid-filled is inconsistent with a very shallow flow, and neither Vid Flumina nor Saraswati Flumen appears to consist of multithread channels. These observations argue against cohesionless banks in the scenario in which these rivers are suspended load-dominated. At the other extreme, if Titan’s riverbanks are similarly cohesive to, or even more cohesive than, those on Earth, perhaps due to tholin materials (62), the flows required to mobilize bank sediment would be deeper than our estimates, and our reconstructed flow discharges and sediment fluxes would be underestimates. We cannot rule out such a scenario. Our hydraulic geometry calculations implicitly assume that suspended load-dominated rivers on Titan have bank cohesion that is dynamically similar to Earth’s with respect to gravity and sediment buoyancy, an assumption that cannot be tested until Dragonfly makes measurements on Titan’s surface. However, given the trends observed in the terrestrial data (Fig. 2) despite the wide range of environmental conditions (SI Appendix, Fig. S2), we do not consider bank cohesion effects to be a dominant source of error in our calculations.
5.5. Sediment and Fluid Compositions.
The composition of Titan’s sediment is unknown, but we assume that it is either water ice, organic solids, or a combination of the two (3, 9). We therefore assume a sediment density of = 0.95 g/cm3, which is within the range of densities expected for organic sediment (SI Appendix, Table S1) while also overlapping with that of water ice. We use fluid densities and viscosities (SI Appendix, Table S1) calculated by Steckloff et al. (21), which range from cold (84 K) methane rain, which might be expected to dominate in a river, to warm (91 K) methane/ethane liquid (70% methane mole fraction), similar in composition to Titan’s seas (7). For both cases, dissolved nitrogen is incorporated into the liquid as a function of the liquid temperature and methane mole fraction (21). For Mars, we assume mafic sediment ( = 2.9 g/cm3) in liquid water (SI Appendix, Table S1).
5.6. Mars Measurements.
We performed calculations for Gale and Jezero Craters, where there are in situ rover observations of the bed grain size for comparison with our results.
5.6.1. Peace Vallis fan (Fig. 1D).
The Peace Vallis fan in Gale Crater is marked by numerous inverted channels that are well resolved in Mars Reconnaissance Orbiter’s High Resolution Imaging Science Experiment (HiRISE) data. Topographic data are also available from a HiRISE digital elevation model (DEM). We use a bankfull channel width of 27 ± 16 m and slopes of 0.003 and 0.01, as reported in Palucis et al. (30). We assume that the lower slope estimate applies to the distal portion of the fan, where Curiosity imaged fluvial conglomerates, and we use this slope to generate predictions of bed grain size for comparison with Curiosity’s measurements. However, there is uncertainty in this slope estimate because the channel width and slope measurements by Palucis et al. (30) were not made in exactly the same the location where Curiosity imaged gravel. By comparing our calculated bed grain size with the grain sizes measured by Curiosity, we therefore assume that the gravel deposits imaged by Curiosity were formed by channels with characteristics similar to those on the Peace Vallis fan. The middle portion of the alluvial fan (Fig. 1D), where most of the resolved channels are located (30), is used to estimate formation timescales, as it most likely represents the bulk of the fan volume and is where slope and channel width can both be measured (30). We use an alluvial fan volume of V = 0.9 km3 and a drainage area upstream of the fan apex of A ~ 730 km2, both estimated by Palucis et al. (30).
5.6.2. Western Jezero delta (Fig. 1E).
Just as for Gale Crater, HiRISE images and DEMs are available over the western Jezero Crater delta and surrounding region, which were used to study the delta in detail (28, 32). However, the measurements are more uncertain at Jezero compared to at Gale, given that the Jezero delta is highly degraded. As argued in Goudge et al. (28) and Lapôtre and Ielpi (33) for these channels on the Jezero delta (Fig. 1E), the full width of the inverted channel likely combines multiple, overlapping inverted channel beds. An empirical scaling corrects for this bias and estimates the active channel width to be 67% of the measured inverted channel width (33). As in Lapôtre & Ielpi (33), we use a channel width of 45 m, with 10th and 90th percentile widths of 19 m and 148 m used as lower and upper bounds.
For the channel slope, Goudge et al. (28) derived slopes of 0.027 ± 0.012. By tracing stratigraphic contacts across the deposit surface, Mangold et al. (32) also measured slopes ranging from 0.003–0.029, with most slopes >0.01. Such slopes (S > 0.01–0.03) would be extraordinarily steep for a river delta. The observations that there are no channels within our terrestrial data compilation (SI Appendix) as wide and steep as those reported in Goudge et al. (28) or at the larger end measured by Mangold et al. (32), and that width and slope should not differ strongly between Mars and Earth (Fig. 4), suggest that such slopes may not be representative of the channel beds when the rivers were active. Moreover, these slopes, when used in the dimensionless hydraulic geometry relationships, yield implausibly large median grain sizes (SI Appendix, Table S4). If these steep slopes are indeed representative of past active flow conditions, then they were likely set by a different process, such as hyper-concentrated flows or debris flows. The approach we use here would not be valid under these scenarios. Alternatively, these steep slopes may correspond to the eroded surface of the delta rather than paleo-channel beds. As such, we adopt the lowest of the slopes measured by Mangold et al. (32), S= 0.003. This slope is consistent with the median slope calculated by Lapôtre and Ielpi (33) as part of their study of the lateral migration rate of fluvial meanders on the Jezero delta. Finally, we use a volume for the western Jezero delta of V ~ 22.5 km3, and a drainage area A ~ 12,700 km2, both of which were calculated by Lapôtre and Ielpi (33) in a manner similar to the measurements by Palucis et al. (30) at Gale Crater.
5.7. Titan Measurements.
We did not include the Huygens probe landing site in our analysis despite having in situ observations of grain size (Fig. 1C) because the topography of the drainage network near the landing site shows that the river channels have incised into the surrounding terrain (63). This, combined with a steep slope of ~0.02 (63), suggests that these channels are or recently were dominantly erosional, so it is likely that their hydraulic geometry was controlled by different mechanisms (64). Indeed, our terrestrial data compilation shows that bedrock rivers have distinct hydraulic geometry (SI Appendix, Fig. S3). There is also no direct evidence that the grains observed at the landing site (Fig. 1C) derive from the nearby channels.
Instead, we selected Vid Flumina and Saraswati Flumen for study, as they are the only two river networks with the possibility of measuring slope that are likely to be self-formed alluvial channels with bed and banks composed of mobile sediment. We also know that Vid Flumina is liquid-filled (26) and assume that Saraswati Flumen is as well by analogy and its proximity to the liquid-filled Ontario Lacus.
5.7.1. Saraswati Flumen (Fig. 1F).
At Saraswati Flumen, we do not have direct measures of the liquid surface elevation. Instead, we adopt the measured slopes of the SAR-dark plain that surrounds Ontario Lacus, and through which the river flows. Because the altimetry track is not parallel to the river’s flow path, (Fig. 1F and SI Appendix, Fig. S4D) and because of the river’s sinuosity, we calculate an adjusted slope , where is the slope measured by the Cassini altimeter [Figure 9 of Hayes et al. (8)], is our measured sinuosity of the river, and is the angle between the shoreline and the altimetry track, making the approximation that the river’s average flow direction is perpendicular to the shoreline (SI Appendix, Fig. S4D). The slope used in our work is therefore .
From SAR images, we estimate a maximum channel width of ~700 m and assume a minimum width equal to the pixel size (175 m), given no other direct altimetric measurements. We measured a minimum drainage area of A ~ 10,000 km2, though this is likely to be an underestimate given that only a single tributary of the river network is resolved by the images (SI Appendix, Fig. S4D). As a result, our runoff rates (M) are likely severe overestimates, with their implications not discussed further in the main text. Our measured widths of Titan’s rivers, particularly Saraswati Flumen, are comparable to the largest rivers in the terrestrial dataset; given the coarse image resolution, the true bankfull channel widths on Titan may be smaller. We suspect that these widths, measured both from SAR images and altimetry data, may convolve channel and floodplain, and we therefore report them as upper limits. We consider the lower end of the estimated flow discharges and sediment fluxes (Qs), and the higher end of the flow (t) and formation timescales, to be most likely. Alternatively, the maximum estimates of channel width provide upper limits on the calculated flow discharge and sediment fluxes and therefore a minimum estimate of the formation timescale for the possible delta in Ontario Lacus, as described below.
5.7.2. Vid Flumina (Fig. 1G).
Cassini directly measured the liquid surface elevation of multiple points across the Vid Flumina river network during the T91 flyby, showing that liquid surface elevations in some of the channels appear to be close to the sea level in Ligeia Mare (26), to which Vid Flumina drains. However, one liquid-filled tributary (Fig. 1G), which clearly connects to the main stem, was elevated, implying active river flow. From this, we calculate an average slope of 1.1–1.5 × 10−3 for this tributary (SI Appendix, Fig. S4 A–C). The power measured by the altimeter also constrains the minimum liquid-filled width of the tributary to be equivalent to the size of the Fresnel zone, estimated to be ~100 m (65). Additional details on the techniques used to measure slopes and minimum channel widths are provided in the SI Appendix. In the highest-resolution SAR images of this region, the tributary is just discernable, suggesting that the maximum liquid-filled channel width is close to the minimum pixel size (~175 m). Vid Flumina appears to have incised valleys into the surrounding terrain (26); we assume that self-formed alluvial channels reside within the broader valleys. By connecting the tips of visible tributaries, we construct a bounding polygon that circumscribes the network and yields a minimum drainage area for the tributary of A~90,000 km2, which is likely to be an underestimate due to the coarse imaging resolution from Cassini (5).
5.8. Sedimentary Deposit Formation Timescales.
We consider various factors that may affect the estimated formation timescales of fluvial deposits, including the relative proportions of the total sediment load that are washload and bed material load, the intermittency of flows, and the influence of sub-bankfull flow events. We calculated the active bankfull flow time t as
| [9] |
where V is the measured sedimentary deposit volume and 0.35 is the assumed porosity of the deposits. For our Mars calculations, we ignore any compaction, as the degree of compaction remains poorly constrained. If considered, however, any compaction would increase the formation timescale in proportion to the decrease in average porosity. The factor is the ratio of washload sediment flux to bed material sediment flux (Qs, estimated from Eq. 6) that is trapped in the sedimentary deposit. Unless reported otherwise, we set = 0 for all calculations involving bedload-dominated rivers, which assumes that washload forms a negligible portion of the resulting sedimentary deposits. For suspended load-dominated rivers on Earth, ranges from 0.4–2 for sandy, washload-poor rivers like the Rhine (47), Brahmaputra, Ganges, and Mississippi to 6–9 for rivers like the Mekong and Ayeyarwady (66). However, such field measurements have large uncertainties, and many washload-rich rivers have been heavily influenced by humans through the construction of dams and changes in land use (66).
Converting the active bankfull flow time to a total formation timescale requires knowledge of the intermittency and duration of bankfull flow events as well as the contributions of nonbankfull flow events to the time-integrated sediment discharge. Paola et al. (43) defined an intermittency factor I as the fraction of time bankfull flow would have to occur to yield the actual time-averaged sediment flux. Given I, the total formation time T can be calculated as T = t/I.
5.8.1. Rhine River.
We use the Rhine River delta as a terrestrial test case for the formation timescale calculations. Field measurements (51) indicate that Rhine River-derived sediments in the current delta include 7.32 km3 of clay and silt and 4.68 km3 of sand and gravel. This equates to a washload factor of ~ 2 and a total volume of clastic sediment of V= 12 km3, which accumulated over ~8,000 y (51). Using the sediment fluxes, we estimated from hydraulic geometry (Fig. 3D) based on field measurements of the widths and slopes of the Rhine River, and assuming a deposit porosity of = 0.35 and an intermittency factor of 0.1, we calculated total formation timescales ranging from 1,200–21,000 y, consistent with the measured timescale.
5.8.2. Mars.
For the Peace Vallis fan, an alluvial fan known to consist of gravel deposits, we assume that = 0, and that the fine material observed near the fan’s toe (41) is not present near the fan center where channel width and slope measurements were made. If a small fraction (up to 20%; ref. 41) of fine material were present, then the formation timescale would decrease in proportion to that fraction. If the channels building the Jezero delta were suspended load-dominated, then was likely greater than 0. However, we suspect for two reasons. First, silt-sized and clay-sized grains would have been less likely to settle out of suspension and be trapped in the delta, especially if flocculation is inefficient on Mars (67), and would more likely have bypassed the delta and settled further toward the crater’s center (33). Second, finer-grained fluvial sediments would have been less likely to survive long periods of erosion than coarser-grained sediments, which would tend to reduce the fraction of washload-sourced material in the partly eroded delta. For our calculations, we therefore set = 2, with the goal of estimating minimum formation times. Even for large washload fractions ( ~ 5), the estimated formation timescale for the Jezero delta is still >25 ky.
Climate models predict that river discharge events on Mars may have occurred seasonally for a few days around the spring equinox during favorable orbital conditions (38–40). If runoff was sourced from snowmelt within the drainage basins of the Peace Vallis fan and Jezero delta and generated bankfull flows for ~5 d per Earth year, this would correspond to an intermittency factor of ~0.01. This assumes that sub-bankfull flow events make a negligible contribution to flow and sediment transport, consistent with abrupt onset and cessation of runoff due to sudden melting (38–40). The assumption that rivers on Mars experienced a similar distribution of flows to ephemeral, arid-region rivers on Earth would also lead to an estimated intermittency factor of ~0.01 (42). Given the limited current understanding of the runoff source and the Martian paleoclimate, however, we also consider an intermittency factor as high as 0.1, representative of the majority of rivers on Earth, including perennial arid region rivers (42). This largest intermittency factor corresponds to the shortest possible formation time. Intermittency factors calculated from Martian climate models with transient rainfall (44, 45) are far smaller than our estimated values and predict formation timescales of hundreds of millions of years or more. Such a climate might have existed, but we consider these very long formation times unlikely.
A few factors could conceivably shorten our already conservatively short estimated formation timescales for sedimentary deposits on Mars. For example, in the case of frequent bankfull flows or major sediment contributions by sub-bankfull flows (intermittency of 0.1) and a washload-dominated sediment load ( = 5), our results suggest that the Jezero delta required ≳25 ky to form. However, we consider such a combination of parameters unlikely. The only scenario we consider to be consistent with proposed formation times less than 10,000 y (32) is one in which the Jezero deposit is an alluvial fan constructed largely by debris flows.
5.8.3. Titan.
We first estimated the volume of Ontario Lacus’ possible river delta by using Cassini SAR images to measure the subaerial portion of the largest delta lobe, closest to the outlet of Saraswati Flumen (SI Appendix, Fig. S4 E and F). This delta lobe has an approximately rectangular shape that is ~12 6 km in size (SI Appendix, Fig. S4 E and F). To estimate the thickness of the delta, we used the liquid depth at the toe of the delta (~10 m) as measured during the T49 altimetry flyby over Ontario Lacus (8). We then assumed that the delta is a wedge with vertical sides and front that does not protrude above the liquid surface (SI Appendix, Fig. S4F). We know that this is not likely the case, but we also have no means to reliably estimate the slope that subaqueously deposited sediment would form under the lake surface. Therefore, we estimated a minimum delta volume of V > 0.36 km3. As we are also estimating maximum flow and sediment discharges, our estimated formation timescales for the delta are likely minima.
To calculate the delta formation timescale, we converted active bankfull flow times into total formation timescales using storm intermittencies and durations in Titan’s south polar region from general circulation model simulations (52, 68–71). Specifically, we assume that there are on average 2 storms per Titan summer (1 storm per 7 Earth years) (52, 68–71) and that they persist for 2 Titan days (32 Earth days) (69), which equates to an intermittency of ~0.01. We summarize these estimates in SI Appendix, Table S5.
We assume that Saraswati Flumen is an alluvial channel and, for simplicity given the unknown properties of Titan’s surface materials (9), that there is no washload deposited in the delta. For the smallest channel width and slope (B = 175 m, S = 0.0004), we predict a formation timescale of 950–2,700 y if suspended load-dominated and up to ~2 Myr if bedload-dominated. Given the width and slope of the river, which are comparable to suspended load-dominated rivers in our dataset, the large drainage area, and the river’s proximity to a river delta and coast of a large lake, Saraswati Flumen is likely to be a suspended load-dominated river. If so, the estimated formation timescale is far shorter than the range of hypothesized timescales of orbitally driven climate change (~104–105 y; 1, 3, 54, 71), even for the smallest estimated width and gentlest estimated slope, which correspond to the longest estimated formation time. This suggests that a suspended load-dominated river could have constructed the Ontario Lacus delta within the most recent sea-level cycle.
5.9. Relative Channel Geometries.
For bedload-dominated rivers, solving Eqs. 1 and 2 for the dimensional width, depth, slope, and sediment flux yields
| [10a] |
| [10b] |
| [10c] |
| [10d] |
Similarly, for suspended load-dominated rivers, using Eqs. 1 and 3 yields
| [11a] |
| [11b] |
| [11c] |
| [11d] |
For a planetary river and a river on Earth with equal sediment flux (Qs) and fluid discharge (Q), using the calibrated hydraulic geometry relationships determined here (Fig. 2 and SI Appendix, Table S2 and Fig. S1), we calculated the relative grain size, width, depth, and slope for bedload-dominated rivers
| [12a] |
| [12b] |
| [12c] |
| [12d] |
where the subscript e refers to the Earth river and the equivalent parameters without subscripts are those of the planetary river (SI Appendix, Table S1). The corresponding ratios for suspended load-dominated rivers are
| [13a] |
| [13b] |
| [13c] |
| [13d] |
These ratios show that the relative geometries scale only weakly with gravity, while both width (B) and slope (S) scale strongly with the sediment buoyancy factor (R). We calculated these ratios for rivers on Mars and Titan (Fig. 4) and discuss their implications in the main text.
As an alternative, we also investigate the relative discharges of rivers on two planets with equal width and slope. Solving (Eqs. 4a and 4b) for the flow discharge, and then substituting Eq. 2 and the fitted regression constants (SI Appendix, Table S2), we find that the discharge scales as
| [14] |
Supplementary Material
Appendix 01 (PDF)
Dataset S01 (XLSX)
Acknowledgments
We thank Jaap Nienhuis, Samuel Goldberg, and Kim Huppert for helpful discussions and directions to relevant terrestrial data. The manuscript was greatly improved due to thoughtful reviews from W.E.D., M.G.L., and P.W. This research was supported by the Heising-Simons Foundation (51 Pegasi b Fellowship to S.P.D.B.), and the Cassini Data Analysis Program (#80NSSC18K1057 and #80NSSC20K0484).
Author contributions
S.P.D.B., G.P., and J.T.P. designed research; S.P.D.B. performed research; G.P., P.C., J.M.S., J.W.M., R.V.P., J.M.L., A.D.A., and A.G.H. contributed new reagents/analytic tools; S.P.D.B., J.W.M., and J.T.P. analyzed data; and S.P.D.B. and J.T.P. wrote the paper.
Competing interests
S.P.D.B. is a coauthor of a white paper with M.G.L.: New Frontiers Titan Orbiter, Bulletin of the American Astronomical Society, p. 317, 2021.
Footnotes
Reviewers: W.E.D., University of California; M.G.L., Stanford University; and P.W., Utah State University.
Contributor Information
Samuel P. D. Birch, Email: sbirch@mit.edu.
Gary Parker, Email: parkerg@illinois.edu.
Data, Materials, and Software Availability
All study data are included in the article and/or SI Appendix.
Supporting Information
References
- 1.Hayes A. G., Lorenz R. D., Lunine J. I., A post-Cassini view of Titan’s methane-based hydrologic cycle. Nat. Geosci. 11, 306–313 (2018). [Google Scholar]
- 2.Turtle E., et al. , Titan’s meteorology over the Cassini mission: Evidence for extensive subsurface methane reservoirs. Geophys. Res. Lett. 45, 5320–5328 (2018). [Google Scholar]
- 3.Birch S. P. D., et al. , Geomorphologic mapping of titan’s polar terrains: Constraining surface processes and landscape evolution. Icarus 282, 214–236 (2017). [Google Scholar]
- 4.Burr D. M., et al. , Fluvial features on Titan: Insights from morphology and modeling. GSA Bulletin 125, 299–321 (2013). [Google Scholar]
- 5.Miller J. W., et al. , Fluvial features on titan and earth: lessons from planform images in low-resolution SAR. Planet. Sci. J. 2, 142 (2021). [Google Scholar]
- 6.Wall S., et al. , Active shoreline of Ontario Lacus, Titan: A morphological study of the lake and its surroundings. Geophys. Res. Lett. 37, L05202 (2010). [Google Scholar]
- 7.Hayes A. G., The lakes and seas of Titan. Annu. Rev. Earth Planet. Sci. 44, 57–83 (2016). [Google Scholar]
- 8.Hayes A. G., et al. , Transient surface liquid in Titan’s polar regions from Cassini. Icarus 211, 655–671 (2011). [Google Scholar]
- 9.Nixon C. A., et al. , Titan’s cold case files – Outstanding questions after Cassini-Huygens. Planet. Space Sci. 155, 50–72 (2018). [Google Scholar]
- 10.Dickson J. L., The global distribution of depositional rivers on early Mars. Geology 49, 504–509 (2021). [Google Scholar]
- 11.Di Achille G., Hynek B. M., Ancient ocean on Mars supported by global distribution of deltas and valleys. Nat. Geosci. 3, 459–463 (2010). [Google Scholar]
- 12.Wordsworth R. D., The climate of early Mars. Annu. Rev. Earth Planet. Sci. 44, 381–408 (2016). [Google Scholar]
- 13.Burr D., et al. , Sediment transport by liquid surficial flow: Application to Titan. Icarus 181, 235–242 (2006). [Google Scholar]
- 14.Morgan A. M., Craddock R. A., Assessing the accuracy of paleodischarge estimates for rivers on Mars. Geo. Phys. Res. Lett. 46, 11738–11746 (2019). [Google Scholar]
- 15.Jacobsen R. E., Burr D. M., Errors in Martian paleodischarges skew interpretations of hydrologic history: Case study of the Aeolis Dorse, Mars, with insights from the Quinn River, NV. Icarus 302, 407–417 (2018). [Google Scholar]
- 16.Konsoer K. M., et al. , Channel slope adjustment in reduced gravity environments and implications for Martian channels. Geology 46, 183–186 (2018). [Google Scholar]
- 17.Parker G., Wilcock P., Paola C., Dietrich W., Physical basis for quasi-universal relationships for bankfull hydraulic geometry of single-thread gravel-bed rivers. J. Geophys. Res. 112, F04005 (2007). [Google Scholar]
- 18.Wilkerson G. V., Parker G., Physical basis for quasi-universal relationships for bankfull hydraulic geometry of sand-bed rivers. J. Hydr. Eng. 137, 7 (2011). [Google Scholar]
- 19.Parker G., Dimensionless Bankfull Hydraulic Relations for Earth and Titan (AGU Fall Meeting, 2005). [Google Scholar]
- 20.Leopold L. B., Maddock T., The hydraulic geometry of stream channels and some physiographic implications, U.S. Geol. Surv. Prof. Pap. 252, 1–57 (1953). [Google Scholar]
- 21.Steckloff J. K., et al. , Stratification Dynamics of Titan’s Lakes via Methane Evaporation. Planetary Sci. J. 1, 26 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Parker G., Self-formed straight rivers with equilibrium banks and mobile bed. Part 1. The sand-silt river. J. Fluid Mech. 89, 109–125 (1978a). [Google Scholar]
- 23.Dingle E. H., Kusack K. M., Venditti J. G., The gravel-sand transition and grain size gap in river bed sediments. Earth-Sci. Rev. 222, 103838 (2021). [Google Scholar]
- 24.Parker G., 1D sediment transport morphodynamics with applications to rivers and turbidity currents, e-book. Natl. Cent. for Earth Surf. Dyn. (2004), http://cee.uiuc.edu/people/parkerg/. [Google Scholar]
- 25.Lamb M. P., Venditti J. G., The grain size gap and abrupt gravel-sand transitions in rivers due to suspension fallout. Geophys. Res. Lett. 43, 3777–3785 (2016). [Google Scholar]
- 26.Poggiali V., et al. , Liquid-filled canyons on Titan. Geophys. Res. Lett. 43, 7887–7894 (2016). [Google Scholar]
- 27.Corlies P., et al. , Titan’s topography and shape at the end of the Cassini mission. Geophys. Res. Lett. 44, 11754–11761 (2017). [Google Scholar]
- 28.Goudge T. A., et al. , Stratigraphy and paleohydrology of delta channel deposits, Jezero crater, Mars. Icarus 301, 58–75 (2017). [Google Scholar]
- 29.Hayden A. T., et al. , Formation of sinuous ridges by inversion of river-channel belts in Utah, USA, with implications for Mars. Icarus 332, 92–110 (2019). [Google Scholar]
- 30.Palucis M. C., et al. , The origin and evolution of the Peace Vallis fan system that drains to the Curiosity landing area, Gale Crater, Mars. J. Geophys. Res. 119, 705–728 (2014). [Google Scholar]
- 31.Hinton D., Hotchkiss R., Ames D. P., Comprehensive and quality-controlled bedload transport database. J. Hyd. Eng. 143, 2 (2016). [Google Scholar]
- 32.Mangold N., et al. , Perseverance rover reveals an ancient delta-lake system and flood deposits at Jezero crater, Mars. Science 374, 711–717 (2021). [DOI] [PubMed] [Google Scholar]
- 33.Lapôtre M. G. A., Ielpi A., The pace of fluvial meanders on Mars and implications for the western delta deposits of Jezero crater. AGU Adv. 1, e2019AV000141 (2020). [Google Scholar]
- 34.Dietrich W. E., et al. , “Gravel-Bed Rivers: Processes and Disasters” in Fluvial Gravels on Mars, Tsutsumi D., Laronne J. B., Eds. (Gravel-Bed Rivers, 2017). https://onlinelibrary.wiley.com/doi/book/10.1002/9781118971437. [Google Scholar]
- 35.Williams R. M. E., et al. , Martian fluvial conglomerates at Gale crater. Science 340, 1068–1072 (2013). [DOI] [PubMed] [Google Scholar]
- 36.Fassett C. I., Head J. W., Fluvial sedimentary deposits on Mars: Ancient deltas in a crater lake in the Nili Fossae region. Geophys. Res. Lett. 32 (2005). [Google Scholar]
- 37.Goudge T. A., et al. , Stratigraphy and paleohydrology of delta channel deposits, Jezero crater, Mars. Icarus 301, 58–75 (2018). [Google Scholar]
- 38.Kite E. S., et al. , Seasonal melting and the formation of sedimentary rocks on Mars, with predictions for the Gale Crater mound. Icarus 223, 181–210 (2013). [Google Scholar]
- 39.Kite E. S., et al. , Persistence of intense, climate-driven runoff late in Mars history. Sci. Adv. 5, eaav7710 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Williams K. E., et al. , Ancient melting of mid-latitude snowpacks on Mars as a water source for gullies. Icarus 200, 418–425 (2009). [Google Scholar]
- 41.Grotzinger J. P., et al. , A habitable fluvio-lacustrine environment at Yellowknife Bay, Gale Crater, Mars. Science 343, 6169 (2014). [DOI] [PubMed] [Google Scholar]
- 42.Hayden A. T., Lamb M. P., McElroy B. J., Constraining the timespan of fluvial activity from the intermittency of sediment transport on Earth and Mars. Geophys. Res. Lett. 48, e2021GL092598 (2021). [Google Scholar]
- 43.Paola C., Heller P. L., Angevine C. L., The large-scale dynamics of grain-size variation in alluvial basins, 1: Theory. Basin Res. 4, 73–90 (1992). [Google Scholar]
- 44.Wordsworth R. D., et al. , Transient reducing greenhouse warming on early Mars. Geophys. Res. Lett. 44, 665–671 (2017). [Google Scholar]
- 45.Wordsworth R. D., et al. , A coupled model of episodic warming, oxidation and geochemical transitions on early Mars. Nat. Geosci. 14, 127–132 (2021). [Google Scholar]
- 46.Fassett C. I., Head J. W., The timing of martian valley network activity: Constraints from buffered crater counting. Icarus 195, 61–89 (2008). [Google Scholar]
- 47.Erkens G., et al. , Holocene sediment budgets of the Rhine Delta (The Netherlands): A record of changing sediment delivery. Sediment Dynamics and the Hydromorphology of Fluvial Systems. IAHS Publ. 306 (2006). [Google Scholar]
- 48.Lapôtre M. G. A., Malaska M. J., Cable M. L., The role of seasonal sediment transport and sintering in shaping Titan’s landscapes: A hypothesis. Geophys. Res. Lett. 49, E2021GL097605 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Comola F., et al. , Titan’s prevailing circulation might drive highly intermittent, yet significant sediment transport. Geophys. Res. Lett. 49, e2022GL097913 (2022). [Google Scholar]
- 50.Tomasko M. G., et al. , Rain, winds and haze during the Huygens probe’s descent to Titan’s surface. Nature 438, 765–778 (2005). [DOI] [PubMed] [Google Scholar]
- 51.Perron J. T., et al. , Valley formation and methane precipitation rates on Titan. J. Geophys. Res. 111, E11001 (2006). [Google Scholar]
- 52.Faulk S. P., Mitchell J. L., Moon S., Lora J. M., Regional patterns of extreme precipitation on Titan consistent with observed alluvial fan distribution. Nat. Geosci. 10, 827–831 (2017). [Google Scholar]
- 53.Tokano T., Lorenz R. D., Modeling of seasonal lake level fluctuations of Titan’s seas/lakes. J. Geophys. Res. Planets 124, 617–635 (2019). [Google Scholar]
- 54.Aharonson O., et al. , An asymmetric distribution of lakes on Titan as a possible consequence of orbital forcing. Nat. Geosci. 2, 851–854 (2009). [Google Scholar]
- 55.Amy L., Dorrell R., Equilibrium sediment transport, grade and discharge for suspended-load-dominated flows on Earth, Mars and Titan. Icarus 360, 114243 (2021). [Google Scholar]
- 56.Filizola N., Guyot J. L., Suspended sediment yields in the Amazon basin: An assessment using the Brazilian national data set. Hydrological Processes 23, 3207–3215 (2009). [Google Scholar]
- 57.Goldberg S. L., Schmidt M. J., Perron J. T., Fast response of Amazon rivers to Quaternary climate cycles. J. Geophys. Res. Earth Surface 126, e2021JF006416 (2021). [Google Scholar]
- 58.Hayden A. T., Lamb M. T., Fluvial sinuous ridges of the Morrison Formation, USA: Meandering, scarp retreat, and implications for Mars. J. Geophys. Res. Planets 125, e2020JE006470 (2020). [Google Scholar]
- 59.Dunne K. J., Jerolmack D. J., What sets river width? Sci Adv. 6, eabc1505 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Matsubara Y., et al. , River meandering on Earth and Mars: A comparative study of Aeolis Dorsa meanders, Mars and possible terrestrial analogs of the Usuktuk River, AK, and the Quinn River, NV. Geomorphology 240, 102–120 (2015). [Google Scholar]
- 61.Lapotre M. G. A., et al. , Model for the formation of single-thread rivers in barren landscapes and implications for pre-Silurian and Martian fluvial deposits. J. Geophys. Res. Earth Surf. 124, 2757–2777 (2019). [Google Scholar]
- 62.Yu X., et al. , Direct measurement of interparticle forces of Titan aerosol analogs (“Tholin”) using atomic force microscopy. J. Geophys. Res. Planets 122, 2610–2622 (2017). [Google Scholar]
- 63.Daudon C., et al. , A new digital terrain model of the Huygens landing site on Saturn’s largest moon, Titan. Earth Space Sci. 7, e2020EA001127 (2020). [Google Scholar]
- 64.Wohl E., David G. C. L., Consistency of scaling relations among bedrock and alluvial channels. J. Geophys. Res. 113, F04013 (2008). [Google Scholar]
- 65.Wye L. C., Radar Scattering from Titan and Saturn’s Icy Satellites using the Cassini Spacecraft (Stanford University, Faculty of Engineering, 2011). [Google Scholar]
- 66.Latrubesse E. M., et al. , The Ayeyarwady River (Myanmar): Washload transport and its global role among rivers in the Anthropocene. PLoS One 16, e0251156 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Zeichner S. S., et al. , Early plant organics increased global terrestrial mud deposition through enhanced flocculation. Science 371, 526–529 (2021). [DOI] [PubMed] [Google Scholar]
- 68.Battalio J. M., Lora J. M., Rafkin S., Soto A., The interaction of deep convection with the general circulation in Titan’s atmosphere. Part 2: Impacts on the climate. Icarus 373, 114623 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Faulk S. P., et al. , Titan’s climate patterns and surface methane distribution due to the coupling of land hydrology and atmosphere. Nat. Astronomy 4, 390–398 (2020). [Google Scholar]
- 70.Battalio J. M., Lora J. M., Global impacts from high-latitude storms on Titan. Geophys. Res. Lett. 48, e2021GL094244 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Mitchell J. L., Lora J. M., The climate of Titan. Annu. Rev. Earth Planet. Sci. 44, 353–380 (2016). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Dataset S01 (XLSX)
Data Availability Statement
All study data are included in the article and/or SI Appendix.