Abstract
Background:
High dose rate (HDR) brachytherapy is commonly used to treat prostate cancer. Existing HDR planning systems solve the dwell time problem for predetermined catheters and a single energy source.
Purpose:
Additional degrees of freedom can be obtained by relaxing the catheters’ pre-designation and introducing more source types, and may have a dosimetric benefit, particularly in improving conformality to spare the urethra. This study presents a novel analytical approach to solving the corresponding HDR planning problem.
Methods:
The catheter and dual-energy source selection problem was formulated as a constrained optimization problem with a non-convex group sparsity regularization. The optimization problem was solved using the fast-iterative shrinkage-thresholding algorithm (FISTA). Two isotopes were considered. The dose rates for the HDR 4140 Ytterbium (Yb-169) source and the Elekta Iridium (Ir-192) HDR Flexisource were modeled according to the TG-43U1 formalism and benchmarked accordingly. 22 retrospective HDR prostate brachytherapy patients treated with Ir-192 were considered. An Ir-192 only (IRO), Yb-169 only (YBO), and dual-source (DS) plan with optimized catheter location was created for each patient with catheters, where is the number of catheters used in the clinically delivered plans. The DS plans jointly optimized Yb-169 and Ir-192 dwell times. All plans and the clinical plans were normalized to deliver a 15 Gy prescription (Rx) dose to 95% of the clinical treatment volume (CTV) and evaluated for the CTV D90%, V150%, and V200%, urethra D0.1cc and D1cc, bladder V75%, and rectum V75%. Dose-volume histograms (DVHs) were generated for each structure.
Results:
The DS plans ubiquitously selected Ir-192 as the only treatment source. IRO outperformed YBO in organ at risk (OARs) OAR sparing, reducing the urethra D0.1cc and D1cc by 0.98% () and 1.09% () of the Rx dose, respectively, and reducing the bladder and rectum V75% by 0.09 () and 0.13 cubic centimeters (cc) (), respectively. The YBO plans delivered a more homogenous dose to the CTV, with a smaller V150% and V200% by 3.20 () and 1.91 cc (), respectively, and a lower CTV D90% by 0.49% () of the prescription dose. The IRO plans reduce the urethral D1cc by 2.82% () of the Rx dose compared to the clinical plans, at the cost of increased bladder and rectal V75% by 0.57 () and 0.21 cc (), respectively, and increased CTV V150% by a mean of 1.46 cc () and CTV D90% by an average of 1.40% of the Rx dose (). While these differences are statistically significant, the clinical differences between the plans are minimal.
Conclusions:
The proposed analytical HDR planning algorithm integrates catheter and isotope selection with dwell time optimization for varying clinical goals, including urethra sparing. The planning method can guide HDR implants and identify promising isotopes for specific HDR clinical goals, such as target conformality or OAR sparing.
1. Introduction
Prostate cancer is a common malignancy in men, with an estimated 1 in 9 American men being diagnosed during their lifetimes1. The prognosis is generally good, with a 98% 5-year survival rate for all stages combined1. The population of prostate cancer survivors in the United States is estimated to be over 3.3 million people and will continue to grow, highlighting the importance of maintaining effective treatment while minimizing side effects and prioritizing long-term quality of life2,3.
There are a wide variety of treatments available, ranging from active surveillance to surgical resection, chemotherapies, and radiotherapies4. The exact course of treatment depends on the disease stage, as well as patient preference4. High dose rate (HDR) brachytherapy is a widely used and effective radiation modality for managing prostate cancer. HDR brachytherapy can be used as a monotherapy or boost treatment in conjunction with external beam radiotherapy (EBRT). While more invasive than EBRT, brachytherapy allows for increased localized dose escalation with a lower risk of toxicity to nearby organs at risk (OARs)5,6. However, there is also evidence that HDR brachytherapy could increase the risk of genitourinary complications, such as urethral stricture, obstruction, and sexual dysfunction7. Urethral stricture is the narrowing of the urethral passage due to scar tissue build-up, causing discomfort and difficulty urinating8. Urethral stricture and other genitourinary toxicities have been shown to correlate with radiation dose to the urethra delivered during brachytherapy, so urethral sparing should be a key objective of dose planning9–11.
Ir-192 and Co-60 are the most prevalent sources for HDR prostate brachytherapy12. Brachytherapy sources are chosen based on several characteristics, including average photon energy, specific activity, and half-life. Yb-169 has also been proposed as an alternative to Ir-19213–16. Yb-169 offers lower energy than Ir-192, at 93 keV on average, as opposed to 380 keV. The lower energy decay products have been suggested to increase the potential for clinical target volume (CTV) homogeneity15,17. Plan optimization studies with hypothetical Yb-169 sources and Ir-192 sources reported that Yb-169 plans could achieve comparable CTV coverage while lowering the dose to OARs and the urethra in particular17,18.
To fully leverage the potential of the Yb-169, catheter location must also be considered. Brachytherapy dosimetry is heavily dependent on the location of the source due to the high local dose rate and rapid fall-off. Typically, catheters are placed using a template and transrectal ultrasound probe, the patient is imaged and catheter positions are reconstructed, and then dwell time optimization is performed19. Dwell time optimization methods in clinical practice and in literature are varied, most prominently including simulated annealing20 and hybrid inverse planning21. These methods rely on anatomical contours and precise catheter locations and have largely replaced slow and user dependent methods such as graphical optimization. Initial catheter placement is often done based on physician and institutional experience, though computational optimization methods are available. Hybrid inverse planning optimization (HIPO), for example, is a popular option that uses stochastic simulated annealing to optimize catheter locations followed by a deterministic dose volume histogram-based optimization of dwell times21. Other heuristics and linear programming-based models for catheter selection have also been presented and shown to improve dosimetry22–25. In 2021, Wang et al. proposed a fast-iterative shrinkage thresholding algorithm (FISTA) with a group sparsity term and adaptive heuristic group sparsity weighting to perform simultaneous dwell time optimization and catheter selection26. They concluded that this was an effective method for catheter selection and improved OAR sparing in the final plans over manual catheter placement26. They observed that a constant weight with an L2,1 norm was ineffective in reducing the number of channels for selection purposes and resorted to a heuristic adaptive weighting based on estimates from previous iterations. While they may work in certain practical cases, such heuristics risk a lack of convergence and general applicability. Here, we propose to use FISTA with a different group sparsity term and systematically updated catheter weights to create a fully analytical method for catheter selection. FISTA scales well with large problems, making it an excellent choice for solving this complex planning problem in linear time.
We hypothesize that by jointly optimizing the catheter locations and the dwell times for both Yb-169 and Ir-192 in a single treatment plan, we can leverage the potential benefits of dual source treatment and generate new insights into source behavior. This study presents a novel analytical inverse planning framework with integrated automated catheter selection and joint dual-energy dwell time optimization to improve urethral sparing.
2. Methods and Materials
2.1. Brachytherapy Sources
We computed the dose rate for the Ir-192 and Yb-169 brachytherapy sources according to the TG-43 report and update,
| (1) |
where is the air kerma strength, is the dose rate constant, is the geometry function, is the radial dose function, and is the anisotropy function27. and are reference points for dosimetry measurements. We used tabulated Monte Carlo generated TG-43 parameters for the HDR 4140 Yb-169 source and the Elekta Ir-192 HDR Flexisource from the CLRP TG-43 Parameter Database28. A line source distribution was assumed for the geometry function. Finally, each source was set to have an activity of 10 Ci. Interpolation and extrapolation from the tabulated data followed the updated TG-43 guidelines27. The dose rate calculation for each source was verified against Lymperopoulou et al.’s 2005 Monte Carlo calculations and found to agree well, with differences being attributed to different source models17. The calculated dose rate distributions for the two sources were also compared directly.
2.2. Problem Formulation and Optimization
The integrated catheter selection and dose optimization is mathematically formulated as
| (2) |
subject to where the variables and parameters are defined in Table 1.
Table 1:
Problem Formulation Symbol Definitions
| Symbol(s) | Definition |
|---|---|
| CTV underdosing penalty weight | |
| CTV overdosing penalty weight | |
| Overdosing penalty weight for OAR | |
| CTV and OAR dose loading matrices | |
| CTV prescription dose | |
| Dose limit for OAR | |
| Vectorized dwell times | |
| Vectorized dwell times for catheter | |
| Group sparsity weight for catheter | |
| Group sparsity norm | |
| Set of candidate catheters | |
| Set of CTV and OARs |
Optimization problem symbols and definitions.
The first and second terms in the objective function penalize cumulative underdosing and overdosing to the CTV with respect to the prescription dose , respectively. The CTV overdosing weight can be set to zero to prevent penalizing dose escalation to the CTV, though in practice, we use a small, nonzero value that does not significantly impact the optimization results. The third term penalizes cumulative OAR overdosing above some threshold . This can be set to 0 to penalize all OAR doses, but by setting for certain OARs, differently shaped dose distributions can be produced29. The final term is a group sparsity penalty that encourages all the dwell times for an individual catheter to be zero, thus eliminating candidate catheters from the plan. The group sparsity weights are chosen to counteract the bias towards short catheters with fewer dwell positions, as will be larger for longer catheters. The weights are assigned as follows
| (3) |
where is the number of dwell positions in catheter is the dose loading matrix for the CTV from catheter , and is a constant parameter that can be used to tune the speed of catheter selection29. is iteratively updated during optimization to achieve the necessary sparsity across all cases without prior knowledge of the optimization results.
Problem (2) was solved using the Fast Iterative Shrinkage-Thresholding Algorithm (FISTA), an accelerated proximal gradient optimization method for linear problems with a line search30. This method was chosen for its computational efficiency and practical implementation for solving large non-differentiable optimization problems. FISTA only requires that the optimization problem can be separated into the form , where is convex and differentiable, and has a known proximal operator. To solve problem (2), we separate out
| (4) |
| (5) |
Here, the group sparsity exponent is chosen to be would make the entire problem convex, which is numerically simpler to optimize but inefficient to converge to a desirable group-sparse solution, as reported in Wang et al.26. Rather than a heuristic modification, we have observed in previous works29,31 that yields good convergence, despite a nonconvex problem formulation, using FISTA and efficient elimination of candidate catheters while still having a computable proximal operator29,31.
The optimization is performed in two distinct steps. Initially, all dwell times are set to 1 second. This was chosen so that in the initial solution, all candidate catheters are considered selected. Next, problem (2) is solved using FISTA until the number of selected catheters is iteratively reduced to by the group sparsity term, and the dwell times for all other candidate catheters have been set to zero. Different from applying a sparsity constraint on all dwell positions, which would reduce the number of active dwell positions but leave a large number of catheters with sparse dwell positions, the group sparsity term resulted in catheters with zero total dwell time that can be eliminated, and catheters with dense dwell positions that are kept.
The group sparsity weights are increased by a constant factor of 1.2 every 500 iterations until the stopping criteria of or fewer catheters with nonzero total dwell time has been met. 500 iterations was chosen to give the problem ample time to converge between each change in weighting. This is the catheter selection portion of the optimization which guarantees that no more than catheters are used in each optimal plan. This approach of iteratively increasing the group sparsity weight until the necessary number of catheters have been removed prevents the need for patient-specific parameter tuning.
Then, the optimization problem is reduced to consider only the selected catheters, and the group sparsity term is turned off, reducing the objective to (4), which is once again minimized by FISTA. This fluence map optimization step smooths the dose distribution and prevents the catheter selection term from exerting too much influence on the final dose plan.
2.3. Patient Set-Up and Catheter Generation
We performed planning on 22 retrospective patients who had received high-dose-rate brachytherapy for prostate cancer using an Ir-192 source. The original HDR plans were created on Oncentra (Elekta Brachytherapy Solutions, Veenendaal, The Netherlands) using inverse planning simulated annealing (IPSA) optimization. For each patient, additional catheter locations were added parallel to the clinical catheter locations with respect to the axial imaging plane, creating a non-uniform distribution of candidate catheter locations around the prostate. For each clinical catheter, a new candidate was added anterior, posterior, left, and right. The clinical catheters were also included in the candidate set. This approach was chosen to maintain the angle of catheter insertion following the patient’s anatomy to approximate clinically feasible placements. A candidate catheter was removed if it intersected the urethral contour, leaving 60–100 candidate catheters per patient. DICOM files with the contoured CT scans, clinical RT plan, and RT dose information were loaded for each patient using CERR, a MATLAB interface for handling DICOM files32. Clinical contours for the CTV, urethra, bladder, rectum, and body were used to define each structure. Then, optimization sampling points were generated for each patient to be uniformly spread out within the prostate and within each OAR, and the dose loading matrices were calculated according to equation (1).
Three plans with catheter selection were created for each patient – an Ir-192 only (IRO) plan, a Yb-169 only (YBO) plan, and a dual-source (DS) plan. For the dual-source plan, both sources can be loaded into each catheter. Each plan used the same set of candidate catheters and the two-step catheter selection and dose-smoothing optimization process. In addition, the clinical plan provided in the DICOM files was evaluated and compared to the optimized plans. Each optimized plan was optimized to have or fewer catheters, where is the number of catheters used clinically for that patient, which ranged from 17–21 by the patient.
All treatment plans were normalized to deliver a prescription dose of 15 Gy in a single fraction to 95% of the CTV. Each plan was evaluated for the CTV D90%, V150% and V200%, urethral D0.1cc and D1cc, rectal V75%, and bladder V75%. The rectum and bladder metrics were chosen based on the recommended dose constraints posed in the prospective prostate brachytherapy Radiation Therapy Oncology Group (RTOG) 0321, which recommends that V75% < 1 cc for both structures33. The urethra dose metrics were chosen to identify hot spots in the urethral dose, defined here as the maximally irradiated 0.1cc of the urethra, and the dose to a larger portion of the organ. Here, V% refers to the volume of the structure receiving % of the prescription dose, D is the minimum dose to the maximally irradiated % of the structure, and Dcc is the minimum dose to the maximally irradiated cubic centimeters of the structure.
The IRO plans were compared individually to the DS, YBO, and clinical plans across each metric. Paired t-tests were used for each comparison. A value of was used to determine the statistical significance of the bladder and rectum metrics. For the CTV and urethra metrics, values of and were used, respectively, to account for the multiple comparisons within a single structure. While a similar dosimetry study does not adjust for multiple comparisons18, Bonferroni correction was selected here due to the small number of comparisons to account for intra-organ metric dependence34.
3. Results
3.1. Dose Rate Comparison
Figure 1 shows a comparison of the radial dose functions, for the Ir-192 and Yb-169 sources. The radial dose function accounts for the different attenuation properties of photons in tissue. Yb-169 has a more prominent peak located at 5 cm followed by a steep fall off, due to the lower energy decay products. However, when the full dose rate is calculated, the geometry function dominates and this effect is no longer significant, as seen in the dose contour lines in Figure 2.
Figure 1:
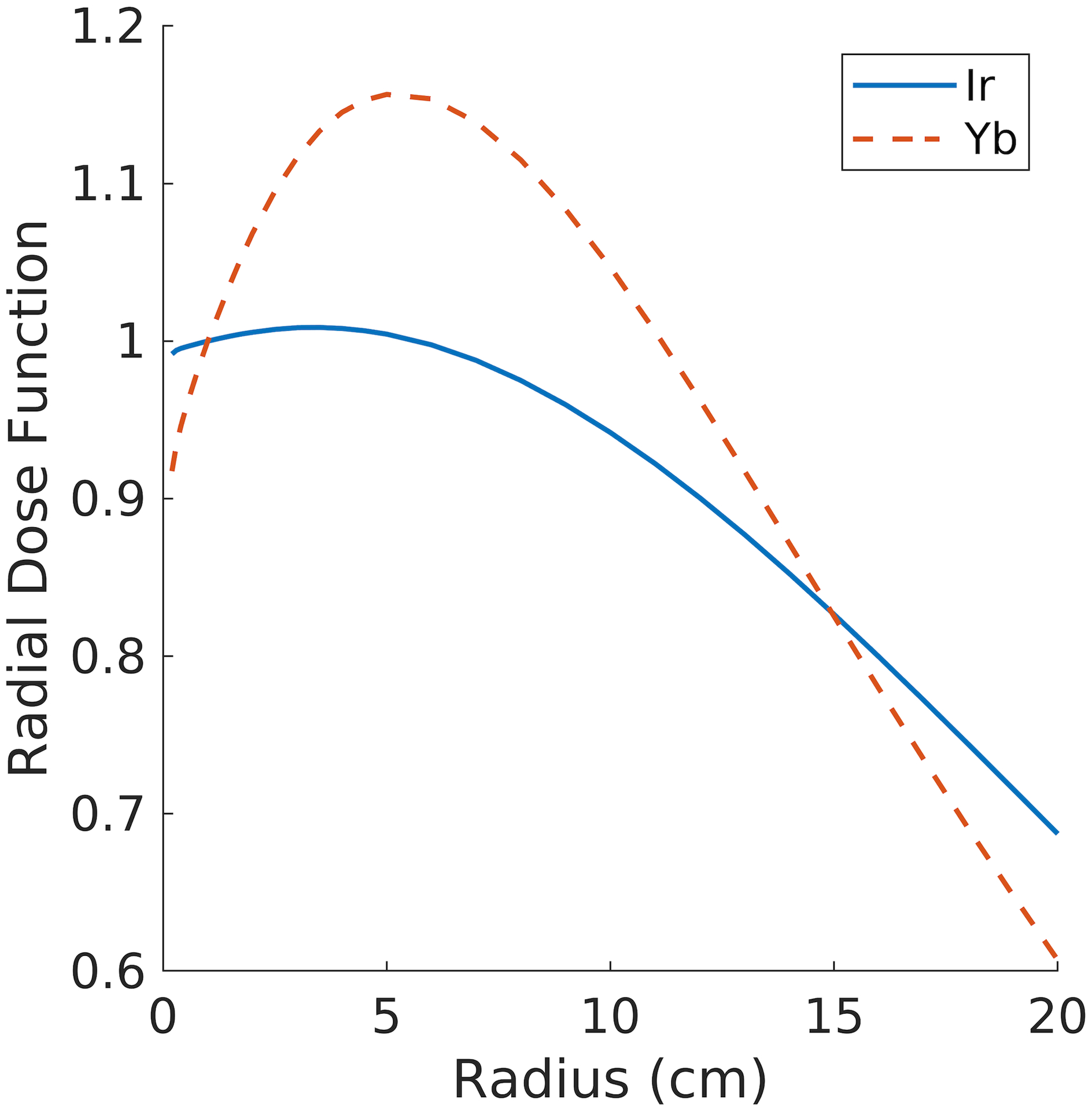
Radial dose function, , for the Yb-169 source (dashed) and the Ir-192 source (solid).
Figure 2:
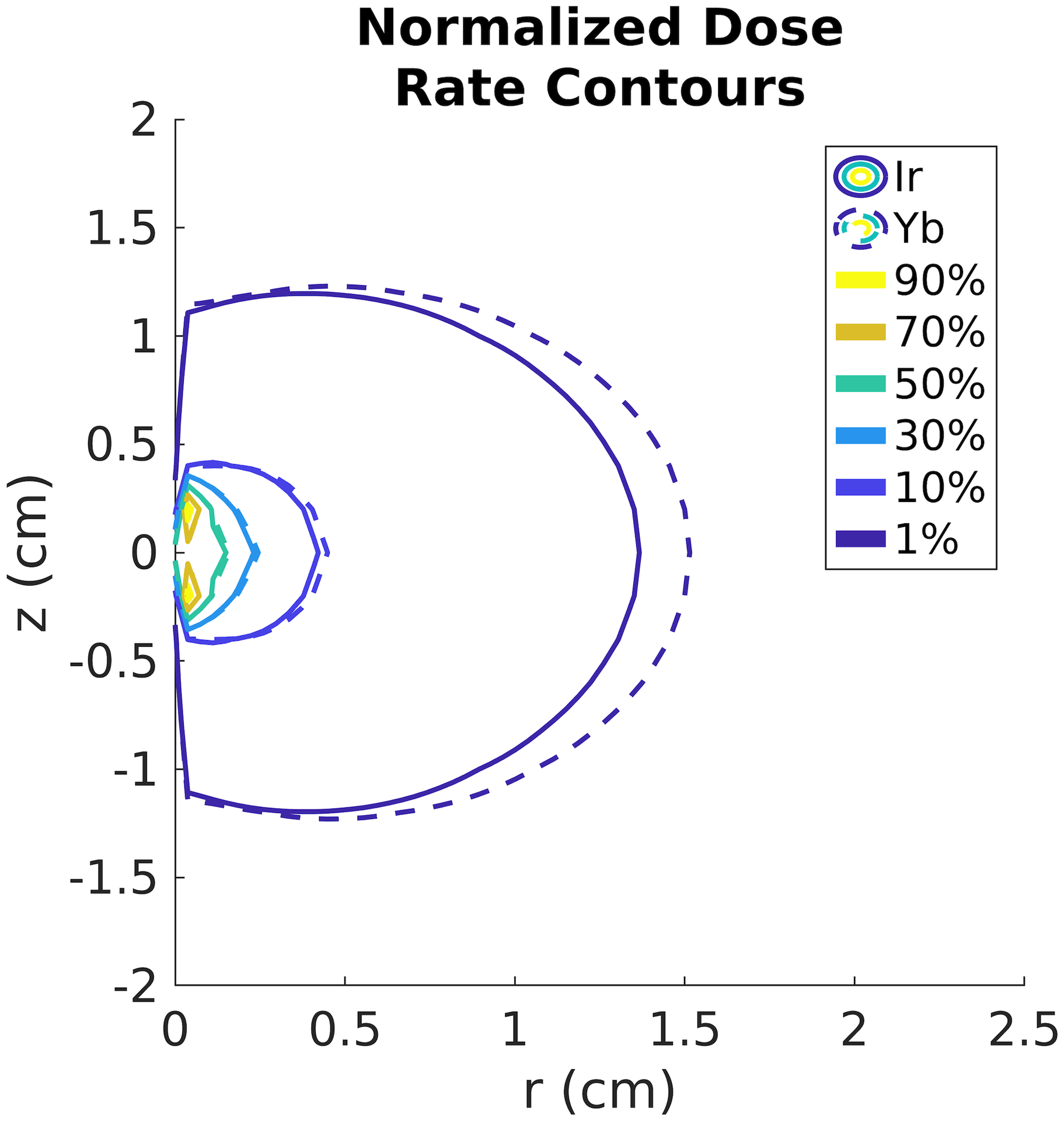
Normalized dose rate contour lines for the Yb-169 source (dashed) and the Ir-192 source (solid).
3.2. Catheter location selection
Figure 3 shows the candidate, and clinical catheter locations and optimized catheters for the IRO, YBO, and DS plans for a typical example patient overlaid on the prostate and urethra contours. The IRO-selected catheters are located closer to the urethra, while the YBO catheters are more peripherally loaded. The DS plan catheters are clustered around the urethra, like the IRO plans. This is because all 22 DS plans selected Ir-192 as the only active source. In this case, the selected catheters are the same for the DS and IRO optimizations. However, in some other cases, the catheter selection between the DS and IRO plans differs slightly due to the catheter weights, which account for the possible inclusion of Yb-169 in the DS plan.
Figure 3:
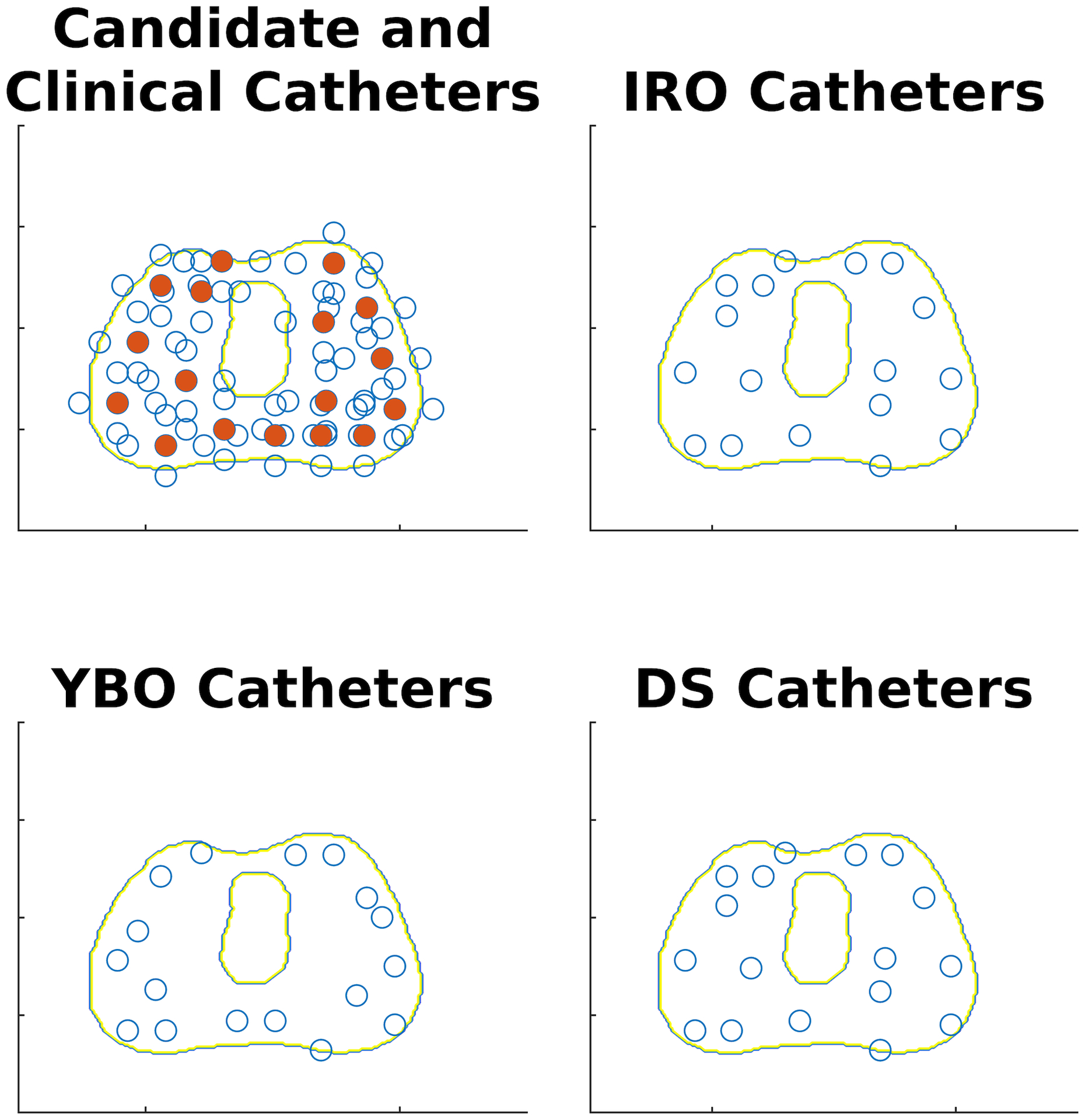
Example catheter selection results overlaid on collapsed prostate and urethra contours. The candidate catheter locations (empty circles) are shown in the upper left, with the clinical catheter locations shown as solid circles. The optimized catheter distributions for the DS, IRO, and YBO plans are shown in the lower right, upper right, and lower left, respectively.
3.3. Dual energy vs. single source comparison
The optimization times for the IRO, YBO, and DS plans were between 1.4 and 9.5 minutes, 0.4 and 5.1 minutes, and 2.8 and 17.9 minutes, respectively. The average objective function values for the final IRO, YBO, and DS plans were 1.90*105 ± 6.18*104, 2.03*105 ± 6.56*104, and 1.90*105 ± 6.17*104. Table 2 compares key CTV and OAR metrics for the IRO, YBO, and DS plans. The DS metrics did not significantly differ from any of the IRO metrics. This is because while the DS plans could utilize both sources, in all 22 plans, the Yb-169 dwell times were optimized to 0. Figure 4 exemplifies a 2D dose colormap for the clinical, DS, YBO, and IRO plans. Further, Figure 5 shows each plan type’s average dose volume histograms. There are no appreciable differences between the IRO plan DVHs and the DS plan DVHs or dose colormaps. There are only minor differences in the dwell time distributions for the IRO and DS plans (Figure 6), and the mean active dwell times were 11.92 ± 16.02 seconds and 11.92 ± 16.02 seconds, respectively with total mean treatment times of 27.63 ± 6.41 minutes and 27.69 ± 6.53 minutes, respectively.
Table 2:
Dosimetry Results
| CTV | Urethra | Bladder | Rectum | ||||
| D90% (% Rx) |
V150% (cc) | V200% (cc) | D0.1cc (% Rx) | D1cc (% Rx) | V75% (cc) | V75% (cc) | |
| IRO | 105.11 ± 0.20 | 21.11 ± 1.30 | 7.53 ± 0.50 | 102.11 ± 0.34 | 92.62 ± 2.05 | 1.14 ± 0.24 | 0.27 ± 0.10 |
| DS | 105.08 ± 0.20 p = 0.33 |
20.95 ± 1.28 * p = 0.045 |
7.50 ± 0.51 p = 0.36 |
102.02 ± 0.35 p = 0.14 |
92.53 ± 2.05 p = 0.056 |
1.10 ± 0.24 p = 0.076 |
0.28 ± 0.10 p = 0.24 |
| YBO | 104.62 ± 0.16 * p = 1.42*10-4 |
17.19 ± 1.03 * p = 4.67*10-10 |
5.62 ± 0.36 * p = 5.79*10-10 |
103.09 ± 0.36 * p = 2.22*10-9 |
93.71 ± 2.03 * p = 1.22*10-10 |
1.23 ± 0.25* p = 0.0048 |
0.40 ± 0.14* p = 0.033 |
| Clinical | 103.71± 0.18 * p = 8.79*10-8 |
19.65 ± 1.37 * p = 0.0094 |
8.07 ± 0.60 p = 0.11 |
103.43 ± 0.67 p = 0.051 |
95.44 ± 1.83 * p = 1.36*10-4 |
0.57 ± 0.10 * p = 0.0022 |
0.06 ± 0.03 * p = 0.019 |
Mean CTV and OAR metrics for the DS, IRO, YBO, and clinical plans with standard deviations. Results where the dual source, Yb-169 only, or clinical metrics differ significantly from the Ir-192 only plans are marked with a *.
Figure 4:
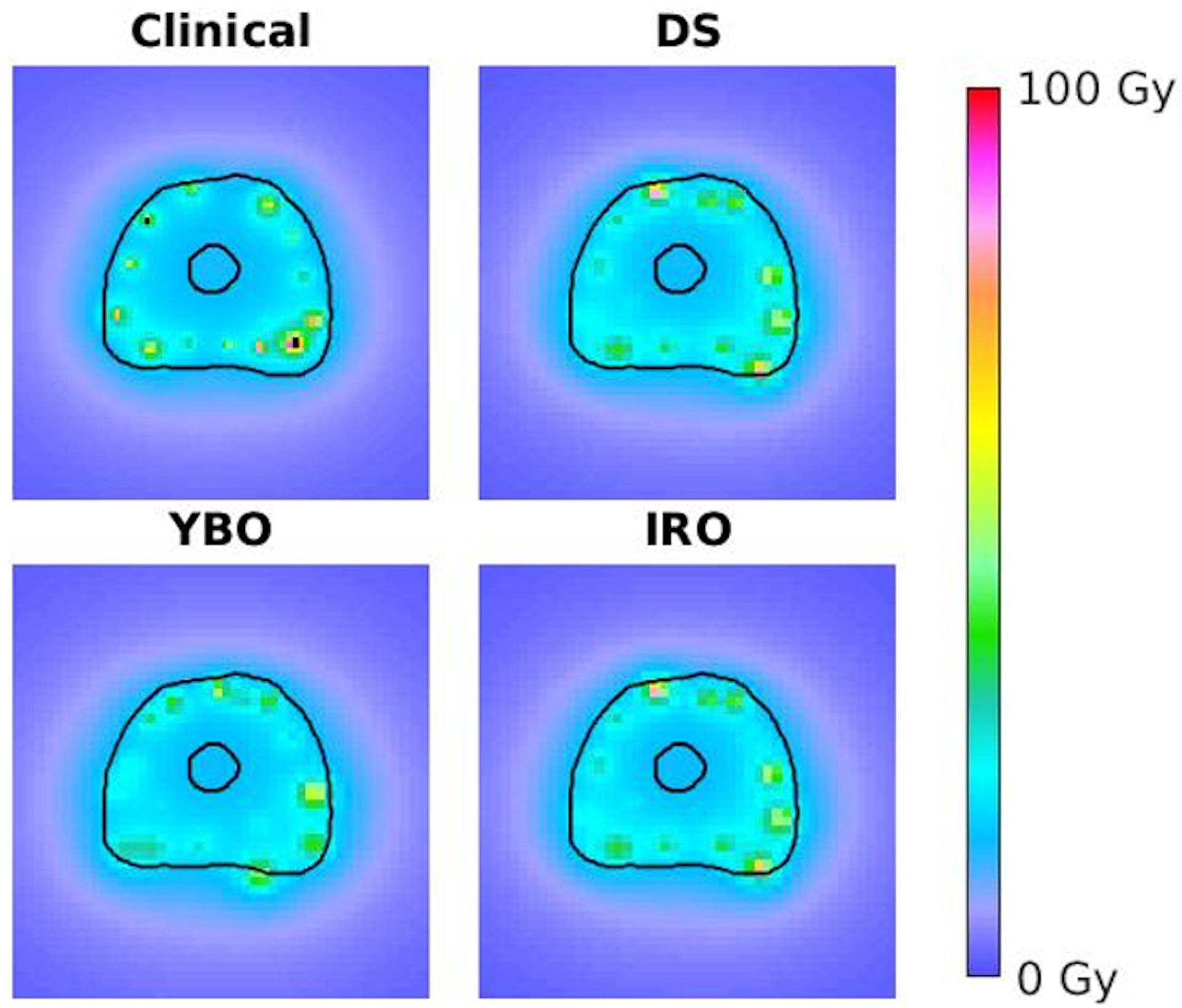
Axial dose distribution for an example patient for the clinical (upper left), DS (upper right), YBO (lower left), and IRO (lower right) plans.
Figure 5:
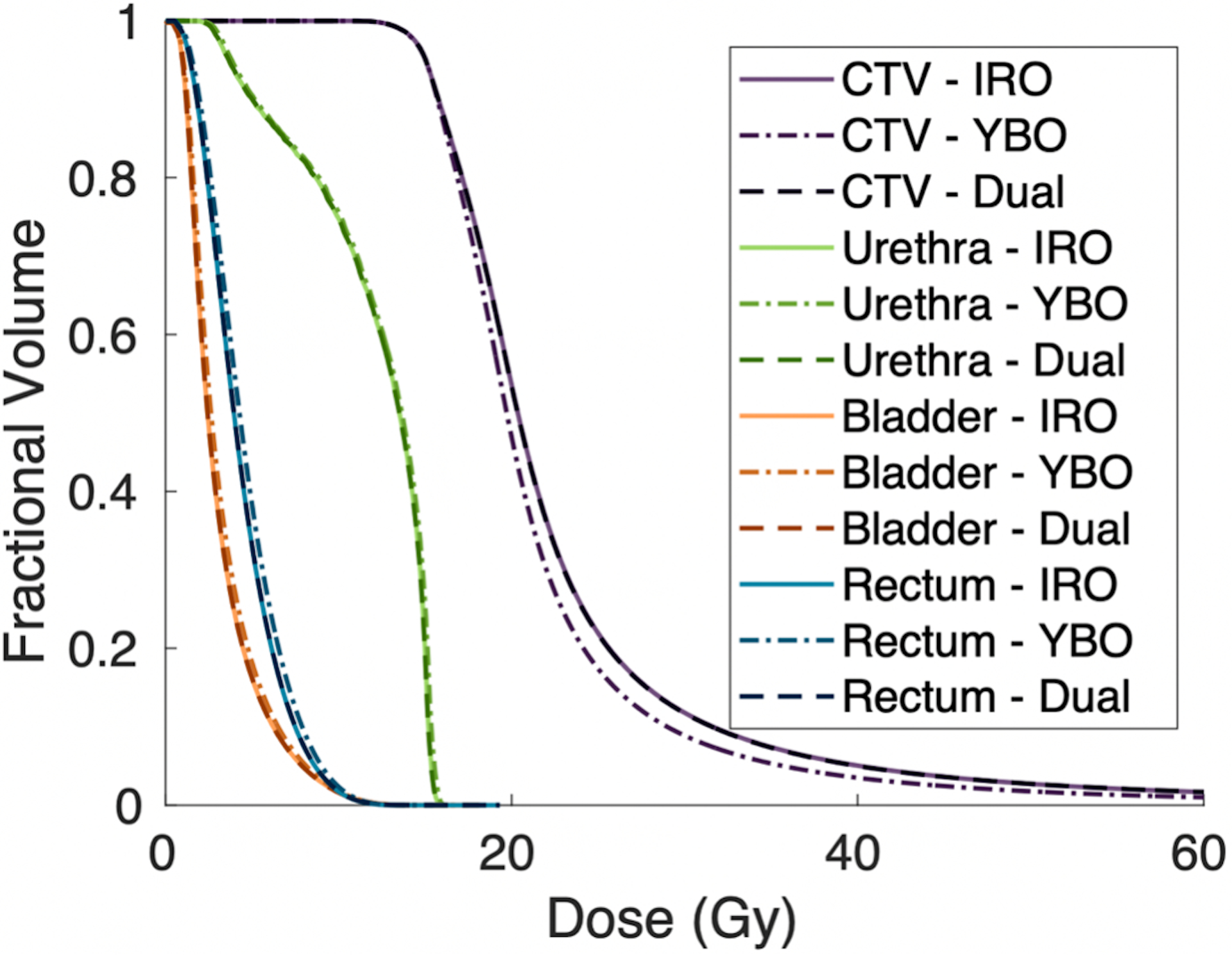
Population averaged CTV and OAR dose volume histograms for the optimized DS, IRO, and YBO plans. All plans are normalized to deliver the prescription dose to 95% of the CTV.
Figure 6:
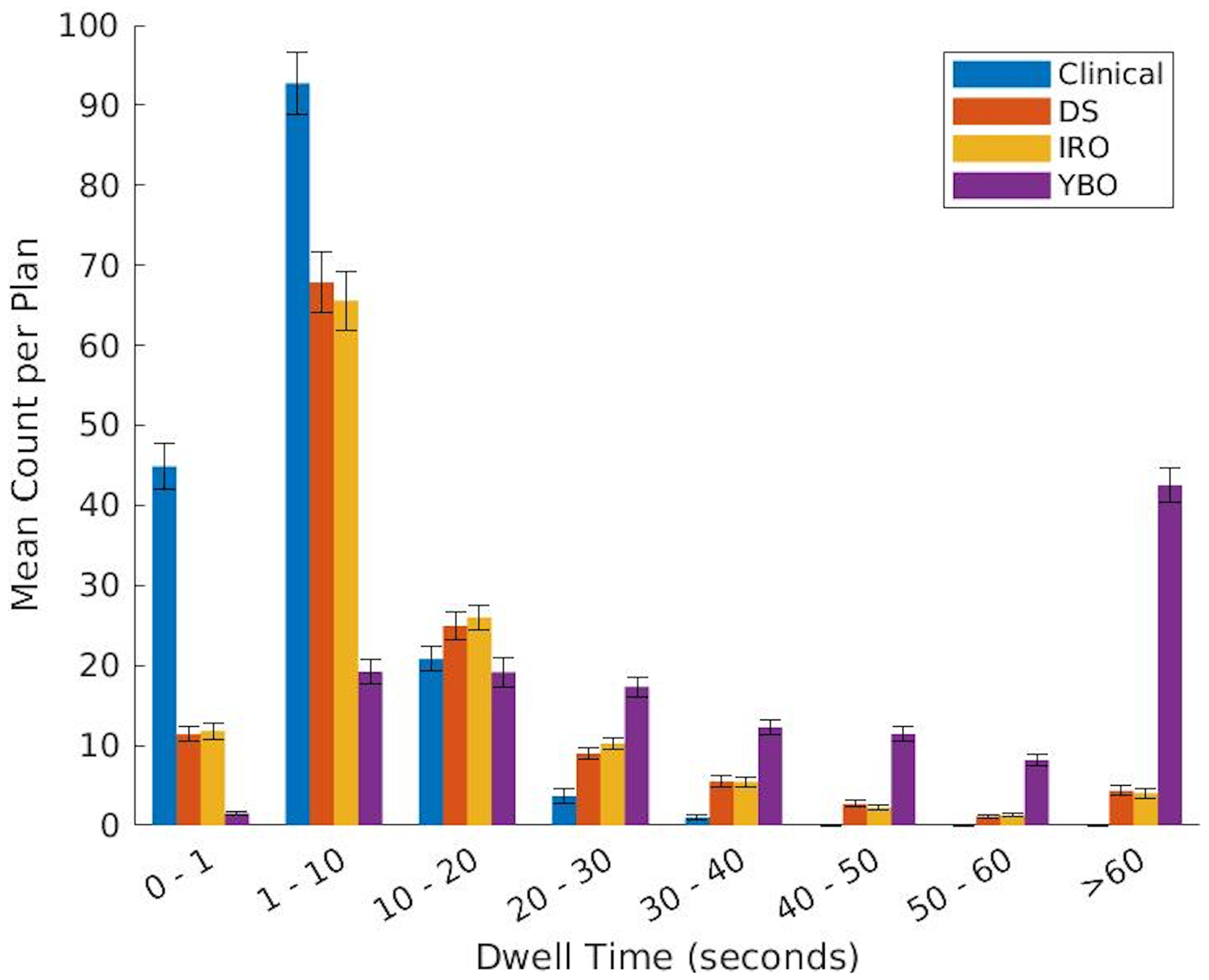
Population averaged dwell time histogram with standard error bars for the clinical, DS, IRO, and YBO plans.
The YBO metrics, on the other hand, all significantly differed from the IRO plans. The dose colormaps (Figure 4) illustrate this difference in dosimetry. Quantitatively, the urethra D0.1cc and D1cc for the Yb-169 plans were, on average, 0.98% and 1.09% of the prescription dose greater, respectively. The bladder and rectum V75% were also larger for the YBO by 0.09 and 0.13 cubic centimeters, respectively. The CTV V150% and V200% were smaller in the YBO plans than the IRO, and the D90% was a smaller percentage of the prescription dose. The dose volume histograms (Figure 5) illustrate these differences, with lower overdosing to the CTV for the Yb-169-only plans but slightly increased doses to all OARs. Additionally, the YBO dwell time distribution is shifted significantly towards longer dwell times, as seen in Figure 6, and the mean active dwell time was 56.79 ± 71.86 seconds with a mean total treatment time of 138.36 ± 31.49 minutes.
3.4. Ir-192 only optimized plan vs. clinical plan comparison
Table 2 also compares the IRO plan and the clinical plan metrics. Significantly, the dose to 90% of the prostate was 1.40% greater for the IRO plans. Additionally, the volume of the prostate receiving 150% of the prescription dose was an average of 1.46 cubic centimeters larger for the Ir-192 optimized plans than the clinical plans. The CTV V200% and urethra D0.1cc did not statistically significantly differ between the two plans. However, the D1cc for the urethra was significantly different, with the clinical plans averaging 95.44% of the prescription dose and the Ir-192 optimized plans averaging 92.62% of the prescription dose. Also significantly, the average bladder and rectum V75% were 1.14 and 0.27 cubic centimeters, respectively, in the Ir-192 only plans, but only 0.57 and 0.06 cubic centimeters, respectively, in the clinical plans. The average dose volume histograms, shown in Figure 7, show that the average urethral dose is lower for the IRO plans than for the clinical plans. However, the clinical plans outperform the optimized plans in bladder and rectum sparing. For the CTV, the clinical plans deliver 15–25 Gy to a smaller structure volume but deliver greater than 25 Gy to a larger structure. The clinical dwell time distribution is shifted towards shorter dwell times, with a mean dwell time of 5.17 ± 5.85 seconds.
Figure 7:
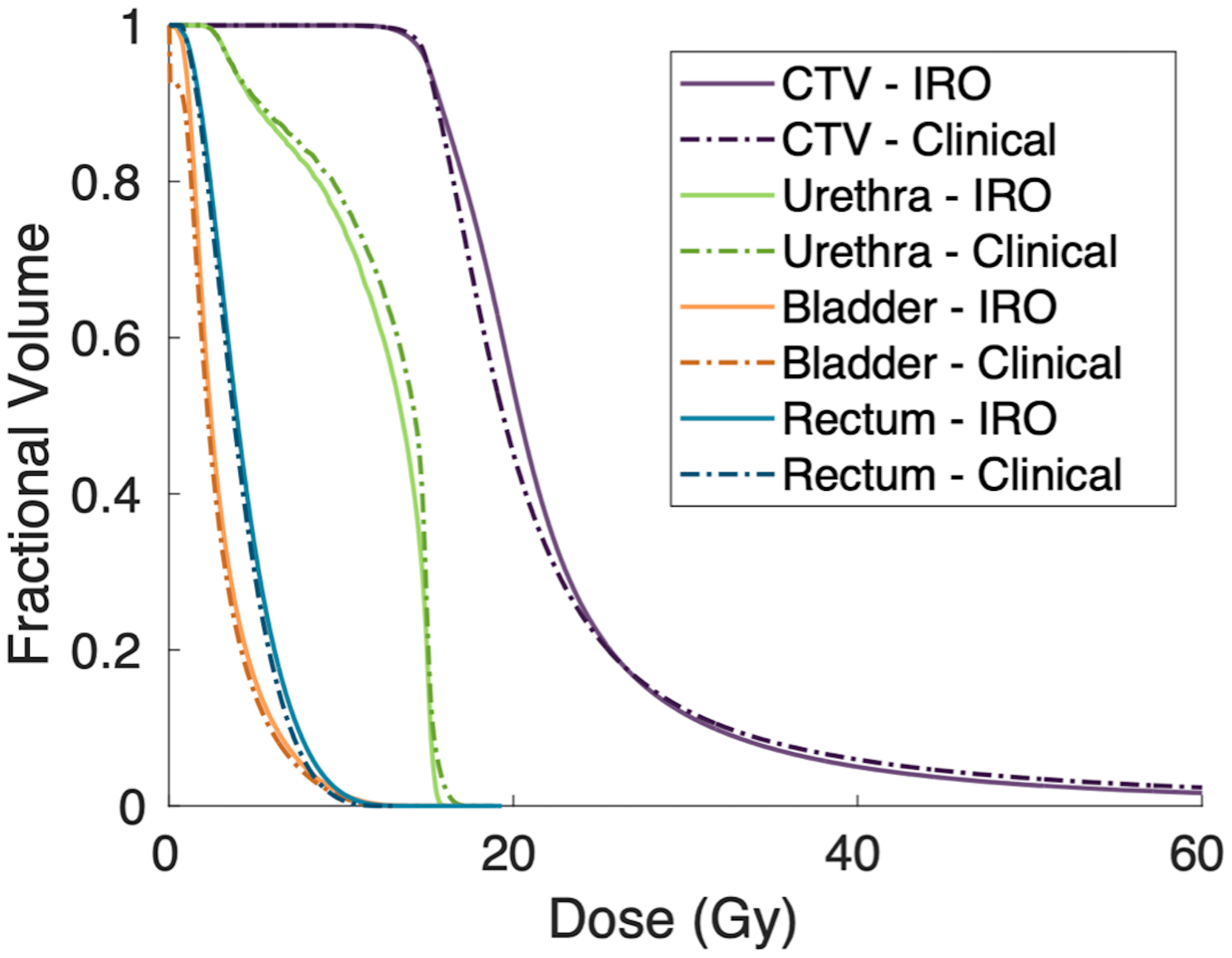
Population averaged CTV and OAR dose volume histograms for the optimized Ir-192 only and clinically delivered plans. All plans are normalized to deliver the prescription dose to 95% of the CTV.
4. Discussion
We have developed an analytical algorithm for high-dose-rate prostate brachytherapy treatment planning with catheter selection and multi-source dwell time optimization. This novel approach affords catheter placement optimization and allows for comparison between source models for flexible clinical goals, including urethral sparing. Additionally, the analytical methods increase plan reproducibility, as the same input parameters always yield the same results. Further, the IRO optimization time is comparable to clinical Ir-192 planning times using simulated annealing. The present work is novel in several aspects. First, a non-convex group sparsity term was used for channel selection. The typical convex L2,1 norm used in external beam orientation optimization problem33 fails to converge to desirable sparsity. In comparison to the heuristically modified L2,1 norm26, our approach rids the dependence on heuristics and improves algorithm generality. While global convergence is not guaranteed, we have observed in previous works that the non-convex norm of allows for good convergence using FISTA and efficient elimination of candidate catheters, while still having an analytical proximal operator29,31. This observation is also supported by the successful use of this non-convex group sparsity in a series of external beam optimization problems29,35–42 and image processing43. Further, in this study, a comparison with the clinical plans shows that the locally optimal solutions are dosimetrically desirable.
Besides the theoretical benefits, the study leads to several novel results regarding the utility of Yb-169 in HDR prostate brachytherapy and the optimal treatment catheter distribution based on source energy.
The differences in source dosimetry shown in Figure 1 and Figure 2 reveal the potential for more conformal dose plans around the OARs using Ir-192 over Yb-169. While the dose build-up from lower energy decay products from the Yb-169 is evident in the shape of the radial dose function, the overall dose rate is dominated by the rapid fall-off in photons further from the source, accounted for in the geometry function. Therefore, the dose rate for Ir-192 falls off faster, allowing for more conformal planning around the OARs. The importance of the geometry function in the final dose rate distribution also highlights that the location of seeds in relation to the patient’s anatomy is a major factor in the final plan dosimetry.
The optimal catheter positions for each plan type reflect the shape of these dose distributions. The optimized YBO catheters are more peripherally located to increase the distance between the dwell positions and urethra, while the optimized IRO catheters are more uniformly distributed throughout the prostate since the steep dose rate drop-off allows for more conformality close to the urethra.
The lower energy of the Yb-169 source also explains the long YBO dwell times of close to a minute on average when compared with the clinical, IRO, and DS dwell times, which averaged 5.17, 11.92, and 11.92 seconds, respectively, as well as the long overall treatment time. The IRO and DS dwell times are, on average, longer than the clinical dwell times due to the low penalty for CTV overdosing in this optimization. Further, the dwell time distributions for the optimized plans have higher variance than the clinical plan, as dwell time homogeneity was not considered in this study.
The dosimetry benefits of the Ir-192 are illustrated in practice by the plan optimization results. Despite having the option to use either Yb-169 or Ir-192, or both, all optimized DS plans chose Ir-192 only. Mathematically, this is reflected in lower final IRO and DS objective function values. Therefore, the DS catheter distribution shown in Figure 3 is identical to the IRO distribution. Additionally, the dose maps in Figure 4 are identical. The ubiquitous Ir-192 selection also accounts for the similar DVHs shown in Figure 5. The metrics also were not significantly different between the Ir-192 only and dual source plans. Thus, for our clinical goals of urethral sparing, we found that Ir-192 was unanimously superior to Yb-169. While this dual-source optimal solution is not guaranteed to be the global optimal solution for this problem, the universal Ir-192 selection for OAR sparing is supported by the differences in source dosimetry and more rapid Ir-192 dose fall off. There has been interest in leveraging the lower energy Yb-169 source for improved brachytherapy dosimetry44. Brachytherapy afterloaders accommodating dual sources were developed for this purpose. The clinical adoption of Yb-169 source has been slow due to the complexity and cost of maintaining the additional isotope, which has a short half-life of 32 days. The current study provides further evidence to suggest a minimal benefit-cost ratio to adopt isotropic Yb-169 for prostate radiotherapy. Therefore, research focus related to Yb-169 should be focused on directionally shielded sources for intensity-modulated brachytherapy45–47.
The plan differences are reflected by the dosimetry metrics. The CTV V150% and V200% were larger in the IRO plans, and the dose to 90% of the CTV was higher. Overall, this indicates that a larger volume of the CTV receives greater than the prescription dose in the IRO plans than in the YBO plans. Since all plans were normalized to deliver 15 Gy to 95% of the prostate, we observe that the CTV dose is more homogenous using Yb-169, consistent with previous reports17,18. This is supported by the dose maps in Figure 4, which show smaller high-dose regions for the YBO plan, and the DVHs in Figure 5, which show a sharper dose drop-off for the CTV in the Yb-169 optimization. The lower CTV V150% and V200% also indicate that Yb-169 is more effective at lowering high-dose regions within the target, however, CTV overdosing was given low significance in this study. Unlike previous studies, we report improved OAR sparing for all organs using the Ir-192 source over the Yb-169 sources17,18. The average OAR DVHs show superior OAR sparing, as do the OAR dose metrics in Table 2. However, it should be noted that while these differences are statistically significant, the clinical difference is not directly evaluated and may be minimal.
Further, the analytical planning algorithm statistically outperformed the clinical system using simulated annealing in improving urethral sparing. The IRO plans reduced the minimum dose to the maximally irradiated 1 cubic centimeter of the urethra by an average of 2.82% of the prescription dose. The overall urethral DVH (Figure 7) is shifted left for the IRO over the clinical plans, meaning the average dose to the urethra is lower. However, this comes at the cost of increased bladder V75% by an average of 0.57 cubic centimeters. Our average optimized bladder V75% falls just above the RTOG 0321 guideline of 1 cubic centimeter for all plan types, but bladder sparing was not a key objective of the optimization33. The average optimized rectum V75% was significantly higher for the optimized plans, but still fell within RTOG 0321 guidelines. Further, the DVHs (Figure 7) show a lower overall rectal and bladder dose in the clinical plans versus the IRO plans. The optimization weights for this study were tuned to prioritize urethral sparing but could be altered to penalize the dose to the bladder and rectum more heavily. Moreover, there was an increase in the CTV D90% and V150% in the IRO plan versus the clinical plan. Overdosing of the prostate was weakly penalized, which accounts for this change. However, there was no significant change in the V200%, and the CTV DVH shows that the IRO plans delivered Gy to a smaller volume of the structure.
Overall, our versatile planning method can optimize prostate HDR brachytherapy treatment plans for specific clinical goals while incorporating additional degrees of freedom, including channel locations and isotope energies.
5. Conclusion
In this paper, we have presented a novel analytical algorithm for HDR brachytherapy treatment planning with automated catheter selection and multi-energy optimization capabilities. We showed that treatment plans created using this framework could outperform the clinical plans in sparing the urethra while maintaining sufficient CTV coverage. Further, we found that Ir-192 is selected over Yb-169 as a more optimal treatment source for prostate planning with a goal of urethral sparing at the cost of higher doses to other OARs. This algorithm allows for repeatable dose optimization and is extendible by tuning the optimization parameters to prioritize other clinical goals, such as CTV homogeneity or bladder and rectal sparing.
Acknowledgments
This work was funded by NIH grants R01CA230278, R01CA255432, R01CA259008, and R44CA183390.
Footnotes
Conflicts of Interest
The authors have no relevant conflicts of interest to disclose.
References
- 1.Siegel RL, Miller KD, Jemal A. Cancer statistics, 2019. CA: A Cancer Journal for Clinicians. 2019;69(1):7–34. doi: 10.3322/caac.21551 [DOI] [PubMed] [Google Scholar]
- 2.Rasper AM, Terlecki RP. Prostate cancer survivorship: Implementation of survivorship care plans to meet the mandate and enhance urologic practice through collaborative care. Rev Urol. 2016;18(4):214–220. doi: 10.3909/riu0733 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Miller KD, Siegel RL, Lin CC, et al. Cancer treatment and survivorship statistics, 2016. CA: A Cancer Journal for Clinicians. 2016;66(4):271–289. doi: 10.3322/caac.21349 [DOI] [PubMed] [Google Scholar]
- 4.Litwin MS, Tan HJ. The Diagnosis and Treatment of Prostate Cancer: A Review. JAMA. 2017;317(24):2532–2542. doi: 10.1001/jama.2017.7248 [DOI] [PubMed] [Google Scholar]
- 5.Crook J, Marbán M, Batchelar D. HDR Prostate Brachytherapy. Seminars in Radiation Oncology. 2020;30(1):49–60. doi: 10.1016/j.semradonc.2019.08.003 [DOI] [PubMed] [Google Scholar]
- 6.Dutta SW, Alonso CE, Libby B, Showalter TN. Prostate cancer high dose-rate brachytherapy: review of evidence and current perspectives. null. 2018;15(1):71–79. doi: 10.1080/17434440.2018.1419058 [DOI] [PubMed] [Google Scholar]
- 7.Chen RC, Basak R, Meyer AM, et al. Association Between Choice of Radical Prostatectomy, External Beam Radiotherapy, Brachytherapy, or Active Surveillance and Patient-Reported Quality of Life Among Men With Localized Prostate Cancer. JAMA. 2017;317(11):1141–1150. doi: 10.1001/jama.2017.1652 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tritschler S, Roosen A, Füllhase C, Stief CG, Rübben H. Urethral stricture: etiology, investigation and treatments. Dtsch Arztebl Int. 2013;110(13):220–226. doi: 10.3238/arztebl.2013.0220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Merrick GS, Butler WM, Wallner KE, et al. Risk factors for the development of prostate brachytherapy related urethral strictures. J Urol. 2006;175(4):1376–1380; discussion 1381. doi: 10.1016/S0022-5347(05)00681-6 [DOI] [PubMed] [Google Scholar]
- 10.Moltzahn F, Dal Pra A, Furrer M, Thalmann G, Spahn M. Urethral strictures after radiation therapy for prostate cancer. Investig Clin Urol. 2016;57(5):309–315. doi: 10.4111/icu.2016.57.5.309 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hsu IC, Hunt D, Straube W, et al. Dosimetric analysis of radiation therapy oncology group 0321: the importance of urethral dose. Pract Radiat Oncol. 2014;4(1):27–34. doi: 10.1016/j.prro.2013.02.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mendez LC, Morton GC. High dose-rate brachytherapy in the treatment of prostate cancer. Transl Androl Urol. 2018;7(3):357–370. doi: 10.21037/tau.2017.12.08 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Reynoso FJ, Manohar N, Krishnan S, Cho SH. Design of an Yb-169 source optimized for gold nanoparticle-aided radiation therapy. Medical Physics. 2014;41(10):101709. doi: 10.1118/1.4895991 [DOI] [PubMed] [Google Scholar]
- 14.Perera H, Williamson JF, Li Z, Mishra V, Meigooni AS. Dosimetric characteristics, air-kerma strength calibration and verification of Monte Carlo simulation for a new Ytterbium-169 brachytherapy source. Int J Radiat Oncol Biol Phys. 1994;28(4):953–970. doi: 10.1016/0360-3016(94)90116-3 [DOI] [PubMed] [Google Scholar]
- 15.Loft SM, Coles IP, Dale RG. The potential of ytterbium 169 in brachytherapy: a brief physical and radiobiological assessment. Br J Radiol. 1992;65(771):252–257. doi: 10.1259/0007-1285-65-771-252 [DOI] [PubMed] [Google Scholar]
- 16.Mason DL, Battista JJ, Barnett RB, Porter AT. Ytterbium-169: calculated physical properties of a new radiation source for brachytherapy. Med Phys. 1992;19(3):695–703. doi: 10.1118/1.596813 [DOI] [PubMed] [Google Scholar]
- 17.Lymperopoulou G, Papagiannis P, Sakelliou L, Milickovic N, Giannouli S, Baltas D. A dosimetric comparison of 169Yb versus 192Ir for HDR prostate brachytherapy. Med Phys. 2005;32(12):3832–3842. doi: 10.1118/1.2126821 [DOI] [PubMed] [Google Scholar]
- 18.Krishnamurthy D, Weinberg V, Cunha JAM, Hsu IC, Pouliot J. Comparison of high–dose rate prostate brachytherapy dose distributions with iridium-192, ytterbium-169, and thulium-170 sources. Brachytherapy. 2011;10(6):461–465. doi: 10.1016/j.brachy.2011.01.012 [DOI] [PubMed] [Google Scholar]
- 19.Morton GC. The emerging role of high-dose-rate brachytherapy for prostate cancer. Clinical Oncology. 2005;17(4):219–227. doi: 10.1016/j.clon.2004.12.005 [DOI] [PubMed] [Google Scholar]
- 20.Lessard E, Pouliot J. Inverse planning anatomy-based dose optimization for HDR-brachytherapy of the prostate using fast simulated annealing algorithm and dedicated objective function. Med Phys. 2001;28(5):773–779. doi: 10.1118/1.1368127 [DOI] [PubMed] [Google Scholar]
- 21.Pokharel S, Rana S, Blikenstaff J, Sadeghi A, Prestidge B. Evaluation of hybrid inverse planning and optimization (HIPO) algorithm for optimization in real-time, high-dose-rate (HDR) brachytherapy for prostate. Journal of Applied Clinical Medical Physics. 2013;14(4):96–107. doi: 10.1120/jacmp.v14i4.4198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.van der Meer MC, Bosman PAN, Niatsetski Y, et al. Bi-objective optimization of catheter positions for high-dose-rate prostate brachytherapy. Med Phys. 2020;47(12):6077–6086. doi: 10.1002/mp.14505 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Guthier CV, Damato AL, Hesser JW, Viswanathan AN, Cormack RA. A fast inverse treatment planning strategy facilitating optimized catheter selection in image-guided high-dose-rate interstitial gynecologic brachytherapy. Medical Physics. 2017;44(12):6117–6127. doi: 10.1002/mp.12590 [DOI] [PubMed] [Google Scholar]
- 24.Guthier CV, Aschenbrenner KP, Müller R, Polster L, Cormack RA, Hesser JW. Real-time inverse high-dose-rate brachytherapy planning with catheter optimization by compressed sensing-inspired optimization strategies. Physics in Medicine and Biology. 2016;61(16):5956–5972. doi: 10.1088/0031-9155/61/16/5956 [DOI] [PubMed] [Google Scholar]
- 25.Ayotte G, D’Amours M, Aubin S, Lessard É, Pouliot J, Beaulieu L. Sci—Thurs AM: YIS—02: Optimizing Number and Position of Catheters within Inverse Planning Simulated Annealing (IPSA) for Prostate and Breast High Dose Rate Brachytherapy. Medical Physics. 2009;36(9Part3): 4315–4315. doi: 10.1118/1.3244162 [DOI] [Google Scholar]
- 26.Wang C, Gonzalez Y, Shen C, Hrycushko B, Jia X. Simultaneous needle catheter selection and dwell time optimization for preplanning of high-dose-rate brachytherapy of prostate cancer. Phys Med Biol. 2021;66(5):055028. doi: 10.1088/1361-6560/abd00e [DOI] [PubMed] [Google Scholar]
- 27.Rivard MJ, Butler WM, DeWerd LA, et al. Supplement to the 2004 update of the AAPM Task Group No. 43 Report. Med Phys. 2007;34(6):2187–2205. doi: 10.1118/1.2736790 [DOI] [PubMed] [Google Scholar]
- 28.Taylor REP, Rogers DWO. An EGSnrc Monte Carlo-calculated database of TG-43 parameters. Med Phys. 2008;35(9):4228–4241. doi: 10.1118/1.2965360 [DOI] [PubMed] [Google Scholar]
- 29.Gu W, O’Connor D, Nguyen D, et al. Integrated beam orientation and scanning-spot optimization in intensity-modulated proton therapy for brain and unilateral head and neck tumors. Medical Physics. 2018;45(4):1338–1350. doi: 10.1002/mp.12788 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM journal on imaging sciences. 2009;2(1):183–202. [Google Scholar]
- 31.O’Connor D, Voronenko Y, Nguyen D, Yin W, Sheng K. Fast non-coplanar beam orientation optimization based on group sparsity. arXiv preprint arXiv:171005308. Published online 2017. [Google Scholar]
- 32.Deasy JO, Blanco AI, Clark VH. CERR: a computational environment for radiotherapy research. Med Phys. 2003;30(5):979–985. doi: 10.1118/1.1568978 [DOI] [PubMed] [Google Scholar]
- 33.Hsu IC, Bae K, Shinohara K, et al. Phase II Trial of Combined High-Dose-Rate Brachytherapy and External Beam Radiotherapy for Adenocarcinoma of the Prostate: Preliminary Results of RTOG 0321. International Journal of Radiation Oncology*Biology*Physics. 2010;78(3):751–758. doi: 10.1016/j.ijrobp.2009.08.048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Groenwold RHH, Goeman JJ, Cessie SL, Dekkers OM. Multiple testing: when is many too much? European Journal of Endocrinology. 2021;184(3):E11–E14. doi: 10.1530/EJE-20-1375 [DOI] [PubMed] [Google Scholar]
- 35.O’Connor D, Yu V, Nguyen D, Ruan D, Sheng K. Fraction-variant beam orientation optimization for non-coplanar IMRT. Phys Med Biol. 2018;63(4):045015. doi: 10.1088/1361-6560/aaa94f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lyu Q, Neph R, Yu VY, Ruan D, Boucher S, Sheng K. Many-isocenter optimization for robotic radiotherapy. Phys Med Biol. 2020;65(4):045003. doi: 10.1088/1361-6560/ab63b8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Gu W, O’Connor D, Ruan D, Zou W, Dong L, Sheng K. Fraction-variant beam orientation optimization for intensity-modulated proton therapy. Med Phys. 2020;47(9):3826–3834. doi: 10.1002/mp.14340 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gu W, Neph R, Ruan D, Zou W, Dong L, Sheng K. Robust beam orientation optimization for intensity-modulated proton therapy. Med Phys. 2019;46(8):3356–3370. doi: 10.1002/mp.13641 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gu W, Ruan D, O’Connor D, et al. Robust optimization for intensity-modulated proton therapy with soft spot sensitivity regularization. Med Phys. 2019;46(3):1408–1425. doi: 10.1002/mp.13344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ramesh P, Lyu Q, Gu W, Ruan D, Sheng K. Reformulated McNamara RBE-weighted beam orientation optimization for intensity modulated proton therapy. Med Phys. 2022;49(4):2136–2149. doi: 10.1002/mp.15552 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ramesh P, Liu H, Gu W, Sheng K. Fixed Beamline Optimization for Intensity Modulated Carbon-Ion Therapy. IEEE Transactions on Radiation and Plasma Medical Sciences. 2022;6(3):288–293. doi: 10.1109/TRPMS.2021.3092296 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lyu Q, Neph R, Yu VY, Ruan D, Sheng K. Single-arc VMAT optimization for dual-layer MLC. Phys Med Biol. 2019;64(9):095028. doi: 10.1088/1361-6560/ab0ddd [DOI] [PubMed] [Google Scholar]
- 43.Lyu Q, O’Connor D, Niu T, Sheng K. Image-domain multimaterial decomposition for dual-energy computed tomography with nonconvex sparsity regularization. J Med Imaging (Bellingham). 2019;6(4):044004. doi: 10.1117/1.JMI.6.4.044004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Cazeca MJ, Medich DC, Munro JJ III. Monte Carlo characterization of a new Yb-169 high dose rate source for brachytherapy application. Medical Physics. 2010;37(3):1129–1136. doi: 10.1118/1.3301607 [DOI] [PubMed] [Google Scholar]
- 45.Dupere JM, Munro JJ 3rd, Medich DC. Shielded high dose rate ocular brachytherapy using Yb-169. Phys Med Biol. 2021;66(12). doi: 10.1088/1361-6560/ac02d6 [DOI] [PubMed] [Google Scholar]
- 46.Adams Q, Hopfensperger KM, Kim Y, Wu X, Flynn RT. (169) Yb-based rotating shield brachytherapy for prostate cancer. Med Phys. 2020;47(12):6430–6439. doi: 10.1002/mp.14533 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Famulari G, Duclos M, Enger SA. A novel (169) Yb-based dynamic-shield intensity modulated brachytherapy delivery system for prostate cancer. Med Phys. 2020;47(3):859–868. doi: 10.1002/mp.13959 [DOI] [PubMed] [Google Scholar]


