Gaming self-consistent field theory: Generative block polymer phase discovery

Significance

Block polymers are an ideal platform for studying soft matter self-assembly. Theory and computation have proven to be powerful explanatory tools, dissecting the relative impact of entropy and enthalpy and providing insights into the arrangements of the polymers that often are experimentally inaccessible. However, using polymer field theory to discover new self-assembled structures runs into a roadblock: Solving the nonlinear equations in the theory requires an initial guess close to the desired solution, but discovering a new phase means the solution’s features are not known in advance. This issue is resolved by using a generative adversarial network to learn useful initial guesses from a small library of previous solutions, thereby enhancing polymer field theory’s power as a predictive tool.

Abstract

Block polymers are an attractive platform for uncovering the factors that give rise to self-assembly in soft matter owing to their relatively simple thermodynamic description, as captured in self-consistent field theory (SCFT). SCFT historically has found great success explaining experimental data, allowing one to construct phase diagrams from a set of candidate phases, and there is now strong interest in deploying SCFT as a screening tool to guide experimental design. However, using SCFT for phase discovery leads to a conundrum: How does one discover a new morphology if the set of candidate phases needs to be specified in advance? This long-standing challenge was surmounted by training a deep convolutional generative adversarial network (GAN) with trajectories from converged SCFT solutions, and then deploying the GAN to generate input fields for subsequent SCFT calculations. The power of this approach is demonstrated for network phase formation in neat diblock copolymer melts via SCFT. A training set of only five networks produced 349 candidate phases spanning known and previously unexplored morphologies, including a chiral network. This computational pipeline, constructed here entirely from open-source codes, should find widespread application in block polymer phase discovery and other forms of soft matter.

Soft matter possesses a remarkable ability to spontaneously self-assemble into nanostructured morphologies through a delicate balance between enthalpic and entropic effects, making a priori prediction challenging. Discovering new ordered states can benefit tremendously from using theory and computation as a screening tool to identify promising materials for experimental investigation. If the target phase is known in advance, the challenge is identifying the molecular building blocks that favor formation of that state, which is known as the “inverse problem” (1). Developing robust solutions to the inverse problem in soft matter remains an outstanding issue and area of intense interest. An equally daunting challenge is using theory and computation for de novo phase discovery, i.e., to uncover previously unanticipated ordered states in a manner similar to a serendipitous experiment. The difficulty in computational phase discovery in soft matter lies in the need for robust initial conditions that drive the solution toward a phase of interest. Without any advance knowledge of the structure of that phase, it is not obvious how to design appropriate initial conditions. This conundrum poses a substantial obstacle for computational phase discovery across a broad range of soft matter.

The present contribution addresses the computational phase discovery question in the context of a model system for understanding self-assembly in soft matter, namely block polymers. Block polymers are the most tractable platform for exposing the general principles of ordered state selection in soft matter, owing to their relatively simple thermodynamics (2), the principle of universality (3), and access to virtually unlimited molecular designs through a plethora of synthetic approaches (4). A block copolymer melt cooled below the order–disorder temperature selects a morphology that balances the interfacial tension created by contact between unlike blocks against the entropic penalty of chain stretching, under the constraint of filling space at constant density (5, 6). Universality in this process emerges at high molecular weights, where the detailed chemical interactions at the monomer scale are subsumed into Gaussian statistics governing the chain configurations, embodied by the statistical segment length and degree of polymerization of the blocks, and Flory–Huggins parameters quantifying the free energy of mixing (3). The resulting thermodynamic model is thus relatively simple compared to other forms of soft matter.

Despite this simplicity, predicting block polymer phase behavior remains challenging due to the rapid expansion of the parameter space as the number of blocks increases (7). As such, identifying new ordered states requires computational methods to guide experiments. Polymer field theory is the most powerful approach here owing to its efficiency for simulating dense systems (5). Within polymer field theory, a mean-field implementation—self-consistent field theory (SCFT)—is widely deployed because it enables facile computation of both the free energy and morphology of block copolymer melts and blends (8–10) by obtaining the self-consistent configurations of a test chain in chemical potential fields created by the other polymers.

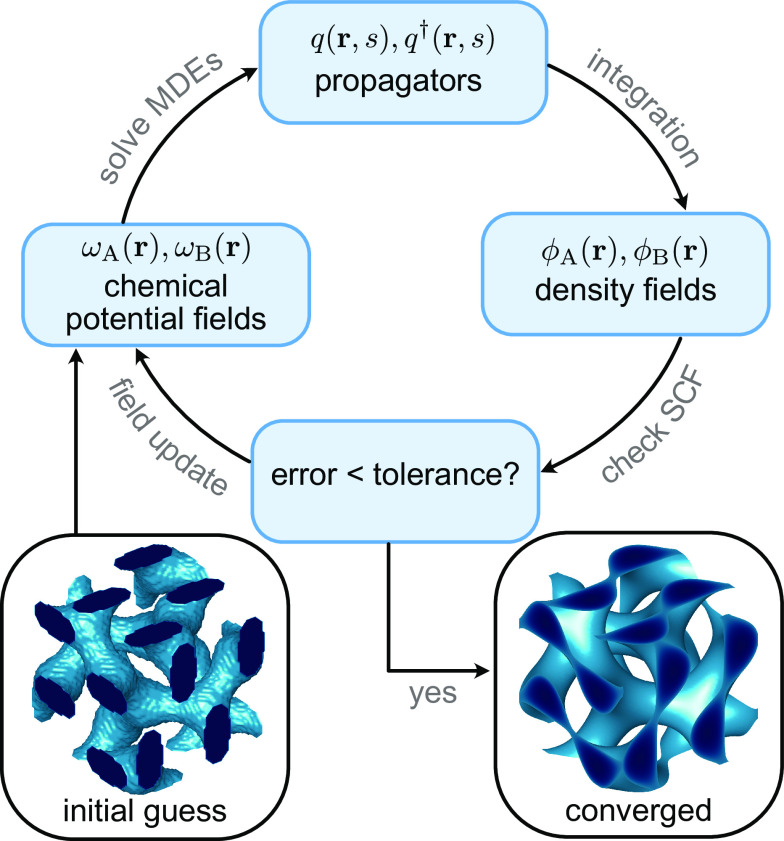
Fig. 1 brings to the fore the challenge in using SCFT for phase discovery, illustrated here in the context of AB copolymers. A given SCFT calculation requires solving modified diffusion equations (MDEs) in the spatially-inhomogeneous chemical potential fields ${\omega }_{\mathrm{A}}(\mathit{r})$ and ${\omega }_{\mathrm{B}}(\mathit{r})$ for the forward and reverse propagators, $q(\mathbf{r},s)$ and $q^{†}(\mathbf{r},s)$, where $s$ is the position on the chain contour, which is done via a pseudospectral method (11). Those solutions permit calculation of the density fields ${\varphi }_{\mathrm{A}}(\mathit{r})$ and ${\varphi }_{\mathrm{B}}(\mathit{r})$, which, in conjunction with a Lagrange multiplier field that imposes the incompressibility constraint ${\varphi }_{\mathrm{A}}(\mathit{r})+{\varphi }_{\mathrm{B}}(\mathit{r})=1$, allows computation of ${\omega }_{\mathrm{A}}(\mathit{r})$ and ${\omega }_{\mathrm{B}}(\mathit{r})$. The resulting system of nonlinear equations, described in detail in refs. 5 and 8–10, thus must be solved self-consistently (12, 13) from an initial guess for the chemical potential fields while also relaxing the unit-cell stress (14). Once the system has converged, the Helmholtz free energy per chain is computed from the SCFT free energy functional. The nonlinear nature of the SCFT equations can give rise to multiple solutions, with many of these corresponding to local minima, i.e., metastable states. Therefore, the initial guess used to initialize an SCFT calculation is a key step in the calculation, as it can significantly affect the solution. In practice, different initial guesses can lead to different solutions, and a poor initial guess can even prevent the algorithm from converging to a physically meaningful solution.

Fig. 1.

Conventional approach to using SCFT to compute block polymer phase behavior. The iterative solution requires initialization using either a previously computed solution or a guess for the structure, e.g., a level set for network phases or form factor for particle phases, to initialize the chemical potential fields. The SCFT iterator refines the chemical potential fields through solutions of the MDEs for the forward and reverse propagators, which are then integrated to compute the density fields for the given blocks. The density fields are then used to compute the error in the self-consistent field (SCF) equations. If the SCF error is below a set tolerance, the solution has converged and the calculation outputs the density field, the optimal unit cell geometry, and the Helmholtz free energy.

SCFT, much like other physics-based simulation methods in soft matter, suffers from a fundamental challenge for materials discovery: How can one initialize a reasonable guess to produce a new candidate phase without advance knowledge of the structure? For example, the most efficient way to initialize an SCFT solution is to use a previously computed result and continue the solution in the parameter space. When no previous solution is available, one can provide an initial guess for the chemical potential fields by using a form-factor approach for particle-forming phases or a level-set method for network phases (9, 15). While these initialization methods are very powerful approaches for investigating the free energy and morphologies of known phases, they are ill-suited for materials discovery because they require a priori knowledge of the structure of the candidate phases, and converging from random initial conditions tends not to be robust.

This longstanding problem for phase discovery can be resolved by leveraging the power of deep generative models to propose new morphologies. Deep generative models, often referred to as generative artificial intelligence, use deep neural networks to identify the hidden patterns within existing data and leverage that information to generate new examples (16). Among these models, generative adversarial networks (GANs) (17), and deep convolutional GANs in particular (18), have emerged as highly effective approaches in image generation that we can deploy here for block polymer phase discovery. A deep convolutional GAN consists of two convolutional neural networks: a generator and a discriminator. The discriminator functions as a binary classifier, trained to distinguish generated fake images from the real images that make up the training set. Meanwhile, the generator is trained to transform a latent space vector into a synthetic image in the data space. This transformation is guided by a designated loss function that rewards the generator’s success in deceiving the discriminator. The training of these two neural networks involves an adversarial interplay, resulting in iterative improvements for both networks throughout the training process.

Here, we leverage the ability of deep convolutional GANs to propose new initial conditions for SCFT calculations in a flexible unit cell (14), by learning from the monomer density field of a few known phases. The density fields, represented on a regular grid with values ranging from 0 to 1, can be treated as 3D gray-scale images for training. The synergy between GANs and SCFT brings out the best in both approaches; SCFT has a remarkable ability to adjust the system morphology during convergence, which puts minimal demands on the generator to propose a precise guess. The power of this approach is demonstrated using network phase formation in a neat, diblock copolymer melt, where the generative polymer field theory not only produced all known network phases in block copolymers using the knowledge of five known network phases, but uncovered hundreds of possible candidate phases including an intriguing chiral network phase with a relatively low free energy.

Integrating Polymer Field Theory with GANs

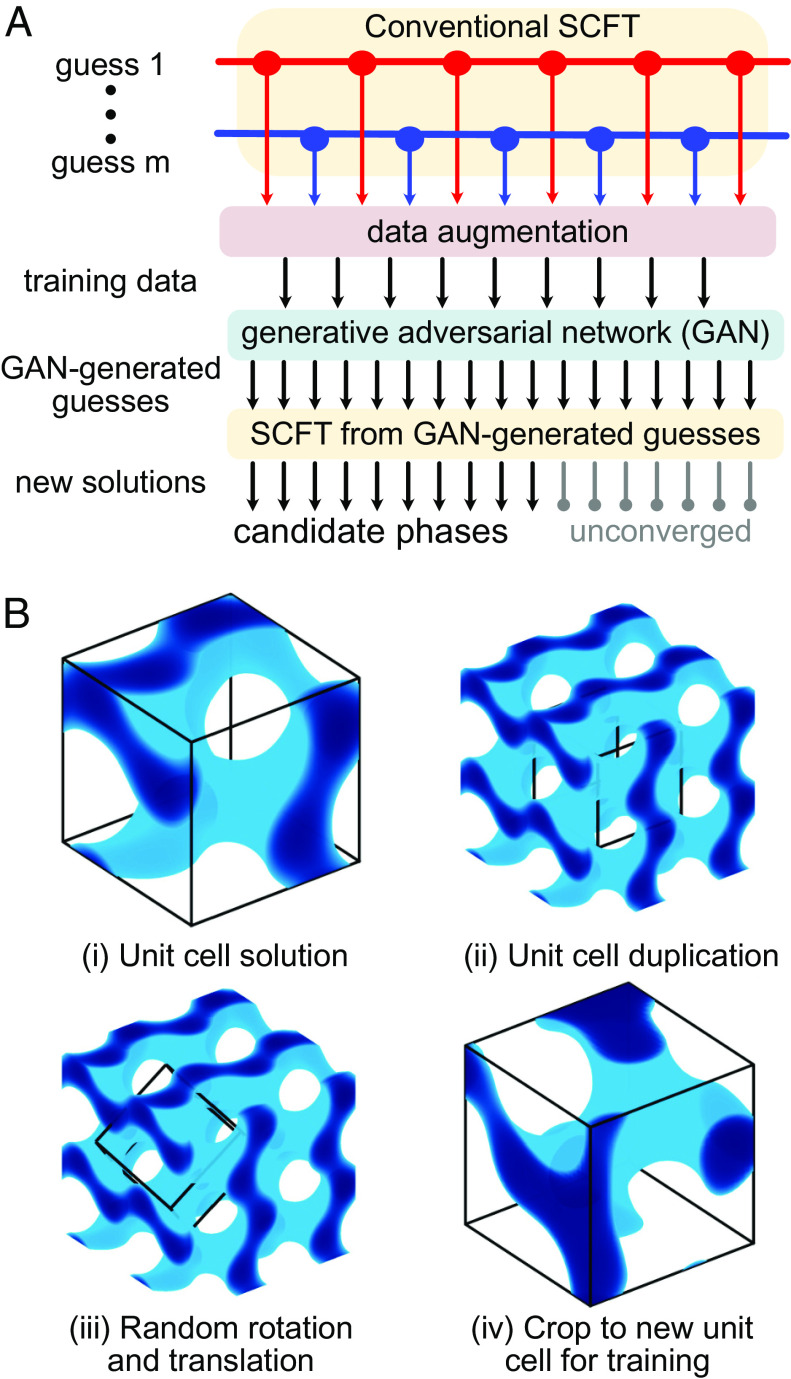
The generative polymer field theory method, illustrated in Fig. 2A in the context of SCFT, consists of three steps. The first step computes unit-cell SCFT solutions for a few known phases, following the standard initialization approach of Fig. 1. Simply using the converged SCFT solutions does not provide enough training data, so the SCFT density fields are output every five iterations during the calculation. The second step trains the GAN from those density fields (SI Appendix, Figs. S1 and S2 and Movie S1). The third step uses guesses produced from the trained GAN to seed a second round of SCFT calculations in a flexible box that, in principle, generates converged morphologies that are distinct from those in the original training set.

Fig. 2.

Generative polymer field theory for block polymer phase discovery. (A) In generative polymer field theory, a small set of $m$ classical field theory calculations are performed first. A set of intermediate states during that calculation are output, randomly transformed, and then used to train the GAN. Following training, the GAN generates thousands of new initial conditions for subsequent field theory calculations. The pipeline illustrates this generative approach in the context of SCFT. (B) Example of data augmentation strategy involving duplication of the unit cell during an SCFT trajectory, random translation and rotation, and then extraction of a new unit cell applied on the training data. In the images in B(ii) and B(iii), the box illustrates the unit cell used for duplication or the unit cell that is extracted from the transformed data.

It is not immediately obvious that this approach will work because GAN training typically requires a diverse data set to enhance generalizability, but there are very few known network phases in block polymers. As a result, the key is to produce sufficiently diverse data to avoid producing a GAN that simply recapitulates the known phases. As part of our data augmentation strategy, we thus applied random translations and rotations to the 3D image, as illustrated in Fig. 2B. We first duplicated and tiled the 3D image containing the monomer density data along three directions. Next, a new cubic box was obtained by randomly translating, rotating the original box that represents the unit cell. The new coordinates of a $32\times 32\times 32$ grid were then calculated based on the coordinates of the new box. Since the original data are also on a grid, the values on the new grid points were obtained by interpolation of the density data from the original grid points. This process breaks the periodic boundary condition of the density fields. The training data are nonetheless periodic because the format for specifying the density fields only uses three of the six faces of the unit cell and enforces periodicity at the other faces. As a result, however, there may be large density gradients near the other three faces of the unit cell. Even if the GAN-generated initial guesses preserve this feature, SCFT is able to smear them out during convergence for the relatively low segregation strengths investigated here (19). Ultimately, data augmentation was essential for the purpose of diversifying the training data and improving the breadth of the domain space available to the GAN. As shown in SI Appendix, Fig. S3, if we did not apply these random transformations, the density fields generated by the GAN generator closely resembled the training inputs and were unlikely to converge to any solutions not represented in the training data during SCFT calculations.

Model Problem: Network Phase Discovery in Diblock Copolymer Melts

The power of this approach is demonstrated using network phase formation in a neat, diblock copolymer melt. Network phases are bicontinuous (or multicontinuous), three-dimensional, periodic systems with a range of possible symmetries and topologies. Historically, SCFT has played a vital role in understanding the emergence of network phases in block polymers, explaining the stability of the double-gyroid phase (20, 21), predicting the O${}^{70}$ phase in diblock melts (22), and rationalizing the stability of different networks (23). Network phases are also important in technological applications; their bicontinuous nature makes them attractive as membranes (24) and optically active materials (25).

To focus the study, we analyzed a conformationally symmetric diblock copolymer melt with a minority block volume fraction $f_{\mathrm{A}}=0.38$ and a segregation strength $\chi N=17.5$, where $\chi$ is the Flory–Huggins parameter and $N$ is the total degree of polymerization. The SCFT phase diagram at this state point predicts double gyroid is the stable morphology (26). The training data were generated from SCFT trajectories for single and double gyroid (threefold connectors), single diamond (fourfold connectors), and single and double primitive (sixfold connectors). To provide sufficient diversity of the density fields for our GAN training data, we obtained SCFT solutions near the double-gyroid window of the linear diblock copolymer melt for state points that uniformly sample from the range $\chi N\in [15,20]$, $f_{\mathrm{A}}\in [0.35,0.45]$, $ϵ\in [0.75,1.33]$. For four of the five training phases, except for double primitive, we used the level-set method to construct initial guesses for $f_{\mathrm{A}}=0.35,0.40$ and $0.45$. For a given sampled state point $(\chi N,f_{\mathrm{A}},ϵ)$, we then randomly selected one of those three initial guesses as the initialization of the fields for the SCFT calculation. For the double-primitive phase, it is difficult to obtain converged solutions for random state points from a level set due to the geometrical packing frustration in the six-connected node (23). Therefore, instead of using the level-set method to initialize the calculation, we randomly selected from three converged solutions with $f_{\mathrm{A}}=0.37,0.40$ and $0.42$ as the initial guess for the double-primitive density field. Following data augmentation (Fig. 2B), the number of images generated from each phase are as follows: double gyroid (3,604), single gyroid (3,130), single diamond (2,793), single primitive (4,142), and double primitive (4,604), for a total of 18,273 3D images after data augmentation. We then used the GAN to generate 5,000 initial conditions for the final step of Fig. 2B and attempted to converge each of them using SCFT.

De Novo Generation of Known Block Polymer Phases.

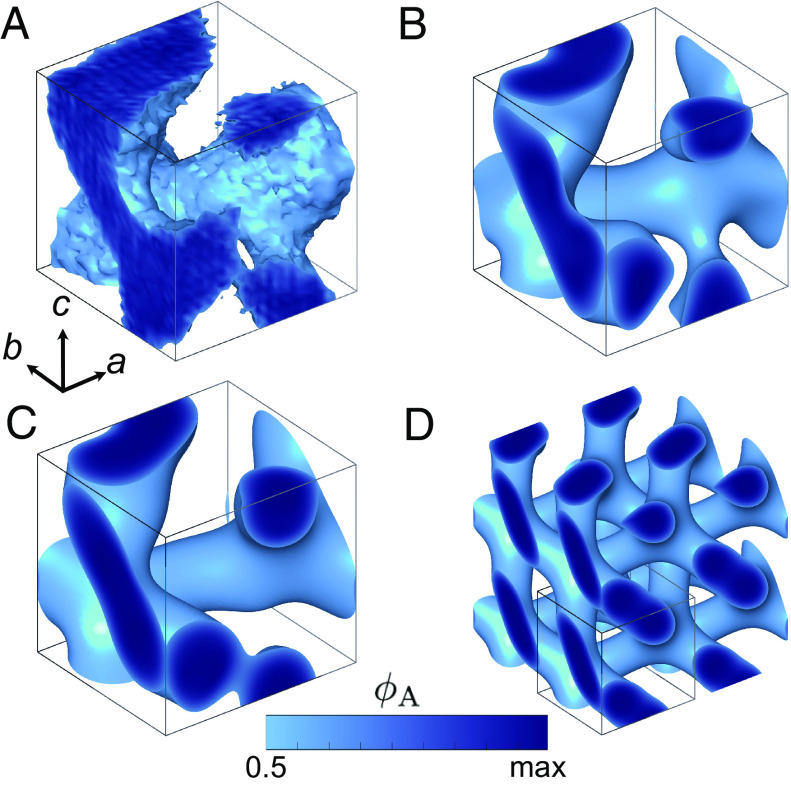
The training data specifically excluded double diamond to determine whether it could be produced from a training set that has knowledge of i) fourfold connectors and ii) the principle of single and double networks. Fig. 3 illustrates this was indeed the case. Moreover, the GAN produced initial guesses that subsequently converged to three other classical block copolymer network phases: the orthorhombic networks O${}^{52}$ ($\mathit{Pnna}$) (27, 28) and O${}^{70}$ ($\mathit{Fddd}$) (22, 29), and hexagonal perforated lamellae with ABC stacking (HPL, $R\overline{3}m$), the latter of which appears as an intermediate state between double gyroid and the disordered melt (30, 31). The SCFT trajectories for these three phases from the GAN-generated guesses are provided as SI Appendix, Figs. S5–S7. The GAN also produced field configurations that converged to the M${}^{15}$ phase (threefold connectors), which can be envisioned as a sheared O${}^{70}$, and T${}^{131}$ (fourfold connectors), both of which were reported recently in self-assembled bottlebrush terpolymers (32).

Fig. 3.

Illustration of the convergence of a GAN-generated initial guess to double-diamond phase in a flexible unit cell via SCFT. Minority block density distributions ${\varphi }_{\mathrm{A}}(\mathit{r})$ in a unit cell (A) for the GAN-generated initial guess; (B) after 11 SCFT iterations; (C) after 19 SCFT iterations; and (D) for the converged solution (205 SCFT iterations). In (D), the unit cell, indicated by the solid lines, is copied into a 2 $\times$ 2 $\times$ 2 system for easier visualization. The lengths of the orthogonal lattice vectors $[a,b,c]$, defined by the coordinate system in (A), are expressed in terms of the unperturbed end-to-end distance of the polymer. The unit-cell lattice vectors and the maximum value of the minority block density ${\varphi }_{\mathrm{A}}$ are (A) [3, 3, 3] and 0.990; (B) [2.73, 2.59, 2.66] and 1.034; (C) [2.62, 2.30, 2.49] and 0.981; and (D) [2.41, 2.17, 2.41] and 0.974. The connection between solutions produced by the generative method and the conventional unit cells is illustrated in SI Appendix, Fig. S4. Movie S2 shows the complete SCFT trajectory for double diamond.

The solution trajectory in Fig. 3 emphasizes the well-known ability of SCFT to substantially modify the morphology while converging toward the saddle point solution (9), in particular by adjusting the unit cell dimensions to minimize stress (14). Using SCFT as the last step in Fig. 2A thus greatly reduces the demands on the GAN when compared to conventional applications of generative neural networks, such as image generation; so long as a subset of the GAN outputs are situated in the SCFT basin of attraction for a new phase, the SCFT iterator often can resolve shortcomings in the generated image. In this sense, this method is also markedly different from a proposed all-machine-learning methodology that uses a GAN for input (33). To circumvent the computational cost of SCFT, the latter method learns the field-theoretic Hamiltonian to estimate free energies from the density field (34), rather than generating an SCFT trajectory. It remains to be seen whether the latter method will have SCFT’s ability to drive the GAN output to a new morphology or the ability to analyze three-dimensional systems, both of which are critical to the success of the present approach.

Emergence of New Candidate Phases.

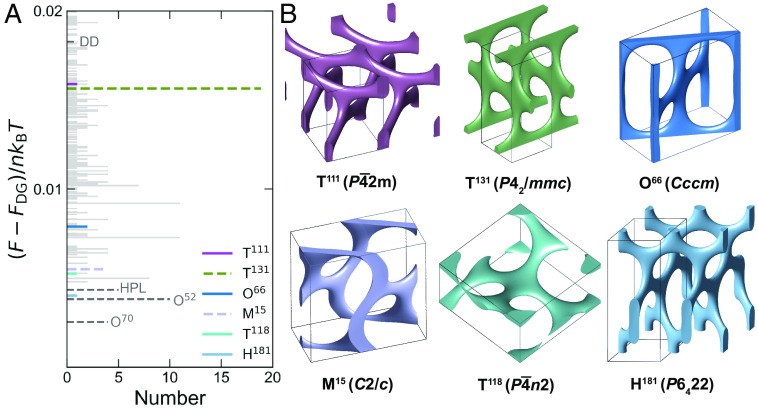
The GAN generated 545 initial guesses that led to converged SCFT solutions. Degeneracy in the converged solutions was assessed by first grouping converged solutions with free energies that differ by less than ${10}^{-5}{k}_{\mathrm{B}}T$ per chain, where $k_{\mathrm{B}}$ is Boltzmann’s constant and $T$ is temperature, and then comparing their density profiles. After accounting for degeneracy, a total of 349 candidate states were produced, which includes the five known block polymer phases previously discussed. The histograms in Fig. 4A and SI Appendix, Fig. S8 reveal, as anticipated, the candidate states are metastable in diblock copolymer melts with free energies that range from $2.5\times {10}^{-3}$ to $5.3\times {10}^{-2}{k}_{\mathrm{B}}T$ per chain above the equilibrium double-gyroid phase.

Fig. 4.

Candidate phase produced by generative polymer field theory with SCFT. (A) Histogram of the free energy per chain of converged SCFT solutions with the lowest free energies, measured relative to the equilibrium double-gyroid (DG) state. The full histogram is reported as SI Appendix, Fig. S8. The classical block polymer network phases produced here using generative polymer field theory, HPL, O${}^{52}$, O${}^{70}$, and double diamond (DD), are labeled. Previously identified network phases in block polymers, including the latter quartet, are indicated by the dashed lines. Solid lines indicate previously unexplored block polymer candidate phases. (B) Representative block polymer candidate phases indicated by the colored data lines in panel (A). The skeletons indicate regions where the minority block density satisfies ${\varphi }_{\mathrm{A}}>0.93$. Analysis of the resulting structures identified the conventional unit cells (monoclinic, orthorhombic, tetragonal, or hexagonal) and symmetries, which are indicated in the labels. The unit cells of H${}^{181}$, T${}^{131}$, and T${}^{111}$ are duplicated for easier visualization. Similar density profiles for ${\varphi }_{\mathrm{A}}>0.50$ and the equilibrated unit cell parameters can be found in SI Appendix, Fig. S9.

The generative approach provides a wealth of morphologies exhibiting different connector valences, network topologies, and symmetries. Several are highlighted in Fig. 4B and SI Appendix, Fig. S9 including the recently discovered M${}^{15}$ and T${}^{131}$ phases (32). In some cases, the candidate phases are related. For example, O${}^{66}$ is a low-symmetry variant of T${}^{131}$ with a non-90${}^{°}$ angle ($55.9^{°}$) between neighboring connectors along the $<$001$>$ directions. Morphologies with mixed connectors were also produced, which should prove promising to probe defect formation in block polymer self-assembly. The lowest free energy phase with mixed connectors is the tetragonal network T${}^{118}$, which has one four-fold node and four three-fold nodes in each unit cell. While most of the candidate phases were single networks, some double networks emerged. The most notable is T${}^{111}$, a (10,3) double network obtained by replacing the four-fold connectors in double diamond with pairs of T-shaped threefold connectors; there is a close analogy between this double-network morphology and its single-network analogue (35).

Importantly, this approach generated previously unanticipated candidate phases with potentially useful material properties. The most intriguing phase is H${}^{181}$ (see SI Appendix, Fig. S10 and Movie S3 for the SCFT trajectory), which has neither been proposed nor realized in soft matter. H${}^{181}$ is a hexagonal network with space group symmetry $P{6}_{4}22$, with lattice parameters $a/c$ = 2.65 at $f_{\mathrm{A}}$ = 0.38 and $\chi N$ = 17.5. The centers of the threefold connectors are located at $[x,y,z]=[0.5,0,0.094\pm 0.002]$ in fractional coordinates and the corresponding symmetry equivalent positions (SI Appendix, Fig. S11), which were determined by the grid points with the highest minority monomer density ${\varphi }_{\mathrm{A}}(\mathit{r})$ in a refined converged solution using a grid resolution of 96 $\times$ 96 $\times$ 512. The A/B interface (Fig. 5A) of H${}^{181}$ encloses a three-connected chiral network that is topologically identical to the bto net (36), which can be obtained by splitting the four-connected nodes of a quartz network with the same space group symmetry into two three-connected nodes along the $c$-axis (SI Appendix, Fig. S11). Such structure modifications transform the (6,4) rings and (8,4) rings of the quartz network into (10,3) rings and (12,3) rings, respectively. The struts of the H${}^{181}$ network can be envisioned as layer stackings of in-plane, threefold connectors with a 60${}^{°}$ twist angle between layers, as illustrated by the colored nodes in Fig. 5 B and C. This arrangement produces a local configuration of the threefold connectors in H${}^{181}$ that closely resembles that of the O${}^{70}$ phase. Each H${}^{181}$ connector is connected to two in-plane connectors and one out-of-plane connector with a 60${}^{°}$ twist angle, while O${}^{70}$ has a local twist angle of 52.6${}^{°}$ in this specific model of diblock copolymer. The 60${}^{°}$ twist angle for H${}^{181}$ is constrained by symmetry, while the twist angle for O${}^{70}$ depends on the exact structure (22).

Fig. 5.

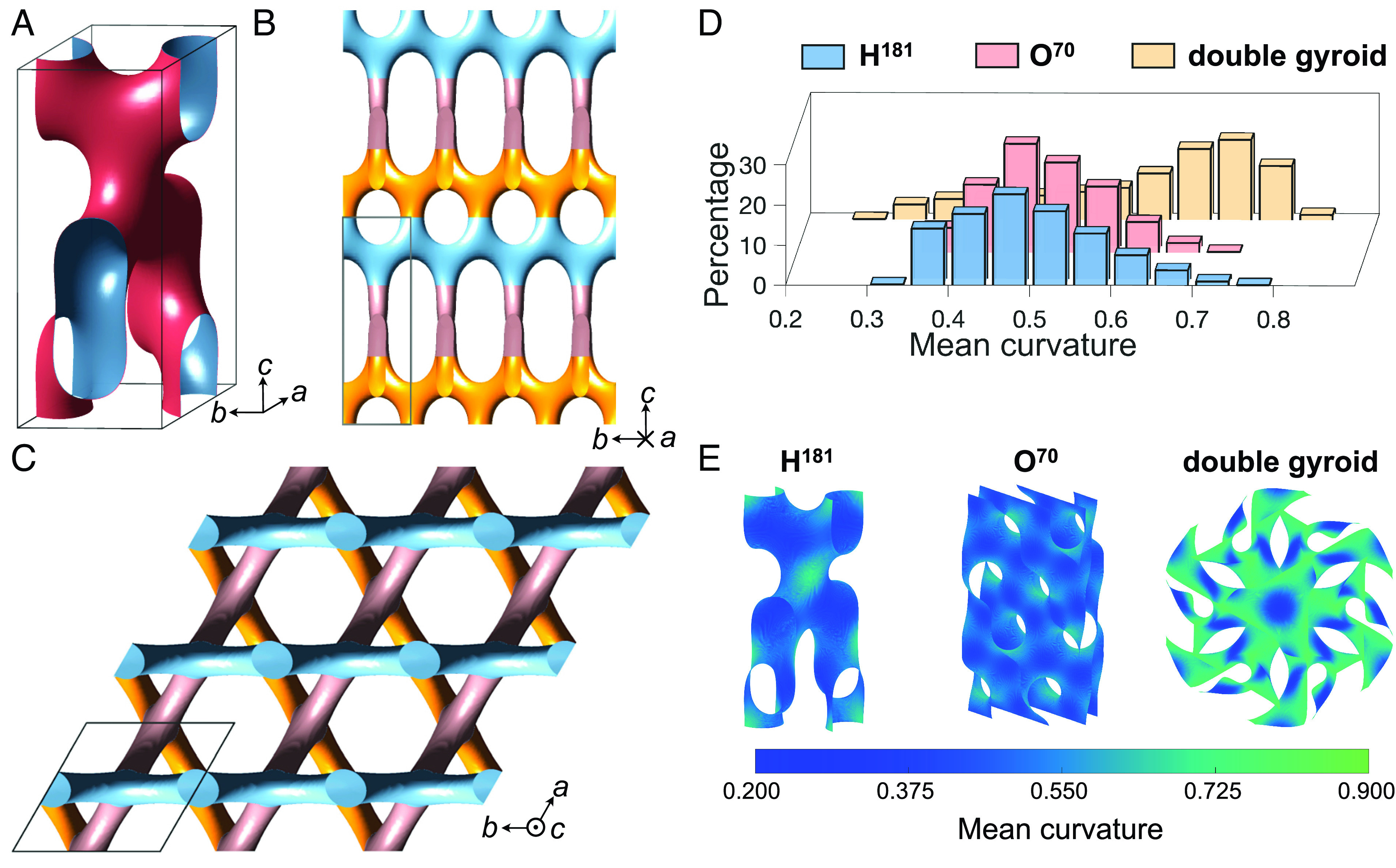
Structure of H${}^{181}$. (A) Interface corresponding to ${\varphi }_{\mathrm{A}}=0.5$. (B) Projection along the [100] direction. (C) Projection along the [00$\overline{1}$] direction. For (B) and (C), the skeletons indicate regions where the minority block density satisfies ${\varphi }_{\mathrm{A}}=0.90$, and the boxes are the unit cell. The coloring in the projections in (B) and (C) indicates the threefold connectors with different orientations within the 3D unit cell of Fig. 4B. (D) Histograms and (E) color maps of the mean curvature of A/B interface of H${}^{181}$, O${}^{70}$, and double gyroid. H${}^{181}$ and O${}^{70}$ have similar average mean curvature (0.498 and 0.506) and curvature distributions in the histogram, while double gyroid has a higher interfacial curvature of 0.621.

The structure of H${}^{181}$ is promising for materials applications. The $6_4$ screw axis implies that H${}^{181}$ is chiral and thus could prove useful as a metamaterial for optical applications; inverting the structure should lead to its chiral counterpart with $P{6}_{2}22$ symmetry. Fig. 5B shows that the [100] direction of H${}^{181}$ provides well-organized channels with two different sizes that could find utility in membrane applications, and Fig. 5C suggests that the $[00\overline{1}]$ (top–down) projection of the network has a trihexagonal tiling pattern (Kagome lattice).

H${}^{181}$ also is a feasible target for materials discovery because it has a lower free energy than HPL; inasmuch as HPL has been accessed as a metastable state in diblock copolymer melts (30, 31), it is plausible that H${}^{181}$ may be accessed there as well, perhaps leveraging shear processing (37), self-assembly of chiral block polymers (38), or multiblock polymers (7). Moreover, Fig. 5 D and E reveal that H${}^{181}$ has a narrow distribution of mean curvature, which is generally associated with higher stability (23), and (ii) additional SCFT calculations in SI Appendix, Fig. S12 reveal that the free energy of H${}^{181}$ is lower than that of double gyroid and O${}^{52}$ in certain regions of the O${}^{70}$ window of the diblock copolymer phase diagram. Indeed, due to the structural relationship between the quartz and the bto networks, the A/B domain interface of H${}^{181}$ shares some similarities with a chiral minimal surface deducted based on a quartz network and its dual (39). According to the mean curvature map of the H${}^{181}$ interface in Fig. 5E, at the region where the quartz node is split into two triangular nodes, the local mean curvature is higher, which can be regarded as the result of locally stretching the minimal surface related to the quartz network along the $c$-direction. The rest of the interface remains relatively low in mean curvature, and the overall mean curvature distribution of H${}^{181}$ resembles that of the O${}^{70}$ phase, as seen in the histogram in Fig. 5D. This is also related to the similarity in local configurations of the three-connected nodes of H${}^{181}$ and O${}^{70}$; the highest curvature region of both structures is near the 60${}^{°}$ (or 52.6${}^{°}$) twist. Double gyroid, on the other hand, has a higher preferred mean curvature and a broader distribution of curvatures. As a result, when the composition of the diblock copolymer becomes more symmetric, the relative stability of H${}^{181}$ and O${}^{70}$ increases compared to double gyroid, which is illustrated by the free energy calculations in the network forming region at $\chi N$ = 12 in SI Appendix, Fig. S12. The difference in preferred curvature eventually leads to a stability region of O${}^{70}$ and a region with lower H${}^{181}$ free energy compared to double gyroid.

Generative Polymer Field Theory Offers Potential for Phase Discovery

The major outstanding problem in the discovery of new block polymer materials lies in not only navigating the high dimensional state space (7), but also uncovering unanticipated morphologies. The number of new phases identified here compares very favorably with previous methods for generating new SCFT candidate phases. The pioneering computational approaches to phase discovery in block polymers used random initial conditions and no preset information about the symmetry using either real-space SCFT (40) or an approximate free energy functional (41) to search for new ordered states. Generative polymer field theory can be viewed as an augmentation of these early studies (40, 41) that leverages advances in machine learning in the ensuing years to improve on the initial conditions, while maintaining their agnostic approach toward symmetry.

More recently, genetic algorithms (42) and particle-swarm optimization (PSO) (43) have been used for similar purposes. While the genetic algorithm was not robust, PSO in reciprocal space uncovered both the double-gyroid phase and several Frank–Kasper phases (43). The PSO approach is appealing because it does not require any training data, since PSO is used as a global optimizer to adjust random SCFT initial guesses for peak locations on a spherical surface in reciprocal space, and it incorporates information about the free energy as well. Our generative approach, on the other hand, entails a significant amount of overhead to generate the training data and then train the GAN. However, the cost of that overhead should be viewed in light of the success of the resulting calculations, which recapitulated almost all known network phases in block copolymers and identified a promising new candidate phase.

The GAN used here is a relatively naïve implementation. There is significant room for advancement by tuning the hyperparameters and architectures of the neural networks, as well as using the latent space to combine information about different types of morphologies in a more systematic manner (18). Moreover, we have demonstrated the power of the approach by intentionally using a small training set (five phases), in part to prove that other known phases could be generated. Increasing the size of the training set should increase the diversity of the output. Indeed, we envision that this approach could be applied recursively, using random transformations of the SCFT solutions produced here to retrain the network. It may also be of interest to include data from SCFT trajectories that did not converge, although one must balance the resulting increased diversity of the training set against the potential that these additional data will hinder convergence of the initial guesses produced from the resultant GAN.

The pipeline of Fig. 2A should be an enabling tool for discovery of new structures, providing candidate phases that can seed either a standard forward search or, more likely, an inverse search that uses an automated method (44–47) to identify a region of the state space that favors formation of the candidate phase. Extending the proof-of-principle example here to other systems (e.g., cylinders, particle packings, and mixed phases) should be straightforward. A particularly fruitful avenue to begin would be triblock terpolymers, where over 30 phases are already known (15, 48) and there are surely more waiting to be uncovered. The fields produced from the present calculations could also be used to seed SCFT calculations for block copolymers with multiple blocks or nonlinear topologies. Indeed, prior SCFT calculations (49) suggest that multiblock copolymers can have a profound impact on network phase selection by relieving packing frustration, and it would be interesting to pursue similar approaches toward stabilizing H${}^{181}$.

SCFT is but one case in soft matter simulation where information about the desired structure is needed in advance, and thus, one encounters challenges searching for novel phases. For example, a GAN can generate similar initial conditions for polymer field-theoretic simulations that sample the field fluctuations (26, 50). Likewise, guiding fields can be used in particle-based simulations to initialize a system in a desired morphology and determine whether it is a stable basin of attraction; this proved especially useful for network phase assembly in oligomers (51). The challenge here is analogous to that in SCFT: How does one select guiding fields without a priori knowledge of the structure? Candidate phases identified for block polymers are a natural answer. Indeed, even if candidate phases produced by generative polymer field theory prove to be metastable for block polymers, the chemical complexity in ligand-grafted colloids (52) or ionic surfactant solutions (53) could provide the additional interactions needed to stabilize them. Thus, this generative approach should find broad utility in the study of self-assembly in soft matter.

Materials and Methods

SCFT Calculations.

Our implementation of SCFT follows that described in ref. 9. The incompressible AB diblock melt is modeled as a system of $n$ Gaussian chains with total degree of polymerization $N$, block degrees of polymerization $N_{\mathrm{A}}$ and $N_{\mathrm{B}}$, and statistical segment lengths $b_{\mathrm{A}}$ and $b_{\mathrm{B}}$. The minority block volume fraction is $f_{\mathrm{A}}=N_{\mathrm{A}}/N$. For GAN training purposes, we consider a range of $f_{\mathrm{A}}$ and conformational asymmetry parameters $ϵ=b_{\mathrm{A}}/b_{\mathrm{B}}$. All data then use GAN-generated guesses to seed SCFT solutions corresponding to $f_{\mathrm{A}}=0.38$ and $ϵ=1$ (conformationally symmetric systems). Additional data obtained elsewhere in the diblock phase diagram are reported for H${}^{181}$ in SI Appendix, Fig. S12. The unfavorable mixing between blocks is quantified by the product $\chi N$, where $\chi$ is the Flory–Huggins parameter.

We performed all SCFT calculations using the open-source Polymer Self-Consistent Field (PSCF) software package developed by Morse and coworkers (9), using an integration step size $\mathrm{\Delta }s=0.01N$ and a convergence tolerance of ${10}^{-6}$ (unless otherwise specified). This code uses Anderson mixing (12) while relaxing the unit-cell stress (14) to a desired tolerance as defined in ref. 13. The grids are either $32\times 32\times 32$ or $64\times 64\times 64$, as indicated in the relevant sections. We initialized the SCFT calculations for known phases using the level-set method of Wohlgemuth et al. (54); the implementation and codes are available in ref. 9. In this method, the A/B domain interface of a network phase is approximated by a level surface using a linear combination of the first few symmetry-adapted basis functions of the corresponding space group and a predetermined minority block volume fraction $f_{\mathrm{A}}$. The corresponding coefficients for the basis functions are available in ref. 54. The generated initial field from the level-set method is a binary density field in a regular real-space grid, with ${\varphi }_{\mathrm{A}}=1$ inside the infinitesimally thin interface and ${\varphi }_{\mathrm{A}}=0$ outside. The chemical potential fields are then initialized by setting the Lagrange multiplier field to zero (9). Fig. 1 shows an example of this initialization approach.

Generation of Training Data.

To produce the training data, the density fields of the minority block, ${\varphi }_{\mathrm{A}}(\mathit{r})$, were saved every 5 iterations for all SCFT calculations that converged within 500 iterations. However, in the early stages of the SCFT trajectory, the incompressibility constraint is often very far from satisfied, leading to grid points with densities ${\varphi }_{\mathrm{A}}(\mathit{r})>1$ or ${\varphi }_{\mathrm{A}}(\mathit{r})<0$. We excluded these density fields from our training set. The grid sizes used for these calculations were $32\times 32\times 32$, and thus the density field of monomer A from each SCFT iteration step can be considered as a gray-scale 3D image with a size equal to ${32}^3$. For each of the five training phases, we performed 150 SCFT calculations with constraints on space group symmetry and an additional 150 SCFT calculations without the constraints. The resulting trajectories generated a total of 18,273 images after removing those images with unphysical densities.

GAN Architecture and Training.

Our implementation is a deep convolutional GAN, which comprises two competing convolutional neural networks, the generator and the discriminator (18). SI Appendix, Table S1 summarizes the architectures of the neural networks. The generator maps a latent vector of size 100 to a 3D gray-scale image of size $1\times 32\times 32\times 32$. The generator consists of four 3D transposed convolutional layers, each of which is followed by batch normalization and rectified linear unit (ReLu) as the activation function, except for the last layer, which uses a sigmoid activation function without batch normalization. The sigmoid activation forces the generated data to lie in the range of [0, 1], which can be considered as density fields without any further transformation. The discriminator functions as a binary classifier that processes a 3D gray-scale image of size $1\times 32\times 32\times 32$ from the generator or from the training set. The discriminator consists of four 3D convolutional layers, each of which is followed by batch normalization and a Leaky ReLu activation function, except for the last layer. The last layer again uses a sigmoid activation, now to produce a score ranging from 0 to 1. The scores represent the prediction of the discriminator on whether the input data is fake to real.

The training process of a GAN involves a minmax game between the generator and the discriminator, where the generator tries to minimize the probability that the discriminator predicts the generated data as fake while the discriminator tries to maximize the probability of correct classification on both the real and fake data (17). To achieve this optimization, the binary cross-entropy (BCE) loss function is used to measure the difference between the ground-truth labels and the predictions of the discriminator. The training of GAN was conducted using the open-source software package PyTorch (55). During each training epoch, the model was trained using batches of real images and fake images mapped from randomly generated latent vectors. The batch size was set as 128. The optimization of both the generator and discriminator was performed using an Adam optimizer with a learning rate of 0.0002 and hyperparameters $({\beta }_1,{\beta }_2)$ of $(0.5,0.999)$. The training was performed iteratively for up to 80 epochs.

Unlike other machine learning methods, determining the stopping criterion for GAN training by tracking the losses is not obvious because it involves two competing neural networks. Instead, it is more straightforward to directly evaluate the quality of the generated data. In our case, tracking the evolution of an isosurface of the generated fields by direct visualizations proved to be an effective strategy. A visualization of the isosurface evolution for a few generated fields is provided in Movie S1. The model used for generating initial guesses for SCFT calculations was chosen by comparing the isosurface plots during the training progress. As shown in SI Appendix, Figs. S1 and S2, the isosurfaces at ${\varphi }_{\mathrm{A}}=0.5$ change little after 30 epochs, but the isosurfaces at 0.9 keep evolving until reaching 45 epochs.

SCFT Calculations with GAN-generated Initial Guesses.

After the training of the GAN, 5,000 initial guesses were created by the passing 5,000 random noise vectors sampled from a normal distribution with a mean of 0 and a SD of 1 through the generator, and then using the resulting density fields with a Lagrange multiplier field of zero to initialize the chemical potential fields (9) for flexible unit cell SCFT calculations without constraints on the space group symmetry ($P1$ space group). Since initializing the SCFT calculations in a unit cell with flexible edge lengths and angles can be unstable, we performed the calculations in two steps. In the first step, outputs from the trained GAN were used to seed new SCFT calculations in a unit cell with flexible edge lengths and fixed angles at 90${}^{°}$, i.e., an orthorhombic box. The initial edge lengths were set to be equal to 3.0 times of the unperturbed end-to-end distance of the polymer, $R_e=\sqrt{N}b$. This initial part of the solution was converged to a tolerance of ${10}^{-4}$ using a grid resolution of $32\times 32\times 32$. In the second step, converged chemical potential fields from the first step were used as inputs for SCFT calculations in a unit cell with both flexible edge lengths and angles. Here, a tolerance of ${10}^{-6}$ and a higher grid resolution of $64\times 64\times 64$ were used to increase the accuracy of the calculated free energies.

Supplementary Material

Appendix 01 (PDF)

Movie S1.

Evolution of the generated density fields during the training process of GAN.

Movie S2.

The convergence of a GAN-generated initial guess to double-diamond phase via SCFT.

Movie S3.

The convergence of a GAN-generated initial guess to H¹⁸¹ phase via SCFT.

Data, Materials, and Software Availability

The GAN training uses PyTorch, which is available at https://pytorch.org/ (56). Self-consistent field theory calculations use the open-source Polymer Self-Consistent Field software package, which is available at https://github.com/dmorse/pscfpp (57). The scripts used for the calculations described here are available on Github at https://github.com/kdorfmanUMN/GANs_SCFT (58). The data supporting this manuscript is available at https://hdl.handle.net/11299/257550 (59).