Abstract
Divergence time estimation is crucial to provide temporal signals for dating biologically important events from species divergence to viral transmissions in space and time. With the advent of high-throughput sequencing, recent Bayesian phylogenetic studies have analyzed hundreds to thousands of sequences. Such large-scale analyses challenge divergence time reconstruction by requiring inference on highly correlated internal node heights that often become computationally infeasible. To overcome this limitation, we explore a ratio transformation that maps the original  internal node heights into a space of one height parameter and
internal node heights into a space of one height parameter and  ratio parameters. To make the analyses scalable, we develop a collection of linear-time algorithms to compute the gradient and Jacobian-associated terms of the log-likelihood with respect to these ratios. We then apply Hamiltonian Monte Carlo sampling with the ratio transform in a Bayesian framework to learn the divergence times in 4 pathogenic viruses (West Nile virus, rabies virus, Lassa virus, and Ebola virus) and the coralline red algae. Our method both resolves a mixing issue in the West Nile virus example and improves inference efficiency by at least 5-fold for the Lassa and rabies virus examples as well as for the algae example. Our method now also makes it computationally feasible to incorporate mixed-effects molecular clock models for the Ebola virus example, confirms the findings from the original study, and reveals clearer multimodal distributions of the divergence times of some clades of interest.
ratio parameters. To make the analyses scalable, we develop a collection of linear-time algorithms to compute the gradient and Jacobian-associated terms of the log-likelihood with respect to these ratios. We then apply Hamiltonian Monte Carlo sampling with the ratio transform in a Bayesian framework to learn the divergence times in 4 pathogenic viruses (West Nile virus, rabies virus, Lassa virus, and Ebola virus) and the coralline red algae. Our method both resolves a mixing issue in the West Nile virus example and improves inference efficiency by at least 5-fold for the Lassa and rabies virus examples as well as for the algae example. Our method now also makes it computationally feasible to incorporate mixed-effects molecular clock models for the Ebola virus example, confirms the findings from the original study, and reveals clearer multimodal distributions of the divergence times of some clades of interest.
Keywords: Bayesian inference, divergence time estimation, effective sample size, Hamiltonian Monte Carlo, pathogens, phylogenetics, ratio transformation
Since Zuckerkandl and Pauling (1962) proposed the first molecular clock model, the development of more reliable divergence time estimation techniques has thrived. Because evolutionary rate and time are confounded in stochastic models for molecular sequence data, one may improve divergence time inference either via advances in treatment of rates or treatment of times. However, the majority of the effort has centered upon improving the model aspects that describe either how evolutionary rates change across the tree or how divergence events happen on the tree resulting as the positions of internal nodes (e.g., coalescent events and/or birth–death events) while improvement of the estimation machinery has received less attention.
This imbalance is partly due to the constraints on the node heights imposed by the tree structure. Assuming a rooted tree with the root node on the top and tip nodes at the bottom, an internal node must be higher than its descendant nodes but lower than its parent node. These constraints pose great challenge for inferring internal node heights jointly, so one typically samples or optimizes the height of one node at a time.
Despite this inference difficulty, divergence time estimation is crucial to provide temporal signals for dating biologically important events, from species divergence to viral transmissions in space and time (Erwin et al. 2011; Meredith et al. 2011; Düx et al. 2020; Lemey et al. 2020). Repeated breakthroughs in sequencing technologies have led to molecular data accumulating at an ever-increasing pace. This often results in data sets that contain so many sequences that the desired divergence time analyses become computationally infeasible. When faced with such obstacles, investigators resort to analyzing only a small proportion of the available data and/or sacrificing statistical rigor and biological plausibility by adopting procedures and models that are flawed but computationally convenient (see, e.g., Simion et al. (2020)). There is, therefore, substantial value in reducing the amount of computation necessary for statistically sound divergence time inference.
In Kishino et al. (2001), the authors transform the internal node heights of a phylogeny with contemporaneous data (sampled at the same time) into a collection of ratios that sum to  . With a Dirichlet prior distribution, Kishino et al. were then able to jointly sample all proportions at one time. Inspired by their pioneering work, we explore a more general ratio transformation, similar to that used in Fourment and Darling (2019), for the internal node heights that one can apply to both serially sampled or contemporaneous data. The ratio transformation serves as a reparameterization that works with any existing phylogenetic models without the need for any specific prior. In fact, the proposed ratio transformation preserves the topology-imposed constraints by its construction, allowing the ratios to be independent so that they are easy to sample from or optimize on.
. With a Dirichlet prior distribution, Kishino et al. were then able to jointly sample all proportions at one time. Inspired by their pioneering work, we explore a more general ratio transformation, similar to that used in Fourment and Darling (2019), for the internal node heights that one can apply to both serially sampled or contemporaneous data. The ratio transformation serves as a reparameterization that works with any existing phylogenetic models without the need for any specific prior. In fact, the proposed ratio transformation preserves the topology-imposed constraints by its construction, allowing the ratios to be independent so that they are easy to sample from or optimize on.
We here show that one can calculate the transformation and the determinant of the Jacobian matrix of the transformation in linear-time with respect to the number of tips (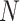 ). With the determinant of the Jacobian matrix, one can set up the phylogenetic model with respect to the untransformed node heights, but sample from the transformed ratio space. To make use of an advanced linear-time gradient of the log-likelihood algorithm (Ji et al. 2020), we show that one can transform the gradient with respect to the untransformed node heights to the gradient with respect to the transformed ratio space with
). With the determinant of the Jacobian matrix, one can set up the phylogenetic model with respect to the untransformed node heights, but sample from the transformed ratio space. To make use of an advanced linear-time gradient of the log-likelihood algorithm (Ji et al. 2020), we show that one can transform the gradient with respect to the untransformed node heights to the gradient with respect to the transformed ratio space with 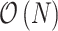 calculations. The linear-time gradient transformation enables the application of gradient-based Monte Carlo samplers such as the Hamiltonian Monte Carlo (HMC) method (Neal 2011) in the Bayesian framework. HMC shows great potential for improving computational efficiency in many phylogenetic applications (Dinh et al. 2017; Ji et al. 2020; Baele et al. 2020).
calculations. The linear-time gradient transformation enables the application of gradient-based Monte Carlo samplers such as the Hamiltonian Monte Carlo (HMC) method (Neal 2011) in the Bayesian framework. HMC shows great potential for improving computational efficiency in many phylogenetic applications (Dinh et al. 2017; Ji et al. 2020; Baele et al. 2020).
We apply the ratio transformation to simultaneously learn the branch-specific evolutionary rates and the internal node heights of 4 viral examples with serially sampled data and an algae example with contemporaneous samples and fossil-informed calibration priors. Our method significantly improves inference efficiency with a 5- to 8-fold computational performance increase for our Lassa and rabies virus examples and an 11-fold increase for the algae example. More interestingly, the West Nile virus example shows that our sampler better approximates the posterior density than do classic univariable samplers that suffer from Markov chain Monte Carlo (MCMC) mixing issues. For an Ebola virus example, we show that our method makes it computationally feasible to employ a mixed-effects relaxed clock model (Bletsa et al. 2019) to account for both clade- and branch-specific effects that reveal clearer multi-modal distribution of divergence times for clades of interest.
Materials and Methods
New Approach
In this section, we define necessary notation and derive the ratio transformation and its related linear-time algorithms.
Notation.
Assume the root node is on the top of a rooted phylogeny with 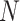 tips and
tips and  internal nodes. We use numbers
internal nodes. We use numbers 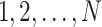 to denote the tip nodes and numbers
to denote the tip nodes and numbers 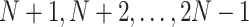 for the internal nodes where the root node is always
for the internal nodes where the root node is always 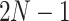 . We use notation
. We use notation 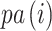 to denote the parent node of node
to denote the parent node of node 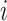 . We denote a branch on the tree by the number of the child node it ends at (i.e., branch
. We denote a branch on the tree by the number of the child node it ends at (i.e., branch 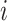 connects node
connects node 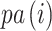 to
to 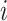 ). We denote the height (i.e., time) of node
). We denote the height (i.e., time) of node 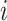 with
with 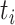 . When
. When 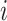 is a tip node (i.e.,
is a tip node (i.e., 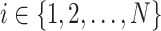 ), its height is the sampling time. In divergence time estimation, one is interested in estimating the heights of internal nodes.
), its height is the sampling time. In divergence time estimation, one is interested in estimating the heights of internal nodes.
Without loss of generality, we derive the ratio transform where the tip nodes can be associated with serially sampled data and where the transformation with contemporaneous data is then a special case where all tip node times are identical. We first define epochs such that any internal node belongs to one and only one epoch. We then define a ratio parameter ascribed to each of the internal nodes except for the root.
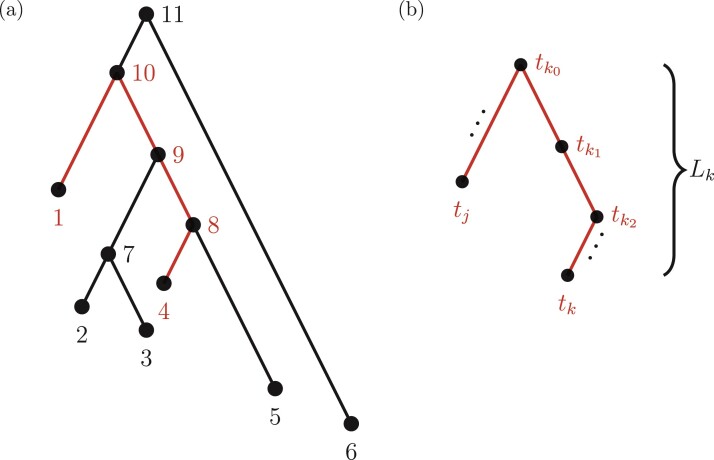
Epoch construction and the ratio transformation.
For aninternal node, we refer to its earliest (i.e., highest) descendant tip node as its anchor node. Therefore, the anchor node of an internal node is its closest descendant tip node. To make the anchor nodes consistent and unique, we assign an arbitrary ordering among tip nodes to distinguish those with the same sampling times. For example, we pick the tip node with the smallest node number as the anchor node from all closest tip nodes sampled at the same time. We group all internal nodes with the same anchor node into an epoch. We refer to an epoch by the number of its anchor node. An epoch is constructed to have a chain structure from its anchor node up to the highest node in the epoch (see Fig. 1a). Except for the epoch to which the root node belongs, we refer to the parent node of the highest node in an epoch as its connecting node such that the connecting node of an epoch belongs to another epoch. We treat the root node as the connecting node for epochs of its immediate descendant nodes.
Figure 1.
Epoch construction on a 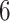 -taxa tree. a) Example tree with serially sampled data. b) One epoch example where epoch
-taxa tree. a) Example tree with serially sampled data. b) One epoch example where epoch 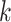 starts from node
starts from node 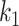 down to its anchor node
down to its anchor node 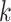 and node
and node 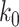 is the connecting node of epoch
is the connecting node of epoch 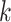 that belongs to epoch
that belongs to epoch 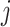 . For the example tree in a) with anchor tip
. For the example tree in a) with anchor tip 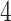 ,
, 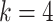 ,
, 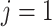 , and
, and 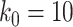 . For anchor tip
. For anchor tip 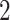 ,
, 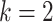 ,
,  , and
, and 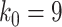 . For anchor tip
. For anchor tip 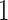 ,
, 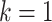 is the starting epoch that contains the root node. Tip nodes
is the starting epoch that contains the root node. Tip nodes 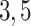 , and
, and 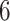 do not anchor any epochs (i.e., their parent nodes belong to epochs anchored at other tip nodes).
do not anchor any epochs (i.e., their parent nodes belong to epochs anchored at other tip nodes).
Let 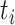 denote the height of node
denote the height of node 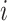 and
and 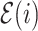 be the epoch to which node
be the epoch to which node 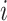 belongs. We refer to the epoch to which the root node belongs as the starting epoch and assign it as
belongs. We refer to the epoch to which the root node belongs as the starting epoch and assign it as 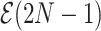 . We abuse notation by referring to the
. We abuse notation by referring to the 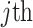 node of epoch
node of epoch 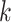 as
as 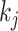 . For epoch
. For epoch 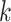 that contains
that contains 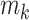 internal nodes with strictly positive branch lengths, we have
internal nodes with strictly positive branch lengths, we have 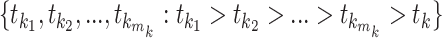 . We refer to the connecting node of an epoch as the
. We refer to the connecting node of an epoch as the 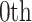 node of an epoch (i.e.,
node of an epoch (i.e., 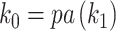 ). We define
). We define 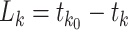 as the length of epoch
as the length of epoch 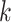 (see Fig. 1b). For the
(see Fig. 1b). For the 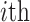 internalnode
internalnode 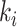 from epoch
from epoch 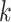 (i.e.,
(i.e., 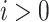 ), we define its ratio parameter
), we define its ratio parameter 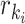 as
as
| (1) |
where 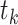 is the height of the anchor node of epoch
is the height of the anchor node of epoch 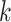 and
and 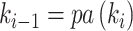 . Note that the anchor node of epoch
. Note that the anchor node of epoch 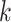 is not necessarily immediately descendant to node
is not necessarily immediately descendant to node 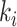 , whereas node
, whereas node 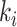 is always immediately descendant to node
is always immediately descendant to node 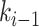 . In fact, the anchor node of epoch
. In fact, the anchor node of epoch 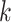 is the highest descendant tip node for all nodes in the epoch (by definition) and is only immediately descendant to the last node
is the highest descendant tip node for all nodes in the epoch (by definition) and is only immediately descendant to the last node 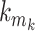 of the epoch. Therefore, when
of the epoch. Therefore, when 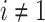 , node
, node 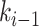 and node
and node 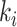 are both from epoch
are both from epoch 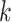 . And when
. And when 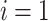 , node
, node 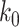 is the connecting node of epoch
is the connecting node of epoch 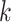 that belongs to another epoch and the denominator in Equation (1) becomes
that belongs to another epoch and the denominator in Equation (1) becomes 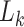 (i.e., the length of epoch
(i.e., the length of epoch 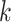 ). One can write the time of an internal node as a function of the ratios and the epoch lengths as
). One can write the time of an internal node as a function of the ratios and the epoch lengths as
| (2) |
To ease notation, let 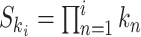 be the product of ratios for internal node
be the product of ratios for internal node 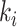 of epoch
of epoch 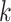 . Equation (2) simplifies to
. Equation (2) simplifies to
| (3) |
Interestingly, there is only one degree of freedom for all epoch lengths because
| (4) |
such that the length of epoch 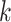 is determined by the length of the epoch of its connecting node (
is determined by the length of the epoch of its connecting node (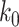 ) and the two associated anchor node times (
) and the two associated anchor node times (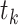 ,
, 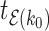 ). We arrive at the following recursive relationship for epoch lengths
). We arrive at the following recursive relationship for epoch lengths
| (5) |
Therefore, there is effectively only one degree of freedom for the scale of time with all ratios denoting the relative height an internal node has using its parent node and the anchor node as reference. There are many choices for modeling this single dimension for time scale (e.g., one may arbitrarily choose one of the epoch lengths). We pick the starting epoch length as the free parameter 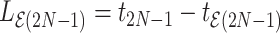 , which we refer to as the height parameter because it represents the height difference from the root node to its closest tip node (all tip nodes are descendants of the root) and is the only dimension. We refer to the space of the height and
, which we refer to as the height parameter because it represents the height difference from the root node to its closest tip node (all tip nodes are descendants of the root) and is the only dimension. We refer to the space of the height and  ratio parameters as the ratio space. We refer to the space of all untransformed internal node heights as the height space. We refer to the transformation from the height space into the ratio space as theratio transform.
ratio parameters as the ratio space. We refer to the space of all untransformed internal node heights as the height space. We refer to the transformation from the height space into the ratio space as theratio transform.
Algorithm 1 illustrates the ratio transform through a single post-order traversal that visits every node on the tree in a descendant-first manner. Likewise, one can perform the inverse ratio transform to get node heights from the ratios by reversing Equation (1) through a pre-order traversal.
Algorithm 1 Ratio transform through a single post-order traversal
-
for node
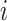 in a post-order traversal do
in a post-order traversal do-
if
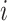 is a tip node then
is a tip node thenSet the anchor tip of epoch
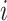 as node
as node 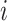 .
.
-
else
Set the anchor tip of
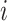 the same as the highest anchor tip of its immediate descendant nodes.
the same as the highest anchor tip of its immediate descendant nodes.Calculate
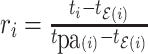 according to Equation (1).
according to Equation (1).
end if
-
end for
Gradient and Jacobian.
Many modern inference machineries benefit from gradient information to find descending directions of the likelihood surface or to efficiently integrate dynamics along the surface for generating Monte Carlo proposals (e.g., Ji et al. (2020) contains gradient applications in non-linear optimization and Bayesian posterior sampling). When transforming probability densities from their original space into another (e.g., the ratio space in this case), one needs the determinant of the Jacobian matrix to correctly “weight” the transformed density (see Theorem 2.1.5 from Casella and Berger (2001)). In this section, we derive algorithms for transforming the “unweighted” likelihood into the ratio space together with the associated quantities from the log-determinant of the Jacobian matrix to correctly set the “weight.”
In Ji et al. (2020), we introduced a linear-time algorithm for calculating the gradient of the log-likelihood with respect to the branch length 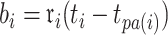 that is the product of the evolutionary rate
that is the product of the evolutionary rate 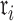 and the time duration
and the time duration 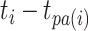 of branch
of branch 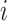 . To calculate the gradient with respect to node heights, one starts with the gradient with respect to branch lengths and finishes via the chain rule. More specifically, for node
. To calculate the gradient with respect to node heights, one starts with the gradient with respect to branch lengths and finishes via the chain rule. More specifically, for node 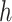 with its two immediate descendant nodes
with its two immediate descendant nodes 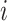 and
and 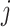 , the derivative of the log-likelihood,
, the derivative of the log-likelihood, 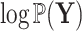 , with respect to
, with respect to 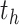 is:
is:
| (6) |
It is important to recall that a ratio parameter is only explicit to the node it assigns to and all its descendant nodes by Equation (2). Therefore, we only need the partial derivatives 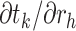 from node
from node 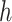 and all its descendant nodes
and all its descendant nodes 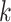 to finish the chain rule
to finish the chain rule
| (7) |
To derive the partial derivative 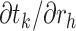 for any two nodes
for any two nodes 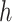 and
and 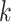 such that node
such that node 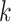 is a descendant of node
is a descendant of node 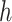 , we separate the node pairs into two cases. The first case considers node
, we separate the node pairs into two cases. The first case considers node 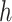 and node
and node 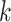 in the same epoch (including the pair where
in the same epoch (including the pair where 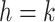 , e.g., Equation (3)), such that
, e.g., Equation (3)), such that
| (8) |
For the other case where node 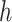 and node
and node 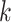 belong to different epochs, we start with revealing the relationship between the partial derivatives of node
belong to different epochs, we start with revealing the relationship between the partial derivatives of node 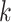 ’s height
’s height 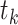 and its connecting node
and its connecting node 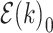 ’s height
’s height 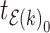 with respect to the same ratio
with respect to the same ratio 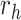 (e.g., plug Equation (5) in Equation (3)), such that
(e.g., plug Equation (5) in Equation (3)), such that
| (9) |
Equation (9) shows that one obtains the partial derivative of a node height 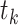 with respect to ratio
with respect to ratio 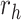 by multiplying the related ratio product (i.e.,
by multiplying the related ratio product (i.e., 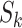 ) and the partial derivative of the node height
) and the partial derivative of the node height 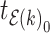 with respect to ratio
with respect to ratio 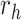 (i.e.,
(i.e., 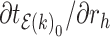 ). Combining Equations (8) and (9), we inductively derive a general expression for the derivatives where node
). Combining Equations (8) and (9), we inductively derive a general expression for the derivatives where node 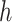 and node
and node 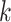 do not belong to the same epoch. We arrive at this derivation through the existence of a series of connecting nodes (when traveling from node
do not belong to the same epoch. We arrive at this derivation through the existence of a series of connecting nodes (when traveling from node 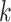 to node
to node 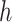 ) starting from epoch
) starting from epoch 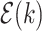 that the last connecting node belongs to the same epoch as node
that the last connecting node belongs to the same epoch as node 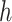 , that is,
, that is, 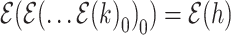 . The general expression for the derivative becomes
. The general expression for the derivative becomes
| (10) |
By naively plugging Equations (8) and (10) into Equation (7), we obtain the gradient with respect to the ratio space. However, this operation amounts to 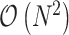 computations for transforming the gradient. To overcome this computational burden, we develop a linear-time
computations for transforming the gradient. To overcome this computational burden, we develop a linear-time 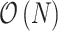 algorithm for transforming the gradient.
algorithm for transforming the gradient.
Post-order traversal
Consider 3 internal nodes 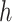 ,
, 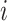 , and
, and 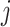 such that node
such that node 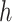 is the parent node of node
is the parent node of node 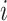 and node
and node 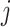 . The linear-time algorithm for transforming the gradient with respect to ratio parameters builds on 2 properties of the ratio transformation. The first property is that any descendant node of node
. The linear-time algorithm for transforming the gradient with respect to ratio parameters builds on 2 properties of the ratio transformation. The first property is that any descendant node of node 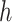 except node
except node 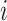 or node
or node 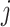 is a descendant node of either node
is a descendant node of either node 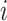 or node
or node 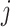 (for bifurcating trees). The other property is that node
(for bifurcating trees). The other property is that node 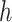 belongs to the same epoch as either node
belongs to the same epoch as either node 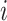 or node
or node 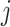 . As is common in dynamic programming algorithms, we want to derive the relationship of
. As is common in dynamic programming algorithms, we want to derive the relationship of 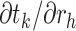 with
with 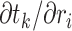 and
and 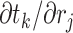 , where node
, where node 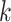 is descendant of node
is descendant of node 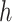 to reuse quantities cached from evaluating Equation (7) on descendant nodes. More specifically, we want to reuse the summations already determined for
to reuse quantities cached from evaluating Equation (7) on descendant nodes. More specifically, we want to reuse the summations already determined for 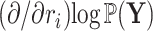 and
and 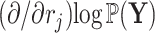 when calculating
when calculating 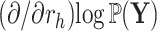 as in Equation (9).
as in Equation (9).
Without loss of generality, we assume node 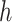 belongs to the same epoch as node
belongs to the same epoch as node 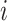 . The following relationships between derivatives with respect to the three ratio parameters
. The following relationships between derivatives with respect to the three ratio parameters  ,
, 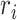 , and
, and 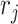 enable the linear-time algorithm through a single post-order traversal to update the gradient from the height space into the ratio space (except for the height parameter). From Equation (8) and Equation (10), when node
enable the linear-time algorithm through a single post-order traversal to update the gradient from the height space into the ratio space (except for the height parameter). From Equation (8) and Equation (10), when node 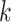 is a descendant of node
is a descendant of node 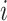 (including
(including 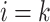 ) such that node
) such that node 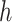 and node
and node 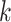 are in the same epoch,
are in the same epoch,
| (11) |
When node 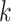 is descendant of node
is descendant of node 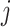 (including
(including 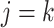 ) such that node
) such that node 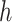 is the connecting node to the epoch
is the connecting node to the epoch 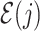 where node
where node 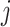 is the first node,
is the first node,
| (12) |
Note that we model the ratio parameters as independent of each other (i.e., 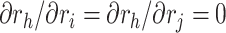 ). Equations (11) and (12) come from the special structure of the transform that the height of an internal node is a product of a series of ratio parameters with one single height parameter. Algorithm 2 illustrates updating the gradient with respect to all ratio parameters (except for the height parameter) where one reuses the derivatives of the log-likelihood with respect to two immediate descendant nodes (i.e., nodes
). Equations (11) and (12) come from the special structure of the transform that the height of an internal node is a product of a series of ratio parameters with one single height parameter. Algorithm 2 illustrates updating the gradient with respect to all ratio parameters (except for the height parameter) where one reuses the derivatives of the log-likelihood with respect to two immediate descendant nodes (i.e., nodes 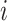 and
and 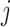 ) to calculate the derivative of the log-likelihood with respect to the parent node (i.e., node
) to calculate the derivative of the log-likelihood with respect to the parent node (i.e., node 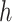 ).
).
Algorithm 2 Transforming the gradient of the log-likelihood with respect to ratio parameters by post-order traversal
-
for node
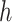 in a post-order traversal do
in a post-order traversal do-
if
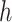 is a tip node then
is a tip node thenSet the gradient of
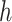 as 0.
as 0.
-
else
Let node
 and node
and node  be the two immediate descendant nodes of node
be the two immediate descendant nodes of node  such that node
such that node  and node
and node 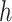 belong to the same epoch.
belong to the same epoch.Set the gradient of
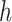 as
as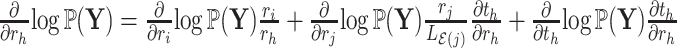 .
.
end if
-
end for
Pre-order traversal
We now update the gradient of the log-likelihood with respect to the height parameter which is the only dimension left in the ratio transform. We use a pre-order traversal to update the gradient in this dimension because the transformation of all internal node heights depends on it. The update is
| (13) |
Based on Equation (4), we calculate all the partial derivatives 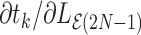 according to Algorithm 3 through a single pre-order traversal.
according to Algorithm 3 through a single pre-order traversal.
Algorithm 3 Transforming gradient of the log-likelihood with respect to the height parameter by pre-order traversal
for node
 in a pre-order traversal do
in a pre-order traversal doif
 is the root node then
is the root node thenSet the derivative of node height
 with respect to height parameter as 1 (i.e.,
with respect to height parameter as 1 (i.e., 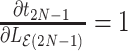 ).
).else
Set the derivative of
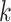 as the product of
as the product of 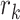 and the derivative of its parent node with respect to height parameter (i.e., ).
and the derivative of its parent node with respect to height parameter (i.e., ).end if
end for
Determinant of the Jacobian matrix
We now derive theJacobian matrix associated with the ratio transform whose determinant sets the weight for the transformed density. One derives the full Jacobian matrix for the ratio transform by applying Equation (8) and Equation (10). Note the special structure that has 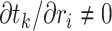 if and only if
if and only if 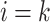 or node
or node  is descendant of node
is descendant of node  , and also note the independence between the height parameter and the ratio parameters. By ordering the entries in a descendant node first fashion that coincides with how nodes are visited in a post-order traversal, the Jacobian matrix becomes triangular (including the height parameter). Because the determinant of a triangular matrix only involves the diagonal entries, the determinant of the Jacobian matrix
, and also note the independence between the height parameter and the ratio parameters. By ordering the entries in a descendant node first fashion that coincides with how nodes are visited in a post-order traversal, the Jacobian matrix becomes triangular (including the height parameter). Because the determinant of a triangular matrix only involves the diagonal entries, the determinant of the Jacobian matrix 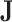 becomes
becomes
| (14) |
Gradient of log-determinant of the Jacobian matrix
We complete this section with a final linear-time algorithm for calculating the gradient of the log-determinant of the Jacobian matrix with respect to the ratio space for applying HMC on this transformed space as described in the next section. This additional gradient component facilitates using HMC to sample all dimensions jointly in the ratio space. Similar to the case of updating the gradient of the log-likelihood from the original space into the ratio space, naively applying Equation (8) and Equation (10) results in an undesired quadratic computational load. One can benefit from the same properties that lead to Algorithm 2 with a modified two-pass linear-time Algorithm 4 that calculates all the derivatives of the log-determinant of the Jacobian matrix with respect to the ratioparameters.
Algorithm 4 Calculating gradient of the log-determinant of the Jacobian matrix with respect to ratio parameters by post-order traversal
for node
 in a post-order traversal do
in a post-order traversal doif
 is a tip node then
is a tip node then
else
Let node
 and node
and node  be the two immediate descendant nodes of node
be the two immediate descendant nodes of node 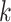 such that node
such that node 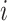 and node
and node 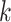 belong to the same epoch, and compute
belong to the same epoch, and compute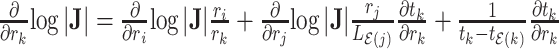 .
.end if
end for
for every internal node
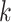 do
doUpdate
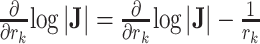 .
.end for
Hamiltonian Monte Carlo.
HMC is a state-of-the-art MCMC method that generates efficient proposals through Hamiltonian dynamics (Neal 2011) for the Metropolis–Hastings algorithm (Metropolis et al. 1953; Hastings 1970). For an arbitrary and unbounded parameter of interest 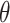 with the posterior density
with the posterior density 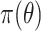 , HMC introduces an auxiliary parameter
, HMC introduces an auxiliary parameter 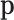 and samples from the product density
and samples from the product density 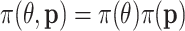 through:
through:
| (15) |
where 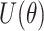 is the “potential energy” often set to the negative log-posterior density and
is the “potential energy” often set to the negative log-posterior density and 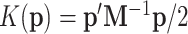 is the “kinetic energy” as the auxiliary parameter
is the “kinetic energy” as the auxiliary parameter 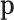 typically follows a multivariate normal distribution
typically follows a multivariate normal distribution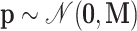 with a “mass matrix”
with a “mass matrix” 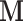 as the covariancematrix. HMC has shown great potential in diversephylogenetic applications (Dinh et al. 2017; Baele et al. 2020; Ji et al. 2020).
as the covariancematrix. HMC has shown great potential in diversephylogenetic applications (Dinh et al. 2017; Baele et al. 2020; Ji et al. 2020).
Naive application of HMC on the space of internal node heights is highly inefficient because of the irregular constraints on these parameters. Instead, the ratio space is trivial to extend such that it is unbounded by applying a logit-transform to each ratio independently and a log-transfrom to the single height parameter. We apply HMC on the (extended) ratio space for efficient sampling of all internal node heights while fixing the tree topology and other model parameters. Finally, we also apply HMC for jointly sampling the evolutionary rates and times (i.e., divergence time estimation) and explore the additional efficiency gain this affords.
Preconditioning with adaptive variance
The geometric structure of the posterior distribution significantly affects the computational efficiency of HMC. For example, when the scales of the posterior distribution vary among individual parameters, failing to account for such structure may reduce the efficiency of HMC (Neal 2011; Stan Development Team 2017; Ji et al. 2020). We can adapt HMC for such structure by modifying the dynamics in Equation (15) via an appropriately chosen mass matrix 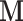 . In Ji et al. (2020), we employ a mass matrix informed by the diagonal entries of the Hessian matrix of the log-posterior to account for the variable scales among dimensions. Unfortunately, one needs the full Hessian matrix in the original height space to transform into the Hessian matrix with respect to the ratio space. This strategy is too computationally expensive toadopt.
. In Ji et al. (2020), we employ a mass matrix informed by the diagonal entries of the Hessian matrix of the log-posterior to account for the variable scales among dimensions. Unfortunately, one needs the full Hessian matrix in the original height space to transform into the Hessian matrix with respect to the ratio space. This strategy is too computationally expensive toadopt.
To incorporate information from the covariance matrix without excessive computational burden, we seek an alternative adaptive MCMC procedure (Haario et al. 1999; Andrieu and Thoms 2008; Roberts and Rosenthal 2009). Adaptive MCMC has previously found its way into Bayesian phylogenetic inference (Baele et al. 2017) and we use this technique here to tune  to the covariance matrix estimated from previous samples in the Markov chain. We further restrict
to the covariance matrix estimated from previous samples in the Markov chain. We further restrict  to remain diagonal and hence to scale the ratio dimensions according to their marginal covariance. This restriction is commonly imposed to regularize the estimate, and a diagonal matrix alone can greatly enhance sampling efficiency of HMC in many situations (Stan Development Team 2017; Ji et al. 2020). We start the HMC sampler with an identity matrix as
to remain diagonal and hence to scale the ratio dimensions according to their marginal covariance. This restriction is commonly imposed to regularize the estimate, and a diagonal matrix alone can greatly enhance sampling efficiency of HMC in many situations (Stan Development Team 2017; Ji et al. 2020). We start the HMC sampler with an identity matrix as  to collect an initial set of samples (e.g., 200 in our analyses), after which we employ the sample covariance to tune
to collect an initial set of samples (e.g., 200 in our analyses), after which we employ the sample covariance to tune  adaptively. Also, we only update the diagonal mass matrix every
adaptively. Also, we only update the diagonal mass matrix every 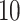 HMC iterations so that the cost of computing the adaptive
HMC iterations so that the cost of computing the adaptive 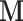 diagonals remains negligible.
diagonals remains negligible.
Data
We examine the molecular evolution of West Nile virus (WNV) in North America (1999–2007), rabies virus (RABV) in the United States (1982–2004), the S segmentof Lassa virus (LASV) in West Africa (2008–2013), Ebolavirus (EBOV) in the Democratic Republic of Congo, Africa (2018–2020), and the coralline red algae subclass Corallinophycidae with contemporaneous data and fossil record informed calibration priors on 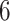 internal nodes (Biek et al. 2007; Pybus et al. 2012; Andersen et al. 2015; Mbala-Kingebeni et al. 2021; Pena et al. 2020). In all data sets, phylogenetic analyses have revealed a high variation of the evolutionary rates across branches in the underlying phylogeny.
internal nodes (Biek et al. 2007; Pybus et al. 2012; Andersen et al. 2015; Mbala-Kingebeni et al. 2021; Pena et al. 2020). In all data sets, phylogenetic analyses have revealed a high variation of the evolutionary rates across branches in the underlying phylogeny.
West Nile virus
West Nile virus is a mosquito-borne RNA virus that involves multiple species of mosquitoes and birds where birds are the primary host. WNV first emerged in the Americas in New York in 1999, and quickly spread across the continent, causing an epidemic of human disease accompanied with massive bird deaths. In total, human infections have resulted in over 48,000 reported cases, 24,000 reported neuroinvasive cases, and over 2300 deaths (Hadfield et al. 2019). The molecular sequence data consist of 104 full genomes, with a total alignment length of 11,029 nucleotides, and were collected from infected human plasma samples from 2003 to 2007 as well as near-complete genomes obtained from GenBank (Pybus et al. 2012).
Rabies virus
Rabies is an RNA virus that can cause zoonotic disease and is responsible for over 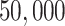 human deaths every year. Besides bats, several terrestrial carnivore species such as raccoons are important rabies reservoirs. Before the detection of a raccoon-specific rabies virus variant in 1970s, there was only limited focus on raccoons as a primary host for rabies in the southeastern United States, specifically Florida. Over the following decades, an emergence of the virus spread along the mid-Atlantic coast and northeastern United States. We analyze the molecular sequences originally described in Biek et al. (2007) that previously served as an example dataset in work on the flexible non-parametric skygrid coalescent model (Gill et al. 2016). The data consist of
human deaths every year. Besides bats, several terrestrial carnivore species such as raccoons are important rabies reservoirs. Before the detection of a raccoon-specific rabies virus variant in 1970s, there was only limited focus on raccoons as a primary host for rabies in the southeastern United States, specifically Florida. Over the following decades, an emergence of the virus spread along the mid-Atlantic coast and northeastern United States. We analyze the molecular sequences originally described in Biek et al. (2007) that previously served as an example dataset in work on the flexible non-parametric skygrid coalescent model (Gill et al. 2016). The data consist of 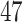 sequences sampled from rabid raccoons between 1982 and 2004 that contain the complete rabies nucleoprotein gene (1365 bp) with part of a noncoding region (87 bp) immediately following its 3
sequences sampled from rabid raccoons between 1982 and 2004 that contain the complete rabies nucleoprotein gene (1365 bp) with part of a noncoding region (87 bp) immediately following its 3 end, and a large portion of the glycoprotein gene (1359 bp).
end, and a large portion of the glycoprotein gene (1359 bp).
Lassa virus
Lassa virus is the causative agent of Lassa fever, a hemorrhagic fever endemic to parts of West Africa that is responsible for thousands of deaths and tens-of-thousands of hospitalizations each year (Andersen et al. 2015). LASV infections can lead to Lassa fever, a hemorrhagic fever similar to that from EBOV and endemic to parts of West Africa. Despite the fact that Lassa fever can lead to over 50% fatality rates among hospitalized patients, an effective vaccine for LASV has yet to be developed and approved. Unlike EBOV (see next paragraph), which passes directly between humans, LASV circulates in a rodent (Mastomys natalensis) reservoir and mainly infects humans through contact with rodent excreta. The LASV genome is comprised of 2 negative-sense single-stranded RNA segments: the L segment is 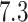 kilobase pairs (kb) long, and the S segment is
kilobase pairs (kb) long, and the S segment is 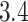 kb long. In this paper, we use the S segment of the LASV sequence data set of Andersen et al. (2015) that consists of
kb long. In this paper, we use the S segment of the LASV sequence data set of Andersen et al. (2015) that consists of 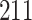 samples obtained at clinics in both Sierra Leone and Nigeria, rodents in the field, laboratory isolates and previously sequenced genomes.
samples obtained at clinics in both Sierra Leone and Nigeria, rodents in the field, laboratory isolates and previously sequenced genomes.
Ebola virus
The Ebola virus disease (EVD) outbreak in North Kivu province in the Democratic Republic of Congo (DRC) during 2018–2020 was the world’s second largest Ebola outbreak on record. It led to 3481 total cases with 2299 deaths (World Health Organization 2021). One patient who received the recombinant vesicular stomatitis virus-based vaccine was diagnosed with EVD and recovered within 14 days after treatment. However, 6 months later, the same patient presented again with severe EVD-like illness and EBOV viremia and died (Mbala-Kingebeni et al. 2021). The molecular sequence data consist of 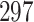 sequenced isolates that contain
sequenced isolates that contain 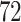 epidemiologically linked cases to the patient’s second infection.
epidemiologically linked cases to the patient’s second infection.
Algae
The coralline red algae (Corallinophycidae) are characterized by the presence of calcite crystals in their cell walls. Corallines, as a group, possess the richest fossil record among marine algae. In their pioneering study, Pena et al. (2020) use a multi-locus dataset with taxon sampling and comprehensive collection of carolline fossil records to reconstruct a time-calibrated phylogeny of the subclass Corallinophycidae. The algae dataset contains 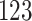 Corallinophycidae taxa and
Corallinophycidae taxa and 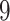 outgroup species with 7 genes (LSU, SSU, 23S, cos1, EF2, psbA, rbcL) concatenated into an alignment of more than
outgroup species with 7 genes (LSU, SSU, 23S, cos1, EF2, psbA, rbcL) concatenated into an alignment of more than 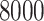 bp. We employ the same fossil-informed normal priors on
bp. We employ the same fossil-informed normal priors on 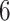 internal nodes as in the original study (Pena et al. 2020). More specifically, we place the same normal priors on the time to most recent common ancestor (tMRCA) with mean
internal nodes as in the original study (Pena et al. 2020). More specifically, we place the same normal priors on the time to most recent common ancestor (tMRCA) with mean 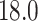 Mya (million years ago) and standard deviation
Mya (million years ago) and standard deviation 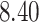 Mya for clade A: Harveylithon, mean
Mya for clade A: Harveylithon, mean 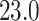 Mya and standard deviation
Mya and standard deviation 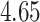 Mya for clade B: Porolithon, mean
Mya for clade B: Porolithon, mean 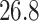 Mya and standard deviation
Mya and standard deviation 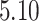 Mya for clade C: Lithophyllum pustulatum, mean
Mya for clade C: Lithophyllum pustulatum, mean 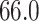 Mya and standard deviation
Mya and standard deviation 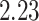 Mya for clade D: Hydrolithoideae, mean
Mya for clade D: Hydrolithoideae, mean 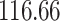 Mya and standard deviation
Mya and standard deviation 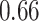 Mya for clade E: Hapalidiales, and mean
Mya for clade E: Hapalidiales, and mean 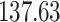 Mya and standard deviation
Mya and standard deviation 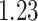 Mya for clade F: Sporolithales as shown in Figure 7.
Mya for clade F: Sporolithales as shown in Figure 7.
Figure 7.
The algae phylogeny explored in the example. Branches are color-coded by the posterior means of the branch-specific evolutionary rates. Horizontal bars represent 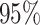 posterior credible intervals for the internal node times. Letters a)–f) indicate where fossil record informed calibration normal priors are placed on the tMRCAs of clade a: Harveylithon, clade b: Porolithon, clade c: Lithophyllum pustulatum, clade d: Hydrolithoideae, clade e: Hapalidiales, and clade f: Sporolithales.
posterior credible intervals for the internal node times. Letters a)–f) indicate where fossil record informed calibration normal priors are placed on the tMRCAs of clade a: Harveylithon, clade b: Porolithon, clade c: Lithophyllum pustulatum, clade d: Hydrolithoideae, clade e: Hapalidiales, and clade f: Sporolithales.
Mixed-effects Relaxed Clock Model
We employ mixed-effects relaxed clock models (as detailed in Bletsa et al. (2019)) to learn the evolutionary rates of the 4 viral datasets and the algae dataset. More specifically, we use the same random-effects relaxed clock model detailed in Ji et al. (2020) for the analysis of WNV, RABV, and LASV datasets. For the EBOV example, we use a mixed-effects relaxed clock model with clade-specific fixed-effects to model clade-specific rate variations among the 3 branches leading to 3 clades of interest (relapse clade, MAN14985 clade, and KAT21596 clade). For the algae example, we use a mixed-effects relaxed clock model with clade-specific fixed-effects to model clade-specific rate variations among the 8 clades of interest as in the original study. The use of the clade-specific fixed-effects mimics a local clock model that allows us to model and compare possibly within-clade rate variations but has previously not been computationally feasible.
Priors
We use the same data partitions, substitution models, and prior distributions as in each example’s original study (Biek et al. 2007; Pybus et al. 2012; Andersen et al. 2015; Pena et al. 2020; Mbala-Kingebeni et al. 2021).
Implementations
We have implemented the algorithms in thismanuscript within the development branch of the software package BEAST (SHA 17da204e2d9bdadb6c8284fd092413054f161bdc) (Suchard et al. 2018) with likelihood computations off-loaded to the high-performance BEAGLE library (SHA 3bdb30bd645e15983f8c8cf952564813e306ad83) (Ayres et al. 2019). We provide instructions and the BEAST XML files for reproducing these analyses on Github at https://github.com/suchard-group/hmc_divergence_time_manuscript_supplement.
Results
We summarize the computational efficiency improvement with HMC on the ratio space followed by our biological findings on divergence time estimations of the 5 examples.
Computational Performance
We infer the posterior distribution of all internal node heights using 2 different MCMC proposal kernels implemented in BEAST (Suchard et al. 2018) with likelihood computations off-loaded to the high-performance BEAGLE library (Ayres et al. 2019). The first kernel proposes new values for one internal node height at a time from their support. This represents the current best-practice approach used in BEAST and we will refer to this kernel as “univariable.” The other proposal kernel utilizes HMC with a diagonal mass matrix informed by adaptive variance on the ratio space that we will refer to as “HMC.” As is conventional for Bayesian phylogenetics, we employ a Metropolis-within-Gibbs (Tierney 1994; Andrieu et al. 2003) approach that cycles between sampling the tree, the evolutionary rates and the other phylogenetic modeling parameters, each from theirrespective full conditional distributions (see, e.g.,Equation (6) in Hassler et al. (2023) for more details).
As expected, sampling the topology and the high-dimensional rate and time (i.e., node height) parameters is computationally rate-limiting. Therefore, we explore 2 scenarios: 1) we sample divergence times only, while keeping the evolutionary rate and all other parameters fixed in scenario “time”; and 2) we sample evolutionary rate and time jointly, while keeping all other parameters fixed in scenario “rate & time.” We compare the efficiency of these proposal kernels through their effective sample size (ESS) per unit time for divergence time estimations. For each analysis, we run the MCMC iterations with each of the kernels for roughly the same run time (more details regarding chain lengths can be found in the supplementary BEAST XML files). This strategy aims to accommodate the difference in computational cost per MCMC iteration among kernels for fair comparisons. To maintain identifiability of internal nodes, we constrain the comparisons of the WNV, RABV, LASV, and algae examples to a fixed topology that was randomly selected from its posterior distribution. Specifically, we set all parameters, except for those of interest in each scenario, fixed to their realized values from a randomly selected MCMC iteration. The topologies and parameter values of the WNV and LASV examples are the same as in Ji et al. (2020). This topology constraint brings no additional work or difficulty for applying our method to integrate over topology space since one typically cycles between sampling the topology, the divergence times and other parameters, each from their respective full conditional distributions as in a Metropolis-within-Gibbs inference strategy (Tierney 1994; Andrieu et al. 2003). To demonstrate, we relax the topology constraint (i.e., we don’t fix the tree topology) for the EBOV example. We also relax the topology constraint when inferring the maximum clade credible evolutionary trees for all 5 examples and report posterior estimates for the evolutionary rate parameters in this scenario in the following section. We present the computational efficiency improvement with HMC in the ratio space for sampling node heights. The application of HMC on the ratio dimensions greatly improves the mixing of the MCMC chain, whereas the univariable samplers are problematic for learning the height of some internal nodes that are close to the root in the WNV example.
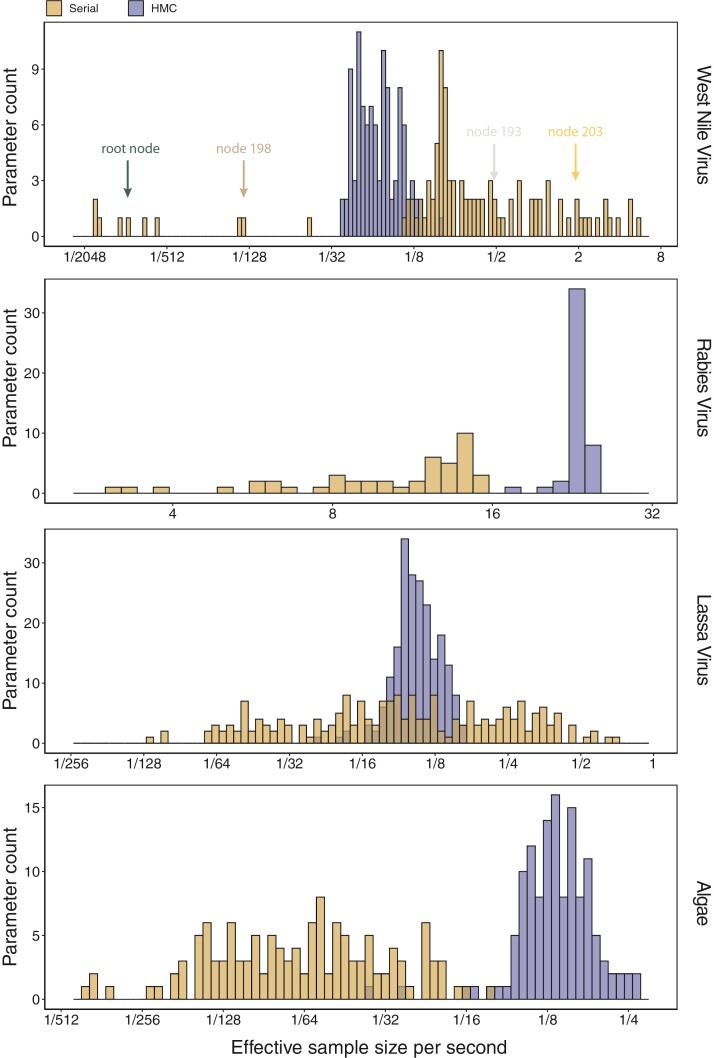
Figure 2 illustrates the posterior sampling efficiency with HMC and univariable samplers in terms of ESS per unit time. Table 1 shows the summary statistics of the efficiency gain of the HMC sampler compared with the univariable samplers for the 3 examples. We exclude the WNV example from the efficiency comparison because the poor mixing with univariable samplers leads to an inflated speed-up for HMC. The HMC sampler yields at least 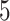 -fold efficiency improvement in terms of the minimum ESS per unit time in the RABV, LASV, and algae examples that have no difficulties of mixing for the univariable sampler.
-fold efficiency improvement in terms of the minimum ESS per unit time in the RABV, LASV, and algae examples that have no difficulties of mixing for the univariable sampler.
Figure 2.
Posterior sampling efficiency on all node height parameters for the WNV, RABV, LASV, and algae examples. We bin parameters by their ESS/s values. The 2 proposal kernels employed in the MCMC are color-coded: a univariable proposal kernel and an HMC proposal kernel with an adaptive mass matrix.
Table 1.
Computational performance of proposal kernels for the RABV, LASV, and algae examples. Computational efficiency measured in terms of effective sample size per second (ESS/s) and effective sample size per proposal (ESS/N). We compare the performance of our HMC proposal kernels operating on the transformed ratio space with a univariable (univariable) proposal kernel on the original node height space. We report speedup with respect to the minimum and median ESS/s and ESS/N (listed in the columns of “univariable” and “HMC”) across parameters for each example and method. We do not report the unreliably high speed-ups for the WNV dataset because of mixing issues under the “univariable” kernel.
| Univariable | HMC | Speedup | ||||||
| Source | Minimum | Median | Minimum | Median | Minimum | Median | ||
| ESS/s | RABV | Time | 3.187 | 12.154 | 17.358 | 23.579 | 5.4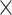
|
1.9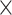
|
| Rate & Time | 0.927 | 4.638 | 6.324 | 8.355 | 6.8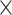
|
1.8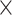
|
||
| LASV | Time | 0.008 | 0.090 | 0.042 | 0.104 | 5.0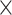
|
1.2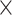
|
|
| Rate & Time | 0.002 | 0.016 | 0.018 | 0.040 | 8.0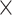
|
2.4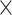
|
||
| Algae | Time | 2.47E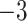
|
1.59E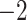
|
2.72E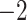
|
1.34E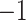
|
11.0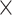
|
8.4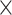
|
|
| Rate & Time | 9.01E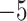
|
7.37E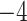
|
1.26E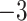
|
4.26E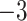
|
14.0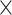
|
5.8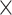
|
||
| ESS/N | RABV | Time | 2.12E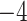
|
8.10E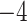
|
3.39E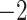
|
4.60E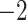
|
159.3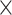
|
56.7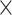
|
| Rate & Time | 2.26E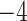
|
1.13E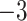
|
2.45E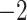
|
3.24E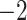
|
108.3
|
28.6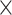
|
||
| LASV | Time | 8.68E 6 6 |
9.45E 5 5 |
1.17E 3 3 |
2.92E 3 3 |
134.8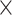
|
30.9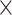
|
|
| Rate & Time | 2.70E 6 6 |
1.98E 5 5 |
1.21E 3 3 |
2.63E 3 3 |
447.3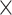
|
132.9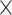
|
||
| Algae | Time | 4.31E 5 5 |
2.77E 4 4 |
1.60E 3 3 |
7.86E 3 3 |
37.2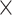
|
28.4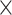
|
|
| Rate & Time | 2.51E 6 6 |
2.05E 5 5 |
2.87E 4 4 |
9.67E 4 4 |
114.2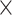
|
47.2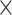
|
||
Divergence Time Estimations
We summarize divergence time estimation results for each of the five examples.
West Nile virus
Our analysis estimates the tree-wise (fixed-effect) rate with posterior mean 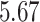 (
(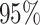 Bayesian credible interval:
Bayesian credible interval: 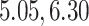 )
) 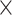
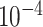 substitutions per site per year and an estimatedvariability characterized by the scale parameter of the lognormal distributed branch-specific random-effects with posterior mean
substitutions per site per year and an estimatedvariability characterized by the scale parameter of the lognormal distributed branch-specific random-effects with posterior mean 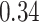
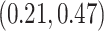 . These values are similar to previous estimates (Pybus et al. 2012; Ji et al. 2020). Figure 3 shows the evolutionary tree explored in the WNV example as well as trace plots of several nodes of interest. Our analysis estimates the date of the epidemic origin to have posterior mean
. These values are similar to previous estimates (Pybus et al. 2012; Ji et al. 2020). Figure 3 shows the evolutionary tree explored in the WNV example as well as trace plots of several nodes of interest. Our analysis estimates the date of the epidemic origin to have posterior mean 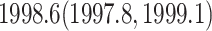 similar to previous estimates. Matching previous findings that the American epidemic was likely to originate from the introduction of a single highly pathogenic lineage, our analysis infers the NY99 lineage to be basal to all other genomes.
similar to previous estimates. Matching previous findings that the American epidemic was likely to originate from the introduction of a single highly pathogenic lineage, our analysis infers the NY99 lineage to be basal to all other genomes.
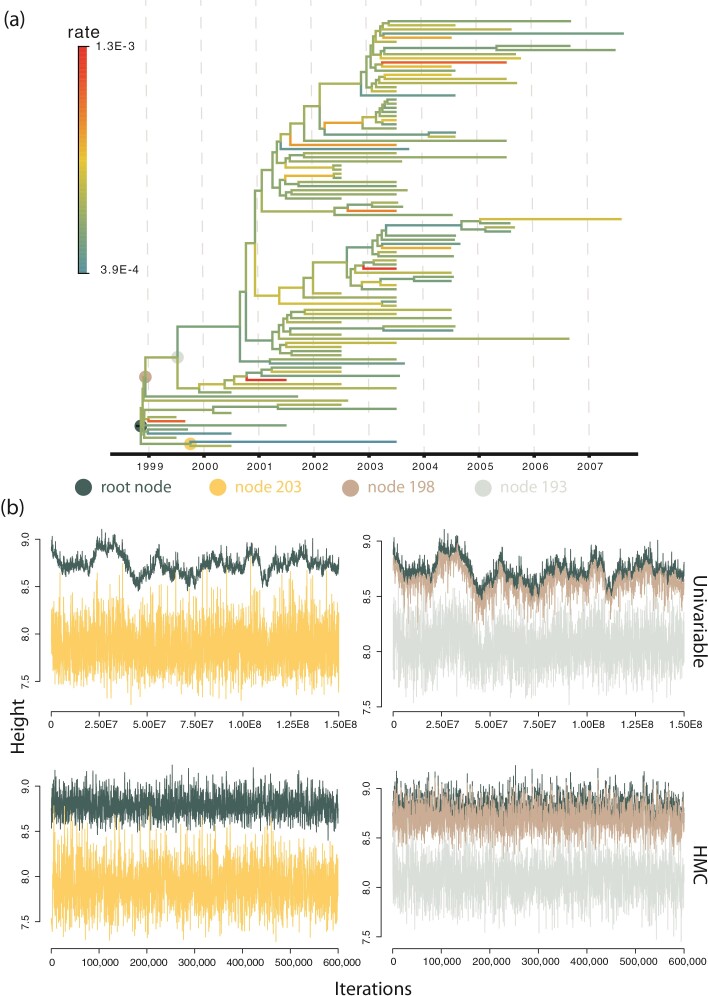
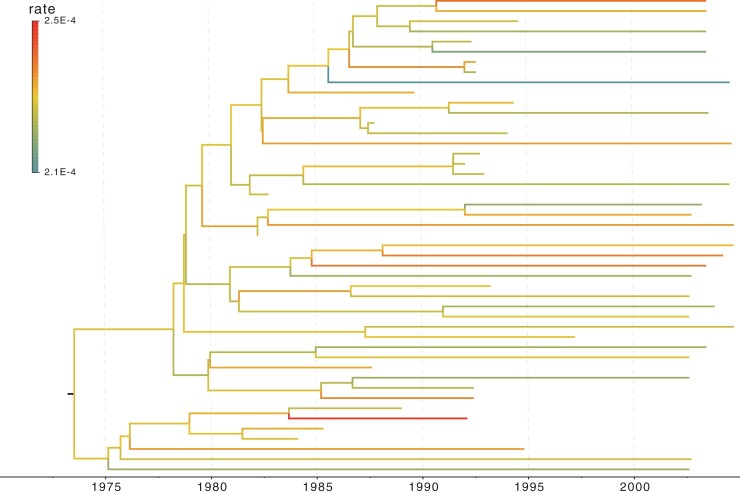
Figure 3.
Trace plot of 4 height parameters indicated on the WNV phylogeny. a) The WNV phylogeny explored in the example. Branches are color-coded by the posterior means of the branch-specific evolutionary rates. Four representative nodes indicated by colored dots illustrate mixing issues at nodes close to the root when learning the posterior distribution of their heights using the univariable samplers. b) The trace plots of the height parameter of the 4 nodes indicated in a) using the same color scheme. The top 2 trace plots are obtained with the univariable samplers for an MCMC chain of length 1.5 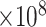 iterations. The bottom 2 trace plots are obtained with the HMC sampler for an MCMC chain of length 600,000. The trace of the root height is shown in both plots for the same sampler to compare with other nodes.
iterations. The bottom 2 trace plots are obtained with the HMC sampler for an MCMC chain of length 600,000. The trace of the root height is shown in both plots for the same sampler to compare with other nodes.
Of important note, the MCMC chain suffers poormixing for some height dimensions close to the root (including the root) under the “univariable” kernel as illustrated by the trace plot in Figure 3b I and II. The mixing issue propagates from the root node to a few of its descendant nodes (e.g., node 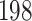 ) that plagues over these dimensions because univariable samplers propose a new value for an internal node’s height from the interval set by the height of its parent and closest descendant node. Such a tree-like boundary structure requires multiple height changes on an internal node and the nodes setting its boundaries in the same direction before a “big” move is possible that often fails by one of these dimensions moving at the oppositedirection.
) that plagues over these dimensions because univariable samplers propose a new value for an internal node’s height from the interval set by the height of its parent and closest descendant node. Such a tree-like boundary structure requires multiple height changes on an internal node and the nodes setting its boundaries in the same direction before a “big” move is possible that often fails by one of these dimensions moving at the oppositedirection.
Rabies virus
Our analysis results in a posterior mean rate of 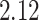
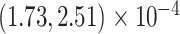 substitutions per site per year. The estimated scale parameter has posterior mean
substitutions per site per year. The estimated scale parameter has posterior mean 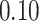
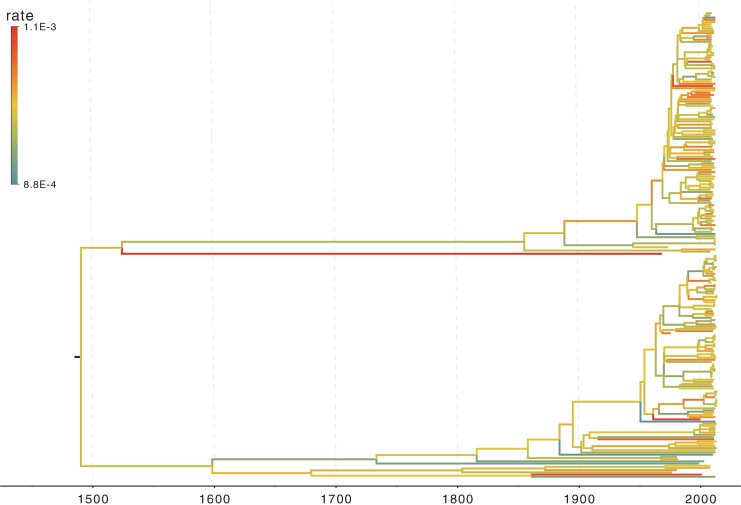
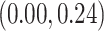 . Figure 4 shows the maximum clade credible evolutionary tree of the RABV example. Our analysis estimates the date of the root of the tree to be
. Figure 4 shows the maximum clade credible evolutionary tree of the RABV example. Our analysis estimates the date of the root of the tree to be 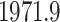
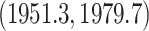 . This is slightly older than the estimate in Biek et al. (2007) and our
. This is slightly older than the estimate in Biek et al. (2007) and our 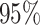 Bayesian credible interval is wider.
Bayesian credible interval is wider.
Figure 4.
The RABV phylogeny explored in the example. Branches are color-coded by the posterior means of the branch-specific evolutionary rates.
Lassa virus
Our analysis yields a posterior mean rate of 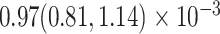 substitutions per site per year. The estimated scale parameter has posterior mean
substitutions per site per year. The estimated scale parameter has posterior mean 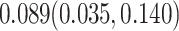 . Figure 5 shows the maximum clade credible evolutionary tree of the LASV example. The date of the root of the tree is inferred to be
. Figure 5 shows the maximum clade credible evolutionary tree of the LASV example. The date of the root of the tree is inferred to be 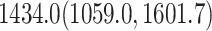 . This agrees with the finding by Andersen et al. (2015) that LASV is a long-standing human pathogen whose most recent common ancestor existed around 600 years ago.
. This agrees with the finding by Andersen et al. (2015) that LASV is a long-standing human pathogen whose most recent common ancestor existed around 600 years ago.
Figure 5.
The LASV phylogeny explored in the example. Branches are color-coded by the posterior means of the branch-specific evolutionary rates.
Ebolavirus
Our analysis yields a posterior mean rate 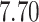
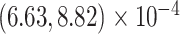 substitutions per site per year. The scale parameter has posterior mean
substitutions per site per year. The scale parameter has posterior mean 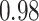
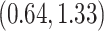 . Figure 6 shows the maximum clade credible evolutionary tree of the EBOV example. The inferred MCC tree shows a significant slow-down in evolutionary rate on the branch leading to the relapse clade with a posterior mean of
. Figure 6 shows the maximum clade credible evolutionary tree of the EBOV example. The inferred MCC tree shows a significant slow-down in evolutionary rate on the branch leading to the relapse clade with a posterior mean of 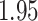
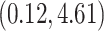
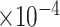 substitutions per site per year that roughly spans over
substitutions per site per year that roughly spans over 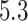 months, similar to the discovery from Mbala-Kingebeni et al. (2021). The posterior mean branch-specific rate of the two branches leading to the MAN4194 and KAT21596 clades are
months, similar to the discovery from Mbala-Kingebeni et al. (2021). The posterior mean branch-specific rate of the two branches leading to the MAN4194 and KAT21596 clades are 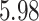
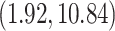
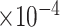 and
and 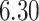
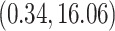
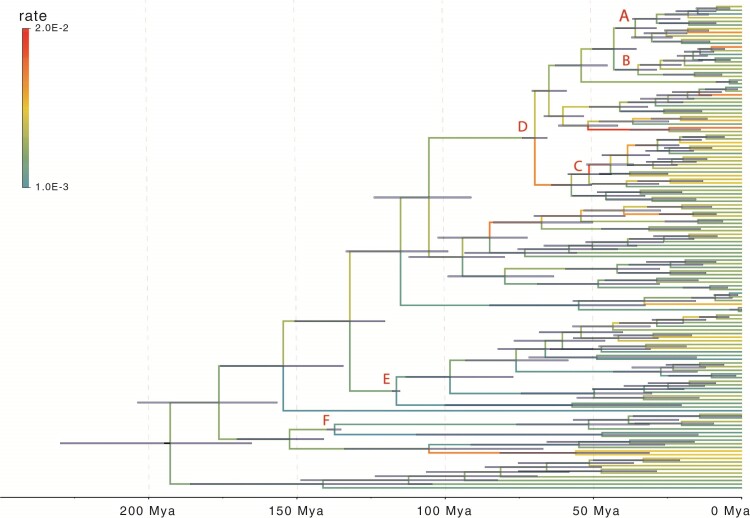
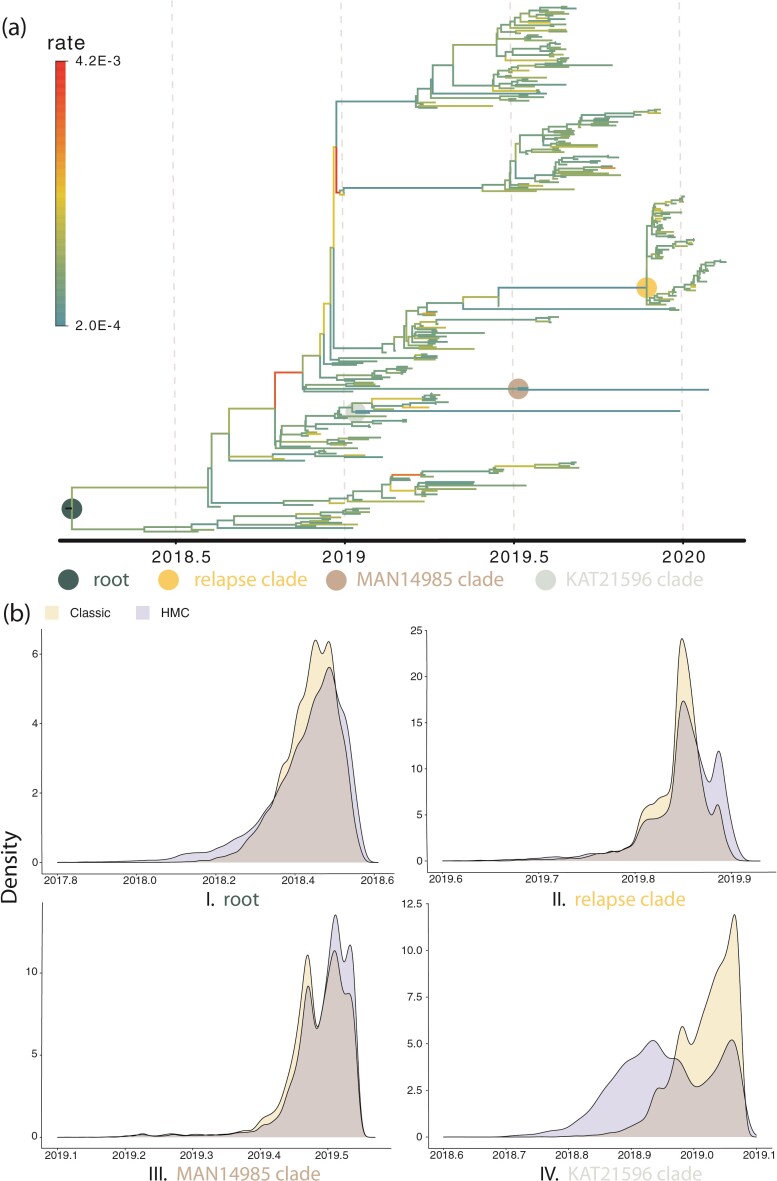
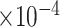 substitutions per site per year respectively (please see section Discussion for more comparisons between the mixed-effects model and the model employed in the original study). However, our results have more variability in evolutionary rates compared to the original study. The MAN4194 sequence that was collected from the individual with the relapsed Ebola infection is basal to all other DRC sequences within the relapse clade. We estimate the date of the most recent common ancestor (MRCA) of the relapse clade (Fig. 6b II) to be
substitutions per site per year respectively (please see section Discussion for more comparisons between the mixed-effects model and the model employed in the original study). However, our results have more variability in evolutionary rates compared to the original study. The MAN4194 sequence that was collected from the individual with the relapsed Ebola infection is basal to all other DRC sequences within the relapse clade. We estimate the date of the most recent common ancestor (MRCA) of the relapse clade (Fig. 6b II) to be 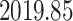
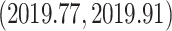 . This is similar to the estimate of Mbala-Kingebeni et al. (2021), but our analysis revealed a clearer bimodal posterior distribution that was previously missed. To confirm that the bimodal posterior distribution was not an artifact, we ran three independent MCMC chains with the same model and confirmed that they converged to the same posterior distribution. Our estimated date of the MRCA of the MAN14985 clade (Fig. 6b III) is
. This is similar to the estimate of Mbala-Kingebeni et al. (2021), but our analysis revealed a clearer bimodal posterior distribution that was previously missed. To confirm that the bimodal posterior distribution was not an artifact, we ran three independent MCMC chains with the same model and confirmed that they converged to the same posterior distribution. Our estimated date of the MRCA of the MAN14985 clade (Fig. 6b III) is 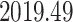
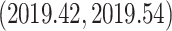 and the estimated date of the MRCA of the KAT21596 set (Fig. 6b IV) is
and the estimated date of the MRCA of the KAT21596 set (Fig. 6b IV) is 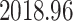
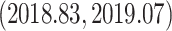 .
.
Figure 6.
Kernel density estimation plot of the tMRCA distribution of 4 clades of interest on the EBOV phylogeny. a) The EBOV phylogeny explored in the example. Branches are color-coded by the posterior means of the branch-specific evolutionary rates. We use 4 colored dots to indicate the 4 MRCA nodes of 4 clades of interest. b) The kernel density estimation plot of the tMRCA of the 4 nodes indicated in a).
Algae
Our analysis yields a posterior mean rate 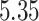
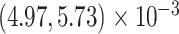 substitutions per site per million years. The scale parameter has posterior mean
substitutions per site per million years. The scale parameter has posterior mean 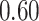
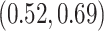 . Figure 7 shows the maximum clade credible evolutionary tree of the algae example. The date of the root of the tree is inferred to be
. Figure 7 shows the maximum clade credible evolutionary tree of the algae example. The date of the root of the tree is inferred to be 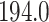
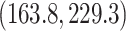 Mya. This is slightly older than the estimate in Pena et al. (2020) and our
Mya. This is slightly older than the estimate in Pena et al. (2020) and our 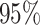 Bayesian credible interval is wider.
Bayesian credible interval is wider.
Discussion
The confounding of evolutionary rate and time has imparted divergence time estimation with high uncertainty and low reliability of the inference. Nonetheless, much effort and improvement have shaped the molecular clock models to better characterize evolutionary rate heterogeneity along phylogenies (Thorne et al. 1998; Kishino et al. 2001; Drummond et al. 2006; Rannala and Yang 2007; Lemey et al. 2010; Lartillot et al. 2016; Bletsa et al. 2019). We here introduce a linear-time transformation of the internal node height parameters into a ratio space with the aim to improve estimation efficiency under complex molecular clock models. Naive transformation of the gradient of the log-likelihood from the original height space into the ratio space results in 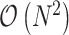 computations. To make the transformation scalable, we present linear-time algorithms that improve the performance of this transformation. With a slight modification, Algorithm 4 builds upon Algorithm 2 to calculate all derivatives of the log-determinant of the Jacobian matrix also in linear-time. This collection of linear-time algorithms enables researchers to employ dynamic-based samplers (e.g., HMC) to sample the internal node heights and substantially improveinference.
computations. To make the transformation scalable, we present linear-time algorithms that improve the performance of this transformation. With a slight modification, Algorithm 4 builds upon Algorithm 2 to calculate all derivatives of the log-determinant of the Jacobian matrix also in linear-time. This collection of linear-time algorithms enables researchers to employ dynamic-based samplers (e.g., HMC) to sample the internal node heights and substantially improveinference.
When applying HMC on all dimensions in the ratio space, the sampler proposes a new set of values for the height parameter and all ratios that corresponds to a set of new values for all internal node heights in the original height space. Alternatively, one may cycle HMC on subsets of dimensions from the ratio space in a Metropolis-within-Gibbs inference strategy such that in each iteration, HMC proposes new values to only a subset of dimensions. For example, one possible choice of these subsets is to separately sample the root height and all the ratios (i.e., one subset containing only the height parameter and one subset containing all ratio parameters). Interestingly, each of the two subsets takes a full traversal for updating the gradient through Algorithms 2 and 3 where the postorder traversal updates the gradient with respect to all ratio parameters ( dimensional) and the preorder traversal updates only the height parameter (single dimensional). Therefore, sometimes it might be more computationally efficient to mix the classic univariable sampling kernels with HMC for the height dimension to benefit from the low computational load for learning the root height dimension. For example, one may apply classic univariable samplers on the height dimension in ratio space instead of HMC. In addition, one may apply classic univariable samplers on the original root height dimension such that with careful caching of the previous iteration, each proposal only needs updating 2 postorder partial likelihood vectors corresponding to the 2 immediate descendant branches from the root. However, as illustrated by the WNVexample, classic univariable samplers may suffer from the constraints on the node heights resulting in poor mixing in some dimensions (e.g., several internal nodes close to the root in this case), where the mixture of samplers may lead to worse computational efficiency. To investigate the univariable sampler’s validity, we ran the chain
dimensional) and the preorder traversal updates only the height parameter (single dimensional). Therefore, sometimes it might be more computationally efficient to mix the classic univariable sampling kernels with HMC for the height dimension to benefit from the low computational load for learning the root height dimension. For example, one may apply classic univariable samplers on the height dimension in ratio space instead of HMC. In addition, one may apply classic univariable samplers on the original root height dimension such that with careful caching of the previous iteration, each proposal only needs updating 2 postorder partial likelihood vectors corresponding to the 2 immediate descendant branches from the root. However, as illustrated by the WNVexample, classic univariable samplers may suffer from the constraints on the node heights resulting in poor mixing in some dimensions (e.g., several internal nodes close to the root in this case), where the mixture of samplers may lead to worse computational efficiency. To investigate the univariable sampler’s validity, we ran the chain 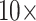 longer for the WNV example. As expected, the trace plot of the longer chain exhibits a normal “caterpillar” shape that indicates both the validity and limitation of the univariable samplers. Interestingly, in other examples where we do not observe MCMC mixing issues for the univariable sampler, the HMC sampler still outperforms the univariable sampler as shown in Figure 2 and Table 1 by generating higher ESS per unit time for the dimension with the minimum ESS (for which one usually waits to grow larger than certain threshold before terminating the MCMC chain). The sampling efficiency is more uniform across dimensions in the HMC sampler as compared to the univariable sampler. This more uniform performance across different dimensions is partly because our adaptive variance informed mass matrix
longer for the WNV example. As expected, the trace plot of the longer chain exhibits a normal “caterpillar” shape that indicates both the validity and limitation of the univariable samplers. Interestingly, in other examples where we do not observe MCMC mixing issues for the univariable sampler, the HMC sampler still outperforms the univariable sampler as shown in Figure 2 and Table 1 by generating higher ESS per unit time for the dimension with the minimum ESS (for which one usually waits to grow larger than certain threshold before terminating the MCMC chain). The sampling efficiency is more uniform across dimensions in the HMC sampler as compared to the univariable sampler. This more uniform performance across different dimensions is partly because our adaptive variance informed mass matrix 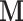 accounts for different levels of variability among dimensions. For example, Ji et al. (2020) show a better performance of an HMC sampler with a mass matrix informed by the diagonal of the Hessian matrix as compared to a vanilla HMC sampler with a mass matrix composed of an identity matrix. Another possible cause is that we do not tune separate univariable samplers for dimensions with different levels of variability where one may propose smaller jumps for dimensions with small variations and larger jumps for dimensions with large variations. However, Fisher et al. (2021) show that allowing each dimension to tune a separate univariable sampler results in little improvement as compared to HMC. The mass matrix employed in this study has only diagonal entries being non-zero that is equivalent to rescaling the dimensions by their variability. Such a rescaling method has already shown its success in divergence time estimations (e.g., such as in Thorne et al. (1998) and Rannala and Yang (2003)).
accounts for different levels of variability among dimensions. For example, Ji et al. (2020) show a better performance of an HMC sampler with a mass matrix informed by the diagonal of the Hessian matrix as compared to a vanilla HMC sampler with a mass matrix composed of an identity matrix. Another possible cause is that we do not tune separate univariable samplers for dimensions with different levels of variability where one may propose smaller jumps for dimensions with small variations and larger jumps for dimensions with large variations. However, Fisher et al. (2021) show that allowing each dimension to tune a separate univariable sampler results in little improvement as compared to HMC. The mass matrix employed in this study has only diagonal entries being non-zero that is equivalent to rescaling the dimensions by their variability. Such a rescaling method has already shown its success in divergence time estimations (e.g., such as in Thorne et al. (1998) and Rannala and Yang (2003)).
The EBOV example employs a more general mixed-effects relaxed clock model with clade-specific fixed-effects and branch-specific random-effects. The originalstudy (Mbala-Kingebeni et al. 2021) incorporates rate variation into a strict molecular clock model by introducing a single parameter to capture fixed-effects from the clades of interest. Their molecular clock modeltherefore has 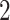 dimensions. The mixed-effects model employed in this study now utilizes a
dimensions. The mixed-effects model employed in this study now utilizes a 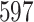 -dimensional parameter (
-dimensional parameter (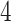 dimensions for clade-specific fixed-effects with an intercept term,
dimensions for clade-specific fixed-effects with an intercept term, 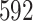 dimensions for branch-specific random-effects, and
dimensions for branch-specific random-effects, and 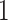 dimension for the scale parameter) to capture multiple sources of rate variation. This more general mixed-effects model detects the same slow-down of the evolutionary rate of the branch leading to the relapse clade. Interestingly, the relapse clade and the MAN14985 clade are monophyletic with posterior probability approaching
dimension for the scale parameter) to capture multiple sources of rate variation. This more general mixed-effects model detects the same slow-down of the evolutionary rate of the branch leading to the relapse clade. Interestingly, the relapse clade and the MAN14985 clade are monophyletic with posterior probability approaching 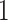 in our analyses whereas the KAT21596 clade is monophyletic withposterior probability
in our analyses whereas the KAT21596 clade is monophyletic withposterior probability 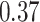 compared to the posterior probability of
compared to the posterior probability of 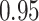 in the original study. The lower posterior probability estimate for the 2 sequences (KAT21596 and BTB4325) forming a monophyletic clade indicates a different mixture of tree topologies partly owing to the more general molecular clock model and potentially better mixing of node heights in each topology. The difference in posterior probability of the KAT21596 clade further affects the multi-modalposterior distribution of tMRCA of the two sequences as in Figure 6b. While our approach reveals clearer multimodal distributions, it remains an important research direction to study its performance in revealing multimodalities and possibly improving mixing efficiency over tree topologies through more intense investigations (e.g., through simulation studies) which, however, is out of the scope of this manuscript.
in the original study. The lower posterior probability estimate for the 2 sequences (KAT21596 and BTB4325) forming a monophyletic clade indicates a different mixture of tree topologies partly owing to the more general molecular clock model and potentially better mixing of node heights in each topology. The difference in posterior probability of the KAT21596 clade further affects the multi-modalposterior distribution of tMRCA of the two sequences as in Figure 6b. While our approach reveals clearer multimodal distributions, it remains an important research direction to study its performance in revealing multimodalities and possibly improving mixing efficiency over tree topologies through more intense investigations (e.g., through simulation studies) which, however, is out of the scope of this manuscript.
The algae example also employs a more general mixed-effects relaxed clock model with clade-specific fixed-effects and branch-specific random effects that expands the dimension of the molecular clock-related parameter from 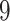 (
(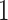 dimension for base-line molecular clock rate and
dimension for base-line molecular clock rate and 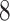 dimensions for fix-effects from clades of interest) to
dimensions for fix-effects from clades of interest) to 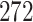 (
(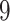 dimensions for clade-specific fixed-effects with an intercept term,
dimensions for clade-specific fixed-effects with an intercept term,  dimensions for branch-specific random-effects, and
dimensions for branch-specific random-effects, and  dimension for the scale parameter) to capture additional sources of rate variation. As shown in Figure 7, our analysis reveals substantial within-clade rate variation that was not modeled previously and a slightly different topology of the maximum clade credible evolutionary tree (e.g., the placement of clade C: L. pustulatum). The large variation in the branch-specific evolutionary rates may also contribute to the wider posterior credible interval estimated for the root time and the tMRCAs of several clades. As demonstrated in their study on the effect of molecular clock rate model choices (dos Reis et al. 2018), it is important for future studies to explore such influence on divergence time estimations with fossil calibration priors under now computationally feasible branch-specific evolutionary rate models.
dimension for the scale parameter) to capture additional sources of rate variation. As shown in Figure 7, our analysis reveals substantial within-clade rate variation that was not modeled previously and a slightly different topology of the maximum clade credible evolutionary tree (e.g., the placement of clade C: L. pustulatum). The large variation in the branch-specific evolutionary rates may also contribute to the wider posterior credible interval estimated for the root time and the tMRCAs of several clades. As demonstrated in their study on the effect of molecular clock rate model choices (dos Reis et al. 2018), it is important for future studies to explore such influence on divergence time estimations with fossil calibration priors under now computationally feasible branch-specific evolutionary rate models.
Recent molecular clock models add additional dependence of evolutionary rate onto time (Aiewsakun and Katzourakis 2015; Ho et al. 2015; Membrebe et al. 2019) that bring in more biological insights into the time-dependency of the evolutionary rates in viral evolution. However, such a dependence structure further complicates the confounding of evolutionary rate and time. Fortunately, the complex dependence structure only affects the derivatives without influencing the ratio transformation or the HMC machinery and is, therefore, the reason Equation (6) uses more general terms 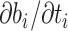 ,
, 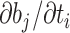 , and
, and 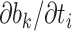 .
.
A caveat of the linear-time algorithms that are introduced here is that they assume sampling dates are given and fixed. Often, viral sequences are associated with various levels of uncertainty, not only in their associated metadata (e.g., sampling dates) but also with regard to sequencing quality. Typically, a quality control step removes unreliable sequences. In addition, fossil records with sequence information may present as ancient tip nodes with associated uncertainties. In a Bayesian framework, one may integrate out sampling date uncertainty through their support so that sampling dates become parameters of the model and are no longer fixed (Pybus et al. 2012). The proposed algorithms and HMC machinery remain unaffected if one cycles between sampling all internal node heights and tip heights from their full conditional distributions. However, the derivative with respect to the height parameter in the ratio space needs to consider contributions from the tip nodes when one samples all node heights (including variable tip heights) jointly. Moreover, the anchor node and epoch constructions become variable and need to be jointly updated with tip heights. Another caveat of our algorithms is that we do not formally consider degree-2 internal nodes such as those employed in a “total-evidence” dating analysis (see, e.g., Stadler (2010) and Gavryushkina et al. (2014)) although one may effectively transform them into regular degree-3 nodes by adding length-zero branches to these degree-2 nodes connected with a tip node with sequences (if any) switched from the original degree-2 internal nodes. In addition, some models may introduce discontinuity or non-smoothness into the target density, such as the “soft-bound” calibration priorsintroduced in Yang and Rannala (2006) that are continuous over the parameter space but that have derivatives with respect to node heights that do not exist for a finite number of points. Although the rejection step in the Metropolis–Hastings algorithm corrects any bias caused by the discontinuity or non-smootheness such that HMC still samples from the correct target density, these issues may increase the numerical integration error in the leap-frog step and thereby reduce sampling efficiency. Fortunately, the pioneering work of Nishimura et al. (2020) has demonstrated a promising HMC variant to solve issues generated by discontinuities. All these remain important avenues of future work.
Acknowledgments
We thank the 3 anonymous reviewers and theeditors for their thoughtful comments that significantly improve the quality of this manuscript.
Contributor Information
Xiang Ji, Department of Mathematics, School of Science & Engineering, Tulane University, 6823 St. Charles Avenue, New Orleans, LA 70118, USA.
Alexander A Fisher, Department of Statistical Science, Duke University, 214 Old Chemistry, Durham, NC 27708, USA.
Shuo Su, MOE International Joint Collaborative Research Laboratory for Animal Health & Food Safety, Jiangsu Engineering Laboratory of Animal Immunology, Institute of Immunology, College of Veterinary Medicine, Nanjing Agricultural University, No. 1 Weigang, Xiaolingwei District, Nanjing, Jiangsu 210095, China.
Jeffrey L Thorne, Bioinformatics Research Center, North Carolina State University, Raleigh, NC, USA; Department of Statistics, North Carolina State University, Raleigh, NC, USA; Department of Biological Sciences, North Carolina State University, Ricks Hall, 1 Lampe Dr, Raleigh, NC 27607, USA.
Barney Potter, Department of Microbiology, Immunology and Transplantation, Rega Institute, Herestraat 49, 3000 Leuven, Belgium.
Philippe Lemey, Department of Microbiology, Immunology and Transplantation, Rega Institute, Herestraat 49, 3000 Leuven, Belgium.
Guy Baele, Department of Microbiology, Immunology and Transplantation, Rega Institute, Herestraat 49, 3000 Leuven, Belgium.
Marc A Suchard, Department of Biomathematics, David Geffen School of Medicine, University of California Los Angeles, Los Angeles, CA, USA; Department of Human Genetics, David Geffen School of Medicine, University of California Los Angeles, Los Angeles, CA, USA; Department of Biostatistics, Fielding School of Public Health, University of California Los Angeles, 695 Charles E Young Dr S, Los Angeles, CA 90095, USA.
Funding
The research leading to these results has received funding from the European Research Council under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 725422—ReservoirDOCS). The Artic Network receives funding from the Wellcome Trust through project 206298/Z/17/Z. M.A.S. and X.J. are partially supported by NIH grants U19 AI135995, R56 AI149004, R01 AI153044, and R01 AI162611. X.J. acknowledges support from the NVIDIA academic hardware grant program. G.B. acknowledges support from the Interne Fondsen KU Leuven / Internal Funds KU Leuven under grant agreement C14/18/094 and from the Research Foundation—Flanders (‘Fonds voor Wetenschappelijk Onderzoek—Vlaanderen’, G0E1420N and G098321N). P.L. acknowledges support by the Research Foundation—Flanders (‘Fonds voor Wetenschappelijk Onderzoek—Vlaanderen’, G066215N, G0D5117N, and G0B9317N). J.L.T. was supported by NSF DEB 1754142.
Conflict of Interest
The authors declare no conflicts of interest.
Supplementary Material
Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.n02v6wx21.
References
- Aiewsakun P., Katzourakis A.. 2015. Time dependency of foamy virus evolutionary rate estimates. BMC Evolut. Biol. 15(1):1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersen K.G., Shapiro B.J., Matranga C.B., Sealfon R., Lin A.E., Moses L.M., Folarin O.A., Goba A., Odia I., Ehiane P.E., Momoh M., England E.M., Winnicki S., Branco L.M., Gire S.K., Phelan E., Tariyal R., Tewhey R., Omoniwa O., Fullah M., Fonnie R., Fonnie M., Kanneh L., Jalloh S., Gbakie M., Saffa S., Karbo K., Gladden A.D., Qu J., Stremlau M., Nekoui M., Finucane H.K., Tabrizi S., Vitti J.J., Birren B., Fitzgerald M., McCowan C., Ireland A., Berlin A.M., Bochicchio J., Tazon-Vega B., Lennon N.J., Ryan E.M., Bjornson Z., Milner D.A., Lukens A.K., Broodie N., Rowland M., Heinrich M., Akdag M., Schieffelin J.S., Levy D., Akpan H., Bausch D.G., Rubins K., McCormick J.B., Lander E.S., Günther S., Hensley L., Okogbenin S., Schaffner S.F., Okokhere P.O., Khan S.H., Grant D.S., Akpede G.O., Asogun D.A., Gnirke A., Levin J.Z., Happi C.T., Garry R.F., Sabeti P.C.. 2015. Clinical sequencing uncovers origins and evolution of Lassa virus. Cell. 162(4):738–750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrieu C., De Freitas N., Doucet A., Jordan M.I.. 2003. An introduction to MCMC for machine learning. Machine Learn. 50(1–2):5–43. [Google Scholar]
- Andrieu C., Thoms J.. 2008. A tutorial on adaptive MCMC. Stat. Comput. 18(4):343–373. [Google Scholar]
- Ayres D.L., Cummings M.P., Baele G., Darling A.E., Lewis P.O., Swofford D.L., Huelsenbeck J.P., Lemey P., Rambaut A., Suchard M.A.. 2019. Beagle 3: improved performance, scaling, and usability for a high-performance computing library for statistical phylogenetics. Syst. Biol. 68(6):1052–1061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baele G., Gill M.S., Lemey P., Suchard M.A.. 2020. Hamiltonian Monte Carlo sampling to estimate past population dynamics using the skygrid coalescent model in a Bayesian phylogenetics framework. Wellcome Open Res. 5(53):53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baele G., Lemey P., Rambaut A., Suchard M.A.. 2017. Adaptive MCMC in Bayesian phylogenetics: an application to analyzing partitioned data in BEAST. Bioinformatics. 33(12):1798–1805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biek R., Henderson J.C., Waller L.A., Rupprecht C.E., Real L.A.. 2007. A high-resolution genetic signature of demographic and spatial expansion in epizootic rabies virus. Proc. Natl. Acad. Sci. U.S.A. 104(19):7993–7998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bletsa M., Suchard M.A., Ji X., Gryseels S., Vrancken B., Baele G., Worobey M., Lemey P.. 2019. Divergence dating using mixed effects clock modelling: an application to HIV-1. Virus Evolut 5(2):vez036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casella G., Berger R.L.. 2001. Statistical inference. 2nd ed. Pacific Grove, CA: Duxbury. [Google Scholar]
- Dinh V., Bilge A., Zhang C., Matsen F.A. IV. Probabilistic path Hamiltonian Monte Carlo. Proceedings of the 34th International Conference on Machine Learning-Volume 7; 2017; p. 1009–1018. JMLR. org. [Google Scholar]
- dos Reis M., Gunnel G.F., Barba-Montoya J., Wilkins A., Yang Z., Yoder A.D.. 2018. Using phylogenomic data to explore the effects of relaxed clocks and calibration strategies on divergence time estimation: primates as a test case. Syst. Biol. 67(4):594–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond A.J., Ho S.Y., Phillips M.J., Rambaut A.. 2006. Relaxed phylogenetics and dating with confidence. PLoS Biol. 4(5):e88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Düx A., Lequime S., Patrono L.V., Vrancken B., Boral S., Gogarten J.F., Hilbig A., Horst D., Merkel K., Prepoint B., Santibanez S., Schlotterbeck J., Suchard M.A., Ulrich M., Widulin N., Mankertz A., Leendertz F.H., Harper K., Schnalke T., Lemey P., Calvignac-Spencer S.. 2020. Measles virus and rinderpest virus divergence dated to the sixth century BCE. Science. 368(6497):1367–1370. doi: 10.1126/science.aba9411 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erwin D.H., Laflamme M., Tweedt S M., Sperling E.A., Pisani D., Peterson K.J.. 2011. The cambrian conundrum: early divergence and later ecological success in the early history of animals. Science. 334(6059):1091–1097. [DOI] [PubMed] [Google Scholar]
- Fisher A.A., Ji X., Zhang Z., Lemey P., Suchard M.A.. 2021. Relaxed random walks at scale. Syst. Biol. 70(2):258–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fourment M., Darling A.E.. 2019. Evaluating probabilistic programming and fast variational Bayesian inference in phylogenetics. PeerJ. 7:e8272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gavryushkina A., Welch D., Stadler T., Drummond A.J.. 2014. Bayesian inference of sampled ancestor trees for epidemiology and fossil calibration. PLoS Comput. Biol. 10(12):e1003919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gill M.S., Lemey P., Bennett S.N., Biek R., Suchard M.A.. 2016. Understanding past population dynamics: bayesian coalescent-based modeling with covariates. Syst. Biol. 65(6):1041–1056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haario H., Saksman E., Tamminen J.. 1999. Adaptive proposaldistribution for random walk Metropolis algorithm. Comput. Stat. 14(3):375–396. [Google Scholar]
- Hadfield J., Brito A.F., Swetnam D.M., Vogels C.B., Tokarz R.E., Andersen K.G., Smith R.C., Bedford T., Grubaugh N.D.. 2019. Twenty years of West Nile virus spread and evolution in the Americas visualized by Nextstrain. PLoS Pathog. 15(10):e1008042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hassler G.W., Magee A.F., Zhang Z., Baele G., Lemey P., Ji X., Fourment M., Suchard M.A.. 2023. Data Integration in Bayesian Phylogenetics. Ann. Rev. Stat. Appl. 10:353–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastings W.K. 1970. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 57(1):97–109. [Google Scholar]
- Ho S.Y., Duchêne S., Molak M., Shapiro B.. 2015. Time-dependent estimates of molecular evolutionary rates: evidence and causes. Mol. Ecol. 24(24):6007–6012. [DOI] [PubMed] [Google Scholar]
- Ji X., Zhang Z., Holbrook A., Nishimura A., Baele G., Rambaut A., Lemey P., Suchard M.A.. 2020. Gradients do grow on trees: a linear-time O (N)-dimensional gradient for statistical phylogenetics. Mol. Biol. Evolut. 37(10):3047–3060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kishino H., Thorne J.L., Bruno W.J.. 2001. Performance of a divergence time estimation method under a probabilistic model of rate evolution. Mol. Biol. Evolut. 18(3):352–361. [DOI] [PubMed] [Google Scholar]
- Lartillot N., Phillips M.J., Ronquist F.. 2016. A mixed relaxed clock model. Phil. Trans. Royal Soc. B: Biol. Sci. 371(1699):20150132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemey P., Hong S.L., Hill V., Baele G., Poletto C., Colizza V., O’toole A., McCrone J.T., Andersen K.G., Worobey M., Nelson M.I., Rambaut A., Suchard M.A.. 2020. Accommodating individual travel history and unsampled diversity in Bayesian phylogeographic inference of SARS-CoV-2. Nat. Commun. 11(1):5110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemey P., Rambaut A., Welch J.J., Suchard M.A.. 2010. Phylogeography takes a relaxed random walk in continuous space and time. Mol. Biol. Evolut. 27(8):1877–1885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mbala-Kingebeni P., Pratt C., Mutafali-Ruffin M., Pauthner M.G., Bile F., Nkuba-Ndaye A., Black A., Kinganda-Lusamaki E., Faye M., Aziza A., Diagne M.M., Mukadi D., White B., Hadfield J., Gangavarapu K., Bisento N., Kazadi D., Nsunda B., Akonga M., Tshiani O., Misasi J., Ploquin A., Epaso V., Sana-Paka E., N’kasar Y.T.T., Mambu F., Edidi F., Matondo M., Bula Bula J., Diallo B., Keita M., Belizaire M.R.D., Fall I.S., Yam A., Mulangu S., Rimion A.W., Salfati E., Torkamani A., Suchard M.A., Crozier I., Hensley L., Rambaut A., Faye O., Sall A., Sullivan N.J., Bedford T., Andersen K.G., Wiley M.R., Ahuka-Mundeke S., MuyembeTamfum J.-J.. 2021. Ebola Virus transmission Initiated by relapse of systemic Ebola virus disease. N. Engl. J. Med. 384(13):1240–1247. doi: 10.1056/NEJMoa2024670 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Membrebe J.V., Suchard M.A., Rambaut A., Baele G., Lemey P.. 2019. Bayesian inference of evolutionary histories under time-dependent substitution rates. Mol. Biol. Evolut. 36(8):1793–1803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meredith R.W., Janečka J.E., Gatesy J., Ryder O.A., Fisher C.A., Teeling E.C., Goodbla A., Eizirik E., Simão T.L., Stadler T., Rabosky D.L., Honeycutt R.L., Flynn J.J., Ingram C.M., Steiner C., Williams T.L., Robinson T.J., Burk-Herrick A., Westerman M., Ayoub N.A., Springer M.S., Murphy W.J.. 2011. Impacts of the cretaceous terrestrial revolution and KPg extinction on mammal diversification. Science. 334(6055):521–524. doi: 10.1126/science.1211028 [DOI] [PubMed] [Google Scholar]
- Metropolis N., Rosenbluth A.W., Rosenbluth M.N., Teller A.H., Teller E.. 1953. Equation of state calculations by fast computing machines. J. Chem. Phys. 21(6):1087–1092. [Google Scholar]
- Neal R.M. 2011. MCMC using Hamiltonian dynamics. Handbook of Markov Chain Monte Carlo. 2(11. [Google Scholar]
- Nishimura A., Dunson D.B., Lu J.. 2020. Discontinuous hamiltonian monte carlo for discrete parameters and discontinuous likelihoods. Biometrika. 107(2):365–380. [Google Scholar]
- Pena V., Vieira C., Braga J.C., Aguirre J., Rösler A., Baele G., De Clerck O., Le Gall L.. 2020. Radiation of the coralline red algae (corallinophycidae, rhodophyta) crown group as inferred from a multilocus time-calibrated phylogeny. Mol. Phylogenet. Evolut. 150:106845. [DOI] [PubMed] [Google Scholar]
- Pybus O.G., Suchard M.A., Lemey P., Bernardin F.J., Rambaut A., Crawford F.W., Gray R.R., Arinaminpathy N., Stramer S.L., Busch M.P., Delwart E.L.. 2012. Unifying the spatial epidemiology and molecular evolution of emerging epidemics. Proc. Natl. Acad. Sci. USA. 109(37):15066–15071. doi: 10.1073/pnas.1206598109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rannala B., Yang Z.. 2003. Bayes estimation of species divergence times and ancestral population sizes using DNA sequences from multiple loci. Genetics. 164(4):1645–1656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rannala B., Yang Z.. 2007. Inferring speciation times under an episodic molecular clock. Syst. Biol. 56(3):453–466. [DOI] [PubMed] [Google Scholar]
- Roberts G.O., Rosenthal J.S.. 2009. Examples of adaptive MCMC. J. Computat. Graph. Stat. 18(2):349–367. [Google Scholar]
- Salvatier J., Wiecki T.V., Fonnesbeck C.. 2016. Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simion P., Delsuc F., Philippe H.. 2020. To what extent current limits of phylogenomics can be overcome? Scornavacca, Celine; Delsuc, Frédéric; Galtier, Nicolas. Phylogenetics in the Genomic Era. No commercial publisher; — Authors open access book, p. 2.1:1–2.1:34. [Google Scholar]
- Stadler T. 2010. Sampling-through-time in birth–death trees. J. Theor. Biol. 267(3):396–404. [DOI] [PubMed] [Google Scholar]
- Stan Development Team (2017). Stan modeling language users guide and reference manual, Version 2.17.0.
- Suchard M.A., Lemey P., Baele G., Ayres D.L., Drummond A.J., Rambaut A.. 2018. Bayesian phylogenetic and phylodynamic data integration using beast 1.10. Virus Evolut. 4(1):vey016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorne J.L., Kishino H., Painter I.S.. 1998. Estimating the rate of evolution of the rate of molecular evolution. Mol. Biol. Evolut. 15(12):1647–1657. [DOI] [PubMed] [Google Scholar]
- Tierney L. 1994. Markov chains for exploring posterior distributions. Ann. Stat: 1701–1728. [Google Scholar]
- World Health Organization. 2021. Ebola outbreak 2018-2020- north kivu/ituri, drc. Available from: https://www.who.int/emergencies/situations/Ebola-2019-drc-.
- Yang Z., Rannala B.. 2006. Bayesian estimation of species divergence times under a molecular clock using multiple fossil calibrations with soft bounds. Mol. Biol. Evolut. 23(1):212–226. [DOI] [PubMed] [Google Scholar]
- Zuckerkandl E., Pauling L.B.. 1962. Molecular disease, evolution and genic heterogeneity. In Kasha M., Pullman B., editors. Horizons in biochemistry. New York, NY: Academic Press. p. 189–225. [Google Scholar]