Online adaptive planning methods for intensity-modulated radiotherapy

Abstract

Online adaptive radiation therapy aims at adapting a patient’s treatment plan to their current anatomy to account for inter-fraction variations before daily treatment delivery. As this process needs to be accomplished while the patient is immobilized on the treatment couch, it requires time-efficient adaptive planning methods to generate a quality daily treatment plan rapidly. The conventional planning methods do not meet the time requirement of online adaptive radiation therapy because they often involve excessive human intervention, significantly prolonging the planning phase. This article reviews the planning strategies employed by current commercial online adaptive radiation therapy systems, research on online adaptive planning, and artificial intelligence’s potential application to online adaptive planning.

1. Introduction

In conventional radiation therapy (RT), a treatment planner designs a treatment plan based on the patient’s anatomy before the treatment starts, and the same plan is intended to be used throughout the course of treatment (Wu et al.; 2002), which usually spans several weeks. If systematic anatomical changes are observed, a new computed tomography (CT) scan can be acquired and the planning process repeated to account for the change in the remaining treatments. As the patient’s anatomy varies from day to day, undesired inter-fraction variations could occur between the daily treatment sessions, such as organ motion, organ deformation, density change, cavity filling, which may significantly compromise the therapeutic effect of the treatment plan (Lomax; 2008; Schmidt et al.; 2013; Müller et al.; 2015; Uchinami et al.; 2019; Ashida et al.; 2020). As a consequence of these variations, the actual target coverage and organ doses may not match the intent of the treatment plan. To alleviate the negative impact of inter-fraction variations, efforts over the past two decades have focused on many approaches such as adding margins to the target structures, improved immobilization devices, image-guided radiotherapy (IGRT), robust optimization, the plan-of-the-day approach, and adaptive radiotherapy.

In IGRT, patients receive daily imaging prior to a daily treatment session. Based on the daily image, the treatment couch is shifted to align the patient with the planning image, such that the target volumes on the daily and planning images match each other to the maximum degree (Dawson and Sharpe; 2006; Den et al.; 2010). This repositioning technique can mitigate setup errors and land the daily target volume of the patients in the planned irradiation area, hence increasing the target coverage and reducing the margin required for daily treatment (Dawson and Sharpe; 2006; Den et al.; 2010; Dhont et al.; 2020). Although IGRT can improve treatment quality to some extent, it is limited to correcting for positional errors with rigid translations and rotations; IGRT is unable to rectify other sources of error such as organ deformation, beam path changes, and weight loss (Sonke et al.; 2019).

On the other hand, robust optimization considers the latent inter-fraction variations as optimization uncertainties and takes them into account beforehand in the optimization process (Chan et al.; 2006; Bortfeld et al.; 2008; Unkelbach et al.; 2009, 2018; Fredriksson et al.; 2021). The first step is to model the scenarios that represent the possible inter-fraction variations. Then, a robust plan is generated that provides a reasonable dose distribution for any scenario considered in the optimization process. This approach has demonstrated a certain level of effectiveness in inter-fraction variation handling (Liu et al.; 2013; Mahmoudzadeh et al.; 2015; Zhang et al.; 2018). However, robust optimization has two inherent limitations that keep it from being the optimal solution to inter-fraction variations. First, robust optimization requires defining uncertainty sets for the optimization model. These usually only include predictable uncertainties that are easy to model, such as range uncertainty and setup uncertainty, and disregard uncertainties that are difficult to precisely predict and model, such as weight loss, organ deformation, and target volume changes. Consequently, the modeled uncertainty scenarios do not realistically represent all possible inter-fraction variations. (Li et al.; 2015). Second, robust optimization finds a solution suitable for a set of possible scenarios. Therefore, when applied to a particular scenario, the robust solution does not provide the optimal therapeutic effect for a particular instance. In other words, robustness comes at a price (Bertsimas and Sim; 2004; van de Water et al.; 2016). Ultimately, the ideal approach is to adapt the treatment plan to the patient’s anatomical changes during the course of treatment.

The plan-of-the-day approach, instead of creating only one treatment plan for one anatomy, prepares a library of treatment plans for different anatomical scenarios that might occur during the course of the treatment. At a daily session, the most suitable plan is selected based on the patient’s current anatomy (Nováková et al.; 2017; Oud et al.; 2022). This method has been presented clinically for photon (Heijkoop et al.; 2014; Buschmann et al.; 2018; Huddart et al.; 2021) and proton radiation therapy (Troost et al.; 2022). The advantage of the plan-of-the-day approach is that it generally does not require additional time or resources as it bypasses daily plan generation and only performs the selection of the daily plan at a treatment session. Compared to robust optimization, which takes all the possible anatomical scenarios into account in one treatment plan, the plan-of-the-day approach, in principle, allows less conservative plans for treatment. However, although the plan-of-the-day approach is a significant step towards adapting to inter-fraction variations, it is difficult to include all the possible situations when preparing the plan library, especially for changes such as internal organ deformation.

The concept of adaptive radiotherapy was invented to account for inter-fraction variations by updating the treatment plan during the course of the treatment. (Yan et al.; 1997; Wu et al.; 2009; Sonke and Belderbos; 2010; Castadot et al.; 2010). The patient would receive re-scan, and a treatment plan that matches the patient’s latest anatomy would be created based on the updated image and contours and undergoes quality assurance (QA) for clinical use. In adaptive radiotherapy, the need for the planning margins used in conventional radiotherapy to account for the inter-fraction variations is hence reduced. The smaller planning margin size leads to less conservative treatment plans with better predicted therapeutic effects (Nuver et al.; 2007; Lu et al.; 2012; van Kranen et al.; 2016; Christiansen et al.; 2021a). Various studies have illustrated adaptive radiotherapy’s potential to reduce toxicity and improve clinical outcomes (Foroudi et al.; 2009; Han et al.; 2008; Wang et al.; 2009; Christiansen et al.; 2021b). Adaptive radiotherapy also exhibited superior efficacy as a method for interfraction variation correction, compared to robust optimization (van de Water et al.; 2018; Jagt et al.; 2020; Lalonde et al.; 2021).

Currently, there are three recognized types of adaptive radiotherapy: offline (OffART), online (OnART), and real-time. The three types differ fundamentally in the time taken for the adaptive process. In OffART, the contouring, plan adaptation, and QA are performed in between fractions when patients are away from the treatment room. OffART is usually performed periodically, e.g., weekly, (Yan and Liang; 2013; Ramella et al.; 2017) or when the patient experiences significant anatomical changes (Lim et al.; 2014; van Beek et al.; 2019), because it usually requires manual intervention for the three steps mentioned above, which is a labor-intensive and time-consuming process. On the other hand, OnART is performed prior to treatment delivery when the patient is immobilized on the treatment couch. Compared to the offline approach, the online approach has two distinct advantages. First, OnART allows treatment with daily plans created based on the latest anatomy, minimizing the time gap between plan creation and delivery. For that reason, patients are expected to receive treatment more conformal to their current anatomy with OnART than with OffART. Second, OnART allows more frequent adaptation since online adaptation can be, in principle, carried out every fraction, whereas OffART can only be made occasionally. Increasing the frequency of adaptation is shown to be able to enhance treatment quality (Bostel et al.; 2019; Bobić et al.; 2021).

Real-time describes a type of adaptive therapy that involves real-time tracking of the target during the delivery rather than creating a new plan based on a static image. This has been described for conventional linacs using the megavoltage (MV) imager and the treatment beam to image and track the target during the delivery, adjusting the multi-leaf collimator (MLC) to follow the target if the position changes (Colvill et al.; 2016; Keall et al.; 2016, 2018, 2019; Muurholm et al.; 2021). Additional methods have been employed using the kilovoltage (kV) imager (Poulsen et al.; 2010) or combining information from both the kV and MV imager for tracking (Cho et al.; 2009). Another method of tracking involves using implanted electromagnetic transponders to guide and monitor target localization in real-time; this has been marketed as the Calypso^® 4D Localization System (Willoughby et al.; 2006; Silva et al.; 2014). Real-time localization and tracking can also be achieved with MR imaging on an MRI-linac (Fast et al.; 2019). A new radiotherapy system (RefleXion Medical, Hayward, CA, USA) combines a linac with a position-emission tomography (PET) detector to use the signal from injected radiotracers to track the target. Two systems designed for real-time target tracking are the CyberKnife (Accuray, Sunnyvale, CA) and Vero systems (Mitsubishi Heavy Industries, Tokyo, Japan and Brainlab AG, Feldkirchen, Germany). Instead of dynamically adjusting the MLC positions, the beam direction is guided by an external-internal correlation model (Seppenwoolde et al.; 2007; Hoogeman et al.; 2009; Sothmann et al.; 2016; Hiraoka et al.; 2020). The correlation model associates the measured signal of the external marker with the position of the internal markers, either implanted fiducials or a visible lung tumor. During treatment, the robotic arm, couch, or gimbal moves according to the measured external marker signal to adjust the beam direction. Since real-time adaptive does not require re-planning, it will not be discussed further in this review.

As promising as OnART sounds, it also comes with various difficulties. One of them is the limited time for adaptation. As the patient is immobilized on the treatment couch while online adaptation is being performed, for the sake of patients’ comfort and to minimize the anatomical variations that occur between plan creation and delivery, the whole process should be accomplished within minutes (Paganetti et al.; 2021). The demanding time restriction is one of the most critical challenges, particularly for plan adaptation, which is the subject of this review. The question then is: how may one create clinically acceptable plans within such a short amount of time and which planning strategies may lead to a better plan from the clinical point of view?

By now, a few review articles have addressed online plan adaptation (Sonke et al.; 2019; Albertini et al.; 2020; Paganetti et al.; 2021). However, these articles were intended to broadly cover the entire online adaptive workflow and only touched briefly on online adaptive planning strategies. This article presents an exhaustive review of existing online adaptive planning strategies as well as commercial OnART systems as a benchmark, providing an overview of the development of online adaptive planning, and describes artificial intelligence (AI) based strategies that may be implemented in the future, as shown in figure 1.

Figure 1.

Review structure

We conducted a literature search using the PubMed search engine. The combination of the following keywords was used initially to identify target articles: one of the following four keywords, “online plan adaptation,” “online adaptive planning,” “automated treatment planning,” and “artificial intelligence treatment planning,” with one of the following three keywords, “intensity-modulated radiation therapy (IMRT),” “intensity-modulated proton therapy (IMPT),” and “volumetric-modulated arc therapy (VMAT).” Then, we expanded our search scope by performing chain searches based on the articles already collected, gathering relevant articles that are cited in them. Finally, we included papers that satisfy the four following criteria in this review:

• The planning methods discussed in the article address inter-fractional anatomical variations.

• The planning methods discussed in the article are highly automated and can be prospectively integrated into the OnART pipeline.

• The planning methods discussed in the article are suitable for intensity-modulated radiotherapy, namely IMRT, including VMAT, and IMPT.

• The written language of the article is English.

Additionally, we conducted a secondary literature search for the commercial online adaptive systems with the keywords: “Ethos online adaptive,” “ViewRay online adaptive,” and “Unity online adaptive,” following the criteria above.

2. Online adaptive radiotherapy and its challenges

The OnART workflow comprises four primary components that must be accomplished before daily treatment delivery: 1. Online imaging, 2. online contour delineation, 3. online treatment plan adaptation, and 4. online plan approval and QA (Albertini et al.; 2020). Besides the technical difficulties associated with each step, the limited amount of time available, minutes, for all four components is the bottleneck that impedes extensive clinical implementation of OnART. To complete the OnART workflow within the restricted time frame, the general idea is to employ high-performance computers and replace human decision-makers with highly automated computerized algorithms.

For offline imaging, CT is commonly used, although magnetic resonance imaging (MRI) is also becoming more popular. For online imaging, in-room CT (Ma and Paskalev; 2006; Knight et al.; 2009; Nesteruk et al.; 2021), cone-beam CT (CBCT) (Yang et al.; 2007; Srinivasan et al.; 2014; Hua et al.; 2017), and MRI (Korhonen et al.; 2014; Prior et al.; 2016; Koivula et al.; 2016; Maspero et al.; 2017) are the imaging modalities for streamlined image acquisition. Currently, images acquired with CBCT or MRI must be registered to the planning CT to create a synthetic CT for dose calculation; CBCT Hounsfield Units (HU) are not sufficiently accurate for dose calculation, and MR images do not contain HU. For proton therapy planning, the conversion of HUs to proton-stopping power is required, and accurate HU are even more crucial than for photons due to the sensitivity of proton dose to the path length.

For online contour delineation, contour propagation and automated segmentation, two highly automated approaches, are taking over the task from human decision-makers. Contour propagation projects the planning contours onto the repeat CT either rigidly (Jagt et al.; 2017; Bernatowicz et al.; 2018; Botas et al.; 2018) or deformably (Bach Cuadra et al.; 2006; Fritscher et al.; 2014; Lustberg et al.; 2018; Nenoff, Matter, Amaya, Josipovic, Knopf, Lomax, Persson, Ribeiro, Visser, Walser, Weber, Zhang and Albertini; 2021). Automated segmentation includes shape modeling methods, such as statistic shape model (Heimann and Meinzer; 2009; Carminati et al.; 2018) and shape representation (Ibragimov et al.; 2014; Tong et al.; 2018), and AI-based methods (Lustberg et al.; 2018; Elmahdy et al.; 2019; Zhu et al.; 2020; Zhou; 2020).

For online plan approval, various AI-based tools, such as dose-volume histogram (DVH) predictor (Zhu et al.; 2011; Tol et al.; 2015; Li et al.; 2017; Hardcastle et al.; 2021), have emerged. The DVH predictor predicts the optimal DVHs for a geometry, which can be used as a reference for plan optimality in the plan evaluation process. For online QA, the traditional phantom-based physical QA is infeasible due to its unwieldy nature. Virtual QA, such as secondary dose calculation has been developed as an alternative approach (Matter et al.; 2018; Johnson et al.; 2019; Zhao et al.; 2021). The secondary dose calculation, which re-calculates the dose distribution with the adapted plan parameters on the planning image, should be done using a dose engine which is independent of the treatment planning system (TPS) and may even use a different calculation algorithm such as Monte Carlo (MC).

By all means, the idea of replacing manual intervention with highly automated algorithms also extends to online adaptive planning. Prior planning knowledge is the key to these highly automated adaptive planning methods. The patient’s original plan, which is regarded as a clinical standard treatment plan for the patient, and population planning knowledge can be utilized in online adaptive planning. The patient’s original plan can be spatially deformed to match the patient’s daily geometry (Mohan et al.; 2005; Court et al.; 2005, 2006; Feng et al.; 2006; Fu et al.; 2009; Ahunbay et al.; 2008, 2009, 2010; Zhang et al.; 2011; Jagt et al.; 2017, 2018; Botas et al.; 2018; Bernatowicz et al.; 2018; Jagt et al.; 2019; Liu et al.; 2020) or used as guidance for re-optimization (Li et al.; 2013; Vestergaard et al.; 2013; Zarepisheh et al.; 2014; Ahunbay and Li; 2015; Tyran et al.; 2018; Olberg et al.; 2018; Kong et al.; 2019). The planning knowledge extracted from similar patients can be used to train AI agents for rapid daily plan generation to meet the time requirement of OnART (Lee et al.; 2013; Boutilier et al.; 2015; McIntosh et al.; 2017; Mahmood et al.; 2018; Shen et al.; 2020; Jihong et al.; 2020; Li et al.; 2020, 2021; Shen, Chen, Gonzalez and Jia; 2021).

3. Treatment planning as an optimization problem

Intensity-modulated treatment planning employs inverse planning techniques. Broadly speaking, the planner starts by defining a set of dosimetric goals in terms of DVH objectives or constraints based on the therapeutic effect they desire for the treatment (Bortfeld; 1999; Xing et al.; 1999; Oelfke and Bortfeld; 2003; Webb; 2003). For example, one can define objectives or constraints such as the minimum dose delivered to 95%, D₉₅, of the planning target volume (PTV) to be no less than 97% in relative dose, or the maximum dose, D_max, delievered to the chiasm to be no more than 30% in relative dose to regulate the dosimetric attributes of the treatment plan. The constraints are the hard criteria that the plan must satisfy, and the objectives are the soft criteria that the plan better satisfies. The established set of objectives is formulated into an optimization problem subject to the constraints (Craft et al.; 2006; Craft; 2013), which computerized optimization algorithms can solve efficiently:

$$\begin{array}{l}\underset{x}{\text{min}}\left\{f_1(d),f_2(d)\dots f_N(d)\right\}\\ \text{s}.\text{t}.g_i(d)\le 0,j=1,\dots ,M,\\ D_x=d,\\ x\ge 0,\end{array}$$ (1)

where f_i(d) denote the objectives, g_j(d) denote the constraints, D denotes the dose influence matrix, d denotes the dose distribution, and x denotes the solution. For IMRT, the solution, x, can be a fluence map (Romeijn et al.; 2004b; Jin et al.; 2010; Aleman; 2018) or a set of MLC apertures weights (Shepard et al.; 2002; Broderick et al.; 2009; Salari and Unkelbach; 2013). For IMPT, the solution is a set of spot weights for the designated proton beamlets (Lomax; 2008; Jagt et al.; 2017; van de Water et al.; 2020). Due to multi-dimensionality, there does not exist an ultimate optimal solution for such an optimization problem. However, there exist Pareto optimal solutions, whose objectives can not be improved without having the others compromised. The Pareto solutions altogether form a Pareto frontier and the treatment planner would search for the treatment plan on the Pareto frontier. Conventionally, the treatment planner assigns a weight to each objective to scalarize problem (1) into the following problem:

$$\begin{array}{l}\underset{x}{\text{min}}\sum _{i=1}^N{w}_i{f}_i(d)\\ \text{s}.\text{t}.g_i(d)\le 0,j=1,\dots ,M,\\ D_x=d,\\ x\ge 0,\end{array}$$ (2)

where w_i denotes the non-negative objective weight assigned to each objective f_i(d). Intuitively speaking, increasing an objective weight w_i results in a Pareto solution that better meets the corresponding objective, f_i(d). The planning procedure includes consecutive tuning of planning parameters, such as objective weights and DVH constraints, and evaluating the intermediate plan generated by the selected planning parameters. The procedure continues until a satisfactory plan is found. However, this trial-and-error-based process can be very lengthy for complex cases with many objectives, as a large number of repetitions of the above steps can be required. Besides the parameter-tuning process, plan generation and evaluation also cost a considerable amount of time. Consequently, a conventional planning session can last from tens of minutes to hours (Hong et al.; 2008; Craft et al.; 2012; Xhaferllari et al.; 2013; Kusters et al.; 2017; Lin et al.; 2020), depending on the complexity of the case. Therefore, conventional planning fails to meet the time requirements of OnART.

Alternative planning techniques, such as Pareto navigation (Craft et al.; 2006; Monz et al.; 2008; Teichert et al.; 2011; Craft and Richter; 2013) and wish-list-driven optimization (Breedveld et al.; 2012; Bijman et al.; 2021), have emerged to improve planning performance and efficiency. The Pareto navigation method first approximates the patient’s daily Pareto frontier by the convex combination of multiple pre-calculated Pareto plans. It allows the planner to navigate through the approximated Pareto frontier and identifies the favorite plan in a real-time fashion. On the other hand, for wish-list-driven optimization, the planner a priori defines a ‘wish list’ that contains objective functions with different priorities and constraints. Then, the ϵ-constraint method (Haimes et al.; 1971) is iteratively performed to solve the optimization problems guided by the wish list. An objective function in the list is minimized in each iteration following the order of priority, subject to the defined constraints and the achieved objective values of the higher-priority objective functions minimized in the previous iterations. Although such planning techniques significantly reduce treatment planning time (Hong et al.; 2008; Craft et al.; 2012; Müller et al.; 2017; Bijman et al.; 2021), the time cost still exceeds the time constraint of OnART because the methods either rely on human intervention in the navigation phase or require multiple rounds of optimization problem solving. Therefore, to meet the time requirement of OnART, it is crucial to employ novel planning strategies that are highly automated and concise in the optimization process.

4. Current commercial OnART systems

Currently, there are no commercial systems that perform online adaptive proton therapy, but three commercial systems are clinically available for online adaptive photon therapy: Ethos, Unity, and MRIdian. The three systems use different modalities for the daily replanning image; Ethos uses CBCT images, Unity uses 1.5 T MR images, and MRIdian uses 0.35 T MR images. The three systems also use different plan adaptation strategies, with different compromises made to achieve faster plan optimization times.

4.1. Varian Ethos

The Varian Ethos (Varian Medical Systems, Palo Alto, CA), introduced in 2019, pairs the closed bore Halcyon linac with dedicated treatment planning and record and verify systems. The Halcyon linac provides a 6 MV flattening filter free (FFF) beam and kV iterative cone-beam CT (iCBCT) imaging, with a minimum CBCT acquisition time of 17 seconds (Netherton et al.; 2019; Pathak et al.; 2021). A streamlined adaptive workflow is enabled in part through artificial intelligence (AI)-based auto-contouring of relevant organs at risk (OARs) and rapid plan re-optimization capabilities.

The Ethos uses Varian’s Intelligent Optimization Engine (IOE) (Pokharel et al.; 2022) for the optimization of the initial treatment plan and the daily adapted plan (Varian; 2021). The user is required to create a prioritized list of clinical goals, using standard optimization goals such as Dmin, Dmax, Dmean, dose or volumetric goals. Each target or organ may have multiple goals, and each goal is assigned a priority group of 1 (Most important), 2 (Very important), 3 (Important), 4 (Less important), or 5 (Report value only; these goals are ignored during optimization). Within each priority group, goals are given sub-priority rankings by ordering the goals within the group. Prior to initiating the optimization, the IOE performs a structure pre-processing step where it examines the goal list and assesses possible conflicts and overlaps between targets and organs. The IOE resolves overlap situations by creating a modified optimization structure set which crops structures assigned a lower-priority goal from those structures with a higher-priority goal, using automatically determined margin structures to ensure the dose gradients are controlled. Extra goals, structures, and optimization objectives are defined by the IOE to control other quality metrics. These include a Normal Tissue Objective (NTO) to ensure that dose falls off appropriately from the target level, a hot-spot control constraint for the body to prevent global hot spots above the highest prescription dose, and ring structures created around each target to keep prescription doses within the target region. There is also a metric that monitors fluence complexity and aims to reduce excessive monitor units (MU) that can arise after leaf motion calculation. During optimization, unmet goals with higher priority are worked on before lower priority goals; the ranking of goals by the user is essential to the creation of optimization structures and the automatic handling of the optimization objectives by the IOE. Byrne et al. (2022) shows that the IOE took around one minute for reoptimization of IMRT lung and brain cases.

RapidPlan (Fogliata et al.; 2019) DVH estimation models can be imported into Ethos and applied to a prescription. However, because there is not a known priority order for the DVH line objective derived from a RapidPlan model, the IOE cannot effectively monitor or modify the strength of this line objective. The cost function from the DVH estimation model is added to the optimization at a level low enough not to overwhelm the IOE’s automatically determined objectives. Thus, RapidPlan models in Ethos serve principally as quality monitors rather than driving the optimization (Varian; 2021).

The Photon Optimization (PO) algorithm optimizes IMRT and volumetric modulated arc therapy (VMAT) plans using the cost function created for each optimization objective by the IOE (Pokharel et al.; 2022). The sum of all objective cost functions is minimized by iteratively conforming the dose distribution to the desired objectives. Fluence smoothing is used for static field IMRT optimization with PO to allow the Leaf Motion Calculator (LMC) to find a good representation of the fluence while keeping the MU low (Spirou and Chui; 1994). The Automated Planning algorithm uses Smart LMC to sequence the leaf positions from the optimized fluence (Varian; 2021). The Sliding Window method is used to minimize the delivery time and avoid extra dose from MLC transmission and leakage.

For Ethos adaptive therapy, the user enters the prescription, clinical goals for each target and organ, and the priority ordering of goals when creating the initial treatment plan. These are saved and used for daily adapted plan generation. To streamline the automated plan generation workflow, the user is not allowed to modify any goals or change the goal ordering for the daily adapted plan. To generate a clinically acceptable adapted plan, the user must understand how the IOE sets up the optimization to order the goals appropriately and ensure the goals are robust to changes in the anatomy. For example, if there is overlap between an organ and a PTV, the PTV will be cropped and underdosed if the organ has a higher priority clinical goal than the PTV, and this behavior cannot be modified for daily adaptive plan generation.

4.2. Elekta Unity

The Unity MR-linac, introduced in 2018, is a hybrid wide-bore 1.5 T MRI (Philips, Best, The Netherlands) and a slip-ring design 7 MV FFF linac (Elekta AB, Stockholm, Sweden) pairing that requires some form of plan adaptation for every daily treatment delivery. The linac treatment couch does not allow making shifts for patient alignment, so every plan at a minimum must be adapted for changes in the patient position relative to treatment isocenter. The primary advantage of MRI over CBCT is improved soft tissue visualization; MRI can also be used for intra-fraction motion monitoring as it does not use ionizing radiation to form the image. The Unity does not have dedicated treatment planning or record and verify systems, instead utilizing Monaco (Elekta AB, Stockholm, Sweden) for treatment planning and Mosaiq (Elekta AB, Stockholm, Sweden) for record and verify.

The initial pre-treatment plan is generated using Monaco. In addition to standard physical cost functions such as DVH and maximum dose, Monaco offers one objective biological cost function for targets, a Poisson statistics cell kills model, and two constraint biological cost functions for OARs based on a general parallel or serial organ model (Semenenko et al.; 2008). These biological indices, which act across the entire DVH rather than only up on a single point like physical cost functions, are included in the overall objective score for plan optimization. The optimization process in Monaco is divided into two stages; during the first stage, the ideal fluence map is optimized based on the objective function and the treatment beam parameters. Dose is calculated for this stage using a pencil beam (PB) algorithm. During the second stage, deliverable fields are generated by an MLC sequencer that simultaneously optimizes the segment shapes and weights. The dose is calculated for this stage using an MC algorithm. Chuter et al. (2019) found that the use of MC for stage I optimization for MR-linac plans was unnecessary as it increased planning time without providing any clinical improvement in plan quality compared to PB.

During an adaptive treatment, an online MRI is acquired and sent to Monaco. The pre-treatment CT, contours, and plan are used with the online MRI to adapt the plan. In Monaco, the user selects one of two adaptive workflows: Adapt To Position (ATP) or Adapt To Shape (ATS). The ATP workflow allows for plan adaptation based only on patient position relative to isocenter; in this workflow, the pre-treatment CT is rigidly registered to the online MRI and the isocenter position on the pre-treatment CT is updated based on this registration. The pre-treatment plan is then either re-calculated or re-optimized on the pre-treatment CT based on the new isocenter position; no contour edits are allowed in this workflow, so the original contours are used for recalculation or re-optimization. If re-optimization is performed, it starts with the same optimization objectives as the original pre-treatment plan. An essential component of Unity adaptive planning is online Segment Aperture Morphing (SAM) (Ahunbay et al.; 2008, 2009, 2010). The SAM algorithm is designed to calculate the MLC morphing (leaf shifts) based on a beam’s eye view (BEV) of the old target projection compared to the new target projection, which allows the segment shapes to adjust for target translations, rotations, and deformations that cause a change in the BEV target projection.

The ATS workflow, on the other hand, allows for plan re-optimization based on changes in patient anatomy. In this workflow, the pre-treatment CT and contours are deformably registered with the online MR and contours are then edited if necessary. The plan is re-calculated or re-optimized on the online MR, with the contours assigned the average electron density value of the corresponding contour on the pre-treatment CT. Similar to ATP, the ATS re-optimization starts with the pre-treatment optimization objectives.

For both the ATP and ATS workflows, six different plan adaptation methods are offered in Monaco, as shown in Table 1. Method A uses the same segments and MU as the pre-treatment plan. Method B uses SAM to morph the segments from the pre-treatment plan based on the rigid registration between the pre-treatment CT and online MR. Method C uses the morphed segments after SAM and optimizes the weights of each segment to minimize the cost function created from user objectives (Ahunbay et al.; 2008, 2009, 2010). Method D discards the pre-treatment segments and first re-optimizes the fluence and creates a new set of segments. The sequencing can be performed with the iterative algorithm, adaptive sequencer (ASEQ), developed by Kontaxis et al. (2015, 2017). The new segments are then further optimized using segment weight optimization. The same is true for the last two methods; Method E uses the morphed segments after SAM for weight and shape optimization, while Method F re-optimizes the fluence and creates new segments, then further optimizes the weights and shapes. The ATP workflow only allows methods that use the morphed segments (A, B, C, and E); the user can switch from the ATP workflow to the ATS workflow within Monaco if they determine that an acceptable plan cannot be generated with any of the methods using the morphed segments. A study simulating online plan adaptation for five cases with varying levels of inter-fraction motion found that the time for re-optimization using the methods available in the ATP workflow ranged between 18 and 376 seconds (Winkel et al.; 2019), but that Methods A and B did not result in plans that met clinical constraints. Method C rarely met clinical constraints. The ATS workflow required longer times than ATP, ranging between 17 and 485 seconds, but was able to meet clinical constraints for most simulated adaptive plans.

Table 1.

Six online plan adaptation methods supported by Unity. SAM = Segment Aperture Morphing

Method	Name	Description
A	Original segments	No modification of segments
B	Adapt segments	Morph segments with SAM
C	Optimize Weights from segments	Method B + segment weight optimization
D	Optimize Weights from fluence	Re-optimize fluence and create new segments + segment weight optimization
E	Optimize Weights and Shapes from segments	Method C + shape optimization
F	Optimize Weights and Shapes from fluence	Method D + shape optimization

4.3. ViewRay MRIdian

The MRIdian (ViewRay Inc, Denver, CO) originated in 2014 with a 0.35 T MRI combined with three ring-gantry mounted ⁶⁰Co sources, and in 2018 was upgraded to use a 6 MV FFF linac instead of ⁶⁰Co. ViewRay provides a dedicated MC-based TPS which is also integrated into the MRIdian treatment console to allow online adaptive re-planning.

The initial pre-treatment plan is generated in the ViewRay TPS using either a CT scan or MR image; for plans based only on an MRI, electron densities must be set for each structure. The dose optimization algorithm uses a separable nonlinear convex voxel-based criteria optimization model with a projected gradient minimizing algorithm (Fox et al.; 2008; Romeijn et al.; 2004a). Contours are determined by the voxels of the image, with contours rounded to the nearest voxel, and all voxels have a penalty function associated with them according to their underlying target or critical structure. If multiple targets and critical structures overlap a given voxel, a user-defined priority list is used to determine which critical structure or target dominates. There are three radiation beam types in the ViewRay TPS: optimized conformal, fixed conformal, and IMRT (ViewRay; 2019). All three types require the user to set the number of beams and beam angles. Optimized conformal beams consist of one segment shaped to fit the target, with the fluence of individual beams optimized by the TPS based on user-defined constraints. Fixed conformal beams consist of one segment that is defined by the user rather than shaped automatically, with the TPS calculating the beam fluence based on prescription weighting points. IMRT beams are discretized into beamlets (bixels) for inverse optimization based on user-defined constraints. After calculating and optimizing the bixel doses to best achieve the desired optimization goals, bixel maps are converted into deliverable segments. An IMRT Efficiency factor is used as a fluence regularization term added to the objective function during optimization to penalize large fluence fluctuations (ie. differences between neighboring bixels). There are three IMRT leaf sequencing options, which also affect the total number of segments and plan quality: accuracy goal, fixed levels, and number of segments. The accuracy goal sequencer tries to minimize the distance between fluence and segment dose, adding more segments if necessary, and is useful when plan quality is more important than the number of segments. The fixed levels sequencer allows the user to specify the number of discretization levels for the bixel fluence map within a range of 2–20, with higher values resulting in more and smaller segments. The number of segments sequencer allows the user to specify the total number of segments as an upper limit; if the number of segments is too low, plan quality may be compromised. Romeijn optimization algorithm allows the user to generate a range of plans from a single cost function, with the plans increasing in number of segments from user-specified minimum to maximum values and is best used with number of segments sequencing to evaluate the appropriate number of segments that achieves desirable plan quality. Da Silva Mendes et al. (2021) found that ViewRay MR-linac IMRT plans for prostate cancer were comparable in plan quality to VMAT plans generated by Monaco for an Elekta Versa HD linac; the IMRT plans also had higher MU and longer predicted delivery times than the VMAT plans.

There are several options available in the online TPS for daily plan adaptation. ‘BOT Optimize’ is a simple segment weight optimization which does not modify the segment shapes and can be used either in place of an optimization or after optimization is complete. ‘Optimize Dose’ is used to start a new optimization or continue an existing optimization. If a new optimization is started, beam angles and structure weights can be edited if needed. Depending on the optimization changes, bixels may need to be re-calculated, which adds to the overall planning time, or only re-optimized. Changes that require bixel re-calculation include editing the bixel size, turning the magnetic field corrections on or off for bixel or dose calculation, editing the number of histories for MC bixel or dose calculation, editing a target structure, or adding or removing a structure as a target. Changes which only require bixel re-optimization include modifying Romeijn parameters, modifying the IMRT efficiency value, selecting a different sequencing option, editing existing objectives or constraints, or adding a new objective or constraint for an already included OAR. ‘Add Segments’ re-runs the segmentation with five additional segments to improve plan quality and can only be used after optimization is complete. The mean time cost for re-planning and QA was 5.91 ± 3.98 minutes based on 154 patients with 962 fractions treated on a MRIdian between 2018 and 2019, with the shortest time cost (3.71 minutes) for fractions treated with the predicted dose and the longest time cost (7.94 minutes) for fractions in which optimization and dose calculations were performed (Güngör et al.; 2021).

5. Research on online adaptive planning

In recent decades, various kinds of research have been conducted to improve the speed and efficacy of online adaptive planning. Two primary classes of methods have emerged for photon adaptive planning: ‘Plan deformation’ (Mohan et al.; 2005; Court et al.; 2005, 2006; Feng et al.; 2006; Ahunbay et al.; 2008; Fu et al.; 2009; Ahunbay et al.; 2009, 2010; Gui et al.; 2010; Liu et al.; 2020) and ‘re-optimization’ (Li et al.; 2013; Vestergaard et al.; 2013; Zarepisheh et al.; 2014; Ahunbay and Li; 2015; Tyran et al.; 2018; Olberg et al.; 2018; Kong et al.; 2019; Padgett et al.; 2020). The ‘plan deformation’ methods assume that the dose distribution is geometrically related to the patient’s anatomy. If a treatment plan, e.g. the fluence maps or MLC apertures, looks the same with respect to the daily anatomy as the original plan looks with respect to the original anatomy, it can deliver a dose similar to the original dose. Therefore, the ‘plan deformation’ methods spatially deform the original plan according to the inter-fraction anatomical changes to retain the relative geometric relationship between the plan and anatomy, as shown in figure 2. On the other hand, the ‘re-optimization’ methods seek a daily plan dosimetrically similar to the original plan through solving mathematical optimization problems established for the daily geometry.

Figure 2.

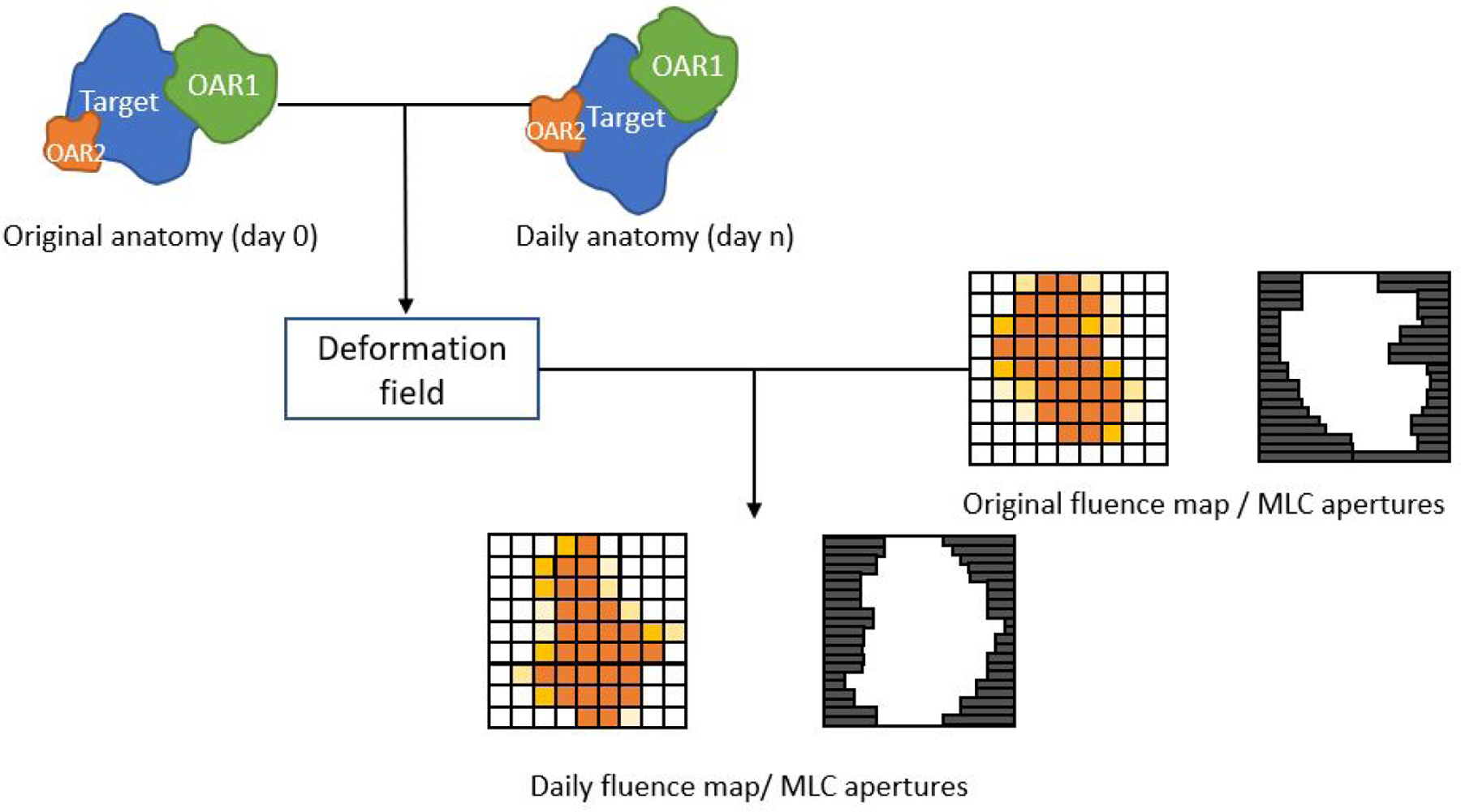
Plan deformation methods derive a deformation field from the inter-fraction anatomical changes that have occurred between day 0 and day n. The deformation field is then applied to the original plan for daily plan generation, in hopes that the original plan-anatomy relationship can be retained.

5.1. Plan deformation methods

Photon treatment planning systems generally either optimize the fluence map or segments; the plan deformation methods can also be subdivided into fluence map deformation methods (Mohan et al.; 2005; Liu et al.; 2020) and segment shape deformation methods (Court et al.; 2005, 2006; Feng et al.; 2006; Ahunbay et al.; 2008; Fu et al.; 2009; Ahunbay et al.; 2009, 2010; Gui et al.; 2010).

Mohan et al. (2005) proposed a method that deforms the original fluence map according to the change of the PTV’s projection in the beam direction. The original and daily PTV contours are first projected on the planning CT and repeat CT along the beam direction, respectively. Then, the PTV projections are deformably registered, resulting in a deformation field. The resultant deformation field represents the PTV changes that have occurred between pre-treatment planning and re-planning days. Finally, the deformation field is applied to the original fluence map, and the resultant fluence map is segmented for daily treatment. It is noteworthy that this method only considers the change of PTVs perpendicular to the beam direction when deforming the fluence maps, neglecting the change along the beam direction. The process was expected to complete within minutes for prostate and head-and-neck cases.

To take the change of PTVs in the beam direction into account, Liu et al. (2020) proposed a method that utilizes a 3-D deformation field to deform the original fluence map. The first step is registering the planning CT and repeat CT, obtaining a 3-D deformation field. Then, for each beamlet, the deformation vectors that reside along the beamlet are projected onto the isocenter plane perpendicular to the beamlet direction. The average of the projected deformation vectors is used to transform the position of the beamlet. This method costed approximately 3 minutes for re-planning for lung cases.

On the segment deformation side, Court et al. (2005) proposed a method that modifies the shape of the original segments using rigid image registration for co-planar IMRT prostate treatment. This method does not change the distance within the MLC leaf pairs of the original plan. The planning and repeat images are first rigidly registered by the target volume. The isocenter shift provides a global translation for the original segments in the superior-inferior (SI), anterior-posterior (AP), and right-left (RL) directions. Then, the individual slices of the planning image and their corresponding slices of the daily image are registered, providing a local translation in the AP direction to the MLC leaf pair above the registered slices, while the relative distance between the pair of MLC leaves remains untouched. Finally, the MLC leaves open up or close in the SI direction in response to the longitudinal extension or shrinkage of the target volume.

A year later, Court et al. (2006) further developed this method for head-and-neck cases, where additional consideration of rotation around the SI axis and translation in the RL direction need to be taken. Before the treatment, a primary plan is created for the planning image. Then, a library of secondary plans is established for the potential rotational changes. The secondary plans are created for the planning image using the primary plan’s objectives, objective weights, and gantry angles with different rotational displacements. Similar to the method previously described (Court et al.; 2005), before the daily fraction, the daily image and planning image are rigidly registered as a whole for the global shift for the MLC leaf pairs. Then, the individual slices are registered, determining the local translational changes in the AP and RL directions and the rotational change. The corresponding MLC leaf pair of the plan that has the most similar angular displacement to the determined rotational change is selected from the library for each daily image slice. Finally, the assembled MLC leaf pairs undergo global and local shifts and open up or close for the longitudinal change. The fixed distance within the MLC leaf pairs is a limitation of this method compared to the segment deformation methods to be presented later, because a segment more conformal to the target volume can be achieved by modifying the intra-leaf distance of the MLC leaf pairs.

In contrast to the rigid-image-registration-based MLC deformation methods, Feng et al. (2006) developed a method that modifies the MLC leaf pairs for each segment with deformable image registration. The underlying concept of this method is akin to the 3-D fluence map deformation method discussed above (Liu et al.; 2020). First, the planning and daily images are deformably registered, producing a 3-D deformation field. The 3-D deformation vectors along each beamlet path are projected onto the isocenter plane, perpendicular to the beam path, and averaged, resulting in a 2-D deformation field. The shape of the original segments is transcribed into a set of points located on their boundary. To deform the original segments, the 2-D deformation field is applied to the boundary points of the corresponding segment. The new boundary points determine the new MLC leaf pairs, which are subsequently converted into a deliverable plan with the original segment weights. The aperture deformation step took 30 seconds for a prostate case.

Fu et al. (2009) proposed a target-volume-projection-based deterministic model that transforms the segment shape. The model determines the new position of MLC leaf pairs from the geometrical center position and lateral extension of the planning and daily targets’ projection in the beam direction. The difference between the geometric center of planning and daily target projections provides a global shift to the MLC leaf pairs in the SI direction. Then, for each individual MLC leaf pair, the geometric center and the lateral boundary position of the part of the new target projection underneath it find the new position of the MLC leaf pair together with the MLC leaves’ original position. Finally, MLC leaf pairs close up if no target projection appears underneath them. Using this method, the adaptive planning process could be completed in 10–20 minutes, including contour delineation.

The segment aperture morphing (SAM) method is another target-volume-projection-based deterministic model that deforms the segment shape for daily plan adaptation (Ahunbay et al.; 2008). Unlike the method presented by Fu et al. (2009), which determines the new position of MLC leaf pairs individually from the part of the target projection underneath them, the SAM method determines the new position of MLC leaf pairs through the position of a group of boundary points created at the edge of the original MLC leaf pairs. For boundary points located within the planning target projection, their distance to the outline of the planning target projection in the x and y (SI) directions are linearly scaled by the ratio of the total extent of the daily target projection to that of the planning target projection in the respective direction. The boundary points located outside the planning target projection hold the point-to-target distance unchanged. Given the daily target projection, the new point-to-target distance decides the new position of the boundary points. The average lateral position of the new boundary points under an MLC leaf pair identifies the new lateral position of the MLC leaf pair. It took 1 second to complete SAM for IMRT head-and-neck and prostate cases (Ahunbay et al.; 2009, 2010) or less than 10 seconds for VMAT prostate, pancreatic, and lung cases treated with flattening filter free beams (Ates et al.; 2016).

Crijns et al. (2015) proposed an online plan adaptation method that combines SAM with internal markers for VMAT prostate cases. First, the initial and daily positions of the internal markers in the BEV are fitted using the least square fit. The resultant transformation is applied to the MLC apertures for translation, rotation, and isotropic scaling. Then, SAM is performed to morph the shape of the MLC apertures. Following that, a regularization factor derived from the target radius scales the apertures to maintain the initial penumbra margin size. Finally, the MU is corrected by a point dose calculation (Khan; 1992) based on the water equivalent path length (WEPL) between the internal maker and the internal markers. The adaptation workflow took less than 13 seconds to complete reportedly.

In summary, the plan deformation methods assume a geometric relationship between the patient’s treatment plan and dose distribution, such that if the patient’s original treatment plan is spatially deformed according to the inter-fractional anatomical changes, the original dose distribution can be retained for the daily fraction. The primary advantage of the plan deformation methods is the speed, which can be in the order of seconds. The deformation methods construct the daily plan by directly modifying an existing plan without solving any plan optimization problem, which can cost a significant amount of time if the problem involves a large number of decision variables and objective functions. However, it is worth noting that the methods that deform fluence maps require a following sequencing step to convert the resultant fluence maps into a deliverable plan, causing additional time cost and deterioration of the dose distribution. Although some plan deformation methods have been successfully implemented in commercial OnART systems, i.e., SAM (Winkel et al.; 2019; Strand et al.; 2021), the intrinsic drawback of this class of online plan adaptation methods is that the geometric relationship it relies on is a false assumption. First, the original plan might not be sufficient to deliver a quality dose distribution to the daily geometry in the first place, even after being spatially modified according to the anatomical variations. Second, the spatial modification does not account for the density changes along the beam path, e.g. transient intestinal gas, cavity filling, and skin folds. Therefore, the plan deformation methods do not guarantee the quality of the obtained daily plan.

5.2. Re-optimization methods

As mentioned in the previous section, the challenge of re-optimizing the treatment plan is the lengthy manual planning parameter tweaking process to establish a proper optimization problem for the daily geometry, such as choosing planning constraints, objectives, and objective weights. One of the most intuitive approaches to avoid the manual tweaking process is to reuse the optimization problem constructed for the initial plan (Vestergaard et al.; 2013; Tyran et al.; 2018; Kong et al.; 2019; Padgett et al.; 2020). This method is currently used in all commercial OnART systems and is the only re-optimization method available in Ethos, while the MR-linac systems allow modification of the original optimization problem if deemed necessary. The initial optimization problem encompasses the treatment planner’s preference. For example, the chosen objective weights reflect the treatment planner’s preferred trade-offs between the structures. If the patient does not undergo drastic anatomical changes, such trade-offs may remain valid in the subsequent days. Therefore, the initial optimization problem might lead to acceptable daily treatment plans, although not truly therapeutically optimal, for the following fractions.

On top of reusing the initial optimization problem for daily plan generation, Olberg et al. (2018) presented an organ grouping method that makes the initial optimization problem more robust to inter-fraction anatomical variations. The proposed method combines several critical OARs into one structure in the planning process instead of treating them individually. The unified OAR structure showed insensitivity to anatomical variations. The treatment with daily plans generated by OAR-grouping optimization problems showed significant improvement in target coverage compared to the treatment with the daily plans generated with the conventionally constructed initial optimization problems for pancreatic cases.

Besides reusing the initial optimization problem, several DVH-guided re-optimization methods have been developed. To make up for deficiencies of the plan deformation methods and further tailor the daily plan, a follow-up procedure that re-optimizes the segment weights after SAM was proposed (Ahunbay et al.; 2008, 2009, 2010). The segment weight optimization (SWO) method uses the DVH values achieved in the original plan as the prescribed dose in the objective functions, aiming to recover the original plan’s DVH values, which are considered clinically acceptable and attainable for the patient, in the daily treatment plan. The initial weight of the objectives is set to 1. During the optimization problem-solving phase, once an objective is fulfilled, its weights is set to 0, leaving space for other objectives yet to be satisfied. The SWO step took about 2 minutes to complete for head-and-neck and prostate cases.

Li et al. (2013) developed a DVH-guided iterative objective weight tuning method for online IMRT plan adaptation. The idea behind this method is to automate the plan evaluation and planning parameter tuning process, which can be time-consuming when conducted manually due to the time cost of decision-making. In the first phase, called the “coarse tuning phase,” a new weight is determined for each structure’s objective functions by the area where the DVH of this structure is worse in the intermediate plan than the original plan. In the second phase, called the “fine tuning phase,” a new weight is determined for each voxel by how much its dose achieved in the intermediate plan deviates from the prescribed dose. The stopping criteria are either that the maximum number of iterations is reached or that no substantial improvement can be made for the intermediate plan. The average time cost of re-optimization was around 30 seconds for each of the three head-and-neck cases.

Zarepisheh et al. (2014) presented a method that seeks objective weights that lead to a daily plan dosimetrically similar to the original plan on the daily Pareto frontier in the objective space, as shown in figure 3. The first step of the method is quadratically approximating the daily Pareto frontier with a pivot plan and a reference plan. The pivot plan is a plan generated with a random set of objective weights on the daily Pareto frontier, which makes the quadratic approximation of the daily Pareto frontier more realistic. The reference plan is the voxel dose permutation of the original plan most similar to the pivot plan. The maximized similarity makes the reference plan the voxel dose permutation most likely feasible for the daily geometry. Given that the gradient of a Pareto frontier at a Pareto solution is the objective weights associated with the solution, the gradient of the reference plan on the quadratic approximation of the daily frontier is calculated and used for daily plan generation. This proposed method can be performed repetitively with different pivot plans, and the best solution is selected as the daily plan in the end. This method took 11.6 seconds to complete adaptive planning for a head-and-neck case.

Figure 3.

2D demonstration of the Zarepisheh et al. (2014) method in the objective space. The yellow and red dots represent the pivot and reference plans. The dashed and solid curves represent the quadratically approximated and actual daily Pareto frontier, the arrow represents the objective weights of the reference plan on the quadratically approximate Pareto frontier, which leads to the daily plan, the green dot, on the actual daily Pareto frontier.

Ahunbay and Li (2015) proposed a method called gradient maintenance (GM), which is based on the idea that the dose gradients towards the OARs around the target in a plan correlate to the dosimetric features of the plan. Therefore, if such dose gradients achieved in the original plan can be preserved in the daily plan, then this daily plan should be dosimetrically similar to the original plan. The author introduced an artificial structure called partial concentric rings (PCR) as surrogates for the dose gradients. The PCRs are the projection of the OARs onto the surface of the isotropically expanded CTV at different extensions. At the daily treatment session, the target contours are delineated, and the original PCR contours are deformably registered to the daily image. An optimization problem that only concerns the target and PCRs is then established to recover the DVH values of the target and PCRs achieved in the original plan and is subsequently solved for a daily plan. This method took 5 minutes reportedly to complete for prostate and pancreas cases.

The re-optimization methods, in principle, are able to generate better quality daily plans than the plan deformation methods by strictly solving inverse optimization problems. However, extra caution is required when implementing this class of methods for online adaptive planning. When using the initial optimization problem for daily plan re-optimization, the initial DVH constraints can become infeasible due to inter-fraction anatomical variations. Therefore, when defining the initial optimization problem, the planner should not ‘over-tune’ the planning parameters for a ‘perfect’ initial plan. Rather, they should prioritize the achievability and flexibility of the optimization problem for the remainder of the treatment. Additionally, the method proposed by Zarepisheh et al. (2014) relies on a randomly generated pivot plan. Therefore, there is no guarantee for the consistent performance of the algorithm.

6. Proton online adaptive planning

While the optimization objectives for proton therapy plans may look similar to those for photon therapy plans, the physics of how protons deposit dose is fundamentally different from photons, and that affects how adaptive planning can be performed for protons. Unlike photons, protons deposit most energy at the end of their path, forming a Bragg peak depth dose distribution. Delivering a prescription dose requires accurate placement of the Bragg peaks of individual IMPT beamlets within the tumor. To place a beamlet’s Bragg peak at the desired location, in addition to the beam direction, the proton energy has to be taken into account to control the beam range, as shown in figure 4, which adds another layer of complexity to proton planning. Moreover, as proton therapy is highly sensitive to range variations caused by anatomical changes, proton therapy urges and benefits more from OnART. Therefore, this section summarizes methods considered specifically for online adaptive planning for IMPT.

Figure 4.

Due to cavity filling, a proton beamlet planned for the day 0 anatomy becomes short in range. After proton energy modulation, the proton beamlet is placed back at the same position.

In addition to using a pre-defined optimization problem for daily treatment plan re-optimization throughout the treatment (Kurz et al.; 2016; Nenoff et al.; 2019; Nenoff, Matter, Charmillot, Krier, Uher, Weber, Lomax and Albertini; 2021), current proton online adaptive planning research primarily focuses on restoring the dose of the original plan. Similar to the fluence map deformation methods for IMRT, the dose restoration method aims to retain the original geometric relationship between the spot pattern and anatomy by modulating proton beamlet’s direction and energy.

Zhang et al. (2011) started the investigation of spot pattern restoration as an online IMPT plan adaptation method on a phantom where only rigid target shift was considered. In this case, the spot pattern only needs to be maintained at the same position with respect to the target. The energy of the beamlets was adjusted correspondingly to maintain the WEPL so that the spots could land at the same position as before. Although the adapted plan showed much fewer cold spots than the re-positioning plan, it failed to show a satisfactory result. A large discrepancy in the DVH values was observed between the adapted plan delivered to phantom and the original plan delivered to the planning CT image. This is due to the fact that the proton beamlet profile varies with energy. Even if the original spots’ position can be maintained by adjusting the spots’ energy, the aggregation of the dose contribution over the individual spots still varies.

The inability of the spot deformation method to correct the errors caused by rigid organ shift, let alone organ deformation and other types of inter-fraction variations, suggests that it is necessary to re-optimize the spot weights after deforming the spot pattern in order to attain an adequate plan. Following this idea, Jagt et al. (2017) developed a dose restoration method, which, on top of spot restoration, involves a succeeding spot weight re-optimization procedure and tested it on IMPT prostate cases. The dose restoration workflow begins with rigidly propagating the planning contours onto the repeat CT. Therefore, this online plan adaptation method does not require a new set of contours for the repeat CT scan. Subsequently, the energy of the beamlets is adjusted accordingly to restore the original spot pattern with respect to the propagated target contour. A quadratic objective function (Voglis and Lagaris; 2004; Breedveld et al.; 2006) is employed to re-optimize the spot weights with heuristically pre-determined objective weights. This method could complete around 4.3 minutes on average for the prostate cases. In addition to the prostate cases, Bernatowicz et al. (2018); Borderías Villarroel et al. (2020) demonstrated the dose restoration method can improve the DVH parameters for 4-D robustly planned IMPT lung cases.

The dose restoration method has displayed a certain level of ability to correct interfraction variations. However, in reality, severe organ deformation and organ motion can occur. In that case, more than the dose restoration method is required because the spot pattern restored in the rigidly propagated target contour might not sufficiently represent the actual daily target volume. To that end, Jagt et al. (2018) introduced the full plan adaptation method, which consists of spot restoration, spot addition, and spot weights re-optimization. Unlike the previous dose restoration method, which only requires rigid organ contour projection, the full plan adaptation method requires organ contour delineation for the repeat CT scans because the spot addition step intends to add spots to the actual target contour. After the contour delineation and spot restoration, 2500 new spots are randomly added to the daily target contour to improve spot coverage further. The reference point method (RPM) used for spot weight re-optimization aims to reproduce the objective values achieved in the original plan, which reflect the DVH parameters in the original plan. The RPM sets the original objective values as the starting point of re-optimization and pushes it towards the daily Pareto frontier along a user-defined direction in the objective space to acquire a daily plan that is dosimetrically similar to the original plan. The average re-optimization time was 2.9 or 4.6 minutes, for one or two iterations. The full plan adaptation method outperformed the dose restoration method according to the sample tested. When combined with a pre-defined plan library so that a plan that matches the daily geometry more can be selected as the “prototype” plan for adaptation, the performance of the full-plan-adaptation method can be further enhanced (Jagt et al.; 2019).

One important advantage of the proposed dose restoration and full plan adaptation method is that they only include the highly relevant spots in the time-consuming calculation steps, i.e., dose influence map calculation and spot weight optimization, by re-using the original spots. In contrast, using a TPS-generated spot pattern, which fully covers the target volume, involves a substantial number of trivial spots in the calculation and hence prolongs plan generation timing. The nature of keeping only highly relevant spots in calculation enables Monte Carlo dose calculation in the planning phase (Botas et al.; 2018), allowing a more accurate dose influence map for planning and alleviating the arduous workload in the subsequent QA process.

7. AI as a potential solution to online adaptive planning

AI-based automated planning methods for radiotherapy have gained increasing attention from researchers over the years. The automation of treatment planning with AI-based methods reduces the need for human intervention and time costs, benefiting both offline and online planning. As limited planning time is the main concern of online adaptive planning, AI-based automated planning methods offer a potential solution to OnART for both photon and proton planning. The AI-based planning methods extract planning knowledge from the previous patient cohorts and generate a daily plan using the trained predictive AI model in a time-efficient manner. The following sections will present three classes of AI-based planning methods potentially suitable for online adaptive planning: 1. direct fluence map prediction (Li et al.; 2020, 2021), 2. optimal dose prediction (McIntosh and Purdie; 2017; Mahmood et al.; 2018; Nguyen et al.; 2019; Fan et al.; 2019; Kajikawa et al.; 2019; Shao et al.; 2021; Gronberg et al.; 2021) and dose-to-plan conversion (Wu et al.; 2008; Chan et al.; 2014; Goli; 2015; McIntosh et al.; 2017; Chan and Lee; 2018; Mahmood et al.; 2018; Fan et al.; 2019; Bakx et al.; 2021; Chan et al.; 2021), 3. planning parameter prediction (Lee et al.; 2013; Boutilier et al.; 2015; Shen et al.; 2020; Jihong et al.; 2020; Shen, Chen, Gonzalez and Jia; 2021), as shown in figure 5.

Figure 5.

Three classes of the AI methods that have the potential for online adaptive planning.

7.1. Direct fluence map prediction

Li et al. (2020, 2021) employed two deep learning networks, Dense-Res Hybrid Network (DHRN) and conditional generative adversarial network (cGAN), to directly predict fluence maps for IMRT prostate and oropharyngeal cases. Both models predict a fluence map for each individual beam from the anatomy representation seen in the beam direction. Two types of 2-D projection inputs characterize the patient’s anatomy: the intra-structure projection and the interface projection. The intra-structure projection is the integration of the photon attenuation coefficient along each beam direction within an important structure. The interface projection is the integration of the photon attenuation coefficient between the beam entrance interface of the patient’s body and the beam exit interface of an important structure along each beam direction. The ground truth plans are the treatment plans re-created by the author’s institute’s knowledge-based planning (KBP) plan generator for consistency. The author reports that the trained AI agents can predict fluence plans comparable to the test cohorts’ clinical and KBP treatment plans. The plan prediction process can be completed in the order of seconds, and the entire AI prediction workflow, from patient data loading to post-processing of the predicted fluence map into a deliverable plan, takes 2–3 minutes to complete.

Yuan et al. (2022) proposed a two-step direct fluence map prediction workflow for IMRT cervical cases. The two-step workflow consists of two convolutional neural network (CNN) models and predicts a fluence map for each individual beam. In the first step, the first CNN model, called CF-CNN, takes the patient’s target and OAR contour masks on each transverse slice of the CT as input and predicts a coarse fluence map, which is a fluence map scaled to speed up the convergence of CNN. In the second step, the second CNN model, called HA-CNN, takes the previously predicted coarse fluence map and the 2-D PTV projection in the beam direction as input and predicts a fine fluence map for the beam. The prediction process reportedly takes less than 1 minute to complete for 7-beam treatment plans.

Unlike the other two classes of AI methods to be presented later, the 3-D dose prediction and dose-to-plan conversion and planning parameter prediction methods, the direct fluence map prediction methods do not require solving a mathematical optimization problem to obtain a fluence map. Therefore, in principle, this class of method has an intrinsic advantage in speed. However, the lack of mathematical optimization also has its downside: the Pareto optimality of the predicted fluence map is not guaranteed. In other words, mathematically, there might exist fluence maps that outperform the predicted one in all the dosimetric aspects a treatment planner would value. Moreover, the predicted fluence map needs to be further converted into a deliverable IMRT plan by sequencing; this step can take extra time and worsen the dose distribution.

7.2. Optimal dose prediction and dose-to-plan conversion

Instead of directly predicting an optimal plan, one can predict the optimal dose distribution and convert it into a deliverable plan using dose mimicking (Wu et al.; 2008; McIntosh et al.; 2017; Fan et al.; 2019; Bakx et al.; 2021), inverse optimization (Chan et al.; 2014; Goli; 2015; Chan and Lee; 2018; Mahmood et al.; 2018; Chan et al.; 2021), or AI (Lee et al.; 2019; Wang et al.; 2020; Wang, Sheng, Palta, Czito, Willett, Hito, Yin, Wu, Ge and Wu; 2021; Wang, Sheng, Palta, Czito, Willett, Yin, Wu, Ge and Wu; 2021). The dose mimicking method penalizes both over and under dose deviation for the voxels in the target, but only over dose for the voxels in the OARs, generating a plan whose dose distribution resembles the input dose. On the other hand, inverse optimization recovers the objective weights for a given dose distribution. Such objective weights should lead to a plan similar to the input dose when combined with the objective functions. The AI methods predict a fluence map for each beam given an “ideal” dose distribution.

Prior to the AI era, Wu et al. (2008) first applied this geometry-to-dose-to-plan concept to the online treatment plan adaptation domain. The proposed method deforms the dose distribution of the original plan by the 3-D deformation field obtained from registering the daily CBCT to the planning CT. The resultant dose distribution is regarded as the ideal dose distribution of the patient’s daily geometry. A linear dose-mimicking algorithm then converts the goal dose distribution into a deliverable plan for the daily geometry. This algorithm demonstrated its capability of correcting interfraction anatomical changes for prostate cases (Wu et al.; 2008; Thongphiew et al.; 2009; Li et al.; 2010, 2011). The reported time cost of this method was around 2 minutes (Wu et al.; 2008; Li et al.; 2010).

After AI became more widely explored as a topic, McIntosh et al. (2017) proposed an AI-based dose prediction with dose-mimicking for plan conversion workflow. The contextual Atlas Regression Forests (cARF) model predicts the dose distribution for a new anatomy. Anatomical features, such as the signed distance transform of the target and the 3-D vector to the closest point on the target contour, are calculated to characterize an anatomy (McIntosh and Purdie; 2017). Based on the anatomical features, the cARF model selects the dose distribution of plans created for the anatomies most similar to the new anatomy from a pre-defined plan library and assembles a probabilistic dose distribution from them, which is later converted into a plan by the dose-mimicking algorithm. This cARF model took 10 minutes on average to make a prediction and the dose mimicking algorithm took 2 minutes for IMRT plans and 3 minutes for VMAT plans (McIntosh et al.; 2017).

Following this, direct (non-library-based) dose prediction models emerged. Mahmood et al. (2018) presented a study that uses the generative adversarial network (GAN) framework for direct dose prediction and inverse optimization for plan conversion. The GAN network takes the 2-D CT slices and the associated structure contours as input and predicts a 2-D dose for each 2-D CT slice. The final 3-D dose distribution is obtained by assembling the predicted 2-D dose. Similarly, Fan et al. (2019) presented an AI-based automated planning study using the ResNet AI model for 3-D dose prediction and a quadratic dose-mimicking function for plan conversion for IMRT head-and-neck cases. The ResNet model took up to 10 seconds to predict a dose distribution for a patient. Sun et al. (2022) compared two different dose mimicking approaches for nasopharyngeal and rectal cancer cases. The quadratic dose mimicking function used in the study of Fan et al. (2019) and a hybrid dose mimicking function, which is the combination of the quadratic dose mimicking function and extra objectives on DVH parameters, were evaluated. The plan generation process, including fluence map optimization, sequencing, and control point optimization, could complete within 1 minute. Lempart et al. (2021) proposed a deep-learning-based model to predict dose distribution for VMAT prostate cases. The proposed model predicts a 2-D dose distribution for a 2-D CT slice from the corresponding image triplet. The image triplet contains the 2-D slice for which the 2-D dose is predicted and the segmentations inferior and superior to the 2-D slice individually stacked with the corresponding target and OAR contours. The mean dose prediction time was 6.6 seconds.

The 3-D dose prediction methods discussed above construct the 3-D dose distribution from the 2-D dose independently predicted for each CT slice, ignoring the inter-slice relation, which can result in a coarse transition of dose between CT slices. To overcome this drawback, multiple true 3-D dose prediction models have been proposed (Kajikawa et al.; 2019; Shao et al.; 2021; Gronberg et al.; 2021; Osman and Tamam; 2022; Sun et al.; 2022).

Besides dose prediction, AI also has an application in converting a given dose distribution into a fluence map, which is functionally the same as the dose mimicking and inverse optimization methods. Lee et al. (2019) proposed a U-Net-based AI agent to predict a fluence map from a given dose distribution for IMRT prostate cases. The U-Net model used in the study takes the desired dose distribution and contours projected in the beam direction as input and predicts a fluence map for each beam separately. The proposed model took about 1 second to generate a fluence map for a patient.

Wang et al. (2020) presented a fully AI-based dose prediction and dose-to-plan conversion pipeline for SBRT pancreas cases. The first CNN model predicts a 3-D dose distribution for each beam from the contour and CT image. Then, the second CNN model predicts a fluence map for each beam from the predicted 3-D dose distribution and PTV contours projected in the beam direction. The entire workflow took 7.1 second on average for each patient.

Ma et al. (2020) proposed a deep-learning-based workflow to predict a fluence map from a given dose distribution for VMAT head-and-neck and prostate cases. The workflow starts with an AI model predicting a fluence map from the given dose distribution projected along the beam directions for a homogeneous water-equivalent cylindrical phantom. The phantom is structurally the same as the patient in terms of isocenter and the position of the targets and OARs. Then, each beamlet in the fluence map predicted for the phantom is scaled according to the tissue phantom ratio, which is the dose delivered by a uniform square field to the isocenter in a fixed 100 cm source axis distance setup. The scaled fluence map should then deliver the same dose to the center plane of the patient as the dose delivered to the phantom by the predicted fluence map. This workflow took about 0.5 seconds to generate a fluence map for a patient, provided the dose distribution.

3-D dose prediction has been one of the most active AI research fields for radiotherapy. Various publications have suggested AI’s capability of predicting 3-D dose distribution to a certain accuracy (Mahmood et al.; 2018; Fan et al.; 2019; Kajikawa et al.; 2019; Shao et al.; 2021; Gronberg et al.; 2021; Osman and Tamam; 2022; Sun et al.; 2022). Dose-mimicking and inverse optimization as an optimization-based dose-to-plan conversion approach can generate treatment plans that are mathematically optimal with respect to a given optimization problem. AI can also be used as an alternative to the optimization-based conversion methods, skipping the optimization solving step and further shortening the planning time. However, the trade-off would be losing the mathematical optimality of the resultant plan.

7.3. Planning parameter prediction

Lee et al. (2013) proposed a logistic-regression model that predicts the rectum’s objective weight for IMRT prostate cases. The study assumes the sum of the bladder and rectum weights is constant and the other OARs’ weights are fixed. Hence, a complete optimization problem for plan generation can be established once the rectum’s weight is determined. The patient’s geometry is characterized by the overlap volume histograms (OVHs) of the bladder and rectum. An OVH presents the overlap volume of an OAR with the PTV at different PTV extensions, which describes the spatial relation between the OAR and PTV. The independent variable and parameters of the logistic-regression model are determined by applying the leave-one-out technique on all the samples, which uses all but the applied sample to train the model and tests the model on the applied sample. The statistically most predictive independent variable and parameters are selected for the prediction model. The ground truth objective weights are the ones determined using inverse optimization from the clinical plans of the prostate cases.

Boutilier et al. (2015) extended the previous study (Lee et al.; 2013) by employing different prediction models and including more independent variables to characterize the patient’s anatomy. Three prediction models were examined: the logistic regression model, the multi-nominal logistic regression model, and the K-nearest neighbor model. The logistic regression model follows the same concept as the one proposed in the previous study, except it predicts the weight of the bladder instead of that of the rectum. The multi-nominal logistic regression model predicts the weights for the important structures individually instead of presuming a fixed relation between the objective weights. The K-nearest neighbor model classifies a patient into three categories, the bladder weighted, the rectum weighted, and balanced groups, where each group is associated with a pre-defined set of objective weights. Then, the K-nearest neighbor algorithm finds the probability of a patient belonging to each of those three groups. The predicted objective weights are the weighted sum of the objective weights over the three patient groups. In addition to the overlap volume ratio of the rectum and bladder, the slope of their OVHs, which is the interpolated slope between two adjacent points in an OVH, also serves as an independent variable in the prediction models. This slope approximates the spatial information between the OAR and the PTV in between the sampled PTV extensions.

Besides predicting the weights for a set of established objectives, two studies proposed using AI to predict the prescribed dose for a list of objectives with fixed weights. Jihong et al. (2020) conducted a study using a CNN model to predict the objectives from the OVHs for IMRT cervical cases. In the study, a list of objectives, where the type and weight of the objectives are fixed, is provided for treatment plan generation. The CNN model predicts the prescribed dose for 15 objectives in the list to complete the plan optimization problem. The OVHs of the structures involved in the 15 objectives are used as the input of the CNN model. On average, the automated planning process took 8.5 minutes.

Bai et al. (2020) presented a study using a neural network (NN) model and a five-fold cross-validation strategy to predict the prescribed dose of objectives for IMRT nasopharyngeal cases. The independent variables of the predictive models are the OVHs and target volume histograms (TVHs). The TVHs indicate the target volume at different isotropic expansion. The five-fold cross-validation divides the patient cohorts into five groups. Each group is chosen as the test group once, and the other four groups are used for model training, resulting in five prediction models. The average of the output of the five prediction models is the final predicted prescribed dose of the objectives. The average time cost of plan generation was 9.85 minutes.

Other than predicting planning parameters directly from the patient’s anatomical information, Shen et al. (2020) proposed a reinforcement learning model, the virtual treatment planner network (VTPN), to predict planning parameters from an intermediate treatment plan. The VTPN iteratively adjusts an objective’s weight or prescribed dose according to the current treatment plan, aiming to attain maximized plan quality improvement. The VTPN can increase, decrease, or keep the value of a planning parameter. After the plan optimization problem is updated, the new problem is solved for another intermediate plan. This procedure repeats until the maximum number of iterations is reached or the VTPN makes no adjustment.

A year later, Shen, Chen and Jia (2021) implemented a hierarchical decision-making scheme in the VTPN because the size of the VTPN increases linearly with the number of planning parameters involved in the network. For more complex cancer sites, such as head-and-neck cancer, the previously proposed VTPN agent will slow down drastically as more planning parameters are involved. Unlike the VTPN, which decides which planning parameter to adjust directly, The hierarchical VTPN (HieVTPN) determines which structure needs adjustment first and then which planning parameter of this structure it should adjust so that the size of the network is insusceptible to the growth of the number of the planning parameters. The average planning time of both VTPN and HierVTPN was 3 minutes.

The advantage of this class of AI methods is that they guarantee the Pareto optimality of the produced treatment plan because a plan optimization problem, established from the predicted planning parameters, is solved in the end for plan generation. A shortcoming of this class of methods is that they only predict planning parameters for sites that use a fixed set of objective functions. When a complex case requires different sets of objective functions across the patients, this class of methods fail to work.

As the use of AI in general for treatment planning increases, the number of studies evaluating AI for adaptive planning can also be expected to increase. New classes of AI methods may emerge that have not yet been investigated. While it is difficult to anticipate which AI methods may make it into clinical implementation first, this remains an active area of research.

8. Future outlook

After twenty years of research aimed at developing fast, high-quality online adaptive planning methods, there is still no clear winner and efforts continue to find a solution that is reliable and robust under all conditions of anatomical variation. However, the ability of OnART to adjust the daily delivered dose to account for inter-fractional motion is still seen as the next step to making radiotherapy more precise. Recent studies on the three current commercial OnART systems confirm the potential benefits of daily adaptation to reduce PTV margins, increase target coverage, and reduce the dose to organs at risk (Henke et al.; 2019; Moazzezi et al.; 2021; Christiansen et al.; 2022). So it is to be expected that OnART will continue its development and become a permanent fixture in the field of radiotherapy. OnART is expected to be particularly beneficial in proton therapy due to the sensitivity of the proton dose deposition to inter-fractional range variations. While no commercial systems for proton OnART are currently available, it is foreseeable that one or more will emerge in the near future.

The crux of the problem for online adaptive planning, as presented in this review, is to minimize treatment planning time while maximizing treatment plan quality. Speeding up the planning process requires automation to replace the human planner who could spend hours finding the best quality plan. All adaptive techniques presented here would benefit from an automated plan quality evaluation, which could be integrated so that if the first automated plan generated is of poor quality, the system could then work to improve the plan quality before turning the final optimized plan over to the user for evaluation. This would minimize the need for manual intervention and thus improve the speed of the OnART process.

While there is currently no clear preference for any of the techniques presented to be the next one implemented clinically, it does seem likely that AI will soon play a larger role in OnART due to its time-efficient nature. AI segmentation is already part of one clinical implementation (Varian Ethos) (Moazzezi et al.; 2021). Given AI’s current prominence as one of the most active research areas across many fields, there may soon be more possibilities to use AI for OnART planning than are presented here.

This review also focused solely on online adaptive planning strategies that operate in physical dose. Another emerging and interesting area of planning research is on biological optimization. Biological response to radiation may be a better predictor of tumor control and normal tissue toxicity than physical dose and integrating biological information with OnART would result in plans that are optimized not only for the patient’s daily anatomy but also for biological tumor control or toxicity reduction. There are many interesting efforts ongoing in this space; the response during treatment could potentially be estimated using bio-markers and tracers that would be visible on an integrated PET image (Fonti et al.; 2019; Ten Eikelder et al.; 2020; Ajdari et al.; 2022). The acquired patient-specific information can be used to update the treatment plan with patient-specific radio-biological parameters (Ajdari et al.; 2022), scale the treatment plan (Ten Eikelder et al.; 2020), or adjust treatment duration (Ajdari et al.; 2018) for the optimal therapeutical effect. Biological adaptation is expected to serve a more crucial role in radiation therapy, providing further personalized treatment and enhancing treatment outcomes.