Addressing substantial covariate imbalance with propensity score stratification and balancing weights: connections and recommendations

Abstract

Objectives

Propensity score (PS) weighting methods are commonly used to adjust for confounding in observational treatment comparisons. However, in the setting of substantial covariate imbalance, PS values may approach 0 and 1, yielding extreme weights and inflated variance of the estimated treatment effect. Adaptations of the standard inverse probability of treatment weights (IPTW) can reduce the influence of extremes, including trimming methods that exclude people with PS values near 0 or 1. Alternatively, overlap weighting (OW) optimizes criteria related to bias and variance, and performs well compared to other PS weighting and matching methods. However, it has not been compared to propensity score stratification (PSS). PSS has some of the same potential advantages; being insensitive extreme values. We sought to compare these methods in the setting of substantial covariate imbalance to generate practical recommendations.

Methods

Analytical derivations were used to establish connections between methods, and simulation studies were conducted to assess bias and variance of alternative methods.

Results

We find that OW is generally superior, particularly as covariate imbalance increases. In addition, a common method for implementing PSS based on Mantel–Haenszel weights (PSS-MH) is equivalent to a coarsened version of OW and can perform nearly as well. Finally, trimming methods increase bias across methods (IPTW, PSS and PSS-MH) unless the PS model is re-fit to the trimmed sample and weights or strata are re-derived. After trimming with re-fitting, all methods perform similarly to OW.

Conclusions

These results may guide the selection, implementation and reporting of PS methods for observational studies with substantial covariate imbalance.

Introduction

There are many tools available to compare interventions in observational data, where the evaluation of outcomes is confounded by differences between patients who receive alternative interventions. These differences are commonly summarized through a propensity score (PS) [1, 2]. The PS can be used to address confounding through weighting, matching, or stratification (sub-classification) [2, 3]. For example, inverse probability of treatment weighting (IPTW) applies weights equal to the inverse probability of receiving the treatment that was actually received, creating a pseudo-sample in which the distributions of patients’ baseline characteristics are similar in both treatment groups [2–4]. Beyond IPTW, recent methodological developments have expanded the possibilities for PS weighting, with particular emphasis on addressing extreme tails (PS values near 0 and 1) that arise in real world data. Various authors have proposed that weights be formulated after excluding or trimming some patients [5–7], whereas [8] developed a weighting scheme that is analogue to pair matching [8, 9]. Li et al. [10] showed that these aforementioned PS weighting methods are members of a class of balancing weights. Within this class, overlap weighting (OW) is optimal on criteria related to bias and precision of the estimated treatment effect. However, OW has not yet been compared to PS stratification.

Propensity score stratification (PSS), often called sub-classification, is widely used in the social sciences, economics, and epidemiology [7, 11, 12]. It can be implemented in a number of ways [2, 3, 12, 13]. The most common approach divides individuals into equal strata based on their estimated PSs. Treatment effect estimates are obtained within strata and then combined over strata, or estimated directly through a stratified regression model [2, 12, 13]. PSS is simple to implement and remains popular despite having slightly larger residual bias when compared to other PS methods [2, 3, 13].

PSS and OW have a number of potential similarities. Unlike IPTW, both PSS and OW are resistant to variance inflation that occurs when some individuals in the sample have extreme PS values near 0 and 1 [14, 15]. OW smoothly down-weights the tails of the PS distribution and emphasizes a target population with uncertainty in the treatment decision [15]. Thus, OW remains efficient and accurate even in the presence of extreme tails or limited overlap of the PS distributions [15]. In this common scenario, PSS might also be considered advantageous. By grouping individuals into PS strata, rather than inverse weighting, no individual becomes too influential. While PSS offers an appealing alternative, increased bias may be expected when individuals are very different within strata [2, 3, 13]. While PS trimming has been employed as a pre-processing step to address this problem [7], it is not clear whether this is beneficial with PSS. We explore these issues through simulations by varying the extent of PS values near 0 and 1.

Moreover, we show that common methods for implementing PSS are equivalent to a coarsened version of overlap weighting. Explicitly, when treatment effects are estimated within strata and then combined over strata by taking a Mantel–Haenszel weighted average (PSS-MH) this is equivalent to overlap weighting at the level of strata. Implicitly, PSS-MH is the estimator that arises when propensity score strata are included as a covariate in a linear regression model for the outcome on treatment. We provide the important insight that the weighting analog to PSS is IPTW, whereas the weighting analog to PSS-MH is OW.

Beyond weighting and stratification, propensity scores are also used for matching. PS matching has many versions, each with different performance characteristics [16]. One-to-one, pair-matching has been addressed, relative to overlap weighting in the previous literature. For example, Li and Greene [8] proposed matching weights as a weighting analog to pair matching. They showed that “Compared with pair matching, the [matching weights] offer more efficient estimation, more accurate variance calculation, better balance, and simpler asymptotic analysis.” Matching weights and overlap weights have been shown to operate similarly with respect to the target population created and performance characteristics [17–19]. As an alternative to 1:1 matching, the features of overlap weighting are relatively clear. In contrast, overlap weighting and propensity score stratification have not been formally compared. Therefore, our focus is to investigate the performance characteristics of overlap weighting and propensity score stratification both analytically and empirically. Our results will better inform the implementation and interpretation of both overlap weighting and propensity score stratification.

Overall, this article explores the advantages and limitations of IPTW, OW, PSS, and PSS-MH through simulation and in the context of a motivating example. Specifically, we evaluate bias and variance across a range of PS distributions that have increasingly limited overlap in the PS distribution and more values near 0 and 1. We consider the interaction between these methods and trimming rules that have been recommended to handle extreme values. Our results highlight strengths and potential pitfalls in the application of these methods and guidance for choosing between them.

Materials and methods

COMPARE-UF example

The COMPARE-UF registry was designed to evaluate treatment options for women with uterine fibroids, recruiting patients from 8 sites across the United States [20, 21]. The procedures in COMPARE-UF include hysterectomy and myomectomy. Randomized studies of these procedures are limited, due to the fact that hysterectomy removes the uterus. Thus, observational treatment comparisons are essential to understand these options for women with fibroids. As the assignment to surgery is not randomized, the treatment comparisons in COMPARE-UF may be confounded by differences in patients who select and receive alternative interventions. The COMPARE-UF data include detailed information about patient characteristics, symptoms, and quality of life, measured prior to the procedure, that can be used to adjust for confounding and support comparative effectiveness and safety conclusions. PS values near 0 and 1 were common in COMPARE-UF. This reflects the preference for myomectomy over hysterectomy among younger women who want to preserve fertility. The decision regarding these procedures is strongly predicted by patient characteristics and their fibroid status. In other words, there is substantial measured confounding and certain types of women almost always (PS~1) or almost never (PS~0) get a hysterectomy. Thus, the current simulation study will inform the best choice of methods for COMPARE-UF.

Notation

We consider the Neyman-Rubin potential outcomes framework where Y _i (1) and Y _i (0), correspond to outcomes that would be observed if, counter to fact, individual i could be observed under two possible interventions; treatment (Z _i =1) and control (Z _i =0), respectively. Here Z _i represents a binary treatment status that could be replaced with any two alternative therapies. We make the Stable Unit Treatment Value Assumption (SUTVA) so that the observed outcome Y _i is equal to the potential outcome under the observed treatment status Z _i , i.e. Y _i =Z _i Y _i (1) + (1 − Z _i )Y _i (0) [1]. We denote N to be the total sample size of the observational study.

Propensity scores

Propensity score methods provide a mechanism to uncover unbiased treatment effects from observational data when the observed pre-treatment covariates, X _i , include all possible confounders of the treatment-outcome relationship, i.e. there is no unmeasured confounding. The PS, p( X _i )=Pr(Z _i =1| X _i ), is the conditional probability of receiving treatment given the observed covariates [1]. While many modeling techniques can be used to estimate the propensity score [22, 23], it is commonly estimated through a logistic model $p({\mathit{X}}_i;\mathit{\beta })=1/\left\{1+\exp \left(-{\mathit{X}}_i^T\mathit{\beta }\right)\right\}$ , where ${\widehat{p}}_i=p({\mathit{X}}_i;\widehat{\mathit{\beta }})$ and $\widehat{\mathit{\beta }}$ the maximum likelihood estimator of β.

PS trimming is a pre-processing step to address extreme PS values, near 0 and 1. First, PS values outside the common area of support are excluded. This means that untreated individuals with PS values below the minimum PS of the treated patients will be excluded, as will those treated individuals with PS values above the maximum of untreated patients [24]. In essence, these patients have no comparable units in the alternative group. An alternative trimming rule extends this idea by excluding anyone outside of the interval [α, 1 − α], with α a chosen threshold (for instance, exclude those with a propensity score less than the 2.5th percentile of the untreated and greater than the 97.5th percentile of the treated) [6]. We employ this approach in subsequent simulations. Trimming changes the target population to focus on individuals with at least a reasonable chance of receiving both treatments. After trimming, the originally estimated PS is not guaranteed to balance covariates. Given a trimmed sample, performance may be improved by re-fitting the PS model to that trimmed population of interest [15].

Inverse probability of treatment weighting

IPTW applies weights to each individual in the sample, proportional to the inverse probability of receiving the treatment that they actually received, i.e., $w_i=1/{\widehat{p}}_i$ for treated units and $w_i=1/(1-{\widehat{p}}_i)$ for untreated units. The target population of IPTW is the entire study cohort, and the causal estimand is the average treatment effect (ATE) if everyone in the sample were to be treated, vs. (possibly counter to fact) no one were treated. An unbiased estimator of the ATE is the weighted difference of the outcome between the groups [2]:

$${\widehat{\mathrm{\Delta }}}_{\text{IPW}}=\frac{\sum _{i=1}^N{Z}_i{Y}_i/{\widehat{p}}_i}{\sum _{i=1}^N{Z}_i/{\widehat{p}}_i}-\frac{\sum _{i=1}^N(1-Z_i)Y_i/(1-{\widehat{p}}_i)}{\sum _{i=1}^N(1-Z_i)/(1-{\widehat{p}}_i)},$$ (1)

Overlap weighting

IPTW and other well-known weighting schemes belong to a general class of balancing weights [10, 25]. Among these, overlap weighting (OW) was developed to minimize the variance of the estimated treatment effect [10, 26]. The overlap weight is $w_i=(1-{\widehat{p}}_i)$ for a treated unit and $w_i={\widehat{p}}_i$ for a control unit. In finite samples, when the PS is estimated by logistic regression, the OW data will have exact mean balance or perfect comparability between the covariate means in each treatment group [10]. In linear models, this is sufficient to eliminate bias, even if the PS model is incorrectly specified [27]. Like trimming, OW emphasizes a target population with a reasonable probability of receiving each treatment. Thus, it estimates the average treatment effect among the overlap population (ATO) [10, 28]. Unlike trimming, OW does not pick an arbitrary threshold α beyond which everyone is excluded. Instead, OW smoothly down-weights the patients in the tails of the PS distribution. An unbiased estimator of the ATO is obtained by the following equation.

$${\widehat{\mathrm{\Delta }}}_{\text{OW}}=\frac{\sum _{i=1}^N{Z}_i{Y}_i(1-{\widehat{p}}_i)}{\sum _{i=1}^N{Z}_i(1-{\widehat{p}}_i)}-\frac{\sum _{i=1}^N(1-Z_i)Y_i{\widehat{p}}_i}{\sum _{i=1}^N(1-Z_i){\widehat{p}}_i},$$ (2)

Propensity score stratification

PSS operates differently from weighting. First patients are sorted into strata based on their PS values. It has been argued that creating 5 PS strata is enough to remove 90 % of the confounding bias [29]. To further decrease residual bias, we define PS strata by deciles. The target estimand for propensity score stratification is generally the ATE, just like IPW. Following Lunceford and Davidian [2] the ATE is estimated by deriving strata-specific estimates and combining them with equal weights [2].

Propensity score stratification with Mantel–Haenszel weights

Alternatively, PSS may be implemented by regression adjustment for strata, i.e. E(Y _i |Z _i , D _i )=δ _Z Z _i  +  δ _D D _i where D _i is a (10 × 1) vector of indicator variables for propensity score deciles. This is appealing because the treatment effect is estimated directly as a model parameter, δ _Z . In our experience, this approach is widely used but rarely made explicit. We show in the Appendix that regression adjustment for strata is equivalent to: (1) Deriving the strata-specific estimates and combining them with Mantel–Haenszel weights (as opposed to equal weights), (2) Overlap weighting at the strata level (coarsened overlap weighting). Subsequently, we refer to this as PSS with Mantel–Haenszel weights (PSS-MH). If the Mantel–Haenszel approach to combining strata is selected, the target of inference is an ATO that is similar to overlap weighting, and some of the advantages of overlap weighting may be expected.

Simulation design

We carried out a series of simulation studies to compare IPTW, OW, PSS, and PSS-MH when the PS distributions had varying degrees of non-overlap and extreme values. Our data-generating mechanism follows previous work in comparing among weighting methods [15]. Specifically, the data-generating process used six variables from a multivariate normal distribution with zero mean, unit marginal variance, and a compound symmetric covariance structure with 0.5 correlation between each pair of covariates. Half the variables were continuous, denoted by X ₁, X ₂, X ₃, and the other half dichotomized at zero to create the binary covariates X ₄, X ₅, X ₆, so that the marginal prevalence of each binary covariate is approximately 0.5. The true PS was then calculated using the following logistic model:

$$p(\mathbf{X})={\{1+\exp -({\alpha }_0+{\alpha }_1{X}_1+{\alpha }_2{X}_2+{\alpha }_3{X}_3+{\alpha }_4{X}_4+{\alpha }_5{X}_5+{\alpha }_6{X}_6)\}}^{-1}$$ (3)

and the observed treatment status was simulated independently from on a Bernoulli distribution with the probability of being treated equal to p(X). The continuous outcome variable Y is from the following linear model,

$$E(Y|Z,\mathbf{X})={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6+\mathrm{\Delta }Z.$$ (4)

This outcome model assumes a homogenous and additive treatment effect Δ for all units, and thus the true causal estimands corresponding to all weights or stratification deciles are identical: Δ_IPTW=Δ_OW=Δ_PSS=Δ_PSS-MH=Δ. This assumption is not required and can be relaxed. However, it facilitates a direct comparison of the finite-sample properties of IPTW, OW, PSS, and PSS-MH, where the methods all have a common target of inference.

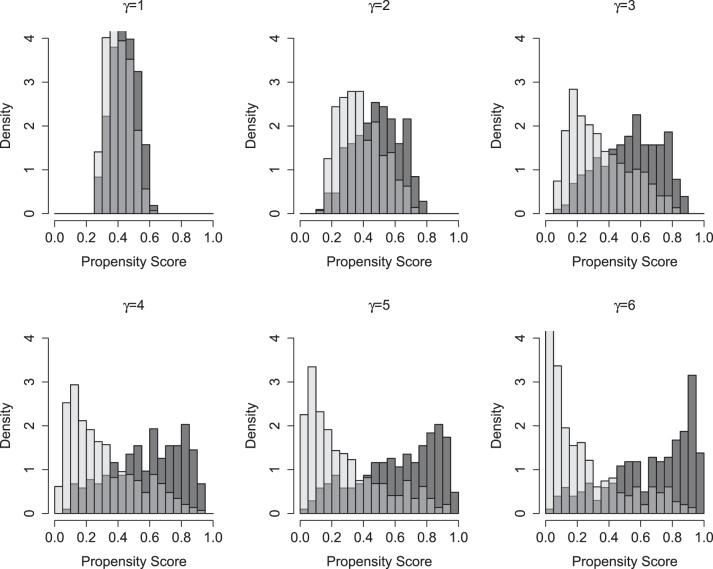
Our simulation considers a range of scenarios with increasingly strong confounding due to increasing separation in the PS distributions. The regression parameters in the PS model are (α ₀, α ₁, α ₂, α ₃, α ₄, α ₅, α ₆)=(0.4, 0.05γ, 0.1γ, 0.1γ, −0.05γ, −0.15γ, −0.15γ), where γ varies from 1 to 6. As γ increases, all coefficients in the PS model increase by the same multiple. Increasing γ further implies decreasing overlap in the PS distribution between treated and untreated patients, and increasing tails in the PS distribution. The C-indices for the models with γ 1 to 6 are 0.59, 0.66, 0.74, 0.77, 0.82 and 0.85. Figure 1 summarizes the PS distributions for each PS model indexed by γ. When γ=1, there is substantial overlap between treatment groups and minimal extreme PS values. As γ increases, the PS distributions between the two treatment groups become more and more polarized. At γ=6, the PS distributions exhibit a U shape where most of the observations have propensity scores near the extremes 0 and 1 of the spectrum.

Figure 1:

Distribution of the propensity scores among untreated (light gray) and treated (dark gray) patients across simulation settings of increasing confounding (i.e. separation in the treated and untreated patients).

We chose the parameters (β ₀, β ₁, β ₂, β ₃, β ₄, β ₅, β ₆)=(0, −0.5, −0.5, −1.5, 0.8, 0.8, 1.0) in the outcome model (4). The observed outcome Y for each unit is generated from a normal distribution with mean, E(Y|Z, X), and a standard deviation 1.5. Throughout, the treatment effect is held fixed at Δ=−0.75 (magnitude equals to one half of the error standard deviation) so that lower values of Y reflect the beneficial effect of the treatment. The simulation parameters are selected so that individuals with a covariate profile indicating worse outcomes are those likely to be treated. Total sample sizes of n=500 and n=2000 were evaluated.

For each scenario, we simulate 1,000 datasets and estimate the treatment effect using IPTW, OW, PSS and PSS-MH. For each method and simulation setting, we calculate the bias and empirical variance for each treatment effect estimator. Bias is defined as the difference between the average treatment effect estimate over 1,000 simulated samples and Δ=−0.75. The empirical variance is defined as the sample variance of the corresponding estimates across 1,000 simulated data sets. Variance is reported relative to OW.

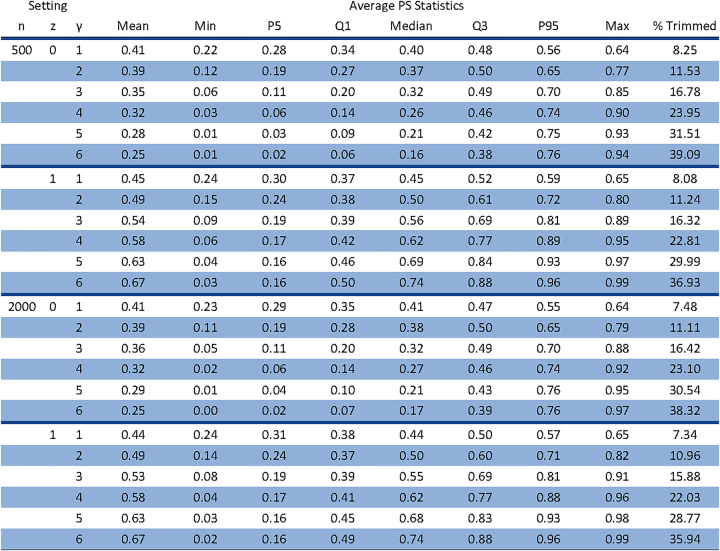
The primary results are interpreted without PS trimming. Subsequently, we explore the sensitivity of IPTW, PSS, and PSS-MH methods to trimming, with and without re-fitting the PS model. Trimming was applied at the 2.5th and 97.5th percentiles of the PS distribution. Trimming was not applied with OW, as one goal of this method is to avoid trimming. Appendix Figure 1 provides details regarding the percentage of patients trimmed in each setting.

Results

Simulation results

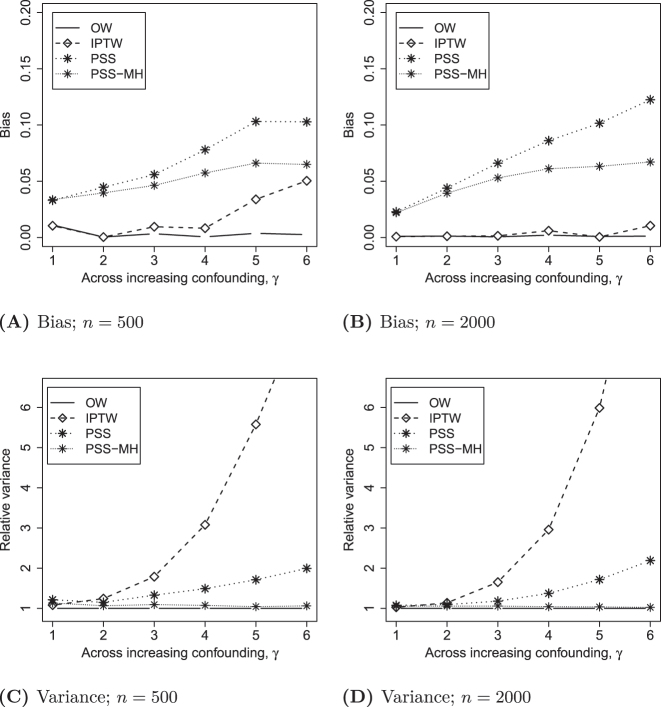
Figure 2A and B displays the bias for each estimator when n=500 and n=2000, across settings of increasing confounding, i.e. γ increases and separation in the PS distribution increases. IPTW has moderate bias for large γ when n=500, but this bias disappears when n=2000. OW demonstrates bias that is consistently near 0 in all settings. Both PSS and PSS-MH exhibited increasing bias with increasing γ that was unrelated to the overall sample size.

Figure 2:

Properties of the estimated treatment effects.

The Monte Carlo variance of alternative estimators, relative to OW, is displayed in Figure 2C and D. The variance of the IPTW estimated treatment effect grows extremely large with increasing separation in the PS distribution. PSS has much lower variance than IPTW, but is still 2-fold that of OW at the highest level of PS separation, γ=6. With respect to variance, PSS-MH is so similar to OW that it is nearly invisible. Results were similar for both sample sizes.

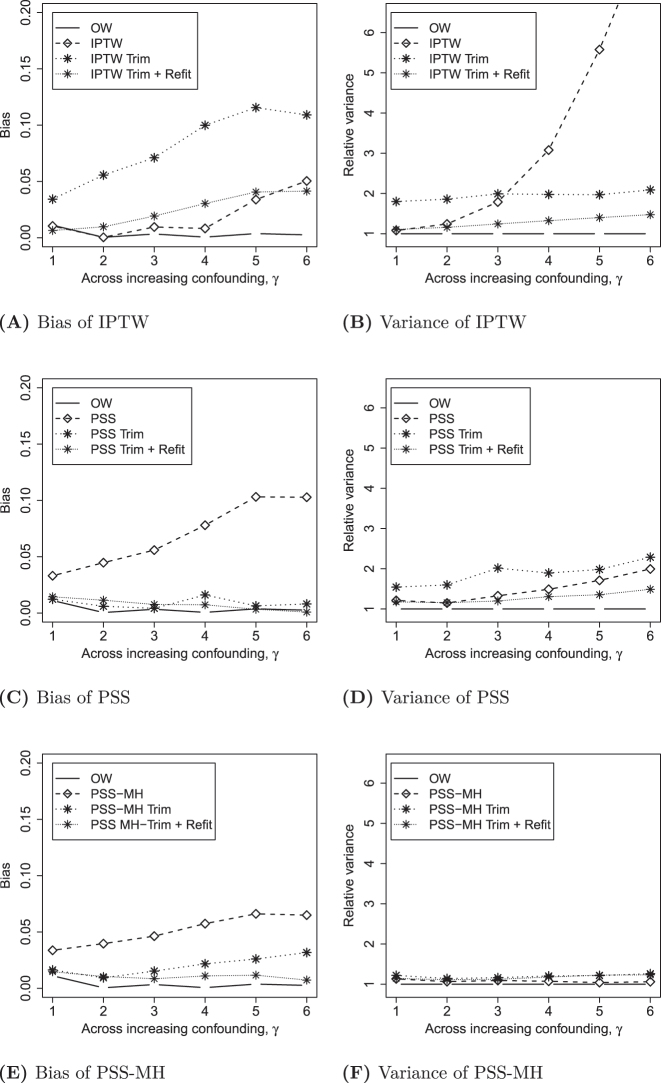
Figure 3 displays the sensitivity analysis where trimming is applied as a pre-processing step for IPTW, PSS and PSS-MH. IPTW with trimming is substantially worse than without trimming, with respect to both bias and variance, unless the PS model is re-fit to the trimmed sample. However, as long as re-fitting is applied, the use of trimming improves the variance associated with IPTW so that it is nearly as good as OW. In contrast, PSS and PSS-MH are improved by trimming, with slight improvements obtained by re-fitting the propensity score model and re-defining propensity strata. These stratification methods with trimming and re-fitting perform as well as OW.

Figure 3:

Properties of different methods with variations of trimming for n=500.

Empirical study

The current data harvest from COMPARE-UF includes 568 patients receiving myomectomy and 727 patients receiving hysterectomy. Here we focus on two quality-of-life scores measured at short-term follow-up (6–12 weeks post-procedure). These are Energy Score and Symptom Severity Score from the UFSQOL instrument. We define the PS as the probability of receiving hysterectomy given observed patient-level characteristics, including demographics, health and operative history as well as baseline quality-of-life measurements. The PSs were estimated via a logistic regression including the main effects of all covariates. The distribution of the estimated scores is presented in Figure 4. There is a clear separation between the two groups; this is not surprising since younger women are more likely to undergo myomectomy for chances of future pregnancy, leading to a lack of overlap. However, the separation is relatively moderate compared to our simulation, likely aligned with γ=3.

Figure 4:

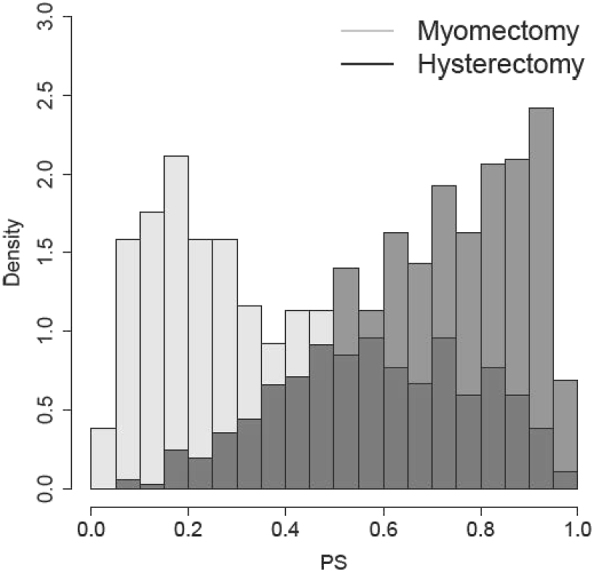
Estimated PS for the myomectomy and hysterectomy groups. The PS is defined as the probability of receiving hysterectomy conditional on the pre-treatment covariates.

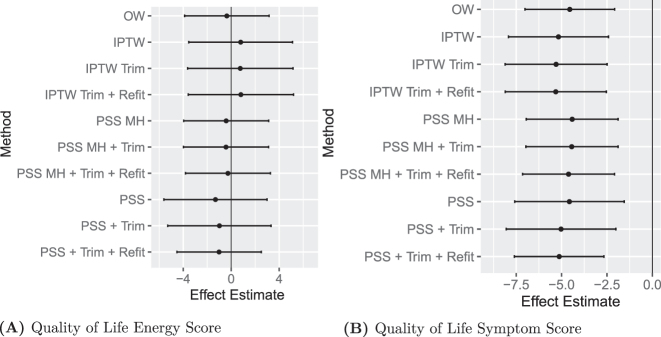
The various PS methods yield consistent results (Figure 5). The only difference is with respect to precision, where IPTW has larger confidence intervals. OW and PSS-MH are virtually identical with respect to the point estimate and confidence intervals.

Figure 5:

Treatment effects in COMPARE-UF.

Discussion

Our results yield a number of important findings. First, OW performs at least as well or better than IPTW, PSS and PSS-MH with respect to bias and variance of the estimated treatment effect, particularly when there is a substantial covariate imbalance. Second, common methods for implementing PSS based on Mantel–Haenszel weights (PSS-MH) are equivalent to a coarsened version of OW. As such, PSS-MH demonstrates similar efficiency to OW, but small residual bias attributable to the coarsening of propensity scores into strata. Third, trimming methods can increase bias and/or variance across methods (IPTW, PSS, and PSS-MH) unless the PS model is re-fit to the newly trimmed sample and the weights or strata are re-defined. Careful application of trimming with re-fitting allows PSS and PSS-MH to perform as well as OW with respect to both bias and variance. In the analysis of COMPARE-UF, point estimates are nearly identical across methods, and differentiation is limited to increased variance with IPTW. This is consistent with the simulation when γ=3, a setting that resembles COMPARE-UF.

One advantage to OW is that it circumvents potential confusion around how to implement trimming and re-fitting. Many different trimming thresholds are used in applications and ad-hoc adaptations of trimming could undermine the performance of PSS. Yet PSS without any trimming is meaningfully worse than OW with respect to bias. In large data sets, this could carry substantial risk.

The advantages of PSS-MH over PSS have been noted previously. Rudolph et al. [12], proposed to efficiently combine propensity score strata by the inverse variance and noted the connection to PSS-MH. They caution that a potential disadvantage of PSS-MH is that, in the presence of treatment effect heterogeneity, it estimates a causal effect for a population that differs from the one that was originally sampled. Like OW, PSS-MH emphasizes a population at greatest clinical equipoise, giving greater weight to strata in which uncertainty about the treatment decision remains high. In samples derived from a well-defined target population, the ATE over that population may be uniquely important. Only IPTW and PSS, without trimming, are designed to target the ATE. However, we show that in the setting of substantial covariate imbalance, the bias/variance tradeoff between IPTW and PSS is amplified; IPTW exhibits rapidly increasing variance, whereas PSS exhibits increasing bias. This is consistent with previous observations [2, 14, 15]. Not only can OW and PSS-MH reduce these problems, but the ATO may be a clinically relevant target parameter when the sample includes individuals for whom the treatment decision is already clear (PS approaching 0 and 1). We may not intend to draw inferences on individuals for whom little uncertainty remains in common practice [15, 17, 28].

Our simulations have a number of limitations. First, we used a constant treatment effect so that the average causal effect was identical for IPTW, OW, PSS, and PSS-MH. This has the advantage of allowing a comparison of bias, in a setting where all three methods estimate the same target of inference. It allows us to focus on the properties of the methods, rather than differences in the target population which have been discussed elsewhere. The differences between PSS and PSS-MH could be even more pronounced in a setting of heterogeneous treatment effects. Second, although we evaluated a range of conditions this simulation is not exhaustive and is limited to linear models. Finally, we have primarily focused on bias and variance as two key metrics to measure the performance of each estimator, and have not considered the properties of the corresponding variance estimators. Prior simulation studies have demonstrated that the nonparametric bootstrap can lead to an interval estimator with nominal coverage with OW, even in the presence of substantial covariate imbalance [15, 30]. However, bootstrap confidence intervals may exhibit under-coverage for IPTW due to bias under substantial covariate imbalance. We expect the findings to apply to our simulations as well Alternatively, Li et al. [15]. provided a closed-form sandwich variance estimator for OW as a computationally convenient alternative to nonparametric bootstrap; these estimators are also implemented in the PSWeight R package [31]. In contrast, variance estimation for PSS and PSS-MH has received relatively less attention and merits additional investigation and comparison in future work. Variance estimation for propensity score stratified analyses may be model-based Lunceford and Davidian [2] or based on bootstrapping Tu and Zhou [32].

Some readers may note that we do not propose to stabilize the propensity weights herein. Stabilization originated with marginal structural models for time-varying treatments Robins et al. [33]. In the setting of marginal structural models, the stabilization factor included baseline confounders which were not addressed via weighting but included in the regression model for the outcome. Therefore, these confounders were available to function as stabilizers in the numerator of the weights. In this time-invariant setting, the stabilizing factor would be the marginal probability of receiving the treatment actually received (not conditional on the confounders). This would introduce a scalar constant in the numerator and denominator of each weighted mean in Equations (1) and (2), thus canceling out. Therefore, our results would be identical with or without stabilization. While stabilization does not matter here, it would be helpful in more complex settings with non-saturated structural models for outcome on treatment.

These results highlight opportunities to improve study design and reporting. Trimming is commonly recommended [7, 34], but OW performs at least as well with fewer risks. When trimming is applied, researchers should clarify whether or not the PS was re-fit to the final population. In addition, the performance of PSS depends on how the strata are combined. Explicit reporting of how strata are combined, and whether regression adjustment for strata was conducted, will facilitate interpretation.

Appendices

Connection between regression adjustment for strata and PSS-MH

Consider the linear model E(Y _i |Z _i , D _i )=δ _Z Z _i  + D _i δ _D where D _i is an (1 × S) vector of indicator (or dummy) variables for the S propensity score strata. The least squares estimator for δ _Z is ${\widehat{\delta }}_Z=[\mathrm{1,0},\dots ,0]{({\mathbf{X}}^{\prime }\mathbf{X})}^{-1}{X}^{\prime }Y$ , with $\mathbf{X}=\left[Z,\mathbf{D}\right]$ the covariate matrix, ${\mathbf{Y}}^{\prime }=\left[Y_1,\dots ,Y_n\right]$ , and n the total sample size. Without loss of generality, let us consider the case where S=2. The least squares estimator for δ _Z is:

$${\widehat{\delta }}_Z=\frac{n_1{n}_2}{n_1\left\{n_2(n_{1z}+n_{2z})-n_{2z}^2\right\}-n_2{n}_{1z}^2}\left[\frac{n_{1z}{n}_{1c}}{n_1}({\overline{Y}}_{1z}-{\overline{Y}}_{1c})+\frac{n_{2z}{n}_{2c}}{n_2}({\overline{Y}}_{2z}-{\overline{Y}}_{2c})\right]$$ (5)

where n _sz and n _sc are the number of treated and untreated patients and n _s is the total number of subjects in stratum, s=1, 2; ${\overline{Y}}_{sz}$ and ${\overline{Y}}_{sc}$ are, respectively, the mean response among treated and untreated patients in stratum s=1, 2. We can further simplify the denominator of ratio outside of the brackets in (5) since n _s =n _sz  + n _sc . Hence,

$$\begin{array}{ll}\hfill n_1\left\{n_2(n_{1z}+n_{2z})-n_{2z}^2\right\}-n_2{n}_{1z}^2& =n_1{n}_2{n}_{1z}+n_1{n}_2{n}_{2z}-n_1{n}_{2z}^2-n_2{n}_{1z}^2\hfill \\ \hfill & =(n_{1z}+n_{1c})n_2{n}_{1z}+n_1(n_{2z}+n_{2c})n_{2z}-n_1{n}_{2z}^2-n_2{n}_{1z}^2\hfill \\ \hfill & =n_2{n}_{1c}{n}_{1z}+n_1{n}_{2c}{n}_{2z}\hfill \end{array}$$

Thus, the ratio outside the bracket in (5) is equal to n ₁ n ₂/(n ₂ n _1c n _1z  + n ₁ n _2c n _2z ).

The Mantel–Haenszel weight for stratum s is defined as $w_s=\frac{n_{sz}{n}_{sc}}{n_s}$ [35]. Taking a weighted average of the stratum-specific mean response, $({\overline{Y}}_{sz}-{\overline{Y}}_{sc})$ , yields.

$$\frac{n_1{n}_2}{n_{1z}{n}_{1c}{n}_2+n_{2z}{n}_{2c}{n}_1}\left[\frac{n_{1z}{n}_{1c}}{n_1}({\overline{Y}}_{1z}-{\overline{Y}}_{1c})+\frac{n_{2z}{n}_{2c}}{n_2}({\overline{Y}}_{2z}-{\overline{Y}}_{2c})\right].$$ (6)

Equations (5) and (6) are identical. Thus the practice of implementing PSS by regression adjustment for strata is equivalent to applying Mantel–Haenszel weights to combine stratum-specific effects PSS-MH.

Connection between PSS-MH and OW

The overlap-weighted population is one for which there is clinical equipoise; it emphasizes those patients for whom there is greatest clinical uncertainty in the treatment decision and successively down-weights smoothly the influence (or contribution to the overall estimation of the treatment effect from) people who get one or the other treatment with increasing clinical certainty [15, 28]. The higher the clinical certainty, the smaller the weight. The overlap weight is $w_i=(1-{\widehat{p}}_i)$ for a treated unit and $w_i={\widehat{p}}_i$ for a control unit [10]. The method does two operations simultaneously. First, it creates a pseudo-population with balanced characteristics by weighting every participant by the inverse propensity of being in their assigned treatment groups. This step employs the usual IPTW weight (1/ $(1-{\widehat{p}}_i)$ or 1/ ${\widehat{p}}_i$ ) to remove differences in the characteristics between treatment groups. Next, it selects from and emphasizes within the pseudo-population participants who, based on their baseline characteristics, are eligible for either treatment via the selection function $h({\widehat{p}}_i)={\widehat{p}}_i(1-{\widehat{p}}_i)$ [10, 19]. The function $h({\widehat{p}}_i)\approx 0$ when ${\widehat{p}}_i\approx 0$ or 1, i.e., it smoothly down-weights to 0 participants with estimated propensity scores at both extremities of the propensity scores spectrum, i.e., [0, 1]. It reaches its maximum $h({\widehat{p}}_i)=0.25$ when ${\widehat{p}}_i=0.5$ and is fairly constant when ${\widehat{p}}_i\in [0.4,0.6]$ since $h({\widehat{p}}_i)\in [0.24,0.25]$ . Hence, it gives more weight to participants for whom there is clinical equipoise, i.e., those with ${\widehat{p}}_i$ in the vicinities of 0.5. Therefore, the overlap weight, as a product of the usual IPTW weights and the selection function, yield the weights $(1-{\widehat{p}}_i)$ and ${\widehat{p}}_i$ [19].

Whereas the overlap weight is defined at the subject level, the Mantel–Haenszel weight for propensity score stratification is defined at the strata level. It functions similarly to the h function; to down-weight those strata with the greatest imbalance in treatment allocation (probability of receiving either treatment is closest to 0 or 1). When the Mantel–Haenszel weights are normalized, so that the weights sum to 1, they become:

$$w_s^{*}=\frac{n_{sz}{n}_{sc}}{n_s\sum _s\frac{n_{sz}{n}_{sc}}{n_s}}=\frac{n_{sz}{n}_{sc}}{\sum _s{n}_{sz}{n}_{sc}},$$ (7)

Because n _s is constant when strata are defined to have equal sizes. If instead of the Mantel–Haenszel weight, the overlap selection function, h(p _s ) = p _s (1 − p _s ), were applied to strata the normalized weight would be:

$$w_{s,h}^{*}=\frac{p_s(1-p_s)}{\sum _s{p}_s(1-p_s)}=\frac{n_{sz}{n}_{sc}}{n_s^2\sum _s\frac{n_{sz}{n}_{sc}}{n_s^2}}=\frac{n_{sz}{n}_{sc}}{\sum _s{n}_{sz}{n}_{sc}}.$$ (8)

We see that the Mantel–Haenszel weighted average is the same as the overlap weighted average, where the weights are based on the selection function h. The IPTW balancing feature of overlap weighting (to create a balanced pseudo-population) is not relevant at the strata level, as the premise of PSS is that patient characteristics are balanced by the creation of strata, in the first place. Thus, the balancing feature of overlap weighting is not relevant, but the population selection feature is.

PSS-MH when implemented directly or via regression adjustment for propensity score strata is equivalent to overlap weighting – applied at the strata level. Therefore all of these methods target a similar overlap population, defined by an emphasis on clinical equipoise.

Details of propensity score distributions and trimmed samples

Figure 6 show the distributions of the propensity scores (averaged over the 1,000 simulation replicates) by treatment group, the sample size, and the degree of overlap γ as well as the percentage of observations that fall outside of the range [0.25, 0.975], which we dropped in the trimmed analysis.

Figure 6:

All values are averaged over the 1,000 simulations under each setting. Larger values of γ indicate a reduction in the common area of support. The common area of support includes PS values that overlap and are between the 97.5th percentile of the treated group (Z _i =1) and the 2.5th percentile of the untreated group (Z _i =0). In trimmed analysis individuals with PSs outside this range are excluded.