Quantum-enhanced greedy combinatorial optimization solver

Abstract

Combinatorial optimization is a broadly attractive area for potential quantum advantage, but no quantum algorithm has yet made the leap. Noise in quantum hardware remains a challenge, and more sophisticated quantum-classical algorithms are required to bolster their performance. Here, we introduce an iterative quantum heuristic optimization algorithm to solve combinatorial optimization problems. The quantum algorithm reduces to a classical greedy algorithm in the presence of strong noise. We implement the quantum algorithm on a programmable superconducting quantum system using up to 72 qubits for solving paradigmatic Sherrington-Kirkpatrick Ising spin glass problems. We find the quantum algorithm systematically outperforms its classical greedy counterpart, signaling a quantum enhancement. Moreover, we observe an absolute performance comparable with a state-of-the-art semidefinite programming method. Classical simulations of the algorithm illustrate that a key challenge to reaching quantum advantage remains improving the quantum device characteristics.

An iterative quantum algorithm solves combinatorial optimization problems with performance guarantees despite hardware noise.

INTRODUCTION

A handful of promising classes of quantum algorithms have been advanced for combinatorial optimization problems, such as quantum adiabatic evolution algorithms (1), variational quantum algorithms (2–4), as well as others (5, 6). In all cases, the problem takes the form of an objective function to extremize, which can be interpreted as an Ising-type Hamiltonian whose ground state is the global extremum of the problem. Solving a generic Ising model is NP-hard (7), and it remains open whether quantum computers can indeed provide a practical advantage over classical methods. A tremendous amount of work has been dedicated to quantum annealers, which leverage adiabatic evolution (8–10), while the focus for gate-based quantum computers has been mainly on parameterized quantum circuits like the quantum approximate optimization algorithm (QAOA) (2, 3, 11–15).

The QAOA has been implemented on several experimental platforms to solve a range of combinatorial optimization problems (13–22). However, a major challenge in these demonstrations has been the stringent technical requirement of reducing hardware noise to provide good quality solutions that are well-separated from trivial classical approaches such as random sampling. In particular, loading arbitrary graph problems, beyond the native topology of the quantum computer, often demands an additional overhead, increasing noise and lowering the performance of the quantum algorithm. For example, while an early implementation of the QAOA on a superconducting quantum system for solving hardware-native maximum cut problems on 19 qubits already showed performance better than random sampling (13), an implementation for solving high-dimensional graph problems beyond the hardware-native topology on 23 qubits found results only as good as random guessing on contemporary devices (15), with similar trends for Rydberg atoms and trapped ions (14, 16, 17, 20, 23). Yet, it is unavoidable for quantum computers to tackle more intricate problem instances en-route to solving universal and real-world problems.

To date, noise has made even the most straightforward classical optimization approaches better candidates for solving real-world optimization. For instance, classical greedy algorithms, which iteratively build a solution by making the locally optimal choice at each stage, are intuitive, easy to implement, and will most likely outperform a modern noisy quantum computer. This raises the question: Can one design algorithms using current quantum technologies to their advantage with performance guarantees, making them realistically competitive against classical ones for arbitrary problems at scale?

Overall, our goal is to minimize the objective function

$$C=u+{\displaystyle \sum _{i=1}^N}{v}_i{Z}_i+{\displaystyle \sum _{j<i}^N}{w}_{ij}{Z}_i{Z}_j$$ (1)

where u, v_i, and w_ij are problem-specific scalar parameters, and Z_i ∈ { − 1, + 1} are Ising spin variables with corresponding bit values B_i = 1/2 − Z_i/2 ∈ {0,1}. The goal is to find a bit string B = (B₁, B₂, …, B_N) minimizing Eq. 1. Substituting the Ising variables for Pauli Z operators (we use the same symbol for both when clear from context) in Eq. 1, the minimization can be achieved on a quantum computer using quantum adiabatic evolution or variational algorithms. The latter, such as the QAOA [2, 3], are better suited for near-term digital devices with their theoretical performance at least on par with a discretized adiabatic evolution with a fixed number of layers. A QAOA circuit with p layers reads

$$\mid \mathrm{\gamma },\mathrm{\beta }⟩=[{\displaystyle \prod _{d=1}^p}{U}_{\mathrm{M}}({\mathrm{\beta }}_d)U_{\mathrm{PS}}({\mathrm{\gamma }}_d)]H^{\otimes N}\mid 0⟩{}^{\otimes N}$$ (2)

where H is the one-qubit Hadamard gate. The unitaries U_PS and U_M are called the phase separator and the mixer, respectively, and are parametrized with the real-valued angles γ_d and β_d, respectively. They are defined as

$$U_{\mathrm{PS}}({\mathrm{\gamma }}_d)=e^{i{\mathrm{\gamma }}_{d}C}\mathrm{and}{U}_{\mathrm{M}}({\mathrm{\beta }}_d)=e^{i{\mathrm{\beta }}_d{\displaystyle \sum _{j=1}^N}{X}_j}$$ (3)

where C is the operator corresponding to the objective function of Eq. 1 and where X_j is the Pauli operator on qubit j. The search for optimal angles γ^* and β^* is done in a quantum-classical hybrid fashion by minimizing the expectation value 〈C〉 = 〈γ, β ∣ C ∣ γ, β〉. Candidate bit string solutions {B} are obtained by sampling the quantum state ∣γ^*, β^*〉.

The quality of a solution is ranked by its cost value C^* with respect to the maximum (worst) and minimum (optimal) ones, C_max and C_min, respectively, through the approximation ratio

$$r=(C_{\max }-C^{\ast })/(C_{\max }-C_{\min })$$ (4)

which is equal to 1 for an optimal solution C^* = C_min. On difficult problem instances, it is proven to be NP-hard to achieve an ensemble-average approximation ratio greater than a given value r^⋆, and intensive ongoing theoretical efforts (2, 3, 11, 24–30) are attempting to establish whether QAOA with p layers can lead to an average approximation ratio larger than the best-known classical methods on some problem classes. Because of noise, when QAOA is run on current generation (noisy) quantum hardware, it leads to approximation ratios much smaller than theoretical bounds and those obtained on small-scale classical emulations (13–15). In a strong noise regime where the quantum state tends to be described as a maximally mixed state, the expected performance is that of a random bit string sampling. Under the assumption that the spectrum of C (Eq. 1) is symmetric about u, this corresponds to r = 1/2.

In the following, we develop a hybrid classical-quantum algorithm performing as good as a randomized classical greedy algorithm in the presence of strong noise. For instance, the classical greedy approach has a performance r ≃ 0.848497… for Sherrington-Kirkpatrick (SK) Ising spin glass problems (see Methods), much larger than random guessing and a very noisy vanilla QAOA execution. We implement the quantum algorithm on Rigetti Aspen-M-3 programmable superconducting quantum system using up to 72 qubits and find that it systematically outperforms its classical greedy counterpart, signaling a quantum enhancement.

RESULTS

We introduce an iterative algorithm for solving discrete optimization problems which bears similarities with divide-and-conquer methods (31) and more closely with other iterative/recursive techniques referred as RQAOA (32,33) or greedy decompositions in quantum annealing (34)—the main difference being the freezing procedure. At each iteration, a set of variables are frozen to their classical values depending on the output returned by a quantum computer—although, as discussed later, the approach works with any sampleable distribution over bit strings, quantum or classical. These variables are removed, and an updated, smaller optimization problem is generated. The procedure is repeated until all variables are frozen or until the remaining problem is small enough for brute force.

A main difference between the quantum-enhanced greedy algorithm that we develop and prior iterative approaches is its robustness to noise, which is key when executing quantum algorithms at scale on current quantum hardware. In a strong depolarizing noise regime, our quantum algorithm maps to a classical randomized greedy algorithm for which one can analytically estimate its average performance for problems such as SK Ising spin glasses. In the same strong noise regime, as expectation values, such as two-point correlations ⟨ZiZj⟩, tend towards zero, other existing iterative algorithms (31–34) would perform as well as a random sampling strategy in the absence of a mapping to a classical greedy baseline.

Each iteration 𝓁 of our quantum-enhanced greedy algorithm follows the steps,

#1. Obtain a list of M^(𝓁) bit strings {B^(𝓁)} that encode candidate solutions to the problem. In the quantum version, these bit strings are sampled from the output of the quantum computer, where the quantum circuit optimizes the objective function C^(𝓁) (Eq. 1). In the classical randomized greedy version, these bit strings are sampled from a uniform distribution of all bit strings.

#2. Find a set {k} of K variables to freeze. Different heuristics can be envisioned (32, 33), including a majority vote based on one-body expectation values, i.e., max_i ∣ 〈Z_i〉∣, or based on two-body expectation values, as well as many others. In the following, we use a two-body expectation strategy developed in Methods to select K = 1 variable.

#3. Find the frozen value of each variable selected in #2: For each variable in {k}, loop over all the possible values {s} of the variable (i.e., s = 0 or 1 for a binary variable), substitute them for all bit string of the list such that $\{{\mathbf{B}}_k^{(\ell )}\leftarrow s\}$, and compute the expectation value of the cost based on the modified {B^(𝓁)}. The assignment s leading to the best expectation value of the cost is taken as the variable’s frozen value (see Methods).

#4. Update the problem C^(𝓁) by replacing each of the operators in {Z_k} by a constant based on the expectation value of 〈Z_k〉. The scalars are absorbed into u, v_i, and w_ij in Eq. 1 to create a new problem C^{(𝓁 + 1)} with at least K fewer variables (see Methods).

Other strategies can be implemented in the third step (#3). The essential point is that for random bit strings {B^(𝓁)}, the freezing decisions are locally optimal with respect to the objective function, independently of the selected variables. As such, the average approximation ratio from random bit strings and optimal freezing is r ≃ 0.848497⋯ (see Methods). Also, if {B^(𝓁)} is replaced by optimal bit strings with respect to the objective function, then the above algorithm will preserve an optimal solution, and yield r = 1. Therefore, the intuition is that for bit strings which are between random and optimal, there should be a performance boost with respect to the classical greedy baseline. Better-than-random bit strings, on average, should help make better-informed decisions for the selection and thus guide an otherwise randomized greedy process. The complexity of the above algorithm is O[(N/K)N_edges] with N_edges the number of two-body terms in the graph problem. Taking K ∼ O(1) and N_edges ∼ O(N²) for the SK instances considered in the following leads to O(N³) complexity. We note that the complexity of the classical randomized version of the algorithm can be reduced to O(N²) when not working with explicit bit strings and considering that all expectation values average to zero.

We implement the quantum-enhanced greedy algorithm on SK problem instances (35) by setting u = v_i = 0 in Eq. 1 and draw the parameters w_ij uniformly from { + 1, − 1}. SK models correspond to paradigmatic Ising spin glasses. Although it was recently proven that the ground state energy of SK models can be efficiently approximated with an approximation ratio (1 − ɛ) by an approximate message passing algorithm (36), SK models remain a relevant benchmark for combinatorial optimization methods.

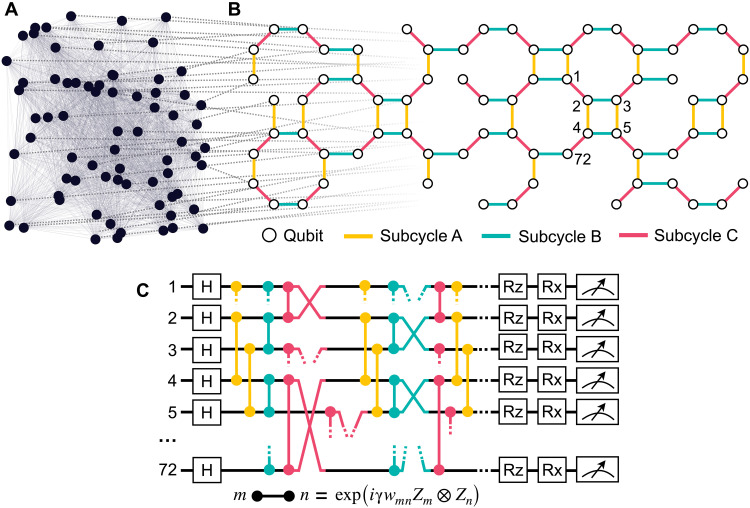
We run the algorithm on Rigetti’s superconducting quantum processor Aspen-M-3 with a planar square-octagon topology of 79 qubits (see the Methods for the parameters used in practice and more details). The limited connectivity of the hardware, displayed in Fig. 1, requires an extensive swap network to cover two-qubit gates between arbitrary qubits (37). Consequently, implementation of the phase separator unitary of Eq. 2 is not practical (due to noise) for SK problems with large N (Fig. 1, A and B]. Instead, we use a truncated one-layer QAOA ansatz: At each iteration of the algorithm, the problem is randomly mapped to the hardware-native architecture, and only gates involving qubits connected within 2 swap cycles are considered, with the others dismissed, as exemplified in Fig. 1C. The circuit (Eq. 2) is compiled into hardware-native gates, resulting in about 400 native $\sqrt{\mathrm{iSWAP}}$ two-qubit gates for the largest problems considered, as detailed in Methods. We collect a total of M^(𝓁) = 256 bit strings for all steps 𝓁.

Fig. 1. Problem mapping and quantum circuit.

(A) Binary optimization problem with N = 72 variables (Eq. 1). (B) Binary variables are randomly mapped to a qubit of the square-octagon topology of the Rigetti Aspen-M-3 quantum processor. The edges are divided into three independent sets A, B, and C on which two-qubit gates can be executed in parallel. (C) QAOA quantum circuit (Eq. 2). We show a truncated version run on hardware: We apply R_zz gates on the yellow edges in subcycle A, then R_zz gates on the teal edges in subcycle B, then R_zz and SWAP gates on the magenta edges in subcycle C, and so on as shown above.

We use the quantum-enhanced greedy algorithm to solve a set of 10 random SK problem instances for sizes N = 8, 24, 40, 56, and 72. We freeze one variable (K = 1) at a time and use two-body expectation values to inform the selection process. We report the estimated expectation value of the approximation ratio r ≡ 〈r〉_{γ^*, β^*} by computing the expectation value of the corresponding objective function over all sampled candidate bit string solutions at angles γ^* and β^*. For N ≤ 24, we use brute force to compute C_max and C_min (Eq. 4) for a given problem instance. For larger N, we rely on the fact that the cost of the optimal solution is self-averaging, known exactly for N → + ∞, and that finite-size corrections have also been studied over an ensemble of random instances (38). This gives access to a proxy for approximating r, assuming one is not interested in the performance for an individual problem but that of an ensemble. Additional detail is given in Methods.

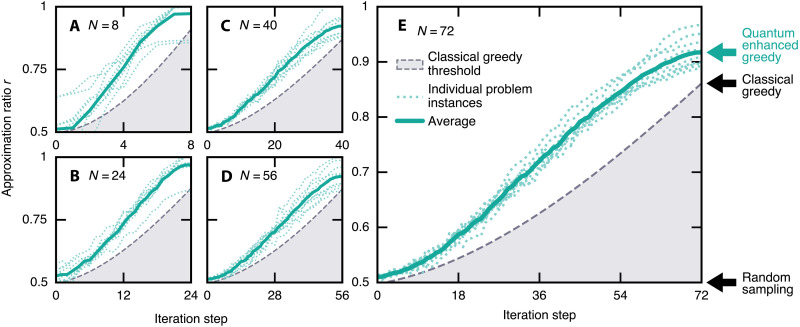
We show the obtained approximation ratio as a function of the iteration step in Fig. 2. Iteration step 0 corresponds to a truncated one-layer QAOA ansatz run on the initial problem of N variables. For all sizes, this is slightly above the r = 1/2 random sampling bar, emphasizing that the QAOA displays a low average performance on current hardware. The last step corresponds to the final solution of the quantum-enhanced greedy algorithm. Its average performance is systematically above that of the classical greedy baseline. We note that the approximation ratio in both the classical greedy and the quantum-enhanced algorithms have a distribution around the average. This is more evident at small N, for example, N = 8 and N = 24 in Fig. 2, where the quantum greedy results for some problem instances dip below the average classical greedy results. The estimated approximation ratio at the last step is displayed in Fig. 3 as a function of problem size N. We observe a decrease in performance with increasing problem size, which has two primary causes. First, the larger the size, the larger the quantum circuit, leading to a higher error rate. Second, the phase separator unitary of the truncated QAOA ansatz only covers an O(1/N) density of edges of the graph problem, which accounts for a vanishing fraction of two-body terms in the SK problem instances (about 3% for N = 72). For comparison, a noiseless simulation of a nontruncated standard single-layer QAOA circuit leads to an average approximation ratio $r=1/2+1/4\mathrm{P}\sqrt{e}\simeq 0.698688\dots$ on large SK problem instances (29), where P is the Parisi constant (39, 40).

Fig. 2. Approximation ratio versus iteration step.

Each panel corresponds to an SK problem instance of different size: (A) N = 8, (B) N = 24, (C) N = 40, (D) N = 56, and (E) N = 72. A random sampling strategy leads to an average approximation ratio r = 0.5. The performance of the classical greedy baseline is shown by the shaded region with a final average approximation ratio r ≃ 0.848497… for N → + ∞ (see Methods). The quantum-enhanced greedy data show the expectation value of the approximation ratio for 10 randomly generated problem instances (see Fig. 1). The performance at iteration step 0 is that of the truncated one-layer QAOA. The performance at iteration step N is that of the quantum-enhanced algorithm, also reported in Fig. 3. Because we display all individual instances, we omit the error bar for the average case.

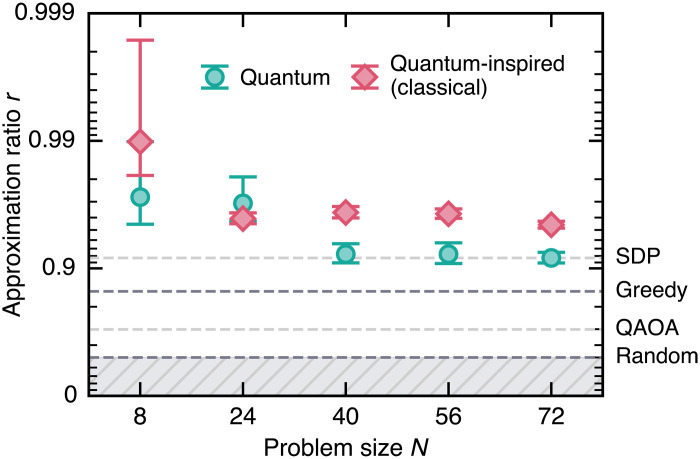
Fig. 3. Performance boost.

Approximation ratio based on different bit string generators: The hardware-run QAOA of Fig. 2, averaged over 10 problem instances, and quantum-inspired classical tensor network simulations (see Methods), averaged over 100 random SK problem instances. The different horizontal dashed lines correspond to the average performance of various algorithms in the limit N → + ∞. From bottom to top: Random sampling r = 1/2, a perfectly executed single-layer, nontruncated, QAOA circuit $r=1/2+1/4\mathrm{P}\sqrt{e}\simeq 0.698688\dots$ (29), the classical greedy baseline $r=1/2+\sqrt{2/\mathrm{\pi }}/3\mathrm{P}\simeq 0.848497\dots$ (see Methods), a classical SDP approach r = 1/2 + 1/πP ≃ 0.917090… (41–43) where P is the Parisi constant (39, 40). Error bars indicate 1 standard deviation. Numerical values are tabulated in the Supplementary Materials.

Embedding the QAOA into the quantum-enhanced algorithm greatly enhances the quality of the end result. From step 0 to step N of the iterative loop (Fig. 2), we experimentally obtain a six- to sevenfold increase in the average approximation ratio for N = 72 where 1 − r ≃ 0.49 → 0.08 (Fig. 3). A fairer comparison point is the classical greedy baseline which runs the same algorithm with random bit strings as input instead. For the SK problem instances considered here, the expected approximation ratio of this classical heuristic is r ≃ 0.848497… as N → + ∞ (see Methods). It is a high absolute bar to pass, much higher than what we obtain from a noisy and truncated one-layer QAOA run at iteration step 0. For reference, it requires at least a perfectly executed nontruncated four- to five-layer QAOA circuit to meet this classical performance [see the Supplementary Materials and (29)]. Here, the quantum-enhanced greedy algorithm run on noisy quantum hardware improves upon the average approximation ratio of its classical counterpart by about a factor 2 (1 − r ≃ 0.151503… → 0.08) for the largest problem size N = 72 (Fig. 3), empirically confirming the intuition that better-than-random bit strings should, on average, help make better-informed decisions in the freezing process. An explanation is that while bit strings look close to random as a whole because of noise, they might still locally retain relevant information. Here, we look for the most correlated variable (see Methods), as this suggests a well-defined value for the corresponding bit, making it a good candidate for freezing. We observe an absolute performance comparable with state-of-the-art semidefinite programming (SDP) method, corresponding to a spectral relaxation rounding to ±1 each entry of the leading eigenvector of the adjacency matrix of the graph problem (41–43).

DISCUSSION

While our empirical results demonstrate that the quantum-enhanced algorithm can outperform the classical greedy threshold, signaling a quantum boost, proving this rigorously remains as future work. All the iterative algorithm needs is a bit string generator at step #1, analogous to classical methods such as genetic algorithms and Monte Carlo methods. We highlight the work ahead for reaching a quantum advantage by using noiseless classical tensor network simulations to generate bit strings from a truncated one-layer QAOA circuit with two swap cycles embedded into a one-dimensional lattice (see Methods). This leads to an average approximation ratio r ≃ 0.95 for the largest problems considered (Fig. 3), higher than what we obtained with the quantum runs. We, therefore, expect that the performance of the quantum-enhanced greedy algorithm will continue to improve with advances in hardware fidelity. The algorithm can use expectation-based error mitigation techniques (44) for improving the freezing decisions—and therefore, the final solution—, which are otherwise not usable for more traditional quantum optimization methods when one is typically interested in enhancing an individual bit string. Further, classical postprocessing methods (45) may be leveraged to develop and explore more sophisticated variable freezing procedures, such as postselecting only bit strings that do at least as well as random guessing. Ultimately, the backbone remains the quantum device, and the overarching goal should be to improve its characteristics. Improving those will allow running deeper QAOA circuits as well as other state-of-the-art quantum circuits, leading to an overall performance increase through better-informed decisions (see the Supplementary Materials). This would warrant additional, comprehensive benchmarks against a panoply of state-of-the-art classical algorithms and techniques, such as Ising machines (46), to assess on the existence of a practical quantum speedup or advantage.

The freezing decisions have a classical component that can be adapted to deal with some hard constraints; such as postselecting on valid solutions. Hard constraints are ubiquitous in real-world optimization problems and are notoriously difficult to handle in practice. A possible strategy is to design quantum circuits working within the in-constraint space with dynamics restricted to the subspace of feasible solutions (12, 47, 48), but these methods may require greater quantum resources. Another typical approach uses penalty terms that will disfavor the appearance of out-of-constraint bit strings, but implementing them on near-term devices and tuning their strength can be similarly challenging. Here, the idea is to make only freezing decisions which do not violate any constraints. Note that this is only possible for some classes of constraints, as a general satisfiability problem is NP-complete. We investigate a proof of concept of the modified algorithm on a constrained binary portfolio optimization problem in the Supplementary Materials, comparing it to the state of the art (49).

In practice, scaling to hundreds of qubits will require freezing variables simultaneously to keep the runtime under control. We suggest the following modification (32): After selecting K variables in step #2, the decision in step #3 attempts the 2^K substitutions in {B^(𝓁)} and keeps the best one.

Last, it is interesting to think of iterative hybrid classical-quantum setups with performance guarantees on noisy hardware in the context of quantum problems rather than classical ones. For instance, can one enhance the performance of variational quantum eigensolvers (4, 50) for chemistry and other quantum many-body problems by embedding ideas from real-space renormalization group methods, such as linked-cluster expansions or the contractor renormalization group technique (51)?

METHODS

Rigetti Aspen-M-3 superconducting platform

Rigetti’s Aspen-M-3 is a programmable and universal superconducting quantum computer based on transmon qubits. There are 79 qubits arranged on a planar square-octagon topology. We make use of one-qubit rotation gates about the x axis Rx(ϕ ∈ ℤ) = exp ( − iXϕπ/4), one-qubit rotation gates about the z axis Rz(θ ∈ ℝ) = exp ( − iZθ/2), and the two-qubit gate $\sqrt{\mathrm{iSWAP}}=\exp [i\mathrm{\pi }(XX+YY)/8]$ (52). X, Y, and Z are Pauli operators. The qubits have an average relaxation time T₁ = 25(2) μs, an average dephasing time T₂ = 28(2) μs, an average readout fidelity of 94.6(7)%, and an average one-qubit Rx fidelity of 99.4(2)% estimated by randomized benchmarking (53).

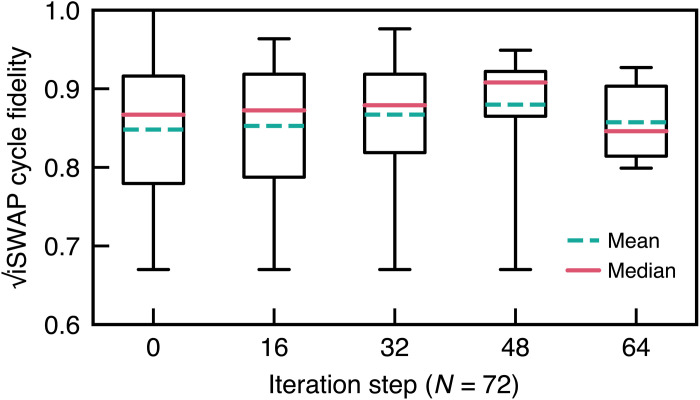
To estimate the fidelity of the operations $\sqrt{\mathrm{iSWAP}}$, we use cycle benchmarking (54). In the circuit, cycles were constructed by splitting the three independent edge groups of Fig. 1C each into two clock cycles (for a total of six), where the $\sqrt{\mathrm{iSWAP}}$ gates are separated by at least one idle qubit. This is done to minimize cross-talk between the $\sqrt{\mathrm{iSWAP}}$ gates. Cycle benchmarking provides a measurement of fidelity that is less forgiving, but more realistic, than isolated randomized benchmarking. The cycles are benchmarked the same way they are played in the application circuit, accumulating additional error from decoherence while idling and from the single-qubit gates which precede each two-qubit gate in the cycle. We report in Fig. 4 the marginal process fidelity contributed by each pair of qubits playing an entangling gate in the cycle. In general, the majority of the infidelity is contributed by the entangling operations. We expect further refinements to the cycle calibration process to reduce control errors and yield better cycle performance.

Fig. 4. Cycle fidelity for two-qubit gates.

Statistics for the cycle fidelity of $\sqrt{\mathrm{iSWAP}}$ at different iteration steps for a problem size N = 72. The boxes cover the first to the third quartile. The whiskers cover the whole range of the data. With each iteration step of the algorithm, the size of the problem is reduced and we successively target smaller and smaller subsets of qubits of higher and higher overall quality resulting in an increasing mean and median with decreasing spread.

As the quantum-enhanced greedy algorithm iteratively reduces the size of the problem and thus the number of qubits at each iteration step, we successively target smaller and smaller subsets of qubits of higher and higher overall quality. This is visible from the general trends of Fig. 4 where the mean and median fidelities increase and the spread decreases with each iteration step.

Hardware-native quantum circuits

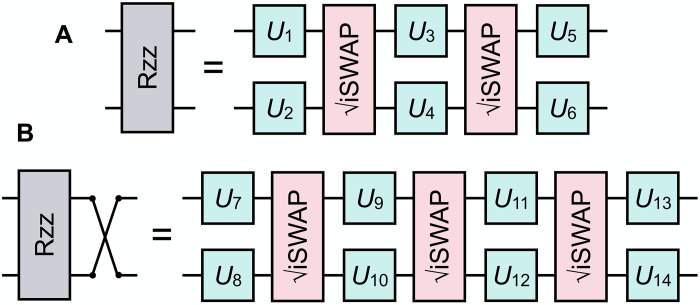
The unitaries of the QAOA in Eq. 3 are expressed through one- and two-qubit gates exclusively, as pictured in Fig. 1C. These gates are further decomposed into the hardware native gate set. For instance, the one-qubit gate Rx(ϕ) is implemented for arbitrary angles using the standard “ZXZXZ” decomposition (55). We use the hardware-native two-qubit $\sqrt{\mathrm{iSWAP}}$ gate to express Rzz(ϕ) = exp ( − iϕZZ/2) and SWAP. Because we always precede a SWAP gate by Rzz(ϕ), we decompose directly the combination of these two gates. Both Rzz and Rzz × SWAP can be implemented using hardware-native one-qubit gates and at most two and three two-qubit $\sqrt{\mathrm{iSWAP}}$ gates (56), respectively, as shown in Fig. 5; the precise decomposition is given in the Supplementary Materials. While this may not be the optimal synthesis in general, it is optimal in terms of number of pulses for the Rigetti Aspen-M-3 quantum processor with respect to alternatives.

Fig. 5. Two-qubit gate decompositions.

(A) Decomposition of the parametric two-qubit gate Rzz(ϕ) = exp ( − iϕZZ/2) using two hardware-native $\sqrt{\mathrm{iSWAP}}=\exp [i\mathrm{\pi }(XX+YY)/8]$ gates. X, Y, and Z are Pauli operators. (B) Decomposition of the parametric two-qubit gate Rzz(ϕ) directly followed by a SWAP using three hardware-native $\sqrt{\mathrm{iSWAP}}$ gates. In each case, the one-qubit gates U_1...14 carry the angle ϕ and are decomposed explicitly as a function of Rx and Rz gates (see the Supplementary Materials for details).

Optimization of QAOA circuits and sampling bit strings

A QAOA circuit with p layers is defined in Eq. 2. It is parameterized by 2p angles, which should be such that the resulting quantum state minimizes the expectation value of the objective function C of Eq. 1. In this work, we consider truncated one-layer QAOA circuits (Fig. 1B) with only two angles γ and β. As such, we optimize them through a 16 × 16 grid search in the range γ ∈ [0,2π] and β ∈ [0, π]. For each of the 16 × 16 = 256 pairs of angles, we collect M = 256 bit strings {B} by sampling the quantum state ∣γ, β〉 to compute the expectation value

$${⟨C⟩}_{\mathrm{\gamma },\mathrm{\beta }}=⟨\mathrm{\gamma },\mathrm{\beta }\mid C\mid \mathrm{\gamma },\mathrm{\beta }⟩=\frac{1}{M}{\sum }_{\{\mathbf{B}\}}⟨\mathbf{B}\mid C\mid \mathbf{B}⟩$$ (5)

The angles leading to the minimum expectation value of 〈C〉_{γ, β} are γ^* and β^*. The M bit strings that led to the minimum expectation value 〈C〉_{γ^*, β^*} during the grid search are used in the first step (#1) of the iterative quantum-enhanced greedy algorithm. Examples of 〈C〉_{γ, β} are shown in the Supplementary Materials.

Iterative process

We provide additional detail on our implementation of the iterative steps #2, #3, and #4 of the algorithm. At this stage, we have already obtained a list of bit strings {B} sampled from the quantum state of the optimized QAOA circuit at angles γ^* and β^*. At step #2, we find K = 1 variable to freeze based on a two-body expectation strategy. Precisely, for each active node k of the graph, we compute

$$F_k=\frac{1}{M}[{\sum }_{i\in \{\mathrm{active}\}\ne k}\mid w_{ik}{\sum }_{\{\mathbf{B}\}}⟨\mathbf{B}\mid Z_i{Z}_k\mid \mathbf{B}⟩\mid +\mid v_k{\sum }_{\{\mathbf{B}\}}⟨\mathbf{B}\mid Z_k\mid \mathbf{B}⟩\mid ]$$ (6)

where we find k such that max_kF_k. The function F_k corresponds to the expectation value of the objective function at the given iteration step where all the terms involving the node k have been individually sandwiched by a modulus symbol. We now move to step #3 and generate two modified versions of the bit strings {B} by setting the bit k on all the M bit strings to either 0 or 1. We then compute the expectation value of the cost 〈C₀〉 = ∑_{{Bk ← 0}} ‍ 〈B ∣ C ∣ B〉/M and 〈C₁〉 = ∑_{{Bk ← 1}} ‍ 〈B ∣ C ∣ B〉/M. The value B_k = 0 or 1 which provided the smallest of 〈C₀〉 and 〈C₁〉 will be used as the variable’s frozen value σ_k = ( − 1)^B_k. Following the freezing decision of the variable k, the problem is updated as follows

$$\begin{array}{c}{w}_{ik}{Z}_i{Z}_k\to v{\mathrm{\prime }}_i{Z}_i\mathrm{\forall }i\mathrm{with}v{\mathrm{\prime }}_i=v_i+w_{ik}{\mathrm{\sigma }}_k,\\ v_k{Z}_k\to u^{\mathrm{\prime }}=u+v_k{\mathrm{\sigma }}_k\end{array}$$ (7)

where the notation of Eq. 1 is used for scalar parameters u, v_i, and w_ij.

Classical simulations of quantum circuits

We supplement the quantum experimental results with classical simulations of the circuits. We use two methods throughout this work. The first one, used in the Supplementary Materials, is based on a state vector approach where the quantum state for N qubits is represented as a complex vector of 2^N components. It is an exact method. The second one, used for generating the data of Fig. 3, is a tensor network approach based on matrix product states (57). The circuits we simulate with matrix product states are a truncated one-layer QAOA circuit with two swap cycles embedded into a one-dimensional lattice with open boundary conditions. The circuits are shallow enough to be executed exactly with a relatively low bond dimension (the bond dimension is a control parameter of a matrix product state simulator), independent of the number of qubits involved, thus enabling exact classical simulations at N = 72. Precisely, the circuits have a brick wall pattern of two-qubit gates with a total of four layers in addition to one-qubit gates. Additional details on matrix product states are given in the Supplementary Materials.

Optimal cost of SK instances

Computing the approximation ratio of Eq. 4 requires the extremum (best C_min and worst C_max) cost values for the SK problem instance of interest. For problems N ≤ 24, we compute them through brute force by enumerating the 2^N bit strings. For larger N, we rely on the fact that the cost of the optimal solution is self-averaging, known exactly for N → + ∞, and that finite-size corrections have also been studied over an ensemble of random instances (38). In particular, one has,

$$C_{\min }\times N^{-3/2}\simeq -\mathrm{P}+a{N}^{-\mathrm{\omega }}$$ (8)

where P = 0.763166726566547… is a universal constant known as the Parisi value (39, 40), ω = 2/3 is a universal exponent accounting for finite-N corrections, and a ≃ 0.70(1) is a nonuniversal constant (38). Moreover, on average, C_max = − C_min since it corresponds to solving an equivalent problem with flipped signs for the parameters w_ij (Eq. 1) (see the Supplementary Materials). Hence, for an ensemble of SK problems leading to an average cost value of C^*, we approximate the obtained approximation ratio as

$$r\simeq \frac{1}{2}(1+\frac{C^{\ast }}{C_{\min }})$$ (9)

where C_min is evaluated numerically using Eq. 8. For randomly generated bit strings, C^* is symmetrically distributed between C_min and C_max, i.e., C^* = 0 in expectation, and the corresponding average approximation ratio is r ≃ 1/2.

Classical greedy baseline

The classical greedy algorithm iteratively builds a solution by making the locally optimal choice at each stage. There are as many iteration steps as variables in the problem. We note Z_i = ± 1 the contribution to the cost function of the frozen variable i. We consider the SK problem instances of the main text (Eq. 1 with w_ij = ± 1, u = v_i = 0) for which the freezing decisions go as follows. Iteration step 1, freeze Z₁ arbitrarily to ±1. Iteration step 2, freeze Z₂ such that w₁₂Z₁Z₂ is minimized, i.e., min_Z2[w₁₂Z₁Z₂]. Iteration step 3, freeze Z₃ such that min_Z3[Z₃(w₁₃Z₁ + w₂₃Z₂)]. At iteration step 𝓁, freeze Z_𝓁 such that $Z_{\ell }{\sum }_{i=1}^{\ell -1}{w}_{i\ell }{Z}_i$ is minimized. This is repeated until iteration step N. The final cost value is

$$C_{\mathrm{greedy}}=-{\displaystyle \sum _{\ell =2}^N}\mid {\displaystyle \sum _{i=1}^{\ell -1}}{w}_{i\ell }{Z}_i\mid$$ (10)

The absolute value terms in Eq. 10 can be seen as individual random walks containing 𝓁 − 1 steps of length ±1. As such, for 𝓁 → + ∞, their average contribution will be $\simeq \sqrt{2(\ell -1)/\mathrm{\pi }}$. This step is analogous to averaging over different freezing orders for the variables. Under the hood, this corresponds to running the algorithm of the main text with a finite number of random bit strings from which statistical fluctuations will lead to different freezing selections in #2 from one run to the next. Hence, one finds that, on average,

$$C_{\mathrm{greedy}}\simeq -\sqrt{2/\mathrm{\pi }}{\displaystyle \sum _{\ell =1}^{N-1}}\sqrt{\ell }$$ (11)

As N → + ∞, an asymptotic expansion based on Euler-Maclaurin formula leads to ${\sum }_{\ell =1}^{N-1}\sqrt{\ell }\sim (2/3)N^{3/2}+\dots ,$, which makes it possible to evaluate the average approximation ratio of the classical greedy algorithm using Eqs. 8 and 9 for an infinite-size SK problem instance

$$\frac{C_{\mathrm{greedy}}}{C_{\min }}=\frac{2\sqrt{2/\mathrm{\pi }}}{3\mathrm{P}}\Rightarrow r=\frac{1}{2}+\frac{\sqrt{2/\mathrm{\pi }}}{3\mathrm{P}}\simeq 0.848497\dots$$ (12)

The case of finite N is studied numerically in the Supplementary Materials. By definition, this is also the average approximation ratio of the quantum-enhanced algorithm with random input. Physically, this would mean that the quantum computer generates a maximally mixed state ρ = I/2^N, as the result of, e.g., strong depolarizing noise: Here, ρ is the density matrix describing N qubits and I the Identity matrix of dimensions 2^N × 2^N.

For comparison, other algorithms yield the following average performance: Random sampling r = 1/2, a perfectly executed single-layer, nontruncated, QAOA circuit $r=1/2+1/4\mathrm{P}\sqrt{e}\simeq 0.698688\dots$ (29), a classical SDP approach r = 1/2 + 1/πP ≃ 0.917090… (41–43). We extend nonexhaustively the analytical analysis of the classical greedy baseline to other problems in the Supplementary Materials.

Supplementary Materials

This PDF file includes:

Supplementary text

Figs. S1 to S11

Table S1

References