Abstract
Unlike steam turbines, electricity production in gas turbines is inherently independent of freshwater consumption. However, the thermal efficiency of gas turbines decreases as the temperature of input air increases. As a result, many methods of cooling the inlet air require the use of fresh water. Moreover, when it comes to humid gas turbine technology, the practice of injecting steam or humid air into the turbine to improve its thermal efficiency and output power consumes a substantial amount of freshwater. Therefore, reducing the use of fresh water to enhance the output power and thermal efficiency of gas turbines can be a necessary option, especially in hot and dry regions. Alternatively, considering the significant amounts of waste heat in gas turbines, one solution to reduce fresh water consumption is to connect them to thermal desalination units. However, conventional thermal desalination is only practical for seawater desalination in coastal areas. Therefore, this study explores the possibility of linking a direct contact membrane distillation (DCMD) unit to a Steam-injected gas turbine (STIG), which can use high salinity water sources like reverse osmosis (RO) brine in inland regions. The freshwater generated by the DCMD is used to chill the input air to the compressor and produce steam injected within the turbine. Simulation results show that this connection can raise the net output power by [9 to 17.2] MW and thermal efficiency by [3.3 to 15.6] % for compressor pressure ratios between [5 to 30], when compared to a simple gas turbine.
Keywords: Direct contact membrane distillation, Steam injected gas turbine, Reverse osmosis brine
1. Introduction
The production of power and freshwater are closely linked. When using a steam turbine or a combination of a steam and gas turbine, freshwater is commonly used for steam condensation in the steam cycle [1]. This has led to a growing interest in constructing power plants near rivers or coastal areas [2]. But despite gas turbines not inherently requiring freshwater, they still consume it indirectly. As the ambient temperature rises, the gas turbine's output power and thermal efficiency decrease due to the drop in air density. This decrease in air density causes an increase in compressor power consumption and a decrease in air mass flow rate across the turbine at constant volume [3]. To address this problem, have developed turbine inlet air cooling (TIAC) methods. However, many of these methods rely on the use of fresh water. For instance, evaporation methods like evaporative media cooling and high-pressure fogging systems use direct contact between water and air to chill the input air to the turbine. Using this method, it is possible to lower the temperature to nearly the wet-bulb temperature [4]. However, it should be noted that these evaporative cooling methods require a substantial amount of fresh water. For example, according to a calculation for evaporation cooling process, for each degree of temperature reduction is required 300 lit/s of fresh water per 300 kg/s of air flow rate [5]. In another investigation, Dawoud et al. have conducted a thermodynamic evaluation of the evaporative and fogging cooling systems for the incoming air to a 40 MW gas turbine in a region in the southeast of Saudi Arabia at the temperature of 48.8 °C in the summer. The results indicated that employing evaporative cooling and fogging systems raised the net output power of the turbine by 9.4 % and 11 % respectively. However, for this evaporation and fogging system, the annual water requirement was 13155 and 10485 tons of water, respectively. This amount is roughly equivalent to the yearly fresh water requirement for a community of 1344 residents near the Saudi Arabia-Oman border [6].
Refrigeration systems, such as compression refrigeration or absorption refrigeration with indirect heat transfer, can cool the input air to the gas turbine below the wet bulb temperature. However, it has to be noted that the absorption refrigeration system requires a cooling tower and freshwater consumption [4,7].
Humid gas turbines (HGT) also are a type of gas turbine that uses injected water to boost their output power. Therefore, in these turbines, the operating fluid is a blend of air and water. Steam-injected gas turbines (STIG) and evaporative gas turbines (EvGT) are two major forms of HGTs that involve injecting steam or humid air into the turbine. Additionally, the TIAC that requires water injection into the inlet air can also be considered a subset of HGT [8]. However, the high consumption of fresh water in HGT technology also restricts employment of them, especially in dry areas with scarce water resources. For instance, an LM5000 STIG™ plant belonging to General Electric company consumes approximately 1450 tons of water per day for a 50.7 MW power plant, when operating under a complete steam injection [9].
Therefore, due to the significant need for fresh water to improve the output and efficiency of gas turbines, an optimal solution is to use saline water sources by connecting thermal desalination units to these turbines. As an example, Wanga and Lior explored the relationship between multi-effect thermal vapor compression (METVC) units with STIG and EvGT systems in two papers [10,11]. However, typically, traditional thermal desalination units like multi-stage flash (MSF), multi-effect distillation (MED), and METVC are suitable to desalinate seawater, and connection of them to a gas turbine is generally done in the coastal regions [12].
However, in hot and dry inland regions, high salinity water, like reverse osmosis (RO) brine, can be an unconventional source of water. Therefore, to avert the power dissipation of gas turbines due to rising air temperatures, it can be suitable to use this type of water to produce fresh water. One way to use this unconventional water is by the membrane distillation (MD) process, which can desalinate high-salinity water. This process can supply the freshwater required by a humid gas turbine, like STIG, using high-salinity water, such as RO brine. This is particularly beneficial in hot and dry regions where over 60 % of the aquifers have high salinity levels and groundwater is the main source of drinking water [13]. Desalination of groundwater water in these areas with RO technology will be accompanied by brine disposal. However, the disposal of RO brine in inland areas has always been one of the environmental challenges [14]. Therefore, using this brine as a source of fresh water for a STIG in these regions would also be environmentally beneficial.
The MD technology chosen for desalinating RO brine in this study is a non-isothermal hydrophobic membrane that lets only water vapor pass through. The membrane's driving force in the MD is the difference in vapor pressure between its two sides, caused by temperature differences [15]. According to several ways to collect permeate, different configurations have been developed for this membrane process. These include direct contact membrane distillation (DCMD), vacuum membrane distillation (VMD), air gap membrane distillation (AGMD), and sweeping gas membrane distillation (SGMD) [16].
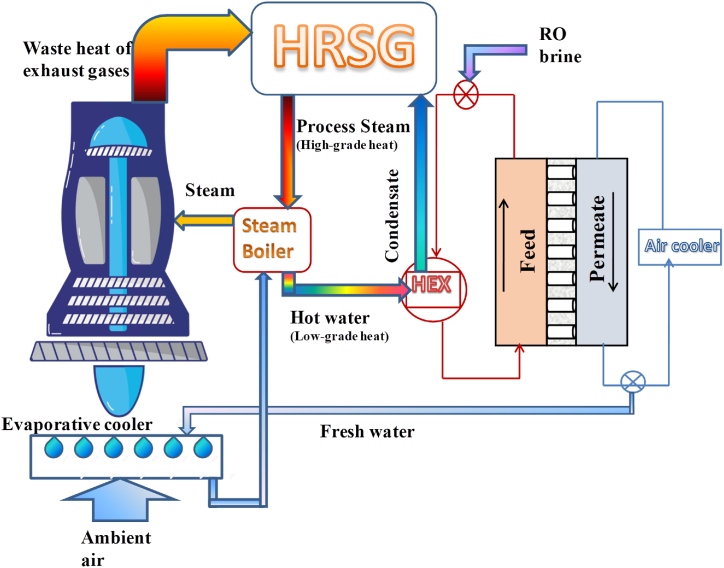
Fig. 1 indicates the conceptual drawing of how a DCMD module is connected to the STIG. This study simulates this connection using the Aspen Plus software. However, since Aspen Plus lacks a specific membrane model, a separate module must be defined for it. To model the membrane distillation, previous studies used the 1D equations in the FORTRAN language, which can be used in the Aspen Plus [[17], [18], [19]]. In the 1D equations, cannot be accounted for the effect of polarization of temperature and concentration on the membrane surface that reduces its permeability. Therefore, in the previous studies to prevent a positive error in the penetration of the membrane in the 1D equations, a polarization coefficient obtained experimentally has been used. In this investigation, the computational fluid dynamics (CFD) method was used to model a 2D flat sheet membrane in COMSOL Multiphysics software, taking into account temperature and concentration polarizations. Then the CFD simulation results for the membrane module were imported to Aspen Plus using the user model block. Next, the analysis of energy and exergy has been done for this process and the results have been compared with a simple gas turbine in the same operating conditions. The comparison with a simple gas turbine has been made with the assumption of being located in a hot and arid region where exists the limitation of using freshwater resources to increase the thermal efficiency of the gas turbine.
Fig. 1.
Conceptual schematic of the connection of a DCMD to the STIG.
2. CFD modeling of a 2D flat sheet DCMD
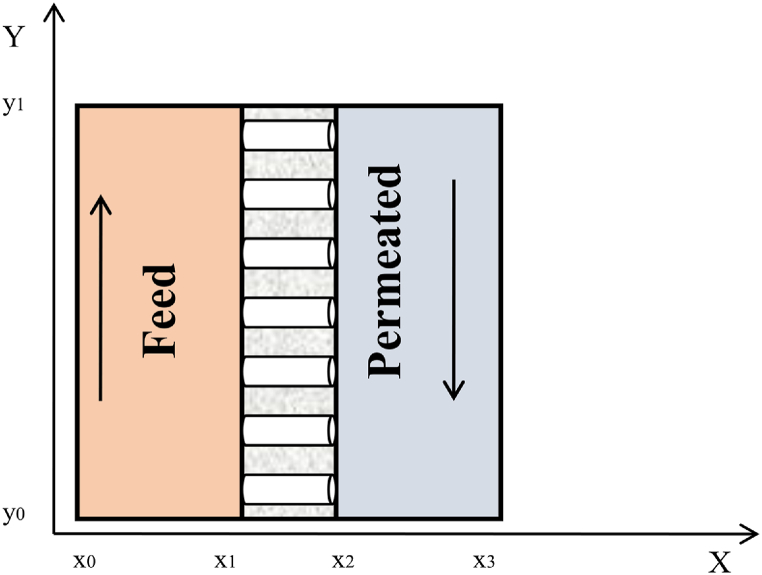
CFD or Computational Fluid Dynamics is a powerful tool used to model systems that involve transfer phenomena like momentum, heat, and mass transfer. In a DCMD model, all of these transfer phenomena occur simultaneously. A flat sheet membrane that separates feed saline water and permeated fresh water is displayed in Fig. 2. There is a counter-current flow present on two sides of the membrane. The gradient in temperature on both sides of the membrane caused a gradient in water vapor pressure. This will lead to water evaporation on the feed side of the membrane. The water vapor passes via the pores of the membrane and condenses on the cold permeate side. Therefore, based on this description, heat, mass, and momentum transfer occur simultaneously in this membrane. To create a 2D flat sheet CFD model for a DCMD in the COMSOL software, we assumed a steady-state condition, 100 % rejection of salt by a non-wetting membrane, and no-slip condition at the surface.
Fig. 2.
The flat sheet membrane placed between the feed salt water and permeated fresh water.
2.1. Feed side domain
To determine the velocity profile of hot saline water on the feed side of the membrane, it is necessary to solve the continuity and Navier-Stokes equations simultaneously in accordance with equations (1), (2)), using the format provided by the Comsol software.
| (1) |
| (2) |
where is liquid density, is the velocity vector in the feed channel, is the pressure, is the fluid dynamic viscosity, and is the body force term. In equations (3), (4), (5), (6)), the boundary conditions of the Navier-Stokes equations in the feed side domain are shown:
| (3) |
| (4) |
| (5) |
| (6) |
Because the salt concentration in water affects the water vapor pressure on the surface of the membrane, it is necessary to calculate the distribution of NaCl concentration on the feed side. Hence, according to equation (7), both convective and diffusive terms in the mass transfer equation are considered for calculating of NaCl concentration in the feed channel.
| (7) |
The boundary conditions needed to solve this mass transfer equation are represented in equations (8), (9), (10), (11)):
| (8) |
| (9) |
| (10) |
| (11) |
which , , and are the diffusion coefficient of the solution, molar concentration, and mass flux of NaCl, respectively.
Also, the heat transfer equation, including conduction and convection, has been used according to equation (12) in the Comsol software.
| (12) |
The boundary conditions for this equation are shown in equations (13), (14), (15), (16)):
| (13) |
| (14) |
| (15) |
| (16) |
where is heat capacity at constant pressure, is the thermal conductivity of feed solution, is the feed saline water temperature on the feed side, is the enthalpy of vaporization of water, effective diffusion coefficient of the membrane and is the molar concentration of water on the membrane surface in the feed side. To calculate the enthalpy of vaporization, a third-order empirical relation according to equation (17) is used [20].
| (17) |
can be calculated according to relation 18
| (18) |
that is the mole fraction of water, is the activity of water in the solution, is the saturated vapor pressure of water, is gas constant, and is the temperature. The is calculated by thermodynamics function in COMSOL software. This function can be calculated by external physical and thermodynamic property calculator software such as Aspen Properties with an open interface standard for chemical process simulation named CAPE-OPEN. In this simulation, the COMSOL is linked to the Aspen Properties software by this interface. Also, the saturated vapor pressure of water is attained by the Antoine equation in equation (19).
| (19) |
2.2. Membrane domain
The transfer phenomena in the membrane are described by mass and heat transfer equations. The conductive heat transfer in the membrane is shown using the relation 20.
| (20) |
The boundary conditions according to equations (21), (22), (23), (24)) have been used to solve this heat transfer equation in the membrane domain
| (21) |
| (22) |
| (23) |
| (24) |
In these equations, is the thermal conductivity of the membrane, is the temperature inside the membrane, is the heat flux required to evaporate water in the feed side, and is the heat flux released from water vapor in the permeate side. To calculate , equation (25) is used
| (25) |
where is the porosity of the membrane. Also; and are the thermal conductivities of the membrane material and the gas within the membrane pores, respectively. In the membrane pores, there is a blend of air and water vapor, which the thermal conductivity of it is determined by equation (26).
| (26) |
In this equation, and are the thermal conductivity of water vapor and air, is the total pressure inside the membrane pore, and is the air pressure in the membrane pore that is achieved by equation (27).
| (27) |
To model the mass transfer of water vapor inside the membrane pores, the mass transfer equation has been presented in equation (28). Also the boundary conditions for this mass transfer equation are developed as equations (29), (30), (31), (32)).
| (28) |
| (29) |
| (30) |
| (31) |
| (32) |
The effective diffusion coefficient inside membrane pores is calculated by the Knudsen and ordinary molecular diffusion mechanisms in equation [15]:
| (33) |
where is the tortuosity of the membrane, is the average pore radius, is the molecular weight of water, and is the molecular diffusion coefficient of water. For water/air, (Pa m2/s) can be calculated from equation (34):
| (34) |
2.3. Permeate side domain
The velocity profile in the permeate side can be determined by continuity and Navier-Stokes equations according to equations (35), (36)):
| (35) |
| (36) |
The boundary conditions for the Navier-Stokes equation are given according to equations (37), (38), 39, (40)).
| (37) |
| (38) |
| 39 |
| (40) |
In this equatins is the velocity vector in the permeate side.
In the following, the heat transfer in the permeate side is presented in equation (41). The boundary conditions for this equation are shown by equations (42), (43), (44), (45)).
| (41) |
| (42) |
| (43) |
| (44) |
| (45) |
In this equations and are the temperature and thermal conductivity of water in the permeate side.
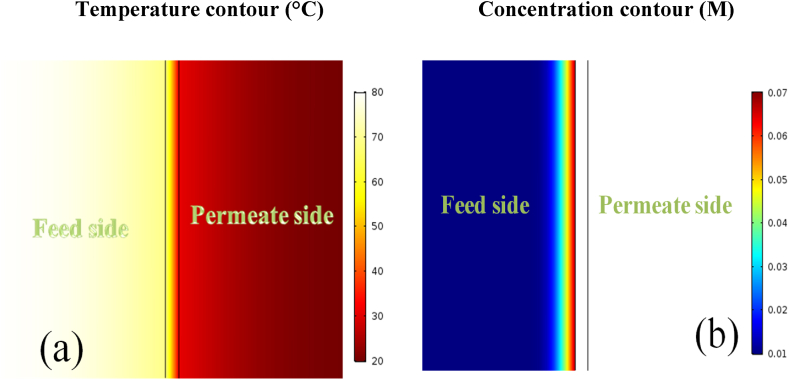
Fig. 3(a) and (b), shows the temperature and NaCl concentration contours for the simulated DCMD. According to these figures, thermal and concentration polarization are evident around the membrane surface, especially on the feed side. In the 2D simulation, because of the possibility of including this polarizations, the accuracy of the results increases compared to the one-dimensional model.
Fig. 3.
(a) Temperature contour and (b) NaCl concentration contour.
2.4. Validation of membrane model
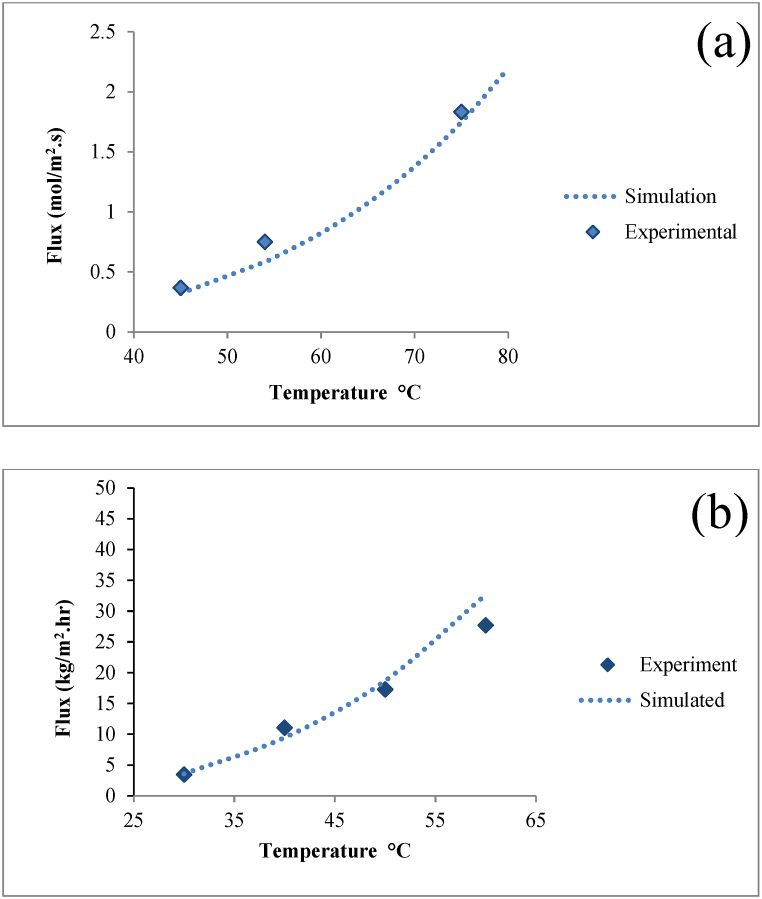
The presented mathematical model for the DCMD was evaluated by comparing the permeated flux calculated by the CFD model with available experimental data for two commercial membranes. In Fig. 4(a), the effect of the temperature of the feed side on the permeate flux for a membrane with the commercial name 3 ME is shown. The experimental data for this membrane can be found in Ref. [21]. In this Fig, the model results are shown along with the experimental data for a NaCl solution at = 20 °C, with a mole fraction of 1.3 %, and feed and permeate flow rates of 63 cm3/s. Additionally, the calculated permeated flux was compared with experimental data for another commercial membrane named PP22, by varying the feed temperature [22]. This comparison was made at = 20 °C, with a mass flow rate of 1.75 m/s, and NaCl concentration at 0.6 g/l, is shown in Fig. 4(b). These results show a compliance between the model and experimental data.
Fig. 4.
Validation of CFD results with the experiential data. (a) membrane 3 ME at =20°C, NaCl solution of 1.3 % mol and flow rate of 63cm3/s. (b) membrane PP22 at=20°C, flow rate of 1.75 m/s and feed salt concentration at 0.6 g/l NaCl.
2.5. Modeling of the membrane module
Considering the use of commercial membrane 3 ME in the process, first, a simulation of a 2D flat sheet membrane has been done in the COMSOL software. The operating parameters and membrane characteristics for this simulation are presented in Table 1.
Table 1.
Membrane characteristics and operating parameters used for CFD model of DCMD.
| Parameter | Values |
|---|---|
| Membrane material | polypropylene (PP) |
| Dimensions of one flat sheet membrane | 0.4 m × 0.5 m. |
| Average pore diameter | 0.73 (μm) |
| Porosity | 85 % |
| Thickness | 79 (μm) |
| Tortuosity | 1.3 |
| Thermal conductivity of (PP)- | 0.17 (W/m.K) |
| Thermal conductivity of air- | 0.02 (W/m.K) |
| Thermal conductivity of vapor- | 0.027 (W/m.K) |
| Feed and permeate channel depth | 3 (mm) |
| Mass flow rate in feed and permeate channels | 2 (kg/s) |
| Temperature in feed channel | 80 (°C) |
| Temperature in permeate channel | 40 (°C) |
| TDS (total dissolved solids) of NaCl | 250000 (ppm) |
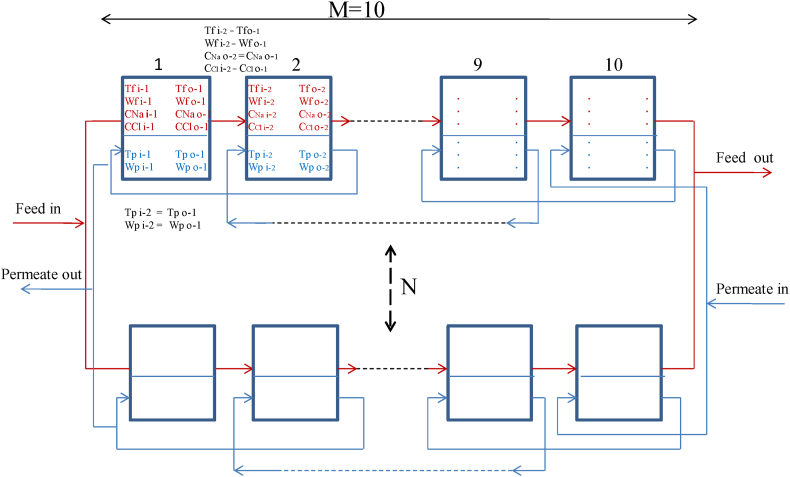
Then, the set of series-parallel membranes with dimensions of N × M (N row and M column) is considered for modeling the membrane module according to Fig. 5.
Fig. 5.
Schematic of series-parallel membranes module.
To model this membrane module, the first 10 membranes were considered in series. In order to reduce the amount of RAM required for the modeling process, the ability to connect COMSOL and MATLAB was considered. After conducting CFD modeling for the first flat sheet membrane in COMSOL, the outlet parameters of the feed for this membrane, such as outlet temperature (), outlet mass flow rate (), outlet concentration of Na+ () and Cl− () were mapped to the corresponding inlet parameters of the feed for the second membrane. These included inlet temperature (), inlet mass flow rate (), inlet concentration of Na+ () and Cl− () respectively in the MATLAB environment. Also; in the penetration side of the first membrane, the outlet temperature () and, the outlet mass flow rate () were mapped to the corresponding inlet's parameters in the second membrane for the inlet temperature () and the inlet mass flow rate () respectively. This process was repeated for the next nine membranes using MATLAB software. The value of N was then determined to ensure that the sum of the low-grade heat required for freshwater production in the DCMD and the high-grade heat required for injected steam production from this freshwater equaled the recovered waste heat in HRSG. The total area of the membrane module was obtained by multiplying N × M by one flat sheet membrane's dimensions. The flux of the membrane module was obtained by multiplying one membrane's flux by N × M. Two output flow rates from the DCMD module were obtained by decreasing the feed stream's flux and adding it to the permeate stream. These two flow rates, along with the NaCl output concentration on the feed side and the temperature of the membrane in the output of the feed and permeate sides, provide the necessary data to utilize in Aspen Plus software. The ability to link COMSOL to MATLAB and Aspen Plus to Microsoft Excel allowed for using CFD results in Aspen Plus software. A schematic of these software's connection is shown in Fig. 6.
Fig. 6.
Link of COMSOL, MATLAB, Microsoft Excel and Aspen plus software's.
3. Proposed process
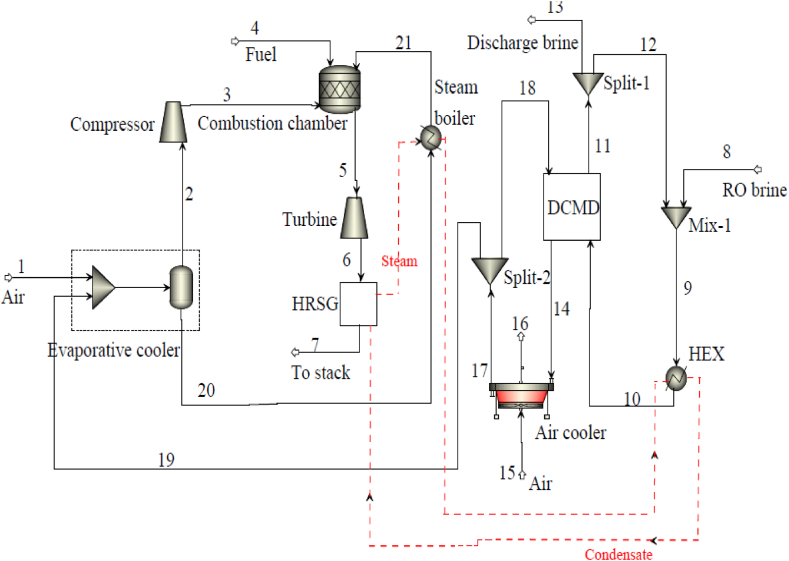
The diagram in Fig. 7 illustrates how a DCMD is connected to a STIG using the Aspen Plus software.
Fig. 7.
Flow diagram of proposed process for connecting a DCMD to a STIG.
According this Figure, the process begins with input air entering a direct evaporative cooler through stream 1. The freshwater produced in DCMD cools this input air to approach the wet-bulb temperature. The temperature of the air coming out of the evaporative cooler will theoretically be slightly higher than the wet-bulb temperature due to two reasons. Firstly, because the temperature of the input water is slightly higher than the temperature of input air, and secondly, due to the assumption of a 3 °C approach temperature in the evaporative cooler. The cooled air then goes into the compressor through stream 2 to increase its pressure. Then, the compressed air passes through a combustion chamber through stream 3 along with the fuel through stream 4. As the fuel burns, the temperature of the compressed air rises, and air with high pressure and temperature enters the turbine by stream 5. Some of the mechanical work generated in the turbine powers the compressor, while the remaining energy is used for the production of electrical energy in the generator. Then the turbine's exhaust gases are recovered for waste heat in the HRSG. The HRSG is used in a closed steam cycle to provide both the high-grade heat necessary for injected steam from the generated fresh water and the low-grade heat required for the production of this freshwater in the DCMD. This closed steam cycle is shown by the red dashed line in the process. After heat recovery, the exhaust gases leave the stack through stream 7 at around 150 °C.
The process of desalination through the membrane begins by introducing the RO brine through stream 8 into the warm saline water cycle on the feed side of the DCMD module. The stream is then heated in a heat exchanger (HEX) through stream 9 to reach a temperature of approximately 80 °C before entering the membrane module. The necessary thermal energy is transferred from the closed steam cycle to the HEX. The hot saline water then enters to feed side of the membrane module through stream 10 after leaving the HEX. After losing some water vapor on the surface of the membrane and passing across the pores to the other side, the feed stream finally exits the membrane module through stream 11. To avoid salt build-up in the feed cycle of the membrane, the more concentrated brine is expelled through stream 13, so that the mass balance of its salt with stream 8 is maintained. Following the removal of excess salt, the saline water cycle on the feed side continues through stream 12.
There is a cycle of cold, fresh water on the other side of the membrane. The freshwater exits the membrane module through stream 14 after condensing the vapor that passes across the pores of the membrane. The exited fresh water is then cooled in a forced air cooler to remove the heat absorbed during vapor condensation. This water with an approximate temperature of 48 °C is entered into the air cooler, and the ambient air with a temperature of 40 °C is used to cool it. If the air comes out at a temperature of 42 °C and assuming a ΔT approach of 1 °C, the cold fresh water exits the air cooler through stream 17 at a temperature of 43 °C. To maintain a balance in the freshwater cycle, fresh water equivalent to the mass of condensed steam exits through stream 19 while the remaining fresh water returns to the membrane module through stream 18. This excess fresh water is then used to chill the input air in the direct evaporative cooler. After exiting the air cooler, the water passes through a steam boiler and is heated by stream 20 to produce injected steam. The required thermal energy for this process is provided by the closed steam cycle. It's important to note that if there are suspended particles in the water entering the boiler, a water filter at the boiler entrance is necessary. However, in this simulation, the installation of the filter has been omitted because the presence of any suspended particles has not been assumed in the water entering the boiler. Finally, the superheated steam produced in the steam boiler is injected into the combustion chamber through stream 21 to increase the output power of the turbine.
4. Analysis of the simulated process
For the described process the simulation is done based on the process operating conditions presented in Table 2. In this simulation, the Peng Robinson equation is used as the property method for the STIG. Also, the electrolyte NRTL has been employed as the property method for the DCMD in Aspen Plus software, assuming the presence of NaCl solution.
Table 2.
Process operating conditions.
| Parameter | Values |
|---|---|
| Ambient Temperature | 40 °C |
| Relative humidity | 40 % |
| Mass flow rate of air | 118 kg/s |
| Isentropic efficiency of compressor | 0.9 |
| Pressure ratio of compressor | [5, 10, 15, 20, 25,30] |
| Isentropic efficiency of turbine | 0.92 |
| Turbine inlet temperature | 943 °C |
| Temperature of feed side of membrane | 80 °C |
| Temperature of permeate side of membrane | 43 °C |
| TDS of RO brine | 80000 |
| TDS of discharge brine | 250000 |
| Stack inlet temperature | 150 °C |
| Heat exchanger pinch temperature | 10 °C &50 °C for HRSG |
| Heat exchanger efficiency | 0.9& 0.8 for HRSG |
| Pressure of steam injected in STIG cycle | 5 bar higher than the combustor pressure |
| Fuel | methane |
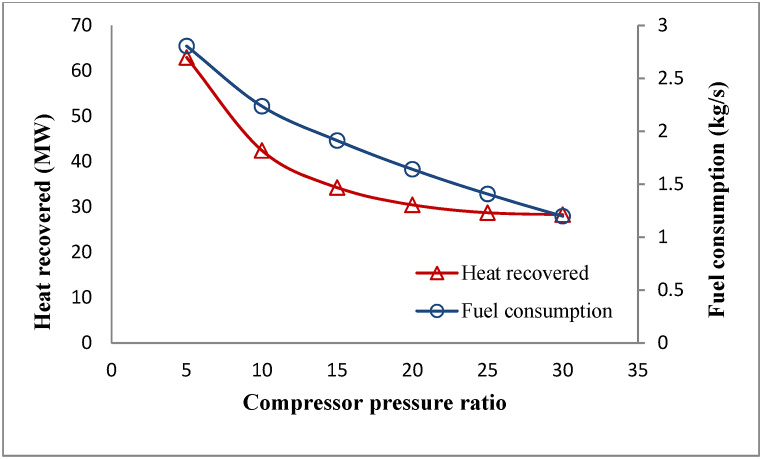
The computer simulation for this process is done for compressor pressure ratios ranging from [5 to 30], as indicated in Table 2. Assuming a constant turbine inlet temperature, with raising the compressor pressure ratio, fuel consumed decreases to maintain the constant turbine inlet temperature. Reducing fuel consumption reduces heat that can be recycled in the HRSG, shown in Fig. 8.
Fig. 8.
Changes in fuel consumption and waste heat recovered by changing compressor pressure ratio.
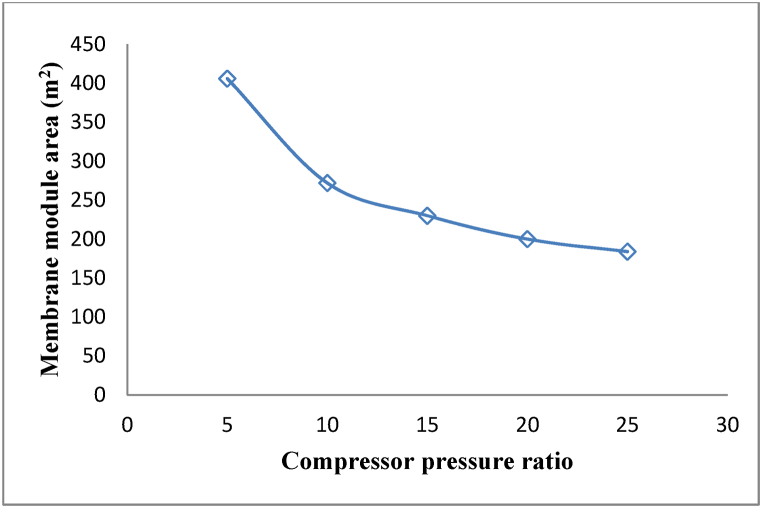
The required area of the membrane module is commensurate with the amount of waste heat recovered for heating the brine. Therefore, as shown in Fig. 9, the used membrane area decreases by increasing the compressor pressure ratio, similar to the reduced waste heat recovered with an increasing compressor pressure ratio in Fig. 8
Fig. 9.
Changes in the area of the membrane module by the changing compressor pressure ratio.
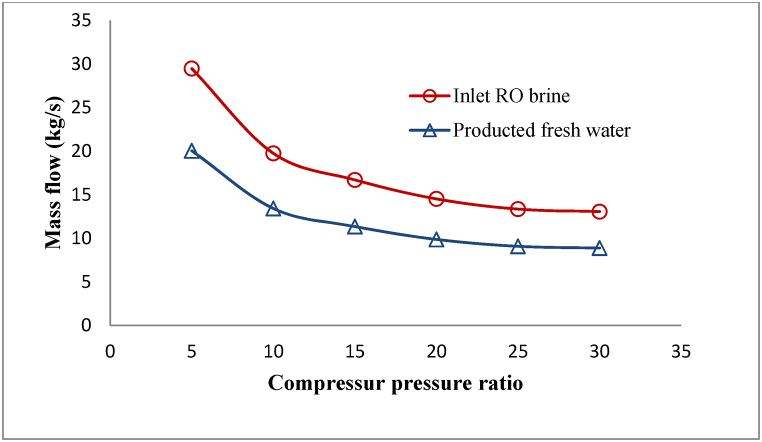
Reducing the area of the used membrane by increasing the pressure ratio of the compressor will also decrease the quantity of RO salt water entering the membrane module, which will result in a decrease in freshwater, produced in the membrane. These changes are shown in Fig. 10.
Fig. 10.
Changes in inlet RO brine and produced fresh water by changing compressor pressure ratio.
In the following, the results of net output power and thermal efficiency are compared with a simple gas turbine to show the effect of connecting the DCMD to the gas turbine. This comparison has been made with the assumption of using this process in hot in hot and arid regions. In these areas, the simple cycle gas turbine is usually used to generate electric power. Also; due to the high demand for freshwater, the employment of steam turbines and the combined cycle have been limited in these areas.
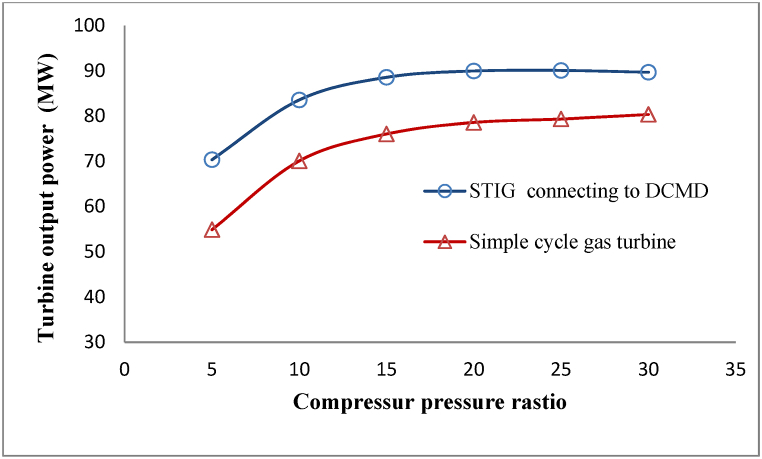
The influence of rising steam injection in increasing turbine output power is shown by comparison with a simple gas turbine in Fig. 11. The difference in output power observed with a simple cycle gas turbine is due to the exergy of the steam injected into the turbine. On the other hand, as shown in Fig. 10, raising the compressor pressure ratio decreases the flow of freshwater which is employed to generate injected steam into the turbine. However, the pressure of the combustion chamber and thus the pressure of the injected steam to it must be increased according to the increase in pressure ratio of the compressor. This increased pressure of injected steam somewhat prevents the reduction of the output power difference of this process compared with a simple gas turbine in the higher compressor pressure ratios.
Fig. 11.
Comparison of turbine output power in the proposed process with a simple cycle gas turbine.
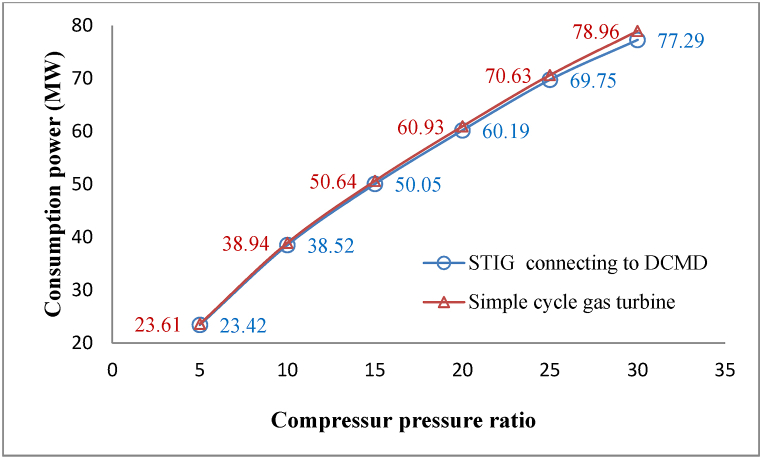
The influence of evaporative cooling on consumption power in the compressor is shown in Fig. 12. In this process, the incoming fresh water from the DCMD unit is employed to chill the incoming air. The temperature of this water is 3 °C higher than the input air. Therefore, the cooling of the air here occurs only because of the latent heat required for the surface evaporation of the water to saturated humidity, and the sensible heat of the water cannot contribute to the cooling of the air.
Fig. 12.
Comparison of compressor consumption power in the proposed process and a simple cycle gas turbine.
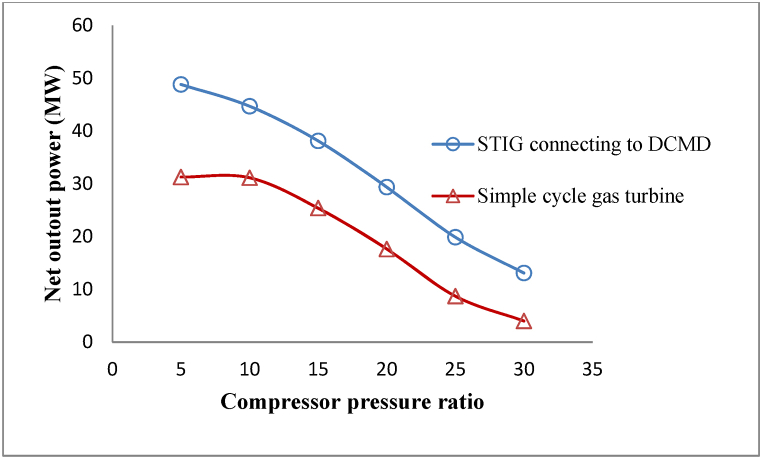
Fig. 13 also indicated the net output power changes in different pressure ratios and their comparison with a simple gas turbine. As the pressure ratio increases, the net output power of the process decreases, as shown in this figure. This occurs because the compressor's power consumption increases more than the turbine's output power with the rise in pressure ratio. This can be inferred by considering the slope of the graphs in Fig. 11, Fig. 12. On the other hand, the net output power rising compared to a simple gas turbine with changes in the compressor pressure ratio in the range between [5 to 30] has been quantitatively calculated in the range between [9 to 17.2] MW. So the greatest increase in net output power occurred at lower pressure ratios. This can be explained by considering that at lower pressure ratios, it is possible to produce more fresh water and inject more steam into the turbine due to more waste heat recovery.
Fig. 13.
Comparison of net output power in the proposed process and a simple cycle gas turbine.
Equation (46) can be utilized to calculate the thermal efficiency of the process indicated by .
| (46) |
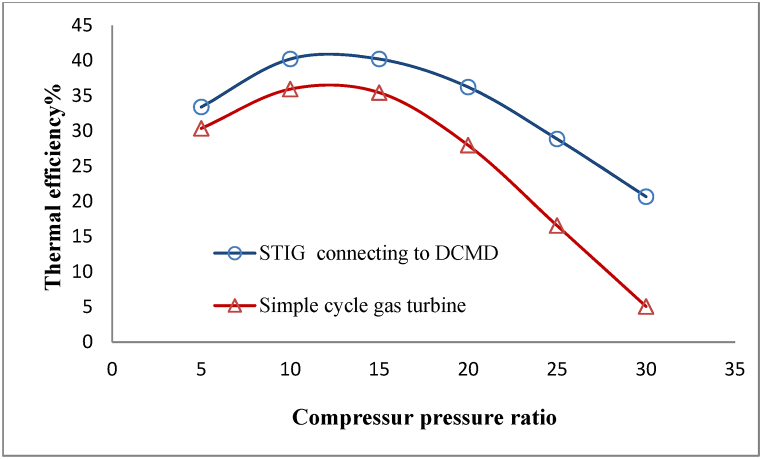
In this equation, is the net output power, is the lower heating value of methane, and is the fuel mass flow rate. Typically, a gas turbine's thermal efficiency increases as the compressor pressure ratio rises. However, this increase in efficiency has a limit and is unable to exceed the efficiency of the Carnot cycle. Therefore, the thermal efficiency of a gas turbine will always have a maximum point against the compressor pressure ratio [23]. In Fig. 14, the thermal efficiency of the proposed process is compared to that of a simple cycle gas turbine in various compressor pressure ratios. The process's thermal efficiency has a maximum value at a compressor pressure ratio of approximately 12. The simulations performed have shown that, within the range of compressor pressure from [5 to 30], the proposed process has the more thermal efficiency than a simple gas turbine, with an increase ranging from [3.3 to 15.6] %. The most significant difference in thermal efficiency occurs at high-pressure ratios, where a sudden increase in the required power by the compressor in a simple gas turbine leads to a sharp decrease in thermal efficiency. However, using a DCMD in connection with a STIG, and recovering waste heat to generate injected steam to the turbine, has partially prevented the severe decrease in thermal efficiency at high-pressure ratios.
Fig. 14.
Comparison of thermal efficiency in the proposed process and a simple cycle gas turbine.
The simulation of the proposed process was conducted at a pressure ratio of 12 to analyze its exergy. The results are given in Table 3, which includes the temperature, mass flow pressure, enthalpy, and exergy of each stream. The calculation of these streams' exergy has been done by Aspen software according to Equation (47).
| (47) |
In this equation, is the exergy per unit mass of stream, is the enthalpy per unit mass, is entropy per unit mass, is pressure, and is temperature, while and indicate pressure and temperature in ambient conditions [24]. Aspen Plus software uses libraries of chemical entropy and enthalpy to use this equation to compute the entropy and enthalpy of each stream [25]. In the following, the exergy destruction of each element in the process can be calculated using equation (48).
| (48) |
In this equation, is the exergy destruction of the component, is the sum of the exergy of input streams to the element, is the sum of the output streams exergy for each element, mechanical work done by the element, heat transferred from the element, temperature of element, and the environmental temperature.
Table 3.
Results of the simulation.
| Stream | From | To | Temperature (°C) | Pressure (bar) | Flow rate (kg/s) | Enthalpy flow rate (kj/s) | Exergy flow rate (kj/s) |
|---|---|---|---|---|---|---|---|
| 1 | Air | Evaporative cooler | 40 | 1 | 118 | −33387.5 | 0 |
| 2 | Evaporative cooler | Compressor | 33.54 | 1 | 118.753 | −43945.6 | −135.34 |
| 3 | Compressor | Combustion chamber | 377 | 12 | 118.753 | −571.78 | 40797.96 |
| 4 | Fuel | Combustion chamber | 30 | 20 | 2.074 | −9710.47 | 108058.6 |
| 5 | Combustion chamber | Turbine | 943 | 12 | 131.92 | −156328 | 114098.2 |
| 6 | Turbine | HRSG | 449.3 | 1 | 131.92 | −241776 | 24752.39 |
| 7 | HRSG | Stack | 150 | 1 | 131.92 | −289044 | 3510.34 |
| 8 | RO brine | Mix-1 | 30 | 1 | 17.42 | −263947 | 9.817 |
| 9 | Mix-1 | HEX | 71.2 | 1 | 240 | −3243276 | 1037.60 |
| 10 | HEX | DCMD | 80 | 1 | 240 | −3236539 | 1733.92 |
| 11 | DCMD | Spli-1 | 75.02 | 1 | 228.15 | −3053979 | 1232.28 |
| 12 | Spli-1 | Mix-1 | 75.02 | 1 | 228.15 | −2979328 | 1202.16 |
| 13 | Spli-1 | Discharge brine | 75.02 | 1 | 5.58 | −74650.79 | 30.12 |
| 14 | DCMD | Air cooler | 47.84 | 1 | 251.85 | −3974301 | 94.94 |
| 15 | Air | Air cooler | 40 | 1 | 2000 | −565799 | 0 |
| 16 | Air cooler | Air | 42 | 1 | 2000 | −560024 | 25.53 |
| 17 | Air cooler | Spli-2 | 43 | 1 | 251.85 | −3979397 | 11.96 |
| 18 | Spli-2 | DCMD | 43 | 1 | 240 | −3792147 | 11.39 |
| 19 | Spli-2 | Evaporative cooler | 43 | 1 | 11.85 | −187249.4 | 0.563 |
| 20 | Evaporative cooler | Steam boiler | 30.66 | 1 | 11.12 | −176320 | 7.206 |
| 21 | Steam boiler | Combustion chamber | 204.37 | 17 | 11.12 | −146045 | 9173.45 |
By evaluating the exergy of each stream for the main elements of the process, it is possible to calculate the exergy destruction in terms of the percentage of exergy of the fuel. It is noted that the fuel exergy is brought from the sum of the physical exergy obtained by the software, and the chemical exergy calculated by relation 49.
| (49) |
In this relation, is the specific chemical exergy of the fuel and is estimated by equation (49). This approximation equation is employed to estimate the specific chemical exergy of hydrocarbon known as [26].
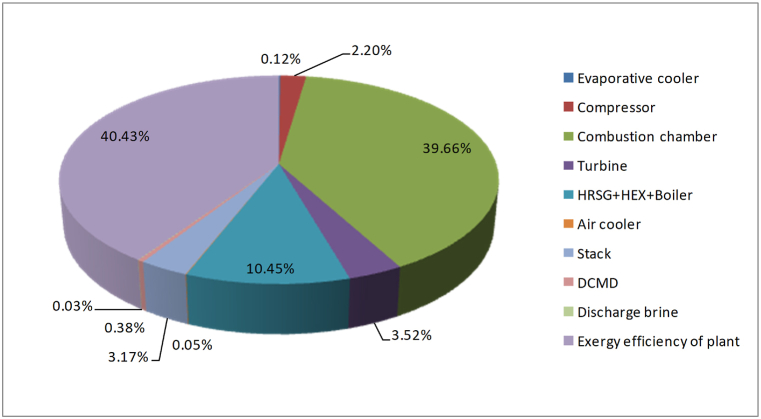
Fig. 15 indicates the pie diagram of the exergy destruction of main plant components and the exergy efficiency of the plant which is defined as a percent of input fuel exergy. According to this diagram, more than 40 % of fuel exergy that inputs the process is converted to mechanical work. Also, the DCMD has a negligible part in exergy destruction. While the largest part of exergy destruction has occurred in the combustion chamber, which is because of the irreversibility and great temperature difference of the combustion reaction with the environment.
Fig. 15.
Pie diagram of exergy destruction in plant components and exergy efficiency of the plant expressed as a percent of input fuel exergy.
5. Conclusions
This study proposes the use of an unconventional water source with high salinity, to enhance the thermal efficiency and out power of gas turbines in hot and arid regions. The method involves connecting a DCMD module to a STIG. Unlike conventional thermal desalination methods used for seawater desalination, membrane distillation can desalinate waters with higher salinity. Thus, in this process, it is possible to utilize non-consecutive water sources such as RO brine in inland regions for humid gas turbine technology. This matter reduces the consumption of fresh water for electricity production and environmental problems related to the disposal of the Ro brine in these areas. The study here only connected DCMD to STIG, but future studies can consider connecting other configurations of membrane distillation to various configurations of humidified gas turbines. The simulations in this study were performed only for the commercial 3 ME membrane, but different membranes have different fluxes depending on their physical properties. Suitable membranes should be selected only after experimental study, computer simulation, and economic analysis, which should be done in future studies.
Data availability statement
Data will be made available on request.
CRediT authorship contribution statement
Alireza Peymani: Conceptualization, Investigation, Methodology, Software, Validation, Writing – original draft, Writing – review & editing. Jafar Sadeghi: Supervision. Farhad Shahraki: Validation. Abdolreza Samimi: Validation.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors thank the financial support of the Research Council of the University of Sistan and Baluchestan.
Contributor Information
Alireza Peymani, Email: alirezapeymani@pgs.usb.ac.ir.
Jafar Sadeghi, Email: sadeghi@eng.usb.ac.ir.
Farhad Shahraki, Email: fshahraki@eng.usb.ac.ir.
Abdolreza Samimi, Email: a.samimi@eng.usb.ac.ir.
Nomenclature
Abbreviations
- AGMD
air gap membrane distillation
activity
- CFD
computational fluid dynamics
molar concentration(mol/m3), heat capacity(J/k)
diffusion coefficient(m2/s)
- DCMD
direct contact membrane distillation
- EvGT
evaporative gas turbine
exergy per unit mass of stream
body force(N/m3)
enthalpy(J/mol)
- HGT
humidified gas turbine
- HRSG
heat recovery steam generation
thermal conductivity(W/m.k)
lower heating Value(MJ)
molecular weight
mass flow rate(kg/s)
- MD
membrane distillation
- MED
multi-effect distillation
- MED-TVC
multi effect distillation thermal vapor compression
mass flux(mol/m2.s)
- MSF
multiple-stag flash
pressure(pa)
heat flow rate(kj/s)
heat flux(J/s.m2)
gas constant(J/mol.k)
pore radius(m)
- RO
reverse osmosis
- SGMD
sweeping gas membrane distillation
- STIG
Steam-injected gas turbine
temperature(k)
- TDS
total dissolved solid
Velocity(m/s)
- VMD
vacuum membrane distillation
output work (MJ)
x-coordinates axis, mole fraction
y-coordinates axis
Greek symbols
porosity
thermal efficiency
viscosity(pa.s)
density(kg/m3)
tortuosity
specific chemical exergy of the fuel
Subscripts
locations inside the membrane
air
atmosphere
effective
element
feed, fuel
gas
- in
membrane
sodium chloride
- net
net
- out
output
pressure, permeate
solid
saturated
solution
thermal
vapor
Water
References
- 1.Sanders K.T. Critical review: uncharted waters? The future of the electricity-water nexus. Environ. Sci. Technol. 2015;49:51–66. doi: 10.1021/es504293b. [DOI] [PubMed] [Google Scholar]
- 2.Deabes E.A.M. The impact of thermal power stations on coastline and benthic fauna: case study of El-Burullus power plant in Egypt. Results Eng. 2020;7 doi: 10.1016/j.rineng.2020.100128. [DOI] [Google Scholar]
- 3.dos Santos A.P.P., Andrade C.R., Zaparoli E.L. Comparison of different gas turbine inlet air cooling methods. World Acad. Sci. Eng. Technol. 2012;61:40–45. [Google Scholar]
- 4.Al-Ibrahim A.M., Varnham A. A review of inlet air-cooling technologies for enhancing the performance of combustion turbines in Saudi Arabia. Appl. Therm. Eng. 2010;30:1879–1888. doi: 10.1016/j.applthermaleng.2010.04.025. [DOI] [Google Scholar]
- 5.Meher-Homji C.B., Mee T.R., III . Turbo Expo Power Land, Sea, Air. American Society of Mechanical Engineers; 2000. Inlet fogging of gas turbine engines: Part B—practical considerations, control, and O&M aspects. [DOI] [Google Scholar]
- 6.Dawoud B., Zurigat Y.H., Bortmany J. Thermodynamic assessment of power requirements and impact of different gas-turbine inlet air cooling techniques at two different locations in Oman. Appl. Therm. Eng. 2005;25:1579–1598. doi: 10.1016/j.applthermaleng.2004.11.007. [DOI] [Google Scholar]
- 7.Deng C., Al-Sammarraie A.T., Ibrahim T.K., Kosari E., Basrawi F., Ismail F.B., Abdalla A.N. Air cooling techniques and corresponding impacts on combined cycle power plant (CCPP) performance: a review. Int. J. Refrig. 2020;120:161–177. doi: 10.1016/j.ijrefrig.2020.08.008. [DOI] [Google Scholar]
- 8.Jonsson M., Yan J. Humidified gas turbines—a review of proposed and implemented cycles. Energy. 2005;30:1013–1078. doi: 10.1016/j.energy.2004.08.005. [DOI] [Google Scholar]
- 9.De Paepe M., Dick E. Technological and economical analysis of water recovery in steam injected gas turbines. Appl. Therm. Eng. 2001;21:135–156. doi: 10.1016/S1359-4311(00)00029-6. [DOI] [Google Scholar]
- 10.Wang Y., Lior N. Performance analysis of combined humidified gas turbine power generation and multi-effect thermal vapor compression desalination systems—Part 1: the desalination unit and its combination with a steam-injected gas turbine power system. Desalination. 2006;196:84–104. doi: 10.1016/j.desal.2006.01.010. [DOI] [Google Scholar]
- 11.Wang Y., Lior N. Performance analysis of combined humidified gas turbine power generation and multi-effect thermal vapor compression desalination systems: Part 2: the evaporative gas turbine based system and some discussions. Desalination. 2007;207:243–256. [Google Scholar]
- 12.Shah K.M., Billinge I.H., Chen X., Fan H., Huang Y., Winton R.K., Yip N.Y. Drivers, challenges, and emerging technologies for desalination of high-salinity brines: a critical review. Desalination. 2022;538 doi: 10.1016/j.desal.2022.115827. [DOI] [Google Scholar]
- 13.Ketharani J., Hansima M., Indika S., Samarajeewa D.R., Makehelwala M., Jinadasa K., Weragoda S.K., Rathnayake R., Nanayakkara K.G.N., Wei Y. A comparative study of community reverse osmosis and nanofiltration systems for total hardness removal in groundwater. Groundw. Sustain. Dev. 2022;18 doi: 10.1016/j.gsd.2022.100800. [DOI] [Google Scholar]
- 14.Gabelich C.J., Xu P., Cohen Y. Concentrate treatment for inland desalting. Sustain. Sci. Eng. 2010;2:295–326. doi: 10.1016/S1871-2711(09)00210-4. [DOI] [Google Scholar]
- 15.Souhaimi M.K., Khayet M., Matsuura T. 2011. Membrane Distillation: Principles and Applications. [Google Scholar]
- 16.He K., Hwang H.J., Woo M.W., Moon I.S. Production of drinking water from saline water by direct contact membrane distillation (DCMD) J. Ind. Eng. Chem. 2011;17:41–48. doi: 10.1016/j.jiec.2010.10.007. [DOI] [Google Scholar]
- 17.Guan G., Yang X., Wang R., Fane A.G. Evaluation of heat utilization in membrane distillation desalination system integrated with heat recovery. Desalination. 2015;366:80–93. doi: 10.1016/j.desal.2015.01.013. [DOI] [Google Scholar]
- 18.Lokare O.R., Tavakkoli S., Rodriguez G., Khanna V., Vidic R.D. Integrating membrane distillation with waste heat from natural gas compressor stations for produced water treatment in Pennsylvania. Desalination. 2017;413:144–153. doi: 10.1016/j.desal.2017.03.022. [DOI] [Google Scholar]
- 19.Zuo G., Wang R., Field R., Fane A.G. Energy efficiency evaluation and economic analyses of direct contact membrane distillation system using Aspen Plus. Desalination. 2011;283:237–244. doi: 10.1016/j.desal.2011.04.048. [DOI] [Google Scholar]
- 20.Yau M.K., Rogers R.R. Elsevier Science; 1996. A Short Course in Cloud Physics. [Google Scholar]
- 21.Lawson K.W., Lloyd D.R. Membrane distillation. II. Direct contact MD. J. Memb. Sci. 1996;120:123–133. doi: 10.1016/0376-7388(96)00141-X. [DOI] [Google Scholar]
- 22.Cath T.Y., Adams V.D., Childress A.E. Experimental study of desalination using direct contact membrane distillation: a new approach to flux enhancement. J. Memb. Sci. 2004;228:5–16. doi: 10.1016/j.memsci.2003.09.006. [DOI] [Google Scholar]
- 23.Jansohn P. 2013. Modern Gas Turbine Systems: High Efficiency, Low Emission, Fuel Flexible Power Generation. [Google Scholar]
- 24.Querol E., Gonzalez-Regueral B., Perez-Benedito J.L. Springer; 2013. Practical Approach to Exergy and Thermoeconomic Analyses of Industrial Processes. [DOI] [Google Scholar]
- 25.Gray T. An introduction to exergy and its evaluation using Aspen Plus. J. Chem. Inf. Model. 2019;53:1689–1699. http://hdl.handle.net/2097/40025 [Google Scholar]
- 26.Moran M.J., Shapiro H.N., Boettner D.D., Bailey M.B. John Wiley & Sons; 2010. Fundamentals of Engineering Thermodynamics. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.