SuSiE PCA: A scalable Bayesian variable selection technique for principal component analysis

Summary

Latent factor models, like principal component analysis (PCA), provide a statistical framework to infer low-rank representation in various biological contexts. However, feature selection is challenging when this low-rank structure manifests from a sparse subspace. We introduce SuSiE PCA, a scalable sparse latent factor approach that evaluates uncertainty in contributing variables through posterior inclusion probabilities. We validate our model in extensive simulations and demonstrate that SuSiE PCA outperforms other approaches in signal detection and model robustness. We apply SuSiE PCA to multi-tissue expression quantitative trait loci (eQTLs) data from GTEx v8 and identify tissue-specific factors and their contributing eGenes. We further investigate its performance on the large-scale perturbation data and find that SuSiE PCA identifies modules with a higher enrichment of ribosome-related genes than sparse PCA (false discovery rate [FDR] $=9.2\times {10}^{-82}$ vs. $1.4\times {10}^{-33}$), while being $\sim$ 18x faster. Overall, SuSiE PCA provides an efficient tool to identify relevant features in high-dimensional biological data.

Graphical abstract

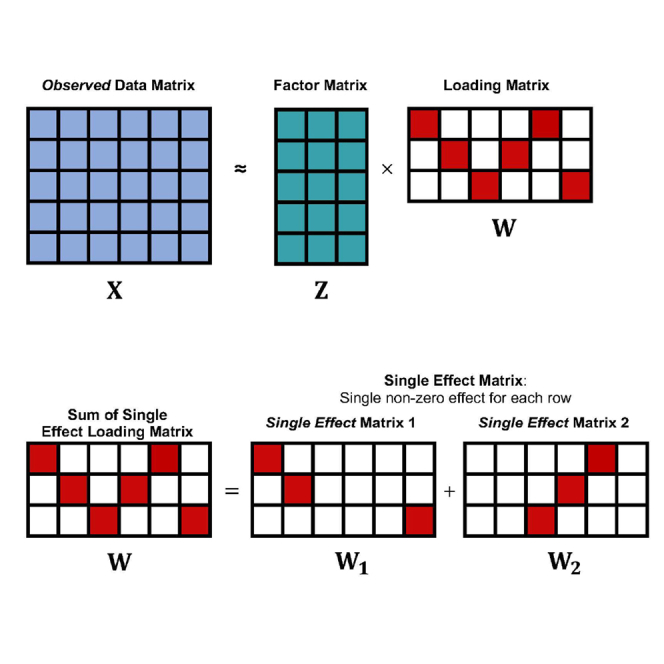
Highlights

• •Efficient PCA feature selection via posterior inclusion probabilities
• •Learned model prior enhances inferential robustness
• •Seamless CPU/GPU/TPU implementation enables efficient inference

Biocomputational method; Classification of bioinformatical subject; Data processing in systems biology; Algorithms

Introduction

Principal component analysis (PCA) is a popular dimension reduction technique¹ that has been widely applied for exploratory data analysis in many fields. One notable functionality of PCA is to synthesize crucial information across features into a small number of principal components (PCs). For example, PCA is commonly used to infer population structure from large-scale genetic data.^2,3 The top PCs explain differences in genetic variation arising from different geographic origins and ancestry of individuals, due to historical migration, admixture, etc.⁴ Moreover, PCA provides a means to rank contributing relevant variables for each latent component, as Tipping and Bishop (1986) proposed the probabilistic reformulation of principal component analysis (PPCA).⁵ Specifically, each PC is independent of other PCs and has its unique weights to represent the “importance” of original features, suggesting different latent components arise from different combinations of variables, or distinct aspects of information from the data.

However, one disadvantage of conventional PCA is that PCs provide limited interpretability, as each results from a linear combination of variables in the data.⁶ To improve the interpretability of PCs, while providing an identifiable solution in high-dimensional data, a common approach is to impose sparsity on the PCA loadings. Broadly speaking, there are two types of approaches to achieving sparsity on the loading matrix. The first is the regularization methods such as sparse PCA,⁶ which rewrites the PCA as a regression-based optimization problem and then includes a $L_1$ penalty on the objective function to achieve sparse loadings. The second type of method is the Bayesian treatment of PPCA, which imposes sparsity-induced prior on the factor loading matrix.^{7,8,9,10,11,12} Despite various methods that focus on inducing sparse solutions for PCA, few provide a statistically rigorous way to select variables relevant to each factor in a post hoc manner. Although several sparse models are capable of shrinking the loadings of uninformative variables to zero, for those variables with non-zero weights, neither a reasonable threshold nor a formal statistical test is provided to inform feature prioritization for validation or follow-up.

Here, we propose SuSiE PCA, a highly scalable Bayesian framework for sparse PCA, that quantifies the uncertainty of contributing features for each latent component. Specifically, SuSiE PCA leverages the recent “sum of single effects” (SuSiE) approach¹³ to model a loading matrix such that each latent factor contains at most L contributing features. Latent factors and sparse loading weights are learned through an efficient variational algorithm. In addition to providing a sparse loading matrix, SuSiE PCA computes posterior inclusion probabilities (PIPs) for each feature, which enables defining $\rho -$ level credible sets for feature selection. We demonstrate through extensive simulations that SuSiE PCA outperforms sparse PCA⁶ and empirical Bayes matrix factorization (EBMF)¹² in identifying relevant features contributing to structured data while being robust to data-generating assumptions. Next, we apply SuSiE PCA to multi-tissue expression quantitative trait loci (eQTLs) data from the the genotype-tissue expression (GTEx) v8^12,14 study to identify tissue-specific components of regulatory genetic features and contributing eGenes (genes that have an associated eQTL). We also apply SuSiE PCA to high-dimensional perturb-seq data (CRISPR-based screens with single-cell RNA-sequencing readouts)¹⁵ and identify gene sets more enriched in the ribosome and coronavirus disease pathways when compared with sparse PCA (false discovery rate (FDR) $=9.2\times {10}^{-82}$, 63 genes involved vs. $1.4\times {10}^{-33}$, 35 genes involved) while requiring 17.8 times less computing time. Overall, we find that SuSiE PCA provides an efficient approach to compute interpretable latent factors from high-dimensional biological data. We provide an open-source python implementation that can run seamlessly on central processing unit (CPU), graphics processing unit (GPU), or tensor processing unit (TPU) available at http://www.github.com/mancusolab/susiepca.

Results

PIPs from SuSiE PCA outperform existing approaches for PCA feature selection

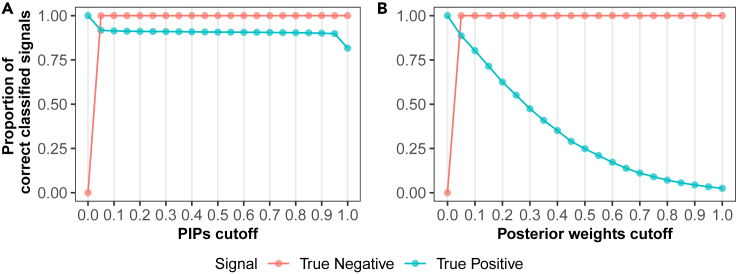
To evaluate the performance of SuSiE PCA, we performed extensive simulations (see details in STAR Methods). Briefly, we performed 100 simulations by varying model parameters one at a time and performed inference using SuSiE PCA with the true number of latent variables (K) and effects (L) known. First, we evaluated the ability of inferred PIPs to discriminate between relevant and non-relevant features for latent factors. Specifically, we compared the sensitivity and specificity of inferred PIPs to normalized posterior mean weights from SuSiE PCA (see Figure 1). When selecting variables based on $\text{PIPs}>0.90$, SuSiE PCA identifies 88.9% of true positive (non-zero) signals, demonstrating largely calibrated posterior inference. We observed nearly all true negative signals exhibited $\text{PIPs}<0.05$. As a comparison, the normalized posterior weights performed well on excluding the true negative signals but failed to capture true positive signals as rapidly as PIP thresholds. Overall, the simulation demonstrates that PIPs provide an intuitive and more efficient indicator for feature selection than normalized posterior weights in SuSiE PCA. In addition, we also examined the sensitivity and specificity using weights estimated from sparse PCA and EBMF (see Figure S1), which have similar trends to the curves in Figure 1B and can only capture a small proportion of the true positive signals as the cutoff threshold increases.

Figure 1.

PIPs exhibit a higher efficiency in selecting the true signals than the posterior weights in SuSiE PCA

The proportion of correct classified signals using PIPs as cutoff (A) or posterior weights as cutoff (B). The green dots represent sensitivity, i.e., $\mathrm{Pr}\left(\text{PIPs}\ge \text{cutoff}|\text{True}\text{positive}\text{signal}\right)$, and the red dots represent specificity, i.e., $\mathrm{Pr}\left(\text{PIPs}<\text{cutoff}|\text{True}\text{false}\text{signal}\right)$. For consistency and to ensure comparability between PIPs and weights, the weights are normalized to be ranged from 0 to 1.

SuSiE PCA is robust to model mis-specification

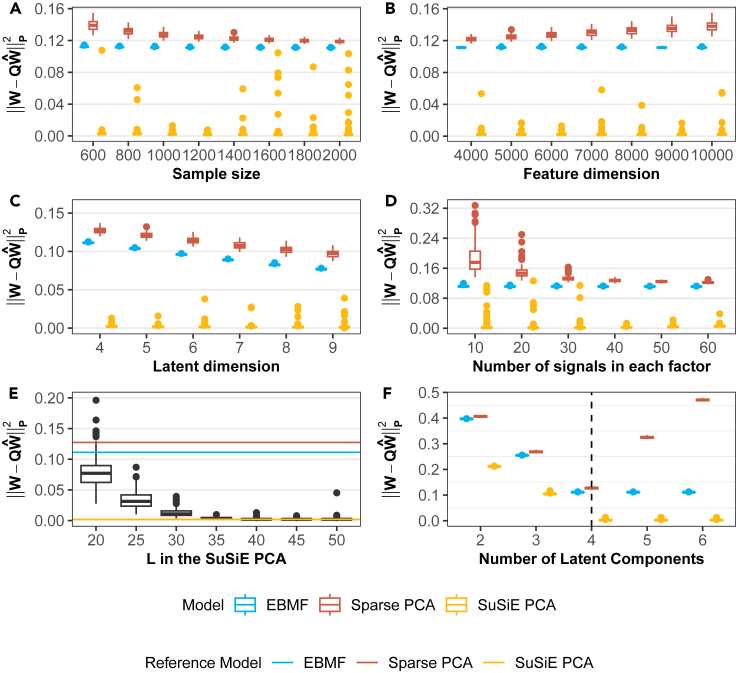
Next, we examined the estimation accuracy of the loading matrix as a function of sample size (N), feature dimension (P), latent dimension (K), and the number of single effects (or sparsity level) (L), via the Procrustes errors¹⁶ (the Frobenius norm after Procrustes transformation,¹⁷ see STAR Methods) (Figures 2A–2D). We found that SuSiE PCA has the smallest Procrustes errors across all simulation settings compared to sparse PCA and EBMF. And we noticed that the Bayesian methods including SuSiE PCA and EBMF maintain a low error even with a small sample size or high feature dimension. Moreover, we found that SuSiE PCA has the lowest relative root mean squared error (RRMSE) across all simulations compared with other methods (Figure S2); and EBMF and SuSiE PCA have a lower level of Procrustes error of factor $\mathbf{Z}$ than sparse PCA (Figure S3). In summary, SuSiE PCA exhibits the highest estimation accuracy, which is consistent with its superior performance in variable selection.

Figure 2.

SuSiE PCA outperforms sparse PCA and EBMF in estimation accuracy and model robustness

SuSiE PCA generates the smallest Procrustes error in weight matrix than sparse PCA and EBMF (A–D) and is robust to over-specified K and L (E and F). For each scenario in (A–D) we vary one of the parameters at a time to generate the simulation data while fixing the other three parameters, and then input the true parameters ( $N,P,K,L$) into models. Finally, we compute the Procrustes error and plot them as a function of $N,P,K,L$. For (E and F), we use the same simulation setting in Figure 1 to generate data but vary the specified L in SuSiE PCA (E) and K in all three models (F). Reference lines refer to the error from the models with correctly specified parameters (i.e., $L=40,K=4$).

We next investigated model robustness under model mis-specification. Similar to other latent factor models, SuSiE PCA could be mis-specified as it requires manually inputting the latent dimension K and the number of single effects L. Considering the potential model mis-specification setting, the simulation datasets are generated based on $K=4,L=40$ and then input into SuSiE PCA, sparse PCA, and EBMF with two mis-specified situations: vary L while fixing K, or vary K while fixing L. The model estimation accuracy is then compared among three models with Procrustes error (see Figures 2E and 2F). We observed that as K and L in the model approach the true value (i.e., $K=4$ or $L=40$), the Procrustes error decreases rapidly to the lower level in SuSiE PCA and remains the same even when $K>4$ or $L>40$. However, the error for sparse PCA has a V shape and reaches its minimum at the real K. The explanation is that when there are over-specified latent factors in the model, SuSiE PCA and EBMF will not extract any information from the data due to their probabilistic model structure; the sparse PCA, on the other hand, cannot handle the weights since it does not impose a probabilistic assumption on them. Instead, the value of the redundant latent factor in sparse PCA is close to 0, which ensures the latent component does not contribute.

Finally, to compare the generative capacity, we computed and compared the log likelihood of held-out data between sparse PCA and SuSiE PCA. We observed that SuSiE PCA outperforms sparse PCA and obtains higher log likelihoods for simulations (Figure S5). In addition to the overall superior model performance, SuSiE PCA remains faster on both CPU and GPU than sparse PCA and EBMF due to the efficient variational algorithm we implement (see STAR Methods) with the JAX library developed by Google.¹⁸

Dissecting cross-tissue eQTLs in GTEx

To illustrate the utility of SuSiE PCA to make inferences in biological data, we analyzed multi-tissue eQTL Z score results computed from GTEx v8^12,14 (see STAR Methods). Specifically, we sought to identify latent factors corresponding to tissue-specific and tissue-shared eQTLs similar to ref. 12. Overall, we found that 27 latent factors explained 53.1% of the variance in the data (see Figure S6). Although we set $L=18$ across all factors, we found the number of tissues with $\text{PIP}>0.9$ is frequently lower than 18 in different factors (see Figure S9), which is due to inferred ${\tau }_{0kl}$ acting to “shut off” uninformative features. Indeed, we observed 30 out of 486 ${\tau }_{0kl}$ with estimates greater than $e^{10}$ (see Figure S7) which effectively shrink the effect size of the corresponding single effect toward 0, driving the number of non-zero single effects in some factors smaller than specified L. We found this behavior also reflected in estimated level-0.9 credible sets, where 456 out of 486 contained a single tissue, and the remaining 30 credible sets contained at least two tissues.

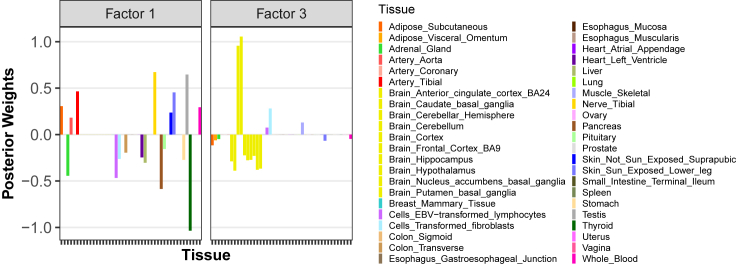
To understand what each factor represents, we examined inferred PIPs (Figure S9) and posterior mean weights of each tissue across 27 factors (Figure S8). Here we present the results from factor ${\mathbf{z}}_1$ and ${\mathbf{z}}_3$ through the posterior weights (Figure 3; see Figure S8 for the remainder). We observed that the latent factor ${\mathbf{z}}_1$ with the second largest percentage of variance (PVE) demonstrates high absolute weights on most tissues except for the brain tissues, while the latent factor ${\mathbf{z}}_3$ has large weights almost exclusively on brain tissues. Moreover, we observed that brain tissue tends to appear as a group and has similar effects, implying the eQTLs in brain tissue are different from those in other tissue and those strong signals are specifically captured by the factor ${\mathbf{z}}_1$. For the rest of the factors, we noticed that factors with large PVE such as ${\mathbf{z}}_2,{\mathbf{z}}_4,{\mathbf{z}}_5$ tended to have large weights on multiple tissues; for example, factor ${\mathbf{z}}_2$ has large weights on esophagus and thyroid, suggesting the eQTLs signals are mostly shared across those tissues, while the factors with small PVE usually have large weights exclusively on one or a few tissues, for example, liver-specific component ${\mathbf{z}}_{12}$, lung-specific component ${\mathbf{z}}_{15}$, etc. The only exception is that the factor ${\mathbf{z}}_0$ with the largest PVE has an exclusively large weight only on the testis, implying the ${\mathbf{z}}_0$ captures the testis-specific eQTL signals. This is consistent with the investigation of the latent factor values of ${\mathbf{z}}_0$: the gene with the largest factor value in ${\mathbf{z}}_{\mathbf{0}}$ is D-dopachrome tautomerase (DDT) (Figure S10), which is shown to be associated with testis cancer.¹⁹ To make a comparison with the existing method, we expanded our investigation by applying sparse PCA to the GTEx Z score dataset and observed comparable tissue weights and factor scores across components in both SuSiE PCA and sparse PCA (Figure S11). However, a notable distinction arises where certain tissues exhibit tiny weights and can potentially be neglected in sparse PCA; in contrast, the SuSiE PCA can successfully capture the signals in those tissues through the PIP. For example, from the original analysis, both models identify adipose gland as the most relevant tissue in factor 10, while the remaining tissues have a much smaller relative weight and can effectively be ignored. Despite this, SuSiE PCA assigns a PIP of 1 to the lowly weighted tissues, suggesting that important signals would be missed if weights alone were used to provide insight. Overall, we find that SuSiE PCA is able to identify tissue-specific components from multi-tissue eQTL data in an intuitive, interpretable manner.

Figure 3.

Factor ${\mathbf{z}}_1$ and ${\mathbf{z}}_3$ captures different types of tissues (tissues without brain vs. brain tissues)

The posterior weights refer to the inferred $\mathbf{W}$ matrix from the SuSiE PCA. The clustering pattern in different factors is found as there are only a limited number of tissues with non-zero weights in each factor since we set L = 18 while the feature dimension is 44.

Identifying regulatory modules from perturb-seq data

To identify gene regulatory modules from genome-wide perturbation data, we ran SuSiE PCA on perturb-seq in cell lines¹⁵ (see STAR Methods) with $K=10$ and $L=300$. Briefly, we inputted the normalized expression data ($2057\times 8563$) to SuSiE PCA to identify gene regulatory modules (i.e., $\mathbf{Z}$) and downstream-regulated networks (i.e., $\mathbf{W}$). To ensure our results were robust to K and L, we explored a grid of possible combinations and found that K = 10 and L = 300 retain the most important information while keeping the relevant gene set much smaller (see Figure S12 for a detailed explanation).

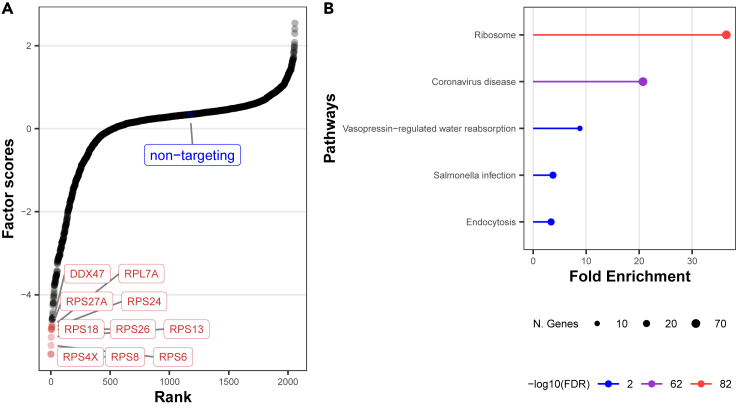
Overall, we found the total PVE was 10.71% across all components (Figure S13), with each component exhibiting 299 downstream genes with PIP $>0.9$ on average. Focusing on the leading component, we found that perturbations with the top 10 largest absolute factor scores are primarily related to Ribosomal Protein Small (RPS) subunit genes and Ribosomal Protein Large (RPL) subunit family (Figure 4A). To provide a broader characterization of the module function, we extracted downstream genes with PIP greater than 0.9 (298 genes) as input into ShinyGO²⁰ to perform a gene set enrichment analysis (Figure 4B). We observed the most enriched pathway was related to ribosome function (FDR = $9.2\times {10}^{-82}$, 63 genes involved), followed by coronavirus disease (FDR = $2.5\times {10}^{-62}$, 62 genes involved). Inspecting the loadings at these downstream genes, we found nearly all weights were positive, suggesting that the knockout of RPS and RPL genes downregulates the expression level of those downstream genes. We found multiple elongation factor genes (EEF1G, EEF1A1, EEF1B2, EIF4B, EIF3L) among the leading downstream genes, which are known to be involved in ribosome function. Additionally, recent studies have suggested that the decreased expression of elongation factor genes is associated with less severe conditions among COVID-19 patients.^21,22 We repeated pathway analysis for each latent factor using corresponding loadings at genes with PIP greater than 0.9 (see Figures S14–S22).

Figure 4.

Dominant factor scores in top component link to RPL and RPS family with subsequent gene enrichment in Ribosome and Coronavirus disease

The perturbations with top factor scores in the first component mostly belong to RPL and RPS family(A), and the enrichment analysis results of downstream genes in the same component are enriched for ribosome and coronavirus disease(B). Each point in (A) represents the latent factor value of each perturbation. The top 9 points as well as the control group are labeled in the plot and colored red and blue, respectively. In gene set enrichment analysis, we input the downstream genes with $\text{PIP}>0.9$ and show the top enriched pathways with log(FDR) and the number of genes included in the corresponding pathways.

To compare with sparse PCA, we performed the same pathway analysis on factor loadings and assessed enrichments. From the sparse PCA with the largest PVE (alpha = 1), we observed components identified by sparse PCA to be less enriched with biological pathways when compared to SuSiE PCA (80 unique enriched pathways in sparse PCA versus 88 pathways in SuSiE PCA), and the top enriched pathways such as ribosome and coronavirus disease are less significant and contain less number of selected genes (FDR $=1.4\times {10}^{-33}$, 35 genes; FDR $=2.9\times {10}^{-18}$, 29 genes). We noticed that, when alpha equals 17, the sparse PCA achieves an approximate similar total PVE (10.91%) with that of our model (10.71%) but with lower sparsity level (Figure S23). We then extracted the top 300 genes with non-zero weights in sparse PCA with alpha = 17 and performed the gene set enrichment analysis and found that the significance level is almost similar to that in SuSiE PCA (Figure S24). However, this is a post hoc analysis that suggests SuSiE PCA is more suitable for sparse data analysis while maintaining the power to perform the feature selection in a more statistical and reasonable manner.

Overall, we find distinct biological functions identified by each component, with groupings consistent with those reported in previous works.^23,24,25

Discussion

In this paper, we propose SuSiE PCA, an efficient Bayesian variable selection approach to PCA for structured biological data. The sparsity of the loading matrix is achieved by restricting the number of features associated with each factor to be at most L. Through simulations and real-data application, we find that SuSiE PCA outperforms existing approaches to sparse latent structure learning in identifying contributing features, while maintaining a more efficient run time.

There are several advantages of SuSiE PCA as compared to other sparse factor models. First, SuSiE PCA generates the PIPs for each feature that quantifies the uncertainty of the selected feature, which can not be provided by other sparse models, such as sparse PCA with regularization¹³ or the Bayesian treatment of PPCA. And assessing the selected variables based on the probability is more reasonable and convenient than using weights. Second, PIPs are capable of selecting more signals with high confidence. In simulations, we demonstrated that using weights for variable selection from SuSiE PCA, sparse PCA, and EBMF can deliver a high specificity (low FDR) but with low sensitivity as the cutoff value increases, while using PIPs as selection tools can maintain a high sensitivity for any positive cutoff value between 0 and 1. Third, SuSiE PCA provides a more precise estimate of the loadings and higher prediction accuracy, even in the mis-specified case, as we impose a probabilistic distribution over the loadings that enables a much more accurate inference on the posterior distribution. Finally, the inference procedure of SuSiE PCA works on the dimension of K and L, which is typically set to be much smaller than feature dimension P; therefore, it is scalable to high-dimensional data and requires less computational demands. We implement the SuSiE PCA with the JAX library developed by Google¹⁸ to enable fast convergence on CPU, GPU, or TPU. The comparison of run time among SuSiE PCA, sparse PCA, and EBMF is listed in Table 1.

Table 1.

Comparison of mean and standard deviation of running time (seconds) between models

Modela	Simulationb	GTEx Z score	Perturb-seq
SuSiE PCA	3.14(0.49)	1.20	68.11
Sparse PCA	51.96(33.50)	41.22	1213.21
EBMF	39.83(5.80)	498.60	243.03

^aAll run time data in the table are based on the analyses performed on the same CPU for consistency. The CPU we used is the Apple M2 chip with 16 GB memory.

^bRun time for simulation is recorded based on simulation setting in Figure 1, i.e., $N=1000,P=6000,K=4,L=40$; the average run time and corresponding standard deviation are computed for 100 simulations. We presented a more detailed run time comparison in simulation in Figure S4.

In the SuSiE PCA, two parameters, the number of components K, and the number of single effects L, need to be prespecified by the user before fitting the model. The selection of K follows a similar strategy as conventional PCA, often informed by researchers’ domain expertise. The merit of SuSiE PCA is that when there are excessive latent components being specified, the variance explained for those components would be extremely minimal with a near-zero count of single effects exhibiting $\text{PIP}>0.9$. This effectively allows for an initial choice of a relatively large K and subsequently inspecting the PVE and PIPs in each component to decide the most suitable K.

The choice of L determines the sparsity in the SuSiE PCA. Although SuSiE PCA only allows one common L specified across all factors, the number of non-zero effects captured across factors can be varied and learned from the data. This is because we treat the inverse of variance ${\tau }_{0kl}$ of the $l_{th}$ single effect in factor ${\mathbf{z}}_k$ as a random variable. As the Algorithm 1 demonstrates, the maximum likelihood estimate (MLE) of ${\tau }_{0kl}$ at the step 3 is derived before inference of other parameters. When the L specified in the model, for a certain factor k, is greater than the true number of signals associated with that factor, the MLE of the ${\tau }_{0kl}$ will be extremely large for those excessive single effects, which then shrinks the ${\mathbf{w}}_{kl}$ and PIP to be 0 or close to 0, and therefore removes the redundant single effects from the model. For example, in the simulation and GTEx Z score data analysis, we have shown that when the user-specified L is larger than the data-generating L, the automatic relevance determination-like (ARD) prior over loadings will shrink effects toward 0, thus adding little additional predictive power and overall mean square error (MSE) from the true loadings matrix. Although it seems like the L parameter may be automatically set to the total number of variables (and thus “shut off” if necessary), we emphasize that this still comes with an added computational cost, albeit a low one due to the scalability of our approach. Therefore, we allow users to specify their own choice of L. From this point of view, without prior knowledge of the data, one can specify a relatively larger L during the initial model fitting and then examine the estimates of ${\tau }_{0kl}$ to explore how many single effects are reasonable for the dataset.

Algorithm 1. Algorithm for SuSiE PCA.

Require: Data ${\mathbf{X}}_{N\times P}$

Require: Number of Factors K; Number of single effects in each factor L

Require: Initialize variational parameters $\left({\mathit{\mu }}_{\mathbf{Z}},{\mathbf{\Sigma }}_{\mathbf{Z}};{\mathit{\mu }}_{{\mathbf{w}}_{kl}},{\mathit{\sigma }}_{{\mathbf{w}}_{kl}};{\mathit{\alpha }}_{kl}\right)$; hyperparameters $\tau ,{\tau }_{0kl}$, for $l=1,\cdots ,L;k=1,\cdots ,K$

Require: update equations on different variables $F_{\mathbf{Z}};F_{{\mathbf{w}}_{kl}};F_{{\mathit{\alpha }}_{kl}};F_{{\mathit{\tau }}_0};F_{\tau }$:

Require: function to compute $\text{ELBO},F_{\text{ELBO}}$

Ensure: ELBO increase

1: repeat

2:  $\mathbf{W}\leftarrow {\sum }_{l=1}^L{\mathit{\mu }}_{\mathbf{w}}\circ \mathit{\alpha }$. $▷$ Define ${\mathit{\mu }}_{\mathbf{w}},\mathit{\alpha }$ as $\left(L,K,P\right)$ arrays by arranging ${\mathit{\mu }}_{{\mathbf{w}}_{kl}},{\mathit{\alpha }}_{kl}$

3:  ${\mathit{\tau }}_0\leftarrow F_{{\mathit{\tau }}_0}\left({\mathit{\mu }}_{\mathbf{w}},{\mathit{\sigma }}_{\mathbf{w}},\mathit{\alpha }\right)$

4:  for k in $1,\cdots ,K$ do

5:   $\mathbb{E}{\left[{\mathbf{R}}_{kl}^{⊺}{\mathbf{Z}}_k\right]}^{\left(1\right)}={\mathbf{X}}^{⊺}{\mathit{\mu }}_{{\mathbf{z}}_k}-\sum _{k^{\prime }\ne k}\mathbb{E}\left[{\mathbf{w}}_{k^{\prime }}\right]\mathbb{E}\left[{\mathbf{Z}}_{k^{\prime }}^{⊺}{\mathbf{Z}}_k\right]$ $▷$ compute the first two terms in Eq

6:   for l in $1,\cdots ,L$ do

7:    $\mathbb{E}\left[{\mathbf{w}}_{k{l}^{\prime }}\right]={\mathbf{w}}_k-{\mathit{\mu }}_{{\mathbf{w}}_{kl}}\circ {\mathit{\alpha }}_{kl}$ $▷$ removing the $l_{th}$ effect from ${\mathbf{w}}_k$

8:    $\mathbb{E}\left[{\mathbf{R}}_{kl}^{⊺}{\mathbf{Z}}_k\right]=\mathbb{E}{\left[{\mathbf{R}}_{kl}^{⊺}{\mathbf{Z}}_k\right]}^{\left(1\right)}-{\mathbf{w}}_k\mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]$ $▷$ complete the calculation of $\mathbb{E}\left[{\mathbf{R}}_{kl}^{⊺}{\mathbf{Z}}_k\right]$

9:    $\left({\mathit{\mu }}_{{\mathbf{w}}_{kl}},{\mathit{\sigma }}_{{\mathbf{w}}_{kl}}\right)\leftarrow F_{{\mathbf{w}}_{kl}}\left(\mathbb{E}\left[{\mathbf{R}}_{kl}^{⊺}{\mathbf{Z}}_k\right],\mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right],{\tau }_{0kl},\tau \right)$

10:    ${\mathit{\alpha }}_{kl}\leftarrow F_{{\mathit{\alpha }}_{kl}}\left(\mathbb{E}\left[{\mathbf{R}}_{kl}^{⊺}{\mathbf{Z}}_k\right],{\mathit{\mu }}_{{\mathbf{w}}_{kl}},{\mathit{\sigma }}_{{\mathbf{w}}_{kl}}\right)$

11:    ${\mathbf{w}}_k=\mathbb{E}\left[{\mathbf{w}}_{k{l}^{\prime }}\right]+{\mu }_{{\mathbf{w}}_{kl}}\circ {\mathit{\alpha }}_{kl}$ $▷$ Update the ${\mathbf{w}}_k$

12:   end for

13:  end for

14:  $\left({\mathit{\mu }}_{\mathbf{Z}},{\mathbf{\Sigma }}_{\mathbf{Z}}\right)\leftarrow F_Z\left(\mathbf{X},\tau ,\mathbb{E}\left[\mathbf{W}\right]\right)$

15:  $\tau =F_{\tau }\left(\mathbf{X},\tau ,\mathbb{E}\left[\mathbf{W}\right],\mathbb{E}\left[\mathbf{Z}\right]\right)$

16: $ELBO\leftarrow F_{\text{ELBO}}$

17: until ELBO convergence criterion satisfied

Overall, SuSiE PCA provides a flexible approach to high-dimensional biological data with a low-rank structure and allows for feature selection in sparse PCA.

Limitations of the study

One limitation of SuSiE PCA is that under the mean-field approximation, all the posteriors, i.e., $\text{Q}\left(\mathbf{W}\right)$ and $\text{Q}\left(\mathbf{Z}\right)$, are factorized to facilitate inference. Under this factorization, estimation for mean terms (i.e., $\text{E}\left[\mathbf{W}\right]$ and $\text{E}\left[\mathbf{Z}\right]$) is approximately unbiased.²⁶ However, it produces overconfident covariance structures within variables (W, Z, etc) due to the assumed independence across Q functions.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
The Genotype-Tissue Expression Z score data	Wei Wang and Matthew Stephens, Empirical Bayes Matrix Factorization, 20211	https://github.com/ysfoo/sparsefactor
Genome-scale Perturb-seq experiment data	Joseph Replogle and Jonathan Weissman, Mapping information-rich genotype-phenotype landscapes with genome-scale Perturb-seq, 20222	https://plus.figshare.com/articles/dataset/_Mapping_information-rich_genotype-phenotype_landscapes_with_genome-scale_Perturb-seq_Replogle_et_al_2022_processed_Perturb-seq_datasets/20029387
Software and algorithms
Scikit-learn library: sparse principal component analysis	Python library scikit-learn	https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.SparsePCA.html; RRID:SCR_002577
R Package: Factors and Loadings by Adaptive SHrinkage in R (flashr)	Wei Wang and Matthew Stephens, Empirical Bayes Matrix Factorization1	https://stephenslab.github.io/flashr/index.html
Variational algorithm in SuSiE PCA	This paper	http://www.github.com/mancusolab/susiepca
Python 3.9	Python Software Foundation	https://www.python.org/
R 4.0.0	R Software	https://www.r-project.org
ShinyGO v0.77	Ge SX, Jung D & Yao R3	http://bioinformatics.sdstate.edu/go/; RRID:SCR_019213

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Dong Yuan (dongyuan@usc.edu).

Material availability

This study did not generate new unique materials or reagents.

Experimental model and subject details

This study did not include experiments with a specific model or subject.

Method details

Overview of SuSiE PCA

In this section, we will give a detailed description of SuSiE PCA. Let ${\mathbf{X}}_{N\times P}$ be the observed data matrix, ${\mathbf{Z}}_{N\times K}$ be the K dimensional latent vectors, and ${\mathbf{W}}_{K\times P}$ be the loading matrix. We denote the normal distribution with mean μ and variance ${\sigma }^2$ as $\mathcal{N}\left(\mu ,{\sigma }^2\right)$, the multinomial distribution with n choices and probabilities $\mathit{\pi }$ as $\text{Multi}\left(n,\mathit{\pi }\right)$ and the matrix normal distribution with dimension $N\times K$, mean $\mathbf{M}$, row-covariance $\mathbf{R}$, and column-covariance $\mathbf{C}$ as $\mathcal{M}{\mathcal{N}}_{N,K}\left(\mathbf{M},\mathbf{R},\mathbf{C}\right)$. We denote the basis vector in which $k^{th}$ coordinate is 1 and 0 elsewhere as ${\mathbf{e}}_k$. The sampling distribution of $\mathbf{X}$ under the SuSiE PCA model is given by,

$$\mathbf{X}|\mathbf{Z},\mathbf{W},{\sigma }^2\sim \mathcal{M}{\mathcal{N}}_{N,P}\left(\mathbf{Z}\mathbf{W},{\mathbf{I}}_N,{\sigma }^2{\mathbf{I}}_P\right)$$ (Equation 1)

$$\mathbf{Z}\sim \mathcal{M}{\mathcal{N}}_{N,K}\left(0,{\mathbf{I}}_N,{\mathbf{I}}_K\right)$$ (Equation 2)

$$\mathbf{W}=\sum _{k=1}^K{\mathbf{e}}_k{\mathbf{w}}_k^{⊺}$$ (Equation 3)

$${\mathbf{w}}_k=\sum _{l=1}^L{\mathbf{w}}_{kl}$$ (Equation 4)

$${\mathbf{w}}_{kl}=w_{kl}{\mathit{\gamma }}_{kl}$$ (Equation 5)

$$w_{kl}|{\sigma }_{0kl}^2\sim \mathcal{N}\left(0,{\sigma }_{0kl}^2\right)$$ (Equation 6)

$${\mathit{\gamma }}_{kl}|\mathit{\pi }\sim \text{Multi}\left(1,\mathit{\pi }\right)\text{,}$$ (Equation 7)

where ${\mathbf{w}}_k$ corresponds to the $k^{th}$ row of $\mathbf{W}$, and contains at most L non-zero elements determined by the sum of L single-effect vectors ${\mathbf{w}}_{kl}$. These single-effect vectors are described by a single random effect $w_{kl}$ and indicator vector ${\mathit{\gamma }}_{kl}$ which assigns the effect to a feature with prior probabilities $\mathit{\pi }=\frac{1}{p}\mathbf{1}$.

Posterior inclusion probability

One of the distinguishing features that the SuSiE model¹³ provides is a posterior inclusion probability (PIP). The PIP reflects the posterior probability that a given variable has a non-zero effect given the observed data. Here we extend the PIP definition to include latent factors. Specifically, given variational parameters ${\mathit{\alpha }}_{kl}$ we can define the PIP that the $i^{th}$ variable has a non-zero effect in the $k^{th}$ latent component as,

$${\text{PIP}}_{ki}:=\mathrm{Pr}\left(w_{ki}\ne 0|\mathbf{X}\right)=1-\prod _{l=1}^L\left(1-{\alpha }_{kli}\right)$$ (Equation 8)

Similarly, a level-$\rho$ credible set (CS) refers to a subset of variables that cumulatively explain at least ρ of the posterior density. Here, we define factor-specific level-$\rho$ CSs, which can be computed across each ${\mathit{\alpha }}_{kl}$ independently, resulting in $K\times L$ total level-ρ credible sets. This lets us reflect on the uncertainty in identified variables to explain a single-effect for each latent factor.

Variational inference in SuSiE PCA

We seek to perform inference of model variables $\mathbf{Z}\mathbf{,}{\mathbf{w}}_{kl}$ and ${\mathit{\gamma }}_{kl}$ conditional on observed data $\mathbf{X}$, however, the marginal likelihood is intractable to compute and therefore, we cannot evaluate the posterior exactly. While sampling based approaches such as Markov Chain Monte Carlo (MCMC) methods provide a numerical approximation of the exact posterior distribution,²⁷ they often lack computational efficiency in high-dimensional settings. As an alternative, we leverage recent advancements in the variational inference that provides an analytical approximation to the posterior distribution²⁸ and remains computationally efficient.

Briefly, To approximate the conditional distribution of latent variables $\mathbf{Z}$ given the observed samples $\mathbf{X}$, variational methods first impose a family of densities over the latent variables, $Q\left(\mathbf{Z}\right)$, usually predefined as known distributions parameterized with a set of variational parameters. Then the goal is to infer those variational parameters such that the variational distribution $Q\left(\mathbf{Z}\right)$ is as similar as possible to the true posterior distribution $P\left(\mathbf{Z}|\mathbf{X}\right)$. A quantity commonly used to measure dissimilarity between distributions is Kullback-Leibler divergence $D_{KL}\left(Q\parallel P\right)$.²⁹ However, since KL divergence contain the unknown true posterior distribution $P\left(\mathbf{Z}|\mathbf{X}\right)$, it cannot be directly computed. Instead, we can show that the log-likelihood of data, $\log P\left(\mathbf{X}\right)$ can be decomposed as:

$$\log P\left(\mathbf{X}\right)=D_{KL}\left(Q\parallel P\right)+\mathcal{L}\left(Q\right)$$ (Equation 9)

Where $\mathcal{L}\left(Q\right)={\mathbb{E}}_Q\left[\log P\left(\mathbf{Z},\mathbf{X}\right)-\log Q\left(\mathbf{Z}\right)\right]$, which is also known as the Evidence Lower Bound (ELBO). Since the $\log P\left(\mathbf{X}\right)$ is a constant with respect to the variational parameters, minimizing KL divergence is equivalent to maximizing ELBO. As the ELBO does not contain the unknown posterior distribution and therefore is tractable to compute and maximize for variational parameters.

Mean-field approximation

Mean field approximation³⁰ is a common solution to find the optimal solution that maximizes ELBO. The basic assumption is that we can factorize the variational distribution into independent components. Then using the calculus of variations, one can show that the distribution $Q_j^{\ast }\left({\mathbf{z}}_j\right)$ minimizing KL divergence for each factor ${\mathbf{Z}}_j$ can be expressed as:

$$\ln Q_j^{\ast }\left({\mathbf{z}}_j|\mathbf{X}\right)={\mathbb{E}}_{i\ne j}\left[\ln P\left(\mathbf{Z},\mathbf{X}\right)\right]+constant$$ (Equation 10)

Applying the Mean-Field approximation to SuSiE PCA the approximate posterior given by,

$$Q\left(\mathbf{Z},\mathbf{W}\right)=Q\left(\mathbf{Z}\right)Q\left(\mathbf{W}\right)$$ (Equation 11)

$$Q\left(\mathbf{W}\right)=\prod _{k=1}^K\prod _{l=1}^{L}Q\left({\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kl}\right)Q\left({\mathit{\gamma }}_{kl}\right)$$ (Equation 12)

Equation 11 factorizes the variational densities of the latent variables $\mathbf{Z}$ and the loading matrix $\mathbf{W}$ into independent parts. We further assume that the variational distribution of loadings ${\mathbf{w}}_{kl}$ from each factor across L single effects are independent as well, leading to Equation 12. For ease of notation we first define $\tau =\frac{1}{{\sigma }^2},{\tau }_{0kl}=\frac{1}{{\sigma }_{0kl}^2}$. Based on the factorization, the complete-data log-likelihood of data and parameters of SuSiE PCA is given by:

$$\begin{array}{l}{\mathcal{l}}_c\left({\sigma }^2,{\sigma }_0^2,\mathit{\pi }|\mathbf{X},\mathbf{Z},\mathbf{W}\right)=\log \mathrm{Pr}\left(\mathbf{X}|\mathbf{Z},\mathbf{W},{\sigma }^2\right)+\log \mathrm{Pr}\left(\mathbf{Z}\right)+\log \mathrm{Pr}\left(\mathbf{W}|{\sigma }_0^2,\mathit{\pi }\right)=\log \mathcal{M}{\mathcal{N}}_{n,p}\left(\mathbf{X}|\mathbf{Z}\mathbf{W},{\mathbf{I}}_n,{\mathbf{I}}_p{\sigma }^2\right)+\log \mathcal{M}{\mathcal{N}}_{n,k}\left(\mathbf{Z}|0,{\mathbf{I}}_n,{\mathbf{I}}_k\right)+\\ \sum _{l=1}^L\sum _{k=1}^K\left[\text{logMulti}\left({\mathit{\gamma }}_{kl}|1,\mathit{\pi }\right)+\log \mathcal{N}\left(w_{kl}|0,{\sigma }_0^2\right)\right]\end{array}$$

Helpful definitions

Before proceeding to the full derivation of variational distribution of parameters $\mathbf{Z},{\mathbf{w}}_{kl},\text{and}{\mathit{\gamma }}_{kl}$, we first give some helpful definitions, including the expansion of the first and second moment of $\mathbf{W}$ and $\mathbf{Z}$.

The second moment of $\mathbf{Z}$ is:

$$\begin{array}{l}\mathbb{E}\left[{\mathbf{Z}}^{⊺}\mathbf{Z}\right]=\text{tr}\left({\mathbf{I}}_n\right){\mathbf{\Sigma }}_{\mathbf{Z}}+\mathbb{E}{\left[\mathbf{Z}\right]}^{⊺}\mathbb{E}\left[\mathbf{Z}\right]=n{\mathbf{\Sigma }}_{\mathbf{Z}}+\mathbb{E}{\left[\mathbf{Z}\right]}^{⊺}\mathbb{E}\left[\mathbf{Z}\right]\\ \mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]=\text{tr}\left(\mathbb{V}\left[{\mathbf{Z}}_k\right]\right)+\mathbb{E}{\left[{\mathbf{Z}}_k\right]}^{⊺}\mathbb{E}\left[{\mathbf{Z}}_k\right]=\text{tr}\left({\mathbf{I}}_n{\left({\mathbf{\Sigma }}_{\mathbf{Z}}\right)}_{kk}\right)+\mathbb{E}{\left[{\mathbf{Z}}_k\right]}^{⊺}\mathbb{E}\left[{\mathbf{Z}}_k\right]=n{\left({\mathbf{\Sigma }}_{\mathbf{Z}}\right)}_{kk}+\mathbb{E}{\left[{\mathbf{Z}}_k\right]}^{⊺}\mathbb{E}\left[{\mathbf{Z}}_k\right]\end{array}$$

The first and second moments of ${\mathbf{w}}_k$ are listed as follows:

$$\begin{gathered} \begin{array}{l}\mathbb{E}\left[{\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kl}\right]=\mathrm{p}-\text{vector}\text{of}\text{posterior} \\ \text{conditional}\text{means}\\ \mathbb{V}\left[{\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kl}\right]=\mathrm{p}-\text{vector}\text{of}\text{posterior} \\ \text{conditional}\text{variances}\\ \mathbb{E}\left[{\mathbf{w}}_k\right]=\mathbb{E}\left[\sum _l{\mathbf{w}}_{kl}\right]=\sum _l\mathbb{E}\left[{\mathbf{w}}_{kl}\right]\\ \mathbb{E}\left[{\mathbf{w}}_{kl}\right]=\sum _l\mathbb{E}\left[w_{kl}|{\mathit{\gamma }}_{kl}\right]\circ \mathbb{E}\left[{\mathit{\gamma }}_{kl}\right]\\ \mathbb{V}\left[{\mathbf{w}}_k\right]=\mathbb{V}\left[\sum _l{\mathbf{w}}_{kl}\right]=\sum _l\mathbb{V}\left[{\mathbf{w}}_{kl}\right]\\ \mathbb{V}\left[{\mathbf{w}}_{kl}\right]=\mathbb{E}\left[{\mathbf{w}}_{kl}{\mathbf{w}}_{kl}^{⊺}\right]-\mathbb{E}\left[{\mathbf{w}}_{kl}\right]\mathbb{E}{\left[{\mathbf{w}}_{kl}\right]}^{⊺}=\mathbb{E}\left[w_{kl}^2{\mathit{\gamma }}_{kl}{\mathit{\gamma }}_{kl}^{⊺}\right]-\mathbb{E}\left[{\mathbf{w}}_{kl}\right]\mathbb{E}{\left[{\mathbf{w}}_{kl}\right]}^{⊺}=\text{diag}\left(\mathbb{E}\left[{\mathbf{w}}_{kl}\circ {\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kl}\right]\circ \mathbb{E}\left[{\mathit{\gamma }}_{kl}\right]\right)-\mathbb{E}\left[{\mathbf{w}}_{kl}\right]\mathbb{E}{\left[{\mathbf{w}}_{kl}\right]}^{⊺}\\ \text{diag}\left(\mathbb{V}\left[{\mathbf{w}}_{kl}\right]\right)=\mathbb{E}\left[{\mathbf{w}}_{kl}\circ {\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kl}\right]\circ \mathbb{E}\left[{\mathit{\gamma }}_{kl}\right]-{\left(\mathbb{E}\left[{\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kl}\right]\circ \mathbb{E}\left[{\mathit{\gamma }}_{kl}\right]\right)}^2\\ \mathbb{E}\left[{\mathbf{w}}_k^{⊺}{\mathbf{w}}_k\right]=\text{tr}\left(\mathbb{V}\left[{\mathbf{w}}_k\right]\right)+\mathbb{E}{\left[{\mathbf{w}}_k\right]}^{⊺}\mathbb{E}\left[{\mathbf{w}}_k\right]\\ \mathbb{E}\left[w_{kl}^2\right]=\left[{\mathbb{E}}^2\left[w_{kl}|{\mathit{\gamma }}_{kl}\right]+\mathbb{V}\left[w_{kl}|{\mathit{\gamma }}_{kl}\right]\right]\circ \mathbb{E}\left[{\mathit{\gamma }}_{kl}\right]\end{array} \end{gathered}$$

The first and second moments of $\mathbf{W}$ are listed as follows:

$$\begin{array}{c}\mathbb{E}\left[\mathbf{W}\right]=\mathbb{E}\left[\sum _k{\mathbf{e}}_k{\mathbf{w}}_k^{⊺}\right]=\sum _k{\mathbf{e}}_k\mathbb{E}{\left[{\mathbf{w}}_k\right]}^{⊺}\\ \mathbb{E}\left[\mathbf{W}{\mathbf{W}}^{⊺}\right]=\mathbb{E}\left[\left(\sum _k{\mathbf{e}}_k{\mathbf{w}}_k^{⊺}\right){\left(\sum _{k^{\prime }}{\mathbf{e}}_{k^{\prime }}{\mathbf{w}}_{k^{\prime }}^{⊺}\right)}^{⊺}\right]=\mathbb{E}\left[\sum _k\sum _{k^{\prime }}{\mathbf{e}}_k{\mathbf{w}}_k^{⊺}{\mathbf{w}}_{k^{\prime }}{\mathbf{e}}_{k^{\prime }}^{⊺}\right]=\sum _k\sum _{k^{\prime }}{\mathbf{e}}_k{\mathbf{e}}_{k^{\prime }}^{⊺}\mathbb{E}\left[{\mathbf{w}}_k^{⊺}{\mathbf{w}}_{k^{\prime }}\right]=\sum _k\sum _{k^{\prime }}{\mathbf{e}}_k{\mathbf{e}}_{k^{\prime }}^{⊺}\mathbb{E}{\left[{\mathbf{w}}_k\right]}^{⊺}\mathbb{E}\left[{\mathbf{w}}_{k^{\prime }}\right]+\sum _k{\mathbf{e}}_k{\mathbf{e}}_k^{⊺}\left(\mathbb{E}\left[{\mathbf{w}}_k^{⊺}{\mathbf{w}}_k\right]-\mathbb{E}{\left[{\mathbf{w}}_k\right]}^{⊺}\mathbb{E}\left[{\mathbf{w}}_k\right]\right)=\mathbb{E}\left[\mathbf{W}\right]\mathbb{E}{\left[\mathbf{W}\right]}^{⊺}+\sum _k{\mathbf{e}}_k{\mathbf{e}}_k^{⊺}\left(\mathbb{E}\left[{\mathbf{w}}_k^{⊺}{\mathbf{w}}_k\right]-\mathbb{E}{\left[{\mathbf{w}}_k\right]}^{⊺}\mathbb{E}\left[{\mathbf{w}}_k\right]\right)=\mathbb{E}\left[\mathbf{W}\right]\mathbb{E}{\left[\mathbf{W}\right]}^{⊺}+\sum _k{\mathbf{e}}_k{\mathbf{e}}_k^{⊺}\text{tr}\left(\mathbb{V}\left[{\mathbf{w}}_k\right]\right)=\mathbb{E}\left[\mathbf{W}\right]\mathbb{E}{\left[\mathbf{W}\right]}^{⊺}+\text{diag}\left(\text{tr}\left(\mathbb{V}\left[{\mathbf{w}}_1\right]\right),\dots ,\text{tr}\left(\mathbb{V}\left[{\mathbf{w}}_k\right]\right)\right)\end{array}$$

Other terms in likelihood function:

$$\begin{array}{l}\log \mathcal{M}{\mathcal{N}}_{n,p}\left(\mathbf{X}|\mathbf{Z}\mathbf{W},{\mathbf{I}}_n,{\mathbf{I}}_p{\sigma }^2\right)=-\frac{1}{2{\sigma }^2}\mathrm{t}\mathrm{r}\left[{\left(\mathbf{X}-\mathbf{Z}\mathbf{W}\right)}^{⊺}\left(\mathbf{X}-\mathbf{Z}\mathbf{W}\right)\right]-\frac{np}{2}\log \left(2\pi {\sigma }^2\right)\\ \log \mathcal{M}{\mathcal{N}}_{n,k}\left(\mathbf{Z}|0,{\mathbf{I}}_n,{\mathbf{I}}_k\right)=-\frac{1}{2}\mathrm{t}\mathrm{r}\left[{\mathbf{Z}}^{⊺}\mathbf{Z}\right]-\frac{nk}{2}\log \left(2\pi \right)\\ \text{logMulti}\left({\mathit{\gamma }}_{kl}|1,\mathit{\pi }\right)=\sum _{i=1}^p{\mathit{\gamma }}_{kli}\log \left({\pi }_i\right)\\ \log \mathcal{N}\left(w_{kl}|0,{\sigma }_0^2\right)=-\frac{1}{2{\sigma }_0^2}{w}_{kl}^2-\frac{1}{2}\log \left(2\pi {\sigma }_0^2\right)\\ \text{tr}\left[{\mathbb{E}}_{\neg \mathbf{Z}}\left[{\left(\mathbf{X}-\mathbf{Z}\mathbf{W}\right)}^{⊺}\left(\mathbf{X}-\mathbf{Z}\mathbf{W}\right)\right]\right]=\text{tr}\left[{\mathbb{E}}_{\neg \mathbf{Z}}\left({\mathbf{X}}^{⊺}\mathbf{X}-{\mathbf{X}}^{⊺}\mathbf{Z}\mathbf{W}-{\mathbf{W}}^{⊺}{\mathbf{Z}}^{⊺}\mathbf{X}+{\mathbf{W}}^{⊺}{\mathbf{Z}}^{⊺}\mathbf{Z}\mathbf{W}\right)\right]=\text{tr}\left({\mathbf{X}}^{⊺}\mathbf{X}\right)-2\mathrm{t}\mathrm{r}\left(\mathbb{E}\left[\mathbf{W}\right]{\mathbf{X}}^{⊺}\mathbf{Z}\right)+\text{tr}\left({\mathbf{Z}}^{⊺}\mathbf{Z}\mathbb{E}\left[\mathbf{W}{\mathbf{W}}^{⊺}\right]\right)=\text{tr}\left({\mathbf{X}}^{⊺}\mathbf{X}\right)-2\mathrm{t}\mathrm{r}\left(\mathbb{E}\left[\mathbf{W}\right]{\mathbf{X}}^{⊺}\mathbf{Z}\right)+\sum _{i=1}^p\text{tr}\left(\mathbf{Z}{\mathit{\sigma }}_{{\mathbf{W}}_i}{\mathbf{Z}}^{⊺}\right)+\mathbb{E}\left[{\mathbf{W}}^{⊺}\right]{\mathbf{Z}}^{⊺}\mathbf{Z}\mathbb{E}\left[\mathbf{W}\right]\\ \text{tr}\left[{\mathbb{E}}_{\neg \mathbf{W}}\left[{\left(\mathbf{X}-\mathbf{Z}\mathbf{W}\right)}^{⊺}\left(\mathbf{X}-\mathbf{Z}\mathbf{W}\right)\right]\right]=\text{tr}\left[{\mathbb{E}}_{\neg \mathbf{W}}\left({\mathbf{X}}^{⊺}\mathbf{X}-{\mathbf{X}}^{⊺}\mathbf{Z}\mathbf{W}-{\mathbf{W}}^{⊺}{\mathbf{Z}}^{⊺}\mathbf{X}+{\mathbf{W}}^{⊺}{\mathbf{Z}}^{⊺}\mathbf{Z}\mathbf{W}\right)\right]=\text{tr}\left({\mathbf{X}}^{⊺}\mathbf{X}\right)-2\mathrm{t}\mathrm{r}\left({\mathbf{X}}^{⊺}\mathbb{E}\left[\mathbf{Z}\right]\mathbf{W}\right)+\text{tr}\left(\mathbb{E}\left[{\mathbf{Z}}^T\mathbf{Z}\right]\mathbf{W}{\mathbf{W}}^{⊺}\right)\end{array}$$

$$\begin{array}{l}\mathbb{E}\left[\text{tr}\left({\left(\mathbf{X}-\mathbf{Z}\mathbf{W}\right)}^{⊺}\left(\mathbf{X}-\mathbf{Z}\mathbf{W}\right)\right)\right]=\mathbb{E}\left[\text{tr}\left({\mathbf{X}}^{⊺}\mathbf{X}-{\mathbf{X}}^{⊺}\mathbf{Z}\mathbf{W}-{\mathbf{W}}^{⊺}{\mathbf{Z}}^{⊺}\mathbf{X}+{\mathbf{W}}^{⊺}{\mathbf{Z}}^{⊺}\mathbf{Z}\mathbf{W}\right)\right]=\text{tr}\left({\mathbf{X}}^{⊺}\mathbf{X}-{\mathbf{X}}^{⊺}\mathbb{E}\left[\mathbf{Z}\right]\mathbb{E}\left[\mathbf{W}\right]-\mathbb{E}\left[{\mathbf{W}}^{⊺}\right]\mathbb{E}\left[{\mathbf{Z}}^{⊺}\right]\mathbf{X}+\mathbb{E}\left[{\mathbf{W}}^{⊺}{\mathbf{Z}}^{⊺}\mathbf{Z}\mathbf{W}\right]\right)=\text{tr}\left({\mathbf{X}}^{⊺}\mathbf{X}\right)-2\mathrm{t}\mathrm{r}\left({\mathbf{X}}^{⊺}\mathbb{E}\left[\mathbf{Z}\right]\mathbb{E}\left[\mathbf{W}\right]\right)+\text{tr}\left(\mathbb{E}\left[{\mathbf{Z}}^{⊺}\mathbf{Z}\right]\mathbb{E}\left[\mathbf{W}{\mathbf{W}}^{⊺}\right]\right)\\ {\overline{\mathbf{R}}}_{kl}:=\mathbf{X}-\mathbb{E}\left[\mathbf{Z}\right]\left(\sum _{k^{\prime }\ne k}{\mathbf{e}}_{k^{\prime }}\mathbb{E}{\left[{\mathbf{w}}_{k^{\prime }}\right]}^{⊺}+\sum _{l^{\prime }\ne l}{\mathbf{e}}_k\mathbb{E}{\left[{\mathbf{w}}_{k{l}^{\prime }}\right]}^{⊺}\right)=\mathbf{X}-\sum _{k^{\prime }\ne k}\mathbb{E}\left[{\mathbf{Z}}_{k^{\prime }}\right]\mathbb{E}{\left[{\mathbf{w}}_{k^{\prime }}\right]}^{⊺}-\sum _{l^{\prime }\ne l}\mathbb{E}\left[{\mathbf{Z}}_k\right]\mathbb{E}{\left[{\mathbf{w}}_{k{l}^{\prime }}\right]}^{⊺}\end{array}$$

Derivation of model parameters

In this section, we present the detailed derivation of the optimal variational distributions of variables $\mathbf{Z},{\mathbf{w}}_{kl}$, and ${\mathit{\gamma }}_{kl}$. First, we derived the $\log Q\left(\mathbf{Z}\right)\text{:}$

$$\begin{array}{l}\log Q\left(\mathbf{Z}\right)={\mathbb{E}}_{\neg \mathbf{Z}}\left[{\mathcal{l}}_c\left({\sigma }^2,{\sigma }_0^2,\mathit{\pi }|\mathbf{X},\mathbf{Z},\mathbf{W}\right)\right]={\mathbb{E}}_{\neg \mathbf{Z}}\left[\log \mathcal{M}{\mathcal{N}}_{n,p}\left(\mathbf{X}|\mathbf{Z}\mathbf{W},{\mathbf{I}}_n,{\mathbf{I}}_p{\sigma }^2\right)\right]+\log \mathcal{M}{\mathcal{N}}_{n,k}\left(\mathbf{Z}|0,{\mathbf{I}}_n,{\mathbf{I}}_k\right)=-\frac{\tau }{2}\left[-\text{tr}\left({\mathbf{X}}^{⊺}\mathbf{Z}\mathbb{E}\left[\mathbf{W}\right]\right)-\text{tr}\left(\mathbb{E}\left[{\mathbf{W}}^{⊺}\right]{\mathbf{Z}}^{⊺}\mathbf{X}\right)+\text{tr}\left({\mathbf{Z}}^{⊺}\mathbf{Z}\mathbb{E}\left(\mathbf{W}{\mathbf{W}}^{⊺}\right)\right)\right]-\frac{1}{2}\mathrm{t}\mathrm{r}\left({\mathbf{Z}}^{⊺}\mathbf{Z}\right)+O\left(1\right)=-\frac{1}{2}\left[\text{tr}\left(\tau {\mathbf{Z}}^{⊺}\mathbf{Z}\mathbb{E}\left(\mathbf{W}{\mathbf{W}}^{⊺}\right)\right)+\text{tr}\left({\mathbf{Z}}^{⊺}\mathbf{Z}\right)-\text{tr}\left(\tau {\mathbf{X}}^{⊺}\mathbf{Z}\mathbb{E}\left[\mathbf{W}\right]\right)-\text{tr}\left(\tau \mathbb{E}\left[{\mathbf{W}}^{⊺}\right]{\mathbf{Z}}^{⊺}\mathbf{X}\right)\right]+O\left(1\right)=-\frac{1}{2}\left[\text{tr}\left({\mathbf{Z}}^{⊺}\mathbf{Z}\left(\mathbb{E}\left(\mathbf{W}{\mathbf{W}}^{⊺}\right)\tau +{\mathbf{I}}_k\right)\right)-\text{tr}\left(\tau {\mathbf{X}}^{⊺}\mathbf{Z}\mathbb{E}\left[\mathbf{W}\right]\right)-\text{tr}\left(\tau \mathbb{E}\left[{\mathbf{W}}^{⊺}\right]{\mathbf{Z}}^{⊺}\mathbf{X}\right)\right]+O\left(1\right)=-\frac{1}{2}\left[\text{tr}\left(\mathbf{Z}\underset{{\mathbf{\Sigma }}_{\mathbf{Z}}^{-1}}{\underbrace{\left(\mathbb{E}\left(\mathbf{W}{\mathbf{W}}^{⊺}\right)\tau +{\mathbf{I}}_k\right)}}{\mathbf{Z}}^{⊺}\right)-\text{tr}\left(\mathbf{Z}\mathbb{E}\left[\mathbf{W}\right]{\mathbf{X}}^{⊺}\tau \right)-\text{tr}\left(\tau \mathbf{X}\mathbb{E}\left[{\mathbf{W}}^{⊺}\right]{\mathbf{Z}}^{⊺}\right)\right]+O\left(1\right)=-\frac{1}{2}\left[\text{tr}\left(\mathbf{Z}{\mathbf{\Sigma }}_{\mathbf{Z}}^{-1}{\mathbf{Z}}^{⊺}\right)-\text{tr}\left(\mathbf{Z}{\mathbf{\Sigma }}_{\mathbf{Z}}^{-1}\underset{{\mathit{\mu }}_{\mathbf{Z}}^{⊺}}{\underbrace{{\mathbf{\Sigma }}_{\mathbf{Z}}\mathbb{E}\left[\mathbf{W}\right]{\mathbf{X}}^{⊺}\tau }}\right)-\text{tr}\left(\underset{{\mathit{\mu }}_{\mathbf{Z}}}{\underbrace{\tau \mathbf{X}\mathbb{E}\left[{\mathbf{W}}^{⊺}\right]{\mathbf{\Sigma }}_{\mathbf{Z}}}}{\mathbf{\Sigma }}_{\mathbf{Z}}^{-1}{\mathbf{Z}}^{⊺}\right)\right]+O\left(1\right)=-\frac{1}{2}\left[\text{tr}\left({\mathbf{\Sigma }}_{\mathbf{Z}}^{-1}{\mathbf{Z}}^{⊺}\mathbf{Z}\right)-\text{tr}\left({\mathbf{\Sigma }}_{\mathbf{Z}}^{-1}{\mathit{\mu }}_{\mathbf{Z}}^{⊺}\mathbf{Z}\right)-\text{tr}\left({\mathbf{\Sigma }}_{\mathbf{Z}}^{-1}{\mathbf{Z}}^T{\mathit{\mu }}_{\mathbf{Z}}\right)+\text{tr}\left({\mathbf{\Sigma }}_{\mathbf{Z}}^{-1}{\mathit{\mu }}_{\mathbf{Z}}^T{\mathit{\mu }}_{\mathbf{Z}}\right)-\text{tr}\left({\mathbf{\Sigma }}_{\mathbf{Z}}^{-1}{\mathit{\mu }}_{\mathbf{Z}}^T{\mathit{\mu }}_{\mathbf{Z}}\right)\right]+O\left(1\right)=-\frac{1}{2}\left[\text{tr}\left({\mathbf{\Sigma }}_{\mathbf{Z}}^{-1}\left({\mathbf{Z}}^{⊺}\mathbf{Z}-{\mathbf{Z}}^T{\mathit{\mu }}_{\mathbf{Z}}-{\mathit{\mu }}_{\mathbf{Z}}^T\mathbf{Z}+{\mathit{\mu }}_{\mathbf{Z}}^T{\mathit{\mu }}_{\mathbf{Z}}\right)\right)\right]+O\left(1\right)=-\frac{1}{2}\text{tr}\left({\mathbf{\Sigma }}_{\mathbf{Z}}^{-1}{\left(\mathbf{Z}-{\mathit{\mu }}_{\mathbf{Z}}\right)}^{⊺}\left(\mathbf{Z}-{\mathit{\mu }}_{\mathbf{Z}}\right)\right)+O\left(1\right)\Rightarrow \\ Q\left(\mathbf{Z}\right)=\mathcal{M}{\mathcal{N}}_{n,k}\left(\mathbf{Z}|{\mathit{\mu }}_{\mathbf{Z}},{\mathbf{I}}_n,{\mathbf{\Sigma }}_{\mathbf{Z}}\right)\end{array}$$

Second, we derive the $\log Q\left(w_{kl}|{\mathit{\gamma }}_{kli}=1\right)$:

$$\log Q\left(w_{kl}|{\mathit{\gamma }}_{kli}=1\right)=-\frac{\tau }{2}{\mathbb{E}}_{\neg w_{kl}}\left[\text{tr}\left({\left({\mathbf{R}}_{kl}-{\mathbf{Z}}_k{\mathbf{w}}_{kl}^{⊺}\right)}^{⊺}\left({\mathbf{R}}_{kl}-{\mathbf{Z}}_k{\mathbf{w}}_{kl}^{⊺}\right)\right)\right]-\frac{{\tau }_0}{2}{\mathbb{E}}_{\neg w_{kl}}\left[\sum _{l=1}^L\sum _{k=1}^K{w}_{kl}^2\right]+O\left(1\right)=-\frac{\tau }{2}{\mathbb{E}}_{\neg w_{kl}}\left[-2\text{tr}\left({\mathbf{R}}_{kl}^{⊺}{\mathbf{Z}}_k{\mathbf{w}}_{kl}^{⊺}\right)+\text{tr}\left({\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k{\mathbf{w}}_{kl}^{⊺}{\mathbf{w}}_{kl}\right)\right]-\frac{{\tau }_0}{2}{w}_{kl}^2+O\left(1\right)=-\frac{\tau }{2}{\mathbb{E}}_{\neg w_{kl}}\left[-2\text{tr}\left({\left(\mathbf{X}-\sum _{k^{\prime }\ne k}{\mathbf{Z}}_{k^{\prime }}{\mathbf{w}}_{k^{\prime }}^{⊺}-\sum _{l^{\prime }\ne l}{\mathbf{Z}}_k{\mathbf{w}}_{k{l}^{\prime }}^{⊺}\right)}^{⊺}{\mathbf{Z}}_k{\mathbf{w}}_{kl}^{⊺}\right)+\text{tr}\left({\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k{w}_{kl}^2\right)\right]-\frac{{\tau }_0}{2}{w}_{kl}^2+O\left(1\right)=-\frac{\tau }{2}{\mathbb{E}}_{\neg w_{kl}}\left[-2\text{tr}\left(\left({\mathbf{X}}^{⊺}{\mathbf{Z}}_k-\sum _{k^{\prime }\ne k}{\mathbf{w}}_{k^{\prime }}{\mathbf{Z}}_{k^{\prime }}^{⊺}{\mathbf{Z}}_k-\sum _{l^{\prime }\ne l}{\mathbf{w}}_{k{l}^{\prime }}{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right){\mathbf{w}}_{kl}^{⊺}\right)+\text{tr}\left({\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k{w}_{kl}^2\right)\right]-\frac{{\tau }_0}{2}{w}_{kl}^2+O\left(1\right)=-\frac{\tau }{2}{\mathbb{E}}_{\neg w_{kl}}\left[-2\left({\mathbf{X}}_i^{⊺}{\mathbf{Z}}_k-\sum _{k^{\prime }\ne k}{\mathbf{w}}_{k^{\prime },i}{\mathbf{Z}}_{k^{\prime }}^{⊺}{\mathbf{Z}}_k-{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\sum _{l^{\prime }\ne l}\mathbf{w}{i}_{k{l}^{\prime }}\right)w_{kl}+{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k{w}_{kl}^2\right]-\frac{{\tau }_0}{2}{w}_{kl}^2+O\left(1\right)=-\frac{1}{2}\left[-2\tau \left({\mathbf{X}}_i^{⊺}\mathbb{E}\left[{\mathbf{Z}}_k\right]-\sum _{k^{\prime }\ne k}\mathbb{E}\left[{\mathbf{w}}_{k^{\prime },i}\right]\mathbb{E}\left[{\mathbf{Z}}_{k^{\prime }}^{⊺}{\mathbf{Z}}_k\right]-\mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]\sum _{l^{\prime }\ne l}\mathbb{E}\left[\mathbf{w}{i}_{k{l}^{\prime }}\right]\right)w_{kl}+\tau \mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]w_{kl}^2\right]-\frac{{\tau }_0}{2}{w}_{kl}^2+O\left(1\right)=-\frac{1}{2}[-2\tau \left({\mathbf{X}}_i^{⊺}\mathbb{E}\left[{\mathbf{Z}}_k\right]-\sum _{k^{\prime }\ne k}\mathbb{E}\left[{\mathbf{w}}_{k^{\prime },i}\right]\mathbb{E}\left[{\mathbf{Z}}_{k^{\prime }}^{⊺}{\mathbf{Z}}_k\right]-\mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]\sum _{l^{\prime }\ne l}\mathbb{E}\left[\mathbf{w}{i}_{k{l}^{\prime }}\right]\right)w_{kl}+\tau \mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]w_{kl}^2+{\tau }_0{w}_{kl}^2]+O\left(1\right)=-\frac{1}{2}[-2\tau \left({\mathbf{X}}_i^{⊺}\mathbb{E}\left[{\mathbf{Z}}_k\right]-\sum _{k^{\prime }\ne k}\mathbb{E}\left[{\mathbf{w}}_{k^{\prime },i}\right]\mathbb{E}\left[{\mathbf{Z}}_{k^{\prime }}^{⊺}{\mathbf{Z}}_k\right]-\mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]\sum _{l^{\prime }\ne l}\mathbb{E}\left[\mathbf{w}{i}_{k{l}^{\prime }}\right]\right)w_{kl}+\underset{1/{\sigma }_{w_{kl}}^2}{\underbrace{\left(\tau \mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]+{\tau }_0\right)}}{w}_{kl}^2]+O\left(1\right)=-\frac{1}{2{\sigma }_{w_{kl}}^2}\left[w_{kl}^2-2\underset{{\mu }_{w_{kl}}}{\underbrace{\tau {\sigma }_{w_{kl}}^2\left({\mathbf{X}}_i^{⊺}\mathbb{E}\left[{\mathbf{Z}}_k\right]-\sum _{k^{\prime }\ne k}\mathbb{E}\left[{\mathbf{w}}_{k^{\prime },i}\right]\mathbb{E}\left[{\mathbf{Z}}_{k^{\prime }}^{⊺}{\mathbf{Z}}_k\right]-\mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]\sum _{l^{\prime }\ne l}\mathbb{E}\left[\mathbf{w}{i}_{k{l}^{\prime }}\right]\right)}}{w}_{kl}\right]\Rightarrow =\log \mathcal{N}\left({\mu }_{{\mathbf{w}}_{kl}},{\sigma }_{{\mathbf{w}}_{kl}}^2\right)$$

Noticed that we can update ${\mathbf{w}}_{kl}$ for all feature at once:

$${\mathit{\mu }}_{{\mathbf{w}}_{kl}}=\tau {\sigma }_{w_{kl}}^2\mathbb{E}\left[{\mathbf{R}}_{kl}^{⊺}{\mathbf{Z}}_k\right],{\mathit{\sigma }}_{{\mathbf{w}}_{kl}}={\sigma }_{w_{kl}}^2{\mathbf{I}}_p$$

Finally we derive the $\log Q\left({\mathit{\gamma }}_{kl}\right)$: Note that $\tau {\mathbf{R}}_{kl}^{⊺}\mathbb{E}\left[{\mathbf{Z}}_k\right]=\mathbb{E}\left[w_{kl}|{\mathit{\gamma }}_{kl}\right]/{\sigma }_{w_{kl}}^2={\mathit{\mu }}_{{\mathbf{w}}_{kl}}/{\sigma }_{w_{kl}}^2\text{.}$

$$\begin{array}{c}\log Q\left({\mathit{\gamma }}_{kli}=1\right)={\mathbb{E}}_{\neg {\mathit{\gamma }}_{kl}}\left[{\mathcal{l}}_c\left({\sigma }^2,{\sigma }_0^2,\mathit{\pi },|\mathbf{X},\mathbf{Z},\mathbf{W}\right)\right]+\text{logMulti}\left({\mathit{\gamma }}_{kl}|\mathit{\pi }\right)+O\left(1\right)=-\frac{\tau }{2}{\mathbb{E}}_{\neg {\mathit{\gamma }}_{kl}}\mathrm{t}\mathrm{r}\left({\left({\mathbf{R}}_{kl}-{\mathbf{Z}}_k{\mathbf{w}}_{kl}^{⊺}\right)}^{⊺}\left({\mathbf{R}}_{kl}-{\mathbf{Z}}_k{\mathbf{w}}_{kl}^{⊺}\right)\right)+\text{logMulti}\left({\mathit{\gamma }}_{kl}|\mathit{\pi }\right)+O\left(1\right)=-\frac{\tau }{2}\left[-2\text{tr}\left({\mathbf{R}}_{kl}^{⊺}\mathbb{E}\left[{\mathbf{Z}}_k\right]\mathbb{E}\left[w_{kl}|{\mathit{\gamma }}_{kli}=1\right]{\mathit{\gamma }}_{kl}^{⊺}\right)+\text{tr}\left(\mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]\mathbb{E}\left[w_{kl}^2|{\mathit{\gamma }}_{kli}=1\right]\right)\right]+\log {\mathit{\pi }}_i+O\left(1\right)=-\frac{\tau }{2}\left[-2{\mathbf{R}}_{kli}^{⊺}\mathbb{E}\left[{\mathbf{Z}}_k\right]\mathbb{E}\left[w_{kl}|{\mathit{\gamma }}_{kli}=1\right]+\mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]\mathbb{E}\left[w_{kl}^2|{\mathit{\gamma }}_{kl}\right]\right]+\log {\mathit{\pi }}_i+O\left(1\right)⟨⟩=\tau {\mathbf{R}}_{kli}^{⊺}\mathbb{E}\left[{\mathbf{Z}}_k\right]\mathbb{E}\left[w_{kl}|{\mathit{\gamma }}_{kli}=1\right]-\frac{\tau }{2}\mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]\mathbb{E}\left[w_{kl}^2|{\mathit{\gamma }}_{kli}=1\right]+\log {\mathit{\pi }}_i+O\left(1\right)=\frac{1}{{\sigma }_{w_{kl}}^2}\mathbb{E}{\left[w_{kl}|{\mathit{\gamma }}_{kli}=1\right]}^2-\frac{\tau }{2}\mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]\mathbb{E}\left[w_{kl}^2|{\mathit{\gamma }}_{kli}=1\right]+\log {\mathit{\pi }}_i-\frac{{\tau }_0}{2}\mathbb{E}\left[w_{kl}^2|{\mathit{\gamma }}_{kli}=1\right]+O\left(1\right)=\frac{1}{{\sigma }_{w_{kl}}^2}\mathbb{E}{\left[w_{kl}|{\mathit{\gamma }}_{kli}=1\right]}^2-\frac{1}{2}\mathbb{E}\left[w_{kl}^2|{\mathit{\gamma }}_{kli}=1\right]\left(\tau \mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]+{\tau }_0\right)+\log {\mathit{\pi }}_i+O\left(1\right)=\frac{1}{{\sigma }_{w_{kl}}^2}\mathbb{E}{\left[w_{kl}|{\mathit{\gamma }}_{kli}=1\right]}^2-\frac{1}{2{\sigma }_{w_{kl}}^2}\mathbb{E}\left[w_{kl}^2|{\mathit{\gamma }}_{kli}=1\right]+\log {\mathit{\pi }}_i+O\left(1\right)=-\frac{1}{2{\sigma }_{w_{kl}}^2}\left[-2\mathbb{E}{\left[w_{kl}|{\mathit{\gamma }}_{kli}=1\right]}^2+\mathbb{E}\left[w_{kl}^2|{\mathit{\gamma }}_{kli}=1\right]\right]+\log {\mathit{\pi }}_i+O\left(1\right)=-\frac{1}{2{\sigma }_{w_{kl}}^2}\left[-2\mathbb{E}{\left[w_{kl}|{\mathit{\gamma }}_{kli}=1\right]}^2+{\sigma }_{w_{kl}}^2+\mathbb{E}{\left[w_{kl}|{\mathit{\gamma }}_{kli}=1\right]}^2\right]+\log {\mathit{\pi }}_i+O\left(1\right)=\frac{1}{2{\sigma }_{{\mathbf{w}}_{kl}}^2}\mathbb{E}{\left[{\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kli}=1\right]}^2+\log {\mathit{\pi }}_i+O\left(1\right)\Rightarrow \\ \log {\tilde{\mathit{\alpha }}}_{kli}=\log {\mathit{\pi }}_i-\log \mathcal{N}\left(0|{\mu }_{{\mathbf{w}}_{kl}},{\sigma }_{{\mathbf{w}}_{kl}}^2\right)\\ Q\left({\mathit{\gamma }}_{kl}\right)=\text{Multi}\left(1,{\mathit{\alpha }}_{kl}=\text{softmax}\left(\log {\tilde{\mathit{\alpha }}}_{kl}\right)\right)\end{array}$$

In summary, the optimal variational distribution of model parameters can be summarized as:

$$Q\left(\mathbf{Z}\right):=\mathcal{M}{\mathcal{N}}_{n,k}\left(\mathbf{Z}|{\mathit{\mu }}_{\mathbf{Z}},{\mathbf{I}}_n,{\mathbf{\Sigma }}_{\mathbf{Z}}\right)$$ (Equation 13)

$$Q\left(w_{kl}|{\mathit{\gamma }}_{kl}\right):=\mathcal{N}\left({\mu }_{{\mathbf{w}}_{kl}},{\sigma }_{{\mathbf{w}}_{kl}}^2\right)$$ (Equation 14)

$$Q\left({\mathit{\gamma }}_{kl}\right):=\text{Multi}\left(1,{\mathit{\alpha }}_{kl}\right)\text{.}$$ (Equation 15)

The corresponding update rules for variational parameters from $Q(·)$ can be expressed as,

$${\mathit{\mu }}_{\mathbf{Z}}=\tau \mathbf{X}\mathbb{E}\left[{\mathbf{W}}^{⊺}\right]{\mathbf{\Sigma }}_{\mathbf{Z}}$$ (Equation 16)

$${\mathbf{\Sigma }}_{\mathbf{Z}}={\left(\mathbb{E}\left[\mathbf{W}{\mathbf{W}}^{⊺}\right]\tau +{\mathbf{I}}_k\right)}^{-1}$$ (Equation 17)

$${\mathit{\mu }}_{{\mathbf{w}}_{kl}}=\tau {\sigma }_{w_{kl}}^2\mathbb{E}\left[{\mathbf{R}}_{kl}^{⊺}{\mathbf{Z}}_k\right]$$ (Equation 18)

$${\mathbf{\Sigma }}_{{\mathbf{w}}_{kl}}={\sigma }_{{\mathbf{w}}_{kl}}^2{\mathbf{I}}_p$$ (Equation 19)

$${\sigma }_{{\mathbf{w}}_{kl}}^2={\left(\tau \mathbb{E}\left[{\mathbf{Z}}_k^{⊺}{\mathbf{Z}}_k\right]+{\tau }_{0kl}\right)}^{-1}$$ (Equation 20)

$${\mathit{\alpha }}_{kl}=\text{softmax}\left(\log \mathit{\pi }-\log \mathcal{N}\left(0|{\mu }_{{\mathbf{w}}_{kl}},{\sigma }_{{\mathbf{w}}_{kl}}^2\right)\right)\text{.}$$ (Equation 21)

Derivation of evidence lower bound (ELBO)

The ELBO provides a natural criterion for evaluating model performance during model training, and also provides a means to perform hyperparameter optimization for model variance τ and ${\tau }_0$ (or equivalently precision) parameters. Given the above definitions for Q, we derive the ELBO for SuSiE PCA as

$$\begin{array}{l}\text{ELBO}\left(\mathbf{W},\mathbf{Z}\right)={\mathbb{E}}_Q\left[\text{logPr}\left(\mathbf{X},\mathbf{Z},\mathbf{W}\right)-\log Q\left(\mathbf{Z},\mathbf{W}\right)\right]={\mathbb{E}}_Q\left[\text{logPr}\left(\mathbf{X}|\mathbf{Z},\mathbf{W}\right)\right]+{\mathbb{E}}_Q\left[\text{logPr}\left(\mathbf{Z},\mathbf{W}\right)-\log Q\left(\mathbf{Z},\mathbf{W}\right)\right]={\mathbb{E}}_Q\left[\text{logPr}\left(\mathbf{X}|\mathbf{Z},\mathbf{W}\right)\right]+{\mathbb{E}}_{Q\left(\mathbf{Z}\right)}\left[\text{logPr}\left(\mathbf{Z}\right)-\log Q\left(\mathbf{Z}\right)\right]+\\ \sum _{l=1}^L\left[{\mathbb{E}}_{Q\left({\mathbf{w}}_l|{\mathbf{\Gamma }}_l\right)}\left[\text{logPr}\left({\mathbf{w}}_l|{\mathbf{\Gamma }}_l\right)-\log Q\left({\mathbf{w}}_l|{\mathbf{\Gamma }}_l\right)\right]+{\mathbb{E}}_{Q\left({\mathbf{\Gamma }}_l\right)}\left[\text{logPr}\left({\mathbf{\Gamma }}_l\right)-\log Q\left({\mathbf{\Gamma }}_l\right)\right]\right]={\mathbb{E}}_Q\left[\text{logPr}\left(\mathbf{X}|\mathbf{Z},\mathbf{W}\right)\right]+{\mathbb{E}}_{Q\left(\mathbf{Z}\right)}\left[\text{logPr}\left(\mathbf{Z}\right)-\log Q\left(\mathbf{Z}\right)\right]+{\mathbb{E}}_{Q\left(\mathbf{W},\mathbf{\Gamma }\right)}\left[\text{logPr}\left(\mathbf{W},\mathbf{\Gamma }\right)-\log Q\left(\mathbf{W},\mathbf{\Gamma }\right)\right]\end{array}$$

Based on the above derivation, ELBO can be decomposed into three parts. The first term is the expectation of the data with respect to all the parameters in the model:

$${\mathbb{E}}_Q\left[\text{logPr}\left(\mathbf{X}|\mathbf{Z},\mathbf{W},\mathbf{\Gamma }\right)\right]={\mathbb{E}}_Q\left[-\frac{1}{2{\sigma }^2}\mathrm{t}\mathrm{r}\left[{\left(\mathbf{X}-\mathbf{Z}\mathbf{W}\right)}^{⊺}\left(\mathbf{X}-\mathbf{Z}\mathbf{W}\right)\right]-\frac{np}{2}\log \left(2\pi {\sigma }^2\right)\right]=-\frac{1}{2{\sigma }^2}\left[\text{tr}\left({\mathbf{X}}^{⊺}\mathbf{X}\right)-2\mathrm{t}\mathrm{r}\left({\mathbf{X}}^{⊺}\mathbb{E}\left[\mathbf{Z}\right]\mathbb{E}\left[\mathbf{W}\right]\right)+\text{tr}\left(\mathbb{E}\left[{\mathbf{Z}}^{⊺}\mathbf{Z}\right]\mathbb{E}\left[\mathbf{W}{\mathbf{W}}^{⊺}\right]\right)\right]-\frac{np}{2}\log \left(2\pi {\sigma }^2\right)$$

The second term is the negative KL divergence of $\mathbf{Z}$.

$$\begin{array}{l}{\mathbb{E}}_{Q\left(\mathbf{Z}\right)}\left[\text{logPr}\left(\mathbf{Z}\right)-\log Q\left(\mathbf{Z}\right)\right]=\mathbb{E}[-\frac{1}{2}\mathrm{t}\mathrm{r}\left({\mathbf{Z}}^{⊺}\mathbf{Z}\right)-\frac{nk}{2}\log \left(2\pi \right)+\frac{1}{2}\mathrm{t}\mathrm{r}\left({\mathbf{\Sigma }}_{\mathbf{Z}}^{-1}{\left(\mathbf{Z}-{\mathit{\mu }}_{\mathbf{Z}}\right)}^{⊺}\left(\mathbf{Z}-{\mathit{\mu }}_{\mathbf{Z}}\right)\right)\\ +\frac{nk}{2}\log \left(2\pi \right)+\frac{n}{2}\log \left(\left|{\mathbf{\Sigma }}_{\mathbf{Z}}\right|\right)]\\ =-\frac{1}{2}\text{tr}\left(\mathbb{E}\left[{\mathbf{Z}}^{⊺}\mathbf{Z}\right]\right)+\frac{1}{2}\mathrm{t}\mathrm{r}\left[{\mathbf{\Sigma }}_{\mathbf{Z}}^{-1}\left(E\left[{\mathbf{Z}}^{⊺}\mathbf{Z}\right]-{\mathit{\mu }}_{\mathbf{Z}}^{⊺}{\mathit{\mu }}_{\mathbf{Z}}\right)\right]+\frac{N}{2}\log \left(\left|{\mathbf{\Sigma }}_{\mathbf{Z}}\right|\right)\\ =-\frac{1}{2}\text{tr}\left(\mathbb{E}\left[{\mathbf{Z}}^{⊺}\mathbf{Z}\right]\right)+\frac{1}{2}\mathrm{t}\mathrm{r}\left[{\mathbf{\Sigma }}_{\mathbf{Z}}^{-1}\left(N{\mathbf{\Sigma }}_{\mathbf{Z}}+{\mathit{\mu }}_{\mathbf{Z}}^{⊺}{\mathit{\mu }}_{\mathbf{Z}}-{\mathit{\mu }}_{\mathbf{Z}}^{⊺}{\mathit{\mu }}_{\mathbf{Z}}\right)\right]+\frac{N}{2}\log \left(\left|{\mathbf{\Sigma }}_{\mathbf{Z}}\right|\right)\\ =-\frac{1}{2}\text{tr}\left(\mathbb{E}\left[{\mathbf{Z}}^{⊺}\mathbf{Z}\right]\right)+\frac{NK}{2}+\frac{N}{2}\log \left(\left|{\mathbf{\Sigma }}_{\mathbf{Z}}\right|\right)\end{array}$$

The last term contains joint negative KL divergence of $\mathbf{W}\text{and}\mathbf{\Gamma }$ can be further decomposed as following:

$$\begin{array}{l}{\mathbb{E}}_{Q\left(\mathbf{W},\mathbf{\Gamma }\right)}\left[\text{logPr}\left(\mathbf{W},\mathbf{\Gamma }\right)-\log Q\left(\mathbf{W},\mathbf{\Gamma }\right)\right]={\mathbb{E}}_{Q\left(\mathbf{W},\mathbf{\Gamma }\right)}\left[\text{logPr}\left(\mathbf{W}|\mathbf{\Gamma }\right)\mathrm{Pr}\left(\mathbf{\Gamma }\right)-\log Q\left(\mathbf{W}|\mathbf{\Gamma }\right)Q\left(\mathbf{\Gamma }\right)\right]={\mathbb{E}}_{Q\left(\mathbf{W},\mathbf{\Gamma }\right)}\left[\text{logPr}\left(\mathbf{W}|\mathbf{\Gamma }\right)-\log Q\left(\mathbf{W}|\mathbf{\Gamma }\right)\right]+{\mathbb{E}}_{Q\left(\mathbf{W},\mathbf{\Gamma }\right)}\left[\text{logPr}\left(\mathbf{\Gamma }\right)-\log Q\left(\mathbf{\Gamma }\right)\right]=\sum _{k=1}^K\sum _{l=1}^L{\mathbb{E}}_{Q\left({\mathbf{w}}_{kl},{\mathit{\gamma }}_{kl}\right)}\left[\text{logPr}\left({\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kl}\right)-\log Q\left({\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kl}\right)\right]+\\ \sum _{k=1}^K\sum _{l=1}^L{\mathbb{E}}_{Q\left({\mathit{\gamma }}_{kl}\right)}\left[\text{logPr}\left({\mathit{\gamma }}_{kl}\right)-\log Q\left({\mathit{\gamma }}_{kl}\right)\right]=\sum _{k=1}^K\sum _{l=1}^L\sum _{i=1}^P{\mathit{\alpha }}_{kli}{\mathbb{E}}_{Q\left({\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kl}\right)}[\log \mathrm{Pr}\left({\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kli}=1\right)-\log Q\left({\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kli}=1\right)]+\\ \sum _{k=1}^K\sum _{l=1}^L\sum _{i=1}^P{\mathbb{E}}_{{\mathit{\gamma }}_{kl}}\left[\text{logPr}\left({\mathit{\gamma }}_{kli}=1\right)-\log Q\left({\mathit{\gamma }}_{kli}=1\right)\right]\end{array}$$

The first expectation term of the last line of equation ${\mathbb{E}}_{Q\left({\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kl}\right)}$ can be expanded as following:

$$\begin{array}{l}{\mathbb{E}}_{Q\left({\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kl}\right)}\left[\log \frac{\mathrm{Pr}\left({\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kl}\right)}{Q\left({\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kl}\right)}\right]=\sum _{i=1}^P{\mathbb{E}}_{Q\left({\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kli}=1\right)}\left[\log \frac{\mathrm{Pr}\left({\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kli}=1\right)}{Q\left({\mathbf{w}}_{kl}|{\mathit{\gamma }}_{kli}=1\right)}\right]=\mathbb{E}\sum _{i=1}^P\left[-\frac{{\tau }_0}{2}{\left(w_{kli}\right)}^2+\frac{1}{2{\sigma }_{w_{kl}}^2}{\left(w_{kli}-{\mathit{\mu }}_{w_{kli}}\right)}^2\right]=\sum _{i=1}^P\left[\left(-\frac{{\tau }_0}{2}+\frac{1}{2{\sigma }_{w_{kl}}^2}\right)\left[{\mu }_{w_{kli}}^2+{\sigma }_{w_{kl}}^2\right]-\frac{1}{2{\sigma }_{w_{kl}}^2}{\mu }_{w_{kli}}^2\right]+\frac{P}{2}\log \left({\sigma }_{w_{kl}}^2{\tau }_0\right)+\frac{P}{2}\log \left({\sigma }_{w_{kl}}^2{\tau }_0\right)=\sum _{i=1}^P\left[-\frac{{\tau }_0}{2}{\mu }_{w_{kli}}^2-\frac{{\tau }_0}{2}{\sigma }_{w_{kli}}^2+\frac{1}{2}\right]+\frac{P}{2}\log \left({\sigma }_{w_{kl}}^2{\tau }_0\right)\\ -\frac{p}{2}\log \left(2\pi /{\tau }_0\right)+\frac{p}{2}\log \left(2\pi {\sigma }_{w_{kl}}^2\right)]\\ =\sum _{i=1}^P\left[\left(-\frac{{\tau }_0}{2}+\frac{1}{2{\sigma }_{w_{kl}}^2}\right)\mathbb{E}\left[{\left(w_{kli}\right)}^2\right]-\frac{1}{2{\sigma }_{w_{kl}}^2}{\mu }_{w_{kli}}^2\right]-\frac{P}{2}\mathit{log}\left(2\pi /{\tau }_0\right)+\frac{P}{2}\log \left(2\pi {\sigma }_{w_{kl}}^2\right)\end{array}$$

And the second expectation term ${\mathbb{E}}_{{\mathit{\gamma }}_{kl}}$ can be decomposed as

$${\mathbb{E}}_{Q\left(\mathbf{\Gamma }\right)}\left[\text{logPr}\left(\mathbf{\Gamma }\right)-\log Q\left(\mathbf{\Gamma }\right)\right]=\sum _{k=1}^K\sum _{l=1}^L\sum _{i=1}^P{\mathbb{E}}_{Q\left({\mathit{\gamma }}_{kli}=1\right)}\left[\left({\mathit{\gamma }}_{kli}\log {\pi }_i-{\mathit{\gamma }}_{kli}\log {\alpha }_{kli}\right)\right]=\sum _{k=1}^K\sum _{l=1}^L\sum _{i=1}^P\left[\mathbb{E}\left({\mathit{\gamma }}_{kli}\right)\log \left({\pi }_i\right)-\mathbb{E}\left({\mathit{\gamma }}_{kli}\right)\log \left({\alpha }_{kli}\right)\right]=\sum _{k=1}^K\sum _{l=1}^L\sum _{i=1}^P\left[{\alpha }_{kli}\left(\log \left({\pi }_i\right)-\log {\alpha }_{kli}\right)\right]$$

With the explicit form of ELBO, we obtained the maximum likelihood estimates of model precision parameters $\tau ,{\tau }_{0kl}$ by setting the derivative of ELBO with respect to each variance parameter to be 0, which results in closed-form update equations given by,

$${\hat{\tau }}_{0kl}=\frac{{\sum }_{i=1}^P{\alpha }_{kli}}{{\sum }_{i=1}^P{\alpha }_{kli}\left({\mu }_{{\mathbf{w}}_{kli}}^2+{\sigma }_{{\mathbf{w}}_{kli}}^2\right)}$$ (Equation 22)

$$\hat{\tau }=\frac{NP}{{\sum }_{i,j}{X}_{ij}^2-2\mathrm{t}\mathrm{r}\left(\mathbb{E}\left[\mathbf{W}\right]{\mathbf{X}}^{⊺}{\mathit{\mu }}_{\mathbf{Z}}\right)}\text{.}$$ (Equation 23)

Simulations

To investigate the performance of SuSiE PCA in variable selection and model fitting, we simulated various data sets that are controlled by 4 parameters: the sample size N, number of features P, number of latent factors K, and number of single effects L in each of the factors. For simplicity, we assume L is the same across different factors. The simulated data $\mathbf{X}$ is generated according to equation ((0.1)), where $N=1000,P=6000$, and ${\mathbf{z}}_k$ and ${\mathbf{w}}_k$, for $k=1,\cdots ,4$ are simulated such that each factor only contain 40 non-zero effects (0.67%) given by,

$${\mathbf{z}}_k\sim \mathcal{N}\left(0,{\mathbf{I}}_N\right)$$ (Equation 24)

$$w_{1,i}\sim \mathcal{N}\left(\mathrm{0,1}\right)i=1,\cdots ,40$$ (Equation 25)

$$w_{2,i}\sim \mathcal{N}\left(\mathrm{0,1}\right)i=41,\cdots ,80$$ (Equation 26)

$$w_{3,i}\sim \mathcal{N}\left(0,2^2\right)i=81,\cdots ,120$$ (Equation 27)

$$w_{4,i}\sim \mathcal{N}\left(\mathrm{0,1}\right)i=121,\cdots ,160$$ (Equation 28)

with the remaining effects set to zero. Considering the scale of the estimates of loadings may differ from various types of methods, we normalized the loading matrix with respect to Frobenius norm, i.e. $\text{tr}\left(A^{⊺}A\right)=\text{tr}\left(B^{⊺}B\right)=1$.

To evaluate the accuracy of SuSiE PCA, we compared inferred posterior expectations with the true latent variables. However, due to the rotational invariance property in latent factor models, evaluating loading or latent factor accuracy can be challenging. To account for possible rotation, we leverage the Procrustes transformation,¹⁷ which finds an orthogonal rotation matrix $\mathbf{P}$ to transform the estimated loading matrix to the true loading matrix space. Specifically, given an estimated loading matrix $\hat{\mathbf{W}}:={\mathbb{E}}_Q\left[\mathbf{W}\right]$ under approximate posterior distribution Q and true effect matrix $\mathbf{W}$, the “Procrustes Norm” can be obtained as following:

$${\Vert \mathbf{W}-\hat{\mathbf{W}}\Vert }_P^2:=\underset{\left\{\mathbf{P}|{\mathbf{P}}^{-1}={\mathbf{P}}^{⊺}\right\}}{\min }{\Vert \hat{\mathbf{W}}\mathbf{P}-\mathbf{W}\Vert }_F^2$$ (Equation 29)

Here we perform the Procrustes analysis via Procrustes package,¹⁶ from which $\mathbf{P}$ is obtained by performing a singular value decomposition on matrix ${\hat{\mathbf{W}}}^{⊺}{\hat{\mathbf{W}}}^{}$ (padding zeros on matrix $\hat{\mathbf{W}}$ would ensure the above operation process correctly).

In addition, we employ the relative root mean squared error (RRMSE) to evaluate the reconstructed data loss as,

$$\text{RRMSE}\left(\hat{\mathbf{X}},\mathbf{X}\right)=\sqrt{\frac{{\sum }_{i,j}{\left({\hat{x}}_{ij}-x_{ij}\right)}^2}{{\sum }_{i,j}{x}_{ij}^2}}$$ (Equation 30)

Lastly, to assess generative modeling proficiency, we computed the log-likelihood under held-out data. Specifically, we first trained the model on simulated training data. Next, we computed latent space representations for the testing data under each of the trained models. Lastly, we computed log-likelihoods under normality assumptions given the latent representations and learned loadings and parameters.

For model comparison, we also evaluate the performance of sparse PCA⁶ and Empirical Bayes Matrix Factorization (EBMF) (a recently described variational approach)¹² on the same simulation data sets with the same K, and compare the model performance with SuSiE PCA via criterion described above.

GTEx Z score dataset

To illustrate the application of SuSiE PCA in genetic research, we downloaded the Genotype-Tissue Expression (GTEx)¹⁴ summary statistics data, composed of z-scores computed from the testing association between genetic variants and the gene expression levels across 44 different human tissues.¹² The GTEx project collected genotype data and gene expression data from 49 non-disease tissues across $n=838$ individuals, providing an ideal resource database to study the relationship between genetic variants and gene expression levels.¹⁴ The genetic variants that are statistically associated with gene expression levels are referred to as expression quantitative trait loci (eQTLs). To identify eQTLs, the GTEx project tested the association between each nearby genetic variant of a certain gene with its expression levels using linear regression to yield a Z score. The summary data we explored reflects the most significant eQTL (equivalently, the largest absolute Z score in each SNP and gene pair) at each of 16069 genes (row) from 44 tissues (column) curated from GTEx v8,^12,14 as those 16069 genes show indication of being expressed in 44 of all 49 human tissues. To identify tissue-specific components of regulatory genetic features and contributing genes, we applied SuSiE PCA across this Z score matrix with a latent dimension of 27 and the number of single effects of 18. The prior information on the number of latent dimensions comes from Wang et al. (2021)¹² who contribute to the Z score dataset and run the EBMF model with 27 factors. To determine the appropriate L that fits the data, we run the SuSiE PCA with L ranged from 10 to 25, and select the model when the increase in the total percentage of variance explained (PVE) is less than 5%. PVE is a measure of the amount of signals in the data captured by the latent component, the PVE of the factor ${\mathbf{z}}_k$ is calculated based on the following equation:

$${\text{PVE}}_k=\frac{s_k}{{\sum }_k{s}_k+NP/\tau }$$ (Equation 31)

where $s_k={\sum }_{i=1}^N{\sum }_{j=1}^P{\left(\mathbb{E}\left[z_{ik}\right]\mathbb{E}\left[w_{kj}\right]\right)}^2$.

Purturb-seq dataset

We next investigated genome-scale Perturb-seq data¹⁵ to discover the co-regulated gene sets affected by some common type of perturbations. The Perturb-seq data originated from Perturb-seq experiments performed by Replogle et al.¹⁵ Perturb-seq is a cutting-edge technique combining CRISPR-based perturbations with single-cell RNA-sequencing readouts, enabling the investigation of co-regulated gene sets affected by various perturbations. The researchers employed three cell lines: K562 cells, hTERT-immortalized RPE1 cells, and HEK293T cells. CRISPRi technology was used to generate cell lines expressing dCas9-BFP-KRAB (KOX1-derived) for the perturbation experiments. Since we focus our analyses on the expression data from the K562 cell line, we give a brief description of the experiments performed on the K562 cell lines. Namely, the authors targeted genes expressed in K562 cells, transcription factors, Cancer Dependency Map common essential genes, and included non-targeting control sgRNAs accounting for 5% of the total library. The gene sets were defined based on a combination of bulk RNA-seq data from ENCODE and 10x Genomics 3′ single-cell RNA-seq data. Libraries were constructed with dual-sgRNA pairs targeting each gene, expressed from tandem U6 expression cassettes in a single lentiviral vector, and ranked based on empirical data and computational predictions. Subsequently, the author conducted Perturb-seq experiments on the K562 cells, with 2056 distinct knocked-out genes and one non-targeting control group over an average of 150 different single cells, and then measured the expression levels of the downstream 8563 genes from each cell.

The final dataset contains 310385 rows, each representing one perturbation in a specific cell, and the expression levels of 8563 downstream genes as the column. As an exploratory analysis, we omitted the single-cell level information and aggregated the expression levels of downstream genes with the same perturbation over all the cells, which resulted in a “psuedo-bulk” data matrix with 2057 rows and 8563 columns. We then performed the SuSiE PCA and Sparse PCA to investigate the regulatory modules from the common perturbations. To exclude the batch effects and other non-genetic covariates, we regressed out the germ-line group and the mitochondrial percent from the original expression data and then aggregated the expression level of downstream genes with the same perturbation. Finally, the aggregated data is centered and standardized before input into SuSiE PCA.

As a comparison, we also run the sparse PCA with the same K in both datasets. While choosing an appropriate sparsity parameter alpha in sparse PCA is less straightforward than tuning L in the SuSiE PCA, as we cannot directly pull all of the non-zero genes even with a fairly large alpha (higher sparsity). To make a reasonable comparison, we run sparse PCA with a set of alpha from 1 to 20 and choose two models to compare: first, choose the model giving the highest PVE, then investigate the model having a similar level of PVE with SuSiE PCA.

Published: October 13, 2023

Data and code availability

• •This paper analyzes existing, publicly available data, i.e., the GTEx z-score dataset¹⁴ and the perturb-seq data.¹⁵ These accession numbers for the datasets are listed in the key resources table.
• •All original codes related to SuSiE PCA have been deposited and are publicly available on GitHub (https://github.com/mancusolab/susiepca).
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.