Abstract
Nowadays, many people worldwide suffer from brain disorders, and their health is in danger. So far, numerous methods have been proposed for the diagnosis of Schizophrenia (SZ) and attention deficit hyperactivity disorder (ADHD), among which functional magnetic resonance imaging (fMRI) modalities are known as a popular method among physicians. This paper presents an SZ and ADHD intelligent detection method of resting-state fMRI (rs-fMRI) modality using a new deep learning method. The University of California Los Angeles dataset, which contains the rs-fMRI modalities of SZ and ADHD patients, has been used for experiments. The FMRIB software library toolbox first performed preprocessing on rs-fMRI data. Then, a convolutional Autoencoder model with the proposed number of layers is used to extract features from rs-fMRI data. In the classification step, a new fuzzy method called interval type-2 fuzzy regression (IT2FR) is introduced and then optimized by genetic algorithm, particle swarm optimization, and gray wolf optimization (GWO) techniques. Also, the results of IT2FR methods are compared with multilayer perceptron, k-nearest neighbors, support vector machine, random forest, and decision tree, and adaptive neuro-fuzzy inference system methods. The experiment results show that the IT2FR method with the GWO optimization algorithm has achieved satisfactory results compared to other classifier methods. Finally, the proposed classification technique was able to provide 72.71% accuracy.
Keywords: Diagnosis, Schizophrenia, ADHD, fMRI, CNN-AE, IT2FR, GWO
Introduction
The human brain consists of a complex and large network of neurons responsible for controlling and monitoring all parts of the body (Górriz et al. 2021; Villringer and Chance 1997). The brain network has different areas that are constantly connected. Many neurons in different parts of the brain are connected and coordinated to perform any function in the body, creating complex brain patterns (Rogers et al. 2016; Broyd et al. 2009). Whenever connectivity is not well-connected in different areas of the brain, it can cause changes in the function of the brain and disorders such as attention deficit hyperactivity (ADHD) (Konrad and Eickhoff 2010), Schizophrenia (SZ) (Shoeibi et al. 2021a; Sadeghi et al. 2022), epilepsy (Shoeibi et al. 2021b, c; Ghassemi et al. 2019), and Parkinson's disease (PD) (Pagano et al. 2016). Initially, the diagnosis of various brain disorders was based on the DSM. The experience of a specialist physician plays a critical role in diagnosing the type of brain disorder (Volkow and O’Brien 2007; Wortzel and Arciniegas 2014). Therefore, examining and diagnosing the type of brain disorder is not possible for all physicians (Bracha 2006). For example, ADHD has some of the same symptoms as other brain disorders, such as PD and SZ, and is difficult for some specialists to diagnose (Tandon et al. 2013; Austerman 2015).
To overcome these challenges, functional neuroimaging modalities have been developed to diagnose a variety of brain disorders that are highly popular with physicians (Shoeibi et al. 2021d, e). Functional neuroimaging modalities include electroencephalography (EEG) (Sanei and Chambers 2013), functional magnetic resonance imaging (fMRI) (Wang et al. 2021), positron emission tomography (PET) (Choi et al. 2019), single-photon emission computed tomography (SPECT) (Mohammed et al. 2021), magnetoencephalography (MEG) (Aoe et al. 2019) and functional near-infrared spectroscopy (fNIRS) (Fernandez Rojas et al. 2019). FMRI modalities are the most important non-invasive techniques for assessing brain function during brain disorders (Wang et al. 2021). fMRI includes task fMRI (T-fMRI) and resting-state fMRI (rs-fMRI) modalities and shows spatial resolution in the brain, making fMRI modalities popular for examining functional connectivity in different parts of the brain (Khodatars et al. 2021). The fMRI data contains a 4-dimensional tensor so that the 3D volume of the brain is segmented into small areas, and the activity of each area is recorded for a certain period of time (Khodatars et al. 2021). In this modality, the two brain regions are functionally related if they have simultaneous functional activity (Khodatars et al. 2021). FMRI modalities have been used to analyze brain connectivity patterns in diagnosing various brain disorders by physicians and have yielded promising results (Eslami et al. 2019; Shoeibi et al. 2022a; Suk et al. 2016).
In recent years, studies have shown that functional connectivity analysis based on fMRI modalities plays a significant role in the diagnosis of brain disorders such as SZ (Shoeibi et al. 2021a), Alzheimer's disease (AD) (Castillo-Barnes et al. 2020), epilepsy (Luckett et al. 2022; Anter et al. 2022), ADHD (Konrad and Eickhoff 2010), and BD (Highland and Zhou 2022). Brain disorders alter functional connectivity in the brain, which fMRI modalities can see. However, diagnosis of brain disorders with fMRI modalities is a difficult and time-consuming task for physicians (Khodatars et al. 2021). For example, ADHD is a developmental disorder with some of the same symptoms as other brain disorders, such as SZ (Sadeghi et al. 2022), making it difficult for physicians to diagnose the type of brain disorder. The main issue with only relying on physicians for the diagnosis of mental disorders such as ADHD and Schizophrenia is that it is time-consuming and subjective measures may influence the final assessments of subjects. Hence, the possibility of misdiagnosis may increase. Application of machine learning approaches for the diagnosis, can overcome these limitations and provide fast, and accurate classification.
In some cases, both ADHD and SZ disorders have been observed simultaneously in patients, but it does not mean that one disease necessarily causes the other (Park et al. 2018; Groom et al. 2008). Other research has shown that people with close relatives with ADHD are more likely to develop SZ (Ross et al. 2000; Grimm et al. 2022). Dopamine is known as one of the causes of ADHD and SZ. Dopamine, as a neurotransmitter, may affect attention, concentration, pleasure, happiness, and motivation (Verdoux and Sutter 2002). In addition, other researchers have shown that perinatal risk factors may be involved in both diseases (Marsh and Williams 2006). According to references (Vovou et al. 2021; Bitsch et al. 2021), there may be an overlap between ADHD and SZ. ADHD and SZ disorders usually have a detrimental effect on memory and attention (https://www.wjgnet.com/2220-3206/full/v5/i1/47.htm). Similar to ADHD, SZ sufferers may experience challenges such as clarity of thinking. On the other hand, there are distinct differences between ADHD and SZ disorders regarding symptoms, diagnosis, and treatment (Pallanti and Salerno 2015; Wang et al. 2014). To address these challenges, in recent years, artificial intelligence (AI) methods have been used to diagnose various brain disorders from fMRI data, and researchers are trying to create working tools to diagnose these diseases (Feng et al. 2021; Khosla et al. 2019). In this paper, the authors aim to present new deep learning (DL)-based method for the simultaneous diagnosis of SZ and ADHD, so a brief description of SZ and ADHD is provided below.
SZ is a severe and chronic mental disorder characterized by impaired thinking, perception, and behavior. In addition, SZ causes psychosis, which is associated with significant disability (Sadeghi et al. 2022). DSM-5 is a guide for assessing and diagnosing mental disorders (Volkow and O’Brien 2007; Wortzel and Arciniegas 2014). According to the DSM-5, two or more of the symptoms of delusions, hallucinations, disorganized speech, grossly disorganized or catatonic behavior, and negative symptoms must frequently occur over one month (Volkow and O’Brien 2007; Wortzel and Arciniegas 2014). Numerous factors in SZ include genetic factors, environmental factors, and brain structure and function. While there is still no cure for SZ, research has led to more innovative and safer treatments. Researchers are also trying to diagnose the disease and identify its causes by studying and conducting research and using fMRI neuroimaging techniques to study the function of the brain.
ADHD is a neurodevelopmental disorder that is very common in children ages 3 and 6 (Loh et al. 2022; Zhao et al. 2022). ADHD includes three types of inattention, hyperactivity-impulsivity, and combination (Loh et al. 2022; Zhao et al. 2022). ADHD always causes many challenges for children, including forgetting simple things, talking non-stop, being distracted, etc. (Loh et al. 2022). ADHD has different symptoms for each person. Therefore, its accurate diagnosis is challenging for specialist doctors (Zhao et al. 2022).
Nowadays, a lot of research is being done to diagnose brain disorders using DL techniques (Rivera et al. 2021; Shoeibi et al. 2022b; Vieira et al. 2017). The DL models are inspired by the human nervous system, consisting of several interconnected layers of processing units with nonlinear activation functions called artificial neurons (Sharifrazi et al. 2020; Alizadehsani et al. 2021; Buchlak et al. 2022). One of the advantages of DL networks is their ability to directly process large raw data or data with little preprocessing on them to automatically extract the best features for the task (Sharifrazi et al. 2020; Alizadehsani et al. 2021; Buchlak et al. 2022).
So far, various researches have been done on diagnosing SZ (Sadeghi et al. 2022) and ADHD (Loh et al. 2022) using fMRI modalities and DL techniques. The main purpose of these pieces of research is to increase the performance for SZ or ADHD detection using MRI modalities. In addition, the researchers hope to be able to provide a working DL-based tool for the diagnosis of SZ and ADHD in the future. Further details of these studies are summarized in Table 6. However, among the presented studies, simultaneous diagnosis of SZ and ADHD from fMRI data using DL techniques has not been performed.
Table 6.
Results for ANFIS classifier models
| Methods | Acc (%) | Prec (%) | Rec (%) | F1 (%) |
|---|---|---|---|---|
| ANFIS | 64.91 | 64.58 | 65.01 | 64.54 |
| ANFIS-GA | 67.05 | 66.37 | 66.31 | 66.20 |
| ANFIS-PSO | 67.22 | 67.04 | 67.48 | 66.88 |
| ANFIS-GWO | 68.15 | 67.65 | 68.17 | 67.64 |
This paper presents a new SZ and ADHD detection method in rs-fMRI modality using 2D convolutional Autoencoder (CNN-AE) and interval type-2 fuzzy regression (IT2FR)- gray wolf optimization (GWO) methods. First, rs-fMRI data from the University of California Los Angeles (UCLA) dataset were used for SZ and ADHD detection (https://legacy.openfmri.org/dataset/ds000030/). The FMRIB software library (FSL) (Jenkinson et al. 2012) toolbox is used to preprocess rs-fMRI data. The preprocessing performed on rs-fMRI data includes various steps that are discussed in detail in the next section of this manuscript. Afterward, a CNN-AE model with the proposed layers is used to extract features from preprocessed fMRI data. Finally, the classification of features is done by different classifier methods, namely, decision tree (DT) (Safavian and Landgrebe 1991), multilayer perceptron (MLP) (Windeatt 2006), k-nearest neighbors (KNN) (Liao and Vemuri 2002), support vector machine (SVM) (Noble 2006), random forest (RF) (Belgiu and Drăguţ 2016), adaptive neuro-fuzzy inference system (ANFIS) (Shoeibi et al. 2022c), ANFIS-GA (genetic algorithm), ANFIS-PSO (particle swarm optimization), ANFIS-GWO, IT2FR-GA, IT2FR-PSO, and IT2FR-GWO. In this step, the IT2FR technique is introduced as a pioneering work and optimized using GA (Whitley 1994), PSO (Oca et al. 2009), and WGO (Sun et al. 2021) optimization algorithms. Also, combining the IT2FR with WGO is another novelty of this paper.
In the following, other sections of the paper are described. The second section introduces the proposed method of SZ detection from rs-fMRI data and the CNN-AE model. The third section is dedicated to the introduction of evaluation parameters. In the fourth section, the test results of the proposed method are presented. Finally, the discussion, conclusions, and future work are presented in the fifth section.
Proposed method
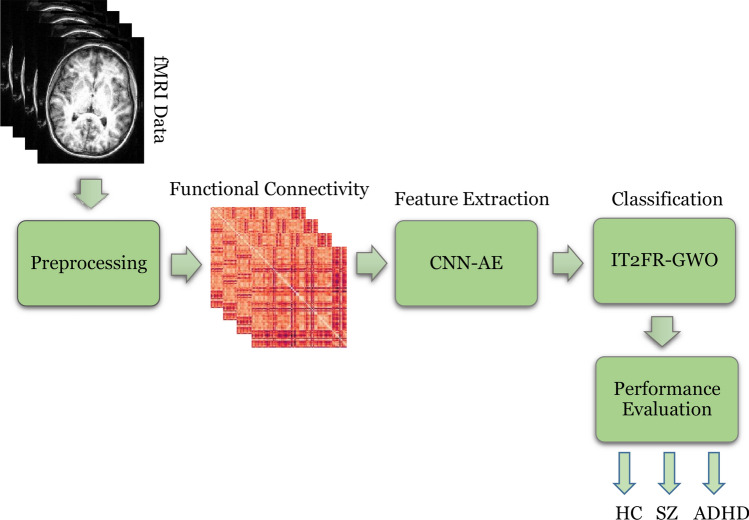
The proposed methods for SZ and ADHD detection from rs-fMRI modalities are introduced in this section. In Fig. 1, the steps of the proposed method are shown in the form of a diagram. First, the UCLA dataset containing rs-fMRI modalities was used. In the second step, preprocessing is performed on rs-fMRI data using FSL software. This step is based on standard preprocessing methods for rs-fMRI modalities. The following feature extraction method is based on the CNN-AE architecture with the suggested number of layers. Finally, various classification algorithms including MLP, KNN, SVM, RF, ANFIS, ANFIS-GA, ANFIS-PSO, ANFIS-GWO, IT2FR-GA, IT2FR-PSO, and IT2FR-GWO are used. In the following, each of these sections is presented.
Fig. 1.
Block diagram of the proposed method
Dataset
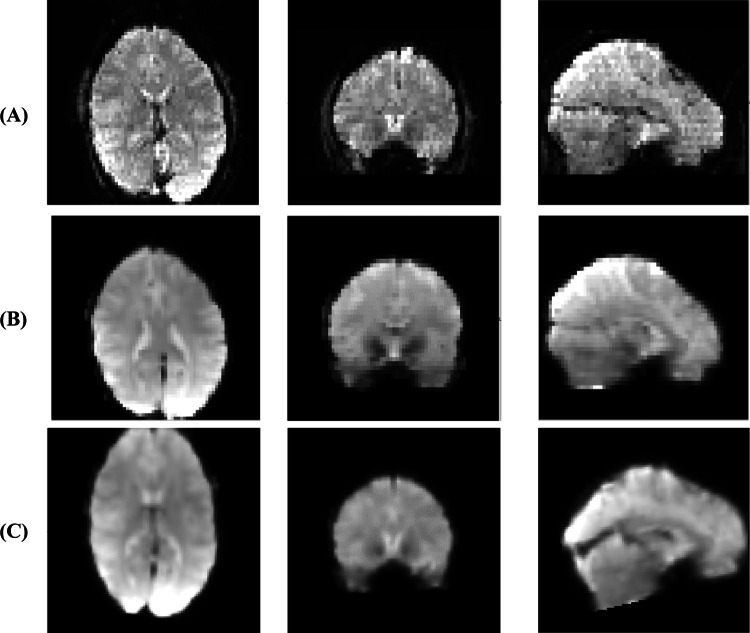
This paper used the UCLA dataset for our experiments (https://legacy.openfmri.org/dataset/ds000030/). This dataset has different versions; the first version is presented in reference (Culbreth et al. 2021). The dataset includes fMRI data from 138 healthy subjects, patients with Schizophrenia (58), Bipolar disorder (49), and ADHD (45). Additional information about the dataset (sex, age and etc.) can be found in Culbreth et al. (2021) (https://legacy.openfmri.org/dataset/ds000030/). In this paper, we used the healthy control (60 subjects), SZ (58 subjects), and ADHD (45 subjects) classes. We selected 60 HC subjects randomly from 138 subjects to make the dataset balanced between different classes. Figure 2 depicts some samples of rs-fMRI data from the UCLA dataset.
Fig. 2.
Sample rs-fMRI data from HC subjects (row A) and patients (row B)
Images were acquired using a 3 T Siemens Trio scanner. The rs-fMRI data with 304 s (eyes-open) was collected from each subject using T2*-weighted echo-planar imaging (EPI) pulse sequence with parameters: axial slices, number of slices = 34, slice thickness = 4 mm, TR = 2 s, TE = 30 ms, flip angle = 90°, matrix = 64 × 64, FOV = 192 × 192 mm2. Also, a T1-weighted high-resolution anatomical scan (MPRAGE) was acquired from each subject with the following parameters: sagittal slices, number of slices = 176, slice thickness = 1 mm, TR = 1.9 s, TE = 2.26 ms, matrix = 256 × 256, FOV = 250 × 250 mm2. The traditional statistical analyses (i.e., ANOVA and t-test) are conducted on demographic information and functional connectivity. Table 1 provides the details about the data used in this work with statistical analysis.
Table 1.
Details about the data used in this work with statistical analysis
| Variables | HC | SZ | ADHD | P value |
|---|---|---|---|---|
| No | 60 | 58 | 45 | – |
| Age (mean ± s.t.d) | 31.59 ± 8.78 | 36.46 ± 8.78 | 32.05 ± 10.27 | 0.019 |
| Hand Score (mean ± s.t.d)** | 0.91 ± 0.15 | 0.95 ± 0.09 | 0.91 ± 0.10 | 0.23 |
| Sex (Male: Female)*** | 29: 23 | 38: 12 | 21: 19 | 0.03 |
*The P value was computed using a one-way Anova analysis
**A measure between 0 and 1. 1: Completely right-handed, 0: completely left-handed
***P Value computed using chi Square test
A one-way ANOVA (p-value < 0.0005, Uncorrected) has been conducted on the functional connectivities. Table 2 shows the summary of one-way ANOVA results obtained for the functional connectivity.
Table 2.
Summary of one-way ANOVA results obtained for the functional connectivity
| Region Pairs | P value |
|---|---|
| Right Temporal Pole–Right Frontal Medial Cortex | 0.0004 |
| Right Frontal Medial Cortex–Right Frontal Orbital Cortex | 0.0001 |
| Right Subcallosal Cortex–Right Frontal Orbital Cortex | 0.0002 |
| Left Central Opercular Cortex–Left Thalamus | 0.0002 |
| Left Central Opercular Cortex–Left Brain-Stem | 0.0002 |
| Left Central Opercular Cortex–Right Brain-Stem | 0.0001 |
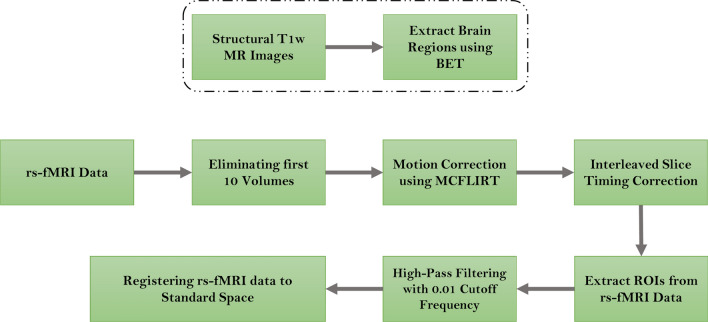
Preprocessing
All preprocessing steps were conducted using the FSL software (Jenkinson et al. 2012). A general overview of the preprocessing steps can be seen in Fig. 3 and are as follow:
Eliminating non-brain regions from the T1 high-resolution images using BET
Eliminating the first 10 volume images to allow for magnetization equilibrium
Applying a temporal Gaussian high-pass filter with a cut-off frequency of 0.01 HZ
Applying motion correction using FSLs MCFLIRT
Applying interleaved slice timing correction
Applying a Gaussian Smoothing with FWHM = 5 mm for noise reduction
Registering all images to standard space (MNI152_T1_2mm)
Fig. 3.
Overview of the preprocessing steps
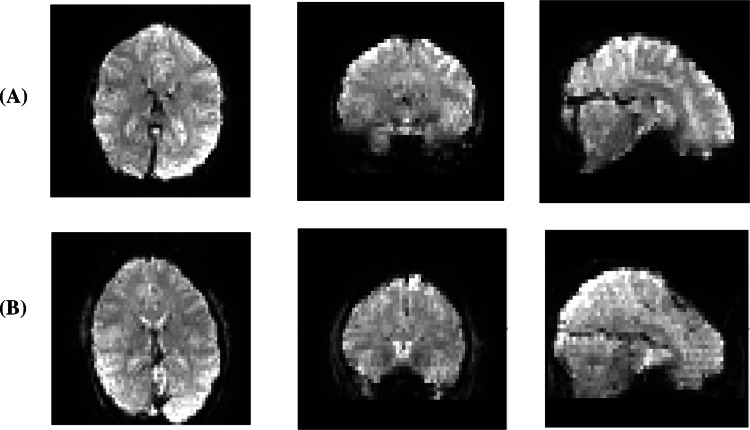
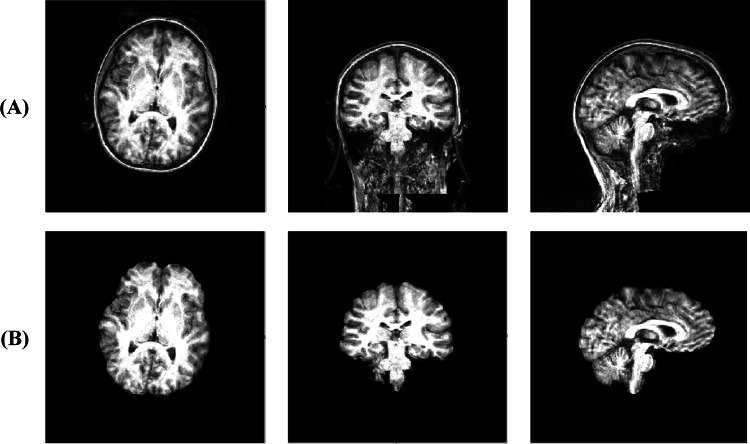
The outcome of the main preprocessing steps (filtering and registration) on a sample image can be seen in Figs. 4 and 5.
Fig. 4.
Sample images before and after applying BET on raw T1-images
Fig. 5.
Sample images after three main preprocessing steps. Row (A): raw rs-fMRI data. Row (B): Raw rs-fMRI data after brain extraction, slice timing correction, and filtering. Row (C): Registered Image to standard space
Connectivity
In fMRI modalities, functional connectivity expresses the temporal correlation between the time series of different brain regions (Bastos and Schoffelen 2016; Kelly et al. 2010). In other words, the presence of statistical dependencies between two neurophysiological data is investigated by functional connectivity (Bastos and Schoffelen 2016; Kelly et al. 2010). Assuming that the data fit Gaussian assumptions, then second-order dependencies are discussed and include covariance's or correlations (Bastos and Schoffelen 2016; Kelly et al. 2010). For non-Gaussian processes, higher-order dependencies are also investigated by some methods such as independent component analysis (ICA) (Cisler et al. 2014). The most important methods of functional connectivity are correlation (Sun et al. 2004), coherence (Wang et al. 2015), mutual information (Mäki-Marttunen et al. 2013), transfer entropy (Astolfi et al. 2006), directed coherence (Havlicek et al. 2010), Granger causality (Lombardi et al. 2017), generalized synchronization (Warnick et al. 2018), and Bayes net (Dalsgaard et al. 2014).
In this paper. the Pearson correlation coefficient was used to estimate the functional connectivity between regions. Regions of interest (ROI) were defined according to the Harvard–Oxford cortical and sub-cortical (lateralized) atlas. Based on this atlas, a total of 118 ROIs were considered. Next, regional time series were obtained by averaging the time series of all voxels inside each of the 118 ROIs. Finally, the Pearson correlation coefficient between the time series was used to extract the connectivity matrices for each subject. In conclusion, a connectivity matrix with a shape of 118 × 118 is obtained. Figures 6, 7, 8 demonstrate connectivity heat maps from healthy control (HC) and SZ subjects.
Fig. 6.
Sample correlation matrices obtained for HC subjects
Fig. 7.
Sample correlation matrices obtained for SZ subjects
Fig. 8.
Sample correlation matrices obtained for ADHD subjects
Proposed CNN-AE Model
The introduction of DL techniques in various fields, including medicine (Khodatars et al. 2021; Eslami et al. 2019; Shoeibi et al. 2022a; Suk et al. 2016; Castillo-Barnes et al. 2020; Luckett et al. 2022), has made significant progress, and valuable results have been achieved in detecting different diseases (Feng et al. 2021; Khosla et al. 2019). So far, several models of DL techniques have been proposed, with different training schemes, including supervised, semi-supervised, and unsupervised methods (Shoeibi et al. 2020; Goodfellow et al. 2016). Autoencoders (AEs) are an important class of DLs trained unsupervised and are widely used for feature extraction (Goodfellow et al. 2016; Khozeimeh et al. 2021). AE architectures consist of two important parts: decoder and encoder (Goodfellow et al. 2016).
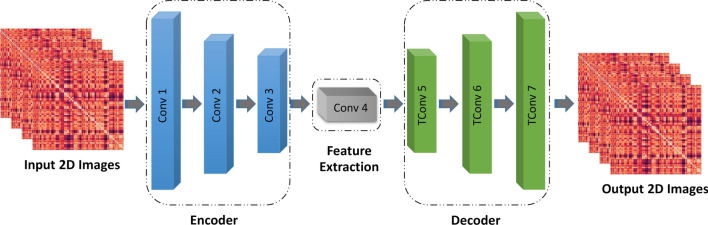
AEs have different architectures (Goodfellow et al. 2016), and the idea of this paper is based on the CNN-AE technique with the proposed layers. In the proposed model, the connectivity matrices are fed to the input of the encoder section. Then, it passes through the convolutional layers to reach the last layer of the encoder. Afterwards, this data is entered into the decoder, which aims to perform data reconstruction. This paper uses seven convolutional layers in the encoder and decoder; three of these are in the encoder (along with activation function and followed by a max pooling), and four are in the decoder (the first three are followed by an upsampling layer, while the last one is used to generate images with the same shape as input). The output of the forth convolution layer (before upsampling) is used for feature extraction. This structure was picked by empirically testing a few alternatives. Figure 9 and Table 3 detail the proposed CNN-AE model.
Fig. 9.
Proposed CNN-AE model for diagnosis of SZ from rs-fMRI modality
Table 3.
Details for the proposed CNN-AE model
| Architecture | Layers | Output Shape | Kernel Size | Stride | Param | Activation | |
|---|---|---|---|---|---|---|---|
| Width | Depth | ||||||
| Encoder | Input Layer | (118, 118) | 1 | – | – | 0 | – |
| Conv2D | (118, 118) | 32 | 32 | 1 | 320 | ReLU | |
| Max Pooling | (59, 59) | 32 | – | 1 | 0 | – | |
| Conv2D | (59, 59) | 32 | 32 | 1 | 9248 | ReLU | |
| Max Pooling | (30, 30) | 32 | – | 1 | 0 | – | |
| Conv2D | (30, 30) | 1 | 32 | 1 | 289 | ReLU | |
| Max Pooling | (15, 15) | 1 | – | 1 | 0 | – | |
| Decoder | Conv2D | (15, 15) | 1 | 32 | 1 | 10 | ReLU |
| Upsampling | (30, 30) | 1 | – | 1 | 0 | – | |
| Conv2D | (30, 30) | 32 | 32 | 1 | 320 | ReLU | |
| Upsampling | (60, 60) | 32 | – | 1 | 0 | – | |
| Conv2D | (60, 60) | 32 | 32 | 1 | 9248 | ReLU | |
| Upsampling | (120, 120) | 32 | – | 1 | 0 | – | |
| Zero Pad | (118, 118) | 1 | – | – | 0 | – | |
| Conv2D | (118, 118) | 1 | 1 | 1 | 289 | Tanh | |
Classifiers
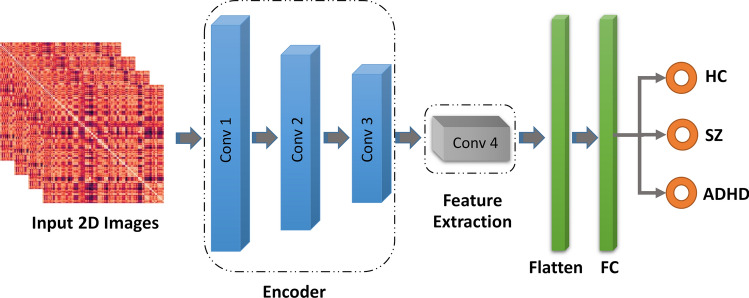
First, the decoder part is deleted to use an autoencoder for feature extraction. Next, a dense layer followed by a SoftMax classifier is inserted after the encoder, and the encoder is fine-tuned. Afterward, the representations from the last convolutional layer (last layer of the encoder) are extracted as features for each image. Figure 10 shows the overall structure of the fine-tuned network. After performing these steps, a representation for each image is generated which can be fed to different classifier methods. In this paper, the used classification algorithms consist of MLP, KNN, SVM, RF, ANFIS, ANFIS-GA, ANFIS-PSO, ANFIS-GWO, IT2FR-GA, IT2FR-PSO, and IT2FR-GWO. In the following, the details of classifier algorithms are presented.
Fig. 10.
AE-based Classifier block diagram
Machine learning classifiers
To compare the results of the proposed method and show its superiority, several classification algorithms are picked and evaluated on the dataset. Decision trees (DT) (Safavian and Landgrebe 1991), KNN (Liao and Vemuri 2002), MLP (Windeatt 2006), SVM (Noble 2006) and Random Forest (Belgiu and Drăguţ 2016) are used. These methods have different complexities, and each has its strength and weaknesses; for example, random forest is fast and robust against outliers but tends to fail where features are highly entangled, whereas SVM with the proper kernel can solve those problems, but its performance decreases for massive datasets. Moreover, some of these methods have hyper-parameters, k in KNN and kernel in SVM; these values are picked as three and RBF, respectively.
ANFIS models
Nowadays, various applications use fuzzy systems, including medical data classification (Shoeibi et al. 2022c). The ANFIS model is one of the most popular classification methods, which combines fuzzy logic and adaptive network. More information about the ANFIS method is given in Shoeibi et al. 2022c. In this work, the Genfis-3 function is used to implement ANFIS based on the FCM clustering algorithm. Furthermore, this function uses the Gaussian membership function for input data. Finally, the training step is based on the hybrid method. In (Shoeibi et al. 2022c), ANFIS model training with intelligent optimization methods is presented, and we have done the same in this research.
Improving Type-2 fuzzy regression based on TSK
Linear regression (LR) has been extensively utilized in many applications, such as the medical one (Schober and Vetter 2020; Marill 2004). According to the definition of LR, there will be a linear relationship between independent variables and the dependent variable. LR-based approaches are among well-known and widely used machine learning tools (ML) (Maulud and Abdulazeez 2020).
Due to uncertainty in medical data and the capability of Fuzzy Logic Systems (FLSs) in modelling uncertainties, Type-1 and Type-2 Fuzzy Regression methods have been proposed, which have more potential and efficiency to outperform LR techniques.
Moreover, taking advantage of additional degrees of freedom provided by the footprint of uncertainty (FOU), Interval Type-2 Fuzzy Logic Systems (IT2 FLSs) are able to effectively handle the high levels of uncertainty in comparison with T1 FLS (Bajestani et al. 2017).
The following definitions will be presented before analyzing the Interval Type-2 Fuzzy Regression (IT2 FR).
Definition 1
Pan et al. (2021): The T2FS is represented by a type-2 membership function as follows:
| 1 |
where is the primary variable in , is the second variable which has the domain , and the amplitude of is known as the second grade. The T2FS can also denoted as:
| 2 |
Definition 2
The footprint of uncertainty (FOU) of a T2FS is defined as.
| 3 |
Definition 3
Pan et al. (2021): Due to the complexity and abstraction of T2FS, IT2FS is defined by setting all , which can be shown as.
| 4 |
The th IF–THEN rule of T2 FLSs is expressed by
| 5 |
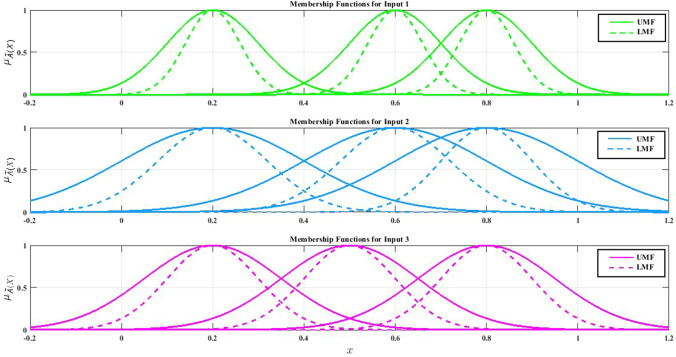
where are antecedent type-2 sets, are consequent type-2 sets. Further studies about the structure of T2FLSs and their applications are proposed in Mittal et al. (2020). Figure 11 demonstrates that IT2 FS could adopt the Gaussian MFs for its premise parts.
Fig. 11.
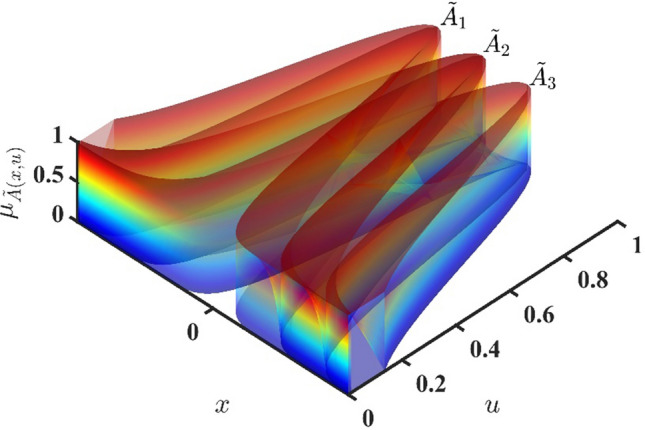
Gaussian IT2F membership functions
Definition 4
Pan et al. 2021): Gaussian IT2FS is a special case of IT2FS which has a fixed mean (), and an uncertain standard deviation that takes on values in . The lower membership function (LMF) and Upper membership function (UMF) of the Gaussian IT2FS are expressed as follows:
| 6 |
| 7 |
Figure 12 shows LMFs and UMFs of an IT2FS with three Gaussian MFs.
Fig. 12.
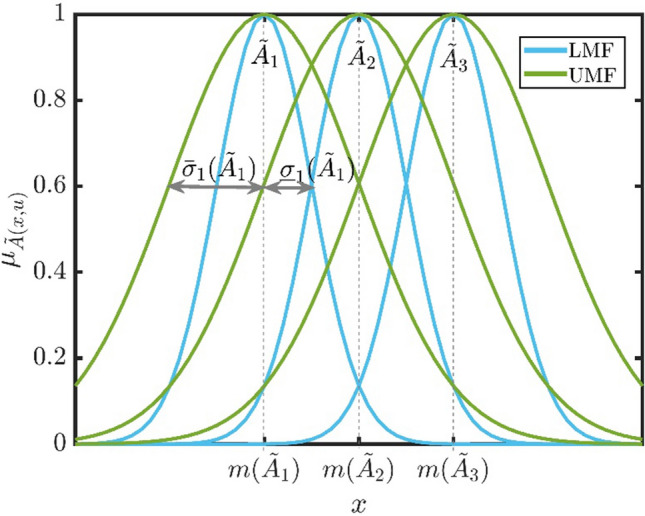
Upper MFs and lower MFs of Gaussian IT2F
When data in a regression problem follow an almost certain linear trend in a region, linear regression methods will be efficient. On the other hand, piecewise linear regression is employed if the linear trend does not exist. The number and location of breakpoints need to be detected in the estimation process. This issue raises complexity and additionally leads to an algorithm whose behavior changes due to added data. This issue could be the leading cause of repeating all calculations.
In this section, IT2 FR is developed to overcome the abovementioned difficulty. Moreover, this method will be independent of the behavior of a trend in a data set. For IT2FR, output is defined by an interval type-2 fuzzy linear model in which and are fuzzy coefficients and crisp inputs:
| 8 |
The above equation does not apply to data with various behavior patterns. To solve this problem, data with similar behavior will be allocated to a cluster, and then linear IT2FR will be used for each cluster. Only that particular cluster will be trained in analyzing new data if new data is placed in the existing clusters. Otherwise, a new cluster will be generated, and IT2FR associated with this cluster will be studied. As a result, the previous calculations are valid, while new behavior patterns are also investigated with minimum computational cost.
Assume that and are the number of data and clusters, respectively, for th cluster with members, the following rule could be expressed:
| 9 |
In fact, one rule is defined for each cluster in which are interval type-2 fuzzy sets (IT2FSs) for th rule and will be determined as follows:
First, with the help of Fuzzy C-Mean clustering (FCM) method, the optimal number of clusters, the cluster members and T2Fs are determined.
The fuzzy regression function based on input and output variables is obtained for each cluster. Consequently, the fuzzy coefficients are calculated.
The final output is defined as follows:
| 10 |
where
| 11 |
| 12 |
The above relation demonstrates a nonlinear fuzzy regression dealing with data complexity. is a coefficient to activate th rule and is:
| 13 |
When data belongs only to a single cluster, it could obviously determine only one FR relation in the output part.
Data patterns that simultaneously belong to many clusters affect more than one FR relations. The degree of each data effectiveness could be specified by its membership grade.
Remark 1: If a cluster's members do not overlap another cluster's members, then , and we have exclusive fuzzy linear regression.
The output of FS after type-reduction and defuzzification (Runkler et al. 2018) stages will be
| 14 |
where is the center of T2FS . The final output is
| 15 |
Optimal IT2FR classifiers
Fuzzy c-mean clustering (FCM) method (Shoeibi et al. 2022c) is the most useful approach to generating a primary fuzzy inference system (FIS) among the ANFIS and IT2FR classifiers. In FIS, direct learning methods influence the Gaussian membership functions (MFs), inputs, and outputs of FIS. This section employs PSO, GA, and GWO methods to train IT2FR and ANFIS models. Firstly, based on FCM, the proposed FR model obtains T1 and T2 Gaussian MFs, and then optimization algorithms are used to decrease the error. Finally, the objective function is defined by Shoeibi et al. 2022c:
| 16 |
where
| 17 |
and we have
| 18 |
where and are the number of FS inputs and error, respectively. are inputs (features) (Shoeibi et al. 2022c). , , and denote the IT2FR and ANFIS method parameters, the number of samples, and the output of FS, respectively.
Genetic algorithm
The genetic algorithm (GA) is one of the most important optimization methods developed by John Holland (Whitley 1994). This algorithm starts with a set of chromosomes called populations. Chromosomes are taken from a population and used as a new population. Then, the hypothesis begins with a unique random population and continues through generations (Whitley 1994). The fitness of the whole population is assessed in each generation. Then, several individuals are randomly selected from the current generation (based on fitness) and modified to form a new generation. The next iteration converts the algorithm to the current generation (Whitley 1994). You can find more information on GA in Whitley (1994).
Particle swarm optimization (PSO)
The PSO optimizes a problem by trying iteratively to enhance a candidate solution to an estimated quality in computational science (Oca et al. 2009). It moves the particles in the search space using a mathematical formula over the particle’s velocity and position. The local best-known position influences the particle's movement, but the best-known positions in the search space also guide them. Hence, the better positions found by other particles are also updated. This makes the swarm move toward the best solutions (Oca et al. 2009). One of the most significant advantages of this algorithm is that it does not use the gradient of the problem being optimized, eliminating all the overheads of gradient calculation and derivative computation. Nevertheless, given the nature of the local search, it does not guarantee an optimal solution (Oca et al. 2009).
Gray Wolf optimization
The GWO algorithm was first proposed in 2014 by Mirjalili et al. (Sun et al. 2021). GWO is a metaheuristic optimization method inspired by how gray wolves hunt (Sun et al. 2021). This technique is in the category of swarm intelligence algorithms, and it is based on population. Gray wolves are predators and often prefer to live in groups (Sun et al. 2021). Each group consists of 5 to 12 wolves on average in a hierarchical manner. This hierarchy is divided into four categories: alpha (group leaders), beta (advisors and orders to lower groups), delta (observers and hunters), and omega (protectors) (Sun et al. 2021). The GWO algorithm is based on the mass hunting of wolves, which will be examined in detail below.
For the design of GWO, the most important factors include best position (α), second solution (β), third solution (δ), and other solutions (ω). For example, the mathematical equation for the siege of prey by gray wolves is defined as follows (Sun et al. 2021):
In the above relations, represents the position of the gray wolf in the i-th repeat, and represents the hunting position in the t repeat. Also, component is reduced linearly from 2 to zero (Sun et al. 2021).
In the search space, we do not know , so we consider the hunting position . Therefore, hunting equations are presented as follows (Sun et al. 2021):
Figure 13 shows the steps of the GWO algorithm. More details of the GWO method are provided in Sun et al. (2021).
Fig. 13.
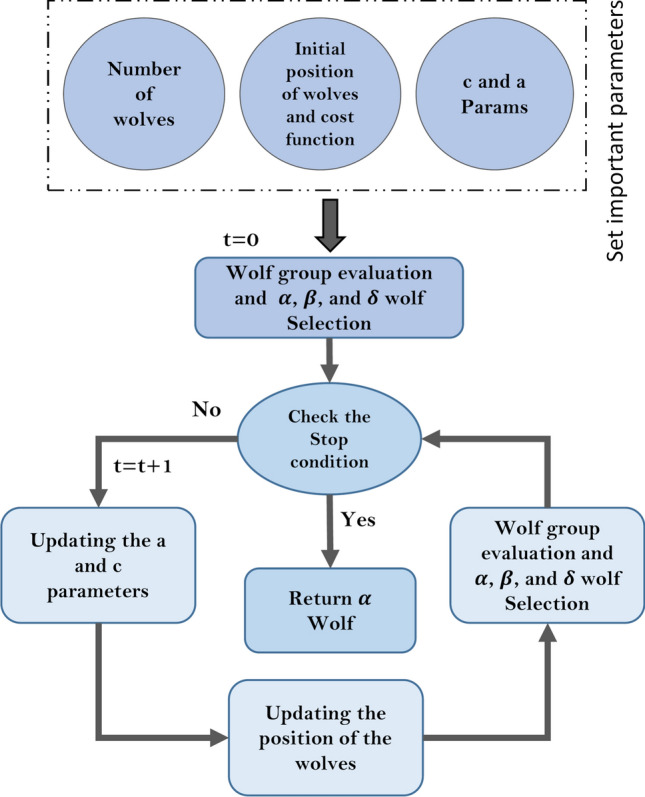
Block diagram of GWO optimization method
Statistical metrics
This section introduces the statistical parameters for evaluating the proposed method of SZ detection from the rs-fMRI modality. In this research, the K-Fold cross-validation with k = 10 is used. Evaluation parameters include accuracy (Acc), precision (Prec), recall (Rec), and F1-Score (F1). The equations of evaluation parameters are shown below (Ayoobi et al. 2021; Appaji et al. 2022).
| 19 |
| 20 |
| 21 |
| 22 |
Experiment results
This section reports the results of the proposed SZ and ADHD detection method from the rs-fMRI modality. To implement the proposed method, a PC with NVidia 1070 GPU, 16 GB RAM, and Core i7 CPU is used. The rs-fMRI preprocessing steps are performed by the FSL toolbox. Also, all the simulations were done by Scikit-learn (Pedregosa et al. 2011) and TensorFlow 2 toolboxes (Dillon et al. 2017) in Python 3.7 environment.
As mentioned in the previous sections, all simulations are performed on the UCLA dataset (https://legacy.openfmri.org/dataset/ds000030/), which contains rs-fMRI data from HC, BD, ADHD, and SZ subjects. Then, as explained in previous sections, preprocessing, feature extraction and classification steps are performed. For model evaluation, we used k-fold cross validation with k = 10. The authors introduced the proposed CNN-AE method, which is the paper's primary novelty. Also, the hyperparameters of the conventional ML classifiers are selected by trial and error to obtain the highest performance. In Sect. 2 to 3, the details for the proposed CNN-AE model is provided. The experiment results of the proposed CNN-AE model with ML classifier techniques are shown in Table 4. It can be noted from the table that the KNN algorithm has achieved better results than other ML classifiers. The confusion matrix for the KNN model is shown in Fig. 14; given that we have used k-fold cross-validation, we have averaged the confusion matrices of each fold to get a final one. Also, Fig. 15 displayed the results of statistical metrics for all ML classifiers.
Table 4.
Results for ML classification methods
| Methods | Acc(%) | Prec(%) | Rec(%) | F1-score (%) |
|---|---|---|---|---|
| DT | 60.90 | 64.66 | 54.83 | 64.27 |
| MLP | 57.18 | 51.678 | 52.03 | 55.63 |
| KNN | 67.72 | 65.61 | 71.94 | 68.45 |
| SVM | 66.90 | 64.57 | 64.20 | 67.70 |
| RF | 62.72 | 65.21 | 55.92 | 63.61 |
Fig. 14.
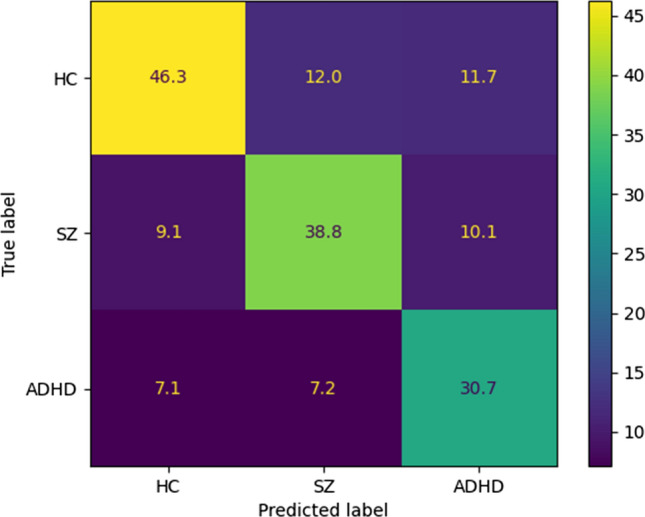
Confusion matrix for KNN method
Fig. 15.
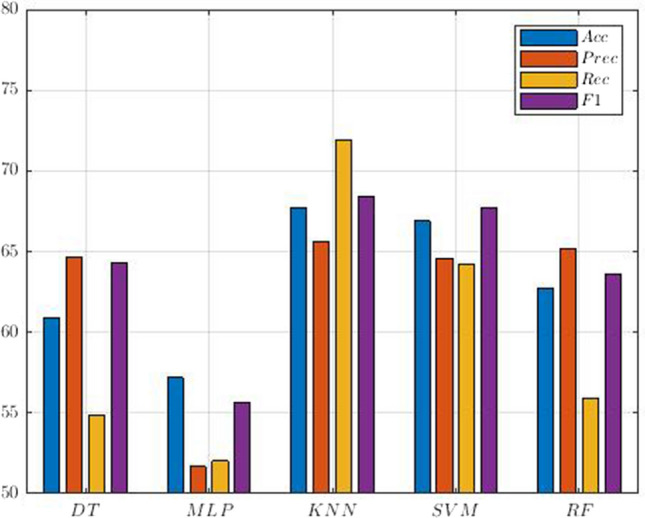
Comparison of performances (%) for SZ and ADHD detection
In the following, the experiment results of the proposed CNN-AE model with ANFIS classifier methods are presented. The ANFIS is one of the most important type-1 fuzzy systems (Coupland and John 2007). This method is based on a Takagi–Sugeno-Kang (TSK) system (Shoeibi et al. 2022c) and has achieved successful results in various medical research (Thirumurugan and Shanthakumar 2016; Al-Ali et al. 2021). There are several training methods for ANFIS, and the hybrid technique is used in this paper. Also, in another part of the simulations, the GA (Whitley 1994), PSO (Oca et al. 2009), and GWO (Sun et al. 2021) optimization algorithms were used for the training of the ANFIS model.
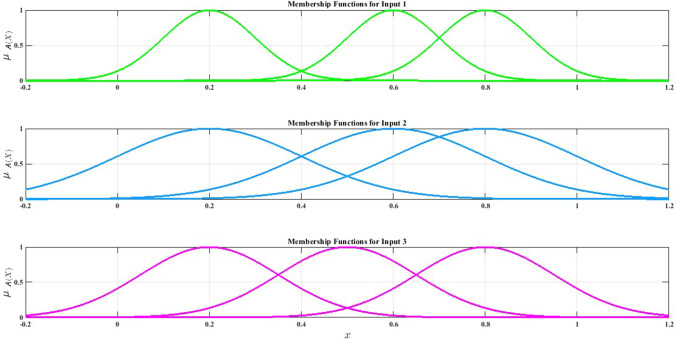
In different studies, the researchers have used optimization techniques in ANFIS training and achieved promising results (Wei 2013; Suleymani and Bemani 2018; Tien Bui et al. 2018). To implement the ANFIS model, the FCM method is first used, which is based on Gaussian MFs (Shoeibi et al. 2022c). Since it is a classification problem, three Gaussian MFs are provided for each input data. Figure 16 shows several Gaussian MFs for SZ and ADHD detection. Then, the hybrid method and optimization techniques expressed to train the ANFIS model were tested and compared. In Table 5, the hyper-parameters of GA (Whitley 1994), PSO (Oca et al. 2009), and GWO (Sun et al. 2021) algorithms are presented for ANFIS training. Finally, the results of the CNN-AE model with ANFIS, ANFIS-GA, ANFIS-PSO, and ANFIS-GWO classifier algorithms are shown in Table 6.
Fig. 16.
Three Gaussian membership functions in ANFIS classifier
Table 5.
Hyper-parameters to optimization methods
| PSO | GA | GWO |
|---|---|---|
| C1 = 2 | Selection = tournament | Search agents = 5 |
| C2 = 2 | Mutation rate = 0.05 | Dimension = 30 |
| W = 0.2 | Crossover fraction = 0.8 | – |
| – | Elite Count = 5 | – |
| N_pop = 60 | ||
| Var_min = min (Feature_Matrix) | ||
| Var_max = max (Feature_Matrix) | ||
| MAX_IT = 400 | ||
The experiment results in Table 6 show the superiority of the ANFIS-GWO method compared to the other ANFIS algorithms. The reason for the high accuracy of ANFIS-GWO compared to other ANFIS models is the use of the GWO method in the training step. Researchers have not used the GWO algorithm to train fuzzy systems such as ANFIS (Shoeibi et al. 2022c), which is another novelty of this paper. The confusion matrix for the ANFIS-GWO technique is displayed in Fig. 17. Also, Fig. 18 displays the results of statistical metrics for the ANFIS classifier.
Fig. 17.
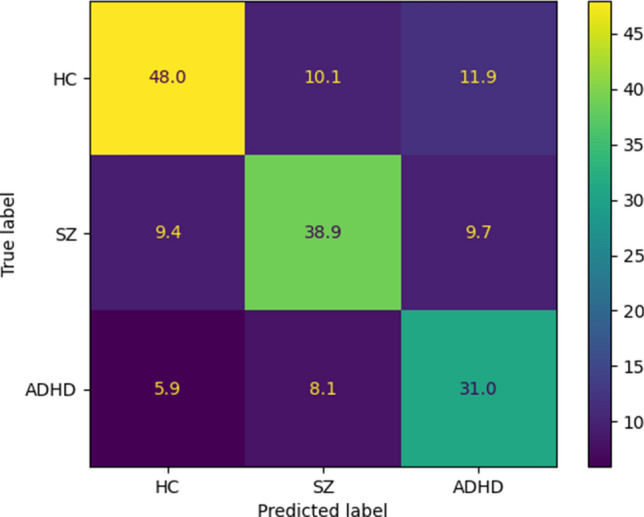
Confusion matrix for ANFIS-GWO
Fig. 18.
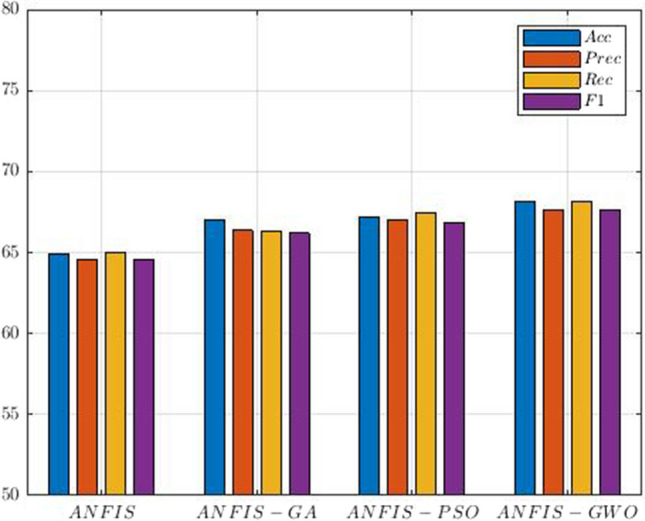
Comparison of ANFIS classifiers results for SZ and ADHD detection
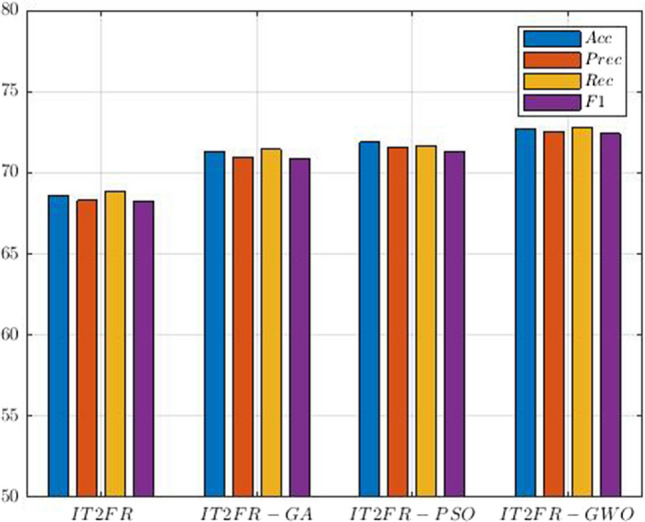
In the following, we present the results of the proposed CNN-AE model alongside IT2FR classifiers. The authors have proposed the IT2FR model for the first time, and it is considered the most important novelty of this paper. Similar to ANFIS, the proposed IT2FR technique is optimized by GA (Whitley 1994), PSO (Oca et al. 2009), and GWO (Sun et al. 2021) methods. To implement of IT2FR model, three interval type-2 Gaussian MFs are provided for each input data. Figure 19 shows several intervals of type-2 Gaussian MFs for SZ and ADHD detection. Table 7 reports the results obtained from IT2FR, IT2FR-GA, IT2FR-PSO, and IT2FR-GWO methods. According to Table 7, it is clear that the IT2FR-GWO method has achieved the most accuracy. The confusion matrix for the IT2FR-GWO method is shown in Fig. 20. Also, Fig. 21 displayed the results of statistical metrics for IT2RF classifiers.
Fig. 19.
Three Gaussian membership functions in IT2FR classifier
Table 7.
Results for IT2FR classifier models
| Methods | Acc (%) | Prec (%) | Rec (%) | F1 (%) |
|---|---|---|---|---|
| IT2FR | 68.61 | 68.29 | 68.84 | 68.27 |
| IT2FR-GA | 71.27 | 70.94 | 71.43 | 70.87 |
| IT2FR-PSO | 71.90 | 71.56 | 71.64 | 71.34 |
| IT2FR-GWO | 72.71 | 72.52 | 72.81 | 72.41 |
Fig. 20.
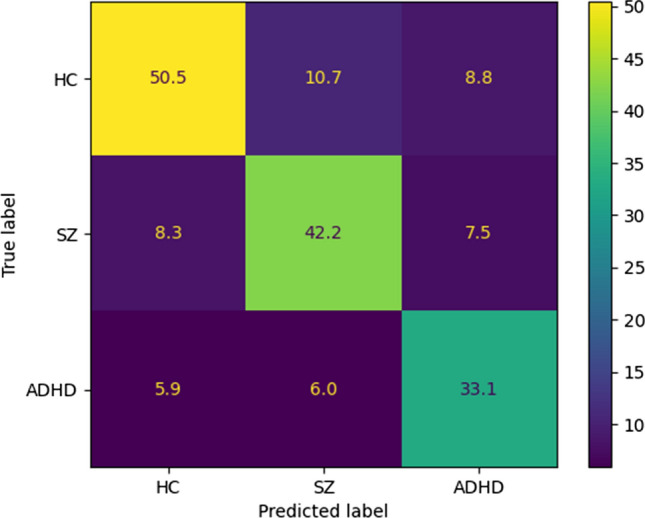
Confusion matrix for IT2FR-GWO
Fig. 21.
Comparison of IT2RF classifiers results for SZ and ADHD detection
In this section, the results of the proposed method for the diagnosis of SZ and ADHD disorders were discussed. The proposed method of this research has three important novelties, including introducing the CNN-AE model with proposed layers, the IT2FR method, and the GWO optimization method to train the proposed IT2FR technique. In Tables 4, 6, and 7, the accuracy of different classification algorithms are shown and compared. It can be seen that the IT2FR-GWO method has achieved state-of-the-art results in comparison with other classification methods.
Limitations of study
This section is dedicated to the limitations of this study. The UCLA dataset has limited rs-fMRI data to diagnose various brain disorders, including SZ and ADHD. This challenge has made it still impossible to provide advanced DL models for the diagnosis of SZ and ADHD. Also, this dataset contains rs-fMRI data and does not have T-fMRI modalities from subjects with mental disorders. The UCLA dataset is used to diagnose SZ, BD, and ADHD disorders, while diagnosing brain disorders of varying severity is very important. The proposed method of this paper consists of DL, fuzzy logic, and optimization algorithms. Implementing the proposed method is very complicated because the CNN-AE model, IT2FR, and GWO methods have different adjustment parameters. Also, the proposed method has a long execution time, which is another limitation.
Discussion, conclusion, and future works
Brain disorders such as SZ and ADHD are among the most important brain diseases that seriously threaten many people's health worldwide (Sadeghi et al. 2022; Loh et al. 2022). ADHD and SZ disorders have many differences and similarities. In some studies, the presence of ADHD symptoms has been reported in people who are diagnosed with SZ in adulthood (Pallanti and Salerno 2015; Wang et al. 2014). Also, ADHD is diagnosed in many children at genetic risk for SZ (Peralta et al. 2011; Jepsen et al. 2018; O'Driscoll et al. 2014). People with SZ in early adolescence often have symptoms of other mental disorders such as ADHD (Peralta et al. 2011; Jepsen et al. 2018; O'Driscoll et al. 2014). A diagnosis of ADHD in childhood may be a better predictor of adult SZ. For example, the risk of SZ in children with ADHD is approximately 4.3 times higher than in other adults (Peralta et al. 2011; Jepsen et al. 2018; O'Driscoll et al. 2014). The co-occurrence of ADHD and SZ may be due to shared genetic factors. ADHD and SZ may also have similarities in clinical treatment (Park et al. 2018; Groom et al. 2008). ADHD is often diagnosed during childhood, while SZ is often diagnosed in the 20 s or 30 s (Pallanti and Salerno 2015; Wang et al. 2014). ADHD is treated with behavioral therapy methods, while SZ can be controlled with cognitive and emotional therapy (CET) (Langberg et al. 2008). ADHD does not require medication to treat it, but doctors may prescribe a stimulant to help the patient to focus (Castle et al. 2007; Poldrack et al. 2016). SZ can be treated with antipsychotic drugs (Pallanti and Salerno 2015; Wang et al. 2014).
ADHD and SZ negatively affect brain function. So, various diagnostic methods have been introduced by specialist physicians to treat them (Khodatars et al. 2021). Currently, the most used methods for the diagnosis of SZ and ADHD disorders include psychological tests and neuroimaging techniques (Sadeghi et al. 2022) (Loh et al. 2022). fMRI modalities are one of the best functional neuroimaging modalities, and physicians and doctors can use them to diagnose brain disorders (Khodatars et al. 2021). Diagnosis of SZ and ADHD disorders using fMRI modalities is challenging. To overcome this, there has been significant growth over the years in research to diagnose various brain disorders, including SZ (Shoeibi et al. 2021a; Sadeghi et al. 2022), ADHD (Loh et al. 2022), etc. using AI (ML and DL) techniques.
|In this paper, we presented a new computer-aided diagnosis system (CADS) based on the proposed CNN-AE architecture and IT2FR-GWO classifier for diagnosing SZ and ADHD disorders using rs-fMRI data. The steps of the proposed method comprise the dataset, preprocessing, feature extraction, and classification. First, the UCLA dataset (https://legacy.openfmri.org/dataset/ds000030/) is used for experiments. As mentioned earlier, this dataset has rs-fMRI modality from HC, SZ, ADHD, and BD patients. We used the HC, SZ, and ADHD data for our experiments. In the second step, the rs-fMRI modality is preprocessed using FSL toolbox (Jenkinson et al. 2012). Then, we extracted the correlation coefficients matrices with 118 × 118 size as 2D images from rs-fMRI data of each subject for post-processing.
The third step is dedicated to feature extraction, which is performed by a proposed 2D CNN-AE architecture. In this step, the 2D images are fed to the input of the proposed CNN-AE model. The first novelty of this paper is an improved CNN-AE architecture. Figure 9 and Table 1 show that the proposed CNN-AE architecture has 7 CNN layers.
The last step of the proposed method is classification. A few ML-based, fuzzy type-1, and fuzzy type-2 methods are used for the classification of CNN-AE features. The DT (Safavian and Landgrebe 1991), MLP (Windeatt 2006), KNN (Liao and Vemuri 2002), SVM (Noble 2006), and RF (Belgiu and Drăguţ 2016) are ML classifier methods. Also, Type-1 fuzzy classification techniques include ANFIS (Shoeibi et al. 2022c), ANFIS-GA, ANFIS-POS, and ANFIS-GWO. The IT2FR, IT2FR-GA, IT2FR-PSO, and IT2FR-GWO are type-2 fuzzy classifier techniques. In this work, the IT2FR method was first introduced by the authors and is considered the most important novelty of the paper. In addition, another novelty of this paper is combining the IT2FR and GWO methods for classification. It should be noted that in the classification section, the K-Fold cross-validation with k = 10 is also used. The experiment results of the proposed method show that the use of the CNN-E model and the IT2FR-GWO method has led to increased accuracy in diagnosing SZ and ADHD disorders. Our findings suggest that significant different functional connectivity exists within these regions which are in line with previous literature (Culbreth 2021; Johnsen 2020; Salmi 2020; Hilland 2022).
In Table 8, the proposed method results are compared with related works in the diagnosis of SZ and ADHD using fMRI modalities. Table 8 shows that the researchers used different MRI datasets for SZ and ADHD detection. In related works, researchers have identified SZ from HC. However, our paper uses the UCLA dataset; the classes presented to the classifier in this paper include HC, SZ, and ADHD. Table 8 shows that this paper's proposed method has higher accuracy than other related works.
Table 8.
Comparison of the proposed method with past works
| Works | Dataset | Modality | Type of classes | Feature extraction | Feature selection | Classifier | Acc (%) |
|---|---|---|---|---|---|---|---|
| Yang et al. (2020) | Clinical | T-fMRI | HC and SZ | Multivariate connectome features | Chi-squared test | SVM | Acc = 71.6 |
| Singh et al. (2016) | COBRE | rs-fMRI | HC and SZ | Different graph theoretical features | – | SVM | Acc = 65 |
| Sendi et al. (2020) | COBRE | rs-fMRI, sMRI | HC and SZ | Dynamic functional connectivity | ENR | LR | Acc = 71 |
| Dillon and Wang (2016) | Multi-Site | rs-fMRI, T-fMRI | HC and SZ | Different features | – | Backus-Gilbert | Acc = 58.6 |
| Pierrefeu et al. (2018) | COBRE | sMRI | HC and SZ | Local grey matter volume | LASSO | Enet-TV | Acc = 68 |
| NMorphCH | |||||||
| NUSDAST | |||||||
| Liang et al. (2020) | Clinical | rs-fMRI | HC and SZ | Brain-wide seed based voxel-wise analysis | SelectFdr | GBDT | Acc = 72.28 |
| Cai et al. (2020) | Clinical | rs-fMRI | HC and SZ | Spatial–temporal reconstruction based on the ICA | T-Test | Majority Voting | Acc = 73 |
| PCA | |||||||
| Fisher | |||||||
| Moura et al. (2018) | Clinical | sMRI | HC and SZ | Structure’s brain volumes | – | MLDA | Acc = 73 |
| Chen et al. (2020) | Different | rs-fMRI | HC and SZ | Demographic and clinical features | PCA | FCM | Acc = 73 |
| Ramkiran et al. (2019) | COBRE | rs-fMRI, sMRI | HC and SZ | FCM | Mann–Whitney U test | SVM | Acc = 69 |
| Li et al. (2019) | COBRE | rs-fMRI | HC and SZ | Consensus functional connections with high discriminative power | T-Test | LDA | Acc = 76.34 |
| Hu et al. (2020) | NUSDAST | sMRI | HC and SZ | Inception ResNet | – | SVM | Acc = 70.98 |
| IMH | |||||||
| Oh et al. 2020) | SchizConnect | sMRI | HC and SZ | 3D-CNN | – | Softmax | Acc = 70 |
| Matsubara et al. (2019) | OpenfMRI | rs-fMRI | HC and SZ | GAN | – | Different Methods | Acc = 71.3 |
| Zhu et al. (2020) | COBRE | rs-fMRI | HC and SZ | Weighted Deep Forest | – | Softmax | Acc = 61 |
| UCLA | |||||||
| Hashimoto et al. (2021) | COBRE | rs-fMRI | HC and SZ | DNN | – | Softmax | Acc = 77.8 |
| Riaz et al. 2018) | ADHD-200 | rs-fMRI | HC and ADHD | 1D-CNN | – | Softmax | Acc = 71.3 |
| Farzi et al. (2017) | ADHD-200 | rs-fMRI | HC and ADHD | DBN | – | Softmax | Acc = 69.83 |
| Zou et al. (2017a) | ADHD-200 | rs-fMRI | HC and ADHD | 3D-CNN | – | – | Acc = 65.67 |
| R-fMRI Maps Project | |||||||
| Hao et al. (2015) | Different Datasets | rs-fMRI | HC and ADHD | DBN | – | SVM | Acc = 72.72 |
| Kuang et al. (2014) | ADHD-200 | rs-fMRI | HC and ADHD | DBN | – | Softmax | Acc = 72.73 |
| Zou et al. (2017b) | ADHD-200 | rs-fMRI | HC and ADHD | 3D-CNN | – | Softmax | Acc = 69.15 |
| Mao et al. (2019) | ADHD-200 | rs-fMRI | HC and ADHD | DCNN | – | Sigmoid | Acc = 71.30 |
| Zhang et al. (2020) | ADHD-200 | rs-fMRI | HC and ADHD | SC-CNN-attention | – | Softmax | Acc = 68.60 |
| Dou et al. (2020) | ADHD-200 | rs-fMRI | HC and ADHD | C4D network | – | Softmax | Acc = 70.4 |
| Proposed Method | UCLA | rs-fMRI | HC, SZ, and ADHD | CNN-AE | – | IT2FR-GWO | Acc = 72.71 |
The proposed method of this paper can help physicians accurately diagnose SZ and ADHD from rs-MRI data. Also, the proposed method can be used in the future as application software for diagnosing SZ or ADHD in hospitals or specialized medical centers. Furthermore, in future works, new DL models such as transformers (Rodriguez-Rivero et al. 2020; Li et al. 2020), attention mechanism (Niu et al. 2021; Liu and Milanova 2018), graph theory (Ma et al. 2021; Georgousis et al. 2021), etc., can be used for the diagnosis of SZ and ADHD.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Al-Ali A, Elharrouss O, Qidwai U, Al-Maaddeed S. ANFIS-Net for automatic detection of COVID-19. Sci Rep. 2021;11(1):1–13. doi: 10.1038/s41598-021-96601-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alizadehsani R, Sharifrazi D, Izadi NH, Joloudari JH, Shoeibi A, Gorriz JM, Acharya UR. Uncertainty-Aware Semi-supervised method using large unlabeled and limited labeled COVID-19 Data. ACM Trans Multimed Comput Commun Appl (TOMM) 2021;17(3):1–24. [Google Scholar]
- Anter AM, Abd Elaziz M, Zhang Z. Real-time epileptic seizure recognition using Bayesian genetic whale optimizer and adaptive machine learning. Futur Gener Comput Syst. 2022;127:426–434. doi: 10.1016/j.future.2021.09.032. [DOI] [Google Scholar]
- Aoe J, Fukuma R, Yanagisawa T, Harada T, Tanaka M, Kobayashi M, Kishima H. Automatic diagnosis of neurological diseases using MEG signals with a deep neural network. Sci Rep. 2019;9(1):1–9. doi: 10.1038/s41598-019-41500-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Appaji A, Harish V, Korann V, Devi P, Jacob A, Padmanabha A, Rao NP. Deep learning model using retinal vascular images for classifying schizophrenia. Schizophr Res. 2022;241:238–243. doi: 10.1016/j.schres.2022.01.058. [DOI] [PubMed] [Google Scholar]
- Astolfi L, Cincotti F, Mattia D, Marciani MG, Baccala LA, Fallani FDV, Babiloni F. Assessing cortical functional connectivity by partial directed coherence: simulations and application to real data. IEEE Trans Biomed Eng. 2006;53(9):1802–1812. doi: 10.1109/TBME.2006.873692. [DOI] [PubMed] [Google Scholar]
- Ayoobi N, Sharifrazi D, Alizadehsani R, Shoeibi A, Gorriz JM, Moosaei H, Mosavi A. Time series forecasting of new cases and new deaths rate for COVID-19 using deep learning methods. Results Phys. 2021;27:104495. doi: 10.1016/j.rinp.2021.104495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajestani NS, Kamyad AV, Esfahani EN, Zare A. Nephropathy forecasting in diabetic patients using a GA-based type-2 fuzzy regression model. Biocybern Biomed Eng. 2017;37(2):281–289. doi: 10.1016/j.bbe.2017.01.003. [DOI] [Google Scholar]
- Bastos AM, Schoffelen JM. A tutorial review of functional connectivity analysis methods and their interpretational pitfalls. Front Syst Neurosci. 2016;9:175. doi: 10.3389/fnsys.2015.00175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belgiu M, Drăguţ L. Random forest in remote sensing: a review of applications and future directions. ISPRS J Photogramm Remote Sens. 2016;114:24–31. doi: 10.1016/j.isprsjprs.2016.01.011. [DOI] [Google Scholar]
- Bitsch F, Berger P, Fink A, Nagels A, Straube B, Falkenberg I. Antagonism between brain regions relevant for cognitive control and emotional memory facilitates the generation of humorous ideas. Sci Rep. 2021;11(1):1–12. doi: 10.1038/s41598-021-89843-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bracha HS. Human brain evolution and the “Neuroevolutionary Time-depth Principle:” Implications for the Reclassification of fear-circuitry-related traits in DSM-V and for studying resilience to warzone-related posttraumatic stress disorder. Prog Neuropsychopharmacol Biol Psychiatr. 2006;30(5):827–853. doi: 10.1016/j.pnpbp.2006.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broyd SJ, Demanuele C, Debener S, Helps SK, James CJ, Sonuga-Barke EJ. Default-mode brain dysfunction in mental disorders: a systematic review. Neurosci Biobehav Rev. 2009;33(3):279–296. doi: 10.1016/j.neubiorev.2008.09.002. [DOI] [PubMed] [Google Scholar]
- Buchlak QD, Milne MR, Seah J, Johnson A, Samarasinghe G, Hachey B, Brotchie P. Charting the potential of brain computed tomography deep learning systems. J Clin Neurosci. 2022;99:217–223. doi: 10.1016/j.jocn.2022.03.014. [DOI] [PubMed] [Google Scholar]
- Cai XL, Xie DJ, Madsen KH, Wang YM, Bögemann SA, Cheung EF, Chan RC. Generalizability of machine learning for classification of schizophrenia based on resting-state functional MRI data. Hum Brain Mapp. 2020;41(1):172–184. doi: 10.1002/hbm.24797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castillo-Barnes D, Su L, Ramírez J, Salas-Gonzalez D, Martinez-Murcia FJ, Illan IA, Network DIA. Autosomal dominantly inherited alzheimer disease: analysis of genetic subgroups by machine learning. Inform Fusion. 2020;58:153–167. doi: 10.1016/j.inffus.2020.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castle L, Aubert RE, Verbrugge RR, Khalid M, Epstein RS. Trends in medication treatment for ADHD. J Atten Disord. 2007;10(4):335–342. doi: 10.1177/1087054707299597. [DOI] [PubMed] [Google Scholar]
- Chen J, Patil KR, Weis S, Sim K, Nickl-Jockschat T, Zhou J, Visser E. Neurobiological divergence of the positive and negative schizophrenia subtypes identified on a new factor structure of psychopathology using non-negative factorization: an international machine learning study. Biol Psychiat. 2020;87(3):282–293. doi: 10.1016/j.biopsych.2019.08.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi H, Ha S, Kang H, Lee H, Lee DS, Initiative ADN. Deep learning only by normal brain PET identify unheralded brain anomalies. EBioMedicine. 2019;43:447–453. doi: 10.1016/j.ebiom.2019.04.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cisler JM, Bush K, Steele JS. A comparison of statistical methods for detecting context-modulated functional connectivity in fMRI. Neuroimage. 2014;84:1042–1052. doi: 10.1016/j.neuroimage.2013.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coupland S, John R. Geometric type-1 and type-2 fuzzy logic systems. IEEE Trans Fuzzy Syst. 2007;15(1):3–15. doi: 10.1109/TFUZZ.2006.889764. [DOI] [Google Scholar]
- Culbreth AJ, Wu Q, Chen S, Adhikari BM, Hong LE, Gold JM, Waltz JA. Temporal-thalamic and cingulo-opercular connectivity in people with schizophrenia. NeuroImage Clin. 2021;29:102531. doi: 10.1016/j.nicl.2020.102531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dalsgaard S, Mortensen PB, Frydenberg M, Maibing CM, Nordentoft M, Thomsen PH. Association between attention-deficit hyperactivity disorder in childhood and schizophrenia later in adulthood. Eur Psychiatry. 2014;29(4):259–263. doi: 10.1016/j.eurpsy.2013.06.004. [DOI] [PubMed] [Google Scholar]
- De Oca MAM, Stutzle T, Birattari M, Dorigo M. Frankenstein's PSO: a composite particle swarm optimization algorithm. IEEE Trans Evol Comput. 2009;13(5):1120–1132. doi: 10.1109/TEVC.2009.2021465. [DOI] [Google Scholar]
- de Pierrefeu A, Löfstedt T, Laidi C, Hadj-Selem F, Leboyer M, Ciuciu P, Duchesnay E (2018) Interpretable and stable prediction of schizophrenia on a large multisite dataset using machine learning with structured sparsity. In: 2018 international workshop on pattern recognition in neuroimaging (PRNI) (pp. 1–4). IEEE
- de Moura AM, Pinaya WHL, Gadelha A, Zugman A, Noto C, Cordeiro Q, Sato JR. Investigating brain structural patterns in first episode psychosis and schizophrenia using MRI and a machine learning approach. Psychiatr Res Neuroimaging. 2018;275:14–20. doi: 10.1016/j.pscychresns.2018.03.003. [DOI] [PubMed] [Google Scholar]
- Dillon JV, Langmore I, Tran D, Brevdo E, Vasudevan S, Moore D, Saurous RA (2017) Tensorflow distributions. http://arxiv.org/abs/arXiv:1711.10604
- Dillon K, Wang YP (2016) An image resolution perspective on functional activity mapping. In: 2016 38th Annual international conference of the IEEE engineering in medicine and biology society (EMBC) (pp 1139–1142). IEEE [DOI] [PubMed]
- Do Austerman J. ADHD and behavioral disorders: Assessment, management, and an update from DSM-5. Cleveland Clin J Med. 2015;82:S3. doi: 10.3949/ccjm.82.s1.01. [DOI] [PubMed] [Google Scholar]
- Dou C, Zhang S, Wang H, Sun L, Huang Y, Yue W. ADHD fMRI short-time analysis method for edge computing based on multi-instance learning. J Syst Architect. 2020;111:101834. doi: 10.1016/j.sysarc.2020.101834. [DOI] [Google Scholar]
- Eslami T, Mirjalili V, Fong A, Laird AR, Saeed F. ASD-DiagNet: a hybrid learning approach for detection of autism spectrum disorder using fMRI data. Front Neuroinform. 2019;13:70. doi: 10.3389/fninf.2019.00070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farzi S, Kianian S, Rastkhadive I (2017) Diagnosis of attention deficit hyperactivity disorder using deep belief network based on greedy approach. In: 2017 5th International symposium on computational and business intelligence (ISCBI) (pp. 96–99). IEEE
- Feng W, Liu G, Zeng K, Zeng M, Liu Y (2021) A review of methods for classification and recognition of ASD using fMRI data. J Neurosci Methods, 109456 [DOI] [PubMed]
- Fernandez Rojas R, Huang X, Ou KL. A machine learning approach for the identification of a biomarker of human pain using fNIRS. Sci Rep. 2019;9(1):1–12. doi: 10.1038/s41598-019-42098-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgousis S, Kenning MP, Xie X. Graph deep learning: State of the art and challenges. IEEE Access. 2021;9:22106–22140. doi: 10.1109/ACCESS.2021.3055280. [DOI] [Google Scholar]
- Ghassemi N, Shoeibi A, Rouhani M, Hosseini-Nejad H (2019) Epileptic seizures detection in EEG signals using TQWT and ensemble learning. In: 2019 9th International conference on computer and knowledge engineering (ICCKE) (pp 403–408). IEEE
- Goodfellow I, Bengio Y, Courville A. Deep learning. MIT press; 2016. [Google Scholar]
- Grimm O, Thomä L, Kranz TM, Reif A. Is genetic risk of ADHD mediated via dopaminergic mechanism? A study of functional connectivity in ADHD and pharmacologically challenged healthy volunteers with a genetic risk profile. Transl Psychiatr. 2022;12(1):1–9. doi: 10.1038/s41398-022-02003-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groom MJ, Jackson GM, Calton TG, Andrews HK, Bates AT, Liddle PF, Hollis C. Cognitive deficits in early-onset schizophrenia spectrum patients and their non-psychotic siblings: a comparison with ADHD. Schizophr Res. 2008;99(1–3):85–95. doi: 10.1016/j.schres.2007.11.008. [DOI] [PubMed] [Google Scholar]
- Górriz JM, Jimenez-Mesa C, Romero-Garcia R, Segovia F, Ramirez J, Castillo-Barnes D, Suckling J. Statistical agnostic mapping: a framework in neuroimaging based on concentration inequalities. Information Fusion. 2021;66:198–212. doi: 10.1016/j.inffus.2020.09.008. [DOI] [Google Scholar]
- Hao AJ, He BL, Yin CH (2015) Discrimination of ADHD children based on Deep Bayesian Network
- Hashimoto Y, Ogata Y, Honda M, Yamashita Y. Deep feature extraction for resting-state functional mri by self-supervised learning and application to schizophrenia diagnosis. Front Neurosci. 2021 doi: 10.3389/fnins.2021.696853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Havlicek M, Jan J, Brazdil M, Calhoun VD. Dynamic Granger causality based on Kalman filter for evaluation of functional network connectivity in fMRI data. Neuroimage. 2010;53(1):65–77. doi: 10.1016/j.neuroimage.2010.05.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Highland D, Zhou G. A review of detection techniques for depression and bipolar disorder. Smart Health. 2022 doi: 10.1016/j.smhl.2022.100282. [DOI] [Google Scholar]
- Hilland E, Johannessen C, Jonassen R, Alnæs D, Jørgensen KN, Barth C, Agartz I. Aberrant default mode connectivity in adolescents with early-onset psychosis: a resting state fMRI study. NeuroImage Clin. 2022;33:102881. doi: 10.1016/j.nicl.2021.102881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- https://legacy.openfmri.org/dataset/ds000030/
- https://www.wjgnet.com/2220-3206/full/v5/i1/47.htm
- Hu M, Sim K, Zhou JH, Jiang X, Guan C (2020) Brain MRI-based 3D convolutional neural networks for classification of schizophrenia and controls. In: 2020 42nd annual international conference of the IEEE engineering in medicine and biology society (EMBC) (pp 1742–1745). IEEE [DOI] [PubMed]
- Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. Fsl Neuroimage. 2012;62(2):782–790. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- Jepsen JRM, Rydkjaer J, Fagerlund B, Pagsberg AK, Glenthøj BY, Oranje B. Overlapping and disease specific trait, response, and reflection impulsivity in adolescents with first-episode schizophrenia spectrum disorders or attention-deficit/hyperactivity disorder. Psychol Med. 2018;48(4):604–616. doi: 10.1017/S0033291717001921. [DOI] [PubMed] [Google Scholar]
- Johnsen LK, Loren V, van Themaat AH, Larsen KM, Burton BK, Baare WFC, Madsen KS, Plessen KJ. Alterations in task-related brain activation in children, adolescents and young adults at familial high-risk for schizophrenia or bipolar disorder-a systematic review. Front Psych. 2020;11:632. doi: 10.3389/fpsyt.2020.00632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly RE, Wang Z, Alexopoulos GS, Gunning FM, Murphy CF, Morimoto SS, Hoptman MJ. Hybrid ICA-seed-based methods for fMRI functional connectivity assessment: a feasibility study. Int J Biomed Imag. 2010 doi: 10.1155/2010/868976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khodatars M, Shoeibi A, Sadeghi D, Ghaasemi N, Jafari M, Moridian P, Berk M. Deep learning for neuroimaging-based diagnosis and rehabilitation of autism spectrum disorder: a review. Comput Biol Med. 2021;139:104949. doi: 10.1016/j.compbiomed.2021.104949. [DOI] [PubMed] [Google Scholar]
- Khosla M, Jamison K, Ngo GH, Kuceyeski A, Sabuncu MR. Machine learning in resting-state fMRI analysis. Magn Reson Imaging. 2019;64:101–121. doi: 10.1016/j.mri.2019.05.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khozeimeh F, Sharifrazi D, Izadi NH, Joloudari JH, Shoeibi A, Alizadehsani R, Islam SMS. Combining a convolutional neural network with autoencoders to predict the survival chance of COVID-19 patients. Sci Rep. 2021;11(1):1–18. doi: 10.1038/s41598-021-93543-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konrad K, Eickhoff SB. Is the ADHD brain wired differently? A review on structural and functional connectivity in attention deficit hyperactivity disorder. Hum Brain Mapp. 2010;31(6):904–916. doi: 10.1002/hbm.21058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuang D, Guo X, An X, Zhao Y, He L (2014) Discrimination of ADHD based on fMRI data with deep belief network. In: International conference on intelligent computing (pp 225–232). Springer, Cham
- Langberg JM, Epstein JN, Graham AJ. Organizational-skills interventions in the treatment of ADHD. Expert Rev Neurother. 2008;8(10):1549–1561. doi: 10.1586/14737175.8.10.1549. [DOI] [PubMed] [Google Scholar]
- Li J, Sun Y, Huang Y, Bezerianos A, Yu R. Machine learning technique reveals intrinsic characteristics of schizophrenia: an alternative method. Brain Imaging Behav. 2019;13(5):1386–1396. doi: 10.1007/s11682-018-9947-4. [DOI] [PubMed] [Google Scholar]
- Li C, Zhang S, Qin Y, Estupinan E. A systematic review of deep transfer learning for machinery fault diagnosis. Neurocomputing. 2020;407:121–135. doi: 10.1016/j.neucom.2020.04.045. [DOI] [Google Scholar]
- Liang S, Deng W, Li X, Wang Q, Greenshaw AJ, Guo W, Li T. Aberrant posterior cingulate connectivity classify first-episode schizophrenia from controls: a machine learning study. Schizophr Res. 2020;220:187–193. doi: 10.1016/j.schres.2020.03.022. [DOI] [PubMed] [Google Scholar]
- Liao Y, Vemuri VR. Use of k-nearest neighbor classifier for intrusion detection. Comput Secur. 2002;21(5):439–448. doi: 10.1016/S0167-4048(02)00514-X. [DOI] [Google Scholar]
- Liu X, Milanova M. Visual attention in deep learning: a review. Int Rob Auto J. 2018;4(3):154–155. [Google Scholar]
- Loh HW, Ooi CP, Barua PD, Palmer EE, Molinari F, Acharya U. Automated detection of ADHD: Current trends and future perspective. Comput Biol Med. 2022 doi: 10.1016/j.compbiomed.2022.105525. [DOI] [PubMed] [Google Scholar]
- Lombardi A, Tangaro S, Bellotti R, Bertolino A, Blasi G, Pergola G, Guaragnella C. A novel synchronization-based approach for functional connectivity analysis. Complexity. 2017 doi: 10.1155/2017/7190758. [DOI] [Google Scholar]
- Luckett PH, Maccotta L, Lee JJ, Park KY, Dosenbach NU, Ances BM, Leuthardt EC. Deep learning resting state fMRI lateralization of temporal lobe epilepsy. Epilepsia. 2022 doi: 10.1111/epi.17233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma G, Ahmed NK, Willke TL, Yu PS. Deep graph similarity learning: a survey. Data Min Knowl Disc. 2021;35(3):688–725. doi: 10.1007/s10618-020-00733-5. [DOI] [Google Scholar]
- Mao Z, Su Y, Xu G, Wang X, Huang Y, Yue W, Xiong N. Spatio-temporal deep learning method for ADHD fMRI classification. Inf Sci. 2019;499:1–11. doi: 10.1016/j.ins.2019.05.043. [DOI] [Google Scholar]
- Marill KA. Advanced statistics: linear regression, part II: multiple linear regression. Acad Emerg Med. 2004;11(1):94–102. doi: 10.1111/j.1553-2712.2004.tb01379.x. [DOI] [PubMed] [Google Scholar]
- Marsh PJ, Williams LM. ADHD and schizophrenia phenomenology: visual scanpaths to emotional faces as a potential psychophysiological marker? Neurosci Biobehav Rev. 2006;30(5):651–665. doi: 10.1016/j.neubiorev.2005.11.004. [DOI] [PubMed] [Google Scholar]
- Matsubara T, Tashiro T, Uehara K. Deep neural generative model of functional MRI images for psychiatric disorder diagnosis. IEEE Trans Biomed Eng. 2019;66(10):2768–2779. doi: 10.1109/TBME.2019.2895663. [DOI] [PubMed] [Google Scholar]
- Maulud D, Abdulazeez AM. A review on linear regression comprehensive in machine learning. J Appl Sci Technol Trends. 2020;1(4):140–147. doi: 10.38094/jastt1457. [DOI] [Google Scholar]
- Mittal K, Jain A, Vaisla KS, Castillo O, Kacprzyk J. A comprehensive review on type 2 fuzzy logic applications: past, present and future. Eng Appl Artif Intell. 2020;95:103916. doi: 10.1016/j.engappai.2020.103916. [DOI] [Google Scholar]
- Mohammed F, He X, Lin Y (2021) Retracted: An easy-to-use deep-learning model for highly accurate diagnosis of Parkinson's disease using SPECT images [DOI] [PubMed]
- Mäki-Marttunen V, Diez I, Cortes JM, Chialvo DR, Villarreal M. Disruption of transfer entropy and inter-hemispheric brain functional connectivity in patients with disorder of consciousness. Front Neuroinform. 2013;7:24. doi: 10.3389/fninf.2013.00024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niu Z, Zhong G, Yu H. A review on the attention mechanism of deep learning. Neurocomputing. 2021;452:48–62. doi: 10.1016/j.neucom.2021.03.091. [DOI] [Google Scholar]
- Noble WS. What is a support vector machine? Nat Biotechnol. 2006;24(12):1565–1567. doi: 10.1038/nbt1206-1565. [DOI] [PubMed] [Google Scholar]
- O'Driscoll C, Laing J, Mason O. Cognitive emotion regulation strategies, alexithymia and dissociation in schizophrenia, a review and meta-analysis. Clin Psychol Rev. 2014;34(6):482–495. doi: 10.1016/j.cpr.2014.07.002. [DOI] [PubMed] [Google Scholar]
- Oh J, Oh BL, Lee KU, Chae JH, Yun K. Identifying schizophrenia using structural MRI with a deep learning algorithm. Front Psych. 2020;11:16. doi: 10.3389/fpsyt.2020.00016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pagano G, Niccolini F, Politis M. Imaging in Parkinson’s disease. Clin Med. 2016;16(4):371. doi: 10.7861/clinmedicine.16-4-371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pallanti S, Salerno L. Raising attention to attention deficit hyperactivity disorder in schizophrenia. World J Psychiatr. 2015;5(1):47. doi: 10.5498/wjp.v5.i1.47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan X, Wang Y, He S. The evidential reasoning approach for renewable energy resources evaluation under interval type-2 fuzzy uncertainty. Inf Sci. 2021;576:432–453. doi: 10.1016/j.ins.2021.06.091. [DOI] [Google Scholar]
- Park MTM, Raznahan A, Shaw P, Gogtay N, Lerch JP, Chakravarty MM. Neuroanatomical phenotypes in mental illness: identifying convergent and divergent cortical phenotypes across autism, ADHD and schizophrenia. J Psychiatr Neurosci. 2018;43(3):201–212. doi: 10.1503/jpn.170094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Duchesnay E. Scikit-learn: machine learning in python. J Mach Learn Res. 2011;12:2825–2830. [Google Scholar]
- Peralta V, de Jalón EG, Campos MS, Zandio M, Sanchez-Torres A, Cuesta MJ. The meaning of childhood attention-deficit hyperactivity symptoms in patients with a first-episode of schizophrenia-spectrum psychosis. Schizophr Res. 2011;126(1–3):28–35. doi: 10.1016/j.schres.2010.09.010. [DOI] [PubMed] [Google Scholar]
- Poldrack RA, Congdon E, Triplett W, Gorgolewski KJ, Karlsgodt KH, Mumford JA, Sabb FW, Freimer NB, London ED, Cannon TD, Bilder RM. A phenome-wide examination of neural and cognitive function. Sci Data. 2016;3(1):1–12. doi: 10.1038/sdata.2016.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramkiran S, Sharma A, Rao NP. Resting-state anticorrelated networks in schizophrenia. Psychiatr Res Neuroimaging. 2019;284:1–8. doi: 10.1016/j.pscychresns.2018.12.013. [DOI] [PubMed] [Google Scholar]
- Riaz A, Asad M, Al Arif SMR, Alonso E, Dima D, Corr P, Slabaugh G (2018) Deep fMRI: An end-to-end deep network for classification of fMRI data. In: 2018 IEEE 15th international symposium on biomedical imaging (ISBI 2018) (pp 1419–1422). IEEE
- Rivera MJ, Teruel MA, Maté A, Trujillo J (2021) Diagnosis and prognosis of mental disorders by means of EEG and deep learning: a systematic mapping study. Artif Intell Rev, 1–43
- Rodriguez-Rivero J, Ramirez J, Martínez-Murcia FJ, Segovia F, Ortiz A, Salas D, Górriz JM. Granger causality-based information fusion applied to electrical measurements from power transformers. Inf Fusion. 2020;57:59–70. doi: 10.1016/j.inffus.2019.12.005. [DOI] [Google Scholar]
- Rogers GB, Keating DJ, Young RL, Wong ML, Licinio J, Wesselingh S. From gut dysbiosis to altered brain function and mental illness: mechanisms and pathways. Mol Psychiatry. 2016;21(6):738–748. doi: 10.1038/mp.2016.50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross RG, Olincy A, Harris JG, Sullivan B, Radant A. Smooth pursuit eye movements in schizophrenia and attentional dysfunction: adults with schizophrenia, ADHD, and a normal comparison group. Biol Psychiatr. 2000;48(3):197–203. doi: 10.1016/S0006-3223(00)00825-8. [DOI] [PubMed] [Google Scholar]
- Runkler TA, Chen C, John R. Type reduction operators for interval type–2 defuzzification. Inf Sci. 2018;467:464–476. doi: 10.1016/j.ins.2018.08.023. [DOI] [Google Scholar]
- Sadeghi D, Shoeibi A, Ghassemi N, Moridian P, Khadem A, Alizadehsani R, Acharya UR. An overview of artificial intelligence techniques for diagnosis of Schizophrenia based on magnetic resonance imaging modalities: Methods, challenges, and future works. Comput Biol Med. 2022 doi: 10.1016/j.compbiomed.2022.105554. [DOI] [PubMed] [Google Scholar]
- Safavian SR, Landgrebe D. A survey of decision tree classifier methodology. IEEE Trans Syst Man Cybern. 1991;21(3):660–674. doi: 10.1109/21.97458. [DOI] [Google Scholar]
- Salmi J, Metwaly M, Tohka J, Alho K, Leppämäki S, Tani P, Laine M. ADHD desynchronizes brain activity during watching a distracted multi-talker conversation. Neuroimage. 2020;216:116352. doi: 10.1016/j.neuroimage.2019.116352. [DOI] [PubMed] [Google Scholar]
- Sanei S, Chambers JA. EEG signal processing. Wiley; 2013. [Google Scholar]
- Schober P, Vetter TR. Linear regression in medical research. Anesth Analg. 2020;132(1):108. doi: 10.1213/ANE.0000000000005206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sendi MS, Zendehrouh E, Fu Z, Mahmoudi B, Miller RL, Calhoun VD (2020) A machine learning model for exploring aberrant functional network connectivity transition in schizophrenia. In: 2020 IEEE Southwest Symposium on Image Analysis and Interpretation (SSIAI) (pp 112–115). IEEE
- Sharifrazi D, Alizadehsani R, Joloudari JH, Shamshirband S, Hussain S, Sani ZA, Alinejad-Rokny H (2020) CNN-KCL: Automatic myocarditis diagnosis using convolutional neural network combined with k-means clustering [DOI] [PubMed]
- Shoeibi A, Ghassemi N, Alizadehsani R, Rouhani M, Hosseini-Nejad H, Khosravi A, Nahavandi S. A comprehensive comparison of handcrafted features and convolutional autoencoders for epileptic seizures detection in EEG signals. Expert Syst Appl. 2021;163:113788. doi: 10.1016/j.eswa.2020.113788. [DOI] [Google Scholar]
- Shoeibi A, Ghassemi N, Khodatars M, Moridian P, Alizadehsani R, Zare A, Gorriz JM. Detection of epileptic seizures on EEG signals using ANFIS classifier, autoencoders and fuzzy entropies. Biomed Signal Process Control. 2022;73:103417. doi: 10.1016/j.bspc.2021.103417. [DOI] [Google Scholar]
- Shoeibi A, Khodatars M, Ghassemi N, Jafari M, Moridian P, Alizadehsani R, Acharya UR. Epileptic seizures detection using deep learning techniques: a review. Int J Environ Res Public Health. 2021;18(11):5780. doi: 10.3390/ijerph18115780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shoeibi A, Khodatars M, Jafari M, Moridian P, Rezaei M, Alizadehsani R, Acharya UR. Applications of deep learning techniques for automated multiple sclerosis detection using magnetic resonance imaging: a review. Comput Biol Med. 2021;136:104697. doi: 10.1016/j.compbiomed.2021.104697. [DOI] [PubMed] [Google Scholar]
- Shoeibi A, Sadeghi D, Moridian P, Ghassemi N, Heras J, Alizadehsani R, Gorriz JM. Automatic diagnosis of schizophrenia in EEG signals using CNN-LSTM models. Front Neuroinformatics. 2021 doi: 10.3389/fninf.2021.777977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shoeibi A, Rezaei M, Ghassemi N, Namadchian Z, Zare A, Gorriz JM (2022a) Automatic diagnosis of schizophrenia in EEG signals using functional connectivity features and CNN-LSTM model. In: International work-conference on the interplay between natural and artificial computation (pp 63–73). Springer, Cham
- Shoeibi A, Ghassemi N, Heras J, Rezaei M, Gorriz JM (2022b). Automatic diagnosis of myocarditis in cardiac magnetic images using CycleGAN and deep PreTrained models. In: International work-conference on the interplay between natural and artificial computation (pp 145–155). Springer, Cham
- Shoeibi A, Khodatars M, Alizadehsani R, Ghassemi N, Jafari M, Moridian P, Shi P (2020) Automated detection and forecasting of covid-19 using deep learning techniques: a review. http://arxiv.org/abs/arXiv:2007.10785
- Shoeibi A, Ghassemi N, Khodatars M, Jafari M, Moridian P, Alizadehsani R, Nahavandi S (2021b) Applications of epileptic seizures detection in neuroimaging modalities using deep learning techniques: methods, challenges, and future works. http://arxiv.org/abs/arXiv:2105.14278 [DOI] [PubMed]
- Singh M, Badhwar R, Bagler G (2016) Graph theoretical biomarkers for schizophrenic brain functional networks. In: 2016 International conference on signal processing and communication (ICSC) (pp 289–294). IEEE
- Suk HI, Wee CY, Lee SW, Shen D. State-space model with deep learning for functional dynamics estimation in resting-state fMRI. Neuroimage. 2016;129:292–307. doi: 10.1016/j.neuroimage.2016.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suleymani M, Bemani A. Application of ANFIS-PSO algorithm as a novel method for estimation of higher heating value of biomass. Energy Sour Part A Recover Util Environ Eff. 2018;40(3):288–293. [Google Scholar]
- Sun FT, Miller LM, D'esposito M. Measuring interregional functional connectivity using coherence and partial coherence analyses of fMRI data. Neuroimage. 2004;21(2):647–658. doi: 10.1016/j.neuroimage.2003.09.056. [DOI] [PubMed] [Google Scholar]
- Sun X, Zhang Y, Tian X, Cao J, Zhu J (2021) Speed sensorless control for IPMSMs using a modified MRAS with grey wolf optimization algorithm. IEEE Trans Transp Electrif
- Tandon R, Gaebel W, Barch DM, Bustillo J, Gur RE, Heckers S, Carpenter W. Definition and description of schizophrenia in the DSM-5. Schizophr Res. 2013;150(1):3–10. doi: 10.1016/j.schres.2013.05.028. [DOI] [PubMed] [Google Scholar]
- Thirumurugan P, Shanthakumar P. Brain tumor detection and diagnosis using ANFIS classifier. Int J Imaging Syst Technol. 2016;26(2):157–162. doi: 10.1002/ima.22170. [DOI] [Google Scholar]
- Tien Bui D, Khosravi K, Li S, Shahabi H, Panahi M, Singh VP, Bin Ahmad B. New hybrids of anfis with several optimization algorithms for flood susceptibility modeling. Water. 2018;10(9):1210. doi: 10.3390/w10091210. [DOI] [Google Scholar]
- Verdoux H, Sutter AL. Perinatal risk factors for schizophrenia: diagnostic specificity and relationships with maternal psychopathology. Am J Med Genet. 2002;114(8):898–905. doi: 10.1002/ajmg.10906. [DOI] [PubMed] [Google Scholar]
- Vieira S, Pinaya WH, Mechelli A. Using deep learning to investigate the neuroimaging correlates of psychiatric and neurological disorders: methods and applications. Neurosci Biobehav Rev. 2017;74:58–75. doi: 10.1016/j.neubiorev.2017.01.002. [DOI] [PubMed] [Google Scholar]
- Villringer A, Chance B. Non-invasive optical spectroscopy and imaging of human brain function. Trends Neurosci. 1997;20(10):435–442. doi: 10.1016/S0166-2236(97)01132-6. [DOI] [PubMed] [Google Scholar]
- Volkow ND, O’Brien CP. Issues for DSM-V: should obesity be included as a brain disorder? Am J Psychiatry. 2007;164(5):708–710. doi: 10.1176/ajp.2007.164.5.708. [DOI] [PubMed] [Google Scholar]
- Vovou F, Hull L, Petrides KV. Mental health literacy of ADHD, autism, schizophrenia, and bipolar disorder: a cross-cultural investigation. J Ment Health. 2021;30(4):470–480. doi: 10.1080/09638237.2020.1713999. [DOI] [PubMed] [Google Scholar]
- Wang HE, Bénar CG, Quilichini PP, Friston KJ, Jirsa VK, Bernard C. A systematic framework for functional connectivity measures. Front Neurosci. 2014;8:405. doi: 10.3389/fnins.2014.00405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Celebi ME, Zhang YD, Yu X, Lu S, Yao X, Tyukin I. Advances in data preprocessing for biomedical data fusion: an overview of the methods, challenges, and prospects. Inf Fusion. 2021;76:376–421. doi: 10.1016/j.inffus.2021.07.001. [DOI] [Google Scholar]
- Wang Z, Alahmadi A, Zhu D, Li T (2015) Brain functional connectivity analysis using mutual information. In: 2015 IEEE global conference on signal and information processing (GlobalSIP) (pp 542–546). IEEE
- Warnick R, Guindani M, Erhardt E, Allen E, Calhoun V, Vannucci M. A Bayesian approach for estimating dynamic functional network connectivity in fMRI data. J Am Stat Assoc. 2018;113(521):134–151. doi: 10.1080/01621459.2017.1379404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei LY. A hybrid model based on ANFIS and adaptive expectation genetic algorithm to forecast TAIEX. Econ Model. 2013;33:893–899. doi: 10.1016/j.econmod.2013.06.009. [DOI] [Google Scholar]
- Whitley D. A genetic algorithm tutorial. Stat Comput. 1994;4(2):65–85. doi: 10.1007/BF00175354. [DOI] [Google Scholar]
- Windeatt T. Accuracy/diversity and ensemble MLP classifier design. IEEE Trans Neural Networks. 2006;17(5):1194–1211. doi: 10.1109/TNN.2006.875979. [DOI] [PubMed] [Google Scholar]
- Wortzel HS, Arciniegas DB. The DSM-5 approach to the evaluation of traumatic brain injury and its neuropsychiatric sequelae. NeuroRehabilitation. 2014;34(4):613–623. doi: 10.3233/NRE-141086. [DOI] [PubMed] [Google Scholar]
- Yang J, Pu W, Wu G, Chen E, Lee E, Liu Z, Palaniyappan L. Connectomic underpinnings of working memory deficits in schizophrenia: evidence from a replication fMRI study. Schizophr Bull. 2020;46(4):916–926. doi: 10.1093/schbul/sbz137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang T, Li C, Li P, Peng Y, Kang X, Jiang C, Xu P. Separated channel attention convolutional neural network (SC-CNN-attention) to identify ADHD in multi-site Rs-fMRI dataset. Entropy. 2020;22(8):893. doi: 10.3390/e22080893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao K, Duka B, Xie H, Oathes DJ, Calhoun V, Zhang Y. A dynamic graph convolutional neural network framework reveals new insights into connectome dysfunctions in ADHD. Neuroimage. 2022;246:118774. doi: 10.1016/j.neuroimage.2021.118774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Y, Fu S, Yang S, Liang P, Tan Y. Weighted deep forest for schizophrenia data classification. IEEE Access. 2020;8:62698–62705. doi: 10.1109/ACCESS.2020.2983317. [DOI] [Google Scholar]
- Zou L, Zheng J, Miao C, Mckeown MJ, Wang ZJ. 3D CNN based automatic diagnosis of attention deficit hyperactivity disorder using functional and structural MRI. IEEE Access. 2017;5:23626–23636. doi: 10.1109/ACCESS.2017.2762703. [DOI] [Google Scholar]
- Zou L, Zheng J, McKeown MJ (2017a) Deep learning based automatic diagnoses of attention deficit hyperactive disorder. In: 2017a IEEE global conference on signal and information processing (GlobalSIP) (pp 962–966). IEEE