Skeletal Maturation and Long Bone Growth Patterns of Patients with Progeria: A Retrospective Study

Abstract

Background

Hutchinson-Gilford Progeria Syndrome (HGPS) is a rare sporadic genetic disorder. One early clinical manifestation of Progeria is abnormal skeletal growth, yet this has not been fully characterized. The objective of this study is to characterize the skeletal maturation and long bone growth patterns of patients with the clinical phenotype of Progeria.

Methods

Skeletal surveys obtained over a 9.5 year period of patients (<20 years-old) with Progeria were reviewed. Most surveys included radiographs of the hands and long bones (humeri, radii, ulnas, tibias, and fibulas). Bone ages of these patients were estimated by the standards of Greulich and Pyle. Following the established methodology for studying long bone growth, the study cohort was separated into 2 overlapping age groups. For the childhood group (≤12 years old), longitudinal bone length measurements were made between physes. For the adolescent group (≥10 years old), longitudinal bone length measurements were made from the upper margins of the proximal to the lower margin of the distal ossified epiphyses. Bone age estimates and bone length measurements were plotted against patient chronologic age and compared to reference standards.

Findings

Eighty-five patients with 250 skeletal surveys were included. Bone age estimates showed a slightly more advanced skeletal maturation rate throughout all chronologic ages, on average 9% and 14% higher than normal males and females, respectively. Longitudinal long bone lengths began to deviate from normal standards by age 1–2 years. Growth curves for these long bones plateaued at about half the normal plateau, and the time taken to reach the plateau, as measured by the half-life, was also about half the normal time.

Interpretation

Our study established growth curves that may serve as reference standards for skeletal maturation and long bone growth of patients with the clinical phenotype of Progeria.

Introduction

Hutchinson Gilford Progeria Syndrome (HGPS) is an extremely rare sporadic autosomal dominant disorder affecting approximately 1 in 20 million people [1]. The classic gene mutation for this disease entity is a single base mutation within the LMNA gene located in a limited region of chromosome 1q [2–4]. The LMNA gene mutation usually results in production of a mutant lamin A protein product called progerin. The cellular accumulation of progerin leads to decreased cellular life span and early cell death [5], with most patient deaths attributed to progressive atherosclerosis and heart failure, between 7–21 years of age [6]. Prior to their deaths, these patients often have advanced cardiovascular disease, including hypertension, transient ischemia attacks, and strokes. Due to the disease rarity and short patient life-span, there are approximately only 350–400 patients with Progeria alive worldwide at any given time [1]. Occasionally, the gene mutations in the lamin pathway do not produce progerin, and patients in this category are called progeroid laminopathies (PL). This subset of patients is phenotypically similar to those who do produce progerin. Therefore, in this study, the term Progeria refers to both progerin producing HGPS and non-progerin producing PL.

Patients with Progeria have a normal physical appearance at birth, but by one year of age they progressively develop the distinctive phenotype of alopecia, generalized growth failure with poor weight gain and loss of subcutaneous fat, joint contractures, and abnormally short stature [6, 7]. They also develop characteristic facial features of retrognathia, crowded dentition, and narrowed nasal bridge. Progeria is considered a unique skeletal dysplasia [8] with notable skeletal manifestations of gracile long bones, hip abnormalities (including coxa valga alignment, hip dysplasia, and avascular necrosis), acro-osteolysis, narrow chest apices, small clavicles with distal resorption, thin ribs with anterior resorption, ovoid vertebral bodies, diastasis of the cranial sutures, and Wormian bones. These skeletal findings are progressive over time and have been well documented [9, 10].

One of the earliest clinical skeletal manifestations in Progeria is abnormal skeletal growth, yet to date this has not been fully characterized. Specifically, the longitudinal growth curves of the long bones in these patients relative to those of the normal population are unknown. As skeletal growth and maturation are intimately related, it is natural to also understand the skeletal maturation pattern. By understanding the natural history of skeletal growth and maturation pattern, reference standards can be established for these measurements for patients with Progeria. In addition, these 2 measures have the potential to provide objective assessments with which to evaluate the efficacy and response of these patients undergoing future drug trials. Therefore, the objective of this study is to establish the skeletal maturation and long bone growth patterns of patients with the clinical phenotype of Progeria.

Methods

Study design and participants

Our large tertiary-care children’s hospital serves as the international referral center for Progeria research. We included patients identified by The Progeria Research Foundation International Registry (www.progeriaresearch.org) as having the clinical phenotype of Progeria as well as the genotypes of HGPS and PL, with clinical and genetic confirmation by the Progeria study investigators (to include both progerin producing HGPS and non-progerin producing PL). As part of the clinical work-up and testing, sequential skeletal surveys are routinely obtained for each patient, thus creating a large centralized imaging database. These serial skeletal surveys were used to characterize the bone phenotype of Progeria patients and assess potential treatment effects on the bones. Skeletal survey radiographs of patients younger than 20 years (obtained between 1/2009 – 7/2018) were reviewed. Skeletal surveys performed prior to 2009 did not routinely include hand or long bone radiographs, and hence could not be used to assess skeletal maturation or long bone growth. Patient gender and age at each imaging session were recorded. Most of these patients participated in clinical trials, including NCT00425607 (lonafarnib monotherapy), NCT00879034 and NCT00916747 (lonafarnib, zoledronate, and pravastatin combination therapy) [1, 6, 11, 12, 13]. This study has the ongoing approval by the institutional Committee on Clinical Investigation. Prior to participating in these clinical trials, written informed consent was obtained for all patients (including consent for performing serial skeletal surveys).

Procedures

Skeletal surveys

The protocol for the standard Progeria skeletal survey varied over time, but since 2009, the majority of surveys included posteroanterior radiographs of the left hand/wrist, and anteroposterior radiographs of each humerus, radius, ulna, tibia, and fibula. No dedicated femur radiographs were acquired in order to reduce the amount of radiation exposure to the patient, as the proximal femurs were imaged on the dedicated pelvic radiographs and the distal femurs were imaged on the dedicated tibia and fibula radiographs. Separate frontal radiographs centered on the left hand/wrist and on each long bone were obtained to maximize image sharpness, minimize image magnification, and reduce geometric distortion.

Bone age measurements

The bone ages were estimated by a pediatric radiologist (with 9 years post fellowship experience) based on left hand radiographs, using the method of Greulich and Pyle, and employing the Brush Foundation standards [14].

Bone length measurements

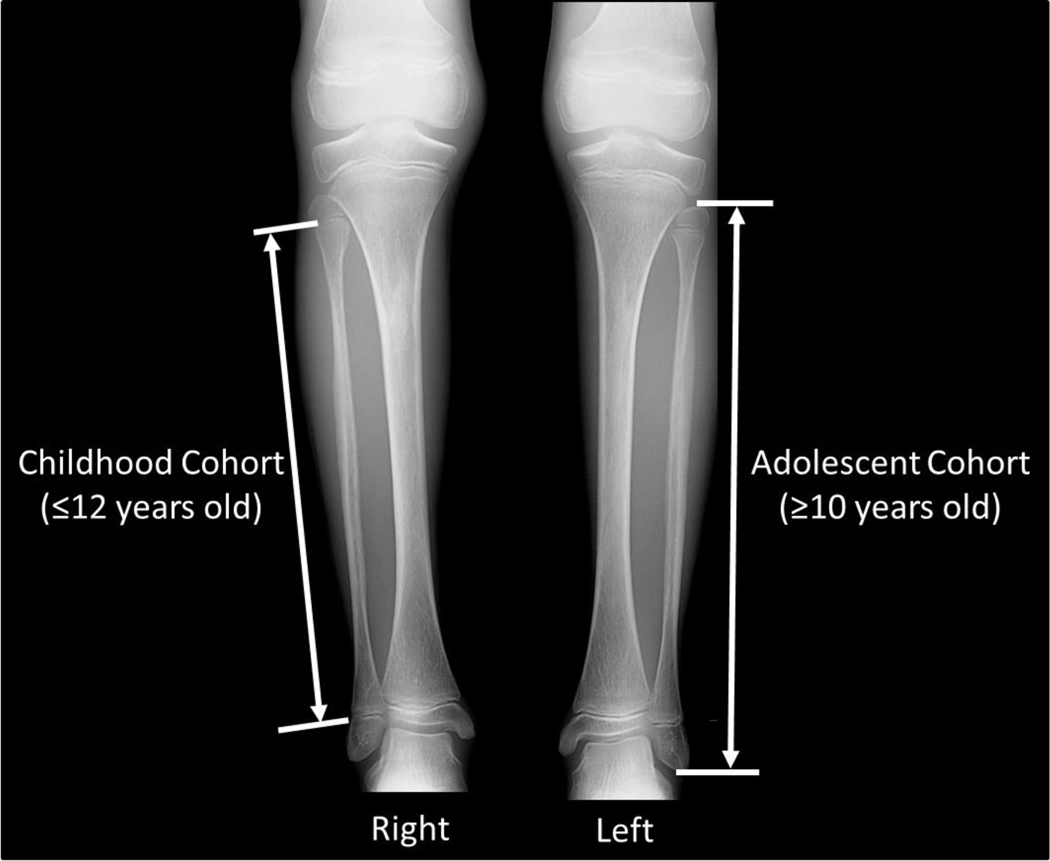
Bone length measurements were performed by the same pediatric radiologist using the picture archiving and communication system measurement tool (0.01 mm resolution). Following standard methodology previously established in the literature for studying long bone growth [15], the study cohort was separated into 2 overlapping age groups: childhood (≤12 years old) and adolescent (≥10 years old). For those in the childhood cohort, bone length measurements were made between physes along the midline long axis of the bone (Fig. 1). In line with the literature, this length measurement technique was necessarily chosen because it does not include the epiphyses that are variably ossified at young ages and therefore not always radiographically apparent. For those in the adolescent cohort, bone length measurements were made along the midline long axis of the bone from the upper margins of the proximal to the lower margin of the distal ossified epiphyses (Fig. 1). The side to be measured was chosen randomly (utilizing the output of a pseudo-random binary-number generator) to avoid any possible systemic right-left laterality bias, unless there was a unilateral fracture, in which case the opposite side was measured.

Fig. 1.

Methodology for long bone length measurements, using lower extremity radiographs of a 10-year 11-month-old girl with Progeria as illustration. For the childhood cohort (≤12 years old), bone length measurements were made between the physes along the midline long axis of the bone (right fibula measurement of above). For the adolescent cohort (≥10 years old), bone length measurements were made along the midline long axis of the bone from the upper margins of the proximal to the lower margin of the distal ossified epiphyses (left fibula measurement of above). This allowed for overlap in the 10–12 year old range.

Statistical analysis

All statistical analyses outlined below were performed using SAS/STAT^® 14.1 [16]. The NLMIXED procedure was used to fit all mixed models, and the MODEL procedure was used to solve the half-life equations for bone length. Tests were 2-sided and at the 5% level.

Models for bone ages and bone lengths for Progeria boys and girls were mixed models (containing both fixed and random effects) [17]. Separate linear spline mixed models for bone ages were fit to boys and girls with Progeria (2 models). Normal bone age data was not modeled. Separate growth mixed models for bone lengths were fit to each of the 5 long bones for boys and girls with Progeria (10 models). These models, excluding the random effects, were also fit to normal medians, 5th percentiles, and 95th percentiles (30 models).

Data from the normal population was construed to be known in this study, on the grounds that it was based on summary statistics of a very large quantity of (unavailable) data. As a result, modeling for the purpose of inference was not relevant for the normal population. However, although normal bone age data was not modeled, normal bone length data was modeled for purposes other than inference, as explained below.

For both bone age and bone length, we assumed Normal distributions for both the random effects and the conditional distributions. This allowed us to interpret parameters as components of median bone ages and bone lengths, which provided appropriate comparisons to medians and other percentiles from the corresponding normal populations.

Model choice was based on considerations of ability to fit, goodness of fit, plausibility, and interpretability. As all of our models are nonlinear in the parameters, the ability to fit primarily concerned the convergence of iterative estimates to their maximum likelihood values. This was aided by careful choices of parameter starting values, and by the exclusion of negligible, if plausible, random effects (for this reason, bone length random effects were used only for the upper asymptote and not for other parameters). Goodness of fit was gauged by AIC and R-square statistics. While AIC was more powerful for comparing models, R-square provided a useful measure of absolute fit, being the proportion of variation in the data explained by our model.

Plausible models for bone age should start at the origin, increase until maturity, and flatten out thereafter. These features were embodied in our constrained linear spline model. Plausible models for bone length growth should start at a lower intercept or asymptote, and increase to an upper asymptote. We considered such models based on exponential, logistic, and extreme value cumulative distribution functions, ultimately choosing the exponential for reasons of simplicity and goodness of fit. The interpretability of bone age models centered on parameters representing the rate of maturation and the age of maturity; while the interpretability of bone length models centered on asymptotes and half-lives.

Bone age models

For patients with Progeria, bone age, $y$, was modeled as a function of chronologic age, $x$, using the “broken stick” linear spline model: $y=\alpha x$ for $x\le \kappa$, and $y=\alpha \kappa$ for $x>\kappa$. This is a constrained linear spline model comprising a sequence of 2 lines, line₁ and line₂, joining at a join point with $x$-coordinate $\kappa$, the knot. The intercept of line₁ was constrained to 0, the slope of line₂ was constrained to 0, and the knot was estimated from the data. Thus our linear spline model starts at $(x,y)=(0,0)$, increases between $x=0$ and $x=\kappa$ by $\alpha$ per year, and is horizontal thereafter. In the context of this model, $\alpha$ is the rate of bone age maturation, and $\kappa$ is the age of bone age maturity. A stylized plot illustrating these parameters in the context of the bone age model is shown in the Appendix (Fig. A1). This model allowed us to compare the maturation rate for Progeria patients with that of their normal counterparts (who have a slope of 1 by definition), and also allowed us to compare the ages of maturity.

Each subject was allowed to vary about line₁ according to a random effect $a_i$, specific to the $i^{th}$ subject. That is, each subject was allowed their own maturation rate. This random effect was assumed to follow a Normal ($N$) distribution with between-subject variance $v_a$. Given the value of the random effect, bone age for the $i^{th}$ subject and $j^{th}$ chronologic age, $y_{ij}\mid a_i$, was assumed to follow a Normal distribution with within-subject variance $v$. Thus the 4-parameter ($\alpha$, $\kappa$, $v$, $v_a$) mixed model for bone age for the $i^{th}$ subject and $j^{th}$ chronologic age was:

$$y_{ij}\mid a_i\sim N\left(\alpha x_{ij}-\alpha Max\left(0,x_{ij}-\kappa \right)+a_i{x}_{ij},v\right)\text{,}\text{where}{a}_i\sim N\left(0,v_a\right)\text{.}$$

Bone length models

Bone length, $y$, was modeled as a function of age, $x$, using the exponential growth model [18]:

$$y=L+(H-L)(1-\exp \left(-\left({\beta }_{1}x+{\beta }_2{x}^2+{\beta }_3{x}^3\right)\right).$$

The lower intercept was denoted by $L$. The upper asymptote, $H$, was allowed to depend on the bone measurement method, $M$, in a systematic way: $H$ for the adolescent measurement method ($M=0$), and $H+\delta$ for the childhood measurement method ($M=1$). This enabled us to estimate parameters using all of the sample data, and to predict lengths in adolescence for a subject measured in childhood. A stylized plot illustrating these parameters in the context of the bone length model is shown in the Appendix (Fig. A2). Additionally, for each subject, the upper asymptote was allowed to vary about the systematic component according to a random effect, $h_i$, specific to the $i^{th}$ subject. This random effect was assumed to follow a Normal distribution with between-subject variance $v_h$. Given the value of the random effect, bone length for the $i^{th}$ subject and $j^{th}$ age, $y_{ij}\mid h_i$, was assumed to follow a Normal distribution with within-subject variance $v$. Thus the 8-parameter ($L$, $H$, $\delta$, ${\beta }_1$, ${\beta }_2$, ${\beta }_3$, $v$, $v_a$) mixed model for bone length for the $i^{th}$ subject and $j^{th}$ age was:

$$y_{ij}\mid h_i\sim N(L+\left(\left(H+\delta M_{ij}+h_i\right)-L\right)\left(1-\exp \left(-\left({\beta }_1{x}_{ij}+{\beta }_2{x}_{ij}^2+{\beta }_3{x}_{ij}^3\right)\right),v\right),$$

where $h_i\sim N\left(0,v_h\right)$.

Normal bone length data was modeled, even though this data is construed to be known in this study. Specifically, we fit the same growth models as above (excluding random effects) to 3 series of normal data: median, 5th percentile, and 95th percentile. This enabled a comparison of Progeria and normal groups via growth model parameters. It also enabled us to improve the fit of the Progeria models near the origin, where the data was very sparse, by the use of the modeled normal $L$ in place of the estimated $L$ from the Progeria data (on the grounds that at birth, normal and Progeria bones should be similar in length). Thus the 8-parameter mixed model for Progeria patients actually contained only 7 parameters ($H$, $\delta$, ${\beta }_1$, ${\beta }_2$, ${\beta }_3$, $v$, $v_a$) estimated from the Progeria data. In addition to these advantages, the modeling of normal data allowed us to interpolate and extrapolate smoothed curves for normal medians and ranges.

Role of the funding source

The funders for this study were instrumental for data collection. They play no role in the study design, data analysis, data interpretation, or writing of this manuscript. The corresponding author (AT) had full access to all the demographic, radiographic and measurement data, and had final responsibility to submit for publication. The biostatistician (PJ) had full access to the measurement data.

Results

Study population

Eighty-five patients (male=45, female=40) with 250 skeletal surveys (male=119, female=131; age range=2 months to 19.8 years) were included in the study, for an average of 2.9 skeletal surveys per patient. Of the 85 patients analyzed, 74 (87%) had the classic HGPS genotype (G608G), 7 (8%) had the nonclassic progerin-producing mutations within intron 11 of the LMNA gene, 2 (2%) had a progeroid laminopathy produced by a mutation in the ZMPSTE24 gene, 1 (1%) had a mutation in exon 11of the LMNA gene that produced a progerin-like protein, and 1 (1%) had a progeroid laminopathy produced by a mutation in exon 9 of the LMNA gene. Of the 68/85 patients with serial skeletal surveys, the minimal, average, and maximum time spans between the first and last skeletal surveys were 0.42, 4.62, and 8.23 years, respectively.

Of the 250 skeletal surveys, 17 did not have hand radiographs for bone age estimation. In total there were 84 patients (male=44, female=40) with 233 hand radiographs (male=113, female=120) available for bone age estimation.

For the long bone length measurements, the childhood cohort consisted of 73 patients (male=38, female=35) for a total of 181 skeletal surveys (male=88, female=93). All of these skeletal surveys had radiographs of the humerus, radius, ulna, tibia, and fibula, except for one male which did not have a radiograph of the radius or ulna. The adolescent cohort consisted of 48 patients (male=23, female=25) for a total of 106 skeletal surveys (male=49, female=57). All of these skeletal surveys have radiographs of the humerus, radius, ulna, tibia, and fibula. Implicit in these numbers is the fact that 16 males and 20 females had both childhood and adolescent skeletal surveys.

Bone age

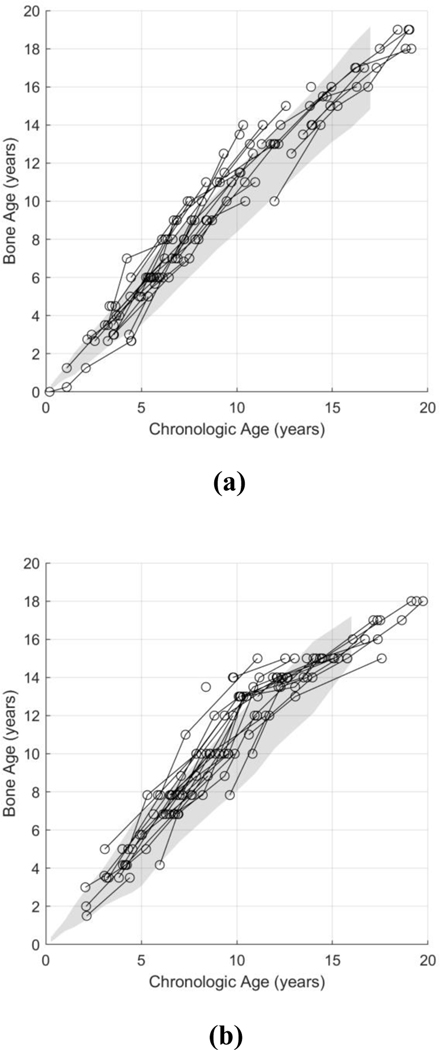
For visual assessment, bone age measurements of patients with Progeria were plotted against their respective chronologic ages, and compared to published normal reference standards [14] (Fig. 2). For both genders, 75% of Progeria bone age measurements fell within ±2 standard deviations of normal (85/113 for boys and 90/120 for girls), but were clearly on the high side of the normal range. Of the remaining 25% of Progeria measurements outside the normal range, almost all were above (rather than below) the normal range. In combination, this suggests that Progeria populations have a tendency toward slightly advanced bone age.

Fig. 2.

Longitudinal bone ages of boys (a) and girls (b) with Progeria, estimated via the method of Greulich and Pyle [14]. The graphs showed that 85/113 (75%) estimated bone ages for boys and 90/120 (75%) estimated bone ages for girls fell within ±2 standard deviation of normal (gray shaded region). Of note, for the calculation of the number of bone ages falling within ±2 standard deviation of normal, the normal gray shaded region was extrapolated to adulthood (i.e. beyond the provided age limits of 17-year-old for boys and 16-year-old for girls).

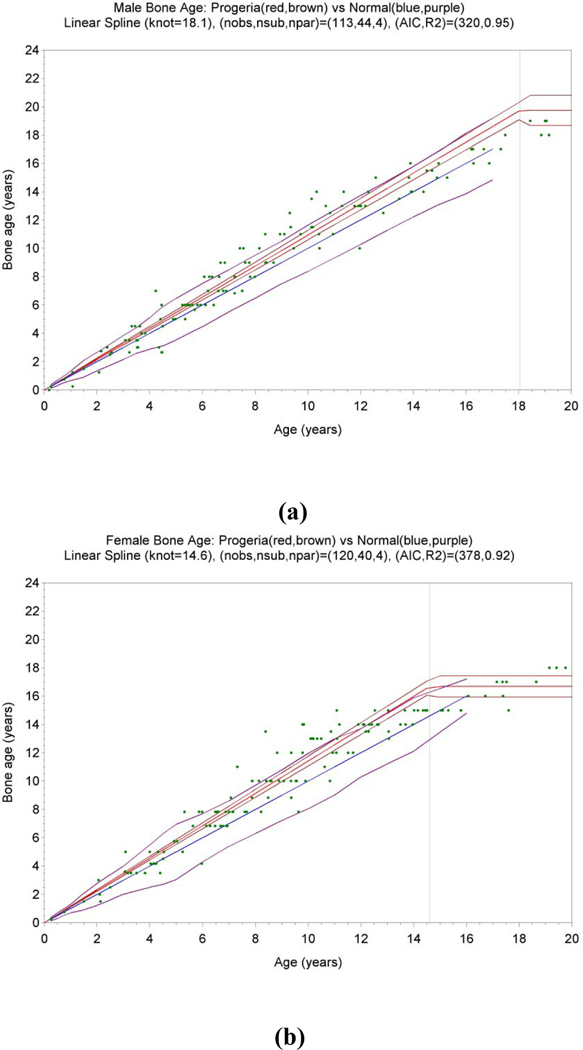
Statistical analysis via mixed modeling confirmed this impression (Fig. 3). For both males and females, the rate of maturation (the relationship between bone age and chronologic age prior to maturity) for patients with Progeria was statistically significantly higher than the normal rate of 1 (p<0.001). For males, the rate of maturation (standard error) was 1.09 (0.02), while for females it was 1.14 (0.02). The age of maturity was estimated to be 18.1 (0.4) for males and 14.6 (0.3) for females, both rather less than their normal counterparts.

Fig. 3.

Fitted statistical models for bone age vs age for 44 boys (a) and 40 girls (b) with Progeria. For each gender, the Progeria median (red line) with confidence interval (brown lines) are plotted in comparison to the normal median with slope 1 (blue line) and range (purple lines). Measurement data are shown as green dots (113 observations for boys and 120 for girls). The age of maturity (standard error) in years is the knot, $k$, of the linear spline, and was estimated to be 18.1 (0.4) for boys and 14.6 (0.3) for girls. The rate of maturation per year prior to maturity is the slope of the first line segment, $\alpha$, and was estimated to be 1.09 (0.02) for boys and 1.14 (0.02) for girls.

Long bone growth

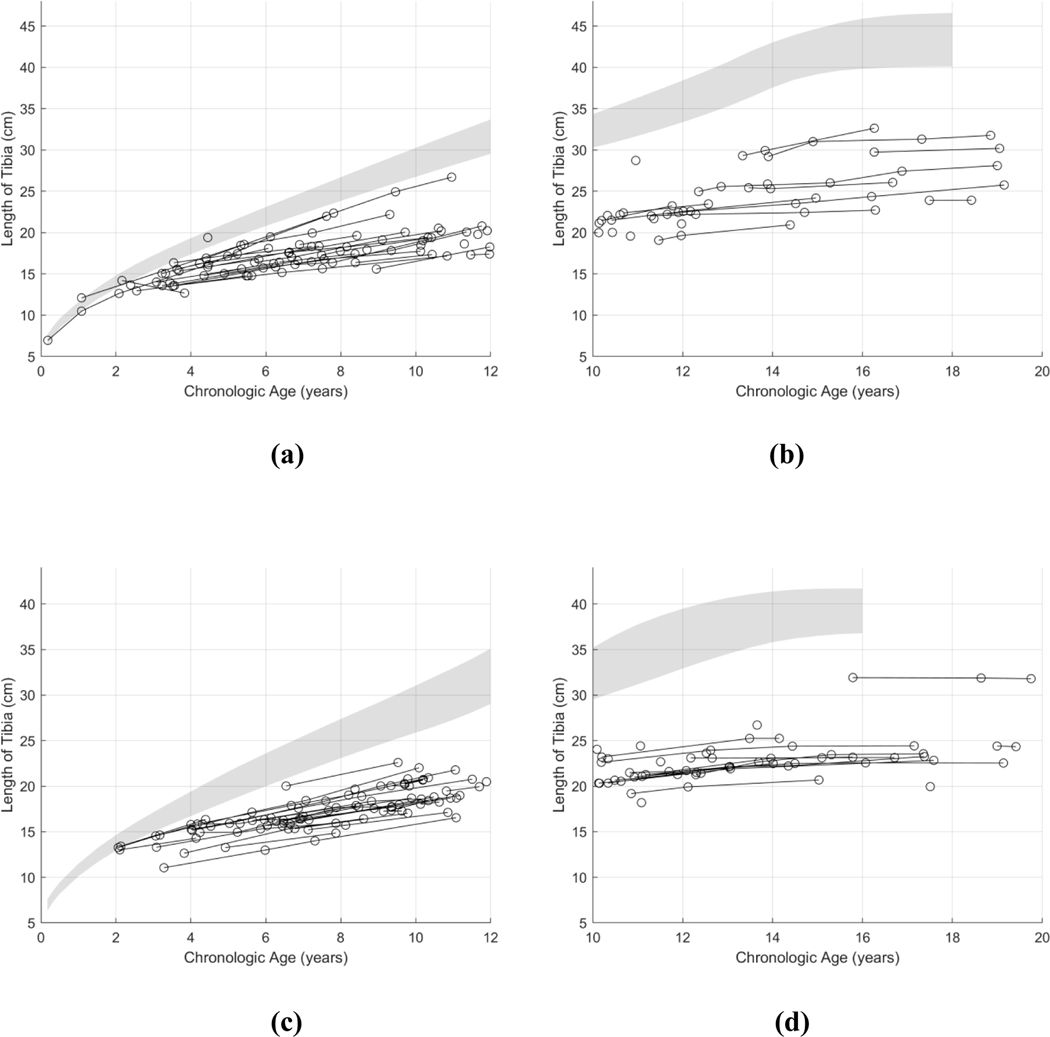
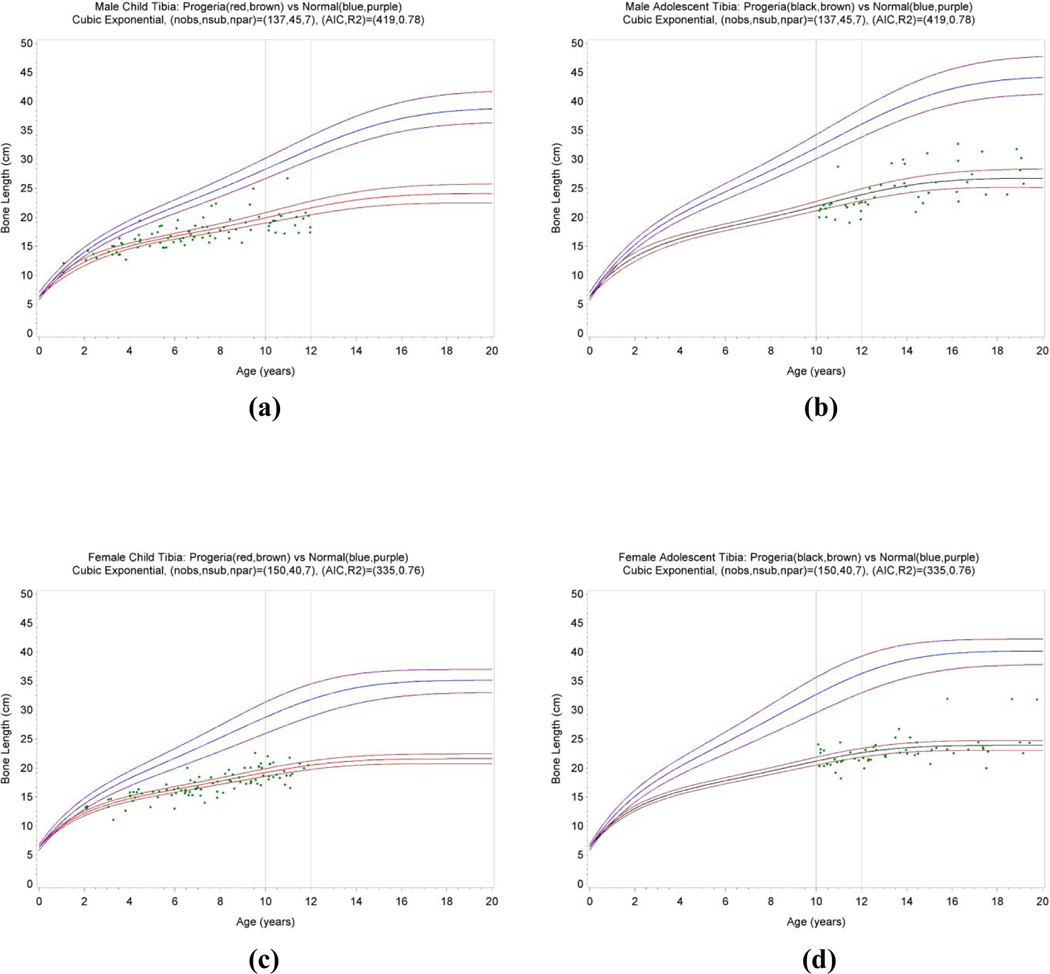
Visually, the long bone growth curves of the humerus, radius, ulna, tibia, and fibula appeared to deviate from their respective normal reference standards in similar fashions. Plots of growth curve data are shown in Fig. 4, using the tibia as the exemplar long bone. Plots of growth curve data for the other long bones are shown in the Appendix (Figs. B1–B4). The longitudinal long bone lengths from these patients appear to begin deviating from normal growth standards by age 1–2 years. The growth curves of these long bones appear to plateau at around age 14–16 years for boys and 12–14 years for girls with physeal fusion, reaching a final bone length that is approximately half of normal.

Fig. 4.

Longitudinal growth patterns of the tibia in patients with Progeria. The tibia growth curves of 38 boys ≤12 years old (a), 23 boys ≥10 years old (b), 35 girls ≤12 years old (c), and 25 girls ≥10 years old (d) were plotted in comparison to their respective reference growth standards of Maresh [15]. The population variance, shown in gray, denotes the 10–90% range of normal.

Estimated model parameters for all long bones are tabulated in Tables 1 and 2. Plots corresponding to the fitted statistical models are shown in Fig. 5 for the tibia, while plots for other long bones are shown in the Appendix (Figs. C1–C4). The major differences between Progeria and normal long bone growth were: (1) patients with Progeria had lower asymptotes (shorter eventual bone lengths), and (2) patients with Progeria had shorter half-lives and thus approached these asymptotes more rapidly. The half-life is the time taken to grow to half the eventual bone length, that is, the time to grow from $L$ to $(L+H)/2$, where $L$ is the length at birth and $H$ is the eventual bone length. We quantified the magnitudes of the two Progeria effects by Progeria/normal ratios for asymptotes and Progeria/normal ratios for half-lives for each of the 5 long bones and each gender. For males, the (humerus, radius, ulna, tibia, fibula), asymptote ratios were (0.61, 0.56, 0.57, 0.60, 0.57) while the half-life ratios were (0.66, 0.44, 0.53, 0.64, 0.52). For females, the asymptote ratios were (0.61, 0.55, 0.58, 0.60, 0.57) while the half-life ratios were (0.67, 0.38, 0.49, 0.61, 0.51). Averaging over genders and bones, the ratio for asymptotes was 0.58 (range 0.55 to 0.61), while the ratio for half-lives was 0.54 (range 0.38 to 0.67). Thus the magnitudes of the two Progeria effects were similar on average, but with more variation for half-lives than asymptotes.

Table 1.

Parameter estimates for the bone length models for boys with Progeria in comparison to those of normal boys. $L$ is the length at birth, $H$ is the eventual bone length, (${\beta }_1$, ${\beta }_2$, ${\beta }_3$) determine the growth rate, and $\delta$ is the difference in eventual bone lengths based on childhood ($H_{child}$) and adolescent ($H_{adol}$) measurement methods. Ratios refer to Progeria/normal ratios for adolescent asymptotes and Progeria/normal ratios for half-lives (the time taken to grow from $L$ to half the distance between $L$ and H). For each bone, all parameters ($L$, $H$, $\delta$ and (${\beta }_1$, ${\beta }_2$, ${\beta }_3$) taken as a group) were significant (p<0.001).

		$L$ (cm)	$H+\delta$ $H_{child}$ (cm)	$H$ $H_{adol}$ (cm)	ratio for asymptote	${\beta }_1$	${\beta }_2$	${\beta }_3$	half-life	ratio for half-life
Humerus	Normal	6.9	34.6	37.4	-	0.14	−0.012	0.0007	7.4	-
	Progeria	6.9	20.8	22.8	0.61	0.19	−0.013	0.0006	4.9	0.66
Radius	Normal	5.6	26.0	28.1	-	0.14	−0.012	0.0008	7.8	-
	Progeria	5.6	14.6	15.8	0.56	0.29	−0.030	0.0015	3.4	0.44
Ulna	Normal	6.2	28.6	30.0	-	0.14	−0.013	0.0008	7.9	-
	Progeria	6.2	16.6	17.2	0.57	0.25	−0.027	0.0015	4.2	0.53
Tibia	Normal	6.3	38.9	44.3	-	0.16	−0.015	0.0010	6.5	-
	Progeria	6.3	24.1	26.7	0.60	0.25	−0.028	0.0017	4.1	0.64
Fibula	Normal	6.0	38.6	43.1	-	0.16	−0.014	0.0009	6.4	-
	Progeria	6.0	21.8	24.5	0.57	0.28	−0.028	0.0015	3.4	0.52

Table 2.

Parameter estimates for the bone length models for girls with Progeria, in comparison to those of normal girls. $L$ is the length at birth, $H$ is the eventual bone length, (${\beta }_1$, ${\beta }_2$, ${\beta }_3$) determine the growth rate, and $\delta$ is the difference in eventual bone lengths based on childhood ($H_{child}$) and adolescent ($H_{adol}$) measurement methods. Ratios refer to Progeria/normal ratios for adolescent asymptotes and Progeria/normal ratios for half-lives (the time taken to grow from $L$ to half the distance between $L$ and $H$). For each bone, all parameters ($L$, $H$, $\delta$ and (${\beta }_1$, ${\beta }_2$, ${\beta }_3$) taken as a group) were significant (p<0.001).

		$L$ (cm)	$H+\delta$ $H_{child}$ (cm)	H $H_{adol}$ (cm)	ratio for asymptote	${\beta }_1$	${\beta }_2$	${\beta }_3$	half-life	ratio for half-life
Humerus	Normal	6.6	30.4	33.1	-	0.18	−0.018	0.0013	5.7	-
	Progeria	6.6	18.5	20.1	0.61	0.25	−0.024	0.0013	3.8	0.67
Radius	Normal	5.3	22.8	24.8	-	0.16	−0.016	0.0012	6.2	-
	Progeria	5.3	12.8	13.7	0.55	0.40	−0.049	0.0030	2.3	0.38
Ulna	Normal	6.0	24.6	26.3	-	0.18	−0.018	0.0013	5.9	-
	Progeria	6.0	14.6	15.2	0.58	0.35	−0.048	0.0031	2.9	0.49
Tibia	Normal	6.3	35.1	40.2	-	0.18	−0.017	0.0015	5.4	-
	Progeria	6.3	21.6	23.9	0.60	0.30	−0.034	0.0023	3.3	0.61
Fibula	Normal	6.0	34.9	38.9	-	0.18	−0.016	0.0013	5.3	-
	Progeria	6.0	19.7	22.2	0.57	0.34	−0.039	0.0025	2.7	0.51

Fig. 5.

Fitted statistical models of the tibia in patients with Progeria. The models for 38 boys ≤12 years old (a), 23 boys ≥10 years old (b), 35 girls ≤12 years old (c), and 25 girls ≥10 years old (d) are plotted in comparison to the normal median (blue line) and range (purple lines).

Measurement data are shown as green dots (88 observations for boys and 93 for girls). In (a) and (b), the Progeria median and its 95% confidence intervals are shown as red and brown lines. In (c) and (d), the Progeria model and its 95% confidence intervals were shown as black and brown lines.

The correlation between the 10 ratios for asymptotes and 10 ratios for half-lives was high (0.97, p<0.001), implying that a particular bone and gender combination having a high Progeria effect for the asymptote tended to have a high Progeria effect for the half-life. The following patterns emerged: firstly, ratios were slightly lower for females than males for half-lives (0.53 vs 0.56), and were the same for asymptotes (0.58 vs 0.58); and secondly, ratios were slightly lower for shorter bones in both the arm and leg for both asymptotes and half-lives. For the leg, the ratios of asymptotes for (fibula vs tibia) were (0.57 vs 0.60), while those for half-lives were (0.52 vs 0.62). For the upper extremity, the ratios of asymptotes for (radius and ulna vs humerus) were (0.56 and 0.58 vs 0.61), while those for half-lives were (0.41 and 0.51 vs 0.66).

Discussion

Progeria is an extremely rare disease that results in a shortened life-span. Because this ill-fated combination results in a very small worldwide population, performing a study to characterize the longitudinal skeletal maturation and growth pattern of this disease entity is exceptionally difficult, with scarcity of data being the largest impediment. However, one institution, serving as the international center for Progeria clinical trials, allows participation of patients with Progeria worldwide to contribute to a large centralized imaging database. This study utilized this unique and rich database to characterize the longitudinal skeletal maturation and growth patterns of these affected patients.

The hand/wrist method of Greulich and Pyle for bone age estimation is subjective, and derived based on historical data. It may not be appropriate for the current population, and may not be applicable across all ethnicities and socioeconomic classes. Despite these limitations, it is still the most commonly used bone age estimation technique across all age groups [14, 19]. Prior cross-sectional skeletal maturation studies using the standards of Greulich and Pyle found that Progeria patients have normal skeletal maturation [9, 10]. However, our longitudinal study, utilizing a much larger dataset with multiple bone age estimates per patient and mixed effects statistical modeling, found that the skeletal maturation pattern of patients with Progeria is slightly more advanced than normal (9% for boys and 14% for girls).

Prior studies have shown generalized growth failure in patients with Progeria. Gordon et al [9] found that the average weight of patients with Progeria increased at a rate of 0.44 kg/year, which was below 2 standard deviations of normal weight gain for any age. In that same study, the heights for these patients were found to be extremely short but the height measurements were thought to be underestimated because of joint contractures. Within this limitation, the heights of these patients at birth ranged between the 13^th and 99.6^th percentile. From birth to 34 months, patient heights were below the 3^rd percentile. Over the age of 34 months, their heights were more than 2 standard deviations below normal (i.e. below the 2^nd percentile, assuming Normality). To better elucidate skeletal growth, our longitudinal study which used the lengths of upper and lower extremity long bones, showed that both the eventual bone lengths (asymptotes), and the times taken to reach (half) these lengths (half-lives) are substantially less than normal (by a factor of about 2 for both phenomena). The shorter half-lives of skeletal growth are consistent with, but more pronounced than, the more advanced skeletal maturation of these Progeria patients.

Finally, we note a potentially important clinical utility of our mixed effects growth models, namely their ability to predict long bone lengths over time. Parameter estimates from our study can be combined with even a single bone length measurement from a new patient to forecast the future trajectory for this patient. An example of such a clinical application is illustrated in the Appendix (Fig. D1).

Our study is limited by its retrospective methodology. Flexion contractures of the hands (mostly of the fingers) and acro-osteolysis of the distal phalanges limit bone age estimates by the standards of Greulich and Pyle. The flexion contractures of the extremities result in suboptimal positioning of some of the long bones for the radiographs, potentially causing foreshortening of the long bones. This is evident by the occasional negative growth trends of the long bone lengths over time. The bowing deformities involving some of these long bones also may limit accurate length measurements. Although interventions of the clinical trials for these patients have centered on preventing cardiovascular disease, it is possible that these interventions may potentially also alter the skeletal maturation and growth of these patients. However, published results from a recent clinical trial reported that treatment with farnesyltransferase inhibitor improved the rigidity of their skeleton but did not alter their appearance radiographically [11]. Finally, the lack of data on medications that may interfere with growth (such as growth hormone and steroids) further limits our study.

In conclusion, our study establishes reference standards for skeletal maturation and long bone growth of patients with the clinical phenotype of Progeria. In addition, these 2 measurements have the potential to provide objective assessments with which to evaluate the efficacy of treatments for patients with Progeria.

Research in context

Evidence before this study

It is well-known that patients with Progeria have short stature. However, the precise pattern of this abnormal height growth is unknown, likely due to the severe contractures that affect these individuals preventing accurate height measurements. Based on available recorded heights, these patients were found to be below the 3^rd percentile of normal height from birth to 34 months, and below the 2^nd percentile thereafter [9]. A surrogate in understanding the pattern of height growth in patients with Progeria is to know the growth pattern of their long bones. However, there has been no such study in patients with Progeria.

Strongly associated with long bone growth is skeletal maturation, and this has also not been fully characterized in patients with Progeria. Prior cross-sectional skeletal maturation studies in this population found that they have normal skeletal maturation [9, 10]. However, these studies utilize a small dataset consisting of a single bone age estimate per patient. Although easier to perform, these cross-sectional studies are not well suited to assess complex changes over an extended period of time. Rather, a longitudinal study such as ours, utilizing multiple measurements per patient, and over a long period of time, is more suited.

There is limited evidence in the literature on skeletal maturation and long bone growth patterns of patients with Progeria. We searched PubMed with no language restrictions. The time frame for the search was from inception till January 8, 2019. Search terms for skeletal maturation pattern in patients with Progeria included “Progeria [MESH] AND bone age [MESH]”, “Progeria [MESH] AND skeletal maturation [MESH]”, “Progeria [MESH] AND bone maturation [MESH]”, “Progeria [MESH] AND skeletal age [MESH]”, and “Progeria [MESH] AND maturation [MESH]”. Search terms for long bone growth pattern in patients with Progeria included “Progeria [MESH] AND bone growth [MESH]”, “Progeria [MESH] AND skeletal growth [MESH]”, “Progeria [MESH] AND long bone [MESH]”, and Progeria [MESH] AND height [MESH]”. Aside from the two studies previously mentioned [9, 10], these two search strategies did not yield any relevant studies that pertain to the patterns of skeletal maturation and long bone growth in patients with Progeria.

Added value of this study

Our study characterizes the long bone growth and skeletal maturation patterns of patients with clinical features of Progeria. Their long bone growth pattern was found to be substantially different from that of the normal population. Specifically, in patients with Progeria, their eventual bone lengths and the times needed to reach their final bone lengths were both found to be much less than normal, by a factor of about 2. Additionally, the skeletal maturation pattern of these patients was found to be slightly more advanced than normal. These skeletal maturation patterns and (particularly) long bone growth patterns have the potential to provide objective assessments with which to evaluate the efficacy of treatments for patients with Progeria.

Implications of all the available evidence

An objective measure to assess disease evolution is necessary to determine drug treatment efficacy and effect on bone growth. We have established the long bone growth and skeletal maturation patterns of patients with Progeria, which can now be used as objective outcome measures to assess the efficacy of future drug treatments.