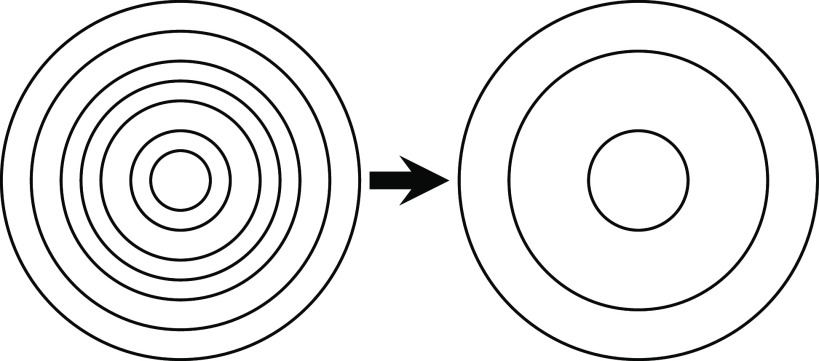
Abstract
We discuss a new theoretical framework for modeling molecular electron densities. Our approach decomposes the total density into contributions from basis function products and then approximates each product using constrained least–squares approximation in a tailored local basis of functions with adjustable non–linear parameters. We show how to solve directly for the expansion coefficients and Lagrange multipliers and present an iterative method to optimize the non–linear parameters. Example products from the Dunning cc-pVTZ basis set are discussed.
1. Introduction
1.1. Background
The central tenet of density functional theory (DFT) is that, notwithstanding its conceptual simplicity, the electron density D(r) in a system is a molecular property from which all others can be derived.1 Consequently, its computation, representation, and visualization are among the most fundamental features of all modern electronic structure software packages. Our goal in this work is to develop a systematic scheme for efficiently constructing accurate approximations to D(r).
In terms of a set of orthonormal orbitals ψi(r), we can write the electron density as2,3
| 1 |
and, if each of these orbitals is expanded in a one-electron basis set ϕμ(r), we obtain
| 2 |
where Pμν is a density matrix. If each basis function is a contracted Gaussian
| 3 |
where Yμ(r) is the angular factor, Ckμ is a contraction coefficient, αkμ is an exponent, and Aμ is the Gaussian center, then the function products in (2) are
| 4 |
where we have introduced the Gaussian density
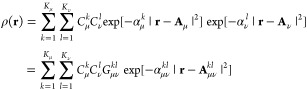 |
5 |
and its primitive prefactors, exponents and centers are, respectively,
| 6 |
| 7 |
| 8 |
The electrostatic energy between two products is given by the two-electron integral
| 9 |
and these integrals yield the Coulomb, exchange, and correlation energies.4 The evaluation of the (μν|λσ) is one of the key bottlenecks of quantum chemistry, and research over many decades has led to an impressive array of algorithms for their computation, including the methods of Boys,5 Dupuis et al.,6 McMurchie and Davidson,7 Obara and Saika,8 Head-Gordon and Pople,9 Hamilton and Schaefer,10 Lindh et al.,11 Gill and Pople,12,13 Adams et al.,14 Ishida,15 Makowski,16 and Komornicki and King.17 Nonetheless, although some of these are very computationally efficient, all become expensive when the degrees of contraction KμKν and KλKσ are large. For this reason, it was recognized long ago that it is desirable to construct approximations for products.
In the 20th century, a variety of methods for fitting function products in an auxiliary basis were introduced and we note the seminal contributions by Reeves and Fletcher,18 O-ohata et al.,19 Newton et al.,20 Hehre et al.,21 Stewart,22 Billingsley and Bloor,23 Baerends et al.,24 Whitten,25 Beebe and Linderberg,26 Dunlap et al.,27 Fortunelli and Salvetti,28 Feyereisen et al.,29 and Eichkorn et al.30 Helpful discussions of the underlying theory were published subsequently by a number of workers.31−37
In the present paper, however, we eschew a global auxiliary basis in favor of approximating each product on its own locally generated basis. More specifically, we seek an approximation to the Gaussian density (5) that uses a few Gaussians whose coefficients, exponents and centers are explicitly optimized.
Throughout this paper, we will use italic symbols to denote scalars and bold (or double-struck) symbols to denote vectors or matrices.
1.2. Least-Squares Functional
We seek to approximate a given density ρ(r) by a model χ(r) where
| 10 |
| 11 |
where d = (d1, ..., dn) is a list of positive coefficients, c = (c1, ..., cm) is a list of expansion coefficients, a = [a1(r), ..., an(r)] and b = [b1(r), ..., bm(r)] are lists of normalized Gaussians
| 12 |
| 13 |
α = (α1, ...,αn) and β = (β1, ...,βm) are lists of inverted exponents, and A = (A1, ..., An) and B = (B1, ..., Bm) are lists of Gaussian centers on the z axis. The assumption that all di > 0 sometimes requires that the basis set be reconstructed and this is discussed in Section 2.1. We assume that m < n, and we regard all of the cj, βj, and Bj as optimizable parameters.
For simplicity, we recast the problem in Fourier space and model ρ̂(k) by χ̂(k) where
| 14 |
| 15 |
and the elements of â and b̂ are the Fourier transforms
| 16 |
| 17 |
Our models seek to minimize by least-squares the residual
| 18 |
over all of space and, to achieve this, we introduce a Fourier weight function
| 19 |
In general, our models must also satisfy l linear constraints on the expansion coefficients ci. These are conveniently captured by the matrix equation
| 20 |
where 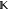 is an m × l matrix and
is an m × l matrix and 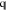 is a vector of length l. For example, if we seek a model that conserves charge in an ss density,
is a vector of length l. For example, if we seek a model that conserves charge in an ss density, 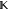 must contain a column of ones and the corresponding
element of
must contain a column of ones and the corresponding
element of 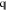 must hold ρ̂(0), i.e. the charge of ρ(r). We therefore introduce
a vector
must hold ρ̂(0), i.e. the charge of ρ(r). We therefore introduce
a vector 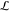 of Lagrange multipliers and seek a stationary
point of the functional
of Lagrange multipliers and seek a stationary
point of the functional
| 21 |
1.3. Weight Function
The parameter p in (19) determines the type of model that we form and we will write Lp(m) to denote an m-Gaussian least-squares model with parameter p and charge conservation
| 22 |
constrained. If p > 0, the fit emphasizes high-frequency components of the density; if p < 0, it emphasizes low-frequency components. Historically, p = 3/2, 1/2, or −1/2 have been advocated, but these are just three points on a continuum of possibilities.
L3/2(m) models minimize the square of the residual density R(r) itself. Such models were used by Reeves and Fletcher18 to perform approximate Slater orbital calculations, O-ohata et al.19 to construct expansions of Slater functions, Newton et al.20 in the PDDO approximation, Hehre et al.21,22 to construct the STO-nG basis sets, Billingsley and Bloor23 in the LEDO approximation and Baerends et al.24 in their Hartree–Fock–Slater algorithm. Most of these authors used unconstrained fits, but Baerends et al. constrained charge conservation.
L1/2(m) models minimize the squared norm of the electric field of R(r). Such models were advocated by Whitten25 for modeling densities without charge conservation, used by Dunlap et al.27 in his Coulomb fitting approach, developed further by Feyereisen et al.29 and Eichkorn et al.30 and analyzed in detail by Hall and Martin.31
L–1/2(m) models minimize the square of the potential value of R(r). They were introduced by Fortunelli and Salvetti28 and defined rigorously by Gill et al.32
The constraint (22) ensures that the integral in (21) exists when weight functions with −2 < p ≤ 0 are used but, for p ≤ −2, additional constraints must be applied. For certain isolated p values, for example p = 0, the weight function (19) is not positive definite and the functional (21) does not have a well-defined stationary point. However, if they are needed, such models can be obtained by taking limits in the neighborhood of p.
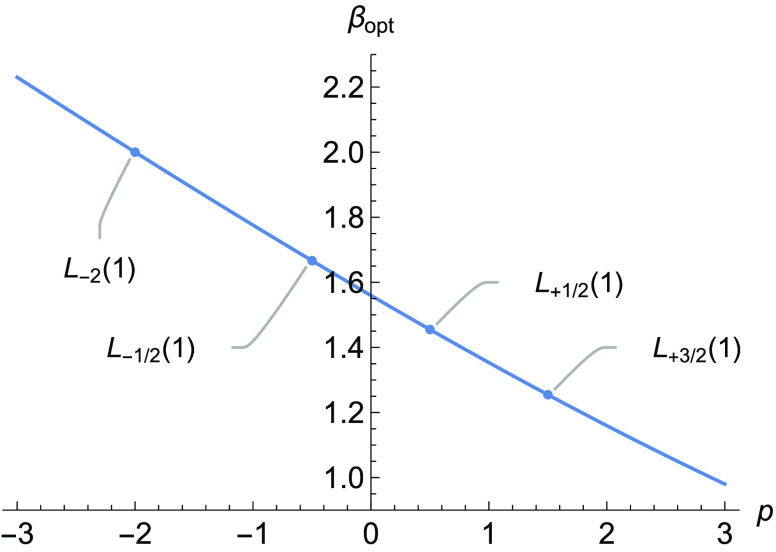
To illustrate this, we modeled a single Slater function by a single Gaussian function. In Fourier space, this corresponds to modeling ρ̂(k) = (1 + k2)−2 by χ̂(k) = exp(−βk2). By minimizing (21), one finds that the optimal β satisfies
| 23 |
where U is the Tricomi hypergeometric function.38 Analysis of (23) reveals that
| 24 |
and Figure 1 shows that the optimal β varies smoothly and almost linearly over a wide domain.
Figure 1.
Optimal β for modeling a Slater function as the weight function ωp(k) varies.
1.4. Cost-Benefit Analysis
In a spatially extended system, most pairs of basis functions ϕμ and ϕν are well separated, and the product ϕμ(r)ϕν(r) can therefore be neglected. It is easy to show that the number of significant ϕμ(r)ϕν(r) products grows only linearly with N and, thus, because the shell pair economizations are independent, the cost of economizing all significant shell pairs is O(N). However, it is reasonable to ask whether this effort is worthwhile. There are two types of calculations where the cost is easy to justify.
First, calculations in which the electron density D(r) will be evaluated at a large number K of points r as, for example, on a van der Waals surface. The cost of evaluating (2) at a point r is O(N) and the total cost for all points is therefore O(KN). In such situations, the economization cost will be more than compensated by the subsequent savings in density evaluations.
Second, calculations in which the shell pairs will be used to calculate two-electron integrals (9) as, for example, in a hybrid density functional calculation. The number of significant shell quartets, and therefore the number of significant ERIs, is O(N2). Thus, whereas the cost of economization scales linearly with N, the savings that accrue from the use of economized shell pairs to form ERIs scale quadratically with N and will more than compensate for the economization cost if N is sufficiently large.
2. Methods
2.1. Basis Set Reconstruction
To facilitate the modeling process, we required all contraction coefficients to be positive. This is true of some basis functions (for example, the 5-fold contracted function on H atoms in the Dunning cc-pVTZ basis,39 see Table 1) but it is not true of many basis functions (for example, the 10-fold contracted functions on C atoms in the same basis, see Table 2). However, it is often possible (at least, in shared-exponent basis sets such as those of Dunning39 and Jensen40) to reconstruct the basis on each atom, creating all-positive basis functions by linearly combining the originals. Because the reconstructed basis set necessarily has the same span as the original, it is equivalent for quantum chemical purposes.
Table 1. cc-pVTZ Exponents and Coefficients39,41 of an s Function on H.
| Primitive | Exponent | Coefficient |
|---|---|---|
| 1 | 33.87 | +0.006068 |
| 2 | 5.095 | +0.045308 |
| 3 | 1.159 | +0.202822 |
| 4 | 0.3258 | +0.503903 |
| 5 | 0.1027 | +0.383421 |
Table 2. cc-pVTZ Exponents and Coefficients39,41 of Two s Functions on C.
| Coefficient |
|||||
|---|---|---|---|---|---|
| cc-pVTZ |
rec-cc-pVTZ |
||||
| Primitive | Exponent | v1 | v2 | u1 | u2 |
| 1 | 8236. | +0.000531 | –0.000113 | +0.000529 | +0.000133 |
| 2 | 1235. | +0.004108 | –0.000878 | +0.004094 | +0.001026 |
| 3 | 280.8 | +0.021087 | –0.004540 | +0.021012 | +0.005238 |
| 4 | 79.27 | +0.081853 | –0.018133 | +0.081555 | +0.019875 |
| 5 | 25.59 | +0.234817 | –0.055760 | +0.233901 | +0.053661 |
| 6 | 8.997 | +0.434401 | –0.126895 | +0.432330 | +0.077970 |
| 7 | 3.319 | +0.346129 | –0.170352 | +0.343379 | 0 |
| 8 | 0.9059 | +0.039378 | +0.140382 | +0.041603 | +0.143342 |
| 9 | 0.3643 | –0.008983 | +0.598684 | +0.000529 | +0.533186 |
| 10 | 0.1285 | +0.002385 | +0.395389 | +0.008666 | +0.355805 |
We formulate our problem as follows. Given a set V of linearly independent vectors 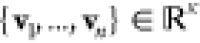 , we seek a set U of all-positive
vectors {u1, ..., un} with span(U) = span(V).
, we seek a set U of all-positive
vectors {u1, ..., un} with span(U) = span(V).
We define vmini as the minimum (i.e., most negative) component of vi and we then reorder the vi so that vmin1 > vmin2 >··· > vminn. We then try to construct a single all-positive vector u1 from V by writing
| 25 |
and seeking the γi that maximize umin1. This maps onto the linear programming problem
| 26 |
with the auxiliary variable t, and solved, for example, by converting to canonical form and applying the Simplex Method.42 The optimized t is maximized umin1.
If the resulting umin1 value is positive, the original vectors are reconstructible. We then form
| 27 |
where δi is the smallest value that yields umini = 0, and normalize the resulting basis functions. This has the additional benefit of reducing the order of contraction by one even before modeling. We add the prefix “rec-” to the name of a reconstructed basis set.
It is important to note that the reconstructed basis functions are not orthogonal and, in some cases, can be almost parallel. As a consequence, we hope that, in the future, (a) improved reconstruction algorithms will be devised and (b) basis set developers will produce basis sets with all-positive coefficients, so that reconstruction is unnecessary.
If this method is applied to the 10-fold contracted functions on C in the cc-pVTZ basis set (Table 2), we find that umin1 is a concave piecewise linear function of γ2 given by
 |
28 |
which reaches its maximum value (+0.000529) at γ2 = 0.0158885. We then form
| 29 |
and renormalize both u1 and u2. The rec-cc-pVTZ basis functions are shown in Table 2 and we note that their overlap integral is S12 = 0.456.
2.2. Modeling Theory
2.2.1. Linear Parameters
The basic units of the optimization are the scalar
| 30 |
the vector
| 31 |
and the matrix
| 32 |
From these, we can assemble the augmented vector
| 33 |
and the augmented matrix
| 34 |
and then write (21) as
| 35 |
where the coefficients and Lagrange multipliers have been conflated into the vector
| 36 |
Requiring that the gradient of (35) with respect to x vanish yields the optimal coefficients and Lagrange multipliers
| 37 |
and the resulting minimal value
| 38 |
For greatest numerical stability, (37) should be computed by solving a linear system.
Having thus solved for the linear parameters ci and 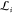 , we now have a functional (38) that depends only on the nonlinear parameters βi and Bi. We now discuss the minimization of (38) with respect to those parameters.
, we now have a functional (38) that depends only on the nonlinear parameters βi and Bi. We now discuss the minimization of (38) with respect to those parameters.
2.2.2. Initial Guesses: Spherical Density
If ρ(r) has spherical (Kh) symmetry, we choose all Bi = 0 and eschew further optimization. The exponents β are more challenging, and to construct an initial guess for these, we convert the modeling problem into a quadrature problem. First, we form the integral representation
| 39 |
where β0 > 0 is a scale factor and an Inverse Mellin Transform38 provides the weight function
| 40 |
We then approximate (39) by the m-point Gauss–Christoffel quadrature formula43
| 41 |
where the weights ci > 0 and roots 0 < ui < 1 are related to polynomials that are orthogonal on [0, 1] with respect to w(u). In the Golub-Welsch method44 (see Supporting Information), the ci and ui are found from the moments
| 42 |
and, in order to sample ρ̂(k) well, we choose the arbitrary scale factor to be
| 43 |
Finally, by substituting ui = exp(−βi/β0) into (41), we obtain an approximation that we call the Q(m) model
| 44 |
Although this model is less accurate than least-squares fitting, it may sometimes be useful in its own right. However, its low cost and reasonable accuracy make it a useful initial guess.
There is an important caveat to the use of a quadrature scheme to generate an initial guess. There is no guarantee45 that the Gauss–Christoffel roots ui and weights ci will exist or be satisfactory unless the weight function w(u) in (39) is a non-negative function on [0, 1]. It was to ensure this that we assumed that all of the coefficients di in (10) are positive.
2.2.3. Initial Guesses: Cylindrical Density
Generating guesses for the exponents βi and centers Bi when ρ(r) has cylindrical (C∞v) symmetry is not difficult. In general, because of the primitive prefactors (6), the coefficients di of the n primitives in ρ(r) range over many orders of magnitude and ρ(r) is therefore dominated by the primitives with the largest absolute coefficients |di|. We exploit this by using the αi and Ai of the m primitives with the largest |di| as our guesses.
We start by ordering the αi and Ai by |di| value and take the first m primitives that are not already “covered” by a larger primitive. A primitive i is considered “covered” if its Ai value is within 0.25 au of the position Aj of a larger primitive j (|dj| > |di|). This is because primitives that are close to each other tend to be represented by a single Gaussian in models, even if they both have large coefficients.
In the case of a tie for the mth largest “uncovered” primitive, there are two options. If it would not break another tie, the (m – 1)th largest primitive is excluded, and the αi and Ai of the mth and (m + 1)th largest primitives are used. Otherwise, the average of the mth and (m + 1)th largest primitives’ quantities are taken.
Finally, if the guess formed this way has k < m primitives, the m – k largest previously excluded “covered” primitives are included as well.
2.2.4. Matrix Elements and Their Derivatives
For the basis functions (17), one can show from eq (6.631.1) of Gradshteyn and Ryzhik46 that both the matrix (32) and its derivatives with respect to the nonlinear parameters (βi and Bi) can be conveniently expressed in terms of the function
| 45 |
where Γ is the gamma function38 and M is the Kummer hypergeometric function.38 The matrix itself is given by
| 46 |
and, using properties of the hypergeometric function, one finds the first derivatives
| 47 |
| 48 |
and the second derivatives
| 49 |
| 50 |
| 51 |
For half-integer values of p, all six of these can be expressed in terms of Gaussians and the error function.38
To construct the gradient of Z, we require the first derivative vectors and matrices
| 52 |
| 53 |
and, to construct its Hessian, we need the second derivative vectors and matrices
| 54 |
| 55 |
| 56 |
Differentiating (38) shows the gradient and Hessian of Z with respect to β and B are
| 57 |
| 58 |
where
| 59 |
| 60 |
| 61 |
| 62 |
| 63 |
and X = diag(x). The square brackets in (57) and (58) indicate that only the first m elements of the enclosed vector, or the first m-by-m block of the enclosed matrix, is retained.
It is well-known, however, that the optimal exponents of Gaussian expansions of exponential densities form a roughly geometrical sequence35,47 and that the exponents typically span several orders of magnitude. We therefore choose to work with the log-exponents
| 64 |
which are roughly evenly spaced and typically of the order of unity. By the chain rule, the elements of the gradient and Hessian of Z with respect to the λi are
| 65 |
| 66 |
| 67 |
| 68 |
2.2.5. Optimization Step
Given the gradient (g) and Hessian (H) of (38), we are in a position to find the optimal β and B via an iterative scheme. Although the Newton–Raphson method could be used, it is effective only if current β and B are near-optimal and can be disastrous otherwise. We prefer the slower (but more robust) approach taken by the Levenberg–Marquardt method,48,49 wherein a small fraction σ > 0 of the identity matrix is added to the Hessian to form the shifted-Newton step
| 69 |
The shift σ should decay as the optimization proceeds and we have found that σ = 10|g| is effective for all the densities discussed below and hundreds of others that we have explored.
When optimizing β and B, our goal is to reduce Z to within 1% of its minimum value. This is usually achieved when H is positive definite and |Δ| < 10–4.
2.2.6. Algorithm
The inputs to our algorithm
are the density ρ(r), the number m of Gaussians in the desired model, the weight function parameter p, the constraint matrix 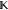 and the constraint vector
and the constraint vector 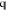 . The way in which we generate initial guesses
for the nonlinear (β and B) parameters
depends on whether the Gaussian density is spherical or cylindrical,
but after that, the algorithm becomes the same. The overall algorithm,
together with links to key equations, is shown in Table 3.
. The way in which we generate initial guesses
for the nonlinear (β and B) parameters
depends on whether the Gaussian density is spherical or cylindrical,
but after that, the algorithm becomes the same. The overall algorithm,
together with links to key equations, is shown in Table 3.
Table 3. Construction of an m-Gaussian Model for a Gaussian Density.
| Step | Description | Equations | Cost |
|---|---|---|---|
| 1 | Input 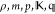
|
O(1) | |
| If ρ is spherical | |||
| 2a | Compute ⟨uj⟩ and β0 | (42), (43) | O(m) |
| 3a | Compute initial guess for β | (44) | O(m2) |
| 4a | Set B = 0 | O(m) | |
| else if ρ is cylindrical | |||
| 2b | Sort primitives by |di| value | O(n) | |
| 3b | Compute initial guess for β and B | O(m) | |
| end if | |||
| 5 | Compute f00, f10, f01, f20, f11, f02 | (33), (52)–(56) | O(m) |
| 6 | Compute F00, F10, F01, F20, F11, F02 | (34), (52)–(56) | O(m2) |
| 7 | Compute E10, E01, E20, E11, E02 | (59) – (63) | O(m) |
| 8 | Compute U10, U01, H20, H11, H02 | (59) – (63) | O(m3) |
| 9 | Compute x | (37) | O(m3) |
| 10 | Compute g | (57) | O(m2) |
| 11 | Compute H | (58) | O(m3) |
| 12 | Compute (β, B) ← (β, B) – Δ | (69) | O(m3) |
| 13 | If |Δ| > 10–4 or H is not positive definite, go to Step 5 | O(m3) |
3. Results and Discussion
3.1. Spherical Densities
3.1.1. Preamble
Armed with the necessary theory, we now consider how it can be applied in calculations using the Dunning cc-pVTZ basis set.39 If the basis functions are concentric, their density is spherical and has the Fourier transform (14)
| 70 |
and the associated weight function (40) is
| 71 |
where δ is the Dirac delta. If all di > 0, then w(u) is non-negative and, from (43), we have
| 72 |
To find the Q(m), we need the moments
| 73 |
and, to find the Lp(m), we need the integrals
| 74 |
| 75 |
The Q(m) and Lp(m) models are constructed to mimic the original density ρ(r) as well as possible over all space. It is also important, however, to assess the resulting models χ(r) by measuring the largest pointwise difference between ρ(r) and χ(r). For a spherical density, it is natural to measure this through the maximum Jacobian-weighted error
| 76 |
and we report this for each of the models described below.
3.1.2. H(1s1s) Density
Our first example comes from the 5-fold contracted basis function on an H atom in the cc-pVTZ basis set (see Table 1). The product of this function with itself yields a density with n = 15 distinct Gaussians and its Q(m) and Lp(m) models are listed in Table 4.
Table 4. Models for the H(1s2) cc-pVTZ Density.
| Q(m) | L–1/2(m) | L+1/2(m) | L+3/2(m) | |||||
|---|---|---|---|---|---|---|---|---|
| m | λi | ci | λi | ci | λi | ci | λi | ci |
| 1 | +1.032 | 1.000 | +0.876 | 1.000 | +1.011 | 1.000 | +1.159 | 1.000 |
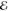 = 1.8 × 10–1 = 1.8 × 10–1
|
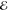 = 1.7 × 10–1 = 1.7 × 10–1
|
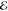 = 1.8 × 10–1 = 1.8 × 10–1
|
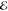 = 2.1 × 10–1 = 2.1 × 10–1
|
|||||
| 2 | +0.421 | 0.610 | +0.315 | 0.572 | +0.497 | 0.700 | +0.719 | 0.824 |
| +1.827 | 0.390 | +1.802 | 0.428 | +2.083 | 0.300 | +2.455 | 0.176 | |
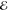 = 5.1 × 10–2 = 5.1 × 10–2
|
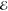 = 5.5 × 10–2 = 5.5 × 10–2
|
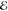 = 4.2 × 10–2 = 4.2 × 10–2
|
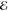 = 6.7 × 10–2 = 6.7 × 10–2
|
|||||
| 3 | +0.004 | 0.262 | +0.027 | 0.308 | +0.219 | 0.456 | +0.439 | 0.621 |
| +0.935 | 0.533 | +1.102 | 0.563 | +1.396 | 0.476 | +1.741 | 0.348 | |
| +2.250 | 0.204 | +2.583 | 0.129 | +2.974 | 0.068 | +3.430 | 0.031 | |
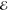 = 2.8 × 10–2 = 2.8 × 10–2
|
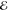 = 1.8 × 10–2 = 1.8 × 10–2
|
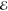 = 1.2 × 10–2 = 1.2 × 10–2
|
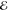 = 2.0 × 10–2 = 2.0 × 10–2
|
|||||
| 4 | –0.174 | 0.161 | –0.139 | 0.186 | –0.036 | 0.249 | +0.316 | 0.519 |
| +0.660 | 0.465 | +0.765 | 0.521 | +0.908 | 0.521 | +1.478 | 0.412 | |
| +1.564 | 0.295 | +1.849 | 0.260 | +2.027 | 0.208 | +2.838 | 0.066 | |
| +2.776 | 0.080 | +3.361 | 0.032 | +3.581 | 0.022 | +4.621 | 0.003 | |
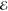 = 1.2 × 10–2 = 1.2 × 10–2
|
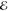 = 5.4 × 10–3 = 5.4 × 10–3
|
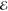 = 4.5 × 10–3 = 4.5 × 10–3
|
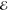 = 1.2 × 10–2 = 1.2 × 10–2
|
|||||
| 5 | –0.196 | 0.147 | –0.165 | 0.169 | –0.130 | 0.189 | –0.057 | 0.228 |
| +0.550 | 0.325 | +0.707 | 0.499 | +0.758 | 0.506 | +0.831 | 0.496 | |
| +1.008 | 0.254 | +1.709 | 0.278 | +1.787 | 0.261 | +1.854 | 0.238 | |
| +1.833 | 0.233 | +2.917 | 0.050 | +3.074 | 0.042 | +3.148 | 0.037 | |
| +3.183 | 0.041 | +4.455 | 0.004 | +4.810 | 0.002 | +4.924 | 0.002 | |
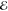 = 5.7 × 10–3 = 5.7 × 10–3
|
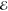 = 1.6 × 10–3 = 1.6 × 10–3
|
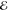 = 6.6 × 10–4 = 6.6 × 10–4
|
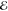 = 7.1 × 10–4 = 7.1 × 10–4
|
|||||
| 6 | –0.196 | 0.147 | –0.190 | 0.152 | –0.176 | 0.161 | –0.135 | 0.183 |
| +0.539 | 0.305 | +0.610 | 0.412 | +0.660 | 0.459 | +0.730 | 0.490 | |
| +0.961 | 0.255 | +1.225 | 0.211 | +1.436 | 0.214 | +1.684 | 0.254 | |
| +1.738 | 0.219 | +1.927 | 0.187 | +2.043 | 0.132 | +2.421 | 0.046 | |
| +2.411 | 0.049 | +3.147 | 0.036 | +3.192 | 0.033 | +3.268 | 0.026 | |
| +3.456 | 0.024 | +4.874 | 0.002 | +4.936 | 0.002 | +4.975 | 0.002 | |
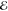 = 4.7 × 10–3 = 4.7 × 10–3
|
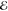 = 2.5 × 10–4 = 2.5 × 10–4
|
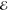 = 1.5 × 10–4 = 1.5 × 10–4
|
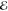 = 1.8 × 10–4 = 1.8 × 10–4
|
|||||
The exponents of the Lp(m) change smoothly and predictably as p and m are varied. The L–1/2(m) are the most diffuse (i.e., their λi are most negative) and the L+3/2(m) are the most compact (i.e., their λi are the most positive). This is reasonable because, whereas the L–1/2(m) use a Fourier weight 1/(2π k4) that emphasizes low-frequency components of the density and therefore its tail, the L+3/2(m) use a weight 1/(2πk0) that places greater emphasis on the high-frequency components and therefore the region near the nuclear cusp. The L+1/2(m) exponents are remarkably close to the average of the analogous L–1/2(m) and L+3/2(m) exponents, thus generalizing the near-linear behavior seen in Figure 1.
The exponents of Q(m) also change smoothly with m. Their most diffuse exponents are similar to those in L+1/2(m) when m is small and similar to those in L–1/2(m) when m is larger but the range λm – λ1 of the Q(m) exponents is smaller than in any of the least-squares models. For applications for which a quick and reasonably accurate approximation is required, the Q(m) models appear useful.
3.1.3. C(1s2s) Density
Our second example comes from the product of the two 10-fold contracted rec-cc-pVTZ basis functions on a C atom (see Table 2). Their product yields a density with n = 55 distinct Gaussians and its Q(m) and Lp(m) models are listed in Table 5.
Table 5. Models for the rec-cc-pVTZ C(1s2s) Density (S = 0.456).
|
Q(m) |
L–1/2(m) |
L+1/2(m) |
L+3/2(m) |
|||||
|---|---|---|---|---|---|---|---|---|
| m | λi | ci/S | λi | ci/S | λi | ci/S | λi | ci/S |
| 1 | 4.031 | 1.000 | 3.386 | 1.000 | 3.685 | 1.000 | 3.976 | 1.000 |
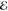 = 6.3 × 10–1 = 6.3 × 10–1
|
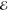 = 4.3 × 10–1 = 4.3 × 10–1
|
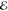 = 4.9 × 10–1 = 4.9 × 10–1
|
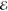 = 6.0 × 10–1 = 6.0 × 10–1
|
|||||
| 2 | 3.273 | 0.725 | 2.349 | 0.441 | 2.835 | 0.642 | 3.284 | 0.796 |
| 5.098 | 0.275 | 4.445 | 0.559 | 4.954 | 0.358 | 5.454 | 0.204 | |
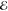 = 1.5 × 10–1 = 1.5 × 10–1
|
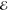 = 1.6 × 10–1 = 1.6 × 10–1
|
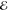 = 1.4 × 10–1 = 1.4 × 10–1
|
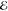 = 2.1 × 10–1 = 2.1 × 10–1
|
|||||
| 3 | 2.855 | 0.524 | 1.423 | 0.117 | 2.334 | 0.382 | 2.872 | 0.615 |
| 4.150 | 0.332 | 3.159 | 0.572 | 3.958 | 0.484 | 4.657 | 0.342 | |
| 5.561 | 0.144 | 5.036 | 0.312 | 5.699 | 0.134 | 6.423 | 0.043 | |
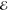 = 6.1 × 10–2 = 6.1 × 10–2
|
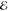 = 1.1 × 10–1 = 1.1 × 10–1
|
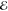 = 5.1 × 10–2 = 5.1 × 10–2
|
 = 8.7 × 10–2 = 8.7 × 10–2
|
|||||
| 4 | 2.625 | 0.416 | 0.854 | 0.046 | 1.708 | 0.155 | 2.574 | 0.467 |
| 3.703 | 0.298 | 2.622 | 0.396 | 3.165 | 0.485 | 4.104 | 0.396 | |
| 4.715 | 0.216 | 4.027 | 0.419 | 4.646 | 0.307 | 5.504 | 0.127 | |
| 6.015 | 0.070 | 5.646 | 0.139 | 6.272 | 0.053 | 7.218 | 0.010 | |
 = 3.1 × 10–2 = 3.1 × 10–2
|
 = 4.8 × 10–2 = 4.8 × 10–2
|
 = 1.9 × 10–2 = 1.9 × 10–2
|
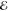 = 4.0 × 10–2 = 4.0 × 10–2
|
|||||
| 5 | 2.544 | 0.370 | 0.494 | 0.023 | 1.195 | 0.071 | 2.273 | 0.321 |
| 3.369 | 0.167 | 2.117 | 0.187 | 2.750 | 0.403 | 3.596 | 0.412 | |
| 3.941 | 0.220 | 3.216 | 0.416 | 4.018 | 0.352 | 4.874 | 0.221 | |
| 4.877 | 0.190 | 4.554 | 0.306 | 5.279 | 0.156 | 6.180 | 0.044 | |
| 6.191 | 0.053 | 6.098 | 0.068 | 6.871 | 0.018 | 7.879 | 0.003 | |
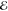 = 2.6 × 10–2 = 2.6 × 10–2
|
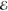 = 2.5 × 10–2 = 2.5 × 10–2
|
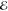 = 9.8 × 10–3 = 9.8 × 10–3
|
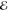 = 2.1 × 10–2 = 2.1 × 10–2
|
|||||
| 6 | 2.182 | 0.143 | 0.217 | 0.013 | 0.957 | 0.049 | 1.958 | 0.201 |
| 2.768 | 0.281 | 1.602 | 0.081 | 2.534 | 0.318 | 3.208 | 0.416 | |
| 3.682 | 0.266 | 2.775 | 0.369 | 3.609 | 0.341 | 4.437 | 0.276 | |
| 4.457 | 0.156 | 3.924 | 0.331 | 4.732 | 0.225 | 5.576 | 0.093 | |
| 5.177 | 0.119 | 5.109 | 0.179 | 5.920 | 0.062 | 6.875 | 0.013 | |
| 6.424 | 0.035 | 6.624 | 0.028 | 7.503 | 0.006 | 8.583 | 0.001 | |
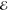 = 1.7 × 10–2 = 1.7 × 10–2
|
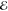 = 1.1 × 10–2 = 1.1 × 10–2
|
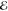 = 3.7 × 10–3 = 3.7 × 10–3
|
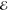 = 1.2 × 10–2 = 1.2 × 10–2
|
|||||
3.1.4. Other Densities
We have applied our algorithm for spherical densities to all of the concentric ss products arising in the cc-pVDZ and cc-pVTZ basis sets of Dunning and the pc-1 and pc-2 basis set of Jensen, constructing L–1/2(m), L1/2(m) and L3/2(m) models with m = 1,..., 6.
The maximum error 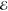 does not show a strong dependence on p but we find that the smallest
does not show a strong dependence on p but we find that the smallest 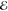 is often obtained by L3/2(m) if m is small,
and by L1/2(m) if m is larger.
is often obtained by L3/2(m) if m is small,
and by L1/2(m) if m is larger.
In many cases, the number m of Gaussians required to accurately model a density with a large number n of Gaussians is surprisingly small. The explanation for this encouraging discovery appears to lie in the distribution of exponents αklμν in a typical basis function product. We see from (7) that the αklμν are simple sums of the αkμ and αlν of the parent basis functions but, because the latter typically form a roughly geometrical sequence, the distribution of αklμν is clustered. To illustrate this, consider a hypothetical basis function with αkμ = {1000, 100, 10, 1}. The product of this with itself generates a Gaussian density with αklμμ = {2000, 1100, 1010, 1001, 200, 110, 101, 20, 11, 2}, and although these 10 exponents are strictly distinct, the second, third and fourth Gaussians are similar (as are the sixth and seventh Gaussians) and can be modeled quite well by a single Gaussian.
3.2. Cylindrical Densities
3.2.1. Preamble
If two basis functions are on different centers, separated by a distance R > 0, their product yields a Gaussian density ρ(r) with cylindrical symmetry and, to find the Lp(m), we need
| 77 |
| 78 |
The overlap S = ∫ρ(r) dr of the functions decays rapidly as R increases and it is interesting to compare the accuracies of the Lp(m) models as a function of R.
The Lp(m) models are constructed to mimic the original density ρ(r) as well as possible over all space. It is also important, however, to assess the resulting models χ(r) by measuring the largest pointwise difference between ρ(r) and χ(r). For a cylindrical density, it is natural to measure this through the maximum axial error
| 79 |
and we report this for each of the models described below.
3.2.2. H(1s)H(1s) Density
Our first example is the product of the 5-fold contracted cc-pVTZ basis functions (Table 1) on two hydrogen atoms centered at (0, 0, ±R/2). The density consists of 25 Gaussians, and L–1/2(m) models with m = 1 to 6 Gaussians are shown in Table 6.
Table 6. L–1/2(m) Models for cc-pVTZ H(1s)H(1s) Densities with Various R.
|
R = 4.928, S = 0.100 |
R = 7.725, S = 0.010 |
R = 9.995, S = 0.001 |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| m | Bi | λi | ci/S | Bi | λi | ci/S | Bi | λi | ci/S |
| 1 | +0.000 | +0.015 | 1.000 | +0.000 | –0.239 | 1.000 | +0.000 | –0.262 | 1.000 |
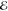 = 3.6 × 10–3 = 3.6 × 10–3
|
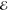 = 2.2 × 10–4 = 2.2 × 10–4
|
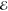 = 1.0 × 10–5 = 1.0 × 10–5
|
|||||||
| 2 | –1.142 | +0.282 | 0.500 | –1.287 | +0.019 | 0.500 | –0.990 | –0.125 | 0.500 |
| +1.142 | +0.282 | 0.500 | +1.287 | +0.019 | 0.500 | +0.990 | –0.125 | 0.500 | |
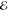 = 1.8 × 10–3 = 1.8 × 10–3
|
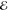 = 9.1 × 10–5 = 9.1 × 10–5
|
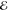 = 3.9 × 10–6 = 3.9 × 10–6
|
|||||||
| 3 | –1.382 | +0.709 | 0.274 | –2.320 | +0.657 | 0.133 | –2.743 | +0.561 | 0.062 |
| +0.000 | –0.182 | 0.452 | +0.000 | –0.165 | 0.734 | +0.000 | –0.193 | 0.875 | |
| +1.382 | +0.709 | 0.274 | +2.320 | +0.657 | 0.133 | +2.743 | +0.561 | 0.062 | |
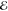 = 1.1 × 10–3 = 1.1 × 10–3
|
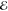 = 3.6 × 10–5 = 3.6 × 10–5
|
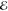 = 9.6 × 10–7 = 9.6 × 10–7
|
|||||||
| 4 | –1.763 | +0.913 | 0.168 | –2.323 | +0.670 | 0.132 | –2.744 | +0.561 | 0.062 |
| +0.000 | –0.163 | 0.510 | +0.000 | –0.184 | 0.717 | +0.000 | +3.312 | –0.0001 | |
| +0.000 | +0.662 | 0.155 | +0.000 | +0.583 | 0.018 | +0.000 | –0.192 | 0.875 | |
| +1.763 | +0.913 | 0.168 | +2.323 | +0.670 | 0.132 | +2.744 | +0.561 | 0.062 | |
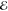 = 8.0 × 10–4 = 8.0 × 10–4
|
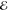 = 3.6 × 10–5 = 3.6 × 10–5
|
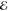 = 9.6 × 10–7 = 9.6 × 10–7
|
|||||||
| 5 | –2.229 | +1.761 | 0.030 | –3.276 | +1.640 | 0.013 | –4.252 | +1.696 | 0.002 |
| –1.137 | +0.554 | 0.290 | –1.982 | +0.531 | 0.146 | –2.607 | +0.541 | 0.062 | |
| +0.000 | –0.273 | 0.361 | +0.000 | –0.198 | 0.683 | +0.000 | –0.196 | 0.870 | |
| +1.137 | +0.554 | 0.290 | +1.982 | +0.531 | 0.146 | +2.607 | +0.541 | 0.062 | |
| +2.229 | +1.761 | 0.030 | +3.276 | +1.640 | 0.013 | +4.252 | +1.696 | 0.002 | |
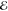 = 3.1 × 10–4 = 3.1 × 10–4
|
 = 1.1 × 10–5 = 1.1 × 10–5
|
 = 1.8 × 10–7 = 1.8 × 10–7
|
|||||||
| 6 | –2.138 | +1.915 | 0.025 | –3.327 | +1.785 | 0.010 | |||
| –1.368 | +0.596 | 0.220 | –2.037 | +0.550 | 0.144 | ||||
| +0.000 | –0.186 | 0.445 | +0.000 | –0.195 | 0.689 | ||||
| +0.000 | +0.872 | 0.064 | +0.000 | +0.886 | 0.002 | ||||
| +1.368 | +0.596 | 0.220 | +2.037 | +0.550 | 0.144 | ||||
| +2.138 | +1.915 | 0.025 | +3.327 | +1.785 | 0.010 | ||||
 = 2.7 × 10–4 = 2.7 × 10–4
|
 = 9.0 × 10–6 = 9.0 × 10–6
|
||||||||
We have considered three values of R, chosen so that the resulting overlap S is close to 0.1, 0.01, or 0.001. These correspond roughly to the most distant H atoms in the equilibrium structures of ethane, propane and butane, respectively.
In the least-squares approximation of smooth functions by other
smooth functions, pointwise convergence is expected to be exponential50 and this seems to be observed here. As the number m of Gaussians in the model grows, the maximum error 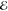 decays rapidly. In all cases, the optimal
centers Bi are symmetrically
and more or less uniformly distributed on the z axis,
the central Gaussian is the most diffuse (its λi is the most negative) and the Gaussians furthest
from the origin are the least diffuse and have the smallest coefficients ci.
decays rapidly. In all cases, the optimal
centers Bi are symmetrically
and more or less uniformly distributed on the z axis,
the central Gaussian is the most diffuse (its λi is the most negative) and the Gaussians furthest
from the origin are the least diffuse and have the smallest coefficients ci.
It is particularly
encouraging to note that, for R ≈ 10, the
25-Gaussian density can be approximated very accurately 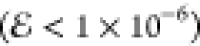 by a model with just three Gaussians, or
accurately (
by a model with just three Gaussians, or
accurately (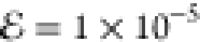 ) by a model with just a single Gaussian!
) by a model with just a single Gaussian!
The reported m = 4 model for R ≈ 10 is a local minimum, with a Z value
0.5% larger than the global minimum. The 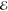 values are the same. It seems clear that
adding a fourth Gaussian to the model provides negligible improvement,
so its precise λi and ci have little bearing on the overally
accuracy. The fifth Gaussian is needed to noticeably lower both Z and
values are the same. It seems clear that
adding a fourth Gaussian to the model provides negligible improvement,
so its precise λi and ci have little bearing on the overally
accuracy. The fifth Gaussian is needed to noticeably lower both Z and 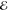 , but this is unimportant since this density
can be modeled so accurately with even a single Gaussian.
, but this is unimportant since this density
can be modeled so accurately with even a single Gaussian.
3.2.3. C(2s)H(1s) Density
Our second example is the product of the 10-fold contracted rec-cc-pVTZ 2s basis function on a C atom at (0, 0, −R/2) with the 5-fold contracted cc-pVTZ basis function on a H atom at (0, 0, +R/2) (see Tables 1 and 2). The product consists of 50 Gaussians, and L–1/2(m) models with m = 1 to 6 Gaussians are shown in Table 7.
Table 7. L–1/2(m) Models for rec-cc-pVTZ C(2s)H(1s) Densities with Various R.
|
R = 4.669, S = 0.100 |
R = 7.305, S = 0.010 |
R = 9.446, S = 0.001 |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| m | Bi | λi | ci/S | Bi | λi | ci/S | Bi | λi | ci/S |
| 1 | –0.285 | +0.158 | 1.000 | –0.593 | –0.090 | 1.000 | –0.712 | –0.134 | 1.000 |
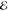 = 3.8 × 10–3 = 3.8 × 10–3
|
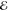 = 3.2 × 10–4 = 3.2 × 10–4
|
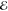 = 1.8 × 10–5 = 1.8 × 10–5
|
|||||||
| 2 | –1.179 | +0.418 | 0.561 | –1.779 | +0.310 | 0.480 | –2.135 | +0.266 | 0.303 |
| +0.889 | +0.378 | 0.439 | +0.567 | +0.025 | 0.520 | –0.072 | –0.082 | 0.697 | |
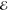 = 3.1 × 10–3 = 3.1 × 10–3
|
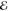 = 1.2 × 10–4 = 1.2 × 10–4
|
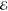 = 4.6 × 10–6 = 4.6 × 10–6
|
|||||||
| 3 | –1.320 | +0.761 | 0.344 | –2.306 | +0.758 | 0.196 | –2.797 | +0.677 | 0.120 |
| –0.289 | –0.099 | 0.387 | –0.437 | –0.041 | 0.699 | –0.537 | –0.073 | 0.838 | |
| +1.079 | +0.733 | 0.270 | +1.869 | +0.662 | 0.105 | +2.171 | +0.595 | 0.041 | |
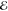 = 2.9 × 10–3 = 2.9 × 10–3
|
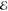 = 1.1 × 10–4 = 1.1 × 10–4
|
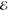 = 3.0 × 10–6 = 3.0 × 10–6
|
|||||||
| 4 | –1.691 | +0.948 | 0.197 | –3.396 | +2.405 | 0.006 | –4.158 | +1.924 | 0.003 |
| –0.274 | –0.039 | 0.487 | –2.197 | +0.707 | 0.203 | –2.710 | +0.653 | 0.121 | |
| –0.170 | +0.776 | 0.171 | –0.434 | –0.052 | 0.681 | –0.533 | –0.076 | 0.834 | |
| +1.529 | +0.954 | 0.145 | +1.813 | +0.646 | 0.110 | +2.136 | +0.594 | 0.042 | |
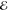 =2.7 × 10–3 =2.7 × 10–3
|
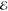 =8.6 × 10–5 =8.6 × 10–5
|
 =2.4 × 10–6 =2.4 × 10–6
|
|||||||
| 5 | –2.280 | +3.202 | 0.008 | –3.232 | +1.878 | 0.012 | –4.037 | +1.686 | 0.005 |
| –1.345 | +0.719 | 0.329 | –2.068 | +0.649 | 0.222 | –2.675 | +0.641 | 0.122 | |
| –0.230 | –0.152 | 0.345 | –0.418 | –0.080 | 0.640 | –0.530 | –0.078 | 0.831 | |
| +0.652 | +0.625 | 0.274 | +1.487 | +0.568 | 0.115 | +2.061 | +0.595 | 0.041 | |
| +1.978 | +1.429 | 0.044 | +2.849 | +1.438 | 0.011 | +3.881 | +1.783 | 0.001 | |
 = 1.6 × 10–3 = 1.6 × 10–3
|
 = 9.4 × 10–5 = 9.4 × 10–5
|
 = 2.5 × 10–6 = 2.5 × 10–6
|
|||||||
| 6 | –2.249 | +3.354 | 0.007 | –3.573 | +3.933 | 0.002 | –4.647 | +3.942 | 0.0004 |
| –1.460 | +0.796 | 0.257 | –2.812 | +1.213 | 0.032 | –3.766 | +1.398 | 0.007 | |
| –0.318 | –0.053 | 0.436 | –1.959 | +0.590 | 0.211 | –2.646 | +0.625 | 0.121 | |
| +0.013 | +0.918 | 0.093 | –0.406 | –0.083 | 0.631 | –0.527 | –0.078 | 0.829 | |
| +1.131 | +0.611 | 0.184 | +1.523 | +0.582 | 0.116 | +2.052 | +0.598 | 0.041 | |
| +1.915 | +1.868 | 0.024 | +2.929 | +1.587 | 0.009 | +3.830 | +1.672 | 0.001 | |
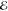 = 1.5 × 10–3 = 1.5 × 10–3
|
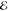 = 3.5 × 10–5 = 3.5 × 10–5
|
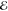 = 8.7 × 10–7 = 8.7 × 10–7
|
|||||||
As before, we have considered three values of R, chosen so that the resulting overlap S is close to 0.1, 0.01, or 0.001. These correspond roughly to the most separated C and H atoms in the equilibrium structures of ethane, propane and butane, respectively.
Although the maximum pointwise error 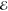 of the models almost always decreases as m grows, its decay is slower than for the H(1s)H(1s) densities
above. More detailed investigation revealed that the pointwise error
is usually largest (and oscillating) in a small region close to the
carbon nucleus, but because of volume effects, this error contributes
relatively little to the integral in (21) and
is therefore only slowly reduced as more Gaussians are added to the
model.
of the models almost always decreases as m grows, its decay is slower than for the H(1s)H(1s) densities
above. More detailed investigation revealed that the pointwise error
is usually largest (and oscillating) in a small region close to the
carbon nucleus, but because of volume effects, this error contributes
relatively little to the integral in (21) and
is therefore only slowly reduced as more Gaussians are added to the
model.
As was observed for the H(1s)H(1s) densities, the models
in Table 7 are usually
dominated
by a diffuse Gaussian near the origin, flanked by tighter Gaussians
with smaller coefficients, and the central dominance is even more
marked in the large-R densities. It is clear from
the 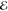 values that the 50-Gaussian densities arising
from the overlap of well separated C(2s) and H(1s) functions can be
very accurately modeled by models with very small numbers of Gaussians.
values that the 50-Gaussian densities arising
from the overlap of well separated C(2s) and H(1s) functions can be
very accurately modeled by models with very small numbers of Gaussians.
4. Conclusions
The electron density D(r) is a fundamental quantity in all quantum chemical calculations and, in order that those calculations be efficient, it is desirable that D(r) be represented as compactly as possible. Most of the successful previous work in this area projects D(r) into a global auxiliary basis set but, in the present work, we have sought instead to approximate each basis function product that contributes to D(r) in a small, local basis that is explicitly tailored to that product. This is achieved by performing a nonlinear optimization with a few adjustable parameters for each product, and we have presented expressions for all of the first and second derivatives required to use Newton’s method or a similar second-order scheme.
We have applied our algorithm to many of the products that arise when Dunning’s cc-pVnZ or Jensen’s pc-n basis sets are used, and we find that, in many cases, products consisting of many primitive Gaussians can be accurately approximated by models with only a few, well-optimized Gaussians. We anticipate that when such models are used in quantum chemical calculations, the resulting errors will be small while the computational speed will be significantly enhanced.
Acknowledgments
E.K.G.B. thanks the University of Sydney for a Ph.D. scholarship and a Postgraduate Teaching Fellowship.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.3c04363.
The Golub-Welsch algorithm (PDF)
The authors declare no competing financial interest.
Special Issue
Published as part of The Journal of Physical Chemistry Avirtual special issue “Krishnan Raghavachari Festschrift”.
Supplementary Material
References
- Hohenberg P.; Kohn W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
- Davidson E. R.Reduced density matrices in quantum chemistry; Academic: New York, 1976; pp 1–2. [Google Scholar]
- Parr R. G.; Yang W.. Density-functional theory of atoms and molecules; Clarendon Press: Oxford, U.K., 1989; pp 24–26. [Google Scholar]
- Szabo A.; Ostlund N. S.. Modern quantum chemistry; McGraw-Hill: New York, 1989; pp 108–230. [Google Scholar]
- Boys S. F. Electronic wave functions. 1. A general method of calculation for the stationary states of any molecular system. Proc. R. Soc. London, Ser. A 1950, 200, 542–554. 10.1098/rspa.1950.0036. [DOI] [Google Scholar]
- Dupuis M.; Rys J.; King H. F. Evaluation of molecular integrals over Gaussian basis functions. J. Chem. Phys. 1976, 65, 111–116. 10.1063/1.432807. [DOI] [Google Scholar]
- McMurchie L. E.; Davidson E. R. One- and two-electron integrals over Cartesian Gaussian functions. J. Comput. Phys. 1978, 26, 218–231. 10.1016/0021-9991(78)90092-X. [DOI] [Google Scholar]
- Obara S.; Saika A. Efficient recursive computation of molecular integrals over cartesian gaussian functions. J. Chem. Phys. 1986, 84, 3963–3974. 10.1063/1.450106. [DOI] [Google Scholar]
- Head-Gordon M.; Pople J. A. A method for two-electron gaussian integral and integral derivative evaluation using recurrence relations. J. Chem. Phys. 1988, 89, 5777–5786. 10.1063/1.455553. [DOI] [Google Scholar]
- Hamilton T. P.; Schaefer H. F. III New variations in two-electron integral evaluation in the context of direct SCF procedures. Chem. Phys. 1991, 150, 163–171. 10.1016/0301-0104(91)80126-3. [DOI] [Google Scholar]
- Lindh R.; Ryu U.; Liu B. The reduced multiplication scheme of the Rys quadrature and new recurrence relations for auxiliary function based two-electron integral evaluation. J. Chem. Phys. 1991, 95, 5889–5897. 10.1063/1.461610. [DOI] [Google Scholar]
- Gill P. M. W.; Pople J. A. The PRISM algorithm for two-electron integrals. Int. J. Quantum Chem. 1991, 40, 753–772. 10.1002/qua.560400605. [DOI] [Google Scholar]
- Gill P. M. W. Molecular integrals over gaussian basis functions. Adv. Quantum Chem. 1994, 25, 141–205. 10.1016/S0065-3276(08)60019-2. [DOI] [Google Scholar]
- Adams T. R.; Adamson R. D.; Gill P. M. W. A tensor approach to two-electron matrix elements. J. Chem. Phys. 1997, 107, 124–131. 10.1063/1.474359. [DOI] [Google Scholar]
- Ishida K. Rigorous algorithm for the electron repulsion integral over the generally contracted solid harmonic Gaussian-type orbitals. J. Chem. Phys. 2000, 113, 7818–7829. 10.1063/1.1316013. [DOI] [Google Scholar]
- Makowski M. Simple yet powerful techniques for optimization of horizontal recursion steps in gaussian-type two-electron integral evaluation algorithms. Int. J. Quantum Chem. 2007, 107, 30–36. 10.1002/qua.21056. [DOI] [Google Scholar]
- Komornicki A.; King H. F. A general formulation for the efficient evaluation of n-electron integrals over products of gaussian charge distributions with gaussian geminal functions. J. Chem. Phys. 2011, 134, 244115. 10.1063/1.3600745. [DOI] [PubMed] [Google Scholar]
- Reeves C. M.; Fletcher R. Use of gaussian functions in the calculation of wavefunctions for small molecules. III. The orbital basis and its effect on valence. J. Chem. Phys. 1965, 42, 4073–4081. 10.1063/1.1695896. [DOI] [Google Scholar]
- O-ohata K.; Taketa H.; Huzinaga S. Gaussian expansions of atomic orbitals. J. Phys. Soc. Jpn. 1966, 21, 2306–2313. 10.1143/JPSJ.21.2306. [DOI] [Google Scholar]
- Newton M. D.; Ostlund N. S.; Pople J. A. Projection of diatomic differential overlap: Least-squares projection of two-center distributions onto one-center functions. J. Chem. Phys. 1968, 49, 5192–5194. 10.1063/1.1670022. [DOI] [Google Scholar]
- Hehre W. J.; Stewart R. F.; Pople J. A. Self-consistent molecular-orbital methods. I. Use of gaussian expansions of Slater-type atomic orbitals. J. Chem. Phys. 1969, 51, 2657–2664. 10.1063/1.1672392. [DOI] [Google Scholar]
- Stewart R. F. Small gaussian expansions of atomic orbitals. J. Chem. Phys. 1969, 50, 2485–2495. 10.1063/1.1671406. [DOI] [Google Scholar]
- Billingsley F. P. II; Bloor J. E. Limited expansion of diatomic overlap (LEDO): A near-accurate approximate ab initio LCAO MO method. I. Theory and preliminary investigations. J. Chem. Phys. 1971, 55, 5178–5190. 10.1063/1.1675655. [DOI] [Google Scholar]
- Baerends E. J.; Ellis D. E.; Ros P. Self-consistent molecular Hartree-Fock-Slater calculations. I. The computational procedure. Chem. Phys. 1973, 2, 41–51. 10.1016/0301-0104(73)80059-X. [DOI] [Google Scholar]
- Whitten J. Coulombic potential energy integrals and approximations. J. Chem. Phys. 1973, 58, 4496–4501. 10.1063/1.1679012. [DOI] [Google Scholar]
- Beebe N. H. F.; Linderberg J. Simplifications in the generation and transformation of two-electron integrals in molecular calculations. Int. J. Quantum Chem. 1977, 12, 683–705. 10.1002/qua.560120408. [DOI] [Google Scholar]
- Dunlap B. I.; Connolly J.; Sabin J. On some approximations in applications of Xα theory. J. Chem. Phys. 1979, 71, 3396–3402. 10.1063/1.438728. [DOI] [Google Scholar]
- Fortunelli A.; Salvetti O. A simplified representation of the potential produced by gaussian charge distributions. J. Comput. Chem. 1991, 12, 36–41. 10.1002/jcc.540120105. [DOI] [Google Scholar]
- Feyereisen M.; Fitzgerald G.; Komornicki A. Use of approximate integrals in ab initio theory. An application in MP2 energy calculations. Chem. Phys. Lett. 1993, 208, 359–363. 10.1016/0009-2614(93)87156-W. [DOI] [Google Scholar]
- Eichkorn K.; Treutler O.; Öhm H.; Häser M.; Ahlrichs R. Auxiliary basis sets to approximate Coulomb potentials. Chem. Phys. Lett. 1995, 240, 283–289. 10.1016/0009-2614(95)00621-A. [DOI] [Google Scholar]
- Hall G. G.; Martin D. Approximate electron densities for atoms and molecules. Isr. J. Chem. 1980, 19, 255–259. 10.1002/ijch.198000028. [DOI] [Google Scholar]
- Gill P. M. W.; Johnson B. G.; Pople J. A.; Taylor S. W. Modeling the potential of a charge distribution. J. Chem. Phys. 1992, 96, 7178–7179. 10.1063/1.462530. [DOI] [Google Scholar]
- Weigend F.; Kattannek M.; Ahlrichs R. Approximated electron repulsion integrals: Cholesky decomposition versus resolution of the identity methods. J. Chem. Phys. 2009, 130, 164106. 10.1063/1.3116103. [DOI] [PubMed] [Google Scholar]
- Pedersen T. B.; Aquilante F.; Lindh R. Density fitting with auxiliary basis sets from Cholesky decompositions. Theor. Chem. Acc. 2009, 124, 1–10. 10.1007/s00214-009-0608-y. [DOI] [PubMed] [Google Scholar]
- McKemmish L. K.; Gill P. M. W. Gaussian expansions of orbitals. J. Chem. Theory Comput. 2012, 8, 4891–4898. 10.1021/ct300559t. [DOI] [PubMed] [Google Scholar]
- Kutzelnigg W. Expansion of a wave function in a gaussian basis. I. Local versus global approximation. Int. J. Quantum Chem. 2013, 113, 203–217. 10.1002/qua.24224. [DOI] [Google Scholar]
- García V.; Zorrilla D.; Sánchez-Márquez J.; Fernández-Núnez M. Software to obtain accurate gaussian expansions for a wide range of radial functions. J. Mol. Model 2017, 23, 165. 10.1007/s00894-017-3340-x. [DOI] [PubMed] [Google Scholar]
- Olver F. W. J., Lozier D. W., Boisvert R. F., Clark C. W., Eds. NIST Handbook of Mathematical Functions; Cambridge University Press: New York, 2010. [Google Scholar]
- Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
- Jensen F. Polarization consistent basis sets: Principles. J. Chem. Phys. 2001, 115, 9113–9125. 10.1063/1.1413524. [DOI] [Google Scholar]
- Pritchard B. P.; Altarawy D.; Didier B.; Gibson T. D.; Windus T. L. A new Basis Set Exchange: An open, up-to-date resource for the molecular sciences community. J. Chem. Inf. Model. 2019, 59, 4814–4820. 10.1021/acs.jcim.9b00725. [DOI] [PubMed] [Google Scholar]
- Dantzig G. B.; Thapa M. N.. Linear Programming 1: Introduction; Springer: New York, 1997; pp 63–97. [Google Scholar]
- Gautschi W. Construction of Gauss-Christoffel quadrature formulas. Math. Comp. 1968, 22, 251–270. 10.1090/S0025-5718-1968-0228171-0. [DOI] [Google Scholar]
- Golub G. H.; Welsch J. H. Calculation of Gauss quadrature rules. Math. Comp. 1969, 23, 221–230. 10.1090/S0025-5718-69-99647-1. [DOI] [Google Scholar]
- Szegö G.Orthogonal polynomials; American Mathematical Society: New York, 1959; pp 9, 111–158. [Google Scholar]
- Gradshteyn I. S.; Ryzhik I. M. In Table of Integrals, Series, and Products, 7th ed.; Jeffrey A., Zwillinger D., Eds.; Academic Press: London, 2007; pp 635–793. [Google Scholar]
- Bardo R. D.; Ruedenberg K. Even-tempered atomic orbitals. VI. Optimal orbital exponents and optimal contractions of Gaussian primitives for hydrogen, carbon, and oxygen in molecules. J. Chem. Phys. 1974, 60, 918–931. 10.1063/1.1681168. [DOI] [Google Scholar]
- Levenberg K. A method for the solution of certain non-linear problems in least squares. Quart. Appl. Math. 1944, 2, 164–168. 10.1090/qam/10666. [DOI] [Google Scholar]
- Marquardt D. W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Indust. Appl. Math. 1963, 11, 431–441. 10.1137/0111030. [DOI] [Google Scholar]
- Boyd J. P.Chebyshev and Fourier spectral methods, 2nd ed.; Dover: New York, 2000; p 67. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.