Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Oct 27;14(44):9834–9841. doi: 10.1021/acs.jpclett.3c02367

Heat Transfer Enhancement in Tree-Structured Polymer Linked Gold Nanoparticle Networks

Xingfei Wei †, Rigoberto Hernandez †,‡,¶,*
PMCID: PMC10642580  PMID: 37890034

Abstract

graphic file with name jz3c02367_0005.jpg

Human brains use a tree-like neuron network for information processing at high efficiency and low energy consumption. Tree-like structures have also been engineered to enhance mass and heat transfer in various applications. In this work, we reveal the heat transfer mechanism in tree-structured polymer linked gold nanoparticle (AuNP) networks using atomistic simulations. We report both upward and downward heat fluxes between root and leaf nodes in tree-structured polyethylene (PE) and poly(p-phenylene) (PPP) linked AuNP networks at tree levels from 1 to 5. We found that the heat conductance increases with an increasing polymer tree level. The heat transfer enhancement is due to the resulting increase in the low-frequency vibrational modes. This and other thermal properties are affected by the location of the AuNPs in the tree. Moreover, complex tree structures with at least five levels were found to be robust in the sense that disabling half of the leaves did not change the overall heat conductance.

Information processing is effectively realized by the network of neurons and synapses in the brain which can be represented in an elegant and complex tree structure.1,2 Here we look for fundamental relationships between variations of such tree structures and their material physical properties. For example, tree-structured nanosilver dendrites have been seen to improve the sensitivity of surface enhanced Raman scattering (SERS) for molecular detection.3,4 Membrane materials with tree-like hierarchical structures have large specific surface area, which is beneficial for air filtration5,6 and ion transport.7,8 Moreover, tree-like copper dendrites can increase catalytic sites and improve CO2 electrochemical reduction.9,10 In the constructal theory of Bejan and co-workers,11−16 the tree structure network was found to be the optimum architecture for fluid flow and heat transfer. In a multiscale tree structure, the nanoscale thermal transport mechanism dominates in the smallest branches, where the phonon mean free path is comparable with the branch size.15 Comparing to traditional parallel channels, in a microelectronic chip cooling system, the tree network channel can enhance the heat transfer rate and reduce the fluid pressure drop.17 In bulk composite materials, the thermal conductivity increases by internally embedding the tree structure with shorter branch length and larger branch diameter.18 In tree-structured networks, the macroscopic scaling laws for electron, heat, and flow transport were summarized by Xu and Yu.19 However, the nanoscale thermal physics is different from that of bulk materials.20 The heat transfer mechanism at the molecular level remains to be uncovered in tree structures.

Soft materials have the potential to be used as surrogates for components of the brain in creating brain-like computing structures because their morphology is similar to that of the soft tissues (gray matter and white matter) of the brain. For example, in prior work,21−23 we demonstrated that polymer linked nanoparticle networks can be used as primitives for data storage and computing. Dendrons and dendrimers are popular choices for tree-structured polymers—which are in turn regarded as unique building blocks for nanoscale materials engineering,24—and have been useful in applications for drug delivery, gene transfection, and biomedical imaging.24−27 A system with digital dendrimers—distinctly mapped into two types of subunits identifiable as 0 or 1 in a binary code—were seen to exhibit high capacity for data storage.28,29 Polymeric materials are also popular in energy management; for example, the thermal conductivity of polymer composites can be engineered by functionalizing the filler and polymer matrix with different chemical groups.30−32 In polymers, thermal conductivity is a result of the complex relationship between chemical structure, chain conformation, length, and stiffness.33−36 Specifically, in polymer linked nanoparticle systems, the internal connection and the polymer network structure determine the heat transfer mechanism and rate.37−39 The heat conductance in polyethylene (PE) molecular junctions has been seen to increase with increasing PE chain length from 2 to 10 CH2 units in alkanedithiol molecules.40 We also found that the heat flux through polymer linked dimers is related to the polymer stiffness and the number of polymer linkers between two gold nanoparticles (AuNPs).39

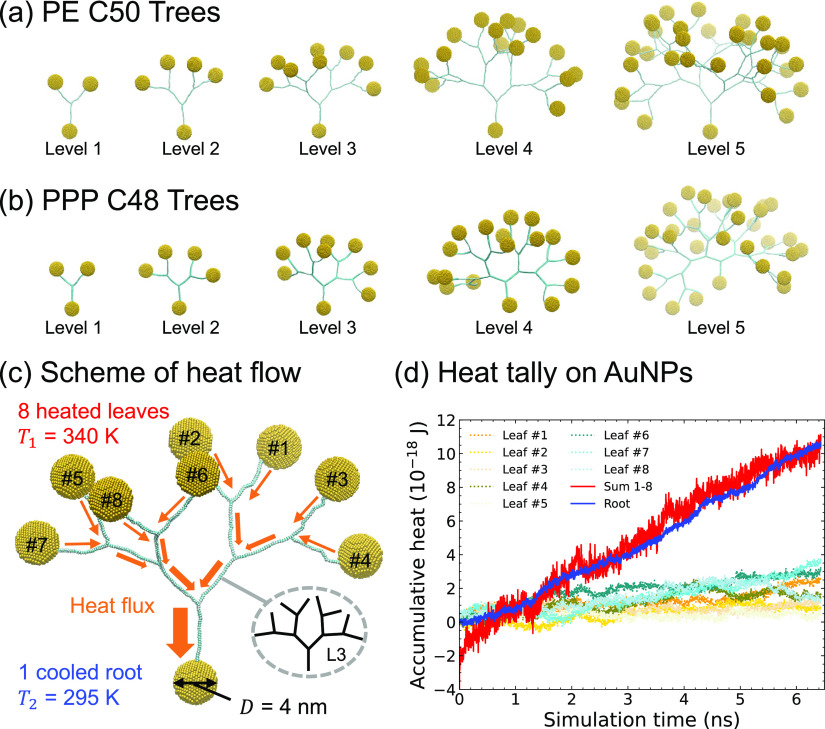
In this Letter, we report heat conductance between the root and the outer leaves in PE and poly(p-phenylene) (PPP) linked AuNP tree-structured networks with up to 5 branching levels; see Figure 1a,b. Nonequilibrium molecular dynamics (MD) is used to calculate the heat conductance between heat sinks maintained by Langevin thermostats on AuNPs; see Figure 1c,d. The energy tally on each AuNP (of diameter D = 4 nm) is monitored in calculating the resulting heat fluxes. Both upward and downward heat fluxes corresponding to heat diffusion from the hot root up to cold leaves and from hot leaves down to the cold root, respectively, are calculated between the temperature gap from T1 = 340 K to T2 = 295 K. Additional details about the simulation methods are summarized in section S-2, illustrated in Figures S1–S3 and detailed in Tables S1 and S2 in the Supporting Information (SI). As reported below, we found a new heat transfer mechanism in tree-structured polymer–AuNP networks with increasing tree complexity. The resulting thermal transport enhancement in these networks is due to the increase of low-frequency vibrational modes (as seen in the vibrational density of state (VDOS) spectra) with an increasing number of tree levels. By choosing different AuNPs as thermostats, we also found a spatial correlation between the heat flux and the position of AuNPs.

Figure 1.

Figure 1

Open in a new tab

Representative tree structures of PE trees and PPP trees from level 1 to 5 are shown in (a) and (b), respectively. When a AuNP is located deeper into the plane, it is shown in a lighter color, The underlying scheme for the heat conductance calculation up is shown in (c). Using the level 3 PE tree as an example, the 8 AuNP leaves on top are heat sources at 340 K and the 1 AuNP root at the bottom is the heat sink at 295 K. The tree branch lengths are all the same. PE branches are 50 carbons, and PPP branches are 48 carbons (12 rings). (d) The accumulative heat additions at the 8 different AuNP leaves are shown in 8 different colored dotted lines, and the energy subtraction at the 1 AuNP root is shown in blue. As noted in the text, the sum of the accumulated heat across all 8 leaves exceeds the energy subtraction by the initial transient energy addition needed to compensate the mismatch in heat capacities between the leaves and the root. The red curve thus displays the sum of the 8 leaves subtracted by this transient energy. (All colors are in grayscale in colorless prints and indicated by the legend.).

In determining heat fluxes, we calculate the heat conductance40,41G and not the conventional thermal conductivity κ because the heat transfer mechanism is not diffusive—as might be required for the latter—at the nanoscale. In our previous work, we found that heat conductance (G) of a linear PE chain with 100 carbons C100 is 24.8 ± 2.4 pW/K.39 Though not shown, we converted our results39 from G to κ and confirmed agreement with Zhang and Luo42 for unstretched unbranched PE chains. If we branch a chain in the middle to obtain the level 1 tree, we find an increased conductance of G = 33.1 ± 3.9 pW/K, as indicated in Figure 2a. Alternatively, a single linear PE chain with 50 carbons C50 has a reported conductance of 31.9 ± 2.5 pW/K.39 Again, the addition of a level increases the heat conductance because more heat flow channels are created through the additional branch. Indeed, the conductance continues to increase with increasing levels, as shown in Figure 2a. The VDOS spectra of PE trees can be used to explain the origin of increasing the heat conductance; see Figure 2b. We find that the VDOS peaks at ∼16 THz in PE levels 4 and 5 trees are higher than that in the level 1 tree. Consequently, the values of G at levels 4 and 5 are larger than those at level 1. The molecular vibration frequency at 15–30 THz is in the far-IR fingerprint region of 500–1000 cm–1. It was reported that vibration frequencies at 2.4–16.8 THz are diffusons, those above 16.8 THz are locons, and those below 2.4 THz are propagons.43 Locons are localized and do not contribute to heat transfer,43,44 which is why we use the VDOS peaks at ∼16 THz for comparison. Extended VDOS spectra up to 100 THz are given in Figure S5 in the SI. In all, increasing the PE tree level can enhance heat transfer through an increasing number of low-frequency vibrational modes.

Figure 2.

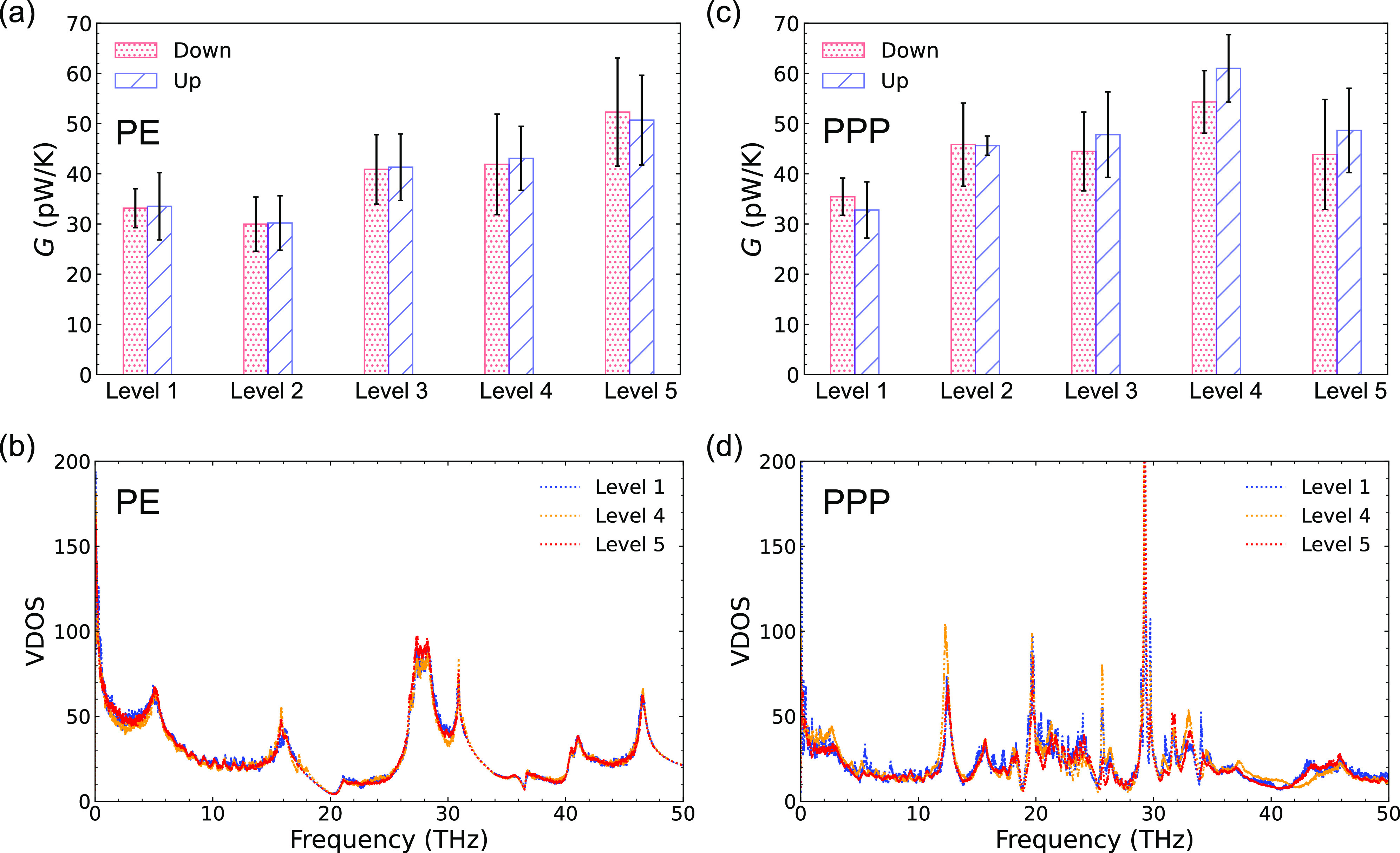
Figure 2

Open in a new tab

(a) Heat conductance of PE C50 tree polymer networks from level 1 to level 5. (b) VDOS spectra of PE C50 tree level 1, level 4, and level 5 polymer networks. (c) Heat conductance of PPP C48 tree polymer networks from level 1 to level 5. (d) VDOS spectra of PPP C48 tree level 1, level 4, and level 5 polymer networks. The large error bar in heat conductance is due to the high uncertainty in single molecule systems, which is also found in experiments40 and similar simulation systems.41,42,45 The VDOS spectra are obtained from the Fourier transform of the velocity autocorrelation function, which is, in turn, calculated from 20 randomly selected carbon atoms within the middle of the polymer to avoid effects from the thermostats; see, e.g., the selection of carbon atoms shown in Figure S4 in the SI. Due to the uncertainty, the VDOS spectra are relevant only for qualitative comparison. For convenience, the VDOS for only three of the levels (as listed in the legends) is shown here. All five of the VDOS spectra over a wider frequency range (from 0 to 100 THz) are shown in Figure S5 in the SI. The y-axis of the VDOS spectra is in arbitrary units.

Earlier, Ma and Tian45 reported a thermal rectification of 70% in tapered bottlebrush tree-like polymers when the temperature gap was between 100 and 300 K. They found that a higher fraction of the vibrational modes in direct thermal transport was diffusive rather than ballistic and ballistic rather than diffusive in the inverse direction.45 However, in our tree-structured PE–AuNP network systems, we found that the upward and downward heat fluxes were the same for trees at different levels; see Figure 2a. The origin of the differing behavior is that the temperature gap employed here, 295–340 K, is much narrower. In our smaller gap, all of the temperatures are near room temperature (300 K), where diffusive vibrational modes are dominant. Thus, the polymer chain remains in a similar structure (or phase) that does not give rise to directed transport and no thermal rectification is observed at 300 K. Experiments of vibrational energy transport inside molecules also show that at room temperature near 300 K diffusive mode transport dominates and at low temperature 10–150 K ballistic modes become important.46,47 When we set up the simulation using the temperature gap 100–300 K, we found the up direction heat flux is higher than the down direction. For PE C50 tree polymer networks, the thermal rectification ratio increases from 12 to 25% when the tree level increase from 1 to 5; see Figure S6a,b in the SI. However, PPP C48 tree polymer networks do not show thermal rectification; see Figure S6c in the SI.

In stiffer polymer PPP, increasing the chain length can either reduce heat transfer through phonon boundary scattering or enhance heat transfer through the opening of long-wavelength phonon modes.39 The reduced heat conductance in the phonon boundary scattering mechanism is due to long-wavelength phonons hitting the end of the polymer chain. The reduced heat conductance in the intrinsic phonon scattering mechanism is due to the collision of short-wavelength phonons inside of a polymer chain. Earlier, we reported that in linear PPP with chain length C50–C200 G ≈ 40 pW/K.39 Here, we find that the level 1 PPP tree drops to G ≈ 34 pW/K at a chain length of 96 carbons; see Figure 2c. This significant reduction in the thermal transport is a result of the induced intrinsic phonon scattering arising from broken symmetry when the linear PPP chain is branched in the middle. More importantly, Figure 2c also shows that G increases with increasing numbers of levels in the tree, reaching a maximum G ≈ 60 pW/K at level 4. This trend in the enhancement is consistent with the VDOS spectra in Figure 2d, which shows that the low-frequency vibrational modes increase in the level 4 tree at specific frequencies, such as near 2, 12, and 30 THz, but not others. However, Figure 2c also shows drops in G at level 5, which is consistent with the corresponding decrease in the VDOS spectra for the vibrational modes near 2 and 12 THz. For stiffer polymers, the relationship between the structure and thermal transport properties is even more complicated. We found that the vibrational modes in the level 5 PPP tree are more localized than those in the level 4 PPP tree. Thus, the heat transfer through these trees is the sum of competing effects: enhancements from the formation of additional low-frequency vibrational modes and reductions from phonon scattering, which tend to be larger with increasing PPP tree level. At temperatures near room temperature, we did not see thermal rectification because vibrational modes in PPP trees are the same in both—namely, up and down—heat flow directions.

Xu and Yu19 reported that the observed electric and heat transfer in network structures obeys the same analogous resistance equation and scaling laws. In our model, each PE branch is 50 carbons in length. In Figure 3, we compare the polymer tree structure in panel (a), the thermal resistance model in panel (b), the cut polymer tree structure in panel (c), and the linear polymer structure in panel (d). The thermal resistance model is based on a conventional electrical circuit with the assumption that the thermal resistance is constant. That is, each polymer branch is assumed to affect the same thermal resistance R1 within the scheme shown in Figure 3b. 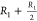Connecting two resistances R in parallel, the total resistance is Inline graphic, and in series the total resistance is R + R = 2R. 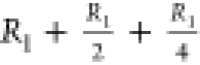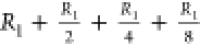Thus, the total resistance in the thermal resistance model for tree level 1 is Inline graphic, tree level 2 is Inline graphic, tree level 3 is Inline graphic, tree level 4 is 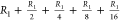Inline graphic, and tree level 5 is 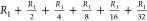Inline graphic. As a consequence, it predicts that the heat conductance values of the tree polymers decrease with an increasing tree level, which is the opposite trend of our simulation result. Thus, at the molecular level, the classical heat transfer rule is broken by the unique tree-structured polymer network.

Figure 3.

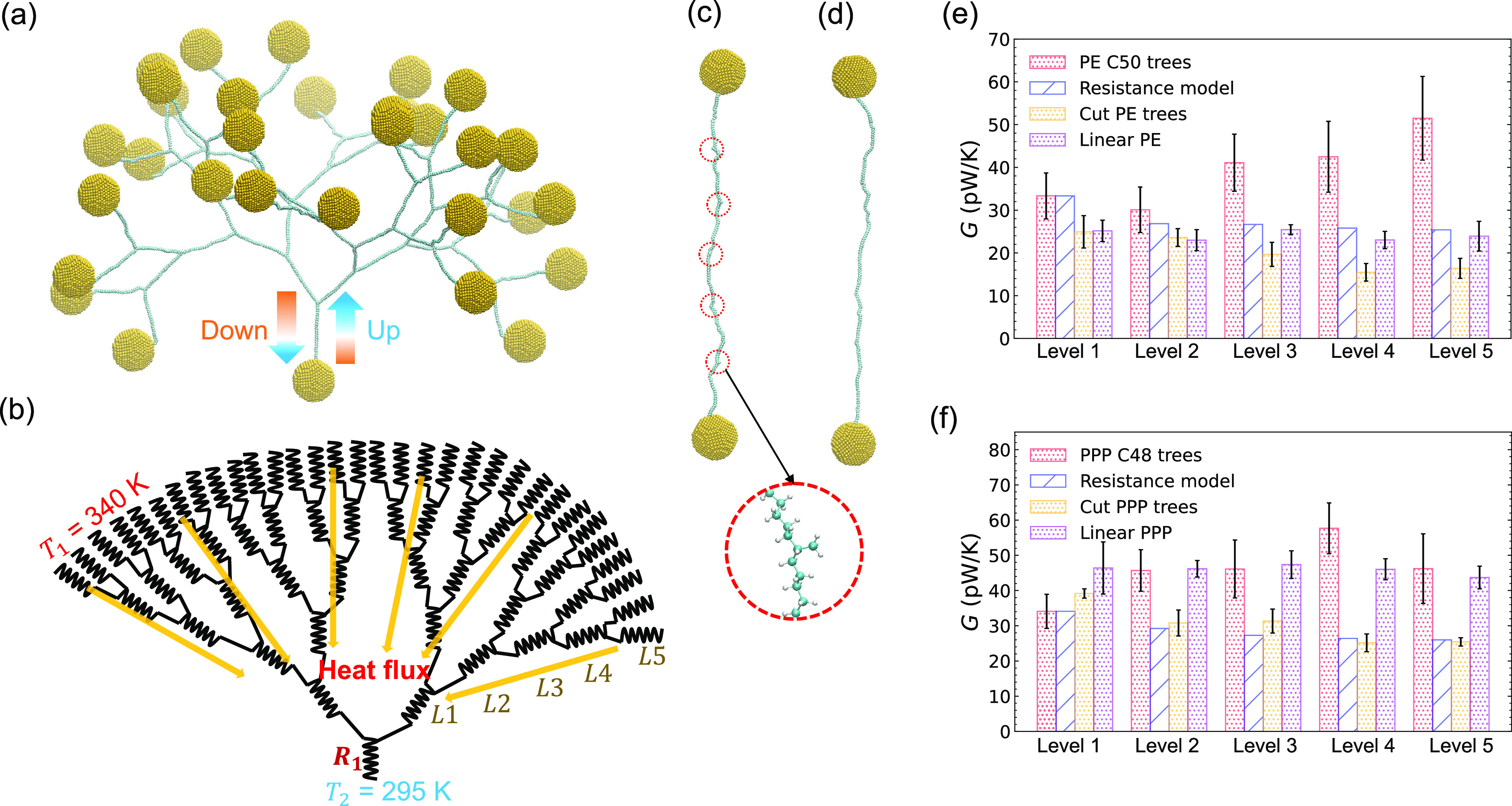
Figure 3

Open in a new tab

Representative level 5 structures of (a) a PE tree MD simulation model, (b) a general thermal resistance model, (c) a PE cut tree (red circles indicate positions of the cut branches), and (d) a linear PE chain at 300 carbon length. The cut tree structure has one CH3 residue group at each of the branching positions. The heat conductance results of four models in (a)–(d) are compared in (e) and (f) for both PE and PPP networks, respectively. Schemes of cut tree structures are shown in parts S8 and S9 in the SI. The G values are averaged from both upward and downward heat flow results since no rectification is observed at this temperature gap.

With even higher tree levels, the network structure should be more complex than our level 5 simulation models, but the trends should remain. The thermal resistance model predicts that the heat conductance monotonically decreases with increasing tree level; see Figure 3e,f for PE and PPP, respectively. In our MD simulations, we found that heat transfer in tree polymer structures follows a new mechanism as G increases with increasing the tree level. This new mechanism trend is a result of the increasing low-frequency vibrational modes with increasing tree level and the resulting increase in additional heat transfer channels. In the cut tree structures, we keep one branch only and cut all other branches with one residue unit (CH3 or benzene ring) at the branching position; see Figure 3c. Since tree, cut tree, and linear chain all have the same longest chain, it appears that the heat transfer enhancement is not due to the longest chain. Instead, the low-frequency modes emerge from the branching chains. Comparing with the cut tree and the linear PE chain networks, the PE tree polymer network also shows higher heat conductance, which is due to the additional heat transfer channels in the tree structure; see Figure 3e. However, in stiffer PPP networks, the linear PPP structure has the largest G, which is related to the highest symmetry in the linear chain; see Figure 3f. We also compared the linear chain with a cut tree structure and found that the cut tree structure has a lower heat conductance because the CH3 residue or benzene group on the cut chain causes intrinsic phonon scattering and reduces heat conductance. The PPP tree network has larger G than the cut tree, as the additional heat transfer channels in the tree structure. For stretched single polymer chains, the thermal conductivity generally increases with increasing chain length.48 We found that when the polymer chain is unstretched and free, the heat conductance values of PE and PPP both stay almost constant or slightly decrease. This is a consequence of the net cancellation between the additional heat transfer modes and the added heat resistance with an increasing chain length.

It may not be obvious if the behavior of G for PE trees from level 1 to level 2 is an increase because it appears to fall within the statistical error that the small decrease of G from level 1 to level 2 is a result of the net contributions due to competing effects from increased thermal resistance and additional heat transfer channels. However, if we use the corresponding thermal resistance model as a benchmark, we do see an increase of G in the level 2 PE tree. Meanwhile the decrease in the heat conductance in the PPP tree from level 4 to level 5 comes through the lens of intrinsic scattering in which some low-frequency vibrational modes shift to higher frequency. Figure S7a (SI) also shows that the heat conductance of PE C12 trees increases with increasing tree level from 1 to 5 in agreement with the behavior in a PE C50 tree. The G of PE C12 branching trees increases from ∼42 pW/K at level 1 to ∼55 pW/K at level 5. We use small 1 nm diameter AuNPs in PE C12 trees because otherwise there is not enough room to connect 4 nm AuNPs. However, these 1 nm AuNPs are not sufficiently pushed apart by the polymers, and they end up aggregated in simulation; see Figure S7b in the SI. In contrast, as shown in Figure 1a,b, we find stable PE C50 and PPP C48 tree structures connected to 4 nm AuNPs.

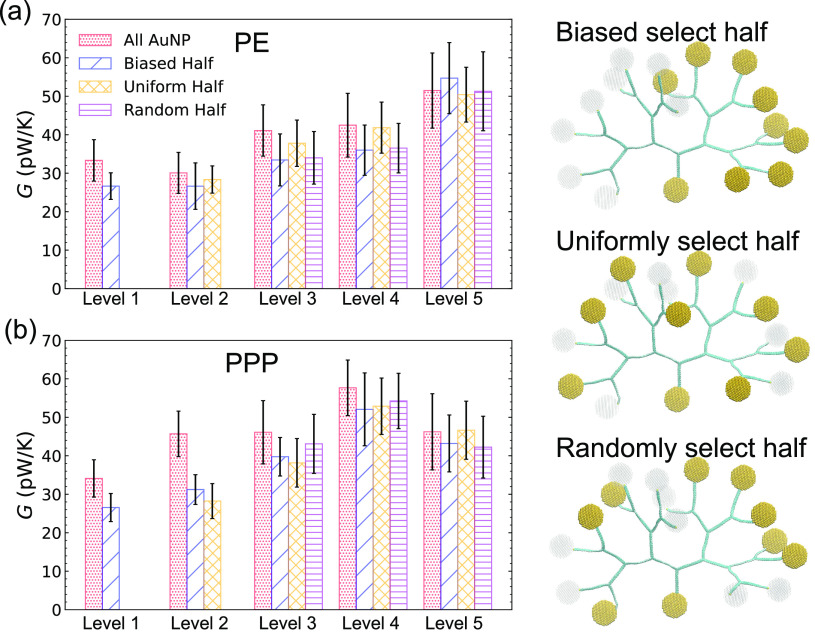
We now consider neuron network-like tree polymer–AuNP networks. We choose heating or cooling of the AuNPs at different positions to explore the spatial variation effect on the heat transfer. In both PE and PPP level 1 trees, we show in Figure 4a,b that removal of one heat source or sink leads the heat conductance to decrease by ∼20%. This arises because in the special case of a level 1 tree the removal of a heat source or sink is equivalent to the removal of half of the sources or sinks, and this is a very significant perturbation. Moreover, PE and PPP have different degrees of stiffness, and this leads to variations in heat transfer. In particular, the PPP branches are stiffer and lead the phonon boundary scattering mechanism to play a more important role. The heat transfer channel in PPP is more directly related to the number of heat sources or sinks. As a result, freezing half of the leaves in level 2 trees leads to a reduction in G by ∼10 and 30–40% for PE and PPP, respectively. This behavior is also found in level 3 and 4 trees in Figure 4a,b. For trees with more than 3 levels, there are at least three ways of freezing half of the leaves—namely, biased, uniform, and random; see the right side of Figure 4. In PE trees at level 3 or 4, we find that uniformly freezing half of the leaves can achieve G values comparable to freezing all leaves, but the biased or random freezing of half of the leaves leads to a decrease in G by ∼10%. This result demonstrates the hypothesized spatial relationship of heat transfer in tree-structured PE networks. Moreover, in level 5 PE and PPP trees, we find no difference in G between the freezing of half of the leaves and the freezing of none of the leaves; see Figure 4a,b. This result further demonstrates that in complex tree polymer–AuNP networks at level ≥5, when half of the heating or cooling leaves are malfunctioning, the thermal transport remains unchanged.

Figure 4.

Figure 4

Open in a new tab

Comparison of the resulting heat conductances when all the leaves are thermostated to when only half of the leaves are thermostated for (a) PE C50 trees and (b) PPP C48 trees from level 1 to level 5. The selection of the leaves that are thermostated is performed in 3 possible ways: biased, uniform, and random. Level 1 trees admit only 1 way (biased). Level 2 trees admit 2 ways (biased and uniform). Level 3–5 trees admit all 3 of the listed approaches.

In conclusion, using all-atom MD simulations, we demonstrated the possibility of heat conductance enhancement in tree polymer networks. In PE trees, the heat conductance increases from level 1 (G ≈ 33 pW/K) to level 5 (G ≈ 50 pW/K). Through analysis of the VDOS, we found that the fundamental mechanism is due to the increase in 0–20 THz low-frequency vibrational modes with an increasing number of tree levels. Meanwhile, in PPP trees, heat conductance also increases from level 1 to level 4 because of the same mechanism. The highest such value is G ≈ 60 pW/K at level 4 PPP trees. However, due to a drop in the low-frequency vibrational modes drop at level 5 in the PPP tree, the G value also drops. In contrast to the thermal resistance model, where G decreases with increasing tree level, we found a new heat conductance mechanism in tree polymer networks. That is, heat conductance increases with increasing tree level complexity because of the addition of new heat transfer channels from low-frequency vibrational modes. We demonstrated a spatial relationship in tree polymer networks with respect to the choice of leaf nodes. We also found that for both level 5 PE and PPP trees, when half of the leaves are malfunctioning, the thermal transport property remains the same.

The analogy to the persistence of brain function, even when half of the brain is damaged, to the persistence of function—namely heat transport, to analogous thermally conducting networks is notable. Specifically, we found here that we can freeze half of the nodes in a sufficiently large tree network without affecting the outputs. We speculate that this analogy is not accidental.

Simulation Methods

The tree polymer networks are simulated in a vacuum cubic box of 100 × 100 × 100 nm3. We require the separation of the system from a solvent, as is satisfied by the vacuum, because otherwise heat would immediately dissipate into the surrounding solvent. The tree polymers are built in the Materials Studio Software;49 see schemes in Figure 1a,b. We used thiol functional groups (−S, without hydrogen) to terminate the polymer chains. The AuNPs are bonded to the S atoms on each tree branch and at the tree root; see Figure 1c. Typically, we use 4 nm diameter AuNPs and PE branch length C50 or PPP branch length C48 to build different levels of tree networks; see Figure S1 in the SI. The AuNP model is cut from a bulk gold FCC crystal with a lattice constant of 4.078 Å. We use the Lennard-Jones (LJ) force field derived by Heinz et al.50 to describe Au–Au interactions. We also simulate tree networks with 1 nm diameter AuNPs and PE branch length C12 for comparison; see Figure S2 in the SI. Figure 1a shows representative structures of PE trees with a branch length of C50 and PPP trees with a branch length of C48. The optimized potentials for liquid simulations (OPLS) all-atom force field is used to describe interactions inside the polymers.51,52 The Au–S bonding interaction is described by a Morse potential.53 All other interactions between the polymer and Au are described by a LJ potentials.22,53 All force field parameters are listed in Tables S1 and S2 in the SI and in our previous paper.39

Our MD simulations are propagated using the large-scale atomic molecular massively parallel simulator (LAMMPS) package.54 The simulation time step is 0.25 fs. Figure 1c shows a representative scheme for calculating the heat conductance down from 8 AuNP leaves to 1 AuNP root through a level 3 PE C50 tree. The simulation models are relaxed for more than 2 ns under the canonical ensemble (NVT) at 300 K using Langevin thermostats. The tree polymers in these systems are unstretched; see schemes in Figure 1a,b. Previously, we had found that unstretched polymers have converged heat flux values,39,41,42 and thus they are sufficient to reveal the tree structure effect on heat transfer. After the relaxation step, the nonequilibrium MD simulation method is applied to calculate the heat flux through the tree networks. For comparison with previously reported systems,39,40 we set the heat source on 8 AuNP leaves at 340 K and the heat sink on the 1 AuNP root at 295 K, ΔT = 45 K. The heat conductance is known to vary dramatically as the polymer is stretched.39,41,42 Consequently, we chose to employ unstretched polymers because they are closer to free polymers in a polymer–nanoparticle composite material under typical experimental conditions. Doing so is equivalent to a setup maintaining constant heat fluxes constant at the thermostats, as had earlier been used in treating the linear case.48 The cumulative heat energy gains at the leaves and loss at the root are recorded by the dissipating Langevin thermostats; see Figure 1d. At steady state, the sum of the values on 8 leaves gives the total energy gain, which should balance the total energy loss at the root. Assuming linearity, we fit the last 2 ns of each productive run (more than 5 ns) to find the heating rate at both the heat source (Pin) and the heat sink (Pout) AuNPs, which gives 2 resulting data points for each productive run.

We simulate more than 5–8 independent productive runs for each model. As a result, the heating rates (P in pW) are calculated from averaging more than 10 data points. The resulting heat conductance is calculated using G = P/ΔT. We calculate the upward heat conductance in the same way by setting the 8 leaves AuNPs at 295 K and 1 AuNP root at 340 K; see scheme in Figure S3 in the SI. The difference between the red profile (sum 1–8 leaves) and the blue profile (1 root) seen in the downward direction reported in Figure 1 but not seen in the upward direction reported in Figure S3 of the SI arises from the relative heat capacities of the root and leaf nodes in the two cases. Specifically, in the upward heat flow case, the temperature of the 8 AuNP leaves must first increase to the target 340 K, and the 40 K increase causes more accumulative heat than required for the 1 AuNP root to reach the target 295 K with 5 K in temperature difference. That is, there is a net cumulative change in temperature of (40 K × 8) – (5 K × 1), which is 315 K. Similarly, in the backward heat flow case, all 8 AuNP leaves must decrease to the target 295 K with a 5 K difference, while the 1 AuNP root increases by 40 K to 340 K. That is, there is a net cumulative change in temperature of (−5 K × 8) + (40 K × 1) which is 0 K. As these are cumulative heat gains, the difference remains across the entire simulation and we see that the rate curves are appropriately parallel because of the equivalence between the forward and backward heat flows at steady state.

At the nanoscale, heat transfer is not diffusive, the temperature drop along the polymer chain is not linear, and the cross-sectional area for the tree structure is ambiguous; as a result, we use G to compare thermal transport properties.

Acknowledgments

This work has been partially supported by the National Science Foundation (NSF) through Grant No. CHE 2102455. The computing resources necessary for this work were performed in part on Expanse at the San Diego Supercomputing Center through allocation CTS090079 provided by Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support ACCESS, which is supported by National Science Foundation (NSF) Grants #2138259, #2138286, #2138307, #2137603, and #2138296. Additional computing resources were provided by the Advanced Research Computing at Hopkins (ARCH) high-performance computing (HPC) facilities supported by the NSF MRI Grant (OAC-1920103).

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.3c02367.

  • Detailed information about simulation model force field parameters, detailed molecular dynamics (MD) simulation force field parameters, gold nanoparticle (AuNP), PE, and PPP tree polymer models, positions of the randomly selected 20 carbons for calculating vibrational density of state (VDOS), extended VDOS results, heat conductance results, and PE and PPP cut tree networks (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz3c02367_si_001.pdf (3.4MB, pdf)

References

  1. Gomez-Marin A. Drawing the Mind, One Neuron at a Time. Science 2022, 375, 1237–1237. 10.1126/science.abo0190. [DOI] [PubMed] [Google Scholar]
  2. Ramón y Cajal S.Texture of the Nervous System of Man and the Vertebrates; Springer-Verlag Wien: New York, 1999; Vol. 1. [Google Scholar]
  3. Razek S. A.; Ayoub A. B.; Swillam M. A. One Step Fabrication of Highly Absorptive and Surface Enhanced Raman Scattering (SERS) Silver Nano-Trees on Silicon Substrate. Sci. Rep. 2019, 9, 1–8. 10.1038/s41598-019-49896-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Vendamani V. S.; Rao S. V. S. N.; Pathak A. P.; Soma V. R. Robust and Cost-Effective Silver Dendritic Nanostructures for SERS-Based Trace Detection of RDX and Ammonium Nitrate. RSC Adv. 2020, 10, 44747–44755. 10.1039/D0RA08834J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Li Z.; Kang W.; Zhao H.; Hu M.; Ju J.; Deng N.; Cheng B. Fabrication of a Polyvinylidene Fluoride Tree-Like Nanofiber Web for Ultra High Performance Air Filtration. RSC Adv. 2016, 6, 91243–91249. 10.1039/C6RA17097H. [DOI] [Google Scholar]
  6. Lu T.; Cui J.; Qu Q.; Wang Y.; Zhang J.; Xiong R.; Ma W.; Huang C. Multistructured Electrospun Nanofibers for Air Filtration: a Review. ACS Appl. Mater. Interfaces 2021, 13, 23293–23313. 10.1021/acsami.1c06520. [DOI] [PubMed] [Google Scholar]
  7. Jing D.; He L.; Wang X. Optimization Analysis of Fractal Tree-Like Microchannel Metwork for Electroviscous Flow to Realize Minimum Hydraulic Resistance. Int. J. Heat Mass Transfer 2018, 125, 749–755. 10.1016/j.ijheatmasstransfer.2018.04.115. [DOI] [Google Scholar]
  8. Li Z.; Liu Y.; Yan J.; Wang K.; Xie B.; Hu Y.; Kang W.; Cheng B. Electrospun Polyvinylidene Fluoride/Fluorinated Acrylate Copolymer Tree-Like Nanofiber Membrane with High Flux and Salt Rejection Ratio for Direct Contact Membrane Distillation. Desalination 2019, 466, 68–76. 10.1016/j.desal.2019.05.005. [DOI] [Google Scholar]
  9. Zhu Q.; Yang D.; Liu H.; Sun X.; Chen C.; Bi J.; Liu J.; Wu H.; Han B. Hollow Metal-Organic-Framework-Mediated in situ Architecture of Copper Dendrites for Enhanced CO2 Electroreduction. Angew. Chem., Int. Ed. 2020, 59, 8896–8901. 10.1002/anie.202001216. [DOI] [PubMed] [Google Scholar]
  10. Shen Y.; Han Q.; Hu J.; Gao W.; Wang L.; Yang L.; Gao C.; Shen Q.; Wu C.; Wang X.; Zhou X.; Zhou Y.; Zou Z. Artificial Trees for Artificial Photosynthesis: Construction of Dendrite-Structured α-Fe2O3/g-C3N4 Z-scheme System for Efficient CO2 Reduction into Solar Fuels. ACS Appl. Energy Mater. 2020, 3, 6561–6572. 10.1021/acsaem.0c00750. [DOI] [Google Scholar]
  11. Bejan A. Constructal-Theory Network of Conducting Paths for Cooling a Heat Generating Volume. Int. J. Heat Mass Transfer 1997, 40, 799–816. 10.1016/0017-9310(96)00175-5. [DOI] [Google Scholar]
  12. Bejan A.; Errera M. R. Deterministic Tree Networks for Fluid Flow: Geometry for Minimal Flow Resistance Between a Volume and One Point. Fractals 1997, 5, 685–695. 10.1142/S0218348X97000553. [DOI] [Google Scholar]
  13. Neagu M.; Bejan A. Constructal-Theory Tree Networks of “Constant” Thermal Resistance. J. Appl. Phys. 1999, 86, 1136–1144. 10.1063/1.370855. [DOI] [Google Scholar]
  14. Neagu M.; Bejan A. Three-Dimensional Tree Constructs of “Constant” Thermal Resistance. J. Appl. Phys. 1999, 86, 7107–7115. 10.1063/1.371799. [DOI] [Google Scholar]
  15. Gosselin L.; Bejan A. Constructal Heat Trees at Micro and Nanoscales. J. Appl. Phys. 2004, 96, 5852–5859. 10.1063/1.1782278. [DOI] [Google Scholar]
  16. Bejan A.; Lorente S. Constructal Theory of Generation of Configuration in Nature and Engineering. J. Appl. Phys. 2006, 100, 041301. 10.1063/1.2221896. [DOI] [Google Scholar]
  17. Chen Y.; Cheng P. Heat Transfer and Pressure Drop in Fractal Tree-Like Microchannel Nets. Int. J. Heat Mass Transfer 2002, 45, 2643–2648. 10.1016/S0017-9310(02)00013-3. [DOI] [Google Scholar]
  18. Yu B.; Li B. Fractal-Like Tree Networks Reducing the Thermal Conductivity. Phys. Rev. E 2006, 73, 066302. 10.1103/PhysRevE.73.066302. [DOI] [PubMed] [Google Scholar]
  19. Xu P.; Yu B. The Scaling Laws of Transport Properties for Fractal-Like Tree Networks. J. Appl. Phys. 2006, 100, 104906. 10.1063/1.2392935. [DOI] [Google Scholar]
  20. Chen G.Nanoscale Energy Transport and Conversion: A Parallel Treatment of Electrons, Molecules, Phonons, and Photons; Oxford University Press: New York, 2005. [Google Scholar]
  21. Bathe M.; Hernandez R.; Komiyama T.; Machiraju R.; Neogi S. Autonomous Computing Materials. ACS Nano 2021, 15, 3586–3592. 10.1021/acsnano.0c09556. [DOI] [PubMed] [Google Scholar]
  22. Wei X.; Zhao Y.; Zhuang Y.; Hernandez R. Building Blocks for Autonomous Computing Materials: Dimers, Trimers and Tetramers. J. Chem. Phys. 2021, 155, 154704. 10.1063/5.0064988. [DOI] [PubMed] [Google Scholar]
  23. Wei X.; Zhao Y.; Zhuang Y.; Hernandez R. Engineered Nanoparticle Network Models for Autonomous Computing. J. Chem. Phys. 2021, 154, 214702. 10.1063/5.0048898. [DOI] [PubMed] [Google Scholar]
  24. Tomalia D. A. Birth of a New Macromolecular Architecture: Dendrimers as Quantized Building Blocks for Nanoscale Synthetic Polymer Chemistry. Prog. Polym. Sci. 2005, 30, 294–324. 10.1016/j.progpolymsci.2005.01.007. [DOI] [Google Scholar]
  25. Svenson S.; Tomalia D. A. Dendrimers in Biomedical Applications-Reflections on the Field. Adv. Drug Delivery Rev. 2012, 64, 102–115. 10.1016/j.addr.2012.09.030. [DOI] [PubMed] [Google Scholar]
  26. Kaup R.; ten Hove J. B.; Velders A. H. Dendroids, Discrete Covalently Cross-Linked Dendrimer Superstructures. ACS Nano 2021, 15, 1666–1674. 10.1021/acsnano.0c09322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Evans C. W.; Ho D.; Marlow J. B.; King J. J.; Hee C.; Wong L. N.; Atkin R.; Smith N. M.; Warr G. G.; Norret M.; Iyer K. S. Intracellular Communication between Synthetic Macromolecules. J. Am. Chem. Soc. 2022, 144, 14112–14120. 10.1021/jacs.2c02793. [DOI] [PubMed] [Google Scholar]
  28. Huang Z.; Zhao J.; Wang Z.; Meng F.; Ding K.; Pan X.; Zhou N.; Li X.; Zhang Z.; Zhu X. Combining Orthogonal Chain-End Deprotections and Thiol-Maleimide Michael Coupling: Engineering Discrete Oligomers by an Iterative Growth Strategy. Angew. Chem., Int. Ed. 2017, 56, 13612–13617. 10.1002/anie.201706522. [DOI] [PubMed] [Google Scholar]
  29. Huang Z.; Shi Q.; Guo J.; Meng F.; Zhang Y.; Lu Y.; Qian Z.; Li X.; Zhou N.; Zhang Z.; Zhu X. Binary Tree-Inspired Digital Dendrimer. Nat. Commun. 2019, 10, 1918. 10.1038/s41467-019-09957-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Wei X.; Zhang T.; Luo T. Thermal Energy Transport Across Hard-Soft Interfaces. ACS Energy Lett. 2017, 2, 2283–2292. 10.1021/acsenergylett.7b00570. [DOI] [Google Scholar]
  31. Wei X.; Zhang T.; Luo T. Molecular Fin Effect from Heterogeneous Self-Assembled Monolayer Enhances Thermal Conductance Across Hard-Soft Interfaces. ACS Appl. Mater. Interfaces 2017, 9, 33740–33748. 10.1021/acsami.7b07169. [DOI] [PubMed] [Google Scholar]
  32. Wei X.; Wang Z.; Tian Z.; Luo T. Thermal Transport in Polymers: A Review. J. Heat Transfer 2021, 143, 072101. 10.1115/1.4050557. [DOI] [Google Scholar]
  33. Wei X.; Zhang T.; Luo T. Chain Conformation-Dependent Thermal Conductivity of Amorphous Polymer Blends: The Impact of Inter- and Intra-Chain Interactions. Phys. Chem. Chem. Phys. 2016, 18, 32146–32154. 10.1039/C6CP06643G. [DOI] [PubMed] [Google Scholar]
  34. Wei X.; Luo T. Chain Length Effect on Thermal Transport in Amorphous Polymers and a Structure-Thermal Conductivity Relation. Phys. Chem. Chem. Phys. 2019, 21, 15523–15530. 10.1039/C9CP02397F. [DOI] [PubMed] [Google Scholar]
  35. Subramanyan H.; Zhang W.; He J.; Kim K.; Li X.; Liu J. Role of Angular Bending Freedom in Regulating Thermal Transport in Polymers. J. Appl. Phys. 2019, 125, 095104. 10.1063/1.5086176. [DOI] [Google Scholar]
  36. Zhou J.; Xi Q.; He J.; Xu X.; Nakayama T.; Wang Y.; Liu J. Thermal Resistance Network Model for Heat Conduction of Amorphous Polymers. Phys. Rev. Materials 2020, 4, 015601. 10.1103/PhysRevMaterials.4.015601. [DOI] [Google Scholar]
  37. Liu J.; Alhashme M.; Yang R. Thermal Transport Across Carbon Nanotubes Connected by Molecular Linkers. Carbon 2012, 50, 1063–1070. 10.1016/j.carbon.2011.10.014. [DOI] [Google Scholar]
  38. Zhong J.; Xi Q.; He J.; Liu J.; Zhou J. Thermal Percolation and Electrical Insulation in Composite Materials with Partially Metallic coated fillers. Appl. Phys. Lett. 2021, 119, 211602. 10.1063/5.0067875. [DOI] [Google Scholar]
  39. Wei X.; Harazinska E.; Zhao Y.; Zhuang Y.; Hernandez R. Thermal Transport Through Polymer Linked Gold Nanoparticles. J. Phys. Chem. C 2022, 126, 18511–18519. 10.1021/acs.jpcc.2c05816. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Cui L.; Hur S.; Akbar Z. A.; Klöckner J. C.; Jeong W.; Pauly F.; Jang S.-Y.; Reddy P.; Meyhofer E. Thermal Conductance of Single-Molecule Junctions. Nature 2019, 572, 628–633. 10.1038/s41586-019-1420-z. [DOI] [PubMed] [Google Scholar]
  41. Dinpajooh M.; Nitzan A. Heat Conduction in Polymer Chains with Controlled End-to-End Distance. J. Chem. Phys. 2020, 153, 164903. 10.1063/5.0023085. [DOI] [PubMed] [Google Scholar]
  42. Zhang T.; Luo T. Morphology-Influenced Thermal Conductivity of Polyethylene Single Chains and Crystalline Fibers. J. Appl. Phys. 2012, 112, 094304. 10.1063/1.4759293. [DOI] [Google Scholar]
  43. Allen P. B.; Feldman J. L.; Fabian J.; Wooten F. Diffusons, Locons and Propagons: Character of Atomie Vibrations in Amorphous Si. Philos. Mag., B 1999, 79, 1715–1731. 10.1080/13642819908223054. [DOI] [Google Scholar]
  44. Seyf H. R.; Henry A. A Method for Distinguishing Between Propagons, Diffusions, and Locons. J. Appl. Phys. 2016, 120, 025101. 10.1063/1.4955420. [DOI] [Google Scholar]
  45. Ma H.; Tian Z. Significantly High Thermal Rectification in An Asymmetric Polymer Molecule Driven by Diffusive Versus Ballistic Transport. Nano Lett. 2018, 18, 43–48. 10.1021/acs.nanolett.7b02867. [DOI] [PubMed] [Google Scholar]
  46. Rubtsov I. V.; Burin A. L. Ballistic and Diffusive Vibrational Energy Transport in Molecules. J. Chem. Phys. 2019, 150, 020901. 10.1063/1.5055670. [DOI] [PubMed] [Google Scholar]
  47. Mackin R. T.; Leong T. X.; Rubtsova N. I.; Burin A. L.; Rubtsov I. V. Low-Temperature Vibrational Energy Transport via PEG Chains. J. Phys. Chem. Lett. 2020, 11, 4578–4583. 10.1021/acs.jpclett.0c01273. [DOI] [PubMed] [Google Scholar]
  48. Liu J.; Yang R. Length-Dependent Thermal Conductivity of Single Extended Polymer Chains. Phys. Rev. B 2012, 86, 104307. 10.1103/PhysRevB.86.104307. [DOI] [Google Scholar]
  49. Dassault System̀es BIOVIA Materials Studio Software, version 8; 2014.
  50. Heinz H.; Vaia R. A.; Farmer B. L.; Naik R. R. Accurate Simulation of Surfaces and Interfaces of Face-Centered Cubic Metals Using 12–6 and 9–6 Lennard-Jones Potentials. J. Phys. Chem. C 2008, 112, 17281–17290. 10.1021/jp801931d. [DOI] [Google Scholar]
  51. Jorgensen W. L.; Maxwell D. S.; Tirado-Rives J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. 10.1021/ja9621760. [DOI] [Google Scholar]
  52. Kaminski G. A.; Friesner R. A.; Tirado-Rives J.; Jorgensen W. L. Evaluation and Reparameterization of the OPLS-AA Force Field for Proteins via Comparison with Accurate Quantum Chemical Calculations on Peptides. J. Phys. Chem. B 2001, 105, 6474–6487. 10.1021/jp003919d. [DOI] [Google Scholar]
  53. Ahn Y.; Saha J. K.; Schatz G. C.; Jang J. Molecular Dynamics Study of the Formation of a Self-Assembled Monolayer on Gold. J. Phys. Chem. C 2011, 115, 10668–10674. 10.1021/jp200447k. [DOI] [Google Scholar]
  54. Plimpton S. J. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz3c02367_si_001.pdf (3.4MB, pdf)

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES