Measuring and modeling forces generated by microtubules

Abstract

Tubulins are essential proteins, which are conserved across all eukaryotic species. They polymerize to form microtubules, cytoskeletal components of paramount importance for cellular mechanics. The microtubules combine an extraordinarily high flexural rigidity and a non-equilibrium behavior, manifested in their intermittent assembly and disassembly. These chemically fueled dynamics allow microtubules to generate significant pushing and pulling forces at their ends to reposition intracellular organelles, remodel membranes, bear compressive forces, and transport chromosomes during cell division. In this article, we review classical and recent studies, which have allowed the quantification of microtubule-generated forces. The measurements, to which we owe most of the quantitative information about microtubule forces, were carried out in biochemically reconstituted systems in vitro. We also discuss how mathematical and computational modeling has contributed to the interpretations of these results and shaped our understanding of the mechanisms of force production by tubulin polymerization and depolymerization.

Introduction

Eukaryotic cytoskeletons are highly dynamic structures, which not only mechanically support cells, but also impart to them an ability to change shape and reorganize their interior in response to internal or external signals (Pegoraro et al. 2017). Microtubules are key components of the cytoskeleton (Olmsted and Borisy 1973). They are hollow cylinders made of αβ-tubulin dimers. Owing to their structure, microtubules have remarkable flexural rigidity (Gittes et al. 1993). When reinforced by a surrounding elastic cytoskeleton, they can withstand significant compressive loads in cells (Stamenović et al. 2002; Brangwynne et al. 2006). Recent work demonstrates that they may also act as compression sensors (Li et al. 2023). However, as microtubules are not just static beams, but rather dynamic polymers, they may do more than just bearing and sensing compression; they can actively generate force. When microtubules assemble, they can convert the free energy of their polymerization into pushing work. The associated forces have been implicated in the positioning of a cell’s nucleus in yeast and fly oocytes (Fig. 1a) (Tran et al. 2001; Daga et al. 2006; Zhao et al. 2012), and pronuclear migration in worm embryos (De Simone et al. 2018), albeit some cases of nuclear centering are mediated by the pulling action of cortical dynein (Laan et al. 2012).

Fig. 1.

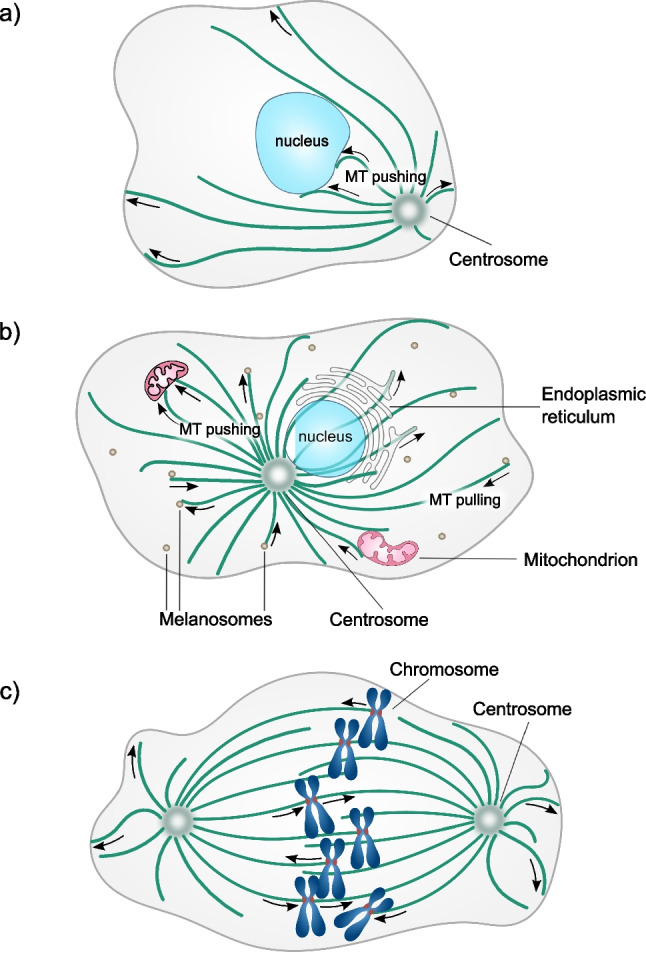
Examples of microtubule-generated forces in cells. a Positioning of the nucleus by microtubule pushing forces in the drosophila oocytes. b Positioning and remodeling membranous organelles by microtubule pushing and pulling forces. c Transport of chromosomes by microtubule pulling-pushing forces during mitosis

Microtubule pushing forces also contribute to the centering of mitotic spindles in yeast (Tolić-Nørrelykke et al. 2005; Tolić-Nørrelykke et al. 2004) and perhaps in worm embryos (Garzon-Coral et al. 2016). Moreover, forces developed by growing microtubules change the architecture of membranous organelles (Fig. 1b), such as endoplasmic reticulum (Waterman-Storer et al. 1995; Waterman-Storer and Salmon 1998; Grigoriev et al. 2008; Wang et al. 2013; Guo et al. 2018; Rodríguez-García et al. 2020) and mitochondria in yeast (Yaffe et al. 2003; Kanfer et al. 2017).

Intriguingly, shortening microtubules perform mechanical work by coupling their disassembling ends with a motion of intracellular cargoes. Probably the most remarkable example of this is the microtubule-driven segregation of chromosomes in mitosis (Fig. 1c) (Grishchuk and McIntosh 2006; Tanaka et al. 2007). Other known examples include microtubule-dependent motion of melanophores (Lomakin et al. 2011; Lomakin et al. 2009), pulling tubes from endoplasmic reticulum (Waterman-Storer et al. 1995; Waterman-Storer and Salmon 1998; Grigoriev et al. 2008; Wang et al. 2013; Guo et al. 2018; Rodríguez-García et al. 2020) and mitochondria (Yaffe et al. 2003; Kanfer et al. 2017) by shortening microtubule ends.

Excellent comprehensive reviews about forces, generated by both growing and shortening microtubules, were written by pioneers of the field (Dogterom et al. 2005; Grishchuk et al. 2012; Vleugel et al. 2016). Here, we briefly summarize previously collected data and models and overview the most recent progress on the measurements and the simulations of the microtubule-generated forces.

Microtubule structure, thermodynamic cycle, and force generation

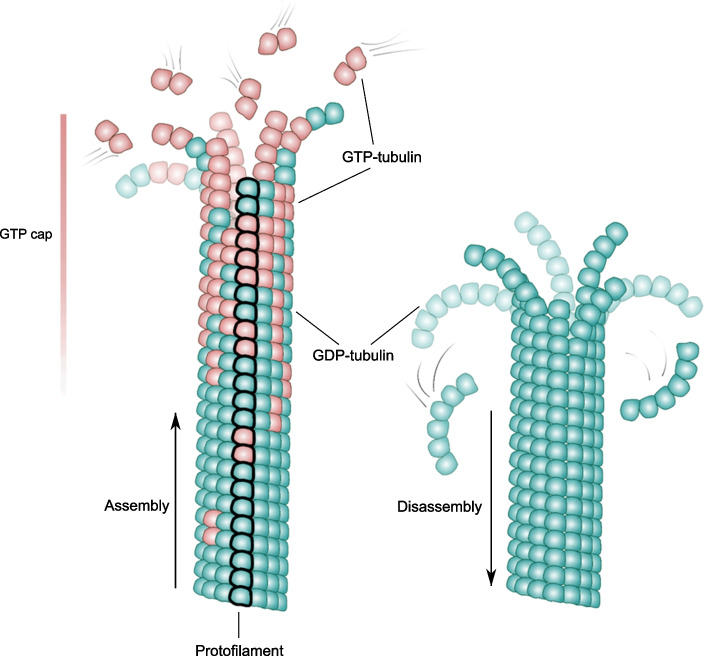
The microtubule wall is built from tubulin dimers organized in a helical lattice, usually comprising 13 linear chains of longitudinally bound tubulin dimers, termed protofilaments (Fig. 2). In this arrangement, each tubulin subunit contacts at least four neighbors: two lateral and two longitudinal ones. The only tubulin subunits with fewer contacts are those exposed at the microtubule ends, where new tubulin dimers can associate from the solution. In the cytoplasm, the tubulin dimer concentration has been measured to be up to 24 μM (Gard and Kirschner 1987). Several small molecules are important for tubulin’s ability to polymerize: guanosine triphosphate (GTP) and guanosine diphosphate (GDP), whose cytoplasmic concentrations are 100–200 μM and 10–20 μM, respectively (Traut 1994), as well as magnesium and phosphate ions, whose concentrations are ~ 15–25 mM and 1 mM, respectively (Romani and Scarpa 1992; Traut 1994). Under these conditions, the majority of free tubulin dimers are associated with the GTP molecules and magnesium ions, so they tend to polymerize; conversely, tubulins associated with GDP, the product of GTP hydrolysis, tend to disassemble. Upon incorporation of Mg-GTP-tubulins into microtubule lattice, the hydrolysis rate of tubulin-bound GTP increases by two orders of magnitude, because longitudinally attached tubulin dimers lower the barrier of this reaction (Nogales et al. 1998; Beckett and Voth 2023). Therefore, the majority of tubulin-associated GTP molecules become hydrolyzed soon after their incorporation into the microtubule (Carlier and Pantaloni 1981). A terminal microtubule region, containing freshly associated tubulins, whose GTP molecules have not yet experienced hydrolysis, forms a stabilizing cap at the growing microtubule end (Fig. 2) (Carlier and Pantaloni 1981; Duellberg et al. 2016). This “GTP cap” protects the microtubule from the transition from assembly to disassembly (Hyman et al. 1992). Although there are multiple lines of evidence supporting of the existence of the GTP cap, its size and the stabilizing mechanism remain debated (reviewed in Bowne-Anderson et al. (2013); Gudimchuk and McIntosh (2021)). When the GTP cap is lost due to stochastic hydrolysis or loosening due to asynchronous elongation of protofilaments (Gardner et al. 2011; Coombes et al. 2013; Alexandrova et al. 2022), a transition to shortening, termed a catastrophe, takes place (Farmer and Zanic 2023). The opposite transition from shortening to growth, termed a rescue, is thought to occur when the GTP cap is regained.

Fig. 2.

Microtubule structure and dynamics. Schematics of an assembling and a disassembling microtubule. GTP-tubulins are shown in red; GDP-tubulins are shown in green. One of the 13 protofilaments is highlighted in bold to illustrate how tubulin dimers are stacked longitudinally into linear strands. The GTP cap with a fuzzy lower boundary is indicated by the scale bar at the left

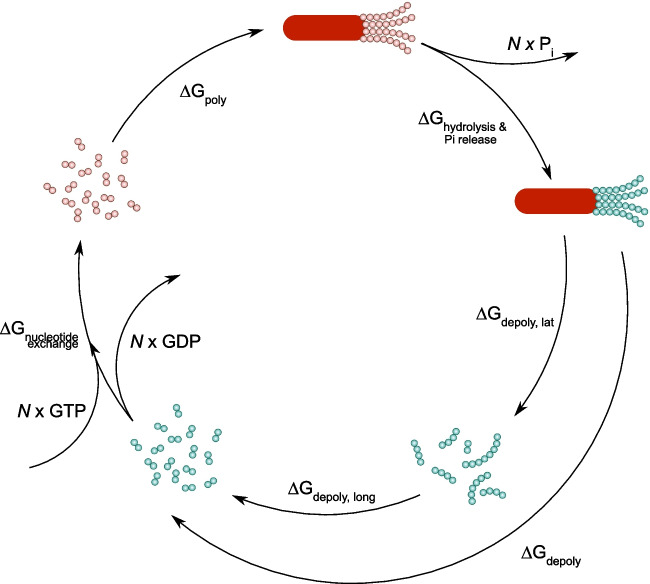
Thus, microtubule dynamics is a non-equilibrium process that is fueled by the energy of GTP hydrolysis. We illustrate this point in Fig. 3 considering a cycle of microtubule polymerization from a nucleating seed followed by complete depolymerization to the seed.

Fig. 3.

Thermodynamic cycle of microtubule polymerization and depolymerization. Nucleating seed is shown as a red oval. GTP-tubulins are shown as red circles; GDP-tubulins are shown as green circles

The main stages of that cycle are (1) microtubule polymerization from GTP-tubulins; (2) GTP hydrolysis in the microtubule lattice, followed by phosphate release; (3) depolymerization of GDP-microtubule lattice into GDP-tubulin oligomers; (4) longitudinal breakage of the GDP oligomers; and finally (5) nucleotide exchange, i.e., release of GDP molecules and binding of GTP molecules to the tubulin dimers. It is clear, that N GTP molecules are converted into N GDP molecules and N inorganic phosphates as a result of the cycle. The free energy change in the system, which equals the energy of hydrolysis of N GTP molecules, is distributed among the stages of the cycle (Desai and Mitchison 1997):

$$\mathrm{\Delta }{G}_{\mathit{GTP}}=\mathrm{\Delta }{G}_{\mathit{poly}}+\mathrm{\Delta }{G}_{hydrolysis,Pirelease}+\mathrm{\Delta }{G}_{\mathit{depoly}}+\mathrm{\Delta }{G}_{nucleotideexchange}$$ 1

where ΔG_poly is the energy of GTP-tubulin polymerization; ∆G_{hydr. , Pi release} is the energy of GTP hydrolysis and phosphate release from the lattice; ∆G_depoly is the energy of GDP-lattice disassembly; ∆G_{nucl. exchange} is the energy of exchange of GDP for GTP in free tubulin dimers. Equation (1) here is written per one molecule of GTP. This equation imposes important thermodynamic limits on the magnitudes of forces that can be developed by growing and shortening microtubules.

The maximal force, generated during microtubule polymerization, can be estimated assuming that the entire free energy ΔG_poly, driving this process, is used to perform mechanical work over the distance d, corresponding to an increment of microtubule length per addition of one tubulin dimer (Hill 1987; Dogterom and Yurke 1997):

$$F={\Delta G}_{\mathit{poly}}/d=RTln\left(\frac{c}{c_{\mathit{cr}}}\right)/d$$ 2

where c is the tubulin concentration in solution, c_cr is the critical concentration of microtubule assembly, R is the universal gas constant, T is the absolute temperature, and d =8 nm/13 is a ratio of the tubulin dimer length and the number of protofilaments in the microtubule. c_cr has been estimated to be 1–3 μM (Wieczorek et al. 2015). Thus, from Eq. (2), it follows that at a tubulin concentration of 20 μM, the maximal thermodynamically possible force a growing microtubule can generate is ~35 pN.

Analogously, the maximal force generated by microtubule depolymerization can be estimated assuming that the entire energy ∆G_depoly is converted into mechanical work over the distance d:

$$F=\mathrm{\Delta }{G}_{\mathit{depoly}}/d$$ 3

The energy of GDP-lattice depolymerization, ∆G_depoly, can be calculated from Eq. (1), as described by Desai and Mitchison (1997). Despite about three decades since the estimates were first published, no significant clarifications have been presented in the literature, so we reproduce the numbers as follows. The total energy of GTP hydrolysis in the cells is about −12.5 kcal/mol, ${\Delta G}_{\mathit{poly}}=RTln\left(\frac{c}{c_{\mathit{cr}}}\right)=-3$ kcal/mol; the free energy of the nucleotide exchange is ∆G_{nucl. exchange} =  − 2 kcal/mol; the free energy of GTP hydrolysis and phosphate release from the lattice has been estimated to be about −2.5 kcal/mol. Hence, ∆G_depoly is about −5 kcal/mol. The corresponding force would be ~60 pN per microtubule.

Forces generated by growing microtubules

Measuring pushing forces developed by growing microtubules

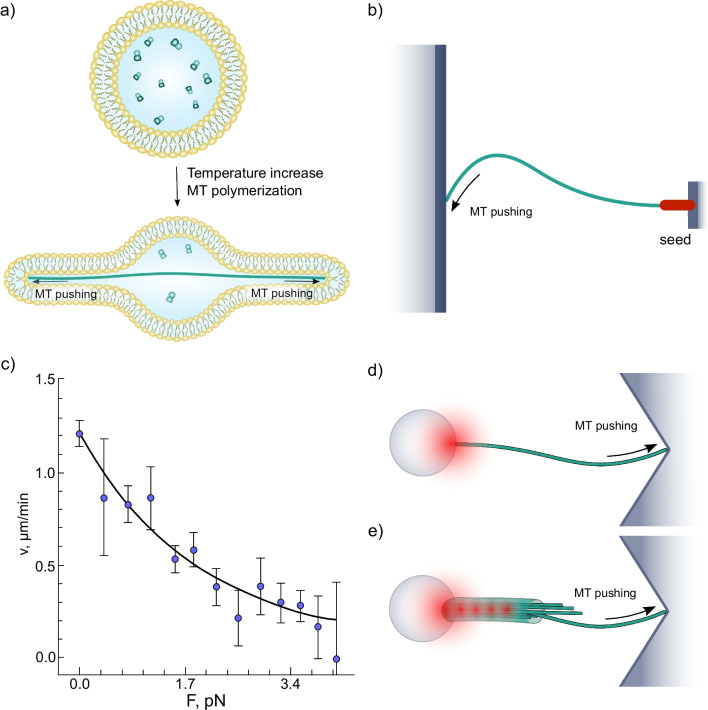
The first clear experimental demonstration of force production by polymerizing tubulin in vitro was provided by Hotani, who formed liposomes that contained soluble tubulin, then induced polymerization. As the polymer length exceeded the diameter of the liposome, the membrane was deformed, demonstrating force development (Fig. 4a) (Hotani and Miyamoto 1990; Kaneko et al. 1998). Further insights came from observations of elastic deformations of microtubules polymerizing against a rigid barrier (Fig. 4b) (Dogterom and Yurke 1997). Following Gittes et al. (1996), Dogterom and Yurke (1997) regarded buckling microtubules as elastic rods with a given bending stiffness and fixed boundary conditions at the ends. Using this approach, they determined the buckling forces and derived the first force-velocity curve of growing microtubules (Dogterom and Yurke 1997) (Fig. 4c). At 20 μM tubulin, microtubule elongation was detectable up to forces at least as high as 4 pN.

Fig. 4.

Reconstitution and quantification of microtubule pushing in vitro. a Deformation of a liposome by pushing forces generated by tubulin polymerization. b Microtubule, growing from a coverslip-immobilized nucleating seed and pushing into a microfabricated barrier. c Force-velocity curve of a growing microtubule. The black line is an exponential fit proposed by Dogterom and Yurke (1997). d Microbead attached to the minus end of the microtubule is trapped in laser tweezers, while the plus end of the microtubule is pushing into a corner-shaped microfabricated barrier. e Axoneme, trapped into a “keyhole”-shaped laser tweezers, is oriented in such a way that dynamic microtubules, nucleated from the axoneme, push against the corner-shaped microfabricated barrier

In another series of studies, tubulin polymerization force was quantified with a laser trapping approach (Kerssemakers et al. 2006; Schek et al. 2007; Laan et al. 2008). Although by that time, laser trapping was already a well-developed and widely used method to measure forces of various molecular motors (Svoboda and Block 1994a; Simmons et al. 1996), it took several novel technical advances to adapt the technique for assessing the forces produced by the growing microtubules. Schek and Hunt (2005) developed a corner-shaped microstructure with an overhanging edge (Fig. 4d), which helped fix the growing end in the direction tangential to the vector of microtubule assembly. Kerssemakers et al. (2006) came up with an idea of using a keyhole-shaped trap (a combination of a single point trap and a line trap) to capture and orient axonemes, serving as a microtubule nucleator (Fig. 4e). These studies have estimated the maximal pushing force to be at least 2.5 pN. The real value may be even larger for a single microtubule at close-to-physiological tubulin concentrations. Schek et al. (2007) who investigated microtubule growth in a feedback-controlled constant force regime, found somewhat less steep dependence of microtubule growth rate on the compressive force than Laan et al. (2008) although the measurements from both groups reported forces that were overall consistent with the estimates from earlier buckling-based experiments.

Modeling pushing forces developed by growing microtubules

The in vitro observations have documented the magnitudes of pushing forces, which are considerably lower than allowed by thermodynamics (Eq. 2), suggesting that the efficiency of energy transformation in this process is fairly modest. Mathematical and computational modeling was used to clarify the origin of this deviation and quantitatively describe microtubule assembly under load.

In the most general case, the rate of microtubule growth under a load F can be expressed as:

$$v(F)=d\left(k_{\mathit{on}},(F),*,c,-,k_{\mathit{off}},(F)\right)$$ 4

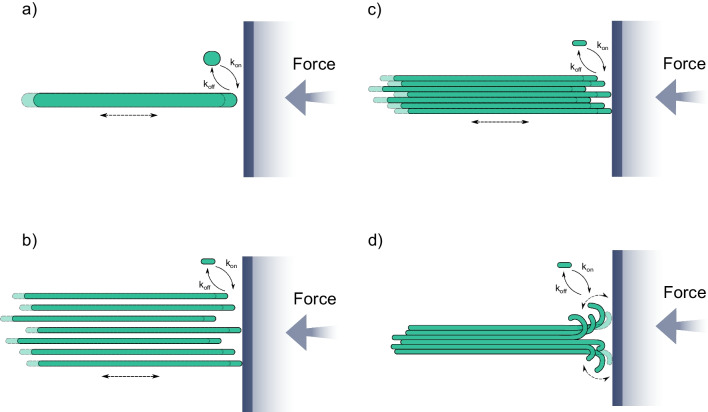
where d = 8 nm/13 is the increment of microtubule length per tubulin dimer addition; k_on(F), k_off(F) are the force-dependent tubulin on- and off-rate constants. When this equation was applied to fit experimental force-velocity data, it was found that k_off  was not dependent on force (Dogterom and Yurke 1997; Janson and Dogterom 2004). Hence, a growing microtubule can be described as a Brownian ratchet (Peskin et al. 1993; Dogterom and Yurke 1997). This mechanism implies that filament elongation can occur when thermal fluctuations separate the end of the microtubule from the barrier to accommodate the attachment of a new tubulin subunit (Fig. 5a). An analogous theory was shown applicable for the description of force production by actin polymers growing against a barrier (Peskin et al. 1993; Mogilner and Oster 1996).

Fig. 5.

Models of pushing force development by a growing microtubule. a Single filament. b Multiple non-interacting protofilaments. c Multiple laterally interacting protofilaments. d Multiple flexible, laterally interacting, curved protofilaments

Interestingly, when the dependence of microtubule growth velocity on opposing load was fitted with Eq. (4) (Fig. 4c), the steepness of the fit was found higher than a theoretical prediction, obtained assuming that all microtubule protofilaments equally shared the load (Dogterom and Yurke 1997). Analytical and Monte Carlo multi-protofilament extensions of the Brownian ratchet model have lifted the assumption of equal load sharing among the protofilaments (Mogilner and Oster 1999; van Doorn et al. 2000). Treatment of a microtubule as an ensemble of 13 independently growing ratchets pointed to what the authors called a “subsidy” effect, where a subset of protofilaments could be involved in pushing the barrier, while others were responsible for microtubule elongation (Fig. 5b). Mogilner and Oster (1999) originally deduced a sublinear scaling of the stalling force with the number of protofilaments, but a later study (van Doorn et al. 2000) using the same model argued that the force should be proportional to the number of pushing protofilaments. An elegant way to verify the latter prediction has been recently found by reconstituting pushing by bacterial microtubules, which are composed of only 4–5 protofilaments (Amini et al. 2023). Consistent with linear scaling, the stall force was about threefold lower than with a eukaryotic microtubule, 1.6 pN.

Thus, the generalized multi-protofilament Brownian ratchet models can quantitatively describe pushing force generation (Mogilner and Oster 1999; van Doorn et al. 2000). However, to consider this phenomenon in the bigger picture of microtubule dynamics, the force generation needs to be derived from molecular parameters of tubulin-tubulin interactions. Several models, considering microtubules at the level of dimers, have successfully accomplished that task (VanBuren et al. 2002; Stukalin and Kolomeisky 2004; Schek and Hunt 2005; Son et al. 2005) (Fig. 5c). All of these studies, however, made an explicit or implicit assumption that microtubules elongate with straight protofilaments at their ends. This assumption has been recently debated in the field (reviewed in Gudimchuk and McIntosh (2021)). Specifically, currently, two other views of microtubule elongation are also discussed: assembly with sheet-like ends (Chrétien et al. 1995) and assembly with flared ends (McIntosh et al. 2018). Our group has recently constructed and analyzed a flared end model for microtubule growth, based on a Brownian dynamics approach (Fig. 5d). The thermally driven straightening of curved protofilaments in the simulation allows the formation of lateral bonds, which support microtubule elongation under a range of pushing loads (Gudimchuk et al. 2020). Despite a distinct morphology of the growing tip in this simulation, we found that the microtubule behavior under compressive load is still reminiscent of the Brownian ratchet. This is explained by the fact that at low loads, it is not the protofilament straightening rate but rather the tubulin on-rate that limits elongation speed. Under high forces, the lengths of curved protofilaments decrease, similar to low tubulin concentrations, and the microtubule ends become almost blunt, behaving like a classical Brownian ratchet. As a result, the simulations predict a close-to-exponential decay of velocity under load, in good agreement with experimental data.

Measuring and modeling pulling forces developed by growing microtubules

Pulling by assembling tubulin polymers is a comparatively under-studied modality of microtubule force generation. The tips of growing microtubules can associate with various cellular cargoes through adaptor proteins and exert forces that drag the cargoes along with their growing ends (Waterman-Storer et al. 1995; Waterman-Storer and Salmon 1998; Grigoriev et al. 2008; Wang et al. 2013; Yaffe et al. 2003; Kanfer et al. 2017). Through in vitro experiments, this kind of pulling has been demonstrated to be capable of membrane remodeling, likely to be important for endoplasmic reticulum tubulation in vivo (Rodríguez-García et al. 2020); linking actin filaments to the growing microtubule ends (Alkemade et al. 2022); and the formation of parallel microtubule bundles, like the ones that contribute to both spindle assembly and cell polarization (Molodtsov et al. 2016). All reported examples of pulling forces by growing microtubule tips in vitro rely on end-binding (EB) proteins, which recognize the ends of growing microtubules, forming a comet-like distribution. The EB-comet serves as a platform for binding various scaffolds through EB-interacting cross-linkers. Using optical trapping (Fig. 6a), Rodríguez-García et al. (2020) and Alkemade et al. (2022) quantified the magnitude of forces, associated with this process, concluding that they fall in the subpiconewton range from 0.1 to 0.5 pN. Molodtsov et al. (2016) estimated the pulling forces indirectly. They first demonstrated that coupling of kinesin-14 with growing microtubules was enough to make this minus end–directed motor step “backward,” moving it toward the plus microtubule end. In a separate experiment, they used laser trapping to assess the magnitude of the plus end–directed load, which was sufficient for this effect, concluding that growing microtubule could pull kinesin-14 with at least 0.25 pN force.

Fig. 6.

Pulling forces by growing microtubule. a Schematic of pulling force measurement using optical trapping. EB-proteins form a comet-like distribution, shown in orange. The microbead is coated with adaptor proteins (TipAct, MTLS), which can interact with EB-proteins. b Schematic of the pulling force measurement using a DNA spring. c Generalized schematic of a stochastic model to describe motion of a scaffold with the growing end of the microtubule

Recently, a novel approach based on calibrated DNA origami springs was put forward as an alternative to optical trapping for measuring micromolecule-generated forces (Iwaki et al. 2016). Maleki et al. (2022) used that method to quantify such forces. The authors attached one end of their DNA spring to the coverslip surface, while the other end was linked to the multimerized scaffold, binding EB-proteins that were interacting with a growing microtubule (Fig. 6b). The extension of the spring was assessed by fluorescence, using labels along the entire DNA length, or/and by monitoring the displacement of a bright fluorescent label at the microtubule-proximal end of the spring. Quantification of dynein-generated forces by this method was consistent with previous measurements using optical trapping. Advantages of DNA spring force measurements include (i) the low cost (no need to use a sophisticated laser tweezers setup); (ii) the lack of necessity to use large microbeads as protein handles, thereby eliminating any significant leverage effect; and (iii) the compatibility of the method with single-molecule fluorescence to quantify the number of coupler molecules interacting with the microtubule tip.

Stochastic computational simulations were employed to gain insights into the mechanism of microtubule pulling by growing microtubules. By considering a 1D model of a scaffold with multiple cross-linkers, which could associate with and dissociate from the EB-comet at the growing tip and diffuse along the microtubule (Fig. 6c), it was possible to reproduce the pulling, and qualitatively describe the forces in the systems of actin-microtubule and membrane-microtubule interactions (Alkemade et al. 2022; Rodríguez-García et al. 2020). The mechanism of microtubule tip tracking in this case can be described as biased diffusion: the motion of the scaffold, pulled by the growing tip, is fueled by thermal fluctuations. The scaffold’s diffusion under force is not completely random, but rather favored in the direction of the EB-comet motion, because the scaffold can bind to the EB-comet region more strongly than to the rest of the microtubule lattice.

Forces generated by shortening microtubules

Measurements of pulling forces generated by microtubule disassembly

In the seminal work by Koshland et al. (1988), microtubules depolymerizing in vitro have been shown to stick by their plus ends to kinetochores of isolated chromosomes, a result consistent with microtubules playing a role in chromosome-to-pole motion. However, any forces developed during this depolymerization were not assessed. A clear demonstration that shortening microtubules can pull was obtained when isolated chromosomes were attached to MTs growing from the basal bodies of lysed Tetrahymena. Microtubule depolymerization pulled chromosomes against a flow of buffer, even when soluble nucleotide triphosphate concentrations were subnanomolar, far below the K_m for any known motor enzyme (Coue et al. 1991). Further experiments showed that both minus and plus end–directed motor-coated microbeads could also do so in vitro (Lombillo et al. 1995). It thereby became clear that shortening MTs could pull, but a key question was, how hard?

A pioneering collaborative study from the McIntosh and Ataullakhanov laboratories used pure brain tubulin to grow labile microtubules from seeds attached to coverslips then stabilized with a photo-labile cap. Laser tweezers were used to attach a microbead coated with streptavidin to the biotinylated microtubule wall (Grishchuk et al. 2005) (Fig. 7a, b). The cap was removed with a burst of light, and the bead position was monitored with a quadrant photodetector. As the end of the shortening microtubule came past the bead, bead displacement demonstrated the generation of force. The displacement was interpreted as a result of a power stroke, coming from one or a few protofilaments, as they splayed out from the microtubule lattice and adopted a curved conformation. The force signal was below 0.5 pN, but the geometry of the assay suggested that a significant leverage should exist, because the radius of the microbead created a lever arm much longer than that of the protofilament(s). Therefore, the actual force generated by the protofilament(s) was likely significantly higher than that measured at the center of the trap. If the leverage were ~10×, as it was suggested by Grishchuk and colleagues, then the protofilament(s) could produce about as much force as a single kinesin motor (Svoboda and Block 1994b). The presence of the leverage was supported by observations that beads with different radii produced different forces; force magnitude was inversely proportional to bead radius (Grishchuk et al. 2008b).

Fig. 7.

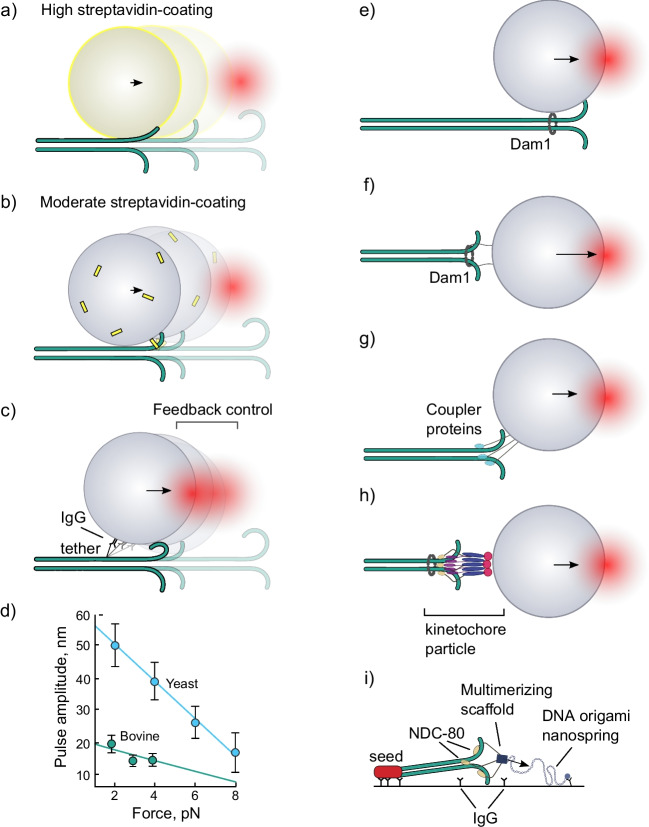
Measurements of forces from splaying protofilaments of depolymerizing microtubules. Two interpretations of the experiments of Grishchuk et al. (2005): a in the high-streptavidin-coating case, the bead radius is effectively increased by the size of streptavidin (shown as yellow shell). The protofilaments stick to the streptavidin as they touch it; b in the moderate streptavidin-coating case, the bead is attached to the microtubule via a single or a few streptavidin molecules; the bead pivots around the anchor point as the protofilament(s) push on it during depolymerization. The schematic is drawn not to scale. c “Lateral push” interpretation of experiments of Driver et al. (2017) and Murray et al. (2022). The schematic is drawn not to scale. d Bead displacement amplitude vs. force graph for yeast (blue) and bovine tubulin (green). Data for 1 mM magnesium concentration are from Driver et al. (2017) and Murray et al. (2022). Lines are linear fits. Panels e–h show schematics of the assays for measurements of depolymerizing microtubule force with different coupling proteins and geometries: e the microbead is laterally attached to the microtubule through the Dam1 ring complex (Asbury et al. 2006; Franck et al. 2007; Grishchuk et al. 2008a); f the microbead is end-on attached to the microtubule tip via Dam1-ring on fibrillar tethers (Volkov et al. 2013); g the microbead is coupled to the microtubule via non-circular couplers, such as NDC80 complex, CENP-F, Ska1, TOG-domain polymerase, etc. (McIntosh et al. 2010; Volkov et al. 2018; Schwietert et al. 2022; Polley et al. 2023; Huis in’t Veld et al. 2019; Schmidt et al. 2012; Trushko et al. 2013; Volkov et al. 2015). The bead is intentionally depicted in between the lateral and the end-on attachment, because actual the geometry of attachment is rarely established with certainty; h the microbead is coupled to the microtubule via a yeast kinetochore particle (Akiyoshi et al. 2010; Miller et al. 2016); i schematic of the DNA spring assay for measuring force (Maleki et al. 2022)

Asbury, Rice, and colleagues have re-designed this experiment by tethering the bead to the microtubule through an antibody to the 6HIS tag genetically fused to the unstructured 30-amino-acid-long C-terminus of yeast β-tubulin (Driver et al. 2017) (Fig. 7c). This tether was intended to give more control over the attachment of the bead to the microtubule. The number of tethers per bead is small and the rotation of the bead is less affected by the properties of the linkage. In this experiment, the most likely force development scenario is a lateral push by one or several curling protofilaments, which leads to the pivoting of the bead, resulting in a detectable displacement of its center along the microtubule. Depending on the size of the microbead, forces as high as 8–16 pN were directly measured in the center of the trap, and the corresponding calculated force at the surface of the bead was reported to be up to ~2-fold higher because of the leverage. Another technical advancement, the feedback-controlled constant force regime, has allowed that team of researchers to explore the displacement amplitude vs. applied load (Fig. 7d). The Y-intercept of this graph corresponds to the maximal displacement amplitude of the bead in the assay. The displacement amplitude appeared to be linearly dependent on the force, pointing to an elastic response of the protofilaments to load. Therefore, the mechanical work output W of the assay was calculated as:

$$W={\int }_0^{\mathit{Fstall}}xdF$$ 5

where F is the applied constant load; x is the corresponding displacement amplitude.

The estimated energy output of the assay was about ~300 pN·nm (~43 kcal/mol) for yeast tubulin; the value was not dependent on the bead size, in contrast to the force, measured in the optical trap. The authors estimated the maximal number of the tubulin dimers, involved in a power stroke, to be about 16, and hence the work output per dimer to be at least 19 pN·nm. Recently, the same experiment was repeated with yeast tubulin–decorated microbeads. Yeast tubulins incorporated into microtubules, polymerized from bovine brain tubulin, allowing the study of predominantly mammalian microtubules with the same assay (Murray et al. 2022). Surprisingly, the measured force was lower, and the work output about threefold smaller with mammalian tubulin compared to the yeast tubulin (Fig. 7d). The authors proposed that the origin of this difference could be related to stronger longitudinal bonds of the yeast tubulin, leading to longer protofilament curls at the ends of yeast microtubules. This interpretation is in line with the observation that increased magnesium concentration in solution leads to a higher force and work output of the assay, as magnesium is known to increase the rate of microtubule shortening and the length of protofilaments curls during this process (Tran et al. 1997).

Discovery of the ability of the yeast heterodecamer kinetochore protein complex Dam1c, aka DASH, to form a ring around a microtubule provided a powerful tool with which to measure forces developed by microtubule dynamics in a more natural setting, one in which force could be collected from all the protofilaments of a depolymerizing microtubule (Miranda et al. 2005; Westermann et al. 2006). The force signal, obtained in such experiments, was several-fold higher compared to experiments with microspheres laterally bound to microtubules via biotin-streptavidin linkage (Grishchuk et al. 2005), as expected for the situation when more protofilaments are involved in force generation (Grishchuk et al. 2008a) (Fig. 7e). The Dam1 complex could support coupling with microtubule forces during both assembly and disassembly, under assisting and opposing forces (Asbury et al. 2006; Westermann et al. 2006; Franck et al. 2007). Using the Dam1 ring as a tool has allowed investigators to explore the impact of assay geometry on the magnitude of the measured force. Achieving an end-on attachment of the microbead to the microtubule was essential for measuring the force without a leverage effect. It is in that configuration that microtubules are thought to develop forces upon proper attachment to kinetochores during cell division (McIntosh et al. 2012). Re-orientation of the ring from the lateral to the end-on position was facilitated in vitro by using ~100-nm-long engineered recombinant linkers (Fig. 7f) (Volkov et al. 2013). When such linkers between the Dam1 subunits and the microbead were used, it was possible to directly measure forces over 30 pN from a single, end-on attached depolymerizing microtubule.

Besides the yeast Dam1 complex, several other ways of coupling beads to microtubules have been explored using optical trapping approach (Fig. 7g, h), including proteins from kinetochores, such as NDC80 complex (McIntosh et al. 2010; Volkov et al. 2018; Schwietert et al. 2022; Polley et al. 2023) and/or the Ska complex (Huis in’t Veld et al. 2019; Schmidt et al. 2012), TOG-domain containing polymerases (Trushko et al. 2013), CENP-F (Volkov et al. 2015), and reconstituted or purified yeast kinetochore assemblies (Akiyoshi et al. 2010; Miller et al. 2016; Hamilton et al. 2020). Maleki et al. (2022) used DNA springs linked to NDC80 complex trimers to measure the forces, generated by depolymerizing microtubules. Expectedly, the magnitude of force was dependent on the number of molecules involved, and reached up to 10 pN for complexes as large as ~two NDC80 complex trimers.

The forces measured in these experiments depended on the geometry of the assays, temperature, buffer conditions, and the type and number of the coupler molecules involved in the force transduction. Interestingly, although the kinetochore particles championed in tests of the duration of coupling, remaining attached for many minutes even under load, their measured forces (up to 11 pN) were not the highest among published reports, which might reflect some differences in the experimental assays that were used. It is also conceivable that in the presence of soluble tubulin, microtubules may not develop the highest forces because the mechanical load promotes their rescue before stall. We speculate that depolymerization factors, like MCAK, may, in principle, act to counteract this possibility in order to maximize the force production and processivity of motion with the shortening microtubule end (Oguchi et al. 2011). It is of course possible that microtubules and their couplers were not designed by nature to generate the maximal forces in cells; other parameters of these structures, such as the persistence of their attachment to each other or some aspects of their regulation, may be more crucial. We emphasized the magnitudes of forces in this section because they imply some limits on the mechanism of their generation, as will be discussed below.

Modeling pulling forces generated by microtubule disassembly

Mathematical and computational modeling of microtubule dynamics has provided deep insights into the basic physics of microtubule polymerization and depolymerization. The models, which operate with molecular and energetic parameters of tubulin-tubulin interactions to describe such characteristics of microtubule behavior as the growth and shortening rates, catastrophe and rescue frequencies, and sometimes other features of tubulin polymers, can also be used to provide an independent estimate of the free energy of microtubule depolymerization, ∆G_depoly, besides the data presented in “Microtubule structure, thermodynamic cycle, and force generation.” Table 1 summarizes the reported differences in free energy between tubulins in the GTP and GDP states, used by different models of microtubule dynamics. The corresponding forces in the table are estimated using Eq. (3).

Table 1.

Estimates of the microtubule disassembly energy and maximal forces, based on the difference of the tubulin-free energy in the GTP and GDP states. $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{lat}}^{T\to D}$, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{long}}^{T\to D}$, and $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{total}}^{T\to D}$ are the nucleotide-dependent energy differences of the lateral bonds, longitudinal bonds, and their totals, respectively

Study	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{lat}}^{T\to D}$, kcal/mol	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{long}}^{T\to D}$, kcal/mol	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{total}}^{T\to D}$, kcal/mol	Fmax, pN
VanBuren et al. (2002)	1.25 to 1.5	0	1.25 to 1.5	14 to 17
VanBuren et al. (2005)	2.2 to 2.5	0	2.2 to 2.5	25 to 28
Margolin et al. (2012)	1.1	4.2	5.3	60
Coombes et al. (2013)	2.5	0	2.5	28
Zakharov et al. (2015)	0	0	3.6	41
Castle et al. (2017)	2.2	0	2.2	25
Schaedel et al. (2019)	1.1	2.3	3.4	38
Gudimchuk et al. (2020)	3.3	0	3.3	37
Alexandrova et al. (2022)	2.3	0.2	2.5	28

As one can see from this table, the majority of estimates of the maximal forces based on models of microtubule dynamics exceed the experimentally obtained values, described in the previous section of this review. This seems reasonable, because no molecular process is 100% efficient. The efficiency of force generation, however, should depend on the architecture of the coupling device, which is used for converting the free energy of tubulin depolymerization into mechanical work. A number of computational models have attempted to describe forces of microtubule disassembly, implicitly or explicitly considering some specific coupler designs. The general difficulty with this approach is that establishing the architecture of the coupler device and the molecular details of its interaction with a microtubule is a hard problem on its own. Therefore, only three main coupler devices have been considered.

Before any structural information about kinetochore coupler proteins was available, Hill (1987) suggested the first hypothetical model of a coupler, a “sleeve,” tightly surrounding the microtubule tip and providing multiple binding sites to the tubulins at the kinetochore. When the microtubule shortened, the sleeve lost some contact with the microtubule end, so thermally driven displacements back to the sleeve were more favorable than the motions in the opposite direction. This model was interpreted by Joglekar and Hunt (2002), and by Molodtsov et al. (2005b) to estimate the maximal force as the slope in the energy vs. coordinate graph, which resulted in estimates of 15 and 9 pN, respectively.

Molodtsov et al. (2005b) developed a molecular-mechanical model of the microtubule end, which was applied to predict the efficiency of a theoretical ring-shaped coupler (Molodtsov et al. 2005b). A microtubule was modeled as a set of interacting spheres, with empirical lateral and longitudinal energy potentials. The lateral bond energies were described with an energy function having an activation barrier, selected to reproduce the temperature dependence of microtubule disassembly rate. The bending energy of the longitudinal bond was described with a quadratic potential of a high enough stiffness to store about 7.3 kcal/mol energy when a tubulin interdimer interface was straightened. Using that model, it was found that each bending protofilament could push on a circular ring of an optimal diameter with the force of about 5 pN, converting almost all the bending energy into mechanical work. Excitingly, in the very same year, a yeast kinetochore-associated protein, the Dam1 complex, was discovered to be a circular complex. Its measured diameter was close to the predicted optimum (Miranda et al. 2005; Westermann et al. 2005), suggesting that this protein complex could be a very efficient force transducer.

Understandably, the majority of further theoretical studies have focused on the couplers with a ring-shaped design. A significantly smaller interaction interface between this type of coupler and the microtubule, compared to the interface between the sleeve and the microtubule, excludes the possibility of analogous coupling principles in these two cases. If so, what makes the Dam1 ring track the depolymerizing end? Two main hypotheses have been put forward in the literature. One group has proposed that the Dam1 complex is weakly bound to the microtubule wall, so it is free to diffuse randomly over the microtubule surface, being restricted only by the flaring protofilaments at the depolymerizing end (Asbury et al. 2006; Franck et al. 2007; Ramey et al. 2011). This mode of motion has been referred to as “biased diffusion.” Another group of authors has argued that the binding of the Dam1 ring to the microtubule wall is strong, so the Dam1 ring can only move when physically pushed by the curling protofilaments (Efremov et al. 2007; Grishchuk et al. 2008a). This wobbling mode of motion was called the “forced walk.” It needs to be clarified that these hypotheses are maybe two extremes of the same continuous relationship: the stronger the binding of a coupler to the microtubule end, the more effect it would have on microtubule shortening, and the more efficiency of force transduction it may achieve.

To distinguish between these two models, the McIntosh and Ataullakhanov team extended their previously developed model of a microtubule (Molodtsov et al. 2005a) by introducing an explicit and detailed realization of the Dam1 ring and applying a dynamic Metropolis Monte Carlo approach for simulating the motion of the Dam1 ring with the disassembling microtubule end (Efremov et al. 2007; Grishchuk et al. 2008a). The Dam1 ring was proposed to interact with the microtubule lattice via flexible linkers, whose tubulin-binding strength was varied to examine its effect on the load-velocity curve for depolymerizing microtubules. This analysis revealed that the strength of Dam1-tubulin interactions was an important determinant of the ring’s ability for processive coupling and bearing high loads. A weakly bound ring, which would be able to move via a biased diffusion mechanism, slipped easily off the tip of the microtubule. Conversely, a strongly bound Dam1 ring, which exhibited a forced walk, could sustain forces up to 35 pN for over a second—a period, which could be measured experimentally. The binding energy of about 7.8 kcal/mol (13 kT) per Dam1 subunit was found optimal. The strong binding of Dam1 subunits to tubulins was supported by experimental in vitro evidence for rates of diffusion dropping with the degree of Dam1 oligomerization on the microtubule wall and the ability of Dam1 assemblies to slow down or even stall microtubule disassembly (Grishchuk et al. 2008b; Volkov et al. 2013).

Finally, as the circular couplers have not been found outside fungi (McIntosh et al. 2013), a fibrillar coupling geometry was also considered in the literature, although the efforts in this direction have so far been quite limited. The specific candidates for this type of coupler are the long proteins of the outer kinetochore, such as NDC80, which appears to be essentially universal, and many other proteins that may contribute to kinetochore-microtubule interactions in different species, such as dynein and CENP-E and CENP-F in vertebrates and a broad set of kinesins, which vary from cell type to cell type across phylogeny. In the study by McIntosh et al. (2008), the authors modeled a coupling device as a set of elastic fibrils, which could associate with curved protofilaments at random positions and dissociated when the peeling oligomers fell from the depolymerizing end. The microtubule was modeled previously (Efremov et al. 2007). It was shown that this type of coupling could sustain a significant opposing load, provided that the number of fibrils and their binding rates are high (k₊ > 50 s⁻¹). By comparing the morphologies of the curved protofilaments, observed at the tips of kinetochore-associated microtubule electron tomography, with the shapes of model protofilaments under variable loads, it was suggested that each protofilament of a kinetochore microtubule could be under 3–4 pN tension during mitosis (McIntosh et al. 2008). Despite the ability of this model to predict efficient coupling, it is limited in value by the assumptions that fibrils are present in high numbers and that they interact with the curved parts of the protofilaments at the microtubule tip. The only long kinetochore fibrillar protein that has been reported to have a preference for binding to curved tubulin oligomers over straight tubulin is CENP-F (Volkov et al. 2015), not NDC80 complex, which is currently thought to be the major contributor to a kinetochore’s grip on microtubules (Wimbish and DeLuca 2020). Moreover, as few as three NDC80 complexes, multimerized via a single scaffold, have been shown sufficient for tracking depolymerizing ends and force development (Volkov et al. 2018). The mechanism of this coupling remains unclear, and further modeling work be required to build a clearer picture of microtubule disassembly–driven motions of mammalian chromosomes and potentially other intracellular cargoes too.

Conclusions and outlook

In vitro measurements and computational modeling have contributed significantly to our understanding of microtubule force generation. Owing to these advances, we now have a comprehensive understanding of pushing force generation by growing microtubules in purified systems in vitro. An extensive body of current evidence speaks in favor of the Brownian ratchet mechanism of this phenomenon. The data suggest that this process is not very efficient in terms of energy usage, at least under the conditions that have so far been explored in vitro. One of the potentially exciting perspectives of this work is answering the question of whether and how microtubule-associated proteins could modulate force development in cells. One issue of particular interest in this respect may be the proteins that can affect the critical concentration for tubulin polymerization and catalyze increased rates of microtubule growth. Another is the post-translational modification of tubulin, which often acts on tubulin polymers, altering the charge distribution on their surfaces and therefore both polymer stability and the identity of other proteins with which the microtubule will interact. Microtubule pulling is a new modality of force generation by growing microtubules. Despite the low forces associated with this type of force generation, this action has already been shown important in several essential biological contexts. We expect to see new discoveries in this field in the near future.

Pulling forces by depolymerizing microtubules have been also studied extensively, despite the difficulties associated with the gaps in knowledge about the coupling devices necessary to maintain attachment to the microtubule tips and convert depolymerization energy into force. Interpretation of experimental measurements in this field has relied heavily on theoretical modeling. Furthermore, more explicit and detailed models of force measurements will be useful to gain further insights into the mechanisms of force generation and energy conversion by microtubules as molecular machines and the designs and mechanisms of molecular couplers that link microtubule disassembly with the motion of intracellular cargos.

New interesting approaches, such as DNA springs and FRET force sensors, may become helpful new options for validation and extending previous measurements of microtubule-based forces, especially in the light of continuing efforts and recent progress in the reconstitution of yeast and mammalian kinetochores in vitro (Hamilton et al. 2020; Tarasovetc et al. 2021; Torvi et al. 2022; Sissoko et al. 2023).

Funding

Analysis of in vitro studies of microtubules was supported by the Russian Science Foundation grant # 23-74-00007, https://rscf.ru/project/23-74-00007/. Analysis of mathematical and computational models was supported by the Scientific and Educational Mathematical Center “Sofia Kovalevskaya Northwestern Center for Mathematical Research” (agreement no. 075-02-2023-937, 16.02.2023).

Declarations

Ethics approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.