Estimating heritability explained by local ancestry and evaluating stratification bias in admixture mapping from summary statistics

Summary

The heritability explained by local ancestry markers in an admixed population ($h_{\gamma }^2$) provides crucial insight into the genetic architecture of a complex disease or trait. Estimation of $h_{\gamma }^2$ can be susceptible to biases due to population structure in ancestral populations. Here, we present heritability estimation from admixture mapping summary statistics (HAMSTA), an approach that uses summary statistics from admixture mapping to infer heritability explained by local ancestry while adjusting for biases due to ancestral stratification. Through extensive simulations, we demonstrate that HAMSTA $h_{\gamma }^2$ estimates are approximately unbiased and are robust to ancestral stratification compared to existing approaches. In the presence of ancestral stratification, we show a HAMSTA-derived sampling scheme provides a calibrated family-wise error rate (FWER) of ∼5% for admixture mapping, unlike existing FWER estimation approaches. We apply HAMSTA to 20 quantitative phenotypes of up to 15,988 self-reported African American individuals in the Population Architecture using Genomics and Epidemiology (PAGE) study. We observe ${\hat{h}}_{\gamma }^2$ in the 20 phenotypes range from 0.0025 to 0.033 (mean ${\hat{h}}_{\gamma }^2$ = 0.012 ± 9.2 × 10⁻⁴), which translates to ${\hat{h}}^2$ ranging from 0.062 to 0.85 (mean ${\hat{h}}^2$ = 0.30 ± 0.023). Across these phenotypes we find little evidence of inflation due to ancestral population stratification in current admixture mapping studies (mean inflation factor of 0.99 ± 0.001). Overall, HAMSTA provides a fast and powerful approach to estimate genome-wide heritability and evaluate biases in test statistics of admixture mapping studies.

This study reports a method to estimate heritability explained by local ancestry using admixture mapping summary statistics and evaluates potential biases in admixture mapping. The method provides a strategy for summary statistic-based heritability estimation in admixed populations and controlling false positives due to ancestral population stratification in admixture mapping studies.

Introduction

Admixture mapping (AM) aims to identify genomic regions associated with a disease or quantitative trait in recently admixed populations^{1,2,3,4,5,6,7} by leveraging the differences in allele frequencies between local ancestries.⁸ AM provides a powerful approach to complement genome-wide association studies (GWASs) in admixed populations due to local ancestry information better tagging uncommon or poorly imputed causal variants⁵ and spanning larger genomic regions, thus reducing the multiple testing burden,⁹ enabling discoveries with relatively smaller sample sizes.^3,10 Similarly, recent work¹¹ demonstrated that local ancestry information, which is summarized by heritability explained by local ancestry $h_{\gamma }^2$, can be leveraged to estimate narrow-sense heritability h² in admixed populations, unlike the genotype-based lower bounds (i.e., $h_g^2$). Multiple works have shown that population structure can bias association tests and estimates of $h_g^2$.^12,13 However, it is less understood how similar demographic phenomena bias AM and $h_{\gamma }^2$ inference in admixed populations.

Admixed populations are typically modeled as a mixture of multiple continental ancestries (e.g., African, European, or Native American) with finer-scale structure within ancestral populations left unmodeled. Nevertheless, human populations are often structured across both space and time. For example, European ancestry individuals can be modeled as a mixture of at least three ancient populations,¹⁴ and Native American ancestry components found in Latinos can also be derived across multiple subpopulations spread across Latin America.¹⁵ This unmodeled fine-scale structure could lead to potential biases in downstream association testing. Indeed, this phenomenon has been demonstrated in European populations,^16,17 and could similarly impact inference in admixed populations when it is not fully accounted for.¹⁸ When estimating ${h_g}^2$ using SNP data of large sample size, a robust approach to population stratification is to estimate h² and test statistic inflation simultaneously.¹⁹ Examples of this approach include linkage disequilibrium score regression (LDSC)¹³ and cov-LDSC.¹² While these methods are designed for SNP data, it remains unclear how applicable they are on estimating $h_{\gamma }^2$ using summary statistics from admixture mapping studies.

In this study we propose HAMSTA (heritability estimation from admixture mapping summary statistics), a likelihood-based approach to infer $h_{\gamma }^2$ from admixture mapping summary statistics. To achieve robust and efficient computation, HAMSTA transforms the correlated test statistics using a truncated singular value decomposition (tSVD) and performs maximum-likelihood inference while accounting for residual inflation due to stratification within ancestral populations. We perform extensive simulations and demonstrate that HAMSTA provides approximately unbiased estimates of $h_{\gamma }^2$ and outperforms existing approaches to detect evidence of stratification bias. We demonstrate that estimates from HAMSTA can be leveraged to efficiently compute well-calibrated family-wise error rates for admixture mapping, particularly in the presence of ancestral stratification which previous approaches do not consider.²⁰ Next, we apply HAMSTA to admixture mapping summary statistics for 20 traits from 15,988 self-identified African American individuals in the Population Architecture using Genomics and Epidemiology (PAGE) study.²¹ We find the h² estimates of 0.85 (standard error: 0.085) and 0.42 (SE: 0.086) for height and BMI, respectively. Compared with LDSC on admixture mapping summary statistics, HAMSTA offers more precise estimates for $h_{\gamma }^2$ and better quantifies the inflation in the test statistics due to unknown confounding biases. Overall, we demonstrate that HAMSTA provides a fast and powerful way to estimate genome-wide heritability that controls biases using summary statistics from admixture mapping studies.

Material and methods

Model for complex trait and ancestral stratification

We consider a two-way admixed population, with ancestral populations pop1 and pop2, the last of which is recently structured into pop2a and pop2b (Figure S1). This demographic model mimics the African and European admixture in African American and the finer-scale structure in their ancestral European population. We let α, δ, and −δ denote the population mean phenotype values of pop1, pop2a, and pop2b. We denote A_i,k as the centered and standardized local ancestry calls for individual i at marker k, such that its sample mean is zero and sample variance is 1. We denote indexing over n individuals at the k^th marker as A_.,k and index over M markers for the i^th individual as A_i,.. We define the phenotype y_iof an admixed individual i as

$$y_i=A_{i,.}\beta +{\pi }_i\alpha +d_i\delta +{ϵ}_i\text{,}$$

where β is the M × 1 vector of local ancestry effects, ${\pi }_i$ is defined as the global ancestry proportion due to pop1, $d_i={{\pi }_i}^{\left(2a\right)}-{{\pi }_i}^{\left(2b\right)}$ is the difference between the global ancestry proportions of pop2a and pop2b, and ${ϵ}_i\sim N\left(0,{\sigma }_{ϵ}^2\right)$ is residual environmental noise. Furthermore, we assume that ${\beta }_k\sim N\left(0,\frac{h_{\gamma }^2}{M}\right)$, where $h_{\gamma }^2$ is defined as the heritability explained by local ancestry.¹¹ Lastly, we define $\frac{{\alpha }^2}{n}{\pi }^{\prime }\pi$ as the phenotypic variance explained (PVE) by global ancestry and $\frac{{\delta }^2}{n}{d}^{\prime }d$ as PVE by ancestral stratification.

Test statistics for admixture mapping

We model the marginal association statistics from an admixture mapping study where only global ancestry proportions ${\pi }_i$ (and not d_i) are estimated beforehand. If the stratification term is not adjusted, the test statistics for marker k will be $Z_k={s_R}^{-1}{\left({A_{.,k}}^{\prime }P{A}_{.,k}\right)}^{-1/2}\left({A_{.,k}}^{\prime }Py\right)$, where ${s_R}^2$ is the residual variance after the global ancestry $\pi$ is projected out by matrix $P=I-\pi {\left({\pi }^{\prime }\pi \right)}^{-1}{\pi }^{\prime }$. Extending this to all M markers we have, $Z={s_R}^{-1}{D}^{-1/2}\left(A^{\prime }Py\right)$, where D is the diagonal elements of $A^{\prime }PA$. Given this and distributional assumptions regarding y, we can derive the expectation and covariance of Z as

$$E\left[Z\right]={s_R}^{-1}{D}^{-1/2}{A}^{\prime }Pd\delta$$

$$Cov\left[Z\right]={s_R}^{-2}\left[\frac{h_{\gamma }^2}{M}{D}^{-\frac{1}{2}}{\left(A^{\prime }PA\right)}^2{D}^{-\frac{1}{2}}+D^{-\frac{1}{2}}\left(A^{\prime }PA\right)D^{-\frac{1}{2}}{\sigma }_{ϵ}^2\right]\text{.}$$

The $D^{-1/2}\left(A^{\prime }PA\right)D^{-1/2}$ is local ancestry disequilibrium (LAD) matrix analogous to the LD matrix. When sample size n is large, the test statistics Z are well approximated by a multivariate normal distribution. The mean reflects the bias due to correlation between local ancestry and ancestral stratification conditional on the global ancestry. In the covariance, the first term is related to the heritability explained by local ancestry and LAD score matrix. The second term in the covariance is related to LAD matrix and nongenetic effects. In the null scenario, where $h_{\gamma }^2=0$, $\delta =0$, the distribution of Z has means of zeros and covariances simply equal to the LAD matrix.

We then use singular value decomposition (SVD) to decorrelate the association statistics. We let the SVD of $A\text{'}P=USV\text{'}$, $A\text{'}PA=U{S}^{2}U\text{'}$, and ${\left(A^{\prime }PA\right)}^2=U{S}^4{U}^{\prime }$. We define $Z^{\ast }=S^{-1}{s}_R{U}^{\prime }{D}^{1/2}Z$, which follows $Z^{\ast }\sim N\left(V^{\prime }d\delta ,\frac{h_{\gamma }^2}{M}{S}^2+I{\sigma }_{ϵ}^2\right)$, where the components are uncorrelated. Since the mean of Z^∗ reflects the bias in association statistics induced by the unknown difference in sub-continental ancestries, we then assume $V^{\prime }d\delta$ to be random and follow a normal distribution N(0, C^∗) such that $Z^{\ast }\sim N(0,\frac{h_{\gamma }^2}{M}{S}^2+(I{\sigma }_{ϵ}^2+C^{\ast }))$. The parameters $h_{\gamma }^2$ and $C={(I\sigma }_{ϵ}^2+C^{\ast })$ are the parameters to be inferred. We refer to the parameter C as “intercept” as it is analogous to LDSC intercept. To allow heterogeneous C across Z^∗, we allow C to be different every 500 elements, i.e., $C=diag\left(c_1{\cdots }_{\times 500},c_2{\cdots }_{\times 500},\cdots \right)$. Test statistics from different chromosomes are rotated separately and do not share elements in C.

Inferring ${\mathit{h}}_{\mathit{\gamma }}^{\mathbf{2}}$ and biases using HAMSTA

HAMSTA first applies $Z^{\ast }=S^{-1}{s}_R{U}^{\prime }{D}^{1/2}Z$ to obtain the rotated Z scores and then finds the estimates for $h_{\gamma }^2$ and C that maximize the likelihood given $Z^{\ast }\sim N\left(0,\frac{h_{\gamma }^2}{M}{S}^2+C\right)$. Parameters $h_{\gamma }^2$ and C were log-transformed to ensure positivity during optimization. First, we test for ancestral stratification using a likelihood ratio test between models with multiple intercepts and single intercepts in which C is a scalar shared by all elements in Z^∗. If the test is significant with p < 0.05, we determine the maximum likelihood estimates ${\hat{h}}_{\gamma }^2$ and $\hat{C}$ under the multiple intercept model. Otherwise, we find ${\hat{h}}_{\gamma }^2$ and $\hat{C}$ under the single intercept model. To test for the significance of ${\hat{h}}_{\gamma }^2$, we use a likelihood ratio test that test the hypothesis $h_{\gamma }^2=0\text{.}$ The standard errors of the estimates were determined using the jackknife method over 10 blocks.

Estimating h² from ${\mathit{h}}_{\mathit{\gamma }}^{\mathbf{2}}$

Previous work¹¹ demonstrated a relationship between narrow-sense heritability h² and $h_{\gamma }^2$ as $h_{\gamma }^2=2F_{STC}\theta \left(1-\theta \right)h^2$. The $h_{\gamma }^2$ was formulated as the variance of the expected phenotype conditioned on local ancestries, assuming only the genotypes are dependent on local ancestry. Assuming a distribution of genotypic effect size with respect to the ancestral allele frequencies, the F_STC is defined as the average genetic distance between the ancestral populations at causal loci weighted by the squared of genotypic effect sizes. At each site, the genetic distance is computed as $\frac{{\left(f_1-f_2\right)}^2}{2f\left(1-f\right)}$, where f₁, f₂, and f are the allele frequency in the ancestral populations and the admixed population. We provided h² estimates based on (1) F_STC = 0.1692 reported in the original study,¹¹ which was estimated from HapMap 3 dataset, and (2) F_STC = 0.1152 estimated in this study using a subset of African and European descent from the 1000 Genome and HGDP subset in gnomAD v.3.1,²² assuming common variants explain 90% of h². The average admixture proportion $\pi$ was observed to be 78% African ancestry.

Simulation design

To validate and assess performance of HAMSTA, we performed simulations using realistic demographic scenarios. Specifically, we simulated ancestral populations pop1 and pop2 mirroring African and European populations in the Out-of-Africa demography model.²³ We additionally introduced structure into pop2 by subdividing it into two subpopulations (denoted by pop2a and pop2b below, Figure S1). We set pop2a and pop2b to have diverged 200 generations ago with a migration rate of 10⁻³. These parameters were selected to result in a genetic differentiation similar to that within European populations ($F_{ST}\approx 0.003$) estimated from the HGDP and 1000 Genome subsets in gnomAD.²² We simulated this demography for a 250 Mb region with a uniform recombination rate of 10⁻⁸ per bp using msprime.²⁴ Using the true genealogies from simulations, we extracted the true local ancestry of each individual by tracing their lineage to each ancestral population (pop1, pop2a, or pop2b). Global ancestries were computed from local ancestry information by computing the total proportion of the 250 Mb region that is inherited from an ancestral population. We sampled 50,000 admixed individuals and 20,000 local ancestry markers according to the demography mode.

Next, we simulated phenotypes according to our phenotype model $y=A\beta +\pi \alpha +d\delta +ϵ$. Given a sparsity α, we drew the effect of a local ancestry marker ${\beta }_k$ from $N\left(0,\frac{h_{\gamma }^2}{\alpha M}\right)$ with probability α and $ϵ$ from $N\left(0,{\sigma }_{ϵ}^2\right)$. Then we set the true $h_{\gamma }^2$, PVE by global ancestry, PVE by ancestral stratification, and ${\sigma }_{ϵ}^2$ by varying the values of γ and δ. Finally, test statistics were computed using linear regression adjusting for π using PLINK 2.0.²⁵

Estimate ${\mathit{h}}_{\mathit{\gamma }}^{\mathbf{2}}$ with other approaches

To compare HAMSTA with existing methods in $h_{\gamma }^2$ estimation, we applied BOLT-REML,²⁶ GCTA,²⁷ LD score regression (LDSC),¹³ and cov-LDSC¹² to the simulated and real-world data. In GCTA, the same set of covariates included in the admixture mapping were used in $h_{\gamma }^2$ estimation. Following previous studies, we compute the genetic relatedness matrix using local ancestry in place of genotypes.¹¹ In LDSC and cov-LDSC, we define the “local ancestry linkage disequilibrium” (LAD) score for marker i as $l_i={\sum }_{j\in W}{r}_{i,j}^2$ with r being the local ancestry correlation between marker i and marker j within W, the set of markers in a given window size. In cov-LDSC, the correlation is conditioned on the global ancestry. Window sizes of 1 cM and 20 cM were used. The LAD scores were used as the regressors and weights in LDSC and cov-LDSC.

Significance threshold estimation

Specifically, to determine the significance threshold for a given admixture mapping study, we randomly generated test statistics $Z=s_R^{-1}{D}^{-1/2}USQ$, where Q is a vector of random variable sampled from $N\left(0,{\sigma }_q^2\right)$. We set ${\sigma }_q^2$ to be the maximum intercept if the test for multiple intercepts is significant, and ${\sigma }_q^2$ to be the inferred intercept if the test is not significant. We repeated the sampling procedure 2,000 times to determine the critical value as the 95% percentile of $\mathit{max}\left(Z^2\right)$. The significance threshold was determined as the tail probability of a chi-square distribution (degree of freedom = 1) at the critical value. To determine the threshold for multiple chromosomes, we estimate the threshold for each chromosome separately and then combine the thresholds by summing up the effective testing burden, i.e., $Combinedthres=0.05/\sum _{i=1}^{22}\left(0.05/thre{s}_{chromosomei}\right)$. For comparison, we also estimated the significance threshold using STEAM,²⁰ which sampled from $Z=MVN\left(0,\Sigma \right)$, where $\Sigma$ is a local ancestry correlation matrix based on genetic distance and admixture parameters. Family-wise error rates (FWERs) were computed as the percentage of times at least one significant signal is identified out of 500 null simulations.

Local ancestry inference and genome-wide mapping for admixed individuals in PAGE cohort

We obtained phenotypes and genotyping data measured on Multi-Ethnic Genotyping Array (MEGA) from the PAGE study.²¹ The complete dataset included 17,299 participants who self-identified as African American. Our analysis included 20 quantitative phenotypes: body mass index (BMI), height, waist-to-hip ratio, diastolic blood pressure, systolic blood pressure, PR interval, QRS interval, QT interval, fasting glucose, fasting insulin, C-reactive protein, mean corpuscular hemoglobin concentration, platelet count, estimated glomerular filtration rate, cigarettes per day, cups of coffee per day, high-density lipoprotein (HDL), low-density lipoprotein (LDL), triglycerides, and total cholesterol. Filters and transformations were applied, and covariates were selected according to the original PAGE analysis within the African American subset (Table S1).²¹

To infer the local ancestry, a subset of African and European genomes from the 1000 Genome and HGDP subset in gnomAD were used as reference individuals.²² After filtering out SNPs with missingness >10%, lifting over, and merging, 516,731 SNPs were used in the local ancestry inference, resulting in 101,292 local ancestry markers. The genotypes of PAGE and reference individuals were re-phased together using EAGLE,²⁸ and the ancestry probabilities were inferred as the local ancestry of the haplotype in a region using RFMIX2.²⁹ The global ancestry of an individual was computed by taking the average of all predicted local ancestries. We analyzed up to 15,988 individuals who have >5% of one of the inferred ancestries and have no missing values in the covariates in the 20 quantitative phenotypes. Admixture mapping was performed using linear regression adjusting for the study center, inferred global ancestry, and phenotype-specific covariates used in PAGE. The average estimate of $h_{\gamma }^2$ across phenotypes was calculated by weighting the estimate of each phenotype by the inverse of the squared standard error. The run time was measured on a machine with an Intel Xeon 4116 processor and 48 GB memory.

Results

HAMSTA provides unbiased estimates of ${\mathit{h}}_{\mathit{\gamma }}^{\mathbf{2}}$ under ancestral stratification

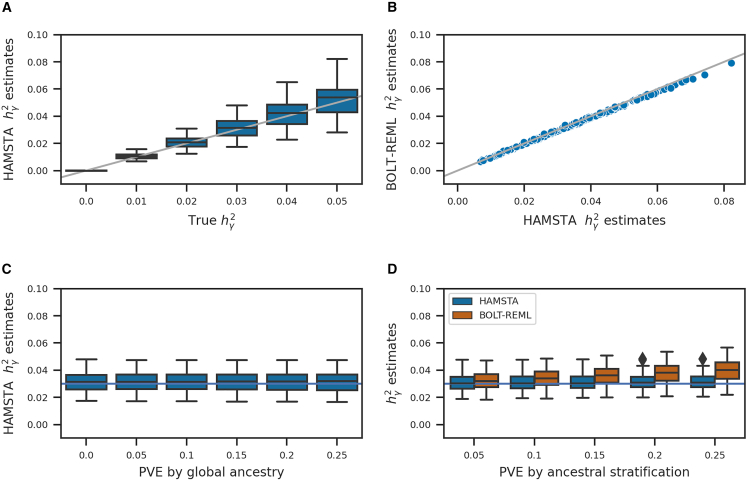
To evaluate the accuracy of $h_{\gamma }^2$ estimates under various scenarios, we performed simulation studies using local ancestry data simulated under a population demographic model that mirrors African American admixture history with an addition of recent population structure in one of the ancestral populations (see material and methods). In brief, we simulated phenotypes without stratification effects where we varied $h_{\gamma }^2$ from 0 to 0.05 (corresponding to h² from 0 to 1 according to Zaitlen et al.¹¹), which reflects $h_{\gamma }^2$ estimates reported in previous African American samples,³⁰ and performed admixture mapping to compute summary statistics. Overall, we found HAMSTA produced approximately unbiased estimates of $h_{\gamma }^2$ (Figure 1A), irrespective of the sparsity of causal markers (Figure S2). The jackknife standard errors for $h_{\gamma }^2$ were also insensitive to the choice of jackknife blocks. For example, in a simulation of $h_{\gamma }^2$ = 0.03, the average standard error was 0.00535, 0.00531, and 0.00513 when using 10, 20, and 50 blocks, respectively. We observed that the summary statistics-based estimates from HAMSTA were highly correlated with those computed from individual-level data using BOLT-REML (Figure 1B), suggesting that when stratification bias is not present, there is no loss in accuracy across data settings. Next, to compare our method with existing summary statistics-based methods, we applied LD score regression (LDSC; see material and methods) and cov-LDSC and observed both methods produced biased estimates exhibiting large standard errors (Figure S3). Importantly, we found LDSC estimates remained biased after re-estimating “LAD scores” using a larger window size of 20 cM (Figure S3). Next, we varied effect of global ancestry while fixing the $h_{\gamma }^2$ and PVE by ancestral stratification and found that HAMSTA $h_{\gamma }^2$ estimates remained unbiased (Figure 1C). Together, our results suggest that when stratification does not inflate summary statistics, HAMSTA provides unbiased estimates of $h_{\gamma }^2$ , unlike existing summary-based approaches.

Figure 1.

Simulation results from 50,000 admixed individuals and phenotypes under different levels of variance explained by local ancestry, global ancestry, and ancestral stratification

The boxplots show the range and quartiles of the estimates

(A) Results of $h_{\gamma }^2$ estimation when varying true $h_{\gamma }^2$. Phenotypic variance explained (PVE) by global ancestry and ancestral stratification were set to 0. A gray identity line is plotted.

(B) Comparison of $h_{\gamma }^2$ estimates between HAMSTA and BOLT-REML applied to simulation data when true $h_{\gamma }^2=\left\{0.01,0.02,0.03,0.05\right\}$ in (A).

(C) Results when varying the PVE by global ancestry, setting $h_{\gamma }^2=0.03$ (horizontal line) and PVE by ancestral stratification = 0.

(D) Comparison of $h_{\gamma }^2$ estimates between HAMSTA and BOLT-REML under various levels of ancestral stratification. True $h_{\gamma }^2$ were fixed at 0.03 (horizontal line). The extremes are capped at 1.5 times of the interquartile range away from the lower and upper quartiles. Estimates beyond the extremes are represented by diamonds.

Next, we sought to evaluate HAMSTA in the presence of ancestral stratifications. We determined that the $h_{\gamma }^2$ estimates in our method were more robust to the presence of unadjusted ancestral stratification (Figure 1D). In contrast, BOLT-REML, where the inference model is not aware of ancestral stratification, produced biased results and elevated variance as the PVE by ancestral stratification increases.

Further, we demonstrate that our method is still robust to other scenarios of structures in the ancestral populations (Figure S4). We explored the cases where (1) both ancestral populations are structured, (2) the proportion of ancestries from the subpopulations are unequal in the admixed population, and (3) the subpopulations are introduced to the admixture event at different times. In all the scenarios, the unbiasedness of our estimator is not affected by the ancestral stratification.

Overall, we demonstrated HAMSTA provides unbiased estimates of $h_{\gamma }^2$ under various levels of effects from local ancestry, global ancestry, and stratification in ancestral populations.

HAMSTA estimates inflation in admixture mapping statistics due to stratification

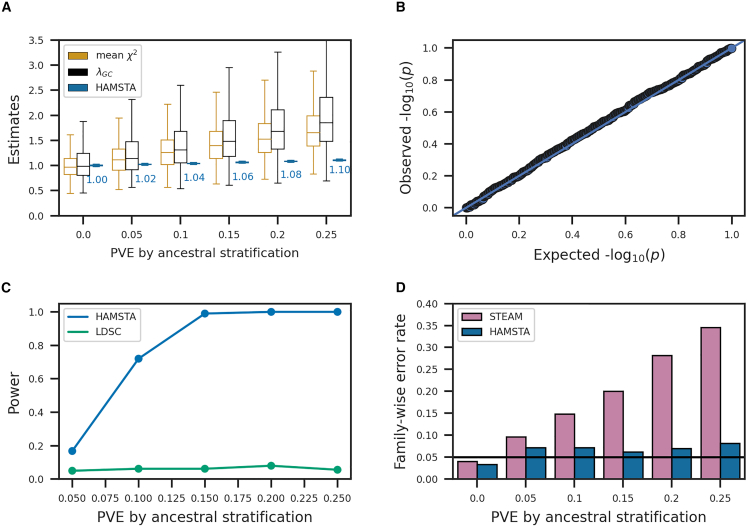
Having established the unbiasedness in $h_{\gamma }^2$ estimates, we next sought to evaluate the ability of HAMSTA to identify inflation in admixture mapping statistics due to ancestral population stratification. Specifically, intercepts estimated by HAMSTA, which signify test statistics inflation and analogous to LDSC intercepts, can be tested against the null (i.e., 1) to evaluate stratification bias. Overall, we observed HAMSTA produced estimates greater than 1 as the PVE by ancestral stratification increased (Figure 2A), demonstrating the ability of HAMSTA-inferred intercepts to capture stratification-induced inflation. Although we noted similar trends in other measures of inflation, including mean ${\chi }^2$ and genomic inflation factor ${\lambda }_{GC}$, their inability to distinguish between polygenicity and confounding prevent their use for complex disease analyses.¹³ Next, we evaluated the ability of LDSC to identify stratification in admixture mapping statistics through its intercept estimates and observed biased results with large variability (Figure S5). We observed that HAMSTA is well calibrated (Figure 2B) and significantly more powerful to detect stratification bias compared with LDSC (Figure 2C). For example, HAMSTA has 80% power when stratification explains 10% of PVE, compared with 5% power of LDSC. These relative differences in performance held when we increased the LAD score window size for LDSC (Figure S5). Overall, HAMSTA provides unbiased estimates of inflation in admixture mapping statistics due to ancestral bias and has greater power to reject its null compared to alternative approaches.

Figure 2.

Evaluating ancestral stratification by HAMSTA in 500 simulation replicates of 50,000 admixed individuals and phenotypes under ${\mathit{h}}_{\mathit{\gamma }}^{\mathbf{2}}=\mathbf{0}$ and various levels of variance explained by local ancestral stratification

(A) Boxplots of measures of test statistic inflation reflecting ancestral stratification. The average estimates of HAMSTA’s intercepts are labeled.

(B) Quantile-quantile plot of p values for the test for ancestral stratification.

(C) Power comparison between HAMSTA and LDSC in detecting ancestral stratification. The p value cutoff for each approach was determined such that the significance level = 0.05 in null simulation.

(D) Family-wise error rate before and after correcting p value cutoff in admixture mapping using the estimated intercepts.

HAMSTA improves estimation of p value thresholds to control family-wise error rate

The number of approximately independent ancestry blocks depends on the demographic history of the population being studied, so there is no universal threshold to determine genome-wide significance in admixture mapping studies. Admixture mapping often relies on permutation-based approaches to estimate the FWER, but these approaches can be computationally intractable for large datasets. Although a recently developed summary-static sampling scheme (STEAM) bypasses the need for individual-level permutations and speeds up the FWER estimation,²⁰ its assumption that there exists no inflation in the test statistics may be unmet in the presence of population structure and polygenicity.

Here, we demonstrated that inferences from HAMSTA can be leveraged to produce significance thresholds for association testing to achieve calibrated FWERs compared with STEAM. First, when PVE due to stratification is zero, we found STEAM and HAMSTA estimated similar significance thresholds (HAMSTA mean: 1.12 × 10⁻⁴; STEAM: 1.57 × 10⁻⁴), yielding comparable FWERs at ∼5% (Figure 2D), which suggests that HAMSTA-based FWER estimates do not deflate overall power despite increased model complexity. Importantly, in presence of ancestral stratification, we found that HAMSTA estimates resulted in approximately calibrated FWERs unlike STEAM, which produced a considerable number of false positive associations (Figures 2D and S6). For example, when PVE due to stratification is 0.25, HAMSTA estimates resulted in FWER of 8% compared to the FWER of 34% from STEAM. Together, these findings demonstrate that intercepts estimated by HAMSTA can be incorporated into significance threshold estimation, producing better calibrated FWERs and thereby reducing false positive findings.

Application to African American in the PAGE study

To illustrate the ability of HAMSTA to estimate $h_{\gamma }^2$ from summary data, we applied it to admixture mapping summary statistics of 20 quantitative phenotypes computed from the African American participants in PAGE study²¹ (mean n = 8,383, SD n = 3,901; see material and methods). In brief, we performed admixture mapping using 101,292 markers adjusting for the study center, global ancestry, and phenotype-specific covariates. The average genomic inflation factor ${\lambda }_{GC}$ across phenotypes is 1.53 (SD = 0.64). Next, we applied HAMSTA to generated summary statistics to infer $h_{\gamma }^2$ and evaluate potential stratification biases. To estimate h² from $h_{\gamma }^2$, we estimated the average African ancestry to be 78% and F_STC = 0.12 from the admixed individuals in PAGE and reference individuals from HGDP and 1000 Genomes.

We estimated the $h_{\gamma }^2$ ranges from 0.0025 for systolic blood pressure to 0.033 for height (mean $h_{\gamma }^2$ = 0.012; SE = 9.2 × 10⁻⁴) across the 20 phenotypes, of which 13/20 were individually significantly different from 0 (nominal p value < 0.05 in Table S2). Translating $h_{\gamma }^2$ to estimates of h², we observed the h² ranging from 0.062 for systolic blood pressure to 0.85 for height (mean h² = 0.30; SE = 0.023), of which 13/20 were individually significant. We found these results were robust to different values of F_STC (see Table S2).

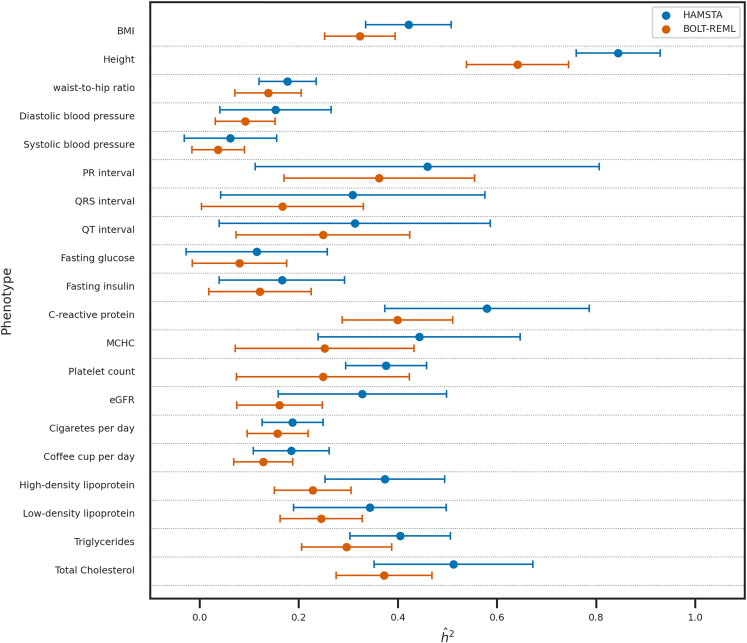
Consistent with the simulation results, HAMSTA estimates were correlated more strongly with BOLT-REML estimates (r = 0.99, Figure 3) than those computed from LDSC (r = 0.44) (Figure S7). This was largely attributable to statistical precision, with standard errors in HAMSTA estimates (range from 0.0023 to 0.014, mean = 0.0058) being slightly, but not significantly (paired t test: p = 0.051), greater than those from BOLT-REML (range from 0.0021 to 0.0076, mean = 0.0042), and noticeably lower than those computed from LDSC (range from 0.0064 to 0.021, mean = 0.012). Since 5/20 phenotypes had limited sample sizes (n < 5,000), which is known to impact the performance of BOLT,²⁶ we also estimated $h_{\gamma }^2$ via GCTA. Of the 16 estimates computed by GCTA that converged, we observed they were in general bounded by the estimates by HAMSTA and BOLT-REML (Figure S8). Overall, we find that HAMSTA estimates of $h_{\gamma }^2$ are consistent with those computed from individual-level approaches in real data, while requiring much less computation time: HAMSTA takes 1–29 min for SVD of each chromosome and 49 s for the inference, but GCTA requires 1 h to compute the relatedness matrix and 1 h for the inference step.

Figure 3.

Comparison of ${\hat{\mathit{h}}}_{\mathit{\gamma }}^{\mathbf{2}}$ -based ${\hat{\mathit{h}}}^{\mathbf{2}}$ between HAMSTA and BOLT-REML for the 20 quantitative traits in African American in PAGE

Results on 20 PAGE quantitative traits. Comparison between the estimates from HAMSTA and BOLT-REML. Each point shows the ${\hat{h}}^2$, and the lengths of the error bars represent the standard errors.

To substantiate the translated h² estimates computed from HAMSTA, we compared with previous h² estimates reported from admixed individuals¹¹ as well as those from twin studies. Overall, we found our h² estimates are significantly correlated with the previously reported $h_{\gamma }^2$-based estimates¹¹ (r = 0.84, p = 0.03). Focusing on height and BMI, HAMSTA estimated $h_{\gamma }^2$ = 0.033 (SE: 3.4 × 10⁻⁴) and $h_{\gamma }^2$ = 0.017 (3.4 × 10⁻⁴), respectively, corresponding to h² of 0.85 (0.085) and 0.42 (0.086), respectively. The estimated height h² was similar to the h² = 0.68–0.84 in twin studies,³¹ whereas the estimated BMI h² was smaller than the h² = 0.57–0.77 in twin studies³² and higher than the h² = 0.30 in an estimation from whole-genome sequence data in European ancestry populations.³³

HAMSTA-estimated intercepts suggested limited evidence for inflated summary statistics due to ancestral stratification in the admixture mapping (range from 0.97 to 1.01, average = 0.99; Table S2), with 0/20 phenotypes differing significantly from the expectation of 1. Although LDSC suggested no significant deviation of intercepts from 1 (range from 0.18 to 1.95, average = 1.07), individual intercepts varied more greatly under LDSC (mean SE = 0.34) than those computed under HAMSTA (mean SE = 5.6 × 10⁻³) (Table S2).

Since in simulation we demonstrated that the significance threshold for admixture mapping corresponding to FWER of 5% is sensitive to ancestral stratification, we estimated the thresholds based on the HAMSTA intercepts. Under no ancestral stratification (i.e., intercept = 1), HAMSTA estimated the significance threshold required to be 2.80 × 10⁻⁵, which agrees with the threshold of 2.10 × 10⁻⁵ reported by STEAM for African Americans.²⁰ Based on the estimated intercepts in HAMSTA for the 20 phenotypes, the estimated thresholds range from 2.70 × 10⁻⁵ to 3.52 × 10⁻⁵. To conclude, HAMSTA found no evidence of inflation in admixture mapping statistics and provided estimates for $h_{\gamma }^2$ and hence h² of the complex traits of African Americans in PAGE study.

Discussion

In this study, we demonstrated the use of summary statistics from admixture mapping to quantify the contribution of genetic variations to a trait. We developed a tool, HAMSTA, that unbiasedly estimates $h_{\gamma }^2$ under the various trait architectures, including in the presence of unknown population stratification in ancestral populations. Using the summary statistic-based approach, HAMSTA distinguishes the effect tagged by local ancestry on test statistics from unknown confounding biases. We also demonstrated that the estimated biases could be used to correct the significance threshold such that FWERs are better controlled. Lastly, we applied HAMSTA to real-world data, showing that it can recover the $h_{\gamma }^2$ and hence h² from admixture mapping summary statistics.

Our method addresses several limitations in existing approaches estimating $h_{\gamma }^2$. First, because of the long-range correlations between local ancestry markers, LDSC requires a large window size to capture correlations with distant effect markers. Also, regression weights may not be sufficient to solve the problem of correlated ${\chi }^2$ statistics, which could lead to inefficient estimation.³⁴ Our analysis shows that the efficiency can be improved when admixture mapping test statistics are rotated to an independent space. Second, although REML could provide an unbiased estimate, we showed in simulation that it is susceptible to ancestral stratification. Also, it is computationally expensive as the sample size increases. In real data analysis, the REML approach in GCTA failed to converge in waist-to-hip ratio, QT-interval, cigarette-per-day, and HDL. In contrast, we showed that HAMSTA would be a more robust approach to ancestral stratification and has no convergence problem in our analysis. Finally, existing methods assume uniform test statistics inflation although it has been shown that this assumption could be inaccurate.^35,36 HAMSTA relaxes this assumption by allowing multiple intercepts to represent non-uniform inflation. Overall, HAMSTA offers advantages over existing methods in the above aspects.

We are aware of several limitations of HAMSTA. First, HAMSTA provides estimates of heritability explained by local ancestries only in two-way admixtures, which may limit the use of the method in admixed populations with more than two ancestral populations. Currently, the relationship between $h_{\gamma }^2$ and h² are established only in two-way admixed populations such as African American, but models for $h_{\gamma }^2$ multi-way admixture have not yet been proposed. Incorporating the contribution of multiple ancestries in $h_{\gamma }^2$ and h² will be a possible extension in the future. Second, the standard error of HAMSTA $h_{\gamma }^2$ is larger than that from methods that use individual-level data like BOLT-REML (mean SE = 0.0058 in HAMSTA versus mean SE = 0.0042 in BOLT-REML). Nevertheless, HAMSTA $h_{\gamma }^2$ is robust to ancestral stratification, unlike BOLT-REML showing upward biases in the $h_{\gamma }^2$ estimates (Figure 1D). Third, HAMSTA models only summary statistics computed from linear regression on quantitative traits. The scope of this study is not extended to modeling binary traits. Future work can explore phenotypes under the liability-scale model and evaluate the use of summary statistics from logistic regression models. Lastly, since HAMSTA relies on an accurate LAD, factors that the LAD depends on, such as global ancestries, could potentially impact the accuracy of the estimates. These factors are required to be adjusted for when estimating the LAD.

Similar to previous summary statistic-based methods in GWASs such as LDSC, HAMSTA requires admixture mapping statistics and LAD information from individual-level local ancestry data. In LDSC or cov-LDSC, the LD scores need to be computed from an individual-level genotype data in which the LD is consistent with the study sample before proceeding with the downstream inference. Other summary-based methods such as h2-GRE³⁷ also use in-sample LD estimates before estimating heritability. Likewise, HAMSTA requires the SVD results of individual-level local ancestry data to capture the LAD information. In a cohort involving multiple phenotypes, LAD captured in the SVD results can be re-used in different phenotypes for fast and robust summary statistics analysis in admixture mapping studies.

In summary, our work opens a direction of summary statistics analysis in admixture mapping studies. Our method will facilitate studies of genetic architecture in large cohorts of admixed populations.

Data and code availability

The codes for HAMSTA are available at https://github.com/tszfungc/HAMSTA.

Published: October 23, 2023

Web resources

• BOLT-REML, https://alkesgroup.broadinstitute.org/BOLT-LMM/BOLT-LMM_manual.html

• GCTA, https://cnsgenomics.com/software/gcta/

• GNOMAD HGDP and 1KG subsets, https://gnomad.broadinstitute.org/downloads#v3-hgdp-1kg

• LDSC, https://github.com/bulik/ldsc

• MSPRIME, https://github.com/tskit-dev/msprime

• PLINK, https://www.cog-genomics.org/plink/

• RFMIX2, https://github.com/slowkoni/rfmix

• STEAM, https://github.com/kegrinde/STEAM