Power of inclusion: Enhancing polygenic prediction with admixed individuals

Summary

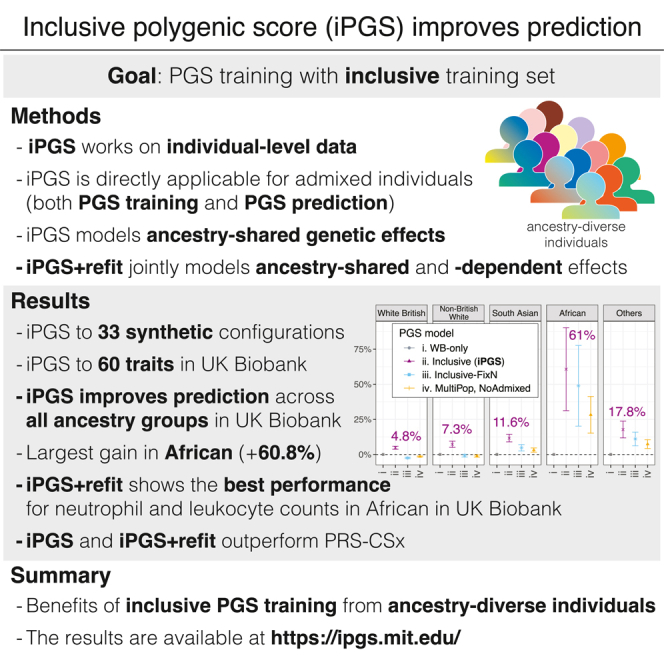
Admixed individuals offer unique opportunities for addressing limited transferability in polygenic scores (PGSs), given the substantial trans-ancestry genetic correlation in many complex traits. However, they are rarely considered in PGS training, given the challenges in representing ancestry-matched linkage-disequilibrium reference panels for admixed individuals. Here we present inclusive PGS (iPGS), which captures ancestry-shared genetic effects by finding the exact solution for penalized regression on individual-level data and is thus naturally applicable to admixed individuals. We validate our approach in a simulation study across 33 configurations with varying heritability, polygenicity, and ancestry composition in the training set. When iPGS is applied to n = 237,055 ancestry-diverse individuals in the UK Biobank, it shows the greatest improvements in Africans by 48.9% on average across 60 quantitative traits and up to 50-fold improvements for some traits (neutrophil count, R² = 0.058) over the baseline model trained on the same number of European individuals. When we allowed iPGS to use n = 284,661 individuals, we observed an average improvement of 60.8% for African, 11.6% for South Asian, 7.3% for non-British White, 4.8% for White British, and 17.8% for the other individuals. We further developed iPGS+refit to jointly model the ancestry-shared and -dependent genetic effects when heterogeneous genetic associations were present. For neutrophil count, for example, iPGS+refit showed the highest predictive performance in the African group (R² = 0.115), which exceeds the best predictive performance for the White British group (R² = 0.090 in the iPGS model), even though only 1.49% of individuals used in the iPGS training are of African ancestry. Our results indicate the power of including diverse individuals for developing more equitable PGS models.

Graphical abstract

Introduction

Polygenic scores (PGSs), used for aggregating genetic effects into the individual-level genetic liability of diseases or non-disease traits,^1,2 have attracted significant research interest as a result of the recent expansion of genotyped cohort sample sizes, increased recognition of the polygenicity of complex traits, and recent methodological innovations in PGS training. For some traits, the predictive performance indicates the potential clinical relevance of PGS.^1,2,3 However, most PGS models suffer from limited transferability across populations,⁴ despite the fact that some complex traits manifest substantial trans-ancestry genetic correlation.^5,6,7 The limited transferability is partly due to the underrepresentation of non-European individuals in genetic studies and results in delaying the realization of equitable healthcare benefits from advancements in genetic research.⁸

Several efforts are underway to improve the transferability of PGS models. On the one hand, active recruitment of non-European individuals in genetic studies along with global partnerships and capacity building are greatly increasing,⁹ but most genome-wide association study (GWAS) cohorts have not realized the diversity that proportionally represents global populations. On the other hand, the development of computational methods can complement these efforts and provide immediate benefits to individuals of diverse ancestry groups.¹⁰ Existing efforts include performing PGS modeling by prioritizing variants present in diverse populations¹¹ and cell-type-specific regulatory elements¹² and combining multiple polygenic predictors characterized for multiple ancestry groups.^13,14,15,16

Admixed individuals, whose genomes consist of haplotypes from more than one ancestry group and account for one in seven newborns in the U.S.,¹⁷ are often excluded in PGS model training given the technical limitations. Most modern PGS methods apply Bayesian multivariate regression by including GWAS summary statistics and ancestry-matched linkage disequilibrium (LD) reference panels. Although methods of applying GWAS analysis to admixed individuals exist,¹⁸ dependencies on the LD reference panels and computational complexities in representing LD for admixed individuals present challenges in the estimation of variant effect sizes in PGS modeling. However, including admixed individuals offers valuable insights into the genomic basis of common complex traits.^6,19,20 A recent study indicates that the individual-level PGS performance shows linear decay as a function of genomic distance defined as the Euclidean distance on the genotype PCA projection from the PGS training set, highlighting the importance of considering the continuum of genomic ancestry in PGS evaluation.²¹ Given the substantial trans-ancestry genetic correlation in some complex traits,^5,6 one might expect that admixed individuals also offer unique opportunities to train PGS models with improved transferability.

Here, we overcome the technical limitations and present inclusive PGS (iPGS), a PGS training strategy that considers individuals across the continuum of genetic ancestry. Applying penalized regression directly to individual-level data, iPGS captures genetic effects shared across population groups while avoiding the need for LD reference panels and is applicable to admixed individuals. We indicate the improved performance of iPGS in 33 simulation configurations and systematic application across 60 anthropometric and hematological traits in the UK Biobank. We also develop an iPGS+refit strategy to jointly model the ancestry-shared and ancestry-dependent effects and indicate its utility in improving prediction in a few hematological traits in the African population in the UK Biobank. Our work highlights the benefits of inclusive PGS training in improving predictive performance and transferability.

Material and methods

Compliance with ethical regulations and informed consent

This research has been conducted through UK Biobank Resource under application number 21942, “Integrated models of complex traits in the UK Biobank.” All participants from UK Biobank provided written informed consent (more information is available at https://www.ukbiobank.ac.uk/2018/02/gdpr/).

Synthetic genotype and phenotype data

We prepared synthetic genotype and phenotype data to investigate the behavior of iPGS. We used the recently released simulated genotypes from the INTERVENE consortium and used their HAPNEST pipeline to generate synthetic quantitative phenotypes.²² The HAPNEST pipeline is capable of generating synthetic genotypes and phenotypes for hundreds of thousands of individuals across multiple continental ancestry groups, thanks to its computational efficiency. The synthetic genotype data preserves the key statistics, such as minor-allele frequency and LD in ancestry-matched reference panels, and has lower relatedness with the reference panels. The pipeline allowed us to simulate phenotypes under the specified heritability and polygenicity.

We downloaded the HAPNEST synthetic dataset (BioStudies: S-BSST936; EMBL-EBI’s BioStudies repository, https://www.ebi.ac.uk/biostudies/studies/S-BSST936) and focused on synthetic genotype data on chromosome 22 for 168,000 individuals each in African and European ancestry groups.²² We split each ancestry group into training (n = 110,000), validation (n = 20,000), and held-out test sets (n = 38,000) without using phenotypes. We used the training set to fit models, the validation set to determine the sparsity of the models, and the held-out test sets to evaluate the predictive performance of the models. We used the same training, validation, and test sets for all tested synthetic traits.

With the phenotype simulation pipeline in HAPNEST, we generated synthetic phenotypes under three polygenicity and heritability parameters: (1) a low polygenicity of 0.01% and equal heritability of 0.1 (h²_AFR = 0.1 and h²_EUR = 0.1); (2) a higher polygenicity of 0.5% and equal heritability of 0.1 in synthetic African and synthetic European samples (h²_AFR = 0.1 and h²_EUR = 0.1); and (3) the higher polygenicity of 0.5% and different heritability between two ancestry groups (h²_AFR = 0.03 and h²_EUR = 0.1). We used the default value of the trans-ancestry genetic correlation of 1.0, assumed no covariate effects on the synthetic phenotypes, and restricted the model to sample causal variants from chromosome 22 alone.

The study population in the UK Biobank

The UK Biobank is a population-based cohort study with genomic and phenotypic datasets across about 500,000 volunteers collected across multiple sites in the United Kingdom.^23,24 We performed sample-level quality control (QC). We focused on n = 406,659 unrelated individuals with genetic data based on the following criteria^25,26,27: (1) used to compute principal components (UK Biobank data field 22020); (2) removal of sex mismatch between the sex field in the genotype dataset and phenotype sex (data field 31); (3) not reported in “outliers for heterozygosity or missing rate” (data field 22027); (4) not reported in "sex chromosome aneuploidy" (data field 22019); and (5) do not have ten or more third-degree relatives (data field 22021).

We subsequently used a combination of self-reported ethnic background (data field 21000) and genetic principal components (data field 22009) to define population groups.²⁷ In brief, we first identified self-reported European, self-reported African, and self-reported Asian individuals. We applied aberrant, a Bayesian-outlier-detection algorithm,²⁸ to the first six genotype PCs to detect outliers to refine population-group assignment.²⁴ We subsequently focused on unrelated individuals. We used the self-reported ethnic background to subdivide European individuals into White British and non-British White. We defined four population groups, as follows: White British (WB), non-British White (NBW), African (Afr), and South Asian (SA). We kept the remaining unrelated individuals as “others.”

We randomly split each population group into training (70%), validation (10%), and test (20%) sets without using phenotypes. As in the case of the synthetic data, we used the training, validation, and test sets for model fitting, determination of the sparsity hyperparameter, and predictive performance evaluation, respectively. We used the same training, validation, and test sets for all tested traits in the UK Biobank.

For iPGS training, we considered four different subsets of the training set (Table 1). For MultiPop, NoAdmixed, and Inclusive-FixN PGS models, we randomly sub-sampled White British individuals in the training set so that the total number of individuals used in the iPGS training would match that of the WB-only model. We applied a similar procedure to define four subsets of the validation-set individuals for PGS training.

Table 1.

The number of unrelated individuals in UK Biobank analysis

A. Population assignment
	WB	NBW	SA	Afr	Others	Total
Training set	237,055	10,130	5,206	4,246	28,024	284,661
Validation set	33,865	1,448	744	607	4,003	40,667
Held-out test set	67,730	2,894	1,487	1,213	8,007	81,331
Total	338,650	14,472	7,437	6,066	40,034	406,659

B. The number of unrelated individuals used in polygenic score training
	Model	WB	NBW	SA	Afr	Others	Total
	i. WB-only	237,055	0	0	0	0	237,055
	ii. Inclusive	237,055	10,130	5,206	4,246	28,024	284,661
	iii. Inclusive-FixN	189,449	10,130	5,206	4,246	28,024	237,055
	iv. iMultiPop, NoAdmixed	217,473	10,130	5,206	4,246	0	237,055
	v. iPGS+refit in Afr (wo/ interaction)	237,055	10,130	5,206	4,246	28,024	284,661
	vi. iPGS+refit in Afr	237,055	10,130	5,206	4,246	28,024	284,661
	vii. PRS-CSx	270,920	11,578	5,950	4,853	0	293,301
	viii. PRS-CSx (n = 256k)	237,055	10,130	5,206	4,246	0	256,637

(A) The number of training, validation, and test-set individuals across population groups is shown. (B) The number of individuals used to train PGS models is shown. In the iPGS+refit in Afr models (models v and vi), n_train = 284,661 individuals were used to train the iPGS model, whereas a subset of n = 4,853 individuals were used in the population-specific refit model (material and methods). Abbreviations are as follows: WB, White British; NBW: non-British White; SA, South Asian; and Afr, African.

Variant annotation and quality control in the UK Biobank

We used the directly genotyped dataset (release version 2), imputed genotypes (release version 3), imputed HLA allelotype (release version 2), and the GRCh37 human reference genome throughout the study.²⁴ We performed variant annotation with Ensembl’s Variant Effect Predictor (VEP) (version 101)^29,30 with the LOFTEE plugin (https://github.com/konradjk/loftee).³¹ Using ClinVar,³² we annotated “pathogenic” and “likely pathogenic” variants. We grouped the VEP-predicted consequence of the variants into six groups: protein-truncating variants (PTVs), protein-altering variants (PAVs), proximal coding variants (PCVs), intronic variants (intronic), genetic variants on untranslated regions (UTRs), and other non-coding variants (others).³³ For the directly genotyped dataset, we focused on variants passing the following criteria: (1) the missingness of the variant is less than 1%, considering that the two genotyping arrays (the UK BiLEVE Axiom array and the UK Biobank Axiom array) cover a slightly different set of variants²⁴ and (2) Hardy-Weinberg disequilibrium test p value greater than 1.0 × 10⁻⁷. For the imputed-genotype dataset, we used the following criteria: (1) the missingness of the variant is less than 1%; (2) the minor-allele frequency (MAF) is greater than 0.01%; (3) the imputation quality score (INFO score) is greater than 0.3; (4) the variant does not present in the directly genotyped dataset; and (5) the variant is present in the HapMap phase 3 dataset. For the HLA allelotype, we kept the imputed allelotype dosage within [0, 0.1), (0.9, 1.1), or (1.9, 2.0] and converted it to a hard call.³⁴ We focused on the HLA allelotype with (1) missingness no more than 1% and (2) Hardy-Weinberg disequilibrium test p value greater than 1.0 × 10⁻⁴. We concatenated all variants and allelotypes into one dataset by using PLINK 2.0 (v. 2.00a3.3LM, 3 Jun 2022).³⁵ The procedure outlined above resulted in a total of 1,316,181 variants considered in the analysis.

Phenotype definition in the UK Biobank

We focused on 60 anthropometric and hematological traits in the UK Biobank (Table S1). Some of those phenotypes are collected at up to four instances, each of which corresponds to (1) the initial assessment visit (2006–2010), (2) the first repeat assessment visit (2012–2013), (3) the imaging visit (2014–present), and (4) first repeat imaging visit (2019–present). We defined phenotype data by using the median of non-missing values for each individual across the 60 quantitative traits as described elsewhere.^26,33,36

Sparse-polygenic-score training from individual-level data

We fit sparse-polygenic-score models by using batch screening iterative lasso (BASIL) implemented in the R snpnet package (version 2) on the individual-level data.^37,38 We considered the additive effects of genetic variants on the phenotypes and fit a polygenic score model by finding the exact solution for L₁-and L₂-penalized multivariate regression (Elastic Net).³⁹ Specifically, BASIL directly operates on the individual-level data and performs variable selection and effect-size estimation simultaneously. Given a continuous phenotype $y\in {\mathrm{R}}^n$ of n individuals, a covariate matrix $Z\in {\mathrm{R}}^{n\times r}$ of n individuals and r covariates, and a genotype matrix $X\in {\mathrm{R}}^{n\times p}$ of n individuals and p variants, we consider the following regularized regression problem:

$$\left(\widehat{y_0},\hat{\gamma },\hat{\beta }\left(\lambda \right)\right)={\mathrm{argmin}}_{y0},{\gamma ,}_{\beta }\frac{1}{2n}{\Vert y-y_0-Z\gamma -X\beta \Vert }_2^2+\lambda \sum _{j=1}^p{v}_j\left[\frac{1-\alpha }{2}{\beta }_j^2+\alpha \left|{\beta }_j\right|\right]$$ (Equation 1)

where λ is a tuning parameter that controls the sparsity of the solution, α is an elastic net parameter that controls the balance between the L₁ (Lasso) and L₂ (Ridge) penalization, and ν_j is the penalty factor for the j-th variable; the penalty factors allow different levels of shrinkage to variables according to prior knowledge. We optimized the tuning parameter, λ, on the basis of the predictive performance on the validation set and use α = 0.99. We set penalty factors of ν_j = 1 for all genetic variants in the application with synthetic data. In contrast, we assigned lower penalty factors for non-synonymous coding variants in the application to the UK Biobank, as described below. Note that the covariate terms are unpenalized in the regression. When fitting a polygenic score model from large-scale cohorts, it is not uncommon to have a large number of individuals (n ≈ 300,000) and genetic variants (p ≈ 1,000,000). Instead of loading all the large-scale data on memory and fitting a regularized regression, BASIL efficiently solves the exact solution of the penalized regression in an iterative procedure by taking advantage of strong rules⁴⁰ that guide the variable selection in each iteration step.³⁷ A similar model can be used for binary phenotypes (logistic regression), time-to-event phenotypes (Cox proportional hazards regression), or joint modeling of multiple phenotypes, as shown in our previous studies.^{33,37,38,41,42,43}

Inclusive polygenic scores with synthetic data

In our application of iPGS to the synthetic genotype and phenotype data from the HAPNEST pipeline,²² we assessed the impact of the composition of the training-set individuals on the predictive performance by using the held-out synthetic individuals of African and European ancestry groups.

We fit 11 models on n_train = 110,000 individuals for each of the three synthetic phenotypes. The training set included individuals with synthetic African and synthetic European ancestry, each with different ratios. The ratios tested were 100%, 95%, 90%, 75%, 60%, 50%, 40%, 25%, 10%, 5%, and 0%. We constructed the validation set of n = 40,000 individuals, matching the ratio in the training set. We applied iPGS to n_train = 110,000 individuals and p = 116,524 variants in chromosome 22. Given that we do not model the covariate effects in phenotype simulation, we did not include covariate terms in the regression. We used the default value of 1.0 for all variants for penalty factors. We used the same n = 76,000 individuals (n = 38,000 each for African and European) in the held-out test set for predictive performance evaluation.

Inclusive polygenic scores in the UK Biobank

In our application of iPGS to the UK Biobank, we included age (UK Biobank data field 34), sex (data field 31), age², age^∗sex, Townsend deprivation index (data field 22189), and the first 18 genotype PCs (data field 22009) provided by the UK Biobank²⁴ as unpenalized covariates. We considered p = 1,316,181 variants for n = 237,055 individuals or n = 284,661 individuals, as shown in Table 1B. We used the validation set metric to select the sparsity of the model.^33,37 We prioritized the protein-truncating and protein-altering variants as previously described.³³ In brief, we assigned a penalty factor of 0.5 to putative protein-truncating variants and pathogenic variants; 0.75 to putative protein-altering variants, likely pathogenic variants, and HLA allelotypes; 1.2 for genetic variants that are not present in the HapMap phase 3 dataset; and 1.0 for the other remaining variants. The specific values of penalty factors are based on heuristics,³³ and finding the optimal values of penalty factors would be an important direction for follow-up studies.

Inclusive polygenic score with population-specific refit

To model the ancestry-dependent genetic effects on top of the ancestry-shared effects captured in iPGS, we developed the iPGS+refit procedure. We focused on the individuals in the training and validation sets and also of African ancestry and fit unpenalized regression by using the individual-level data to characterize the covariate effects: phenotype ∼ age + sex + age² + age^∗sex + Townsend deprivation index + genotype PCs, where genotype PCs represent the first 18 genotype PCs as in the iPGS training. We obtained the covariate-only score term by predicting the phenotype values using the covariate terms alone.

For the iPGS+refit model in the training set without interaction effects, we focused on the individuals in the training and validation sets and also of African ancestry and fit the following elastic-net penalized regression model:

$$\text{phenotype}\sim \text{covariate}-\text{only}\text{score}+\text{iPGS}+\sum _{v\in G}v$$ (Equation 2)

where, the covariate-only score and iPGS represent the predicted phenotype value from the covariate-only model and iPGS model (genotype-only model), respectively, and G represents the set of genetic variants with heterogeneous associations. To nominate the set of genetic variants with heterogeneous associations (G), we used the heterogeneity test in GWAS meta-analysis by using nominal p value = 5 × 10⁻⁸ as the statistical-significance threshold. We imputed the missing values in the genetic variants with heterogeneous associations in the individual-level data by using the allele frequency computed in the African population in the UK Biobank. We assigned a penalty factor of 1.1 for the genetic variants and 1.0 for the covariate-only score and iPGS.

For the iPGS+refit model with interaction effects, we also considered variant ^∗ PC1 and variant ^∗ PC2 terms for genetic variants with heterogeneous associations in the penalized regression model:

$$\text{phenotype}\sim \text{covariate}-\text{only}\text{score}+\text{iPGS}+\sum _{v\in G}\left(v+v\cdot \text{PC}1+v\cdot \text{PC}2\right)$$ (Equation 3)

We assigned a penalty factor of 1.2 for the interaction terms, 1.1 for the genetic variants, and 1.0 for both covariate-only and iPGS scores. For both models, we fit the elastic-net penalized regression by setting elastic-net parameter α to be 0.99 and optimized the tuning parameter by using 10-fold cross-validation with the cv.glmnet function implemented in the glmnet package in R.^39,40,44

Genome-wide association analysis

We applied genome-wide association analysis with PLINK (v. 2.00 alpha).³⁵ We first computed population-specific genotype PCs for White British, non-British White, South Asian, and African individuals in the UK Biobank by using the randomized algorithm (“approx” modifier)⁴⁵ implemented as the “--pca allele-wts 20 approx vzs” command in PLINK2. We subsequently applied the GWAS analysis by using age, sex, Townsend deprivation index, array, and the top ten population-specific genotype PC loadings as covariates and using the approximation algorithm (“cc-residualize” modifier)⁴⁶ implemented as the “--glm zs omit-ref no-x-sex log10 hide-covar skip-invalid-pheno cc-residualize firth-fallback” command in PLINK2. The participants from the UK Biobank were genotyped on two different arrays: about 10% of participants were genotyped on the UK BiLEVE Axiom array, and the rest were genotyped on the UK Biobank Axiom array.²⁴ When genetic variants were directly measured on both arrays, we included an indicator variable “array” in the covariates and denoted whether the UK Biobank Axiom array or UK BiLEVE Axiom array was used in the genotyping.

For the GWAS meta-analysis and heterogeneity test, we applied quantile normalization by using the “--pheno-quantile-normalize” option in PLINK2. We conducted GWAS analysis by using the individuals in the training set for the following populations: White British, non-British White, South Asian, and African.

For PGS modeling with PRS-CSx,¹⁶ we used the same GWAS summary statistics for the meta-analysis. We also conducted GWAS analysis by using the union of the training and validation-set individuals in each of the four populations. We used those two sets of GWAS summary statistics as the input of the PRS-CSx model (n_train = 293,301) and the "PRS-CSx (n = 256k)" model (n_train = 256,637) (Table 1).

For heritability estimation analysis, we applied GWAS analysis by using all the individuals in the White British group in the UK Biobank without applying the quantile normalization.

GWAS meta-analysis and heterogeneity test

Using the GWAS summary statistics for four analyzed populations (White British, non-British White, South Asian, and African), we performed inverse-variance weighted (IVW) meta-analysis by using METAL⁴⁷ (version 2020-05-05) and included a heterogeneity-of-effects analysis.

Heritability analysis

We applied linkage disequilibrium (LD) score regression (LDSC)⁴⁸ and estimated the SNP-based heritability. We compared the predictive performance of the PRS models and the LDSC-based heritability estimates.

Allele frequency and LD pruning

We computed the non-reference allele frequency with PLINK2³⁵ by using the individuals in the training set and in the following population groups in the UK Biobank: White British, non-British White, South Asian, and African. We compute the cumulative frequency of the minor-allele frequency distribution for all the 1,316,181 genetic variants considered in the study. We also repeated the analysis by focusing on the subset of variants selected in at least one of the PGS models across 60 anthropometric and hematological traits.

We applied LD pruning with widow size 200 kb and pairwise threshold r² of 0.5 by using the “--indep-pairwise 200kb 0.5” command implemented in PLINK2.³⁵ We prioritized protein-truncation, protein-altering, or proximal-coding variants by using the “--indep-preferred” command. We repeated the procedure for White British, non-British White, South Asian, and African individuals in UK Biobank. We used the selected variants as approximately LD-independent variants.

PGS training with PRS-CSx

We fit PGS models by using PRS-CSx, a cross-population polygenic prediction method based on Bayesian multivariate regression using continuous shrinkage priors.¹⁶ We downloaded the pre-computed LD reference panels constructed from the UK Biobank data from GitHub (https://github.com/getian107/PRScsx) and used them for our analysis. Specifically, we used the European (EUR) reference for our White British and non-British White populations, the South Asian (SAS) reference for our South Asian population, and the African (AFR) reference for our African population in the UK Biobank. We fit the Bayesian regression model implemented in PRScsx.py for each chromosome independently. Following the tutorial and recommendations in the GitHub repository, we applied a small-scale grid search for the global shrinkage parameter, phi, by fitting four models corresponding to the following phi values: 1 × 10⁻⁶, 1 × 10⁻⁴, 1 × 10⁻², and 1. We used the default values for the other parameters and obtained posterior SNP effect-size estimates for each discovery super-population (i.e., EUR, SAS, and AFR). We subsequently learned the optimal linear combination of the three scores. Specifically, we used the individuals in the validation set, computed the super-population-specific scores for each individual by using the “--score” command implemented in PLINK2,³⁵ applied scaling so that the super-population-specific scores have zero mean and unit variance, and learned the coefficients of linear combinations of the population-specific scores according to the recommendations provided in the GitHub repository. For each target population (i.e., the White British, non-British White, South Asian, African, and others groups in the UK Biobank), we selected the global shrinkage parameter on the basis of the predictive performance evaluated in the individuals in the validation set. We fit two versions of the PRS-CSx models, corresponding to the individuals in the training set (the "PRS-CSx [n = 256k]" model, n_train = 256,637) and the individuals in the union of training and validation set (the PRS-CSx model, n_train = 293,301), where we used the optimal phi values and the weights for linear combination of population-specific scores learned from the "PRS-CSx (n = 256k)" model.

The similarity of PGS models

To assess the similarity of PGS models trained for the same phenotype, we computed the Pearson’s correlation between the pair of PGS values across the individuals in the held-out test set.

PGS performance evaluation

We used the held-out test set to evaluate the predictive performance (R²) of (1) PGS (genotype-only) models, (2) covariate-only models, and (3) full models that considered both covariates and genotypes (Tables S2 and S3). We reported the predictive performance of genotype-only models in the remainder of the main text unless indicated otherwise. We evaluated the 95% confidence interval of predictive performance by using the approximate standard error of R².^49,50

In our application of iPGS to the UK Biobank, we used the predictive performance computed for the WB-only model as the baseline to evaluate the significance of improvements in predictive performance (R²) in the held-out-test-set individuals. We assessed the significance of the difference in R² between the iPGS model and the WB-only model by using the delta method implemented in the r2redux package in R.^49,51 We report the average improvements in PGS models across traits. For each White British, non-British White, South Asian, African, and “others” population in the held-out test set individuals, we fit generalized Deming regression models, R² ∼ 0 + R²_WB-only, accounting for the uncertainties in both predictor and response variables (i.e., standard errors for R²_WB-only and R², respectively) by using the Deming package in R.⁵² We report the slope of the regression model and its 95% confidence interval as the average improvements in the predictive performance.

Statistics

For computational and statistical analysis, we used Jupyter Notebook,⁵³ R,⁵⁴ the R Tidyverse package,⁵⁵ and GNU parallel⁵⁶ (https://www.gnu.org/software/parallel/). For visualization, we used ggplot2⁵⁷ with ggrepel⁵⁸ (https://github.com/slowkow/ggrepel) and ggrastr⁵⁹ (https://CRAN.R-project.org/package=ggrastr) packages. The p values were computed from two-sided tests unless otherwise specified.

Results

Overview of inclusive polygenic score (iPGS) methodology

In iPGS, we characterize PGS models by applying the batch screening iterative lasso (BASIL) algorithm that we previously developed^37,38 to ancestry-diverse individuals. Unlike most modern PGS methods, which take GWAS summary statistics and LD reference panels as input, BASIL directly operates on the individual-level data and fits a PGS model as the exact solution of penalized multivariate regression via the iterative procedure. We characterize ancestry-shared genetic effects from large-scale individual-level data of more than one million genetic variants across hundreds of thousands of ancestry-diverse individuals by taking advantage of efficient variable screening rules in BASIL. One may provide genotype principal-component loadings as unpenalized covariates to account for genome-wide admixture fractions and population structure. We randomly split the individuals into training, validation, and held-out test sets and fit a PGS model on the training-set individuals. We used the validation set to select the sparsity of the penalized regression model and the held-out test set for performance evaluation.

Application to synthetic data

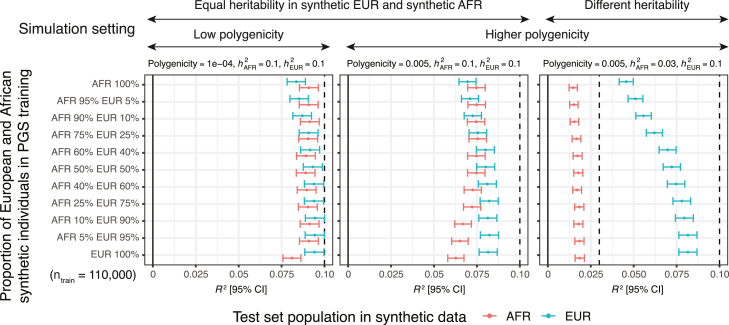
We first tested our approach with a synthetic individual-level dataset generated by HAPNEST.²² We used simulated genotypes in chromosome 22 and created three synthetic phenotypes with different polygenicity and heritability for 168,000 individuals each in African and European ancestry groups (material and methods). We split each of the ancestry groups into a training set (n_train = 110,000), a validation set (n = 20,000), and a held-out test set (n = 38,000) for evaluation. To systematically assess the impact of the composition of individuals in PGS training on predictive performance, we constructed 11 training sets with varying numbers of synthetic African and synthetic European individuals (n_train = 110,000), fit iPGS models, and evaluated their predictive performance for each of the three synthetic traits (Figure 1).

Figure 1.

Simulation study with synthetic data

Across three heritability and polygenicity scenarios (top), we fit PGS models with 110,000 individuals of synthetic African and synthetic European ancestry of 11 different compositions. We quantified the predictive performance in the held-out test set. Error bars represent 95% confidence intervals.

The lower polygenicity scenario showed the highest predictive performance in both synthetic African and synthetic European individuals, as expected, given that the accuracy of PGS depends on the polygenicity, heritability, and sample size.⁶⁰ With the equal heritability between the two ancestry groups, we found that the difference between synthetic African and synthetic European groups in the test-set predictive performance is the smallest when the iPGS models were trained on 75% of synthetic African and and 25% of synthetic European individuals. The fact that the transferability of PGS models from synthetic European individuals to synthetic African individuals was lower than in the opposite direction possibly reflects that African genomes have greater genetic diversity (e.g., lower degree of LD) than European genomes.⁶¹

We found an increase in the transferability with ancestry-diverse training in synthetic African and synthetic European groups when they were the minority samples in the training set. Our results indicate that the inclusion of the minority target population, even 5%, in PGS training would help improve the transferability of PGS models. When the heritability was different between the two ancestry groups, the predictive performance for both populations increased as we increased the samples from high heritability. Those results validate the utility of ancestry-diverse training to enhance the transferability of PGS models and motivated us to apply iPGS to the UK Biobank, one of the largest cohorts with readily available individual-level data.

Application to 60 traits in the UK Biobank

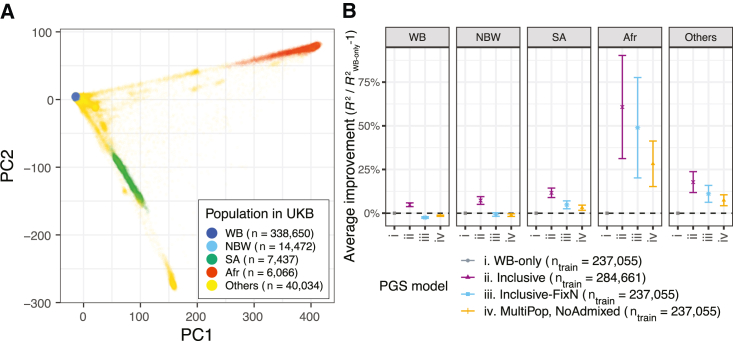
In our application of iPGS to the UK Biobank,^23,24 we assigned unrelated individuals to four ancestry groups: White British (WB, n = 338,650), non-British White (NBW, n = 14,472), South Asian (SA, n = 7437), and African (Afr, n = 6066) by using the combination of genotype principal-component (PC) loadings and self-reported ethnicity data (material and methods, Figure 2A). The remaining individuals (others, n = 40,034) accounted for nearly 10% of unrelated individuals in the UK Biobank and consisted of many admixed individuals and a smaller number of East Asian individuals (Table 1A). We randomly split each of the ancestry groups into a training set (70%), a validation set (10%), and a held-out test set for evaluation (20%) (Table 1A). To assess the effects of ancestry composition of the PGS training sets on predictive performance, we fit four PGS models by using different subsets of the training-set individuals: (1) White British population (WB-only [model i], n_train = 237,055), (2) all of the unrelated individuals in the training set (inclusive [model ii], n_train = 284,661), (3) individuals across the continuum of ancestry, where the number of individuals was kept the same as for the WB-only model (inclusive-FixN [model iii], n_train = 237,055), and (4) individuals from White British, non-British White, South Asian, and African ancestry groups with population stratification (MultiPop, NoAdmixed [model iv], n_train = 237,055) (Table 1B). We fit PGS models across 60 quantitative traits, consisting of anthropometric and hematological measures (material and methods, Table S1).

Figure 2.

Inclusive PGS (iPGS) training with diverse ancestry enhances the transferability of polygenic scores in the UK Biobank

(A) Principal-component projection of the unrelated individuals in the UK Biobank and population-label assignment.

(B) Relative average improvements of PGS model performance against the baseline model trained only with White British individuals (material and methods). Error bars represent 95% confidence intervals of average improvements.

The resulting sparse-PGS model contained from 2,827 (inclusive-FixN model for mean corpuscular hemoglobin concentration) to 62,419 (inclusive model for standing height) genetic variants, with a median of 30,787 variants for the inclusive model (Figure S1; Table S4). Given the nature of penalized multivariate regression, we observed shrinkage of effect-size estimates in inclusive PGS models compared GWASs (Figure S2). The direction of the effects is more consistent with European ancestry groups than with non-European ancestry groups, as expected, given that most individuals used to train inclusive PGS models are of European ancestry. When we compared the predicted scores in the individuals in the held-out test set across the four models, the scores were largely consistent with substantial variability across ancestry groups. For instance, the median value of Pearson’s correlation between the PGSs from the WB-only and the inclusive models was 0.94 for white British individuals and 0.84 for African individuals (Figure S3; Table S5).

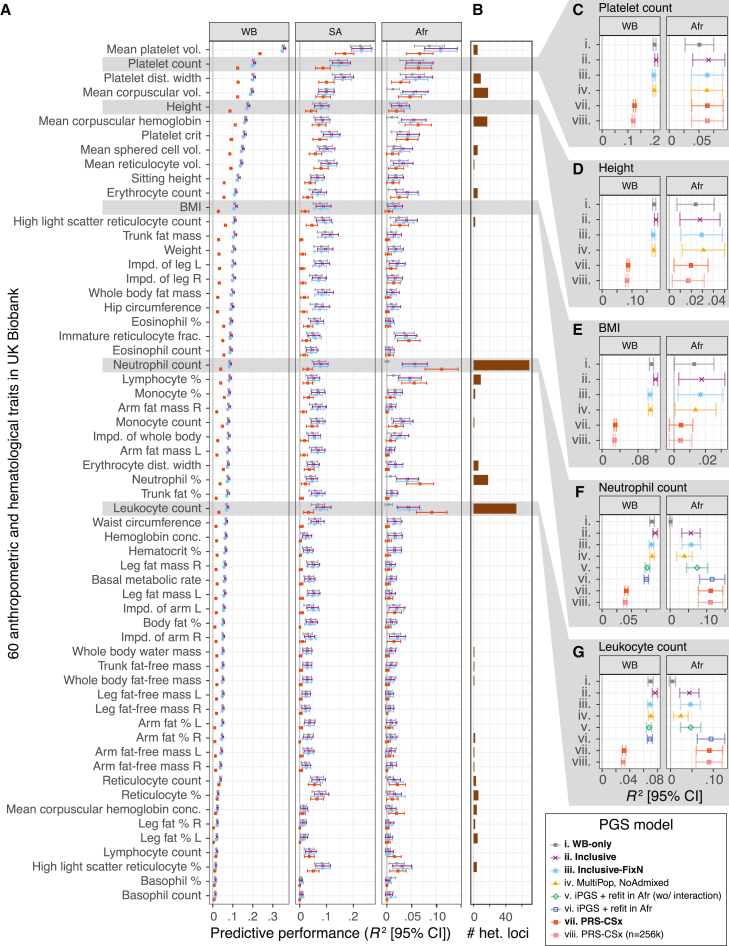
Our systematic application of iPGS and evaluation of our predictive performance (R²) across 60 quantitative traits indicates that the direct inclusion of diverse-ancestry individuals increases predictive performance in held-out-test-set individuals of non-European ancestry (material and methods, Figures 2B, 3, S4, and S5; Table S2). Overall, iPGS showed the greatest improvements for individuals of African ancestry; there were an average of 48.9% (95% confidence interval [CI] = [20.2%, 77.7%]) improvements across 60 quantitative traits when the models were trained on the same number of individuals (inclusive-FixN, n_train = 237,055, material and methods, Figure 2B; Table S6). For some traits (e.g., neutrophil count), our inclusive-FixN PGS model showed substantial improvements (R² = 0.0577 for the genotype-only model, nominal p value = 1.3 × 10⁻¹⁶) in the held-out test-set individuals of African ancestry in comparison to the baseline model trained only on White British individuals (R² = 0.0011, nominal p > 0.05, more than a 50-fold increase in R²), even though both models were trained with the same number of individuals of n = 237,055 (Figure 3F). The difference in R² values was statistically significant, with a nominal p value of 2.9 × 10⁻⁶ (material and methods). Similarly, we observed improvements in prediction for leukocyte (red blood cell) count in African individuals (R² = 0.0465, nominal p = 1.2 × 10⁻¹³ vs. R² = 0.0044, nominal p = 0.024 for inclusive-FixN and WB-only models, respectively) (Figure 3G).

Figure 3.

Systematic predictive performance evaluation of inclusive PGS (iPGS) models and PRS-CSx across 60 anthropometric and hematological traits in the UK Biobank

(A) The predictive performance (R²) in White British (WB), South Asian (SA), and African (Afr) groups in the UK Biobank are shown for four select models: (i) WB-only, (ii) inclusive, (iii) inclusive-FixN, and (vii) PRS-CSx.

(B) The number of approximately LD-independent (R² < 0.2 in the African population in the UK Biobank) variants with heterogeneous GWAS associations (material and methods).

(C–G). The predictive performance of up to eight PGS models in White British (WB) and African (Afr) populations in the UK Biobank are shown for five select traits. The refit models are trained only for the neutrophil and leukocyte counts, where genetic variants with heterogeneous GWAS effects were observed. The predictive performance for other models and ancestry groups is shown in Figures S4 and S5. BMI: body mass index. Vol.: volume. Dist.: distribution. Impd.: impedance. Frac.: fraction. Conc.: concentration. %: percentage. R: right. L: left. Error bars represent 95% confidence intervals.

With the inclusion of all individuals across the continuum of genomic ancestry (inclusive, n_train = 284,661), we observed that our inclusive model showed improved or equally competitive performance over our WB-only model across all of the five populations tested in our study (Figure 2B; Table S7). Overall, we found an average improvement of 60.8% (95% CI: [31.2%, 90.3%]) for individuals of African ancestry, 11.6% (95% CI: [8.9%, 14.4%]) for South Asian, 7.3% (95% CI: [5.0%, 9.5%]) for non-British White, 4.8% (95% CI: [3.7%, 5.9%]) for White British, and 17.8% (95% CI: [11.8%, 23.8%]) for the remaining individuals (“others”) for the held-out test-set, indicating the power gain in inclusive PGS training (Figures 2B and S6; Table S6). With a fixed number of training individuals (n_train = 237,055), our inclusive-FixN PGS model (trained on 189,449 WB and 47,606 individuals of the other ancestry groups, instead of 237,055 WB) led to a very modest drop in performance (2.5%, 95% CI: [2.1%, 2.9%]) in White British, as expected given the smaller ancestry-matched sample size in the training set (Figure 2B). However, when we used all the unrelated individuals in the training set (inclusive, n_train = 284,661), there was no drop in the performance across all population groups.

Heritability and allele-frequency analysis

We next investigated the relationship between heritability and predictive performance of the iPGS model by focusing on White British individuals because they had the largest sample size in the UK Biobank. Because we model the additive genetic effects in our iPGS model, the narrow-sense SNP heritability provides the theoretical upper bound of predictive performance. We estimated the heritability by using LD score regression⁴⁸ and compared it with the predictive performance of our iPGS model. We found that the predictive performance of the iPGS models for hematological traits was closer to the heritability estimates than it was for the anthropometric traits (Figure S7; Table S8). The observed difference most likely reflects the difference in the power across traits with n_train = 284,661 individuals in the UK Biobank. The sample size required to achieve predictive performance at the estimated heritability depends on the genetic architecture of each trait, and anthropometric traits might require a larger sample size. Indeed, a saturated map of genetic associations for standing height has recently been reported for the European population through meta-analysis of GWAS results from 4 million European individuals.⁶²

We examined the allele frequency of the genetic variants selected in the PGS model across 60 traits and found that our PGS models capture common variants (Figure S8). Across the 1,316,181 genetic variants analyzed in the study, some variants were of lower frequency in non-European individuals (Figures S8 and S9). We observed a similar difference between ancestry groups when we restricted the analysis to ∼300,000 genetic variants selected for at least one of the 60 traits (Figure S9; Table S9). Although the difference between PGS models was much smaller than the difference between ancestry groups, the variants selected in iPGS models were more common in European than in African individuals (Figures S8 and S9).

Detecting ancestry-dependent genetic effects with heterogeneity tests

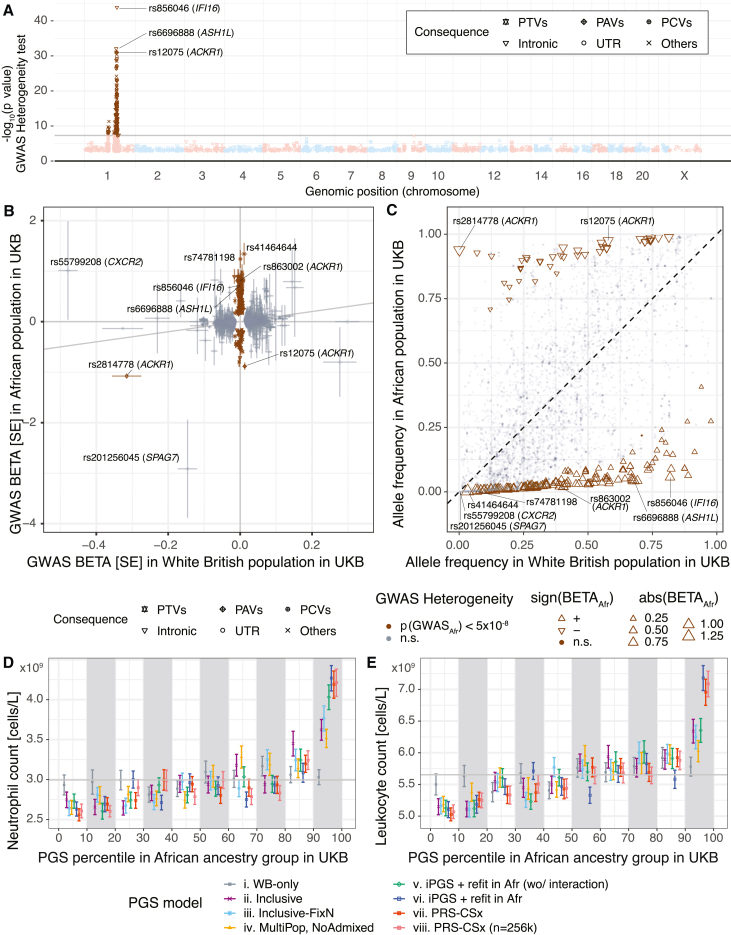
Although our results across 60 quantitative traits highlight the benefits of modeling genetic effects shared across ancestry groups, in some cases, ancestry-dependent or ancestry-specific genetic effects might result in reduced performance. Previous analyses have revealed a relatively small number of loci with substantial differences in allele frequency between ancestry groups, and some of these loci show associations with complex traits.^63,64,65 To identify genetic variants with heterogeneous associations across ancestry groups in the UK Biobank, we systematically applied the heterogeneity test by using GWAS meta-analysis (material and methods, Figure 3B; Table S10). Applying the heterogeneity test across 60 traits, we found a limited number of approximately LD-independent (R² < 0.5) heterogeneous associations (median of 0) with a few exceptions. Neutrophil counts showed the greatest level of heterogeneity; approximately 69 LD-independent loci had statistically significant heterogeneous GWAS associations, all located in chromosome 1 (Figures 3B and 4A, S10, and S11). Most of those variants had population-specific effects in individuals of African ancestry (Figure 4B). The neutrophil-count-lowering alleles with heterogeneous associations were of higher allele frequency in individuals of African ancestry in UK Biobank (Figure 4C).

Figure 4.

Enhanced predictive performance with iPGS+refit that additionally accounts for ancestry-dependent genetic effects

(A) GWAS meta-analysis heterogeneity test in the UK Biobank for the neutrophil count. Genetic variants with heterogeneity p value < 5 × 10⁻⁸ are highlighted in brown.

(B) GWAS effect size comparison between White British (x axis) and African (y axis) populations in the UK Biobank. The color indicates whether the variants show heterogeneous GWAS associations. Error bars represent the standard error of the GWAS effect-size estimates.

(C) Allele frequency comparison for 5,890 genetic variants associated with neutrophil count (material and methods). The color indicates whether the variants show heterogeneous GWAS associations. The shape and size represent the direction and the magnitude of GWAS associations in the African population in the UK Biobank.

(D and E) Phenotype mean values of neutrophil count (D) and leukocyte count (E) stratified by decile of PGS in the held-out test set of individuals of the African population in the UK Biobank are shown. Error bars represent the standard error-of-mean estimates.

PTVs: protein-truncating variants. PAVs: protein-altering variants. PCVs: proximal coding variants. Intronic: intronic variants. UTR: genetic variants on untranslated regions. Others: other non-coding variants.

The lead GWAS-associated variant for neutrophil counts in African ancestry groups is a well-characterized upstream untranslated region (UTR) variant rs2814778 in ACKR1 (atypical chemokine receptor 1, also known as Duffy blood group gene [DARC] [MIM: 613665]) (Figure S10), which encodes the subunit of the Duffy receptor and serves as the basis of the Duffy blood group system. The UTR variant rs2814778 disrupts binding sites of the GATA1 transcription factor and shuts down expression of the receptor in erythrocytes;⁶⁶ thus, it is considered the null allele. The null allele is under positive selection in the African population (allele frequency of 83% in the African population and 0.3% in the non-Finish European population),^31,63,67 given that the Duffy receptor works as the canonical entry point for the malaria parasite, Plasmodium vivax, and the null allele is protective against malaria infection.^68,69 Beyond its roles in erythrocytes, the null allele is also known as the causal variant for neutrophil-count-lowering associations from admixture mapping studies.⁶⁷ A recent GWAS meta-analysis of hematological traits supports the association between rs2814778 and neutrophil counts in individuals of African ancestry.⁷⁰ When we looked at the variants selected in the PGS models, the causal UTR variant rs2814778 was captured in the inclusive PGS model but not in the WB-only model (Figure S12), highlighting the benefits of inclusive PGS training.

Joint modeling of ancestry-shared and -dependent effects

To account for ancestry-shared and ancestry-dependent genetic effects, we developed a series of new models, named iPGS+refit models (material and methods). In these models, we fit a regression model to the individual-level data in a specific ancestry group. We considered an additive combination of covariate effects, iPGS, and genetic variants with ancestry-dependent genetic associations as predictors. We also explored an iPGS+refit model that additionally considers the interaction between the first two genotype principal components and the genetic variants with ancestry-dependent genetic effects. We named these two models "iPGS+refit in Afr (wo/interaction)" (model v) and "iPGS+refit in Afr" (model vi), respectively (material and methods). For neutrophil counts, for example, we identified 186 genetic variants with heterogeneous genetic associations from a GWAS meta-analysis in the UK Biobank (Figure 4A). We then focused on the 4,853 individuals of African ancestry in our training and validation sets and applied the iPGS+refit regression models to their individual-level data. For the "iPGS+refit in Afr (wo/interaction)" model (model v), we used 188 variables as predictors, which included one term each representing the covariate effects and iPGS score as well as the 186 genetic variants. For the "iPGS+refit in Afr" model (model vi), we used as predictors a total of 560 variables, consisting of an additional 372 variables that model the interaction between the 186 genetic variants and the first two genotype principal components (material and methods). We evaluated the predictive performance of these models by using the individuals in the held-out test set.

The iPGS+refit model improved predictive performance when we observed the genetic variants with heterogeneous GWAS associations across ancestry groups. For neutrophil counts, we saw further improvements with population-specific iPGS+refit, even beyond the improvements in the inclusive PGS model without the population-specific refit in the African population (Figures 3F and 4D). We found the iPGS+refit in Afr (wo/interaction) (model v) showed the improvements over the vanilla iPGS model without refit (R² = 0.0737 vs. R² = 0.0567). Furthermore, the iPGS+refit in Afr (model vi), which considers the interaction between genotype PCs and genetic variants with heterogeneous effects, showed the best predictive performance (R² = 0.1148) for African individuals. The performance measure exceeded the best-performing model we observed for White British individuals (R² = 0.0902 in iPGS, model ii), even though only 1.49% (4246/284,661, Table 1) of individuals used in the iPGS training were of African ancestry, highlighting the benefits of population-specific refit using the genetic variants with ancestry-dependent associations. We observed similar improvements in iPGS+refit models in leukocyte counts (R² = 0.0947, 0.0470, and 0.0441 in iPGS+refit in Afr [model vi], iPGS+refit in Afr [wo/interactions, model v], and iPGS [model ii], respectively) (Figures 3G and 4E).

Comparison with summary-statistics-based PGS approach

Lastly, we compared our iPGS with PRS-CSx, a recently developed multi-ancestry-aware PGS approach.¹⁶ Specifically, PRS-CSx fits Bayesian multiple-linear-regression models by using GWAS summary statistics from multiple population groups and a series of ancestry-matched LD reference panels. We compared its predictive performance across European (White British and non-British White), South Asian, African, and the remaining “other” individuals in the held-out test set. We fit two sets of models for each of the 60 traits: PRS-CSx (model vii, trained on n_train = 293,301 individuals) and PRS-CSx (n = 256k) (model viii, trained on n_train = 256,637 individuals), which we used for hyperparameter tuning for both models (Table 1, material and methods). Overall, our iPGS (model ii) outperformed the PRS-CSx model trained on up to n_train = 293,301 individuals in most tested traits and ancestry groups even though we trained iPGS models on a smaller number of n_train = 284,661 individuals (Figures 3, S4, and S5; Table S6). The few exceptions were all in the African population and when there were genetic variants with ancestry-dependent effects (Figures 3A and 3B). Ancestry-dependent genetic effects violate the modeling assumption in iPGS; inclusive PGS training works best to capture ancestry-shared genetic effects. Nonetheless, for neutrophil and leukocyte counts, where PRS-CSx outperformed the vanilla iPGS models without population-specific refit, iPGS+refit showed the best predictive performance for African individuals (Figures 3F, 3G, 4D, and 4E). Those results highlight the advantage of iPGS and the flexibility of iPGS+refit in jointly modeling ancestry-dependent and ancestry-shared genetic effects.

Discussion

We present inclusive PGS (iPGS), a PGS training strategy that includes ancestry-diverse individuals. By working directly on the individual-level data, iPGS does not require LD reference panels in PGS fitting and naturally provides a way to include admixed individuals in PGS training. Our empirical results, in 33 simulation configurations and 60 anthropometric and hematological traits in the UK Biobank, indicate the power of iPGS training in capturing genetic effects shared across ancestry groups. Across all population groups in the held-out test set, we see the largest improvements in predictive performance when we use ancestry-diverse individuals, including admixed individuals, in training, highlighting the increase in sample size and power.

We also developed iPGS+refit, a method to model ancestry-dependent effects on top of the shared effects captured in iPGS. We showed its utility when genetic variants have heterogeneous associations, by using neutrophil and leukocyte counts as examples. A systematic benchmarking across the 60 traits revealed the competitive advantage of iPGS and iPGS+refit against the commonly used summary-statistics-based PGS model, PRS-CSx.¹⁶

Unlike other existing methods,¹⁴ our iPGS is directly applicable to admixed individuals without the need for local-ancestry inference. In our application of iPGS to the UK Biobank, we report the predictive performance for the “others” group (Figure S4). The average improvement is 17.8% (95% CI: [11.8%, 23.8%]) for the inclusive model over the WB-only model (Figure 2B). Given the diverse ancestral background, individual-level quantification of the predictive performance would be more appropriate for this group of individuals. A recent study reports a Bayesian approach to evaluate the predictive performance of PGS at the individual level.²¹ However, the Bayesian method depends on resampling from Bayesian Markov chain Monte Carlo (MCMC). It is not directly applicable to other statistical models, such as the ones based on the penalized regression on the individual-level data, as ours is, and fast Bayesian PGS based on variational inference.⁷¹ Further methodological innovations will be needed to evaluate the individual-level performance of PGS models for a wider class of PGS models.

When fitting inclusive PGS models, we assume shared genetic effects across ancestry groups, and our iPGS works the best under this assumption. Our empirical analysis across 60 traits in the UK Biobank shows that iPGS improves the transferability for most situations. However, there is no guarantee as to whether the genetic variants selected in the PGS model have causal roles because iPGS is not designed for fine-mapping analysis. In our application of iPGS to the UK Biobank, we observe that genetic variants selected in the iPGS model are more common in the White British than in the African population, consistent with the difference in the allele-frequency distribution across 1.3 million genetic variants considered in the study.

Moreover, we observe some cases where ancestry-dependent or ancestry-specific associations violate our modeling assumptions. In some cases, there are extreme differences in allele frequency across population groups—for example, as a result of the positive selections in some populations, as we see in the UTR variant rs2814778 in ACKR1. For neutrophil count, our inclusive PGS model captures the causal UTR variant, but that is not the case for our WB-only model. We develop an iPGS+refit strategy to jointly model ancestry-shared and ancestry-dependent effects in a specific population when our modeling assumption in the vanilla iPGS does not hold. In our applications of iPGS+refit to hematological traits in the UK Biobank, we selected the candidate genetic variants with ancestry-dependent effects by using the heterogeneity test implemented in a GWAS meta-analysis. We empirically report that the interaction effects between the genetic variants and genotype PCs help improve the predictive performance in iPGS+refit. However, there is no guarantee that the predictive models constructed from iPGS and iPGS+refit capture the causal effects. Investigating how best to combine the ancestry-shared and ancestry-dependent effects warrants further follow-up analysis.

We envision three directions for future improvements in our strategy. First, we consider genome-wide admixture fractions along with age, sex, age², age^∗sex, and Townsend deprivation index as covariates in PGS modeling: integration with local ancestry inference⁷² and emerging methodologies to efficiently represent LD and genealogical relationships among haplotypes⁷³ might provide opportunities to model the interaction between polygenic effects and local ancestry. Second, we prioritize coding variants by using heuristics-based penalty factors (material and methods) as in our previous study³³: incorporating the biomedical domain knowledge to prioritize specific classes of variants, perhaps with functional genomics¹² and single-cell genomics data, could prioritize causal variants and further improve the transferability. Third, we currently focus on the UK Biobank only as proof of principle, given the challenges in sharing individual-level data across cohorts, but future studies will benefit greatly from combining multiple cohorts.

Overall, our results highlight the importance and the benefits of inclusive PGS training: it naturally offers a way to include admixed individuals in PGS training and increases the power to model ancestry-shared polygenic effects. We also indicate that joint modeling of ancestry-shared and -dependent effects, as in our iPGS+refit model, would be beneficial for further improvements of the transferability of PGS models. We make iPGS coefficients publicly available via an online browser (https://ipgs.mit.edu), figshare dataset (https://doi.org/10.6084/m9.figshare.22905368),⁷⁴ and in the PGS catalog (PGP publication ID: PGP000502).⁷⁵ Our work enables future studies to build more equitable PGS models and apply them to translational research.

Data and code availability

The supplementary data files are available as a dataset at figshare (https://doi.org/10.6084/m9.figshare.22905368). The sparse iPGS model weights generated from this study are also available at our online browser (http://ipgs.mit.edu/) and in the PGS catalog (https://www.pgscatalog.org/publication/PGP000502; score IDs are listed in Table S1). The analyses presented in this study were based on the individual-level data accessed through UK Biobank: https://www.ukbiobank.ac.uk. The BASIL algorithm implemented in the R snpnet package version 2 (https://github.com/rivas-lab/snpnet/tree/compact) was used in the PGS analysis.

Published: October 26, 2023