Factorizing polygenic epistasis improves prediction and uncovers biological pathways in complex traits

Summary

Epistasis is central in many domains of biology, but it has not yet been proven useful for understanding the etiology of complex traits. This is partly because complex-trait epistasis involves polygenic interactions that are poorly captured in current models. To address this gap, we developed a model called Epistasis Factor Analysis (EFA). EFA assumes that polygenic epistasis can be factorized into interactions between a few epistasis factors (EFs), which represent latent polygenic components of the observed complex trait. The statistical goals of EFA are to improve polygenic prediction and to increase power to detect epistasis, while the biological goal is to unravel genetic effects into more-homogeneous units. We mathematically characterize EFA and use simulations to show that EFA outperforms current epistasis models when its assumptions approximately hold. Applied to predicting yeast growth rates, EFA outperforms the additive model for several traits with large epistasis heritability and uniformly outperforms the standard epistasis model. We replicate these prediction improvements in a second dataset. We then apply EFA to four previously characterized traits in the UK Biobank and find statistically significant epistasis in all four, including two that are robust to scale transformation. Moreover, we find that the inferred EFs partly recover pre-defined biological pathways for two of the traits. Our results demonstrate that more realistic models can identify biologically and statistically meaningful epistasis in complex traits, indicating that epistasis has potential for precision medicine and characterizing the biology underlying GWAS results.

Epistasis has been difficult to study in complex traits due to the statistical challenges of fitting polygenic interactions. Here, we develop a model called Epistasis Factor Analysis and demonstrate its utility for modeling epistasis effects in complex traits.

Introduction

Epistasis refers to interactions between genetic effects on a trait and is central to many domains of biology, including rare human disorders,^1,2,3 protein evolution,^4,5 natural selection,^6,7 and functional genomics.⁸ Statistical models of epistasis can be useful for characterizing genetic architecture,^{9,10,11,12,13,14,15,16} improving genomic selection,^17,18 and unbiasedly screening for unknown genomic mechanisms^19,20,21,22 in model systems. Nonetheless, it remains debated whether epistasis is relevant for studying complex traits.^23,24,25 This is primarily because complex-trait biology is poorly understood, which severely limits our ability to study epistatic interactions between causal genetic mechanisms.

Unbiased genome-wide statistical tests for epistasis could quantify and characterize epistasis in complex traits. However, modeling epistasis in complex traits is challenging because they are affected by a large number of genetic variants, i.e., they are polygenic (Figure 1A). Although studies have identified some specific examples of epistasis in complex traits,^26,27,28 they have not explained significant missing heritability.^29,30 We hypothesize this is partly due to shortcomings in current models of complex-trait epistasis. Specifically, prior studies have assumed that each SNP-SNP interaction is independent of all other additive and interaction effects (Figure 1B).^31,32 This model is mathematically simple but biologically unrealistic and statistically under-powered.

Figure 1.

Three genetic architectures consistent with a typical GWAS

(A) Additive: Each SNP has an independent effect on the phenotype, Y.

(B) Uncoordinated: Each SNP interacts randomly with all other SNPs.

(C) Coordinated: SNPs can be grouped into interacting factors. EFA uses the P1xP2 interaction to (1) improve statistical power to detect epistasis and (2) sort GWAS loci into factors enriched in distinct biological pathways.

Here, we develop a complex trait epistasis model called Epistasis Factor Analysis (EFA). EFA assumes a “coordinated” form of epistasis where SNP-SNP interactions are structured by interactions between a few latent polygenic components, which we call epistasis factors (EFs) (Figure 1C).^33,34 EFA simultaneously partitions genome-wide association study (GWAS) effects into latent EFs and estimates the interactions between the EFs. The inferred EFs can be validated with known genomic annotations and, in principle, be used to discover novel biological pathways underlying GWAS results. A key feature of EFA is leveraging additive effects to improve estimates of epistasis effects, which is important because additive effects are usually much stronger in complex traits.

We illustrate the advantages of EFA over standard models in realistic simulations where heritability is mostly additive. We also show that EFA improves phenotype prediction over the additive model for traits with modest epistasis heritability in two multi-trait yeast datasets. We then apply EFA to the four UK Biobank (UKB) traits characterized by Sinnott-Armstrong et al.³⁵ and find significant epistasis in all four, including two that are robust to phenotype scale. Finally, we find that the inferred EFs partly recover predefined biological pathways. Our results show that structured models of polygenic epistasis can improve statistical performance and biological understanding in complex traits.

Subjects and methods

EFA intuition and overview

Nearly all complex trait studies assume the additive model, and it remains debated whether epistasis matters in complex traits.^24,25 However, this debate has largely been predicated on an “uncoordinated” model of epistasis that assumes that epistasis effects are independent of both additive effects and other epistasis effects.^30,31,36 Uncoordinated epistasis is neither interpretable, nor realistic, nor statistically supported.³⁰ In contrast, we recently proposed a more realistic “coordinated” model of epistasis where epistasis and additive effects are structured by latent factors (Figure 1C).³⁴ Coordination is motivated by known forms of epistasis in simpler traits, such as genetic modifiers of a Mendelian disease.²

Here, we introduce a coordinated epistasis model to identify these latent factors called EFA. EFA makes two key assumptions (A1 and A2) on the nature of epistasis in complex traits: (A1) SNP effects are mediated through a few distinct polygenic factors and (A2) these polygenic factors interact.

A1 and A2 are biologically motivated. For example, the factors in A1 could reflect distinct causal tissues,^37,38 core genes,^39,40 or heritable exposures like smoking.⁴¹ In accordance with A2, causal tissues might signal each other, core genes might encode proteins that physically interact, or an exposure’s effect may depend on underlying genetic risk. These assumptions are the same as the assumptions required for the coordinated epistasis model proposed in Sheppard et al.³⁴ (Note S1).

The key idea in EFA is to share information between additive effects and epistasis effects. This connection is central to both of EFA’s goals: (1) leveraging additive signals greatly improves power to detect epistasis, and (2) leveraging epistasis signals provides a way to unbiasedly partition SNPs into distinct factors, which is impossible in the additive model without external data or biological annotations.

Mathematical description of EFA

EFA applies to a quantitative trait measured on N individuals, y, and a matrix of genotypes measured on N individuals at M loci, G. The EFA model is

$$y_i=P_{i1}+P_{i2}+2\lambda P_{i1}{P}_{i2}+{\epsilon }_i;P_{ik}:=\sum _{j=1}^M{G}_{ij}{U}_{jk}\text{,}$$ (Equation 1)

where $P_{ik}$ is the level of EF k for sample i, $U_{jk}$ is the weight of SNP j on EF k, and λ is the interaction between EFs. In practice, we recommend using roughly 10 to 100 linkage disequilibrium (LD)-pruned SNPs in EFA that are chosen based on their additive effects. However, the optimal number will depend on the sample size and SNP effect-size distribution, and EFA can scale up to hundreds of SNPs (Figure S1).

While we primarily focus on the EFA model defined in Equation 1, we also present a generalized model in Equation 2 that allows for $K>2$ pathways and quadratic effects of each EF. We refer to this generalized model as EFA^∗.

$$y=GU{1}_K+\left(\left(GU\right)\bullet \left(GU\right)\right)\mathrm{v}\mathrm{e}\mathrm{c}\left(\mathrm{\Lambda }\right)+\epsilon$$ (Equation 2)

In Equation 2, U is an $M\times K$ matrix of SNP effects on each of K factors, $\mathrm{\Lambda }$ is a symmetric $K\times K$ matrix of factor-level interactions, $\bullet$ is the face-splitting product ($A\bullet B$ is a matrix where each column is the element-wise product of a column of A and a column of B), and ε is independent and identically distributed (i.i.d.) Gaussian noise. Note that EFA^∗ is still a pairwise interaction model; K refers to the number of latent pathways and EFA^∗ considers all $K\left(K+1\right)/2$ second-order interactions.

Intuitively, each column of U represents the SNP weights on a different EF, and $P_{,k}:=G{U}_{,k}$ is an individual’s weight on the k-th EF. ${\mathrm{\Lambda }}_{k{k}^{\prime }}$ represents the factor-level interaction between EFs k and $k^{\prime }$. When ${\mathrm{\Lambda }}_{k{k}^{\prime }}>0$, factors k and $k^{\prime }$ interact synergistically, meaning that their combined phenotypic effect is greater than the sum of their individual effects. The reverse is true for antagonistic factors, when ${\mathrm{\Lambda }}_{k{k}^{\prime }}<0$. When ${\mathrm{\Lambda }}_{k{k}^{\prime }}=0$, factors k and $k^{\prime }$ do not interact. Finally, ${\mathrm{\Lambda }}_{kk}$ refers to the quadratic effect of pathway k, which can help identify the pathway weights in U and improve prediction. Nonetheless, our primary interest is in the ${\mathrm{\Lambda }}_{k{k}^{\prime }}$ terms where $k\ne k^{\prime }$, as we are motivated by unraveling interactions across distinct biological factors. We note that the generalized EFA^∗ model with quadratic terms is not identified without further assumptions, such as that U is sparse. We prove these facts and comprehensively characterize the theoretical properties of EFA^∗ in Note S1.

EFA and EFA^∗ are special cases of the standard pairwise polygenic epistasis model for complex traits,

$$y_i=\sum _j{G}_{ij}{\beta }_j+\sum _{j,j^{\prime }}{G}_{ij}{G}_{i{j}^{\prime }}{\omega }_{j{j}^{\prime }}+{\epsilon }_{i,}$$ (Equation 3)

where ${\beta }_j$ is the additive effect of SNP j and ${\omega }_{j{j}^{\prime }}$ is the epistatic interaction between SNPs j and $j^{\prime }$. We can derive these SNP-level effects from EFA post hoc by

$$\beta =\sum _k{U}_{,k};\omega =U\mathrm{\Lambda }{U}^T\text{.}$$ (Equation 4)

This implicit, low-rank factorization of the genome-wide epistasis matrix is where EFA derives its name. Moreover, the linked factorization across β and ω gives rise to a certain level of coordination as defined in Sheppard et al.³⁴ (Note S1) and is how EFA leverages additive effects to estimate epistasis effects; the constraint on the EFs summing to β improves power to estimate ω when epistasis is coordinated.

Pragmatically, EFA outputs SNP weights on each EF (U) and the interaction between EFs (λ). These outputs can be used to reconstruct individual-level EFs (P), additive SNP effects (β, Equation 4), and SNP-SNP interaction effects (ω, Equation 4).

Fitting EFA parameters

We estimate U and $\mathrm{\Lambda }$ in Equation 2 using maximum likelihood (Note S1). In general, we fit parameters using gradient descent based on automatic differentiation. We evaluate multiple random restarts, each initialized with $U_{,k}$ drawn from a neighborhood around 0. We use this approach in simulations and in the yeast analyses. This generic, flexible estimation method can easily accommodate future model extensions, e.g., introducing sparsity in U with ${\mathcal{l}}_1$ penalties or “anchoring” EFs to specific SNPs (Note S1).

To scale our method to UKB sample size, we derive a block coordinate descent algorithm applicable only to the special case where we disallow quadratic terms (Note S1). The updates are remarkably simple, requiring only iterative least-squares regressions that scale linearly in sample size and quadratically in SNPs (i.e., $O\left(N{M}^2\right)$). The key to this efficiency is that we only evaluate EF-EF interactions and never explicitly evaluate SNP-SNP interactions, which would cost $O\left(N{M}^4\right)$. With 100 SNPs, as in our UKB analyses, this is a 10,000-fold speedup.

Uncoordinated models of polygenic epistasis

We compare EFA with other polygenic models in simulations and real data analyses. All comparison methods are special cases of the overarching polygenic pairwise epistasis model in Equation 3.

First, we compare with the standard additive model, which ignores epistasis by setting ${\omega }_{j{j}^{\prime }}=0$ for all $j,j^{\prime }$. Because we mostly study scenarios with $M<N$, we primarily fit the additive model with fixed effects (by ordinary least squares). The predictions from this model are then essentially polygenic scores. We also fit the additive model with random effects (assuming each ${\beta }_j$ is i.i.d. Gaussian, Note S2) in the real yeast analysis, enabling us to fit the full genome-wide data without pruning.

Second, we compare with the standard pairwise epistasis model in Equation 3 fit with fixed effects. Because this model has $O\left(M^2\right)$ parameters, jointly fitting all pairwise epistasis effects is often noisy or even impossible. Instead, we fit each pairwise interaction ${\omega }_{j{j}^{\prime }}$ one at a time (for $j\le j^{\prime }$) while controlling for additive fixed effects (note that only ${\omega }_{j{j}^{\prime }}+{\omega }_{j^{\prime }j}$ is identified).

Third, we compare with the uncoordinated random effect model for pairwise epistasis.³¹ This model assumes that ${\omega }_{j{j}^{\prime }}$ are drawn i.i.d. Gaussian. This assumption simplifies computation because the ω can be easily marginalized out of the likelihood function. We fit the variance components (one for β and one for ω) with maximum likelihood. We derive the best linear unbiased predictors (BLUPs) for both ω and for phenotype prediction in Note S2. We note that EFA is more similar to the fixed-effects uncoordinated model than the random-effect model.

Finally, we also develop an approach to estimate latent pathways from uncoordinated estimates by applying principal component analysis (PCA) to the estimated ω matrix. This is a naive baseline approach that only involves post-processing uncoordinated estimates. In contrast, EFA directly learns pathways, linking the low-dimensional components of ω with the additive effects.

Simulations

We used a polygenic simulation framework that is fully described in Note S3. In brief, we simulated allele frequencies at independent SNPs from a $\text{beta}\left(\mathrm{2,2}\right)$ distribution and diploid genotypes from a binomial distribution parameterized by the randomly chosen allele frequency. We centered and scaled genotypes to remove the ambiguity between variance “attributable to” vs. variance “caused by” additive effects, which can cause confusion.^24,25

We then simulated phenotypes under the EFA model Equation 2 with the simulated genotypes. We simulated the latent pathways, $U_{,k}$, from i.i.d. Gaussians to assign SNP weights on each EF and then rescaled the EFs to give the appropriate additive heritability (recall that the additive effect is related to the latent pathways by $\beta =\sum _k{U}_{,k}$). Next, we simulated the upper triangular entries of $\mathrm{\Lambda }$ from i.i.d. Gaussians with variance chosen to give the appropriate epistasis heritability. Using these key parameters, we generated the pairwise polygenic epistasis effects by $\omega =\sum _{k,k^{\prime }}{\mathrm{\Lambda }}_{k{k}^{\prime }}{U}_{,k}{U}_{,k^{\prime }}^T$.

We also simulated partly coordinated epistasis by adding i.i.d. Gaussian random variables to each entry of the ω matrix simulated above from the EFA model. By varying the relative contribution of these two pieces, we can interpolate between the EFA model (coordinated) and the classical epistasis model (uncoordinated). By choosing the relative variances of these different parameters appropriately, we are able to simulate the standard additive model, the standard uncoordinated model, and the coordinated EFA model.

Unless otherwise specified, we simulated $N=1000$ individuals and $M=20$ SNPs. We fixed the broad-sense heritability at $H^2=0.5$ and set both the additive and epistasis heritabilities at $h_{add}^2=h_{epi}^2=0.25$ such that the total heritability was evenly partitioned between additive and epistasis effects. As a baseline, we simulated $K=2$ pathways without quadratic terms and perfect coordination between additive and epistasis effects.

Finally, we used two alternative simulation frameworks to evaluate the calibration of our bootstrap test with respect to LD and dominance, which we described fully in Note S3.

Yeast data

We downloaded genotype and phenotype data for prototrophic haploid segregants from a cross between a laboratory strain and a wine strain of yeast.¹³ This dataset consisted of 46 quantitative traits for 1,008 samples genotyped at 11,623 unique markers. We standardized each phenotype and SNP to mean 0 and variance 1. Each phenotype represented growth rate on a different medium as measured by endpoint colony size assays. To account for LD in fixed-effect models, we used PLINK 1.9⁴² to clump and threshold variants at a threshold of $r^2<0.2$, minimum distance of 250 kb, and marginal additive $\mathrm{p}<0.05$. We performed clumping and thresholding separately on each cross-validated fold to avoid bias from overfitting.⁴³

Additionally, we downloaded a second yeast growth trait dataset from the same group with a larger sample size ($N=4390$).¹⁴ This second dataset contained 20/46 of the growth phenotypes in the first dataset, and it included 28,220 unique genotype markers for each sample. We preprocessed this dataset in the same manner as above.

We evaluated phenotype prediction accuracy with 10-fold cross-validation using the same 10-folds across all methods so we could test for differential prediction accuracy with paired t tests.

UKB data

This project used the UKB Resource under application number 30397 and application number 89052. All UKB participants provided informed consent. We studied the same four traits in UKB that were extensively characterized in Sinnott-Armstrong et al.³⁵: urate, insulin growth factor 1 (IGF-1), testosterone in males, and testosterone in females. We mainly focused on analyzing unrelated “White British” individuals as defined by UKB. We used the top 100 LD-pruned GWAS hits from Sinnott-Armstrong et al.³⁵ or all 77 GWAS hits for female testosterone. Prior to fitting EFA, we regressed out sex, age, batch, assessment center, and the top 10 genotype PCs from the phenotype.

We assessed statistical significance using 499 bootstrap samples to estimate standard errors and confidence intervals on the pathway-level interaction, λ. We computed empirical p values as $2·\min \left(B_{\lambda <0},B_{\lambda >0}\right)$, where $B_{\lambda <0}$ is the number of bootstrap samples where EFA estimates $\lambda <0$ (and vice versa for $B_{\lambda >0}$). We also report Gaussian p values obtained from Z scores computed as the bootstrap mean divided by the bootstrap standard deviation.

To test the biological significance of our inferred EFs, we used the annotations of GWAS hits to biological pathways provided in Sinnott-Armstrong et al.³⁵ We note that EFA outputs a continuous assignment of SNPs to EFs via the effect sizes in U; discretely mapping SNPs to EFs requires setting thresholds on EF-specific effect sizes.

We assigned SNPs to the epistasis factors by (1) polarizing SNPs to have positive additive effect sizes and (2) choosing the largest 10 effects on each EF after subtracting out additive effects from the EFs. To test robustness, we also evaluated results using the top 15 or 20 SNPs per EF (Tables S3–S7). We calculated p values for enrichment of these top SNPs in biological pathways with a hypergeometric test comparing the top 10 SNPs for each EF with the other 90 SNPs.

To test the portability of the EFs estimated in White British individuals, we performed ordinary linear regression in other populations by

$$\left(Y_{pop}-G_{pop}{\hat{U}}_1^{\left(wB\right)}-G_{pop}{\hat{U}}_2^{\left(wB\right)}\right)\sim 2·G_{pop}{\hat{U}}_1^{\left(wB\right)}\times G_{pop}{\hat{U}}_2^{\left(wB\right).}\text{.}$$ (Equation 5)

This yielded estimates and p values for population-specific values of $\hat{\lambda }$ based on the same EFs learned in the White British population, ${\hat{U}}^{\left(wB\right)}$. In this regression, $Y_{pop}$ and $G_{pop}$ are the (covariate residualized) phenotypes and genotypes of individuals from a given ancestry and ${\hat{U}}^{\left(wB\right)}$ is the EF effect sizes learned in White British individuals. As with most portability analyses, we expect these population-specific estimates of λ to be attenuated relative to the estimate in the White British population because our EFs are learned in that population.

We defined these populations based on self-reported “ethnic background” (UKB datafield 21,000). Specifically, we use two top-level categories (Asian or Asian British, shortened to “Asian,” and Black or Black British, shortened to “Black”). The third population we consider are the “White” individuals after excluding “British,” which we term non-British European. We exclude all White British individuals used to fit EFA and all individuals related to another individual in UKB.

Results

EFA recovers true pathways and improves prediction in simulations

We performed simulations to characterize EFA as a function of additive heritability ($h_{add}^2$), epistasis heritability ($h_{epi}^2$), and the fraction of epistasis heritability due to coordinated vs. uncoordinated effects (subjects and methods). We compared EFA with uncoordinated epistasis estimates fit either by fixed or random effects (subjects and methods). For each parameter setting, we ran 100 independent simulations and report the mean estimation accuracy for the pairwise SNP-SNP interactions ${\omega }_{j{j}^{\prime }}$ and for the EFs $U_{jk}$. EFA directly fits EFs and implicitly fits ω (using Equation 3 in the subjects and methods). Uncoordinated methods directly fit ω, and we derive uncoordinated EFs post hoc using PCs of the estimated ω matrix (subjects and methods).

First, we varied the relative contribution of additive and epistasis effects ($h_{add}^2$ vs. $h_{epi}^2$). We find that EFA outperforms uncoordinated estimates of ω across the range of $h_{epi}^2$, which is expected as we simulate from the EFA model (Figure 2A). EFA’s gain is greatest when $h_{add}^2\gg h_{epi}^2$, illustrating how EFA’s epistasis estimates borrow strength from additive effects. Analogously, EFA improves additive effect estimates over standard additive models when $h_{epi}^2\gg h_{add}^2$ (Figure S2), though this scenario is highly unlikely in practice. Additionally, EFA substantially outperforms uncoordinated estimates of EFs, which is expected because EFA specifically targets these low-dimensional factors (Figure 2B). This also shows how EFA leverages additive signals to improve EF estimates: when $h_{add}^2=0$, EFA actually underperforms the uncoordinated model, whereas EFA remains accurate even when heritability is 90% additive.

Figure 2.

Simulations characterize the accuracy of polygenic epistasis estimates

Points show the average across 100 simulation replicates, and the error bars depict the standard errors. Accuracy is quantified by the squared correlation between estimated and true pairwise SNP epistasis effects, ω (A, C, E) or between estimated and true EFs, U (B, D).

(A and B) Simulations under the EFA model vary the fraction of heritability due to additive vs. epistasis effects.

(C and D) Partial coordination is simulated by combining epistasis effects from the EFA model with uncoordinated epistasis effects.

(E) Model misspecification is evaluated by simulating and fitting EFA with different values of K, the number of EFs in the EFA^∗ model. In (B) and (D), the EF $R^2$ is nonzero even without any coordinated epistasis because the EFs still capture the additive effects in our simulation framework.

Next, we fixed $h_{add}^2=h_{epi}^2=25\%$ and varied the level of coordination by adding in uncoordinated epistasis effects (subjects and methods). EFA’s performance decays as coordination weakens, while the uncoordinated estimates remain stable because the uncoordinated model is agnostic to the structure of epistasis (Figure 2C). Nonetheless, EFA produces accurate estimates of the EFs even at mild levels of correlation (Figure 2D). Moreover, EFA always outperforms the uncoordinated estimates because EFA directly targets the coordinated component of epistasis.

To investigate EFA’s performance when the number of latent factors, K, is misspecified, we simulated from the EFA^∗ model (subjects and methods) with a true K and fit different EFA^∗ models with K being potentially misspecified. As expected, ω estimates are more accurate when fitting ${\text{EFA}}^{\ast }$ with the true value of K, though the base EFA model is robust to modest misspecification of K (Figure 2E). Again, the uncoordinated estimates remain stable as K increases and eventually outperform the EFA estimates. This is unsurprising, as the $K=\infty$ case is equivalent to uncoordinated epistasis³⁴; intuitively, the independent pathways become individually negligible and wash out. We did not consider EF estimation accuracy because EFs are not identified for $K>2$ (Note S1).

We next profiled the computational and statistical scalability of EFA by varying the number of SNPs, M, and sample size, N, while simulating from the EFA model with $h_{add}^2=9\%$ and $h_{epi}^2=1\%$ (Figure S1). Across all N and M, EFA always outperforms uncoordinated estimates of ω and the EFs. Performances for all methods decay as M grows because each individual SNP effect is smaller. This illustrates why modeling epistasis in complex traits is difficult. Likewise, all methods improve as N grows. In terms of run time, EFA is comparable with the uncoordinated model, fitting hundreds of SNPs with a reasonable computational demand. However, we note that fitting EFA requires an iterative algorithm, meaning that the EFA’s run times depend on its convergence rate while the uncoordinated model has a steady run time guaranteed by its analytic solution.

Finally, we asked whether EFA can improve phenotype prediction in our baseline EFA simulation. We found that EFA performs well, with out-of-sample prediction $R^2$ near the theoretical limit of $H^2$ (Figure 3A). EFA always outperforms the fixed-effect uncoordinated model as we vary the fraction of heritability that is additive, and EFA outperforms the random-effect uncoordinated model except when epistasis is absent.

Figure 3.

Phenotype prediction accuracy in simulations

Simulations and plots were conducted and created as in Figure 2. The y axis depicts the out-of-sample phenotype prediction accuracy as measured by $R^2$. The x axis varies the fraction of total heritability due to additive vs. epistasis effects (A) or the fraction of epistasis heritability due to coordinated vs. uncoordinated epistasis (B). The black dotted line indicates the broad-sense heritability, $H^2$, which is the upper bound for $R^2$, and the pink dotted line indicates the narrow-sense heritability, $h^2$, which is the upper bound for $R^2$ with the additive model.

We then fixed $h_{epi}^2=h_{add}^2=25\%$ and varied the fraction of epistasis that is coordinated, as above. Results were similar to ω estimation accuracy in Figure 2C: when epistasis is mostly coordinated, EFA is optimal, but EFA performs poorly when epistasis is uncoordinated (Figure 3A). Overall, EFA improves estimation of latent pathways in all our tests and improves prediction when epistasis is sufficiently strong and coordinated.

EFA improves prediction in complex yeast traits

We next asked whether EFA could improve phenotype prediction in complex traits. Using data from Bloom et al., we generated genetic predictions of 46 quantitative yeast traits measured on 1,008 samples, where each trait is defined as the yeast's growth rate on a different medium.¹³ These traits have varying levels of epistasis heritability, as defined by the difference between the phenotypic similarity of clones ($H^2$) and the additive heritability estimated from genotype data ($h^2$). We measured prediction accuracy by the squared correlation between predicted and observed phenotypes using 10-fold cross-validation. For each trait, we clumped+thresholded SNPs, which yielded 30–70 roughly independent SNPs ($r^2<0.2$, subjects and methods).

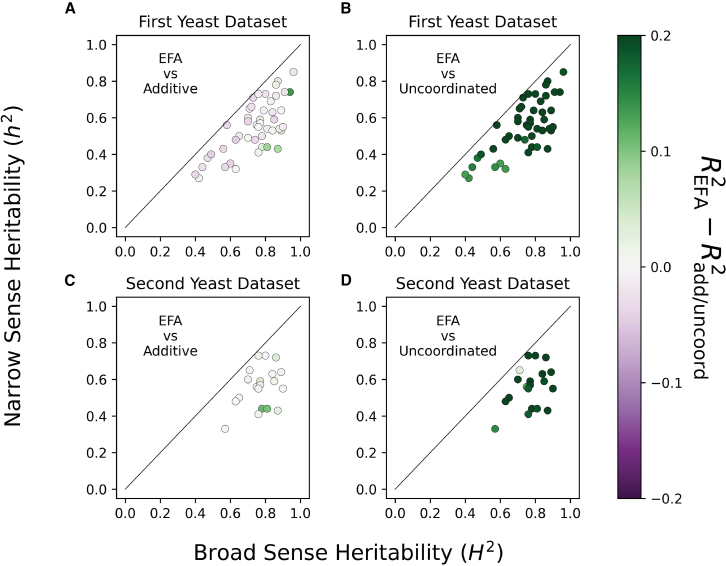
We first compared EFA with the additive model and found that EFA significantly improved prediction accuracy for 6/46 traits ($\mathrm{p}<0.05$, paired t test, subjects and methods, Table S1). These 6 traits all had large epistasis heritability as indicated by differences between $H^2$ and $h^2$ (Figure 4A). More generally, the traits that are furthest to the bottom-right of the diagonal in Figure 4A tended to be the traits for which EFA has the largest improvement over the additive model. Concretely, the difference between $R_{EFA}^2$ and $R_{add}^2$ correlated with the epistasis heritability (Spearman’s $\rho =0.48$, $\mathrm{p}<0.001$). This is consistent with our simulations showing that EFA can outperform additive predictions when $h_{epi}^2$ is higher. By comparison, the additive model significantly improved prediction over EFA for 20/46 traits. Finally, EFA predictions were superior to uncoordinated epistasis predictions using fixed effects for all 46 traits (Figure 4B).

Figure 4.

Phenotype prediction accuracy across complex yeast traits. Prediction accuracy is measured by $R^2$ between the out-of-sample predicted phenotypes and the true phenotypes in 10-fold cross-validation

Each point is a trait whose x and y coordinates are the broad- and narrow-sense heritability estimates from¹³ (A, B) or¹⁴ (C, D). Traits are colored by the difference between EFA prediction $R^2$ and the prediction $R^2$ of the additive model (A, C) or the uncoordinated epistasis model (B, D), where green indicates EFA is superior and purple indicates EFA is inferior.

(A) EFA significantly outperforms the additive model for 6/46 traits from Bloom et al., 2013 data.

(C) EFA significantly outperforms the additive model for 7/20 traits from Bloom et al., 2015 data.

(B and D) EFA always outperforms the uncoordinated fixed-effect epistasis model.

Next, we compared EFA with additive and epistasis random-effects models. Unlike fixed-effect models, including EFA, random-effect models can fit the whole genome without LD pruning, which is often a major advantage for prediction in complex traits.^18,44,45 Nonetheless, EFA significantly outperforms both additive and uncoordinated epistasis random-effect models for 7/46 traits ($\mathrm{p}<0.05$, Figure S3). We also compared the 2 random-effect models, and we found that the uncoordinated epistasis model significantly outperformed the additive model for 9/46 traits ($\mathrm{p}<0.05$). Intriguingly, these 9 traits only overlap 1 of the 7 traits where EFA outperforms the additive random-effect model. Together with our simulations in Figure 3B, this suggests that the degree of coordination varies across traits.

Finally, we evaluated replication in a second dataset from the same group with 4,390 samples measured on 20 of the above 46 traits (Bloom et al.,¹⁴ Figure S4). We analyze all 20 traits measured in Bloom et al.,¹⁴ which are a subset of the 46 traits in Bloom et al. 2013.¹³ We replicated the superiority of EFA over the additive model for all 3 traits where EFA beat the additive model in the first dataset ($\mathrm{p}<0.05$; the other 3/6 traits were not measured in the second dataset). Further, at this larger sample size, we find 4 additional traits where EFA significantly outperforms the additive fixed-effect model (Figure 4C; Table S2). We also replicate that EFA always outperforms the uncoordinated fixed-effects model (Figure 4D). Overall, EFA improves prediction over the additive model for some complex traits, and the utility of EFA will likely grow with larger sample sizes.

EFA detects epistasis and recovers known pathways in complex human traits

We applied EFA to complex human traits in UKB. We studied the same 4 traits that were extensively characterized in Sinnott-Armstrong et al.:³⁵ IGF-1, urate, testosterone in males, and testosterone in females. We used the top 100 LD-pruned GWAS hits for each trait (or all 77 for female testosterone) and fit EFA using our coordinate descent algorithm on the genotypes and phenotypes of unrelated White British individuals in the UKB (subjects and methods). While recent work has suggested that regions of long-range LD may be enriched for epistasis,⁴⁶ we chose conservatively to prune our SNPs as LD can generate subtle, non-additive statistical signals.^47,48

We first asked whether EFA detects statistically significant epistasis using the bootstrap to test whether $\lambda =0$. Specifically, we resample individuals to calculate the sampling distribution of $\hat{\lambda }$, the factor-level epistasis, which yields empirical p values and confidence intervals (subjects and methods). We used simulations to confirm that this bootstrap test is calibrated under the null model where SNPs are additive (Figure S5). Additionally, we performed realistic simulations with true epistasis and found that EFA’s λ estimates are unbiased and that EFA’s bootstrap test is powerful. A caveat is that our bootstrap confidence intervals are liberal in the presence of true epistasis, but this does not cause false-positive tests of epistasis.

The EFA bootstrap test finds significant epistasis for all 4 tested traits (all empirical $\mathrm{p}<0.05/4$; Figures 5E–5H and Table 1). For IGF-1 and male and female testosterone, λ is positive, while λ is negative for urate. Because we use 499 bootstrap replicates, the empirical p values are noisy and cannot be lower than 1/500. If we further assume that our estimate of λ is roughly Gaussian under the additive model, we get much lower and more numerically precise p values (Table 1). Our simulations suggest that this Gaussian approximation is conservative (Figure S6). To test robustness under the null, we repeated our analysis after permuting phenotypes. As expected, our bootstrap test was null (Table 1 and Figure S7).

Figure 5.

EFA identifies statistically and biologically significant epistasis in 4 complex human traits

(A–D) EFA jointly partitions the additive effects of GWAS-significant SNPs (x axis) into two EFs (y axis: difference between the EFs and the additive effects, i.e., $U_{jk}-{\beta }_j/2$).

(E and F) Bootstrap replicates show that EFA identifies significant epistasis in all 4 traits. Each histogram displays the distribution of $\hat{\lambda }$ across bootstrap replicates. Red lines indicate the symmetric $95\%$ confidence intervals calculated empirically from the bootstrap distribution. For visualization, 14 values of λ are excluded across all plots (out of a total of 6,000). See Figure S7 for comparable plots on quantile-normalized and permuted phenotypes.

(I–L) Distribution of estimated interaction between White British EFs in the Black, Asian, and non-British European populations in UK Biobank. Distributions obtained from standard linear regression of phenotypes on the product between EFs estimated in White British UK Biobank participants (see subjects and methods). Gaussian distribution mean and standard deviation given by the regression coefficient point estimate and standard errors, respectively.

Table 1.

EFA finds statistically significant evidence of epistasis in complex human traits

	IGF-1	Urate	Testosterone (male)	Testosterone (female)
Standard
Confidence interval	(0.25, 0.60)	(−0.50, −0.27)	(0.39, 0.70)	(1.19, 1.78)
Empirical p val	0.002	0.006	0.002	0.002
Gaussian p val	3.52e−04	1.16e−07	0.011	2.75e−04
QNorm
Confidence interval	(−0.30, 0.37)	(−0.57, −0.36)	(−0.46, 0.42)	(0.63, 1.04)
Empirical p val	0.570	0.002	0.826	0.002
Gaussian p val	0.689	7.67e−15	0.846	3.72e−2
Permuted
Confidence interval	(−0.28, 0.32)	(−0.47, 0.00)	(−0.46, 0.41)	(−1.48, 0.75)
Empirical p val	0.730	0.066	0.618	0.274
Gaussian p val	0.749	0.090	0.642	0.984

Empirical 95% confidence intervals were computed using the 0.025 and 0.975 quantiles of the bootstrap distribution. All p values are two sided.

Certain forms of epistasis can be entirely removed by a non-linear transformation of the phenotype onto a scale in which all effects are additive.⁴⁹ Therefore, we tested robustness to scale by quantile-normalizing phenotypes (Figure S7). We found that urate and female testosterone remained highly significant after quantile normalization (empirical $\mathrm{p}=0.002,0.002$; Gaussian $\mathrm{p}=7.7\mathrm{e}-15,3.7\mathrm{e}-13$). Moreover, the sign and magnitude of λ remained stable after this transformation. However, quantile normalization eliminated the EFA signal for male testosterone and IGF-1, which emphasizes the importance of evaluating scale dependence in interaction tests. Overall, our results increase confidence that the EFA signals for urate and female testosterone are not scale dependent, while the discrepancies for IGF-1 and male testosterone could either be false positives on the original scale or false negatives on the transformed scale.³⁴

Next, given the complexities of testing epistasis in complex traits, we performed a new set of simulations to evaluate our bootstrap-based test in several realistic scenarios that cause false positives in many epistasis tests. These simulations use the same broad framework as in Figure 2 in that they simulate from the EFA model, but instead of evaluating estimation accuracy, these simulations measure power and false-positive rates of our bootstrap-based tests.

First, we simulated a dominance model without any epistasis between distinct SNPs (Note S3). Under modest levels of dominance ($h_{dom}^2=0.1\%$^30,50), the bootstrap test is roughly null (Figure S5). Under stronger dominance ($h_{dom}^2=1\%$), however, the bootstrap test becomes significant (Figure S5). Both results are expected: dominance is not technically a false positive under EFA (unlike our prior even-odd test³⁴), but EFA primarily targets inter-SNP epistasis; hence, the EFA test has low power if dominance effects are the only form of epistasis.

Second, we simulated an additive model with unobserved causal variants in LD with measured variants. Our simulation meets the necessary condition for “phantom” epistasis in de Los Campos et al.,⁴⁷ which can cause severe bias in pairwise SNP-SNP epistasis tests (Note S3). For EFA, however, we do not observe any bias from ungenotyped variants (Figure S5). Intuitively, the phantom epistasis generated by this particular form of unmodeled LD is uncoordinated, so it cancels out at the level of pathway interactions. Nonetheless, in principle, other forms of LD could bias EFA estimates. Overall, the structured and polygenic nature of EFA substantially mitigates the LD biases that can plague other epistasis tests.^{18,48,51,52,53}

We next asked whether EFA captures biologically meaningful epistasis by comparing estimated EFs with the known biological pathways defined in Sinnott-Armstrong et al.³⁵ Specifically, we used a hypergeometric test for enrichment of the top 10 SNPs per EF, defined by EF-specific effect size, in each predefined biological pathway (relative to the other 90 GWAS SNPs, Table 2, subjects and methods).

Table 2.

Epistasis factors are enriched in predefined biological pathways

Trait	Biological pathway	# SNPs in EF1	# SNPs in EF2	# Top marginal SNPs	# SNPs total
IGF-1	downstream signaling	1 ($\mathrm{p}=0.284$)	0 ($\mathrm{p}=1.000$)	0 ($\mathrm{p}=1.000$)	3
	growth horm. secr.	0 ($\mathrm{p}=1.000$)	1 ($\mathrm{p}=0.361$)	2 ($\mathrm{p}=0.053$)	4
	IGF-1 secretion	0 ($\mathrm{p}=1.000$)	1 ($\mathrm{p}=0.361$)	0 ($\mathrm{p}=1.000$)	4
	IGF-1 serum balance	0 ($\mathrm{p}=1.000$)	1 ($\mathrm{p}=0.549$)	3 ($\mathrm{p}=0.023$)	7
	Ras signaling	0 ($\mathrm{p}=1.000$)	1 ($\mathrm{p}=0.430$)	0 ($\mathrm{p}=1.000$)	5
Urate	solute transport	3 ($\mathrm{p}=0.175$)	5 ($\mathrm{p}=0.007$)	7 ($\mathrm{p}=4.1\mathrm{e}-5$)	15
Testosterone (male)	steroid synthesis and metabolism	0 ($\mathrm{p}=1.000$)	1 ($\mathrm{p}=0.478$)	2 ($\mathrm{p}=0.109$)	6
	HPG signaling	0 ($\mathrm{p}=1.000$)	0 ($\mathrm{p}=1.000$)	2 ($\mathrm{p}=0.077$)	5
	serum homeostasis	0 ($\mathrm{p}=1.000$)	3 ($\mathrm{p}=0.001$)	1 ($\mathrm{p}=0.273$)	3
Testosterone (female)	steroid synthesis and metabolism	1 ($\mathrm{p}=0.638$)	0 ($\mathrm{p}=1.000$)	2 ($\mathrm{p}=0.223$)	7

We show pathways that have been assigned $>2$ SNPs used in EFA. p values are from a hypergeometric test of the top 10 EF SNPs in each biological pathway relative to the other 90 SNPs.

We find that EF2 for male testosterone is enriched in “serum homeostasis” ($\mathrm{p}=0.0001$). This enrichment is driven by SNPs assigned to SHBG and SLCO1B3, which live on different chromosomes (17 and 12). In urate, EF2 is enriched in “solute transport” ($\mathrm{p}=0.007$, Table 2), which is driven solely by a single locus with large effect (SLC2A9). This urate signal could either reflect genuine cis-trans interactions or could merely reflect subtle LD with unmeasured additive effects and/or dominance effects.³⁰ We confirmed these enrichments are robust if we instead use the top 15 or 20 SNPs per EF (Tables S3–S6). The results are also robust if we increase the window size used to assign SNPs to genes (Tables S3–S6). Altogether, EFA is capable of recovering biologically meaningful pathways using the SNPs that contribute to each EF.

For comparison, we next asked whether the top 10/100 additive SNPs are enriched in these pathways compared with the bottom 90/100 using the same hypergeometric test (subjects and methods). We find exactly 1 significant enrichment, which is for the same solute transport pathway in urate that EFA identifies. While these analyses provide context for the EFA enrichments, they are not directly comparable as they evaluate different parameters (additive vs. epistasis enrichments).

Finally, we examined whether EFA is portable across ancestries. Specifically, we tested replication in each of 3 additional populations defined by self-reported ethnicity (subjects and methods): non-British European, Asian, and Black. Because the sample sizes for these populations are much smaller in UKB, we did not attempt to fully replicate our EFA results. Instead, we built EFs from the EFs learned in the White British population, akin to constructing polygenic scores in a test dataset. We then estimate λ by fitting a regression of the phenotype onto the interactions between these EFs in each population (subjects and methods).

Overall, the regression-based estimates of λ are consistent across the Black, Asian, and non-British European populations (Figures 5I–5L). These estimates are attenuated but sign consistent with the EFA estimates from the White British population, which is expected when porting genetic scores between populations. However, the power of these tests varied substantially due to differences across traits and sample size differences across populations. In urate, for example, all populations had highly significant and similar estimates of λ (all three $\mathrm{p}<4\mathrm{e}-5$, Table S7). In male testosterone, at the other extreme, the estimates were insignificant and inconsistent across populations. IGF-1 and female testosterone lie between, with consistent estimates of λ across populations that were significant in the larger non-British European population but not the smaller Black and Asian populations. Altogether, this suggests that the interactions learned by EFA are generally portable across ancestries.

Discussion

Despite strong evidence for epistasis in many domains of biology, it remains unclear whether modeling epistasis adds biological or statistical value in complex traits. We introduced a model called EFA to address this question. In contrast to existing uncoordinated models of polygenic epistasis, which lack biological motivation, EFA assumes a structured form of polygenic epistasis driven by latent factors (Figure 1C). We showed that EFA outperforms additive predictions in several yeast traits and replicated this result in a second dataset. Additionally, we found that EFA can identify epistasis in complex human traits where standard models fail and that the EFs can partly recover known biological pathways without prior information. Finally, we showed the EF interaction replicates well across populations.

We found that EFA can improve prediction in model organisms and simulations, and it is likely that epistasis will eventually improve prediction in natural populations. However, the within-population prediction gain will likely be modest because additive models partly capture epistasis effects—especially when causal variants have been driven to lower frequencies by natural selection.^24,54 It is possible that epistasis predictions will improve portability across ancestries and it is promising that the EFs are somewhat portable, but epistasis has not yet been shown to contribute to this important problem.^55,56 Therefore, the greater promise of epistasis models in complex human traits is not better statistical prediction but rather better biological understanding of GWAS results. Our results showing that EFs are enriched in predefined genomic annotations provide support for this idea.

Many polygenic epistasis models have been previously developed. The standard model, which we call “uncoordinated,”³⁴ assumes that all SNP-SNP epistasis effects are independent of each other and of additive effects.³¹ While uncoordinated models are rigorous and easy to fit, they are biologically implausible and statistically under-powered.³⁰ More recent polygenic epistasis models make parsimonious assumptions to improve power and interpretation. For example, autosome-sex interactions represent a particular form of structured epistasis that is strongly supported in diverse complex traits^57,58,59,60 (though many of these interactions are at least partly due to gender, not sex). As another example, interactions between a single locus and a polygenic background can identify epistasis hubs.^{61,62,63,64,65,66} Finally, biologically annotated neural network (BANN) models complex traits as epistatic compositions of simpler pathways, like EFA, though BANN pathways are more numerous, less polygenic, and require prior biological annotations.⁶⁷

There are several important limitations to our study. First, like linear regression, EFA can fit dozens to thousands of genetic variants (Figure S1) but cannot jointly fit the entire genome. In practice, we pre-screen SNPs based on additive signals, such as selecting only GWAS-significant SNPs in UKB. This is because SNPs with additive effects are enriched in SNPs with epistasis effects.^24,68 Second, our polygenic epistasis tests do not establish interactions between any given SNP pair. In the future, sparse models (Bayesian or frequentist) could test which SNPs affect which EFs. Third, following Sinnott-Armstrong et al.,³⁵ we have only studied 4 relatively simple complex human traits, and it will be important in the future to evaluate EFA more broadly across more complex traits.

Another set of concerns is statistical false positives from phenotype scale and/or complex LD patterns. First, it is obvious that scale transformations of an additive trait can induce interactions.^34,49,69,70 Nonetheless, 2/4 of our human EFA signals are qualitatively identical on the natural and quantile-normalized scales, and coordination is theoretically robust to modest rescaling.³⁴ Second, LD with unmeasured causal variants can cause dramatic and replicating false positives, especially in small cis windows with large effects.^{18,48,51,52,53} We partly address this by LD-pruning SNPs, and we also use simulations to show that EFA’s polygenic nature reduces sensitivity to locus-specific LD biases. More broadly, EFA’s utility for prediction and biological characterization persists even if EFA signals reflect scaling and/or subtle LD patterns. Overall, these caveats are crucial for interpreting interactions, but they are not likely to impact our central conclusions.

There are several extensions to EFA that may prove useful. First, EFA could jointly model multiple traits that partly share EFs. This would add power to detect shared EFs and provide a rich decomposition of pleiotropy that goes beyond simple genetic correlation.^{71,72,73,74,75} Second, EFA could model complex diseases in a generalized linear-model framework, which is closely related to the idea of limiting disease pathways³³ and disease subtyping.⁵⁹ While the heterogeneous genetic architectures of binary case-control disease traits are naturally explained by the pathway-level model in EFA,^34,59 extending EFA to model such traits requires care as the forms of scale-dependence issues that generate non-additive signals can be particularly extreme for binary traits.^49,76 Third, we have focused on SNP interactions, but in principle, EFA is capable of modeling more powerful and/or interpretable genetic features such as imputed gene expression,^77,78 copy number variants,^27,28,79 or polygenic scores for secondary traits⁸⁰ or exposures.⁴¹ EFA could also incorporate non-genetic variables such as epigenomic marks, medical image-derived features,⁸¹ disease symptoms, or comorbidities from electronic health records. Fourth, it would be useful to quantify the variance explained by coordinated vs. uncoordinated epistasis, but extending EFA to a variance component model remains challenging because coordination cannot be modeled as a simple Gaussian random effect. Ultimately, we hope that the EFA model and its strong results in real data provide a solid step toward unraveling epistasis in complex human traits.

Data and code availability

• •We downloaded the first yeast dataset from http://genomics-pubs.princeton.edu/YeastCross_BYxRM/data/cross.Rdata and the second yeast dataset from https://static-content.springer.com/esm/art%3A10.1038%2Fncomms9712/MediaObjects/41467_2015_BFncomms9712_MOESM729_ESM.zip.
• •A python implementation of EFA is available at https://github.com/tangdavid/efa. This link also contains the code for all analyses in this paper, though the UKB analysis is not fully reproducible because the raw data is not public. An R implementation is available at https://github.com/andywdahl/EFA.

Published: November 2, 2023