Abstract
Mammalian and Drosophila melanogaster model mitochondrial membrane compositions are constructed from experimental data. Simplified compositions for inner and outer mitochondrial membranes are provided, including an asymmetric inner mitochondrial membrane. We performed atomistic molecular dynamics simulations of these membranes and computed their material properties. When comparing these properties to those obtained by extrapolation from their constituting lipids, we find good overall agreement. Finally, we analyzed the curvature effect of cardiolipin, considering ion concentration effects, oxidation, and pH. We draw the conclusion that cardiolipin-negative curvature is most likely due to counterion effects, such as cation adsorption, in particular of H3O+. This oft-neglected effect might account for the puzzling behavior of this lipid.
Graphical abstract
Significance
Mitochondrial membranes are of fundamental interest to the pathogenesis of neurodegenerative diseases. The biophysics of mitochondrial membranes can be expected to profoundly influence both the electron transport chain and larger-scale mitochondrial morphology. We provide model mitochondrial membrane compositions and examine their mechanical properties. Reconstructing these properties from their constituent lipids, we facilitate the creation of mesoscopic models. Cardiolipin, as the key mitochondrial lipid is given special attention. We find that its mechanical properties, in particular its curvature, are not constant, but highly dependent on specific ion effects, concentration, and oxidation state.
Introduction
Mitochondrial membranes have a number of unique properties that distinguish them from other cellular and intracellular membranes. At the molecular level, their most prominent features are the almost complete absence of cholesterol and the prevalence of cardiolipin (CL) in the inner mitochondrial membrane (IMM) (1), while the outer mitochondrial membrane (OMM) hosts machinery for lipid and protein transport. Mitochondrial lipids are increasingly studied for their relevance to disease pathogenesis. In particular, neurodegenerative diseases, such as Parkinson’s and Alzheimer’s disease are known to be associated with the oxidation of mitochondrial lipids (2,3,4,5) and Barth’s disease is the result of a failure of CL remodeling (6,7).
Mitochondria exposed to oxidative stress as well as undergoing other ion and lipid imbalances, exhibit distinct changes in their external and internal morphology (8,9). Internally, mitochondria contain folded lamellar membrane structures of their inner membranes, the so-called cristae (10). Mitochondrial membrane remodeling is known to be driven by an array of fusion and fission proteins, such as Drp1, the mitofusins, and Opa1 (11), as well as contact sites to the endoplasmic reticulum (12,13). These proteins require specific interaction with mitochondrial lipids to function (14,15), and the interplay of mitochondrial membrane lipids and the global shape of mitochondria is at present hardly understood. A particular source of confusion continues to be CL. CL is essential for the cristae’s structure and functioning and was originally considered a proton conductor (5). This hypothesis is particularly appealing as the lipid also appears in chloroplasts and strongly interacts with the electron transport chain, in particular complex IV. However, it has been shown that, at physiological pH, CLs are not protonated (16,17). At the same time, it is often claimed that CL has a strongly negative curvature and is very fluid. This hypothesis is supported by lipid sorting experiments (18,19). However, CL is also stable in the lamellar phase (20)—which is seemingly at odds with such behavior. Moreover, relatively high bending rigidities have been reported for it (21).
Perhaps the special features of mitochondrial membranes result from their complex lipid compositions. In experimental setups, typically mixtures of PE, CL, and PC lipids, containing a single component for each headgroup are employed as model mitochondrial membranes (22).
Therefore, we begin this study with the construction of model mitochondrial bilayers for mammalian mitochondria as well as Drosophila. In the next step, we compute the bulk mechanical properties of the resulting systems and compare them to the bulk properties extrapolated from their constituent lipids. For this purpose, we use a recently developed methodology that allows the extraction of bending rigidity as well as tilt moduli and spontaneous curvatures for these lipids (23,24) from molecular dynamics (MD) simulations.
In the next step, we consider the effect of membrane asymmetry, lipid oxidation, curvature, and lipid imbalances as well as the presence of ions. Specific ion-membrane interactions elucidate how the interplay of electrostatics and curvature are the key to understanding mitochondrial membrane structure.
Methods
Computational details
Most of the solvated bilayers were constructed using the CHARMM-GUI input generator (25). Typically, the systems contain 200 lipids (i.e., 100 lipids per leaflet) and ca. 10k water molecules. For detailed system compositions, see Table S9. To maintain a near physiological salt concentration, 150 mM KCl was added on top of the counterions necessary to neutralize the membranes (where applicable). The lipid types used in this paper are—1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (POPE), 1,2-dioleoyl-sn-glycero-3-phos-phocholine (DOPC), 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE), 1,2-dipalmitoleoyl-sn-glycero-3-phosphoethanolamine (DYPE), 1,2-dipalmitoleoyl-sn-glycero-3-phosphocholine (DYPC), 1,3-bis-[1,2-di-(9,12-octadecadienoyl)-sn-glycero-3-phospho]-snglycerol (tetralinoleoyl cardiolipin, TLCL), 1-stearoyl-2-linoleoyl-sn-glycero-3-phospho-L-serine (SLPS), and 1-palmitoyl-2-linoleoyl-sn-glycero-3-phosphoinositol (PLPI, e.g. from soy PI). We also refer to the headgroups of these lipids, using the second part of the four-letter abbreviations, e.g., PE refers to phosphoethanolamine. In our simulations, CL is fully deprotonated (–2e charge), as it is known to be at physiological pH values (16). Unless mentioned otherwise, all lipids were modeled using the CHARMM36 force field (26). For one of the CL bilayer system preparations, we used the OPLS-AA force field (27) and, in that particular case, we used SPC/E water model (28). Whereas, for all other systems we used the TIP3P model to hydrate the systems (29). Furthermore, when we checked the effect of ionization on the CL bilayer, we replaced half of the K+ ions in the system with H3O+ (30,31). Simulations were performed at 303.15 K temperature, using the Nosé-Hoover thermostat (32) with a time constant of 1.0 ps. Our choice of temperature was made according to availability of data and falls within the interval of common biological (Drosophila/mammal) and laboratory environments. Pressure was maintained at 1 bar using the Parrinello-Rahman barostat (33) in a semi-isotropic setup (coupling the membrane plane separately from its normal) with a coupling constant of 5.0 ps. Long-range electrostatic forces were treated using the particle mesh Ewald method (34) with a real-space cutoff of 1.2 nm. Lennard Jones interactions were cut off at 1.2 nm with a force switching starting at 1.0 nm and a 2 fs timestep was used for integration. Covalent bonds were constrained using the LINCS algorithm (35). All simulations were performed at a constant pressure of 1 bar with a compressibility of 4.5 × 10−5 bar−1.
After initial relaxation, all the systems were run for 200 ns in an NpT ensemble for lipid bilayer equilibration. For production, the systems were run for 400 ns in an NpT ensemble using GROMACS 2020.3 (36,37). Bilayer simulations were performed using semi-isotropic pressure coupling. The lateral pressure profile calculation was carried out using the Sega code (38), modified with a Goetz and Lipowsky (39) force decomposition. To compute lateral pressure profiles, we ran a separate simulation of 200 ns length with triangular water molecules (as SETTLES are unsupported), which was carried out after pre-equilibration. The neighbor list was updated every 20th step and covalent bond lengths were constrained using the LINCS algorithm. Here, we have increased the LINCS order to 5 to deal with the nonlinearity introduced by the constrained H2O ring and turned off force switching. Pressures and velocities were sampled for 25,000 frames to compute the lateral pressure profile.
Extraction of material properties
The spontaneous curvature (C0), bending modulus (κc), and tilt modulus () parametrize the Hamm-Kozlov Helfrich free energy functional (40,41,42,43,44,45,46). These membrane elastic properties are sufficient to model mesoscopic membrane structure, including membrane fusion and fission (47,48). In addition to the curvature elastic parameters, we also compute the area compressibility modulus , which is useful, e.g., for surface tension computations. Our previously developed a computational (ReSIS) approach was used to quantify the κc and value from local fluctuations of lipid splay and tilt degree of in real space (23,49,50,51,52).
The first moment of the lateral pressure distribution is linked to the monolayer spontaneous curvature () and bending modulus (κc) by (53)
| (1) |
The integration must be carried out along to the z axis from the bulk (z = –l) to the center of the lipid bilayer (z = 0), the integration is carried out over each monolayer separately and then averaged. Using the ReSIS value of κ, we computed the spontaneous curvature () from Eq. 1. We ensured the membranes to be tension free by requiring the surface tension σ to be zero, i.e., subtracting an adequate constant normal pressure from the averaged local, diagonal stress components . We verified the freedom from surface tension by making sure that the required normal pressure, , was close to 1 bar and by checking the z component of the virial in the simulation. We have set l to be either half the box z dimension, or 6 nm for very large systems, as pressure fluctuations and uncertainties contribute proportionally to l. 6 nm was sufficient to achieve a charge neutral bulk in all examples considered.
| (2) |
The lateral pressure profile can be rigorously connected to the surface tension and will provide a valid bending moment for the Helfrich functional. It is not clear, however, if the Helfrich functional has the same coefficients for very large curvatures, such as in an inverted hexagonal phase.
Results and discussion
Model lipid distribution of mammalian IMM and OMM
A model lipid distribution for mitochondrial membranes is useful for experiments and MD simulations, e.g., of mitochondrial membrane proteins. To build a realistic mitochondrial membrane model, we considered both the acyl chain composition of mitochondrial membranes and their headgroup composition. We follow Daum’s example by using a rat liver mitochondrial headgroup composition to represent mammalian cells (54). Details and literature are given in Tables S1 and S4. The composition of acyl chains for lipids in living organisms is very diverse; nevertheless, there are usually only a few species that dominate the fatty acid composition of each lipid. Thus, the number of species was limited in a pragmatic manner to a few, ideally commercially available lipids. The data by Daum does not contain any assignment of the acyl chains to lipid headgroups. Assigning these to the tails is nontrivial. We departed from the membrane specific acyl chain determination by Ardail et al. (55). We consider the length of acyl chains to be less important to the lipid physical properties than lipid (un)saturation. Accordingly, we simplified the total acyl chain composition based on the saturation type, interpolating between data by Daum (56) and lipidomics data by Oemer et al. (57). Arachidonic acid (C20:4) and linoleic acid (C18:2) are grouped as unsaturated lipid type. It is known that 18:2 CL is dominant in rat liver (58). Hence, we chose this as the exclusive CL tail. Due to our simplification of 20:4 to 18:2 tails, we chose 16:0/18:2 for PI and 18:0/18:2 for PS lipids, with good experimental support from rodent mitochondria, in the sense that there is a dominant species with a saturated and a polyunsaturated tail for both PS and PI (59,60). We note, that arachidonic acid appears as the dominant unsaturated species, especially for PI, but expect the effect on bulk properties to be minor.
Further details on our simplification are given in Tables S2 and S3. The distribution of lipid tails for PC seems broad; we choose two variants of PC, 1-palmitoyl-2-oleoyl (C16:0/18:1) and di-palmitoyl (C16:1/16:1) (60). As a result, our final composition has a lower 18:0, and higher 18:1 content than the experimental data. The resulting, slightly lower fraction of fully saturated chains is necessary to keep all components of the membrane fluid at the simulation temperature, for separate mechanical evaluation. For PE, we chose POPE to fulfill the total (simplified) composition with a typical acyl configuration. The simplified acyl chain for the OMM was constructed in an analogous manner. Here, we considered two acyl variants (16:0/18:1 and 16:1/16:1) for PC and PE, a single variant for PI (16:0/18:2), CL (18:2/18:2), and PS (18:0/18:2). We then estimate each acyl chain variant that is distributed among each phospholipid, as done before. The calculated percentages of acyl chain variants are shown in Table S3. The final model lipid compositions in mammals based on acyl chain and headgroups for IMM and OMM are shown in Fig. 1.
Figure 1.
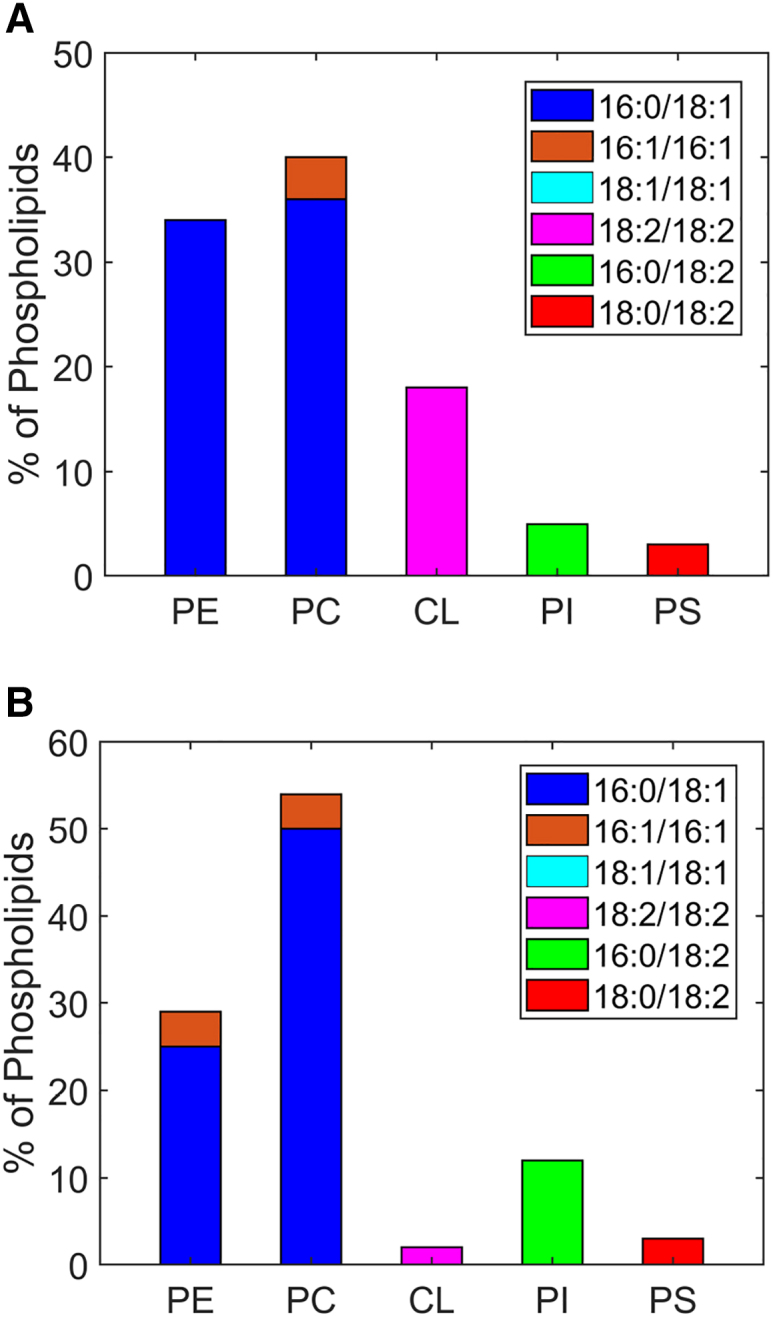
Model lipid compositions of mammalian mitochondrial membranes. Lipid distribution in mammalian (A) IMM and (B) OMM showing headgroup as well as fatty acyl chains of the lipids. To see this figure in color, go online.
Mammalian mitochondrial membranes have more PC content in both IMM and OMM than PE. As is well established, CL content is far higher in the IMM than in the OMM.
Construction of IMM and OMM model lipid compositions for Drosophila
Acehan et al. (61) determined the total headgroup composition of Drosophila mitochondrial membranes. However, the compositions of IMM and OMM were not measured separately. Hence, we started by creating a model of Drosophila mitochondrial membranes in combination with other data. The first step was to estimate the distribution of headgroups across the mitochondrial membranes.
The percentage of phospholipid headgroups in IMM and OMM of mammals is known from the literature and given in Table S1. To build a membrane model for Drosophila, for each lipid headgroup we estimate its distribution via the ratio of IMM to OMM (NIMM/NOMM). Furthermore, we determine the global lipid fraction of IMM (χIMM) and OMM (χOMM). Then, the average total percentage, or, in our case of 100 lipids per leaflet, the number of phospholipids is decomposed as follows:
| (3) |
where χIMM and χΟΜΜ are the fractions of lipid in the inner and outer membranes, respectively. We take these fractions to be 0.8 and 0.2, meaning that 80% of total lipids are in the IMM. Knowing the total lipid composition from literature and taking the headgroup distribution ratio to be equal to that found in mammals (i.e., estimating the ratio of, e.g., PE in inner versus outer membrane to be conserved), it becomes possible to estimate the headgroup composition for OMM and IMM of Drosophila.
We controlled our estimate of χIMM and χΟΜΜ by reproducing the average headgroup composition of phospholipids from the data of Horvath and Daum (54). Furthermore, we find that our estimate also reproduces the total lipid compositions of plants well (for which total and relative data are given by Daum). The resulting headgroup composition is shown in Table S5.
Full lipid distribution of IMM and OMM for Drosophila by combining acyl chain and headgroup compositions
We obtained the acyl chain composition from Dubessay et al. (62) and used it to estimate the lipid distribution of the IMM for Drosophila. Following the simplification and headgroup assignment procedure described model lipid distribution of mammalian IMM and OMM and construction of IMM and OMM model lipid compositions for Drosophila, we considered three acyl chain variants for PC, PE, and a single variant for the charged PI, CL, and PS lipids. These were based on the lipid simplification given in Tables S6 and S7. After assigning PI, CL, and PS as before, we distributed the rest of the acyl chains into the neutral lipids equally into the IMM and OMM to fulfill the total acyl chain composition requirement given in Table S5. Results are shown in Fig. 2.
Figure 2.
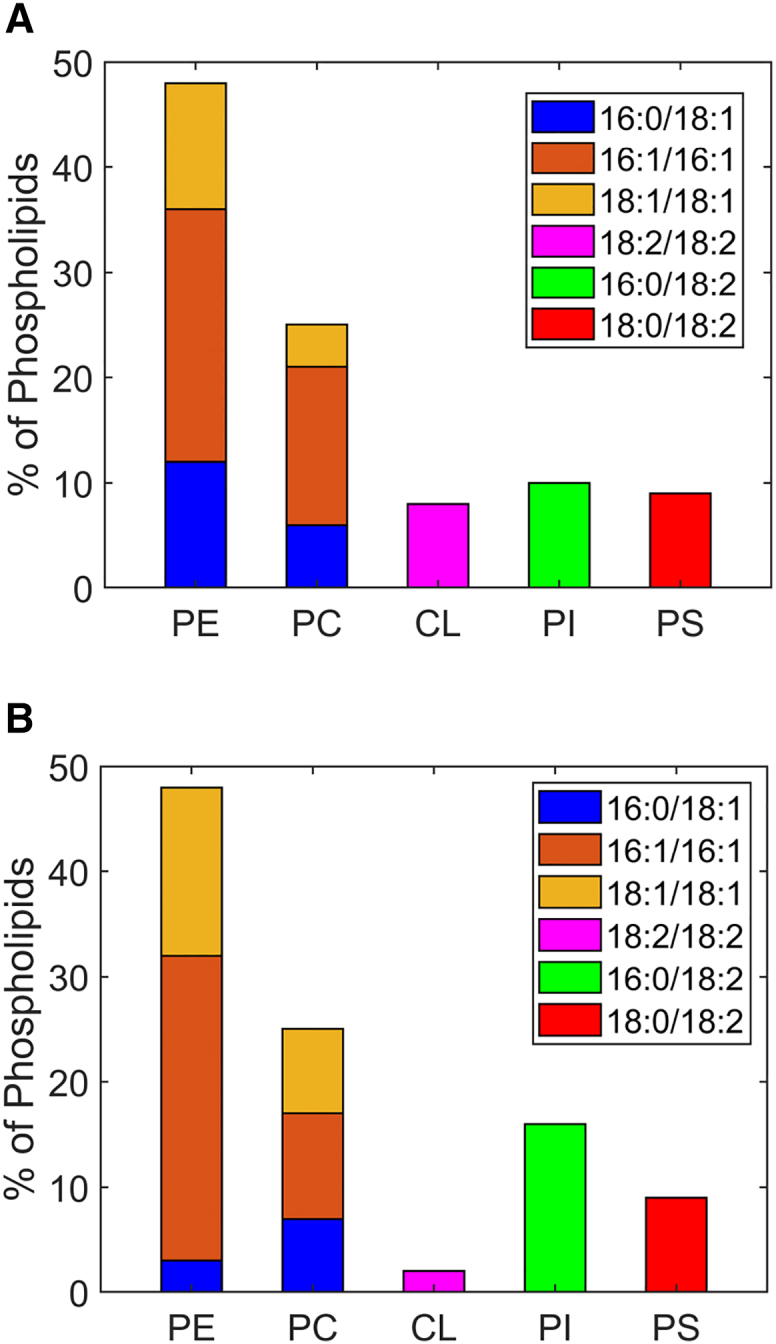
Model lipid composition of Drosophila IMM and OMM. Lipid distribution in (A) IMM and (B) OMM showing headgroup as well as acyl chains of the lipids. To see this figure in color, go online.
It follows from our approach that, due to the higher PE content found in the mitochondria, both in IMM and OMM, PE is the dominant headgroup. Accordingly, the main differences between IMM and OMM arise from their CL and PI lipid contents. CL is present predominantly in the IMM, whereas PI is typical for the OMM.
Model of the asymmetric lipid distribution of the mammalian IMM
Lipids are asymmetrically distributed in the inner and outer leaflets of biological membranes. In particular, CL is localized mostly in the matrix side of the IMM. An asymmetric membrane lipid distribution between outer and inner leaflets might show some significant changes in their biophysical properties such as bending, rigidity, and spontaneous curvature for each monolayer. To build an asymmetrical IMM model, we selected the mammalian system as there is a known lipid headgroup distribution for the inner and outer leaflets of IMM and OMM (54). Area mismatch between two asymmetrical leaflets (in the sense of a stress-free reference area) can lead to one of the leaflets being under tension, whereas another might be compressed. To avoid this, we simulated each membrane leaflet in a separate, symmetrical configuration. We verified that the total area difference was small (see Fig. S2) and then we assembled the asymmetrical mitochondrial membrane by combining the two leaflets. In principle, the leaflets also do not need to be independent from each other, and interdigitation may affect the packing of the opposing leaflet (63,64). However, our combined membrane has an area that corresponds closely to what would be expected for a simple combination of independent leaflets. The lipid distribution in the asymmetrical membrane model was obtained by sorting the mammalian IMM model composition according to (54). However, the data in that reference does not really admit to matching the areas due to the area per lipid (APL) of CL being approximately twice that of other lipids. Accordingly, we distributed some PC and PS into the CL-depleted intermembrane space side (see Table S8 for full details). Our proposed asymmetrical IMM model composition for mammals is shown in Fig. 3.
Figure 3.
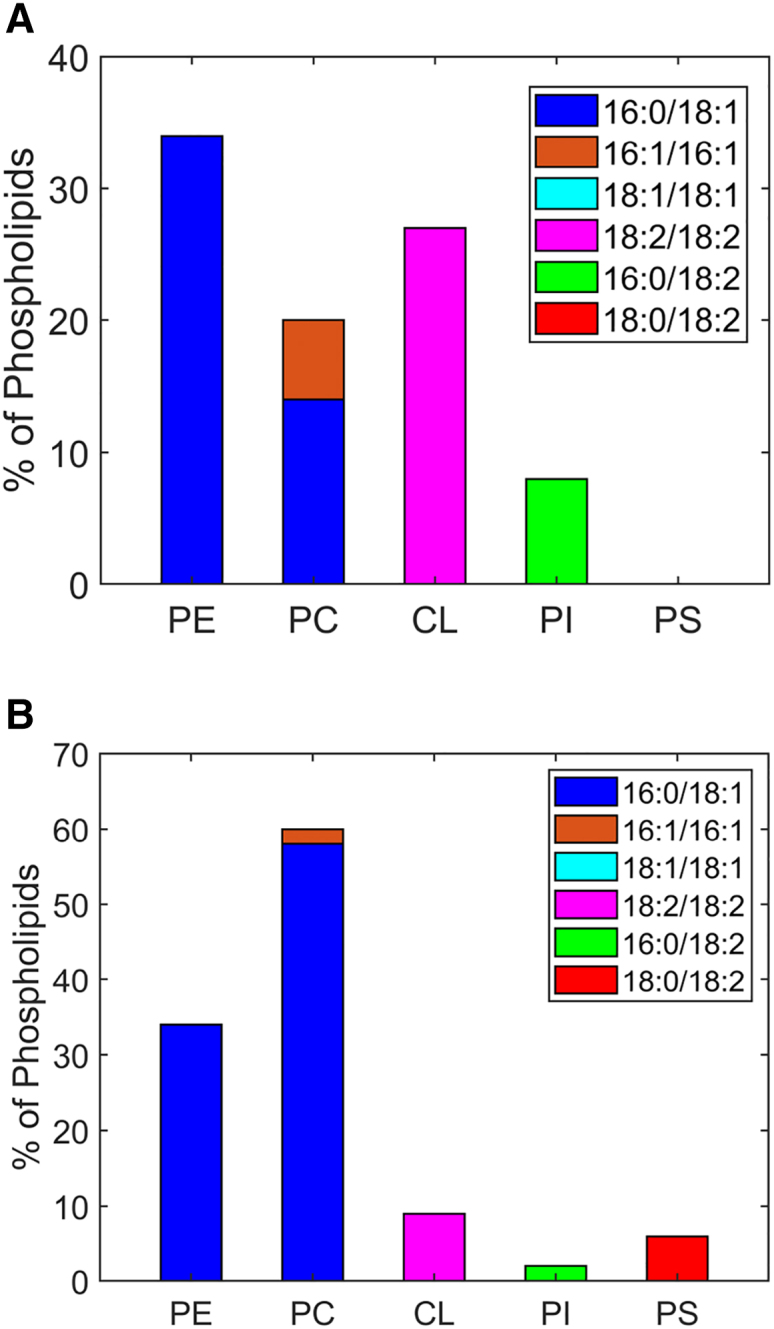
Asymmetric lipid distribution of inner (matrix) and outer (intermembrane space) leaflets of mammalian IMM. Lipid distribution in inner leaflet (A) and outer leaflet (B). To see this figure in color, go online.
Material properties of the membranes
APL and thickness of the lipid bilayers
To understand the structural properties of the bilayers, we first computed the APL and lipid bilayer thickness of the model mitochondrial membranes (IMM and OMM) for both symmetric and asymmetric membranes as listed in Table S10. In addition to the model mitochondrial membranes, we also computed the properties for single-component lipid membranes for all their components, using the CHARMM36 force field with the ultimate goal of checking the validity of commonly used mixing rules for membranes. APL and bilayer thickness of these lipid variants are also listed in Table S10. The APLs and bilayer thicknesses of single-component DOPC, POPC, DOPE, and POPE bilayer systems are in agreement with previously reported data (48,65,66).
We will now focus on CL. Because of the relevance of this lipid, we computed its structural and elastic properties using different force fields, namely CHARMM36 and OPLS-AA. The APL for the CL [(18:2)4] system using the CHARMM36 force field is 137.1 Å2, which is slightly higher than the corresponding value when using the OPLS-AA force field (132.5 Å2). The CL-OPLS-AA force field shows better agreement with the reported experimental data (129.8 Å2) by Pan et al. for TOCL [(18:1)2:(18:1)2] (67). CL oxidation is considered an important potential factor for mitochondrial diseases. Therefore, to examine the potential changes due to CL oxidation, we have also considered an oxidized form of cardiolipin (CLox) by substituting one of the acyl chains with 13-hydroperoxy-trans-11,cis-9-octadecadienoic acid (13-tc) in OPLS-AA (68). CLox has higher APL (∼142.8 Å2) than CL (∼132.5 Å2) using OPLS-AA. Note that this is far from the only possible oxidation product, but simulating single-component membranes composed of more oxidized forms, such as Lysolipids, will destabilize the bilayer too much. Area compressibility moduli were computed using Eq. 3 and are reported in Fig. S3. They do not show large differences between mitochondrial membranes across species.
Monolayer bending rigidities, spontaneous curvatures, and tilt moduli
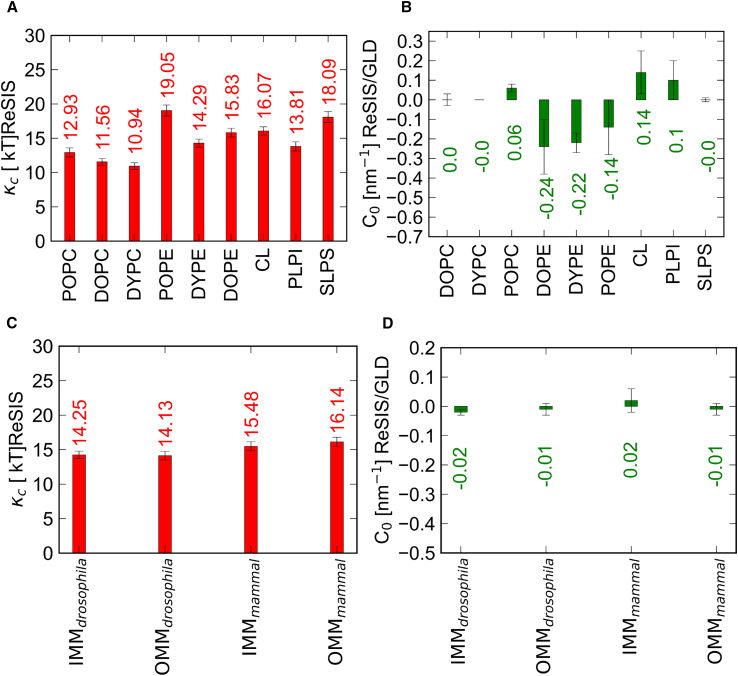
The bending modulus κc and the spontaneous curvature C0 are some of the most important parameters that determine the mesoscopic behavior of membranes, as they describe the resistance against bending deformations and the preferred membrane geometry. If we want our mitochondrial membrane models to be available for mesoscopic modeling studies, we need to determine the membrane elastic properties under different conditions, including mixtures. We want to address the question—“Will the different mitochondrial membrane lipid composition found across species affect the mechanical properties of the membrane or not?” While different types of ions (divalent and monovalent) modulate the membrane elasticity (69,70,71,72,73), we probe the case of the noncoordinating salt KCl. The lipid composition of IMM/OMM for Drosophila significantly differs from the lipid composition for mammals. To find out whether this difference leads to important changes in the elasticity of the membrane, we calculated κc, C0, and the tilt modulus, for the model membrane systems (shown in Figs. 4, C, D, and S1 B). Simultaneously, we calculated κc and for the bulk lipid systems (Figs. 4, A, B, and S1 A).
Figure 4.
Elastic properties and spontaneous curvature of the bulk system and model mitochondrial membranes (IMM and OMM) for both species. (A) Monolayer bending rigidities (κc) (in kT) and (B) spontaneous curvature (C0 value in nm−1) of bulk systems. (C) Monolayer bending rigidities (κc) (in kT) and (D) spontaneous curvature (C0 value in nm−1) of IMM and OMM of Drosophila and mammal. Error bars show the ΔC0 value (it is calculated based on the difference of the C0 values of each leaflet) or the standard error on κc estimated from subsamples, respectively. To see this figure in color, go online.
Although the IMM and OMM compositions of the model membranes (Drosophila and mammal) are different from each other, their κc and values do not differ strongly. In contrast to this, large differences in all of these parameters occur for the single-component lipids. We do not know whether the homogeneity of bending elastic parameters is a coincidence or that it reflects the diversity of evolutional outcomes, which lead to functional membranes.
C0 is an important parameter as well as lipid-specific property, hence we computed the C0 values for our model mitochondrial membranes. Fig. 5 D shows the C0 values for IMM and OMM for two types of species and the asymmetric membrane. Although, the IMM compositions of Drosophila and mammals differ, their C0 values are close to each other. The expected C0 values for Drosophila are slightly below those of the mammalian ones due to their higher PE content (34 vs. 53%) (for the IMM, see Fig. 5 D). The values from direct simulation and estimates from extrapolation agree well: in contrast to recent coarse-grained (CG)-MD studies the atomistic simulations of mitochondrial membranes (74) have very small amounts of spontaneous curvature. The small differences in the estimated values are mainly due to PE and CL content, which act in opposite directions. In simulation, all mitochondrial membranes are close to ∼0 nm−1. Considering the uncertainties on the single-component values for C0 (see error bars in Fig. 4 B), the agreement with the prediction is quite good. In conclusion, we observed no major difference in the bending rigidity and spontaneous curvature between these two models. This stands in marked contrast to the behavior of the single-component lipids, which show marked differences in spontaneous curvature, as is expected (24,48). The material properties suggest that the unique biological properties of mitochondrial membranes are not due to global curvature elastic terms but might significantly change via local demixing induced, e.g., by proteins.
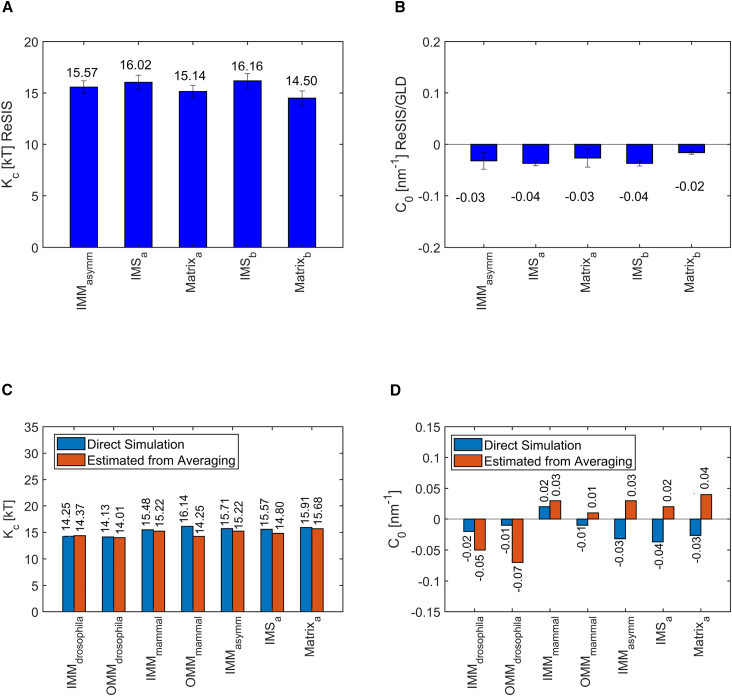
Figure 5.
Comparison of the elastic properties of the asymmetrical model IMM. (A) Bending rigidity (κc) (in kT). (B) Spontaneous curvature (C0 in nm−1) of IMM for mammals, asymmetric membrane, and inner and outer leaflet of IMM, respectively. (C) Monolayer bending rigidity (κc) (in kT) of mitochondrial membranes of Drosophila and mammals comparing ReSIS methodology and the direct simulation method with values computed from single component mixing rules. (D) Equivalent comparison of the spontaneous curvature (C0 in nm−1) of the corresponding membranes. Error bars show standard errors estimated from subsamples. To see this figure in color, go online.
Another potential issue is whether the curvature elastic properties of mitochondrial membranes are significantly affected by their asymmetric lipid composition. Several known examples of asymmetric membranes suggest that important differences are possible, especially for domain forming lipids (75,76). Fig. 5, A and B shows the bending rigidities (κc) and spontaneous curvatures (C0) for the asymmetric membranes. Initially, we found that the κc of the symmetrized IMM (mammals) and asymmetric IMM (IMMasymm) are almost the same, i.e., 15.4 and 15.6 kT. We calculated κc for IMM and separately for both leaflets (inner and outer leaflets) of the IMM. Here, is the outer leaflet and is the inner leaflet of asymmetric IMM, where inner refers to the mitochondrial matrix side, and outer leaflet represents part of the membrane in the intramembrane space side. We observed only a small difference between the κc for each leaflet of the IMMasymm. We further examined asymmetry and possible interdigitation effects by comparing the monolayer values and with properties computed from a symmetric bilayer of the inner and outer IMM composition. These are marked with and do not differ significantly from the monolayer values. Similarly, the C0 and κc for and are within the margin of error for the C0 for IMM (mammals) and asymmetric IMM. This result clearly suggests that for the purpose of global material properties of mitochondrial membranes, asymmetry is not a strong factor and does not introduce additional complications in the computation of bending rigidities and curvatures of fluid membranes beyond the need to match equilibrium areas. Our membrane simulations setups are tension free (σ = 0 pN/nm), the differential stress from the pressure profile (the difference between surface tensions of the leaflets) is 0.9 pN/nm. Comparing this value with existing literature data (77), the monolayer surface tensions are very small and can be considered negligible.
Extrapolation of elastic properties of IMM and OMM by simple mixing rules
Just like any other biological membrane, mitochondrial membranes are locally inhomogeneous. CL is known to be strongly sorted by negative curvature in experiments (18,19). This stands in direct, apparent contradiction to our results that show negligible curvature. To make a useful mesoscopic model without the need to re-extract properties for any composition, we need a way to generate the elastic properties for different compositions. Our simulation of all lipid components as one component systems and the consistent extraction of their simulated properties enables us to test well-established empirical equations for the mixing of membrane properties. As proposed (52), the bending rigidity of a lipid mixture is estimated via a harmonic mean of the corresponding values of its constituents. Accordingly, the bending rigidity ( ) of the mitochondrial membrane can be calculated using,
| (4) |
where represents the area fraction of the individual lipid component (PC, PE, or CL) present in the mitochondrial membrane. The index runs over the individual lipid types present in the IMM or OMM. The values for each bulk lipid system are shown in Fig. 4 A. Likewise, the spontaneous curvatures () of different IMM and OMM compositions are typically estimated in the literature (78,79) by direct averaging over the spontaneous curvatures of the constituent lipids (here the areas per lipid are neglected, see Fig. 4 B for the values used):
| (5) |
| (6) |
Here, represents the area fraction, refers to an APL of the lipid species i, and refers to the number of lipids of type present in the bilayer. In addition, it is assumed that the APL does not change during lipid mixing.
Fig. 5C shows the estimated values for obtained by using these averaging procedures. The predicted average value of matches well with the ReSIS method for both species of mitochondrial membrane (IMM and OMM) (Fig. 5 A). This is a very encouraging result, as it allows us to simultaneously confirm the consistency of the ReSIS results and explain the very similar properties found for the different types of mitochondrial membranes.
Fig. 5D shows the values for IMM and OMM of Drosophila and mammals as estimated by Eq. 6. Here, the predicted average value of spontaneous curvature shows some differences with the values obtained by the direct simulation method (Fig. 5 B), mainly due to the higher DOPE content. However, this difference is not very large. Thus, we conclude that these two equations are helpful in predicting the elastic nature of the membrane when its composition is known. The estimation from the components allows us to construct curvature elastic properties for any realistic mitochondrial membrane headgroup composition. That might be of value in future, more detailed mesoscopic models.
We have noted that the predicted curvature from the components somewhat deviates from the curvature found in direct simulation. The deviation is definitely not large (with respect to the method errors), but it may point toward some potential sources of disagreement. For example, we have not considered the effect of counterion distribution and the reduced charge density when going, e.g., from single-component CL or PS to a membrane mixture. Overall, it is surprising that the combined deviation seems this small, considering the rough approximations made.
The puzzle of CL
Our extraction of mitochondrial membrane material properties has not resulted in any special properties for CL; we have not obtained a low spontaneous curvature for CL. Boyd et al. already predicted a very small absolute C0 value of the bulk CL system (6). It is of particular interest to mitochondrial pathologies to also check the effect of lipid oxidation for CL.
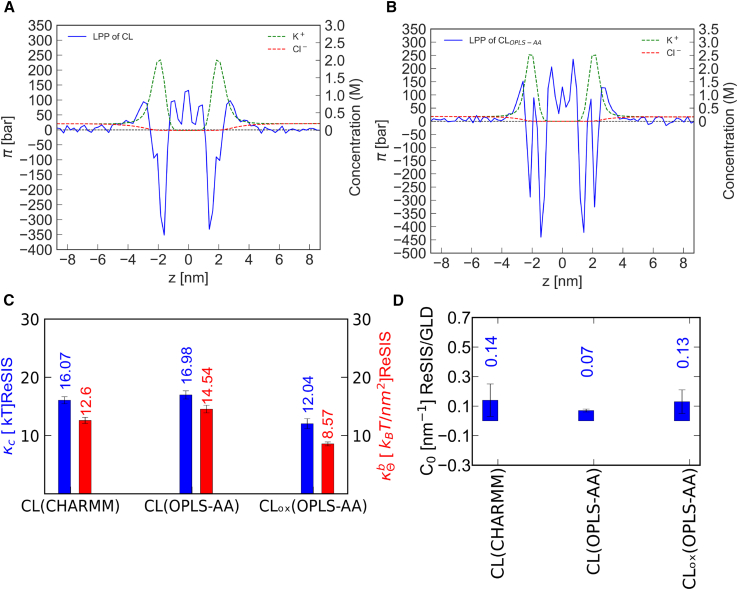
The monoperoxide form of CL has a lower κc (12.0 kT) than the native form (17.0 kT), which can be explained by the less favorable lipid tail packing and the concomitant increase in APL (∼140 Å2). Overall, the tilt modulus of all CL variants is low in comparison with its bending rigidity (Fig. 6 C). This may have profound structural implications, e.g., by privileging tilt deformations over bending deformations. It might also explain the widely held view that CL is a “soft” lipid. The apparent softness of CL would then be due to its chain tilt and not due to its susceptibility to bending deformations.
Figure 6.
Comparison of lateral pressure profiles of CL. Lateral pressure profile of CL (A) using the CHARMM force field and (B) the using OPLS-AA force field (left axis), with K+ and Cl− ion concentration (right axis) along the bilayer normal. (C) Elastic properties of CL using different force fields. Bending rigidity (κc) (in kT) and tilt modulus () (in kT/nm2 unit) of cardiolipin (CL) for different force fields as well as normal and oxidized forms. In this figure, CL(OPLS-AA) represents the normal form of CL, whereas CLox(OPLS-AA) represents the oxidized form of CL using the OPLS-AA force field. (D) Spontaneous curvature of CL for different force fields. The spontaneous curvature (C0 in nm−1) of CL is given at different hydration levels, force fields (CHARMM and OPLS-AA), and in its oxidized form. In this figure, CLox(OPLS-AA) represents the oxidized form of CL using the OPLS-AA force field. Error bars show the ΔC0 value (it is calculated based on the difference of the C0 values of each leaflet) or the standard error on κc estimated from subsamples, respectively. To see this figure in color, go online.
Conventional wisdom suggests that, due to its small headgroup and relatively large tail (four acyl chains), CL must have a negative intrinsic curvature. The main empirical support for an extremely low spontaneous curvature of CL stems from lipid sorting experiments: it was found that CL sorts toward the inner leaflet of LUVs and membrane tubes with a high degree of selectivity (18,19). Assuming ideal mixing entropy for CL, this fact can only be explained by extremely high negative values for C0. However, there are good reasons to assume that such strong negative curvature is unrealistic. For example, it is possible to create lamellar phases made of pure CL. In addition, spontaneous curvatures are often measured in inverted hexagonal phases, these phases have differences in packing and only a small aqueous phase, potentially affecting C0. For example, we conducted a simulation of a small CHARMM-CL box, finding a spontaneous curvature of 0.05 nm−1, which is lower than that of the large system reported here.
The ability of CL to form lamellar phases is highly dependent on the salt concentration (20,80). Recently, Allolio and Harries proposed that a long-range lipid clustering by divalent Ca2+ ion induces a negative curvature formation. In this study, it was discovered that the distribution of the counterions will also affect the spontaneous curvature of lipids, independently of them being bound to headgroups or not. Due to screening, an increased salt concentration leads to a decreased ion-ion repulsion, as expressed by the Debye length. Thus, salt concentration might play a very important role in regulating the intrinsic curvature of CL. Indeed, this is well established experimentally, as CL can be transferred from a lamellar phase into an inverted hexagonal phase by increasing the salt concentration (81); however, this effect is not usually part of the discussion on CL in the biological community. Our simulations allow to refine the discussion above simple considerations of the Debye length showing that both salt concentration and the distance of the counterion density influence the curvature of CL, as larger distances have a higher weight in the moment calculation (see Eq. 1). In Fig. 6, A and B, we show the lateral pressure profiles of a CL bilayer using different force fields. We immediately notice the very strong negative lateral stress contribution of the CL headgroup region. This finding confirms the geometric reasoning based on the small headgroup size. However, the contribution of the counterion density offsets the negative pressure of the headgroup by its levered positive contributions of the Maxwell (and osmotic) stress.
The balance between ion dissociation, CL electrostatics, and curvature might be highly force field dependent and, therefore, in Fig. 6 C, the κc value of CL in both CHARMM and OPLS-AA force fields are reported. They are found to be similar. For identical box sizes, the values of C0 are also comparable. This allows us to rationalize the stability of the lamellar phase of CL at low ion concentrations.
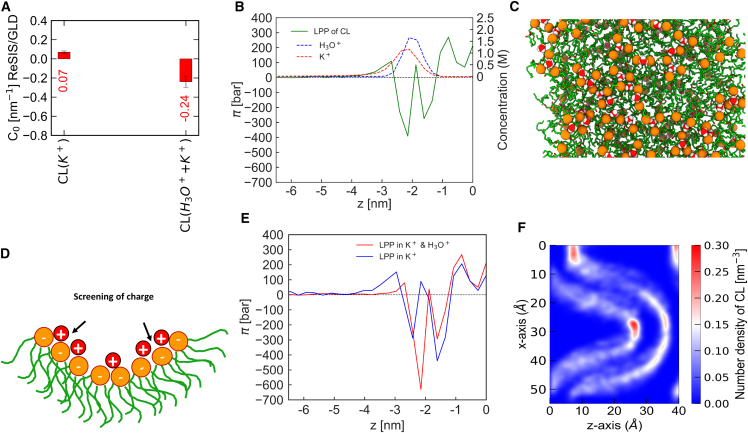
It thus becomes evident that the integration of CL into any sort of mesoscopic model necessitates the incorporation of electrostatic terms generated by the counterion profile. It also raises obvious questions with respect to the validity of CG models of CL without correct long-range electrostatics and water polarization. To check for ion-specific effects, we replaced half of the K+ ions with the H3O+ ions and repeated the MD simulation of the single-component CL system. In Fig. 7 A, the C0 values of CL in the presence of K+ ions and both K+ and H3O+ ions are shown. The data show that the addition of H3O+ ions in the bulk CL system induces negative spontaneous curvature in the bilayer. Fig. 7 B shows the lateral pressure profile of CL and the number density of K+ and H3O+ ions. Our data show that the headgroup region of CL is strongly enriched in the H3O+ ions over the K+ ions. The reason for the induction of negative curvature is to be found both in the depletion of ions at a large distance to the bilayer center and in the screening and binding effects of the H3O+ ions at the membrane interface. At this point, it should be noted that we have not protonated the CL lipids but merely have put them in contact with water self-ions. Therefore, it is expected that no sharp transition should be visible in a titration curve, i.e., that lipid properties gradually change in a qualitative manner before the protonation of CL is achieved. An enhanced presence of H3O+ at the CL interface is thus not in contradiction with the results of Olofsson and Sparr, of a pKA2 of 2.9–3.1 for CL (16). What has been neglected is the fact that H3O+ adsorption may cause drastic changes without covalent binding to CL. The absence of H3O+ dissociation in our simulation indicates a low H3O+ in the solution and hence H3O+ concentration near the interface might be significant even at near-neutral conditions. This effect might be important in explaining part of the sorting behavior of CL.
Figure 7.
Spontaneous curvature of CL and lateral pressure profile of CL in the presence of K+ + H3O+ ions. (A) Spontaneous curvature (C0 value in nm−1) of CL (OPLS-AA) in the presence of K+ and K+ + H3O+ ions, respectively. Error bars show the ΔC0 value (it is calculated based on the difference of the C0 values of each leaflet). (B) Symmetrized lateral pressure profile of CL (left axis) alongside K+ and H3O+ concentration (right axis). (C) Top view of a frame from a 200 ns simulation trajectory where H3O+ is adsorbed between the CL headgroups (marked by orange spheres on the phosphate atoms). (D) Cartoon representation of CL clustering in the presence of H3O+. (E) Comparison of symmetrized lateral pressure profiles of CL in the presence of K+ only and a mixture of H3O+ and K+. (F) Density profile of CL in a buckled membrane system. To see this figure in color, go online.
When examining the trajectory of our simulation, and we found that H3O+ ions are bridging headgroups of CL via hydrogen bonds. Fig. 7 C shows a simulation snapshot of a CL bulk system where the H3O+ ion is trapped between the headgroups. Here, the H3O+ ion is screening the repulsion between two negatively charged headgroups of CL. As the repulsion between these two headgroups is screened, the CLs are clustered.
The binding of the H3O+ ion to CL should affect the pressure profile of the lipid bilayer thus we have compared the profiles of CL in the presence and the absence of the H3O+ ion. This difference in the lateral pressure profiles of CL is shown in Fig. 7 E. The data suggest that H3O+ ion binding leads to a decline in the first moment of the pressure profile when compared with K+ ions. Apart from the significant differences in the headgroup region, the counterion concentration in bulk is also drastically affected, as can be seen in Fig. 7 B. The hydronium force field has been carefully validated for the air-water interface, but not on CL. Data for experimental validation is hard to find, but H3O+-generated spontaneous curvature at intermediate pH is plausible from micromanipulation data (82,83).
Pressure profiles of bilayers in the lamellar phase only allow the computation of the bending free energy to linear order. Elastic energy functional modifications due to, e.g., adjustment of chain packing do not enter any linear response calculation. Therefore, we have simulated CL in a strongly curved geometry with K+ counterions. The results are shown in Fig. 7 F. Results here are interesting, because they show the enrichment of CL at strongly negatively curved parts of the system. But, on the other hand, the positively curved parts of the system also display enrichment of CL. We explain this phenomenon again using the counterion density. At the strongly negatively curved interface, the counterion distribution is closer to the membrane due to the lack of space for dissociation as well as due to the reduced permittivity of the adjacent bilayers. Whereas, at the positively curved interfaces, there is a large gap for counterions to distribute. Our findings show that CL curvature is not a unique number but is shaped by the counterion distribution, its geometry and specific interactions. It is, therefore, no longer sufficient to speak of a “negative curvature” of CL. Instead, one must consider the CL counterion system and its geometry.
Conclusions
We have constructed mitochondrial membrane models based on available data for mammals and Drosophila. These simple models contain commercially available lipids and may guide experimental research. The models are based on simplified membrane compositions and various simplifying estimates, but they reflect the significantly different membrane compositions across species. The difference becomes even more pronounced when considering lipid membrane asymmetry. Simulation of these mitochondrial membrane models with all-atom molecular dynamics allowed us to extract their bulk mechanical properties. We find these properties to be remarkably similar across species, even when including asymmetry. In addition, we find these properties to be in good agreement with common extrapolation schemes. This indicates that the previous approaches to modeling complex membrane compositions agree with detailed simulations.
The main exception is CL, whose elastic properties, in particular its curvature, are heavily affected by the counterion distribution as exemplified by the adsorption of H3O+. This finding illustrates that it is not permissible to assign a constant spontaneous curvature to charged lipids without considering the detailed boundary conditions and ion-specific effects. We believe that this insight will also be crucial when explaining curvature sorting observations of CL and gives a hint toward the role of CL inside proton gradient-generating organelles. Furthermore, we examined the effects of force fields and CL oxidation and provided elastic parameters for single lipids.
Author contributions
C.A. designed and supervised the research, while S.K. and H.A. performed simulations and analysis. C.A. and S.K. wrote the paper. All authors read and approved the final manuscript.
Acknowledgments
This work was funded by the Charles University PRIMUS grant PRIMUS/20/SCI/015 (to C.A., H.A., and S.K.). H.A. was also funded by the Charles University grant UNCE/SCI/023. We thank Prof. Luke H. Chao for bringing to our attention the challenges of mitochondrial membrane morphology and Dr. Piotr Jurkiewicz for discussing CL biophysics with us.
Declaration of interests
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Editor: Frederick Heberle.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2023.10.002.
Supporting material
References
- 1.Enkavi G., Javanainen M., et al. Vattulainen I. Multiscale Simulations of Biological Membranes: The Challenge To Understand Biological Phenomena in a Living Substance. Chem. Rev. 2019;119:5607–5774. doi: 10.1021/acs.chemrev.8b00538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chew H., Solomon V.A., Fonteh A.N. Involvement of Lipids in Alzheimer’s Disease Pathology and Potential Therapies. Front. Physiol. 2020;11:598–628. doi: 10.3389/fphys.2020.00598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ellis C.E., Murphy E.J., et al. Nussbaum R.L. Mitochondrial Lipid Abnormality and Electron Transport Chain Impairment in Mice Lacking α-Synuclein. Mol. Cell Biol. 2005;25:10190–10201. doi: 10.1128/MCB.25.22.10190-10201.2005/FORMAT/EPUB. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kagan V.E., Bayir H.A., et al. Borisenko G. Cytochrome c/cardiolipin relations in mitochondria: a kiss of death. Free Radic. Biol. Med. 2009;46:1439–1453. doi: 10.1016/J.FREERADBIOMED.2009.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Paradies G., Paradies V., et al. Petrosillo G. Functional role of cardiolipin in mitochondrial bioenergetics. BBA. 2014;1837:408–417. doi: 10.1016/j.bbabio.2013.10.006. [DOI] [PubMed] [Google Scholar]
- 6.Boyd K.J., Alder N.N., May E.R. Molecular Dynamics Analysis of Cardiolipin and Monolysocardiolipin on Bilayer Properties. Biophys. J. 2018;114:2116–2127. doi: 10.1016/j.bpj.2018.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Acehan D., Khuchua Z., et al. Schlame M. Distinct effects of tafazzin deletion in differentiated and undifferentiated mitochondria. Mitochondrion. 2009;9:86–95. doi: 10.1016/j.mito.2008.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jendrach M., Mai S., et al. Bereiter-Hahn J. Short- and long-term alterations of mitochondrial morphology, dynamics and mtDNA after transient oxidative stress. Mitochondrion. 2008;8:293–304. doi: 10.1016/j.mito.2008.06.001. [DOI] [PubMed] [Google Scholar]
- 9.Wilson J.D., Bigelow C.E., et al. Foster T.H. Light Scattering from Intact Cells Reports Oxidative-Stress-Induced Mitochondrial Swelling. Biophys. J. 2005;88:2929–2938. doi: 10.1529/biophysj.104.054528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ikon N., Ryan R.O. Cardiolipin and mitochondrial cristae organization. BBA. 2017;1859:1156–1163. doi: 10.1016/j.bbamem.2017.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ge Y., Boopathy S., et al. Chao L.H. Absence of Cardiolipin From the Outer Leaflet of a Mitochondrial Inner Membrane Mimic Restricts Opa1-Mediated Fusion. Front. Mol. Biosci. 2021;8 doi: 10.3389/fmolb.2021.769135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.De Vecchis D., Brandner A., et al. Taly A. A Molecular Perspective on Mitochondrial Membrane Fusion: From the Key Players to Oligomerization and Tethering of Mitofusin. J. Membr. Biol. 2019;252:293–306. doi: 10.1007/s00232-019-00089-y. [DOI] [PubMed] [Google Scholar]
- 13.Abrisch R.G., Gumbin S.C., et al. Voeltz G.K. Fission and fusion machineries converge at ER contact sites to regulate mitochondrial morphology. J. Cell Biol. 2020;219 doi: 10.1083/JCB.201911122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Stepanyants N., MacDonald P.J., et al. Ramachandran R. Cardiolipin’s propensity for phase transition and its reorganization by dynamin-related protein 1 form a basis for mitochondrial membrane fission. Mol. Biol. Cell. 2015;26:3104–3116. doi: 10.1091/mbc.E15-06-0330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Liu R., Chan D.C. OPA1 and cardiolipin team up for mitochondrial fusion. Nat. Cell Biol. 2017;19:760–762. doi: 10.1038/ncb3565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Olofsson G., Sparr E. Ionization Constants pK a of Cardiolipin. PLoS One. 2013;8 doi: 10.1371/journal.pone.0073040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gorbenko G.P., Molotkovsky J.G., Kinnunen P.K.J. Cytochrome c Interaction with Cardiolipin/Phosphatidylcholine Model Membranes: Effect of Cardiolipin Protonation. Biophys. J. 2006;90:4093–4103. doi: 10.1529/BIOPHYSJ.105.080150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Beltrán-Heredia E., Tsai F.C., et al. Monroy F. Membrane curvature induces cardiolipin sorting. Commun. Biol. 2019;2:225. doi: 10.1038/s42003-019-0471-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Elmer-Dixon M.M., Hoody J., et al. Bowler B.E. Cardiolipin Preferentially Partitions to the Inner Leaflet of Mixed Lipid Large Unilamellar Vesicles. J. Phys. Chem. B. 2019;123:9111–9122. doi: 10.1021/acs.jpcb.9b07690. [DOI] [PubMed] [Google Scholar]
- 20.Seddon J.M., Kaye R.D., Marsh D. Induction of the lamellar-inverted hexagonal phase transition in cardiolipin by protons and monovalent cations. BBA - Biomembr. 1983;734:347–352. doi: 10.1016/0005-2736(83)90134-7. [DOI] [Google Scholar]
- 21.Wilson B.A., Ramanathan A., Lopez C.F. Cardiolipin-Dependent Properties of Model Mitochondrial Membranes from Molecular Simulations. Biophys. J. 2019;117:429–444. doi: 10.1016/j.bpj.2019.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sennato S., Bordi F., et al. Rufini S. Evidence of Domain Formation in Cardiolipin-Glycerophospholipid Mixed Monolayers. A Thermodynamic and AFM Study. J. Phys. Chem. B. 2005;109:15950–15957. doi: 10.1021/jp051893q. [DOI] [PubMed] [Google Scholar]
- 23.Allolio C., Haluts A., Harries D. A local instantaneous surface method for extracting membrane elastic moduli from simulation: Comparison with other strategies. Chem. Phys. 2018;514:31–43. doi: 10.1016/j.chemphys.2018.03.004. [DOI] [Google Scholar]
- 24.Allolio C., Harries D. Calcium ions promote membrane fusion by forming negative-curvature inducing clusters on specific anionic lipids. ACS Nano. 2021;15:12880–12887. doi: 10.1021/ACSNANO.0C08614. [DOI] [PubMed] [Google Scholar]
- 25.Lee J., Cheng X., et al. Im W. CHARMM-GUI Input Generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM Simulations Using the CHARMM36 Additive Force Field. J. Chem. Theor. Comput. 2016;12:405–413. doi: 10.1021/acs.jctc.5b00935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Klauda J.B., Venable R.M., et al. Pastor R.W. Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types. J. Phys. Chem. B. 2010;114:7830–7843. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Róg T., Martinez-Seara H., et al. Vattulainen I. Role of cardiolipins in the inner mitochondrial membrane: Insight gained through atom-scale simulations. J. Phys. Chem. B. 2009;113:3413–3422. doi: 10.1021/jp8077369. [DOI] [PubMed] [Google Scholar]
- 28.Berendsen H.J.C., Grigera J.R., Straatsma T.P. The Missing Term in Effective Pair Potentials1. J. Phys. Chem. 1987;91:6269–6271. doi: 10.1021/j100308a038. [DOI] [Google Scholar]
- 29.Jorgensen W.L., Chandrasekhar J., et al. Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. doi: 10.1063/1.445869. [DOI] [Google Scholar]
- 30.Bonthuis D.J., Mamatkulov S.I., Netz R.R. Optimization of classical nonpolarizable force fields for OH− and H3O+ J. Chem. Phys. 2016;144 doi: 10.1063/1.4942771. [DOI] [PubMed] [Google Scholar]
- 31.Mamatkulov S.I., Allolio C., et al. Bonthuis D.J. Orientation-Induced Adsorption of Hydrated Protons at the Air–Water Interface. Angew. Chem., Int. Ed. Engl. 2017;56:15846–15851. doi: 10.1002/ANIE.201707391. [DOI] [PubMed] [Google Scholar]
- 32.Nosé S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984;81:511–519. doi: 10.1063/1.447334. [DOI] [Google Scholar]
- 33.Parrinello M., Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981;52:7182–7190. doi: 10.1063/1.328693. [DOI] [Google Scholar]
- 34.Darden T., York D., Pedersen L. Particle mesh Ewald: An N. log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. doi: 10.1063/1.464397. [DOI] [Google Scholar]
- 35.Hess B., Bekker H., et al. Fraaije J.G.E.M. LINCS: A Linear Constraint Solver for molecular simulations. J. Comput. Chem. 1997;18:1463–1472. doi: 10.1002/(SICI)1096-987X(199709)18:12<1463::AID-JCC4>3.0.CO;2-H. [DOI] [Google Scholar]
- 36.Abraham M.J., Murtola T., et al. Lindahl E. Gromacs: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 2015;1–2:19–25. doi: 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- 37.Berendsen H.J.C., van der Spoel D., van Drunen R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995;91:43–56. doi: 10.1016/0010-4655(95)00042-E. [DOI] [Google Scholar]
- 38.Sega M., Fábián B., Jedlovszky P. Pressure Profile Calculation with Mesh Ewald Methods. J. Chem. Theor. Comput. 2016;12:4509–4515. doi: 10.1021/ACS.JCTC.6B00576. [DOI] [PubMed] [Google Scholar]
- 39.Goetz R., Lipowsky R. Computer simulations of bilayer membranes: Self-assembly and interfacial tension. J. Chem. Phys. 1998;108:7397–7409. doi: 10.1063/1.476160. [DOI] [Google Scholar]
- 40.Canham P.B. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J. Theor. Biol. 1970;26:61–81. doi: 10.1016/S0022-5193(70)80032-7. [DOI] [PubMed] [Google Scholar]
- 41.Evans E.A. Bending resistance and chemically induced moments in membrane bilayers. Biophys. J. 1974;14:923–931. doi: 10.1016/S0006-3495(74)85959-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C Biosci. 1973;28:693–703. doi: 10.1515/ZNC-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 43.Hamm M., Kozlov M.M. Elastic energy of tilt and bending of fluid membranes. Eur. Phys. J. A E. 2000;3:323–335. doi: 10.1007/s101890070003. [DOI] [Google Scholar]
- 44.May S., Kozlovsky Y., et al. Kozlov M.M. Tilt modulus of a lipid monolayer. Eur. Phys. J. A E. 2004;14:299–308. doi: 10.1140/epje/i2004-10019-y. [DOI] [PubMed] [Google Scholar]
- 45.Fošnarič M., Iglič A., May S. Influence of rigid inclusions on the bending elasticity of a lipid membrane. Phys. Rev. E. 2006;74 doi: 10.1103/PhysRevE.74.051503. [DOI] [PubMed] [Google Scholar]
- 46.Kozlovsky Y., Kozlov M.M. Stalk model of membrane fusion: Solution of energy crisis. Biophys. J. 2002;82:882–895. doi: 10.1016/S0006-3495(02)75450-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Pieffet G., Botero A., et al. Leidy C. Exploring the Local Elastic Properties of Bilayer Membranes Using Molecular Dynamics Simulations. J. Phys. Chem. B. 2014;118:12883–12891. doi: 10.1021/jp504427a. [DOI] [PubMed] [Google Scholar]
- 48.Venable R.M., Brown F.L.H., Pastor R.W. Mechanical properties of lipid bilayers from molecular dynamics simulation. Chem. Phys. Lipids. 2015;192:60–74. doi: 10.1016/j.chemphyslip.2015.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Johner N., Harries D., Khelashvili G. Implementation of a methodology for determining elastic properties of lipid assemblies from molecular dynamics simulations. BMC Bioinf. 2016;17:161. doi: 10.1186/s12859-016-1003-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Johner N., Harries D., Khelashvili G. Curvature and lipid packing modulate the elastic properties of lipid assemblies: Comparing HII and lamellar phases. J. Phys. Chem. Lett. 2014;5:4201–4206. doi: 10.1021/jz5022284. [DOI] [PubMed] [Google Scholar]
- 51.Doktorova M., Harries D., Khelashvili G. Determination of bending rigidity and tilt modulus of lipid membranes from real-space fluctuation analysis of molecular dynamics simulations. Phys. Chem. Chem. Phys. 2017;19:16806–16818. doi: 10.1039/c7cp01921a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Khelashvili G., Kollmitzer B., et al. Harries D. Calculating the bending modulus for multicomponent lipid membranes in different thermodynamic phases. J. Chem. Theor. Comput. 2013;9:3866–3871. doi: 10.1021/ct400492e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Szleifer I., Kramer D., et al. Safran S.A. Molecular theory of curvature elasticity in surfactant films. J. Chem. Phys. 1990;92:6800–6817. doi: 10.1063/1.458267. [DOI] [Google Scholar]
- 54.Horvath S.E., Daum G. Lipids of mitochondria. Prog. Lipid Res. 2013;52:590–614. doi: 10.1016/j.plipres.2013.07.002. [DOI] [PubMed] [Google Scholar]
- 55.Ardail D., Privat J.P., et al. Louisot P. Mitochondrial contact sites. Lipid composition and dynamics. J. Biol. Chem. 1990;265:18797–18802. doi: 10.1016/S0021-9258(17)30583-5. [DOI] [PubMed] [Google Scholar]
- 56.Daum G. Lipids of mitochondria. Biochim. Biophys. Acta. 1985;822:1–42. doi: 10.1016/0304-4157(85)90002-4. [DOI] [PubMed] [Google Scholar]
- 57.Oemer G., Koch J., et al. Keller M.A. Phospholipid Acyl Chain Diversity Controls the Tissue-Specific Assembly of Mitochondrial Cardiolipins. Cell Rep. 2020;30:4281–4291.e4. doi: 10.1016/j.celrep.2020.02.115. [DOI] [PubMed] [Google Scholar]
- 58.Pennington E.R., Funai K., et al. Shaikh S.R. The role of cardiolipin concentration and acyl chain composition on mitochondrial inner membrane molecular organization and function. BBA. 2019;1864:1039–1052. doi: 10.1016/j.bbalip.2019.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kiebish M.A., Han X., et al. Seyfried T.N. Lipidomic analysis and electron transport chain activities in C57BL/6J mouse brain mitochondria. J. Neurochem. 2008;106:299–312. doi: 10.1111/j.1471-4159.2008.05383.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kim J., Hoppel C.L. Comprehensive approach to the quantitative analysis of mitochondrial phospholipids by HPLC–MS. J. Chromatogr. B. 2013;912:105–114. doi: 10.1016/j.jchromb.2012.10.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Acehan D., Malhotra A., et al. Schlame M. Cardiolipin Affects the Supramolecular Organization of ATP Synthase in mitochondria. Biophys. J. 2011;100:2184–2192. doi: 10.1016/j.bpj.2011.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Dubessay P., Garreau-Balandier I., et al. Alziari S. Aging impact on biochemical activities and gene expression of Drosophila melanogaster mitochondria. Biochimie. 2007;89:988–1001. doi: 10.1016/j.biochi.2007.03.018. [DOI] [PubMed] [Google Scholar]
- 63.Doktorova M., Weinstein H. Accurate in silico modeling of asymmetric bilayers based on biophysical principles. Biophys. J. 2018;115:1638–1643. doi: 10.1016/j.bpj.2018.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Hossein A., Deserno M. Spontaneous Curvature, Differential Stress, and Bending Modulus of Asymmetric Lipid Membranes. Biophys. J. 2020;118:624–642. doi: 10.1016/j.bpj.2019.11.3398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Hills R.D., McGlinchey N. Model parameters for simulation of physiological lipids. J. Comput. Chem. 2016;37:1112–1118. doi: 10.1002/jcc.24324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Ding W., Palaiokostas M., et al. Orsi M. Effects of Lipid Composition on Bilayer Membranes Quantified by All-Atom Molecular Dynamics. J. Phys. Chem. B. 2015;119:15263–15274. doi: 10.1021/acs.jpcb.5b06604. [DOI] [PubMed] [Google Scholar]
- 67.Pan J., Cheng X., et al. Katsaras J. Structural and mechanical properties of cardiolipin lipid bilayers determined using neutron spin echo, small angle neutron and X-ray scattering, and molecular dynamics simulations. Soft Matter. 2015;11:130–138. doi: 10.1039/c4sm02227k. [DOI] [PubMed] [Google Scholar]
- 68.Vähäheikkilä M., Peltomaa T., et al. Vattulainen I. How cardiolipin peroxidation alters the properties of the inner mitochondrial membrane? Chem. Phys. Lipids. 2018;214:15–23. doi: 10.1016/j.chemphyslip.2018.04.005. [DOI] [PubMed] [Google Scholar]
- 69.Lekkerkerker H.N.W. Contribution of the electric double layer to the curvature elasticity of charged amphiphilic monolayers. Physica A. 1989;159:319–328. doi: 10.1016/0378-4371(89)90400-7. [DOI] [Google Scholar]
- 70.Winterhalter M., Helfrich W. Effect of surface charge on the curvature elasticity of membranes. J. Phys. Chem. 2002;92:6865–6867. doi: 10.1021/J100335A004. [DOI] [Google Scholar]
- 71.Bossa G.V., Berntson B.K., May S. Curvature Elasticity of the Electric Double Layer. Phys. Rev. Lett. 2018;120 doi: 10.1103/PhysRevLett.120.215502. [DOI] [PubMed] [Google Scholar]
- 72.Guttman G.D., Andelman D. Electrostatic interactions in two-component membranes. J. Phys. II France. 1993;3:1411–1425. doi: 10.1051/JP2:1993210. [DOI] [Google Scholar]
- 73.Avital Y.Y., Grønbech-Jensen N., Farago O. Elasticity and mechanical instability of charged lipid bilayers in ionic solutions. Eur. Phys. J. A E. 2014;37:26. doi: 10.48550/arxiv.1407.3603. [DOI] [PubMed] [Google Scholar]
- 74.Venkatraman K., Lee C.T., et al. Rangamani P. Cristae formation is a mechanical buckling event controlled by the inner membrane lipidome. bioRxiv. 2023 doi: 10.1101/2023.03.13.532310. Preprint at. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Rickeard B.W., Nguyen M.H.L., et al. Marquardt D. Transverse lipid organization dictates bending fluctuations in model plasma membranes. Nanoscale. 2020;12:1438–1447. doi: 10.1039/C9NR07977G. [DOI] [PubMed] [Google Scholar]
- 76.Karamdad K., Law R.V., et al. Ces O. Studying the effects of asymmetry on the bending rigidity of lipid membranes formed by microfluidics. Chem. Commun. 2016;52:5277–5280. doi: 10.1039/C5CC10307J. [DOI] [PubMed] [Google Scholar]
- 77.Saeedimasine M., Montanino A., et al. Villa A. Role of lipid composition on the structural and mechanical features of axonal membranes: a molecular simulation study. Sci. Rep. 2019;9:8000–8012. doi: 10.1038/s41598-019-44318-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Andelman D., Kozlov M.M., Helfrich W. Phase Transitions between Vesicles and Micelles Driven by Competing Curvatures. Europhys. Lett. 1994;25:231–236. doi: 10.1209/0295-5075/25/3/013. [DOI] [Google Scholar]
- 79.Khelashvili G., Harries D., Weinstein H. Modeling Membrane Deformations and Lipid Demixing upon Protein-Membrane Interaction: The BAR Dimer Adsorption. Biophys. J. 2009;97:1626–1635. doi: 10.1016/j.bpj.2009.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Rand R.P., Sengupta S. Cardiolipin forms hexagonal structures with divalent cations. BBA. 1972;255:484–492. doi: 10.1016/0005-2736(72)90152-6. [DOI] [PubMed] [Google Scholar]
- 81.Ortiz A., Killian J.A., et al. Wilschut J. Membrane Fusion and the Lamellar-to-Inverted-Hexagonal Phase Transition in Cardiolipin Vesicle Systems Induced by Divalent Cations. Biophys. J. 1999;77:2003–2014. doi: 10.1016/S0006-3495(99)77041-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Khalifat N., Fournier J.B., et al. Puff N. Lipid packing variations induced by pH in cardiolipin-containing bilayers: the driving force for the cristae-like shape instability. BBA-Biomembr. 2011;1808:2724–2733. doi: 10.1016/j.bbamem.2011.07.013. [DOI] [PubMed] [Google Scholar]
- 83.Khalifat N., Puff N., et al. Angelova M.I. Membrane deformation under local pH gradient: mimicking mitochondrial cristae dynamics. Biophys. J. 2008;95:4924–4933. doi: 10.1529/biophysj.108.136077. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.