Abstract
Background
To investigate the predictive ability of high-throughput MRI with deep survival networks for biochemical recurrence (BCR) of prostate cancer (PCa) after prostatectomy.
Methods
Clinical-MRI and histopathologic data of 579 (train/test, 463/116) PCa patients were retrospectively collected. The deep survival network (iBCR-Net) is based on stepwise processing operations, which first built an MRI radiomics signature (RadS) for BCR, and predicted the T3 stage and lymph node metastasis (LN+) of tumour using two predefined AI models. Subsequently, clinical, imaging and histopathological variables were integrated into iBCR-Net for BCR prediction.
Results
RadS, derived from 2554 MRI features, was identified as an independent predictor of BCR. Two predefined AI models achieved an accuracy of 82.6% and 78.4% in staging T3 and LN+. The iBCR-Net, when expressed as a presurgical model by integrating RadS, AI-diagnosed T3 stage and PSA, can match a state-of-the-art histopathological model (C-index, 0.81 to 0.83 vs 0.79 to 0.81, p > 0.05); and has maximally 5.16-fold, 12.8-fold, and 2.09-fold (p < 0.05) benefit to conventional D’Amico score, the Cancer of the Prostate Risk Assessment (CAPRA) score and the CAPRA Postsurgical score.
Conclusions
AI-aided iBCR-Net using high-throughput MRI can predict PCa BCR accurately and thus may provide an alternative to the conventional method for PCa risk stratification.
Subject terms: Prognostic markers, Prostate cancer, Outcomes research
Introduction
The tumour progression and outcome of prostate cancer (PCa) are widely variable due to its complex biological properties [1]. Approximately 20–50% of patients undergoing radical prostatectomy (RP) experienced biochemical recurrence (BCR), and two-thirds of these recurrences occurred within 2 years after surgery [2–4]. BCR is considered a surrogate predictor of clinical recurrence and distant metastasis [5]. Therefore, it is critical to preoperatively assess BCR risk to assist with better treatment decision-making and follow-up schedules for patients.
Several state-of-the-art scoring systems have been proposed to predict BCR for subsequent treatment. For example, the D’Amico classification system categorises patients into low-, intermediate-, and high-risk using measurements such as prostate-specific antigen (PSA), Gleason score (GS) and clinical T stage [6]. The Cancer of the Prostate Risk Assessment (CAPRA) adds variables as age and percent of biopsy core positives (core+%) [7], and the CAPRA Postsurgical (CAPRA-S) score consists of more granular clinicopathological characteristics: PSA, pathologic GS, positive surgical margins (SM), extracapsular extension (ECE), seminal vesicle invasion (SVI), and pelvic lymph node metastasis (PLNM) [8]. Unfortunately, these systems were mainly validated in western cohorts with a C-index roughly around 0.67–0.81, so the accuracy and repeatability still require extensive external validation [9–12].
Magnetic resonance imaging (MRI) is a state-of-the-art tool to detect, localise and stage PCa [13, 14]. MRI assessments such as Prostate Imaging Reporting and Data System (PI-RADS) score, tumour size, ECE, SVI and PLNM were reflected as prognostic biomarkers of PCa [15, 16]. Additionally, radiomics, using high-throughput mining of quantitative image features to reveal intra-tumoral heterogeneity, had proven predictive value for postsurgical outcome of PCa [17–19]. In a 120-patient cohort study, a machine learning classifier trained with radiomic features from biparametric MRI achieved an AUC of 0.73 for the prediction of BCR [18]. In another cohort study of 107 patients, an ADC-derived GLSZM-based feature was associated with tumour heterogeneity and achieved an AUC of 0.76 for the prediction of BCR [19]. Even with encouraging results, these studies were limited by small sample sizes and ignored the time dependence in survival analysis. Nevertheless, no single factor alone appears to accurately predict tumour prognosis. We have still little understanding of the multimodal interaction and relationship of multimodal data features such as clinical variables, imaging features and histopathological findings for time-dependent survival analysis in PCa. The conventional method for time-to-event data analysis is Cox proportional hazards (Cox-PH) regression. Although it generates interpretable regression coefficients, Cox-PH makes linear assumptions and thus cannot simulate nonlinear relationships that may occur in real life. Recently, Cox regression ensembled with artificial intelligence (AI) algorithms such as machine learning or deep learning, allowing the integration of high-dimensional features with nonlinear and complex interactions, might be an alternative to provide reliable prognostic information [20, 21].
Hence, this study attempts to investigate whether a multimodal integrative deep survival network, namely iBCR-Net, especially relying on AI-aided high-throughput MRI assessment, can predict the BCR-free survival of PCa after RP. In addition, the clinical benefit of iBCR-Net is compared to the start-of-the-art scoring systems such as D’Amico, CAPRA, and CAPRA-S.
Materials and methods
Patients
The retrospective study included 579 histologically confirmed PCa patients in a single tertiary care medical centre (the First Affiliated Hospital of Nanjing Medical University) between Jan 2013 and Dec 2019. Ethics approval was granted by the hospital Institutional Review Board (grant no. 2021-SR-396), and informed patient consent was waived. The patient enrolment procedure is listed in Supplementary Materials (Supplementary Fig. 1).
All patients underwent a standardised prostate examination at 3.0-T MRI (u770, United Imaging, Shanghai, China; and Verio/Skyra, Siemens, Erlangen, Germany), which complied with the PI-RADS document requirements [13]. Details of acquirement protocols are provided in Supplementary Materials (Supplementary Table 1). All imaging data were retrospectively interpreted using PI-RADS ver. 2.1 [13] by two uroradiologists (YH and JZ, with 5-year and 15-year experience in prostate imaging, respectively) who were blinded to all clinical, biopsy and surgical findings. For patients with multiple neoplastic lesions, only index lesion (highest PI-RADS score and/or largest lesion size) was analysed, and specific imaging features evaluated included: (1) lesion location (peripheral zone [PZ] or transitional zone [TZ]); (2) lesion size (the max diameter); (3) PI-RADS score; (4) MRI-based ECE, SVI, and PLNM (absent or present). During the image interpretation, any inter-reader disagreement in qualitative assessments was discussed until a consensus was reached.
Clinical variables included the age, PSA, and PSA density (PSAD) level. TRUS/MRI-fusion targeted biopsy in conjunction with extended systematic biopsy was performed standardly according to the Ginsburg protocol [22]. Histopathological examinations were performed by two experienced uropathologists with more than 10 years of experience in uropathology in accordance with the International Society of Urological Pathology (ISUP) 2005 and 2014 recommendations [23, 24]. Biopsy variables included biopsy GS, core+%, and the presence of perineural invasion (Peri-NI). Postsurgical histopathological variables included pathological GS, negative or positive of SM, ECE, SVI and PLNM if a pelvic lymph node dissection (PLND) or extended PLND (ePLND) is adopted. The GS of the tumour was recorded and grouped into four categories, as per ISUP grade group (GG): GS 3+3 (GG 1), GS 3+4 (GG 2), GS 4+3 (GG 3), and GS ≥ 4+4 (GG 4).
Postoperative follow-up was based on PSA, MRI, and/or positron emission tomography or bone scans [25]. Routinely patients were followed up every 3 months for the first 2 years post-operatively, every 6 months thereafter until 5 years, and then annually according to institutional practice. The primary endpoint was BCR-free survival, which was calculated from the date of surgery to the date of BCR or censored at the date of last follow-up (up to 5 years). BCR was defined as three postoperative consecutive increasing PSA values >0.1 ng/ml at least 6 weeks with final PSA > 0.2 ng/ml or PSA ≥ 0.4 ng/ml once at least 6 weeks post-operatively, or secondary treatment due to elevated PSA level, referenced to a previous report and related to the probability of subsequent PSA progression [26].
The iBCR-Net construction
The iBCR-Net model works on three key steps: (1) first, we performed processing operations to derive an MRI radiomics prognostic signature (RadS) that allows to indicate the BCR-free survival probability. (2) Second, we measured two AI-derived predictions that allow to assess the T3 stage and PLNM of PCa, respectively, using two predefined AI models described in previous studies [27, 28]. (3) Last, the new MRI predictors, including RadS, AI-predicted T3 stage, and AI-predicted PLNM, were combined with 17 ordered clinical indicators from clinical, radiological, and pathological documents to develop a multimodal integrative deep survival network, i.e., the iBCR-Net, for the prediction of BCR-free survival. The iBCR-Net was constructed by a concept of multimodal data integration and multialgorithm ensemble, the detailed architecture of which is illustrated in Fig. 1. Additionally, we evaluated the predictive accuracy and clinical applicability of iBCR-Net model by comparing with D’Amico, CAPRA, and CAPRA-S scoring schemes in the independent test dataset.
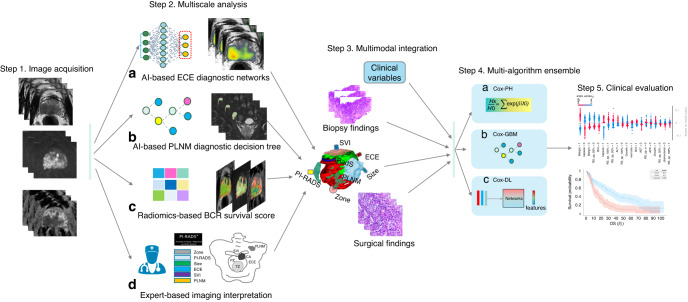
Fig. 1. Flowchart of iBCR-Net construction.
The study consists of the following primary steps: first, individual prostate MRI within the cohort of study, in response to each pathological status, is acquired by a panel of experts and is evaluated with a pretrained AI-based network for diagnosing ECE (a) and a pretrained diagnostic model for PLNM (b), respectively. Tumour radiomics features are extracted on T2WI, b1500 DWI and ADC images and processed with a Lasso-Cox regression algorithm to derive a radiomics survival (RadS) score that connects to BCR survival outcome (c). Additionally, expert-based interpretation for PI-RADS score, tumour size, tumour zone, T stage and N stage, etc., is done by the panel of radiologists (d). Then, the newly determined imaging biomarkers, together with clinicopathologic variables, are fed into a stack of Cox-based algorithms, including Cox-PH, Cox-GBM and Cox-DL, to derive a prognostic model for BCR survival outcome. Last, the model is validated clinically in independent test data. ECE extracapsular extension, PLNM pelvic lymph node metastasis, BCR biochemical recurrence, SVI seminal vesicle invasion, Cox-PH Cox proportional hazards, Cox-GBM Cox gradient boosting machine, Cox-DL deep learning-based Cox model.
BCR-related radiomics signature (RadS)
The entire volumetric region-of-interest (ROI) of the tumour was drawn by another two dedicated radiologists (KWJ and YDZ) and in consultation with uropathologists. Generally, the ROI of the target lesion was predefined once the patient received an MRI exam and following MRI/TRUS-fusion biopsy in a clinical routine, while PI-RADS was reevaluated by the dedicated investigators with a retrospective blinded reviewing process when the patient was compliant with enrolment criteria for this study. Details of ROI identification and image preprocessing are described in Supplementary Materials (Supplementary E1). To avoid the risk of bias and overfitting in high-dimensional survival data, a Cox-based least absolute shrinkage and selection operator (Lasso-Cox) regression analysis was utilised for feature selection and shrinkage to construct RadS [29].
AI-predicted ECE and PLNM
The ECE and PLNM status (absence vs presence) of all patients in this study were assessed using two predefined AI models described previously [27, 28], in which the ECE (T3 stage) model is built on a ResNeXt network in 596 PCa patients with RP [27], and the PLNM model is built on a random forest analysis using 18 integrative clinic-imaging features on 248 PCa patients with both RP and ePLND [28].
Development of iBCR-Net
Patients were randomly assigned into train (n = 463) and test group (n = 116). The inputs of iBCR-Net contained: (1) clinical variables such as age, PSA, and PSAD; (2) expert-interpreted radiological identifications such as lesion location, lesion size, PI-RADS score, expert-based ECE, SVI, and PLNM; (3) AI-derived predictions including RadS, AI-predicted ECE and PLNM; (4) biopsy findings including biopsy GG, core+%, and Peri-NI; (5) postsurgical-pathological findings such as pathological GG, SM, ECE, SVI, and PLNM. In real-world clinical settings, not all patients are candidates for PLND or ePLND; therefore, compromisingly, patients without PLND were assumed to have no PLNM at histopathology by default.
To achieve a model allowing to accurately predict BCR-free survival, we proposed three baseline algorithms for iBCR-Net: (1) a state-of-the-art Cox-PH, specifically included independent prognostic indicators related to BCR in the multivariate analysis; (2) a powerful gradient boosting model using Gradient Boosting Machine (Cox-GBM), using a forward stage-wise decision tree strategy to build an additive model [30]; (3) a deep learning-based Cox model (Cox-DL) using 7 baseline frameworks such as a DL-based Cox proportional hazard model (DeepSurv) [31], a non-proportional and a proportional Cox referred to as Cox-Time and Cox-CC model [32], respectively, a linear Cox regression (Deep-Hit) [33], a neural multi-task logistic regression (N-MTLR) [34], a regression parametrising the probability mass function (PMF) and a piecewise constant hazard regression assuming the continuous-time hazard function is constant in predefined intervals (PC-Hazard) [35]. Primarily, we selected the desired model for Cox-DL with a stepwise ablation experience by comparing Harrell’s concordance index (C-index) on a five-fold cross-validation in the train group, then validated it in the test group. The detail of the analysis is summarised in Supplementary Materials (Supplementary E2).
In total, we trained 18 iBCR-Net models using multimodal integrations to answer the critical questions about current clinical concerns on PCa treatment and management [36]: (1) preoperative (pre-Op) vs postoperative (post-Op) variables; (2) AI-aided vs expert-based assessment; (3) MRI-added vs MRI-spared (e.g., D’Amico, CAPRA, and CAPRA-S). We postulated a simple model relying on clinical and automatic AI detections that can be comparable to a state-of-the-art model relying on presurgical and postsurgical indicators (see more details in Supplementary Materials in Supplementary Fig. 2).
Statistical analysis
The Mann–Whitney U test and chi-square test were used to calculate group-difference in terms of baseline characteristics. Model discrimination was evaluated based on Harrell’s C-index, calibration curves and decision curve analysis. Kaplan–Meier and log-rank were used to calculate survival curves. X-tile software (version 3.6.1) was applied to determine the cutoff value of RadS and risk scores for prognostic model in the training cohort and classified patients into high- and low-risk groups [37]. Model building and statistical analyses were performed using the R package (version 4.1.2; http://www.Rproject.org). All tests were two-tailed, with statistical significance set at 0.05.
Results
Baseline characteristics
The characteristics of the 579 enrolled patients are summarised in Table 1. Overall, 137/463 (29.6%) and 34/116 (29.3%) patients experienced BCR in the train and test cohort, respectively. About 94.7% of biochemical relapses occurred within the first 2 years in the whole cohort. The median follow-up time was 26.1 (95% confidence intervals [CIs], 24.1–28.1) months.
Table 1.
The baseline characteristics of the patients.
| Variable | Train group n = 463 | Test group n = 116 | p-value |
|---|---|---|---|
| Age (yr), median (IQR) | 69 (65–74) | 69 (63–75) | 0.952 |
| PSA (ng/ml), median (IQR) | 14.9 (8.8–26.5) | 16.8 (9.0–34.5) | 0.407 |
| PSAD (ng/ml/cc), median (IQR) | 0.5 (0.2–0.9) | 0.4 (0.2–0.9) | 0.598 |
| PI-RADS score | 0.589 | ||
| 1–2 | 23/463 (5.0%) | 4/116 (3.4%) | |
| 3 | 79/463 (17.1%) | 25/116 (21.6%) | |
| 4 | 158/463 (34.1%) | 41/116 (35.3%) | |
| 5 | 203/463 (43.8%) | 46/116 (39.7%) | |
| Lesion location | 0.099 | ||
| TZ | 150/463 (32.4%) | 47/116 (40.5%) | |
| PZ | 313/463 (67.6%) | 69/116 (59.5%) | |
| Lesion size (cm), median (IQR) | 1.5 (1.0–2.2) | 1.4 (0.9–2.5) | 0.949 |
| Expert-based ECE | 0.252 | ||
| Present | 142/463 (30.7%) | 42/116 (36.2%) | |
| Absent | 321/463 (69.3%) | 74/116 (63.8%) | |
| Expert-based SVI | 0.404 | ||
| Present | 70/463 (15.1%) | 14/116 (12.1%) | |
| Absent | 393/463 (84.9%) | 102/116 (87.9%) | |
| Expert-based PLNM | 0.718 | ||
| Present | 45/463 (9.7%) | 10/116 (8.6%) | |
| Absent | 418/463 (90.3%) | 106/116 (91.4%) | |
| Biopsy Gleason score | 0.915 | ||
| GS 3+3 | 119/463 (25.7%) | 33/116 (28.4%) | |
| GS 3+4 | 97/463 (21.0%) | 25/116 (21.6%) | |
| GS 4+3 | 120/463 (25.9%) | 29/116 (25.0%) | |
| GS ≥ 4+4 | 127/463 (27.4%) | 29/116 (25.0%) | |
| Percentage of positive cores, median (IQR) | 0.4 (0.2–0.6) | 0.3 (0.1–0.6) | 0.222 |
| Perineural invasion | 0.187 | ||
| Present | 70/463 (15.1%) | 12/116 (10.3%) | |
| Absent | 393/463 (84.9%) | 104/116 (89.7%) | |
| Surgical Gleason Score | 0.949 | ||
| GS 3+3 | 69/463 (14.9%) | 17/116 (14.7%) | |
| GS 3+4 | 129/463 (27.9%) | 30/116 (25.9%) | |
| GS 4+3 | 141/463 (30.5%) | 35/116 (30.2%) | |
| GS ≥ 4+4 | 124/463 (26.8%) | 34/116 (29.3%) | |
| Pathological ECE | 0.349 | ||
| Present | 116/463 (25.1%) | 34/116 (29.3%) | |
| Absent | 347/463 (74.9%) | 82/116 (70.7%) | |
| Pathological SVI | 0.321 | ||
| Present | 74/463 (16.0%) | 23/116 (19.8%) | |
| Absent | 389/463 (84.0%) | 93/116 (80.2%) | |
| Pathological SM | 0.488 | ||
| Present | 199/463 (43.0%) | 54/116 (46.6%) | |
| Absent | 264/463 (57.0%) | 62/116 (53.4%) | |
| Pathological PLNM | 0.774 | ||
| Present | 41/463 (8.9%) | 10/116 (8.6%) | |
| Absenta | 422/463 (91.1%) | 106/116 (91.4%) | |
Unless indicated otherwise, data are the number of tumours, with percentages in parentheses. The Mann–Whitney U test for continuous variables. The chi-square test was used for categoric variables.
PSA prostate serum antigen, PSAD prostate serum antigen density, PI-RADS Prostate Imaging and Reporting and Data System version 2.1, TZ transition zone, PZ peripheral zone, ECE extracapsular extension, SVI seminal vesicle invasion, PLNM pelvic lymph node metastasis, GS Gleason Score, SM surgical margin, PLND pelvic lymph node dissection, ePLND extended PLND.
a299/579 (51.6%) patients without PLND or ePLND were assumed to have no lymph node involvement by default.
New MRI signatures for BCR
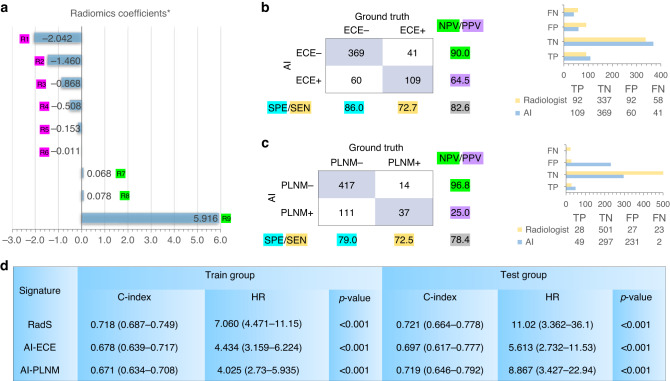
The stepwise Lasso-Cox analysis selected a total of 9 significant radiomics features (one feature on T2WI, 5 features on DWI, and 3 features on ADC) associated with BCR-free survival in the training cohort. The RadS was calculated through a linear combination of selected feature weights by their respective coefficients, as plotted in Fig. 2a. It resulted in a C-index of 0.718 (95% CIs, 0.687–0.749) and 0.721 (95% CIs, 0.664–0.778) in train and test group for predicting BCR-free survival, respectively. Using the cutoff value of 0.80 for staging ECE, the predefined AI model produced an overall accuracy of 82.6% (478/579) with 72.7% (109/150) sensitivity and 86.0% (369/429) specificity in diagnosis of ECE (Fig. 2b). The C-index of AI-predicted ECE score was 0.678 (95% CIs, 0.639–0.717) and 0.697 (95% CIs, 0.617–0.777) in train and test group, respectively, for predicting BCR-free survival. Simultaneously, using the cutoff value of 0.83 for PLNM, the dedicated model produced an overall accuracy of 78.4% (454/579) with 72.5% (37/51) sensitivity and 79% (417/528) specificity in determining PLNM (Fig. 2c). The AI-predicted PLNM score resulted in a C-index of 0.671 (95% CIs, 0.634–0.708) and 0.719 (95% CIs, 0.646–0.792) in train and test group for predicting BCR-free survival, respectively (Fig. 2d).
Fig. 2. The performance of AI-derived predictions including RadS, AI-detected ECE and PLNM for BCR-free survival.
The selected radiomics features (RadS) using Lasso-Cox is plotted in (a). The results of AI-detected ECE and AI-predicted PLNM are summarized in (b) and (c), respectively Values highlighted with different colours in (b) and (c) correspond to SEN, SPE, PPV, NPV, and overall accuracy (grey colour), respectively. Diagnostic performances (TP, TN, FP, and FN) for ECE and PLNM between AI and radiologist are compared. The C-index and HR of RadS, AI-predicted ECE and PLNM for BCR-free survival are displayed in (d). SEN sensitivity, SPE specificity, PPV positive predictive value, NPV negative predictive value, TP true positives, TN true negatives, FP false positives, FN false negatives, HR hazard ratio. R1 = ADC (wavelet LHL glszm Small Area Low Grey Level Emphasis); R2 = b1500_DWI (wavelet LHH glrlm Short Run Low Grey Level Emphasis); R3 = T2WI (original shape Sphericity); R4 = b1500_DWI (original glcm Imc1); R5 = b1500_DWI (original shape Sphericity); R6 = ADC (original shape Sphericity); R7 = b1500_DWI (wavelet LLH glszm Zone Entropy); R8 = b1500_DWI (wavelet LHL glszm Zone Entropy); R9 = ADC (wavelet HLL glcm Idn).
Ablation experience of Cox-DL
The results of dynamic performance tuning of Cox-DL models are summarised in Supplementary Materials (Supplementary Fig. 3 and Supplementary Table 3), where DeepSurv outperformed other DL survival models regarding the best C-index (0.804) over the five-fold cross-validation. The output of DeepSurv was selected as the desired model for Cox-DL for the estimation of BCR-free survival in an individual patient.
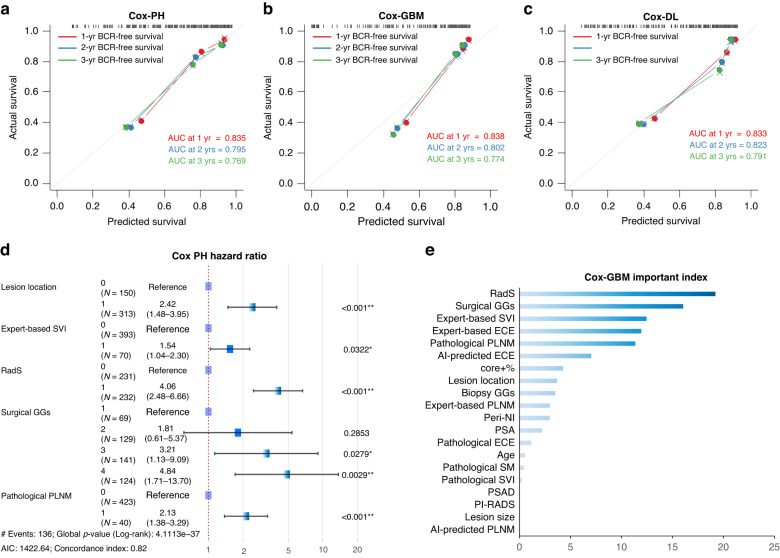
Performance of iBCR-Net
The C-index of 18 iBCR-Net models based on multimodal integration and multialgorithm ensemble is summarised in Table 2. The predicted vs observed BCR-free survival rate of baseline Cox-PH, Cox-GBM, and Cox-DL model (including all clinical-imaging-pathological variables) is plotted with a calibration curve in Fig. 3a, b and c, respectively. The RadS, pathological ISUP GG, lesion location, surgical PLNM, and expert-based SVI were independent predictors of BCR-free survival at Cox-PH model (HRs > 1.50, p < 0.05) (Fig. 3d). Similar results are observed in Cox-GBM, where RadS and pathological ISUP GG are two top-ranked predictors of BCR-free survival by calculating average decrease in accuracy with dynamically adding variables in Cox-GBM analysis (Fig. 3e). The 1-year, 2-year and 3-year survival Receiver-Operating-Characteristic (ROC) analysis of the models for predicting BCR-free survival are plotted with area-under-the-curves (AUC) values in Supplementary Fig. 4a. Based on the optimal cutoff value determined by X-tile software, patients are stratified as low-risk and high-risk categories, whereas the low-risk patients have longer median BCR-free survival time than high-risk patients at the Kaplan–Meier plots (Supplementary Fig. 4b). The detail results of predictive performance of M1 to M5 are illustrated in Supplementary Figs. 5–7.
Table 2.
The C-index of iBCR-Net with multimodal integration using Cox-PH, Cox-GBM and Cox-DL in the test group.
| Model | Cox-PH | Cox-GBM | Cox-DL |
|---|---|---|---|
| Pre/Post-Op M0 | 0.791 (0.712–0.870) | 0.800 (0.722–0.878) | 0.808 (0.738–0.878) |
| Pre-Op M1 | 0.772 (0.694–0.850) | 0.783 (0.704–0.862) | 0.783 (0.715–0.851) |
| Pre-Op M2 | 0.761 (0.683–0.839) | 0.779 (0.703–0.855) | 0.783 (0.712–0.854) |
| Pre-Op M3 | 0.746 (0.655–0.837) | 0.746 (0.661–0.831) | 0.765 (0.685–0.845) |
| Pre-Op M4 | 0.808 (0.740–0.876) | 0.811 (0.746–0.876) | 0.815 (0.753–0.877) |
| Pre-Op M5 | 0.812 (0.750–0.874) | 0.816 (0.756–0.876) | 0.826 (0.770–0.882) |
The numbers in parentheses are the 95% confidence interval.
Cox-PH Cox proportional hazards, Cox-GBM Cox gradient boosting machine, Cox-DL a deep learning-based Cox proportional hazard model.
Fig. 3. Results of baseline iBCR-Net M0 using Cox-PH, Cox-GBM and Cox-DL.
Calibration curve plot of predicted vs observed BCR-free survival rates and time-dependent area-under-the-curve (AUC) at 1-year, 2-year and 3-year endpoint (a–c). Forest plots of hazard ratio and importance index of multimodal factors for BCR at Cox-PH (d) and Cox-GBM (e).
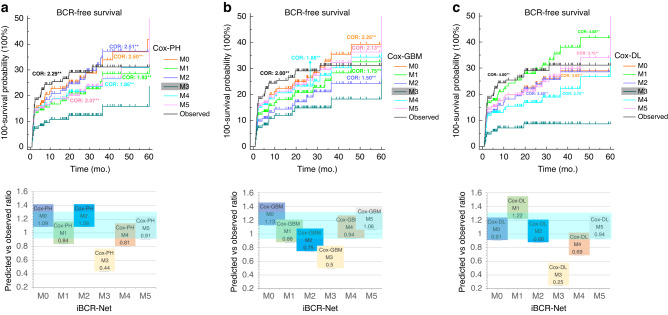
To determine the agreement of iBCR-Net prediction with ground truth observation, the cross-odds ratio (COR) and BCR-free survival curves between iBCR-Net predictions and true observations are plotted using a pairwise log-rank test (Fig. 4). It shows that M1, M2, M4 and M5 are competitive to baseline M0 model (all CORs vs ground truth, p > 0.05), while M3 is significantly lower than M0 (0.21–0.67 vs ground truth, p < 0.01) in either Cox-PH, or Cox-GBM, or Cox-DL model. Details of the pairwise comparison of CORs between M0 to M5 and observed outcomes, with a specific interpretation of Q1–4 referred to in Supplementary Fig. 2, are summarised in Supplementary Materials (Supplementary Tables 4–6 and Supplementary E3).
Fig. 4. Plots of predicted vs observed BCR-free survival curves.
There is no significant (p > 0.05 at the pairwise log-rank test) of predicted survival rates by M0, M1, M2, M4, M5 using Cox-PH (a), Cox-GBM (b) and Cox-DL (c) against true observations. There is a significant (**, p < 0.01 at the pairwise log-rank test) difference in predicted survival rates by M3 compared to those by M0, M1, M2, M4, M5 and true observations. Cross-odds ratio (COR) indicates the relative benefit of the desired model against M3 for survival prediction (e.g., in the upper row, a COR of 2.5 for desired M0 against M3 implicates the use of M0 results in 2.5-fold odds compared to M3 for predicting BCR survival). Plot of the ratio between prediction and observation (lower row) indicates relative agreement between prediction and observation, in which a ratio of 1:1 indicates fully consistent, and <0.8 or >1.2 suggests significant prediction deviation.
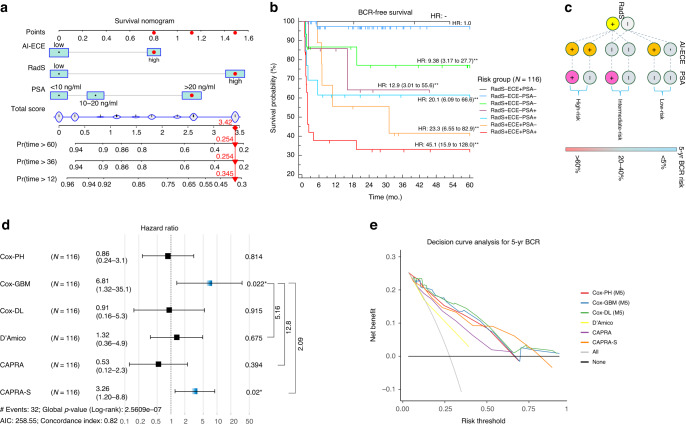
With advances in simplicity, noninvasiveness, and non-reduced diagnostic accuracy, the M5 model, consisting of three presurgical predictors (RadS, AI-predicted ECE, and serum PSA), is regarded as the optimal model for BCR assessment in real-world clinical settings. The Cox-PH M5 is transformed into an easy-to-use nomogram by summing the coefficients of dedicated predictors (Fig. 5a). Survival curves of the 7-level risk categories based on M5 model are plotted (Fig. 5b), relying on which a more simplified triple-stratifying scheme combining RadS (low- vs high-risk), AI-predicted ECE (absent vs present) and PSA (≤20 ng/ml vs >20 ng/ml) is determined (Fig. 5c). It shows that triple-positive patients (RadS+, AI-predicted ECE+, and PSA > 20 ng/ml) have 45.1-fold recurrence risk compared to triple-negative patients within 5 years after surgery.
Fig. 5. Cox-PH M5 expressed as a simplified survival nomogram for clinical application, by which, with AI-determined ECE and RadS at MRI, as well as with PSA, the predicted 1-year, 3-year and 5-year relapse-free survival rate can be calculated preoperatively.
Red dots mark the prediction process of a case with PSA > 20 ng/ml, high-risk RadS and high-risk AI-predicted ECE (a). The resulting nomogram outputs 7-level risk categories, showing different BCR-free survival rates (b). Relying on M5, a more simplified triple-stratifying scheme for 5-year BCR risk is presented with a decision tree (c), where triple-positive patients have extremely higher relapse risk than triple-negative patients 5 years after surgery. The net clinical benefit of iBCR-Net (Cox-PH M5, Cox-GBM M5, Cox-DL M5) against conventional D’Amico, CAPRA, and CAPRA-S tested with a pairwise log-rank test (d) and a decision curve analysis (e).
In pairwise comparison with a hazard regression plot, the iBCR-Net, especially Cox-GBM M5, resulted in 5.16-fold, 12.8-fold, and 2.09-fold (p < 0.05 with the log-rank test) benefit, respectively, against D’Amico, CAPRA, and CAPRA-S for BCR-free survival prediction (Fig. 5d). Decision curve analysis showed that iBCR-Net produced relatively higher net benefits against D’Amico and CAPRA in diagnosing 5-year BCR at all threshold probabilities, and relatively higher net benefit against CAPRA-S at threshold probabilities below 50% (Fig. 5e).
Discussion
Precise stratification of BCR risk of PCa patients after RP is desirable to guide appropriate therapeutic strategy. Preoperative identification of low-risk BCR may enhance the clinician’s decision confidence to delay additional therapy; while high-risk PCa patients are potential candidates to initiate adjuvant therapy [25]. Therefore, we developed a novel iBCR-Net model by a concept of multimodal integration and multialgorithm ensemble, which allows to preoperatively assess BCR risk in PCa patients with RP. The proposed iBCR-Net, especially the biopsy-free AI-aided M5 model, can match the state-of-the-art referred postsurgical model or, in some cases, outperform conventional scoring systems such as D’Amico, CAPRA, and CAPRA-S, thereby provides patients and clinicians more information for administrative decisions.
Recent research suggests that MRI-derived features, especially radiomics, are relevant for identifying men at high risk of BCR [18, 19]. In our study, a more comprehensive radiomics analysis was implemented based on a large-scale sample. Partly in accordance with Bourbonne et al. [19], we found that the ADC-derived Grey Level feature is the most important contributor of RadS. The integrative RadS score, indicating tumour heterogeneity and aggressiveness, was associated with poor BCR-free survival of PCa.
In accordance with previous studies [4, 38, 39], higher ISUP GGs, presence of ECE, or presence of PLNM, implying higher aggressiveness of PCa, were associated with shorter BCR-free survival in our patients. The expert-based performance of MRI in the diagnosis of ECE and PLNM has potential limitations. A single-centre retrospective study reported a sensitivity of 16–44% for ECE diagnosis and a sensitivity of 27–40% for PLNM diagnosis, respectively [28, 40]. With our proposed AI models [27, 28], it resulted in an improved accuracy for staging ECE and PLNM. Additionally, the use of AI may provide a potential way to overcome inter-reader and intra-centre variance during image interpretation. Our results also demonstrated a significant difference in BCR-free survival between low-risk and high-risk patients stratified by AI-aided ECE and PLNM assessment. Notice that the proportion of surgical PLNMs is relatively low compared with previous reports (8.9% vs 15%) [41]. This may be caused by the fact that only 48.4% of our patients underwent PLND or ePLND. Compromission in defining surgical PLNM may produce bias in model assessment. It is thus urgent to further expand the sample size to test the performance of our AI model for PLNM.
In the process of integrating multimodal data for survival analysis, we found that all three Cox-based models provided outstanding risk stratification ability and prediction accuracy. Our findings in the pre-op M5 model supported a critical issue in PCa treatment and management that deserves special attention: the incorporation of AI predictions does not degrade model performance even in the absence of postoperative or biopsy variables, suggesting that M5, avoiding complications caused by invasive procedures or biopsy sampling errors, had promising validity and feasibility in recurrence prediction. This result ties well with the report by Meissner et al. that validated the feasibility of primary RP avoiding invasive prior biopsy in patients with strong PSMA uptake and positive MRI [36]. This indicates the urgent need for noninvasive examination and prediction in clinic. The preoperative simplified triple-stratifying scheme had great potential as a noninvasive tool for prognostic assessment, especially for patients who are not candidates for RP. In our cohort, the performance of D’Amico, CAPRA, and CAPRA-S was better than those reported previously [10] while inferior to our M5 except CAPRA-S. This indicated the potential of our iBCR-Net for preoperative prognostic prediction, which will provide clinicians with more treatment strategy choices.
We acknowledge that our study had potential limitations. First, inherent bias may exist because of its retrospective character. Second, the validation dataset was limited to a single institution. To validate the reproducibility of our iBCR-Net, further prospective multicenter studies are warranted. Third, although about two-thirds of patients experienced biochemical relapse within 2 years after surgery and this percentage in our study reached nearly 90%, the short follow-up is still a potential issue. Long-term follow-up of PCa patients will be conducted further to verify our model. Last, our M5 had a relatively lower net benefit against the CAPRA-S model at a risk threshold larger than 0.5. This may leave a gap for missing patients with high recurrence risk with M5. We can understand that CAPRA-S is a postoperative approach with predictable predictive accuracy. Compared with some accepted preoperative models, such as D’Amico and CAPRA, our M5 is superior and does not even require biopsy results. Therefore, M5 can be easier and more noninvasive against CAPRA-S.
In conclusion, our study confirmed the clinical application value of iBCR-Net in the prognostic task of PCa. The M5 featured with biopsy-free and AI assistance can match state-of-the-art baseline M0 and, in some cases, outperform D’Amico, CAPRA, and CAPRA-S in predicting BCR. Therefore, we support that our iBCR-Net provides a potential way for risk stratification in PCa patients prior to surgery.
Supplementary information
Author contributions
YH: Conceptualization, Data curation, Formal analysis, Writing—original draft. K-WJ: Conceptualisation, Data curation, Formal analysis, Investigation, Methodology, Validation, Writing—original draft, Writing—review & editing. L-LW: Data curation, Formal analysis. RZ: Data curation, Formal analysis. M-LB: Data curation, Formal analysis. QL: Data curation, Formal analysis. JZ: Data curation, Formal analysis. F-PZ, J-RQ, and Y-DZ: Conceptualisation, Data curation, Formal analysis, Investigation, Methodology, Validation, Project administration, Resources, Software, Supervision, Writing—original draft, Writing—review & editing.
Funding
This work was supported by the Key Research and Development Program of Jiangsu Province (BE2017756, Y-DZ) and the Outstanding Postdoctoral Program of Jiangsu Province (2023ZB612, YH).
Data availability
Requests for the raw images and associated imaging data used to train and evaluate the model can be directed to Y-DZ and made available after specific IRB approvals and bespoke data agreement is established between the hospital health network and the requesting party.
Code availability
Source code of Lasso-Cox and Cox-GBM is archived on GitHub (https://github.com/scikitting/ethan/releases/tag/ibcr). Source code of Cox-DL is archived on GitHub (https://github.com/havakv/pycox/). Source code of AI-based ECE staging model is archived on GitHub (https://github.com/Cherishzyh/ProstateECE). The PLNM risk is calculated using the formula: Y = 0.34 × log (D-max) - 4.63× log (ADC) + 0.28 × log (PI-RADS v2 score) + 0.18 ×log (MRI T-stage) + 0.61× log (MRI-SVI) + 0.85 × log (number of positive cores) + 1.12 × log (MRI-LNI).
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Ying Hou, Ke-Wen Jiang.
These authors jointly supervised this work: Jin-Rong Qu, Fei-Peng Zhu, Yu-Dong Zhang.
Supplementary information
The online version contains supplementary material available at 10.1038/s41416-023-02441-5.
References
- 1.Rebello RJ, Oing C, Knudsen KE, Loeb S, Johnson DC, Reiter RE, et al. Prostate cancer. Nat Rev Dis Prim. 2021;7:9. doi: 10.1038/s41572-020-00243-0. [DOI] [PubMed] [Google Scholar]
- 2.Han M, Partin AW, Zahurak M, Piantadosi S, Epstein JI, Walsh PC. Biochemical (prostate specific antigen) recurrence probability following radical prostatectomy for clinically localized prostate cancer. J Urol. 2003;169:517–23. doi: 10.1016/S0022-5347(05)63946-8. [DOI] [PubMed] [Google Scholar]
- 3.Liesenfeld L, Kron M, Gschwend JE, Herkommer K. Prognostic factors for biochemical recurrence more than 10 years after radical prostatectomy. J Urol. 2017;197:143–8. doi: 10.1016/j.juro.2016.07.004. [DOI] [PubMed] [Google Scholar]
- 4.Walz J, Chun FK, Klein EA, Reuther A, Saad F, Graefen M, et al. Nomogram predicting the probability of early recurrence after radical prostatectomy for prostate cancer. J Urol. 2009;181:601–7. doi: 10.1016/j.juro.2008.10.033. [DOI] [PubMed] [Google Scholar]
- 5.Simmons MN, Stephenson AJ, Klein EA. Natural history of biochemical recurrence after radical prostatectomy: risk assessment for secondary therapy. Eur Urol. 2007;51:1175–84. doi: 10.1016/j.eururo.2007.01.015. [DOI] [PubMed] [Google Scholar]
- 6.D’Amico AV, Whittington R, Malkowicz SB, Schultz D, Blank K, Broderick GA, et al. Biochemical outcome after radical prostatectomy, external beam radiation therapy, or interstitial radiation therapy for clinically localized prostate cancer. JAMA. 1998;280:969–74. doi: 10.1001/jama.280.11.969. [DOI] [PubMed] [Google Scholar]
- 7.Cooperberg MR, Pasta DJ, Elkin EP, Litwin MS, Latini DM, DuChane J, et al. The University of California, San Francisco cancer of the prostate risk assessment score: a straightforward and reliable preoperative predictor of disease recurrence after radical prostatectomy. J Urol. 2005;173:1938–42. doi: 10.1097/01.ju.0000158155.33890.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cooperberg MR, Hilton JF, Carroll PR. The CAPRA-S score: a straightforward tool for improved prediction of outcomes after radical prostatectomy. Cancer. 2011;117:5039–46. doi: 10.1002/cncr.26169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zelic R, Garmo H, Zugna D, Stattin P, Richiardi L, Akre O, et al. Predicting prostate cancer death with different pretreatment risk stratification tools: a head-to-head comparison in a nationwide cohort study. Eur Urol. 2020;77:180–8. doi: 10.1016/j.eururo.2019.09.027. [DOI] [PubMed] [Google Scholar]
- 10.Punnen S, Freedland SJ, Presti JC, Aronson WJ, Terris MK, Kane CJ, et al. Multi-institutional validation of the CAPRA-S score to predict disease recurrence and mortality after radical prostatectomy. Eur Urol. 2014;65:1171–7. doi: 10.1016/j.eururo.2013.03.058. [DOI] [PubMed] [Google Scholar]
- 11.Lughezzani G, Budaus L, Isbarn H, Sun M, Perrotte P, Haese A, et al. Head-to-head comparison of the three most commonly used preoperative models for prediction of biochemical recurrence after radical prostatectomy. Eur Urol. 2010;57:562–8. doi: 10.1016/j.eururo.2009.12.003. [DOI] [PubMed] [Google Scholar]
- 12.Brajtbord JS, Leapman MS, Cooperberg MR. The CAPRA score at 10 years: contemporary perspectives and analysis of supporting studies. Eur Urol. 2017;71:705–9. doi: 10.1016/j.eururo.2016.08.065. [DOI] [PubMed] [Google Scholar]
- 13.Turkbey B, Rosenkrantz AB, Haider MA, Padhani AR, Villeirs G, Macura KJ, et al. Prostate Imaging Reporting and Data System version 2.1: 2019 update of Prostate Imaging Reporting and Data System version 2. Eur Urol. 2019;76:340–51. doi: 10.1016/j.eururo.2019.02.033. [DOI] [PubMed] [Google Scholar]
- 14.Morlacco A, Sharma V, Viers BR, Rangel LJ, Carlson RE, Froemming AT, et al. The incremental role of magnetic resonance imaging for prostate cancer staging before radical prostatectomy. Eur Urol. 2017;71:701–4. doi: 10.1016/j.eururo.2016.08.015. [DOI] [PubMed] [Google Scholar]
- 15.Ho R, Siddiqui MM, George AK, Frye T, Kilchevsky A, Fascelli M, et al. Preoperative multiparametric magnetic resonance imaging predicts biochemical recurrence in prostate cancer after radical prostatectomy. PLoS ONE. 2016;11:e0157313. doi: 10.1371/journal.pone.0157313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gandaglia G, Ploussard G, Valerio M, Marra G, Moschini M, Martini A, et al. Prognostic implications of multiparametric magnetic resonance imaging and concomitant systematic biopsy in predicting biochemical recurrence after radical prostatectomy in prostate cancer patients diagnosed with magnetic resonance imaging-targeted biopsy. Eur Urol Oncol. 2020;3:739–47. doi: 10.1016/j.euo.2020.07.008. [DOI] [PubMed] [Google Scholar]
- 17.Lambin P, Leijenaar RTH, Deist TM, Peerlings J, de Jong EEC, van Timmeren J, et al. Radiomics: the bridge between medical imaging and personalized medicine. Nat Rev Clin Oncol. 2017;14:749–62. doi: 10.1038/nrclinonc.2017.141. [DOI] [PubMed] [Google Scholar]
- 18.Shiradkar R, Ghose S, Jambor I, Taimen P, Ettala O, Purysko AS, et al. Radiomic features from pretreatment biparametric MRI predict prostate cancer biochemical recurrence: preliminary findings. J Magn Reson Imaging. 2018;48:1626–36. doi: 10.1002/jmri.26178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bourbonne V, Vallières M, Lucia F, Doucet L, Visvikis D, Tissot V, et al. MRI-derived radiomics to guide post-operative management for high-risk prostate cancer. Front Oncol. 2019;9:807. doi: 10.3389/fonc.2019.00807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wang P, Li Y, Reddy CK. Machine learning for survival analysis: a survey. ACM Comput Surv. 2019;51:110.
- 21.Bello GA, Dawes TJW, Duan J, Biffi C, de Marvao A, Howard L, et al. Deep learning cardiac motion analysis for human survival prediction. Nat Mach Intell. 2019;1:95–104. doi: 10.1038/s42256-019-0019-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hansen N, Patruno G, Wadhwa K, Gaziev G, Miano R, Barrett T, et al. Magnetic resonance and ultrasound image fusion supported transperineal prostate biopsy using the ginsburg protocol: technique, learning points, and biopsy results. Eur Urol. 2016;70:332–40. doi: 10.1016/j.eururo.2016.02.064. [DOI] [PubMed] [Google Scholar]
- 23.Epstein JI, Egevad L, Amin MB, Delahunt B, Srigley JR, Humphrey PA, et al. The 2014 International Society of Urological Pathology (ISUP) Consensus Conference on Gleason Grading of Prostatic Carcinoma: definition of grading patterns and proposal for a new grading system. Am J Surg Pathol. 2016;40:244–52. doi: 10.1097/PAS.0000000000000530. [DOI] [PubMed] [Google Scholar]
- 24.Epstein JI, Allsbrook WC, Jr, Amin MB, Egevad LL, Committee IG. The 2005 International Society of Urological Pathology (ISUP) Consensus Conference on Gleason Grading of Prostatic Carcinoma. Am J Surg Pathol. 2005;29:1228–42. doi: 10.1097/01.pas.0000173646.99337.b1. [DOI] [PubMed] [Google Scholar]
- 25.Cornford P, van den Bergh RCN, Briers E, den Broeck TV, Cumberbatch MG, De Santis M, et al. EAU-EANM-ESTRO-ESUR-SIOG Guidelines on Prostate Cancer. Part II—2020 update: treatment of relapsing and metastatic prostate cancer. Eur Urol. 2021;79:263–82. [DOI] [PubMed]
- 26.Brockman JA, Alanee S, Vickers AJ, Scardino PT, Wood DP, Kibel AS, et al. Nomogram predicting prostate cancer-specific mortality for men with biochemical recurrence after radical prostatectomy. Eur Urol. 2015;67:1160–7. doi: 10.1016/j.eururo.2014.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hou Y, Zhang YH, Bao J, Bao ML, Yang G, Shi HB, et al. Artificial intelligence is a promising prospect for the detection of prostate cancer extracapsular extension with mpMRI: a two-center comparative study. Eur J Nucl Med Mol Imaging. 2021;48:3805–16. doi: 10.1007/s00259-021-05381-5. [DOI] [PubMed] [Google Scholar]
- 28.Hou Y, Bao ML, Wu CJ, Zhang J, Zhang YD, Shi HB. A machine learning-assisted decision-support model to better identify patients with prostate cancer requiring an extended pelvic lymph node dissection. BJU Int. 2019;124:972–83. doi: 10.1111/bju.14892. [DOI] [PubMed] [Google Scholar]
- 29.Tibshirani R. The lasso method for variable selection in the Cox model. Stat Med. 1997;16:385–95. doi: 10.1002/(SICI)1097-0258(19970228)16:4<385::AID-SIM380>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
- 30.Friedman JH. Greedy function approximation: a gradient boosting machine. Ann Stat. 2001;29:1189–232. doi: 10.1214/aos/1013203451. [DOI] [Google Scholar]
- 31.Katzman JL, Shaham U, Cloninger A, Bates J, Jiang T, Kluger Y. DeepSurv: personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Med Res Methodol. 2018;18:24. doi: 10.1186/s12874-018-0482-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Håvard Kvamme ØB, Scheel I. Time-to-event prediction with neural networks and Cox regression. J Mach Learn Res. 2019;20:1–30. [Google Scholar]
- 33.Lee C, Zame W, Yoon J, van der Schaar M. Deephit: a deep learning approach to survival analysis with competing risks. Thirty-Second AAAI Conference on Artificial Intelligence; 2018.
- 34.Fotso S. Deep neural networks for survival analysis based on a multi-task framework. [Preprint]. 2018. Available from: https://arxiv.org/abs/1801.05512.
- 35.Kvamme H, Borgan Ø. Continuous and discrete-time survival prediction with neural networks. [Preprint]. 2019. Available from: https://arxiv.org/abs/1910.06724. [DOI] [PMC free article] [PubMed]
- 36.Meissner VH, Rauscher I, Schwamborn K, Neumann J, Miller G, Weber W, et al. Radical prostatectomy without prior biopsy following multiparametric magnetic resonance imaging and prostate-specific membrane antigen positron emission tomography. Eur Urol. 2022;82:156–60. [DOI] [PubMed]
- 37.Camp RL, Dolled-Filhart M, Rimm DL. X-tile: a new bio-informatics tool for biomarker assessment and outcome-based cut-point optimization. Clin Cancer Res. 2004;10:7252–9. doi: 10.1158/1078-0432.CCR-04-0713. [DOI] [PubMed] [Google Scholar]
- 38.Wilczak W, Wittmer C, Clauditz T, Minner S, Steurer S, Buscheck F, et al. Marked prognostic impact of minimal lymphatic tumor spread in prostate cancer. Eur Urol. 2018;74:376–86. doi: 10.1016/j.eururo.2018.05.034. [DOI] [PubMed] [Google Scholar]
- 39.Jeong BC, Chalfin HJ, Lee SB, Feng Z, Epstein JI, Trock BJ, et al. The relationship between the extent of extraprostatic extension and survival following radical prostatectomy. Eur Urol. 2015;67:342–6. doi: 10.1016/j.eururo.2014.06.015. [DOI] [PubMed] [Google Scholar]
- 40.Wang J, Wu CJ, Bao ML, Zhang J, Shi HB, Zhang YD. Using support vector machine analysis to assess PartinMR: a new prediction model for organ-confined prostate cancer. J Magn Reson Imaging. 2018;48:499–506. doi: 10.1002/jmri.25961. [DOI] [PubMed] [Google Scholar]
- 41.von Bodman C, Godoy G, Chade DC, Cronin A, Tafe LJ, Fine SW, et al. Predicting biochemical recurrence-free survival for patients with positive pelvic lymph nodes at radical prostatectomy. J Urol. 2010;184:143–8. doi: 10.1016/j.juro.2010.03.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Requests for the raw images and associated imaging data used to train and evaluate the model can be directed to Y-DZ and made available after specific IRB approvals and bespoke data agreement is established between the hospital health network and the requesting party.
Source code of Lasso-Cox and Cox-GBM is archived on GitHub (https://github.com/scikitting/ethan/releases/tag/ibcr). Source code of Cox-DL is archived on GitHub (https://github.com/havakv/pycox/). Source code of AI-based ECE staging model is archived on GitHub (https://github.com/Cherishzyh/ProstateECE). The PLNM risk is calculated using the formula: Y = 0.34 × log (D-max) - 4.63× log (ADC) + 0.28 × log (PI-RADS v2 score) + 0.18 ×log (MRI T-stage) + 0.61× log (MRI-SVI) + 0.85 × log (number of positive cores) + 1.12 × log (MRI-LNI).