Multimodal imaging-based material mass density estimation for proton therapy using supervised deep learning

Abstract

Objective

Mapping CT number to material property dominates the proton range uncertainty. This work aims to develop a physics-constrained deep learning-based multimodal imaging (PDMI) framework to integrate physics, deep learning, MRI, and advanced dual-energy CT (DECT) to derive accurate patient mass density maps.

Methods:

Seven tissue substitute MRI phantoms were used for validation including adipose, brain, muscle, liver, skin, spongiosa, 45% hydroxyapatite (HA) bone. MRI images were acquired using T ₁ weighted Dixon and T ₂ weighted short tau inversion recovery sequences. Training inputs are from MRI and twin-beam dual-energy images acquired at 120 kVp with gold/tin filters. The feasibility investigation included an empirical model and four residual networks (ResNet) derived from different training inputs and strategies by PDMI framework. PRN-MR-DE and RN-MR-DE denote ResNet (RN) trained with and without a physics constraint (P) using MRI (MR) and DECT (DE) images. PRN-DE stands for RN trained with a physics constraint using only DE images. A retrospective study using institutional patient data was also conducted to investigate the feasibility of the proposed framework.

Results:

For the tissue surrogate study, PRN-MR-DE, PRN-DE, and RN-MR-DE result in mean mass density errors: −0.72%/2.62%/−3.58% for adipose; −0.03%/−0.61%/−0.18% for muscle; −0.58%/−1.36%/−4.86% for 45% HA bone. The retrospective patient study indicated that PRN-MR-DE predicted the densities of soft tissue and bone within expected intervals based on the literature survey, while PRN-DE generated large density deviations.

Conclusion

The proposed PDMI framework can generate accurate mass density maps using MRI and DECT images. The supervised learning can further enhance model efficacy, making PRN-MR-DE outperform RN-MR-DE. The patient investigation also shows that the framework can potentially improve proton range uncertainty with accurate patient mass density maps.

Advances in knowledge:

PDMI framework is proposed for the first time to inform deep learning models by physics insights and leverage the information from MRI to derive accurate mass density maps.

Introduction

Compared to traditional photon radiation therapy, proton therapy has demonstrated a reduction in patients’ side-effects and unplanned hospitalizations while achieving comparable tumor control. ^1,2 Protons offer the physical advantage of stopping just after depositing highest dose, sparing healthy tissues beyond the tumor volume. ³ One of the critical factors that dominates the quality of proton treatment planning is the accuracy of the dose calculation algorithm. Dose calculation algorithms, which may be analytical ⁴ or Monte Carlo-based, ^5–7 require the relative stopping power (RSP) or mass density of materials to simulate transport phenomena within patients. Conventional treatment planning systems use CT numbers to material property curves calibrated by the stoichiometric method ⁸ to convert Hounsfield units (HUs) to material RSP or mass densities from CT images. However, this approach is based on fitting data to a bilinear model which is limited in how mass densities are categorized for different tissue types, ^9,10 and materials with different compositions may result in the same attenuation measured by CT scanners. To account for this uncertainty in HU-to-RSP or HU-to-mass-density conversion, a 2.5–3.5% proton range margin is usually adapted for treatment planning. ^11,12

Dual-energy computed tomography (DECT) can effectively characterize tissues and detect lesions. ¹³ The parametric maps inferred from DECT images, such as the effective atomic number and relative electron density, can be used to derive proton RSP for analytical dose calculation. ^14,15 Virtual monochromatic images (VMIs) derived from DECT can also increase image quality and reduce beam-hardening artifacts compared to CT images from a polychromatic spectrum. ¹⁶ VMI can provide images with less noises ¹⁶ and metal artifacts ^17–19 than the images acquired from a CT machine with polychromatic energy spectra. In more recent work by Medrano et al, ²⁰ they developed an RSP prediction method based on the sinogram domain that achieved bony-tissue uncertainty of 0.8%. In general, accurate proton RSP maps can be acquired from DECT images, ²¹ and this approach leads to more accurate proton dose calculation than the method using conventional CT imaging. ^22,23 Wohlfahrt et al ²⁴ recommended patient-specific DECT-based RSP prediction for treatment planning. They concluded that intrapatient adipose and soft tissue diversity were 5.6 and 9.8% by taking the difference of 97.5th and 2.5th RSP percentiles weighted by CT voxel ratios of each individual tissue, and the mean RSP deviation was 1.2% between the Hounsfield look-up table and patient specific RSP map.

Meanwhile, MRI demonstrates favorable soft tissue contrast relative to CT and its utility in radiation oncology has seen a significant increase over the past decade. Synthetic CT-based MRI-only proton therapy has been investigated, and while others have concluded that an MRI-only treatment planning is feasible, but inaccurate bone delineation has the potential to lead to significant uncertainty. ²⁵ Sudhyadhom ²⁶ proposed a method to directly determine material mean ionization potential (I) from MRI. Using this method, Scholey et al ²⁷ predicted RSP by using the Bethe-Bloch formula with material I and relative electron densities (based on the CT stoichiometric method) from MRI and CT separately, and achieved RSP uncertainty within 1% for soft tissues. It would be of great interest to develop a model that can directly assimilate MRI and DECT information to generate material properties.

However, a fixed form of the linear model is used for the DECT-based stoichiometric method ^28,29 to fit data, and it is non-trivial for the model to utilize MRI directly. It typically requires extensive time and effort to gain the mechanistic understanding necessary to develop a new model that can simultaneously assimilate MRI and DECT data. Alternatively, modern machine learning (ML) methods can deploy models with flexible forms to effectively discover the underlying correlations between MRI/CT images and material characteristics. Su et al ³⁰ demonstrated that ML models could generate RSP mapping with the uncertainty of ~3% for cortical bone from DECT images. In Scholey et al, ³¹ they show that ML from low energy CT to higher energy CT (kVCT to MVCT) may be useful in the accurate generation of RSP maps with error reductions primarily due to improvements in electron density. RSP accuracy in that study was limited by a lack of compositional (elemental or molecular) information as available in DECT ^32,33 or MRI. ²⁶

Many conventional ML methods favor the principle of Occam’s razor: simplicity leads to the optimal model because of its generalizability and interpretability. ³⁴ However, the strategy may not be applicable when dealing with a substantial amount of data. ³⁵ In contrast, neural networks have been proven universal approximators, ³⁶ and modern deep learning (DL) models with hierarchical structures can learn complex patterns from data.

In the present work, we propose a physics-constrained DL-based multimodal imaging (PDMI) framework to predict patient mass density maps from MRI and DECT images. To evaluate the feasibility of the proposed method for clinical applications, we explore conditions by which DL models can benefit from the PDMI framework to infer material mass density maps accurately and effectively from MRI and DECT images.

Methods and materials

Tissue substitute phantoms and data acquisition

Five tissue substitute phantoms were created following the recipe by Scholey et al, ²⁷ including adipose, muscle, skin, and spongiosa. We also added 45% hydroxyapatite (HA) bone as that’s a typical composition of “standard” bone (whereas spongiosa is less dense and contains fat). The phantoms were made by homogeneous mixtures of deionized water, gelatin from porcine skin (surrogate of protein), porcine lard (surrogate of fat), and HA. A small amount of sodium dodecyl sulfate (SDS) was added to the phantoms with water and lard to promote mixing and enhance homogeneity. Scholey et al ²⁷ investigated each mixture to ensure that their physical characteristics were similar to actual biological tissues for the respective modality. Table 1 gives mass percent compositions of each mixture for tissue surrogates.

Table 1.

Mass percent compositions of mixtures for tissue substitute phantoms

Tissue surrogate	Water	Gelatin (Protein)	Lard (Fat)	Hydroxyapatite	SDS
Adipose			100
Muscle	74.78	19.97	5.0		0.25
Skin	75.0	25.0
Spongiosa	26.61	11.83	47.43	12.81	1.32
45% HA bone	55.0			45.0

HA, hydroxyapatite; SDS, sodium dodecyl sulfate.

Two additional fresh animal tissue phantoms were made from ex vivo porcine blood with either porcine brain (brain phantom) or porcine liver (liver phantom). To determine the elemental compositions of these phantoms, multiple small brain and liver samples were weighed, dehydrated, crushed, and sent off for combustion analysis to determine their elemental compositions. These results, along with the known amount of blood (assumed to have the same elemental composition as water) and hydrated tissue comprising the brain and liver phantoms, were then used to compute the elemental compositions of the animal tissue phantoms. The mass densities of each tissue substitute and animal tissue phantom were measured by a high-precision scale (HK-3200A, Mars Scale Corporation, Canada) and volumetric pipettes. Table 2 summarizes each tissue surrogate’s measured mass density and physical properties.

Table 2.

Physically measured mass densities (ρ_meas ), mean excitation energies (I), and elemental mass percent compositions for tissue substitute phantoms

Tissue surrogate	ρ meas (g/cm3)	I (eV)	H	C	N	O	Na	P	S	Ca
Adipose	0.936	61.9	12.37	77.70	0.16	9.77
Brain	1.028	77.3	10.96	6.02	0.73	82.24			0.05
Muscle	1.064	76.7	10.37	12.44	3.06	73.86	0.02		0.25
Liver	1.065	77.2	10.60	8.98	2.05	78.25			0.12
Skin	1.077	77.5	10.09	10.55	3.82	75.26			0.28
Spongiosa	1.091	76.1	9.79	42.50	1.88	37.96	0.11	2.37	0.28	5.11
45% HA bone	1.417	108.5	6.24			67.48		8.32		17.96

HA, hydroxyapatite.

Tissue substitute phantoms were scanned with a Siemens SOMATOM Definition Edge scanner using a head-and-neck (HN) TwinBeam dual-energy (TBDE) protocol with a CT dose index (CTDI_{vol, 32cm}) of 8.6 mGy and effective milliampere-seconds (mAs_eff) of 400. TBDE protocols acquire images at 120 kVp with gold (Au) and tin (Sn) filters, and we refer to images from low- and high-energy spectra as DECT HighE and DECT LowE images. DECT parametric maps were generated from Siemens Syngo.Via including relative electron density and VMI of 80 keV. A Siemens MAGNETOM Aera 1.5 T scanner was used to acquire MR images of the phantoms using a 3D T ₁ weighted Dixon VIBE sequence, generating water-only (T ₁DW) and fat-only (T ₁DF) images, and a 3D T ₂ weighted short tau inversion recovery SPACE sequence (T ₂-STIR).

Table 3 summarizes the acquisition parameters used to acquire DECT and MR images. Figure 1 depicts the axial view of phantom images acquired from MRI and DECT scans. The dimension of each phantom was 5.7 × 5.7 × 12.9 cm³, and each phantom was placed in a cylindrical water container with a diameter and height equal to 16.83 cm and 25.4 cm. MRI T1 and T2 scans contain 208 × 288 × 176 and 256 × 256 × 208 voxels, and DECT scans include 512 × 512 × 545 voxels.

Table 3.

DECT and MRI acquisition parameters

Scanner		Siemens SOMATOM Definition Edge
Collimation		64 × 0.6 mm
Voxel size		0.977 × 0.977 × 0.5 mm3
Field of view		500 mm
X-ray tube voltage		120 kVp with Au and Sn filters
Scanner		Siemens MAGNETOM Aera 1.5T
T1	3D DIXON VIBE voxel size	1.247 × 1.247 × 1.2 mm3
	TR	7.76 ms
	TE	2.39 ms
T2	3D STIR SPACE voxel size	1.016 × 1.016 × 1.1 mm3
	TR	3500 ms
	TE	248 ms

3D, three-dimensional; DECT, dual-energy CT; STIR, short tau inversion recovery; TE, echo time; TR, repetition time.

Figure 1.

Transversal representation of tissue substitute phantom images acquired from (a1–a4) T ₁ DW MRI, (b1–b4) T ₁DF MRI, (c1–c4) T ₂-STIR, (d1–d4) high-energy spectrum imaging of twin-beam DECT (DECT HighE), and low-energy spectrum imaging of twin-beam DECT (DECT LowE). The dimensions of squared phantoms are 5.7 × 5.7 × 12.9 cm³, and the sizes of the cylindrical water containers are 16.83 cm and 25.4 cm in diameter and height. DECT, dual-energy CT; HA, hydroxyapatite; T ₁DW, T ₁ weighted Dixon water-only; T ₁DF, T ₁ weighted Dixon fat-only; T ₂-STIR, T ₂ weighted short tau inversion recovery.

A retrospective HN patient study was conducted for a proof-of-concept test of the proposed framework due to the lack of ground-truth mass density maps. The HN patient was scanned with identical MRI and DECT imaging protocols as the phantom study. Since patient images were heterogeneous, MRI images were first rigidly registered to DECT images, and then deformable image registration was applied using Velocity^TM (Varian Medical Systems, Palo Alto), a multimodality image registration software. Ultimately, MRI images were resampled to match the resolution of DECT images, which includes 512 × 512 × 470 voxels with a voxel size of 0.977 × 0.977 × 1 mm³.

Physics-constrained deep learning-based multimodal imaging framework

The PDMI framework relies on supervised learning to train DL models that can infer material mass densities from MRI and DECT images. Figure 2 shows the PDMI framework to generate material mass density maps from MRI and DECT images and validate the phantom results through a proton experiment. The model inputs from MRI include T ₁DF, T ₁DW, and T ₂-STIR, while the inputs from DECT images are HighE, LowE, ρ_e , and 80-keV VMI. The HighE and LowE are images acquired from TBDE protocols using a 120 kVp X-ray spectrum with tin (Sn) and gold (Au) filters. The ρ_e , and 80-keV VMI are derived from Siemens Syngo.Via, and they are relative electron density maps to that of water and virtual monochromatic images obtained from the 80-keV spectrum.

Figure 2.

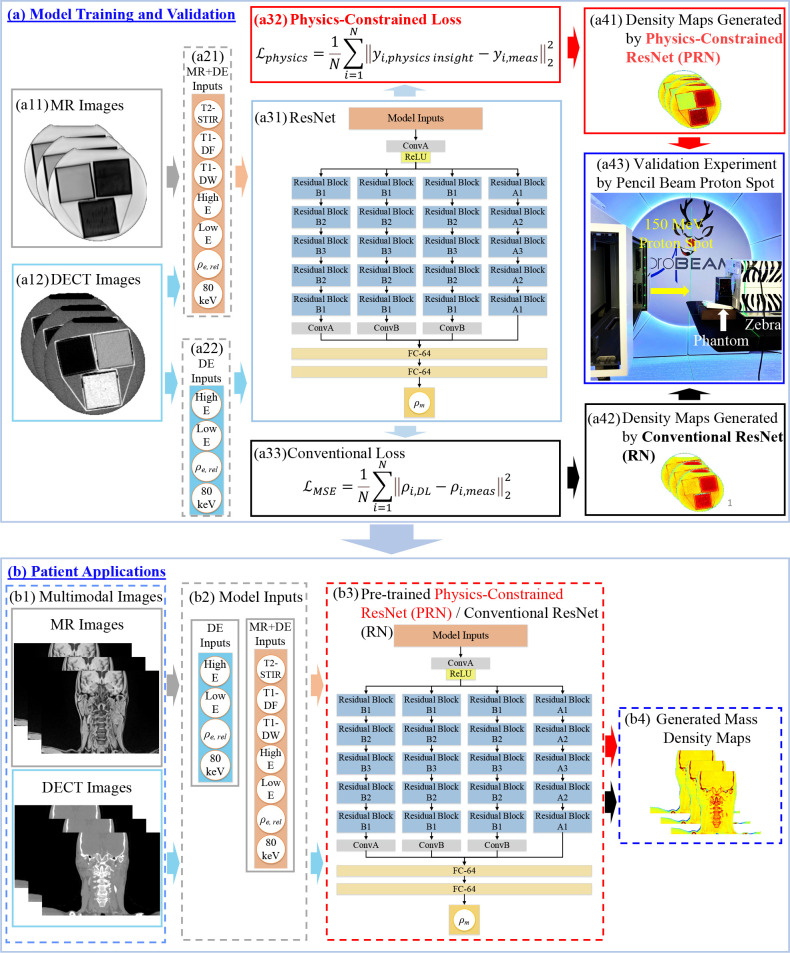
PDMI framework for material mass density inference including (a) model training and validation and (b) patient application. At training phase, model inputs are (a11) MRI and (a12) DECT images. (a31) DL models used in the framework. ResNet was implemented where ConvA, ConB, and Residual Blocks represent different convolutional components. (a32) Physics-constrained loss and (a33) conventional mass density loss for training. Material mass densities generated by (a41) conventional RN and (a42) PRN. (a43) Validation experiment to obtain measured RSP for tissue substitute phantoms using a 150 MeV proton spot and Zebra (IBA Dosimetry, Germany). For patient application, (b1–b4) inference of mass density map for patient applications using MRI and DECT images as inputs for PRN and RN. DECT, dual energy CT; DL, deep learning; PDMI, physics-constrained deep learning-based multimodal imaging; PRN, physics-constrained ResNet.

We used PyTorch ³⁷ to implement residual networks (ResNet) in the proposed framework. Figure 2(a) illustrates the training workflow that involves two branches (Figure 2(a31)→(a32) and Figure 2(a31)→(a33)) to train DL models with different loss functions. Figure 2(a33) shows a conventional mass density loss function ( ${\mathcal{L}}_{\rho }$ ) defined by mean square error with ground truth mass density (ρ_meas ) from the physical measurement of mass density for tissue substitute phantoms. Unlike conventional DL training, Figure 2(a32) shows the proposed physics-constrained loss function ( ${\mathcal{L}}_{\rho hysics}$ ) using physics insights without requiring ground truth mass density, which requires separate measurement that can introduce additional uncertainty. The physics insights can be quantified from a well-established physics-based models to constrained DL models. Section 2.2.2. describes how we tightly integrate physics insights (Eq. (4)) into DL training in this work. Figure 2(a43) shows the experiment setup for proton measurement (see Section 0) that can be used to validate the accuracy of DL models. The measured RSP can be derived through proton experiment, and then the reference mass density can be obtained by Eq. (7). The model uncertainty can be evaluated for physics-constrained ResNet (PRN) in Figure 2(a41) and conventional ResNet (RN) in Figure 2(a42). Figure 2(b) depicts the workflow for patient applications. Patients’ DECT and MRI images will be input to the pre-trained and validated ResNet models (RN and PRN) from Figure 2(a). Then, the ResNet will generate the corresponding mass density map to support potential proton Monte Carlo dose calculation for treatment planning.

Deep learning model and training data

ResNet is used in Figure 2(a31) due to its accuracy in learning from data through hierarchical modelling. ³⁸ The ConvA in Figure 2(a31) denotes the convolutional layer with channel numbers, kernel size, stride number, and padding size of 64, 7, 2, and 3, while the parameters are 64, 3, 1, and 0 for another convolutional layer (ConvB). Each residual block includes two convolutional and one residual layers. The convolutional layers include channel numbers of 64, 128, 256 for residual block A1/B1, A2/B2, and A3/B3, while the stride numbers and padding sizes are 2 and 1 for all convolutional layers in each residual block. The kernel sizes are 3 and 2 for residual block A1-A3 and B1-B3. The ResNet in Figure 2(a31)/(b3) has identical model structures, and Figure 2(b3) is for patient application that the model parameters are trained based on the calibration data used at the training phase as depicted by Figure 2(a). The Adam optimizer ³⁹ is used for training ResNet.

The ResNet networks trained by the physics-constrained loss and conventional loss are named physics-constrained ResNet (PRN) and conventional RN. We also add a suffix, “-MR-DE” or “-DE,” to PRN and RN to indicate whether the model is trained with MRI and DECT images or DECT-only images. For instance, PRN-MR-DE presents the ResNet trained with the physics-constrained loss using MRI and DECT images. ReLU ⁴⁰ is the activation function used in the network.

MATLAB was used to pre-process the DICOM image files from MRI and CT for training, and all image files were normalized within the range of [−1, 1] based on each imaging modality. Circular volumes of interest (VOIs) were manually contoured for each tissue surrogate with diameters of 40 and 28 pixels for MRI and DECT images. Data from each VOI were subsequently arranged in a one-dimensional (1D) array to form a DL input matrix with the size of n_vox ×n_inp where n_vox and n_inp denote the total voxels within VOI from each material and input images such as T ₁DF, T ₁DW, T ₂-STIR, HighE, LowE, ρ_e , and 80-keV VMI for PRN-MR-DE. The n_vox contained 444,465 and 226,590 voxels for training and testing from each VOI on MRI and DECT images for seven materials. Since the DL training was based on 1D data, there was no need to perform image interpolation.

Mass density and physics-constrained loss functions

The PDMI framework is based on supervised learning DL to find the underlying correlations behind the data. This inverse modelling is ill-posed, and it can be solved by optimizing the loss function defined by Eq. (1), which includes conventional mass density ( ${\mathcal{L}}_{\rho }$ ) and physics-constrained ( ${\mathcal{L}}_{physics}$ ) losses. For $\delta$ =1, physics-constrained training is performed, and conventional training is used when $\delta$ =0.

$${\displaystyle \mathfrak{L}=\left(1-\delta \right)\times {\mathfrak{L}}_{\rho }+\delta \times {\mathfrak{L}}_{physics}}$$ (1)

Eq. (2) defines a conventional mass loss function that requires measured material mass density (ρ_meas ) as the targets. The ρ_DL , N, and i denote the predicted mass density from DL models, total number of voxels, and i^th voxel.

$${\displaystyle {\displaystyle {\mathfrak{L}}_{\rho }=\frac{1}{N}\sum _{i=1}^N{\Vert {\rho }_{i,DL}-{\rho }_{i,meas}\Vert }_2^2}}$$ (2)

Meanwhile, the PDMI framework also adapts physics insights to form physics-constrained loss functions given by Eq. (3), where y_{physics insight} and y_meas denote the physics insights and corresponding measured quantities of the physics insights, respectively. We select y_{physics insight} as the empirical HU model from the stoichiometric calibration method, ⁸ and y_meas becomes the CT numbers in this study.

$${\displaystyle {\displaystyle {\mathfrak{L}}_{physics}=\frac{1}{N}\sum _{i=1}^N{\Vert y_{i,physicsinsight}-y_{i,meas}\Vert }_2^2}}$$ (3)

Eq. (4) gives the empirical HU model with the assumption that HU = 1000(µ/µ_w-1) where µ and µ_w are linear attenuation coefficients of the material and water. The k_ph , k_coh , and k_incoh are energy-dependent coefficients associated with the photon-electric, coherent, incoherent effects, respectively. These constants can be determined from the stoichiometric calibration method ⁸ with least-square fitting. In this work, the estimated k_ph , k_coh , and k_incoh coefficients are 9.094 × 10⁻⁶, 1.064 × 10⁻³, and 5.988 × 10⁻¹.

$${\displaystyle y_{\text{physics insight }}\equiv H{U}_{80keV}=1000\left[\tilde{\rho }\frac{k_{ph}{\tilde{z}}^{3.62}+k_{\text{coh }}{\hat{z}}^{1.86}+k_{\text{incoh }}}{k_{ph}{z}_w^{3.62}+k_{\text{coh }}{\hat{z}}_w^{1.86}+k_{\text{incoh }}}-1\right]}$$ (4)

By defining $\tilde{z}\equiv z_{3.62}$ and $\widehat{z}\equiv z_{1.86}$ , the material z_n values can be derived by Eq. (5) ²⁸ where n is 3.62 or 1.86. The i, ω, Z, and A denote ith element, weight fraction, atomic number, and atomic mass number. The z_3.62 and z_1.86 are 7.522 and 7.115 for water.

$${\displaystyle {\displaystyle z_n={\left(\sum _i\frac{{\omega }_i\frac{Z_i}{A_i}}{\sum _i{\omega }_i\frac{Z_i}{A_i}}{Z}_i^n\right)}^{\frac{1}{n}}}}$$ (5)

The relative electron density derived using the DL model output ( $\tilde{\rho }$ ) is defined by Eq. (6) with the electron density of water (ρ_e,w ) equal to 3.343 × 10²³ e^-/cm³.

$${\displaystyle {\displaystyle \stackrel{\sim }{\rho }\equiv \frac{{\rho }_{DL}\sum _i{\omega }_i\frac{Z_i}{A_i}}{{\rho }_{e,w}}}}$$ (6)

The value of ρ_DL is queried from DL models during each training iteration that allows Eq. (4) to be updated and the physics loss given by Eq. (3). The target is 80-keV VMI for the physics-constrained training because the image provides the optimal image-noise and beam-hardening ratios. ^15,16

Validation experiment: proton RSP measurement for tissue substitute phantoms

A 150 MeV proton spot delivered by Varian ProBeam System (Varian Medical Systems, Palo Alto) was used to determine the measured RSP of seven tissue substitute phantoms including adipose, brain, muscle, liver, skin, spongiosa, and 45% HA bone. The dimension of each phantom container was 5.7 (width) x 5.7 (height) x 12.9 (length) cm³ Figure 2(a43) illustrates the setup for the experiment with Zebra (IBA Dosimetry, Germany) to measure proton 80% distal range (R80). The water equivalent thickness (WET) was computed by taking differences between R80 measurements with and without phantoms. WET values were divided by the physical width of phantom containers to obtain measured RSP for each material given in Table 2.

The Bethe-Bloch equation can be rearranged as Eq. (7) to obtain the reference mass density (ρ_ref ) using measured RSP (RSP_meas ) where m_e , c, β, and I are the electron mass, speed of light, proton (150 MeV) velocity relative to the speed of light, and mean ionization potential of materials. The mean ionization potential of water (I_water ) is 75 eV. ⁴¹ Table 4 gives the measured RSP, reference mass densities, and other material characteristics defined by Eq. (5) for each phantom.

Table 4.

Material characteristics for tissue substitute phantoms

Tissue surrogate	RSPmeas	ρ ref (g/cm3)	$\tilde{z}$	$\widehat{z}$
Adipose	0.979	0.947	5.902	5.502
Brain	1.014	1.020	7.445	7.023
Muscle	1.056	1.067	7.406	6.954
Liver	1.054	1.063	7.421	6.993
Skin	1.067	1.082	7.447	7.004
Spongiosa	1.076	1.093	9.711	7.673
45% HA bone	1.344	1.476	13.152	11.025

HA, hydroxyapatite.

$${\displaystyle {\displaystyle {\rho }_{ref}=RS{P}_{meas}{\left\{\frac{\sum _i{\omega }_i\frac{Z_i}{A_i}}{{\rho }_{e,w}}\cdot \frac{ln\left[\frac{2m_e{c}^2{\beta }^2}{I\left(1-{\beta }^2\right)}\right]-{\beta }^2}{ln\left[\frac{2m_e{c}^2{\beta }^2}{I_{water}\left(1-{\beta }^2\right)}\right]-{\beta }^2}\right\}}^{-1}}}$$ (7)

Empirical model for DECT parametric mapping

Eq. (8) shows the empirical model ⁴² to estimate material mass densities using DECT parametric maps of relative electron density (ρ_e ) and effective atomic number (Z_eff ) obtained from Siemens Syngo.Via. This linear fitting model is not valid for low-density material such as an inflated lung, so a constant value of 0.26 g/cm³ is used when materials’ relative electron densities are lower than 0.37. We implemented the empirical model in Matlab R2021b and compared it to ResNet models trained by the PDMI framework.

$${\displaystyle p\left(\frac{g}{c{m}^3}\right)=\{\begin{array}{l}-0.1746+1.176{\rho }_e\\ 0.26\end{array}\frac{{\rho }_e\ge 0.37}{{\rho }_e<0.37}}$$ (8)

Evaluation

To evaluate the performance of the PDMI framework, we compare the proposed physics-constrained DL model to conventional DL and empirical models. The implemented ResNet can take inputs from both DECT and MRI (MR-DE) or merely DECT (DE). We refer to the ResNet models trained by the physics-constrained loss function (Eq. (3)) as PRN-MR-DE and PRN-DE. The ResNet models trained by the conventional loss function (Eq. (2)) are denoted as RN-MR-DE and RN-DE. The empirical model is given by Eq. (8).

The mean percentage error (MPE) is the evaluation metric to quantify model accuracy for tissue surrogate phantom analyses with the reference mass densities from proton measurement. Eq. (9) defines MPE where x, REF, i, and N denote the voxel quantity, reference values, ith voxel, and total voxels.

$${\displaystyle {\displaystyle MPE=\frac{1}{N}\sum _{i=1}^N\left(\frac{x_i-x_{i,REF}}{x_{i,REF}}\right)\times 100\mathrm{\%}}}$$ (9)

Results

The PDMI framework allows ResNet to be trained with a physics-constrained loss or a conventional mass density loss. The investigated models include ResNet trained with a physics-constrained loss using MRI and DECT images or DECT-only images (PRN-MR-DE or PRN-DE) and ResNet trained with a conventional mass density loss using MRI and DECT images or DECT-only images (RN-MR-DE or RN-DE).

Inference of material mass densities for tissue substitute phantoms

MPE results for the empirical, conventional, and physics-constrained models are shown in Table 5, with lowest MPE value for each phantom in bold. PRN-MR-DE yields the lowest MPE values for most phantom materials. The additional MRI data adapted by PRN-MR-DE improve the model accuracy for all phantoms compared to PRN-DE. For example, PRN-MR-DE improves the errors from PRN-DE by 1.9 and 1.08% for adipose and skin. In the case where RN-MR-DE results in considerable uncertainty, the physics-constrained training usually can regularize ResNet to deliver lower model errors. For instance, PRN-MR-DE reduces the errors from RN-MR-DE by 2.86 and 4.28% for adipose and 45% HA bone. The empirical model achieves the optimal error of −0.62% for adipose.

Table 5.

Comparisons of mass densities between the reference and different models

Phantom	MPE
	Empirical model	Conventional		Physics-constrained
		RN-DE	RN-MR-DE	PRN-DE	PRN-MR-DE
Adipose	−0.62%	7.65%	−3.58%	2.62%	−0.72%
Brain	−0.37%	0.37%	0.49%	0.34%	−0.29%
Muscle	0.09%	−0.93%	−0.18%	−0.61%	−0.03%
Liver	0.27%	−0.71%	0.34%	−0.68%	0.22%
Skin	0.56%	0.51%	−0.13%	1.24%	0.16%
Spongiosa	1.02%	1.20%	0.05%	3.83%	3.13%
45% HA bone	−0.78%	−5.72%	−4.86%	−1.36%	−0.58%

HA, hydroxyapatite; MPE, mean percentage error; PRN, physics-constrained ResNet.

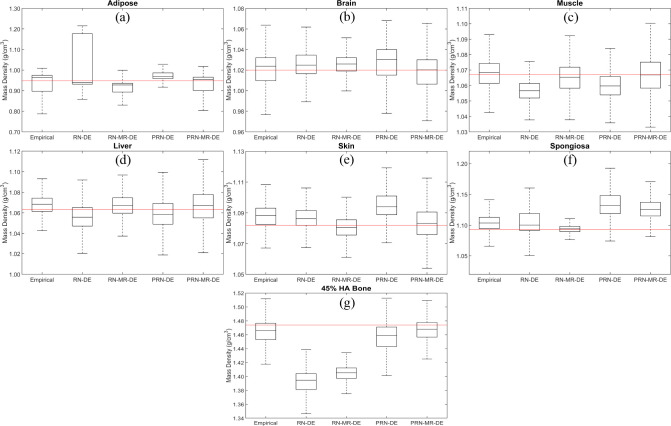
Figure 3 shows the boxplot of different models’ mass density distributions for each phantom. RN-DE yields an unreasonable density range for adipose, since the upper bound reaches 1.2 g/cm³. When the reference mass densities of adipose and 45% HA bone are not included in interquartile ranges by RN-MR-DE, the physics-constrained training can regularize the model responses. For instance, PRN-MR-DE predicts the median adipose and 45% HA bone values close to the reference. The empirical model delivers median values within interquartile ranges for most phantoms except skin and spongiosa. RN-MR-DE results in the optimal median value prediction for spongiosa. For most phantoms, the median values predicted by PRN-MR-DE are the closest to the reference compared to other models.

Figure 3.

Boxplot of mass density distributions generated by the empirical model, RN-DE, RN-MR-DE, PRN-DE, and PRN-MR-DE for tissue substitute phantoms including (a) adipose, (b) brain, (c) muscle, (d) liver, (e) skin, (f) spongiosa, and (g) 45% HA bone. The red line presents the reference mass densities. HA, hydroxyapatite; PRN, physics-constrained ResNet.

Retrospective head-and-neck patient analysis

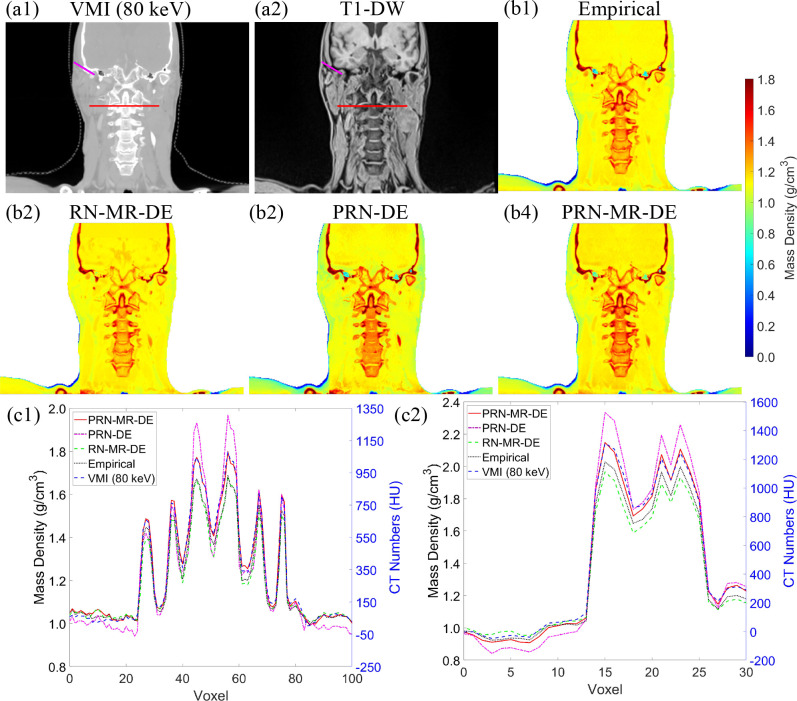
Figure 4 depicts a retrospective density map prediction using HN patient images. Figure 4(a1)–(a2) show the patient anatomy acquired from MRI and DECT scans. Figure 4(b1)–(b4) illustrate the density maps generated from different models. Figure 4(c1) portrays the line profile from the red line in Figure 4(a1)–(a2) across regions of spine vertebrae. At voxel 22 and 91, PRN-DE estimates the mass density equal to 0.95 g/cm³, while the empirical model and PRN-MR-DE predict the value of 1.04 g/cm³. Based on the MRI image from Figure 4(a2), these two voxels correspond to soft tissue, and a typical mass density of soft tissue should range from 1.04 to 1.07 g/cm³ according to ICRU 44. ⁴³ Figure 4(c1) also shows that the densities of cervical vertebrae at voxel 56 are: 1.69 g/cm³ from the empirical model and RN-MR-DE; 1.97 g/cm³ from PRN-DE; 1.80 g/cm³ from PRN-MR-DE. Based on ICRP 70, ⁴⁴ the mass density of hydrated trabecular bone is about 1.87 g/cm³. Figure 4(c2) gives the line profile from the purple line in Figure 4(a1)–(a2). From the MRI image (Figure 4(a2)), the voxel 1–8 and voxel 9–13 correspond to adipose and soft tissue, and average mass densities for voxel over these two regions are: 0.93 and 1.03 g/cm³ from PRN-MR-DE; 0.88 and 0.98 g/cm³ from PRN-DE. The expected mass density of adipose is 0.92 g/cm³ from ICRU 44. Figure 4(c2) also shows that the mass densities of the temporal bone at voxel 15 are: 2.33 g/cm³ from PRN-DE; 2.15 g/cm³ from PRN-MR-DE; 2.03 g/cm³ from the empirical model. Based on the literature, ⁴⁵ 99.7% of temporal bone data ranges from 1.63 to 2.22 g/cm³. Both Figure 4(c1)–(c2) display that PRN-MR-DE agrees with the trend of VMI HU profiles.

Figure 4.

Images from (a1) 80-keV VMI and (b1) T ₁DW for the same patient. Mass density maps of a patient from an HN site generated by (b1) the empirical model (Eq. (8)), (b2) conventional ResNet trained by MRI and DECT (RN-MR-DE) images, (b3) PRN trained by DECT (PRN-DE) images, and (b4) PRN trained by MRI and DECT (PRN-MR-DE) images. (c1) The line profile of the red line from (a1)–(a2). (c2) The line profile of the purple line from (a1)–(a2). DECT, dual energy CT; PRN, physics-constrained ResNet; VMI, irtual monochromatic image; T ₁DW, T ₁ weighted Dixon water-only

Discussion

DECT has been clinically evaluated and investigated to derive accurate RSP maps, which can be adapted by commercial treatment planning systems for proton treatment planning. These approaches can be classified into physics-based ^22,28,46 and ML-based ³⁰ dual-energy models, and both approaches aim to support proton analytical dose calculation. Conventional ML methods require a separate measurement for phantoms’ RSP or mass density values as the ground truth to train ML models (Eq. (2)) such that the phantom measurement or manufacturing uncertainty from calibration phantoms is inherently rooted in the ML models, especially when an independent measurement is not possible due to phantom designs and vendor data must be used. For the first time, we propose a PDMI framework to embed physics insights into DL training and exclude the uncertainty from material mass density measurement. The loss function defined by Eq. (3) does not require separate measurements for material mass densities; instead, the training target can be obtained by imaging the calibration phantoms. Eq. (4) correlates the images (y_meas ) in Eq. (3) and model predicted mass density (ρ_DL ) in Eq. (6) such that the physics-constrained loss function (Eq. 3) does not require separate measurement of material mass density. The proposed framework provides an alternative approach to leverage MRI to improve the uncertainty for radiotherapy.

The physics-constrained training does not require separate measurement of mass densities for calibration phantoms as the ground-truth targets; instead, the targets are CT numbers from VMI that can be consistently acquired from DECT images as the acquisition for DL model inputs. For instance, Table 5 indicates that RN-MR-DE without physics training underestimates the mass densities for adipose and 45% HA bone by 2.86 and 4.28%, compared to PRN-MR-DE with physics training. Additional MRI information can also improve the accuracy of mass density inference for DL models. For example, by training DL models with additional MRI images, conventional RN-MR-DE improve the errors by 4.07 and 1.15% for adipose and spongiosa, compared to RN-DE trained from DECT-only images. Although Table 5 shows that the empirical model achieves the minimum error for adipose, PRN-MR-DE still shows comparable results since the difference is 0.1%. Figure 3 depicts that PRN-MR-DE predicts the closest median values of mass density for most phantoms. PRN-MR-DE generally can reach the optimal error values for most tissue substitute phantoms.

For the retrospective patient analysis, the line profiles in Figure 4(c1)–(c2) show that the mass density curves by PRN-MR-DE agree with the trend of 80-keV VMI, and the density values for adipose, soft tissue, and bone are within a reasonable range published in literature. ^43–45 However, Figure 4(c1) shows that the empirical model tends to underestimate the mass density for cervical vertebrae. Figure 4(c2) displays that PRN-DE underrates the mass density for adipose and soft tissue and results in temporal density variations larger than the range found in the literature. ⁴⁵ These observations indicate that the additional MRI information can increase the accuracy of DL models. Meanwhile, RN-MR-DE without physics constraints could underestimate temporal density in some regions. For example, Figure 4(c2) depicts that RN-MR-DE predicts the temporal density of 1.59 g/cm³ at voxel 18, outside 99.7% of the temporal density data. ⁴⁵ ResNet trained without MRI images and physics insights exhibited similar patterns between the phantom and retrospective patient studies. Without physics constraints, both models could underestimate the mass densities for low- and high-density materials.

Hünemohr et al ⁴⁷ concluded that the uncertainty of RSP was dominated by mass density prediction. Proton Monte Carlo dose calculation has been recommended for treatment planning when patient images involve heterogeneous tissues or surgical implants. ⁴⁸ Consequently, we aim to use physics insights to regularize DL models and combine MRI and DECT data to derive accurate mass density maps. The proposed physics-constrained method is based on image domain training, and model accuracy can be compromised by image noise, artifacts, or calibration phantom inhomogeneities. The accuracy of the empirical model given by Eq. (8) is also impacted by the noise of relative electron density maps. Table 5 indicates that RN-MR-DE can deliver minimal spongiosa error due to the phantom inhomogeneity. In contrast, conventional DL model training corresponds each input image voxel to a constant material mass density so that conventional DL models can demonstrate effective noise suppression capability.

Model inference from data belongs to inverse problems, which are ill-posed, ⁴⁹ and the physics-constrained loss can potentially regularize DL models to remedy this ill-posedness. However, additional biological equivalent and MRI-visible tissue substitute phantoms are essential to extend training data coverage and validate the robustness of DL models for clinical applications. Future investigation will likely include the development of biological equivalent and MRI-visible tissue substitute phantoms to cover the mass density distribution for most human tissues. Furthermore, MRI signal intensity is dependent upon T1 and T2 relaxation time constants of the constituent hydrogen nuclei, or spins, within the water molecules in these calibration phantoms, which themselves vary based on molecular motion, size, and interactions between other spins and the surrounding lattice. For instance, cortical bone has a long T1 because water molecules are tightly bound to rigid HA crystals, which does not allow for motion near the Larmor frequency required for efficient T1 relaxation of a spin back to its surrounding lattice, and a very short T2 because there is efficient spin-spin relaxation among the tightly bound water molecules; these effects typically make cortical bone dark on T ₁- and T ₂ weighted MR images. While most of the tissue substitute phantoms demonstrate appropriate contrast on the T ₁DW, T ₁DF, and T ₂-STIR MR images, the 45% HA phantom does not display the same contrast as cortical bone. Although the 45% HA phantom is also dark on T ₁-STIR imaging, it is uncharacteristically bright on T ₁DW imaging. This is likely due to differences in the micro-structure of the HA phantom and in vivo cortical bone, which result in the water molecules in the phantom not as tightly bound to HA crystals as in bone. Meanwhile, customized MRI-visible phantoms usually are made with water, fat, or other organic matter, and this approach can introduce additional uncertainty for phantom mass densities from volumetric and weight measurement and phantom preservation. Physics-constrained training has the potential to be a promising tool to eliminate this uncertainty. Future investigation will likewise integrate the proposed PDMI framework into clinical workflows to evaluate dosimetry impacts ⁵⁰ for treatment planning with mass density maps generated from different models.

Conclusions

A PDMI framework was developed to demonstrate the feasibility of using MRI to improve patient mass density maps generated by DECT-only DL methods using tissue substitute surrogates. Physics-constrained training can regularize DL models and enhance model efficacy, especially when the measurement of mass densities for calibration phantoms includes significant uncertainty. The retrospective patient density map showed that tissue mass densities obtained from the proposed physics-constrained model were within expected intervals. The proposed framework has the potential to improve the quality of treatment planning for proton therapy through accurate material mass density maps derived from MRI and DECT images.